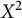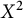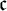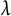1 Introduction
As is common in the literature for countable dense homogeneous spaces by a space, we will always mean a separable metrizable topological space. Given a space X we will denote by
$\mathcal {H}(X)$
the space of homeomorphisms of X. A space X is called countable dense homogeneous (CDH) if for every two
$A, B$
countable dense subsets of X there exists
$h \in \mathcal {H}(X)$
such that
$h(A) = B$
. Some basic positive results about CDH spaces include that
$2^\omega $
,
$\mathbb {R}^n$
for
$n \in \mathbb {N}$
,
$\omega ^\omega $
or
$[0,1]^\omega $
are all CDH spaces. In fact, the CDH property is very well understood for
$0$
-dimensional Polish spaces. Recall that a space is Polish if it is completely metrizable and
$0$
-dimensional if it has a base consisting of clopen sets. Let us denote
$$\begin{align*}\mathcal{C} = \{X; X \approx \kappa \oplus (\lambda \times 2^\omega) \oplus (\mu \times \omega^\omega), \text{where } 0 \leq \kappa, \lambda, \mu \leq \omega\}.\end{align*}$$
We have the following result due to Hrušák and Avilés.
Theorem 1 [Reference Hrušák and Zamora Avilés6]
Let X be a Polish
$0$
-dimensional CDH space. Then
$X \in \mathcal {C}$
.
Remark This result, in fact holds even for Borel
$0$
-dimensional CDH spaces [Reference Hrušák and Zamora Avilés6, Corollary 2.5] and consistently for projective sets [Reference Hrušák and Zamora Avilés6, Corollary 2.7].
Note that the class
$\mathcal {C}$
is closed under finite and even countable products. Thus the following questions asked by Medini [Reference Medini9] and later repeated in a survey paper of Hrušák and van Mill [Reference Hrušák and van Mill5] are very natural.
Question 1 [Reference Hrušák and van Mill5, Problem 14]
Is there a
$0$
-dimensional CDH space X such that
$X^2$
is not CDH?
Question 2 [Reference Hrušák and van Mill5, Problem 28]
For which cardinals
$\kappa $
is there a
$0$
-dimensional CDH space X such that
$X^2$
has exactly
$\kappa $
many types of countable dense subsets?
Or the following.
Question 3 [Reference Medini9, Question 1.9]
Can the space from Question 1 be consistently analytic or consistently co-analytic?
Note that due to the remark after Theorem 1 we cannot get in ZFC the space answering Question 1 analytic or co-analytic.
We will construct a
$0$
-dimensional CDH space X, such that
$X^2$
has exactly
$\mathfrak {c}$
many types of countable dense subsets, which is consistently co-analytic. Thus answering Question 1 in the negative and partially answering Question 2 and Question 3. In [Reference Medini9] it has been shown that a space answering Question 1 exists under MA(
$\sigma $
-centered). However, our construction works in ZFC and uses more elementary tools.
2 Preliminary results
In the construction, we will use the notion of a
$\lambda $
-set.
Definition 1 A set
$X \subset 2^\omega $
is called a
$\lambda $
-set if every countable subset of X is
$G_\delta $
in X, i.e., for any
$D \subset X$
countable
$D = \bigcap _{n=1}^{\infty }\left (G_n \bigcap X\right )$
, where
$G_n$
are open in
$2^\omega $
.
Remark Note that being a
$\lambda $
-set is a hereditary property and that the space
$2^{\omega }$
is not a
$\lambda $
-set. Thus, no
$\lambda $
-set contains a copy of
$2^\omega $
.
By Theorem 1, Polish zero-dimensional CDH-spaces behave very predictably. If we want any non-standard behavior we need to focus on non Polish zero-dimensional spaces. One such class of spaces are meager spaces and if we restrict our attention to those, it has been shown in [Reference Fitzpatrick and Zhou2] that the notion of a
$\lambda $
-set arises very naturally in the study of CDH-spaces.
In [Reference Hernández-Gutiérrez, Hrušák and van Mill4] it has been shown that there are uncountable
$\lambda $
-sets that are CDH.
Definition 2
$$\begin{align*} &\mathfrak{b} = \min(\{|F|; F \subset \omega^\omega \text{ and } \forall g \in \omega^\omega \, \exists f \in F \text{ such that } \\ &\quad \{x \in \omega; g(x) \leq f(x)\} \text{ is infinite}\}).\end{align*}$$
Theorem 2 [Reference Hernández-Gutiérrez, Hrušák and van Mill4]
For any cardinal number
$\kappa \leq \mathfrak {b}$
there exists
$\lambda $
-set X such that X is CDH.
Remark Note that we have
$\aleph _1 \leq \mathfrak {b} \leq \mathfrak {c}$
. More details regarding
$\mathfrak {b}$
can be found in [Reference Jech8].
As we want to show that the square of the constructed space is not CDH we will need some tools for finding many distinct countable dense sets.
The following has been used in [Reference Hrušák and van Mill7] for studying spaces with more types of countable dense subsets.
Lemma 3 [Reference Brian, van Mill and Suabedissen1]
There exist
$\mathfrak {c}$
many nonhomeomorphic nowhere dense subsets of
$\mathbb {Q}$
.
In [Reference Hernández-Gutiérrez3] the relation of products and CDH spaces has been studied. The following can be seen as an obstruction for product spaces to be CDH.
Theorem 4 [Reference Hernández-Gutiérrez3]
Let
$X, Y$
be two spaces. If
$X \times Y$
is CDH, then X contains a subspace homeomorphic to
$2^{\omega }$
if and only if Y contains a subspace homeomorphic to
$2^{\omega }$
.
However, we will need a finer tool as we not only want to show that the second power is not CDH but also that it has exactly
$\mathfrak {c}$
many types of countable dense sets. We will actually use the following which follows from the proof of [Reference Hernández-Gutiérrez3, Theorem 4].
Corollary 5 Let
$X, Y$
be spaces such that X contains a copy of
$2^\omega $
and Y does not contain a copy of
$2^\omega $
. Then there exists a countable dense subset C of
$X \times Y$
such that for no
$D \subset C$
we have
$\mkern 1.5mu\overline {\mkern -1.5muD\mkern -1.5mu}\mkern 1.5mu \approx 2^\omega $
.
When dealing with the descriptive complexity of the constructed space, the following will be needed.
Theorem 6 [Reference Miller10]
Suppose MA
$+ \neg $
CH
$+ \omega _1 = (\omega _1)^{\text {L}}$
. Then every
$A \subset 2^\omega $
of cardinality
$\aleph _1$
is
$\boldsymbol {\Pi }_1^{1}$
.
More details regarding the set theoretic axioms can be found in [Reference Jech8].
3 Main results
We have all the tools needed and can proceed to the construction.
Theorem 7 There exists a
$0$
-dimensional CDH space X with the following properties:
-
•
$X^2$
has exactly
$\mathfrak {c}$
many types of countable dense subsets. -
• If MA +
$\neg $
CH +
$\omega _1 = (\omega _1)^{\text {L}}$
holds, then X is
$\boldsymbol {\Pi }_1^{1}$
.
Proof By Theorem 2 we can find Y, a
$\lambda $
-set of cardinality
$\aleph _1$
such that Y is CDH. Consider
$X = Y \oplus 2^\omega $
. This space is clearly CDH, since both Y and
$2^\omega $
are CDH. By Theorem 6, if MA +
$\neg $
CH +
$\omega _1 = \omega _1^{\text {L}}$
holds then Y is
$\boldsymbol {\Pi }_1^{1}$
thus also X is
$\boldsymbol {\Pi }_1^{1}$
. Now, note that
$X^2 \approx Y^2 \oplus 2^\omega \oplus 2^\omega \times Y$
. First we will show that for any
$h \in \mathcal {H}(X^2)$
we have
$h(2^\omega \times Y) = 2^\omega \times Y$
.
To this end let
$h \in \mathcal {H}(X^2)$
. Since any clopen subset of
$2^\omega \times Y$
contains a copy of the Cantor set and
$Y^2$
does not contain a copy of the the Cantor set, we have that
$h(2^\omega \times Y) \bigcap Y^2 = \emptyset $
. By the same argument, we have
$h(2^\omega ) \bigcap Y^2 = \emptyset $
. Now suppose
$h(2^\omega )\bigcap (2^\omega \times Y) \neq \emptyset $
. Denote by
$\pi _2: 2^\omega \times Y \to Y$
the projection to the second coordinate. Then we have that
$\pi _2(h(2^\omega )\bigcap (2^\omega \times Y))$
is compact, zero-dimensional metric space. It is also a clopen subset of Y therefore it is a crowded space. But this means that
$\pi _2(h(2^\omega )\bigcap 2^\omega \times Y) \approx 2^\omega $
which cannot be since Y does not contain a copy of the Cantor set. This and the fact that
$h(2^\omega ) \bigcap Y^2 = \emptyset $
implies that
$h(2^\omega ) = 2^\omega $
and thus
$h(2^\omega \times Y) = 2^\omega \times Y$
. Now we will show that
$Y \times 2^\omega $
has exactly
$\mathfrak {c}$
many types of countable dense sets, this together with the fact that it is preserved by any
$h \in \mathcal {H}(X^2)$
will yield the desired.
Since
$|2^\omega \times Y| = \mathfrak {c}$
we have that the space
$2^\omega \times Y$
has at most
$\mathfrak {c}$
many types of countable dense subsets. Thus, it is enough to find
$\mathfrak {c}$
many countable dense subsets of
$2^\omega \times Y$
of a different type.
Let
$s \in 2^\omega $
and let
$A, B \subset 2^\omega $
be open disjoint such that
$A \cup B \cup \{s\} = 2^\omega $
and
$\partial A = \partial B = s$
. Note that we have
$A \approx B \approx 2^\omega \setminus \{0\}$
.
By Corollary 5, we can find
$Q_0 \subset A \times Y$
countable dense such that for no
$E \subset Q_0$
we have
$\mkern 1.5mu\overline {\mkern -1.5muE\mkern -1.5mu}\mkern 1.5mu \approx 2^\omega $
. Let
$\{U_n\}_{n\in \omega }$
be a countable base of the space
$B \times Y$
. For
$n \in \omega $
let
$F_n \subset U_n$
be countable such that
$\mkern 1.5mu\overline {\mkern -1.5muF_n\mkern -1.5mu}\mkern 1.5mu \approx 2^\omega $
. Let
$Q_1 = \bigcup _{n \in \omega }F_n$
and put
$D = Q_0 \cup Q_1$
. Then the set D is by construction a countable dense subset of
$2^\omega \times Y$
. By Lemma 3, there is a collection
$\{C_r; r \in (0,1)\}$
of countable pairwise nonhomeomorphic nowhere dense subsets of
$ \{s\} \times Y$
. For
$r \in (0,1)$
let
$D_r = D \cup C_r $
.
Now let
$p,r \in (0,1)$
,
$p \neq r$
and suppose there is
$h \in \mathcal {H}(2^\omega \times Y)$
such that
$h(D_p) = D_r$
. Let
$a \in \{s\} \times Y $
. First suppose
$h(a) \in A \times Y$
, then we can find an open neighborhood
$V_0$
of a such that
$h(V_0) \subset A \times Y$
. We have that
$V_0 \cap (B \times Y) \neq \emptyset $
. There exists
$n \in \omega $
such that
$U_n \subset V_0$
thus also
$F_n \subset V_0$
which means
$h(F_n) \subset Q_0$
. This contradicts the fact that for no countable subset
$E \subset Q_0$
we have
$\mkern 1.5mu\overline {\mkern -1.5muE\mkern -1.5mu}\mkern 1.5mu \approx 2^\omega $
. Now suppose
$h(a) \in B \times Y$
. Then there is an open neighborhood
$V_1$
of a such that
$h(V_1) \subset B \times Y$
, thus also
$h(V_1 \cap (A \times Y)) \subset B \times Y$
. Again, we can find
$n \in \omega $
and
$F_n \subset h(V_1 \cap (A \times Y))$
. However, this means
$h^{-1}(F_n) \subset Q_0$
, which cannot be. This means that
$h(\{s\} \times Y) = \{s\} \times Y$
, thus
$h(C_p) = C_r$
, which is a contradiction. Thus all the sets
$D_r$
for
$r \in (0,1)$
are of a different type.
Acknowledgements
The author is very grateful to Benjamin Vejnar for his helpful comments and insights.
