Hostname: page-component-686fd747b7-8s9h2 Total loading time: 0 Render date: 2025-02-13T13:35:32.833Z Has data issue: false hasContentIssue false
  • English
  • Français

Zero-dimensional metrizable CDH space X such that 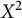$X^2$ is not CDH

Part of: Peculiar spaces Connections with other structures, applications

Published online by Cambridge University Press:  22 January 2025

Michal Hevessy Open the ORCID record for Michal Hevessy [Opens in a new window]
Michal Hevessy*
Affiliation:
Department of Mathematical Analysis, Faculty of Mathematics and Physics, Charles University, Prague, Czechia
*
e-mail: hevessy@karlin.mff.cuni.cz
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, a construction of a metrizable zero-dimensional CDH space X such that 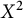$X^2$ has exactly 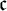$\mathfrak {c}$ many types of countable dense subsets is provided. Furthermore, it is shown that the space can be constructed consistently co-analytic. Thus answering an open question asked by Medini. To do so we use the notion of a 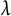$\lambda $-set.

Keywords

Countable dense homogeneousλ-setmetrizablezero-dimensional

MSC classification

Primary: 54G20: Counterexamples
Secondary: 54H05: Descriptive set theory (topological aspects of Borel, analytic, projective, etc. sets)
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 4
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work on this article was supported by the Czech Science Foundation grant 24-10705S.

References

Brian, W., van Mill, J., and Suabedissen, R., Homogeneity and generalizations of 2-point sets . Houston J. Math. 40(2014), no. 3, 885–898.Google Scholar
Fitzpatrick, B. Jr. and Zhou, H. X., Countable dense homogeneity and the Baire property . Topol. Appl. 43(1992), no. 1, 1–14.Google Scholar
Hernández-Gutiérrez, R., Countable dense homogeneity and the double arrow space . Topol. Appl. 160(2013), no. 10, 1123–1128.Google Scholar
Hernández-Gutiérrez, R., Hrušák, M., and van Mill, J.. Countable dense homogeneity and $\lambda$ -sets . Fund. Math. 226(2014), no. 2, 157–172.Google Scholar
Hrušák, M and van Mill, J., Open problems on countable dense homogeneity . Topol. Appl. 241(2018), 185–196.Google Scholar
Hrušák, M. and Zamora Avilés, B., Countable dense homogeneity of definable spaces . Proc. Amer. Math. Soc. 133(2005), no. 11, 3429–3435.Google Scholar
Hrušák, M. and van Mill, J., Nearly countable dense homogeneous spaces . Canad. J. Math. 66(2014), no. 4, 743–758.Google Scholar
Jech, T., Set theory: Millennium edition, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Medini, A., Products and countable dense homogeneity . Topol. Proc. 46(2015), 135–143.Google Scholar
Miller, A. W., Descriptive set theory and forcing: How to prove theorems about Borel sets the hard way, Lecture Notes in Logic, 4, Springer-Verlag, Berlin, 1995.Google Scholar