Hostname: page-component-6dbcb7884d-q4sxc Total loading time: 0 Render date: 2025-02-14T06:37:42.166Z Has data issue: false hasContentIssue false
  • English
  • Français

The Values of Modular Functions and Modular Forms

Published online by Cambridge University Press:  20 November 2018

So Young Choi
So Young Choi*
Affiliation:
Department of Mathematics, Korea Advanced Institude of Science and Technology, Taejon 305-701, Republic of Korea e-mail: young@math.kaist.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 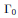${{\Gamma }_{0}}$ be a Fuchsian group of the first kind of genus zero and 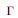$\Gamma$ be a subgroup of 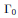${{\Gamma }_{0}}$ of finite index of genus zero. We find universal recursive relations giving the 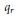${{q}_{r}}$-series coefficients of ${{j}_{0}}$ by using those of the 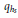${{q}_{{{h}_{s}}}}$ -series of 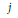$j$, where 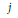$j$ is the canonical Hauptmodul for 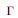$\Gamma$ and ${{j}_{0}}$ is a Hauptmodul for 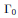${{\Gamma }_{0}}$ without zeros on the complex upper half plane $\mathfrak{H}\left( \text{here}\,\,{{q}_{\ell }}\,:=\,{{e}^{2\pi iz/\ell }} \right)$. We find universal recursive formulas for $q$-series coefficients of any modular form on 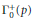$\Gamma _{0}^{+}\left( p \right)$ in terms of those of the canonical Hauptmodul $j_{p}^{+}$.

Keywords

10D1211F11
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 4 , 01 December 2006 , pp. 526 - 535
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Ahlgren, S., The theta-operator and the divisors of modular forms on genus zero subgroups. Math. Res. Lett. 10(2003), no. 5–6, 787–798.Google Scholar
[2] Bruinier, J. H., Kohnen, W., and Ono, K., The arithmetic of the values of modular functions and the divisors of modular forms. Comp. Math. 140(2004), no. 3, 552–566.Google Scholar
[3] Choi, D., Values of a modular form on Γ 0(N). Acta Arith. 121(2006), no. 4, 299–311.Google Scholar
[4] Helling, H., Note über das Geschlecht gewisser arithmetischer Gruppen. Math. Ann. 205(1973), 173–179.Google Scholar
[5] Kim, C. H. and Koo, J. K., Arithmetic of the modular function j 1,4 . Acta Arith. 84(1998), no. 2, 129–143.Google Scholar
[6] Kim, C. H. and Koo, J. K., Self-recursion formulas satisfied by Fourier coefficients of some modular functions. J. Pure Appl. Algebra 160(2001), no. 1, 53–65.Google Scholar
[7] Macdonald, I. G., Symmetric Functions and Hall Polynomials. Second edition, Oxford University Press, New York, 1995.Google Scholar