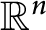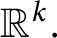1 Introduction
A tight frame in
![]() $\mathbb {R}^k$
is a set of vectors that is the orthogonal projection of some orthonormal basis of
$\mathbb {R}^k$
is a set of vectors that is the orthogonal projection of some orthonormal basis of
![]() $\mathbb {R}^n$
onto
$\mathbb {R}^n$
onto
![]() $\mathbb {R}^k.$
Or, equivalently, it is a set of vectors
$\mathbb {R}^k.$
Or, equivalently, it is a set of vectors
![]() $\{v_1, \dots , v_n\}$
that satisfy identity
$\{v_1, \dots , v_n\}$
that satisfy identity
 $$ \begin{align} \sum\limits_1^n v_i \otimes v_i = I_k, \end{align} $$
$$ \begin{align} \sum\limits_1^n v_i \otimes v_i = I_k, \end{align} $$
where
![]() $I_k$
is the identity operator in
$I_k$
is the identity operator in
![]() $\mathbb {R}^k.$
$\mathbb {R}^k.$
Tight frames appear and are used naturally in different branches of mathematics: from quantum mechanics and approximation theory (see [Reference Aubrun and Szarek1] for details) to classical problems of convex analysis, starting with the well-known John condition [Reference John11] for the ellipsoid of maximal volume in a convex body.
We study properties of tight frames from the algebraic point of view. For this purpose, we use exterior algebra for studying properties of the exterior powers of the projection operators in Section 3. The necessary definitions on exterior algebra are included in Section 2.1 for completeness. Among other results on projection operators, we prove the following theorem.
Theorem 1.1 A set of vectors
![]() $\{v_1, \dots , v_n \} \subset \mathbb {R}^k $
is a tight frame if and only if the set of cross products
$\{v_1, \dots , v_n \} \subset \mathbb {R}^k $
is a tight frame if and only if the set of cross products
![]() $[v_{i_1}, \dots , v_{i_{k-1}}]$
for all
$[v_{i_1}, \dots , v_{i_{k-1}}]$
for all
![]() $(k-1)$
-tuples
$(k-1)$
-tuples
 $\{i_1, \dots , i_{k-1}\} \in \binom {[n]}{k-1}$
is a tight frame.
$\{i_1, \dots , i_{k-1}\} \in \binom {[n]}{k-1}$
is a tight frame.
There are standard geometric objects that can be described either in terms of Grassmannian
![]() $\operatorname {Gr}\!\left ( n, k \right )$
of k-dimensional subspace of
$\operatorname {Gr}\!\left ( n, k \right )$
of k-dimensional subspace of
![]() $\mathbb {R}^n$
or in terms of tight frames. Let us give some examples.
$\mathbb {R}^n$
or in terms of tight frames. Let us give some examples.
Let
![]() $\{v_1, \dots , v_n\}$
be the orthogonal projection of the standard basis onto k-dimensional subspace
$\{v_1, \dots , v_n\}$
be the orthogonal projection of the standard basis onto k-dimensional subspace
![]() $H \subset \mathbb {R}^n$
. Consider the following classes of convex polytopes:
$H \subset \mathbb {R}^n$
. Consider the following classes of convex polytopes:
-
(1) Projections of the cross-polytope. Let
 $\diamondsuit ^n = \{ x \in \mathbb {R}^n \mid |x_1| + \cdots + |x_n| \leq 1\}$
be the standard cross-polytope. Then, the projection of
$\diamondsuit ^n = \{ x \in \mathbb {R}^n \mid |x_1| + \cdots + |x_n| \leq 1\}$
be the standard cross-polytope. Then, the projection of
 $\diamondsuit ^n$
onto H is the absolute convex hull of the projection of the standard basis of
$\diamondsuit ^n$
onto H is the absolute convex hull of the projection of the standard basis of
 $\mathbb {R}^n$
, that is
$\mathbb {R}^n$
, that is
 $\mathop {\mathrm {co}} \{\pm v_1, \dots , \pm v_n\}.$
$\mathop {\mathrm {co}} \{\pm v_1, \dots , \pm v_n\}.$
-
(2) Sections of the cube. Let
 $\boxed {}^n = [-1,1]^n$
be the standard n-dimensional cube. The section
$\boxed {}^n = [-1,1]^n$
be the standard n-dimensional cube. The section
 $\boxed {}^n \cap H$
is the intersection of strips
$\boxed {}^n \cap H$
is the intersection of strips
 $\left \{x \in H : |\left \langle x,v_i\right \rangle | \leq 1 \right \}.$
$\left \{x \in H : |\left \langle x,v_i\right \rangle | \leq 1 \right \}.$
-
(3) Projections of the cube. Then, the projection of
 $\boxed {}^n$
onto H is the Minkowski sum of the segments
$\boxed {}^n$
onto H is the Minkowski sum of the segments
 $[-v_i, v_i].$
$[-v_i, v_i].$
Identifying H with
![]() $\mathbb {R}^k,$
we identify the set
$\mathbb {R}^k,$
we identify the set
![]() $\{v_1, \dots , v_n\}$
with a tight frame. Clearly, the volumes of these polytopes can be considered as functions on the set of tight frames.
$\{v_1, \dots , v_n\}$
with a tight frame. Clearly, the volumes of these polytopes can be considered as functions on the set of tight frames.
Of course, much more types of convex bodies can be described in both ways. We list these three examples, since they can be considered as a standard position of special types of centrally symmetric polytopes. For example, any convex centrally symmetric polytope is an affine image of a central section of the cube or a projection of the cross-polytope of some dimension. The problems of finding the minimal and maximal volumes of these types of polytopes are well-studied (see [Reference Ball2
, Reference Barthe and Naor3
, Reference Lutwak, Yang and Zhang12
, Reference Meyer and Pajor14
]). However, there are still a lot of open questions. For example, the tight upper bound on the volume of a projection of cross-polytope
![]() $\diamondsuit ^n$
onto a k-dimensional subspace H of
$\diamondsuit ^n$
onto a k-dimensional subspace H of
![]() $\mathbb {R}^n$
is unknown. The reasonable conjecture is that the upper bound is
$\mathbb {R}^n$
is unknown. The reasonable conjecture is that the upper bound is
![]() $\operatorname {vol}_{k} \diamondsuit ^k,$
and it can be considered as a dual to Vaaler’s theorem [Reference Vaaler18] that states that
$\operatorname {vol}_{k} \diamondsuit ^k,$
and it can be considered as a dual to Vaaler’s theorem [Reference Vaaler18] that states that
 $\operatorname {vol}_{k} (\boxed {}^n \cap H_k) \geq \operatorname {vol}_{k} \boxed {}^k.$
$\operatorname {vol}_{k} (\boxed {}^n \cap H_k) \geq \operatorname {vol}_{k} \boxed {}^k.$
In Section 4, we show how to reformulate problems about extrema of the volume of sections and projections of regular polytopes in the language of tight frames. For example, one can apply our results for listed above types of polytopes. A similar to ours approach was used by Filliman in [Reference Filliman5–Reference Filliman8]. However, Filliman preferred to consider the volume functions as the functions on the Grassmannian. Instead of this, we consider functions on the set of tight frames in
![]() $\mathbb {R}^k;$
extend the domain of such functions to the set of the ordered sets of n vectors of
$\mathbb {R}^k;$
extend the domain of such functions to the set of the ordered sets of n vectors of
![]() $\mathbb {R}^k$
in a natural way; and give in Lemma 4.2 a necessary and sufficient condition for local extremum of such functions. Thus, we avoid working in the Grassmannians. The only thing we need the Grassmannians for is to prove a first-order approximation formula for a perturbation of a tight frame. As a consequence of Theorem 1.1 and the Cauchy–Binet formula, we obtain the following theorem.
$\mathbb {R}^k$
in a natural way; and give in Lemma 4.2 a necessary and sufficient condition for local extremum of such functions. Thus, we avoid working in the Grassmannians. The only thing we need the Grassmannians for is to prove a first-order approximation formula for a perturbation of a tight frame. As a consequence of Theorem 1.1 and the Cauchy–Binet formula, we obtain the following theorem.
Theorem 1.2 Let
![]() $\{v_1, \dots , v_n \}$
be a tight frame in
$\{v_1, \dots , v_n \}$
be a tight frame in
![]() $\mathbb {R}^k, \tau $
be a scalar, and
$\mathbb {R}^k, \tau $
be a scalar, and
![]() $\{x_i\}_1^n$
be an arbitrary set of vectors of
$\{x_i\}_1^n$
be an arbitrary set of vectors of
![]() $\mathbb {R}^k.$
Then,
$\mathbb {R}^k.$
Then,
 $$ \begin{align*} {\det \sum\limits_1^n (v_i + \tau x_i) \otimes (v_i + \tau x_i) } = 1 + 2 \tau\sum\limits_{i = 1}^{n} \left\langle x_i,v_i\right\rangle + o \left(\tau\right). \end{align*} $$
$$ \begin{align*} {\det \sum\limits_1^n (v_i + \tau x_i) \otimes (v_i + \tau x_i) } = 1 + 2 \tau\sum\limits_{i = 1}^{n} \left\langle x_i,v_i\right\rangle + o \left(\tau\right). \end{align*} $$
We illustrate our technique on the problem of maximizing function
where
![]() $[0,1]^n | H$
is the projection of the cube
$[0,1]^n | H$
is the projection of the cube
![]() $[0,1]^n$
onto
$[0,1]^n$
onto
![]() $H.$
The projections of the cube
$H.$
The projections of the cube
![]() $[0,1]^n$
may be considered as a special position of Minkowski sum of finitely many linear segments, so-called zonotopes.
$[0,1]^n$
may be considered as a special position of Minkowski sum of finitely many linear segments, so-called zonotopes.
Using the results of Section 4, we give a complete system of the first-order necessary conditions of a maximizer of (1.2) in Lemma 5.5. It yields the following geometric result.
Corollary 1.3 Let H be a local maximizer of (1.2) and
![]() $Q = [0,1]^n |H.$
Let
$Q = [0,1]^n |H.$
Let
![]() $v_i$
denote the orthogonal projection of the standard basis vector
$v_i$
denote the orthogonal projection of the standard basis vector
![]() $e_i$
onto
$e_i$
onto
![]() $H,$
for
$H,$
for
![]() $i \in [n],$
and
$i \in [n],$
and
![]() $Q | v_i^{\perp } $
be the projection of Q onto the orthogonal complement of the line
$Q | v_i^{\perp } $
be the projection of Q onto the orthogonal complement of the line
![]() $\left \{ \lambda v_i \middle \vert \ \lambda \in \mathbb {R}\right \}$
in
$\left \{ \lambda v_i \middle \vert \ \lambda \in \mathbb {R}\right \}$
in
![]() $H.$
Then,
$H.$
Then,
Also, we obtain some properties of the maximizers.
Theorem 1.4 Let the maximum of (1.2) be attained at
![]() $H.$
Let
$H.$
Let
![]() $v_i$
denote the projection of the standard basis vector
$v_i$
denote the projection of the standard basis vector
![]() $e_i$
onto
$e_i$
onto
![]() $H,$
for
$H,$
for
![]() $i \in [n].$
Then, for any
$i \in [n].$
Then, for any
![]() $i,j \in [n],$
the inequality
$i,j \in [n],$
the inequality
 $$ \begin{align*} |v_i|^2 \geq (\sqrt{2} - 1) |v_j|^2 \end{align*} $$
$$ \begin{align*} |v_i|^2 \geq (\sqrt{2} - 1) |v_j|^2 \end{align*} $$
holds.
As a consequence of Theorem 1.4 and McMullen’s symmetric formula [Reference McMullen13], which is
where
![]() $H^{\perp }$
is the orthogonal complement of
$H^{\perp }$
is the orthogonal complement of
![]() $H,$
we prove the following corollary.
$H,$
we prove the following corollary.
Corollary 1.5 Fix
![]() $q \in \mathbb {N}.$
Let
$q \in \mathbb {N}.$
Let
![]() $H_{n - q}$
be a maximizer of (1.2) for
$H_{n - q}$
be a maximizer of (1.2) for
![]() $k = n-q, n \geq q.$
By
$k = n-q, n \geq q.$
By
![]() $M_{n}$
and
$M_{n}$
and
![]() $m_{n}$
, we denote the maximum and the minimum length of the projections of the standard basis vectors of
$m_{n}$
, we denote the maximum and the minimum length of the projections of the standard basis vectors of
![]() $\mathbb {R}^n$
onto
$\mathbb {R}^n$
onto
![]() $H_{n-q},$
respectively. Then,
$H_{n-q},$
respectively. Then,
 $$ \begin{align*} \frac{m_n}{M_n} \to 1 \qquad \text{as} \qquad n \to \infty. \end{align*} $$
$$ \begin{align*} \frac{m_n}{M_n} \to 1 \qquad \text{as} \qquad n \to \infty. \end{align*} $$
2 Definitions and preliminaries
We use
![]() $\operatorname {C}^n$
to denote an n-dimensional cube
$\operatorname {C}^n$
to denote an n-dimensional cube
![]() $\{x : 0 \leq x[i] \leq 1\}$
in
$\{x : 0 \leq x[i] \leq 1\}$
in
![]() $\mathbb {R}^n.$
Here and throughout the paper,
$\mathbb {R}^n.$
Here and throughout the paper,
![]() $x[i]$
stands for the ith coordinate of a vector
$x[i]$
stands for the ith coordinate of a vector
![]() $x.$
As usual,
$x.$
As usual,
![]() $\{e_i\}_1^n$
is the standard orthonormal basis of
$\{e_i\}_1^n$
is the standard orthonormal basis of
![]() $\mathbb {R}^n.$
We use
$\mathbb {R}^n.$
We use
![]() $\left \langle p,x\right \rangle $
to denote the value of a linear functional p at a vector
$\left \langle p,x\right \rangle $
to denote the value of a linear functional p at a vector
![]() $x.$
$x.$
For a convex body
![]() $K \subset \mathbb {R}^n$
and a k-dimensional subspace H of
$K \subset \mathbb {R}^n$
and a k-dimensional subspace H of
![]() $\mathbb {R}^n$
, we denote by
$\mathbb {R}^n$
, we denote by
![]() $K \cap H$
and
$K \cap H$
and
![]() $K | H$
the section of K by H and the orthogonal projection of K onto
$K | H$
the section of K by H and the orthogonal projection of K onto
![]() $H,$
respectively. For a k-dimensional subspace H of
$H,$
respectively. For a k-dimensional subspace H of
![]() $\mathbb {R}^n$
and a convex body
$\mathbb {R}^n$
and a convex body
![]() $K \subset H$
, we denote by
$K \subset H$
, we denote by
![]() $\operatorname {vol}_{k} K$
the k-dimensional volume of K. We use
$\operatorname {vol}_{k} K$
the k-dimensional volume of K. We use
![]() $P^H$
to denote the orthogonal projection onto
$P^H$
to denote the orthogonal projection onto
![]() $H.$
$H.$
For a positive integer
![]() $n,$
we refer to the set
$n,$
we refer to the set
![]() $\{1, 2, \dots , n\}$
as
$\{1, 2, \dots , n\}$
as
![]() $[n].$
The set of all
$[n].$
The set of all
![]() $\ell $
-element subsets (or
$\ell $
-element subsets (or
![]() $\ell $
-tuple) of a set
$\ell $
-tuple) of a set
![]() $M \subset [n]$
is denoted by
$M \subset [n]$
is denoted by
 $ \binom {M}{\ell }.$
For two
$ \binom {M}{\ell }.$
For two
![]() $\ell $
-tuples
$\ell $
-tuples
 $I \in \binom {[a]}{\ell } , J \in \binom {[b]}{\ell }$
, we will use
$I \in \binom {[a]}{\ell } , J \in \binom {[b]}{\ell }$
, we will use
![]() $M_{\{I, J\}}$
to denote the determinant of the corresponding
$M_{\{I, J\}}$
to denote the determinant of the corresponding
![]() $\ell $
minor of the
$\ell $
minor of the
![]() $a \times b$
matrix
$a \times b$
matrix
![]() $M.$
For the sake of convenience, we will write
$M.$
For the sake of convenience, we will write
![]() $M_I$
whenever
$M_I$
whenever
![]() $I = J.$
We use
$I = J.$
We use
![]() $M_{[i,j]}$
to denote the entry in the ith row and the jth column of a matrix
$M_{[i,j]}$
to denote the entry in the ith row and the jth column of a matrix
![]() $M.$
$M.$
For the sake of convenience, we denote by
![]() $d_S (\{M \})$
the determinant of
$d_S (\{M \})$
the determinant of
![]() $ \{ v_i \;: \; i \in M \}$
for an ordered set of vectors
$ \{ v_i \;: \; i \in M \}$
for an ordered set of vectors
![]() $S = \{v_1, \dots , v_n\} \subset \mathbb {R}^k$
and a set M of k indexes from
$S = \{v_1, \dots , v_n\} \subset \mathbb {R}^k$
and a set M of k indexes from
![]() $[n]$
(the indexes may repeat).
$[n]$
(the indexes may repeat).
Recall that a zonotope in a vector space is the Minkowski sum of finitely many line segments, i.e.,
![]() $\sum _{i=1}^{n} [a_i, b_i],$
where
$\sum _{i=1}^{n} [a_i, b_i],$
where
![]() $\sum $
stands for the Minkowski sum, and
$\sum $
stands for the Minkowski sum, and
![]() $[a,b]$
means the line segment between points a and
$[a,b]$
means the line segment between points a and
![]() $b.$
$b.$
Definition 2.1 We will say that an ordered n-tuple of vectors
![]() $\{v_1, \dots , v_n\} \subset H$
forms a tight frame in a vector space H if
$\{v_1, \dots , v_n\} \subset H$
forms a tight frame in a vector space H if
 $$ \begin{align} \left. \left(\sum\limits_1^n v_i \otimes v_i \right) \right|_H = I_H, \end{align} $$
$$ \begin{align} \left. \left(\sum\limits_1^n v_i \otimes v_i \right) \right|_H = I_H, \end{align} $$
where
![]() $I_H$
is the identity operator in H and
$I_H$
is the identity operator in H and
![]() $\left . A\right |{}_H$
is the restriction of an operator A onto
$\left . A\right |{}_H$
is the restriction of an operator A onto
![]() $H.$
$H.$
We use
![]() $\Omega (n,k)$
to denote the set of all tight frames with n vectors in
$\Omega (n,k)$
to denote the set of all tight frames with n vectors in
![]() $\mathbb {R}^k.$
$\mathbb {R}^k.$
2.1 Exterior algebra
For the sake of completeness and clarity, all needed definitions from exterior algebra are given here in a brief and noncanonical way. We assume that the equivalence of our definitions to the usual ones is quite obvious. As a proper introduction to multilinear algebra, we refer to Greub’s book [Reference Greub9].
Let H be a finite-dimensional vector space with inner product
![]() $\left \langle \cdot , \cdot \right \rangle .$
We define the vector space
$\left \langle \cdot , \cdot \right \rangle .$
We define the vector space
![]() $\Lambda ^{\ell } (H )$
as the space of the multilinear skew-symmetric functions on
$\Lambda ^{\ell } (H )$
as the space of the multilinear skew-symmetric functions on
![]() $\ell $
vectors of H with the natural linear structure. The vectors of
$\ell $
vectors of H with the natural linear structure. The vectors of
![]() $\Lambda ^{\ell } (H )$
are called
$\Lambda ^{\ell } (H )$
are called
![]() $\ell $
-forms. As we consider only linear spaces with inner products, we assume that a space H and its dual
$\ell $
-forms. As we consider only linear spaces with inner products, we assume that a space H and its dual
![]() $H^{*}$
coincide. This allows us to simplify the following definitions.
$H^{*}$
coincide. This allows us to simplify the following definitions.
For a sequence of
![]() $\ell $
vectors
$\ell $
vectors
![]() $\{x_1, \dots , x_{\ell } \} \subset H,$
we define an
$\{x_1, \dots , x_{\ell } \} \subset H,$
we define an
![]() $\ell $
-form
$\ell $
-form
![]() $x_1 \wedge \dots \wedge x_{\ell }$
by its evaluation on vectors
$x_1 \wedge \dots \wedge x_{\ell }$
by its evaluation on vectors
![]() $\{y_1, \dots , y_{\ell }\} \subset H$
given by
$\{y_1, \dots , y_{\ell }\} \subset H$
given by
 $$ \begin{align*} x_1 \wedge \dots \wedge x_{\ell} (y_1, \dots, y_{\ell}) = \det M, \qquad \text{where} \qquad M_{[ij]} = \left\langle x_i,y_j\right\rangle, \quad i,j \in [\ell]. \end{align*} $$
$$ \begin{align*} x_1 \wedge \dots \wedge x_{\ell} (y_1, \dots, y_{\ell}) = \det M, \qquad \text{where} \qquad M_{[ij]} = \left\langle x_i,y_j\right\rangle, \quad i,j \in [\ell]. \end{align*} $$
By the properties of the determinant,
![]() $x_1 \wedge \dots \wedge x_{\ell }$
is a multilinear skew-symmetric function of
$x_1 \wedge \dots \wedge x_{\ell }$
is a multilinear skew-symmetric function of
![]() $\ell $
vectors of H. For the sake of convenience, for given n vectors
$\ell $
vectors of H. For the sake of convenience, for given n vectors
![]() $\{x_i\}_1^{n}$
and
$\{x_i\}_1^{n}$
and
![]() $\ell $
-tuple
$\ell $
-tuple
 $L =\{i_1, \dots , i_{\ell }\} \in \binom {[n]}{\ell },$
we denote by
$L =\{i_1, \dots , i_{\ell }\} \in \binom {[n]}{\ell },$
we denote by
![]() $x_L$
the
$x_L$
the
![]() $\ell $
-form
$\ell $
-form
![]() $x_{i_1} \wedge \dots \wedge x_{i_{\ell }}$
.
$x_{i_1} \wedge \dots \wedge x_{i_{\ell }}$
.
As usual, we use the set of
![]() $\ell $
-forms
$\ell $
-forms
![]() $e_{i_1} \wedge \dots \wedge e_{i_{\ell }},$
where
$e_{i_1} \wedge \dots \wedge e_{i_{\ell }},$
where
 $\{i_1, \dots , i_{\ell }\} \in \binom {[n]}{\ell }$
, as the standard basis of
$\{i_1, \dots , i_{\ell }\} \in \binom {[n]}{\ell }$
, as the standard basis of
![]() $\Lambda ^{\ell } \left ( \mathbb {R}^n \right ).$
We use the lexicographical order on
$\Lambda ^{\ell } \left ( \mathbb {R}^n \right ).$
We use the lexicographical order on
![]() $\ell $
-tuples
$\ell $
-tuples
 $\{i_1, \dots , i_{\ell }\} \in \binom {[n]}{\ell }$
to assign a number to
$\{i_1, \dots , i_{\ell }\} \in \binom {[n]}{\ell }$
to assign a number to
![]() $e_{i_1} \wedge \dots \wedge e_{i_{\ell }}$
in this basis.
$e_{i_1} \wedge \dots \wedge e_{i_{\ell }}$
in this basis.
Recall that for a vector space
![]() $H,$
an
$H,$
an
![]() $\ell $
-form
$\ell $
-form
![]() $w \in \Lambda ^{\ell } (H)$
is said to be decomposable if it can be represented in the form
$w \in \Lambda ^{\ell } (H)$
is said to be decomposable if it can be represented in the form
![]() $x_1 \wedge \dots \wedge x_{\ell }$
for
$x_1 \wedge \dots \wedge x_{\ell }$
for
![]() $\{x_i\}_1^{\ell } \subset H.$
Every
$\{x_i\}_1^{\ell } \subset H.$
Every
![]() $\ell $
-form is a linear combination of some decomposable
$\ell $
-form is a linear combination of some decomposable
![]() $\ell $
-forms (e.g., of the forms from the standard basis), but not all
$\ell $
-forms (e.g., of the forms from the standard basis), but not all
![]() $\ell $
-forms are decomposable, e.g.,
$\ell $
-forms are decomposable, e.g.,
![]() $e_1 \wedge e_2 + e_3 \wedge e_4 \in \Lambda ^2 (\mathbb {R}^4)$
is not decomposable. A line
$e_1 \wedge e_2 + e_3 \wedge e_4 \in \Lambda ^2 (\mathbb {R}^4)$
is not decomposable. A line
![]() $l \subset \Lambda ^{\ell } \left ( \mathbb {R}^n \right )$
has a decomposable directional vector iff l is “generated” by some
$l \subset \Lambda ^{\ell } \left ( \mathbb {R}^n \right )$
has a decomposable directional vector iff l is “generated” by some
![]() $\ell $
-dimensional subspace
$\ell $
-dimensional subspace
![]() $H_{\ell } \subset \mathbb {R}^n.$
$H_{\ell } \subset \mathbb {R}^n.$
By linearity, it suffices to define a linear operator (or an inner product) on
![]() $\Lambda ^{\ell }(\mathbb {R}^n)$
only for decomposable
$\Lambda ^{\ell }(\mathbb {R}^n)$
only for decomposable
![]() $\ell $
-forms, since the decomposable forms span
$\ell $
-forms, since the decomposable forms span
![]() $\Lambda ^{\ell } (\mathbb {R}^n).$
$\Lambda ^{\ell } (\mathbb {R}^n).$
Recall that the exterior
![]() $\ell $
-power of an operator A on
$\ell $
-power of an operator A on
![]() $\mathbb {R}^n$
is a linear operator on
$\mathbb {R}^n$
is a linear operator on
![]() $\Lambda ^{\ell } (\mathbb {R}^n),$
which is defined on decomposable forms by
$\Lambda ^{\ell } (\mathbb {R}^n),$
which is defined on decomposable forms by
Recall that the inner product of two decomposable
![]() $\ell $
-forms
$\ell $
-forms
![]() $a = a_1 \wedge \dots \wedge a_{\ell }$
and
$a = a_1 \wedge \dots \wedge a_{\ell }$
and
![]() $b = b_1 \wedge \dots \wedge b_{\ell }$
is defined by
$b = b_1 \wedge \dots \wedge b_{\ell }$
is defined by
In this way, once we fix an inner product on
![]() $\mathbb {R}^n$
, we fix the inner product on
$\mathbb {R}^n$
, we fix the inner product on
![]() $\Lambda ^{\ell } (\mathbb {R}^n).$
Then, for
$\Lambda ^{\ell } (\mathbb {R}^n).$
Then, for
![]() $\ell \in [n]$
, we can define a special isometry
$\ell \in [n]$
, we can define a special isometry
![]() $ \star : \Lambda ^{\ell } (\mathbb {R}^n) \to \Lambda ^{n - \ell } (\mathbb {R}^n),$
the so-called Hodge star operator, by the following equation:
$ \star : \Lambda ^{\ell } (\mathbb {R}^n) \to \Lambda ^{n - \ell } (\mathbb {R}^n),$
the so-called Hodge star operator, by the following equation:
where
![]() $a,b$
are
$a,b$
are
![]() $\ell $
-forms.
$\ell $
-forms.
Using this, one can show the following. For given
![]() $a=a_1 \wedge \dots \wedge a_{\ell } \in \Lambda ^{\ell } (\mathbb {R}^n)$
and
$a=a_1 \wedge \dots \wedge a_{\ell } \in \Lambda ^{\ell } (\mathbb {R}^n)$
and
![]() $b = b_1 \wedge \dots \wedge b_{n - \ell } \in \Lambda ^{n -\ell } (\mathbb {R}^n),$
we have
$b = b_1 \wedge \dots \wedge b_{n - \ell } \in \Lambda ^{n -\ell } (\mathbb {R}^n),$
we have
 $$ \begin{align} \left\langle a,\star (b)\right\rangle = (-1)^{\ell (n - \ell)}\det \{a_1, \dots, a_{\ell}, b_1, \dots,b_{n - \ell}\}. \end{align} $$
$$ \begin{align} \left\langle a,\star (b)\right\rangle = (-1)^{\ell (n - \ell)}\det \{a_1, \dots, a_{\ell}, b_1, \dots,b_{n - \ell}\}. \end{align} $$
For a k-dimensional subspace
![]() $H_k \subset \mathbb {R}^n,$
we use
$H_k \subset \mathbb {R}^n,$
we use
![]() $\wedge ^{\ell } H_k$
to denote the linear hull of forms
$\wedge ^{\ell } H_k$
to denote the linear hull of forms
![]() $x_1 \wedge \dots \wedge x_{\ell }$
in
$x_1 \wedge \dots \wedge x_{\ell }$
in
![]() $\Lambda ^{\ell } \left ( \mathbb {R}^n \right )$
such that
$\Lambda ^{\ell } \left ( \mathbb {R}^n \right )$
such that
![]() $\{x_1, \dots , x_{\ell }\} \subset H_k.$
Since
$\{x_1, \dots , x_{\ell }\} \subset H_k.$
Since
![]() $H_k$
inherits the inner product of
$H_k$
inherits the inner product of
![]() $\mathbb {R}^n$
, the space
$\mathbb {R}^n$
, the space
![]() $\wedge ^{\ell } H_k$
inherits the inner product of
$\wedge ^{\ell } H_k$
inherits the inner product of
![]() $\Lambda ^{\ell } (\mathbb {R}^n)$
and thus can be identified with the space
$\Lambda ^{\ell } (\mathbb {R}^n)$
and thus can be identified with the space
![]() $\Lambda ^{\ell } (H_k)$
in a tautological way. This allows us to use the Hodge star operator for the spaces
$\Lambda ^{\ell } (H_k)$
in a tautological way. This allows us to use the Hodge star operator for the spaces
![]() $\Lambda ^{\ell } (H_k)$
and
$\Lambda ^{\ell } (H_k)$
and
![]() $\Lambda ^{(k -\ell )} (H_k)$
for
$\Lambda ^{(k -\ell )} (H_k)$
for
![]() $\ell \in [k].$
Also, identity (2.2) can be rewritten in the following form. For given
$\ell \in [k].$
Also, identity (2.2) can be rewritten in the following form. For given
![]() $a=a_1 \wedge \dots \wedge a_{\ell } \in \Lambda ^{\ell } (H_k)$
and
$a=a_1 \wedge \dots \wedge a_{\ell } \in \Lambda ^{\ell } (H_k)$
and
![]() $b = b_1 \wedge \dots \wedge b_{k - \ell } \in \Lambda ^{k -\ell } (H_k),$
we get
$b = b_1 \wedge \dots \wedge b_{k - \ell } \in \Lambda ^{k -\ell } (H_k),$
we get
 $$ \begin{align} \left\langle a,\star (b)\right\rangle = (-1)^{\ell (k - \ell)}\det \{a_1, \dots, a_{\ell}, b_1, \dots,b_{k - \ell}\}, \end{align} $$
$$ \begin{align} \left\langle a,\star (b)\right\rangle = (-1)^{\ell (k - \ell)}\det \{a_1, \dots, a_{\ell}, b_1, \dots,b_{k - \ell}\}, \end{align} $$
where we understand the determinant as the determinant of k-vectors in a k-dimensional space
![]() $H_k$
.
$H_k$
.
The next result is a straightforward consequence of the definitions. We show that the outer product and the tensor product commute for the exterior powers of operators in our case. Usually, definitions of the outer product involve some kind of (anti)symmetrization, which can give an additional factor when we exchange the
![]() $\wedge $
-product and
$\wedge $
-product and
![]() $\otimes $
-product. To avoid misunderstandings, we prove the following statement.
$\otimes $
-product. To avoid misunderstandings, we prove the following statement.
Lemma 2.1 Let
 $A = \sum \limits _{i=1}^{t} v_i \otimes v_i$
for some integer t and vectors
$A = \sum \limits _{i=1}^{t} v_i \otimes v_i$
for some integer t and vectors
![]() $\{v_i\}_1^t \subset \mathbb {R}^n.$
Then,
$\{v_i\}_1^t \subset \mathbb {R}^n.$
Then,
 $\wedge ^{\ell } A = \sum \limits _{L \in \binom {[t]}{\ell }} v_{L} \otimes v_L.$
$\wedge ^{\ell } A = \sum \limits _{L \in \binom {[t]}{\ell }} v_{L} \otimes v_L.$
Proof We can assume that
![]() $\ell \leq \mathop {\mathrm {dim}} \mathop {\mathrm {Lin}} \{v_1, \dots , v_t\} \leq t,$
otherwise
$\ell \leq \mathop {\mathrm {dim}} \mathop {\mathrm {Lin}} \{v_1, \dots , v_t\} \leq t,$
otherwise
 $\wedge ^{\ell } A = 0 = \sum \limits _{L \in \binom {[n]}{\ell }} v_{L} \otimes v_L.$
It suffices to prove the identity only for the decomposable
$\wedge ^{\ell } A = 0 = \sum \limits _{L \in \binom {[n]}{\ell }} v_{L} \otimes v_L.$
It suffices to prove the identity only for the decomposable
![]() $\ell $
-forms. Fix
$\ell $
-forms. Fix
![]() $\{x_1, \dots , x_{\ell }\} \subset \mathbb {R}^n.$
We have
$\{x_1, \dots , x_{\ell }\} \subset \mathbb {R}^n.$
We have
 $$ \begin{align*} \wedge^{\ell} A (x_{1} \wedge \dots \wedge x_{\ell}) = Ax_{1} \wedge \dots \wedge Ax_{\ell} = \sum\limits_{i=1}^t \left\langle v_i,x_1\right\rangle v_i \wedge \dots \wedge \sum\limits_{i=1}^t \left\langle v_i,x_{\ell}\right\rangle v_i. \end{align*} $$
$$ \begin{align*} \wedge^{\ell} A (x_{1} \wedge \dots \wedge x_{\ell}) = Ax_{1} \wedge \dots \wedge Ax_{\ell} = \sum\limits_{i=1}^t \left\langle v_i,x_1\right\rangle v_i \wedge \dots \wedge \sum\limits_{i=1}^t \left\langle v_i,x_{\ell}\right\rangle v_i. \end{align*} $$
By linearity and by skew symmetry, we expand the last identity, and the coefficient at
![]() $v_L = v_{i_1} \wedge \dots \wedge v_{i_{\ell }}$
is
$v_L = v_{i_1} \wedge \dots \wedge v_{i_{\ell }}$
is
 $$ \begin{align*} \sum\limits_{\sigma} \operatorname{sgn}{\sigma} \prod\limits_{j = 1}^{\ell} \left\langle v_{i_j}, x_{\sigma(j)}\right\rangle, \end{align*} $$
$$ \begin{align*} \sum\limits_{\sigma} \operatorname{sgn}{\sigma} \prod\limits_{j = 1}^{\ell} \left\langle v_{i_j}, x_{\sigma(j)}\right\rangle, \end{align*} $$
where the summation is taken over all permutations of
![]() $[\ell ].$
This is the determinant of the matrix
$[\ell ].$
This is the determinant of the matrix
 $M_{ij} = \left \langle v_{i_j}, x_i\right \rangle ,$
where
$M_{ij} = \left \langle v_{i_j}, x_i\right \rangle ,$
where
![]() $i,j \in [\ell ].$
By the definition of the inner product, this determinant is just
$i,j \in [\ell ].$
By the definition of the inner product, this determinant is just
![]() $\left \langle v_L,(x_{1} \wedge \dots \wedge x_{\ell })\right \rangle\! ,$
that is,
$\left \langle v_L,(x_{1} \wedge \dots \wedge x_{\ell })\right \rangle\! ,$
that is,
 $$ \begin{align*} \wedge^{\ell} A (x_{i_1} \wedge \dots \wedge x_{i_{\ell}}) = \sum\limits_{L \in \binom{[t]}{\ell}} \left\langle v_{L}, (x_{1} \wedge \dots \wedge x_{\ell})\right\rangle v_L = \sum\limits_{L \in \binom{[t]}{\ell}} v_{L} \otimes v_L (x_{1} \wedge \dots \wedge x_{\ell}). \end{align*} $$
$$ \begin{align*} \wedge^{\ell} A (x_{i_1} \wedge \dots \wedge x_{i_{\ell}}) = \sum\limits_{L \in \binom{[t]}{\ell}} \left\langle v_{L}, (x_{1} \wedge \dots \wedge x_{\ell})\right\rangle v_L = \sum\limits_{L \in \binom{[t]}{\ell}} v_{L} \otimes v_L (x_{1} \wedge \dots \wedge x_{\ell}). \end{align*} $$
This completes the proof. ▪
Identifying
![]() $\wedge ^{k-1} H_k$
with
$\wedge ^{k-1} H_k$
with
![]() $\Lambda ^{k-1}(H_k)$
, we identify
$\Lambda ^{k-1}(H_k)$
, we identify
![]() $H_k$
with
$H_k$
with
![]() $\wedge ^{k-1}{H_k}$
using the Hodge star operator. Now, we can define the cross product of
$\wedge ^{k-1}{H_k}$
using the Hodge star operator. Now, we can define the cross product of
![]() $k-1$
vectors
$k-1$
vectors
![]() $\{x_1, \dots , x_{k-1}\}$
by
$\{x_1, \dots , x_{k-1}\}$
by
Or, in other words, by linearity of the determinant, the cross product
![]() $x = [x_1, \dots , x_{k-1}]$
of
$x = [x_1, \dots , x_{k-1}]$
of
![]() $k-1$
vectors
$k-1$
vectors
![]() $\{x_1, \dots , x_{k-1}\}$
in a k-dimensional space
$\{x_1, \dots , x_{k-1}\}$
in a k-dimensional space
![]() $H_k$
with the fixed inner product
$H_k$
with the fixed inner product
![]() $\left \langle \cdot ,\cdot \right \rangle $
is the vector defined by
$\left \langle \cdot ,\cdot \right \rangle $
is the vector defined by
3 Properties of the exterior power of a projection operator
As a tight frame is a projection of an orthonormal basis, it is natural that its properties are connected with the properties of a projection operator. Moreover, sometimes it is useful to consider a lifting of a tight frame up to an orthonormal basis.
In the following trivial lemma, we understand
![]() $\mathbb {R}^k \subset \mathbb {R}^n$
as the subspace of vectors, whose last
$\mathbb {R}^k \subset \mathbb {R}^n$
as the subspace of vectors, whose last
![]() $n-k$
coordinates are zero. For convenience, we will consider
$n-k$
coordinates are zero. For convenience, we will consider
![]() $\{w_i\}_1^n \subset \mathbb {R}^k \subset \mathbb {R}^n$
to be k-dimensional vectors.
$\{w_i\}_1^n \subset \mathbb {R}^k \subset \mathbb {R}^n$
to be k-dimensional vectors.
Lemma 3.1 The following assertions are equivalent:
-
(1) a set of vectors
 $\{w_1, \dots , w_n\} \subset \mathbb {R}^k$
is a tight frame;
$\{w_1, \dots , w_n\} \subset \mathbb {R}^k$
is a tight frame; -
(2) there exists an orthonormal basis
 $\{ f_1, \dots , f_n \}$
of
$\{ f_1, \dots , f_n \}$
of
 $\mathbb {R}^n$
such that
$\mathbb {R}^n$
such that
 $w_i$
is the orthogonal projection of
$w_i$
is the orthogonal projection of
 $f_i$
onto
$f_i$
onto
 $\mathbb {R}^k,$
for any
$\mathbb {R}^k,$
for any
 $i \in [n];$
$i \in [n];$
-
(3)
 $\mathop {\mathrm {Lin}}\{w_1, \dots ,w_n\} = \mathbb {R}^k$
and the Gram matrix
$\mathop {\mathrm {Lin}}\{w_1, \dots ,w_n\} = \mathbb {R}^k$
and the Gram matrix
 $\Gamma $
of vectors
$\Gamma $
of vectors
 $\{w_1, \dots ,w_n\} \subset \mathbb {R}^k$
is the matrix of the projection operator from
$\{w_1, \dots ,w_n\} \subset \mathbb {R}^k$
is the matrix of the projection operator from
 $\mathbb {R}^n$
onto the linear hull of the rows of matrix
$\mathbb {R}^n$
onto the linear hull of the rows of matrix
 $M = (w_1, \dots , w_n).$
$M = (w_1, \dots , w_n).$
-
(4) the
 $k\times n$
matrix
$k\times n$
matrix
 $M = (w_1, \dots , w_n )$
is a submatrix of an orthogonal matrix of order n.
$M = (w_1, \dots , w_n )$
is a submatrix of an orthogonal matrix of order n.
The main observation is that P is the Gram matrix of vectors
![]() $\{v_1, \dots , v_n\} \subset H_k.$
Since
$\{v_1, \dots , v_n\} \subset H_k.$
Since
 $\left \langle P e_i,e_j\right \rangle = \left \langle P^2 e_i,e_j\right \rangle = \left \langle P e_i,P e_j\right \rangle = \left \langle v_i,v_j\right \rangle ,$
we have that for fixed
$\left \langle P e_i,e_j\right \rangle = \left \langle P^2 e_i,e_j\right \rangle = \left \langle P e_i,P e_j\right \rangle = \left \langle v_i,v_j\right \rangle ,$
we have that for fixed
![]() $\ell \in [k]$
and
$\ell \in [k]$
and
![]() $\ell $
-tuple
$\ell $
-tuple
 $L \subset \binom {[n]}{\ell },$
the corresponding
$L \subset \binom {[n]}{\ell },$
the corresponding
![]() $\ell \times \ell $
submatrix of P is the Gram matrix of vectors
$\ell \times \ell $
submatrix of P is the Gram matrix of vectors
![]() $\{v_i\}_{i \in L}$
, and the determinant of this Gram matrix is
$\{v_i\}_{i \in L}$
, and the determinant of this Gram matrix is
![]() $P_L.$
It is well known that for
$P_L.$
It is well known that for
![]() $\ell $
vectors
$\ell $
vectors
![]() $\{w_i\}_1^{\ell } \subset \mathbb {R}^{\ell },$
their squared determinant is equal to the determinant of their Gram matrix.
$\{w_i\}_1^{\ell } \subset \mathbb {R}^{\ell },$
their squared determinant is equal to the determinant of their Gram matrix.
Lemma 3.2 Let P be the orthogonal projection from
![]() $\mathbb {R}^n$
onto a k-dimensional subspace
$\mathbb {R}^n$
onto a k-dimensional subspace
![]() $H_k.$
Then, for
$H_k.$
Then, for
![]() $\wedge ^{\ell } P,$
where
$\wedge ^{\ell } P,$
where
![]() $1 \leq \ell \leq k,$
we have
$1 \leq \ell \leq k,$
we have
-
(1)
 $\wedge ^{\ell } P$
is an
$\wedge ^{\ell } P$
is an
 $\binom {n}{\ell } \times \binom {n}{\ell }$
matrix such that (3.1)
$\binom {n}{\ell } \times \binom {n}{\ell }$
matrix such that (3.1) $$ \begin{align} \wedge^{\ell} P_{[I, J]} = P_{\{I,J\}} \quad \text{for} \quad I,J \in \binom{[n]}{\ell}; \end{align} $$
$$ \begin{align} \wedge^{\ell} P_{[I, J]} = P_{\{I,J\}} \quad \text{for} \quad I,J \in \binom{[n]}{\ell}; \end{align} $$
-
(2)
 $\wedge ^{\ell } P : \Lambda ^{\ell } \left ( \mathbb {R}^n \right ) \to \Lambda ^{\ell } \left ( \mathbb {R}^n \right )$
is the orthogonal projection onto
$\wedge ^{\ell } P : \Lambda ^{\ell } \left ( \mathbb {R}^n \right ) \to \Lambda ^{\ell } \left ( \mathbb {R}^n \right )$
is the orthogonal projection onto
 $ \wedge ^{\ell } H_k.$
$ \wedge ^{\ell } H_k.$
Proof (1) By definition,
![]() $\wedge ^{\ell } P$
is an
$\wedge ^{\ell } P$
is an
 $\binom {n}{\ell } \times \binom {n}{\ell }$
matrix. Identity (3.1) is the consequence of the definition of the inner product in
$\binom {n}{\ell } \times \binom {n}{\ell }$
matrix. Identity (3.1) is the consequence of the definition of the inner product in
![]() $\Lambda ^{\ell } \left ( \mathbb {R}^n \right ).$
$\Lambda ^{\ell } \left ( \mathbb {R}^n \right ).$
(2) For any decomposable
![]() $\ell $
-form
$\ell $
-form
![]() $x_1 \wedge \dots \wedge x_{\ell },$
we have
$x_1 \wedge \dots \wedge x_{\ell },$
we have
By linearity, we have that
![]() $ \wedge ^{\ell } P x \in \wedge ^{\ell } H_k$
for an arbitrary
$ \wedge ^{\ell } P x \in \wedge ^{\ell } H_k$
for an arbitrary
![]() $\ell $
-form
$\ell $
-form
![]() $x.$
For
$x.$
For
![]() $x \in {\wedge ^{\ell }} H_k,$
we see that
$x \in {\wedge ^{\ell }} H_k,$
we see that
![]() $\wedge ^{\ell } P x = x.$
Thus, we showed that
$\wedge ^{\ell } P x = x.$
Thus, we showed that
![]() $\operatorname {Im} \wedge ^{\ell } P ={\wedge ^{\ell }} H_k$
and
$\operatorname {Im} \wedge ^{\ell } P ={\wedge ^{\ell }} H_k$
and
 $\left (\wedge ^{\ell } P\right )^2 = \wedge ^{\ell } P.$
By this and since
$\left (\wedge ^{\ell } P\right )^2 = \wedge ^{\ell } P.$
By this and since
![]() $P^2 = P,$
we have that
$P^2 = P,$
we have that
![]() $\wedge ^{\ell } P$
is symmetric. This completes the proof. ▪
$\wedge ^{\ell } P$
is symmetric. This completes the proof. ▪
In the following Lemma, we understand
![]() $\mathbb {R}^k \subset \mathbb {R}^n$
as the subspace of vectors, whose last
$\mathbb {R}^k \subset \mathbb {R}^n$
as the subspace of vectors, whose last
![]() $n-k$
coordinates are zero. This embedding induces a natural embedding
$n-k$
coordinates are zero. This embedding induces a natural embedding
![]() $\Lambda ^{\ell } (\mathbb {R}^k) \subset \Lambda ^{\ell } (\mathbb {R}^n)$
for
$\Lambda ^{\ell } (\mathbb {R}^k) \subset \Lambda ^{\ell } (\mathbb {R}^n)$
for
![]() $\ell \in [n].$
$\ell \in [n].$
Theorem 3.3 The following assertions are equivalent for
![]() $\{v_1, \dots , v_n\} \subset \mathbb {R}^k:$
$\{v_1, \dots , v_n\} \subset \mathbb {R}^k:$
-
(1) there exists an orthonormal basis
 $\{ f_1, \dots , f_n \}$
of
$\{ f_1, \dots , f_n \}$
of
 $\mathbb {R}^n$
such that
$\mathbb {R}^n$
such that
 $v_i$
is the orthogonal projection of
$v_i$
is the orthogonal projection of
 $f_i$
onto
$f_i$
onto
 $\mathbb {R}^k,$
for any
$\mathbb {R}^k,$
for any
 $i \in [n];$
$i \in [n];$
-
(2)
 $P_k = \sum \limits _{1}^{n} v_i \otimes v_i, $
where
$P_k = \sum \limits _{1}^{n} v_i \otimes v_i, $
where
 $P_k$
is the projector from
$P_k$
is the projector from
 $\mathbb {R}^n$
onto
$\mathbb {R}^n$
onto
 $\mathbb {R}^k$
;
$\mathbb {R}^k$
; -
(3) for any fixed
 $\ell \in [k-1]$
, there exists an orthonormal basis
$\ell \in [k-1]$
, there exists an orthonormal basis
 $\{ f_L \}$
of
$\{ f_L \}$
of
 $\Lambda ^{\ell } (\mathbb {R}^n)$
such that
$\Lambda ^{\ell } (\mathbb {R}^n)$
such that
 $v_L$
is the orthogonal projection of
$v_L$
is the orthogonal projection of
 $f_L$
onto
$f_L$
onto
 $\Lambda ^{\ell } (\mathbb {R}^k),$
for all
$\Lambda ^{\ell } (\mathbb {R}^k),$
for all
 $L \in \binom {[n]}{\ell }$
;
$L \in \binom {[n]}{\ell }$
; -
(4) for any fixed
 $\ell \in [k-1]$
, the following identity is true: where
$\ell \in [k-1]$
, the following identity is true: where $$ \begin{align*} \Lambda^{\ell} P_k = \sum\limits_{L \in \binom{[n]}{\ell}} v_L \otimes v_L, \end{align*} $$
$$ \begin{align*} \Lambda^{\ell} P_k = \sum\limits_{L \in \binom{[n]}{\ell}} v_L \otimes v_L, \end{align*} $$
 $\Lambda ^{\ell } P_k$
is the projector from
$\Lambda ^{\ell } P_k$
is the projector from
 $\Lambda ^{\ell } (\mathbb {R}^n)$
onto
$\Lambda ^{\ell } (\mathbb {R}^n)$
onto
 $\Lambda ^{\ell } (\mathbb {R}^k).$
$\Lambda ^{\ell } (\mathbb {R}^k).$
Proof By the equivalence (1)
![]() $\Leftrightarrow $
(2) in Lemma 3.1 and since
$\Leftrightarrow $
(2) in Lemma 3.1 and since
![]() $I_k$
is the restriction of
$I_k$
is the restriction of
![]() $P_k$
onto
$P_k$
onto
![]() $\mathbb {R}^k,$
we have that (1)
$\mathbb {R}^k,$
we have that (1)
![]() $\Leftrightarrow $
(2).
$\Leftrightarrow $
(2).
Identifying
![]() $f_i$
and
$f_i$
and
![]() $e_i$
for
$e_i$
for
![]() $i \in [n],$
we identify
$i \in [n],$
we identify
![]() $\mathbb {R}^k$
with some subspace
$\mathbb {R}^k$
with some subspace
![]() $H_k \subset \mathbb {R}^n,$
$H_k \subset \mathbb {R}^n,$
![]() $\Lambda ^{\ell } (\mathbb {R}^k) \subset \Lambda ^{\ell } (\mathbb {R}^n)$
with
$\Lambda ^{\ell } (\mathbb {R}^k) \subset \Lambda ^{\ell } (\mathbb {R}^n)$
with
![]() $ \wedge ^{\ell } (H^k) \subset \Lambda ^{\ell } (\mathbb {R}^n),$
and
$ \wedge ^{\ell } (H^k) \subset \Lambda ^{\ell } (\mathbb {R}^n),$
and
![]() $P_k$
with
$P_k$
with
![]() $P.$
$P.$
Lemma 3.2 says that
![]() $ \Lambda ^{\ell } P_k$
is exactly
$ \Lambda ^{\ell } P_k$
is exactly
![]() $\wedge ^{\ell } P_k.$
Thus, identifying
$\wedge ^{\ell } P_k.$
Thus, identifying
![]() $f_i$
and
$f_i$
and
![]() $e_i$
for
$e_i$
for
![]() $i \in [n],$
we identify
$i \in [n],$
we identify
![]() $ \Lambda ^{\ell } P_k$
with
$ \Lambda ^{\ell } P_k$
with
![]() $\wedge ^{\ell } P.$
Again, since (1)
$\wedge ^{\ell } P.$
Again, since (1)
![]() $\Leftrightarrow $
(2) in Lemma 3.1, we get that (3)
$\Leftrightarrow $
(2) in Lemma 3.1, we get that (3)
![]() $\Leftrightarrow $
(4).
$\Leftrightarrow $
(4).
By assertion (2) in Lemma 3.2, we have that (2)
![]() $\Rightarrow $
(4).
$\Rightarrow $
(4).
Hence, we must show that the implication (2)
![]() $\Leftarrow $
(4) holds to complete the proof.
$\Leftarrow $
(4) holds to complete the proof.
Let
![]() $\{v_1, \dots , v_n \} \subset H_k$
such that
$\{v_1, \dots , v_n \} \subset H_k$
such that
 $ \wedge ^{\ell } P = \sum \limits _{L \in \binom {[n]}{\ell }} v_L \otimes v_L$
for a fixed
$ \wedge ^{\ell } P = \sum \limits _{L \in \binom {[n]}{\ell }} v_L \otimes v_L$
for a fixed
![]() $\ell \in [k-1].$
Let us prove that
$\ell \in [k-1].$
Let us prove that
 $P = \sum \limits _1^n v_i \otimes v_i$
to complete the proof. Assume the contrary, i.e.,
$P = \sum \limits _1^n v_i \otimes v_i$
to complete the proof. Assume the contrary, i.e.,
 $P \neq \sum \limits _1^n v_i \otimes v_i,$
and define
$P \neq \sum \limits _1^n v_i \otimes v_i,$
and define
 $A = \sum \limits _1^n v_i \otimes v_i.$
By Lemma 2.1, we have that
$A = \sum \limits _1^n v_i \otimes v_i.$
By Lemma 2.1, we have that
![]() $\wedge ^l P = \wedge ^l A.$
Since the restriction of A on
$\wedge ^l P = \wedge ^l A.$
Since the restriction of A on
![]() $H_k$
is a positive semi-definite operator, the restriction of A has an orthonormal basis of eigenvectors in
$H_k$
is a positive semi-definite operator, the restriction of A has an orthonormal basis of eigenvectors in
![]() $H_k$
. Let us denote these eigenvectors by
$H_k$
. Let us denote these eigenvectors by
![]() $x_1, \dots , x_k$
and the corresponding eigenvalues by
$x_1, \dots , x_k$
and the corresponding eigenvalues by
![]() $\lambda _1, \dots , \lambda _k.$
Since
$\lambda _1, \dots , \lambda _k.$
Since
![]() $\{x_1, \dots , x_k\} \subset H_k$
and
$\{x_1, \dots , x_k\} \subset H_k$
and
![]() $\wedge ^{\ell } P= \wedge ^{\ell } A$
is the projection onto
$\wedge ^{\ell } P= \wedge ^{\ell } A$
is the projection onto
![]() $\wedge ^{\ell } H_k,$
we have that
$\wedge ^{\ell } H_k,$
we have that
 $$ \begin{align*} 0 & \neq x_{i_1} \wedge \dots \wedge x_{i_{\ell}} = Px_{i_1} \wedge \dots \wedge Px_{i_{\ell}} = \wedge^{\ell} P (x_{i_1} \wedge \dots \wedge x_{i_{\ell}}) \\ & =\wedge^{\ell} A (x_{i_1} \wedge \dots \wedge x_{i_{\ell}}) = Ax_{i_1} \wedge \dots \wedge Ax_{i_{\ell}} = \left(\prod\limits_{j = 1}^{\ell} \lambda_{i_j} \right) \cdot x_{i_1} \wedge \dots \wedge x_{i_{\ell}} \end{align*} $$
$$ \begin{align*} 0 & \neq x_{i_1} \wedge \dots \wedge x_{i_{\ell}} = Px_{i_1} \wedge \dots \wedge Px_{i_{\ell}} = \wedge^{\ell} P (x_{i_1} \wedge \dots \wedge x_{i_{\ell}}) \\ & =\wedge^{\ell} A (x_{i_1} \wedge \dots \wedge x_{i_{\ell}}) = Ax_{i_1} \wedge \dots \wedge Ax_{i_{\ell}} = \left(\prod\limits_{j = 1}^{\ell} \lambda_{i_j} \right) \cdot x_{i_1} \wedge \dots \wedge x_{i_{\ell}} \end{align*} $$
for any
![]() $\ell $
-tuple
$\ell $
-tuple
 $\{i_1, \dots , i_{\ell }\} \subset \binom {[n]}{\ell }.$
Therefore,
$\{i_1, \dots , i_{\ell }\} \subset \binom {[n]}{\ell }.$
Therefore,
 $\left (\prod \limits _{j = 1}^{\ell } \lambda _{i_j} \right ) = 1$
for any
$\left (\prod \limits _{j = 1}^{\ell } \lambda _{i_j} \right ) = 1$
for any
![]() $\ell $
-tuple
$\ell $
-tuple
 $\{i_1, \dots , i_{\ell }\} \subset \binom {[n]}{\ell }.$
Obviously, since
$\{i_1, \dots , i_{\ell }\} \subset \binom {[n]}{\ell }.$
Obviously, since
![]() $0 < \ell < k,$
it implies that all eigenvalues are one. Hence, the restriction of A onto
$0 < \ell < k,$
it implies that all eigenvalues are one. Hence, the restriction of A onto
![]() $H_k$
is the identity operator in
$H_k$
is the identity operator in
![]() $H_k.$
This means that
$H_k.$
This means that
![]() $A = P.$
▪
$A = P.$
▪
The implication (2)
![]() $\Leftarrow $
(4) of Theorem 3.3 still holds for
$\Leftarrow $
(4) of Theorem 3.3 still holds for
![]() $\ell =k.$
By the same arguments as in the proof, we have that (4) implies
$\ell =k.$
By the same arguments as in the proof, we have that (4) implies
 $\det \left . \left (\sum \limits _1^n v_i \otimes v_i\right )\right |_{\mathbb {R}^k} =1.$
Thus, we have the following corollary.
$\det \left . \left (\sum \limits _1^n v_i \otimes v_i\right )\right |_{\mathbb {R}^k} =1.$
Thus, we have the following corollary.
Corollary 3.4 The following assertions are equivalent for
![]() $\{v_1, \dots , v_n\} \subset \mathbb {R}^k \subset \mathbb {R}^n$
:
$\{v_1, \dots , v_n\} \subset \mathbb {R}^k \subset \mathbb {R}^n$
:
-
(1)
 $\det \left . \left (\sum \limits _1^n v_i \otimes v_i\right )\right |_{\mathbb {R}^k} =1.$
$\det \left . \left (\sum \limits _1^n v_i \otimes v_i\right )\right |_{\mathbb {R}^k} =1.$
-
(2) the following identity is true:
 $$ \begin{align*} \Lambda^{k} P_k = \sum\limits_{L \in \binom{[n]}{k}} v_L \otimes v_L. \end{align*} $$
$$ \begin{align*} \Lambda^{k} P_k = \sum\limits_{L \in \binom{[n]}{k}} v_L \otimes v_L. \end{align*} $$
Proof of Theorem 1.1
By the definition of the cross product, Theorem 1.1 is the equivalence (1)
![]() $\Leftrightarrow $
(3) of Theorem 3.3 with
$\Leftrightarrow $
(3) of Theorem 3.3 with
![]() $\ell = k-1$
. ▪
$\ell = k-1$
. ▪
By identity
![]() $(\wedge ^{\ell } P)^2 = \wedge ^{\ell } P,$
we have
$(\wedge ^{\ell } P)^2 = \wedge ^{\ell } P,$
we have
 $$ \begin{align*} P_{\{I,J\}} = \sum_{L \in \binom{[n]}{\ell}} P_{\{I,L\}} P_{\{L,J\}}\\[-16pt] \end{align*} $$
$$ \begin{align*} P_{\{I,J\}} = \sum_{L \in \binom{[n]}{\ell}} P_{\{I,L\}} P_{\{L,J\}}\\[-16pt] \end{align*} $$
for a fixed
![]() $\ell \in [k]$
and two
$\ell \in [k]$
and two
![]() $\ell $
-tuples
$\ell $
-tuples
 $I,J \subset \binom {[n]}{\ell }.$
But Theorem 3.3 gives us another identity, which connects the squared
$I,J \subset \binom {[n]}{\ell }.$
But Theorem 3.3 gives us another identity, which connects the squared
![]() $\ell $
-dimensional volume (that is,
$\ell $
-dimensional volume (that is,
![]() $P_I$
) with the sum of the squared k-dimensional volumes.
$P_I$
) with the sum of the squared k-dimensional volumes.
Lemma 3.5 Let
![]() $\{v_1, \dots , v_n\}$
is a tight frame in
$\{v_1, \dots , v_n\}$
is a tight frame in
![]() $H_k.$
Then, the following identity holds:
$H_k.$
Then, the following identity holds:
 $$\begin{align*}P_{I} = \sum_{Q \in \binom{[n]}{ k - \ell}; |Q \cap I| = \emptyset} P_{I \cup Q} = \sum_{\left. T \in \binom{[n]}{k} \right| I \subset T} P_T\\[-16pt] \end{align*} $$
$$\begin{align*}P_{I} = \sum_{Q \in \binom{[n]}{ k - \ell}; |Q \cap I| = \emptyset} P_{I \cup Q} = \sum_{\left. T \in \binom{[n]}{k} \right| I \subset T} P_T\\[-16pt] \end{align*} $$
for a fixed
![]() $\ell \in [k]$
and an
$\ell \in [k]$
and an
![]() $\ell $
-tuple
$\ell $
-tuple
 $I \in \binom {[n]}{\ell }.$
$I \in \binom {[n]}{\ell }.$
Proof Now, we identify
![]() $\wedge ^p H_k$
with
$\wedge ^p H_k$
with
![]() $\Lambda ^p (H_k)$
for a fixed integer
$\Lambda ^p (H_k)$
for a fixed integer
![]() $p \in [k].$
Then, the Hodge star operator maps a p-form
$p \in [k].$
Then, the Hodge star operator maps a p-form
![]() $w \in \Lambda ^p (H_k)$
to a
$w \in \Lambda ^p (H_k)$
to a
![]() $(k-p)$
-form
$(k-p)$
-form
![]() $\nu \in \Lambda ^{k-p} (H_k).$
By Theorem 3.3, we know that the set of
$\nu \in \Lambda ^{k-p} (H_k).$
By Theorem 3.3, we know that the set of
![]() $(k-\ell )$
-forms
$(k-\ell )$
-forms
![]() $v_Q,$
where
$v_Q,$
where
 $Q \in \binom {[n]}{k -\ell },$
is a tight frame in
$Q \in \binom {[n]}{k -\ell },$
is a tight frame in
![]() $\wedge ^{(k - \ell )} H_k \equiv \Lambda ^{(k - \ell )}( H_k).$
Using the Hodge star operator, we get that the set of
$\wedge ^{(k - \ell )} H_k \equiv \Lambda ^{(k - \ell )}( H_k).$
Using the Hodge star operator, we get that the set of
![]() $\ell $
-forms
$\ell $
-forms
![]() $\star (v_Q),$
where
$\star (v_Q),$
where
 $Q \in \binom {[n]}{k -\ell },$
is a tight frame in
$Q \in \binom {[n]}{k -\ell },$
is a tight frame in
![]() $\wedge ^{\ell } H_k \equiv \Lambda ^{\ell }( H_k).$
By the definition of the inner product of two
$\wedge ^{\ell } H_k \equiv \Lambda ^{\ell }( H_k).$
By the definition of the inner product of two
![]() $\ell $
-forms, we have
$\ell $
-forms, we have
![]() $P_I = \left \langle v_I,v_I\right \rangle .$
Now, we can expand this using properties of the
$P_I = \left \langle v_I,v_I\right \rangle .$
Now, we can expand this using properties of the
![]() $\ell $
-forms
$\ell $
-forms
![]() $\star (v_Q),$
where
$\star (v_Q),$
where
 $Q \in \binom {[n]}{k -\ell }.$
So,
$Q \in \binom {[n]}{k -\ell }.$
So,
 $$ \begin{align} P_I = \left\langle v_I,v_I\right\rangle = \sum\limits_{Q \in \binom{[n]}{k -\ell}} \left\langle v_I,\star(v_Q)\right\rangle \left\langle\star(v_Q), v_I\right\rangle.\\[-16pt]\nonumber \end{align} $$
$$ \begin{align} P_I = \left\langle v_I,v_I\right\rangle = \sum\limits_{Q \in \binom{[n]}{k -\ell}} \left\langle v_I,\star(v_Q)\right\rangle \left\langle\star(v_Q), v_I\right\rangle.\\[-16pt]\nonumber \end{align} $$
By identity (2.3),
![]() $\left \langle v_I, \star (v_Q)\right \rangle $
is the determinant of k vectors
$\left \langle v_I, \star (v_Q)\right \rangle $
is the determinant of k vectors
![]() $(v_i)_{i \in I}, (v_q)_{q \in Q}$
of
$(v_i)_{i \in I}, (v_q)_{q \in Q}$
of
![]() $H_k$
. Thus,
$H_k$
. Thus,
![]() $\left \langle v_I,\star (v_Q)\right \rangle = 0$
whenever
$\left \langle v_I,\star (v_Q)\right \rangle = 0$
whenever
![]() $I \cap Q \neq \emptyset ,$
and
$I \cap Q \neq \emptyset ,$
and
 $ \left \langle v_I,\star (v_Q)\right \rangle ^2 = P_{I \cup Q}$
whenever
$ \left \langle v_I,\star (v_Q)\right \rangle ^2 = P_{I \cup Q}$
whenever
![]() $I \cap Q = \emptyset .$
Combining these formulas with (3.2), we obtain
$I \cap Q = \emptyset .$
Combining these formulas with (3.2), we obtain
 $$ \begin{align*} P_I = \sum\limits_{Q \in \binom{[n]}{k -\ell}; Q \cap I = \emptyset} \left\langle v_I,\star(v_Q)\right\rangle \left\langle \star(v_Q),v_I\right\rangle = \sum_{Q \in \binom{[n]}{k - \ell}; |Q \cap I| = \emptyset} P_{I \cup Q}.\\[-55pt] \end{align*} $$
$$ \begin{align*} P_I = \sum\limits_{Q \in \binom{[n]}{k -\ell}; Q \cap I = \emptyset} \left\langle v_I,\star(v_Q)\right\rangle \left\langle \star(v_Q),v_I\right\rangle = \sum_{Q \in \binom{[n]}{k - \ell}; |Q \cap I| = \emptyset} P_{I \cup Q}.\\[-55pt] \end{align*} $$
▪
3.1 Lagrange’s identity and McMullen’s formula
McMullen’s formula (1.3) follows from Shepard’s formula [Reference Shephard17] for the volume of a
![]() $\sum _{i=1}^{n} [0, b_i] \subset \mathbb {R}^k$
$\sum _{i=1}^{n} [0, b_i] \subset \mathbb {R}^k$
 $$ \begin{align} \operatorname{vol}_{k} \left(\sum\limits_{i=1}^{n} [0, b_i]\right) = \sum\limits_{\{i_1, \dots, i_k\} \in \binom{[n] }{k}} \left|\det \{b_{i_1}, \dots, b_{i_k}\} \right|, \end{align} $$
$$ \begin{align} \operatorname{vol}_{k} \left(\sum\limits_{i=1}^{n} [0, b_i]\right) = \sum\limits_{\{i_1, \dots, i_k\} \in \binom{[n] }{k}} \left|\det \{b_{i_1}, \dots, b_{i_k}\} \right|, \end{align} $$
and identity
![]() $\left |d_S (\{L\})\right | = \left |d_S (\{[n] \backslash L\})\right |$
for a tight frame S and a subset L of
$\left |d_S (\{L\})\right | = \left |d_S (\{[n] \backslash L\})\right |$
for a tight frame S and a subset L of
![]() $[n].$
By assertion (4) of Lemma 3.1, this identity is equivalent to identity
$[n].$
By assertion (4) of Lemma 3.1, this identity is equivalent to identity
![]() $|U_L| = |U_{[n] \backslash L}|$
for an orthogonal matrix U of rank n and any
$|U_L| = |U_{[n] \backslash L}|$
for an orthogonal matrix U of rank n and any
![]() $L \subset [n],$
which is known as Lagrange’s identity. However, it is natural to prove it in terms of properties of a projection operator.
$L \subset [n],$
which is known as Lagrange’s identity. However, it is natural to prove it in terms of properties of a projection operator.
Lemma 3.6 Let
![]() $H_{n-k}$
be the orthogonal complement of
$H_{n-k}$
be the orthogonal complement of
![]() $H_k$
in
$H_k$
in
![]() $\mathbb {R}^n.$
Denote by P and
$\mathbb {R}^n.$
Denote by P and
![]() $P^\perp $
the projections onto
$P^\perp $
the projections onto
![]() $H_k$
and
$H_k$
and
![]() $H_{n-k},$
respectively. Then,
$H_{n-k},$
respectively. Then,
 $$ \begin{align*} \star \left(\wedge^k P [x] \right) = \left( \wedge^{(n- k)} P^\perp \right) [\star x] \end{align*} $$
$$ \begin{align*} \star \left(\wedge^k P [x] \right) = \left( \wedge^{(n- k)} P^\perp \right) [\star x] \end{align*} $$
for any
![]() $x \in \Lambda ^k \left (\mathbb {R}^n \right ).$
$x \in \Lambda ^k \left (\mathbb {R}^n \right ).$
Proof We use
![]() $\pi $
to denote a unit directional vector of the line
$\pi $
to denote a unit directional vector of the line
![]() ${\wedge ^k} H_k$
generated by
${\wedge ^k} H_k$
generated by
![]() $H_k$
in
$H_k$
in
![]() $\Lambda ^k \left (\mathbb {R}^n \right ).$
Clearly,
$\Lambda ^k \left (\mathbb {R}^n \right ).$
Clearly,
![]() $\star \pi $
is the unit directional vector (with a proper orientation) of the line
$\star \pi $
is the unit directional vector (with a proper orientation) of the line
![]() $\wedge ^{(n-k)} H_{n-k}$
generated by
$\wedge ^{(n-k)} H_{n-k}$
generated by
![]() $H_{n-k}$
in
$H_{n-k}$
in
![]() $\Lambda ^{n-k} \left (\mathbb {R}^n \right ).$
For an arbitrary
$\Lambda ^{n-k} \left (\mathbb {R}^n \right ).$
For an arbitrary
![]() $x \in \Lambda ^k \left (\mathbb {R}^n \right )$
and
$x \in \Lambda ^k \left (\mathbb {R}^n \right )$
and
![]() $y \in \Lambda ^{n-k} \left (\mathbb {R}^n \right ),$
we have
$y \in \Lambda ^{n-k} \left (\mathbb {R}^n \right ),$
we have
![]() ${\wedge ^k}P [x] = c_1 \pi \in {\wedge ^k} H_k$
and
${\wedge ^k}P [x] = c_1 \pi \in {\wedge ^k} H_k$
and
 $\left ({\wedge ^{(n - k)}} P^\perp \right ) [ y ] = c_2 (\star \pi ) \in {\wedge ^{(n - k)}}H_{n-k}$
for some scalars
$\left ({\wedge ^{(n - k)}} P^\perp \right ) [ y ] = c_2 (\star \pi ) \in {\wedge ^{(n - k)}}H_{n-k}$
for some scalars
![]() $c_1, c_2.$
From this and by linearity of operators
$c_1, c_2.$
From this and by linearity of operators
 $\star \left ({\wedge ^k} P\right )$
and
$\star \left ({\wedge ^k} P\right )$
and
 $\left (\wedge ^{(n - k)} P^\perp \right ) \star ,$
we obtain that
$\left (\wedge ^{(n - k)} P^\perp \right ) \star ,$
we obtain that
 $\star \left ({\wedge ^k} P\right ) [x] = c \left (\wedge ^{(n - k)} P^\perp \right ) [\star x]$
for some scalar c. From the chain
$\star \left ({\wedge ^k} P\right ) [x] = c \left (\wedge ^{(n - k)} P^\perp \right ) [\star x]$
for some scalar c. From the chain
 $$ \begin{align*} \star \left({\wedge^k} P\right) \pi = \star \pi = \left(\wedge^{(n - k)} P^\perp \right) [\star \pi], \end{align*} $$
$$ \begin{align*} \star \left({\wedge^k} P\right) \pi = \star \pi = \left(\wedge^{(n - k)} P^\perp \right) [\star \pi], \end{align*} $$
we conclude that
![]() $c=1.$
This completes the proof. ▪
$c=1.$
This completes the proof. ▪
So, Lagrange’s identity takes the following form with a simple geometric meaning.
Corollary 3.7 In the notation of Lemma 3.6 , we have
 $$ \begin{align} P_L = P^\perp_{[n]\backslash L} \end{align} $$
$$ \begin{align} P_L = P^\perp_{[n]\backslash L} \end{align} $$
for
 $L \in \binom {[n]}{k}.$
$L \in \binom {[n]}{k}.$
4 The tight frames and related geometric problems
4.1 Equivalent formulation
Tight frame
![]() $\{P^H e_1, \dots , P^H e_n \},$
where H is a k-dimensional subspace of
$\{P^H e_1, \dots , P^H e_n \},$
where H is a k-dimensional subspace of
![]() $\mathbb {R}^n$
and
$\mathbb {R}^n$
and
![]() $P^H$
is the orthogonal projection onto
$P^H$
is the orthogonal projection onto
![]() $H,$
can be considered as the ordered set of n vectors of
$H,$
can be considered as the ordered set of n vectors of
![]() $\mathbb {R}^k.$
That allows us to avoid working in Grassmannian
$\mathbb {R}^k.$
That allows us to avoid working in Grassmannian
![]() $\operatorname {Gr}\!\left ( n, k \right )\!.$
However, there is an ambiguity in correspondence
$\operatorname {Gr}\!\left ( n, k \right )\!.$
However, there is an ambiguity in correspondence
![]() $H \to \{P^H e_1, \dots , P^H e_n \}.$
Any choice of orthonormal basis of H gives its own tight frame in
$H \to \{P^H e_1, \dots , P^H e_n \}.$
Any choice of orthonormal basis of H gives its own tight frame in
![]() $\mathbb {R}^k,$
all of them are isometric but different from each other. Let us formalize our technique and explain how one can deal with this ambiguity.
$\mathbb {R}^k,$
all of them are isometric but different from each other. Let us formalize our technique and explain how one can deal with this ambiguity.
We endow
![]() $\Omega (n,k)$
with the metric
$\Omega (n,k)$
with the metric
 $$ \begin{align*} \operatorname{dist}\!\left( \{v_1, \dots, v_n\}, \{w_1, \dots, w_n\} \right) = \sqrt{\sum\limits_1^n |v_i - w_i|^2}. \end{align*} $$
$$ \begin{align*} \operatorname{dist}\!\left( \{v_1, \dots, v_n\}, \{w_1, \dots, w_n\} \right) = \sqrt{\sum\limits_1^n |v_i - w_i|^2}. \end{align*} $$
The orthogonal group
![]() $\operatorname {O}\left ( k \right )$
acts on
$\operatorname {O}\left ( k \right )$
acts on
![]() $\Omega (n,k)$
in a usual way
$\Omega (n,k)$
in a usual way
The equivalence classes of this action are called O-classes, and the O-class of a tight frame S is denoted as
![]() $\left [ S \right ].$
We say that a function
$\left [ S \right ].$
We say that a function
![]() $\Psi : \Omega (n, k) \to \mathbb {R}$
is O-invariant if it is constant on each O-class.
$\Psi : \Omega (n, k) \to \mathbb {R}$
is O-invariant if it is constant on each O-class.
There is a one-to-one correspondence between
![]() $\operatorname {Gr}\!\left ( n, k \right )$
and
$\operatorname {Gr}\!\left ( n, k \right )$
and
 $\frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )}:$
$\frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )}:$
-
• the map
 $\alpha : \operatorname {Gr}\!\left ( n, k \right ) \to \frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )}$
is defined by
$\alpha : \operatorname {Gr}\!\left ( n, k \right ) \to \frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )}$
is defined by  $$ \begin{align*} \alpha(H) = \left[ P^H e_1, \dots, P^H e_n \right] \quad \text{for} \quad H \in \operatorname{Gr}\!\left( n, k \right). \end{align*} $$
$$ \begin{align*} \alpha(H) = \left[ P^H e_1, \dots, P^H e_n \right] \quad \text{for} \quad H \in \operatorname{Gr}\!\left( n, k \right). \end{align*} $$
-
• the map
 $\beta : \frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )} \to \operatorname {Gr}\!\left ( n, k \right )$
is defined as follows. Let
$\beta : \frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )} \to \operatorname {Gr}\!\left ( n, k \right )$
is defined as follows. Let
 $\{v_1, \dots , v_n\} \in \Omega (n,k).$
By Lemma 3.1, the Gram matrix P of
$\{v_1, \dots , v_n\} \in \Omega (n,k).$
By Lemma 3.1, the Gram matrix P of
 $\{v_1, \dots , v_n\}$
is the matrix of projection onto a k-dimensional subspace
$\{v_1, \dots , v_n\}$
is the matrix of projection onto a k-dimensional subspace
 $H.$
Then,
$H.$
Then,
 $\beta \left ( \left [\{v_1, \dots , v_n\} \right ] \right ) = H.$
Clearly, an orthogonal transformation does not change the Gram matrix. Therefore,
$\beta \left ( \left [\{v_1, \dots , v_n\} \right ] \right ) = H.$
Clearly, an orthogonal transformation does not change the Gram matrix. Therefore,
 $\beta $
is defined correctly.
$\beta $
is defined correctly.
By assertion (4) of Lemma 3.1, the sets of vectors
![]() $\{v_1, \dots , v_n\}$
and
$\{v_1, \dots , v_n\}$
and
![]() $\{P e_1, \dots , P e_n\}$
are isometric. Thus,
$\{P e_1, \dots , P e_n\}$
are isometric. Thus,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are the inverse functions of each other.
$\beta $
are the inverse functions of each other.
Consequently, there is a one-to-one correspondence between the space of functions
![]() $\operatorname {Gr}\!\left ( n, k \right ) \to \mathbb {R}$
and the space of O-invariant functions
$\operatorname {Gr}\!\left ( n, k \right ) \to \mathbb {R}$
and the space of O-invariant functions
![]() $\Omega (n,k) \to \mathbb {R}.$
For any function
$\Omega (n,k) \to \mathbb {R}.$
For any function
![]() $\Psi : \operatorname {Gr}\!\left ( n, k \right ) \to \mathbb {R},$
we define its frame-function
$\Psi : \operatorname {Gr}\!\left ( n, k \right ) \to \mathbb {R},$
we define its frame-function
![]() $\gamma (\Psi ): \Omega (k, n) \to \mathbb {R}$
by
$\gamma (\Psi ): \Omega (k, n) \to \mathbb {R}$
by
Clearly, the frame-function is O-invariant. Thus, by the above argument,
![]() $\Psi $
and
$\Psi $
and
![]() $\gamma (\Psi )$
have the same global extrema. Let us show that the local extrema of any continuous function
$\gamma (\Psi )$
have the same global extrema. Let us show that the local extrema of any continuous function
![]() $\operatorname {Gr}\!\left ( n, k \right ) \to \mathbb {R}$
and its frame-functions are the same up to factorization by
$\operatorname {Gr}\!\left ( n, k \right ) \to \mathbb {R}$
and its frame-functions are the same up to factorization by
![]() $\operatorname {O}\left ( k \right )\!.$
Of course, we need to specify a topology or metric on
$\operatorname {O}\left ( k \right )\!.$
Of course, we need to specify a topology or metric on
![]() $\operatorname {Gr}\!\left ( n, k \right )\!.$
We consider the natural one as a topology of a homogeneous space
$\operatorname {Gr}\!\left ( n, k \right )\!.$
We consider the natural one as a topology of a homogeneous space
![]() $\left (\operatorname {Gr}\!\left ( n, k \right ) = \operatorname {O}\left ( n \right )/ (\operatorname {O}\left ( k \right ) \times \operatorname {O}\left ( n-k \right )) \right )$
, which is the metric topology generated by metric
$\left (\operatorname {Gr}\!\left ( n, k \right ) = \operatorname {O}\left ( n \right )/ (\operatorname {O}\left ( k \right ) \times \operatorname {O}\left ( n-k \right )) \right )$
, which is the metric topology generated by metric
 $$ \begin{align*} \operatorname{Dist} (H, H') = \left\| P^H - P^{H'} \right\|, \end{align*} $$
$$ \begin{align*} \operatorname{Dist} (H, H') = \left\| P^H - P^{H'} \right\|, \end{align*} $$
where
![]() $\left \| \cdot \right \|$
denotes the operator norm.
$\left \| \cdot \right \|$
denotes the operator norm.
Lemma 4.1 Let
![]() $\Psi : \operatorname {Gr}\!\left ( n, k \right ) \to \mathbb {R}$
be a continuous function. Then, the following assertions are equivalent:
$\Psi : \operatorname {Gr}\!\left ( n, k \right ) \to \mathbb {R}$
be a continuous function. Then, the following assertions are equivalent:
-
(1)
 $S \in \Omega (n,k)$
is a local extremum of
$S \in \Omega (n,k)$
is a local extremum of
 $\gamma (\Psi ).$
$\gamma (\Psi ).$
-
(2)
 $[S] \subset \Omega(n,k)$
in the identity. At the moment, it is written
$[S] \subset \Omega(n,k)$
in the identity. At the moment, it is written
 $[S] \in.$
$[S] \in.$
-
(3)
 $\beta ([S])$
is a local extremum of
$\beta ([S])$
is a local extremum of
 $\Psi .$
$\Psi .$
Proof The equivalence of the first two assertions is trivial as
![]() $\gamma (\Psi )$
is O-invariant. Let us show that they are equivalent to the third one.
$\gamma (\Psi )$
is O-invariant. Let us show that they are equivalent to the third one.
We define a metric on
 $\frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )}$
as follows:
$\frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )}$
as follows:
Obviously, the minimum is attained. Let us check the triangle inequality for arbitrary O-classes
![]() $O_1, O_2$
, and
$O_1, O_2$
, and
![]() $O_3.$
Since
$O_3.$
Since
![]() $\operatorname {O}\left ( k \right )$
acts transitively on each O-class, there is
$\operatorname {O}\left ( k \right )$
acts transitively on each O-class, there is
![]() $S_2 \in O_2$
such that
$S_2 \in O_2$
such that
![]() $\rho \left (O_1, O_2 \right ) = \operatorname {dist}\!\left ( S_1, S_2 \right )$
for any
$\rho \left (O_1, O_2 \right ) = \operatorname {dist}\!\left ( S_1, S_2 \right )$
for any
![]() $S_1 \in O_1.$
We assume that the minimum in (4.1) is attained at
$S_1 \in O_1.$
We assume that the minimum in (4.1) is attained at
![]() $S_1$
and
$S_1$
and
![]() $S_2$
for
$S_2$
for
![]() $O_1$
and
$O_1$
and
![]() $O_2,$
and at
$O_2,$
and at
![]() $S_2$
and
$S_2$
and
![]() $S_3$
for
$S_3$
for
![]() $O_2$
and
$O_2$
and
![]() $O_3.$
Then,
$O_3.$
Then,
Clearly, the tight frames of
![]() $[S]$
are the local extrema of
$[S]$
are the local extrema of
![]() $\gamma (\Psi )$
iff
$\gamma (\Psi )$
iff
![]() $[S]$
is a local extremum of the function
$[S]$
is a local extremum of the function
 $\Psi _O : \frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )} \to \mathbb {R}$
defined by
$\Psi _O : \frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )} \to \mathbb {R}$
defined by
![]() $\Psi _O\left (\left [S\right ]\right ) = \gamma (\Psi (S)).$
To complete the proof, it suffices to show that
$\Psi _O\left (\left [S\right ]\right ) = \gamma (\Psi (S)).$
To complete the proof, it suffices to show that
![]() $\operatorname {Gr}\!\left ( n, k \right )$
and
$\operatorname {Gr}\!\left ( n, k \right )$
and
 $\frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )}$
are homeomorphic. This follows from the observation that the operator norm is equivalent to the Hilbert–Schmidt operator norm
$\frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )}$
are homeomorphic. This follows from the observation that the operator norm is equivalent to the Hilbert–Schmidt operator norm
 $\left (\left \| P^H \right \|_{HS} = \sqrt {\sum \limits _1^n |P^H e_i|^2} \right ),$
and the latter is equivalent to metric
$\left (\left \| P^H \right \|_{HS} = \sqrt {\sum \limits _1^n |P^H e_i|^2} \right ),$
and the latter is equivalent to metric
![]() $\rho $
on
$\rho $
on
 $\frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )}.$
▪
$\frac {\Omega (n,k)}{\operatorname {O}\left ( k \right )}.$
▪
4.2 Perturbation of frames
Our main idea of finding local extrema of an O-invariant function
![]() $\Psi $
is to transform a given tight frame S to a new one
$\Psi $
is to transform a given tight frame S to a new one
![]() $S'.$
However, it is not convenient to restrict ourselves to the set of tight frames. For example, consider function
$S'.$
However, it is not convenient to restrict ourselves to the set of tight frames. For example, consider function
![]() $\Psi _1 : \Omega (n,k) \to \mathbb {R}_+$
given by
$\Psi _1 : \Omega (n,k) \to \mathbb {R}_+$
given by
![]() $\Psi _1 \left (\{v_1, \dots , v_n\} \right ) = \operatorname {vol}_{k} \mathop {\mathrm {co}} \{\pm v_1, \dots , \pm v_n\}$
(that is, the frame-function of the volume of a projection of the cross-polytope). It is clear what happens with the convex hull when we move one or several vectors of the tight frame, but we may destroy the tight frame condition with such a transformation. It is not a problem as we can easily extend the domain.
$\Psi _1 \left (\{v_1, \dots , v_n\} \right ) = \operatorname {vol}_{k} \mathop {\mathrm {co}} \{\pm v_1, \dots , \pm v_n\}$
(that is, the frame-function of the volume of a projection of the cross-polytope). It is clear what happens with the convex hull when we move one or several vectors of the tight frame, but we may destroy the tight frame condition with such a transformation. It is not a problem as we can easily extend the domain.
Definition 4.1 We will say that the ordered set
![]() $S = \{v_1, \dots , v_n\}$
of n vectors of
$S = \{v_1, \dots , v_n\}$
of n vectors of
![]() $\mathbb {R}^k$
is a frame if vectors of S span
$\mathbb {R}^k$
is a frame if vectors of S span
![]() $\mathbb {R}^k.$
We consider the following objects related to frames:
$\mathbb {R}^k.$
We consider the following objects related to frames:
-
(1) the operator
 $ \sum \limits _{i \in [n]} v_i \otimes v_i.$
We use
$ \sum \limits _{i \in [n]} v_i \otimes v_i.$
We use
 $A_S$
to denote this operator and the matrix of this operator in the standard basis.
$A_S$
to denote this operator and the matrix of this operator in the standard basis. -
(2) The operator
 $B_S = A_S^{-\frac {1}{2}}.$
$B_S = A_S^{-\frac {1}{2}}.$
-
(3) The subspace
 $H_k^{S} \subset \mathbb {R}^n$
, which is the linear hull of the rows of the
$H_k^{S} \subset \mathbb {R}^n$
, which is the linear hull of the rows of the
 $k \times n$
matrix
$k \times n$
matrix
 $(v_1, \dots , v_n)$
and the projection operator
$(v_1, \dots , v_n)$
and the projection operator
 $P^S$
from
$P^S$
from
 $\mathbb {R}^n$
onto
$\mathbb {R}^n$
onto
 $H_k^S$
. We use the same notation
$H_k^S$
. We use the same notation
 $P^S$
for the matrix of this operator in the standard basis.
$P^S$
for the matrix of this operator in the standard basis.
For a frame
![]() $S = \{v_1, \dots , v_n\}$
and a linear transformation
$S = \{v_1, \dots , v_n\}$
and a linear transformation
![]() $L,$
we denote
$L,$
we denote
![]() $\{Lv_1, \dots , Lv_n\}$
by
$\{Lv_1, \dots , Lv_n\}$
by
![]() $LS.$
The operator
$LS.$
The operator
![]() $B_S$
is well-defined as the condition
$B_S$
is well-defined as the condition
![]() $\mathop {\mathrm {Lin}} S = \mathbb {R}^k$
implies that
$\mathop {\mathrm {Lin}} S = \mathbb {R}^k$
implies that
![]() $A_S$
is a positive definite operator. Clearly, for any frame
$A_S$
is a positive definite operator. Clearly, for any frame
![]() $S,$
the frame
$S,$
the frame
![]() $B_S S$
is a tight frame:
$B_S S$
is a tight frame:
 $$ \begin{align*} \sum_{i=1}^{n} B_S v_i \otimes B_S v_i = B_S \left( \sum_{i=1}^{n} v_i \otimes v_i \right) B_S^T = B_S A_S B_S = I_k. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{n} B_S v_i \otimes B_S v_i = B_S \left( \sum_{i=1}^{n} v_i \otimes v_i \right) B_S^T = B_S A_S B_S = I_k. \end{align*} $$
It is easy to see that the metric
![]() $\operatorname {dist}\!\left ( \cdot , \cdot \right )$
on
$\operatorname {dist}\!\left ( \cdot , \cdot \right )$
on
![]() $\Omega (n,k)$
extends to the set of all frames. Also, a small enough perturbation of a frame S yields a small perturbation of
$\Omega (n,k)$
extends to the set of all frames. Also, a small enough perturbation of a frame S yields a small perturbation of
![]() $B_S.$
$B_S.$
Typically, O-invariant functions can be extended to the set of all frames in a tautological way, for example, the extensions of O-invariant functions for the objects listed above might be:
-
(1)
 $\Psi _1 \left ( \{v_1, \dots , v_n\} \right ) = \operatorname {vol}_{k} \mathop {\mathrm {co}}\{ \pm v_1, \dots , \pm v_n\};$
$\Psi _1 \left ( \{v_1, \dots , v_n\} \right ) = \operatorname {vol}_{k} \mathop {\mathrm {co}}\{ \pm v_1, \dots , \pm v_n\};$
-
(2)
 $\Psi _2 \left ( \{v_1, \dots , v_n\} \right ) = \operatorname {vol}_{k} \left (\bigcap \limits _1^n \left \{x \in \mathbb {R}^k : |\left \langle x,v_i\right \rangle | \leq 1 \right \} \right );$
$\Psi _2 \left ( \{v_1, \dots , v_n\} \right ) = \operatorname {vol}_{k} \left (\bigcap \limits _1^n \left \{x \in \mathbb {R}^k : |\left \langle x,v_i\right \rangle | \leq 1 \right \} \right );$
-
(3)
 $\Psi _3 \left ( \{v_1, \dots , v_n\} \right ) = \operatorname {vol}_{k}\left ( \sum \limits _{1}^{n} [-v_i, v_i]\right ).$
$\Psi _3 \left ( \{v_1, \dots , v_n\} \right ) = \operatorname {vol}_{k}\left ( \sum \limits _{1}^{n} [-v_i, v_i]\right ).$
We prefer to extend the functions as follows:
 $$ \begin{align} \Psi \!\! \left( \tilde{S}\right) = \frac{\Psi\!\! \left(B_{\tilde{S}} \tilde{S} \right)}{\det B_{\tilde{S}}} \quad \text{for a frame}\ \tilde{S}. \end{align} $$
$$ \begin{align} \Psi \!\! \left( \tilde{S}\right) = \frac{\Psi\!\! \left(B_{\tilde{S}} \tilde{S} \right)}{\det B_{\tilde{S}}} \quad \text{for a frame}\ \tilde{S}. \end{align} $$
One can see that
![]() $\Psi _1$
and
$\Psi _1$
and
![]() $\Psi _3$
satisfy this condition, and
$\Psi _3$
satisfy this condition, and
![]() $\overline {\Psi }_2 = 1 / \Psi _2$
satisfies it as well. It looks as a natural extension at least for problems related to the volume of projections or sections of bodies because of the positive homogeneity of the volume
$\overline {\Psi }_2 = 1 / \Psi _2$
satisfies it as well. It looks as a natural extension at least for problems related to the volume of projections or sections of bodies because of the positive homogeneity of the volume
![]() $\operatorname {vol}_{k} L(K) = |\det L| \operatorname {vol}_{k} K,$
where K is a convex set and L is a linear transformation.
$\operatorname {vol}_{k} L(K) = |\det L| \operatorname {vol}_{k} K,$
where K is a convex set and L is a linear transformation.
In order to obtain properties of extremizers, we consider a composition of two operations:
 $$ \begin{align} S \quad \stackrel{\mathbf{T}}{\longrightarrow} \quad \tilde{S} \quad \stackrel{B_{\tilde{S}}}{\longrightarrow} \quad S', \end{align} $$
$$ \begin{align} S \quad \stackrel{\mathbf{T}}{\longrightarrow} \quad \tilde{S} \quad \stackrel{B_{\tilde{S}}}{\longrightarrow} \quad S', \end{align} $$
where
![]() $\mathbf {T}$
is a map from a subset of
$\mathbf {T}$
is a map from a subset of
![]() $\Omega (n, k)$
to the set of frames in
$\Omega (n, k)$
to the set of frames in
![]() $\mathbb {R}^k$
and
$\mathbb {R}^k$
and
![]() $B_{\tilde {S}}$
just maps
$B_{\tilde {S}}$
just maps
![]() $\tilde {S} = T (S)$
to a new tight frame
$\tilde {S} = T (S)$
to a new tight frame
![]() $S'.$
$S'.$
Using our setting, it is easy to write a necessary and sufficient condition for a local extremum of an O-invariant function.
Lemma 4.2 A tight frame
![]() $S = \{v_1, \dots , v_n\}$
is a local maximum (or minimum) of a non-negative O-invariant function
$S = \{v_1, \dots , v_n\}$
is a local maximum (or minimum) of a non-negative O-invariant function
![]() $\Psi $
iff the following inequality holds for any frame
$\Psi $
iff the following inequality holds for any frame
![]() $\tilde {S}$
of some open neighborhood
$\tilde {S}$
of some open neighborhood
![]() $U(S)$
of S in the set of frames:
$U(S)$
of S in the set of frames:
 $$ \begin{align} \frac{\Psi(\tilde{S})}{\Psi\! \left(S\right)} \leq \sqrt{\det A_{\tilde{S}}} \quad ( or \geq). \end{align} $$
$$ \begin{align} \frac{\Psi(\tilde{S})}{\Psi\! \left(S\right)} \leq \sqrt{\det A_{\tilde{S}}} \quad ( or \geq). \end{align} $$
In addition, S is a global maximum (or minimum) iff inequality (4.4) holds for all frames
![]() $\tilde {S}.$
$\tilde {S}.$
Proof As mentioned above,
 $B_{\tilde {S}} \tilde {S}$
is a tight frame and, by continuity, it belongs to a small enough neighborhood of S in
$B_{\tilde {S}} \tilde {S}$
is a tight frame and, by continuity, it belongs to a small enough neighborhood of S in
![]() $\Omega (n,k)$
if
$\Omega (n,k)$
if
![]() $\tilde {S} \in U(S).$
Using these observations and the definition of
$\tilde {S} \in U(S).$
Using these observations and the definition of
![]() $B_S,$
we have
$B_S,$
we have
 $$ \begin{align*} \frac{\Psi(\tilde{S})}{\Psi\! \left(S\right)} = \frac{1}{ \det B_{\tilde{S}}} \frac{\Psi(B_{\tilde{S}} \tilde{S})}{\Psi\! \left(S\right)} \leq \frac{1}{ \det B_{\tilde{S}}} = \sqrt{\det A_{\tilde{S}}}. \end{align*} $$
$$ \begin{align*} \frac{\Psi(\tilde{S})}{\Psi\! \left(S\right)} = \frac{1}{ \det B_{\tilde{S}}} \frac{\Psi(B_{\tilde{S}} \tilde{S})}{\Psi\! \left(S\right)} \leq \frac{1}{ \det B_{\tilde{S}}} = \sqrt{\det A_{\tilde{S}}}. \end{align*} $$
The equivalence for a global extremum is trivial. ▪
Choosing a proper simple operation
![]() $\mathbf {T}$
( e.g., scaling one or several vectors, moving one vector to the origin, and mapping one vector to another), we may understand the geometric meaning of the left-hand side of (4.4). On the other hand, the determinant in the right-hand side of (4.4) can be calculated directly. In particular, the first-order approximation of the determinant is obtained in Theorem 1.2.
$\mathbf {T}$
( e.g., scaling one or several vectors, moving one vector to the origin, and mapping one vector to another), we may understand the geometric meaning of the left-hand side of (4.4). On the other hand, the determinant in the right-hand side of (4.4) can be calculated directly. In particular, the first-order approximation of the determinant is obtained in Theorem 1.2.
4.3 Computation of the determinants
Proof of Theorem 1.2
First of all, by the Cauchy–Binet formula, we have
 $$ \begin{align} \det \left( \sum\limits_1^n v_i \otimes v_i\right) = \sum\limits_{I \in \binom{[n]}{k}} P_I^S. \end{align} $$
$$ \begin{align} \det \left( \sum\limits_1^n v_i \otimes v_i\right) = \sum\limits_{I \in \binom{[n]}{k}} P_I^S. \end{align} $$
By linearity and identity
![]() $P_I^S = ( d_S(\{I\}))^2,$
it suffices to prove the theorem for the case when only one vector of the set
$P_I^S = ( d_S(\{I\}))^2,$
it suffices to prove the theorem for the case when only one vector of the set
![]() $\{x_i\}_1^n$
is nonzero. Thus, the theorem follows from the following lemma. ▪
$\{x_i\}_1^n$
is nonzero. Thus, the theorem follows from the following lemma. ▪
Lemma 4.3 Let
![]() $S = \{v_1, \dots , v_n \}$
be a tight frame and
$S = \{v_1, \dots , v_n \}$
be a tight frame and
![]() $S'$
be a frame obtained from S by substitution
$S'$
be a frame obtained from S by substitution
![]() $v_i \to v_i + t x,$
where
$v_i \to v_i + t x,$
where
![]() $t \in \mathbb {R}, x \in \mathbb {R}^k.$
Then,
$t \in \mathbb {R}, x \in \mathbb {R}^k.$
Then,
 $$ \begin{align*} \sqrt{\det A_{S'}} = 1 + t \left\langle v_i,x\right\rangle + o(t). \end{align*} $$
$$ \begin{align*} \sqrt{\det A_{S'}} = 1 + t \left\langle v_i,x\right\rangle + o(t). \end{align*} $$
That is,
![]() $\sqrt {\det A_{S'}}$
is a differentiable function of t at
$\sqrt {\det A_{S'}}$
is a differentiable function of t at
![]() $t =0,$
and the derivative equals
$t =0,$
and the derivative equals
![]() $\left \langle v_i,x\right \rangle .$
$\left \langle v_i,x\right \rangle .$
Proof Given a substitution
![]() $v_i \to v_i + t x,$
we modify the minor
$v_i \to v_i + t x,$
we modify the minor
![]() $P_I^S$
iff
$P_I^S$
iff
![]() $i \in I.$
By the properties of minors of
$i \in I.$
By the properties of minors of
![]() $P^S$
and definition of the Hodge star operator, we have that
$P^S$
and definition of the Hodge star operator, we have that
 $P_I^S = (\left \langle v_i,\star (v_{I\backslash i})\right \rangle )^2$
if
$P_I^S = (\left \langle v_i,\star (v_{I\backslash i})\right \rangle )^2$
if
![]() $i \in I.$
After the substitution, we get
$i \in I.$
After the substitution, we get
 $$ \begin{align*} \left(\left\langle v_i + t x, \star (v_{I\backslash i})\right\rangle\right)^2 = \left(\left\langle v_i, \star (v_{I\backslash i})\right\rangle\right)^2 + 2 t \left\langle v_i,\star (v_{I\backslash i})\right\rangle \left\langle \star (v_{I\backslash i}), x\right\rangle + o(t). \end{align*} $$
$$ \begin{align*} \left(\left\langle v_i + t x, \star (v_{I\backslash i})\right\rangle\right)^2 = \left(\left\langle v_i, \star (v_{I\backslash i})\right\rangle\right)^2 + 2 t \left\langle v_i,\star (v_{I\backslash i})\right\rangle \left\langle \star (v_{I\backslash i}), x\right\rangle + o(t). \end{align*} $$
Hence,
 $$ \begin{align*} \det A_{S'} = \sum\limits_{I \in {\binom{[n] \backslash i}{k}}} P_I^S + \sum\limits_{I \in \binom{[n]}{k}, i \in I} P_I^S + 2 t \sum\limits_{I \in \binom{[n]}{k}, i \in I } \left\langle v_i,\star (v_{I\backslash i})\right\rangle \left\langle\star (v_{I\backslash i}),x\right\rangle + o(t). \end{align*} $$
$$ \begin{align*} \det A_{S'} = \sum\limits_{I \in {\binom{[n] \backslash i}{k}}} P_I^S + \sum\limits_{I \in \binom{[n]}{k}, i \in I} P_I^S + 2 t \sum\limits_{I \in \binom{[n]}{k}, i \in I } \left\langle v_i,\star (v_{I\backslash i})\right\rangle \left\langle\star (v_{I\backslash i}),x\right\rangle + o(t). \end{align*} $$
If
![]() $i \in J$
for
$i \in J$
for
 $J \in \binom {[n]}{k-1},$
then we have
$J \in \binom {[n]}{k-1},$
then we have
![]() $ \left \langle v_i,\star (v_{J})\right \rangle = 0.$
Therefore, we can rewrite the last identity
$ \left \langle v_i,\star (v_{J})\right \rangle = 0.$
Therefore, we can rewrite the last identity
 $$ \begin{align*} \det A_{S'} &= \sum\limits_{I \in \binom{[n]}{ k}} P_I^S + 2t \sum\limits_{J \in \binom{[n]}{k-1}} \left\langle v_i,\star (v_{J})\right\rangle \left\langle\star (v_{J}), x\right\rangle + o(t). \end{align*} $$
$$ \begin{align*} \det A_{S'} &= \sum\limits_{I \in \binom{[n]}{ k}} P_I^S + 2t \sum\limits_{J \in \binom{[n]}{k-1}} \left\langle v_i,\star (v_{J})\right\rangle \left\langle\star (v_{J}), x\right\rangle + o(t). \end{align*} $$
By Theorem 1.1, we know that the vectors
 $(\star (v_J))_{J \in \binom {[n]}{k-1} }$
form a tight frame in
$(\star (v_J))_{J \in \binom {[n]}{k-1} }$
form a tight frame in
![]() $H_k.$
Therefore,
$H_k.$
Therefore,
 $$ \begin{align*} \sum\limits_{J \in \binom{[n]}{k-1}} \left\langle v_i,\star (v_{J})\right\rangle \left\langle\star (v_{J}),x\right\rangle = \left\langle v_i,x\right\rangle. \end{align*} $$
$$ \begin{align*} \sum\limits_{J \in \binom{[n]}{k-1}} \left\langle v_i,\star (v_{J})\right\rangle \left\langle\star (v_{J}),x\right\rangle = \left\langle v_i,x\right\rangle. \end{align*} $$
Using this and by (4.5), we obtain
 $$ \begin{align*} \sqrt{\det A_{S'}} = \sqrt{\det A_S + 2 t \left\langle v_i,x\right\rangle + o(t)} = 1 + t \left\langle v_i,x\right\rangle + o(t). \\[-35pt]\end{align*} $$
$$ \begin{align*} \sqrt{\det A_{S'}} = \sqrt{\det A_S + 2 t \left\langle v_i,x\right\rangle + o(t)} = 1 + t \left\langle v_i,x\right\rangle + o(t). \\[-35pt]\end{align*} $$
▪
Theorem 1.2 gives the first-order approximation of the left-hand side in inequality (4.4). It implies the first-order necessary condition for a differentiable O-invariant function
![]() $\Psi .$
$\Psi .$
Corollary 4.4 Let
![]() $\Psi $
be an O-invariant function,
$\Psi $
be an O-invariant function,
![]() $S = \{v_1, \dots , v_n\}$
be a local extremum of
$S = \{v_1, \dots , v_n\}$
be a local extremum of
![]() $\Psi $
on
$\Psi $
on
![]() $\Omega (n,k),$
and
$\Omega (n,k),$
and
![]() $\Psi $
is differentiable at
$\Psi $
is differentiable at
![]() $S.$
Then,
$S.$
Then,
 $$ \begin{align*} \Psi \!\left( \tilde{S}\right) = \Psi(S) \left(1 + \tau \sum\limits_{i = 1}^{n} \left\langle x_i,v_i\right\rangle \right) + o \left(\tau \right) \end{align*} $$
$$ \begin{align*} \Psi \!\left( \tilde{S}\right) = \Psi(S) \left(1 + \tau \sum\limits_{i = 1}^{n} \left\langle x_i,v_i\right\rangle \right) + o \left(\tau \right) \end{align*} $$
for an arbitrary
![]() $\tilde {S} = \{v_1 + \tau x_1, \dots , v_n + \tau x_n\}.$
$\tilde {S} = \{v_1 + \tau x_1, \dots , v_n + \tau x_n\}.$
By the dimension argument, Corollary 4.4 gives a complete system of the first-order necessary conditions. As a small enough perturbation of a frame is still a frame, we see that the set of frames looks like
![]() $\mathbb {R}^{nk}$
locally, and we can speak about local convexity of O-invariant functions. By a basic fact from subdifferential calculus, inequality (4.4) implies the differentiability of a locally convex function
$\mathbb {R}^{nk}$
locally, and we can speak about local convexity of O-invariant functions. By a basic fact from subdifferential calculus, inequality (4.4) implies the differentiability of a locally convex function
![]() $\Psi $
at its local maximum.
$\Psi $
at its local maximum.
Corollary 4.5 Let
![]() $\Psi $
be an O-invariant function,
$\Psi $
be an O-invariant function,
![]() $S = \{v_1, \dots , v_n\}$
be a local extremum of
$S = \{v_1, \dots , v_n\}$
be a local extremum of
![]() $\Psi $
on
$\Psi $
on
![]() $\Omega (n,k),$
and
$\Omega (n,k),$
and
![]() $\Psi $
is locally convex at
$\Psi $
is locally convex at
![]() $S.$
Then,
$S.$
Then,
![]() $\Psi $
is a differentiable function at
$\Psi $
is a differentiable function at
![]() $S,$
and it satisfies the identity of Corollary
4.4
.
$S,$
and it satisfies the identity of Corollary
4.4
.
Actually, the local convexity of
![]() $\Psi $
is a rather typical situation when we consider the volume of the projection of a polytope in
$\Psi $
is a rather typical situation when we consider the volume of the projection of a polytope in
![]() $\mathbb {R}^n$
onto a k-dimensional subspace, as the latter is piecewise linear on the corresponding Grassmannian by Theorem 1 in [Reference Filliman7]. Another example is the so-called linear parameter systems (see [Reference Rogers and Shephard15]).
$\mathbb {R}^n$
onto a k-dimensional subspace, as the latter is piecewise linear on the corresponding Grassmannian by Theorem 1 in [Reference Filliman7]. Another example is the so-called linear parameter systems (see [Reference Rogers and Shephard15]).
Here is another observation. One can notice that
 $\mathop {\mathrm {tr}} A_S = \sum \limits _1^n |v_i|^2$
for a tight frame
$\mathop {\mathrm {tr}} A_S = \sum \limits _1^n |v_i|^2$
for a tight frame
![]() $S = \{v_1, \dots , v_n\}.$
Hence,
$S = \{v_1, \dots , v_n\}.$
Hence,
![]() $\mathop {\mathrm {tr}} A_S = k$
for a tight frame
$\mathop {\mathrm {tr}} A_S = k$
for a tight frame
![]() $S.$
Let
$S.$
Let
![]() $\Omega ' (n,k)$
denote the class of frames
$\Omega ' (n,k)$
denote the class of frames
![]() $S = \{v_1, \dots , v_n \}$
such that
$S = \{v_1, \dots , v_n \}$
such that
 $ \sum \limits _1^n |v_i|^2 = k( = \mathop {\mathrm {tr}} A_S).$
The same arguments as in Lemma 4.2 imply the following corollary.
$ \sum \limits _1^n |v_i|^2 = k( = \mathop {\mathrm {tr}} A_S).$
The same arguments as in Lemma 4.2 imply the following corollary.
Corollary 4.6 Let
![]() $\Psi $
be an O-invariant function. Then,
$\Psi $
be an O-invariant function. Then,
 $$ \begin{align*} \max\limits_{S \in \Omega'(n,k)} \Psi (S) = \max\limits_{S \in \Omega(n,k)} \Psi(S). \end{align*} $$
$$ \begin{align*} \max\limits_{S \in \Omega'(n,k)} \Psi (S) = \max\limits_{S \in \Omega(n,k)} \Psi(S). \end{align*} $$
Proof Since
![]() $\Omega (n, k) \subset \Omega '(n,k),$
it is enough to show that for any
$\Omega (n, k) \subset \Omega '(n,k),$
it is enough to show that for any
![]() $S' \in \Omega '(n,k), S' \notin \Omega (n,k),$
there exists a tight frame S such that
$S' \in \Omega '(n,k), S' \notin \Omega (n,k),$
there exists a tight frame S such that
![]() $ \Psi (S') < \Psi (S).$
We put
$ \Psi (S') < \Psi (S).$
We put
![]() $S = B_{S'} S'.$
Then, by Lemma 4.2, it is enough to prove that
$S = B_{S'} S'.$
Then, by Lemma 4.2, it is enough to prove that
![]() $\det A_{S'} < 1.$
Considering
$\det A_{S'} < 1.$
Considering
![]() $A_{S'}$
in the basis of its eigenvectors (in which it is a diagonal operator) and using the inequality of arithmetic and geometric means, we obtain
$A_{S'}$
in the basis of its eigenvectors (in which it is a diagonal operator) and using the inequality of arithmetic and geometric means, we obtain
 $$ \begin{align*} \det A_{S'} \leq \left( \frac{\mathop{\mathrm{tr}} A_{S'}}{k}\right)^k = 1, \end{align*} $$
$$ \begin{align*} \det A_{S'} \leq \left( \frac{\mathop{\mathrm{tr}} A_{S'}}{k}\right)^k = 1, \end{align*} $$
where equality is attained iff all eigenvalues of
![]() $A_{S'}$
are ones. This means, the equality is attained iff
$A_{S'}$
are ones. This means, the equality is attained iff
![]() $S' \in \Omega (n,k).$
This completes the proof. ▪
$S' \in \Omega (n,k).$
This completes the proof. ▪
Remark 4.7 Corollary 4.6 was proved in [Reference Filliman5, Theorem 1] with the same idea but different notation for the projections of regular polytopes, particularly, for the mentioned functions
![]() $\Psi _1$
and
$\Psi _1$
and
![]() $\Psi _3.$
However, Corollary 4.6 gives a nice property of function
$\Psi _3.$
However, Corollary 4.6 gives a nice property of function
![]() $1/\Psi _2$
as well.
$1/\Psi _2$
as well.
4.4 Lifting of frames
Vectors
![]() $\{v_1, \dots , v_n\}$
of a tight frame
$\{v_1, \dots , v_n\}$
of a tight frame
![]() $S \in \Omega (n,k)$
have a nice isometric embedding in
$S \in \Omega (n,k)$
have a nice isometric embedding in
![]() $\wedge ^{k-1} (H^S).$
Fix
$\wedge ^{k-1} (H^S).$
Fix
![]() $i \in [n]$
and let
$i \in [n]$
and let
![]() $d_S(i)$
be the vector in
$d_S(i)$
be the vector in
![]() $\Lambda ^{k-1} (\mathbb {R}^n)$
such that its Lth coordinate in the standard basis of
$\Lambda ^{k-1} (\mathbb {R}^n)$
such that its Lth coordinate in the standard basis of
![]() $\Lambda ^{k-1} (\mathbb {R}^n)$
is
$\Lambda ^{k-1} (\mathbb {R}^n)$
is
![]() $d_S(\{i, L\}).$
$d_S(\{i, L\}).$
Lemma 4.8 Let
![]() $S = \{v_1, \dots , v_n\}$
be an arbitrary tight frame. Then, the vectors
$S = \{v_1, \dots , v_n\}$
be an arbitrary tight frame. Then, the vectors
![]() $d_S(i), i \in [n],$
belong to
$d_S(i), i \in [n],$
belong to
![]() $\wedge ^{k-1} (H^S) \subset \Lambda ^{k-1} (\mathbb {R}^n).$
Moreover, they form a tight frame in
$\wedge ^{k-1} (H^S) \subset \Lambda ^{k-1} (\mathbb {R}^n).$
Moreover, they form a tight frame in
![]() $\wedge ^{k-1} (H^S),$
and the following identity holds:
$\wedge ^{k-1} (H^S),$
and the following identity holds:
 $$ \begin{align} \left\langle d_S (i), d_S (j)\right\rangle = \left\langle v_i, v_j\right\rangle \end{align} $$
$$ \begin{align} \left\langle d_S (i), d_S (j)\right\rangle = \left\langle v_i, v_j\right\rangle \end{align} $$
for all
![]() $i,j \in [n].$
$i,j \in [n].$
Proof Let
![]() $a_j, j \in [k],$
be the rows of the
$a_j, j \in [k],$
be the rows of the
![]() $k \times n$
matrix
$k \times n$
matrix
![]() $M^S = (v_1, \dots , v_n ).$
By the definition of
$M^S = (v_1, \dots , v_n ).$
By the definition of
![]() $H^S,$
we know that
$H^S,$
we know that
 $a_j \in H_k^{S}, j \in [k],$
and that they form an orthonormal system in
$a_j \in H_k^{S}, j \in [k],$
and that they form an orthonormal system in
![]() $H^{S}.$
Hence, the
$H^{S}.$
Hence, the
![]() $(k-1)$
-forms
$(k-1)$
-forms
 $(a_{[k] \backslash j})_{j=1}^k$
are an orthonormal basis of
$(a_{[k] \backslash j})_{j=1}^k$
are an orthonormal basis of
![]() $\wedge ^{k-1} (H^S).$
Consider the
$\wedge ^{k-1} (H^S).$
Consider the
![]() $(k-1)$
-forms
$(k-1)$
-forms
 $b_i = \sum \limits _{j=1}^k (-1)^{j +1} v_i[j] \cdot a_{[k] \backslash j},$
where
$b_i = \sum \limits _{j=1}^k (-1)^{j +1} v_i[j] \cdot a_{[k] \backslash j},$
where
![]() $i \in [n].$
Then, by the definition of the inner product in
$i \in [n].$
Then, by the definition of the inner product in
![]() $\Lambda ^{k-1} (\mathbb {R}^n)$
and the Laplace expansion of the determinant, we have
$\Lambda ^{k-1} (\mathbb {R}^n)$
and the Laplace expansion of the determinant, we have
 $$ \begin{align*} b_i[L] &= \left\langle b_i,e_L\right\rangle = \sum\limits_{j=1}^k (-1)^{j+1} v_i[j] \left\langle a_{[k] \backslash j}, \right\rangle{e_L} \\ &= \sum\limits_{j=1}^k (-1)^{j+1} v_i[j] M^S_{[k] \backslash j, L} = M^S_{\{i,L\}, \{i, L\}} = d_S(i)[L] \end{align*} $$
$$ \begin{align*} b_i[L] &= \left\langle b_i,e_L\right\rangle = \sum\limits_{j=1}^k (-1)^{j+1} v_i[j] \left\langle a_{[k] \backslash j}, \right\rangle{e_L} \\ &= \sum\limits_{j=1}^k (-1)^{j+1} v_i[j] M^S_{[k] \backslash j, L} = M^S_{\{i,L\}, \{i, L\}} = d_S(i)[L] \end{align*} $$
for
 $L \in \binom {[n]}{k-1}, i \notin L.$
We get
$L \in \binom {[n]}{k-1}, i \notin L.$
We get
![]() $b_i[L] = d_{S}(i)[L] = 0$
if
$b_i[L] = d_{S}(i)[L] = 0$
if
![]() $i \in L.$
Thus,
$i \in L.$
Thus,
![]() $d_S(i) = b_i \in \Lambda ^{k-1} (H^{S})$
and, clearly, identity (4.6) holds. ▪
$d_S(i) = b_i \in \Lambda ^{k-1} (H^{S})$
and, clearly, identity (4.6) holds. ▪
Lemma 3.1 allows us to describe all substitutions
![]() $w_i \to w^{\prime }_i, i \in [n],$
which preserve the operator
$w_i \to w^{\prime }_i, i \in [n],$
which preserve the operator
![]() $A_S$
for a frame
$A_S$
for a frame
![]() $S = \{w_1, \dots , w_n\}.$
But we need a more suitable geometric description. So, let
$S = \{w_1, \dots , w_n\}.$
But we need a more suitable geometric description. So, let
![]() $S = \{w_1, \dots , w_n\}$
be a frame and
$S = \{w_1, \dots , w_n\}$
be a frame and
 $\ell \in [k], L = \{i_1, \dots , i_{\ell }\}\subset \binom {[n]}{\ell }.$
Consider a substitution
$\ell \in [k], L = \{i_1, \dots , i_{\ell }\}\subset \binom {[n]}{\ell }.$
Consider a substitution
![]() $w_i \to w^{\prime }_i,$
for
$w_i \to w^{\prime }_i,$
for
![]() $i \in L,$
and
$i \in L,$
and
![]() $w^{\prime }_i = w_i,$
for
$w^{\prime }_i = w_i,$
for
![]() $i \notin L,$
which preserves
$i \notin L,$
which preserves
![]() $A_S,$
and denote by
$A_S,$
and denote by
![]() $S' = \{w^{\prime }_1,\dots , w^{\prime }_n\}$
the new frame.
$S' = \{w^{\prime }_1,\dots , w^{\prime }_n\}$
the new frame.
In this notation, we get the following.
Lemma 4.9 The substitution preserves
![]() $A_S$
(i.e.,
$A_S$
(i.e.,
![]() $A_S = A_{S'}$
) iff there exists an orthogonal matrix U of rank
$A_S = A_{S'}$
) iff there exists an orthogonal matrix U of rank
![]() $\ell $
such that
$\ell $
such that
 $$ \begin{align} \begin{pmatrix} w^{\prime}_{i_1}, & \dots, & w^{\prime}_{i_{\ell}} \end{pmatrix} = \begin{pmatrix} w_{i_1}, & \dots , & w_{i_{\ell}} \end{pmatrix} U. \end{align} $$
$$ \begin{align} \begin{pmatrix} w^{\prime}_{i_1}, & \dots, & w^{\prime}_{i_{\ell}} \end{pmatrix} = \begin{pmatrix} w_{i_1}, & \dots , & w_{i_{\ell}} \end{pmatrix} U. \end{align} $$
Additionally, in case S is a tight frame, let
![]() $\{f_1, \dots , f_n\}$
be any orthonormal basis of
$\{f_1, \dots , f_n\}$
be any orthonormal basis of
![]() $\mathbb {R}^n$
given by the assertion (3.1) of Lemma
3.1
. Then, the substitution preserves
$\mathbb {R}^n$
given by the assertion (3.1) of Lemma
3.1
. Then, the substitution preserves
![]() $A_S$
iff the vectors of
$A_S$
iff the vectors of
![]() $S'$
are the projection of an orthonormal basis
$S'$
are the projection of an orthonormal basis
![]() $\{f^{\prime }_1, \dots , f^{\prime }_n\}$
of
$\{f^{\prime }_1, \dots , f^{\prime }_n\}$
of
![]() $\mathbb {R}^n,$
which is obtained from
$\mathbb {R}^n,$
which is obtained from
![]() $\{f_1, \dots , f_n\}$
by an orthogonal transformation of
$\{f_1, \dots , f_n\}$
by an orthogonal transformation of
![]() $\{f_i\}_{i \in I}$
in their linear hull.
$\{f_i\}_{i \in I}$
in their linear hull.
Proof The identity
![]() $A_{S'} = A_S$
holds if and only if
$A_{S'} = A_S$
holds if and only if
 $$ \begin{align*} \sum_{i \in I} w_i \otimes w_i = \sum_{i \in I} w^{\prime}_i \otimes w^{\prime}_i. \end{align*} $$
$$ \begin{align*} \sum_{i \in I} w_i \otimes w_i = \sum_{i \in I} w^{\prime}_i \otimes w^{\prime}_i. \end{align*} $$
Writing this in a matrix form, we get another equivalent statement that the Gram matrices of the rows of the matrices
 $\begin {pmatrix} w^{\prime }_{i_1}, & \dots , & w^{\prime }_{i_{\ell }} \end {pmatrix} $
and
$\begin {pmatrix} w^{\prime }_{i_1}, & \dots , & w^{\prime }_{i_{\ell }} \end {pmatrix} $
and
 $ \begin {pmatrix} w_{i_1}, & \dots , & w_{i_{\ell }} \end {pmatrix}$
are the same. The latter is equivalent to the existence of an isometry of
$ \begin {pmatrix} w_{i_1}, & \dots , & w_{i_{\ell }} \end {pmatrix}$
are the same. The latter is equivalent to the existence of an isometry of
![]() $\mathbb {R}^{\ell }$
, which maps the rows of the first matrix to the rows of the second. This isometry defines an orthogonal matrix
$\mathbb {R}^{\ell }$
, which maps the rows of the first matrix to the rows of the second. This isometry defines an orthogonal matrix
![]() $U,$
which satisfies the assumptions of the lemma.
$U,$
which satisfies the assumptions of the lemma.
In case of a tight frame, extending U as the orthogonal transformation of
![]() $\mathop {\mathrm {Lin}} \{f_i \; : \; {i \in I}\},$
we obtain the suitable
$\mathop {\mathrm {Lin}} \{f_i \; : \; {i \in I}\},$
we obtain the suitable
![]() $\{f^{\prime }_1, \dots , f^{\prime }_n\}.$
▪
$\{f^{\prime }_1, \dots , f^{\prime }_n\}.$
▪
Also, we can reformulate the second claim of Lemma 4.9 in the following equivalent way: given a block matrix
 $M = \begin {pmatrix} A & B \\ C & D \end {pmatrix}$
such that the rows of
$M = \begin {pmatrix} A & B \\ C & D \end {pmatrix}$
such that the rows of
 $\begin {pmatrix} A & B \end {pmatrix}$
are orthonormal and the columns of
$\begin {pmatrix} A & B \end {pmatrix}$
are orthonormal and the columns of
 $\begin {pmatrix} A \\ C \end {pmatrix}$
are orthonormal, then D can be chosen in such a way that M will be an orthogonal matrix.
$\begin {pmatrix} A \\ C \end {pmatrix}$
are orthonormal, then D can be chosen in such a way that M will be an orthogonal matrix.
5 Zonotopes and their volume
5.1 Definitions and history
A zonotope is the Minkowski sum of several segments in
![]() $\mathbb {R}^k$
. Every zonotope can be represented (up to an affine transformation) as a projection of a higher-dimensional cube
$\mathbb {R}^k$
. Every zonotope can be represented (up to an affine transformation) as a projection of a higher-dimensional cube
![]() $\operatorname {C}^n = [0,1]^n.$
For example, it follows from the definition of
$\operatorname {C}^n = [0,1]^n.$
For example, it follows from the definition of
![]() $B_S.$
To get more information about zonotopes, we refer the reader to Zong’s book [Reference Zong20, Chapter 2] and to [Reference Schneider and Weil16].
$B_S.$
To get more information about zonotopes, we refer the reader to Zong’s book [Reference Zong20, Chapter 2] and to [Reference Schneider and Weil16].
Several different bounds for the maximum in (1.2) are known. For example, G. D. Chakerian and P. Filliman [Reference Chakerian and Filliman4] prove
 $$ \begin{align*} \operatorname{vol}_{k} (\operatorname{C}^n | H) \leq \sqrt{\frac{n!}{(n-k)! k!}} \quad \text{and} \quad \operatorname{vol}_{k} (\operatorname{C}^n | H) \leq \frac{\omega_{k-1}^k}{\omega_{k}^{k-1}} \left(\frac{n}{k} \right)^{k/2}, \end{align*} $$
$$ \begin{align*} \operatorname{vol}_{k} (\operatorname{C}^n | H) \leq \sqrt{\frac{n!}{(n-k)! k!}} \quad \text{and} \quad \operatorname{vol}_{k} (\operatorname{C}^n | H) \leq \frac{\omega_{k-1}^k}{\omega_{k}^{k-1}} \left(\frac{n}{k} \right)^{k/2}, \end{align*} $$
where
![]() $w_i$
is the volume of the i-dimensional Euclidean unit ball. The right-hand side inequality is asymptotically tight, as was shown in [Reference Filliman5], and the left-hand side inequality is tight in the cases
$w_i$
is the volume of the i-dimensional Euclidean unit ball. The right-hand side inequality is asymptotically tight, as was shown in [Reference Filliman5], and the left-hand side inequality is tight in the cases
![]() $k =1,n-1.$
The tight upper and lower bounds in the limit case for the volume of a zonotope in a specific position (even for so-called
$k =1,n-1.$
The tight upper and lower bounds in the limit case for the volume of a zonotope in a specific position (even for so-called
![]() $L_p$
-zonoids) were obtained in [Reference Lutwak, Yang and Zhang12, Theorem 2].
$L_p$
-zonoids) were obtained in [Reference Lutwak, Yang and Zhang12, Theorem 2].
Among different upper bounds, all maximizers of (1.2) were described in the cases
![]() $k =1,2,n-2,n-1$
and
$k =1,2,n-2,n-1$
and
![]() $k=3, n=6$
in [Reference Filliman5]. It appears that projections of the standard basis vectors onto
$k=3, n=6$
in [Reference Filliman5]. It appears that projections of the standard basis vectors onto
![]() $H_k$
have the same length whenever H is a maximizer of (1.2) for all cases mentioned above, which gives a rather reasonable conjecture.
$H_k$
have the same length whenever H is a maximizer of (1.2) for all cases mentioned above, which gives a rather reasonable conjecture.
Conjecture 5.1 Let the maximum volume projection of
![]() $\operatorname {C}^n = [0,1]^n$
onto a k-dimensional subspace be attained on
$\operatorname {C}^n = [0,1]^n$
onto a k-dimensional subspace be attained on
![]() $H.$
Then, the projections of the vectors of the standard basis onto H have the same length.
$H.$
Then, the projections of the vectors of the standard basis onto H have the same length.
We note that there are k-dimensional subspaces of
![]() $\mathbb {R}^n$
such that the projections of the vectors of the standard basis onto them have the same length. An explicit construction of such subspaces can be found in [Reference Zimmermann19]. In [Reference Ivanov10, Lemma 2.4], the author describes all possible lengths of the projections of the vectors of the standard basis.
$\mathbb {R}^n$
such that the projections of the vectors of the standard basis onto them have the same length. An explicit construction of such subspaces can be found in [Reference Zimmermann19]. In [Reference Ivanov10, Lemma 2.4], the author describes all possible lengths of the projections of the vectors of the standard basis.
Summarizing the observations of Section 4, we have that the problem to find and to study maximizers of
 $$ \begin{align} F_2(S) = \operatorname{vol}_{k} \left(\sum\limits_1^n [0, v_i]\right), \qquad \text{where} \qquad \{v_1, \dots, v_n\} \in \Omega(n,k), \end{align} $$
$$ \begin{align} F_2(S) = \operatorname{vol}_{k} \left(\sum\limits_1^n [0, v_i]\right), \qquad \text{where} \qquad \{v_1, \dots, v_n\} \in \Omega(n,k), \end{align} $$
is equivalent to that of (1.2). We illustrate the developed technique and write the first-order necessary condition of local maximum for (5.1) together with some geometric consequences.
5.2 The first-order necessary condition
We start with showing that
![]() $F_2(S)$
is a differentiable function at its local maximum.
$F_2(S)$
is a differentiable function at its local maximum.
Lemma 5.2 Let
![]() $S = \{v_1, \dots , v_n\}$
be a local maximizer of (5.1) and
$S = \{v_1, \dots , v_n\}$
be a local maximizer of (5.1) and
![]() $S'$
be a frame obtained from S by substitution
$S'$
be a frame obtained from S by substitution
![]() $v_i \to v_i + t x,$
where
$v_i \to v_i + t x,$
where
![]() $t \in \mathbb {R}, x \in \mathbb {R}^k.$
Then,
$t \in \mathbb {R}, x \in \mathbb {R}^k.$
Then,
 $\frac {F_2(S')}{F_2(S)}$
is a differentiable function of t at
$\frac {F_2(S')}{F_2(S)}$
is a differentiable function of t at
![]() $t =0$
, and the derivative equals
$t =0$
, and the derivative equals
![]() $\left \langle v_i, x\right \rangle .$
$\left \langle v_i, x\right \rangle .$
Proof Given a substitution
![]() $v_i \to v_i + t x,$
we change
$v_i \to v_i + t x,$
we change
![]() $d_S(\{L\})$
for
$d_S(\{L\})$
for
 $L \in \binom {[n]}{k}$
in (3.3) iff
$L \in \binom {[n]}{k}$
in (3.3) iff
![]() $i \in L.$
Since the determinant is a linear function of each vector, this means that
$i \in L.$
Since the determinant is a linear function of each vector, this means that
![]() $|d_{S'} (\{L\})|$
as function of t (even as function of
$|d_{S'} (\{L\})|$
as function of t (even as function of
![]() $x' = tx$
) is a convex function of t (or even of
$x' = tx$
) is a convex function of t (or even of
![]() $x' = tx \in \mathbb {R}^k$
). Therefore,
$x' = tx \in \mathbb {R}^k$
). Therefore,
![]() ${ F_2(S')}/{F_2(S)}$
as function of t (or
${ F_2(S')}/{F_2(S)}$
as function of t (or
![]() $x' = tx$
) is a convex function. The result follows from Corollary 4.5. ▪
$x' = tx$
) is a convex function. The result follows from Corollary 4.5. ▪
Corollary 5.3 Let
![]() $S = \{v_1, \dots , v_n\}$
be a local maximizer of (5.1). Then, the vectors of S are in general position in
$S = \{v_1, \dots , v_n\}$
be a local maximizer of (5.1). Then, the vectors of S are in general position in
![]() $\mathbb {R}^k,$
i.e.,
$\mathbb {R}^k,$
i.e.,
![]() $d_S (\{L\}) \neq 0$
for each
$d_S (\{L\}) \neq 0$
for each
 $L \in \binom {[n]}{{k}}.$
$L \in \binom {[n]}{{k}}.$
Proof Assume the contrary that there is a k-tuple J such that
![]() $d_S(\{J\}) = 0.$
As the rank of the vectors of S is
$d_S(\{J\}) = 0.$
As the rank of the vectors of S is
![]() $k,$
this implies that there is an
$k,$
this implies that there is an
 $L = \{i_1, \dots , i_k\} \in \binom {[n]}{k}$
such that the vectors
$L = \{i_1, \dots , i_k\} \in \binom {[n]}{k}$
such that the vectors
![]() $\{v_{i_1}, \dots , v_{i_{k-1}}\}$
are linearly independent and the vectors
$\{v_{i_1}, \dots , v_{i_{k-1}}\}$
are linearly independent and the vectors
![]() $\{v_{i_1}, \dots , v_{i_{k-1}}, v_{i_k}\}$
are linearly dependent (i.e.,
$\{v_{i_1}, \dots , v_{i_{k-1}}, v_{i_k}\}$
are linearly dependent (i.e.,
![]() $d_S(\{L\}) = 0$
). Taking
$d_S(\{L\}) = 0$
). Taking
![]() $x \neq 0$
in the orthogonal complement of
$x \neq 0$
in the orthogonal complement of
![]() $\mathop {\mathrm {Lin}} \{v_{i_1}, \dots , v_{i_{k-1}}\}$
and obtaining
$\mathop {\mathrm {Lin}} \{v_{i_1}, \dots , v_{i_{k-1}}\}$
and obtaining
![]() $S'$
by a substitution
$S'$
by a substitution
![]() $v_{i_k} \to v_{i_k} +t x,$
we get that
$v_{i_k} \to v_{i_k} +t x,$
we get that
![]() ${ F_2(S')}/{F_2(S)}$
as well as the absolute value of
${ F_2(S')}/{F_2(S)}$
as well as the absolute value of
![]() $d_{S'} (\{L\})$
is not differentiable at
$d_{S'} (\{L\})$
is not differentiable at
![]() $t =0.$
This contradicts Lemma 5.2. ▪
$t =0.$
This contradicts Lemma 5.2. ▪
Lemma 5.4 The function
![]() $F_2(\cdot )$
is differentiable at a local maximizer of (5.1).
$F_2(\cdot )$
is differentiable at a local maximizer of (5.1).
Proof Let
![]() $S = \{v_1, \dots , v_n\}$
be a local maximizer of (5.1) and
$S = \{v_1, \dots , v_n\}$
be a local maximizer of (5.1) and
![]() $S'$
be a frame obtained from S by substitution
$S'$
be a frame obtained from S by substitution
![]() $v_i \to v_i + t_i x_i, i \in [n].$
$v_i \to v_i + t_i x_i, i \in [n].$
The function
![]() $|d_{S'}(\{L\})|$
as a function of
$|d_{S'}(\{L\})|$
as a function of
![]() $(t_1, \dots , t_n)$
is the absolute value of a polynomial of
$(t_1, \dots , t_n)$
is the absolute value of a polynomial of
![]() $(t_1, \dots , t_n).$
Hence, it is differentiable at a point
$(t_1, \dots , t_n).$
Hence, it is differentiable at a point
![]() $(t_1, \dots , t_n)$
whenever
$(t_1, \dots , t_n)$
whenever
![]() $d_{S'}(\{L\}) \neq 0.$
By Corollary 5.3, we have
$d_{S'}(\{L\}) \neq 0.$
By Corollary 5.3, we have
![]() $d_S(\{L\}) \neq 0$
for all k-tuples. Therefore, the function
$d_S(\{L\}) \neq 0$
for all k-tuples. Therefore, the function
 $$ \begin{align*} {F_2(S')} = {\sum\limits_{L \in \binom{[n]}{k}}|d_{S'}(\{L\})| } \end{align*} $$
$$ \begin{align*} {F_2(S')} = {\sum\limits_{L \in \binom{[n]}{k}}|d_{S'}(\{L\})| } \end{align*} $$
as a function of
![]() $(t_1, \dots , t_n)$
is differentiable at the origin. ▪
$(t_1, \dots , t_n)$
is differentiable at the origin. ▪
Now, we show the geometric meaning of identities of Corollary 4.4 for the function
![]() $F_2.$
We define a sign function
$F_2.$
We define a sign function
![]() $\sigma _S(i, L)$
by
$\sigma _S(i, L)$
by
 $$ \begin{align*} \sigma_S(i, L) = \begin{cases} 1/{F_2(S)} , \qquad \text{if} \qquad d(\{i, L\})>0; \\ -1/{F_2(S)} , \qquad \text{if} \qquad d(\{i, L\}) <0; \\ 0, \qquad \text{if} \qquad d(\{i, L\}) = 0, \end{cases} \end{align*} $$
$$ \begin{align*} \sigma_S(i, L) = \begin{cases} 1/{F_2(S)} , \qquad \text{if} \qquad d(\{i, L\})>0; \\ -1/{F_2(S)} , \qquad \text{if} \qquad d(\{i, L\}) <0; \\ 0, \qquad \text{if} \qquad d(\{i, L\}) = 0, \end{cases} \end{align*} $$
for a frame
![]() $S, i \in [n]$
and
$S, i \in [n]$
and
 $L \in \binom {[n]}{k-1}.$
$L \in \binom {[n]}{k-1}.$
In the same way as with the vectors
![]() $d_S(i), i \in [n],$
we identify
$d_S(i), i \in [n],$
we identify
![]() $\sigma _S (i)$
with a vector in
$\sigma _S (i)$
with a vector in
![]() $\Lambda ^{k-1} (\mathbb {R}^n)$
such that its Lth coordinate in the standard basis of
$\Lambda ^{k-1} (\mathbb {R}^n)$
such that its Lth coordinate in the standard basis of
![]() $\Lambda ^{k-1} (\mathbb {R}^n)$
is
$\Lambda ^{k-1} (\mathbb {R}^n)$
is
![]() $\sigma _S({i, L}).$
As a direct consequence of Lemma 5.4, we obtain the following lemma.
$\sigma _S({i, L}).$
As a direct consequence of Lemma 5.4, we obtain the following lemma.
Lemma 5.5 Let
![]() $S = \{v_1, \dots , v_n\}$
be a local maximizer of (5.1). Then,
$S = \{v_1, \dots , v_n\}$
be a local maximizer of (5.1). Then,
 $$ \begin{align} \wedge^{k-1} P^S (\sigma_S (i)) = d_S (i) \qquad \text{and} \qquad \left\langle\sigma_S (i), d_S (j)\right\rangle = \left\langle v_i, v_j\right\rangle, \;\;\; i,j \in [n]. \end{align} $$
$$ \begin{align} \wedge^{k-1} P^S (\sigma_S (i)) = d_S (i) \qquad \text{and} \qquad \left\langle\sigma_S (i), d_S (j)\right\rangle = \left\langle v_i, v_j\right\rangle, \;\;\; i,j \in [n]. \end{align} $$
Proof By Lemma 4.8, we have that the vectors
![]() $(d_S(i))_{i=1}^{n}$
form a tight frame in
$(d_S(i))_{i=1}^{n}$
form a tight frame in
 $\wedge ^{k-1} H_k^S.$
Therefore, by Theorem 3.3, it is enough to show that the rightmost identity in (5.2) is true.
$\wedge ^{k-1} H_k^S.$
Therefore, by Theorem 3.3, it is enough to show that the rightmost identity in (5.2) is true.
Fix
![]() $i, j \in [n].$
Let
$i, j \in [n].$
Let
![]() $S'$
be a frame obtained from S by the substitution
$S'$
be a frame obtained from S by the substitution
![]() $v_i \to v_i + t v_j.$
By Corollary 5.3, we have that
$v_i \to v_i + t v_j.$
By Corollary 5.3, we have that
![]() $d_S(\{L\}) \neq 0$
for every k-tuple
$d_S(\{L\}) \neq 0$
for every k-tuple
![]() $L.$
Therefore,
$L.$
Therefore,
![]() $d_{S'}(\{L\}) \neq 0$
and
$d_{S'}(\{L\}) \neq 0$
and
![]() $d_{S'}(\{L\})$
has the same sign as
$d_{S'}(\{L\})$
has the same sign as
![]() $d_S(\{L\})$
for all k-tuples L and for a small enough
$d_S(\{L\})$
for all k-tuples L and for a small enough
![]() $t.$
Using the substitution
$t.$
Using the substitution
![]() $v_i \to v_i + t v_j,$
we only change the determinants of type
$v_i \to v_i + t v_j,$
we only change the determinants of type
![]() $d_S(\{i, J\}),$
where
$d_S(\{i, J\}),$
where
 $i \notin J \subset \binom {[n]}{{k-1}}.$
Thus, by the properties of absolute value (for a small enough t), we get
$i \notin J \subset \binom {[n]}{{k-1}}.$
Thus, by the properties of absolute value (for a small enough t), we get
 $$ \begin{align*} \frac{F_2(S')}{F_2(S)} = \frac{1}{F_2(S)}{\sum\limits_{L \in \binom{[n]}{k}}|d_{S'}(\{L\})| } = 1 + t \sum\limits_{J \in \binom{[n]}{k-1} , i \notin J} \sigma_S(i, J) d_S(\{j, J\}). \end{align*} $$
$$ \begin{align*} \frac{F_2(S')}{F_2(S)} = \frac{1}{F_2(S)}{\sum\limits_{L \in \binom{[n]}{k}}|d_{S'}(\{L\})| } = 1 + t \sum\limits_{J \in \binom{[n]}{k-1} , i \notin J} \sigma_S(i, J) d_S(\{j, J\}). \end{align*} $$
Since
![]() $\sigma _S(i, J) = 0$
whenever
$\sigma _S(i, J) = 0$
whenever
![]() $i \in J,$
we have that the coefficient at t in the previous formula is
$i \in J,$
we have that the coefficient at t in the previous formula is
 $$ \begin{align*} \sum\limits_{J \in \binom{[n]}{k-1}} \sigma_S(i, J) d_S(\{j, J\}). \end{align*} $$
$$ \begin{align*} \sum\limits_{J \in \binom{[n]}{k-1}} \sigma_S(i, J) d_S(\{j, J\}). \end{align*} $$
But this is the inner product
![]() $\left \langle \sigma _S (i), d_S(j)\right \rangle $
of the
$\left \langle \sigma _S (i), d_S(j)\right \rangle $
of the
![]() $(k-1)$
-forms
$(k-1)$
-forms
![]() $\sigma _S(i)$
and
$\sigma _S(i)$
and
![]() $d_S(j)$
written in the standard basis of
$d_S(j)$
written in the standard basis of
![]() $\Lambda ^{k-1} (\mathbb {R}^n).$
By Lemma 5.4 and Corollary 4.4, we have that
$\Lambda ^{k-1} (\mathbb {R}^n).$
By Lemma 5.4 and Corollary 4.4, we have that
 $ \left \langle \sigma _S (i),d_S (j)\right \rangle = \left \langle v_i, v_j\right \rangle .$
▪
$ \left \langle \sigma _S (i),d_S (j)\right \rangle = \left \langle v_i, v_j\right \rangle .$
▪
5.3 Proofs of Corollary 1.3, Theorem 1.4, and Corollary 1.5
Corollary 1.3 is a direct consequence of Lemma 5.5 with a simple geometric meaning.
Proof of Corollary 1.3
By Corollary 5.3,
![]() $|v_i| \neq 0$
for all
$|v_i| \neq 0$
for all
![]() $i \in [n].$
Let
$i \in [n].$
Let
![]() $S' = \{v^{\prime }_1, \dots , v^{\prime }_n\}$
be projections of the vectors
$S' = \{v^{\prime }_1, \dots , v^{\prime }_n\}$
be projections of the vectors
![]() $\{v_1, \dots , v_n\}$
onto
$\{v_1, \dots , v_n\}$
onto
![]() $v_i^\perp .$
Clearly,
$v_i^\perp .$
Clearly,
![]() $v^{\prime }_i = 0.$
By Shepard’s formula (3.3) and the properties of the determinant, we have
$v^{\prime }_i = 0.$
By Shepard’s formula (3.3) and the properties of the determinant, we have
 $$ \begin{align*} \operatorname{vol}_{k-1} \left(Q | v_i^\perp \right) = \sum\limits_{J \in \binom{[n]}{{k-1}}} \left| d_{S'}(\{J\}) \right| = \frac{1}{|v_i|} \sum\limits_{J \in \binom{[n]}{{k-1}}} \left| d_{S}(\{i,J\}) \right|. \end{align*} $$
$$ \begin{align*} \operatorname{vol}_{k-1} \left(Q | v_i^\perp \right) = \sum\limits_{J \in \binom{[n]}{{k-1}}} \left| d_{S'}(\{J\}) \right| = \frac{1}{|v_i|} \sum\limits_{J \in \binom{[n]}{{k-1}}} \left| d_{S}(\{i,J\}) \right|. \end{align*} $$
By Lemma 5.5, the latter is
![]() $|v_i| \operatorname {vol}_{k} Q.$
▪
$|v_i| \operatorname {vol}_{k} Q.$
▪
The idea of the proof of Theorem 1.4 is the following. We use Lemma 4.9 to rotate vectors by
![]() $\pi /4$
(i.e.,
$\pi /4$
(i.e.,
![]() $v_i \to \cos (\pi /4) v_i - \sin (\pi /4) v_j, v_j \to \sin (\pi /4) v_i + \cos (\pi /4) v_j$
), and after some simple calculations along with Corollary 4.4, we get the inequality of Theorem 1.4.
$v_i \to \cos (\pi /4) v_i - \sin (\pi /4) v_j, v_j \to \sin (\pi /4) v_i + \cos (\pi /4) v_j$
), and after some simple calculations along with Corollary 4.4, we get the inequality of Theorem 1.4.
Proof of Theorem 1.4
We prove the theorem for a maximizer
![]() $S = \{ v_1, \dots , v_n\}$
of (5.1). Fix i and j in
$S = \{ v_1, \dots , v_n\}$
of (5.1). Fix i and j in
![]() $[n].$
We assume that
$[n].$
We assume that
![]() $|v_i|^2 < |v_j|^2,$
otherwise there is nothing to prove. Using Lemma 4.9, we have that the substitution
$|v_i|^2 < |v_j|^2,$
otherwise there is nothing to prove. Using Lemma 4.9, we have that the substitution
![]() $v_i \to \cos (\pi /4) v_i - \sin (\pi /4) v_j, v_j \to \sin (\pi /4) v_i + \cos (\pi /4) v_j$
preserves
$v_i \to \cos (\pi /4) v_i - \sin (\pi /4) v_j, v_j \to \sin (\pi /4) v_i + \cos (\pi /4) v_j$
preserves
![]() $A_S$
and the absolute value of
$A_S$
and the absolute value of
![]() $d_S(\{L\})$
for all
$d_S(\{L\})$
for all
 $L \subset \binom {[n]}{k}$
such that
$L \subset \binom {[n]}{k}$
such that
![]() $i,j \in L.$
Let
$i,j \in L.$
Let
![]() $S'$
be the tight frame obtained by this substitution. From the choice of
$S'$
be the tight frame obtained by this substitution. From the choice of
![]() $S,$
we have
$S,$
we have
![]() $F_2(S') \leq F_2(S).$
Expanding these volumes by formula (3.3) and reducing common determinants, we get
$F_2(S') \leq F_2(S).$
Expanding these volumes by formula (3.3) and reducing common determinants, we get
 $$ \begin{align*} \frac{\sqrt{2}}{2} \sum\limits_{J \in \binom{[n]}{{k-1}}, \; i,j \notin J} & \left( \left|d_{S}(\{i,J\}) - d_{S}(\{j,J\}) \right| + \left|d_{S}(\{i,J\}) + d_{S}(\{j,J\}) \right|\right) \\ &\quad \leq \sum\limits_{J \in \binom{[n]}{{k-1}},\; i,j \notin J} (\left|d_{S}(\{i,J\})\right| + \left| d_{S}(\{j,J\}) \right|). \end{align*} $$
$$ \begin{align*} \frac{\sqrt{2}}{2} \sum\limits_{J \in \binom{[n]}{{k-1}}, \; i,j \notin J} & \left( \left|d_{S}(\{i,J\}) - d_{S}(\{j,J\}) \right| + \left|d_{S}(\{i,J\}) + d_{S}(\{j,J\}) \right|\right) \\ &\quad \leq \sum\limits_{J \in \binom{[n]}{{k-1}},\; i,j \notin J} (\left|d_{S}(\{i,J\})\right| + \left| d_{S}(\{j,J\}) \right|). \end{align*} $$
By identity
![]() $|a + b| + |a-b| = 2 \max \{|a|, |b|\},$
we obtain that each summand in the left-hand side is at least
$|a + b| + |a-b| = 2 \max \{|a|, |b|\},$
we obtain that each summand in the left-hand side is at least
![]() $2 \max \{ \left |d_{S}(\{i,J\})\right | , \left | d_{S}(\{i,J\}) \right |\}$
and, consequently, is at least
$2 \max \{ \left |d_{S}(\{i,J\})\right | , \left | d_{S}(\{i,J\}) \right |\}$
and, consequently, is at least
![]() $2 \left |d_{S}(\{j,J\})\right |.$
Hence, we show that
$2 \left |d_{S}(\{j,J\})\right |.$
Hence, we show that
 $$ \begin{align*} (\sqrt{2} -1)\sum\limits_{J \in \binom{[n]}{k-1},\; i,j \notin J} \left| d_{S}(\{j,J\}) \right| \leq \sum\limits_{J \in \binom{[n]}{{k-1}},\; i,j \notin J} \left| d_{S}(\{i,J\}) \right|. \end{align*} $$
$$ \begin{align*} (\sqrt{2} -1)\sum\limits_{J \in \binom{[n]}{k-1},\; i,j \notin J} \left| d_{S}(\{j,J\}) \right| \leq \sum\limits_{J \in \binom{[n]}{{k-1}},\; i,j \notin J} \left| d_{S}(\{i,J\}) \right|. \end{align*} $$
Consider the one-to-one correspondence between the set of all
![]() $(k-1)$
-tuples L with
$(k-1)$
-tuples L with
![]() $i \in L$
and
$i \in L$
and
![]() $j \notin L$
and the set of all
$j \notin L$
and the set of all
![]() $(k-1)$
-tuples J with
$(k-1)$
-tuples J with
![]() $i \notin J$
and
$i \notin J$
and
![]() $j \in J$
given by
$j \in J$
given by
![]() $L \to (L\backslash \{i\}) \cup \{j\}.$
In this case,
$L \to (L\backslash \{i\}) \cup \{j\}.$
In this case,
![]() $|d_S(\{j, L\})| = |d_S(\{i, (L\backslash \{i\}) \cup \{j\}\})|.$
Adding all such determinants to the last inequality, we obtain
$|d_S(\{j, L\})| = |d_S(\{i, (L\backslash \{i\}) \cup \{j\}\})|.$
Adding all such determinants to the last inequality, we obtain
 $$ \begin{align*} &\sum\limits_{J \in \binom{[n]}{{k-1}},\; i \notin J} \left| d_{S}(\{i,J\}) \right| \\ &\quad\geq (\sqrt{2} -1)\sum\limits_{J \in \binom{[n]}{{k-1}},\; i,j \notin J} \left| d_{S}(\{j,J\}) \right| + \sum\limits_{J \in \binom{[n]}{{k-1}},\; i \in J, \; j \notin J} \left| d_{S}(\{j,J\}) \right| \\&\quad\geq (\sqrt{2} -1)\left(\sum\limits_{J \in \binom{[n]}{{k-1}},\; i,j \notin J} \left| d_{S}(\{j,J\}) \right| + \sum\limits_{J \in \binom{[n]}{{k-1}},\; i \in J, \; j \notin J} \left| d_{S}(\{j,J\}) \right| \right) \\ &\quad =(\sqrt{2} -1) \sum\limits_{J \in \binom{[n]}{{k-1}},\; j \notin J} \left| d_{S}(\{j,J\}) \right|. \end{align*} $$
$$ \begin{align*} &\sum\limits_{J \in \binom{[n]}{{k-1}},\; i \notin J} \left| d_{S}(\{i,J\}) \right| \\ &\quad\geq (\sqrt{2} -1)\sum\limits_{J \in \binom{[n]}{{k-1}},\; i,j \notin J} \left| d_{S}(\{j,J\}) \right| + \sum\limits_{J \in \binom{[n]}{{k-1}},\; i \in J, \; j \notin J} \left| d_{S}(\{j,J\}) \right| \\&\quad\geq (\sqrt{2} -1)\left(\sum\limits_{J \in \binom{[n]}{{k-1}},\; i,j \notin J} \left| d_{S}(\{j,J\}) \right| + \sum\limits_{J \in \binom{[n]}{{k-1}},\; i \in J, \; j \notin J} \left| d_{S}(\{j,J\}) \right| \right) \\ &\quad =(\sqrt{2} -1) \sum\limits_{J \in \binom{[n]}{{k-1}},\; j \notin J} \left| d_{S}(\{j,J\}) \right|. \end{align*} $$
Finally, the sum in the left-hand side is exactly
![]() $F_2(S)\left \langle \sigma _S (i), d_S(i)\right \rangle ,$
and by Lemma 5.2, it is equal to
$F_2(S)\left \langle \sigma _S (i), d_S(i)\right \rangle ,$
and by Lemma 5.2, it is equal to
![]() $F_2(S) |v_i|^2.$
Similarly, we have
$F_2(S) |v_i|^2.$
Similarly, we have
 $(\sqrt {2} - 1) F_2(S) |v_j|^2$
in the right-hand side of the last inequality. Dividing by
$(\sqrt {2} - 1) F_2(S) |v_j|^2$
in the right-hand side of the last inequality. Dividing by
![]() $F_2(S),$
we obtain
$F_2(S),$
we obtain
 $|v_{i}|^2 \geq (\sqrt {2} - 1) |v_{j}|^2.$
▪
$|v_{i}|^2 \geq (\sqrt {2} - 1) |v_{j}|^2.$
▪
As mentioned in the Introduction, Corollary 1.5 is a consequence of Theorem 1.4 and McMullen’s symmetric formula (1.3).
Proof of Corollary 1.5
Let
![]() $H_q$
be the orthogonal complement of
$H_q$
be the orthogonal complement of
![]() $H_{n-q}$
in
$H_{n-q}$
in
![]() $\mathbb {R}^n.$
Let
$\mathbb {R}^n.$
Let
![]() $v_i$
and
$v_i$
and
![]() $v^{\prime }_i$
be the projections of the vector
$v^{\prime }_i$
be the projections of the vector
![]() $e_i$
onto
$e_i$
onto
![]() $H_{n-q}$
and
$H_{n-q}$
and
![]() $H_q,$
respectively. Clearly,
$H_q,$
respectively. Clearly,
![]() $|v_i|^2 + |v^{\prime }_i|^2 = 1.$
By Theorem 1.4, we conclude that
$|v_i|^2 + |v^{\prime }_i|^2 = 1.$
By Theorem 1.4, we conclude that
![]() $|v^{\prime }_i|^2$
is at most
$|v^{\prime }_i|^2$
is at most
![]() $1/(\sqrt {2} - 1)$
and at least
$1/(\sqrt {2} - 1)$
and at least
![]() $(\sqrt {2} -1)$
of the average squared length of the projections of the standard basis, which is
$(\sqrt {2} -1)$
of the average squared length of the projections of the standard basis, which is
![]() $ q/n.$
Therefore,
$ q/n.$
Therefore,
 $$ \begin{align*} 1 \geq \frac{m_n}{M_n} \geq \sqrt{\frac{1 - \frac{1}{\sqrt{2} -1 } \frac{q}{n}}{1 - (\sqrt{2} -1)\frac{q}{n}}}, \end{align*} $$
$$ \begin{align*} 1 \geq \frac{m_n}{M_n} \geq \sqrt{\frac{1 - \frac{1}{\sqrt{2} -1 } \frac{q}{n}}{1 - (\sqrt{2} -1)\frac{q}{n}}}, \end{align*} $$
which tends to 1 as n tends to infinity. ▪