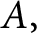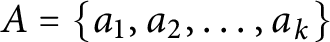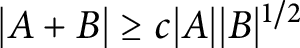1 Introduction
Given two sets of numbers, A and B, the sumset of A and B, denoted by
![]() $A+B,$
is
$A+B,$
is
Let
![]() $A=\{a_1,a_2,\ldots ,a_k\}$
be a finite set of real numbers with the property that
$A=\{a_1,a_2,\ldots ,a_k\}$
be a finite set of real numbers with the property that
for any
![]() $1<i<k.$
Sets with this property are said to be convex sets.
$1<i<k.$
Sets with this property are said to be convex sets.
Improving on a result of Hegyvári [Reference Hegyvári4], Elekes et al. [Reference Elekes, Nathanson and Ruzsa2] proved that if A is convex, then
![]() $|A+B|\geq ck^{3/2}$
for any set B with
$|A+B|\geq ck^{3/2}$
for any set B with
![]() $|B|=k.$
A set,
$|B|=k.$
A set,
![]() $A,$
has distinct consecutive differences if for any
$A,$
has distinct consecutive differences if for any
![]() $1\leq i,j\leq k, a_{i+1}-a_i=a_{j+1}-a_j$
implies
$1\leq i,j\leq k, a_{i+1}-a_i=a_{j+1}-a_j$
implies
![]() $i=j.$
$i=j.$
The following theorem, which was proved in [Reference Ruzsa, Shakan, Solymosi and Szemerédi8], generalizes the result of Elekes et al.
Theorem 1.1 [Reference Ruzsa, Shakan, Solymosi and Szemerédi8]
Let A and B be finite sets of real numbers with
![]() $|A| = k$
and
$|A| = k$
and
![]() $|B| = \ell .$
If A has distinct consecutive differences, then
$|B| = \ell .$
If A has distinct consecutive differences, then
 $$ \begin{align*} |A+B| \geq c{k\sqrt{\ell}}. \end{align*} $$
$$ \begin{align*} |A+B| \geq c{k\sqrt{\ell}}. \end{align*} $$
In particular, if
![]() $k = \ell ,$
then
$k = \ell ,$
then
 $$ \begin{align*} |A+B| \geq c{k^{3/2}}, \end{align*} $$
$$ \begin{align*} |A+B| \geq c{k^{3/2}}, \end{align*} $$
where
![]() $c>0$
is an absolute constant.
$c>0$
is an absolute constant.
Although the above theorem is tight, i.e. there are sets A and B such that the above bound is sharp up to the multiplicative constant (see in [Reference Ruzsa, Shakan, Solymosi and Szemerédi8]), several questions remain open. Below, we list six questions. In all of them, A denotes a set with distinct consecutive differences. Here, and later in the paper, we are using the asymptotic notation
![]() $f(x)\gg g(x)$
when there is a constant c such that
$f(x)\gg g(x)$
when there is a constant c such that
![]() $f(x)\geq g(x)/\log ^cf(x)$
holds as x goes to infinity.
$f(x)\geq g(x)/\log ^cf(x)$
holds as x goes to infinity.
-
(1) What can we say about the structure of A when there is a set
 $B, |B|=|A|=k$
so that
$B, |B|=|A|=k$
so that
 $|A+B| = O({k^{3/2}}) $
?
$|A+B| = O({k^{3/2}}) $
? -
(2) There is no restriction on B in Theorem 1.1. What happens if B also has distinct consecutive differences?
-
(3) What is the minimum size of
 $A+A$
?
$A+A$
? -
(4) What is the best bound on
 $|A+B|$
if A is convex?
$|A+B|$
if A is convex? -
(5) What is the best bound on
 $|A+A|$
if A is convex?
$|A+A|$
if A is convex? -
(6) What is the minimum size of
 $A+B$
if A and B are convex?
$A+B$
if A and B are convex?
All questions above are open. In this paper, we will consider the first three questions. The following list summarises the best known estimates.
-
(1) If there is a set
 $B, |B|=|A|=k$
so that
$B, |B|=|A|=k$
so that
 $|A+B| = O({k^{3/2}}) $
then the sumset is evenly distributed,
$|A+B| = O({k^{3/2}}) $
then the sumset is evenly distributed,
 $E_{1.5}(A,B)\ll k^{9/4}$
(in this paper).
$E_{1.5}(A,B)\ll k^{9/4}$
(in this paper). -
(2) Even if both A and B have distinct consecutive differences, there are examples when
 $|B|=|A|=k$
and
$|B|=|A|=k$
and
 $|A+B| = c{k^{3/2}} $
(in this paper).
$|A+B| = c{k^{3/2}} $
(in this paper). -
(3) There are constructions for sets A such that
 $|A+A|\leq |A|^{2-c}$
with some
$|A+A|\leq |A|^{2-c}$
with some
 $c>0.1$
(in this paper). No better lower bound is known than what follows from Theorem 1.1.
$c>0.1$
(in this paper). No better lower bound is known than what follows from Theorem 1.1. -
(4) What is the best bound on
 $|A+B|$
if A is convex? No better lower bound is known than what follows from Theorem 1.1, and no construction is known showing
$|A+B|$
if A is convex? No better lower bound is known than what follows from Theorem 1.1, and no construction is known showing
 $|A+B|\leq (|A||B|)^{1-c}$
with some
$|A+B|\leq (|A||B|)^{1-c}$
with some
 $c>0.$
$c>0.$
-
(5) If A is convex then
 $|A+A|\gg |A|^{30/19}$
according to a recent result of Rudnev and Stevens in [Reference Rudnev and Stevens7], building on earlier results in [Reference Li and Roche-Newton5, Reference Schoen and Shkredov10, Reference Shkredov12].
$|A+A|\gg |A|^{30/19}$
according to a recent result of Rudnev and Stevens in [Reference Rudnev and Stevens7], building on earlier results in [Reference Li and Roche-Newton5, Reference Schoen and Shkredov10, Reference Shkredov12]. -
(6) If A and B are convex and
 $|A|=|B|$
then
$|A|=|B|$
then
 $|A+B|\gg |A|^{30/19}$
[Reference Shkredov13]. No construction is known showing
$|A+B|\gg |A|^{30/19}$
[Reference Shkredov13]. No construction is known showing
 $|A+B|\leq (|A||B|)^{1-c}$
with some
$|A+B|\leq (|A||B|)^{1-c}$
with some
 $c>0.$
$c>0.$
There are interesting works relaxing and strengthening the notation of convex sequences, like in [Reference Schoen9], [Reference Hanson, Roche–Newton and Rudnev3], and [Reference Stevens and Warren14].
2 Lower bounds using crossing numbers
2.1 Proof of Theorem 1.1
In this section, we offer a new proof for Theorem 1.1 by giving a bound in terms of additive energy. As the original proof in [Reference Ruzsa, Shakan, Solymosi and Szemerédi8], this is also a simple proof, but here, we are using graph theory, the crossing number bound, which gives more information about the structure of
![]() $A.$
The variants of the crossing bounds we are going to use are all originate from the classical crossing bound by Ajtai et al. in [Reference Ajtai, Chvátal, Newborn and Szemerédi1].
$A.$
The variants of the crossing bounds we are going to use are all originate from the classical crossing bound by Ajtai et al. in [Reference Ajtai, Chvátal, Newborn and Szemerédi1].
Proof of Theorem 1.1
For the given sets,
![]() $A=\{a_1,a_2,\ldots ,a_k\}$
in which the consecutive differences are all distinct and an arbitrary set
$A=\{a_1,a_2,\ldots ,a_k\}$
in which the consecutive differences are all distinct and an arbitrary set
![]() $B=\{b_1,\ldots ,b_\ell \}$
we define a geometric graph, G. The vertices of the graph are points on the x axis, the values of the sumset
$B=\{b_1,\ldots ,b_\ell \}$
we define a geometric graph, G. The vertices of the graph are points on the x axis, the values of the sumset
![]() $A+B.$
Two vertices,
$A+B.$
Two vertices,
![]() $u,v\in \{A+B\}$
are connected by an edge, an upper semicircular arc, iff there is an
$u,v\in \{A+B\}$
are connected by an edge, an upper semicircular arc, iff there is an
![]() $a_i\in A$
and
$a_i\in A$
and
![]() $b_j\in B$
such that
$b_j\in B$
such that
![]() $u=a_i+b_j$
and
$u=a_i+b_j$
and
![]() $v=a_{i+1}+b_j.$
So G consists of translates of the path,
$v=a_{i+1}+b_j.$
So G consists of translates of the path,
![]() $P,$
with vertex set A where the consecutive vertices are connected by a semicircular arc (Figure 1). Since the consecutive differences are all different in
$P,$
with vertex set A where the consecutive vertices are connected by a semicircular arc (Figure 1). Since the consecutive differences are all different in
![]() $A,$
the graph has no multiple edges. We are going to bound the crossing number of this graph from below and from above to get a bound on
$A,$
the graph has no multiple edges. We are going to bound the crossing number of this graph from below and from above to get a bound on
![]() $|A+B|.$
For the upper bound, note that any two translates of P have at most
$|A+B|.$
For the upper bound, note that any two translates of P have at most
![]() $2k-1$
crossings, so the number of crossings in G is at most
$2k-1$
crossings, so the number of crossings in G is at most
 $$ \begin{align} cr(G)\leq \binom{|B|}{2}(2k-1)\leq |B|^2{k}. \end{align} $$
$$ \begin{align} cr(G)\leq \binom{|B|}{2}(2k-1)\leq |B|^2{k}. \end{align} $$

Figure 1 The number of crossings between two translates of A is at most
![]() $2k-1$
.
$2k-1$
.
There are various bounds on the crossing number of graphs. In our case, this is the convex crossing number (which is the same as the one-page crossing number) applies. The lower bound is a bit better than for general crossing numbers. It was proved in [Reference Shahrokhi, Sýkora, Székely and Vrt’o11] that for
![]() $|B|(k-1)$
edges and
$|B|(k-1)$
edges and
![]() $|A+B|$
vertices the number of crossings is at least
$|A+B|$
vertices the number of crossings is at least
 $$ \begin{align} cr(G)\geq \frac{(|B|(k-1))^3}{27|A+B|^2}, \end{align} $$
$$ \begin{align} cr(G)\geq \frac{(|B|(k-1))^3}{27|A+B|^2}, \end{align} $$
which proves Theorem 1.1, with the constant
![]() $c=1/\sqrt {27}\approx 0.19,$
since
$c=1/\sqrt {27}\approx 0.19,$
since
 $$ \begin{align} |B|^2{k} \geq \frac{(|B|(k-1))^3}{27|A+B|^2}, \end{align} $$
$$ \begin{align} |B|^2{k} \geq \frac{(|B|(k-1))^3}{27|A+B|^2}, \end{align} $$
implies that
 $$ \begin{align*} |A+B| \geq \frac{|A||B|^{1/2}}{\sqrt{27}}. \end{align*} $$
$$ \begin{align*} |A+B| \geq \frac{|A||B|^{1/2}}{\sqrt{27}}. \end{align*} $$
▪
Our goal is not only to give another simple proof to this result, but also to understand the structure of A a bit better when the above bound is close to being tight. One would expect that uneven degree distributions might improve the bound. If in our graph,
![]() $G,$
a vertex
$G,$
a vertex
![]() $v\in \{A+B\}$
has degree d that means that there are at least
$v\in \{A+B\}$
has degree d that means that there are at least
![]() $d/2$
ways to write v as
$d/2$
ways to write v as
![]() $v=a+b,$
where
$v=a+b,$
where
![]() $a\in A$
and
$a\in A$
and
![]() $b\in B.$
Using the usual notation in additive combinatorics,
$b\in B.$
Using the usual notation in additive combinatorics,
![]() $r_{A+B}(x)$
denotes the number of ways to write x as
$r_{A+B}(x)$
denotes the number of ways to write x as
![]() $x=a+b,$
where
$x=a+b,$
where
![]() $a\in A$
and
$a\in A$
and
![]() $b\in B.$
The additive energy of the two sets is defined as
$b\in B.$
The additive energy of the two sets is defined as
 $$ \begin{align*} E(A,B)=E_2(A,B)=\sum_{x\in\{A+B\}}r_{A+B}^{2}(x). \end{align*} $$
$$ \begin{align*} E(A,B)=E_2(A,B)=\sum_{x\in\{A+B\}}r_{A+B}^{2}(x). \end{align*} $$
In a similar way, for any
![]() $\alpha>1$
one can define
$\alpha>1$
one can define
 $$ \begin{align*} E_\alpha(A,B)=\sum_{x\in\{A+B\}}r_{A+B}^{\alpha}(x). \end{align*} $$
$$ \begin{align*} E_\alpha(A,B)=\sum_{x\in\{A+B\}}r_{A+B}^{\alpha}(x). \end{align*} $$
We are going to use a crossing number bound from [Reference Pach, Solymosi and Tardos6] to get an estimate on
![]() $E_{1.5}(A,B)$
when A has distinct consecutive differences.
$E_{1.5}(A,B)$
when A has distinct consecutive differences.
Theorem 2.1 (Theorem 1 in [Reference Pach, Solymosi and Tardos6])
For any simple graph G on n vertices with vertex degrees
![]() $d_1\geq d_2\geq \cdots \geq d_n$
we have
$d_1\geq d_2\geq \cdots \geq d_n$
we have
 $$ \begin{align*} cr(G)\geq \frac{1}{36000n}\sum_{i=1}^nid_i^3-4.01n^2. \end{align*} $$
$$ \begin{align*} cr(G)\geq \frac{1}{36000n}\sum_{i=1}^nid_i^3-4.01n^2. \end{align*} $$
Note that for any sequence of positive real numbers
![]() $d_1\geq d_2\geq \cdots \geq d_n$
, we have the inequality
$d_1\geq d_2\geq \cdots \geq d_n$
, we have the inequality
 $$ \begin{align*} \sum_{i=1}^nid_i^3\leq \left(\sum_{i=1}^nd_i^{3/2}\right)^2\leq (\ln{n}+1)\sum_{i=1}^nid_i^3, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^nid_i^3\leq \left(\sum_{i=1}^nd_i^{3/2}\right)^2\leq (\ln{n}+1)\sum_{i=1}^nid_i^3, \end{align*} $$
which leads us to
 $$ \begin{align*} |B|^2k+4.01|A+B|^2\geq \frac{c_1}{|A+B|\ln{|A+B|}}\left(\sum_{x\in\{A+B\}}r_{A+B}^{3/2}(x)\right)^2. \end{align*} $$
$$ \begin{align*} |B|^2k+4.01|A+B|^2\geq \frac{c_1}{|A+B|\ln{|A+B|}}\left(\sum_{x\in\{A+B\}}r_{A+B}^{3/2}(x)\right)^2. \end{align*} $$
We use this bound in the case when
![]() $|B|=|A|=k.$
By Theorem 1.1 and the inequality above, we get the following result.
$|B|=|A|=k.$
By Theorem 1.1 and the inequality above, we get the following result.
Theorem 2.2 If A is a set where the consecutive differences are distinct, and B is an arbitrary set such that
![]() $|A|=|B|,$
thenFootnote
1
$|A|=|B|,$
thenFootnote
1
 $$ \begin{align*} |A+B|\gg \left(\sum_{x\in\{A+B\}}r_{A+B}^{3/2}(x)\right)^{2/3}=E_{1.5}(A,B)^{2/3}. \end{align*} $$
$$ \begin{align*} |A+B|\gg \left(\sum_{x\in\{A+B\}}r_{A+B}^{3/2}(x)\right)^{2/3}=E_{1.5}(A,B)^{2/3}. \end{align*} $$
This bound—up to the log factor—is an improved version of Theorem 1.1. By Jensen’s inequality, the right hand side is minimal if
![]() $r_{A+B}(x)$
is the average,
$r_{A+B}(x)$
is the average,
![]() $k^2/|A+B|,$
for all
$k^2/|A+B|,$
for all
![]() $x\in \{A+B\},$
and then
$x\in \{A+B\},$
and then
![]() $|A+B|\approx k^{3/2}.$
$|A+B|\approx k^{3/2}.$
There is another, more direct way to measure the smoothness of the degree sequence, to count the number of
![]() $x\in \{A+B\}$
which have high multiplicity, i.e., there are many ways to express x as a sum. For this, let us choose a set
$x\in \{A+B\}$
which have high multiplicity, i.e., there are many ways to express x as a sum. For this, let us choose a set
![]() $S\subset \{A+B\}$
which is a collection of such elements.
$S\subset \{A+B\}$
which is a collection of such elements.
Theorem 2.3 Suppose that A is a set with consecutive differences being all distinct, and B is an arbitrary set. Let
![]() $S\subset \{A+B\}$
a set such that
$S\subset \{A+B\}$
a set such that
 $$ \begin{align} \sum_{x\in S}r_{A+B}(x)\geq \frac{|A||B|}{\Delta}. \end{align} $$
$$ \begin{align} \sum_{x\in S}r_{A+B}(x)\geq \frac{|A||B|}{\Delta}. \end{align} $$
Then there is a constant,
![]() $c_\Delta>1/(2\Delta )^3,$
so the following inequality holds
$c_\Delta>1/(2\Delta )^3,$
so the following inequality holds
 $$ \begin{align} |A+B|\geq \frac{c_\Delta|B||A|^2}{|S|}. \end{align} $$
$$ \begin{align} |A+B|\geq \frac{c_\Delta|B||A|^2}{|S|}. \end{align} $$
As in the previous theorem, this result implies Theorem 1.1. Setting
![]() $S=\{A+B\}$
gives
$S=\{A+B\}$
gives
 $|A+B|=\Omega \left (|B|^{1/2}|A|\right ),$
as in Theorem 1.1. At the other end, if
$|A+B|=\Omega \left (|B|^{1/2}|A|\right ),$
as in Theorem 1.1. At the other end, if
![]() $|S|\approx |A|,$
then the sumset is as large as possible, it is
$|S|\approx |A|,$
then the sumset is as large as possible, it is
![]() $\Omega (|A||B|).$
$\Omega (|A||B|).$
Proof We will work with G as defined in the proof of Theorem 1.1 and we are going to use a simple crossing bound from [Reference Pach, Solymosi and Tardos6].
Lemma 2.4 (Lemma 2.1 in [Reference Pach, Solymosi and Tardos6])
Let
![]() $G(U,V)$
be a bipartite graph with vertex classes U and
$G(U,V)$
be a bipartite graph with vertex classes U and
![]() $V,$
and suppose that its number of edges satisfies
$V,$
and suppose that its number of edges satisfies
![]() $e \geq 6 \max (|U|,|V|).$
Then we have
$e \geq 6 \max (|U|,|V|).$
Then we have
 $$ \begin{align*} cr(G(U,V))\geq \frac{e^3}{108|U||V|}. \end{align*} $$
$$ \begin{align*} cr(G(U,V))\geq \frac{e^3}{108|U||V|}. \end{align*} $$
▪
From the proof of Theorem 1.1, we know that
![]() $cr(G)\leq |A||B|^2.$
There are two simple cases to consider; when a
$cr(G)\leq |A||B|^2.$
There are two simple cases to consider; when a
![]() $\delta $
-fraction of the edges with an endpoint in S are inside of
$\delta $
-fraction of the edges with an endpoint in S are inside of
![]() $S,$
or the
$S,$
or the
![]() $(1-\delta )$
-fraction of them connect S with the outside of S (we are going to optimize for
$(1-\delta )$
-fraction of them connect S with the outside of S (we are going to optimize for
![]() $0<\delta <1$
at the end of our calculation). For the first case, we apply a classical crossing bound for the induced subgraph of G on
$0<\delta <1$
at the end of our calculation). For the first case, we apply a classical crossing bound for the induced subgraph of G on
![]() $S,$
denoted by
$S,$
denoted by
![]() $H_S.$
By inequality (2.2), we have
$H_S.$
By inequality (2.2), we have
 $$ \begin{align*} |A||B|^2\geq cr(H_S)\geq \frac{(\delta|A||B|/\Delta)^3}{27|S|^2}\geq \frac{(\delta|A||B|/\Delta)^3}{27|A+B||S|}, \end{align*} $$
$$ \begin{align*} |A||B|^2\geq cr(H_S)\geq \frac{(\delta|A||B|/\Delta)^3}{27|S|^2}\geq \frac{(\delta|A||B|/\Delta)^3}{27|A+B||S|}, \end{align*} $$
which gives the required inequality
 $$ \begin{align*} |A+B|\geq \left(\frac{\delta}{3\Delta}\right)^3\frac{|B||A|^2}{|S|}. \end{align*} $$
$$ \begin{align*} |A+B|\geq \left(\frac{\delta}{3\Delta}\right)^3\frac{|B||A|^2}{|S|}. \end{align*} $$
In the second case, we can assume that
![]() $|A||B|^2\geq 6|A+B|,$
so Lemma 2 is applicable with
$|A||B|^2\geq 6|A+B|,$
so Lemma 2 is applicable with
![]() $V=S$
and
$V=S$
and
![]() $U=\{A+B\}\setminus S.$
$U=\{A+B\}\setminus S.$
 $$ \begin{align*} |A||B|^2\geq \frac{e^3}{108|U||V|}> \frac{((1-\delta)|A||B|/\Delta)^3}{125|S||A+B|}, \end{align*} $$
$$ \begin{align*} |A||B|^2\geq \frac{e^3}{108|U||V|}> \frac{((1-\delta)|A||B|/\Delta)^3}{125|S||A+B|}, \end{align*} $$
which gives
 $$ \begin{align*} |A+B|> \left(\frac{1-\delta}{5\Delta}\right)^3\frac{|B||A|^2}{|S|}. \end{align*} $$
$$ \begin{align*} |A+B|> \left(\frac{1-\delta}{5\Delta}\right)^3\frac{|B||A|^2}{|S|}. \end{align*} $$
Choosing
![]() $\delta $
to make the constant multipliers in the two cases equal, we see that one can set
$\delta $
to make the constant multipliers in the two cases equal, we see that one can set
![]() $c_\Delta>1/(2\Delta )^3$
in Theorem 2.3.▪
$c_\Delta>1/(2\Delta )^3$
in Theorem 2.3.▪
One can be more specific in defining
![]() $S,$
we can bound the number of
$S,$
we can bound the number of
![]() $x\in A+B$
such that
$x\in A+B$
such that
![]() $r_{A+B}(x)\geq t.$
$r_{A+B}(x)\geq t.$
Corollary 2.5 Suppose that A is a set with consecutive differences being all distinct, and B is an arbitrary set. Let
![]() $t>1$
an arbitrary integer and
$t>1$
an arbitrary integer and
![]() $S_t\subset \{A+B\}$
a set such that
$S_t\subset \{A+B\}$
a set such that
 $$ \begin{align} \min_{x\in S_t}\{r_{A+B}(x)\}\geq t. \end{align} $$
$$ \begin{align} \min_{x\in S_t}\{r_{A+B}(x)\}\geq t. \end{align} $$
Then
 $$ \begin{align*} |S_t|<\frac{3|A+B|^{1/2}|A|^{1/2}|B|}{t^{3/2}}. \end{align*} $$
$$ \begin{align*} |S_t|<\frac{3|A+B|^{1/2}|A|^{1/2}|B|}{t^{3/2}}. \end{align*} $$
Proof Set
 $$ \begin{align*} \Delta=\frac{|A||B|}{t|S_t|} \end{align*} $$
$$ \begin{align*} \Delta=\frac{|A||B|}{t|S_t|} \end{align*} $$
so the following inequality holds
 $$ \begin{align*} \sum_{x\in S_t}r_{A+B}(x)\geq|S_t|t=\frac{|A||B|}{\Delta}, \end{align*} $$
$$ \begin{align*} \sum_{x\in S_t}r_{A+B}(x)\geq|S_t|t=\frac{|A||B|}{\Delta}, \end{align*} $$
and we can apply Theorem 2.3. Solving inequality (2.5) for
![]() $|S_t|$
we get the desired result. ▪
$|S_t|$
we get the desired result. ▪
Another advantage of using crossing numbers in this context is that there are effective bounds for multigraphs, so we get the following result.
Claim 2.6 Let A and B be finite sets of real numbers with
![]() $|A| = k$
and
$|A| = k$
and
![]() $|B| = \ell .$
If in A any consecutive difference,
$|B| = \ell .$
If in A any consecutive difference,
![]() $a_i-a_{i-1},$
has multiplicity at most m then
$a_i-a_{i-1},$
has multiplicity at most m then
 $$ \begin{align*} |A+B| \geq \frac{ck\sqrt{\ell}}{\sqrt{m}}, \end{align*} $$
$$ \begin{align*} |A+B| \geq \frac{ck\sqrt{\ell}}{\sqrt{m}}, \end{align*} $$
where
![]() $c>0$
is a universal constant.
$c>0$
is a universal constant.
Proof The claim follows directly from the crossing bound for multigraphs (see e.g., in [Reference Székely15]) and from our upper bound in equation (2.1).
 $$ \begin{align*} k\ell^2\geq cr(G)\geq \frac{c(k\ell)^3}{m|A+B|^2}. \end{align*} $$
$$ \begin{align*} k\ell^2\geq cr(G)\geq \frac{c(k\ell)^3}{m|A+B|^2}. \end{align*} $$
▪
2.2 A small improvement on the crossing number bound
In the above results, we used crossing number bounds, however, we could have used a slightly better graph parameter for our purposes. It might be interesting if one would like to improve the constant multiplier in the lower bounds. For any graph,
![]() $G_n,$
an interval drawing is given by a one-to-one map,
$G_n,$
an interval drawing is given by a one-to-one map,
![]() $\Phi : V(G_n)\rightarrow \mathbb {R},$
where an edge
$\Phi : V(G_n)\rightarrow \mathbb {R},$
where an edge
![]() $(v_i,v_j)\in E(V(G_n)$
maps to the interval
$(v_i,v_j)\in E(V(G_n)$
maps to the interval
![]() $[\Phi (v_i),\Phi (v_j)].$
Two vertex-disjoint edges,
$[\Phi (v_i),\Phi (v_j)].$
Two vertex-disjoint edges,
![]() $(v_j,v_j)$
and
$(v_j,v_j)$
and
![]() $(v_k,v_\ell ),$
are intersecting (under the map
$(v_k,v_\ell ),$
are intersecting (under the map
![]() $\Phi $
) if they share an interior point,
$\Phi $
) if they share an interior point,
Definition 2.1 For a given graph
![]() $G_n,$
the intersecting number,
$G_n,$
the intersecting number,
![]() $int(G_n),$
is the lowest number of edge intersections of an interval drawing of
$int(G_n),$
is the lowest number of edge intersections of an interval drawing of
![]() $G_n.$
$G_n.$
Our upper bound in (2.1) holds for the intersection number of
![]() $G_n$
and it is clear that
$G_n$
and it is clear that
The inequality is strict if one edge (interval) contains another inside. The maximum number of crossing-free edges in
![]() $G_n$
is about
$G_n$
is about
![]() $2n,$
while for intersection-free
$2n,$
while for intersection-free
![]() $G_n$
it is at most
$G_n$
it is at most
![]() $1.5n.$
Using the probabilistic approach of Székely (as we will see in the proof of Claim 2.7), one can show that if the number of edges,
$1.5n.$
Using the probabilistic approach of Székely (as we will see in the proof of Claim 2.7), one can show that if the number of edges,
![]() $e,$
is at least
$e,$
is at least
![]() $2.25n,$
then
$2.25n,$
then
 $$ \begin{align*} int(G_n)\geq \frac{0.0658e^3}{n^2}, \end{align*} $$
$$ \begin{align*} int(G_n)\geq \frac{0.0658e^3}{n^2}, \end{align*} $$
which is better than the inequality used in equation (2.3) since
![]() $1/27\approx 0.037 < 0.0658$
. As an example we show the following bound:
$1/27\approx 0.037 < 0.0658$
. As an example we show the following bound:
Claim 2.7 Let
![]() $A=\{a_1,a_2,\ldots ,a_k\}$
be a finite set of real numbers with distinct consecutive differences which are not too far from each other, i.e.,
$A=\{a_1,a_2,\ldots ,a_k\}$
be a finite set of real numbers with distinct consecutive differences which are not too far from each other, i.e.,
for any
![]() $1<i,j\leq k,$
and let
$1<i,j\leq k,$
and let
![]() $B\subset \mathbb {R}$
an arbitrary finite set. Then
$B\subset \mathbb {R}$
an arbitrary finite set. Then
 $$ \begin{align*} |A+B|\geq \frac{2}{3\sqrt{3}}|A||B|^{1/2}. \end{align*} $$
$$ \begin{align*} |A+B|\geq \frac{2}{3\sqrt{3}}|A||B|^{1/2}. \end{align*} $$
Proof To see this, note that by condition (2.7) if a subgraph of
![]() $G_{|A+B|}$
on n vertices is intersection free, then it has at most
$G_{|A+B|}$
on n vertices is intersection free, then it has at most
![]() $n-1$
edges. If the number of edges is at least
$n-1$
edges. If the number of edges is at least
![]() $1.5n$
then there are at least
$1.5n$
then there are at least
![]() $0.5n$
intersections. The number of edges in
$0.5n$
intersections. The number of edges in
![]() $G_{|A+B|}$
is
$G_{|A+B|}$
is
![]() $(k-1)|B|\approx |A||B|,$
so let’s select a random subgraph of
$(k-1)|B|\approx |A||B|,$
so let’s select a random subgraph of
![]() $G_{|A+B|}$
choosing the vertices independently at random with probability
$G_{|A+B|}$
choosing the vertices independently at random with probability
 $p=\frac {1.5|A+B|}{|A||B|}.$
Then the expected number of vertices is
$p=\frac {1.5|A+B|}{|A||B|}.$
Then the expected number of vertices is
 $\frac {1.5|A+B|^2}{|A||B|},$
the number of edges is
$\frac {1.5|A+B|^2}{|A||B|},$
the number of edges is
 $\frac {(1.5|A+B|)^2}{|A||B|},$
and the expected number of intersections is at least
$\frac {(1.5|A+B|)^2}{|A||B|},$
and the expected number of intersections is at least
 $p^4\cdot int(G_{|A+B|}).$
From here, we have
$p^4\cdot int(G_{|A+B|}).$
From here, we have
 $$ \begin{align*} \left(\frac{1.5|A+B|}{|A||B|}\right)^4\cdot int(G_{|A+B|})\geq 0.5\cdot \frac{1.5|A+B|^2}{|A||B|}, \end{align*} $$
$$ \begin{align*} \left(\frac{1.5|A+B|}{|A||B|}\right)^4\cdot int(G_{|A+B|})\geq 0.5\cdot \frac{1.5|A+B|^2}{|A||B|}, \end{align*} $$
and
 $$ \begin{align*} |A||B|^2\geq int(G_{|A+B|})\geq 0.5\cdot \frac{(|A||B|)^3}{1.5^3|A+B|^2}. \end{align*} $$
$$ \begin{align*} |A||B|^2\geq int(G_{|A+B|})\geq 0.5\cdot \frac{(|A||B|)^3}{1.5^3|A+B|^2}. \end{align*} $$
▪
Note that in the proof we only used the weaker condition that
![]() $a_{i+2}-a_i\neq a_j$
for any
$a_{i+2}-a_i\neq a_j$
for any
![]() $1\leq i,j\leq k.$
$1\leq i,j\leq k.$
3 Constructions
3.1 Both A and B have distinct consecutive differences
In this section, we are going to show constructions which indicate the limitations of possible lower bounds on the size of sumsets forced by local conditions, like distinct consecutive differences in a set.
Theorem 3.1 For arbitrary large integer
![]() $k,$
there are sets, A and
$k,$
there are sets, A and
![]() $B,$
such that in both sets the consecutive differences are distinct,
$B,$
such that in both sets the consecutive differences are distinct,
![]() $|A|\approx |B|\geq k$
and
$|A|\approx |B|\geq k$
and
![]() $|A+B|\leq c|A||B|^{1/2},$
where
$|A+B|\leq c|A||B|^{1/2},$
where
![]() $c>0$
is a universal constant.
$c>0$
is a universal constant.
Proof Let n and k be relative prime numbers,
![]() $1 < n < k,$
such that
$1 < n < k,$
such that
![]() $k-n$
is small (we will assign their exact values later). Set A is defined as
$k-n$
is small (we will assign their exact values later). Set A is defined as
Between two consecutive numbers of A there is at least one multiple of
![]() $n.$
Let us choose one of them and add it to
$n.$
Let us choose one of them and add it to
![]() $A.$
In this way, we have
$A.$
In this way, we have
![]() $n-1$
numbers, all below
$n-1$
numbers, all below
![]() $kn/2.$
All consecutive differences are distinct since the difference is either of the form
$kn/2.$
All consecutive differences are distinct since the difference is either of the form
![]() $jk-in$
or
$jk-in$
or
![]() $in-jk.$
If
$in-jk.$
If
![]() $jk-in = j'k-i'n,$
then
$jk-in = j'k-i'n,$
then
![]() $(j-j')k = (i -i')n,$
so
$(j-j')k = (i -i')n,$
so
![]() $n \mid j- j',$
$n \mid j- j',$
![]() $j = j'$
and then
$j = j'$
and then
![]() $i = i'.$
The same holds for the
$i = i'.$
The same holds for the
![]() $in- jk = i'n -j'k$
case. If
$in- jk = i'n -j'k$
case. If
![]() $jk - in = i'n - j'k,$
then
$jk - in = i'n - j'k,$
then
![]() $(j + j')k = (i + i')n,$
so
$(j + j')k = (i + i')n,$
so
![]() $n \mid j + j', j + j' < n,$
so
$n \mid j + j', j + j' < n,$
so
![]() $j = j' = 0,$
which is not possible.
$j = j' = 0,$
which is not possible.
The construction of B follows the same algorithm, using numbers
![]() $m, r.$
$m, r.$
We choose
![]() $m, r$
in a way that
$m, r$
in a way that
![]() $A + B$
is small. To achieve this let
$A + B$
is small. To achieve this let
![]() $1 < a < b < c < d$
be four pairwise relative prime numbers close to each other, e.g.,
$1 < a < b < c < d$
be four pairwise relative prime numbers close to each other, e.g.,
![]() $a = 6t+1, b = 6t+2, c = 6t+3, d = 6t+5.$
Let
$a = 6t+1, b = 6t+2, c = 6t+3, d = 6t+5.$
Let
![]() $n = ab, k = cd, m = ac, r = bd.$
The elements in both sets are less than
$n = ab, k = cd, m = ac, r = bd.$
The elements in both sets are less than
![]() $abcd/2,$
so the sumset is subset of
$abcd/2,$
so the sumset is subset of
![]() $[0, abcd).$
All elements of the sumset are divisible by one of the numbers
$[0, abcd).$
All elements of the sumset are divisible by one of the numbers
![]() $ a, b, c, d,$
so its cardinality is less than
$ a, b, c, d,$
so its cardinality is less than
![]() $4bcd.$
The cardinality of the sets is at least
$4bcd.$
The cardinality of the sets is at least
![]() $a^2$
and
$a^2$
and
 $$ \begin{align*} 4bcd<(4+\varepsilon)(a^2)^{3/2}. \end{align*} $$
$$ \begin{align*} 4bcd<(4+\varepsilon)(a^2)^{3/2}. \end{align*} $$
▪
3.2 Bounding the size of A+A
The best known lower bound on
![]() $|A+A|,$
where A has distinct consecutive differences follows from Theorem 1.1. One can use the structure of the graph G defined by
$|A+A|,$
where A has distinct consecutive differences follows from Theorem 1.1. One can use the structure of the graph G defined by
![]() $A+A$
to improve the constant multiplier in Theorem 1.1, but it is still
$A+A$
to improve the constant multiplier in Theorem 1.1, but it is still
![]() $|A+A|=\Omega (|A|^{3/2}).$
In this direction, the best result is due to Schoen [Reference Schoen9] who proved a better bound if A is a
$|A+A|=\Omega (|A|^{3/2}).$
In this direction, the best result is due to Schoen [Reference Schoen9] who proved a better bound if A is a
![]() $tdcd$
set. Schoen calls a a set a
$tdcd$
set. Schoen calls a a set a
![]() $tdcd$
-set (totally distinct consecutive differences) if for every fixed
$tdcd$
-set (totally distinct consecutive differences) if for every fixed
![]() $1\leq d < |A|,$
all differences
$1\leq d < |A|,$
all differences
![]() $a_i-a_{i-d},$
where
$a_i-a_{i-d},$
where
![]() $d < i < n,$
are distinct. For
$d < i < n,$
are distinct. For
![]() $tdcd$
sets Schoen proved that there is a constant
$tdcd$
sets Schoen proved that there is a constant
![]() $c>0$
such that
$c>0$
such that
![]() $|A+A|\geq c|A|^{3/2+c}.$
$|A+A|\geq c|A|^{3/2+c}.$
The next construction shows that there are sets A with distinct consecutive differences such that
![]() $|A+A|\leq c|A|^{2-c}.$
$|A+A|\leq c|A|^{2-c}.$
Theorem 3.2 There is a constant,
![]() $c>0.1,$
such that for arbitrarily large n there is a set A with distinct consecutive differences,
$c>0.1,$
such that for arbitrarily large n there is a set A with distinct consecutive differences,
![]() $|A|\geq n,$
such that
$|A|\geq n,$
such that
 $|A+A|=O\left (|A|^{2-c}\right ).$
$|A+A|=O\left (|A|^{2-c}\right ).$
Proof For the construction of A, we are going to use a set of integers with larger difference set than sumset. Searching for sets with many more differences than sums, we selected the set
![]() $S=\{0,1,3,7,12,22,30\}.$
S has 43 distinct pairwise differences and 28 sums.
$S=\{0,1,3,7,12,22,30\}.$
S has 43 distinct pairwise differences and 28 sums.
If the reader would like to follow the construction with a smaller set then one can perform all steps using the
![]() $S=\{0,1,3\}$
set, and then
$S=\{0,1,3\}$
set, and then
![]() $c>0$
is a bit below 0.1 (
$c>0$
is a bit below 0.1 (
![]() $ c\approx 0.92 $
), but the steps are easier to check. The selected seven element set is a result of a simple optimization to maximize
$ c\approx 0.92 $
), but the steps are easier to check. The selected seven element set is a result of a simple optimization to maximize
![]() $c.$
We are going to revisit the selection of S at the end of the proof.
$c.$
We are going to revisit the selection of S at the end of the proof.
First, we construct a set of k-dimensional vectors,
![]() $Q_k,$
in a sequence that consecutive vectors have distinct (vector) differences. Let us consider S as the vertex set of a complete digraph on seven vertices, and assign a value to every edge as follows: If the edge is
$Q_k,$
in a sequence that consecutive vectors have distinct (vector) differences. Let us consider S as the vertex set of a complete digraph on seven vertices, and assign a value to every edge as follows: If the edge is
![]() $v_i\rightarrow v_j$
then its value is defined as
$v_i\rightarrow v_j$
then its value is defined as
![]() $w(i,j)=v_i-v_j.$
For example,
$w(i,j)=v_i-v_j.$
For example,
![]() $w(2,4)=-6,$
and
$w(2,4)=-6,$
and
![]() $w(3,3)=0.$
We will consider walks in this digraph. The first walk is an Euler tour starting and ending in
$w(3,3)=0.$
We will consider walks in this digraph. The first walk is an Euler tour starting and ending in
![]() $v_1.$
Listing the indices of the vertices in sequence as the tour goes we have e.g.,
$v_1.$
Listing the indices of the vertices in sequence as the tour goes we have e.g.,
 $$ \begin{align*} E &=\{1,3,5,2,6,4,7,2,4,1,5,7,3,6,1,2,3,4,5,6,7,1,7, \\ &\qquad 5,3,7,4,6,5,1,6,2,5,4,3,1,4,2,7,6,3,2,1\}. \end{align*} $$
$$ \begin{align*} E &=\{1,3,5,2,6,4,7,2,4,1,5,7,3,6,1,2,3,4,5,6,7,1,7, \\ &\qquad 5,3,7,4,6,5,1,6,2,5,4,3,1,4,2,7,6,3,2,1\}. \end{align*} $$
Using the values assigned to the vertices, we have our first multiset of (one dimensional) vectors,
 $$ \begin{align*} Q_1 &= \{0,3,12,1,22,7,30,1,7,0,12,30,3,22,0,1,3,7,12,22,30, \\ &\qquad 0,30,12,3,30,7,22,12,0,22,1,12,7,3,0,7,1,30,22,3,1,0\}. \end{align*} $$
$$ \begin{align*} Q_1 &= \{0,3,12,1,22,7,30,1,7,0,12,30,3,22,0,1,3,7,12,22,30, \\ &\qquad 0,30,12,3,30,7,22,12,0,22,1,12,7,3,0,7,1,30,22,3,1,0\}. \end{align*} $$
By the construction, all consecutive differences are distinct, we used all differences but 0. We define
![]() $Q_{k+1}$
recursively, using
$Q_{k+1}$
recursively, using
![]() $Q_k.$
There will be
$Q_k.$
There will be
![]() $43|Q_k|=43^{k+1},$
not necessarily distinct
$43|Q_k|=43^{k+1},$
not necessarily distinct
![]() $k+1$
dimensional vectors in
$k+1$
dimensional vectors in
![]() $Q_{k+1},$
such that all consecutive differences are distinct. The first k coordinates are periodically repeating vectors, lets take k copies, blocks, of
$Q_{k+1},$
such that all consecutive differences are distinct. The first k coordinates are periodically repeating vectors, lets take k copies, blocks, of
![]() $Q_k,$
one after the other. We choose the last,
$Q_k,$
one after the other. We choose the last,
![]() $(k+1)$
th coordinate for every vector in blocks using
$(k+1)$
th coordinate for every vector in blocks using
![]() $Q_1$
as follows. In the first block all
$Q_1$
as follows. In the first block all
![]() $(k+1)$
th coordinates are 0. In the second block, we alternate 3 and 0, as
$(k+1)$
th coordinates are 0. In the second block, we alternate 3 and 0, as
![]() $3,0,3,0,\ldots ,0,3.$
The third is
$3,0,3,0,\ldots ,0,3.$
The third is
![]() $12,3,12,3,\ldots ,3,12.$
For the ith block,
$12,3,12,3,\ldots ,3,12.$
For the ith block,
![]() $(i>1),$
we use the ith and
$(i>1),$
we use the ith and
![]() $i-1$
th entries of
$i-1$
th entries of
![]() $Q_1$
and alternate them starting (and ending) with the ith. Note that the first and last vectors are identical.
$Q_1$
and alternate them starting (and ending) with the ith. Note that the first and last vectors are identical.
In this way, all consecutive vectors have distinct differences. If the differences in the last coordinate are the same in two pairs of consecutive vectors, then there are three cases.
-
• First, the two pairs are selected from the same
 $Q_k$
block. In this case, the differences of the first k coordinates are distinct by induction.
$Q_k$
block. In this case, the differences of the first k coordinates are distinct by induction. -
• The second case when one of the pairs is between two blocks. There is only one pair of blocks where the last and the first vectors have a given difference in the last coordinate, so the other pair is inside one block. But in the difference vector of pairs between blocks the first k coordinates are zero, while differences of consecutive vectors in the same block have some nonzero coordinates among the first
 $k.$
$k.$
-
• The third case is when one pair is in one block and the other is in another block. It is only possible if one pair is in a block with last coordinates
 $a,b,a,\ldots ,b,a$
and the other is in the block with
$a,b,a,\ldots ,b,a$
and the other is in the block with
 $b,a,\ldots ,a,b,$
but in this case the positions of the two pairs relative to their blocks are different due to parity, so by induction the differences are distinct in the first k coordinates.
$b,a,\ldots ,a,b,$
but in this case the positions of the two pairs relative to their blocks are different due to parity, so by induction the differences are distinct in the first k coordinates.

Figure 2 The recursion getting
![]() $Q_{k+1}$
from
$Q_{k+1}$
from
![]() $Q_k.$
$Q_k.$
Our next step is to construct an increasing sequence of numbers using the vectors in
![]() $Q_k$
keeping the same order and keeping the property that consecutive elements have distinct differences. If
$Q_k$
keeping the same order and keeping the property that consecutive elements have distinct differences. If
![]() $\vec {v_i}\in Q_k$
has coordinates
$\vec {v_i}\in Q_k$
has coordinates
![]() $\vec {v_i}^T=[\nu _1,\nu _2,\ldots ,\nu _k],$
then let us define
$\vec {v_i}^T=[\nu _1,\nu _2,\ldots ,\nu _k],$
then let us define
![]() $b_i=\nu _1+100\nu _2+100^2\nu _3+\ldots +100^{k-1}\nu _k.$
With this definition
$b_i=\nu _1+100\nu _2+100^2\nu _3+\ldots +100^{k-1}\nu _k.$
With this definition
![]() $b_i\leq 100^k,$
and the consecutive differences (in the order of the vectors in
$b_i\leq 100^k,$
and the consecutive differences (in the order of the vectors in
![]() $Q_k$
) are all distinct. To make the sequence monotone increasing, we define
$Q_k$
) are all distinct. To make the sequence monotone increasing, we define
 $$ \begin{align*} A=\left\{a_i \text{ }|\text{ } a_i=b_i+i100^k, 1\leq i\leq 43^k\right\}. \end{align*} $$
$$ \begin{align*} A=\left\{a_i \text{ }|\text{ } a_i=b_i+i100^k, 1\leq i\leq 43^k\right\}. \end{align*} $$
The sumset,
![]() $A+A,$
consists of sums
$A+A,$
consists of sums
 $a_i+a_j=b_i+b_j+(i+j)100^k.$
From the selection of the initial set,
$a_i+a_j=b_i+b_j+(i+j)100^k.$
From the selection of the initial set,
![]() $S,$
we see that
$S,$
we see that
 $\left |\left \{b_i+b_j | 1\leq i,j\leq 43^k\right \}\right |\leq 28^k,$
so we have the bound
$\left |\left \{b_i+b_j | 1\leq i,j\leq 43^k\right \}\right |\leq 28^k,$
so we have the bound
![]() $|A+A|\leq 28^k\cdot 2\cdot 43^k$
while
$|A+A|\leq 28^k\cdot 2\cdot 43^k$
while
![]() $|A|=43^k.$
By this construction we get a set
$|A|=43^k.$
By this construction we get a set
![]() $A,$
with distinct consecutive differences and
$A,$
with distinct consecutive differences and
![]() $|A+A|\leq 2|A|^{2-c}$
where
$|A+A|\leq 2|A|^{2-c}$
where
 $$ \begin{align*} c= \frac{\log{\frac{43}{28}}}{\log{43}}\approx 0.11406. \end{align*} $$
$$ \begin{align*} c= \frac{\log{\frac{43}{28}}}{\log{43}}\approx 0.11406. \end{align*} $$
From the construction, we see that we needed a set S with small sumset and large difference set. We were searching among Sidon sets, i.e., sets where all pairwise sums are distinct. In such sets, if the size of S is x then
 $|S+S|=\binom {x}{2}+x$
and
$|S+S|=\binom {x}{2}+x$
and
![]() $|S-S|= x(x-1)+1$
. As we are looking for a large c above, we want to find the maximum of the function
$|S-S|= x(x-1)+1$
. As we are looking for a large c above, we want to find the maximum of the function
 $$ \begin{align*} \frac{\log{\frac{x(x-1)+1}{\binom{x}{2}+x}}}{\log{x(x-1)+1}}, \end{align*} $$
$$ \begin{align*} \frac{\log{\frac{x(x-1)+1}{\binom{x}{2}+x}}}{\log{x(x-1)+1}}, \end{align*} $$
for positive
![]() $x.$
The maximum is
$x.$
The maximum is
![]() $0.114058\ldots $
when
$0.114058\ldots $
when
![]() $x \approx 6.99618$
, so we selected S to be a seven-element Sidon set,
$x \approx 6.99618$
, so we selected S to be a seven-element Sidon set,
![]() $\{0,1,3,7,12,22,30\}.$
▪
$\{0,1,3,7,12,22,30\}.$
▪
Acknowledgment
We would like to thank Endre Szemerédi and Ilya Shkredov for helpful discussions. We appreciate useful comments from the anonymous referee. Research was supported in part by the OTKA K 119528 and K129335 grants. The second author was supported by NSERC Discovery and NKFI KKP 133819 grants.