2 Proof of Proposition 1

The example of a Stein curve X is obtained by implanting generalized cusp singularities at the points $2,3, \ldots $ , of ${{\mathbb {C}}}$ , and then the existence of the function f is obtained via Cartan’s vanishing theorem on Stein spaces.

In order to proceed, let p and q be coprime integers $\geq $ 2. Consider the cusp-like irreducible and locally irreducible complex curve:

$$ \begin{align*}\Gamma=\{(z_1,z_2) \in {{\mathbb{C}}}^2 \;:\, z_1^p=z_2^q\} \subset {{\mathbb{C}}}^2.\end{align*} $$

Its normalization is ${{\mathbb {C}}}$ and $\pi :{{\mathbb {C}}} \longrightarrow \Gamma $ , $t \mapsto (t^q,t^p)$ , is the normalization map. Note that $\pi $ is a homeomorphism.

A continuous function $h:\Gamma \longrightarrow {{\mathbb {C}}}$ that is holomorphic off its zero set, but fails to be globally holomorphic, is produced as follows.

Select natural numbers m and n with $mq-np=1$ , and define $h:\Gamma \longrightarrow {{\mathbb {C}}}$ by setting for $(z_1,z_2) \in \Gamma $ ,

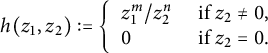$$\begin{align*}h(z_1,z_2):= \left\{ \begin{array}{ll} {z_1^m}/{z_2^n} & \mbox{ if } z_2 \neq 0, \\ 0 & \mbox{ if } z_2=0. \\ \end{array} \right. \end{align*}$$

It is easily seen that h is continuous (as $\pi $ is a homeomorphism, the continuity of h follows from that of $h \circ \pi $ , which is equal to the identity mapping on ${{\mathbb {C}}}$ ), h is holomorphic off its zero set (incidentally, here, the regular part ${\textrm {Reg}}(\Gamma )$ is the complement of this zero set), and h is not holomorphic about $(0,0)$ (use a Taylor series expansion about $(0,0) \in {{\mathbb {C}}}^2$ of a presumably holomorphic extension).

Furthermore, $h^k$ is globally holomorphic provided that $k \geq (p-1)(q-1)$ . (Because every integer at least $(p-1)(q-1)$ can be written in the form $\alpha p + \beta q$ with $\alpha ,\beta \in \{0, 1, 2, \ldots \}$ , and because $h^p$ and $h^q$ are holomorphic being the restrictions of $z_2$ and $z_1$ to $\Gamma $ , respectively.)

In addition, $z_1^a z_2^b h$ is holomorphic on $\Gamma $ provided that $ q \lfloor (m+a)/p \rfloor +b \geq n,$ where $\lfloor \cdot \rfloor $ is the floor function.

It is interesting to note that the stalk of germs of c-holomorphic functions ${\mathcal O}^{\textrm {c}}_0$ at $0$ is generated as an ${\mathcal O}_0$ -module by the germs at $0$ of $1, h, \ldots , h^{r}$ , where $r=\min \{p,q\}-1$ .

Now, for each integer $k \geq 2$ , let $\Gamma _k:=\{(z_1,z_2) \in {{\mathbb {C}}}^2 \;; \, z_1^k=z_2^{k+1}\}$ . As previously noted, $\Gamma _k$ is an irreducible curve whose normalization map is $\pi _k:{{\mathbb {C}}} \longrightarrow \Gamma _k, \, t \mapsto (t^{k+1},t^k)$ , and the function $h_k:\Gamma _k \longrightarrow {{\mathbb {C}}}$ defined for $(z_1,z_2) \in \Gamma _k$ by:

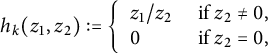$$\begin{align*}h_k(z_1,z_2):= \left\{ \begin{array}{ll} {z_1}/{z_2} & \mbox{ if } z_2 \neq 0, \\ 0 & \mbox{ if } z_2=0, \\ \end{array} \right. \end{align*}$$

has the following properties:

1. a _k ) The function $h_k$ is c-holomorphic.

2. b _k ) The power $h_k^{k-1}$ is not holomorphic.

3. c _k ) The function $z_1^{k-1}h_k$ is holomorphic, because it is the restriction of $z_2^k$ to $\Gamma _k$ .

Here, with these examples of singularities at hand, we change the standard complex structure of ${{\mathbb {C}}}$ at the discrete analytic set $\{2,3, \ldots \}$ by complex surgery, in order to obtain an irreducible Stein complex curve X and a discrete subset $\Lambda =\{x_k: k=2, 3, \ldots \}$ such that, at the level of germs, $(X,x_k)$ is biholomorphic to $(\Gamma _k,0)$ .

The surgery, that we recall for the commodity of the reader (because, in some monographs like [Reference Kaup and Kaup8], the subsequent condition $(\star )$ is missing), goes as follows.

Let Y and $U'$ be complex spaces together with analytic subsets A and $A'$ of Y and $U'$ , respectively, such that there is an open neighborhood U of A in Y and $\varphi :U \setminus A \longrightarrow U' \setminus A'$ that is biholomorphic.

Then, define:

$$ \begin{align*}X:=(Y \setminus A) \sqcup_\varphi U':= (Y \setminus A) \sqcup U'/_{\sim}\end{align*} $$

by means of the equivalence relation $U \setminus A \ni y \sim \varphi (y) \in U' \setminus A'$ .

Then, there exists exactly one complex structure on X such that $U'$ and $Y \setminus A$ can be viewed as open subsets of X in a canonical way provided that the following condition is satisfied:

1. (⋆) For every $y \in \partial U$ and $a' \in A'$ , there are open neighborhoods D of y in Y, $D \cap A=\emptyset $ , and B of $a'$ in $U'$ such that $\varphi (D \cap U) \cap B \subseteq A'.$

Thus, X is formed from Y by “replacing” A with $A'$ .

In practice, the condition $(\star )$ is fulfilled if $\varphi ^{-1}: U' \setminus A' \longrightarrow U \setminus A$ extends to a continuous function $\psi :U' \longrightarrow U$ such that $\psi (A')=A$ . In this case, if D and V are disjoint open neighborhoods of $\partial U$ and A in Y, respectively, then $B=A' \cup \varphi (V \setminus A)$ is open in $U'$ , because it equals $\psi ^{-1}(V)$ and $(\star )$ follows immediately. (This process is employed, for instance, in the construction of the blowup of a point in a complex manifold!)

Coming back to the construction of the example proving Proposition 1, consider $Y={{\mathbb {C}}}$ , $A=\{2,3, \ldots \}$ , and for each $k=2,3, \ldots $ , let $\Delta (k,1/3)$ be the disk in ${{\mathbb {C}}}$ centered at $k $ of radius $1/3$ that is mapped holomorphically onto an open neighborhood $U_k$ of $(0,0) \in \Gamma _k$ through the holomorphic map $t \mapsto \pi _k(z-k)$ . Applying surgery, we get an irreducible Stein curve X and the discrete subset $\Lambda $ with the aforementioned properties.

It remains to produce the function f as stated. For this, we let ${\mathcal I} \subset {\mathcal O}_X$ be the coherent ideal sheaf with support $\Lambda $ and such that ${\mathcal I}_{x_k}= \mathfrak {m}^{k-1}_{x_k}$ for $k=2,3 \ldots $ , where $\mathfrak {m}_{x_k}$ is the maximal ideal of the analytic algebra of the stalk of ${\mathcal O}_X$ at $x_k$ .

From the exact sequence:

$$ \begin{align*}0 \longrightarrow {\mathcal I} \longrightarrow {\mathcal O}^{\textrm{c}} \longrightarrow {\mathcal O}^{ \rm c}/{{\mathcal I}} \longrightarrow 0,\end{align*} $$

we obtain a c-holomorphic function f on X such that, for each $k=2,3, \ldots $ , at germs level, f equals $h_k$ (mod ${\mathcal I}_{x_k}$ ).

By properties ${\textbf { a}}_k)$ , ${\textbf { b}}_k)$ , and ${\textbf { c}}_k)$ from above, it follows that there does exist $\nu \in {{\mathbb {N}}}$ such that $f^\nu $ becomes holomorphic on X. (For instance, if $f=h_k+g_k^{k-1}$ , for certain $g_k \in \mathfrak {m}_{x_k}$ , then $f^{k-1}$ is not holomorphic about $x_k$ .)

3 Proof of Theorem 1

This is divided into four steps. In Step 1, we recall, following [Reference Chirka4], the multiplicity of an analytic set at a point. Then, in Step 2, we estimate the vanishing order of a c-holomorphic function germ at a point of its zero set in terms of the multiplicity of the analytic germ where it is defined. In Step 3, we collect some useful facts about ${\textrm {O}}^N$ -approximability due to Spallek [Reference Spallek13] and Siu [Reference Siu12]. Eventually, the proof of theorem is achieved in the fourth step.

Step 1. Let A be a pure k-dimensional locally analytic subset of ${{\mathbb {C}}}^n$ . Let $a \in A$ and select an $(n-k)$ -dimensional complex subspace $L \subset {{\mathbb {C}}}^n$ such that a is an isolated point of the set $A \cap (\{a\}+L)$ . Then, as we know, there is a domain $U \ni a$ in ${{\mathbb {C}}}^n$ such that $A \cap U \cap (\{a\}+L)=\{a\}$ and such that the projection $\pi _L:A \cap U \longrightarrow U^{\prime }_L \subset L^{\perp }$ along L is a d-sheeted analytic cover, for some $d \in {{\mathbb {N}}}$ , where $L^\perp $ is the orthogonal of L with respect to the canonical scalar product in ${{\mathbb {C}}}^n$ .

The critical analytic set $\Sigma $ of this cover does not partition the domain $U^{\prime }_L$ and is nowhere dense in it; therefore, the number of sheets of this cover does not change when shrinking U. Furthermore, if $z'$ is the projection of z in $L^\perp $ and $z' \in U^{\prime }_L \setminus \Sigma $ , then,

$$ \begin{align*}\sharp \,\, A \cap U \cap (\{z\}+L)=d,\end{align*} $$

and all d points of the fiber above $z'$ tend to a as $z' \to a'$ . This number is called the multiplicity of the projection $\pi _L|_A$ at a, and is denoted by $\mu _a(\pi _L|_A)$ .

For any point $x \in A$ in the above indicated small neighborhood $U \ni a$ , the number of sheets of the cover $A \cap U \longrightarrow U^{\prime }_L$ does not exceed d in a neighborhood of x (it may be less); hence, the function $\mu _x(\pi _L|_A)$ is upper semicontinuous on $A \cap U$ . See [Reference Chirka4, p. 102].

Thus, for every $(n-p)$ -dimensional complex plane $L \subset {{\mathbb {C}}}^n$ such that a is an isolated point in $A \cap (\{a\}+L)$ , the multiplicity of the projection $\mu _a(\pi _L|_A)$ is finite. The minimum of these numbers over all $L \in {\textrm {Gr}}(n-p,n)$ as above is denoted $\mu _a(A)$ and is called the multiplicity of A at a.

Furthermore, it can be shown that the multiplicity $\mu _a(A)$ does not depend on how A is locally embedded at a into a complex euclidean space.

Altogether, we get a function $A \ni x \mapsto \mu _x(A) \in {{\mathbb {N}}}$ that is upper semicontinuous. See [Reference Chirka4, p. 120].

Step 2. For the sake of simplicity, let $a=0$ , and for the complex subspace $L=\{0\} \times {{\mathbb {C}}}^{n-k}$ , the projection $\pi _L|_A$ realizes $\mu _0(A)$ , namely $\mu _0(\pi _L|_A)=\mu _0(A)$ .

With the necessary changes, by Step 1, we arrive at the following setup.

The set A is analytic in $D \times {{\mathbb {C}}}^{n-k}$ with D a domain of ${{\mathbb {C}}}^k$ , the map $\pi :A \longrightarrow D$ is induced by the first projection from ${{\mathbb {C}}}^k_z \times {{\mathbb {C}}}_w^{n-k}$ onto ${{\mathbb {C}}}^k_z$ , $A \ni x=(z,w) \mapsto \pi (x)=z$ , such that $\pi $ is a (finite) branched covering with image D, covering number $d:=\mu _0(A)$ , critical set $\Sigma $ , which is a nowhere dense analytic subset of D, and $\pi ^{-1}(0)=\{0\}$ .

Now, let $h:A \longrightarrow {{\mathbb {C}}}$ be any ${\textrm {c}}$ -holomorphic function. For every point $x=(z,w) \in (D \setminus \Sigma ) \times {{\mathbb {C}}}^{n-k}$ , we define the polynomial:

$$ \begin{align*}\omega(x,t)= \prod_{\pi(x')=z} (t-h(x')) = t^d + a_1(x) t^{d-1}+ \cdots + a_d(x).\end{align*} $$

Because h is holomorphic on the regular part $\text {Reg}(A)$ of A and h is continuous on A, a fortiori h is bounded on any compact subset of A (in particular, on $\pi ^{-1}(K)$ , for every compact set K of D), the coefficients $a_j$ are naturally holomorphic on $(D \setminus \Sigma ) \times {{\mathbb {C}}}^{n-k}$ and locally bounded on $D \times {{\mathbb {C}}}^k$ . Thus, granting Riemann’s extension theorem, they extend holomorphically to $D \times {{\mathbb {C}}}^{n-k}$ (we keep the same notations for the extensions). If, furthermore, $h(0)=0$ , then all coefficients $a_j(0)=0$ , because $\pi $ is proper and $\pi ^{-1}(0)=\{0\}$ .

Therefore, we obtain a distinguished Weierstrass polynomial of degree d, $W(x,t)= t^d + a_1(x) t^{d-1}+ \cdots + a_d(x)$ , which is the unique extension of $\omega $ to $D \times {{\mathbb {C}}}^{n-k}$ and such that $W(x,h(x))=0$ for all $x \in A$ .

Note that, if $W(x,t)=0$ , then the identity $|t|^d={\textrm {O}}(\|x\|)$ holds true as $(x,t) \to 0$ because

$|a_j(x)|= {\textrm {O}}(\|x\|)$ , or equivalently:

$$ \begin{align*}|t|={\textrm{O}}(\|x\|^{1/d}) \mbox{ as } (x,t) \to 0,\end{align*} $$

meaning that there are positive constants M and $\epsilon $ such that, if $W(x,t)=0$ and $\max \{|t|, \|x\|\}<\epsilon $ , then $|t| \leq M \|x\|^{1/d}$ .

To sum up, coming back to the general setting, and using that for two real numbers $\alpha $ and $\beta $ , one has $s^\alpha ={\textrm {O}}(s^\beta )$ as $(0,\infty ) \ni s \to 0$ if and only if $\alpha \geq \beta $ , by routine arguments, from Step 1 and the above discussion, we get the following fact.

1. (†) Let A be a locally analytic subset of ${{\mathbb {C}}}^n$ of pure dimension. Then, the multiplicity function $\mu _x(A)$ on $x \in A$ is upper semicontinuous. Furthermore, any point $a \in A$ admits an open neighborhood U in A such that, for every point $x_0 \in U$ and every nonconstant, ${\textrm {c}}$ -holomorphic germ $h:(A,x_0) \longrightarrow ({{\mathbb {C}}},0)$ , one has,

   $$ \begin{align*}|h(x)| ={\textrm{O}}(\|x-x_0\|^\alpha) \mbox{ as } A \ni x \rightarrow x_0,\end{align*} $$
   where $\alpha =1/{\mu _a(A)}$ .

In general, if $(A,x)= \cup _j (A_j,x)$ is the decomposition of the germ $(A,x)$ into its finitely many irreducible components, whose number might depend on $x \in A$ , then we set $\mu _x(A)= \max _j \mu _x(A_j)$ . The multiplicity function thus defined is upper semicontinuous on A, and the above “identity” in $(\dagger )$ holds for the exponent $\alpha $ given by $1/\alpha =\max _j \mu _a(A_j)$ .

For the commodity of the reader, we mention that, for any complex space X, we get a natural multiplicity function $X \ni x \mapsto \mu _x(X) \in {{\mathbb {N}}}$ that is upper semicontinuous, although this information is not used hereafter.

Step 3. From Spallek [Reference Spallek13], we recall the following notion. Let $A \subset {{\mathbb {C}}}^n$ be a set and a a point of A. We say that a germ function $\varphi :(A,a) \longrightarrow ({{\mathbb {C}}},\varphi (a))$ is ${\textrm {O}}^N$ -approximable at a if there exists a polynomial $P(z,\bar z) $ of degree at most $N-1$ in the variables $z_j-a_j, \overline {z_j-a_j}$ , $j=1, \ldots , n$ , such that,

$$ \begin{align*}|\varphi(z)-P(z,\bar z)|={\textrm{O}}(\|z-a\|^N) \mbox{ as } A \ni z \rightarrow a.\end{align*} $$

The following result due to Siu [Reference Siu12] improves onto Spallek’s similar one from [Reference Spallek13].

Step 4. To conclude the theorem, because the assertion to be proved is local, without any loss in generality, we may assume that X is an analytic subset of some open set of ${{\mathbb {C}}}^n$ .

Now, let K be a compact set of X. We claim that there is $\nu _K \in {{\mathbb {N}}}$ such that, for any ${\textrm {c}}$ -holomorphic function f on X that is holomorphic off its zero set $f^{-1}(0)$ , the power $f^\nu $ is holomorphic about K for all integers $\nu \geq \nu _K$ .

For this, consider a compact neighborhood $K^\ast $ of K in X. Because the function $X \ni x \mapsto \mu _x(X) \in {{\mathbb {N}}}$ is upper semicontinuous, there exists a natural number d such that $\mu _x(X) <d$ for all $x \in K^\ast $ .

We show that $\nu _K=d N$ is as desired, where N is selected according to Proposition 2 corresponding to the compact K of X.

Indeed, in order to show that $f^\nu $ is holomorphic about K for $\nu \in {{\mathbb {N}}}$ that satisfies $\nu \geq \nu _K$ , we apply Proposition 2, and for this, we need to check that the function $\text {Re} f^\nu $ is ${\textrm {O}}^N$ -approximable at any point $x \in K^\ast $ .

This follows by case analysis.

If $f(x) \neq 0$ , because f is holomorphic on the open set $X \setminus f^{-1}(0)$ of X, so that $\text {Re} f$ and ${\textrm {Im}} f$ are $C^\infty $ -smooth there, by Example 1, it follows that $\text {Re} f^\nu $ is ${\textrm {O}}^N$ -approximable at x.

If $f(x)=0$ , then by Example 1, the function $\text {Re} f^\nu $ is ${\textrm {O}}^N$ -approximable at x, because $\nu \geq d N=\nu _K$ .

This completes the proof of the theorem.

4 A final remark

Below we answer a question raised by Th. Peternell at the XXIV Conference on Complex Analysis and Geometry, held in Levico Terme, June 10–14, 2019. He asked whether or not a similar statement like Theorem 1 does hold for nonreduced complex spaces.

More specifically, let $(X,{\mathcal O}_X)$ be a not necessarily reduced complex space and $f:X \longrightarrow {{\mathbb {C}}}$ be continuous such that, if A denotes the zero set of f, then $X \setminus A$ is dense in X, and there is a section $\sigma \in \Gamma (X \setminus A,{\mathcal O}_X)$ whose reduction ${\textrm {Red}}(\sigma )$ equals $f|_{X \setminus A}$ .

Is it true that, for every relatively compact open subset D of X, there is a positive integer n such that $\sigma ^n$ extends to a section in $\Gamma (D,{\mathcal O}_X)$ ?

We show that the answer is “No.”

In order to do this, recall that, if R is a commutative ring with unit and M is an R-module, we can endow the direct sum $R \oplus M$ with a ring structure with the obvious addition, and multiplication defined by:

$$ \begin{align*}(r,m) \cdot (r',m')=(rr',rm'+r'm).\end{align*} $$

This is the Nagata ring structure from algebra [Reference Nagata9].

Now, if $(X,{\mathcal O}_X)$ is a complex space and $\mathcal F$ a coherent ${\mathcal O}_X$ -module, then ${\mathcal H}:={\mathcal O}_X \oplus {\mathcal F}$ becomes a coherent sheaf of analytic algebras and $(X,{\mathcal H})$ a complex space [Reference Forster5, Satz 2.3].

The example is as follows. Let ${}_n{\mathcal O}$ denote the structural sheaf of ${{\mathbb {C}}}^n$ . The above discussion produces a complex space $({{\mathbb {C}}},{\mathcal H})$ such that ${\mathcal H}={}_1{\mathcal O} \oplus {}_1{\mathcal O}$ , which can be written in a suggestive way ${\mathcal H}={}_1{\mathcal O}+\epsilon \cdot {}_1{\mathcal O}$ , where $\epsilon $ is a symbol with $\epsilon ^2=0$ . As a matter of fact, if we consider ${{\mathbb {C}}}^2$ with complex coordinates $(z,w)$ and the coherent ideal ${\mathcal I}$ generated by $w^2$ , then ${\mathcal H}$ is the analytic restriction of the quotient ${}_2{\mathcal O}/{{\mathcal I}}$ to ${{\mathbb {C}}}$ .

The reduction of $({{\mathbb {C}}},{\mathcal H})$ is $({{\mathbb {C}}},{}_1{\mathcal O})$ . A holomorphic section of ${\mathcal H}$ over an open set $U \subset {{\mathbb {C}}}$ consists of couple of ordinary holomorphic functions on U.

Now, take f the identity function ${\textrm {id}}$ on ${{\mathbb {C}}}$ , and the holomorphic section $\sigma \in \Gamma ({{\mathbb {C}}}^\star ,{\mathcal H})$ given by $\sigma = {\textrm {id}} + \epsilon g$ , where g is holomorphic on ${{\mathbb {C}}}^\star $ having a singularity at $0$ , for instance, $g(z)= 1/z$ .

Obviously, the reduction of $\sigma $ is the restriction of ${\textrm {id}}$ on ${{\mathbb {C}}}^\star $ , and no power $\sigma ^k$ of $\sigma $ extends across $0$ to a section in $\Gamma ({{\mathbb {C}}}, {\mathcal H})$ , because $\sigma ^k={\textrm {id}} + \epsilon kg$ and g does not extend holomorphically across $0 \in {{\mathbb {C}}}$ .