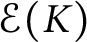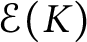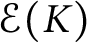1 Introduction
If X is a Banach space with unconditional topological basis
$(f_k)_{k=1}^{\infty }$
, then any permutation
$\sigma : \mathbb {N}\rightarrow \mathbb {N}$
and a sequence of nonzero scalars
$(\rho _k)_{k=1}^{\infty }$
generate another basis
$(e_k)_{k=1}^{\infty }$
with
$e_k=\rho _k\,f_{\sigma (k)}.$
In the case when any unconditional basis
$(e_k)_{k=1}^{\infty }$
of X can be represented in this form, we say that X has unique unconditional basis (up to permutation). The property of unicity of basis is quite exceptional in the context of Banach spaces [Reference Lindenstrauss and Zippin11].
We observe the opposite situation in the class of nuclear Fréchet (NF) spaces, where, by T.9 in [Reference Mityagin14], all bases are absolute. In the field, similar in the above sense, bases are called quasi-equivalent. Namely, two bases
$(e_k)_{k=1}^{\infty }$
and
$(f_k)_{k=1}^{\infty }$
in an NF space X are quasi-equivalent if there exist a permutation
$\sigma $
, scalars
$\rho _k \ne 0$
, and an isomorphism
$T:X\to X$
such that
$Te_k=\rho _k\,f_{\sigma (k)}$
for each k.
Let us note some results for NF spaces on this issue. The first achievement is due to Dragilev who proved in [Reference Dragilev5] that all bases in the space of analytic functions on the unit disc are quasi-equivalent. In [Reference Mitjagin12–Reference Mityagin14], Mityagin generalized this to the case of Hilbert scales. All bases in X are quasi-equivalent if X has a regular basis [Reference Crone and Robinson4, Reference Kondakov10] or a basis of type
$G_1$
or
$G_{\infty }$
[Reference Alpseymen1]. Zaharjuta et al. showed the quasi-equivalence of bases in special Köthe power spaces [Reference Chalov and Zahariuta3, Reference Zaharjuta15], in tensor products of power series spaces with their duals [Reference Goncharov, Terzioğlu and Zahariuta8] and in some other cases. The conjecture on the quasi-equivalence of bases in NF spaces was implicitly stated in [Reference Mitjagin13] (Problem 12) and in [Reference Mitjagin12], see also Problem 8 in [Reference Aytuna, Djakov, Goncharov, Terzioğlu and Zahariuta2]. We can quote Zobin [Reference Zobin16], who wrote 20 years ago: “There was a common belief at that time that the conjecture will be proven very soon. To everybody’s great surprise, it is still an open question.” Two decades later, the status of the conjecture remains the same. In our opinion, the quasi-equivalence problem is one of the most important open problems in the structure theory of NF spaces.
Here, we discuss this problem for the class of Whitney spaces. In [Reference Goncharov6], the first author constructed bases in the spaces
$\mathcal {E}(K^{(\alpha _{n})})$
, see Section 2 for the definition of the set
$K^{(\alpha _{n})}$
. Recently, in [Reference Goncharov and Şengül7], bases were presented in the Whitney spaces for more general Cantor-type sets
$K=K_{(N_{n})}^{(\alpha _{n})}$
. In the case of a “small” set K (here, this means that the logarithmic dimension
$\lambda _{0}(K)$
of the set is smaller than 1), an interpolating Faber basis was presented in
$\mathcal {E}(K)$
. Consequently, each space has many bases, and for small sets, at least one basis consists of polynomials. We answer in the affirmative to the question posed in [Reference Goncharov6] about quasi-equivalence of these bases. The proof is given for the space
$\mathcal {E}(K^{(\alpha _{n})})$
with
$\alpha _{n}\geq 2,$
which implies
$\lambda _{0}(K^{(\alpha _{n})})\leq 1.$
We think that a slight modification of the proof can be applied to other cases as well.
Let X be an NF space with a topology given by an increasing sequence of seminorms
$(||\cdot ||_p)_{p=1}^{\infty }$
and a basis
$(e_n)_{n=1}^{\infty }.$
Then, X is isomorphic to the Köthe echelon space
$K(A)$
with the matrix
$A=(||e_n||_p)_{n,p=1}^{\infty }.$
Beginning with his first papers on this topic, Mityagin proposed a combinatorial technique based on modifications of the Hall–König theorem to compare Köthe matrices for different bases. This method was widely used in the works cited above. In our paper, we explicitly construct the desired isomorphism.
2 Uniform distribution of points on a Cantor-type set
Here, we follow [Reference Goncharov6, Reference Goncharov and Ural9]. Let
$(\ell _{s})_{s=0}^{\infty }$
be a sequence such that
$ \ell _{0}=1$
and
$0<3\ell _{s+1}\leq \ell _{s}$
for
$s \in \Bbb N_0:=\{0,1,\ldots \}.$
For
$E_{0}=I_{0,1}= [0,1]$
and given
$E_{s}$
, a union of
$2^{s}$
closed basic intervals
$I_{j,s}$
of length
$\ell _{s}$
, we obtain
$E_{s+1}$
by replacing each
$I_{j,s}$
for
$1\leq j\leq 2^{s}$
by two adjacent subintervals
$I_{2j-1,s+1}$
and
$I_{2j,s+1}$
. Then,
$h_{s}=\ell _{s}-2\,\ell _{s+1}$
is the distance between them. By assumption,
$h_s\geq \ell _{s+1}$
for each s. We consider a Cantor-type set
$K=\bigcap _{s=0}^{\infty } E_{s}$
, defined by the sequence
$(\ell _{s})_{s=0}^{\infty }$
.
Denote
$\alpha _1=1$
and
$\alpha _s = \frac {\log \ell _s}{\log \ell _{s-1}}$
for
$s\geq 2.$
Thus,
$\ell _s=\ell _1^{\,\alpha _1 \,\cdots \, \alpha _s}.$
By
$K^{(\alpha _{s})}$
, we denote a set associated with the sequence
$(\alpha _{s})_{s=1}^{\infty }$
.
Let x be an endpoint of some basic interval. Then, there exists a minimal number s (the type of x) such that x is the endpoint of some
$I_{j,\,m}$
for every
$m\geq s.$
By
$X_k$
, we denote all endpoints of type k. Hence,
$X_0:=\{0, 1\}, X_1:=\{\ell _1, 1-\ell _1\}, X_2:=\{\ell _2, \ell _1-\ell _2, 1-\ell _1+\ell _2, 1-\ell _2\},$
etc. Set
$Y_s=\cup _{k=0}^s X_k.$
Then,
$\#(Y_s)=2^{s+1}.$
Here and below,
$\#(Z)$
denotes the cardinality of a finite set Z. Given such set, let
$m(j,s,Z):=\#(Z\cap I_{j,s}).$
In addition, for each
$x\in \Bbb R$
, by
$d_{k}(x,Z), k=1, 2, \ldots , \#(Z),$
we denote the distances
$|x-z_{j_k}|$
from x to points of Z arranged in the nondecreasing order. In what follows, we omit the parameter
$ Z $
in
$ m(\cdot ,\cdot ,Z), d_k(\cdot , Z) $
if this does not cause misunderstanding.
We put all points from
$\cup _{k=0}^{\infty } X_k$
in order by means of the rule of increase of type. For the points from
$X_0\cup X_1$
, we take
$ x_1=0, x_2 =1, x_3 = \ell _1, x_4 = 1-\ell _1.$
To put the points from
$X_2$
in order, we increasingly arrange the points from
$Y_1$
, so
$Y_1=\{x_1,x_3,x_4,x_2\}.$
After this, we increase the index of each point by 4. This gives the ordering
$X_2=\{x_5,x_7,x_8,x_6\}.$
Similarly, indices of increasingly arranged points from
$Y_{k-1}=\{x_{i_1},x_{i_2},\cdots , x_{i_{2^k}}\}$
define the ordering
$X_k=\{x_{i_1+2^k},x_{i_2+2^k},\ldots , x_{i_{2^k}+2^k}\}.$
We see that
$x_{j+2^k}=x_j \pm \ell _k,$
where the sign is uniquely defined by
$j.$
More precisely, every natural number N greater than 1 can be uniquely written as
$N=1+2^{p_1}+2^{p_2}+\cdots +2^{p_n}$
with
$0\leq p_1< p_2 < \cdots < p_n.$
Then,
$x_N=\ell _{p_1}-\ell _{p_2}+\cdots +(-1)^{n-1}\ell _{p_n}.$
Thus, for
$j=N-2^{p_n}$
, we have
$x_{j+2^{p_n}}=x_j +(-1)^{n-1}\ell _{p_n},$
where the degree of
$-1$
is the number of terms except 1 in the representation of j. For example,
$x_{12}=x_{4+2^3}=x_4+\ell _3,$
because
$4=1+2^0+2^1.$
A useful property of this order is that for each k, the points
$(x_p)_{p=1}^k$
are distributed uniformly on
$K^{(\alpha _{s})}$
in the following sense.
Suppose we are given a set
$U=(z_p)_{p=1}^{k}$
of points from a Cantor-type set K. We say that points are uniformly distributed on K if, for each
$s\in \Bbb N$
and
$i,j \in \{1,2, \ldots , 2^s\}$
, we have
$$ \begin{align} |m(i,s,U) - m(j,s,U)|\leq 1, \end{align} $$
so any two intervals of the same level contain the same number of points from U or, perhaps, one of the intervals contains one extra point
$z_p,$
compared to another interval.
Suppose points
$Z=(x_p)_{p=1}^k$
are chosen by the rule of increase of type,
$2^q\leq k<2^{q+1}.$
Then, the binary representation
$$ \begin{align} k=2^q+2^r+\cdots+2^t+\cdots +2^w \,\,\,\mbox{with} \,\,\,0\leq w < \cdots<t<\cdots <r<q \end{align} $$
generates the decomposition
$Z=Z_q \cup Z_r \cup \cdots \cup Z_w$
with
$Z_q=Y_{q-1}$
and
$Z_r \cup \cdots \cup Z_w \subset X_q.$
Let
$\mathcal K :=\{w, \cdots , r, q\}$
be the set of exponents in (2.2). For fixed
$i \in \mathcal K,$
each basic interval of ith level contains just one point from
$Z_i.$
Moreover, for each basic interval
$I=I_{j,s},$
the points
$(x_{i,j,s})_{i=1}^m=Z\cap I$
coincide with points selected on I by the rule of increase of type or mirror symmetric to them.
We say that a Cantor-type set K is
$\ell $
-
$regular$
if
$$ \begin{align} \ell^2_{s+1}\geq \ell_{s}\ell_{s+2}\,\,\,\,\,\,\mbox{for }\,\,\, s \in \Bbb N. \end{align} $$
It is easily seen that the following Cantor-type sets have this property.
-
(1)
$K_{\beta },$
where
$\ell _{s}=\beta ^{s}$
for
$s \in \Bbb N_0$
with
$0<\beta <1/2$
. In particular, the Cantor ternary set
$K_{1/3}$
is
$\ell $
-
$regular$
. -
(2)
$K^{\alpha },$
where
$\alpha _s=\alpha $
for
$s\geq 2$
with
$\alpha>1.$
-
(3)
$K^{(\alpha _{s})}$
with
$\alpha _{s}(2-\alpha _{s+1}) \leq 1$
for
$s\geq 2$
. Thus, a set
$K^{(\alpha _{s})}$
with
$\alpha _{s}\geq 2$
for
$s\geq 2$
is
$\ell $
-regular.
Lemma 2.1 If a Cantor-type set K is
$\ell $
-regular, then the value
$\frac {h_s}{\ell _s}$
increases, so
$\min _s \frac {h_s}{\ell _s}=h_0.$
Proof It is evident, because
$\frac {h_s}{\ell _s}=1-2\frac {\ell _{s+1}}{\ell _s}$
. ▪
We consider the space
$\,{\mathcal {E}} (K^{(\alpha _{s})})$
of Whitney functions on s
$K^{(\alpha _{s})}$
with the topology defined by the norms
$$ \begin{align*}||f||_q = |f|_q + \sup \left\{ \frac{|(R_{y}^{q} f)^{(i)}(x)|}{|\,x-y|^{q-i}} : x,y \in K^{(\alpha_{s})} ,x \neq y, i = 0,1,\ldots\ q \right\}, q \in \Bbb N_0,\end{align*} $$
where
$|f|_{\,q}= \sup \{ |f^{(i)} (x)| : x \in K^{(\alpha _s)} , i \leq q \}$
and
$R_{y}^{q}f(x) = f(x) - T_{y}^{q} f(x) $
is the Taylor remainder.
3 Correspondence between bases
Recall two theorems from [Reference Goncharov6]. Let
$(x_i)_{i=1}^{\infty }$
be chosen by the rule of increase of type. Define
$e_0\equiv 1$
and
$e_k(x) = \prod _{j=1}^k(x-x_j)$
. In the case of rarefied sets, these functions form an interpolating Faber basis, that is, basis of polynomials such that degrees of polynomials coincide with numbers of basis elements. Biorthogonal functionals are given as divided differences
$\xi _k(f) =[x_1,x_2,\ldots ,x_{k+1}]f.$
Theorem 3.1 [Reference Goncharov6, T.1]
If
$ \alpha _s \geq 2$
for
$s\geq 2$
, then the sequence
$(e_k)_{k=0}^{\infty }$
is a Schauder basis in the space
${\mathcal E}(K^{(\alpha _{s})})$
.
On the other hand, in any space
${\mathcal E}(K^{(\alpha _{s})})$
, we can present a variety of bases consisting of local polynomials. Let us fix a nondecreasing sequence of natural numbers
$(n_s)_{s=0}^{\infty }$
with
$n_s \nearrow \infty $
such that
$$ \begin{align} {\overline{\lim}}_s [n_s-\log_2(\alpha_1\,\alpha_2\cdots \alpha_s)]<\infty. \end{align} $$
Let
$ N_s= 2^{n_s}.$
The condition above implies that for some
$Q>0$
the sequence
$(2^{N_s}\,\ell _s^Q)_{s=0}^{\infty }$
is bounded and we can apply
Theorem 3.2 [Reference Goncharov6, T.2]
If a nondecreasing unbounded sequence
$\,(N_s)_{s=0}^{\infty }$
of natural numbers of the form
$\,N_s = 2^{n_s}$
is such that for some Q the sequence
$\,(2^{N_s}\,l_{s}^Q)_{s=0}^{\infty }$
is bounded, then the functions
$(e_{n,\,j,\,s})_{s=0,\,j=1,\,n=M_s}^{\,\,\,\infty , \,\,\,j=2^s,\,\,\,n=N_s}$
form a basis in the space
${\mathcal E}(K^{(\alpha _{s})})$
.
Here,
$e_{n,j,\,s} = \prod _{i=1}^n(x-x_{i,j,\,s})$
if
$x\in K^{(\alpha _{s})}\cap I_{j,s}$
and
$e_{n,j,\,s} = 0$
otherwise on
$K^{(\alpha _{s})}$
with the points
$(x_{i,j,\,s})_{i=1}^n$
chosen on
$I_{j,s}$
by the rule of increase of type if j is odd or mirror symmetric to them if j is even.
Our next goal is to number these functions accordingly. We will denote the resulting sequence by
$(f_k)_{k=0}^{\infty }$
. First, for
$s=0$
and
$0\leq k \leq N_0$
, we take
$f_k=e_k=e_{k,1,0}.$
Let us consider functions corresponding to
$s=1.$
The last functional of the previous level
$\xi _{N_0}(f)$
is defined by the points
$(x_i)_{i=1}^{N_0+1},$
where the left subinterval
$I_{1,1}$
contains
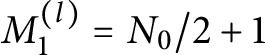$ M_1^{(l)}=N_0/2+1$
of them, whereas the right
$I_{2,1}$
does
$ M_1^{(r)}=N_0/2$
. On both intervals, we consider
$e_{n,\,j,\,1}$
for n starting with the corresponding
$ M_1$
and ending with the same value
$ N_1.$
In order to number them, for each k, we look at the position of
$x_{k+1}.$
For
$k=N_0+1$
, the point
$x_{N_0+2}$
belongs to
$I_{2,1}$
, so we take
$f_{N_0+1}=e_{N_0/2,\,2,\,1}.$
It is important to notice that the functions
$e_{N_0+1}$
and
$f_{N_0+1}$
have the same zeros on
$I_{2,1}$
. For
$k=N_0+2$
, the point
$x_{N_0+3}$
belongs to
$I_{1,1}$
and we take
$f_{N_0+2}=e_{N_0/2+1,\,1,\,1}.$
Here, as above,
$e_{N_0+2}$
and
$f_{N_0+2}$
have the same zeros on
$I_{1,1}$
. We continue in this fashion to obtain
$f_k$
as a certain
$e_{n,\,j,\,1},$
where
$j\in \{1,2\}$
is defined by the condition
$x_{k+1}\in I_{j,1}$
. The functions
$f_k$
and
$e_k$
have the same zeros on
$I_{j,1}$
. The total number of functions
$e_{n,\,j,\,1}$
is
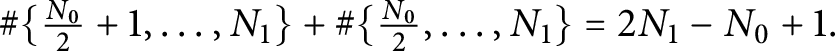$\#\{\frac {N_0}{2}+1,\ldots , N_1\}+\#\{\frac {N_0}{2},\ldots , N_1\}=2N_1-N_0+1.$
Let us calculate the number
$V_1$
of k corresponding to
$s\leq 1.$
It is a sum of
$N_0+1$
functions of the zero level and
$2N_1-N_0+1$
functions of the first level, that is,
$V_1=2N_1+2$
. We start enumeration from 0. Therefore, the value
$s = 1$
corresponds to the functions
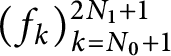$(f_k)_{k=N_0+1}^{2N_1+1}$
.
Continuing in this manner, we obtain the number
$V_s=2^s(N_s+1)$
of k corresponding to levels
$0, 1, \ldots , s.$
Then,
$f_k$
for
$V_{s-1}\leq k<V_s$
correspond to the levels
$s.$
Let us consider these values in detail and, for each k, find
$\deg \tilde {f_k},$
where
$\tilde {f_k}$
is the analytic continuation of the corresponding
$e_{n,j,\,s}$
from
$I_{j,s}$
to
$\Bbb R$
.
As in [Reference Goncharov6], we consider
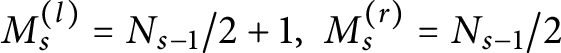$M_s^{(l)}=N_{s-1}/2+1, \,\,M_s^{(r)}= N_{s-1}/2$
. Each
$I_{i,s-1}$
contains subintervals
$I_{2i-1,s}$
and
$I_{2i,s}$
. For
$j=2i-1$
, we consider
$e_{n,j,\,s}$
with
$M_s^{(l)}\leq n \leq N_s$
, while
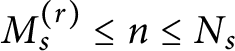$M_s^{(r)}\leq n \leq N_s$
for
$j=2i.$
Hence, there are
$2^{s-1}$
right subintervals
$I_{2i,s}$
and for
$V_{s-1}\leq k<V_{s-1}+2^{s-1}$
, we get
$\deg \tilde {f_k}=N_{s-1}/2$
. After this, each of extra
$2^s$
zeros of
$e_k$
will add one to degrees of
$\tilde {f_k}$
. Hence, for k with
$$ \begin{align*}V_{s-1}+2^{s-1}+(i-1)2^s \leq k<V_{s-1}+2^{s-1}+i\,\,2^s,\end{align*} $$
we have
$\deg \tilde {f_k}=N_{s-1}/2+i.$
Here,
$1\leq i \leq N_s -N_{s-1}/2.$
Indeed, the maximal value of k on sth level is
$V_{s-1}+2^{s-1}+(N_s -N_{s-1}/2)\,2^s-1=V_s-1$
and
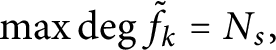$\max \deg \tilde {f_k}=N_s,$
as expected.
Thus, all functions
$e_{n,j,\,s}$
are included in the sequence
$(f_k)_{k=0}^{\infty }$
and, for each
$f_k=e_{n,j,\,s}$
, the functions
$e_k$
and
$e_{n,j,\,s}$
have the same zeros on
$I_{j,s}.$
The bijection
$f_k \leftrightarrow e_k$
will define the desired isomorphism T. We need to find appropriate coefficients
$\rho _k.$
4 Estimations of norms
For each
$n\in \Bbb N,$
let
$\pi _n=\pi _{n,0}:=\ell _n\,\ell _{n-1}\,\ell _{n-2}^2\,\ell _{n-3}^4 \cdots \ell _{j}^{2^{n-j-1}}\cdots \ell _{0}^{2^{n-1}}.$
Similarly, for
$n,s\in \Bbb N,$
set
$\pi _{n,s}:=\ell _{n+s}\,\ell _{n+s-1}\,\ell _{n+s-2}^2 \cdots \ell _{j+s}^{2^{n-j-1}}\cdots \ell _{s}^{2^{n-1}}.$
Each
$\pi _{n,s}$
has
$2^n$
terms.
We proceed to estimate
$||e_k||_p$
. Recall that the set
$Z=(x_i)_{i=1}^k$
of zeros of
$e_k$
is chosen by the rule of increase of type. Suppose
$2^q\leq k<2^{q+1}.$
We use the representation (2.2), the corresponding set
$\mathcal K$
, and the product
$\prod _{i\in \mathcal K} \pi _i.$
Given any product
$\prod _{j=1}^N \lambda _j$
with
$\lambda _j\geq 0$
and
$p<N,$
by
$(\prod _{j=1}^N \lambda _j)_p$
, we denote this product without p smallest terms.
Lemma 4.1 Let
$1\leq p<k.$
Then,
$h_0^k\,(\prod _{i\in \mathcal K} \pi _i)_{p-1}\leq ||e_k||_p\leq 5(3\,k)^p\,(\prod _{i\in \mathcal K} \pi _i)_p.$
Proof Fix
$x\in K^{(\alpha _{s})}.$
Then,
$|e_k(x)|= \prod _{j=1}^k d_j(x, Z)=\prod _{i\in \mathcal K} \prod _{j=1}^{2^i} d_j(x, Z_i).$
Points from
$Z_i$
are distributed uniformly on
$K^{(\alpha _{s})}.$
Hence,
$d_1(x, Z_i)\leq \ell _i, d_2(x, Z_i)\leq \ell _{i-1}.$
For the next two indices, we have
$d_j(x, Z_i)\leq \ell _{i-2},$
etc. Thus,
$\prod _{j=1}^{2^i} d_j(x, Z_i)\leq \pi _i$
and
$|e_k(x)|\leq \prod _{i\in \mathcal K} \pi _i.$
The pth derivative of
$e_k$
at x is a sum of
$k!/(k-p)!$
products, where each product contains
$k-p$
terms of the type
$x-x_j$
. Hence,
$$ \begin{align*}|e_k^{(p)}(x)|\leq k^p\, \prod_{j=p+1}^k d_j(x,Z)=k^p\,\left(\prod_{i\in \mathcal K} \pi_i\right)_p.\end{align*} $$
This gives
$$ \begin{align*}|e_k|_p\leq k^p\,\left(\prod_{i\in \mathcal K} \pi_i\right)_p.\end{align*} $$
As for the norms
$||e_k||_p$
, we completely repeat the reasoning from the proof of Theorem 1 in [Reference Goncharov6], see page 354:
$$ \begin{align} ||e_k||_p\leq 5(3\,k)^p\,\left(\prod_{i\in \mathcal K} \pi_i\right)_p. \end{align} $$
We now turn to lower bound of
$||e_k||_p$
. Clearly,
$||e_k||_p\geq |e_k^{(p)}(0)|.$
As above,
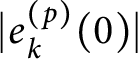$|e_k^{(p)}(0)|$
is a sum of
$k!/(k-p)!$
products, each of
$k-p$
terms. Here, all products have the same sign, so we can neglect all products except one with largest terms:
$$ \begin{align} ||e_k||_p \geq \left(\prod_{j=1}^k d_j(0, Z)\right)_p. \end{align} $$
Of course,
$d_1(0, Z)=0.$
To estimate
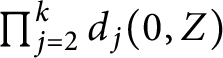$\prod _{j=2}^k d_j(0, Z)$
from below in terms of
$\pi _i$
, let us consider (2.2). We use the method from Lemma 2.2 in [Reference Goncharov and Ural9]. First, consider distances from 0 to the points from
$Z_q:\, d_2(0, Z_q)=\ell _{s-1}>h_{s-1},\, d_3(0, Z_q)=\ell _{q-2}-\ell _{q-1}>h_{q-2}, d_4(0, Z_q)=\ell _{q-2}>h_{q-2}, \ldots $
Continuing in this fashion, we get
$$ \begin{align} \prod_{j=2}^{2^q} d_j(0, Z_q)\geq h_{q-1}\,h_{q-2}^2\,h_{q-3}^4 \cdots h_{0}^{2^{q-1}}= \ell^{-1}_{q}\,\pi_q \, \prod_{i=0}^{q-1}\left(\frac{h_i}{\ell_i}\right)^{2^{q-1-i}}\geq \ell^{-1}_{q}\,\pi_q \,h_0^{2^q-1}, \end{align} $$
by Lemma 4.5.
By the rule of increase of type, the first
$2^q$
points are all endpoints of basic intervals of
$(q-1)$
st type. The next
$2^r$
points (in increasing order) are:
$\ell _q, \ell _{r-1}-\ell _q, \ell _{r-2}-\ell _{r-1}+\ell _q, \ell _{r-2}-\ell _q, \ldots $
They define
$d_j(0, Z_r)$
. As above, we get
$$ \begin{align} \prod_{j=1}^{2^r} d_j(0, Z_r)\geq \frac{\ell_q}{\ell_r}\,\pi_r \,h_0^{2^r}. \end{align} $$
Other indices from the set
$\mathcal K =\{w, v,\ldots ,t, r, q\}$
can be handled in the same way. Combining (4.3) with (4.4) and analogous inequalities for other
$i\in \mathcal K$
yields
$$ \begin{align*}\prod_{j=2}^k d_j(0, Z) \geq h_0^k\,\ell^{-1}_{q}\,\pi_q \,\frac{\ell_q}{\ell_r}\,\pi_r \frac{\ell_r}{\ell_t}\,\pi_t \cdots \frac{\ell_v}{\ell_w}\,\pi_w= h_0^k\,\ell^{-1}_{w}\,\prod_{i\in \mathcal K} \pi_i.\end{align*} $$
We neglect
$\ell ^{-1}_{w}$
and note that
$(\prod _{j=1}^k d_j(0, Z))_p\geq (\prod _{i\in \mathcal K} \pi _i)_{p-1}.$
By (4.2), we have the desired lower bound. ▪
In an exactly similar way, we estimate norms of elements of local bases. Let
$2^m\leq n< 2^{m+1},$
so
$n=\sum _{m_i \in \mathcal M} 2^{m_i}$
, where
$\mathcal M =\{m_y, \ldots , m_2, m_1\}$
with
$0\leq m_y<\cdots < m_2 < m_1=m.$
Here, we replace
$\frac {h_0}{\ell _0}$
with
$\frac {h_s}{\ell _s}$
and, as in [Reference Goncharov6], note that the points from
$K^{(\alpha _s)}\setminus I_{j,s}$
have no influence on the estimation of
$||e_{n,\,j,\,s}||_{p}$
for
$p<n,$
because
$dist(I_{j,s},K^{(\alpha _s)}\setminus I_{j,s}) = h_{s-1}$
is larger than
$\ell _s.$
Lemma 4.2 If
$1\leq p<n$
, then
$$ \begin{align*}\left(\frac{h_s}{\ell_s}\right)^n\,\left(\prod_{m_i\in \mathcal M} \pi_{m_i,s}\right)_{p-1}\leq ||e_{n,j,\,s}||_p\leq 5(3\,n)^p\, \left(\prod_{m_i\in \mathcal M} \pi_{m_i,s}\right)_p.\end{align*} $$
It should be noted that bases above are not regular, so the arguments from [Reference Crone and Robinson4, Reference Kondakov10] cannot be used to show their quasi-equivalence. We recall the definition of regular bases.
A basis
$(b_k)_{k=0}^{\infty }$
in an NF space X is regular if there is a fundamental system of seminorms
$(||\cdot ||_p)_{p=0}^{\infty }$
in X such that for each
$p,q$
with
$p<q$
, the sequence
$\frac {||b_k||_p}{ ||b_k||_q}$
monotonically tends to 0 as
$k\to \infty .$
Let us show that the ratio
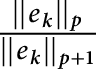$\frac {||e_k||_p}{||e_k||_{p+1}}$
is not decreasing. The exact calculation of the norm
$||e_k||_p$
, in general, is rather sophisticated. We restrict ourselves to small values of
$k, p$
and the case
$\ell _1<\frac {1}{5}.$
We proceed to show that
$$ \begin{align} \frac{||e_2||_0}{||e_2||_1}< \frac{||e_3||_0}{||e_3||_1}. \end{align} $$
For
$e_2(x)=x^2-x$
, it is easily seen that
$|e_2|_0=|e_2(\ell _1)|=\ell _1(1-\ell _1),\,||e_2||_0=2 \ell _1(1-\ell _1)$
, and
$|e_2|_1=e^{\prime }_2(1)=1$
with
$$ \begin{align*}\sup \left\{ \frac{|(R_{y}^{1} e_2)^{(i)}(x)|}{|x-y|^{1-i}}: x,y \in K^{(\alpha_{s})} ,x \neq y, i = 0,1\right\}=(R_{0}^{1} e_2)'(1)=2.\end{align*} $$
Thus, the left-hand side of (4.5) is
$\frac {2}{3}\ell _1(1-\ell _1).$
On the other hand, for
$e_3(x)=x(x-1)(x-\ell _1)$
, we have
$|e_3|_0=|e_3(1-\ell _1)|=\ell _1(1-\ell _1)(1-2\ell _1)$
and
$\sup _{x,y\in K} |e_3(x)-e_3(y)|=e_3(\ell _2)-e_3(1-\ell _1).$
From this,
$||e_3||_0=2 \ell _1(1-\ell _1)(1-2\ell _1)+\ell _2(1-\ell _2)(\ell _1-\ell _2).$
It is straightforward to show that
$|e_3|_1=e^{\prime }_3(1)=1-\ell _1.$
We proceed to analyze
$(R_{y}^{1} e_3)(x)=e_3(x)-e_3(y)-e^{\prime }_3(y)(x-y)=(x-y)[x^2+xy-2y^2-(1+\ell _1)(x-y)].$
We will denote by g the function in square brackets. Now, the task is to find the maximum value of
$|g(x,y)|$
on the set
$K^{(\alpha _{s})}\times K^{(\alpha _{s})},$
which is a subset of
$E_1\times E_1,$
where
$E_1=[0,\ell _1]\cup [1-\ell _1,1].$
The set
$E_1\times E_1$
is a union of four squares. For the squares
$Q_1=[0,\ell _1]\times [0,\ell _1], Q_2=[1-\ell _1,1]\times [0,\ell _1], Q_3=[1-\ell _1,1]\times [1-\ell _1,1]$
, the representation
$g(x,y)=(x-y)(x+2y-1-\ell _1)$
implies
$|g(x,y)|\leq 1-\ell _1,$
as is easy to check. Let us consider
$(x,y)\in Q_4=[0,\ell _1]\times [1-\ell _1,1].$
Here, for a fixed x, the function
$h(y):=|g(x,y)|$
is an upward parabola
$(y-x)(x+2y-1-\ell _1)$
with the vertex below the line
$y=1-\ell _1.$
Hence,
$\max _{1-\ell _1\leq y \leq 1} h(y)=h(1)=-x^2+x\ell _1+1-\ell _1$
. For
$x\in [0,\ell _2]\cup [\ell _1-\ell _2,\ell _1]$
, the function
$-x^2+x\ell _1+1-\ell _1$
attains its maximum at
$x = \ell _2.$
Thus,
$$ \begin{align*}\sup \left\{ \frac{|(R_{y}^{1} e_3)(x)|}{|x-y|}: x,y \in K^{(\alpha_{s})} ,x \neq y \right\}=|g(\ell_2,1)|=1-\ell_1+\ell_1 \ell_2-\ell_2^2.\end{align*} $$
Similarly,
$$ \begin{align*}\sup \Big\{ |(R_{y}^{1} e_3)'(x)|: x,y \in K^{(\alpha_{s})} ,x \neq y \Big\}=|e^{\prime}_3(1)-e^{\prime}_3(\ell_1)|=1-\ell_1^2\end{align*} $$
that exceeds
$1-\ell _1+\ell _1 \ell _2-\ell _2^2.$
Therefore,
$||e_3||_1=2-\ell _1-\ell _1^2.$
It follows that the right-hand side of (4.5) exceeds
$\frac {2\ell _1(1-\ell _1)(1-2\ell _1)}{2-\ell _1-\ell _1^2}$
and (4.5) is proved.
5 Quasi-equivalence of bases
Suppose
$\alpha _s \geq 2$
for
$s\geq 2$
and a sequence
$(n_s)_{s=0}^{\infty }$
satisfying (3.1) is given. Then, the space
${\mathcal E}(K^{(\alpha _{s})})$
has a polynomial basis
$(e_k)_{k=0}^{\infty }$
, by Theorem 3.1, and a local polynomial basis
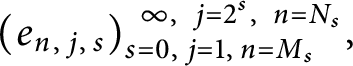$(e_{n,\,j,\,s})_{s=0,\,j=1,\,n=M_s}^{\,\,\,\infty , \,\,\,j=2^s,\,\,\,n=N_s},$
by 3.2. In Section 3, we established a bijection between these bases. We are now in a position to indicate lengths of intervals, which are included in
$\pi _{m,s}$
that define norms of the corresponding basis elements. Let
$f_k=e_{n,\,j,\,s}$
be fixed. For
$n=\deg \tilde f_k$
, by construction, we have
$2^m\leq n<2^{m+1}$
for some
$n_{s-1}-1\leq m \leq n_s.$
Therefore, the product
$\prod _{m_i\in \mathcal M} \pi _{m_i,s}$
in Lemma 4.2 includes
$\pi _{m,s}=\ell _{s+m} \cdots \ell _s^{2^{m-1}}$
and other
$\pi _{m_i,s}$
that start from
$\ell _t$
with
$s\leq t<s+m.$
For the corresponding
$e_k,$
by (2.2), each interval of sth level may contain n or
$n+1$
points. It cannot contain
$n-1$
points, because, given s, we chose first functions
$f_k=e_{n,\,j,\,s}$
on intervals with minimal number of points. Hence,
$n\,2^s\leq k \leq (n+1)2^s$
and
$2^{s+m}\leq k \leq 2^{s+m+1},$
as
$n+1\leq 2^{m+1}$
. This means that the product
$\prod _{i\in \mathcal K} \pi _i$
in Lemma 4.1 includes
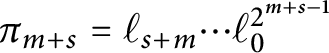$\pi _{m+s}=\ell _{s+m} \cdots \ell _0^{2^{m+s-1}}$
and others
$\pi _i$
that start from
$\ell _i$
with
$0\leq i<s+m.$
The feature of the sequence
$(x_i)_{i=1}^{\infty }$
mentioned above is that, given k with
$f_k=e_{n,j,s},$
the set
$(x_i)_{i=1}^{k}\cap I_{j,s}$
defines zeros of
$f_k$
on this interval. Hence,
$\prod _{m_i\in \mathcal M} \pi _{m_i,s}$
coincides with the product of n smallest terms of
$\prod _{i\in \mathcal K} \pi _i$
. The rest gives the desired coefficient
$$ \begin{align*}\rho_k:=\prod_{i\in \mathcal K} \pi_i / \prod_{m_i\in \mathcal M} \pi_{m_i,s}=\left(\prod_{i\in \mathcal K} \pi_i\right)_n.\end{align*} $$
Of course,
$$ \begin{align} \left(\prod_{i\in \mathcal K} \pi_i\right)_q= \rho_k\,\left(\prod_{m_i\in \mathcal M} \pi_{m_i,s}\right)_q, \end{align} $$
for
$q<n$
, because, by definition, each term in
$\prod _{m_i\in \mathcal M} \pi _{m_i,s}$
does not exceed each term in
$\rho _k$
.
We are able to present the main result of the paper.
Theorem 5.1 Let
$\alpha _s \geq 2$
for
$s\geq 2$
and a sequence
$(n_s)_{s=0}^{\infty }$
satisfy (3.1). Then, the bases
$(e_k)_{k=0}^{\infty }$
and
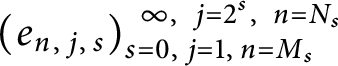$(e_{n,\,j,\,s})_{s=0,\,j=1,\,n=M_s}^{\,\,\,\infty , \,\,\,j=2^s,\,\,\,n=N_s}$
of the space
${\mathcal E}(K^{(\alpha _{s})})$
are quasi-equivalent.
Proof Let
$Te_k=\rho _k\,f_k, \,k\in \Bbb N_0$
, where
$(f_k)_{k=0}^{\infty }$
is the enumeration of the system
$(e_{n,\,j,\,s})_{s,j,n}$
given in Section 3. It can be extended linearly to an operator
$ T $
acting on the whole space. We aim to prove that T is an isomorphism. First, we show that for each p, there are q and
$C_p$
such that
$$ \begin{align} ||Te_k||_p=\rho_k\,||f_k||_p \leq C_p\,||e_k||_q \,\,\,\,\,\mbox {for all} \,\,\,\,k. \end{align} $$
Without loss of generality, we can consider p in the form
$p=2^u$
with
$u\in \Bbb N.$
Fix such p. Let
$q=2^v$
with
$v=u+10.$
Given
$q=q(p)$
, there are only finitely many values k with
$n\leq q,$
where
$n=\deg \tilde {f_k}.$
For such k, (5.2) is valid with an appropriate choice of
$C_p.$
Hence, we can assume that k is so large that we can use above lemmas.
By Lemma 4.2,
$||f_k||_p=||e_{n,j,\,s}||_p\leq 5(3\,n)^p\,(\prod _{m_i\in \mathcal M} \pi _{m_i,s})_p.$
By (5.1),
$$ \begin{align*}\rho_k\,||f_k||_p \leq 5(3\,n)^p\,\left(\prod_{i\in \mathcal K} \pi_i\right)_p.\end{align*} $$
On the other hand, by Lemma 4.1,
$\ell _1^k\,(\prod _{i\in \mathcal K} \pi _i)_{q-1}\leq ||e_k||_q$
, because
$h_0\geq \ell _1.$
To obtain (5.2), it remains to find
$C_p$
such that
$$ \begin{align} 5(3\,n)^p\,\left(\prod_{i\in \mathcal K} \pi_i\right)_p\leq C_p \ell_1^k\,\left(\prod_{i\in \mathcal K} \pi_i\right)_{q-1}. \end{align} $$
Let
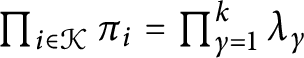$\prod _{i\in \mathcal K} \pi _i=\prod _{\gamma =1}^k \lambda _{\gamma }$
with
$\lambda _1\leq \cdots \leq \lambda _k.$
Then,
$$ \begin{align*}\left(\prod_{i\in \mathcal K} \pi_i\right)_p= \lambda_{p+1}\cdots \lambda_{q-1} \left(\prod_{i\in \mathcal K} \pi_i\right)_{q-1}.\end{align*} $$
We note that
$\prod _{i\in \mathcal K} \pi _i$
contains
$\pi _{m+s}=\ell _{s+m}\, \ell _{s+m-1}\, \ell _{s+m-2}^2\cdots \ell _0^{2^{m+s-1}}= \prod _{\gamma =1}^{2^{s+m}} \lambda ^{\prime }_{\gamma }$
with
$\lambda ^{\prime }_{\gamma } \uparrow $
. The product
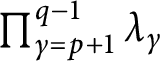$\prod _{\gamma =p+1}^{q-1} \lambda _{\gamma }$
does not exceed
$\prod _{\gamma =p+1}^{q-1} \lambda ^{\prime }_{\gamma },$
because including the terms from other
$\pi _i$
can only reduce the result.
We see that
$\lambda ^{\prime }_{\gamma }=\ell _{s+m-i}$
for
$\gamma \in \{2^{i-1}+1, \ldots , 2^i\}$
with
$2\leq i \leq s+m.$
For
$p=2^u, q=2^v$
, we have
$\prod _{\gamma =p+1}^{q-1} \lambda ^{\prime }_{\gamma }= \ell _{s+m-u-1}^{2^u}\cdots \ell _{s+m-v}^{2^{v-1}-1}=\ell _1^{\kappa }$
with
$$ \begin{align*}\kappa=\sum_{i=u}^{v-2} 2^i\,\alpha_2\,\cdots\, \alpha_{s+m-i-1}+ (2^{v-1}-1)\,\alpha_2\,\cdots\, \alpha_{s+m-v}\geq 2^{s+m-2}(v-u-1).\end{align*} $$
Indeed, we neglect the last summand and use the fact that all
$\alpha _i$
are bounded below by 2. The problem now reduces to establishing that
$$ \begin{align*}5(3\,n)^p\,\ell_1^{2^{s+m-2}(v-u-1)} \leq C_p \ell_1^k,\end{align*} $$
for
$n<2^{m+1}$
and
$k\leq 2^{s+m+1}.$
It is easy to check that our choice
$v=v+10$
provides this inequality together with (5.3) and (5.2).
The same reasoning applies to the inverse inequality: for each p, there are q and
$C_p$
:
$$ \begin{align*}\rho_k\,||T^{-1}f_k||_p=||e_k||_p \leq C_p\,||f_k||_q \,\,\,\,\,\mbox {for all} \,\,\,\,k,\end{align*} $$
but we will not need it.
For each
$f=\sum _{k=0}^{\infty }\xi _k(f)\,e_k\in {\mathcal E}(K^{(\alpha _{s})})$
, we define
$Tf=\sum _{k=0}^{\infty }\xi _k(f)\rho _k\,f_k.$
It is a simple matter to check that T is a bijection. Let us show its continuity.
The basis
$(e_k)_{k=0}^{\infty }$
is absolute. Hence, the norms
$|||f|||_q:=\sum _{k=0}^{\infty }|\xi _k(f)|\,||e_k||_q$
are well-defined for each q. It is a standard fact that the topology given by these norms is complete. By the open mapping theorem, for any q, there exist
$r, \,C>0$
such that
$$ \begin{align} |||\,f\,|||_{\,q} \leq C\,||\,f\,||_{\,r}. \end{align} $$
Fix any
$p\in {\Bbb N}$
and
$f \in {\mathcal E}(K^{(\alpha _{s})}).$
Then, by (5.2) and (5.4),
$$ \begin{align*}||Tf||_p\leq \sum_{k=0}^{\infty}|\xi_k(f)|\, \rho_k\,||f_k||_p\leq C_p \sum_{k=0}^{\infty}|\xi_k(f)|\,||e_k||_q\leq C_p\, C ||f||_r.\end{align*} $$
Thus, T is an isomorphism, which is our claim. ▪
Acknowledgment
We would like to express our sincere gratitude for the referee for suggestions for improving the presentation of the article.
