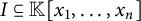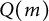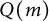1 Introduction
Throughout this paper,
$S = \mathbb {K}[x_1,\ldots ,x_n]$
denotes the polynomial ring over an arbitrary field
$\mathbb {K}$
. Francisco, Mermin, and Schweig [Reference Francisco, Mermin and Schweig12] introduced the notion of a Q-Borel monomial ideal to generalize the properties of Borel monomial ideals, also called strongly stable monomial ideals (see [Reference Francisco, Mermin and Schweig11, Reference Herzog and Hibi15] and their references for more on Borel ideals and their importance). Specifically, we fix a poset Q on the set
$\{x_1,\ldots ,x_n\}$
. Then a monomial ideal I is a Q-Borel ideal if for any monomial
$m \in I$
, if
$x_i|m$
and
$x_j \leq _Q x_i$
, then
$x_j\cdot \frac {m}{x_i} \in I$
. We call
$x_j\cdot \frac {m}{x_i}$
a Q-Borel move of m. A Borel ideal is then the special instance when Q is the chain
$Q = C: x_1 < x_2 < \cdots < x_n$
. A monomial ideal I is a principal Q-Borel ideal, denoted
$Q(m)$
, if there is a monomial m such that all the minimal generators of I can be obtained from m via Q-Borel moves. As shown in [Reference Francisco, Mermin and Schweig12] and Bhat’s thesis [Reference Bhat1], many properties of
$Q(m)$
, e.g., projective dimension, primary decomposition, can be described in terms of the poset Q and order ideals of Q associated with the monomial m.
Our goal in this paper is to study the properties of powers of principal Q-Borel ideals. Understanding powers of ideals figures prominently in commutative algebra. Two examples of this theme are the ideal containment problem and the persistence of primes. The ideal containment problem compares the regular powers of an ideal with its symbolic powers. The persistence of primes asks whether
${\textrm {ass}}(I^s) \subseteq {\textrm {ass}}(I^{s+1})$
for all
$s \geq 1$
, where
${\textrm {ass}}(J)$
denotes the set of associated primes of J. The references [Reference Bocci, Cooper, Guardo, Harbourne, Janssen, Nagel, Seceleanu, Van Tuyl and The2, Reference Bocci and Harbourne3, Reference Cooper, Embree, Hà and Hoefel8, Reference Ein, Lazarsfeld and Smith10, Reference Galetto, Geramita, Shin and Van Tuyl13, Reference Herzog and Qureshi16–Reference Hochster and Huneke18, Reference Martínez-Bernal, Morey and Villarreal20] form a small subset of papers on these topics; see also [Reference Carlini, Hà, Harbourne and Van Tuyl5, Reference Dao, De Stefani, Grifo, Huneke, Núñez-Betancourt, Araujo dos Santos, Menegon Neto, Mond, Saia and Snoussi9] for an introduction.
For principal Q-Borel ideals
$Q(m)$
, we consider these (and other) problems. Many of our results are expressed in terms of the combinatorics of the poset of Q, thus building upon [Reference Francisco, Mermin and Schweig12, Question 1.3] which asked what other properties of Q-Borel ideals are determined by Q. One theme that becomes apparent is that principal Q-Borel ideals satisfy many of the same properties as principal monomial ideals (in fact, results about principal monomial ideals become special cases of our work when Q is the anti-chain).
We first compare the regular and symbolic powers (formal definitions postponed until later in the paper) of principal Q-Borel ideals. Our main result in this direction is the following theorem.
Theorem 1.1 (Theorem 3.8)
Let
$I = Q(m)$
for some monomial m and poset Q. Then
$$ \begin{align*}I^{(d)}=I^d ~~\mbox{for all}\ d \geq 1.\end{align*} $$
Our proof requires Francisco et al. [Reference Francisco, Mermin and Schweig12] characterization of the associated primes of
$Q(m)$
, and Cooper et al. [Reference Cooper, Embree, Hà and Hoefel8] description of the symbolic powers of monomial ideals. As a corollary, we obtain results on the Waldschmidt constant, the symbolic defect, and the resurgence (see Corollary 3.10).
The analytic spread of I, denoted
$\ell (I)$
, is the Krull dimension of the ring
$$ \begin{align*}\mathcal{F}(I) = \bigoplus_{i \geq 0} \frac{I^i}{\textbf{m}I^i} ~~~~\mbox{where}\ I^0 = S\ \mbox{and}\ {\textbf{m}} =\langle x_1,\ldots,x_n\rangle.\end{align*} $$
For principal Q-Borel ideals, we obtain the following formula for the analytic spread in terms of combinatorics of Q.
Theorem 1.2 (Theorem 5.4)
Let
$I=Q(m)$
be a principal Q-Borel ideal, let
$A(m)$
be the order ideal generated by the support of m. Then
$$ \begin{align*}\ell(I)=|A(m)|-K(A(m))+1\end{align*} $$
where
$K(A(m))$
is the number of connected components in the subposet induced by
$A(m)$
.
Our proof uses the fact that for ideals generated by monomials of the same degree, the analytic spread is the rank of the matrix of exponent vectors of the generators. The analytic spread of
$Q(m)$
could also be computed using results of Herzog, Rauf, and Vladoiu [Reference Herzog, Rauf and Vladoiu17], but our result highlights the connection to the poset of Q.
Herzog, Rauf, and Vladoiu’s paper [Reference Herzog, Rauf and Vladoiu17] is used to address the question of persistence of primes. Precisely, we show that
${\textrm {ass}}(I) = {\textrm {ass}}(I^s)$
for all
$s \geq 1$
for any principal Q-Borel ideal (see Theorem 4.3). In fact, we give two different proofs for this result.
We also consider powers of square-free principal Q-Borel ideals, denoted
$sfQ(m)$
. These square-free monomial ideals are generated by the square-free monomial generators of
$Q(m)$
. For this class of ideals, we also compute their analytic spread (see Theorem 5.10) in terms of Q.
Our paper is structured as follows. Section 2 is the background on monomial ideals, posets, and (principal) Q-Borel ideals. In section 3 we prove Theorem 3.8. In Section 4 we examine the persistence of primes problem. Section 5 is devoted to the analytic spread of (square-free) principal Q-Borel ideals.
2 Background
In this section we recall the relevant background and definitions.
2.1 Basics of monomial ideals and posets
Given a monomial
$m = x_1^{a_1}\cdots x_n^{a_n}$
in S, we may write the monomial as
$m = x^\alpha $
with
$\alpha = (a_1,\ldots ,a_n) \in \mathbb {N}^n$
. The monomial m is a square-free monomial if
$a_i = 0$
or
$1$
for all
$i=1,\ldots ,n$
. The support of
$m = x_1^{a_1}\cdots x_n^{a_n}$
is the set
${\textrm {supp}}(m) = \{j ~|~ a_j> 0 \}$
.
An ideal
$I \subseteq S$
is a (square-free) monomial ideal if I is generated by (square-free) monomials. A monomial ideal has a unique set of minimal monomial generators denoted by
$G(I)$
.
Let Q be a poset on the ground set
$\{x_1,\ldots ,x_n\}$
, where the partial order is denoted by
$<_Q$
. A poset
$Q'$
is an induced poset of Q if there exists an injective function
$f:Q' \rightarrow Q$
such that
$x \leq _{Q'} y$
if and only if
$f(x) \leq _Q f(y)$
.
Associated to any poset on a finite ground set is a Hasse diagram. In particular, the elements of Q are represented by vertices, and there exists a line segment from x to y in the “upwards” direction if
$x <_Q y$
and if there is no other
$z \in Q$
such that
$x <_Q z <_Q y$
. The Hasse diagram is an example of directed acyclic graph (a directed graph with no directed cycles). Given a poset Q, the number of connected components of Q, denoted
$K(Q)$
, is the number of connected components of the Hasse diagram, i.e., the connected components of the Hasse diagram when viewed as a undirected graph.
An order ideal of Q is a set
$A \subseteq Q$
such that if
$y \in A$
and if
$x <_Q y$
, then
$x \in A$
. Given any monomial
$m = x_1^{a_1}\cdots x_{n}^{a_n} \in S$
, we can associate with m the order ideal
$$ \begin{align*}A(m) = \left\{x_j ~\left|~ \mbox{there is an}~ x_i ~\mbox{such that} ~x_j \leq_Q x_i ~~\mbox{and}~~ x_i|m\right\}\right..\end{align*} $$
The order ideal
$A(m)$
is an induced poset of Q via the inclusion map. We say an order ideal
$A(m)$
is connected if the Hasse diagram of
$A(m)$
is connected. The next lemma follows directly from the definitions.
Lemma 2.1 Fix a poset Q on
$\{x_1,\ldots ,x_n\}$
, and let
$m_1,m_2 \in S$
be two monomials. If
${\textrm {supp}}(m_1) = {\textrm { supp}}(m_2)$
, then
$A(m_1) = A(m_2)$
.
The next lemma will be used in future calculations.
Lemma 2.2 Fix a poset Q on
$\{x_1,\ldots , x_n\}$
and let
$m_1,m_2\in S$
be two monomials. Then
$$ \begin{align*}A(\mathrm{lcm}(m_1,m_2))=A(m_1m_2)=A(m_1)\cup A(m_2). \\[-18pt] \end{align*} $$
Proof Note that
$$ \begin{align*}\mathrm{supp}(\mathrm{lcm}(m_1,m_2))=\mathrm{supp}(m_1m_2)=\mathrm{supp}(m_1)\cup\mathrm{supp}(m_2).\end{align*} $$
Now apply Lemma 2.1.▪
The next lemma shows the relationships between the components of a monomial and the order subideals of its order ideal.
Lemma 2.3 Fix a poset Q on
$\{x_1,\ldots , x_n\}$
and let
$m \in S$
be a monomial. For any order ideal
$O\subset Q$
such that
$O=A(m')$
for some
$m'|m$
, there is a unique monomial
$m_O$
satisfying:
-
•
$m_O|m$
. -
•
$O=A(m_O)$
. -
• For any other monomial
$m''|m$
such that
$O = A(m'')$
, we have
$m''|m_O$
.
Proof Define
$$ \begin{align*}m_O=\mathrm{lcm}\left\{m''\ \left|~~~ m''\ \mbox{a monomial,} ~~m''|m,\text{ and } A(m'')=O\right\}\right..\end{align*} $$
The set on the right contains
$m'$
so
$m_O$
is well-defined and it is clear that
$m_O|m$
. From the last lemma, we have
$A(m_O)=O$
and from the definition, if any other monomial
$m''|m$
satisfies
$A(m'')=O$
, then we have
$m''|m_O$
.▪
2.2 Q-Borel ideals
Q-Borel ideals were introduced by Francisco, Mermin, and Schweig [Reference Francisco, Mermin and Schweig12] to generalize properties of Borel monomial ideals. We recall this definition.
Definition 2.4 Let
$I \subseteq S$
be a monomial ideal and let Q be a poset on
$\{x_1,\ldots ,x_n\}$
. The ideal I is a Q -Borel ideal if whenever
$x_j \leq _Q x_i$
and
$x_i|m$
for some monomial
$m \in I$
, then
$x_j \cdot (m/x_i) \in I$
. We say that I is Borel with respect to Q.
Remark 2.5 Definition 2.4 generalizes the notion of a Borel monomial ideal. More precisely, a Q-Borel ideal is a Borel ideal if Q is the chain
$Q=C: x_1 <_Q x_2 <_Q < \cdots <_Q x_n$
. Note that any monomial ideal I is a Q-Borel ideal if we take Q to be the antichain.
If
$x_i|m$
and
$x_j \leq _Q x_i$
, then we call
$x_j \cdot (m/x_i)$
a Q-Borel move of the monomial m. It follows that a monomial ideal I is a Q-Borel ideal if I is closed under Q-Borel moves. Observe that if
$m = x^\alpha $
, then a Q-Borel move
$x_j \cdot (m/x_i)$
corresponds to the existence of a vector
$e_{(i,j)} \in \mathbb {N}^n$
whose k-th coordinate is given by
$$ \begin{align} (e_{(i,j)})_k =\begin{cases} 1&k=j\text{ and }x_j\leq_Q x_i\\ -1&k=i\text{ and }x_j\leq_Q x_i\\ 0&\text{otherwise}\end{cases} \end{align} $$
such that
$x^{\alpha +e_{(i,j)}} = x_j\cdot (m/x_i)$
. The following lemma shall be useful.
Lemma 2.6 Fix a poset Q on
$\{x_1,\ldots ,x_n\}$
. Suppose that
$x^\alpha $
and
$ x^\beta $
are monomials of S such that
$x^\beta $
can be obtained via a series of Q-Borel moves on
$x^\alpha $
. Then there exists
$e_{(i_1,j_1)},\ldots ,e_{(i_l,j_l)}$
, not necessarily distinct, with
$i_t \in {\textrm {supp}}(x^\alpha )$
for
$t=1,\ldots ,l$
, such that
$$ \begin{align*} \alpha+e_{(i_1,j_1)}+\cdots + e_{(i_l,j_l)} = \beta.\end{align*} $$
Equivalently, expressed in terms of monomials, we have
$$ \begin{align*}x^{\beta}=x^\alpha\cdot\frac{x_{j_1}\cdots x_{j_l}}{x_{i_1}\cdots x_{i_l}}\end{align*} $$
where
$x_{i_t}$
divdes
$x^\alpha $
for
$t=1,\ldots ,l$
.
Proof Because
$x^\beta $
can be obtained from
$x^\alpha $
by Q-Borel moves, there exists monomials
$x^\alpha =x^{\alpha _1},x^{\alpha _2},\ldots ,x^{\alpha _{r-1}},x^{\alpha _r} =x^{\beta }$
such that
$x^{\alpha _{t+1}}$
is obtained from
$x^{\alpha _{t}}$
via a Q-Borel move for
$t=1,\ldots ,r-1$
. In particular, there exists a vector of the form
$e_{(a_t,b_t)}$
such that
$$ \begin{align*}\alpha_{t} +e_{(a_t,b_t)} = \alpha_{t+1} ~~\mbox{for each}\ t=1,\ldots,r-1\end{align*} $$
where
$a_t \in {\textrm {supp}}(x^{\alpha _t})$
and
$x_{b_t} \leq _Q x_{a_t}$
. Consequently,
$$ \begin{align*}\alpha + e_{(a_1,b_1)}+\cdots + e_{(a_{r-1},b_{r-1})} = \beta.\end{align*} $$
If
$a_t \in {\textrm {supp}}(x^\alpha )$
for all
$t=1,\ldots ,r-1$
, then we are done.
On the other hand, suppose that there is some
$e_{(a_t,b_t)}$
such that
$a_t \not \in {\textrm {supp}}(x^\alpha )$
. Let t be the smallest index such that
$a_t \not \in {\textrm {supp}}(x^\alpha )$
. That is, t is the smallest index such that
$\alpha _{t+1}$
has not been expressed in the form
$\alpha +e_{(i_1,j_1)} + \cdots + e_{(i_t,j_t)}$
with all
$i_k \in {\textrm {supp}}(x^\alpha )$
. Note that
$t \geq 2$
because
$a_1 \in {\textrm {supp}}(x^\alpha )$
. Now
$$ \begin{align*}\alpha_{t+1} = \alpha_t + e_{(a_t,b_t)} = (\alpha + e_{(a_1,b_1)}+\cdots+ e_{(a_{t-1},b_{t-1})})+ e_{(a_t,b_t)}.\end{align*} $$
Because
$a_t$
is not in the support of
$x^\alpha $
, but in the support of
$x^{\alpha _t}$
, this means that
$a_t \in \{b_1,\ldots ,b_{t-1}\}$
since the
$b_k$
’s correspond to the supports of the new variables by which we multiply after dividing by
$a_k$
. Say
$a_t = b_s$
with
$s \in \{1,\ldots ,t-1\}$
. But then by equation (2.1)
$$ \begin{align*}e_{(a_s,b_s)}+e_{(a_t,b_t)} = e_{(a_s,b_t)},\end{align*} $$
that is, the coordinate which is
$1$
in the first vector cancels out with
$-1$
in the second vector. Furthermore,
$b_t \leq _Q a_s$
, because
$b_t \leq _Q a_t = b_s \leq _Q a_s$
. So, we can rewrite
$\alpha _{t+1}$
as
$$ \begin{align*} \alpha_{t+1} &= \alpha + e_{(a_1,b_1)}+\cdots+ (e_{(a_s,b_s)}+e_{(a_t,b_t)})+ \cdots + e_{(a_{t-1},b_{t-1})} \\ &= \alpha +e_{(a_1,b_1)}+\cdots+ e_{(a_s,b_t)} + \cdots + e_{(a_{t-1},b_{t-1})} \end{align*} $$
where all the
$a_k$
’s are in the
${\textrm {supp}}(x^\alpha )$
. So
$\alpha _{t+1}$
has the desired form.
Repeating this process allows
$\beta $
to be expressed in the desired form.▪
Because Q-Borel ideals are closed under Q-Borel moves, the generators of Q-Borel ideals can be described as subsets of monomials of S from which other monomial generators in the ideal can be obtained via Q-Borel moves. The following terminology shall be helpful.
Definition 2.7 Let X be a subset of monomials of S. The smallest Q-Borel ideal I that contains X is denoted
$Q(X)$
, and we say X is a Q -Borel generating set of
$I = Q(X)$
. A square-free monomial ideal J is a square-free Q -Borel ideal if it is generated by the square-free monomials of a Q-Borel ideal. Given a set Y of square-free monomials, we let
$sfQ(Y)$
denote the smallest square-free Q-Borel ideal containing Y.
The following fact follows directly from the definitions.
Lemma 2.8 [Reference Francisco, Mermin and Schweig12, Proposition 2.6]
If all the monomials of X have the same degree, then all the minimal generators of the Q-Borel ideal
$I =Q(X)$
have the same degree.
2.3 Q-Borel principal ideals
We are primarily interested in the following ideals.
Definition 2.9 If
$X = \{m\}$
contains a single monomial, then we call
$I = Q(X)$
a Q -Borel principal ideal, and we abuse notation and write
$I =Q(m)$
. Similarly, if
$Y = \{m\}$
contains a single square-free monomial, then we call
$I = sfQ(Y)$
a square-free Q -Borel principal ideal and write
$I = sfQ(m)$
.
Principal Q-Borel ideals are preserved under ideal multiplication.
Lemma 2.10 Fix a poset Q on
$\{x_1,\ldots ,x_n\}$
, and let
$m_1,m_2 \in S$
be two monomials. Then
$$ \begin{align*}Q(m_1)Q(m_2) = Q(m_1m_2).\end{align*} $$
Proof Let
$p_1 \in Q(m_1)$
, respectively
$p_2 \in Q(m_2)$
, be any monomial generator of
$Q(m_1)$
, respectively
$Q(m_2)$
. So
$p_1$
is a Q-Borel move of
$m_1$
, and similarly for
$p_2$
and
$m_2$
. Thus
$$ \begin{align*}p_1 = m_1\frac{x_{j_1}x_{j_2}\cdots x_{j_r}}{x_{i_1}x_{i_2}\cdots x_{i_r}} \mbox{ with}\ x_{j_\ell} <_Q x_{i_\ell}\ \mbox{for}\ \ell =1,\ldots,r\end{align*} $$
and
$$ \begin{align*}p_2 = m_2\frac{x_{b_1}x_{b_2}\cdots x_{b_s}}{x_{a_1}x_{a_2}\cdots x_{a_s}} \mbox{ with}\ x_{b_\ell} <_Q x_{a_\ell}\ \mbox{for}\ \ell =1,\ldots,s.\end{align*} $$
But this means that
$$ \begin{align*}p_1p_2 = m_1m_2\frac{x_{j_1}x_{j_2}\cdots x_{j_r}}{x_{i_1}x_{i_2}\cdots x_{i_r}}\frac{x_{b_1}x_{b_2}\cdots x_{b_s}}{x_{a_1}x_{a_2}\cdots x_{a_s}}\end{align*} $$
is a Q-Borel move of
$m_1m_2$
, so
$p_1p_2 \in Q(m_1m_2)$
, thus showing
$Q(m_1)Q(m_2) \subseteq Q(m_1m_2)$
.
For the reverse containment, if
$p \in Q(m_1m_2)$
is a generator of
$Q(m_1m_2)$
obtained via a series of Q-Borel moves on
$m_1m_2$
. So, by Lemma 2.6 and Lemma 2.2, we have
$$ \begin{align*}p = m_1m_2\frac{x_{j_1}x_{j_2}\cdots x_{j_r}}{x_{i_1}x_{i_2}\cdots x_{i_r}}\frac{x_{b_1}x_{b_2}\cdots x_{b_s}}{x_{a_1}x_{a_2}\cdots x_{a_s}} \frac{x_{c_1}x_{c_2}\cdots x_{c_t}}{x_{d_1}x_{d_2}\cdots x_{d_t}} \end{align*} $$
where
$x_{j_\ell }<_Q x_{i_\ell }$
,
$x_{b_\ell }<_Q x_{a_\ell }$
,
$x_{c_\ell }<_Q x_{d_\ell }$
and
${i_\ell }\in \mathrm {supp}(m_1){\kern2pt}\backslash{\kern2pt}\mathrm {supp}(m_2)$
,
${a_\ell }\in \mathrm {supp}(m_2){\kern2pt}\backslash{\kern2pt} \mathrm {supp}(m_1)$
and
${d_\ell }\in \mathrm {supp}(m_1)\cap \mathrm {supp}(m_2)$
for all relevant
$\ell $
. Since
$x_{d_1}\cdots x_{d_t}|(\mathrm {gcd}(m_1,m_2))^2$
, we can re-index, if necessary, so that for some
$1\leq t'\leq t-1$
we have
$$ \begin{align*}x_{d_1}\cdots x_{d_{t'}}|{\textrm{gcd}}(m_1,m_2) ~\mbox{and}~ x_{d_{t'+1}}\cdots x_{d_t}|\mathrm{gcd}(m_1,m_2).\end{align*} $$
We then have
$$ \begin{align*}\left(m_1\frac{x_{j_1}\cdots x_{j_r}}{x_{i_1}\cdots x_{i_r}}\frac{x_{c_1}\cdots x_{c_{t'}}}{x_{d_1}\cdots x_{d_{t'}}}\right)\in Q(m_1),\ \left(m_2\frac{x_{b_1}\cdots x_{b_s}}{x_{a_1}\cdots x_{a_s}}\frac{x_{c_{t'+1}}\cdots x_{c_t}}{x_{d_{t'+1}}\cdots x_{d_t}}\right)\in Q(m_2)\end{align*} $$
implying that
$p\in Q(m_1)Q(m_2)$
. Therefore,
$Q(m_1m_2)\subseteq Q(m_1)Q(m_2)$
and we have the conclusion.▪
We also have the following property of ideal intersections.
Lemma 2.11 Fix a poset Q on
$\{x_1,\ldots ,x_n\}$
, and let
$m_1,m_2 \in S$
be two monomials. If
$A(m_1) \cap A(m_2) = \emptyset $
, then
$Q(m_1) \cap Q(m_2) = Q(m_1)Q(m_2).$
Proof It suffices to show that
$Q(m_1) \cap Q(m_2) \subseteq Q(m_1)Q(m_2)$
.
Note that for any monomial m, if
$p \in G(Q(m))$
is a minimal generator of
$Q(m)$
, then
$\{x_j ~|~ j \in {\textrm {supp}}(p)\} \subseteq A(m)$
. In fact, we have
$$ \begin{align*}A(m) = \bigcup_{p\in G(Q(m))} \{x_j ~|~ j \in {\textrm{supp}}(p)\}.\end{align*} $$
That is,
$A(m)$
is precisely the set of variables that divide at least one minimal generator of
$Q(m)$
.
Because
$A(m_1)$
and
$A(m_2)$
are disjoint, this implies that for any Q-Borel movement
$m'$
of
$m_1$
and any Q-Borel movement
$m''$
of
$m_2$
,
$\mathrm {gcd}(m',m'')=1,$
and thus
${\textrm {lcm}}(m',m'') =m'm''$
. It then follows that
$$ \begin{align*} Q(m_1) \cap Q(m_2) &= \langle {\textrm{lcm}}(m',m'') = m'm'' ~|~ m' \in G(Q(m_1)) ~\mbox{and}~ m'' \in G(Q(m_2)) \rangle \\ & = Q(m_1)Q(m_2), \end{align*} $$
as desired.
As first shown by Francisco, et al. [Reference Francisco, Mermin and Schweig12], the associated primes of principal Q-Borel ideals are related to order ideals of Q. Recall that for any ideal
$I \subseteq S$
, a prime ideal P is an associated prime of I if there exists an element
$f \in S$
such that
$$ \begin{align*}I:\langle f \rangle = \{g \in S ~|~ gf \in I\} = P.\end{align*} $$
We denote the set of all associated primes of I by
${\textrm {ass}}(I)$
. We then have the following theorem.
Theorem 2.12 [Reference Francisco, Mermin and Schweig12, Theorem 4.3]
Let
$I = Q(m)$
for some monomial m and poset Q. Then
$P \in {\textrm {ass}}(I)$
if and only if
$$ \begin{align*}P = \langle x_i ~|~ x_i \in A(m')\rangle\end{align*} $$
for some
$m'|m$
with the property that
$A(m')$
is connected.
Remark 2.13 As we will see in Section 4, principal Q-Borel ideals are products of prime monomial ideals, that is, all principal Q-Borel ideals are examples of ideals that are products of ideals generated by linear forms. There are a number of papers on this topic, for example [Reference Conca and Herzog6, Reference Conca and Tsakiris7].
In particular, the primary decomposition of principal Q-Borel ideals can also be deduced from the work of [Reference Conca and Herzog6]. We use the statement of [Reference Francisco, Mermin and Schweig12] since it relates the associated primes directly to the Hasse diagram of Q,
Example 2.14 We illustrate some of the above ideas with the following example. Let
$S=\mathbb {K}[x_1,\ldots ,x_{11}]$
and let Q be the poset on
$\{x_1,\ldots ,x_{11}\}$
with Hasse diagram:
In the above drawing,
$x_i <_Q x_j$
if there is a path from
$x_i$
to
$x_j$
such that the path from
$x_i$
to
$x_j$
only moves “upward”. For example
$x_1 <_Q x_5$
, but
$x_1$
and
$x_3$
are not comparable.
If we consider the monomial
$m =x_4x_9^2$
, then because
$x_1 <_Q x_4$
and
$x_4|m$
, the monomial
$x_1\cdot (m/x_4) = x_1x_9^2$
is a Q-Borel move of m. The Q-Borel principal ideal
$I=Q(x_4x_{9}^2)$
is the monomial ideal generated by all the Q-Borel moves one can obtain from
$x_4x_9^2$
. In particular,
$$ \begin{align*}Q(x_4x_9^2) &= \langle x_1x_6^2,x_1x_6x_7,x_1x_7^2, x_1x_6x_9,x_1x_7x_9, x_1x_9^2, x_4x_6^2,x_4x_6x_7,x_4x_7^2,\\ &\quad x_4x_6x_9,x_4x_7x_9, x_4x_9^2\rangle.\end{align*} $$
Observe that all the generators of
$Q(x_4x_9^2)$
have degree three, as expected by Lemma 2.8.
We apply Theorem 2.12 to compute
${\textrm {ass}}(Q(x_4x_9^2))$
. The monomials that divide
$x_4x_9^2$
are
$x_4,x_9,x_9^2,x_4x_9$
and
$x_4x_9^2$
. Now
$A(x_4x_9) = A(x_4x_9^2) = \{x_1,x_4,x_6,x_7,x_9\}$
is not connected, but the order ideals
$A(x_4) = \{x_1,x_4\}$
and
$A(x_9) = A(x_9^2) =\{x_9,x_6,x_7\}$
are. So
$$ \begin{align*}{\textrm{ass}}(Q(x_4x_9^2)) = \{\langle x_1,x_4\rangle,\langle x_6,x_7,x_9 \rangle\}.\end{align*} $$
3 The ideal containment problem for
$Q(m)$
The d-th symbolic power of an ideal
$I \subseteq S$
, denoted
$I^{(d)}$
, is the ideal
$$ \begin{align*}I^{(d)} = \bigcap_{P \in {\textrm{ass}}(I)} (I^dS_P \cap S) \end{align*} $$
where
$S_P$
is the ring S localized at the ideal P, and the intersection is over the set of all the associated primes of I. (The definition of symbolic powers is not uniform in the literature, where in some references, the indexing set is only over the minimal associated primes, as in [Reference Villarreal21, Definition 4.3.22].)
The regular d-th power of I, that is
$I^d$
, always satisfies
$I^d \subseteq I^{(d)}$
. Ein-Lazersfeld-Smith [Reference Ein, Lazarsfeld and Smith10] and Hochster-Huneke [Reference Hochster and Huneke18] showed that, for every positive integer d, there is an integer
$r \geq d$
such that
$I^{(r)} \subseteq I^d$
. The “ideal containment problem” pertains to the problem of determining, for each positive integer d, the smallest integer r such that
$I^{(r)} \subseteq I^d$
. In this section, we show that for any principal Q-Borel ideal, we can take
$r=d$
.
The following results of Cooper et al. [Reference Cooper, Embree, Hà and Hoefel8] about symbolic powers of monomial ideals will be useful. If
$I = Q_1 \cap \cdots \cap Q_s$
is a primary decomposition of the monomial ideal I, and if
$P \in {\textrm {ass}}(I)$
, then we define
$$ \begin{align*}Q_{\subseteq P} = \bigcap_{\sqrt{Q_i} \subseteq P} Q_i.\end{align*} $$
That is,
$Q_{\subseteq P}$
is the intersection of all the primary ideals in the primary decomposition of I such that
$\sqrt {Q_i}$
is contained in P. Then, we have the following theorem.
Theorem 3.1 [Reference Cooper, Embree, Hà and Hoefel8, Theorem 3.7]
The d-th symbolic power of a monomial ideal I is
$$ \begin{align*}I^{(d)} = \bigcap_{P \in {\textrm{maxass}}(I)} Q_{\subseteq P}^d\end{align*} $$
where
${\textrm {maxass}}(I)$
denotes the maximal associated primes of I, ordered by inclusion.
Thus, to compute the symbolic powers of principal Q-Borel ideals, we need to determine
${\textrm {maxass}}(I)$
. We introduce the following terminology.
Definition 3.2 Let
$S=\mathbb {K}[x_1,\ldots ,x_n]$
and let Q be a poset over its variables. Fix a monomial
$m\in S$
and suppose that
$m'|m$
. We say that
$m'$
is a maximal connected component of m if
-
•
$A(m')$
is connected, -
•
$A(m')$
is maximal with respect to inclusion, i.e., there is no other
$m''$
that divides m such that
$A(m'')$
is connected and
$A(m') \subsetneq A(m'')$
, and -
•
$m'=m_O$
with
$O=A(m')$
, i.e.,
$m'$
is the unique monomial of Lemma 2.3.
Note that by Lemma 2.3, the maximal connected components of a monomial exist and are unique.
Remark 3.3 Using Lemma 2.3, we can give an equivalent definition of a maximal connected component in terms of the poset Q. Specifically, let m be a monomial and Q a poset as before. Let L be the lattice of divisors of m and
$\Lambda $
the subposet of L consisting of
$\{\mu \ |\ A(\mu )\mbox { is connected.}\}$
. Then
$m'$
is a maximal connected component if and only if
$m'$
is a maximal element of
$\Lambda $
. This alternative viewpoint may be helpful.
Lemma 3.4 Let
$I = Q(m)$
for some monomial m and poset Q. Then
$P \in {\textrm {maxass}}(I)$
if and only if
$P = \langle x ~|~ x \in A(m') \rangle $
with
$m'$
a maximal connected component of m.
Proof
$(\Rightarrow )$
Suppose that
$P \in {\textrm {maxass}}(I)$
. By Theorem 2.12, there exists a monomial
$m'$
such that
$m'|m$
,
$A(m')$
is connected, and
$P = \langle x_i ~|~ x_i \in A(m') \rangle $
. We can assume that
$m'=m_O$
with
$O=A(m')$
. If
$m'$
is not a maximal connected component of m, then there is some
$m''$
that divides m such that the connected component
$A(m'')$
properly contains
$A(m')$
. But since
$A(m'')$
is connected,
$P' = \langle x_i ~|~ x_i \in A(m'') \rangle $
is an associated prime of I that properly contains P, contradicting the maximality of P. We now have the desired contradiction.
$(\Leftarrow )$
We reverse the above argument. Let
$m'$
be a maximal connected component of m. By Theorem 2.12, there is a prime ideal
$P \in {\textrm {ass}}(I)$
such that
$P = \langle x_i ~|~ x_i \in A(m') \rangle $
since
$A(m')$
is connected. If P is not a maximal associated prime, then there is a prime ideal
$P'$
with
$P \subsetneq P'$
. But then
$P' = \langle x_i ~|~ x_i \in A(m'') \rangle $
for some
$m''$
such that
$m''|m$
and
$A(m'')$
is connected. But then
$A(m') \subsetneq A(m'')$
contradicting the fact that
$m'$
is a maximal connected component of m.▪
The following lemma on distinct maximal connected components is required.
Lemma 3.5 Let
$m\in S$
be a monomial, and let
$m_1$
an
$m_2$
be two distinct maximal connected components of m. Then
$A(m_1) \cap A(m_2) = \emptyset $
.
Proof Suppose that
$y \in A(m_1) \cap A(m_2)$
. Then y is path connected to every element in
$A(m_1)$
, and similarly, to every element in
$A(m_2)$
since both
$A(m_1)$
and
$A(m_2)$
are connected. But then
$A({\textrm {lcm}}(m_1,m_2))$
is a connected component of
$A(m)$
that properly contains
$A(m_1)$
and
$A(m_2)$
. But this contradicts the fact that
$A(m_1)$
and
$A(m_2)$
are maximal.
Lemma 3.6 Let
$m\in S$
be a monomial and let
$m_1,\ldots ,m_r$
be all the maximal connected components of m. Then
$m = m_1\cdots m_r$
.
Proof Note that by Lemma 3.5, it follows that all the supports of
$m_1,\ldots ,m_r$
are pairwise disjoint, so
$m_1\cdots m_r$
divides m. If
$m_1 \cdots m_r$
strictly divides m, that means that there is either: (1) a variable
$x_j$
that divides m that does not divide any of
$m_1,\ldots ,m_r$
, or (2) a variable
$x_j$
such that
$x_j^d|m$
and
$x_j^a$
divides some
$m_i$
, but
$a <d$
. We show that neither case can happen.
If
$x_j|m$
, then
$A(x_j) \subseteq A(m)$
and
$A(x_j)$
is connected. Consider all
$m'$
such that
$m'|m$
,
$A(x_j) \subseteq A(m')$
, and
$A(m')$
is connected. In addition, suppose
$m'$
is picked to be maximal with the property with respect to both inclusion and the degree of
$m'$
. But then
$m'$
would be a maximal connected component, which is a contradiction.
For case (2), suppose that
$x_j^d|m$
. Since the
$m_1,\ldots ,m_r$
have distinct support,
$x_j$
can only divide one of these monomials. After relabeling, suppose
$x_j|m_1$
. Suppose
$x_j^a$
with
$a \geq 1$
is the largest power of
$x_j$
that divides
$m_1$
. We claim that
$a=d$
. Since
$m_1 |m$
we know
$a\leq d$
. If
$1 \leq a<d$
, then
$A(m_1x_j) = A(m_1)$
since
$m_1$
and
$m_1x_j$
have the same support. But then
$m_1$
is not a maximal connected component since
$\deg m_1x_j> \deg m_1$
and
$m_1x_j|m$
. So case (2) cannot happen.▪
We relate the primary decomposition of
$Q(m)$
with its maximal connected components.
Lemma 3.7 Let
$m\in S$
be a monomial and let
$m_1,\ldots ,m_r$
be all the maximal connected components of m. Then
$$ \begin{align*}Q(m)=Q(m_1)\cap\cdots\cap Q(m_r).\end{align*} $$
Furthermore, if
$Q(m) = Q_1 \cap \cdots \cap Q_s$
is a primary decomposition of
$Q(m)$
, then
$$ \begin{align*}Q(m_i)=Q_{\subseteq \langle A(m_i)\rangle} ~~\mbox{for}\ i=1,\ldots,r\end{align*} $$
where
$\langle A(m_i) \rangle = \langle x ~|~ x \in A(m_i) \rangle $
.
Proof By Lemma 3.6, we have
$m=m_1\cdots m_r$
. By Lemmas 2.2 and 3.5, we have that
$A(m_1\cdots m_{j-1}) \cap A(m_j) = \left (\bigcup _{i=1}^{j-1} A(m_i)\right )\cap A(m_j) = \emptyset $
, for
$j=2,\ldots ,r$
. So by repeatedly applying Lemma 2.11, we have
$$ \begin{align*}Q(m)=\prod_{i=1}^r Q(m_i)=\bigcap_{i=1}^r Q(m_i).\end{align*} $$
For the second claim, observe that any associated prime of
$Q(m)$
is an associated prime of
$Q(m_j)$
for just one j (due to Theorem 2.12 and the definition of a maximal connected component); for the same reason, any associated prime of
$Q(m_i)$
is an associated prime of
$Q(m)$
. Since
$Q(m_i)$
has just one maximal associated prime, namely,
$\langle A(m_i) \rangle $
, we then have
$Q_{\subseteq \langle A(m_i)\rangle }=Q(m_i),$
as desired.▪
We arrive at the main result of this section.
Theorem 3.8 Let
$I = Q(m)$
for some monomial m and poset Q. Then
$$ \begin{align*}I^{(d)}=I^d ~~\mbox{for all}\ d \geq 1.\end{align*} $$
Proof Let
$m_1,\ldots ,m_r$
be the maximal connected components of m. By Lemma 3.4,
${\textrm {maxass}}(I) = \{ \langle A(m_i) \rangle ~|~ i=1,\ldots ,r\}$
. By Theorem 3.1 and Lemma 3.7 we have
$$ \begin{align*}I^{(d)}=\bigcap_{i=1}^r Q^d_{\subseteq \langle A(m_i) \rangle} = \bigcap_{i=1}^r \left(Q(m_i)\right)^d.\end{align*} $$
But, by Lemma 2.10, we have
$$ \begin{align*}\bigcap_{i=1}^r \left(Q(m_i)\right)^d =\bigcap_{i=1}^r \left(Q(m_i^d)\right)\end{align*} $$
Because
$A(m_i) = A(m_i^d)$
, it follows from Lemma 3.5 that all the generators of
$Q(m_i^d)$
are relatively prime with the all generators of
$Q(m_j^d)$
for any
$i\neq j$
. Thus
$$ \begin{align*}I^{(d)}=\bigcap_{i=1}^r \left(Q(m_i^d)\right)=\prod_{i=1}^r Q(m_i^d)=Q(m^d)=Q(m)^d = I^d\end{align*} $$
The third and fourth equality follow from Lemma 2.10 and the fact that
$m=m_1\cdots m_r$
.▪
Theorem 3.8 allows us to compute some invariants related to the ideal containment problem. We recall these definitions (see [Reference Carlini, Hà, Harbourne and Van Tuyl5] for more on the properties of these invariants). For a homogeneous ideal I,
$\alpha (I)$
denotes the smallest degree of an element in a minimal set of homogeneous generators for I. For a graded R-module M,
$\mu (M)$
denotes its minimal number of generators.
Definition 3.9 Let I be a homogeneous ideal of S.
-
(1) (see [Reference Bocci and Harbourne3]) The Waldschmidt constant of I, denoted by
$\widehat {\alpha }(I)$
, is
$$ \begin{align*}\hat\alpha(I) := \lim_{s \rightarrow \infty} \frac{\alpha(I^{(s)})}{s}.\end{align*} $$
-
(2) (see [Reference Galetto, Geramita, Shin and Van Tuyl13]) The d -th symbolic defect of I, denoted by
$\mathrm {sdefect}(I,d)$
, as
$$ \begin{align*}\mathrm{sdefect}(I,d)=\mu\left(I^{(d)}/I^d\right).\end{align*} $$
-
(3) (see [Reference Bocci and Harbourne3]) The resurgence of I, denoted by
$\rho (I)$
, is
$$ \begin{align*}\rho(I)=\mathop{\mathrm{sup}}\limits\left\{\frac{s}{r}\ |\ I^{(s)}\not\subset I^r\right\}. \end{align*} $$
Corollary 3.10 Let
$I = Q(m)$
for some monomial m and poset Q. Then
-
(1)
$\widehat {\alpha }(I) = \deg (m)$
, -
(2)
${\textrm {sdefect}}(I,d) = 0$
for all
$d \geq 1$
, and -
(3)
$\rho (I) = 1$
.
Proof These results follow directly from the fact that
$I^d = I^{(d)}$
for all
$d \geq 1$
.▪
Remark 3.11 Observe that Corollary 3.10 holds for principal ideals in the regular sense, thus illustrating the theme that principal Q-Borel ideals behave like principal ideals.
Remark 3.12 For principal Q-Borel ideals
$I = Q(m)$
, Corollary 3.10 shows that the Waldschmidt constant is very easy to obtain from m. If we consider square-free Q-Borel ideals, it becomes much harder to determine this invariant. In a follow up paper [Reference Camps-Moreno, Kohne, Sarmiento and Van Tuyl4], we look at the Waldschmidt constant of square-free Q-Borel ideals in the special case that Q is the chain
$C:x_1 < \cdots <x_n$
, or in other words, square-free Borel ideals.
4 Associated primes of powers of principal Q-Borel ideals
As noted in the introduction, studying the set of the associated primes of a power of an ideal has been of recent interest. One property that has been studied is the persistence property. Formally, an ideal I is said to have the persistence property if
${\textrm {ass}}(I^i) \subseteq {\textrm {ass}}(I^{i+1})$
for all
$i \geq 1$
. Given this interest, it makes sense to determine if principal Q-Borel ideals have this property. This short section gives two different proofs that principal Q-Borel ideals have this property.
Our first proof relies on the work of Herzog, Rauf, and Vladoiu [Reference Herzog, Rauf and Vladoiu17]; we recall a key definition from [Reference Herzog, Rauf and Vladoiu17].
Definition 4.1 A monomial ideal I is a transversal polymatroidal ideal if
$$ \begin{align*}I = P_1P_2\cdots P_t\end{align*} $$
for prime monomial ideals
$P_1,\ldots ,P_t$
.
Lemma 4.2 Let
$I=Q(m)$
for some monomial m and poset Q. Then, I is a transversal polymatroidal ideal.
Proof This result follows from [Reference Francisco, Mermin and Schweig12, Proposition 2.7], which states that a principal Q-Borel ideal is a product of prime monomial ideals.▪
We then have following result, which implies that principal Q-Borel ideals have the persistence property. Our first proof makes use of a property of polymatroidal ideals, while our second proof uses Lemma 2.10, and is self-contained.
Theorem 4.3 Let
$I=Q(m)$
for some monomial m and poset Q. Then we have
$$ \begin{align*}{\textrm{ass}}(I) = {\textrm{ass}}(I^s) ~~ \mbox{for all}\ s \geq 1.\end{align*} $$
First Proof
By [Reference Herzog, Rauf and Vladoiu17, Corollary 3.6], every transversal polymatroidal ideal J satisfies
${\textrm {ass}}(J) = {\textrm {ass}}(J^s)$
for all
$s \geq 1$
. Now apply Lemma 4.2.▪
Second Proof
By repeatedly applying Lemma 2.10,
$I^s = Q(m)^s = Q(m^s)$
. If
$P \in {\textrm {ass}}(I)$
, then by Theorem 2.12, there is a
$m'$
such
$m'|m$
and
$A(m')$
is connected and
$P = \langle x_i ~|~ x_i \in A(m') \rangle $
. But then
$m'|m^s$
and
$A(m')$
is connected, so P is also an associated prime of
$I^s = Q(m^s)$
.
Conversely, suppose that
$P \in {\textrm {ass}}(I^s) = {\textrm {ass}}(Q(m^s))$
. By Theorem 2.12, there is a monomial
$m'$
that divides
$m^s$
such that
$A(m')$
is connected and
$P = \langle x_i ~|~ x_i \in A(m') \rangle $
. If
$m' = x_{i_1}^{b_{i_1}}\cdots x_{i_r}^{b_{i_r}}$
with
$b_{i_j}>0$
, let
$m'' =x_{i_1}\cdots x_{i_r}$
. Since
$m'|m^s$
, we have
$m''|m$
. Furthermore, because
$m'$
and
$m''$
share the same support,
$A(m') = A(m'')$
by Lemma 2.1. So, we have
$m''$
divides m and
$A(m'')$
is connected. So by Theorem 2.12,
$P = \langle x_i ~|~ x_i \in A(m') = A(m'') \rangle $
is an associated prime of I, as desired.▪
5 The analytic spread of principal Q-Borel ideals
In this section, we compute the analytic spread of principal Q-Borel ideals
$Q(m)$
and square-free principal Q-Borel ideals
$sfQ(m)$
. In particular, this invariant is expressed in terms of the properties of the order ideal
$A(m)$
viewed as an induced subposet of Q. We recall the definition of analytic spread.
Definition 5.1 Let
$I \subseteq S =\mathbb {K}[x_1,\ldots ,x_n]$
be a homogeneous ideal, and let
${\textbf {m}} = \langle x_1,\ldots ,x_n \rangle $
. The analytic spread of I, denoted
$\ell (I)$
, is the Krull dimension of the ring
$$ \begin{align*}\mathcal{F}(I) = \bigoplus_{i \geq 0} \frac{I^i}{\textbf{m}I^i} ~~~~\mbox{where}\ I^0 = S.\end{align*} $$
Remark 5.2 The ring
$\mathcal {F}(I)$
is usually referred to as the special fiber ring. The special fiber ring is also isomorphic to
$\mathcal {R}(I)/{\textbf {m}}\mathcal {R}(I)$
where
$\mathcal {R}(I) = R[It] = \bigoplus _{i \geq 0} I^it^i \subseteq R[t]$
is the Rees algebra of I. Roughly speaking, the analytic spread is the minimum number of generators of an ideal J that is a reduction of I (e.g., see [Reference Huneke and Swanson19, Corollary 8.2.5]).
The next lemma gives us a tool to compute
$\ell (I)$
when I is generated by monomials all of the same degree.
Lemma 5.3 [Reference Martínez-Bernal, Morey and Villarreal20, Lemma 3.2]
Let
$I= \langle x^{\alpha _1},\ldots ,x^{\alpha _r} \rangle $
be a monomial ideal and let A be the matrix with columns
$\alpha _i$
. If
$\deg x^{\alpha _i}=d$
for all i, then the analytic spread of I is
$$ \begin{align*}\ell(I)=\mathrm{rank}\ A.\end{align*} $$
Since
$I = Q(m)$
is generated by monomials of the same degree (see Lemma 2.8), to compute
$\ell (Q(m))$
it is enough compute the rank of the matrix corresponding to the degrees of the generators. The rank of this matrix is encoded in
$A(m)$
, as we now show.
Theorem 5.4 Let
$I = Q(m)$
for some monomial m and poset Q. Then
$$ \begin{align*}\ell(I)=|A(m)|-K(A(m))+1\end{align*} $$
where
$A(m)$
is the order ideal of m and
$K(A(m))$
is the number of connected components of
$A(m)$
as an induced subposet of Q.
Proof We can write
$I = Q(m)$
as
$I = \langle x^{\alpha _1}, \ldots ,x^{\alpha _r} \rangle $
where
$\{x^{\alpha _1},\ldots ,x^{\alpha _r}\}$
are the minimal generators, and
$m = x^{\alpha _r}$
. By Lemma 2.8, the generators all have the same degree.
Let
$A = \begin {bmatrix} \alpha _1 & \cdots & \alpha _r \end {bmatrix}$
be the
$n \times r$
matrix where the i-th column is given by
$\alpha _i$
. By Lemma 5.3 we need to compute
${\textrm {rank}}(A)$
, or equivalently, the rank of the matrix
$$ \begin{align*}A' = \begin{bmatrix} \alpha_1-\alpha_r & \alpha_2-\alpha_r & \cdots & \alpha_{r-1}-\alpha_r & \alpha_r \end{bmatrix}\end{align*} $$
because the column space of A and
$A'$
is the same.
For all
$x_j \leq _Q x_i$
, let
$e_{(i,j)} \in \mathbb {N}^n$
denote the vector defined in (2.1). Note that
$x^{\alpha _k}$
is the monomial obtained from
$m = x^{\alpha _r}$
via a series of Q-Borel moves. In particular by Lemma 2.6 there exists vectors
$e_{(i_1,j_1)},e_{(i_2,j_2)},\ldots ,e_{(i_l,j_l)}$
with
$i_t \in {\textrm {supp}}(x^{\alpha _r})$
for
$t=1,\ldots ,l$
such that
$$ \begin{align*}\alpha_r+e_{(i_1,j_1)} + \cdots + e_{(i_l,j_l)} = \alpha_k.\end{align*} $$
Thus
$\alpha _k-\alpha _r\in \mathrm {Span}\{e_{(i,j)}\ |\ i\in \mathrm {supp}(x^{\alpha _r}) ~~\mbox {and}~~ x_j \leq _Q x_i\}$
for any
$1\leq k\leq r-1$
. Because
$\alpha _r+e_{(i,j)}$
is a column of A for any
$i\in \mathrm {supp}(x^{\alpha _r})$
and
$x_j \leq _Q x_i$
, the vectors
$e_{(i,j)}$
appear as columns of
$A'$
. This implies that
$$ \begin{align*}\mathrm{rank}\ A'=1+\dim_{\mathbb{K}} (\mathrm{Span}\{e_{(i,j)}\ |\ i\in\mathrm{supp}(x^{\alpha_r}) ~~\mbox{and}~~ x_j \leq_Q x_i\}).\end{align*} $$
where the
$1$
corresponds to the column corresponding to
$\alpha _r$
.
Consider the order ideal
$A(x^{\alpha _r})$
and view it as an induced poset of of Q. Let B denote the incidence matrix of the Hasse diagram associated to
$A(x^{\alpha _r})$
. That is, B is the matrix whose rows are indexed by the elements of
$A(x^{\alpha _r})$
and whose columns are indexed by the directed edges in
$A(x^{\alpha _r})$
. Furthermore, in the column indexed by the edge of
$A(x^{\alpha _r})$
between
$x_j$
and
$x_i$
with
$x_j <_Q x_i$
, we put a
$-1$
in the row indexed by
$x_i$
and a
$1$
in the row indexed by j.
It follows from the proof of [Reference Godsil and Royle14, Theorem 8.3.1] that the kernel of B is generated by the vectors
$v_C=\sum _{x_i\in C} e_i$
where C is a connected component of
$A(m)$
. Given that the columns of B belong to
$\mathrm {Span}\{e_{(i,j)}\ |\ i\in \mathrm {supp}(x^{\alpha _r}) ~~\mbox {and}~~ x_j \leq _Q x_i\}$
and the generators of this space are orthogonal to the elements in
$\{v_C\ |\ C\mbox { is a connected component of} A(m)\}$
, then
$$ \begin{align*}\mathrm{Col}(B)=\mathrm{Span}\{e_{(i,j)}\ |\ i\in\mathrm{supp}(x^{\alpha_r}) ~~\mbox{and}~~ x_j \leq_Q x_i\}.\end{align*} $$
Thus,
$$ \begin{align*}\ell(Q(m))=\mathrm{rank}\ A=\mathrm{rank}\ A'=1+\mathrm{rank}\ B\end{align*} $$
and from [Reference Godsil and Royle14, Theorem 8.3.1] we know
$\mathrm {rank}\ B=|A(m)|-K(A(m))$
from where we obtain the desired conclusion.▪
Before considering square-free principal Q-Borel ideals, we make a brief aside to differentiate our work from that of Herzog and Qureshi [Reference Herzog and Qureshi16]. As shown in [Reference Herzog and Qureshi16], the analytic spread of a polymatroidal ideal [Reference Herzog and Qureshi16, Definition 2.3] can be computed via the linear relation graph of the ideal.
Definition 5.5 Let
$G(I)=\{m_1,\ldots ,m_s\}$
be the minimal generators of a monomial ideal I. The linear relation graph
$\Gamma $
of I is the graph with edge set
$$ \begin{align*}E=\{\{i,j\}\ |\ \text{there exists}\ m_k,m_l\in G(I)\text{ such }x_im_k=x_jm_l\}\end{align*} $$
and vertex set
$V=\bigcup _{\{i,j\}\in E}\{i,j\}$
.
The analytic spread of a polymatroidal ideal is related to its linear relation graph.
Lemma 5.6 [Reference Herzog and Qureshi16, Lemma 4.2]
Let I be a polymatroidal ideal with linear relation graph
$\Gamma $
. If r is the number of vertices of
$\Gamma $
and s is the number of connected components of
$\Gamma $
, then
$$ \begin{align*}\ell(I)=r-s+1.\end{align*} $$
As shown in [Reference Francisco, Mermin and Schweig12, Proposition 2.9], a principal Q-Borel ideal
$I=Q(m)$
is a polymatroidal ideal. Consequently, one can compute
$\ell (Q(m))$
via Lemma 5.6. However, our Theorem 5.4 has the advantage of expressing the analytic spread in terms of the poset Q and order ideal
$A(m)$
. As the next example shows, we do not necessarily have
$|A(m)|=r$
and
$K(A(m))=s$
, with r and s as in Lemma 5.6.
Example 5.7 Consider
$S=\mathbb {K}[x_1,x_2,x_3]$
, and let our poset Q on
$\{x_1,x_2,x_3\}$
have Hasse diagram
Consider
$I=Q(x_2x_3) = \langle x_1x_2,x_2x_3 \rangle $
. Then
$|A(x_2x_3)| = 3$
and
$K(A(x_2x_3)) =2$
. However, the linear relation graph
$\Gamma $
of I contains the single edge
$\{1,3\}$
since
$x_3(x_1x_2) = x_1(x_2x_3)$
is the only linear relation among the generators of I. So
$r = 2$
and
$s=1$
.
In light of the above example, it is natural to ask if there is any connection between
$A(m)$
and the linear relation graph
$\Gamma $
of the principal Q-Borel ideal
$I=Q(m)$
. This relationship is explained in the following theorem.
Theorem 5.8 Fix a poset Q on
$X=\{x_1,\ldots ,x_n\}$
and take
$m\in S$
a monomial. Let
$I=Q(m)$
and let
$\Gamma $
be its linear relation graph. Consider H, the Hasse diagram of
$A(m)$
, but as an undirected graph; that is, the vertex set is
$V(H)=A(m)$
and
$\{x_i,x_j\}\in E(H)$
is an edge if
$x_i<_Q x_j$
or
$x_j<_Q x_i$
and there is no element
$y\in X$
with
$x_i <_Q y <_Q x_j$
or
$x_j <_Q y < x_i$
.
Then
$\Gamma $
is the transitive closure of H after removing the isolated vertices of H.
Proof First, it is clear that
$E(H)\subseteq E(\Gamma )$
. Also
$V(H){\kern2pt}\backslash{\kern2pt} V(\Gamma )$
is precisely the set of isolated vertices of H. Now, take
$\{i,j\}\in E(\Gamma )$
. Then there exists
$x^{\alpha },x^{\beta }\in G(I)$
such that
$$ \begin{align*}e_i+\alpha=e_j+\beta.\end{align*} $$
But
$x^\alpha ,x^\beta $
are also Q-Borel movements of
$m =x^\nu $
. Then, by Lemma 2.6, there exists
$i_1,\ldots ,i_t\in \mathrm {supp}(m)$
,
$j_1,\ldots , j_t$
with
$x_{j_k}<_Q x_{i_k}$
for
$1\leq k\leq t$
and
$\{i^{\prime }_1,\ldots ,i^{\prime }_s\}\in \mathrm {supp}(m)$
,
$j^{\prime }_1,\ldots , j^{\prime }_s$
with
$x_{j^{\prime }_k}<_Q x_{i^{\prime }_k}$
,
$1\leq k\leq s$
, such that:
$$ \begin{align*}\nu=\alpha+\sum_{k=1}^t e_{(i_k,j_k)}=\beta+\sum_{k=1}^s e_{(i^{\prime}_k,j^{\prime}_k)}\end{align*} $$
and then
$$ \begin{align*}e_j-e_i=\sum_{k=1}^s e_{(i^{\prime}_k,j^{\prime}_k)}-\sum_{k=1}^t e_{(i_k,j_k)}.\end{align*} $$
But this means that there is a path from i to j along the vertices of H and then
$\{i,j\}$
is in the transitive closure of H.▪
Remark 5.9 The previous theorem implies that if c is the number of isolated vertices of
$A(m)$
, then
$|A(m)| = r+c$
and
$K(A(m))=s+c$
where r and s are as in Lemma 5.6. Using the fact that a principal Q-Borel ideal is a polymatroidal ideal, we could then use Lemma 5.6 and Theorem 5.8 to give a different proof of Theorem 5.4. In particular, if
$\Gamma $
is the linear relation graph of
$Q(m)$
, we have
$$ \begin{align*}\ell(Q(m)) = r-s+1 = (r+c)-(s+c)+1 = |A(m)|-K(A(m))+1.\end{align*} $$
Our proof of Theorem 5.4 avoids using the polymatroidal property.
Our analysis of the square-free principal Q-Borel case is similar to the principal Q-Borel case. We require the following notation. Suppose that Q is a poset on
$X = \{x_1,\ldots ,x_n\}$
. If
$Y = \{x_{j_1},\ldots ,x_{j_s}\}$
is a subset of X, then Q induces a poset
$Q'$
on Y if we define
$x_j <_{Q'} x_i$
if
$x_j <_Q x_i$
.
If m is a monomial only in the variables of Y, then we write
$A_{Q}(m)$
or
$A_{Q'}(m)$
if wish to view the order ideal in Q on the set X or in
$Q'$
on the set Y. Similarly, we write
$sfQ(m)$
or
$sfQ'(m)$
, and
$Q(m)$
and
$Q'(m)$
if we wish to denote which partial order and ground set we are using.
Theorem 5.10 Fix a poset Q on
$X = \{x_1,\ldots ,x_n\}$
, and suppose that
$m \in S$
is a square-free monomial. Let
$m' = {\textrm {gcd}}(G(sfQ(m)))$
be the greatest common divisor of all the generators of the square-free principal Q-Borel ideal
$I = sfQ(m)$
. Then,
$$ \begin{align*}\ell(I) = \ell(Q'(m/m')) = |A_{Q'}(m/m')| - K(A_{Q'}(m/m')) +1, \end{align*} $$
where
$Q'$
is the induced poset on
$Y= X {\kern2pt}\backslash{\kern2pt} \{x_j ~|~ j \in {\textrm {supp}}(m')\}$
.
Proof Let
$m = x^\alpha =x_{i_1}x_{i_2}\cdots x_{i_s}$
and
$m' = x^\delta = x_{j_1}\cdots x_{j_t}$
. Since
$m'$
is the greatest common divisor of all the generators,
$m'|m$
. Furthermore, suppose
$x_j|m'$
, and thus
$x_j|m$
. If
$x_k <_Q x_j$
, then
$\frac {x_k}{x_j}m \not \in I$
because otherwise we would have a generator of I not divisible by
$x_j$
. If
$x_j <_Q x_i$
and
$x_i|m$
, then
$\frac {x_j}{x_i}m$
is a Q-Borel move of m, but it is not in I since this monomial is not square-free. Thus,
$x\in A(m')$
implies that
$A(x)=\{x\}$
or for any
$y\in Q{\kern2pt}\backslash{\kern2pt} \{x\}$
comparable to x, the corresponding Q-Borel movement is not in
$sfQ(m)$
.
We first consider the case that
$m'=1$
. Note that this means that every
$x_i$
that divides m is not a minimal element of
$A(m)$
. Indeed, if
$x_i$
is a minimal element, then
$x_i$
would appear in every generator of I, contradicting the fact
$m'=1$
.
Set
$I = sfQ(m)$
and
$J = Q(m)$
. Let A be the matrix whose column entries have the form
$\beta $
where
$x^\beta $
is a generator of I, and similarly, let B be the matrix whose columns have the form
$\gamma $
where
$x^\gamma $
is a generator of J. By Lemma 5.3 and Theorem 5.4 we have
$$ \begin{align*}\ell(I) = {\textrm{rank}}(A) \leq {\textrm{rank}}(B) = \ell(J) = |A(m)|- K(A(m))+1.\end{align*} $$
The inequality follows from the fact that all of the columns of A are in B.
Fix any
$i \in {\textrm {supp}}(m)$
(and thus,
$x_i|m$
), and suppose
$x_j <_Q x_i$
. If
$x_j \nmid m$
, then
$\frac {x_j}{x_i}m\in G(I)$
, and therefore
$\alpha +e_{(i,j)}$
is a column of A. Since
$\alpha $
is a column of A, we have
$e_{(i,j)} \in {\textrm {Col}}(A)$
. If
$x_j$
also divides m, then there exists a minimal element
$x_k<_Q x_j$
. Since
$x_k$
is minimal, our hypotheses imply that
$x_k \nmid m$
. But then
$$ \begin{align*}\alpha+e_{(i,k)}~~\mbox{and}~~ \alpha+e_{(j,k)}\end{align*} $$
are columns of A, and then
$e_{(i,k)}-e_{(j,k)}=e_{(i,j)}$
is in
$\mathrm {Col}(A)$
. But from Theorem 5.4 we have
$$ \begin{align*}\mathrm{Col}(B)=\mathrm{Span}(\{\alpha\}\cup\{e_{(i,j)}\ |\ i\in\mathrm{supp}(m), x_j \leq_Q x_i\})\subset\mathrm{Col}(A).\end{align*} $$
Consequently,
${\textrm {rank}}(B) \leq {\textrm {rank}}(A)$
, giving the desired result.
Now suppose that
$m'=x^\delta = x_{j_1}\cdots x_{j_k}> 1$
. Since every generator of
$sfQ(m)$
is divisible by
$m'$
, we have
$$ \begin{align*}I=sfQ'(m)=m'\cdot sfQ'(m/m').\end{align*} $$
If A, respectively B, is the matrix whose columns have the form
$\gamma $
with
$x^\gamma $
a generator of
$sfQ'(m)$
, respectively,
$sfQ'(m/m')$
, we can use Lemma 5.3 and the proof of Theorem 5.4 to show that
${\textrm {rank}}(A) = {\textrm {rank}}(B)$
; in particular, one needs to verify
$$ \begin{align*} \dim\ \mathrm{Col}(A) &=\dim\mathrm{Span}(\{\delta+\beta\}\cup\{e_{(i,j)}\in \mathbb{N}^{|Q|}\ |\ i\in\mathrm{supp}(m/m')~~\mbox{and}~~ x_j\leq_{Q'} x_i\}) \\ &=\dim\mathrm{Span}(\{\beta\}\cup\{e_{(i,j)} \in \mathbb{N}^{|Q'|}\ |\ i\in\mathrm{supp}(m/m')~~\mbox{and}~~ x_j\leq_{Q'} x_i\})\\ &=\dim\ \mathrm{Col}(B) \end{align*} $$
where
$m = x^{\delta +\beta }$
and
$m/m' = x^\beta $
. Consequently
$$ \begin{align*}\ell(I) = {\textrm{rank}}(A) = {\textrm{rank}}(B) = \ell(sfQ'(m/m')) = \ell(Q'(m/m'))\end{align*} $$
where the last equality follows from the first part of the proof.▪
Example 5.11 We illustrate the above result. Let Q be the poset with Hasse diagram
Let
$m=x_1x_2x_3x_6$
and
$I=sfQ(m)$
, and thus
$$ \begin{align*}I=\langle x_1x_2x_3x_6,x_1x_2x_3x_5,x_1x_2x_3x_4\rangle.\end{align*} $$
We have
$\mathrm {gcd}(G(I))=x_1x_2x_3$
. Therefore
$Q'$
is the poset on
$\{x_4,x_5,x_6\}$
with Hasse diagram:
Hence,
$\ell (I)=\ell (Q'(x_6))=3$
.
Remark 5.12 It can be shown that
$m' = {\textrm {gcd}}(G(I))$
in Theorem 5.10 is the largest monomial (by degree) that divides m such that
$$ \begin{align*}\{x_j ~|~ j \in {\textrm{supp}}(m')\} = A(m').\end{align*} $$
That is, the variables that divide
$m'$
form an order ideal. Returning to the above example, note that
$\{x_j ~|~ j \in {\textrm {supp}}(x_1x_2x_3)\} = \{x_1,x_2,x_3\} = A(x_1x_2x_3)$
in the poset Q. Note that if no such monomial exists, we use the convention that
$A(1) = \emptyset $
.
Using the above interpretation of
$m'$
, we have the following corollary, which uses the following terminology. Given a poset Q on
$\{x_1,\ldots ,x_n\}$
, the minimal elements of
$\{x_1,\ldots ,x_n\}$
are those
$x_i$
that are minimal with respect to the partial order on Q.
Corollary 5.13 Fix a poset Q and suppose that
$m \in S$
is a square-free monomial. Suppose
$\{x_j ~|~ j \in {\textrm {supp}}(m)\}$
contains no minimal elements of Q. If
$I =sfQ(m)$
, then
$$ \begin{align*}\ell(I) = \ell(Q(m)) = |A(m)| - K(A(m)) +1. \end{align*} $$
Proof No subset of
$\{x_j ~|~ j \in {\textrm {supp}}(m)\}$
is an order ideal in Q. So
$m'= {\textrm {gcd}} (G(I)) = 1$
. Now, apply Theorem 5.10.▪
Acknowledgments
We thank Ashwini Bhat, Chris Francisco, and the two referees for their comments and improvements.
