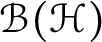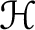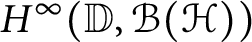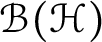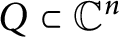1 Introduction and some basic questions
Let
$H^{\infty }(\mathbb {D},X)$
be the space of bounded analytic functions from the unit disk
$\mathbb {D}:=\{z \in \mathbb {C}:|z|<1\}$
into a complex Banach space X with
$\left \lVert f\right \rVert _{H^{\infty }(\mathbb {D},X)}:=\sup _{|z|<1} \left \lVert f(z)\right \rVert $
. Let
$\mathcal {B}(\mathbb {D},X)$
be the class of functions f in
$H^{\infty }(\mathbb {D},X)$
with
$\left \lVert f\right \rVert _{H^{\infty }(\mathbb {D},X)} \leq 1$
. The Bohr radius
$R(X)$
for the class
$\mathcal {B}(\mathbb {D},X)$
is defined by (see [Reference Blasco12])
$$ \begin{align*} R(X):=\sup \left\{r \in (0,1): M_{r}(f)\leq 1 \,\, \mbox{for all} \,\, f(z)= \sum_{k=0}^{\infty} x_{k} z^{k} \in \mathcal{B}(\mathbb{D},X), z \in \mathbb{D}\right\}, \end{align*} $$
where
$M_{r}(f)=\sum _{k=0}^{\infty } \left \lVert x_{k}\right \rVert r^{k}$
is the associated majorant series of
$f \in H^{\infty }(\mathbb {D},X)$
. The remarkable theorem of Harald Bohr [Reference Bohr14] (in improved form) states that
$R(X)=1/3$
for
$X=\mathbb {C}$
, where the norm of X is the usual modulus of complex numbers. The interest in the Bohr’s theorem has been revived when Dixon [Reference Dixon18] used it to answer a long-standing question on the characterization of the Banach algebras satisfying the nonunital von Neumann inequality. For the last two decades, there has been an extensive research carried out to the extensions of analytic functions of several complex variables, to planar harmonic mappings, to polynomials, to solutions of elliptic partial differential equations, and to more abstract settings. In
$1997$
, Boas and Khavinson [Reference Boas and Khavinson13] introduced the n-dimensional Bohr radius
$K_{n}$
for the Hardy space of bounded analytic functions on the unit polydisk, and obtained the upper and lower bounds of
$K_{n}$
. In
$2006$
, an improved version of the lower estimate of
$K_{n}$
was obtained by Defant and Frerick [Reference Defant and Frerick16]. Further estimation of
$K_{n}$
has been obtained by Defant et al. [Reference Defant, Frerick, Ortega-Cerd À, Ounaïes and Seip17] by using the hypercontractivity of the polynomial Bohnenblust-Hille inequality. In
$2014$
, Bayart et al. [Reference Bayart, Pellegrino and Seoane-Sep Úlveda9] obtained the exact asymptotic behaviour of
$K_{n}$
. In
$2019$
, Popescu [Reference Popescu25] extended the Bohr inequality for free holomorphic functions to polyballs. For more interesting aspects and generalization of multidimensional Bohr’s inequality, we refer to [Reference Aizenberg, Aytuna and Djakov3–Reference Alkhaleefah, Kayumov and Ponnusamy5, Reference Aytuna and Djakov8, Reference Djakov and Ramanujan19, Reference Liu and Ponnusamy22]. In
$2004$
, Paulsen and Singh [Reference Paulsen and Singh24] extended Bohr’s theorem to Banach algebras by finding a general version of Bohr inequality which is valid in the context of uniform algebras. In
$2021$
, Bhowmik and Das [Reference Bhowmik and Das11] extensively studied Bohr inequality for operator valued functions. Further results on Bohr radius, we refer to [Reference Bénéteau, Dahlner and Khavinson10, Reference Garcia, Mashreghi and Ross21].
For
$p \in [1, \infty )$
, let
$H^{p}(\mathbb {D},X)$
be the space of analytic functions from
$\mathbb {D}$
into a complex Banach space X such that
$$ \begin{align} \left\lVert f\right\rVert_{H^{p}(\mathbb{D},X)}= \sup \limits {}_{0<r<1} \left(\int_{0}^{2\pi} \left\lVert f(re^{it})\right\rVert^{p} \frac{dt}{2\pi}\right)^{1/p} < \infty. \end{align} $$
In [Reference Bénéteau, Dahlner and Khavinson10], Bénéteau et al. have shown that there is no Bohr phenomenon in the Hardy spaces
$\left \lVert f\right \rVert _{H^{p}(\mathbb {D},\mathbb {C})}$
for
$1 \leq p <\infty $
. In fact, they have shown that there is no Bohr phenomenon in complex valued Hardy spaces
$H^{q}$
for
$q \in (0,\infty )$
. In [Reference Djakov and Ramanujan19], Djakov and Ramanujan have extensively studied the p-Bohr inequality for the power series of the form
$\sum _{k=0}^{\infty } |a_{k}|^{p} r^{k}$
for
$p \in [1,\infty )$
, where
$f(z)=\sum _{k=0}^{\infty } a_{k}z^{k}$
is a bounded analytic function in
$\mathbb {D}$
. In [Reference Djakov and Ramanujan19], the notion of p-Bohr inequality has been extended to the analytic functions of several variables.
1.1 Bohr theorem for operator valued analytic function
One of the main aims of the present paper is to study Bohr inequality in the setting of operator valued analytic functions in the unit disk
$\mathbb {D}$
, to be more specific, for functions in
$H^{\infty }(\mathbb {D},X)$
, where
$X=\mathcal {B}(\mathcal {H})$
is the algebra of all bounded linear operators on a complex Hilbert space
$\mathcal {H}$
. For the rest of our discussion on this, we need to fix some basic notations. For
$T \in \mathcal {B}(\mathcal {H})$
,
$\left \lVert T\right \rVert $
denotes the operator norm of T. The adjoint operator
$T^{*}:\mathcal {H} \rightarrow \mathcal {H}$
of T is defined by
$\left \langle Tx,y\right \rangle =\left \langle x,T^{*}y\right \rangle $
for all
$x, y \in \mathcal {H}$
. The operator T is said to be normal if
$T^{*}T=TT^{*}$
, self-adjoint if
$T^{*}=T$
, and positive if
$\left \langle Tx,x\right \rangle \geq 0$
for all
$x \in \mathcal {H}$
. The absolute value of T is defined by
$\left \lvert T\right \rvert :=\left (T^{*}T\right )^{1/2}$
, while
$S^{1/2}$
denotes the unique positive square root of a positive operator S. Let I be the identity operator on
$\mathcal {H}$
. Let
$f \in H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))$
be a bounded analytic function with the expansion
$$ \begin{align} f(z)= \sum_{k=0}^{\infty} A_{k}z^{k} \,\,\,\, \mbox{for} \,\,\,\, z \in \mathbb{D}, \end{align} $$
where
$A_{k} \in \mathcal {B}(\mathcal {H})$
for all
$k \in \mathbb {N} \cup \{0\}$
. For each
$f \in H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))$
of the form (1.2), the function
$r \mapsto M_{r}(f)$
is an increasing function in
$[0,1)$
with
$M_{0}(f)=\left \lVert A_{0}\right \rVert \leq 1$
, where
$M_{r}(f)$
is the associated majorant series of f defined by
$M_{r}(f)=\sum _{k=0}^{\infty } \left \lVert A_{k}\right \rVert r^{k}$
for
$r \in [0,1)$
. For each fixed
$z \in \mathbb {D}$
, we denote
$\mathcal {G}_{z}:= \left \{f(z)=\sum _{k=0}^{\infty } A_{k}z^{k}: f\in H^{\infty }\right.\! \left.\!(\mathbb {D}, \mathcal {B}(\mathcal {H}))\right \}.$
In [Reference Allu and Halder6], Allu and Halder have proved that the space
$\mathcal {G}_{z}$
with norm
$M_{r}$
constitutes a Banach algebra and have shown that functions in
$\mathcal {G}_{z}$
satisfy a von Neumann type inequality. Set
$\chi =\mathcal {B}(\mathbb {D},\mathcal {B}(\mathcal {H}))$
. By the similar definition as in [Reference Bombieri15] for the complex valued functions, we define
$$ \begin{align} m(\chi,r):=\sup_{f\in \chi} M_{r}(f)\,\,\,\,\, \mbox{for} \,\,\,\, r\in [0,1). \end{align} $$
Clearly,
$m(\chi ,0)=1$
. It is worth mentioning that
$m(\chi ,r)$
is an increasing function of r and hence
$m(\chi ,r)\geq 1$
for
$r \in [0,1)$
. For the arbitrary functions f in
$H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))$
, not necessarily
$\left \lVert f\right \rVert _{H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))} \leq 1$
, we have
$m(\chi ,r) \leq M_{r}(f) \left \lVert f\right \rVert _{H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))}$
. Thus, finding or estimating
$m(\chi ,r)$
, it is relevance to know
$\left \lVert f(z)\right \rVert $
i.e., to understand the rate of the growth of functions in
$H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))$
. However, a precise value for
$m(\chi ,r)$
is not known for all
$r \in [0,1)$
. But we can estimate the bounds for
$m(\chi ,r)$
. In [Reference Bombieri15], Bombieri has obtained upper bounds and lower bounds for
$m(\chi ,r)$
for complex valued bounded analytic functions.
We now generalize the notion of Bohr radius for the class
$z \chi =\{zf:f \in \chi \}$
, i.e., for the class of functions
$f \in \chi $
with
$f(0)=0$
. The Bohr radius for the class
$z \chi $
is the largest radius
$R_{1}$
such that (a)
$M_{r}(f)=\sum _{k=0}^{\infty }\left \lVert A_{k}\right \rVert r^{k+1} \leq 1$
for
$r \in [0,R_{1}]$
and for all
$f(z)=\sum _{k=0}^{\infty } A_{k}z^{k+1} \in z\chi $
, (b) when
$r \in (R_{1},1)$
, there is a function
$f \in z\chi $
such that
$M_{r}(f)>1$
. In view of (1.3), it is easy to see that
$R_{1}$
is the unique root of
$$ \begin{align} r\, m(\chi,r)=1. \end{align} $$
Since
$m(\chi ,r)$
is strictly increasing, the function
$r \mapsto r\, m(\chi ,r)$
is also strictly increasing in
$r\in [0,1)$
, which shows that (1.4) has the unique root in
$(0,1)$
. Bombieri [Reference Bombieri15] has proved that
$R_{1}=1/\sqrt {2}$
for the complex valued bounded functions in
$\mathbb {D}$
. Later, Paulsen et al. [Reference Paulsen23] have extensively studied the radius
$R_{1}$
for complex valued functions. In the present paper, we obtain
$R_{1}$
for operator valued functions in
$\chi =\mathcal {B}(\mathbb {D}, \mathcal {B}(\mathcal {H}))$
in Lemma 3.3.
In
$2019$
, Popescu [Reference Popescu25] proved the following interesting result, which is an analogue of the classical theorem of Bohr for operator valued bounded analytic functions in
$\mathbb {D}$
.
Theorem A [Reference Popescu25]
Let
$f \in H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))$
be an operator valued bounded holomorphic function with the expansion (1.2) such that
$A_{0}=a_{0}I$
,
$a_{0} \in \mathbb {C}$
. Then
$$ \begin{align} \sum\limits_{n=0}^{\infty} \left\lVert A_{n}\right\rVert \, r^{n} \leq \left\lVert f\right\rVert_{H^{\infty}(\mathbb{D},\mathcal{B}(\mathcal{H}))} \,\,\,\,\,\, \mbox{for} \,\,\,\,\, |z|=r \leq \frac{1}{3} \end{align} $$
and
$1/3$
is the best possible constant. Moreover, the inequality is strict unless f is a constant.
The proof of Theorem A relies on the bound of the norm of coefficients
$\left \lVert A_{n}\right \rVert $
, which may be obtained as an application of the operator counterpart of the Schwarz-Pick inequality.
Lemma 1.6 [Reference Anderson and Rovnyak7] (counterpart of Schwarz-Pick inequality)
Let
$B(z)$
be an analytic function with values in
$\mathcal {B}(\mathcal {H})$
and satisfying
$\left \lVert B(z)\right \rVert \leq 1$
on
$\mathbb {D}$
. Then
$$ \begin{align*} (1-|a|)^{n-1}\, \left\lVert\frac{B^{(n)}(a)}{n!}\right\rVert \leq \frac{\left\lVert I-B(a)^{*}B(a)\right\rVert^{1/2} \, \left\lVert I-B(a)B(a)^{*}\right\rVert^{1/2}}{1-|a|^{2}} \end{align*} $$
for each
$a \in \mathbb {D}$
and
$n=1,2,\ldots $
.
We note that for
$f \in \mathcal {B}(\mathbb {D},\mathcal {B}(\mathcal {H}))$
of the form (1.2) with
$A_{0}=a_{0}I$
,
$|a_{0}|<1$
. Without loss of generality, assume that
$\left \lVert f\right \rVert _{H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))} \leq 1$
. Then, by the virtue of Lemma 1.6, putting
$a=0$
, we obtain
$$ \begin{align} \left\lVert A_{n}\right\rVert \leq \left\lVert I-|A_{0}|^{2}\right\rVert=1-|a_{0}|^{2} \,\,\,\,\, \mbox{for} \,\,\,\, n\in \mathbb{N}. \end{align} $$
In view of (1.7), the proof of Theorem A follows immediately. For the sharpness of the constant
$1/3$
, we consider the following function
$$ \begin{align} \psi_{a}(z)= \left(\frac{a-z}{1-az}\right)I= A_{0} + \sum_{k=1}^{\infty} A_{k} z^{k} \,\,\, \, z \in \mathbb{D}, \end{align} $$
where
$A_{0}= aI, A_{k}=-(1-a^{2})a^{k-1} I$
and for some
$a \in [0,1)$
. Then it is easy to see that
$M_{r}(f) =\sum _{k=0}^{\infty } \left \lVert A_{k}\right \rVert r^{k}= (a+(1-2a^{2})r)/(1-ar)> 1$
whenever
$r> 1/(1+2a)$
. Taking a is very close to
$1$
, i.e.,
$a \rightarrow 1^{-}$
, we obtain
$M_{r}(f)>1$
for
$r>1/3$
, which shows that
$1/3$
is the best possible.
We say that
$\mathcal {B}(\mathbb {D},\mathcal {B}(\mathcal {H}))$
satisfies Bohr phenomenon if all the functions in
$\mathcal {B}(\mathbb {D},\mathcal {B}(\mathcal {H}))$
satisfies the inequality (1.5) for
$r \leq 1/3$
. It is worth mentioning that the constant
$1/3$
does not dependent on the coefficients of functions. In the recent years, refined versions and improved versions of Bohr inequality in the case of bounded analytic functions have become central research interest in one and several complex variables. Several authors have established various refined and improved versions of Bohr’s inequality (see [Reference Ahamed, Allu and Halder1, Reference Alkhaleefah, Kayumov and Ponnusamy5]). We now recall some of them. Let
$f \in H^{\infty }(\mathbb {D},\mathbb {C})$
be of the form
$$ \begin{align} f(z)=\sum_{k=0}^{\infty} a_{k}z^{k} \,\,\,\, \mbox{for} \,\,\,\, z \in \mathbb{D}. \end{align} $$
Let
$S_{r}$
be the area of the image of the subdisk
$\mathbb {D}_{r}=\{z:|z|<r\}$
under the map f given by (1.9). Then it is known that
$S_{r}/\pi = \sum _{k=1}^{\infty }k|a_{k}|^{2} r^{2k}$
(see [Reference Evdoridis, Ponnusamy and Rasila20]).
Theorem B Let
$f \in \mathcal {B}(\mathbb {D},\mathbb {C})$
of the form (1.9). Then
-
(a)
$ \sum _{k=0}^{\infty } |a_{k}|r^{k} + \left (\frac {1}{1+|a_{0}|} + \frac {r}{1-r}\right ) \sum _{k=1}^{\infty } |a_{k}|^{2} r^{2k} \leq 1 $
for
$|z|=r\leq 1/3$
. The constant
$1/3$
is the best possible. -
(b)
$\sum _{k=0}^{\infty }|a_{k}|r^{k}+\frac {8}{9}\left (\frac {S_{r}}{\pi }\right )\leq 1\;\;\mbox {for}\;\; r\leq 1/3$
. The bound
$8/9$
and the constant
$1/3$
cannot be replaced by a larger quantity. -
(c)
$ |f(z)| + \sum _{k=N}^{\infty } \left \lvert a_{k}\right \rvert r^{k} \leq 1 \,\,\,\,\,\,\mbox {for} \,\,\,\,\,|z|=r \leq R_{N,1}, $
where
$R_{N,1}$
is the unique root in
$(0,1)$
of
$2(1+r) r^{N} - (1-r)^{2}=0$
. The constant
$R_{N,1}$
is the best possible.
It is important to note that the proof of the part (a) and part (b) can be obtained by putting
$\gamma =0$
in [Reference Evdoridis, Ponnusamy and Rasila20, Theorem 2] and [Reference Evdoridis, Ponnusamy and Rasila20, Theorem 1] respectively. The proof of the part (c) can be obtained by putting
$\gamma =0$
in [Reference Ahamed, Allu and Halder1, Theorem 2.7].
Like the quantity
$S_{r}/\pi = \sum _{k=1}^{\infty }k|a_{k}|^{2} r^{2k}$
for the functions
$f(z)=\sum _{k=0}^{\infty } a_{k} z^{k}$
in
$ H^{\infty }(\mathbb {D},\mathbb {C})$
, we define
$$ \begin{align} S(z)=\sum_{k=1}^{\infty}k \left\lVert A_{k}\right\rVert^{2} r^{2k}, \,\,\, |z|=r<1, \end{align} $$
for the functions
$f(z)=\sum _{k=0}^{\infty } A_{k} z^{k} \in H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))$
. Let
$ G(w) $
be a polynomial defined by
$$ \begin{align} G(w)=c_{1}w+c_{2}w^{2}+\cdots+c_{l}w^{l}\;\; \mbox{for}\;\; c_{i}\in\mathbb{R}^{+},\;\; i=1, 2, \cdots, l. \end{align} $$
1.2 Multidimensional analogues of operator valued Bohr’s inequality
Let
$\alpha $
be an n-tuple
$(\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
of nonnegative integers,
$|\alpha |$
be the sum
$\alpha _{1}+\cdots + \alpha _{n}$
of its components,
$\alpha !$
denotes the product
$\alpha _{1}! \alpha _{2}!\ldots \alpha _{n}!$
, z denotes an n-tuple
$(z_{1},z_{2},\ldots , z_{n})$
of complex numbers, and
$z^{\alpha }$
denotes the product
$z_{1}^{\alpha _{1}} z_{2}^{\alpha _{2}}\ldots z_{n}^{\alpha _{n}}$
. Using the standard multi-index notation, we write an operator valued n-variable power series
$$ \begin{align} f(z)=\sum_{\alpha} A_{\alpha} z^{\alpha}, \,\,\,\,\, A_{\alpha} \in \mathcal{B}(\mathcal{H}). \end{align} $$
Let
$\mathbb {D}^{n}=\{z \in \mathbb {C}^{n}: z=(z_{1}, \ldots ,z_{n}), |z_{j}|<1, j=1,2,\ldots ,n\}$
. Let
$K_{n}(\mathcal {H})$
be the largest nonnegative number such that the power series (1.12) converges in
$\mathbb {D}^{n}$
and
$\left \lVert f\right \rVert _{H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))} \leq 1$
, then
$$ \begin{align} \sum_{\alpha} \left\lVert A_{\alpha}\right\rVert \left\lvert z^{\alpha}\right\rvert\leq 1\,\,\,\, \mbox{for all }\,\,\,\,\, z\in K_{n}(\mathcal{H})\cdot\mathbb{D}^{n}. \end{align} $$
Definition 1.1 A domain
$D \subset \mathbb {C}^{n}$
is said to be a Reinhardt domain centered at
$0 \in D$
if for any
$z=(z_{1},\ldots ,z_{n})\in D$
, and for each
$\theta _{k}\in [0,2\pi ]$
,
$k=1,2,\ldots ,n$
, we have that
$(z_{1}e^{i\theta _{1}},\ldots ,z_{n}e^{i\theta _{n}}) \in D$
. We say that
$D \subset \mathbb {C}^{n}$
is a complete Reinhardt domain if for each
$z=(z_{1},\ldots ,z_{n})\in D$
, and for each
$|\xi _{k}|\leq 1$
,
$k=1,2,\ldots ,n$
, we have that
$\xi .z=(z_{1}\xi _{1}, \ldots ,z_{n}\xi _{n}) \in D$
. A domain
$Q \subset \mathbb {C}^{n}$
is called a circular domain centered at
$0\in Q$
if for any
$z=(z_{1},\ldots ,z_{n})\in Q$
, and for each
$\theta \in [0,2\pi ]$
, we have that
$(z_{1}e^{i\theta },\ldots ,z_{n}e^{i\theta }) \in Q$
. We say that
$Q \subset \mathbb {C}^{n}$
is a complete circular domain if for each
$z=(z_{1},\ldots ,z_{n})\in Q$
, and for each
$|\xi |\leq 1$
, we have that
$\xi .z=(z_{1}\xi _{1}, \ldots ,z_{n}\xi _{n}) \in Q$
.
For a complete circular domain
$Q\subseteq \mathbb {C}^{n}$
centered at
$0\in Q$
, every analytic function in Q can be expressed into the following homogeneous polynomials
$$ \begin{align} f(z)= \sum_{k=0}^{\infty} P_{k}(z)\,\,\,\,\,\, \mbox{for} \,\,\,\, z \in Q, \end{align} $$
where
$P_{k}(z)=\sum _{|\alpha |=k} A_{\alpha } z^{\alpha }$
is a homogeneous polynomial of degree k and
$P_{0}(z)=f(0)$
.
It is natural to raise the following question.
Question 1.15 Can we establish the analogue of Theorem B for the operator valued functions in
$\mathcal {B}(\mathbb {D},\mathcal {B}(\mathcal {H}))$
? If so, then what is the multidimensional analogue of Theorem B for the functions in
$\mathcal {B}(\mathbb {D},\mathcal {B}(\mathcal {H}))$
?
In Theorem B (b), it is worth mentioning that Bohr inequality is improved by adding one degree polynomial in
$S_{r}/\pi $
with the majorant series
$\sum _{k=0}^{\infty } |a_{k}|r^{k}$
. Therefore, we have the following question.
Question 1.16 Is it possible to establish an improved version of Theorem B (b) by adding the polynomial
$G\left (S_{r}/\pi \right )$
with the majorant series
$\sum _{k=0}^{\infty } ||A_{k}||r^{k}$
for
$f \in \mathcal {B}(\mathbb {D},\mathcal {B}(\mathcal {H}))$
? If so, then what is the multidimensional analogue of Theorem B for the functions in
$\mathcal {B}(\mathbb {D},\mathcal {B}(\mathcal {H}))$
?
One of the main aims of this paper is to answer Questions 1.15 and 1.16 affirmatively.
2 Main results
Theorem 2.1 If the series (1.14) converges in the domain Q such that the estimate
$\left \lVert f(z)\right \rVert <1$
holds in Q and
$f(0)=a_{0}I$
,
$a_{0} \in \mathbb {C}$
,
$|a_{0}|<1$
, then
$$ \begin{align} \sum_{k=0}^{\infty} \left\lVert P_{k}(z)\right\rVert <1 \end{align} $$
in the homothetic domain
$(1/3)Q$
. Moreover, if Q is convex, the constant
$1/3$
is the best possible.
In particular, if f is complex valued bounded analytic functions in the domain Q, we can obtain the multidimensional analogues of Bohr’s inequality for complex valued bounded analytic functions in the domain Q, which has been independently proved by Aizenberg [Reference Aizenberg2]. We obtain the Bohr radius for the functions
$f \in \mathcal {B}(\mathbb {D}, \mathcal {B}(\mathcal {H}))$
with the initial coefficients
$f(0)=0$
in the following lemma. Recall that
$R_{1}$
is the unique root of (1.4). In the following lemma, we assume that
$\mathcal{B}(\mathcal{H})$
is complex Hilbert space.
Lemma 2.2 Let
$f \in \chi =\mathcal {B}(\mathbb {D}, \mathcal {B}(\mathcal {H}))$
with
$f(0)=0$
. Then
$R_{1}=1/\sqrt {2}$
.
If
$f \in \mathcal {B}(\mathbb {D}, \mathbb {C})$
, then the well known Bombieri [Reference Bombieri15] result follows from Lemma 2.2. In the following result, we obtain an multidimensional analogues of Lemma 2.2 by assuming
$\mathcal{B}(\mathcal{H})$
is a complex Hilbert space.
Theorem 2.2 If the series (1.14) converges in the domain Q with the estimate
$\left \lVert f(z)\right \rVert <1$
holds in Q and
$f(0)=0$
, then
$$ \begin{align} \sum_{k=1}^{\infty} \left\lVert P_{k}(z)\right\rVert <1 \end{align} $$
in the homothetic domain
$(1/\sqrt {2})Q$
. Moreover, if Q is convex, then the constant
$1/\sqrt {2}$
is the best possible.
Corollary 2.4 Suppose that the series (1.12) converges in the polydisk
$\mathbb {D}^{n}$
such that
$f(0)=0$
and
$\left \lVert f(z)\right \rVert <1$
in
$\mathbb {D}^{n}$
. Then
$$ \begin{align*} \sum_{k=1}^{\infty} \left\lVert\sum_{|\alpha|=k}A_{\alpha}z^{\alpha}\right\rVert \leq 1 \end{align*} $$
in the polydisk
$(1/\sqrt {2})\mathbb {D}^{n}$
. The constant
$1/\sqrt {2}$
is the best possible.
We establish the multidimensional analogues of Theorem B (c) for the operator valued analytic functions in the complete circular domain Q.
Theorem 2.3 Suppose that Q is a complete circular domain centered at
$0 \in Q \subset \mathbb {C}^{n}$
. If the series (1.14) converges in Q such that
$\left \lVert f(z)\right \rVert <1$
for all
$z \in Q$
and
$f(0)=a_{0}I$
,
$a_{0} \in \mathbb {C}$
,
$|a_{0}|<1$
. Then for
$p \in (0,1]$
, we have
$$ \begin{align} \left\lVert f(z)\right\rVert^{p} + \sum_{k=N}^{\infty} \left\lVert P_{k}(z)\right\rVert \leq 1 \end{align} $$
in the homothetic domain
$(R_{N,p})Q$
, where
$R_{N,p}$
is the positive root in
$(0,1)$
of the equation
$$ \begin{align} 2(1+r) r^{N} - p(1-r)^{2}=0. \end{align} $$
Moreover, if Q is convex, then the constant
$R_{N,p}$
is the best possible.
In the following result, we prove the multidimensional version of Theorem B (a) for the operator valued analytic functions in the complete circular domain Q.
Theorem 2.4 Assume that the series (1.14) converges in the domain Q such that
$\left \lVert f(z)\right \rVert <1$
for all
$z \in Q$
and
$f(0)=a_{0}I$
,
$a_{0} \in \mathbb {C}$
,
$|a_{0}|<1$
. Then
$$ \begin{align} \sum_{k=0}^{\infty} \left\lVert P_{k}(z)\right\rVert + \left(\frac{1}{1+\left\lVert f(0)\right\rVert} + \frac{r}{1-r}\right) \sum_{k=1}^{\infty} \left\lVert P_{k}(z)\right\rVert^{2} \leq 1. \end{align} $$
holds in the homothetic domain
$(1/3)Q$
. Moreover, if Q is convex, then
$1/3$
is the best possible.
In the following, we obtain an multidimensional version of Theorem B (b) for the operator valued analytic functions in the complete circular domain Q.
Theorem 2.5 If the series (1.14) and (1.10) converge in the domain Q such that
$\left \lVert f(z)\right \rVert <1$
for all
$z \in Q$
and
$f(0)=a_{0}I$
,
$a_{0} \in \mathbb {C}$
,
$|a_{0}|<1$
. If G is given by (1.11), then
$$ \begin{align} \sum_{k=0}^{\infty} \left\lVert P_{k}(z)\right\rVert + G\left(\sum_{k=1}^{\infty}k \left\lVert P_{k}(z)\right\rVert^{2}\right) \leq 1 \end{align} $$
holds in the homothetic domain
$(1/3)Q$
, where the coefficients of G satisfy
$$ \begin{align} 8c_{1}\left(\frac{3}{8}\right)^{2}+24c_{2}\left(\frac{3}{8}\right)^{4}+\cdots+8(2l-1)c_{l}\left(\frac{3}{8}\right)^{2l} \leq 1. \end{align} $$
Moreover, if Q is convex, then
$1/3$
cannot be replaced by a larger quantity.
3 Key lemmas and their proofs
We first obtain the upper and lower bounds of
$m(\chi ,r) $
for functions in
$\mathcal {B}(\mathbb {D},\mathcal {B}(\mathcal {H}))$
.
Lemma 3.1 Let
$\mathcal{B}(\mathcal{H})$
be a complex Hilbert space and
$f \in \mathcal {B}(\mathbb {D},\mathcal {B}(\mathcal {H}))$
. Then
-
(a)
$m(\chi ,r) \leq 1/\sqrt {1-r^{2}}$
for
$r \in [0,1)$
and -
(b)
$m(\chi ,r) \geq (3-\sqrt {8(1-r^{2})})/(1-r)$
for
$r \in [1/3,1)$
.
Proof Let
$f(z)=\sum _{k=0}^{\infty } A_{k}z^{k}$
, where
$A_{k} \in \mathcal {B}(\mathcal {H})$
for
$k\in \mathbb {N}\cup \{0\}$
.
-
(a) In view of the Cauchy-Schwarz inequality, we have
(3.2)From the given assumption that f is in the unit ball of
$$ \begin{align} M_{r}(f) = \sum_{k=0}^{\infty} \left\lVert A_{k}\right\rVert r^{k} \leq \sqrt{\sum_{k=0}^{\infty} \left\lVert A_{k}\right\rVert^{2}} \, \sqrt{\sum_{k=0}^{\infty} r^{2k}} \,\,\,\,\, \,\,\,\mbox{for} \,\,\, r\in [0,1). \end{align} $$
$H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))$
. That is,
$\left \lVert f\right \rVert _{H^{\infty }(\mathbb {D},\mathcal {B}(\mathcal {H}))} \leq 1$
. In particular, we have
$\left \lVert f\right \rVert ^{2}_{H^{2}(\mathbb {D},\mathcal {B}(\mathcal {H}))} =\sum _{k=0}^{\infty } \left \lVert A_{k}\right \rVert ^{2}\leq 1$
. Then the desired inequality follows from (3.2).
-
(b) To obtain the lower bound of
$m(\chi ,r)$
, we consider the function
$\psi _{a}$
which is defined by (1.8). Now, by the well known argument used in proving [Reference Garcia, Mashreghi and Ross21, Lemma 8.1.13], we can easily obtain the lower bound of
$m(\chi ,r)$
. Hence, we omit the details.▪
In the following result, we establish an operator valued analogues of Theorem B (c) with the term
$|f(z)|$
replaced by
$\left \lVert f(z)\right \rVert ^{p}$
for
$p\in (0,1]$
for functions f in
$ \mathcal {B}(\mathbb {D},\mathcal {B}(\mathcal {H}))$
.
Lemma 3.3 Let
$f : \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be a bounded analytic function of the form (1.2) such that
$A_{0}=a_{0}I$
,
$a_{0} \in \mathbb {C}$
,
$|a_{0}|<1$
. If
$\left \lVert f(z)\right \rVert \leq 1$
in
$\mathbb {D}$
, then for
$p \in (0,1]$
, we have
$$ \begin{align} \left\lVert f(z)\right\rVert^{p} + \sum_{k=N}^{\infty} \left\lVert A_{k}\right\rVert r^{k} \leq 1 \,\,\,\,\,\,\mbox{for} \,\,\,\,\,|z|=r \leq R_{N,p}, \end{align} $$
where
$R_{N,p}$
is the unique root in
$(0,1)$
of the equation (2.6). The constant
$R_{N,p}$
is the best possible.
Proof Let
$\mathcal {B}(\mathcal {H})$
be the set of bounded linear operators on a complex Hilbert space
$\mathcal {H}$
. Then
$\mathcal {B}(\mathcal {H})$
is a complex Banach space with respect to the norm
$$ \begin{align*} \left\lVert A\right\rVert=\sup_{h\in \mathcal{H}\setminus\{0\}} \frac{\left\lVert Ah\right\rVert}{\left\lVert h\right\rVert}= \sup_{h\in \mathcal{H}, \left\lVert h\right\rVert=1} \left\lVert Ah\right\rVert, \end{align*} $$
where
$A \in \mathcal {B}(\mathcal {H})$
. Let
$X^{*}$
be the dual space of
$\mathcal {B}(\mathcal {H})$
. For
$x \in \mathcal {B}(\mathcal {H}) \setminus \{0\}$
, let
$$ \begin{align*} T(x)= \{l_{x} \in X^{*}: l_{x}(x)=\left\lVert x\right\rVert \,\,\, \mbox{and} \,\,\, \left\lVert l_{x}\right\rVert=1 \}. \end{align*} $$
By the Hahn-Banach theorem, we have
$T(x) \neq \phi $
. Fix
$z \in \mathbb {D}\setminus \{0\}$
and let
$\nu = z/|z| \in \partial \mathbb {D}$
. Without loss of generality, we assume
$f(z) \neq 0$
. Let
$\tau \in \mathcal {B}(\mathcal {H})$
be any fixed point such that
$\left \lVert \tau \right \rVert =1$
. We define the following holomorphic function in
$\mathbb {D}$
by
$$ \begin{align*} g(\rho)=l_{\tau}(f(\rho \nu)) \,\,\,\,\, \mbox{for} \,\,\,\, \rho \in \mathbb{D}, \end{align*} $$
where
$l_{\tau } \in T(\tau )$
. Clearly,
$|g(\rho )| \leq 1$
in
$\mathbb {D}$
. By applying the Schwarz-Pick lemma (often referred to as Lindelöf’s inequality) (see [Reference Alkhaleefah, Kayumov and Ponnusamy5]) to the complex-valued function g, we obtain
$$ \begin{align} |g(\rho)| \leq \frac{|g(0)|+|\rho|}{1+|g(0)| |\rho|}, \,\,\,\,\, \rho \in \mathbb{D}. \end{align} $$
It is easy to see that
$$ \begin{align} |g(0)| = |l_{\tau}(f(0))| \leq \left\lVert l_{\tau}\right\rVert \left\lVert f(0)\right\rVert=\left\lVert f(0)\right\rVert. \end{align} $$
Let
$|g(0)|=t$
and
$|\rho |=s$
. Then
$s \in [0,1)$
and hence, the right hand side term
$(t+s)/(1+ts)$
of (3.5) is an increasing function in the variable
$t \in [0,\infty )$
. Thus, (3.5) and (3.6) give
$$ \begin{align} |l_{\tau}(f(\rho \nu))| \leq \frac{\left\lVert f(0)\right\rVert + |\rho|}{1+ \left\lVert f(0)\right\rVert|\rho|}. \end{align} $$
By choosing
$\rho =|z|$
and
$\tau =f(z)/\left \lVert f(z)\right \rVert $
in (3.7), we obtain
$$ \begin{align} \left\lVert f(z)\right\rVert \leq \frac{\left\lVert f(0)\right\rVert + |z|}{1+\left\lVert f(0)\right\rVert |z|} \,\,\,\,\,\mbox{for} \,\,\,\,\, z \in \mathbb{D}. \end{align} $$
Let
$f(z)= \sum _{k=0}^{\infty } A_{k}z^{k}$
be analytic in
$\mathbb {D}$
such that
$A_{k} \in \mathcal {B}(\mathcal {H})$
for all
$k \in \mathbb {N} \cup \{0\}$
and
$A_{0}=a_{0}I$
,
$a_{0} \in \mathbb {C}$
with
$|a_{0}|<1$
. Then, in view of (1.7) and (3.8), we have
$$ \begin{align} \left\lVert f(z)\right\rVert^{p} + \sum_{k=N}^{\infty} \left\lVert A_{k}\right\rVert|z|^{k} \leq \left(\frac{|z|+ |a_{0}|}{1+|z||a_{0}|}\right)^{p} + (1-|a_{0}|^{2}) \frac{|z|^{N}}{1-|z|}=1+\Upsilon_{N,p}(|a_{0}|), \end{align} $$
where
$$ \begin{align*} \Upsilon_{N,p}(|a_{0}|)= \left(\frac{r+|a_{0}|}{1+r|a_{0}|}\right)^{p} -\frac{1-r-(1-|a_{0}|^{2})r^{N}}{1-r} \,\,\,\,\, \mbox{for} \,\,\,\, |z|=r \end{align*} $$
and
$|a_{0}| \in [0,1]$
. Let
$|a_{0}|=\alpha $
. To prove the inequality (3.4), it is enough to show that
$\Upsilon _{N,p}(\alpha ) \leq 0$
for
$\alpha \in [0,1]$
. That is, we have to show that
$\Phi _{N,p}(\alpha ) \leq 0$
, where
$$ \begin{align*} \Phi_{N,p}(\alpha)= (1-r)(r+\alpha)^{p} - (1+r\alpha)^{p} \left(1-r-(1-\alpha^{2})r^{N}\right). \end{align*} $$
Clearly,
$\Phi _{N,p}(1)=0$
. Therefore, if we show that
$\Phi _{N,p}$
is an increasing function in
$\alpha $
under the condition (2.6), then we are done. A simple computation shows that
$$ \begin{align*} \Phi^{\prime}_{N,p}(\alpha) = p(1-r)(r+\alpha)^{p-1} - pr\left(1-r-(1-\alpha^{2})r^{N}\right)(1+r\alpha)^{p-1} - 2 \alpha r^{N} (1+r \alpha)^{p} \end{align*} $$
and
$$ \begin{align*} \Phi^{\prime\prime}_{N,p}(\alpha) &= p(p-1)(1-r)\left((r+\alpha)^{p-2} - r^{2} (1+r\alpha)^{p-2} \right) \\ & \,\,\, \,\,\, + p(p-1)r^{2} (1-\alpha^{2})r^{N} (1+r\alpha)^{p-2} - 2\alpha pr^{N+1}(1+r\alpha)^{p-1} - 2r^{N} (1+r \alpha)^{p}. \end{align*} $$
Note that
$(r+\alpha )^{p-2} - r^{2} (1+r\alpha )^{p-2}$
is positive for
$\alpha \in [0,1]$
and
$p \in (0,1]$
, which shows that the first term in the expression of
$\Phi ^{\prime \prime }_{N,p}(\alpha )$
is negative for
$p \in (0,1]$
. Since the other terms in the expression of
$\Phi ^{\prime \prime }_{N,p}(\alpha )$
are also negative for
$p \in (0,1]$
, it follows that
$\Phi ^{\prime \prime }_{N,p}(\alpha ) \leq 0$
for all
$\alpha \in [0,1]$
and
$p \in (0,1]$
. Thus,
$\Phi ^{\prime }_{N,p}$
is a monotonically decreasing function in
$\alpha \in [0,1]$
for
$p \in (0,1]$
, which gives that
$$ \begin{align} \Phi^{\prime}_{N,p}(\alpha) \geq \Phi^{\prime}_{N,p}(1)=p(1-r)^{2} - 2r^{N}(1+r):= \Psi(r). \end{align} $$
We observe that
$\Psi (r) \geq 0$
for
$r \leq R_{N,p}$
, where
$R_{N,p}$
is the unique root of
$\Psi (r)=0$
. Indeed,
$\Psi ^{\prime }(r)=-2p(1-r)-2\left (Nr^{N-1} + (N+1)r^{N}\right ) \leq 0$
implies that
$\Psi $
is a decreasing function in
$r \in [0,1]$
. On the other hand, since
$\Psi (0)=p>0$
and
$\Psi (1)=-4<0$
,
$\Psi $
has the unique root in
$(0,1)$
and let
$R_{N,p}$
be that root. Since
$\Psi $
is a decreasing function in r, we have
$\Psi (r) \geq \Psi (R_{N,p})=0$
for
$r \leq R_{N,p}$
. Therefore,
$\Phi ^{\prime }_{N,p}(\alpha ) \geq 0$
for
$r \leq R_{N,p}$
and
$p \in (0,1]$
. Thus,
$\Phi _{N,p}$
is an increasing function in
$\alpha $
whenever
$p \in (0,1]$
. Therefore,
$\Phi _{N,p}(\alpha ) \leq \Phi _{N,p}(1)=0$
for
$r \leq R_{N,p}$
for
$p \in (0,1]$
. This shows that
$\Upsilon _{N,p}(\alpha ) \leq 0$
for
$r \leq R_{N,p}$
,
$p \in (0,1]$
and hence, the inequality (3.4) follows from (3.9).
To prove the sharpness of the radius
$R_{N,p}$
, we consider the function
$\psi _{a}$
with
$\psi _{a}(z)=\sum _{k=0}^{\infty } A_{k} z^{k} $
given by (1.8). A simple computation shows that
$$ \begin{align} \left\lVert\psi_{a}(-r)\right\rVert^{p} + \sum_{k=N}^{\infty} \left\lVert A_{k}\right\rVert r^{k} &= \left(\frac{r+a}{1+ra}\right)^{p} + (1-a^{2}) \frac{a^{N-1}r^{N}}{1-ar} \\[3pt] \nonumber & = 1- \frac{(1-a)B_{N,p}(a,r)}{(1+ar)^{p} (1-ar)}, \end{align} $$
where
$$ \begin{align*} B_{N,p}(a,r)= (1-ar)(1+ar)^{p} \left(\frac{1}{1-a}\left(1-\left(\frac{r+a}{1+ra}\right)^{p}\right) - \left(\frac{1+a}{1-ar}\right)a^{N-1}r^{N}\right). \end{align*} $$
We note that the right hand expression of (3.11) is greater than or equals to
$1$
if, and only if,
$B_{N,p}(a,r) \leq 0$
. By letting
$a \rightarrow 1^{-}$
, we obtain
$$ \begin{align*} \lim\limits_{a \rightarrow 1^{-}} B_{N,p}(a,r) = (1-r)(1+r)^{p} \left(p\left(\frac{1-r}{1+r}\right) - \frac{2r^{N}}{1-r}\right)<0 \end{align*} $$
for
$r>R_{N,p}$
. This proves the sharpness of the constant
$R_{N,p}$
. This completes the proof.▪
In the next result, we prove an operator valued analogues of Theorem B (a).
Lemma 3.12 Let
$f : \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be a bounded holomorphic function of the form (1.2) such that
$A_{0}=a_{0}I$
,
$a_{0} \in \mathbb {C}$
with
$|a_{0}|<1$
. If
$\left \lVert f(z)\right \rVert \leq 1$
in
$\mathbb {D}$
, then we have
$$ \begin{align} \sum_{k=0}^{\infty} \left\lVert A_{k}\right\rVert r^{k} + \left(\frac{1}{1+\left\lVert f(0)\right\rVert} + \frac{r}{1-r}\right) \sum_{k=1}^{\infty} \left\lVert A_{k}\right\rVert^{2} r^{2k} \leq 1 \,\,\,\,\,\,\mbox{for} \,\,\,\,\,|z|=r\leq \frac{1}{3}. \end{align} $$
The constant
$1/3$
is the best possible.
Proof Let
$f(z)= \sum _{k=0}^{\infty } A_{k}z^{n}$
in
$\mathbb {D}$
with
$\left \lVert f(z)\right \rVert \leq 1$
in
$\mathbb {D}$
such that
$A_{k} \in \mathcal {B}(\mathcal {H})$
for all
$k \in \mathbb {N} \cup \{0\}$
and
$A_{0}=a_{0}I$
,
$a_{0} \in \mathbb {C}$
. Set
$\left \lVert A_{0}\right \rVert =|a_{0}|=b \in [0,1]$
. Then by (1.7), we obtain
$$ \begin{align*}& \sum_{k=0}^{\infty} \left\lVert A_{k}\right\rVert r^{k} + \left(\frac{1}{1+|a_{0}|} + \frac{r}{1-r}\right) \sum_{k=1}^{\infty} \left\lVert A_{k}\right\rVert^{2} r^{2k}\\ & \leq b+ (1-b^{2})\left(\frac{r}{1-r}\right) + \left(\frac{1}{1+b} + \frac{r}{1-r}\right) (1-b^{2})^{2} \, \frac{r^{2}}{1-r^{2}}:=\Psi_{2}(b). \end{align*} $$
Clearly,
$\Psi _{2}$
can be expressed as
$\Psi _{2}(b)=b+ \alpha (1-b^{2}) +\beta (1-b)(1-b^{2})+ \gamma (1-b^{2})^{2}$
for
$b \in [0,1]$
, where
$$ \begin{align*} \alpha =\frac{r}{1-r},\, \beta =\frac{r^{2}}{1-r^{2}}\,\, \mbox{and} \,\,\, \gamma=\frac{r^{3}}{(1-r)(1-r^{2})}. \end{align*} $$
Clearly,
$\alpha ,\beta $
, and
$\gamma $
are non-negative. We note that
$$ \begin{align*}& \Psi_{2}^{\prime}(b)\,=1-2\alpha b +\beta(3b^{2} -2b-1) + 4\gamma(b^{3} -b), \\ & \Psi_{2}^{\prime\prime}(b)= -2\alpha + 2 \beta (3b -1) + 4\gamma (3 b^{2} -1) \,\, \mbox{and} \,\,\, \Psi_{2}^{\prime\prime\prime}(b)=6\beta b +24 b \gamma. \end{align*} $$
Since
$\beta $
and
$\gamma $
are non-negative, we have
$\Psi _{2}^{\prime \prime \prime }(b)>0$
for all
$b \in [0,1]$
. That is,
$\Psi _{2}^{\prime \prime }$
is an increasing function of b, which implies that
$$ \begin{align*} \Psi_{2}^{\prime\prime}(b) \leq \Psi_{2}^{\prime\prime}(1)= -2 \alpha + 4\beta + 8\gamma= \frac{2r}{(1-r)(1-r^{2})}\, \tau (r), \end{align*} $$
where
$\tau (r)= 4r^{2} + 2r (1-r) - (1-r^{2})= (1+r)(3r -1)$
. It is easy to see that
$\tau (r) \leq 0$
for
$r \leq 1/3$
. Therefore,
$\Psi _{2}^{\prime \prime }(b) \leq 0$
for
$b \in [0,1]$
, which shows that
$\Psi _{2}^{\prime }$
is a decreasing function in
$b \in [0,1]$
. Thus, for
$r \leq 1/3$
, we obtain
$$ \begin{align*} \Psi_{2}^{\prime}(b) \geq \Psi_{2}^{\prime}(1) = 1-2\alpha = \frac{1-3r}{1-r}. \end{align*} $$
Clearly, for
$r \leq 1/3$
, we have
$\Psi _{2}^{\prime }(1)\geq 0$
and hence
$\Psi _{2}^{\prime }(b) \geq 0$
in
$[0,1]$
. This implies that
$\Psi _{2}$
is an increasing function in
$[0,1]$
and hence, we obtain
$\Psi _{2}(b) \leq \Psi _{2}(1)=1$
for
$r \leq 1/3$
. This proves the desired inequality (3.13). For the sharpness of the constant
$1/3$
, we consider the function
$\psi _{a}$
given by (1.8). A simple computation shows that
$$ \begin{align*}& \left\lVert A_{0}\right\rVert+\sum_{k=1}^{\infty} \left\lVert A_{k}\right\rVert r^{k} + \left(\frac{1}{1+|a_{0}|} + \frac{r}{1-r}\right) \sum_{k=1}^{\infty} \left\lVert A_{k}\right\rVert^{2} r^{2k}\\ & = a+ \frac{1-a^{2}}{a}\sum_{k=1}^{\infty} a^{n} r^{n} + \left(\frac{1}{1+a} + \frac{r}{1-r}\right) \, \frac{1-b^{2}}{b}\sum_{k=1}^{\infty}a^{2k} r^{2k}:= 1+(1-a)u(r):=v(r), \end{align*} $$
where
$$ \begin{align*} u(r)= \frac{(1+a)r}{1-ar} + \left(\frac{1}{1+a} + \frac{r}{1-r}\right) \frac{(1+a)(1-a^{2})r^{2}}{1-a^{2} r^{2}} -1. \end{align*} $$
We note that u is strictly increasing function in
$(0,1)$
. Hence, for
$r>1/3$
, we have
$u(r)>u(1/3)$
. By letting a very close to
$1$
, we obtain
$\lim _{a \rightarrow 1^{-}}u(1/3)=0$
. Therefore, u is strictly positive function for
$r>1/3$
, as a is very close to
$1$
. Hence,
$v(r)>1$
for
$r>1/3$
, which shows that the radius
$1/3$
is the best possible.▪
In the following result, we establish an operator valued analogues of Theorem B (b).
Lemma 3.14 Let f be as in Lemma
3.12
. If
$\left \lVert f(z)\right \rVert \leq 1$
in
$\mathbb {D}$
, then we have
$$ \begin{align} \sum_{k=0}^{\infty}\left\lVert A_{k}\right\rVert r^{k}+G(S(z))\leq 1\;\;\mbox{for}\;\; r\leq \frac{1}{3}, \end{align} $$
where the coefficients of
$ G(w) $
are given by (1.11) satisfy (2.9). Furthermore, the constant
$ 1/3 $
cannot be replaced by a larger quantity. Here S is given by (1.10).
Proof Let
$\left \lVert A_{0}\right \rVert =|a_{0}|=b \in [0,1]$
. Then using the inequality (1.7), we obtain
$$ \begin{align} S(z) \leq (1-b^{2})^{2} \sum_{k=1}^{\infty} kr^{2k}= (1-b^{2})^{2} \frac{r^{2}}{(1-r^{2})^{2}}. \end{align} $$
The inequality (3.16) along with (1.7) gives
$$ \begin{align} \left\lVert A_{0}\right\rVert & + \sum_{k=1}^{\infty} \left\lVert A_{k}\right\rVert r^{k} + U(S(z)) \leq b+ (1-b^{2})\frac{r}{1-r} \nonumber \\ & + \sum_{m=1}^{l} c_{m} \left(\frac{(1-b^{2})r}{1-r^{2}}\right)^{2m}=1+H(r), \end{align} $$
where
$$ \begin{align} H(r)= (1-b^{2})\frac{r}{1-r} + \sum_{m=1}^{l} c_{m} \left(\frac{(1-b^{2})r}{1-r^{2}}\right)^{2m} - (1-b). \end{align} $$
It is easy to see that
$H(r)$
is an increasing function and hence
$H(r) \leq H(1/3)$
for
$r\leq 1/3$
. A simple computation shows that
$$ \begin{align*} H(1/3)=\frac{1-b^{2}}{2}\left(1+2F_{l}(b)-\frac{2}{1+b}\right):=\frac{1-b^{2}}{2}J(b), \end{align*} $$
where
$$ \begin{align*} F_{l}(b)=\sum_{m=1}^{l}c_{l} (1-b^{2})^{2m-1}\left(\frac{3}{8}\right)^{2m} \,\,\, \mbox{and} \,\,\, J(b)=1+2F_{l}(b)-\frac{2}{1+b}. \end{align*} $$
To show that
$ H(r)\leq 0 $
, it is enough to show that
$ J(b)\leq 0 $
for
$ b\in [0,1] $
. Since
$ b\in [0,1] $
, a simple computation shows that
$$ \begin{align*} b(1+b)^{2} \left(3/8\right)^{2}\leq 4\left(3/8\right)^{2}, \,\, \dots ,b(1+b)^{2}(1-b^{2})^{2m-2} \left(3/8\right)^{2l}\leq 4\left(3/8\right)^{2l}. \end{align*} $$
It is easy to see that
$$ \begin{align*} J^{\prime}(b)&=\frac{2}{(1+b)^{2}}\bigg(1-2c_{1}b(1+b)^{2} \left(\frac{3}{8}\right)^{2}-6c_{2} b(1+b)^{2}(1-b^{2})^{2} \left(\frac{3}{8}\right)^{4}\\ &\quad\quad-\cdots-2(2l-1)c_{l} b(1+b)^{2}(1-b^{2})^{2l-2} \left(\frac{3}{8}\right)^{2l}\bigg)\\ &\geq \frac{2}{(1+b)^{2}}\left(1-\left(8c_{1}\left(\frac{3}{8}\right)^{2}+24c_{2}\left(\frac{3}{8}\right)^{4}+\cdots+8(2l-1)c_{l}\left(\frac{3}{8}\right)^{2l}\right)\right)\\ &\geq 0,\;\;\;\;\; \text{if}\;\; 8c_{1}\left(\frac{3}{8}\right)^{2}+24c_{2}\left(\frac{3}{8}\right)^{4}+\cdots+8(2l-1)c_{l}\left(\frac{3}{8}\right)^{2l}\leq 1. \end{align*} $$
Therefore,
$ J(b) $
is an increasing function in
$ [0,1] $
if (2.9) holds. Hence,
$ J(b)\leq J(1)= 0 $
for all
$ b\in [0,1] $
, which gives the desired inequality (3.15). To show the sharpness of the constant
$1/3$
, we consider the function
$\psi _{a}$
given by (1.8). A simple computation using (1.7) shows that
$$ \begin{align*} \sum_{n=0}^{\infty}{|a_{n}|}r^{n}+U(S(z))&=a +(1-a^{2})\frac{r}{1-ar}+\frac{c_{1}r^{2}(1-a^{2})^{2}}{(1-a^{2}r^{2})^{2}}+\cdots+\frac{c_{m}r^{2m}(1-a^{2})^{2m}}{(1-a^{2}r^{2})^{2m}} \\ & :\;=1-(1-a)\Phi_{1}(r), \end{align*} $$
where
$$ \begin{align*} \Phi_{1}(r)&=-\frac{(1+a)r}{1-ar}-\frac{c_{1}r^{2}(1-a)(1+a)^{2}}{(1-a^{2}r^{2})^{2}}- \cdots -\frac{c_{m}r^{2m}(1-a)^{2m-1}(1+a)^{2m}}{(1-a^{2}r^{2})^{2m}} +1. \end{align*} $$
It is not difficult to show that
$ \Phi _{1}(r) $
is strictly decreasing function of
$ r$
in
$(0,1) $
. Therefore, for
$ r>1/3 $
, we have
$ \Phi _{1}(r)<\Phi _{1}(1/3) $
. A simple computation shows that
$\lim _{a\rightarrow 1}\Phi _{1}(1/3)= 0$
. Therefore
$ \Phi _{1}(r)< 0 $
for
$ r>1/3 $
. Hence
$ 1-(1-a)\Phi _{1}(r)>1 $
for
$ r>1/3, $
which shows that
$ 1/3 $
is the best possible. This completes the proof.▪
4 Proofs of the main results
Proof of Theorem 2.1
To obtain the inequality (2.1), we convert the multidimensional power series (1.14) into the power series of one complex variable and we want to make use of Lemma 3.3. Let
$L=\{z=(z_{1}, \ldots ,z_{n}):z_{j}=a_{j}t, j=1,2,\ldots ,n; t \in \mathbb {C}\}$
be a complex line. Then, in each section of the domain Q by the line L, the series (1.14) turns into the following power series of complex variable t:
$$ \begin{align} f(at)=\sum_{k=0}^{\infty} P_{k}(a) t^{k}= f(0) + \sum_{k=1}^{\infty} P_{k}(a) t^{k}. \end{align} $$
Since
$\left \lVert f(at)\right \rVert <1$
for
$t \in \mathbb {D}$
and
$f(0)=a_{0}I$
,
$|a_{0}|<1$
, by Lemma 3.3, we obtain
$$ \begin{align} \sum_{k=0}^{\infty} \left\lVert P_{k}(a) t^{k}\right\rVert<1 \end{align} $$
for z in the section
$L \bigcap \left (\frac {1}{3}Q\right )$
. Since L is an arbitrary complex line passing through the origin, the inequality (4.2) is just (2.1). For the sharpness of the constant
$1/3$
, let the domain Q be convex. Then Q is an intersection of half spaces
$$ \begin{align*} Q= \bigcap \limits {}_{a \in J} \{z=(z_{1}, \ldots, z_{n}): {\operatorname{Re}\,} (a_{1}z_{1} + \cdots + a_{n}z_{n})<1\} \end{align*} $$
for some J. Because Q is circular, we obtain
$$ \begin{align*} Q= \bigcap \limits {}_{a \in J} \left\{z=(z_{1}, \ldots, z_{n}): \left\lvert a_{1}z_{1} + \cdots + a_{n}z_{n}\right\rvert<1\right\}. \end{align*} $$
Therefore, to show the constant
$1/3$
is the best possible, it is enough to show that
$1/3$
cannot be improved for each domain
$G_{a}=\{z=(z_{1}, \ldots , z_{n}): \left \lvert a_{1}z_{1} + \cdots + a_{n}z_{n}\right \rvert <1\}$
. In view of Theorem A, for some
$b \in [0,1)$
, there exists a function
$\psi _{b}:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
defined by (1.8) with
$\left \lVert \psi _{b}(\xi )\right \rVert <1$
for
$\xi \in \mathbb {D}$
, but for any
$|\xi |=r>1/3$
, (2.1) fails to hold in the disk
$\mathbb {D}_{r}=\{\xi : |\xi |<r\}$
. On the other hand, consider the function
$\phi : G_{a} \rightarrow \mathbb {D}$
defined by
$\phi (z)=a_{1}z_{1} + \cdots + a_{n}z_{n}$
. Thus, the function
$f(z)=(\psi _{b} \circ \phi ) (z)$
gives the sharpness of the constant
$1/3$
for each domain
$G_{a}$
. This completes the proof.▪
Proof of Lemma 2.2
In view of Lemma 3.1 (a), with
$r=1/\sqrt {2}$
, we have
$m(\chi ,1/\sqrt {2}) \leq \sqrt {2}$
and by Lemma 3.1 (b) with
$r=1/\sqrt {2}$
, we obtain
$m(\chi ,1/\sqrt {2}) \geq \sqrt {2}$
. These together give
$(1/\sqrt {2}) \, m(\chi ,1/\sqrt {2}) =1$
. Hence by (1.4), we conclude that
$R_{1}=1/\sqrt {2}$
.▪
Proof of Theorem 2.2
In view of Lemma 2.2, by going the similar lines of argument as in Theorem 2.1, we can easily show that
$\sum _{k=1}^{\infty } \left \lVert P_{k}(z)\right \rVert <1$
in the homothetic domain
$(1/\sqrt {2})Q$
. To show the constant
$1/\sqrt {2}$
is the best possible, let the domain Q be convex. Therefore, by the analogues proof of Theorem 2.1, it is enough to prove that the constant
$1/\sqrt {2}$
cannot be improved in each domain
$G_{a}=\{z=(z_{1}, \ldots , z_{n}): \left \lvert a_{1}z_{1} + \cdots + a_{n}z_{n}\right \rvert <1\}$
. Since
$1/\sqrt {2}$
is the best possible in Lemma 2.2, there exists an analytic function
$h :\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
defined by
$$ \begin{align*} h(\xi)= \xi \left(\frac{\frac{1}{\sqrt{2}}-\xi}{1-\frac{\xi}{\sqrt{2}}}\right)I= \sum_{k=1}^{\infty} A_{k} \xi {}^{k} \,\,\,\,\, \mbox{for} \,\,\,\,\, \xi \in \mathbb{D}, \end{align*} $$
where
$A_{1}=1/\sqrt {2}$
and
$A_{k}=-(1/2) (1/\sqrt {2})^{k-2}$
for
$k \geq 2$
such that
$\left \lVert h(\xi )\right \rVert <1$
in
$\mathbb {D}$
and
$h(0)=0$
. But for any
$|\xi |=r>1/\sqrt {2}$
,
$$ \begin{align*} \sum_{k=1}^{\infty} \left\lVert A_{k}\right\rVert r^{k} = \frac{r/\sqrt{2}}{1-(r/\sqrt{2})}>1, \end{align*} $$
which shows that (2.2) fails to hold in the disk
$\mathbb {D}_{r}=\{z:|z|<r\}$
. Therefore, the function
$f(z)=(h \circ \phi ) (z)$
gives the sharpness of the constant
$1/\sqrt {2}$
in each domain
$G_{a}$
, where
$\phi : G_{a} \rightarrow \mathbb {D}$
defined by
$\phi (z)=a_{1}z_{1} + \cdots + a_{n}z_{n}$
. This completes the proof.▪
Proof of Theorem 2.3
In view of Lemma 3.3 and the analogues proof of Theorem 2.1, as well as from (3.4), we can easily obtain the inequality (2.5) in the homothetic domain
$(R_{N,p})Q$
, where
$R_{N,p}$
is the positive root in
$(0,1)$
of the equation (2.6). To prove the constant
$R_{N,p}$
is the best possible whenever Q is convex, in view of the analogues proof of Theorem 2.1, it is enough to show that
$R_{N,p}$
cannot be improved for each domain
$G_{a}=\{z=(z_{1}, \ldots , z_{n}): \left \lvert a_{1}z_{1} + \cdots + a_{n}z_{n}\right \rvert <1\}$
. Since
$R_{N,p}$
is the best possible in Lemma 3.3, there exists an analytic function
$h:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
such that
$\left \lVert h(\xi )\right \rVert <1$
in
$\mathbb {D}$
, but (2.5) fails to hold in the disk
$\mathbb {D}_{r}=\{z: |z|<r\}$
for each
$|\xi |=r>R_{N,p}$
. Thus, the function
$f(z)=(h \circ \phi ) (z)$
gives the sharpness of the constant
$R_{N,p}$
in each domain
$G_{a}$
, where
$\phi : G_{a} \rightarrow \mathbb {D}$
is defined by
$\phi (z)=a_{1}z_{1} + \cdots + a_{n}z_{n}$
.▪
Proof of Theorem 2.4
In view of Lemma 3.12 and the analogues proof of Theorem 2.1, as well as from (3.13), we can obtain the inequality (2.7) in the homothetic domain
$(1/3)Q$
. To prove the constant
$1/3$
is the best possible when Q is convex, in view of the analogues proof of Theorem 2.1, it is enough to show that
$1/3$
cannot be improved for each domain
$G_{a}=\{z=(z_{1}, \ldots , z_{n}): \left \lvert a_{1}z_{1} + \cdots + a_{n}z_{n}\right \rvert <1\}$
. Thus, the function
$f(z)=(h \circ \phi ) (z)$
gives the sharpness of the constant
$1/3$
in each domain
$G_{a}$
, where
$\phi : G_{a} \rightarrow \mathbb {D}$
is defined by
$\phi (z)=a_{1}z_{1} + \cdots + a_{n}z_{n}$
.▪
Proof of Theorem 2.5
Using Lemma 3.14 and the analogues proof of Theorem 2.1, from (3.15), we can easily obtain the inequality (2.8) in the homothetic domain
$(1/3)Q$
, where the coefficients of G satisfy (2.9). When Q is convex, to prove the constant
$1/3$
is the best possible, in view of the analogues proof of Theorem 2.1, it is enough to show that
$1/3$
cannot be improved for each domain
$G_{a}=\{z=(z_{1}, \ldots , z_{n}): \left \lvert a_{1}z_{1} + \cdots + a_{n}z_{n}\right \rvert <1\}$
. Thus, the function
$f(z)=(h \circ \phi ) (z)$
gives the sharpness of the constant
$1/3$
in each domain
$G_{a}$
, where
$\phi : G_{a} \rightarrow \mathbb {D}$
defined by
$\phi (z)=a_{1}z_{1} + \cdots + a_{n}z_{n}$
.▪
Acknowledgment
The first author is supported by SERB-CRG and the second author is supported by CSIR (File No: 09/1059(0020)/2018-EMR-I), New Delhi, India.
