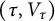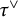1 Introduction
1.1
$\boldsymbol {\tau }$
-isospectrality and representation equivalence
Let G be a connected non-compact semisimple Lie group with finite centre. Let K be a maximal compact subgroup in G. Then
$G/K$
is a symmetric space which carries a G-invariant Riemannian metric induced by the Ad(G)-invariant inner product on the Lie algebra
$\mathfrak {g}$
of G. For any finite dimensional complex representation
$(\tau , V_{\tau })$
of K, one has the homogeneous vector bundle
$E_{\tau }$
on
$G/K$
(see Section 2.3 for the details) whose smooth sections are given by the space
$$\begin{align*}\mathcal A^\infty(G/K, \tau): = \{ \phi : G \rightarrow V_{\tau} \ | \ \text{smooth},\ \phi(gk)=\tau(k^{-1})(\phi(g))\ \text{for all}\ k \in K, g \in G\}. \end{align*}$$
This space
$\mathcal A^\infty (G/K, \tau )$
is
$\mathfrak {U(g)}^K$
-stable. In particular, the centre
$\mathfrak {Z(g)}$
of the universal enveloping algebra acts on
$\mathcal A^\infty (G/K, \tau )$
, and the Casimir element in the centre induces a second order elliptic differential operator
$\Delta _{\tau }$
on
$\mathcal A^\infty (G/K, \tau )$
. When
$\tau $
is the trivial representation of K,
$\Delta _{\tau }$
coincides with the Laplace–Beltrami operator acting on the smooth functions on
$G/K$
.
Let
$\Gamma $
be a uniform lattice in G. Then
$X_{\Gamma }:=\Gamma \backslash G /K$
is a compact locally symmetric space which is manifold if
$\Gamma $
acts freely on
$G/K$
. The space
$X_{\Gamma }$
has a Riemannian metric induced from
$G/K$
. We denote by
$V_{\Gamma , \tau }$
to be the space of all
$\Gamma $
-invariant smooth sections in
$\mathcal A^\infty (G/K, \tau )$
. Then
$V_{\Gamma , \tau }$
is stable under the action of
$\mathfrak {U(g)}^K$
, in particular of the centre
$\mathfrak {Z(g)}$
. The Casimir element C, induces the second order self-adjoint elliptic operator
$\Delta _{\tau , \Gamma }$
on
$V_{\Gamma , \tau }$
, which has non-negative discrete spectrum of eigenvalues with finite multiplicities. The multiset of eigenvalues with multiplicity is denoted by Spec(
$\Delta _{\tau , \Gamma }$
). Such spectrum of a locally symmetric space is closely related to the multiplicity of irreducible representations occurring in the right regular representation
$L^2(\Gamma \backslash G)$
of G. Here we mention the famous Matsushima–Murakami formula (see [Reference Yozô and Shingo9], see also [Reference Lauret, Miatello and Rossetti7, Proposition 2.4]):
$$ \begin{align} \text{Mult}_{\Delta_{\tau, \Gamma}}(\lambda) = \sum_{\pi \in \widehat{G}, \pi(C) =\lambda} m(\pi, \Gamma)\ \mathrm{dim}(\mathrm{Hom}_K(\tau^\vee, \pi|_K)), \end{align} $$
where,
$\tau ^\vee $
is the dual representation of
$\tau $
and
$m(\pi , \Gamma )$
is the multiplicity of
$\pi $
in the right regular representation
$L^2(\Gamma \backslash G).$
Let
$\widehat {G}_{\tau } = \{ \pi \in \widehat {G} : \mathrm {Hom}_K(\tau , \pi |_K) \neq 0\}$
. Two uniform lattices
$\Gamma _1$
and
$\Gamma _2$
are called
$\tau $
-representation equivalent if
$m(\pi , \Gamma _1)=m(\pi , \Gamma _2)$
for all
$\pi \in \widehat {G}_{\tau }$
. From Eq. 1.1, it is easily observed that if
$m(\pi , \Gamma _1)=m(\pi , \Gamma _2)$
for all
$\pi \in \widehat {G}_{\tau ^\vee }$
, then Spec(
$\Delta _{\tau , \Gamma _1}$
) = Spec(
$\Delta _{\tau , \Gamma _2}$
) for
$X_{\Gamma _1}$
and
$X_{\Gamma _2}$
, respectively. Therefore, if two lattices
$\Gamma _1$
and
$\Gamma _2$
are
$\tau ^\vee $
-representation equivalent, then the corresponding elliptic operators have the same spectrum for the locally symmetric spaces
$X_{\Gamma _1}$
and
$X_{\Gamma _2}$
, respectively i.e., they are
$\tau $
-isospectral (see [Reference Lauret, Miatello and Rossetti7, Proposition 2.5]).
Definition 1.1.1 Two co-compact lattices
$\Gamma _1$
and
$\Gamma _2$
are called almost-
$\tau $
-representation equivalent if
$m(\pi , \Gamma _1)$
is equal to
$ m(\pi , \Gamma _2)$
for all but finitely many
$\pi \in \widehat {G}_{\tau }$
.
In the first half of this paper, we give an affirmative answer of the question: whether the almost-
$\tau $
-representation equivalence implies
$\tau $
-representation equivalence between two uniform torsion free lattices
$\Gamma _1$
and
$\Gamma _2$
in non-compact symmetric space
$G/K$
with arbitrary rank, and for any finite dimensional representation
$(\tau , V_{\tau })$
of K.
Theorem 1.1.2
Let G be a non-compact connected semisimple Lie group with finite center. If for two uniform torsion free lattices
$\Gamma _1$
and
$\Gamma _2$
,
$$ \begin{align*}m(\pi, \Gamma_1)=m(\pi, \Gamma_2)\end{align*} $$
for all but finitely many
$\pi \in \widehat {G}_{\tau }$
, then
$\Gamma _1$
and
$\Gamma _2$
are
$\tau $
-representation equivalent lattices.
Remark 1.1.3 Consequently, the above hypothesis implies that
$X_{\Gamma _1}$
and
$X_{\Gamma _2}$
are
$\tau ^\vee $
-isospectral. When
$\tau $
is trivial, Theorem 1.1.2 reduces to [Reference Chandrasheel and Rajan1, Theorem 1.2]. A special case of Theorem 1.1.2 is [Reference Chandrasheel and Gunja2, Theorem 4.1] for the group
$\mathrm {PSL}(2, {\mathbb R})$
.
1.2 Infinitesimal
$\boldsymbol {\tau }$
-isospectrality
For an infinitesimal character
$\chi $
of
$\mathfrak {Z(g)}$
, let
$V_{\chi , \Gamma , \tau }=\{ \phi \in V_{\Gamma , \tau } \ | \ z. \phi = \chi (z) \phi $
for all
$z \in \mathfrak {Z(g)}\}$
.
We define a refinement of the notion of
$\tau $
-isospectrality as follows.
Definition 1.2.1 Two locally symmetric spaces
$X_{\Gamma _1}$
and
$X_{\Gamma _2}$
of non-compact type are infinitesimally
$\tau $
-isospectral if
$$\begin{align*}\mathrm{dim}\ V_{\chi, \Gamma_1, \tau} = \mathrm{dim}\ V_{\chi, \Gamma_2, \tau} \ \text{ for all} \ \chi \in \widehat{\mathfrak{Z(g)}}.\end{align*}$$
Let
$[\chi ]$
be the set of all irreducible representations of G which has infinitesimal character
$\chi $
. It is known that
$[\chi ]$
is a finite subset of
$\widehat {G}$
(see [Reference Knapp4, Corollary 10.37]). We have obtained the following variant of Matsushima–Murakami formula.
Theorem 1.2.2 Let G be a connected non-compact semisimple Lie group. Assume that
$\Gamma $
is a uniform lattice in G. Then for any
$\chi \in \widehat {\mathfrak {Z(g)}}$
and for any finite dimensional representation
$\tau $
of K,
$$\begin{align*}\mathrm{dim}\ V_{\chi, \Gamma, \tau}=\sum_{\pi \in [\chi]} m(\pi, \Gamma)\ \mathrm{dim}(\mathrm{Hom}_K(\tau^\vee, \pi|_K)). \end{align*}$$
Remark 1.2.3 For the rank one semisimple Lie group G, an infinitesimal character
$\chi \in \widehat {\mathfrak {Z(g)}}$
is completely determined by its value on the Casimir element. Therefore the above result becomes the earlier mentioned Matsushima–Murakami formula Eq. 1.1.
Remark 1.2.4 Let
$\tau =\tau _p$
be the p-th exterior power of the adjoint representation of K on
$\mathfrak {p}^*_{\mathbb {C}}$
. The associated homogeneous vector bundle is identified with the p-th exterior product of the co-tangent bundle on
$G/K$
. In [Reference Yozô8], Matsushima proved the relationship between the dimension of harmonic p-forms on
$X_{\Gamma }$
and the multiplicity of irreducible representations in
$L^2(\Gamma \backslash G)$
that occur with a nonzero
$\tau _p$
-isotypic component. Therefore, Theorem 1.2.2 can be seen as an infinitesimal version of Eq. 1.1.
Corollary 1.2.5 If
$\Gamma _1$
and
$\Gamma _2$
are
$\tau ^\vee $
-representation equivalent then the spaces
$X_{\Gamma _1}$
and
$X_{\Gamma _2}$
are infinitesimally
$\tau $
-isospectral.
Remark 1.2.6 If
$\tau $
is trivial, the above formula in Theorem 1.2.2 reduces to [Reference Chandrasheel and Rajan1, Theorem 1.3].
Remark 1.2.7 The finite set
$[\chi ]$
of all irreducible representations of a real reductive group (informally a
$\chi $
-packet) is quite close to Langlands L-packet that consists of irreducible admissible representations having same L-parameter. It is known that the irreducible representations from a fixed L-packet have same infinitesimal character i.e., they cannot be distinguished by the spectral data. According to our knowledge, the converse of this is not known in general. It is interesting to formulate a suitable variant of Matsushima–Murakami formula in terms of L-packet instead, and that might reflect some analogous relationship between the multiplicities of irreducible representations in a given L-packet and isospectrality.
1.3 Literature review
We briefly review some literature related to the main results in this paper. The question: Can the space
$X_{\Gamma }$
(up to isometry) be determined by its spectrum? has been of great interest over last few decades. The works of Milnor (see [Reference Milnor10]) and Vignéras (see [Reference Vignéras14]) are in the frontline to answer this negatively. Later, the construction of non-isometric isospectral manifolds by Sunada brought significant arithmetic flavour in this context (see [Reference Sunada13]). In another important work in this context, C. S. Rajan studied the appropriate arithmetic properties which are determined by the spectrum (see [Reference Rajan, Nakamura and Weng12]). Other than the ambitious inverse spectral problem there is another converse of the above discussion: Given two
$\tau $
-isospectral spaces
$X_{\Gamma _1}$
and
$X_{\Gamma _2}$
, are
$\Gamma _1$
and
$\Gamma _2\ \tau ^\vee $
-representation equivalent? This is called the representation-spectral converse for the pair
$(G, K)$
. This has gotten attention for quite some time. There is a slightly weaker version of this, defined as follows.
Definition 1.3.1 Two locally symmetric spaces
$X_{\Gamma _1}$
and
$X_{\Gamma _2}$
with the same universal cover
$G/K$
are said to be almost-
$\tau $
-isospectral if
$\text {Mult}_{\Delta _{\tau , \Gamma _1}}(\lambda )=\text {Mult}_{\Delta _{\tau , \Gamma _2}}(\lambda )$
for all but finitely many
$\lambda $
.
In the direction of ‘almost-
$\tau $
-representation equivalence implies isospectrality’, several approaches have been made. In [Reference Lauret and Miatello5], E. Lauret and R. Miatello answered this question for the case where K is a closed subgroup of a compact group G, i.e., for the case of compact homogeneous space
$G/K$
for compact group G. They further proved that the multiplicity of an appropriate finite subset of
$\widehat {G}_{\tau }$
determines all multiplicities (see [Reference Lauret and Miatello5, Theorem 1.1]). Later, they studied the representation-spectral converse in the context of simply connected compact Riemannian symmetric space
$G/K$
of rank one and proved there are infinitely many
$\tau \in \widehat {K}$
such that almost-
$\tau $
-isospectrality implies
$\tau ^\vee $
-representation equivalence and hence
$\tau $
-isospectral (see [Reference Lauret and Miatello6, Theorem 1.1]).
For many non-compact Riemannian symmetric spaces, Pesce proved the validity of representation-spectral converse where
$\tau $
is trivial (see [Reference Hubert11]). When
$\tau $
is trivial the
$\tau $
-spectra are called spherical spectra. Bhagwat and Rajan answered that almost-spherical representation equivalence implies spherical representation equivalence (see [Reference Chandrasheel and Rajan1, Theorem 1.2]). In fact, they described that for a spherical irreducible representation
$\pi \in \widehat {G}_1$
, there exists a character
$\lambda _{\pi }$
of the algebra of G-invariant differential operators on
$X_{\Gamma }$
such that
$\text {Mult}(\lambda _{\pi })=m(\pi , \Gamma )$
and conversely. Later, Kelmer obtained several density results which relates the isospectrality and representation equivalence via the notion of length equivalence for the case of
$X_{\Gamma }$
with real rank one and of non-compact type (having non-compact universal cover), in particular for compact hyperbolic manifolds (see [Reference Dubi3]).
1.4 Methodology
Let us briefly outline our methods for obtaining Theorem 1.1.2. We employ the well-established and effective tool, namely the Selberg Trace Formula to study the representation spectra of
$L^2(\Gamma \backslash G)$
with respect to a convolution operator. Since our focus is on the
$\tau $
-spherical irreducible representations in
$L^2(\Gamma \backslash G)$
, we need to annihilate the non
$\tau $
-spherical component using appropriate test functions. To achieve this, we instead consider the right regular representation
$L^2(\Gamma \backslash G, V_{\tau })$
(see 2.1) of G. We also utilize an algebra, denoted by
$C_c^{\infty }(G, K, V_{\tau })$
consisting of compactly supported smooth
$\mathrm {End}({V_{\tau }})$
-valued test functions on G which are
$\tau $
-equivariant (see 2.3). One can suitably define the convolution operator on
$L^2(\Gamma \backslash G, V_{\tau })$
for such test functions. It is straightforward to compute both the spectral and geometric expansions of the trace of these convolution operators, which leads to the required Selberg Trace Formula for
$L^2(\Gamma \backslash G, V_{\tau })$
(see 2.12). The advantage of using such operator valued
$\tau $
-equivariant test functions is the corresponding convolution operator annihilates the non
$\tau $
-spherical representation spectra (see 3.1.3). Moreover, due to our hypothesis, taking the difference between the trace formula for
$\Gamma _1$
and
$\Gamma _2$
yields a finite linear combination of Harish Chandra character distribution associated with finitely many
$\tau $
-spherical irreducible representations. In Proposition 3.1.5, we construct a left K-saturated open set in G that avoids all conjugacy classes
$[\gamma ]_G$
for
$\gamma \in \Gamma _1 \cup \Gamma _2$
. For the aforementioned test functions supported on this K-stable open set, the orbital integrals, and thus the entire geometric side vanish. Finally, the remainder of the argument relies on the analyticity of locally integrable character functions and the linear independence of character distributions for inequivalent irreducible representations.
The organization of the article is as follows: In Section 2, we set up the preliminaries and recall the Harish Chandra character distributions, Isospectrality and Representation equivalence. In Section 2.5, we explicitly calculate the Selberg Trace Formula for
$L^2(\Gamma \backslash G), V_{\tau })$
. In Section 3, we discuss the required lemmas and propositions to prove Theorem 1.1.2. In Section 4, we provide some observations and complete the proof of Theorem 1.2.2. In Section 5, we consider the case where the group G has discrete series representations and using the results from [Reference Williams Floyd16] and Theorem 1.2.2, we show that the dimension of
$\chi $
-eigenspace of the automorphic forms of type
$\tau ^\vee $
is equal to the
$q_{\lambda }$
-th
$L^2$
-cohomology of the automorphic line bundle
$\Gamma \backslash \mathcal {L}_{\lambda }$
associated to the discrete series representation
$\pi $
with minimal K-type
$\tau $
and infinitesimal character
$\chi $
.
2 Preliminaries
2.1 Basic setup
Let G be a connected non-compact semisimple Lie group and let K be a maximal compact subgroup of G with Lie algebras
$\mathfrak {g}$
and
$\mathfrak {k}$
, respectively. Then the homogeneous space
$G /K$
is a symmetric space with a G-invariant metric. Let
$(\tau , V_{\tau })$
be a finite dimensional representation of K. Let
$\Gamma $
be a uniform torsion-free lattice in G.
We consider the right regular representation
$\rho $
of G on the space
$$ \begin{align} L^2(\Gamma \backslash G, V_{\tau}) &: =\{ \phi : G \rightarrow V_{\tau}\ | \ \phi \text{ is measurable}, \nonumber\\ & \phi(\gamma g) =\phi(g) \text{ for all } \gamma \in \Gamma, \int \limits_{\Gamma \backslash G} |\phi(g)|^2\ dg < \infty\}. \end{align} $$
Since
$\Gamma \backslash G$
is compact, the right regular representation
$L^2(\Gamma \backslash G)$
of G is completely reducible and each irreducible subrepresentation occurs with finite multiplicity. In other words,
with
$m(\pi , \Gamma ) < \infty $
for all
$\pi \in \widehat {G}$
.
We choose an orthonormal basis for each copy of
$\pi $
. Taking union of those we get an orthonormal basis
$\mathcal {W}$
of
$L^2(\Gamma \backslash G)$
. Let
$\{v_i\}_{i=1}^{n}$
be an orthonormal basis of
$V_{\tau }$
. For any
$\psi \in \mathcal {W}$
, we let
$\psi _i(x) =\psi (x)v_i$
. Then
$\{ \psi _i \ | \ \psi \in \mathcal {W},\ 1 \leq i \leq n\}$
forms an orthonormal basis of
$L^2(\Gamma \backslash G, V_{\tau })$
. Note that
$L^2(\Gamma \backslash G, V_{\tau }) = L^2(\Gamma \backslash G) \otimes V_{\tau }$
.
Therefore, we get
For each copy of
$W_{\pi } \otimes V_{\tau }$
, we identify a subspace
$V_{\pi }$
in
$L^2(\Gamma \backslash G, V_{\tau })$
. The subspace
$V_{\pi }$
is not an irreducible G-subspace, rather it is direct sum of dim
$V_\tau $
many copies of
$W_{\pi }$
.
We introduce a space
$C_c^{\infty }(G, K, V_{\tau })$
defined by
$$ \begin{align} \{ f : G \rightarrow \mathrm{End}(V_{\tau}) \ | \ & f \text{ is compactly supported and smooth such that } \nonumber\\ & f(kx)=f(x)\tau(k^{-1}) \text{ for all } x \in G, k \in K\}. \end{align} $$
For
$f \in C_c^{\infty }(G, K, V_{\tau })$
, let
$h_f(x) =\mathrm {Trace~}(f(x))$
for all
$x \in G$
. Now for any
$f \in C_c^{\infty }(G, K, V_{\tau })$
, we define the convolution operator
$\rho (f) :L^2(\Gamma \backslash G, V_{\tau } ) \rightarrow L^2(\Gamma \backslash G, V_{\tau })$
by
$$ \begin{align} \rho(f) \phi (x) = \int \limits_G f(y) (\phi(gy)) \ dy \quad \text{for all}\ \phi \in L^2(\Gamma \backslash G, V_{\tau} ). \end{align} $$
Proposition 2.1.1
Each
$V_{\pi }$
is
$\rho (f)$
-stable subspace for all
$f \in C_c^{\infty }(G, K, V_{\tau })$
.
Proof Let
$\mathcal {U} \subset \mathcal {W}$
be the subset such that
$\mathcal {U}$
is an orthonormal basis of
$W_{\pi }$
. Then
$\{ \phi _i : \phi \in \mathcal {U}, 1 \leq i \leq n\}$
is an orthonormal basis of
$V_{\pi }$
. Thus it suffices to show that
$$ \begin{align*}\langle \rho(f) \phi_i, \psi_j \rangle =0 \quad \text{for any}\ \phi \in \mathcal{U}, \psi \in \mathcal{W} \,{\backslash}\, \mathcal{U} \ \text{and any}\ 1 \leq i, j \leq n.\end{align*} $$
We compute,
$$ \begin{align} \langle \rho(f) \phi_{i} , \psi_{j} \rangle & = \int \limits_{\Gamma \backslash G} \langle \rho(f) \phi_{i}(g), \psi_{j}(g) \rangle\ dg \nonumber\\ & = \int \limits_{\Gamma \backslash G} \langle \int\limits_G \phi(gy) f(y) v_i, \psi(g) v_j \rangle\ dy\ dg \nonumber\\ & = \int \limits_{\Gamma \backslash G} \int\limits_G \phi(gy) \overline{\psi(g)} \langle f(y)v_i, v_j \rangle\ dy\ dg\\ & = \int \limits_G \langle f(y)v_i, v_j \rangle \int\limits_{\Gamma \backslash G} \phi(gy)\overline{\psi(g)}\ dg\ dy \nonumber\\ & = 0. \nonumber\\[-32pt]\nonumber \end{align} $$
2.2 Results on Harish–Chandra characters
We will be using the following two important results on Harish–Chandra characters.
Harish–Chandra character distribution: Let
$(\pi , W_{\pi })$
be an irreducible unitary representation of G. Let
$C_c^{\infty }(G)$
be the space of all compactly supported smooth functions on G. For any
$f \in C_c^{\infty }(G)$
, the convolution operator
$\pi (f)$
on
$W_{\pi }$
is defined by
$\pi (f)v=\int \limits _G f(g) \pi (g)v \ dg$
for all
$v \in W_{\pi }$
. It is a trace class operator (see [Reference Knapp4, Theorem 10.2]) and
$$ \begin{align*}\chi_{\pi}(f)=\mathrm{Trace~}(\pi(f)) \ \text{ for all } f \in C_c^{\infty}(G).\end{align*} $$
Theorem 2.2.1
Let
$\{\pi _i\}$
be a finite collection of mutually inequivalent unitary irreducible representations of G. Then their characters
$\{\chi _{\pi _i}\}$
are linearly independent distributions on G.
Proof Reader is referred to [Reference Knapp4, Theorem 10.6].
Theorem 2.2.2
Let
$\pi $
be an irreducible unitary representation of G. Then the distribution character
$\chi _{\pi }$
is given by a locally integrable function
$\phi _{\pi }$
on G i.e., for
$f \in C_c^{\infty }(G)$
,
$$ \begin{align*}\chi_{\pi}(f)=\int \limits_G f(g) \phi_{\pi}(g) \ dg.\end{align*} $$
Moreover, the restriction of
$\phi _{\pi }$
to the regular set of G is a real analytic function invariant under conjugation.
Proof Reader is referred to [Reference Knapp4, Theorem 10.25].
2.3 Isospectrality and representation equivalence
There is a natural homogeneous vector bundle
$E_{\tau }$
on
$G/K$
that is associated with the representation
$(\tau , V_{\tau })$
of K. The space of all smooth global sections of
$E_{\tau }$
can be realized as
$\mathcal A^\infty (G/K, \tau ) =\{ \phi : G \rightarrow V_{\tau }\ |\ \phi $
is smooth,
$\phi (xk)=\tau (k^{-1})(\phi (x)) \text { for all} x \in G, k \in K\}$
. Note that
$\mathcal A^\infty (G/K, \tau )$
is a
$\mathfrak {U(g)}^K$
module. In particular,
$\mathfrak {Z(g)} \subset \mathfrak {U(g)}^K$
acts on
$\mathcal A^\infty (G/K, \tau )$
.
Let
$\mathfrak {g}= \mathfrak {k} \oplus \mathfrak {p}$
be the Cartan decomposition of the Lie algebra
$\mathfrak {g}$
. We choose a basis
$\{X_i\}$
and
$\{Y_j\}$
of
$\mathfrak {k}$
and
$\mathfrak {p}$
, respectively with respect to a bilinear form B on
$\mathfrak {g}$
induced from the killing form such that
$B(X_k, X_l)=-\delta _{kl}$
and
$B(Y_m, Y_n)=\delta _{mn}$
. Let C be the Casimir element given by
$C=-\sum X_i^2 + \sum Y_j^2$
. The Casimir element C induces a second order symmetric elliptic operator
$\Delta _{\tau }$
on
$\mathcal A^\infty (G/K, \tau )$
.
Let
$\Gamma $
be a uniform torsion-free lattice in G, and let
$ X_{\Gamma } = \Gamma \backslash G / K$
be the associated compact locally symmetric space of non-compact type. We consider the vector bundle
$E_{\tau , \Gamma }$
on
$X_{\Gamma }$
defined by the relation
$[\gamma g , w] \sim [g, w]$
for all
$\gamma \in \Gamma \text { and } [g, w] \in E_{\tau }$
. The space of all smooth global sections of
$E_{\tau , \Gamma }$
can be realised as the space
$V_{\Gamma , \tau }=\{ \phi \in \mathcal A^\infty (G/K, \tau ) \ | \ \phi (\gamma x)=\phi (x) \text { for all } \gamma \in \Gamma \}$
. Hence, the centre
$\mathfrak {Z(g)}$
acts on
$V_{\Gamma , \tau }$
.
Let
$\Delta _{\tau , \Gamma }=\Delta _{\tau }|_{V_{\Gamma , \tau }}.$
This is again a second order symmetric elliptic operator on
$X_{\Gamma }$
. Its spectrum Spec
$(\Delta _{\tau , \Gamma })$
is a discrete subset of the non-negative real numbers. Let
$\text {Mult}_{\Delta _{\tau , \Gamma }}(\lambda )=$
the multiplicity of
$\lambda \in $
Spec
$(\Delta _{\tau , \Gamma })$
. Recall Eq. 1.1
$$ \begin{align*}\text{Mult}_{\Delta_{\tau, \Gamma}}(\lambda) = \sum_{\pi \in \widehat{G}, \pi(C)=\lambda} m(\pi, \Gamma)\ \mathrm{dim}(\mathrm{Hom}_K(\tau^\vee, \pi|_K)),\end{align*} $$
where
$\pi (C)$
is the scalar by which the Casimir element C acts on
$W_{\pi }$
.
Definition 2.3.1
$ X_{\Gamma _1}$
and
$X_{\Gamma _2}$
are called
$\tau $
-isospectral if the operators
$\Delta _{\tau , \Gamma _1}$
and
$\Delta _{\tau , \Gamma _2}$
have same spectrum (with multiplicity).
We denote
$\widehat {G}_{\tau }=\{ \pi \in \widehat {G} : \mathrm {Hom}_K(\tau , \pi ) \neq 0\}$
.
Definition 2.3.2
$\Gamma _1$
and
$\Gamma _2$
are called
$\tau $
-representation equivalent if
$m(\pi , \Gamma _1)=m(\pi , \Gamma _2)$
for all
$\pi \in \widehat {G}_{\tau }$
.
It is clear from Eq. 1.1 that, if
$\Gamma _1$
and
$\Gamma _2$
are
$\tau ^\vee $
-representation equivalent, then
$X_{\Gamma _1}$
and
$X_{\Gamma _2}$
are
$\tau $
-isospectral.
2.4 A further refinement
We have seen that
$\mathfrak {Z}(\mathfrak {g})$
acts on
$V_{\Gamma , \tau }$
(see Section 1.1). For any character
$\chi \in \widehat {\mathfrak {Z}(\mathfrak {g})}$
, we have the
$\chi $
-eigenspace defined as
$$ \begin{align*}V_{\chi, \Gamma, \tau} =\{ \phi \in V_{\Gamma, \tau}\ | \ z. \phi =\chi(z) \phi \text{ for all } z \in \mathfrak{Z}(\mathfrak{g})\}.\end{align*} $$
In fact,
$V_{\Gamma , \tau }$
decomposes as
$V_{\Gamma , \tau }=\bigoplus \limits _{\chi \in \widehat {\mathfrak {Z(g)}}} V_{\chi , \Gamma , \tau }$
.
We here introduce a notion of two locally symmetric spaces being infinitesimally
$\tau $
-isospectral, defined as follows.
Definition 2.4.1 Two locally symmetric spaces
$X_{\Gamma _1}$
and
$X_{\Gamma _2}$
are infinitesimally
$\tau $
-isospectral if for all characters
$\chi \in \widehat {\mathfrak {Z(g)}}$
,
$$\begin{align*}\mathrm{dim}\ V_{\chi, \Gamma_1, \tau}= \mathrm{dim}\ V_{\chi, \Gamma_2, \tau}.\end{align*}$$
Remark 2.4.2 If G is a real rank one Lie group, the centre
$\mathfrak Z(\mathfrak g)$
is the polynomial algebra over
${\mathbb C}$
in the Casimir element C. Therefore, the
$\chi $
-eigenspace is simply the
$\lambda $
-eigenspace where
$\lambda $
is an eigenvalue of the Laplace-Beltrami operator
$\Delta _{\tau , \Gamma }$
on
$E_{\tau , \Gamma }$
. In this case, infinitesimal
$\tau $
-isospectrality reduces to
$\tau $
-isospectrality as defined above.
As in [Reference Chandrasheel and Rajan1] and [Reference Chandrasheel and Gunja2], we can expect that the
$\text {dim} \ V_{\chi , \Gamma , \tau }$
is related with the multiplicities
$m(\pi , \Gamma )$
of
$\pi \in \widehat {G}_{\tau ^\vee }$
occurring in
$L^2(\Gamma \backslash G)$
with infinitesimal character
$\chi $
. This is the content of Theorem 1.2.2.
2.5 Selberg trace formula for
$L^2(\Gamma \backslash G, V_{\tau })$
Recall
$\{\psi _{j} : \psi \in \mathcal {W}, j\in {1,...,n}\}$
is an orthonormal basis of
$L^2(\Gamma \backslash G, V_{\tau })$
(recall 2.1). For any
$f \in C_c^{\infty }(G, K, V_{\tau })$
(recall 2.3), let
$[f_{ij}]_{n \times n}$
be the matrix representation of f with respect to the basis
$\{v_i\}_{i=1}^n$
of
$V_{\tau }$
. For
$f \in C_c^{\infty }(G, K, V_{\tau })$
, observe that,
$$ \begin{align} \rho(f) \psi_j(x) & = \int \limits_G f (x^{-1} y ) (\psi_{j}(y))\ dy \nonumber\\ & = \int \limits_G f ( x ^{-1} y ) ( \psi(y) v _j)\ dy \\ & = \sum_{i} \int \limits_G \psi (y)f _{ij}( x ^{-1} y) v_i\ dy. \nonumber \end{align} $$
Then, we have
$$ \begin{align} \mathrm{Trace~} (\rho(f)) & = \sum_{\psi \in \mathcal{W}} \sum_{j} \langle \rho(f) \psi_{j}, \psi_{j}\rangle \nonumber \\ & = \sum_{\psi \in \mathcal{W}} \sum_{j} \int \limits_{\Gamma \backslash G} \langle \sum_{i} \int \limits_G \psi(y) f_{ij}(x ^{-1} y) v_i\ dy , \psi(x) v_j \rangle\ dx \nonumber \\ & = \sum_{\psi \in \mathcal{W}} \sum_{j} \int \limits_{\Gamma \backslash G} \int \limits_{\Gamma \backslash G} \psi(y) \ \psi(x)\ \sum_{\gamma \in \Gamma} \langle \sum_{i} f_{ij}(x ^{-1} \gamma y) v_i,\ v_j \rangle\ dy\ dx \nonumber \\ & = \sum_{\psi \in \mathcal{W}} \ \int \limits_{\Gamma \backslash G \times \Gamma \backslash G} \sum_{\gamma \in \Gamma} \mathrm{Trace~} (f( x^{-1} \gamma y)) \overline{\psi(x)} \psi(y) \ dy\ dx \nonumber \\ & = \sum_{\psi \in \mathcal{W}} \ \int \limits_{\Gamma \backslash G \times \Gamma \backslash G} \sum_{\gamma \in \Gamma} h_f( x^{-1} \gamma y) \overline{\psi(x)} \psi(y)\ dy \ dx. \end{align} $$
Put
$K_f(x,y) =\sum \limits _{\gamma \in \Gamma } h_f(x^{-1}\gamma y)$
. Above equals,
$$ \begin{align} \sum_{\psi \in \mathcal{W}} \ \int\limits_{\Gamma \backslash G \times \Gamma \backslash G} K_f(x,y) \overline{\psi (x)} \psi(y) \ dy \ dx. \end{align} $$
Consider the integral operator T on
$L^2 (\Gamma \backslash G)$
defined by
$$ \begin{align} T \psi(x) & = \int\limits_{\Gamma \backslash G} K_f(x,y) \psi(y)\ dy. \end{align} $$
Then T is a trace class operator and its trace is given by
$$ \begin{align} \mathrm{Trace~}(T) = \sum_{\psi \in \mathcal{W}} \ \int\limits_{\Gamma \backslash G \times \Gamma \backslash G} K_f(x, y) \overline{\psi(x)} \psi(y)\ dy\ dx. \end{align} $$
On the other hand the trace of such an operator T equals
$\int \limits _{\Gamma \backslash G} K_f(x,x)\ dx$
. Therefore,
$$ \begin{align*}\mathrm{Trace~}(\rho(f))= \int\limits_{\Gamma \backslash G} K_f(x,x)\ dx=\int\limits_{\Gamma \backslash G} \sum\limits_{\gamma \in \Gamma } h_f( x^{-1} \gamma x)\ dx.\end{align*} $$
From Proposition 2.1.1, we have
$$ \begin{align*}\mathrm{Trace~}(\rho(f))=\sum\limits_{\pi \in \widehat{G}} m(\pi , \Gamma)\ \mathrm{Trace~}(\rho(f)|_{V_{\pi}}). \end{align*} $$
Now,
$$ \begin{align} \mathrm{Trace~}(\rho(f)|_{V_{\pi}}) & = \sum_{j} \sum_{\psi \in \mathcal{W} \cap W_{\pi}} \langle \rho(f) \psi_j , \psi_j \rangle \nonumber\\ & = \sum_{\psi \in \mathcal{W} \cap W_{\pi}} \ \int\limits_{\Gamma \backslash G} \int\limits_G \psi(xy) \ \overline{\psi(x)}\ \mathrm{Trace~}(f(y))\ dy\ dx\\ & = \mathrm{Trace~}(\pi(h_f)). \nonumber \end{align} $$
Therefore, we have the following Selberg trace formula:
$$ \begin{align} \sum_{\pi \in \widehat{G}} m( \pi, \Gamma)\ \mathrm{Trace~}( \pi(h_f)) & =\int\limits_{\Gamma \backslash G} \sum_{\gamma \in \Gamma} h_f(x^{-1} \gamma x)\ dx \nonumber \\ & = \sum_{[\gamma] \in [\Gamma]_G} \text{vol}\ (\Gamma_{\gamma} \backslash G_{\gamma}) \int\limits_{G_{\gamma} \backslash G} h_f(x^{-1} \gamma x)\ dx \\ & = \sum_{[\gamma] \in [\Gamma]_G} a(\gamma, \Gamma) \ O_\gamma(h_f), \nonumber \end{align} $$
where,
$a(\gamma , \Gamma )$
and
$O_\gamma (h_f)$
denote
$\text {vol}\ (\Gamma _{\gamma } \backslash G_{\gamma }) $
and
$\int \limits _{G_{\gamma } \backslash G} h_f(x^{-1} \gamma x)\ dx,$
respectively.
Remark 2.5.1 This trace formula is a generalisation of the well-known Selberg trace formula. For more explicit description about the “geometric side”, see [Reference Wallach15].
3 Proof of the first main result Theorem 1.1.2
3.1 Some preliminary results
We will describe the lemmas and propositions required to prove Theorem 1.1.2.
Lemma 3.1.1
Let
$Kx$
be a left coset of K in G for some
$x \in G$
. Let U be an open set containing the left coset
$Kx$
. Then there exists
$f \in C_c^{\infty }(G)$
with Supp
$(f)\subset U$
such that
$\int \limits _K f(k x) \chi _{\tau }(k) \ dk \neq 0$
. (Here
$\chi _{\tau }$
is the character function of
$\tau $
.)
Proof For any
$f \in C_c^{\infty }(G)$
with
$\mathrm {Supp}(f) \subset U$
, we define
$\psi \in C^{\infty }(K)$
by
$\psi (k)=f(kx)$
. Conversely, for any
$\psi \in C^{\infty }(K)$
, define
$f(kx)=\psi (k)$
, and extend f smoothly to U.
Now, if
$\int \limits _K f(kx) \chi _{\tau }(k)\ dk =0$
for all
$f \in C_c^{\infty }(G)$
such that
$\mathrm {Supp}(f) \subset U$
, then
$$\begin{align*}\int\limits_K \psi(k)\ \chi_{\tau}(k)\ dk =0\ \text{for all}\ \psi \in C^{\infty}(K).\end{align*}$$
But that implies
$\chi _{\tau }$
is identically zero leading to a contradiction.
Lemma 3.1.2
Let
$Kx \neq Ky$
be two distinct left cosets of K in G. Then there exists
${F \in C_c^{\infty }(G, K, V_{\tau })}$
such that
$h_{F}(x)\neq 0$
and
$h_{F}|_{Ky}=0$
.
Proof
$Kx \neq Ky$
are disjoint compact sets in G. Choose disjoint open sets
$U_1, U_2$
with
$Kx \subset U_1,Ky \subset U_2$
, and
$U_1 \cap U_2 = \emptyset $
. From Lemma 3.1.1, there exists
$f \in C_c^{\infty }(G)$
with
$\mathrm {Supp}\ (f) \subset U_1$
such that
$\int \limits _K f(kx) \chi _{\tau }(k)\ dk \neq 0$
.
Let
$F(g) = \int \limits _K f(kg) \tau (k)\ dk$
. Then,
$F \in C_c^{\infty }(G,K, V_{\tau })$
.
Furthermore,
$h_{F}(g)=\int \limits _K f(kg) \chi _{\tau }(k)\ dk$
. Hence
$h_F(x) \neq 0$
and
$h_F(y)=0$
and hence
$h_{F}|_{Ky}=0$
.
Proposition 3.1.3
Let
$\pi $
be an irreducible representation of G occurring as a subrepresentation of
$\rho $
. Assume that
$\pi $
is not
$\tau $
-spherical i.e.,
$\mathrm {Hom}_K(V_{\tau }, V_{\pi })=0$
. Then
$\rho (f)$
is zero on
$V_{\pi }$
.
Proof It is enough to show that
$\rho (f)$
is zero at each element of the orthonormal basis
$\{\psi _j : \psi \in \mathcal {U}, 1 \leq j \leq n\}$
. Here,
$\mathcal {U}=\mathcal {W} \cap W_{\pi }$
. Recall that (see Eq. 2.4)
$$ \begin{align*}\rho(f)\psi_j(g)= \int\limits_G \psi(gy) f(y)(v_j) \ dy.\end{align*} $$
For a fixed
$\psi \in \mathcal {U}$
, consider the subspace
$U_{\psi }=\text {span}\ \{\psi _j : j \in \{1,\ldots , n\}\} $
. If
${v = \sum \limits _{j=1}^{n} a_j v_j}$
, we write
$\psi _v =\sum _{j=1}^{n} a_j \psi _j$
. Then the subspace
$U_{\psi }$
is same as
$\{ \psi _v : v \in V_{\tau }\}$
. There is an action of K on
$U_{\psi }$
by
$\tau (k)\psi _v=\psi _{\tau (k)v}.$
Clearly,
$U_{\psi }$
is a representation of K isomorphic to
$\tau $
. Note that
$\widehat {\bigoplus \limits _{\psi \in \mathcal {W}}} U_{\psi } = V_{\pi }$
. We show that
$\rho (f)|_{U_{\psi }}=0$
. In fact, we show that
$\rho (f) \in \mathrm {Hom}_K(U_{\psi }, V_{\pi })$
.
Let
$\psi _v \in U_{\psi }$
and
$k_0 \in K$
. Then for every
$g \in G$
, we have
$$ \begin{align} (\rho(k_0) \rho(f) \psi_v )(g) & = (\rho(f) \psi_v)(gk_0) \nonumber \\ & = \int\limits_G f(y)\ (\psi(gk_0y)v)\ dy \nonumber\\ & = \int\limits_G \psi(gy)\ f(k_0^{-1} y) v\ dy\\ & = \int\limits_G \psi(gy)\ f(y) \tau(k_0)v\ dy \nonumber\\ & = \rho(f)\ \tau(k_0)\ \psi_v(g).\nonumber \end{align} $$
Therefore,
$\rho (f)$
is zero on
$U_{\psi }$
for all
$\psi \in \mathcal {W}$
. Consequently,
$\rho (f)$
is zero on
$V_{\pi }$
.
Lemma 3.1.4
Let
$\Gamma $
be a torsion-free uniform lattice in G. For a non-trivial element
$\gamma \in \Gamma $
, the conjugacy class
$[\gamma ]_G$
of
$\gamma $
in G is disjoint from K.
Proof Reader is referred to [Reference Chandrasheel and Rajan1, Lemma 4.2].
Proposition 3.1.5 Let
$\Gamma _1$
and
$\Gamma _2$
be two uniform lattices in G. Then there exists an open set B in G such that
$[\gamma ]_G \cap B$
is empty for all
$\gamma \in \Gamma _1 \cup \Gamma _2$
, and B is stable under left K action on G.
Proof Let
$U'$
be a relatively compact open set containing the identity element e in G. Let
$U=KU'$
. Then U is relatively compact and therefore it intersects at most finitely many conjugacy classes
$[\gamma ]_G$
. Since, the natural map
$G \rightarrow K \backslash G$
is proper,
$K [\gamma ]_G$
is closed in G. Since U is K-stable,
$K[\gamma ]_G \cap U \neq \emptyset $
if and only if
${[\gamma ]_G \cap U \neq \emptyset} $
. Let
$E = \bigcup \limits _{\gamma \neq e} (K [\gamma ]_G \cap U)$
. Since E is a finite union of closed sets, it is closed and K-stable subset of U. If there is
$k \in K$
,
$\gamma \neq e$
and
$ x \in G$
such that
$k x^{-1} \gamma x =e$
, then
$x^{-1} \gamma x \in K$
; which contradicts the previous lemma. Therefore
$e \notin K [\gamma ]_G$
for any
$\gamma \neq e$
and hence
$e \notin E$
. Choose an open set V containing e such that
$E \cap V =\emptyset $
. Now, let
$B=KV \cap K^c$
. Then B is the desired open set in G.
3.2 Proof of Theorem 1.1.2
We have two uniform torsion free lattices
$\Gamma _1$
and
$\Gamma _2$
in G. So by Eq. 2.2,
for
$ i =1, 2$
. Let
$t_{\pi }= m(\pi , \Gamma _1)-m(\pi , \Gamma _2)$
. By hypothesis there exists a finite set
$\mathcal {S} \subset \widehat {G}_{\tau }$
such that
$t_{\pi }=0$
for all
$\pi \in \widehat {G}_{\tau } \smallsetminus \mathcal {S}$
. For
$f \in C^{\infty }_c(G, K, V_{\tau })$
,
$\rho _{\Gamma _i}(f)$
is zero on
$V_{\pi }$
if
${\pi \notin \widehat {G}_{\tau }}$
by Proposition 3.1.3. Recall that
$h_f(y)=\mathrm {Trace~}(f(y))$
. Therefore from the Selberg trace formula (2.12), we have
$$ \begin{align*} \sum\limits_{[\gamma] \in [\Gamma_1]_G \cup [\Gamma_2]_G } (a(\gamma , \Gamma_1) - a(\gamma, \Gamma_2 )) O_{\gamma} (h_f) & = \sum\limits_{\pi \in \mathcal{S} } t_{\pi}\ \mathrm{Trace~} (\pi (h_f))\\ & = \sum\limits_{\pi \in \mathcal{S}} t_{\pi} \int\limits_G h_{f} (y) \phi_{\pi} (y)\ dy\\ & = \int\limits_G h_f(y) \phi(y)\ dy, \end{align*} $$
where,
$\phi =\sum \limits _{\pi \in \mathcal {S}} t_{\pi } \phi _{\pi }$
.
Let B be the open set from Proposition 3.1.5. For any
$f \in C^{\infty }_c(G, K, V_{\tau })$
supported in B, the orbital integrals on the right-hand side is zero. For such functions f, we have
$$ \begin{align*}\int\limits_B h_f(y) \phi(y)\ dy =0.\end{align*} $$
From Lemma 3.1.2, the functions
$h_f$
separates points in B. Hence
$\phi $
must vanish on the open subset B of G. Since
$\phi $
is real analytic (see Theorem 2.2.2), it vanishes on all of G. By the linear independence of functions
$\phi _{\pi }$
(see Theorem 2.2.1), we conclude that
$m(\pi , \Gamma _1)=m(\pi , \Gamma _2)$
for all
$\pi \in \widehat {G}_{\tau }$
.
4 Proof of the second main result Theorem 1.2.2
4.1 Some observations
In this subsection, we make some observations that will be useful in the proof of Theorem 1.2.2.
Recall from Section 2.3 that
$\mathcal A^\infty (G/K, \tau )$
is the space of smooth sections of the vector bundle
$E_\tau $
and
$V_{\Gamma , \tau }$
is the subspace defined by
$$\begin{align*}V_{\Gamma, \tau} = \{ \phi \in \mathcal A^\infty(G/K, \tau) \ | \ \phi(\gamma x)=\phi(x)\ \text{ for all}\ \gamma \in \Gamma, x \in G\}. \end{align*}$$
Let
$n=\text {dim}(V_{\tau })$
. Recall the choice of an orthonormal basis
$\{v_i\}_{i=1}^{n}$
of
$V_{\tau }$
from Section 2.1. For a fixed
$\phi \in V_{\chi , \Gamma , \tau }$
, write
$\phi (x)=\sum \limits _{i=1}^{n} \phi _i(x) v_i$
for all
$x \in G$
, where each
$\phi _i$
is smooth complex valued function on
$\Gamma \backslash G$
. Recall from Section 2.1 that
$V_{\chi , \Gamma , \tau }$
is the
$\chi $
-eigenspace of
$V_{\Gamma , \tau }$
with respect to the action of
$\mathfrak {Z(g)}$
. For any
$X \in \mathfrak {Z(g)}$
and for all
$x \in G$
, we can see that
$$ \begin{align} X \cdot \phi (x) =\sum\limits_{i=1}^{n} X \cdot\phi_i (x)\ v_i. \end{align} $$
Therefore, we conclude that
$X \cdot \phi _i = \chi (X) \phi _i$
for all i.
Each
$\tau (k)$
has a matrix representation with respect to the chosen orthonormal basis of
$V_{\tau }$
. Let the
$(i,j)$
-th entry of
$\tau (k)$
be denoted by
$a_{ij}(k)$
.
Note that
$\phi (xk) =\tau (k^{-1})(\phi (x))$
for all
$x \in G$
and
$k \in K$
. Thus we have
$$ \begin{align} \sum_i \phi_i(xk) \ v_i & = \tau(k^{-1})\left(\sum_j \phi_j(x)\ v_j\right) \nonumber\\ & = \sum_l \left(\sum_j a_{lj}(k^{-1})\phi_j(x) \right)v_l. \end{align} $$
Therefore,
$\phi _i(xk)=\sum \limits _{j=1}^{n} a_{ij}(k^{-1}) \ \phi _j(x)$
for all
$x \in G, \ k \in K$
.
4.2 Proof of Theorem 1.2.2
We denote
$[\chi ]=\{ \pi \in \widehat {G} : \ \text {the infinitesimal character of} \ \pi \ \text {is}\ \chi \}$
. Recall that
There are
$m(\pi , \Gamma )$
copies of
$W_{\pi }$
inside
$L^2(\Gamma \backslash G)$
say,
$\{ W_{\pi _t} : 1 \leq t \leq m(\pi , \Gamma )\}$
. Let
$P_{\pi _t}$
be the projection onto
$W_{\pi _t}$
.
Clearly,
$\phi _i \in L^2(\Gamma \backslash G)$
for all
$\phi \in V_{\chi , \Gamma , \tau }$
. We have
$$\begin{align*}\phi_i= \sum_{\pi \in [\chi]} \sum_{t=1}^{m(\pi, \Gamma)} P_{\pi_t} \phi_i. \end{align*}$$
For any
$1 \leq t \leq m(\pi , \Gamma )$
, clearly
$P_{\pi _t} \in \mathrm {Hom}_G(L^2(\Gamma \backslash G), W_{\pi _t})$
. Using Eq. 4.2, we get
$$ \begin{align} \pi(k) P_{\pi_t} \phi_i & = P_{\pi_t} \rho(k) \phi_i \nonumber\\ & = P_{\pi_t} \sum_{j=1}^{n} a_{ij}(k^{-1})\phi_j\\ & = \sum_{j=1}^{n} a_{ij}(k^{-1}) P_{\pi_t} \phi_j. \nonumber \end{align} $$
Let
$F_{\pi _t}=$
Span of
$\{ P_{\pi _t} \phi _j : 1 \leq j \leq n\}$
. From Eq. 4.3, it follows that
$F_{\pi _t}$
is a finite dimensional representation of K. Let
$\tau ^\vee $
be the dual representation of
$\tau $
of K on the dual space
$V_{\tau }^*$
. Let
$\{v_i^\ast \}_{i=1}^n$
be the dual basis of
$V_{\tau }^*$
. Then there is K-isomorphism between
$F_{\pi _t}$
and
$V_{\tau }^*$
which maps each
$P_{\pi _t} \phi _i$
to
$v_i^*$
.
Now we assume that
$\tau $
is irreducible (and hence
$\tau ^\vee $
as well). For a fixed
$\pi _t$
, let
$W_{\pi _t}(\tau ^\vee )$
be the isotypic component of
$\tau ^\vee $
in
$W_{\pi _t}$
. Then
$F_{\pi _t} \subset W_{\pi _t}(\tau ^\vee )$
. We have a decomposition
$$\begin{align*}W_{\pi_t}(\tau^\vee)=\bigoplus_{p=1}^{M_{\tau^\vee}} H_p, \end{align*}$$
where, each
$H_p$
is an irreducible representation of K isomorphic to
$\tau ^\vee $
. Note that
$M_{\tau ^\vee } = \text {dim}(\mathrm {Hom}_K(\tau ^\vee , \pi ))$
.
For each
$ p$
, let
$\{ \phi _{t, p, s}\}_{s=1}^{n}$
be a basis of
$H_p$
satisfying
$\phi _{p, t, s}(xk)=\sum \limits _{u=1}^{n} a_{us}(k^{-1}) \phi _{t, p, u}(x)$
. Note that this is possible because each
$H_p$
is isomorphic to
$F_{\pi _t}$
.
Now,
$P_{\pi _t} \phi _i = \sum \limits _p \sum \limits _s \alpha _{p,s,i}\ \phi _{t, p, s}$
. For each p, the matrix
$(\alpha _{p,s,i})_{s,i}$
represents a K-homomorphism between
$F_{\pi _t}$
and
$H_p$
. Therefore,
$\alpha _{p, s, i} = \alpha _p \delta _{s, i}$
for some scalar
$\alpha _p$
by Schur’s lemma.
Therefore,
$P_{\pi _t} \phi _i = \sum \limits _p \alpha _p\ \phi _{t, p, i}$
. We define
$\phi _{t, p}(x)= \sum \limits _{i=1}^{n} \phi _{t, p, i}(x)\ v_i$
for all t and p. Hence, we get
$$ \begin{align} \phi & = \sum\limits_{i=1}^{n} \phi_i v_i \nonumber \\ & = \sum_{i=1}^{n} \left(\sum_{\pi \in [\chi]} \sum_{t =1}^{m(\pi, \Gamma)} P_{\pi_t}\ \phi_i\right)\ v_i \nonumber\\ & = \sum_{i=1}^{n} \sum_{\pi \in [\chi]} \sum_{t =1}^{m(\pi, \Gamma)} \sum_{p=1}^{M_{\tau^\vee}} \alpha_p\ \phi_{t, p, i}\ v_i\\ & = \sum\limits_{\pi \in [\chi]} \sum_{t=1}^{m(\pi, \Gamma)} \ \sum_{p=1}^{M_{\tau^\vee}} \alpha_p\ \phi_{t, p}.\nonumber \end{align} $$
We conclude that dim
$V_{\chi , \Gamma , \tau } \leq \sum \limits _{\pi \in [\chi ]}m(\pi , \Gamma ) \ { \mathrm dim}(\mathrm {Hom}_K(\tau ^\vee , \pi ))$
.
Conversely, for every t and for every p, choose a basis
$\{ \phi _{t, p, i}\}_{i=1}^{n}$
of
$H_p$
such that
$$\begin{align*}\phi_{t, p, i}(xk)= \sum\limits_{j=1}^{n} a_{ji}(k^{-1}) \ \phi_{t, p, j}(x).\end{align*}$$
Let
$\phi _{t, p}= \sum \limits _{i=1}^{n}\phi _{t,p,i} \ v_i$
. Then
$\phi _{t, p}(xk)=\tau (k^{-1})(\phi _{t,p}(x))$
. Since
$X \cdot \phi _{t, p, i}= \chi (X)\ \phi _{t, p, i}$
for all
$X \in \mathfrak {Z(g)}$
, it follows that
$\phi _{t, p} \in V_{\chi , \Gamma , \tau }$
.
We conclude that
$\sum \limits _{\pi \in [\chi ]} m(\pi , \Gamma ) \ \mathrm {dim}(\mathrm {Hom}_K(\tau ^\vee , \pi )) \leq \mathrm {dim} \ V_{\chi , \Gamma , \tau }$
. Therefore, we have the equality
$$ \begin{align} \mathrm{dim} \ V_{\chi, \Gamma, \tau} = \sum_{\pi \in [\chi]}m(\pi, \Gamma)\ \mathrm{dim}(\mathrm{Hom}_K(\tau^\vee, \pi))\ \text{ for all}\ \tau \in \widehat{K}. \end{align} $$
Now, let us consider the general case that
$\tau $
is a finite dimensional representation of K (possibly reducible). Let
$\tau \cong \bigoplus \limits _{i=1}^{q} m_i \ \tau _i$
be a decomposition of
$\tau $
into irreducible representations of K. Hence
$\tau ^\vee \cong \bigoplus \limits _{i=1}^{q} m_i \ (\tau _i)^\vee $
.
Let
$V_{\Gamma , \tau }$
be as in Section 2.3. The center
$\mathfrak {Z(g)}$
acts on this space. Therefore for any character
$\chi \in \widehat {\mathfrak {Z(g)}}$
, we can consider the
$\chi $
-eigenspace
$V_{\chi , \Gamma , \tau } \subset V_{\Gamma , \tau }$
. We observe that
$$\begin{align*}\mathrm{dim} \ V_{\chi, \Gamma, \tau}=\sum_{i=1}^{q}\ m_i\ \mathrm{dim}\ V_{ \chi, \Gamma, \tau_i}.\end{align*}$$
We can use the argument culminating into Eq. 4.5 for each
$\tau _i$
and the additivity properties of
$\mathrm {Hom}$
spaces with respect to decomposition of
$\tau $
to complete the proof of Theorem 1.2.2.
5 Discrete series representations and cohomology
In this section, we comment about the case when G is non-compact connected semisimple group that admits a discrete series representation. (This is same as saying rank G = rank T, where T is a “compact” Cartan subgroup.) It is well-known that for a given
$\chi \in \widehat {\mathfrak {Z(g)}}$
, and a K-type
$\tau $
there exists at most one (up to infinitesimal equivalence) discrete series representation
$\pi _{\lambda + \rho }$
with the infinitesimal character
$\chi $
and minimal K-type
$\tau $
where
$\lambda \in \mathfrak {t}^*_{{\mathbb C}}$
such that
$\lambda + \rho $
is regular and integral linear form. Also,
$\mathrm {Hom}_K(\tau , \pi _{\lambda + \rho })=1$
.
Therefore Theorem. 1.2.2 implies the dimension of
$V_{\chi , \Gamma , \tau ^\vee }$
is equal to the multiplicity of the above discrete series
$\pi _{\lambda +\rho }$
in
$L^2(\Gamma \backslash G)$
.
For
$\lambda \in \mathfrak {t}^*_{{\mathbb C}}$
, there exists a G-equivariant holomorphic line bundle
$\mathcal {L}_{\lambda }$
on
$G/T$
. Under a mild condition on
$\lambda $
(see [Reference Williams Floyd16, Equation (7.66)]), [Reference Williams Floyd16, Theorem 7.65] implies the
$L^2$
-cohomology
$H^*_2(\Gamma \backslash \mathcal {L}_{\lambda })$
is non-vanishing in exactly one degree
$q_{\lambda }$
(depends on
$\lambda $
) and
$$ \begin{align*}\mathrm{dim}\ H_2^{q_\lambda}(\Gamma \backslash \mathcal{L}_{\lambda})=m(\pi_{\lambda +\rho}, \Gamma).\end{align*} $$
Hence, the dimension of the
$\chi $
-eigenspace of the automorphic forms of type
$\tau ^\vee $
is equal to the
$q_{\lambda }$
-th
$L^2$
-cohomology of the automorphic line bundle
$\Gamma \backslash \mathcal {L}_{\lambda }$
.
Acknowledgements
K. Mondal thanks the program Zariski dense subgroups, number theory, and geometric application (ICTS/zdsg2024/01) at International Centre for Theoretical Sciences(ICTS), Bengaluru, India in January, 2024. He also sincerely thanks Prof. C. S. Rajan for suggesting him to write the
$\tau $
-equivariant Trace Formula during this workshop. Finally, we are grateful to the anonymous referee for carefully reviewing our manuscript and providing useful suggestions for the betterment of our article.
