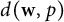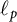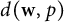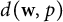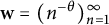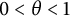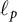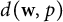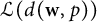1 Introduction
Little is known about the complemented subspace structure of Lorentz sequence spaces
$d(\textbf {w},p)$
. Until recently, the only nontrivial complemented subspace discussed in the literature was
$\ell _p$
[Reference Altshuler, Casazza and LinACL73]. Then, in [Reference WallisWa20], it was shown that for certain weights
$\textbf {w}$
(see Theorem 2.2 below), the space
$d(\textbf {w},p)$
contains a 1-complemented subspace isomorphic to
$(\bigoplus _{n=1}^\infty \ell _\infty ^n)_p$
. Up to now, these were the only nontrivial complemented subspaces known to exist.
In this short note, we show that each Lorentz sequence space admits a 1-complemented subspace Y distinct from
$\ell _p$
(Section 2). We also give an explicit representation of Y for the case
$\textbf {w}=(n^{-\theta })_{n=1}^\infty $
(
$0<\theta <1$
), as the
$\ell _p$
-sum of finite-dimensional copies of
$d(\textbf {w},p)$
(Section 3). Note that this choice of
$\textbf {w}=(n^{-\theta })_{n=1}^\infty $
corresponds to the classical Lorentz sequence spaces
$\ell _{q,p}$
with
$p/q=1-\theta $
. Finally, as an application, we find a sixth distinct element in the lattice of closed ideals in the operator algebra
$\mathcal {L}(d(\textbf {w},p))$
, where only five were previously known in the general case (Section 4).
Let us set up the main notation we need to use. We begin by fixing
$\mathbb {K}\in \{\mathbb {R},\mathbb {C}\}$
. Denote by
$\Pi $
the set of all permutations of
$\mathbb {N}$
, and denote by
$\mathbb {W}$
the set of all sequences
$\textbf {w}=(w_n)_{n=1}^\infty \in c_0\setminus \ell _1$
satisfying
$$ \begin{align*}1=w_1\geqslant w_2\geqslant w_3\geqslant\cdots>0. \end{align*} $$
Fix
$1\leqslant p<\infty $
and
$\textbf {w}\in \mathbb {W}$
. For each
$(a_n)_{n=1}^\infty \in \mathbb {K}^{\mathbb {N}}$
, we set
$$ \begin{align*}\left\|(a_n)_{n=1}^\infty\right\|_{d(\mathbf{w},p)}:=\mathop{\mathrm{sup}}\limits_{\pi\in\Pi}\left(\sum_{n=1}^\infty|a_{\pi(n)}|^pw_n\right)^{1/p}, \end{align*} $$
and let
$d(\textbf {w},p)$
denote the linear space of all
$(a_n)_{n=1}^\infty \in \mathbb {K}^{\mathbb {N}}$
with
$\|(a_n)_{n=1}^\infty \|_{d(\textbf {w},p)}<\infty $
endowed with the norm
$\|\cdot \|_{d(\textbf {w},p)}$
, called a Lorentz sequence space. Recall that if
$(a_n)_{n=1}^\infty \in c_0$
then there exists a “decreasing rearrangement”
$(\hat {a}_n)_{n=1}^\infty $
of
$(|a_n|)_{n=1}^\infty $
. In this case, the rearrangement inequality gives us
$$ \begin{align} \left\|(a_n)_{n=1}^\infty\right\|_{d(\mathbf{w},p)}=\left(\sum_{n=1}^\infty\hat{a}_n^pw_n\right)^{1/p}\;\;\;\text{ for all }(a_n)_{n=1}^\infty\in c_0. \end{align} $$
Because
$d(\textbf {w},p)\subset c_0$
as linear spaces (although not as normed spaces), this represents an alternative formulation of the Lorentz sequence space norm.
For each
$i,k\in \mathbb {N}$
, we define
$$ \begin{align*}W_k:=\sum_{n=1}^kw_n\;\;\text{ and }\;\;w_i^{(k)}:=\frac{1}{W_k}\sum_{n=(i-1)k+1}^{ik}w_n, \end{align*} $$
and
$\textbf {w}^{(k)}:=(w_i^{(k)})_{i=1}^\infty $
. It is readily apparent that
$\textbf {w}^{(k)}\in \mathbb {W}$
. When p is clear from context, we also set
$$ \begin{align*}d_i^{(k)}:=\frac{1}{W_k^{1/p}}\sum_{n=(i-1)k+1}^{ik}d_n, \end{align*} $$
where
$(d_n)_{n=1}^\infty $
is the canonical unit vector basis for
$d(\textbf {w},p)$
. It is routine to verify that
$(d_i^{(k)})_{i=1}^\infty $
is a normalized basic sequence isometrically equivalent to the
$d(\textbf {w}^{(k)},p)$
basis. If necessary, we may sometimes abuse this notation; for instance, if
$(j_k)_{k=1}^\infty $
is a sequence in
$\mathbb {N}$
, then we could write
$((d_i^{(j_k)})_{i=1}^k)_{k=1}^\infty $
for appropriately translated successive normalized constant-coefficient blocks of lengths
$j_k$
.
Our main tool for finding complemented subspaces of
$d(\textbf {w},p)$
is the fact that every constant-coefficient block basic sequence of a symmetric basis spans a 1-complemented subspace (cf., e.g., [Reference Lindenstrauss and TzafririLT77, Proposition 3.a.4]). We will use this well-known fact freely and without further reference.
2 Lorentz sequence spaces contain at least two nontrivial complemented subspaces
The first discovery of a nontrivial complemented subspace in
$d(\textbf {w},p)$
came almost half a century ago, with the following result.
Theorem 2.1 ([Reference Altshuler, Casazza and LinACL73, Lemma 1])
Fix
$1\leqslant p<\infty $
and
$\textbf {w}\in \mathbb {W}$
, and let
$$ \begin{align*}x_i=\sum_{n=p_i}^{p_{i+1}-1}a_nd_n,\;\;\;i\in\mathbb{N}, \end{align*} $$
form a seminormalized block basic sequence in
$d(\textbf {w},p)$
. If
$a_n\to 0$
, then
$(x_i)_{i=1}^\infty $
admits a subsequence equivalent to
$\ell _p$
and complemented in
$d(\textbf {w},p)$
.
By taking sufficiently long constant-coefficient blocks, it follows that
$d(\textbf {w},p)$
contains a 1-complemented copy of
$\ell _p$
. Much later was shown the following.
Theorem 2.2 ([Reference WallisWa20, Theorem 4.3])
Let
$1\leqslant p<\infty $
and
$\textbf {w}=(w_n)_{n=1}^\infty \in \mathbb {W}$
. If
$$ \begin{align*}\inf_{k\in\mathbb{N}}\frac{\sum_{n=1}^{2k}w_n}{\sum_{n=1}^kw_n}=1, \end{align*} $$
then
$d(\textbf {w},p)$
admits a 1-complemented subspace spanned by constant-coefficient blocks and isomorphic to
$(\bigoplus _{n=1}^\infty \ell _\infty ^n)_p$
.
Thanks in large part to the ideas of William B. Johnson, our main result in this section is to generalize this to all Lorentz sequence spaces, as follows.
Theorem 2.3 Let
$1\leqslant p<\infty $
and
$\textbf {w}\in \mathbb {W}$
. Then, there exists an increasing sequence
$(N_k)_{k=1}^\infty \in \mathbb {N}^{\mathbb {N}}$
such that
$((d_i^{(k)})_{i=1}^{N_k})_{k=1}^\infty $
spans a 1-complemented subspace Y which contains no isomorph of
$d(\textbf {w},p)$
and which is not isomorphic to
$\ell _p$
.
To prove it, we need a few preliminaries.
Lemma 2.4 If
$1<p<\infty $
, then every complemented subspace of
$L_p[0,1]$
with a subsymmetric basis
$(x_n)_{n=1}^\infty $
is isomorphic to either
$\ell _p$
or
$\ell _2$
.
Proof The case
$p=2$
is trivial, because every complemented subspace of
$L_2[0,1]$
is isomorphic to
$\ell _2$
. For the case
$p>2$
, recall from [Reference Kadec and PełczyńskiKP62, Corollary 6] that every seminormalized basic sequence in
$L_p[0,1]$
,
$p\in (2,\infty )$
, admits a subsequence equivalent to
$\ell _p$
or
$\ell _2$
, and so because
$(x_n)_{n=1}^\infty $
is also subsymmetric, then it is in fact equivalent to
$\ell _p$
or
$\ell _2$
. In case
$1<p<2$
, because
$(x_n)_{n=1}^\infty $
is complemented in
$L_p[0,1]$
, its corresponding sequence of biorthogonal functionals
$(x_n^*)_{n=1}^\infty $
is contained in
$L_{p'}[0,1]$
, where
$\frac {1}{p}+\frac {1}{p'}=1$
. Because
$p'>2$
, a subsequence of
$(x_n^*)_{n=1}^\infty $
is equivalent to
$\ell _{p'}$
or
$\ell _2$
, whence by subsymmetry
$(x_n)_{n=1}^\infty $
is equivalent to
$\ell _p$
or
$\ell _2$
.▪
Lemma 2.5 Let X be a Banach space whose canonical isometric copy in
$X^{**}$
is complemented. Then, for any free ultrafilter
$\mathcal {U}$
on
$\mathbb {N}$
, the canonical copy of X in
$X^{\mathcal {U}}$
is complemented in
$X^{\mathcal {U}}$
.
Proof Let
$q:X\to X^{**}$
denote the canonical embedding, and define the norm-1 linear operator
$V:\ell _\infty (X)\to X^{**}$
by the rule
$$ \begin{align*}V(x_n)_{n=1}^\infty=\underset{\mathcal{U}}{\text{weak*-lim}}\,qx_n, \end{align*} $$
which exists by the weak*-compactness of
$B_{X^{**}}$
together with the fact that if K is a compact Hausdorff space, then for each
$(k_n)_{n=1}^\infty \in K^{\mathbb {N}}$
, the (unique) limit
$\lim _{\mathcal {U}}k_n$
exists in K. Note that if
$\lim _{\mathcal {U}}x_n=0$
, then
$V(x_n)_{n=1}^\infty =0$
, and so V induces an operator
$\widehat {V}:X^{\mathcal {U}}\to X^{**}$
which agrees with V along the diagonal. In particular,
$\widehat {V}$
sends the canonical copy of X in
$X^{\mathcal {U}}$
isomorphically to the canonical copy of X in
$X^{**}$
.▪
Theorem 2.6 Fix
$1\leqslant p<\infty $
, and let
$(x_n)_{n=1}^\infty $
be a basis for a Banach space X whose canonical copy in
$X^{**}$
is complemented. If the finite-dimensional spaces
$[x_n]_{n=1}^N$
,
$N\in \mathbb {N}$
, are uniformly complemented in
$L_p(\mu )$
for some measure
$\mu $
, then X is complemented in
$L_p[0,1]$
.
Proof Let
$X_N=[x_n]_{n=1}^N$
and
$P_N:X\to X_N$
the projection onto
$X_N$
. By uniform complementedness of
$X_N$
, we can find uniformly bounded linear operators
$A_N:X_N\to L_p(\mu )$
and
$B_N:L_p(\mu )\to X_N$
such that
$B_NA_N$
is the identity on
$X_N$
. Let
$\mathcal {U}$
be any free ultrafilter on
$\mathbb {N}$
. Define the bounded linear operators
$A:X\to L_p(\mu )^{\mathcal {U}}$
by the rule
$Ax=(A_NP_Nx)_{\mathcal {U}}$
, and
$B:L_p(\mu )^{\mathcal {U}}\to X^{\mathcal {U}}$
by
$B(y_N)_{\mathcal {U}}=(B_Ny_N)_{\mathcal {U}}$
. Let
$x\in \text {span}(x_n)_{n=1}^\infty $
, so that, for some
$k\in \mathbb {N}$
,
$$ \begin{align*}BAx=(P_1x,\ldots,P_kx,x,x,\ldots)_{\mathcal{U}}=x^{\mathcal{U}}. \end{align*} $$
By continuity,
$BA$
is the canonical injection of X into
$X^{\mathcal {U}}$
. Because its range is complemented by Lemma 2.5, we have the identity on X factoring through
$L_p(\mu )^{\mathcal {U}}$
.
It was proved in [Reference HeinrichHe80, Theorem 3.3] that ultrapowers preserve
$L_p$
lattice structure, and in particular
$L_p(\mu )^{\mathcal {U}}$
is isomorphic to
$L_p(\nu )$
for some measure
$\nu $
. Although
$L_p(\nu )$
itself is nonseparable, we could pass to the closed sublattice generated by
$AX$
to find a space isomorphic to a separable
$L_p$
containing a complemented copy of X. Due mostly to a famous result of Lacey and Wojtaszczyk, it is known that separable and infinite-dimensional
$L_p$
spaces are isomorphic to either
$\ell _p$
or
$L_p[0,1]$
[Reference Johnson, Lindenstrauss, Johnson and LindenstraussJL01, Section 4, p. 15]. This means an isomorph of X is complemented in
$L_p[0,1]$
.▪
An immediate corollary to Lemma 2.4 and Theorem 2.6 is as follows.
Corollary 2.7 Let
$1<p<\infty $
and
$\textbf {w}\in \mathbb {W}$
. Then, no
$L_p(\mu )$
space contains uniformly complemented copies of
$[d_n]_{n=1}^N$
,
$N\in \mathbb {N}$
.
Now, we are ready to prove the main result of this section, Theorem 2.3.
Proof Fix
$k\in \mathbb {N}$
, and note that
$(d_i^{(k)})_{k=1}^\infty $
is isometric to the
$d(\textbf {w}^{(k)},p)$
basis. Consider the case where
$p=1$
. Then, we can choose the
$N_k$
’s large enough that each
$(d_i^{(k)})_{i=1}^{N_k}$
fails to be k-equivalent to
$\ell _1^{N_k}$
, and hence
$((d_i^{(k)})_{i=1}^{N_k})_{k=1}^\infty $
fails to be equivalent to
$\ell _1$
. As
$\ell _1$
has a unique unconditional basis by a result of Lindenstrauss and Pełczyński, it follows that Y is not isomorphic to
$\ell _1$
.
Next, consider the case where
$1<p<\infty $
. By Corollary 2.7, we can select
$N_k$
’s large enough that
$[d_i^{(k)}]_{i=1}^{N_k}$
fails to be k-complemented in
$\ell _p$
. As
$[d_i^{(k)}]_{i=1}^{N_k}$
’s are all 1-complemented in Y, that means Y is not isomorphic to
$\ell _p$
.
It remains to show that Y contains no isomorph of
$d(\textbf {w},p)$
. Suppose toward a contradiction that it does. As
$(d_n)_{n=1}^\infty $
is weakly null (cf., e.g., [Reference Altshuler, Casazza and LinACL73, Proposition 1]), we can use the gliding hump method together with symmetry to find a normalized block sequence of
$((d_i^{(k)})_{i=1}^{N_k})_{k=1}^\infty $
equivalent to
$(d_n)_{n=1}^\infty $
. However, every such block sequence is also a block sequence w.r.t.
$(d_n)_{n=1}^\infty $
with coefficients tending to zero. By Theorem 2.1, it follows that
$(d_n)_{n=1}^\infty $
admits a subsequence equivalent to
$\ell _p$
, which is impossible.▪
3 A special case
In this section, we show that when
$\textbf {w}=(n^{-\theta })_{n=1}^\infty $
for some fixed
$0<\theta <1$
, the space Y described in Theorem 2.3 can be chosen to be isomorphic to the space
$$ \begin{align*}Y_{\mathbf{w},p}:=\left(\bigoplus_{N=1}^\infty D_N\right)_p, \end{align*} $$
where
$D_N:=[d_n]_{n=1}^N$
, for each
$N\in \mathbb {N}$
. As usual, we require some preliminaries.
Lemma 3.1 Let
$0<\theta <1$
and
$j,k\in \mathbb {N}$
. Then,
$$ \begin{align*}\left(\frac{j+1}{k}+1\right)^{1-\theta}-\left(\frac{j+1}{k}\right)^{1-\theta} \leqslant\frac{\sum_{n=j+1}^{j+k}n^{-\theta}}{\sum_{n=1}^kn^{-\theta}} \leqslant\frac{(j/k+1)^{1-\theta}-(j/k)^{1-\theta}}{2^{1-\theta}-1}. \end{align*} $$
Proof Observe that the map
$$ \begin{align*}f(t)=(1+1/t)^{1-\theta}-(1/t)^{1-\theta} \end{align*} $$
is increasing on
$[1,\infty )$
and hence has a minimum
$f(1)=2^{1-\theta }-1$
. Hence,
$$ \begin{align*} \left(\frac{j+1}{k}+1\right)^{1-\theta}-\left(\frac{j+1}{k}\right)^{1-\theta} &\leqslant\frac{(j+k+1)^{1-\theta}-(j+1)^{1-\theta}}{k^{1-\theta}-\theta} \\&=\frac{\int_{j+1}^{j+k+1}t^{-\theta}\;dt}{1+\int_1^kt^{-\theta}\;dt} \\&\leqslant\frac{\sum_{n=j+1}^{j+k}n^{-\theta}}{\sum_{n=1}^kn^{-\theta}} \\&\leqslant\frac{\int_j^{j+k}t^{-\theta}\;dt}{\int_1^{k+1}t^{-\theta}\;dt} \\&=\frac{(j+k)^{1-\theta}-j^{1-\theta}}{(k+1)^{1-\theta}-1} \\&=\frac{(j/k+1)^{1-\theta}-(j/k)^{1-\theta}}{(1+1/k)^{1-\theta}-(1/k)^{1-\theta}} \\&\leqslant\frac{(j/k+1)^{1-\theta}-(j/k)^{1-\theta}}{2^{1-\theta}-1}.\\[-3.3pc] \end{align*} $$
▪
Lemma 3.2 Let
$0<\theta <1$
and
$\textbf {w}=(w_n)_{n=1}^\infty =(n^{-\theta })_{n=1}^\infty \in \mathbb {W}$
. Then,
$$ \begin{align*}\frac{1-\theta}{2}\cdot w_i \leqslant w_i^{(k)} \leqslant\frac{2-2^\theta}{2^{1-\theta}-1}\cdot w_i \;\;\;\text{ for all }i,k\in\mathbb{N}. \end{align*} $$
In particular, if
$1\leqslant p<\infty $
, then there is a constant
$C\in [1,\infty )$
, depending only on
$\theta $
, such that
$$ \begin{align*}(d_n)_{n=1}^\infty\approx_C(d_i^{(k)})_{i=1}^\infty\;\;\;\text{ for all }k\in\mathbb{N}. \end{align*} $$
Proof We can assume
$i,k\geqslant 2$
. Observe that
$$ \begin{align*}t\mapsto t-(t-1)^{1-\theta}\cdot t^\theta \end{align*} $$
is decreasing on
$[2,\infty )$
, and hence has the maximum
$2-2^\theta $
. Furthermore, the function
$$ \begin{align*}t\mapsto t-(t-1/2)^{1-\theta}\cdot t^\theta \end{align*} $$
is decreasing on
$[2,\infty )$
and hence has infimum
$$ \begin{align*}\lim_{t\to\infty}\left(t-(t-1/2)^{1-\theta}\cdot t^\theta\right)=\frac{1-\theta}{2}. \end{align*} $$
Thus, by the above, and applying Lemma 3.1 with
$j=k(i-1)$
,
$$ \begin{align*} \frac{1-\theta}{2}\cdot i^{-\theta} &\leqslant\left(i-(i-1/2)^{1-\theta}\cdot i^\theta\right)i^{-\theta} \\&=i^{1-\theta}-(i-1/2)^{1/\theta} \\&\leqslant(i+1/k)^{1-\theta}-(i-1+1/k)^{1/\theta} \\&\leqslant\frac{\sum_{n=(i-1)k+1}^{ik}n^{-\theta}}{\sum_{n=1}^kn^{-\theta}} &\left(\text{which is equal to }w_i^{(k)}\right) \\&\leqslant\frac{i^{1-\theta}-(i-1)^{1-\theta}}{2^{1-\theta}-1} \\&=\frac{i-(i-1)^{1-\theta}\cdot i^\theta}{2^{1-\theta}-1}\cdot i^{-\theta} \\&\leqslant\frac{2-2^\theta}{2^{1-\theta}-1}\cdot i^{-\theta}.\\[-3.2pc] \end{align*} $$
▪
Remark 3.3 Suppose
$x=\sum _{n\in A}a_nd_n$
and
$y=\sum _{n\in B}b_nd_n$
for finite and disjoint sets
$A,B\subset \mathbb {N}$
, where
$(a_n)_{n\in A}$
and
$(b_n)_{n\in B}$
are sequences of scalars. Then,
$$ \begin{align*}\|x+y\|^p\leqslant\|x\|^p+\|y\|^p. \end{align*} $$
Lemma 3.4 Let
$(j_k)_{k=1}^\infty $
be a sequence of positive integers, and, for each k, set
$$ \begin{align*}J_k=j_1+2j_2+3j_3+\cdots+kj_k.\end{align*} $$
Suppose that there are constants
$A,B\in (0,\infty )$
such that
$$ \begin{align} w_i^{(j_k)}\leqslant Aw_i \end{align} $$
and
$$ \begin{align} Bw_i\leqslant\frac{1}{W_{j_k}}\sum_{n=J_{k-1}+(i-1)j_k+1}^{J_{k-1}+ij_k}w_n, \end{align} $$
for all
$i=1,\ldots ,k$
and all
$k\in \mathbb {N}$
. Then,
$((d_i^{(j_k)})_{i=1}^k)_{k=1}^\infty $
is equivalent to the canonical
$Y_{\textbf { w},p}$
basis.
Proof Due to (3.1), we have
$(d_i^{(j_k)})_{i=1}^k\lesssim _A d(\textbf {w},p)^k$
. Now, using Remark 3.3, for any finitely supported scalar sequence
$((a_i^{(k)})_{i=1}^k)_{k=1}^\infty $
,
$$ \begin{align*} \left\|\sum_{k=1}^\infty\sum_{i=1}^k a_i^{(k)}d_i^{(j_k)}\right\|^p &\leqslant\sum_{k=1}^\infty\left\|\sum_{i=1}^ka_i^{(k)}d_i^{(j_k)}\right\|^p \\&\leqslant A^p\sum_{k=1}^\infty\left\|(a_i^{(k)})_{i=1}^k\right\|_{d(\mathbf{w},p)}^p \\&=A^p\left\|((a_i^{(k)})_{i=1}^k)_{k=1}^\infty\right\|_{Y_{\mathbf{w},p}}^p. \end{align*} $$
For the reverse inequality, let
$(\hat {a}_i^{(k)})_{i=1}^k$
denote the decreasing rearrangement of
$(|a_i^{(k)}|)_{i=1}^k$
. Then, applying (3.2),
$$ \begin{align*} \left\|\sum_{k=1}^\infty\sum_{i=1}^k a_i^{(k)}d_i^{(j_k)}\right\|^p &=\left\|\sum_{k=1}^\infty\sum_{i=1}^k\frac{a_i^{(k)}}{W_{j_k}^{1/p}}\sum_{n=J_{k-1}+(i-1)j_k+1}^{J_{k-1}+ij_k}d_n\right\|^p \\&\geqslant\sum_{k=1}^\infty\sum_{i=1}^k\frac{\hat{a}_i^{(k)p}}{W_{j_k}}\sum_{n=J_{k-1}+(i-1)j_k+1}^{J_{k-1}+ij_k}w_n &\left(\text{from }(1.1)\right) \\&\geqslant B\sum_{k=1}^\infty\sum_{i=1}^k\hat{a}_i^{(k)p}w_i \\&=B\left\|((a_i^{(k)})_{i=1}^k)_{k=1}^\infty\right\|_{Y_{\mathbf{w},p}}^p.\\[-3.3pc] \end{align*} $$
▪
Theorem 3.5 Let
$(j_k)_{k=1}^\infty $
and
$(J_k)_{k=1}^\infty $
be as in Lemma
3.4
. Suppose there is
$M\in [1,\infty )$
such that
$$ \begin{align*}\frac{J_{k-1}}{j_k}\leqslant M,\;\;\;\text{ for all }k=2,3,4,\ldots. \end{align*} $$
Then,
$((d_i^{(j_k)})_{i=1}^k)_{k=1}^\infty $
is equivalent to the canonical
$Y_{\textbf { w},p}$
basis.
Proof Due to Lemma 3.4, it suffices to show that (3.2) and (3.1) both hold. To do this, fix an arbitrary
$k\in \mathbb {N}$
. We may assume, without loss of generality, that
$j_k\geqslant 2$
. Now, by Lemma 3.1,
$$ \begin{align*} \frac{1}{W_{j_k}}\sum_{n=J_{k-1}+(i-1)j_k+1}^{J_{k-1}+ij_k}w_n &\geqslant\left(\frac{J_{k-1}+(i-1)j_k+1}{j_k}+1\right)^{1-\theta}-\left(\frac{J_{k-1}+(i-1)j_k+1}{j_k}\right)^{1-\theta} \\&=\left(\frac{J_{k-1}}{j_k}+i+\frac{1}{j_k}\right)^{1-\theta}-\left(\frac{J_{k-1}}{j_k}+i-1+\frac{1}{j_k}\right)^{1-\theta} \\&\geqslant\left(\frac{J_{k-1}}{j_k}+i\right)^{1-\theta}-\left(\frac{J_{k-1}}{j_k}+i-1+\frac{1}{2}\right)^{1-\theta} \\&=i^\theta\left[\left(\frac{J_{k-1}}{j_k}+i\right)^{1-\theta}-\left(\frac{J_{k-1}}{j_k}+i-\frac{1}{2}\right)^{1-\theta}\right]w_i. \end{align*} $$
Applying the Mean Value Theorem to the function
$x\mapsto (\phi +x)^{1-\theta }$
,
$\phi \in [1,\infty )$
, we can find
$x_\phi \in (-1/2,0)$
such that
$$ \begin{align*}\phi^{1-\theta}-(\phi-1/2)^{1-\theta}=\frac{(1-\theta)(\phi+x_\phi)^{-\theta}}{2} \geqslant\frac{(1-\theta)\phi^{-\theta}}{2}. \end{align*} $$
Hence, letting
$\phi =J_{k-1}/j_k+i$
, we have
$$ \begin{align*} i^\theta\left[\left(\frac{J_{k-1}}{j_k}+i\right)^{1-\theta}-\left(\frac{J_{k-1}}{j_k}+i-\frac{1}{2}\right)^{1-\theta}\right] &\geqslant i^\theta\left[\frac{(1-\theta)(J_{k-1}/j_k+i)^{-\theta}}{2}\right] \\&=\frac{1-\theta}{2}\left(\frac{i}{J_{k-1}/j_k+i}\right)^\theta \\&\geqslant\frac{1-\theta}{2}\left(\frac{1}{M+1}\right)^\theta. \end{align*} $$
This proves (3.2), and (3.1) follows immediately from Lemma 3.2.▪
Taking inductively
$j_1=1$
and
$j_{k+1}=J_k$
, the following is now immediate.
Corollary 3.6 Let
$1\leqslant p<\infty $
,
$0<\theta <1$
, and
$\textbf {w}=(w_n)_{n=1}^\infty =(n^{-\theta })_{n=1}^\infty \in \mathbb {W}$
. Then,
$d(\textbf {w},p)$
admits a 1-complemented subspace isomorphic to
$Y_{\textbf { w},p}$
.
4 Application to the lattice of closed ideals
In [Reference Kaminska, Popov, Spinu, Tcaciuc and TroitskyKPSTT12], it was shown (among other results) that the lattice of closed ideals for the operator algebra
$\mathcal {L}(d(\textbf {w},p))$
can be put into a chain:
$$ \begin{align*}\{0\} \subsetneq\mathcal{K}(d(\mathbf{w},p)) \subsetneq\mathcal{SS}(d(\mathbf{w},p)) \subsetneq\mathcal{S}_{d(\mathbf{w},p)}(d(\mathbf{w},p)) \subsetneq\mathcal{L}(d(\mathbf{w},p)). \end{align*} $$
Here,
$\mathcal {K}$
denotes the compact operators,
$\mathcal {SS}$
the strictly singular operators, and
$\mathcal {S}_{d(\textbf {w},p)}$
the ideal of operators which fail to be bounded below on any isomorph of
$d(\textbf {w},p)$
. While, in [Reference WallisWa20, Corollary 2.7], for the special case where
$1<p<2$
and
$\textbf {w}\in \mathbb {W}\cap \ell _{2/(2-p)}$
, a chain of distinct closed ideals with cardinality of the continuum were identified lying between
$\mathcal {K}(d(\textbf {w},p))$
and
$\mathcal {SS}(d(\textbf {w},p)$
, for the general case, the only distinct elements known were those of the above chain.
For an operator T, let
$\mathcal {J}_T$
denote the class of operators factoring through T. If Z is any Banach space, we then set
$\mathcal {J}_Z=\mathcal {J}_{Id_Z}$
. By Theorem 4.3 below, we can extend the chain above as follows:
$$ \begin{align*} \{0\} \subsetneq\mathcal{K}(d(\mathbf{w},p)) &\subsetneq\mathcal{SS}(d(\mathbf{w},p)) \subsetneq(\overline{\mathcal{J}_{\ell_p}}\vee\mathcal{SS})(d(\mathbf{w},p)) \\ &\subsetneq\mathcal{S}_{d(\mathbf{w},p)}(d(\mathbf{w},p)) \subsetneq\mathcal{L}(d(\mathbf{w},p)). \end{align*} $$
Furthermore, by [Reference Kaminska, Popov, Spinu, Tcaciuc and TroitskyKPSTT12, Corollary 3.2 and Theorem 5.3] together with the fact that
$d(\textbf {w},p)$
has the approximation property, any additional distinct closed ideals in the above chain must lie between
$\mathcal {K}(d(\textbf {w},p)) $
and
$\mathcal {SS}(d(\textbf {w},p))$
, or else between
$(\overline {\mathcal {J}_{\ell _p}}\vee \mathcal {SS})(d(\textbf {w},p))$
and
$\mathcal {S}_{d(\textbf {w},p)}(d(\textbf {w},p))$
, although there may be other ideals in the lattice which are not a part of the chain.
To prove Theorem 4.3, we need a couple of preliminary results.
Proposition 4.1 Let X and Z be an infinite-dimensional Banach spaces such that
$Z^2\approx Z$
, and X fails to be isomorphic to a complemented subspace of Z. Then,
$\overline {\mathcal {J}_Z}(X)$
is a proper ideal in
$\mathcal {L}(X)$
. Furthermore, if
$P\in \mathcal {L}(X)$
is a projection with image isomorphic to Z, then
$$ \begin{align*}\mathcal{J}_P(X)=\mathcal{J}_Z(X).\end{align*} $$
Proof Because
$Z^2\approx Z$
, [Reference Kaminska, Popov, Spinu, Tcaciuc and TroitskyKPSTT12, Lemma 2.2] guarantees that
$\mathcal {J}_Z(X)$
is an ideal in
$\mathcal {L}(X)$
. Suppose toward a contradiction that
$Id_X\in \mathcal {J}_Z(X)$
. Then,
$Id_X=AB$
for operators
$A\in \mathcal {L}(Z,X)$
and
$B\in \mathcal {L}(X,Z)$
. By [Reference Kaminska, Popov, Spinu, Tcaciuc and TroitskyKPSTT12, Lemma 2.1],
$BX$
is complemented in Z and isomorphic to X, which contradicts our hypotheses. It follows that
$\mathcal {J}_Z(X)$
is a proper ideal in
$\mathcal {L}(X)$
. Recall that the closure of a proper ideal in a unital Banach algebra is again proper; in particular,
$\overline {\mathcal {J}_Z}(X)$
is a proper ideal in
$\mathcal {L}(X)$
.
To prove the “furthermore” part, assume
$A\in \mathcal {L}(Z,X)$
and
$B\in \mathcal {L}(X,Z)$
. Let
$Q:Z\to X$
be the canonical embedding, so that
$PQ=Id_Z$
and hence
$AB=APQB\in \mathcal {J}_P(X)$
. It follows that
$\mathcal {J}_Z(X)\subseteq \mathcal {J}_P(X)$
, and the reverse inclusion is even more obvious.▪
For the next result,
$\mathcal {F}$
denotes the class of finite-rank operators and
$\mathcal {E}$
the class of inessential operators. Recall also that a basis
$\mathcal {B}$
is called semispreading whenever every subsequence of
$\mathcal {B}$
is dominated by
$\mathcal {B}$
itself. In particular, the unit vector basis of
$\ell _p$
is semispreading.
Proposition 4.2 ([Reference Laustsen, Loy and ReadLLR04, Corollary 3.8])
Let Z be a Banach space with a semispreading basis
$(z_n)$
, and let X be a Banach space with basis
$(x_n)$
such that any seminormalized block sequence of
$(x_n)$
contains a subsequence equivalent to
$(z_n)$
and spanning a complemented subspace of X. Then,
$$ \begin{align*}\{0\}\subsetneq\overline{\mathcal{F}}(X)=\mathcal{K}(X)=\mathcal{SS}(X)=\mathcal{E}(X)\subsetneq\overline{\mathcal{J}_Z}(X), \end{align*} $$
and any additional distinct closed ideals must lie between
$\overline {\mathcal {J}_Z}(X)$
and
$\mathcal {L}(X)$
.
In the proof of what follows, we use the fact that if
$\mathcal {I}$
and
$\mathcal {J}$
are ideals in
$\mathcal {L}(X)$
, then
$\overline {\mathcal {I}}\vee \overline {\mathcal {J}}=\overline {\mathcal {I}+\mathcal {J}}$
.
Theorem 4.3 Fix
$1\leqslant p<\infty $
and
$\textbf {w}\in \mathbb {W}$
. Let Y be as in Theorem
2.3
, and
$P_Y\in \mathcal {L}(d(\textbf {w},p))$
any continuous linear projection onto Y. Then,
$$ \begin{align*}P_Y\in\mathcal{S}_{d(\mathbf{w},p)}(d(\mathbf{w},p))\setminus(\overline{\mathcal{J}_{\ell_p}}\vee\mathcal{SS})(d(\mathbf{w},p)).\end{align*} $$
Proof Let
$P_{\ell _p}\in \mathcal {L}(d(\textbf {w},p))$
be any projection onto an isomorphic copy of
$\ell _p$
spanned by basis vectors of Y. (Such a copy exists by Theorem 2.1.) By Theorem 2.3, Y contains no isomorph of
$d(\textbf {w},p)$
and hence
$P_Y\in \mathcal {S}_{d(\textbf {w},p)}(d(\textbf {w},p))$
. Because
$\mathcal {S}_{d(\textbf {w},p)}(d(\textbf {w},p))$
is the unique maximal ideal in
$\mathcal {L}(d(\textbf {w},p))$
, and
$\mathcal {J}_{P_{\ell _p}}(d(\textbf {w},p))=\mathcal {J}_{\ell _p}(d(\textbf {w},p))$
by Proposition 4.1, it is sufficient to prove that
$P_Y\notin (\overline {\mathcal {J}_{P_{\ell _p}}}\vee \mathcal {SS})(d(\textbf {w},p)).$
Next, we claim that
$P_Y\in (\overline {\mathcal {J}_{P_{\ell _p}}}\vee \mathcal {SS})(d(\textbf {w},p))$
only if
$Id_Y\in (\overline {\mathcal {J}_{\ell _p}}\vee \mathcal {SS})(Y)$
. To prove it, fix
$\varepsilon>0$
, and suppose there are
$A,B\in \mathcal {L}(d(\textbf {w},p))$
and
$S\in \mathcal {SS}(d(\textbf {w},p))$
such that
$$ \begin{align*}\left\|AP_{\ell_p}B+S-P_Y\right\|<\varepsilon. \end{align*} $$
Let
$J_Y:Y\to d(\textbf {w},p)$
be an embedding satisfying
$P_YJ_Y=J_Y$
, or
$P_YJ_Y=Id_Y$
when viewed as an operator in
$\mathcal {L}(Y)$
. Composing
$P_Y$
on the left and
$J_Y$
on the right, we have
$$ \begin{align*}\left\|P_YAP_{\ell_p}BJ_Y+P_YSJ_Y-Id_Y\right\|_{\mathcal{L}(Y)}<\|P_Y\|\cdot\varepsilon\cdot\|J_Y\|. \end{align*} $$
On the other hand, because
$AP_{\ell _p}=A|_YP_{\ell _p}$
and
$P_{\ell _p}=P_{\ell _p}P_Y$
, we have
$$ \begin{align*}P_YAP_{\ell_p}BJ_Y =(P_YA|_Y)P_{\ell_p}(P_YBJ_Y), \end{align*} $$
and hence
$$ \begin{align*}\left\|(P_YA|_Y)P_{\ell_p}(P_YBJ_Y)+P_YSJ_Y-Id_Y\right\|_{\mathcal{L}(Y)}<\|P_Y\|\cdot\varepsilon\cdot\|J_Y\|. \end{align*} $$
Because
$\mathcal {J}_{\ell _p}(Y)=\mathcal {J}_{P_{\ell _p}}(Y)$
by Proposition 4.1, where
$P_{\ell _p}$
is likewise viewed as an operator in
$\mathcal {L}(Y)$
, from the above together with the ideal property of
$\mathcal {SS}$
, the claim follows.
Let
$\mathcal {B}_Y=((d_i^{(k)})_{i=1}^{N_k})_{k=1}^\infty $
denote the canonical basis of Y from Theorem 2.3. Note that because
$\mathcal {B}_Y$
is made up of constant coefficient blocks of
$(d_n)$
of increasing length, any seminormalized blocks of
$\mathcal {B}_Y$
will contain a subsequence equivalent to
$\ell _p$
by Theorem 2.1. In fact, in [Reference Casazza and LinCL74, Lemma 15], this result was refined to show that we can choose that subsequence to span a complemented subspace of
$d(\textbf {w},p)$
, and hence of Y itself. We can therefore apply Theorem 4.2 to conclude that
$\mathcal {SS}(Y)\subset \overline {\mathcal {J}_{\ell _p}}(Y)$
. Meanwhile, again by Proposition 4.1,
$\overline {\mathcal {J}_{\ell _p}}(Y)$
is a proper ideal in
$\mathcal {L}(Y)$
, which means
$Id_Y\notin \overline {\mathcal {J}_{\ell _p}}(Y)$
. Hence,
$P_Y\notin (\overline {\mathcal {J}_{P_{\ell _p}}}\vee \mathcal {SS})(d(\textbf {w},p))$
as desired.▪
