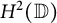1 Introduction
In this paper, we study nearly invariant subspaces from a Brangesian point of view. A subspace
![]() $\mathcal {M}$
of the Hardy space
$\mathcal {M}$
of the Hardy space
![]() $H^2(\mathbb {D})$
is called nearly invariant under the backward shift operator
$H^2(\mathbb {D})$
is called nearly invariant under the backward shift operator
![]() $S^*$
on
$S^*$
on
![]() $H^2(\mathbb {D})$
if
$H^2(\mathbb {D})$
if
![]() $S^*(f)$
belongs to
$S^*(f)$
belongs to
![]() $\mathcal {M}$
whenever f vanishes at zero. These subspaces first arose in the work of Hitt [Reference Hitt11] while characterizing the shift invariant subspaces of the Hardy space of an annulus. The kernels of Toeplitz operators are particular examples of nearly
$\mathcal {M}$
whenever f vanishes at zero. These subspaces first arose in the work of Hitt [Reference Hitt11] while characterizing the shift invariant subspaces of the Hardy space of an annulus. The kernels of Toeplitz operators are particular examples of nearly
![]() $S^*$
-invariant subspaces, and this special case of Hitt’s theorem was independently established by Hayashi [Reference Hayashi10] by developing ideas similar to those used by Hitt. Hitt called these subspaces “weakly invariant” rather than “nearly invariant”. Sarason, [Reference Sarason13], coined the term “nearly invariant subspaces” and—more importantly—gave a new proof of Hitt’s theorem by utilizing ideas based on de Branges–Rovnyak spaces, [Reference de Branges and Rovnyak3]. See also [Reference Sarason14]. In doing so, Sarason engendered new ideas that gave rise to some very interesting papers such as [Reference Aleman, Baranov, Belov and Hedenmalm1, Reference Aleman, Feldman and Ross2, Reference Chevrot8, Reference Yakubovich15]. Since the time [Reference Hayashi10, Reference Hitt11], and particularly [Reference Sarason13] appeared nearly invariant subspaces have established themselves as an important area of research and they can be deemed to be a proper generalization of the concept of invariant subspaces. In addition, they connect with many diverse areas including with mathematical physics. See D. Vukoti
$S^*$
-invariant subspaces, and this special case of Hitt’s theorem was independently established by Hayashi [Reference Hayashi10] by developing ideas similar to those used by Hitt. Hitt called these subspaces “weakly invariant” rather than “nearly invariant”. Sarason, [Reference Sarason13], coined the term “nearly invariant subspaces” and—more importantly—gave a new proof of Hitt’s theorem by utilizing ideas based on de Branges–Rovnyak spaces, [Reference de Branges and Rovnyak3]. See also [Reference Sarason14]. In doing so, Sarason engendered new ideas that gave rise to some very interesting papers such as [Reference Aleman, Baranov, Belov and Hedenmalm1, Reference Aleman, Feldman and Ross2, Reference Chevrot8, Reference Yakubovich15]. Since the time [Reference Hayashi10, Reference Hitt11], and particularly [Reference Sarason13] appeared nearly invariant subspaces have established themselves as an important area of research and they can be deemed to be a proper generalization of the concept of invariant subspaces. In addition, they connect with many diverse areas including with mathematical physics. See D. Vukoti
![]() $\acute {\mathrm {c}}$
(2011). [Review of the book The Hardy spaces of a slit domain, by A. Aleman, N. Feldman, and W. Ross]. MR2548414 (2011m:30095).
$\acute {\mathrm {c}}$
(2011). [Review of the book The Hardy spaces of a slit domain, by A. Aleman, N. Feldman, and W. Ross]. MR2548414 (2011m:30095).
Theorem 1.1 (Hitt’s theorem). Let
![]() $\mathcal {M}$
be a non-trivial nearly invariant subspace of
$\mathcal {M}$
be a non-trivial nearly invariant subspace of
![]() $H^2(\mathbb {D})$
under
$H^2(\mathbb {D})$
under
![]() $S^*,$
and let g be a function in
$S^*,$
and let g be a function in
![]() $\mathcal {M}$
of unit norm that is orthogonal to
$\mathcal {M}$
of unit norm that is orthogonal to
![]() $\mathcal {M}\cap zH^2(\mathbb {D})$
and positive at the origin. Then there exists a
$\mathcal {M}\cap zH^2(\mathbb {D})$
and positive at the origin. Then there exists a
![]() $S^*$
-invariant subspace
$S^*$
-invariant subspace
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $H^2(\mathbb {D})$
such that
$H^2(\mathbb {D})$
such that
![]() $\mathcal {M}=g\mathcal {N}$
and
$\mathcal {M}=g\mathcal {N}$
and
![]() $||gf||=||f||$
for all
$||gf||=||f||$
for all
![]() $f\in \mathcal {N}.$
$f\in \mathcal {N}.$
In 2010, Chalendar, Chevrot, and Partington [Reference Chalendar, Chevrot and Partington4] generalized Hitt’s result to the backward shift operator on a vector-valued Hardy space. A few years later, the first and third author from [Reference Chalendar, Chevrot and Partington4], in collaboration with Gallardo–Gutierrez, introduced and described in [Reference Chalendar, Gallardo-Gutiérrez and Partington5] nearly invariant subspaces with finite defect for the backward shift operator on
![]() $H^2(\mathbb {D}).$
This work was further extended to the vector-valued case by Chattopadhyay, Das, and Pradhan in [Reference Chattopadhyay, Das and Pradhan7].
$H^2(\mathbb {D}).$
This work was further extended to the vector-valued case by Chattopadhyay, Das, and Pradhan in [Reference Chattopadhyay, Das and Pradhan7].
Simultaneously, Erard [Reference Erard9] in 2004 introduced the notion of nearly invariant subspaces in the vastly general situation of multiplication operators that are bounded below on reproducing kernel Hilbert spaces. He first deduced a factorization theorem in the general setting and later used it to describe nearly invariant subspaces of the backward shift on general reproducing kernel Hilbert spaces of analytic functions on the open unit disc
![]() $\mathbb {D}$
on which the operator of multiplication with z is well-defined and bounded below. As a particular case, his result also described nearly invariant subspaces of the backward shift on
$\mathbb {D}$
on which the operator of multiplication with z is well-defined and bounded below. As a particular case, his result also described nearly invariant subspaces of the backward shift on
![]() $H^2(\mathbb {D}).$
His description turns out to be the same as Hitt’s. However, since he was working in a much more general setting, his method could not capture two crucial pieces of information about the representation, namely, the norm equality (as it appears in Hitt’s theorem) and the closedness of the backward shift invariant subspaces that appear in the representation. In 2021, Liang and Partington used Erard’s factorization theorem ([Reference Erard9, Theorem 3.2]) to describe nearly invariant subspaces of Dirichlet-type spaces
$H^2(\mathbb {D}).$
His description turns out to be the same as Hitt’s. However, since he was working in a much more general setting, his method could not capture two crucial pieces of information about the representation, namely, the norm equality (as it appears in Hitt’s theorem) and the closedness of the backward shift invariant subspaces that appear in the representation. In 2021, Liang and Partington used Erard’s factorization theorem ([Reference Erard9, Theorem 3.2]) to describe nearly invariant subspaces of Dirichlet-type spaces
![]() $\mathcal {D}_\alpha , \ -1\le \alpha \le 1$
with respect to the operator of multiplication with a finite Blaschke factor. This work of Liang and Partington has been extended to the finite defect setting in 2022 by Chattopadhyay and Das in [Reference Chattopadhyay and Das6].
$\mathcal {D}_\alpha , \ -1\le \alpha \le 1$
with respect to the operator of multiplication with a finite Blaschke factor. This work of Liang and Partington has been extended to the finite defect setting in 2022 by Chattopadhyay and Das in [Reference Chattopadhyay and Das6].
Let
![]() $\mathcal {H}_1$
and
$\mathcal {H}_1$
and
![]() $\mathcal {H}_2$
be two Hilbert spaces with norms
$\mathcal {H}_2$
be two Hilbert spaces with norms
![]() $||\cdot ||_1$
and
$||\cdot ||_1$
and
![]() $||\cdot ||_2,$
respectively. We say
$||\cdot ||_2,$
respectively. We say
![]() $\mathcal {H}_1$
is contractively contained in
$\mathcal {H}_1$
is contractively contained in
![]() $\mathcal {H}_2$
if
$\mathcal {H}_2$
if
![]() $\mathcal {H}_1$
is a vector subspace (not necessarily closed) of
$\mathcal {H}_1$
is a vector subspace (not necessarily closed) of
![]() $\mathcal {H}_2$
and the inclusion map is a contraction, that is,
$\mathcal {H}_2$
and the inclusion map is a contraction, that is,
![]() $||h||_2\le ||h||_1$
for all
$||h||_2\le ||h||_1$
for all
![]() $h\in \mathcal {H}_1. $
In this paper we shall investigate the above-mentioned avenues of research associated with nearly invariant subspaces for contractively contained Hilbert spaces.
$h\in \mathcal {H}_1. $
In this paper we shall investigate the above-mentioned avenues of research associated with nearly invariant subspaces for contractively contained Hilbert spaces.
The organization of the paper is as follows. Section 2 contains definitions and terminologies that will be used throughout the paper. In Section 3, we describe Hilbert spaces that are contractively contained in the Hardy space
![]() $H^2(\mathbb {D}, \mathbb {C}^n)$
and which are nearly invariant under the backward shift operator on
$H^2(\mathbb {D}, \mathbb {C}^n)$
and which are nearly invariant under the backward shift operator on
![]() $H^2(\mathbb {D}, \mathbb {C}^n ).$
Our result (Theorem 3.3) is, in a sense, the best possible generalization-in the setting of de Branges spaces-of Hitt’s theorem (Theorem 1.1) and also its vector-valued generalization by Chalendar et al. (Theorem 3.1). This is so, since the representations obtained in both these theorems can be easily derived from our version once we assume that our general de Branges space is the special case of the scalar valued Hardy space of Hitt or the n-dimensional valued Hardy space of Chalendar et al. At the same time, we show through specific counterexamples that our characterization per se in the general setting of the contractively contained de Branges space cannot be improved. In other words we show that in the conclusion of Theorem 3.3, our inequality between the de Branges space and the Hardy space cannot be improved to an equality (Example 3.5) nor can we conclude in the general case that the backward shift invariant subspace in our description is closed, see (Example 3.6). Afterwards, in Section 4 (Theorem 4.3), we extend a work of Erard from [Reference Erard9, Theorem 5.1] (stated here as Theorem 4.1) to the case of contractively contained Hilbert spaces. Our Theorem 4.3 is in fact also an extension of Liang and Partington’s result ([Reference Liang and Partington12, Theorem 3.4]) that used Erad’s result to describe subspaces of the Dirichlet-type spaces
$H^2(\mathbb {D}, \mathbb {C}^n ).$
Our result (Theorem 3.3) is, in a sense, the best possible generalization-in the setting of de Branges spaces-of Hitt’s theorem (Theorem 1.1) and also its vector-valued generalization by Chalendar et al. (Theorem 3.1). This is so, since the representations obtained in both these theorems can be easily derived from our version once we assume that our general de Branges space is the special case of the scalar valued Hardy space of Hitt or the n-dimensional valued Hardy space of Chalendar et al. At the same time, we show through specific counterexamples that our characterization per se in the general setting of the contractively contained de Branges space cannot be improved. In other words we show that in the conclusion of Theorem 3.3, our inequality between the de Branges space and the Hardy space cannot be improved to an equality (Example 3.5) nor can we conclude in the general case that the backward shift invariant subspace in our description is closed, see (Example 3.6). Afterwards, in Section 4 (Theorem 4.3), we extend a work of Erard from [Reference Erard9, Theorem 5.1] (stated here as Theorem 4.1) to the case of contractively contained Hilbert spaces. Our Theorem 4.3 is in fact also an extension of Liang and Partington’s result ([Reference Liang and Partington12, Theorem 3.4]) that used Erad’s result to describe subspaces of the Dirichlet-type spaces
![]() $\mathcal {D}_{\alpha } \ (0\le \alpha \le 1)$
which are nearly invariant under “division by a finite Blaschke factor”. Lastly, in Section 5, we extend our study from Section 4 to the finite defect setting. Theorem 5.3 is an extension of Chattopadhay and Das’ result [Reference Chattopadhyay and Das6, Theorem 3.9] to multiplication with inner function on general reproducing kernel Hilbert spaces which in turn is a generalization of Liang and Partington’s above-mentioned work to the finite defect setting.
$\mathcal {D}_{\alpha } \ (0\le \alpha \le 1)$
which are nearly invariant under “division by a finite Blaschke factor”. Lastly, in Section 5, we extend our study from Section 4 to the finite defect setting. Theorem 5.3 is an extension of Chattopadhay and Das’ result [Reference Chattopadhyay and Das6, Theorem 3.9] to multiplication with inner function on general reproducing kernel Hilbert spaces which in turn is a generalization of Liang and Partington’s above-mentioned work to the finite defect setting.
2 Terminologies and definitions
Let
![]() $\mathbb {D}$
be the open unit disc in the complex plane
$\mathbb {D}$
be the open unit disc in the complex plane
![]() $\mathbb {C}.$
For a given Hilbert space
$\mathbb {C}.$
For a given Hilbert space
![]() $\mathcal {K},$
let
$\mathcal {K},$
let
![]() $H^2(\mathbb {D}, \mathcal {K})$
denote the familiar Hardy space of
$H^2(\mathbb {D}, \mathcal {K})$
denote the familiar Hardy space of
![]() $\mathcal {K}$
-valued analytic functions on
$\mathcal {K}$
-valued analytic functions on
![]() $\mathbb {D}.$
Recall that
$\mathbb {D}.$
Recall that
 $$ \begin{align*}H^2(\mathbb{D}, \mathcal{K}) = \left \{\sum_{m=0}^\infty A_m z^m : A_m\in \mathcal{K}, \ \sum_{m=0}^\infty ||A_m||^2_{\mathcal{K}}<\infty\right\} \end{align*} $$
$$ \begin{align*}H^2(\mathbb{D}, \mathcal{K}) = \left \{\sum_{m=0}^\infty A_m z^m : A_m\in \mathcal{K}, \ \sum_{m=0}^\infty ||A_m||^2_{\mathcal{K}}<\infty\right\} \end{align*} $$
and it is a Hilbert space with respect to the norm
![]() $||f||^2_{2,\mathcal {K}} = \sum _{m=0}^\infty ||A_m||^2_{\mathcal {K}},$
where
$||f||^2_{2,\mathcal {K}} = \sum _{m=0}^\infty ||A_m||^2_{\mathcal {K}},$
where
![]() $f(z)=\sum _{m=0}^\infty A_mz^m$
belongs to
$f(z)=\sum _{m=0}^\infty A_mz^m$
belongs to
![]() $H^2(\mathbb {D}, \mathcal {K}).$
The Hardy space
$H^2(\mathbb {D}, \mathcal {K}).$
The Hardy space
![]() $H^2(\mathbb {D},\mathbb {C})$
is denoted simply as
$H^2(\mathbb {D},\mathbb {C})$
is denoted simply as
![]() $H^2(\mathbb {D})$
. Note that if
$H^2(\mathbb {D})$
. Note that if
![]() $\{x_i:i\in I\}$
is an orthonormal basis of
$\{x_i:i\in I\}$
is an orthonormal basis of
![]() $\mathcal {K},$
then
$\mathcal {K},$
then
![]() $H^2(\mathbb {D},\mathcal {K})$
can be identified (under an isometric isomorphism) with
$H^2(\mathbb {D},\mathcal {K})$
can be identified (under an isometric isomorphism) with
![]() $\ell ^2$
-direct sum of I copies of
$\ell ^2$
-direct sum of I copies of
![]() $H^2(\mathbb {D}).$
Thus, each
$H^2(\mathbb {D}).$
Thus, each
![]() $f\in H^2(\mathbb {D}, \mathcal {K})$
can be identified with an I-tuple
$f\in H^2(\mathbb {D}, \mathcal {K})$
can be identified with an I-tuple
![]() $(f_i)_{i\in I}$
, where each
$(f_i)_{i\in I}$
, where each
![]() $f_i\in H^2(\mathbb {D})$
and
$f_i\in H^2(\mathbb {D})$
and
![]() $||f||_{2,\mathcal {K}}^2=\sum _{i\in i} ||f_i||_{2,\mathbb {C}}^2.$
Henceforth, for notational convenience, we shall not mention
$||f||_{2,\mathcal {K}}^2=\sum _{i\in i} ||f_i||_{2,\mathbb {C}}^2.$
Henceforth, for notational convenience, we shall not mention
![]() $\mathcal {K}$
in the norm
$\mathcal {K}$
in the norm
![]() $||\cdot ||_{2,\mathcal {K}}$
; instead, we shall write it as
$||\cdot ||_{2,\mathcal {K}}$
; instead, we shall write it as
![]() $||\cdot ||_2$
.
$||\cdot ||_2$
.
The forward shift or simply the shift operator S on
![]() $H^2(\mathbb {D}, \mathcal {K})$
is defined as
$H^2(\mathbb {D}, \mathcal {K})$
is defined as
![]() $Sf(z)=zf(z)$
and it’s adjoint
$Sf(z)=zf(z)$
and it’s adjoint
![]() $S^*$
, known as the backward shift operator, is given by
$S^*$
, known as the backward shift operator, is given by
for
![]() $f\in H^2(\mathbb {D}, \mathcal {K}).$
$f\in H^2(\mathbb {D}, \mathcal {K}).$
In the introduction, we have used the term subspace to refer to a closed subspace, and we shall keep following the same terminology throughout the paper. But very often, in what follows, we shall encounter subspaces that are not necessarily closed; to make them stand out, we shall refer to them as vector subspaces.
Definition 2.1 A vector subspace
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $H^2(\mathbb {D}, \mathcal {K})$
is said to be nearly invariant under the backward shift
$H^2(\mathbb {D}, \mathcal {K})$
is said to be nearly invariant under the backward shift
![]() $S^*$
if
$S^*$
if
![]() $S^*f\in \mathcal {M}$
whenever
$S^*f\in \mathcal {M}$
whenever
![]() $f\in \mathcal {M}$
and
$f\in \mathcal {M}$
and
![]() $f(0)=0.$
$f(0)=0.$
In light of the fact that
![]() $S^*$
is a left inverse of S, the definition of nearly invariant under
$S^*$
is a left inverse of S, the definition of nearly invariant under
![]() $S^*$
is equivalent to saying
$S^*$
is equivalent to saying
![]() $f\in \mathcal {M}$
whenever
$f\in \mathcal {M}$
whenever
![]() $Sf\in \mathcal {M}$
. This motivated Erard in [Reference Erard9] to extend the notion of nearly invariant to the setting of bounded below multiplication operators on reproducing kernel Hilbert spaces. Before giving Erard’s version, first, we provide the following relevant definitions.
$Sf\in \mathcal {M}$
. This motivated Erard in [Reference Erard9] to extend the notion of nearly invariant to the setting of bounded below multiplication operators on reproducing kernel Hilbert spaces. Before giving Erard’s version, first, we provide the following relevant definitions.
Definition 2.2 A set of complex-valued functions on a set X is called a reproducing kernel Hilbert space (RKHS) if
-
1.
 $\mathcal {H}$
is a vector space with respect to pointwise addition and scalar multiplication;
$\mathcal {H}$
is a vector space with respect to pointwise addition and scalar multiplication; -
2.
 $\mathcal {H}$
has a norm with which it is a Hilbert space;
$\mathcal {H}$
has a norm with which it is a Hilbert space; -
3. for each fixed
 $x\in X,$
the point evaluation map
$x\in X,$
the point evaluation map
 $f\mapsto f(x)$
is continuous on
$f\mapsto f(x)$
is continuous on
 $\mathcal {H}.$
$\mathcal {H}.$
Suppose
![]() $\mathcal {H}$
is an RKHS on a set X. Further, suppose
$\mathcal {H}$
is an RKHS on a set X. Further, suppose
![]() $\phi $
is a function on X which multiplies
$\phi $
is a function on X which multiplies
![]() $\mathcal {H}$
into itself. Let
$\mathcal {H}$
into itself. Let
![]() $M_\phi $
denote this multiplication map. Then it can be seen that
$M_\phi $
denote this multiplication map. Then it can be seen that
![]() $M_\phi $
is linear and bounded. The following is Erard’s analog of nearly invariant in the context of a multiplication operator on an RKHS.
$M_\phi $
is linear and bounded. The following is Erard’s analog of nearly invariant in the context of a multiplication operator on an RKHS.
Definition 2.3 Let
![]() $\mathcal {H}$
be an RKHS on a set X and suppose
$\mathcal {H}$
be an RKHS on a set X and suppose
![]() $M_\phi $
is a multiplication operator on
$M_\phi $
is a multiplication operator on
![]() $\mathcal {H}$
which is bounded below. Then, a vector subspace
$\mathcal {H}$
which is bounded below. Then, a vector subspace
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathcal {H}$
is said to be nearly invariant under division by
$\mathcal {H}$
is said to be nearly invariant under division by
![]() $\phi $
if
$\phi $
if
![]() $\phi f\in \mathcal {M}$
implies
$\phi f\in \mathcal {M}$
implies
![]() $f\in \mathcal {M}.$
$f\in \mathcal {M}.$
Note that when
![]() $M_\phi $
is bounded below on
$M_\phi $
is bounded below on
![]() $\mathcal {H},$
then nearly invariant under a left inverse of
$\mathcal {H},$
then nearly invariant under a left inverse of
![]() $\mathcal {M}_\phi ,$
as we discussed above, would mean
$\mathcal {M}_\phi ,$
as we discussed above, would mean
![]() $f\in \mathcal {M}$
whenever
$f\in \mathcal {M}$
whenever
![]() $\phi f\in \mathcal {M}$
which clearly justifies Erard’s choice for the terminology “nearly invariant under division by
$\phi f\in \mathcal {M}$
which clearly justifies Erard’s choice for the terminology “nearly invariant under division by
![]() $\phi $
”. Moreover, the advantage of this terminology is that it brings to light the essence of the definition for multiplication operators. Also, the absence of an explicit mention of a left inverse makes the definition much simpler to follow.
$\phi $
”. Moreover, the advantage of this terminology is that it brings to light the essence of the definition for multiplication operators. Also, the absence of an explicit mention of a left inverse makes the definition much simpler to follow.
The following are straightforward but yet important observations.
Lemma 2.4 Let
![]() $\mathcal {W}$
be an open subset of the complex plane,
$\mathcal {W}$
be an open subset of the complex plane,
![]() $\mathcal {H}$
be an RKHS on
$\mathcal {H}$
be an RKHS on
![]() $\mathcal {W}$
consisting of analytic functions on
$\mathcal {W}$
consisting of analytic functions on
![]() $\mathcal {W},$
and let
$\mathcal {W},$
and let
![]() $\phi $
be an analytic function on
$\phi $
be an analytic function on
![]() $\mathcal {W}$
that multiplies
$\mathcal {W}$
that multiplies
![]() $\mathcal {H}$
into itself. If
$\mathcal {H}$
into itself. If
![]() $\phi $
vanishes at a point in
$\phi $
vanishes at a point in
![]() $\mathcal {W},$
then the only vector subspace of
$\mathcal {W},$
then the only vector subspace of
![]() $\mathcal {H}$
that is nearly invariant under division by
$\mathcal {H}$
that is nearly invariant under division by
![]() $\phi $
and contained in
$\phi $
and contained in
![]() $\phi \mathcal {H}$
is the zero subspace.
$\phi \mathcal {H}$
is the zero subspace.
Proof Suppose,
![]() $\mathcal {M}$
is a vector subspace of
$\mathcal {M}$
is a vector subspace of
![]() $\mathcal {H}$
that is nearly invariant under division by
$\mathcal {H}$
that is nearly invariant under division by
![]() $\phi $
and it is contained in
$\phi $
and it is contained in
![]() $\phi \mathcal {H}$
. Then for
$\phi \mathcal {H}$
. Then for
![]() $h \in \mathcal {M}$
,
$h \in \mathcal {M}$
,
![]() $h=\phi f$
for some
$h=\phi f$
for some
![]() $ f \in \mathcal {H}$
. Since
$ f \in \mathcal {H}$
. Since
![]() $\mathcal {M}$
is nearly invariant under division by
$\mathcal {M}$
is nearly invariant under division by
![]() $\phi $
, therefore
$\phi $
, therefore
![]() $f \in \mathcal {M}$
. Again, using the fact that
$f \in \mathcal {M}$
. Again, using the fact that
![]() $\mathcal {M}$
is contained in
$\mathcal {M}$
is contained in
![]() $\phi \mathcal {H}$
and it is nearly invariant under division by
$\phi \mathcal {H}$
and it is nearly invariant under division by
![]() $\phi $
, we conclude
$\phi $
, we conclude
![]() $f=\phi f_1$
for some
$f=\phi f_1$
for some
![]() $f_1 \in \mathcal {M}.$
Then
$f_1 \in \mathcal {M}.$
Then
![]() $h=\phi ^{2}f_1$
. Continuing in the similar fashion, we obtain that for each
$h=\phi ^{2}f_1$
. Continuing in the similar fashion, we obtain that for each
![]() $n, \ h=\phi ^{n+1}f_n$
, for some
$n, \ h=\phi ^{n+1}f_n$
, for some
![]() $f_n \in \mathcal {M}$
. Now since
$f_n \in \mathcal {M}$
. Now since
![]() $\phi $
has a zero in
$\phi $
has a zero in
![]() $\mathcal {W},$
say at
$\mathcal {W},$
say at
![]() $z_0$
, we deduce that the analytic function h has a zero at
$z_0$
, we deduce that the analytic function h has a zero at
![]() $z_0$
of every order. This implies that
$z_0$
of every order. This implies that
![]() $h=0.$
Hence
$h=0.$
Hence
![]() $\mathcal {M}=\{0\};$
this completes the proof.
$\mathcal {M}=\{0\};$
this completes the proof.
Lemma 2.5 Let
![]() $\mathcal {M}$
be a non-zero Hilbert space contractively contained as a vector subspace in
$\mathcal {M}$
be a non-zero Hilbert space contractively contained as a vector subspace in
![]() $\mathcal {H}.$
If
$\mathcal {H}.$
If
![]() $\mathcal {R}$
is closed in
$\mathcal {R}$
is closed in
![]() $\mathcal {H},$
then
$\mathcal {H},$
then
![]() $\mathcal {M}\cap \mathcal {R}$
is closed in
$\mathcal {M}\cap \mathcal {R}$
is closed in
![]() $\mathcal {M}.$
$\mathcal {M}.$
Proof Let
![]() $\{h_n\}_{n=0}^{\infty }$
be a sequence in
$\{h_n\}_{n=0}^{\infty }$
be a sequence in
![]() $\mathcal {M}\cap \mathcal {R}$
that converges to h in
$\mathcal {M}\cap \mathcal {R}$
that converges to h in
![]() $\mathcal {M}$
. Since
$\mathcal {M}$
. Since
![]() $\mathcal {M}$
is contractively contained in
$\mathcal {M}$
is contractively contained in
![]() $\mathcal {H}$
, therefore
$\mathcal {H}$
, therefore
![]() $\{h_n\}$
converges to h in
$\{h_n\}$
converges to h in
![]() $\mathcal {H}.$
But, each
$\mathcal {H}.$
But, each
![]() $h_n\in \mathcal {R}$
and
$h_n\in \mathcal {R}$
and
![]() $\mathcal {R}$
is closed in
$\mathcal {R}$
is closed in
![]() $\mathcal {H}.$
Therefore,
$\mathcal {H}.$
Therefore,
![]() $h \in \mathcal {R}$
which implies that
$h \in \mathcal {R}$
which implies that
![]() $h \in \mathcal {M}\cap \mathcal {R}$
. Thus
$h \in \mathcal {M}\cap \mathcal {R}$
. Thus
![]() $\mathcal {M}\cap \mathcal {R}$
is closed in
$\mathcal {M}\cap \mathcal {R}$
is closed in
![]() $\mathcal {M}.$
$\mathcal {M}.$
We end this section by recalling a few more terminologies. If
![]() $\phi $
is a bounded analytic function on
$\phi $
is a bounded analytic function on
![]() $\mathbb {D}$
, then it multiplies
$\mathbb {D}$
, then it multiplies
![]() $H^2(\mathbb {D})$
into itself, and in this case, the multiplication operator
$H^2(\mathbb {D})$
into itself, and in this case, the multiplication operator
![]() $M_{\phi }$
is a particular example of a Toeplitz operator which is generally denoted as
$M_{\phi }$
is a particular example of a Toeplitz operator which is generally denoted as
![]() $T_\phi $
. Further, a bounded analytic function on
$T_\phi $
. Further, a bounded analytic function on
![]() $\mathbb {D}$
is said to be an inner function if
$\mathbb {D}$
is said to be an inner function if
![]() $\lim \limits _{r\to 1^{-}}|\phi (re^{it})|=1$
a.e. If
$\lim \limits _{r\to 1^{-}}|\phi (re^{it})|=1$
a.e. If
![]() $\phi $
is an inner function on
$\phi $
is an inner function on
![]() $\mathbb {D}$
and
$\mathbb {D}$
and
![]() $\phi (0)=0,$
then the composition operator, denoted as
$\phi (0)=0,$
then the composition operator, denoted as
![]() $C_\phi $
, is an isometry on
$C_\phi $
, is an isometry on
![]() $H^2(\mathbb {D}).$
Suppose,
$H^2(\mathbb {D}).$
Suppose,
![]() $\mathcal {K}$
is a Hilbert space with an orthonormal basis indexed by a set
$\mathcal {K}$
is a Hilbert space with an orthonormal basis indexed by a set
![]() $I.$
Then, direct sum of
$I.$
Then, direct sum of
![]() $T_\phi $
and
$T_\phi $
and
![]() $C_\phi $
on
$C_\phi $
on
![]() $H^2(\mathbb {D}, \mathcal {K})$
(identified as
$H^2(\mathbb {D}, \mathcal {K})$
(identified as
![]() $\ell ^2$
-direct sum of I-copies of
$\ell ^2$
-direct sum of I-copies of
![]() $H^2(\mathbb {D})$
are again bounded operator which we shall denote again by
$H^2(\mathbb {D})$
are again bounded operator which we shall denote again by
![]() $T_\phi $
and
$T_\phi $
and
![]() $C_\phi $
.
$C_\phi $
.
3 Nearly invariant Brangesian subspaces for the backward shift on vector-valued Hardy spaces
In [Reference Chalendar, Chevrot and Partington4], Chalendar, Chevrot, and Partington extended Hitt’s theorem (Theorem 1.1) to the vector-valued setting. They described subspaces of
![]() $H^2(\mathbb {D}, \mathbb {C}^n)$
that are nearly invariant under the backward shift operator
$H^2(\mathbb {D}, \mathbb {C}^n)$
that are nearly invariant under the backward shift operator
![]() $S^*$
on
$S^*$
on
![]() $H^2(\mathbb {D}, \mathbb {C}^n)$
. In this section, we investigate their result in the de Branges setting. We describe Hilbert spaces contractively contained in
$H^2(\mathbb {D}, \mathbb {C}^n)$
. In this section, we investigate their result in the de Branges setting. We describe Hilbert spaces contractively contained in
![]() $H^2(\mathbb {D}, \mathbb {C}^n)$
and nearly invariant under
$H^2(\mathbb {D}, \mathbb {C}^n)$
and nearly invariant under
![]() $S^*.$
It is crucial to note that we do not assume these vector subspaces to be closed in the Hardy space.
$S^*.$
It is crucial to note that we do not assume these vector subspaces to be closed in the Hardy space.
Before presenting their description, we explain some notations essential to understanding their result and which will also be used throughout this section. Suppose,
![]() $g_1, \dots , g_m$
be
$g_1, \dots , g_m$
be
![]() $\mathbb {C}^n$
-valued functions on
$\mathbb {C}^n$
-valued functions on
![]() $\mathbb {D}.$
Let G denote
$\mathbb {D}.$
Let G denote
![]() $n\times m$
matrix-valued function that maps
$n\times m$
matrix-valued function that maps
![]() $z\in \mathbb {D}$
to
$z\in \mathbb {D}$
to
![]() $n\times m$
matrix with column vectors
$n\times m$
matrix with column vectors
![]() $g_1(z), \dots , g_m(z).$
Now, suppose f is a
$g_1(z), \dots , g_m(z).$
Now, suppose f is a
![]() $\mathbb {C}^m$
-valued function on
$\mathbb {C}^m$
-valued function on
![]() $\mathbb {D}$
. Clearly, we can write
$\mathbb {D}$
. Clearly, we can write
![]() $f=(f_1,\dots , f_m)$
, where
$f=(f_1,\dots , f_m)$
, where
![]() $f_1, \dots , f_m$
are scalar-valued functions on
$f_1, \dots , f_m$
are scalar-valued functions on
![]() $\mathbb {D}$
. Then for each
$\mathbb {D}$
. Then for each
![]() $z\in \mathbb {D},$
the matrix multiplication
$z\in \mathbb {D},$
the matrix multiplication
 $G(z)f(z) =(g_1(z) \cdots g_m(z)) \begin {pmatrix} f_1(z) \\ \vdots \\ f_m(z)\end {pmatrix}=\sum _{i=1}^m f_i(z)g_i(z)$
is well-defined. We shall use
$G(z)f(z) =(g_1(z) \cdots g_m(z)) \begin {pmatrix} f_1(z) \\ \vdots \\ f_m(z)\end {pmatrix}=\sum _{i=1}^m f_i(z)g_i(z)$
is well-defined. We shall use
![]() $Gf$
to denote the function
$Gf$
to denote the function
![]() $z\mapsto G(z)f(z)=\sum _{i=1}^mf_i(z)g_i(z)$
. Clearly, if each
$z\mapsto G(z)f(z)=\sum _{i=1}^mf_i(z)g_i(z)$
. Clearly, if each
![]() $g_i$
and f are analytic on
$g_i$
and f are analytic on
![]() $\mathbb {D}$
, then
$\mathbb {D}$
, then
![]() $Gf$
is also analytic on
$Gf$
is also analytic on
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
Theorem 3.1 ([Reference Chalendar, Chevrot and Partington4, Theorem 4.4]). Let
![]() $\mathcal {F}$
be a nearly
$\mathcal {F}$
be a nearly
![]() $S^*$
-invariant subspace of
$S^*$
-invariant subspace of
![]() $H^2(\mathbb {D}, \mathbb {C}^n)$
and let
$H^2(\mathbb {D}, \mathbb {C}^n)$
and let
![]() $\{g_1, \dots , g_r\}$
be an orthonormal basis of
$\{g_1, \dots , g_r\}$
be an orthonormal basis of
![]() $\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n))$
. Let G be the
$\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n))$
. Let G be the
![]() $n\times r$
matrix-valued function with columns
$n\times r$
matrix-valued function with columns
![]() $g_1, \dots , g_r$
. Then, there exists an isometric mapping
$g_1, \dots , g_r$
. Then, there exists an isometric mapping
where
![]() ${\mathcal {F}}^{'}:=\{f\in H^2(\mathbb {D}, \mathbb {C}^r): \exists \ h\in \mathcal {F}, \ h=Gf\}.$
Moreover,
${\mathcal {F}}^{'}:=\{f\in H^2(\mathbb {D}, \mathbb {C}^r): \exists \ h\in \mathcal {F}, \ h=Gf\}.$
Moreover,
![]() $\mathcal {F}^{'}$
is subspace of
$\mathcal {F}^{'}$
is subspace of
![]() $H^2(\mathbb {D}, \mathbb {C}^r)$
that is
$H^2(\mathbb {D}, \mathbb {C}^r)$
that is
![]() $S^*$
-invariant.
$S^*$
-invariant.
We shall now present the main result (Theorem 3.3) of this section. It is an analog of Theorem 3.1 for the de Branges setting. We start with the following preliminary observation.
Proposition 3.2 Let
![]() $\mathcal {M}$
be a non-zero Hilbert space contractively contained in the Hardy space
$\mathcal {M}$
be a non-zero Hilbert space contractively contained in the Hardy space
![]() $H^2(\mathbb {D}, \mathbb {C}^n).$
Suppose,
$H^2(\mathbb {D}, \mathbb {C}^n).$
Suppose,
![]() $\mathcal {M}$
is nearly invariant under the backward shift on
$\mathcal {M}$
is nearly invariant under the backward shift on
![]() $H^2(\mathbb {D}, \mathbb {C}^n).$
Then,
$H^2(\mathbb {D}, \mathbb {C}^n).$
Then,
![]() $\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n))$
is non-zero and its dimension can be at most n.
$\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n))$
is non-zero and its dimension can be at most n.
Proof First note that since
![]() $\mathcal {M}$
is non-zero, therefore Lemma 2.4 implies that
$\mathcal {M}$
is non-zero, therefore Lemma 2.4 implies that
![]() $\mathcal {M}$
cannot be contained in
$\mathcal {M}$
cannot be contained in
![]() $zH^2(\mathbb {D}, \mathbb {C}^n).$
$zH^2(\mathbb {D}, \mathbb {C}^n).$
Now as
![]() $\mathcal {M}$
is contractively contained in
$\mathcal {M}$
is contractively contained in
![]() $\mathcal {H}^2(\mathbb {D}, \mathbb {C}^n)$
, for each
$\mathcal {H}^2(\mathbb {D}, \mathbb {C}^n)$
, for each
![]() $w\in \mathbb {D},$
the point evaluation map
$w\in \mathbb {D},$
the point evaluation map
![]() $ E_w : \mathcal {M} \longrightarrow \mathbb {C}^n$
given by
$ E_w : \mathcal {M} \longrightarrow \mathbb {C}^n$
given by
![]() $E_w(f)=f(w)$
is bounded. Let
$E_w(f)=f(w)$
is bounded. Let
![]() $\{e_1,\dots , e_n\}$
be the canonical orthonormal basis of
$\{e_1,\dots , e_n\}$
be the canonical orthonormal basis of
![]() $\mathbb {C}^n.$
We claim that the set
$\mathbb {C}^n.$
We claim that the set
![]() $\{ g_i:=E^*_0(e_i) : 1 \le i \le n\}$
spans
$\{ g_i:=E^*_0(e_i) : 1 \le i \le n\}$
spans
![]() $\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n))$
. For any f in
$\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n))$
. For any f in
![]() $\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n)$
,
$\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n)$
,
Thus, each
![]() $g_i$
belongs to
$g_i$
belongs to
![]() $\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n)).$
Further, if
$\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n)).$
Further, if
![]() $f\in \mathcal {M}$
is orthogonal to each
$f\in \mathcal {M}$
is orthogonal to each
![]() $g_i$
. Then
$g_i$
. Then
![]() $f(0)$
is orthogonal to
$f(0)$
is orthogonal to
![]() $e_i$
for each
$e_i$
for each
![]() $1 \le i \le n$
. This forces
$1 \le i \le n$
. This forces
![]() $f(0)=0$
which means
$f(0)=0$
which means
![]() $f \in \mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n)$
. Hence, the set
$f \in \mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n)$
. Hence, the set
![]() $\{g_i: 1\le i\le n\}$
spans
$\{g_i: 1\le i\le n\}$
spans
![]() $\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n))$
. This completes the proof.
$\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n))$
. This completes the proof.
Theorem 3.3 Let
![]() $\mathcal {M}$
be a non-zero Hilbert space contractively contained in
$\mathcal {M}$
be a non-zero Hilbert space contractively contained in
![]() $H^2(\mathbb {D},\mathbb {C}^n).$
Suppose
$H^2(\mathbb {D},\mathbb {C}^n).$
Suppose
![]() $\mathcal {M}$
is nearly invariant under
$\mathcal {M}$
is nearly invariant under
![]() $S^*$
and
$S^*$
and
![]() $\|z h\|_{\mathcal {M}}\ge \|h\|_{\mathcal {M}}$
whenever
$\|z h\|_{\mathcal {M}}\ge \|h\|_{\mathcal {M}}$
whenever
![]() $zh \in \mathcal {M}$
. If
$zh \in \mathcal {M}$
. If
![]() $\{g_1,\dots , g_r\}, \ 1\le r\le n$
, is an orthonormal basis for
$\{g_1,\dots , g_r\}, \ 1\le r\le n$
, is an orthonormal basis for
![]() $\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n)),$
then there exists a vector subspace
$\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n)),$
then there exists a vector subspace
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $H^2(\mathbb {D},\mathbb {C}^r)$
that is
$H^2(\mathbb {D},\mathbb {C}^r)$
that is
![]() $S^*$
-invariant such that
$S^*$
-invariant such that
![]() $\mathcal {M}$
is in one-to-one correspondence with
$\mathcal {M}$
is in one-to-one correspondence with
![]() $\mathcal {N}$
via the linear map
$\mathcal {N}$
via the linear map
where G is the matrix-valued function whose columns are
![]() $g_1, \dots , g_r.$
Moreover, for each
$g_1, \dots , g_r.$
Moreover, for each
![]() $h\in \mathcal {M}, \ ||h||_{\mathcal {M}} \ge ||f||_2,$
where
$h\in \mathcal {M}, \ ||h||_{\mathcal {M}} \ge ||f||_2,$
where
![]() $h=Gf$
with
$h=Gf$
with
![]() $f\in \mathcal {N}.$
$f\in \mathcal {N}.$
Proof Firstly, using Proposition 3.2,
![]() $\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n )$
is closed in
$\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n )$
is closed in
![]() $\mathcal {M}, \ \mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n))$
is non-zero, and dimension of
$\mathcal {M}, \ \mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n))$
is non-zero, and dimension of
![]() $\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n))$
is at most
$\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n))$
is at most
![]() $n.$
Let P denote the orthogonal projection of
$n.$
Let P denote the orthogonal projection of
![]() $\mathcal {M}$
onto
$\mathcal {M}$
onto
![]() $\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n)$
and let
$\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n)$
and let
![]() $Q=I_{\mathcal {M}}-P.$
$Q=I_{\mathcal {M}}-P.$
Now since
![]() $\mathcal {M}$
is nearly invariant under
$\mathcal {M}$
is nearly invariant under
![]() $S^*,$
therefore
$S^*,$
therefore
![]() $S^*P$
is a well-defined linear mapping of
$S^*P$
is a well-defined linear mapping of
![]() $\mathcal {M}$
into itself. Let us define
$\mathcal {M}$
into itself. Let us define
Then the hypothesis
![]() $||f||_{\mathcal {M}} \le ||zf||_{\mathcal {M}}$
whenever
$||f||_{\mathcal {M}} \le ||zf||_{\mathcal {M}}$
whenever
![]() $zf\in \mathcal {M}$
implies that R is a contraction on
$zf\in \mathcal {M}$
implies that R is a contraction on
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Fix any
![]() $h\in \mathcal {M}$
. We decompose it as
$h\in \mathcal {M}$
. We decompose it as
![]() $h=Qh+Ph.$
Note that
$h=Qh+Ph.$
Note that
![]() $Ph\in zH^2(\mathbb {D}, \mathbb {C}^n).$
This means
$Ph\in zH^2(\mathbb {D}, \mathbb {C}^n).$
This means
![]() $Ph=SS^*Ph=SRh.$
Then, we have
$Ph=SS^*Ph=SRh.$
Then, we have
and
As
![]() $\{g_1,\dots , g_r\}$
is an orthonormal basis for
$\{g_1,\dots , g_r\}$
is an orthonormal basis for
![]() $\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n)),$
therefore we can write
$\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}, \mathbb {C}^n)),$
therefore we can write
where
![]() $a_{01}, \dots , a_{0r}$
are scalars,
$a_{01}, \dots , a_{0r}$
are scalars,
 $A_0=\begin {pmatrix} a_{01} \\ \vdots \\ a_{0r}\end {pmatrix} \in \mathbb {C}^r$
, and G is the
$A_0=\begin {pmatrix} a_{01} \\ \vdots \\ a_{0r}\end {pmatrix} \in \mathbb {C}^r$
, and G is the
![]() $n\times r$
matrix-vaued function on
$n\times r$
matrix-vaued function on
![]() $\mathbb {D}$
with columns
$\mathbb {D}$
with columns
![]() $g_1, \dots , g_r$
. Thus,
$g_1, \dots , g_r$
. Thus,
Further,
![]() $||Qh||^2_{\mathcal {M}}=\sum _{i=1}^r |a_{0i}|^2=||A_0||^2_{\mathbb {C}^r}$
. Thus, Inequality (3.2) yields
$||Qh||^2_{\mathcal {M}}=\sum _{i=1}^r |a_{0i}|^2=||A_0||^2_{\mathbb {C}^r}$
. Thus, Inequality (3.2) yields
Now
![]() $Rh\in \mathcal {M}.$
Then repeating the above arguments for
$Rh\in \mathcal {M}.$
Then repeating the above arguments for
![]() $Rh$
in place of h, we obtain a vector
$Rh$
in place of h, we obtain a vector
![]() $A_1\in \mathbb {C}^r$
such that
$A_1\in \mathbb {C}^r$
such that
and
![]() $||A_1||^2_{\mathbb {C}^r}+||R^2h||^2_{\mathcal {M}}\le ||Rh||^2_{\mathcal {M}}.$
Then, Equations (3.3) and (3.4) yields
$||A_1||^2_{\mathbb {C}^r}+||R^2h||^2_{\mathcal {M}}\le ||Rh||^2_{\mathcal {M}}.$
Then, Equations (3.3) and (3.4) yields
and
Again,
![]() $R^2h\in \mathcal {M}.$
Continuing as above, we obtain a sequence
$R^2h\in \mathcal {M}.$
Continuing as above, we obtain a sequence
![]() $\{A_n\}$
in
$\{A_n\}$
in
![]() $\mathbb {C}^r$
such that for each postive integer m
$\mathbb {C}^r$
such that for each postive integer m
and
 $$ \begin{align} \sum_{i=0}^m ||A_i||^2_{\mathbb{C}^r} + ||R^{m+1}h||_{\mathcal{M}}^2\le ||h||_{\mathcal{M}}^2. \end{align} $$
$$ \begin{align} \sum_{i=0}^m ||A_i||^2_{\mathbb{C}^r} + ||R^{m+1}h||_{\mathcal{M}}^2\le ||h||_{\mathcal{M}}^2. \end{align} $$
The Inequality (3.8) establishes that
 $$ \begin{align*}\sum_{n=0}^{\infty}\|A_n\|^2_{\mathbb{C}^r} < \infty. \end{align*} $$
$$ \begin{align*}\sum_{n=0}^{\infty}\|A_n\|^2_{\mathbb{C}^r} < \infty. \end{align*} $$
Thus,
 $$ \begin{align*}f(z)=\sum_{m=0}^{\infty}A_mz^m \end{align*} $$
$$ \begin{align*}f(z)=\sum_{m=0}^{\infty}A_mz^m \end{align*} $$
belongs to
![]() $H^2(\mathbb {D},\mathbb {C}^r)$
.
$H^2(\mathbb {D},\mathbb {C}^r)$
.
Clearly,
![]() $Gf$
is analytic on
$Gf$
is analytic on
![]() $\mathbb {D}.$
Now comparing the coefficient of
$\mathbb {D}.$
Now comparing the coefficient of
![]() $z^m$
in h,
$z^m$
in h,
![]() $Gf$
, and using Equation (3.7), we conclude,
$Gf$
, and using Equation (3.7), we conclude,
![]() $h=Gf.$
Also, using Equation (3.8),
$h=Gf.$
Also, using Equation (3.8),
Hence, for each
![]() $h\in \mathcal {M}$
there exists an
$h\in \mathcal {M}$
there exists an
![]() $f\in H^2(\mathbb {D}, \mathbb {C}^r)$
such that
$f\in H^2(\mathbb {D}, \mathbb {C}^r)$
such that
![]() $h=G f$
and
$h=G f$
and
![]() $||f||_2\le ||h||_{\mathcal {M}}.$
$||f||_2\le ||h||_{\mathcal {M}}.$
Let
![]() $\mathcal {N}=\{f\in H^2(\mathbb {D}, \mathbb {C}^r): Gf\in \mathcal {M}\}.$
Then,
$\mathcal {N}=\{f\in H^2(\mathbb {D}, \mathbb {C}^r): Gf\in \mathcal {M}\}.$
Then,
![]() $\mathcal {N}$
is a vector subspace of
$\mathcal {N}$
is a vector subspace of
![]() $H^2(\mathbb {D}, \mathbb {C}^r)$
. Clearly, the mapping
$H^2(\mathbb {D}, \mathbb {C}^r)$
. Clearly, the mapping
![]() $\mathcal {G}:\mathcal {N} \to \mathcal {M}$
given by
$\mathcal {G}:\mathcal {N} \to \mathcal {M}$
given by
![]() $\mathcal {G}(f)=Gf$
is a well-defined surjective linear map. To show it is one-to-one, let
$\mathcal {G}(f)=Gf$
is a well-defined surjective linear map. To show it is one-to-one, let
![]() $Gf=0.$
Suppose,
$Gf=0.$
Suppose,
![]() $f(z)=\sum _{m=0}^\infty A_mz^m.$
Write
$f(z)=\sum _{m=0}^\infty A_mz^m.$
Write
![]() $f=A_0+zf_1,$
where
$f=A_0+zf_1,$
where
![]() $f_1(z)=\sum _{m=0}^\infty A_{m+1}z^m.$
Then
$f_1(z)=\sum _{m=0}^\infty A_{m+1}z^m.$
Then
![]() $Gf=GA_0+G(zf_1)$
and
$Gf=GA_0+G(zf_1)$
and
![]() $zGf_1\in \mathcal {M}\cap zH^2(\mathbb {D},\mathbb {C}^n).$
This implies that
$zGf_1\in \mathcal {M}\cap zH^2(\mathbb {D},\mathbb {C}^n).$
This implies that
![]() $GA_0=Q(Gf)=0$
, which further implies that
$GA_0=Q(Gf)=0$
, which further implies that
![]() $A_0=0$
; hence
$A_0=0$
; hence
![]() $f=zf_1.$
Thus,
$f=zf_1.$
Thus,
![]() $Gf_1=0. $
Continuing in this way, we can show that
$Gf_1=0. $
Continuing in this way, we can show that
![]() $A_k=0$
for all
$A_k=0$
for all
![]() $k.$
Hence,
$k.$
Hence,
![]() $f=0.$
Thus
$f=0.$
Thus
![]() $\mathcal {G}$
is one-to-one.
$\mathcal {G}$
is one-to-one.
Finally, we shall show that
![]() $\mathcal {N}$
is invariant under
$\mathcal {N}$
is invariant under
![]() $S^*.$
Let
$S^*.$
Let
![]() $f=\sum _{m=0}^\infty A_m z^m\in \mathcal {N}.$
Then, there exists an
$f=\sum _{m=0}^\infty A_m z^m\in \mathcal {N}.$
Then, there exists an
![]() $h\in \mathcal {M}$
such that
$h\in \mathcal {M}$
such that
![]() $h=Gf$
. Now,
$h=Gf$
. Now,
But
![]() $Q (Gf)=GA_0.$
Therefore,
$Q (Gf)=GA_0.$
Therefore,
which implies
 $$ \begin{align*}SR(Gf)=G(f-A_0)=G \Bigg(\sum_{k=1}^{\infty}A_k z^{k} \Bigg), \end{align*} $$
$$ \begin{align*}SR(Gf)=G(f-A_0)=G \Bigg(\sum_{k=1}^{\infty}A_k z^{k} \Bigg), \end{align*} $$
and hence
 $$ \begin{align*}R(Gf)=G\Bigg(\sum_{k=1}^{\infty}A_k z^{k-1}\Bigg)=G\Bigg(S^*\Bigg(\sum_{k=0}^{\infty}A_k z^{k}\Bigg)\Bigg)=G(S^*f). \end{align*} $$
$$ \begin{align*}R(Gf)=G\Bigg(\sum_{k=1}^{\infty}A_k z^{k-1}\Bigg)=G\Bigg(S^*\Bigg(\sum_{k=0}^{\infty}A_k z^{k}\Bigg)\Bigg)=G(S^*f). \end{align*} $$
Since
![]() $R(Gf) \in \mathcal {M}$
, therefore by definition,
$R(Gf) \in \mathcal {M}$
, therefore by definition,
![]() $S^*f\in \mathcal {N}$
. Hence
$S^*f\in \mathcal {N}$
. Hence
![]() $\mathcal {N}$
is invariant under
$\mathcal {N}$
is invariant under
![]() $S^*$
. This completes the proof.
$S^*$
. This completes the proof.
Remark 3.4 Note that the Hitt’s description of a nearly
![]() $S^*$
-invariant subspace of
$S^*$
-invariant subspace of
![]() $H^2(\mathbb {D})$
(Theorem 1.1) as well as it’s vectorial generalization (Theorem 3.1) both have three parts to them, namely, the representation in terms of
$H^2(\mathbb {D})$
(Theorem 1.1) as well as it’s vectorial generalization (Theorem 3.1) both have three parts to them, namely, the representation in terms of
![]() $S^*$
-invariant subspace, the norm preservation between nearly
$S^*$
-invariant subspace, the norm preservation between nearly
![]() $S^*$
-invariant subspace and the corresponding
$S^*$
-invariant subspace and the corresponding
![]() $S^*$
-invariant subspace, and the closedness of the
$S^*$
-invariant subspace, and the closedness of the
![]() $S^*$
-invariant subspace. Now the description (Theorem 3.3) we obtain for our setting does gives a representation that is similar to the one given in Theorem 1.1 for the scalar case and Theorem 3.1 for the vector case, but our description in the general case neither guarantees the preservation of norm nor does it guarantees the closedness of the
$S^*$
-invariant subspace. Now the description (Theorem 3.3) we obtain for our setting does gives a representation that is similar to the one given in Theorem 1.1 for the scalar case and Theorem 3.1 for the vector case, but our description in the general case neither guarantees the preservation of norm nor does it guarantees the closedness of the
![]() $S^*$
-invariant vector subspace. Interestingly, with the help of the following two examples we show that either of these can’t be promised for our setting in general.
$S^*$
-invariant vector subspace. Interestingly, with the help of the following two examples we show that either of these can’t be promised for our setting in general.
Example 3.5 (Failure of equality of norms). Let
![]() $\mathcal {M}=span\{1+z,z+z^2\}$
and
$\mathcal {M}=span\{1+z,z+z^2\}$
and
![]() $\mathcal {U} : H^2(\mathbb {D}) \longrightarrow H^2(\mathbb {D})$
be the linear operator given by
$\mathcal {U} : H^2(\mathbb {D}) \longrightarrow H^2(\mathbb {D})$
be the linear operator given by
Define a norm
![]() $\|.\|_{\mathcal {M}}$
on
$\|.\|_{\mathcal {M}}$
on
![]() $\mathcal {M}$
by
$\mathcal {M}$
by
Then
![]() $\mathcal {M}$
equipped with norm
$\mathcal {M}$
equipped with norm
![]() $\|\cdot \|_{\mathcal {M}}$
is a Hilbert space contractively contained in
$\|\cdot \|_{\mathcal {M}}$
is a Hilbert space contractively contained in
![]() $H^2(\mathbb {D})$
that is nearly
$H^2(\mathbb {D})$
that is nearly
![]() $S^*$
-invariant.
$S^*$
-invariant.
Clearly,
![]() $\mathcal {M}\cap zH^2(\mathbb {D})=span\{z+z^2\}.$
Let
$\mathcal {M}\cap zH^2(\mathbb {D})=span\{z+z^2\}.$
Let
![]() $f\in \mathcal {M}\cap zH^2(\mathbb {D}).$
Then
$f\in \mathcal {M}\cap zH^2(\mathbb {D}).$
Then
![]() $f=\alpha (z+z^2)$
for some scalar
$f=\alpha (z+z^2)$
for some scalar
![]() $\alpha $
and
$\alpha $
and
![]() $||S^*f||_{\mathcal {M}}=|\alpha ||\mathcal {U}(1+z)||_2=|\alpha |\sqrt {3}.$
On the other hand,
$||S^*f||_{\mathcal {M}}=|\alpha ||\mathcal {U}(1+z)||_2=|\alpha |\sqrt {3}.$
On the other hand,
![]() $||f||_{\mathcal {M}}=|\alpha | ||\mathcal {U}(z+z^2)||_{\mathcal {M}}=|\alpha |2.$
Therefore,
$||f||_{\mathcal {M}}=|\alpha | ||\mathcal {U}(z+z^2)||_{\mathcal {M}}=|\alpha |2.$
Therefore,
![]() $||S^*(f)||_{\mathcal {M}}\le ||f||_{\mathcal {M}}$
for each
$||S^*(f)||_{\mathcal {M}}\le ||f||_{\mathcal {M}}$
for each
![]() $f\in \mathcal {M}\cap zH^2(\mathbb {D})$
which simply means that
$f\in \mathcal {M}\cap zH^2(\mathbb {D})$
which simply means that
![]() $||zh||_{\mathcal {M}}\ge ||h||_{\mathcal {M}}$
whenever
$||zh||_{\mathcal {M}}\ge ||h||_{\mathcal {M}}$
whenever
![]() $zh\in \mathcal {M}.$
Thus,
$zh\in \mathcal {M}.$
Thus,
![]() $\mathcal {M}$
satisfies the hypotheses of Theorem 3.3.
$\mathcal {M}$
satisfies the hypotheses of Theorem 3.3.
Now we can verify that
where
![]() $g(z)=\frac {(z-2)(z+1)}{2\sqrt {2}}$
and
$g(z)=\frac {(z-2)(z+1)}{2\sqrt {2}}$
and
![]() $||g||_{\mathcal {M}}=1.$
$||g||_{\mathcal {M}}=1.$
Then using Theorem 3.3, there exists a
![]() $S^*$
-invariant vector subspace
$S^*$
-invariant vector subspace
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $H^2(\mathbb {D})$
such that
$H^2(\mathbb {D})$
such that
![]() $\mathcal {M}=g\mathcal {N}.$
$\mathcal {M}=g\mathcal {N}.$
For
![]() $1+z \in \mathcal {M}$
, we have
$1+z \in \mathcal {M}$
, we have
![]() $1+z=g\frac {2\sqrt {2}}{z-2}$
. Therefore,
$1+z=g\frac {2\sqrt {2}}{z-2}$
. Therefore,
![]() $f=\frac {2\sqrt {2}}{z-2}\in \mathcal {N}$
. Notice that
$f=\frac {2\sqrt {2}}{z-2}\in \mathcal {N}$
. Notice that
 $$ \begin{align*} \|z+1\|^2_{\mathcal{M}} &=\|\sqrt{2}z+1\|_2^2\\ &=3 \end{align*} $$
$$ \begin{align*} \|z+1\|^2_{\mathcal{M}} &=\|\sqrt{2}z+1\|_2^2\\ &=3 \end{align*} $$
and
 $$ \begin{align*} \|f\|_2^2&=\Big\|\frac{2\sqrt{2}}{z-2}\Big\|_2^2\\ &= 8\Big\|\frac{1}{z-2}\Big\|_2^2\\ &= \frac{8}{3}. \end{align*} $$
$$ \begin{align*} \|f\|_2^2&=\Big\|\frac{2\sqrt{2}}{z-2}\Big\|_2^2\\ &= 8\Big\|\frac{1}{z-2}\Big\|_2^2\\ &= \frac{8}{3}. \end{align*} $$
Hence,
![]() $1+z=gf$
and
$1+z=gf$
and
![]() $\|1+z|\|_{\mathcal {M}}>\|f\|_2.$
$\|1+z|\|_{\mathcal {M}}>\|f\|_2.$
Example 3.6 (Failure of the closedness). Let
![]() $\mathcal {D}$
denote the classical Dirichlet space consisting of analytic functions on the unit disc
$\mathcal {D}$
denote the classical Dirichlet space consisting of analytic functions on the unit disc
![]() $\mathbb {D}$
with the norm
$\mathbb {D}$
with the norm
![]() $||f||_{\mathcal {D}}^2 = \sum _{i=0}^\infty |a_i|^2(i+1)$
for
$||f||_{\mathcal {D}}^2 = \sum _{i=0}^\infty |a_i|^2(i+1)$
for
![]() $f(z)=\sum _{i=0}^\infty a_iz^i\in \mathcal {D}.$
Recall that
$f(z)=\sum _{i=0}^\infty a_iz^i\in \mathcal {D}.$
Recall that
![]() $\mathcal {D}$
is a Hilbert space contractively contained in
$\mathcal {D}$
is a Hilbert space contractively contained in
![]() $H^2(\mathbb {D}),$
and it is not closed in
$H^2(\mathbb {D}),$
and it is not closed in
![]() $H^2(\mathbb {D}).$
$H^2(\mathbb {D}).$
Let
![]() $\theta $
be a bounded analytic function on
$\theta $
be a bounded analytic function on
![]() $\mathbb {D}$
with
$\mathbb {D}$
with
![]() $||\theta ||_\infty =1$
and
$||\theta ||_\infty =1$
and
![]() $\theta (0)>0.$
Set
$\theta (0)>0.$
Set
and define
![]() $||\theta f||_{\mathcal {M}}=||f||_{\mathcal {D}}.$
Clearly,
$||\theta f||_{\mathcal {M}}=||f||_{\mathcal {D}}.$
Clearly,
![]() $\mathcal {M}$
is a vector subspace of
$\mathcal {M}$
is a vector subspace of
![]() $H^2(\mathbb {D}), ||\cdot ||_{\mathcal {M}}$
a norm on
$H^2(\mathbb {D}), ||\cdot ||_{\mathcal {M}}$
a norm on
![]() $\mathcal {M}$
with respect to which
$\mathcal {M}$
with respect to which
![]() $\mathcal {M}$
becomes a Hilbert space contractively contained in
$\mathcal {M}$
becomes a Hilbert space contractively contained in
![]() $H^2(\mathbb {D}).$
$H^2(\mathbb {D}).$
Let,
![]() $f\in \mathcal {M}\cap zH^2(\mathbb {D}).$
Then,
$f\in \mathcal {M}\cap zH^2(\mathbb {D}).$
Then,
![]() $f=\theta h$
for some
$f=\theta h$
for some
![]() $h\in \mathcal {D}$
and
$h\in \mathcal {D}$
and
![]() $f(0)=0.$
Thus,
$f(0)=0.$
Thus,
![]() $h(0)=0$
because
$h(0)=0$
because
![]() $\theta (0)>0.$
This implies that
$\theta (0)>0.$
This implies that
![]() $h=zh_1$
for some
$h=zh_1$
for some
![]() $h_1\in H^2(\mathbb {D}).$
But
$h_1\in H^2(\mathbb {D}).$
But
![]() $zh_1\in \mathcal {D}$
implies
$zh_1\in \mathcal {D}$
implies
![]() $h_1\in \mathcal {D}$
and
$h_1\in \mathcal {D}$
and
![]() $||zh_1||_{\mathcal {D}}\ge ||h_1||_{\mathcal {D}}.$
Therefore,
$||zh_1||_{\mathcal {D}}\ge ||h_1||_{\mathcal {D}}.$
Therefore,
![]() $S^*(f)=\theta h_1\in \mathcal {M}$
and
$S^*(f)=\theta h_1\in \mathcal {M}$
and
![]() $||S^*f||_{\mathcal {M}}=||h_1||_{\mathcal {D}}\le ||zh_1||_{\mathcal {D}} = ||f||_{\mathcal {M}}.$
This means
$||S^*f||_{\mathcal {M}}=||h_1||_{\mathcal {D}}\le ||zh_1||_{\mathcal {D}} = ||f||_{\mathcal {M}}.$
This means
![]() $\mathcal {M}$
is nearly
$\mathcal {M}$
is nearly
![]() $S^*$
-invariant and
$S^*$
-invariant and
![]() $||zg||_{\mathcal {M}}\ge ||g||_{\mathcal {M}}$
whenever
$||zg||_{\mathcal {M}}\ge ||g||_{\mathcal {M}}$
whenever
![]() $zg\in \mathcal {M}.$
Hence,
$zg\in \mathcal {M}.$
Hence,
![]() $\mathcal {M}$
satisfies the hypotheses of Theorem 3.3. Note that
$\mathcal {M}$
satisfies the hypotheses of Theorem 3.3. Note that
![]() $\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}))=span\{\theta \}.$
Therefore, there exists an
$\mathcal {M}\ominus (\mathcal {M}\cap zH^2(\mathbb {D}))=span\{\theta \}.$
Therefore, there exists an
![]() $S^*$
-invariant vector subspace
$S^*$
-invariant vector subspace
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $H^2(\mathbb {D})$
such that
$H^2(\mathbb {D})$
such that
![]() $\mathcal {M}=\theta \mathcal {N}.$
But this simply means
$\mathcal {M}=\theta \mathcal {N}.$
But this simply means
![]() $\mathcal {N}$
equals
$\mathcal {N}$
equals
![]() $\mathcal {D}$
, which is not closed in
$\mathcal {D}$
, which is not closed in
![]() $H^2(\mathbb {D}).$
Hence, this example shows that the
$H^2(\mathbb {D}).$
Hence, this example shows that the
![]() $S^*$
-invariant vector subspace we obtain in the representation given by Theorem 3.3 may not be closed.
$S^*$
-invariant vector subspace we obtain in the representation given by Theorem 3.3 may not be closed.
4 Nearly invariant Brangesian subspaces related to multiplication operators on reproducing kernel Hilbert spaces
In [Reference Erard9], Erard extended the study of nearly invariant subspaces on
![]() $H^2(\mathbb {D})$
to reproducing kernel Hilbert spaces.
$H^2(\mathbb {D})$
to reproducing kernel Hilbert spaces.
Theorem 4.1 (Erard [Reference Erard9, Theorem 5.1]). Let
![]() $\mathcal {H}$
be an RKHS consisting of complex-valued analytic functions on
$\mathcal {H}$
be an RKHS consisting of complex-valued analytic functions on
![]() $\mathbb {D}$
on which multiplication with z is well-defined with dimension of
$\mathbb {D}$
on which multiplication with z is well-defined with dimension of
![]() $\mathcal {H}\ominus z\mathcal {H}$
equals
$\mathcal {H}\ominus z\mathcal {H}$
equals
![]() $1$
and
$1$
and
![]() $||h||_{\mathcal {H}}\le ||zh||_{\mathcal {H}}$
for all
$||h||_{\mathcal {H}}\le ||zh||_{\mathcal {H}}$
for all
![]() $h\in \mathcal {H}.$
Assume also that there exists
$h\in \mathcal {H}.$
Assume also that there exists
![]() $f\in \mathcal {H}$
with
$f\in \mathcal {H}$
with
![]() $f(0)\ne 0.$
Let
$f(0)\ne 0.$
Let
![]() $\mathcal {M}$
be a non-zero subspace of
$\mathcal {M}$
be a non-zero subspace of
![]() $\mathcal {H,}$
which is nearly invariant under the backward shift. Let g be any unit vector of
$\mathcal {H,}$
which is nearly invariant under the backward shift. Let g be any unit vector of
![]() $\mathcal {M}\ominus (\mathcal {M}\cap z\mathcal {H}).$
Then, there exists a linear subspace
$\mathcal {M}\ominus (\mathcal {M}\cap z\mathcal {H}).$
Then, there exists a linear subspace
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $H^2(\mathbb {D})$
such that
$H^2(\mathbb {D})$
such that
 $$ \begin{align*}\mathcal{M}= g\mathcal{N} \ \ \mathrm{and} \ ||h||_{\mathcal{H}}\ge ||\frac{h}{g}||_2. \end{align*} $$
$$ \begin{align*}\mathcal{M}= g\mathcal{N} \ \ \mathrm{and} \ ||h||_{\mathcal{H}}\ge ||\frac{h}{g}||_2. \end{align*} $$
Besides,
![]() $\mathcal {N}$
is invariant under the backward shift and
$\mathcal {N}$
is invariant under the backward shift and
![]() $g(0)\ne 0.$
$g(0)\ne 0.$
Our main result (Theorem 4.3) of this section generalizes Erard’s Theorem. We describe Hilbert spaces that are contractively contained in an RKHS of analytic functions on the unit disc which are nearly invariant under division by an inner function. So, in our result, subspaces have been replaced with contractively contained Hilbert spaces and multiplication with z has been replaced with an inner function.
Before proceeding further, we would like to compare Erard’s theorem with Hitt’s. Erard’s theorem replaces
![]() $H^2(\mathbb {D})$
by a much general RKHS, and also, instead of assuming
$H^2(\mathbb {D})$
by a much general RKHS, and also, instead of assuming
![]() $M_z$
to be an isometry, it only assumes it to be bounded below. However, the drawback of Erard’s theorem is that although the representation of a nearly
$M_z$
to be an isometry, it only assumes it to be bounded below. However, the drawback of Erard’s theorem is that although the representation of a nearly
![]() $S^*$
-invariant subspace when
$S^*$
-invariant subspace when
![]() $\mathcal {H}=H^2(\mathbb {D})$
is very similar to what Hitt’s theorem gives, it does not infer the correspondence between a nearly
$\mathcal {H}=H^2(\mathbb {D})$
is very similar to what Hitt’s theorem gives, it does not infer the correspondence between a nearly
![]() $S^*$
-invariant subspace and the corresponding
$S^*$
-invariant subspace and the corresponding
![]() $S^*$
-invariant vector subspace to be an isometry, and in fact, it doesn’t even guarantee the closedness of the
$S^*$
-invariant vector subspace to be an isometry, and in fact, it doesn’t even guarantee the closedness of the
![]() $S^*$
-invariant vector subspace.
$S^*$
-invariant vector subspace.
Interestingly, we can deduce our Theorem 3.3 (the scalar case) as a corollary from Erard’s Theorem without missing any detail because we have shown, with Examples 3.5 and 3.6, that the two features of the description of a nearly
![]() $S^*$
-invariant subspaces that Erard’s theorem misses do not hold for our setting in general.
$S^*$
-invariant subspaces that Erard’s theorem misses do not hold for our setting in general.
We first prove the following analog of Lemma 2.1 from [Reference Erard9] that played a pivotal role in proving Erard’s Theorem. Indeed, we have proved this result (in disguise) within the proof of Theorem 3.3, and we need it again for Theorem 4.3. We feel that it is a crucial observation and is interesting in its own right; so, we are proving it here as a separate result.
Lemma 4.2 Let T be a bounded operator on a Hilbert space
![]() $\mathcal {H}$
such that
$\mathcal {H}$
such that
![]() $\|Th\|_{\mathcal {H}}\ge \|h\|_{\mathcal {H}}$
for all h in
$\|Th\|_{\mathcal {H}}\ge \|h\|_{\mathcal {H}}$
for all h in
![]() $\mathcal {H}$
. Let
$\mathcal {H}$
. Let
![]() $\mathcal {M}$
be a Hilbert space contractively contained in
$\mathcal {M}$
be a Hilbert space contractively contained in
![]() $\mathcal {H}$
such that
$\mathcal {H}$
such that
![]() $h\in \mathcal {M}$
whenever
$h\in \mathcal {M}$
whenever
![]() $Th\in \mathcal {M}$
and
$Th\in \mathcal {M}$
and
![]() $\|Th\|_{\mathcal {M}}\ge \|h\|_{\mathcal {M}}$
. If P denotes the orthogonal projection of
$\|Th\|_{\mathcal {M}}\ge \|h\|_{\mathcal {M}}$
. If P denotes the orthogonal projection of
![]() $\mathcal {M}$
onto
$\mathcal {M}$
onto
![]() $\mathcal {M}\cap T{\mathcal {H}}$
and
$\mathcal {M}\cap T{\mathcal {H}}$
and
![]() $Q= I_{\mathcal {M}}- P,$
then
$Q= I_{\mathcal {M}}- P,$
then
![]() $R:= (TT^*)^{-1}T^*P$
is a well-defined contraction on
$R:= (TT^*)^{-1}T^*P$
is a well-defined contraction on
![]() $\mathcal {M}$
, and for every positive integer m, we can decompose each
$\mathcal {M}$
, and for every positive integer m, we can decompose each
![]() $h\in \mathcal {M}$
as
$h\in \mathcal {M}$
as
 $$ \begin{align*}h=\sum_{k=0}^{m}T^kQR^kh + T^{m+1}R^{m+1}h \end{align*} $$
$$ \begin{align*}h=\sum_{k=0}^{m}T^kQR^kh + T^{m+1}R^{m+1}h \end{align*} $$
and
 $$ \begin{align*}\|h\|^2_{\mathcal{M}}\ge \sum_{k=0}^m\|QR^kh\|^2_{\mathcal{M}}. \end{align*} $$
$$ \begin{align*}\|h\|^2_{\mathcal{M}}\ge \sum_{k=0}^m\|QR^kh\|^2_{\mathcal{M}}. \end{align*} $$
Proof Let
![]() $h\in \mathcal {M}.$
Then
$h\in \mathcal {M}.$
Then
 $$ \begin{align*} TRh&=T(TT^*)^{-1}T^*P(h)\\ &=T(TT^*)^{-1}T^*Th_0 \ \ (Ph =T h_0 \text{for some} \ h_0\in \mathcal{H})\\ &=Th_0\\ &=P(h) \end{align*} $$
$$ \begin{align*} TRh&=T(TT^*)^{-1}T^*P(h)\\ &=T(TT^*)^{-1}T^*Th_0 \ \ (Ph =T h_0 \text{for some} \ h_0\in \mathcal{H})\\ &=Th_0\\ &=P(h) \end{align*} $$
This shows
![]() $TRh\in \mathcal {M}$
, but then
$TRh\in \mathcal {M}$
, but then
![]() $Rh\in \mathcal {M}$
and
$Rh\in \mathcal {M}$
and
![]() $||TRh||_{\mathcal {M}}\ge ||Rh||_{\mathcal {M}}.$
Thus,
$||TRh||_{\mathcal {M}}\ge ||Rh||_{\mathcal {M}}.$
Thus,
![]() $||Rh||_{\mathcal {M}}\le ||TRh||_{\mathcal {M}}= ||Ph||_{\mathcal {M}}\le ||h||_{\mathcal {M}}$
. Therefore, R is a well-defined contraction on
$||Rh||_{\mathcal {M}}\le ||TRh||_{\mathcal {M}}= ||Ph||_{\mathcal {M}}\le ||h||_{\mathcal {M}}$
. Therefore, R is a well-defined contraction on
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Again, let h in
![]() $\mathcal {M}$
and decompose it as
$\mathcal {M}$
and decompose it as
Then
Now
![]() $Rh \in \mathcal {M}$
. Thus,
$Rh \in \mathcal {M}$
. Thus,
and
Then, using Inequalities (4.1)–(4.4), we have
and
Continuing this process, we obtain that for non-negative integer m, we can write
 $$ \begin{align*}h=\sum_{k=0}^{m}T^kQR^kh + T^{m+1}R^{m+1}h \end{align*} $$
$$ \begin{align*}h=\sum_{k=0}^{m}T^kQR^kh + T^{m+1}R^{m+1}h \end{align*} $$
and
 $$ \begin{align*}\|h\|^2_{\mathcal{M}}\ge \sum_{k=0}^m\|QR^kh\|^2_{\mathcal{M}}. \end{align*} $$
$$ \begin{align*}\|h\|^2_{\mathcal{M}}\ge \sum_{k=0}^m\|QR^kh\|^2_{\mathcal{M}}. \end{align*} $$
This completes the proof.
Theorem 4.3 Let
![]() $\mathcal {H}$
be an RKHS consisting of analytic functions on
$\mathcal {H}$
be an RKHS consisting of analytic functions on
![]() $\mathbb {D}.$
Let
$\mathbb {D}.$
Let
![]() $\phi $
be an inner function such that
$\phi $
be an inner function such that
![]() $\phi (0)=0, \ \phi \mathcal {H}\subseteq \mathcal {H},$
and
$\phi (0)=0, \ \phi \mathcal {H}\subseteq \mathcal {H},$
and
![]() $||h||\le ||\phi h||$
for every
$||h||\le ||\phi h||$
for every
![]() $h\in \mathcal {H}$
. Assume that, if
$h\in \mathcal {H}$
. Assume that, if
![]() $\phi h\in \mathcal {H}$
for an analytic function h on
$\phi h\in \mathcal {H}$
for an analytic function h on
![]() $\mathbb {D},$
then
$\mathbb {D},$
then
![]() $h\in \mathcal {H}.$
Let
$h\in \mathcal {H}.$
Let
![]() $\mathcal {M}$
be a Hilbert space contractively contained in
$\mathcal {M}$
be a Hilbert space contractively contained in
![]() $\mathcal {H}$
which is nearly invariant under division by
$\mathcal {H}$
which is nearly invariant under division by
![]() $\phi $
and
$\phi $
and
![]() $||\phi h||_{\mathcal {M}}\ge ||h||_{\mathcal {M}}$
whenever
$||\phi h||_{\mathcal {M}}\ge ||h||_{\mathcal {M}}$
whenever
![]() $\phi h\in \mathcal {M}.$
Then, there exists a vector subspace
$\phi h\in \mathcal {M}.$
Then, there exists a vector subspace
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $H^2(\mathbb {D},\ell ^2(I))$
invariant under
$H^2(\mathbb {D},\ell ^2(I))$
invariant under
![]() $T_{\phi }^*$
such that
$T_{\phi }^*$
such that
![]() $\mathcal {M}$
is in one-to-one correspondence with
$\mathcal {M}$
is in one-to-one correspondence with
![]() $\mathcal {N}$
via the linear map
$\mathcal {N}$
via the linear map
where
![]() $f=(f_i)_{i\in I}$
and
$f=(f_i)_{i\in I}$
and
![]() $\{g_i:i\in I\}$
is an orthonormal basis of
$\{g_i:i\in I\}$
is an orthonormal basis of
![]() $\mathcal {M}\ominus (\mathcal {M}\cap \phi \mathcal {H}).$
Moreover,
$\mathcal {M}\ominus (\mathcal {M}\cap \phi \mathcal {H}).$
Moreover,
![]() $\|h\|_{\mathcal {M}}\ge \|f\|_{H^2(\mathbb {D},\ell ^2(I))}$
if
$\|h\|_{\mathcal {M}}\ge \|f\|_{H^2(\mathbb {D},\ell ^2(I))}$
if
![]() $h(z)=\sum _{i\in I}g_i(z)f_i(z)$
for
$h(z)=\sum _{i\in I}g_i(z)f_i(z)$
for
![]() $f=(f_i)_{i\in I}\in \mathcal {N}.$
$f=(f_i)_{i\in I}\in \mathcal {N}.$
Proof Let P denote the orthogonal projection of
![]() $\mathcal {M}$
onto it’s closed subspace
$\mathcal {M}$
onto it’s closed subspace
![]() $\mathcal {M}\cap \phi \mathcal {H}$
and
$\mathcal {M}\cap \phi \mathcal {H}$
and
![]() $Q=I_{\mathcal {M}} - P.$
Let
$Q=I_{\mathcal {M}} - P.$
Let
![]() $h\in \mathcal {M}$
. Then using Lemma 4.2,
$h\in \mathcal {M}$
. Then using Lemma 4.2,
 $$ \begin{align} h=\sum_{k=0}^mM_{\phi}^m QR^m h+M^{m+1}_{\phi}R^{m+1}h \ \ \ \mathrm{for \ every} \ m\ge 0, \end{align} $$
$$ \begin{align} h=\sum_{k=0}^mM_{\phi}^m QR^m h+M^{m+1}_{\phi}R^{m+1}h \ \ \ \mathrm{for \ every} \ m\ge 0, \end{align} $$
and
 $$ \begin{align} \sum_{m=0}^\infty ||Q_{\mathcal{M}}R^mh||_{\mathcal{M}}^2\le ||h||_{\mathcal{M}}^2, \end{align} $$
$$ \begin{align} \sum_{m=0}^\infty ||Q_{\mathcal{M}}R^mh||_{\mathcal{M}}^2\le ||h||_{\mathcal{M}}^2, \end{align} $$
where
![]() $R:=(M_{\phi }M_{\phi }^*)^{-1}M_{\phi }P$
is a contraction on
$R:=(M_{\phi }M_{\phi }^*)^{-1}M_{\phi }P$
is a contraction on
![]() $\mathcal {M}.$
$\mathcal {M}.$
Since
![]() $\{g_i: i\in I\}$
is an orthonormal basis of
$\{g_i: i\in I\}$
is an orthonormal basis of
![]() $\mathcal {M}\ominus (\mathcal {M}\cap \phi \mathcal {H})$
, therefore for every
$\mathcal {M}\ominus (\mathcal {M}\cap \phi \mathcal {H})$
, therefore for every
![]() $k\ge 0,$
we have
$k\ge 0,$
we have
for some
![]() $\{c_{ki}\}_{i\in I}\in \ell ^2(I).$
$\{c_{ki}\}_{i\in I}\in \ell ^2(I).$
Then
 $$ \begin{align*}h=\sum_{k=0}^{m}\sum_{i \in I}c_{ki}M^{k}_{\phi }g_{i} + M^{m+1}_{\phi}R^{m+1}h \end{align*} $$
$$ \begin{align*}h=\sum_{k=0}^{m}\sum_{i \in I}c_{ki}M^{k}_{\phi }g_{i} + M^{m+1}_{\phi}R^{m+1}h \end{align*} $$
and
 $$ \begin{align*}\sum_{i \in I}\sum_{k=0}^{\infty} |c_{ki}|^{2}\le \|h\|^{2}_{\mathcal{M}}. \end{align*} $$
$$ \begin{align*}\sum_{i \in I}\sum_{k=0}^{\infty} |c_{ki}|^{2}\le \|h\|^{2}_{\mathcal{M}}. \end{align*} $$
Thus for every
![]() $i \in I, \ q_i(z):=\sum _{k=0}^{\infty }c_{ki}z^k$
is in
$i \in I, \ q_i(z):=\sum _{k=0}^{\infty }c_{ki}z^k$
is in
![]() $H^2(\mathbb {D}).$
Further, since
$H^2(\mathbb {D}).$
Further, since
![]() $\phi $
is an inner function with
$\phi $
is an inner function with
![]() $\phi (0)=0,$
therefore the composition operator
$\phi (0)=0,$
therefore the composition operator
![]() $C_{\phi }$
induced by
$C_{\phi }$
induced by
![]() $\phi $
is an isometry on
$\phi $
is an isometry on
![]() $H^2(\mathbb {D}).$
Thus,
$H^2(\mathbb {D}).$
Thus,
![]() $f_{i}=C_{\phi }(q_i)=\sum _{k=0}^\infty c_{ki}\phi ^k$
belongs to
$f_{i}=C_{\phi }(q_i)=\sum _{k=0}^\infty c_{ki}\phi ^k$
belongs to
![]() $C_\phi (H^2(\mathbb {D}))$
and
$C_\phi (H^2(\mathbb {D}))$
and
![]() $||f_i||_2^2=\sum _{k=0}^\infty |c_{ki}|^2.$
$||f_i||_2^2=\sum _{k=0}^\infty |c_{ki}|^2.$
Then, for any
![]() $w \in \mathbb {D}$
,
$w \in \mathbb {D}$
,
 $$ \begin{align*} & \sum_{i \in I}|(g_i f_i)(w)| \\&\le \Bigg(\sum_{i \in I}|g_i(w)|^2\Bigg)^{1/2}\Bigg(\sum_{i \in I}|f_i(w)|^2\Bigg)^{1/2}\\ & \le \Bigg(\sum_{i \in I}|<g_i,k_w>_{\mathcal{M}}|^2\Bigg)^{1/2}\Bigg(\sum_{i \in I}\Bigg(\sum_{k=0}^{\infty}|c_{ki}|^2\Bigg)\Bigg(\sum_{k=0}^{\infty}|\phi(w)|^{2k}\Bigg)\Bigg)^{1/2}\\ &\le \|Qk_w\|_{\mathcal{M}}\|h\|_{\mathcal{M}}\frac{1}{\sqrt{1-|\phi(w)|^2}}, \end{align*} $$
$$ \begin{align*} & \sum_{i \in I}|(g_i f_i)(w)| \\&\le \Bigg(\sum_{i \in I}|g_i(w)|^2\Bigg)^{1/2}\Bigg(\sum_{i \in I}|f_i(w)|^2\Bigg)^{1/2}\\ & \le \Bigg(\sum_{i \in I}|<g_i,k_w>_{\mathcal{M}}|^2\Bigg)^{1/2}\Bigg(\sum_{i \in I}\Bigg(\sum_{k=0}^{\infty}|c_{ki}|^2\Bigg)\Bigg(\sum_{k=0}^{\infty}|\phi(w)|^{2k}\Bigg)\Bigg)^{1/2}\\ &\le \|Qk_w\|_{\mathcal{M}}\|h\|_{\mathcal{M}}\frac{1}{\sqrt{1-|\phi(w)|^2}}, \end{align*} $$
where
![]() $k_{w}$
is the kernel function of
$k_{w}$
is the kernel function of
![]() $\mathcal {M}$
at the point
$\mathcal {M}$
at the point
![]() $w.$
This shows that the series
$w.$
This shows that the series
![]() $\sum _{i \in I}g_{i}f_{i}$
converges at each point in
$\sum _{i \in I}g_{i}f_{i}$
converges at each point in
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
We shall now prove that
![]() $\sum _{i \in I}g_{i}f_{i}$
is analytic on
$\sum _{i \in I}g_{i}f_{i}$
is analytic on
![]() $\mathbb {D}$
. Suppose
$\mathbb {D}$
. Suppose
![]() $z_0 \in \mathbb {D}$
and choose
$z_0 \in \mathbb {D}$
and choose
![]() $r>0$
such that
$r>0$
such that
![]() $ \overline {D(z_0,r)} \subset \mathbb {D}$
. Let
$ \overline {D(z_0,r)} \subset \mathbb {D}$
. Let
![]() $w \in \overline {D(z_0,r)}$
. Since the kernel function K of
$w \in \overline {D(z_0,r)}$
. Since the kernel function K of
![]() $\mathcal {M}$
is analytic in the first variable and coanalytic in the second variable, therefore K is bounded on compact subsets of
$\mathcal {M}$
is analytic in the first variable and coanalytic in the second variable, therefore K is bounded on compact subsets of
![]() $\mathbb {D}^2.$
Thus, there exists a constant
$\mathbb {D}^2.$
Thus, there exists a constant
![]() $A>0$
, depending on
$A>0$
, depending on
![]() $z_0$
and
$z_0$
and
![]() $r,$
such that
$r,$
such that
![]() $\|k_w\|_{\mathcal {M}}^2=K(w,w)\le A$
. Also,
$\|k_w\|_{\mathcal {M}}^2=K(w,w)\le A$
. Also,
![]() $\text {sup}_{|w-z_0|\le r}|\phi (w)| \le B <1$
, where B depends on
$\text {sup}_{|w-z_0|\le r}|\phi (w)| \le B <1$
, where B depends on
![]() $z_0$
and r. Therefore,
$z_0$
and r. Therefore,
 $$ \begin{align*}\sum_{i \in I}|(g_i f_i)(w)| \le \frac{A}{\sqrt{1-B}}\Bigg( \sum_{i \in I}\sum_{k=0}^{\infty}|c_{ki}|^2\Bigg)^{1/2}. \end{align*} $$
$$ \begin{align*}\sum_{i \in I}|(g_i f_i)(w)| \le \frac{A}{\sqrt{1-B}}\Bigg( \sum_{i \in I}\sum_{k=0}^{\infty}|c_{ki}|^2\Bigg)^{1/2}. \end{align*} $$
This also implies that
![]() ${\{i\in I: f_i(z)g_i(z)\ne 0\}}$
must be countable which means we can assume the above sum on the left must be a countable sum. Then, using the Weierstrass M-test the series converges uniformly on
${\{i\in I: f_i(z)g_i(z)\ne 0\}}$
must be countable which means we can assume the above sum on the left must be a countable sum. Then, using the Weierstrass M-test the series converges uniformly on
![]() $\overline {D(z_0,r)}$
. Thus, the series
$\overline {D(z_0,r)}$
. Thus, the series
![]() $\sum _{i\in I}g_i f_i$
converges locally uniformly on
$\sum _{i\in I}g_i f_i$
converges locally uniformly on
![]() $\mathbb {D}$
. Hence
$\mathbb {D}$
. Hence
![]() $\sum _{i \in I}(g_if_i)$
is analytic on
$\sum _{i \in I}(g_if_i)$
is analytic on
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
Further, using Equation (4.5),
![]() $h - \sum _{i \in I}g_{i}f_{i}$
is an analytic function on
$h - \sum _{i \in I}g_{i}f_{i}$
is an analytic function on
![]() $\mathbb {D}$
having zero of every order at 0. Hence
$\mathbb {D}$
having zero of every order at 0. Hence
![]() $f_i\in C_{\phi }(H^2(\mathbb {D}))$
for each
$f_i\in C_{\phi }(H^2(\mathbb {D}))$
for each
![]() $f_i\in I$
and
$f_i\in I$
and
 $$ \begin{align*}\sum_{i\in I}||f_i||_2^2=\sum_{i\in I}\sum_{k=0}^\infty |c_{ki}|^2\le ||h||_{\mathcal{M}}^2. \end{align*} $$
$$ \begin{align*}\sum_{i\in I}||f_i||_2^2=\sum_{i\in I}\sum_{k=0}^\infty |c_{ki}|^2\le ||h||_{\mathcal{M}}^2. \end{align*} $$
Now, define
 $$ \begin{align*} \mathcal{N}&=\{f = (f_i)_{i\in I}\in H^{2}(\mathbb{D},\ell^2(I)) : f_i\in C_\phi(H^2(\mathbb{D})), \ \exists \ h \in \mathcal{M}, \\ h(z)&=\sum_{i\in I}g_i(z)f_i(z) \ \mathrm{for} \ z\in \mathbb{D}\}. \end{align*} $$
$$ \begin{align*} \mathcal{N}&=\{f = (f_i)_{i\in I}\in H^{2}(\mathbb{D},\ell^2(I)) : f_i\in C_\phi(H^2(\mathbb{D})), \ \exists \ h \in \mathcal{M}, \\ h(z)&=\sum_{i\in I}g_i(z)f_i(z) \ \mathrm{for} \ z\in \mathbb{D}\}. \end{align*} $$
Clearly
![]() $\mathcal {N}$
is a vector subspace of
$\mathcal {N}$
is a vector subspace of
![]() $H^{2}(\mathbb {D},\ell ^2(I)$
and the map
$H^{2}(\mathbb {D},\ell ^2(I)$
and the map
![]() $\mathcal {G}(f)(z)=\sum _{i\in I}g_i(z)f_i(z), z\in \mathbb {D},$
is a well-defined linear surjective map. To show it is one-to-one, we shall show that every
$\mathcal {G}(f)(z)=\sum _{i\in I}g_i(z)f_i(z), z\in \mathbb {D},$
is a well-defined linear surjective map. To show it is one-to-one, we shall show that every
![]() $f\in \mathcal {N}$
is uniquely determined by
$f\in \mathcal {N}$
is uniquely determined by
![]() $\mathcal {G}f.$
Let
$\mathcal {G}f.$
Let
![]() $f=(f_i)_{i\in I}\in \mathcal {N}.$
Then, there exists
$f=(f_i)_{i\in I}\in \mathcal {N}.$
Then, there exists
![]() $h\in \mathcal {M}$
such that
$h\in \mathcal {M}$
such that
![]() $h=\sum _{i\in I}g_if_i.$
Let
$h=\sum _{i\in I}g_if_i.$
Let
![]() $f_i=\sum _{k=0}^\infty a_{ki}\phi ^k.$
Then
$f_i=\sum _{k=0}^\infty a_{ki}\phi ^k.$
Then
![]() $h=\sum _{i\in I}c_{0i}g_i+\phi \left (\sum _{i\in I}g_i\tilde {f_i}\right ),$
where
$h=\sum _{i\in I}c_{0i}g_i+\phi \left (\sum _{i\in I}g_i\tilde {f_i}\right ),$
where
![]() $\tilde {f_i}=\sum _{k=0}^\infty c_{(k+1)i}\phi ^k.$
Then,
$\tilde {f_i}=\sum _{k=0}^\infty c_{(k+1)i}\phi ^k.$
Then,
![]() $\phi \left (\sum _{i\in I}g_i\tilde {f_i}\right )\in \mathcal {H}$
which yields
$\phi \left (\sum _{i\in I}g_i\tilde {f_i}\right )\in \mathcal {H}$
which yields
![]() $\sum _{i\in I}g_i\tilde {f_i}\in \mathcal {H}.$
Thus,
$\sum _{i\in I}g_i\tilde {f_i}\in \mathcal {H}.$
Thus,
![]() $h-\sum _{i\in I}c_{0i}g_i\in \mathcal {M}\cap \phi \mathcal {H}.$
Therefore,
$h-\sum _{i\in I}c_{0i}g_i\in \mathcal {M}\cap \phi \mathcal {H}.$
Therefore,
![]() $Q(h)=\sum _{i\in I}c_{0i}g_i.$
This means,
$Q(h)=\sum _{i\in I}c_{0i}g_i.$
This means,
for each
![]() $i.$
Now,
$i.$
Now,
![]() $Ph=\phi \left (\sum _{i\in I}g_i\tilde {f_i}\right )$
and
$Ph=\phi \left (\sum _{i\in I}g_i\tilde {f_i}\right )$
and
![]() $P=M_\phi R.$
Therefore,
$P=M_\phi R.$
Therefore,
![]() $Rh=\sum _{i\in I}g_i\tilde {f_i}.$
Again, repeating the above arguments,
$Rh=\sum _{i\in I}g_i\tilde {f_i}.$
Again, repeating the above arguments,
![]() $QRh=\sum _{i\in I}c_{1i}g_i$
which implies
$QRh=\sum _{i\in I}c_{1i}g_i$
which implies
Continuing like this, we obtain
This establishes the claim.
Lastly, we shall show that
![]() $\mathcal {N}$
is invariant under
$\mathcal {N}$
is invariant under
![]() $T^*_\phi $
. Let
$T^*_\phi $
. Let
![]() $f=(f_i)_{i\in I}\in \mathcal {N}.$
Then by definition, for each
$f=(f_i)_{i\in I}\in \mathcal {N}.$
Then by definition, for each
![]() $i, \ f_i\in C_\phi (H^2(\mathbb {D}))$
and there exists an
$i, \ f_i\in C_\phi (H^2(\mathbb {D}))$
and there exists an
![]() $h\in \mathcal {M}$
such that
$h\in \mathcal {M}$
such that
![]() $h(z)=\sum _{i\in I}g_i(z)f_i(z)$
for every
$h(z)=\sum _{i\in I}g_i(z)f_i(z)$
for every
![]() $z\in \mathbb {D}.$
We decompose h as
$z\in \mathbb {D}.$
We decompose h as
since
![]() $P=M_{\phi }R.$
Then
$P=M_{\phi }R.$
Then
where for each
![]() $i\in I, \ f_i=\sum _{k=0}^\infty c_{ki}\phi ^k$
which implies
$i\in I, \ f_i=\sum _{k=0}^\infty c_{ki}\phi ^k$
which implies
and therefore
Hence,
![]() $T^*_\phi (f)=(T_{\phi }^* f_i)_{i\in I} \in \mathcal {N}$
which establishes that
$T^*_\phi (f)=(T_{\phi }^* f_i)_{i\in I} \in \mathcal {N}$
which establishes that
![]() $\mathcal {N}$
is invariant under
$\mathcal {N}$
is invariant under
![]() $T^*_\phi $
.
$T^*_\phi $
.
Remark 4.4 In [Reference Liang and Partington12], Liang and Partington used Erard’s methods from [Reference Erard9] to describe subspaces of Dirichet-type spaces
![]() $\mathcal {D}_{\alpha } (-1\le \alpha \le 1)$
that are nearly invariant under division by a finite Blaschke factor. For
$\mathcal {D}_{\alpha } (-1\le \alpha \le 1)$
that are nearly invariant under division by a finite Blaschke factor. For
![]() $\alpha \ge 0, \mathcal {D}_{\alpha }$
posses an equivalent norm with respect to which
$\alpha \ge 0, \mathcal {D}_{\alpha }$
posses an equivalent norm with respect to which
![]() $M_{\phi }$
is bounded below on it with a lower bound 1. Hence, our Theorem extends Theorem 3.4 from [Reference Liang and Partington12] to a vastly general situation.
$M_{\phi }$
is bounded below on it with a lower bound 1. Hence, our Theorem extends Theorem 3.4 from [Reference Liang and Partington12] to a vastly general situation.
5 Nearly invariant Brangesian subspaces with finite defect related to multiplication operators on reproducing kernel Hilbert spaces
Chalendar, Gallardo–Guti
![]() $\mathrm {\acute {e}}$
rrez, and Partington introduced and studied the notion of nearly
$\mathrm {\acute {e}}$
rrez, and Partington introduced and studied the notion of nearly
![]() $S^*$
-invariant subspaces of
$S^*$
-invariant subspaces of
![]() $H^2(\mathbb {D})$
with finite defect in [Reference Chalendar, Gallardo-Gutiérrez and Partington5]. In this Section, we shall extend our work from Section 4 to the finite defect case. This extension is motivated by work of Chattopadhyay and Das from [Reference Chattopadhyay and Das6]. They, following Erard’s ideas, as discussed in Section 4, extended Liang and Partington’s description [Reference Liang and Partington12] of nearly
$H^2(\mathbb {D})$
with finite defect in [Reference Chalendar, Gallardo-Gutiérrez and Partington5]. In this Section, we shall extend our work from Section 4 to the finite defect case. This extension is motivated by work of Chattopadhyay and Das from [Reference Chattopadhyay and Das6]. They, following Erard’s ideas, as discussed in Section 4, extended Liang and Partington’s description [Reference Liang and Partington12] of nearly
![]() $S^*$
-invariant subspaces of Dirichlet-type spaces to the finite defect situation. First, we introduce some definitions and terminologies that we shall need in this section.
$S^*$
-invariant subspaces of Dirichlet-type spaces to the finite defect situation. First, we introduce some definitions and terminologies that we shall need in this section.
Let
![]() $\mathcal {H}$
be a Hilbert space. Suppose
$\mathcal {H}$
be a Hilbert space. Suppose
![]() $\mathcal {M}$
is a vector subspace of
$\mathcal {M}$
is a vector subspace of
![]() $\mathcal {H}$
which is a Hilbert space (with maybe a different norm) and
$\mathcal {H}$
which is a Hilbert space (with maybe a different norm) and
![]() $\mathcal {F}$
is a closed subspace of
$\mathcal {F}$
is a closed subspace of
![]() $\mathcal {H}$
such that
$\mathcal {H}$
such that
![]() $\mathcal {M}\cap \mathcal {F}=\{0\}.$
Then, the vector subspace
$\mathcal {M}\cap \mathcal {F}=\{0\}.$
Then, the vector subspace
![]() $\mathcal {M}+\mathcal {F}$
of
$\mathcal {M}+\mathcal {F}$
of
![]() $\mathcal {H}$
becomes a Hilbert space with respect to the norm given by
$\mathcal {H}$
becomes a Hilbert space with respect to the norm given by
Furthermore,
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {F}$
are closed orthogonal subspaces of
$\mathcal {F}$
are closed orthogonal subspaces of
![]() $(\mathcal {M}+\mathcal {F}, ||\cdot ||_{\oplus })$
. Henceforth, we shall use
$(\mathcal {M}+\mathcal {F}, ||\cdot ||_{\oplus })$
. Henceforth, we shall use
![]() $\mathcal {M}\oplus \mathcal {F}$
to denote
$\mathcal {M}\oplus \mathcal {F}$
to denote
![]() $(\mathcal {M}+\mathcal {F}, ||\cdot ||_{\oplus })$
.
$(\mathcal {M}+\mathcal {F}, ||\cdot ||_{\oplus })$
.
The following result is an anlogue of Lemma 2.1 from [Reference Erard9] and our Lemma 4.2 for the finite defect situation.
Lemma 5.1 Let
![]() $\mathcal {H}$
be a Hilbert space and
$\mathcal {H}$
be a Hilbert space and
![]() $T\in B(\mathcal {H})$
with
$T\in B(\mathcal {H})$
with
![]() $||Th||_{\mathcal {H}}\ge ||h||_{\mathcal {H}}$
for all
$||Th||_{\mathcal {H}}\ge ||h||_{\mathcal {H}}$
for all
![]() $h\in \mathcal {H}.$
Let
$h\in \mathcal {H}.$
Let
![]() $\mathcal {M}$
be a Hilbert space contractively contained in
$\mathcal {M}$
be a Hilbert space contractively contained in
![]() $\mathcal {H}$
for which there exists a finite dimensional subspace
$\mathcal {H}$
for which there exists a finite dimensional subspace
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $\mathcal {H}$
such that
$\mathcal {H}$
such that
![]() $\mathcal {M}\cap \mathcal {F}=\{0\}$
,
$\mathcal {M}\cap \mathcal {F}=\{0\}$
,
![]() $Th\in \mathcal {M}$
implies
$Th\in \mathcal {M}$
implies
![]() $h\in \mathcal {M}\oplus \mathcal {F}$
, and
$h\in \mathcal {M}\oplus \mathcal {F}$
, and
![]() $||Th||_{\mathcal {M}}\ge ||h||_{\oplus }.$
If P and L, respectively, are the orthogonal projections of
$||Th||_{\mathcal {M}}\ge ||h||_{\oplus }.$
If P and L, respectively, are the orthogonal projections of
![]() $\mathcal {M}\oplus \mathcal {F}$
onto
$\mathcal {M}\oplus \mathcal {F}$
onto
![]() $\mathcal {M}\cap T\mathcal {H}$
and
$\mathcal {M}\cap T\mathcal {H}$
and
![]() $\mathcal {F},$
and
$\mathcal {F},$
and
![]() $Q=I_{\mathcal {M}\oplus \mathcal {F}} - P,$
then
$Q=I_{\mathcal {M}\oplus \mathcal {F}} - P,$
then
![]() $R:=(T^*T)^{-1}T^*P$
is a well-defined contraction on
$R:=(T^*T)^{-1}T^*P$
is a well-defined contraction on
![]() $\mathcal {M}\oplus \mathcal {F}$
. Further, for each
$\mathcal {M}\oplus \mathcal {F}$
. Further, for each
![]() $m\ge 0,$
every
$m\ge 0,$
every
![]() $h\in \mathcal {M}$
can be written as
$h\in \mathcal {M}$
can be written as
 $$ \begin{align*}h=\sum_{k=0}^{m}T^kQR^kh + T^{m+1}R^{m+1}h + T\sum_{k=1}^{m}T^{k-1}LR^kh \end{align*} $$
$$ \begin{align*}h=\sum_{k=0}^{m}T^kQR^kh + T^{m+1}R^{m+1}h + T\sum_{k=1}^{m}T^{k-1}LR^kh \end{align*} $$
and
 $$ \begin{align*}\|h\|^2_{\mathcal{M}}\ge \sum_{k=0}^m\|QR^kh\|^2_{\mathcal{M}} + \sum_{k=1}^m\|LR^kh\|^2_{\mathcal{H}}\end{align*} $$
$$ \begin{align*}\|h\|^2_{\mathcal{M}}\ge \sum_{k=0}^m\|QR^kh\|^2_{\mathcal{M}} + \sum_{k=1}^m\|LR^kh\|^2_{\mathcal{H}}\end{align*} $$
Proof For
![]() $g\in \mathcal {M} \oplus \mathcal {F},$
$g\in \mathcal {M} \oplus \mathcal {F},$
 $$ \begin{align*} TRg&=T(T^*T)^{-1}T^*P(g)\\ &=T(T^*T)^{-1}T^*Th_0, \text{ where } Pg=Th_0 \ \ \mathrm{for \ some} \ h_0\in\mathcal{H} \ \\ &=Th_0\\ &= Pg. \end{align*} $$
$$ \begin{align*} TRg&=T(T^*T)^{-1}T^*P(g)\\ &=T(T^*T)^{-1}T^*Th_0, \text{ where } Pg=Th_0 \ \ \mathrm{for \ some} \ h_0\in\mathcal{H} \ \\ &=Th_0\\ &= Pg. \end{align*} $$
Thus
![]() $TRg\in \mathcal {M}$
, which implies
$TRg\in \mathcal {M}$
, which implies
![]() $Rg\in \mathcal {M}\oplus \mathcal {F}.$
Also,
$Rg\in \mathcal {M}\oplus \mathcal {F}.$
Also,
![]() $||Rg||_{\oplus }\le ||TRg||_{\mathcal {M}}=||Pg||_{\mathcal {M}}\le ||Pg||_{\oplus }\le ||g||_{\oplus }.$
Therefore R is a well-defined contraction on
$||Rg||_{\oplus }\le ||TRg||_{\mathcal {M}}=||Pg||_{\mathcal {M}}\le ||Pg||_{\oplus }\le ||g||_{\oplus }.$
Therefore R is a well-defined contraction on
![]() $\mathcal {M}\oplus \mathcal {F}.$
$\mathcal {M}\oplus \mathcal {F}.$
Fix any
![]() $h \in \mathcal {M}.$
Then
$h \in \mathcal {M}.$
Then
and
Since
![]() $Rh \in \mathcal {M} \oplus \mathcal {F}$
, therefore we can decompose it as
$Rh \in \mathcal {M} \oplus \mathcal {F}$
, therefore we can decompose it as
and
Using these in Equations (5.1) and (5.2), we obtain
and
 $$ \begin{align*}||h||_{\mathcal{M}}^2\ge \sum_{k=0}^1||QR^kh||_{\mathcal{M}}^2+||R^2h||_{\oplus}^2+||LRh||_{\mathcal{H}}^2. \end{align*} $$
$$ \begin{align*}||h||_{\mathcal{M}}^2\ge \sum_{k=0}^1||QR^kh||_{\mathcal{M}}^2+||R^2h||_{\oplus}^2+||LRh||_{\mathcal{H}}^2. \end{align*} $$
Continuing like this we can show that
 $$ \begin{align*}h=\sum_{k=0}^mT^kQR^kh+T^{m+1}R^{m+1}h+\sum_{k=1}^mT^kLR^kh \end{align*} $$
$$ \begin{align*}h=\sum_{k=0}^mT^kQR^kh+T^{m+1}R^{m+1}h+\sum_{k=1}^mT^kLR^kh \end{align*} $$
and
 $$ \begin{align*}||h||_{\mathcal{M}}^2\ge \sum_{k=0}^m||QR^kh||_{\mathcal{M}}^2+||R^{m+1}h||_{\oplus}^2+\sum_{k=1}^m||LR^kh||_{\mathcal{H}}^2 \end{align*} $$
$$ \begin{align*}||h||_{\mathcal{M}}^2\ge \sum_{k=0}^m||QR^kh||_{\mathcal{M}}^2+||R^{m+1}h||_{\oplus}^2+\sum_{k=1}^m||LR^kh||_{\mathcal{H}}^2 \end{align*} $$
for every
![]() $m\ge 0.$
This completes the proof.
$m\ge 0.$
This completes the proof.
Definition 5.2 Let
![]() $\mathcal {H}$
be an RKHS on a set X,
$\mathcal {H}$
be an RKHS on a set X,
![]() $\phi $
be a complex-valued function on X such that
$\phi $
be a complex-valued function on X such that
![]() $\phi \mathcal {H}\subseteq \mathcal {H}$
and
$\phi \mathcal {H}\subseteq \mathcal {H}$
and
![]() $M_\phi ,$
the operator of multiplication with
$M_\phi ,$
the operator of multiplication with
![]() $\phi $
is bounded below on
$\phi $
is bounded below on
![]() $\mathcal {H}.$
Then a vector subspace
$\mathcal {H}.$
Then a vector subspace
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathcal {H}$
is said to be nearly invariant under division by
$\mathcal {H}$
is said to be nearly invariant under division by
![]() $\phi $
with defect p if there exists a p-dimensional subspace
$\phi $
with defect p if there exists a p-dimensional subspace
![]() $\mathcal {F}$
(which can assumed to have zero intersection with
$\mathcal {F}$
(which can assumed to have zero intersection with
![]() $\mathcal {M})$
of
$\mathcal {M})$
of
![]() $\mathcal {H}$
such that
$\mathcal {H}$
such that
![]() $\phi f\in \mathcal {M}$
implies
$\phi f\in \mathcal {M}$
implies
![]() $f\in \mathcal {M}\oplus \mathcal {F}$
(algebraic direct sum). The subspace
$f\in \mathcal {M}\oplus \mathcal {F}$
(algebraic direct sum). The subspace
![]() $\mathcal {F}$
(unique upto isomorphism) is said to be the defect space of
$\mathcal {F}$
(unique upto isomorphism) is said to be the defect space of
![]() $\mathcal {M}.$
$\mathcal {M}.$
The following is the main theorem of this section. It an extension of our Theorem 4.3 for the finite defect case.
Theorem 5.3 Let
![]() $\mathcal {H}$
be an RKHS consisting of analytic functions on
$\mathcal {H}$
be an RKHS consisting of analytic functions on
![]() $\mathbb {D}.$
Let
$\mathbb {D}.$
Let
![]() $\phi $
be an inner function such that
$\phi $
be an inner function such that
![]() $\phi (0)=0, \ \phi \mathcal {H}\subseteq \mathcal {H},$
and
$\phi (0)=0, \ \phi \mathcal {H}\subseteq \mathcal {H},$
and
![]() $||h||\le ||\phi h||$
for every
$||h||\le ||\phi h||$
for every
![]() $h\in \mathcal {H}$
. Assume that if
$h\in \mathcal {H}$
. Assume that if
![]() $\phi h\in \mathcal {H}$
for an analytic function h on
$\phi h\in \mathcal {H}$
for an analytic function h on
![]() $\mathbb {D},$
then
$\mathbb {D},$
then
![]() $h\in \mathcal {H}.$
Let
$h\in \mathcal {H}.$
Let
![]() $\mathcal {M}$
be a Hilbert space contractively contained in
$\mathcal {M}$
be a Hilbert space contractively contained in
![]() $\mathcal {H}$
which is nearly invariant under division by
$\mathcal {H}$
which is nearly invariant under division by
![]() $\phi $
with defect space
$\phi $
with defect space
![]() $\mathcal {F}$
of dimension p such that
$\mathcal {F}$
of dimension p such that
![]() $\|\phi h\|_{\mathcal {M}}\ge \|h\|_{\oplus }$
whenever
$\|\phi h\|_{\mathcal {M}}\ge \|h\|_{\oplus }$
whenever
![]() $\phi h \in \mathcal {M}$
.
$\phi h \in \mathcal {M}$
.
-
1. If
 $\mathcal {M}\nsubseteq \phi \mathcal {H},$
then there exists a vector subspace
$\mathcal {M}\nsubseteq \phi \mathcal {H},$
then there exists a vector subspace
 $\mathcal {N}$
of
$\mathcal {N}$
of
 $H^{2}(\mathbb {D},\ell ^2(I)\oplus \mathbb {C}^p)$
invariant under
$H^{2}(\mathbb {D},\ell ^2(I)\oplus \mathbb {C}^p)$
invariant under
 $T^{*}_{\phi }$
such that
$T^{*}_{\phi }$
such that
 $\mathcal {M}$
is in one-to-one correspondence with
$\mathcal {M}$
is in one-to-one correspondence with
 $\mathcal {N}$
via the linear map
$\mathcal {N}$
via the linear map
 $\mathcal {G}:\mathcal {N} \to \mathcal {M}$
given by where
$\mathcal {G}:\mathcal {N} \to \mathcal {M}$
given by where $$ \begin{align*}(\mathcal{G}q)(z)=\sum_{i\in I}g_i(z)f_i(z)+\phi(z)\sum_{i=1}^p e_i(z)t_i(z) \ \ (\mathrm{pointwise}), \end{align*} $$
$$ \begin{align*}(\mathcal{G}q)(z)=\sum_{i\in I}g_i(z)f_i(z)+\phi(z)\sum_{i=1}^p e_i(z)t_i(z) \ \ (\mathrm{pointwise}), \end{align*} $$
 $q=(f,t)\in \mathcal {N}$
, and
$q=(f,t)\in \mathcal {N}$
, and
 $\{g_i:i\in I\}$
and
$\{g_i:i\in I\}$
and
 $\{e_i:i=1,\dots , p\}$
are orthonormal basis of
$\{e_i:i=1,\dots , p\}$
are orthonormal basis of
 $\mathcal {M}\ominus \mathcal {M}\cap \phi \mathcal {H}$
and
$\mathcal {M}\ominus \mathcal {M}\cap \phi \mathcal {H}$
and
 $\mathcal {F},$
respectively. Moreover, for
$\mathcal {F},$
respectively. Moreover, for $$ \begin{align*}||h||_{\mathcal{M}}^2\ge ||(f,t)||_2^2=||f||_2^2+||t||_2^2 \end{align*} $$
$$ \begin{align*}||h||_{\mathcal{M}}^2\ge ||(f,t)||_2^2=||f||_2^2+||t||_2^2 \end{align*} $$
 $h \in \mathcal {M}$
, where
$h \in \mathcal {M}$
, where
 $ h=\mathcal {G}(f,t). $
$ h=\mathcal {G}(f,t). $
-
2. If
 $\mathcal {M} \subseteq \phi \mathcal {H},$
then there exists a vector subspace
$\mathcal {M} \subseteq \phi \mathcal {H},$
then there exists a vector subspace
 $\mathcal {N}$
of
$\mathcal {N}$
of
 $H^{2}(\mathbb {D}, \mathbb {C}^p)$
invariant under
$H^{2}(\mathbb {D}, \mathbb {C}^p)$
invariant under
 $T^{*}_{\phi }$
such that
$T^{*}_{\phi }$
such that
 $\mathcal {M}$
is in one-to-one correspondence with
$\mathcal {M}$
is in one-to-one correspondence with
 $\mathcal {N}$
via the linear map
$\mathcal {N}$
via the linear map
 $\mathcal {G}:\mathcal {N} \to \mathcal {M}$
given by where
$\mathcal {G}:\mathcal {N} \to \mathcal {M}$
given by where $$ \begin{align*}\mathcal{G}(t)(z)=\phi(z)\sum_{i=1}^p e_i(z)t_i(z) \ \ (\mathrm{pointwise}), \end{align*} $$
$$ \begin{align*}\mathcal{G}(t)(z)=\phi(z)\sum_{i=1}^p e_i(z)t_i(z) \ \ (\mathrm{pointwise}), \end{align*} $$
 $t\in \mathcal {N}$
and
$t\in \mathcal {N}$
and
 $\{e_i:i=1,\dots , p\}$
is an orthonormal basis of
$\{e_i:i=1,\dots , p\}$
is an orthonormal basis of
 $\mathcal {F}$
. Moreover, for
$\mathcal {F}$
. Moreover, for $$ \begin{align*}||h||_{\mathcal{M}}\ge ||t||_2 \end{align*} $$
$$ \begin{align*}||h||_{\mathcal{M}}\ge ||t||_2 \end{align*} $$
 $h \in \mathcal {M}$
, where
$h \in \mathcal {M}$
, where
 $ h=\mathcal {G}(t). $
$ h=\mathcal {G}(t). $
Proof Let
![]() $h\in \mathcal {M}.$
Then, using Lemma 5.1 for
$h\in \mathcal {M}.$
Then, using Lemma 5.1 for
![]() $m\ge 0,$
$m\ge 0,$
 $$ \begin{align} h=\sum_{k=0}^m M_{\phi}^mQR^m h+ M^{m+1}_{\phi}R^{m+1}+ M_{\phi}\sum_{k=1}^m M_{\phi}^{k-1}LR^mh \end{align} $$
$$ \begin{align} h=\sum_{k=0}^m M_{\phi}^mQR^m h+ M^{m+1}_{\phi}R^{m+1}+ M_{\phi}\sum_{k=1}^m M_{\phi}^{k-1}LR^mh \end{align} $$
and
 $$ \begin{align} ||h||_{\mathcal{M}}^2\ge \sum_{k=0}^\infty ||QR^kh||_{\mathcal{M}}^2 + \sum_{k=1}^\infty ||LR^kh||_{\mathcal{H}}, \end{align} $$
$$ \begin{align} ||h||_{\mathcal{M}}^2\ge \sum_{k=0}^\infty ||QR^kh||_{\mathcal{M}}^2 + \sum_{k=1}^\infty ||LR^kh||_{\mathcal{H}}, \end{align} $$
where Q and L are the projections of
![]() $\mathcal {M}\oplus \mathcal {F}$
onto
$\mathcal {M}\oplus \mathcal {F}$
onto
![]() $\mathcal {M}\ominus (\mathcal {M}\cap \phi \mathcal {H})$
and
$\mathcal {M}\ominus (\mathcal {M}\cap \phi \mathcal {H})$
and
![]() $\mathcal {F}$
, respectively. Recall that
$\mathcal {F}$
, respectively. Recall that
![]() $\mathcal {M}\oplus \mathcal {F}$
is the Hilbert space
$\mathcal {M}\oplus \mathcal {F}$
is the Hilbert space
![]() $(\mathcal {M}+\mathcal {F}, ||\cdot ||_{\oplus })$
, where
$(\mathcal {M}+\mathcal {F}, ||\cdot ||_{\oplus })$
, where
![]() $||a + b||_{\oplus }^2=||a||_{\mathcal {M}}^2+||b||_{\mathcal {H}}^2$
for
$||a + b||_{\oplus }^2=||a||_{\mathcal {M}}^2+||b||_{\mathcal {H}}^2$
for
![]() $a\in \mathcal {M}$
and
$a\in \mathcal {M}$
and
![]() $b\in \mathcal {F}$
.
$b\in \mathcal {F}$
.
Let
![]() $\{g_i:i\in I\}$
and
$\{g_i:i\in I\}$
and
![]() $\{e_i:i=1,\dots , p\}$
be orthonormal basis of
$\{e_i:i=1,\dots , p\}$
be orthonormal basis of
![]() $Ran(Q)$
and
$Ran(Q)$
and
![]() $Ran(L),$
respectively. Then
$Ran(L),$
respectively. Then
 $$ \begin{align*}QR^{k}h=\sum_{i \in I}c_{ki}g_i \text{ and } LR^kh=\sum_{j=1}^{p}d_{kj}e_j \end{align*} $$
$$ \begin{align*}QR^{k}h=\sum_{i \in I}c_{ki}g_i \text{ and } LR^kh=\sum_{j=1}^{p}d_{kj}e_j \end{align*} $$
for
![]() $\{c_{ki}\}_{i\in I}\in \ell ^2(I)$
and
$\{c_{ki}\}_{i\in I}\in \ell ^2(I)$
and
![]() $\{d_{kj}\}_{j=1}^p\in \mathbb {C}^p.$
Using these representations in Equation (5.3), we obtain
$\{d_{kj}\}_{j=1}^p\in \mathbb {C}^p.$
Using these representations in Equation (5.3), we obtain
 $$ \begin{align*}h=\sum_{k=0}^{m}\sum_{i \in I}c_{ki}M^{k}_{\phi }g_{i} + M^{m+1}_{\phi}R^{m+1}h +M_\phi\sum_{k=1}^{m} \sum_{j=1}^{p}d_{kj}M^{k-1}_\phi e_j \end{align*} $$
$$ \begin{align*}h=\sum_{k=0}^{m}\sum_{i \in I}c_{ki}M^{k}_{\phi }g_{i} + M^{m+1}_{\phi}R^{m+1}h +M_\phi\sum_{k=1}^{m} \sum_{j=1}^{p}d_{kj}M^{k-1}_\phi e_j \end{align*} $$
and
 $$ \begin{align*}\sum_{i \in I}\sum_{k=0}^{\infty} |c_{ki}|^{2} + \sum_{j=1}^{p}\sum_{k=1}^{\infty} |d_{kj}|^{2}\le \|h\|^{2}_{\mathcal{M}}. \end{align*} $$
$$ \begin{align*}\sum_{i \in I}\sum_{k=0}^{\infty} |c_{ki}|^{2} + \sum_{j=1}^{p}\sum_{k=1}^{\infty} |d_{kj}|^{2}\le \|h\|^{2}_{\mathcal{M}}. \end{align*} $$
Thus for every
![]() $i \in I$
and
$i \in I$
and
![]() $j\in \{1,2,\dots ,p\}$
,
$j\in \{1,2,\dots ,p\}$
,
![]() $f_i=\sum _{k=0}^{\infty }c_{ki}\phi ^{k}$
and
$f_i=\sum _{k=0}^{\infty }c_{ki}\phi ^{k}$
and
![]() $t_j=\sum _{k=1}^{\infty }d_{kj}\phi ^{k-1}$
are well-defined functions in
$t_j=\sum _{k=1}^{\infty }d_{kj}\phi ^{k-1}$
are well-defined functions in
![]() $C_{\phi }(H^2(\mathbb {D}))$
and
$C_{\phi }(H^2(\mathbb {D}))$
and
![]() $\sum _{i\in I}||f_i||_2^2+\sum _{j=1}^p||t_j||_2^2\le ||h||_{\mathcal {M}}^2.$
Then using the arguments simiar to the ones used in the proof of Theorem 4.3, we first show that for each
$\sum _{i\in I}||f_i||_2^2+\sum _{j=1}^p||t_j||_2^2\le ||h||_{\mathcal {M}}^2.$
Then using the arguments simiar to the ones used in the proof of Theorem 4.3, we first show that for each
![]() $w\in \mathbb {D},$
$w\in \mathbb {D},$
 $$ \begin{align} \sum_{i \in I}|(g_i f_i)(w)| \le \|Qk_w\|_{\mathcal{M}}\|h\|_{\mathcal{M}}\frac{1}{\sqrt{1-|\phi(w)|^2}} \end{align} $$
$$ \begin{align} \sum_{i \in I}|(g_i f_i)(w)| \le \|Qk_w\|_{\mathcal{M}}\|h\|_{\mathcal{M}}\frac{1}{\sqrt{1-|\phi(w)|^2}} \end{align} $$
and
 $$ \begin{align} \sum_{j=1}^{p}|(e_j t_j)(w)|\le \|Lk_w\|_{\mathcal{H}}\|h\|_{\mathcal{M}}\frac{1}{\sqrt{1-|\phi(w)|^2}}, \end{align} $$
$$ \begin{align} \sum_{j=1}^{p}|(e_j t_j)(w)|\le \|Lk_w\|_{\mathcal{H}}\|h\|_{\mathcal{M}}\frac{1}{\sqrt{1-|\phi(w)|^2}}, \end{align} $$
and then use them to establish that
![]() $\sum _{i \in I}g_{i}f_{i}$
and
$\sum _{i \in I}g_{i}f_{i}$
and
![]() $\phi \sum _{j=1}^{p}e_{j}t_{j}$
are both analytic on
$\phi \sum _{j=1}^{p}e_{j}t_{j}$
are both analytic on
![]() $\mathbb {D}$
. Lastly, using Equation (5.3), we conclude that
$\mathbb {D}$
. Lastly, using Equation (5.3), we conclude that
![]() $h-\sum _{i \in I}g_{i}f_{i}-\phi \sum _{j=1}^{p}e_{j}t_{j}$
is an analytic function on
$h-\sum _{i \in I}g_{i}f_{i}-\phi \sum _{j=1}^{p}e_{j}t_{j}$
is an analytic function on
![]() $\mathbb {D}$
having zero of every order at 0. Hence,
$\mathbb {D}$
having zero of every order at 0. Hence,
 $$ \begin{align} h=\sum_{i \in I}g_{i}f_{i} + \phi\sum_{j=1}^{p}e_{j}t_{j} \ \ \text{ on } \ \ \mathbb{D}. \end{align} $$
$$ \begin{align} h=\sum_{i \in I}g_{i}f_{i} + \phi\sum_{j=1}^{p}e_{j}t_{j} \ \ \text{ on } \ \ \mathbb{D}. \end{align} $$
Note that each
![]() $f_i , t_j\in C_\phi (H^2(\mathbb {D}))$
. Therefore, we have obtained
$f_i , t_j\in C_\phi (H^2(\mathbb {D}))$
. Therefore, we have obtained
![]() $f=(f_i)_{i\in I}\in H^2(\mathbb {D}, \ell ^2(I))$
and
$f=(f_i)_{i\in I}\in H^2(\mathbb {D}, \ell ^2(I))$
and
![]() $t=(t_j)_{j=1}^p\in H^2(\mathbb {D},\mathbb {C}^p)$
with
$t=(t_j)_{j=1}^p\in H^2(\mathbb {D},\mathbb {C}^p)$
with
![]() $f_i, t_j\in C_\phi (H^2(\mathbb {D}))$
such that Equation 5.7 holds and
$f_i, t_j\in C_\phi (H^2(\mathbb {D}))$
such that Equation 5.7 holds and
 $$ \begin{align} \|f\|^2_2 + \|t\|^2_2&=\sum_{i \in I} \|f_i\|^2_2 + \sum_{j=1} ^{p}\|t_j\|^2_2 \le \|h\|^2_{\mathcal{M}}. \end{align} $$
$$ \begin{align} \|f\|^2_2 + \|t\|^2_2&=\sum_{i \in I} \|f_i\|^2_2 + \sum_{j=1} ^{p}\|t_j\|^2_2 \le \|h\|^2_{\mathcal{M}}. \end{align} $$
Define
 $$ \begin{align*} \begin{split} \mathcal{N}=\left \{(f,t) \in H^2(\mathbb{D},\ell^2(I)\oplus \mathbb{C}^p) : f=(f_i)_{i\in I}, t= (t_j)_{j=1}^p, f_i, t_j\in C_\phi(H^2(\mathbb{D})) \right.\\ \left. \mathrm{and} \ \exists \ h \in \mathcal{M} \text{ such that} \ h=\sum_{i\in I}g_if_i+\phi \sum_{j=1}^p e_jt_j, \ \mathrm{and \ for \ each} \ i\in I, \right. \\ \left. 1\le j\le p, \ k\ge 0, \ \ \langle{f_i,\phi^k}\rangle=\langle{QR^kh,g_i}\rangle, \langle{t_j,\phi^{k}}\rangle=\langle{LR^{k+1}h,e_j} \rangle \right\}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \mathcal{N}=\left \{(f,t) \in H^2(\mathbb{D},\ell^2(I)\oplus \mathbb{C}^p) : f=(f_i)_{i\in I}, t= (t_j)_{j=1}^p, f_i, t_j\in C_\phi(H^2(\mathbb{D})) \right.\\ \left. \mathrm{and} \ \exists \ h \in \mathcal{M} \text{ such that} \ h=\sum_{i\in I}g_if_i+\phi \sum_{j=1}^p e_jt_j, \ \mathrm{and \ for \ each} \ i\in I, \right. \\ \left. 1\le j\le p, \ k\ge 0, \ \ \langle{f_i,\phi^k}\rangle=\langle{QR^kh,g_i}\rangle, \langle{t_j,\phi^{k}}\rangle=\langle{LR^{k+1}h,e_j} \rangle \right\}. \end{split} \end{align*} $$
Clearly
![]() $\mathcal {N}$
is a vector subspace of
$\mathcal {N}$
is a vector subspace of
![]() $H^2(\mathbb {D},\ell ^2(I)\oplus \mathbb {C}^p),$
and the map
$H^2(\mathbb {D},\ell ^2(I)\oplus \mathbb {C}^p),$
and the map
![]() $\mathcal {G}:\mathcal {N}\to \mathcal {M}$
given by
$\mathcal {G}:\mathcal {N}\to \mathcal {M}$
given by
 $$ \begin{align*}\mathcal{G}(f,t)=\sum_{i\in I}g_if_i+\phi \left(\sum_{j=1}^pe_jt_j\right) \end{align*} $$
$$ \begin{align*}\mathcal{G}(f,t)=\sum_{i\in I}g_if_i+\phi \left(\sum_{j=1}^pe_jt_j\right) \end{align*} $$
is well-defined one-one, onto, and linear.
Now we will show that
![]() $\mathcal {N}$
is invariant under
$\mathcal {N}$
is invariant under
![]() $T^*_\phi $
. Let
$T^*_\phi $
. Let
![]() $(f,t)\in \mathcal {N}.$
Then, by definition, there exists a
$(f,t)\in \mathcal {N}.$
Then, by definition, there exists a
![]() $h\in \mathcal {M}$
such that
$h\in \mathcal {M}$
such that
 $$ \begin{align*}h=\sum_{i\in I}g_if_i+\phi\sum_{j=1}^pe_jt_j, \end{align*} $$
$$ \begin{align*}h=\sum_{i\in I}g_if_i+\phi\sum_{j=1}^pe_jt_j, \end{align*} $$
and for each
![]() $k\ge 0, \langle {QR^kh,g_i}\rangle =\langle {f_i,\phi ^k}\rangle $
and
$k\ge 0, \langle {QR^kh,g_i}\rangle =\langle {f_i,\phi ^k}\rangle $
and
![]() $\langle {LR^{k+1}h,e_j}\rangle =\langle {t_j,\phi ^k}\rangle $
for every
$\langle {LR^{k+1}h,e_j}\rangle =\langle {t_j,\phi ^k}\rangle $
for every
![]() $i\in I, 1\le j\le p.$
Decompose
$i\in I, 1\le j\le p.$
Decompose
 $$ \begin{align*} h&=Qh + Ph\\ &=Qh+M_\phi Rh\\ &=\sum_{i\in I}c_{0i}g_i+\phi(Rh). \end{align*} $$
$$ \begin{align*} h&=Qh + Ph\\ &=Qh+M_\phi Rh\\ &=\sum_{i\in I}c_{0i}g_i+\phi(Rh). \end{align*} $$
Then
 $$ \begin{align*}\phi(Rh)=h-\sum_{i\in I}c_{0i}g_i=\phi\left(\sum_{i\in I}g_i\tilde{f_i}\right)+\phi\left(\sum_{j=1}^pe_jt_j\right), \end{align*} $$
$$ \begin{align*}\phi(Rh)=h-\sum_{i\in I}c_{0i}g_i=\phi\left(\sum_{i\in I}g_i\tilde{f_i}\right)+\phi\left(\sum_{j=1}^pe_jt_j\right), \end{align*} $$
where
![]() $f_i-c_{0j}=\phi \tilde {f_i}$
. Then
$f_i-c_{0j}=\phi \tilde {f_i}$
. Then
 $$ \begin{align*}Rh= \sum_{i\in I}g_i\tilde{f_i} + \sum_{j=1}^pe_jt_j. \end{align*} $$
$$ \begin{align*}Rh= \sum_{i\in I}g_i\tilde{f_i} + \sum_{j=1}^pe_jt_j. \end{align*} $$
Then
 $$ \begin{align*}\sum_{i\in I}g_i\tilde{f_i} + \sum_{j=1}^pe_jt_j=Rh=L(Rh) +(P+Q)(Rh) = \sum_{j=1}^p d_{0j}e_j + (P+Q)(Rh), \end{align*} $$
$$ \begin{align*}\sum_{i\in I}g_i\tilde{f_i} + \sum_{j=1}^pe_jt_j=Rh=L(Rh) +(P+Q)(Rh) = \sum_{j=1}^p d_{0j}e_j + (P+Q)(Rh), \end{align*} $$
since
![]() $Rh\in \mathcal {M}\oplus \mathcal {F}$
and
$Rh\in \mathcal {M}\oplus \mathcal {F}$
and
![]() $L(Rh)=\sum _{j=1}^p d_{0j}e_j.$
Therefore,
$L(Rh)=\sum _{j=1}^p d_{0j}e_j.$
Therefore,
 $$ \begin{align*}\sum_{i\in I}g_i\tilde{f_i} + \phi \left(\sum_{j=1}^pe_j\tilde{t_j}\right)\in \mathcal{M}, \end{align*} $$
$$ \begin{align*}\sum_{i\in I}g_i\tilde{f_i} + \phi \left(\sum_{j=1}^pe_j\tilde{t_j}\right)\in \mathcal{M}, \end{align*} $$
where
![]() $t_j-d_{0j}=\phi \tilde {t_j}.$
Let
$t_j-d_{0j}=\phi \tilde {t_j}.$
Let
![]() $\tilde {f}=(\tilde {f_i})_{i\in I}$
and
$\tilde {f}=(\tilde {f_i})_{i\in I}$
and
![]() $\tilde {t}=(\tilde {t_j})_{j=1}^p$
Then,
$\tilde {t}=(\tilde {t_j})_{j=1}^p$
Then,
![]() $(\tilde {f},\tilde {t})\in \mathcal {N};$
hence
$(\tilde {f},\tilde {t})\in \mathcal {N};$
hence
![]() $T_\phi ^*(f,t)=(T_{\phi }^*f, T_{\phi }^*t)=(\tilde {f},\tilde {t})\in \mathcal {N}.$
This establishes that
$T_\phi ^*(f,t)=(T_{\phi }^*f, T_{\phi }^*t)=(\tilde {f},\tilde {t})\in \mathcal {N}.$
This establishes that
![]() $\mathcal {N}$
is
$\mathcal {N}$
is
![]() $T_\phi ^*$
invariant; hence completes the proof for the case
$T_\phi ^*$
invariant; hence completes the proof for the case
![]() $\mathcal {M}\nsubseteq \phi \mathcal {H}.$
$\mathcal {M}\nsubseteq \phi \mathcal {H}.$
Lastly, note that
![]() $Q=0$
when
$Q=0$
when
![]() $\mathcal {M}\subseteq \phi \mathcal {H}$
. Then, the proof for the case
$\mathcal {M}\subseteq \phi \mathcal {H}$
. Then, the proof for the case
![]() $\mathcal {M}\subseteq \phi \mathcal {H}$
follows simply by repeating the above arguments with
$\mathcal {M}\subseteq \phi \mathcal {H}$
follows simply by repeating the above arguments with
![]() $Q=0.$
$Q=0.$
Acknowledgement
The authors thank the anonymous referees for their valuable comments, which have greatly improved the paper. The second and third authors thank the Mathematical Sciences Foundation, Delhi for support and facilities needed to complete the present work. The second author also thanks Shiv Nadar Institution of Eminence for providing partial financial support for this research.
Data availability statements
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Competing interests
The authors have no competing interests to declare that are relevant to the content of this article.