Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-05T14:22:38.722Z Has data issue: false hasContentIssue false
  • English
  • Français

Joint Mean Oscillation and Local Ideals in the Toeplitz Algebra II: Local Commutivity and Essential Commutant

Published online by Cambridge University Press:  20 November 2018

Jingbo Xia
Jingbo Xia*
Affiliation:
Department of Mathematics, State University of New York at Buffalo, Buffalo, NY 14260, USA, e-mail: jxia@acsu.buffalo.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A well-known theorem of Sarason [11] asserts that if 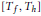$\left[ {{T}_{f}},\,{{T}_{h}} \right]$ is compact for every 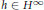$h\,\in \,{{H}^{\infty }}$, then 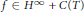$f\,\in \,{{H}^{\infty }}\,+\,C\left( T \right)$. Using local analysis in the full Toeplitz algebra 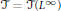$T\,=\,T\left( {{L}^{\infty }} \right)$, we show that the membership 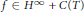$f\,\in \,{{H}^{\infty }}\,+\,C\left( T \right)$ can be inferred from the compactness of a much smaller collection of commutators 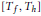$\left[ {{T}_{f}},\,{{T}_{h}} \right]$. Using this strengthened result and a theorem of Davidson [2], we construct a proper 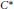${{C}^{*}}$-subalgebra 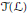$T\left( \mathcal{L} \right)$ of 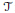$T$ which has the same essential commutant as that of 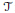$T$. Thus the image of 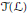$T\left( \mathcal{L} \right)$ in the Calkin algebra does not satisfy the double commutant relation [12], [1]. We will also show that no separable subalgebra 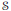$\mathcal{S}$ of 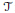$T$ is capable of conferring the membership 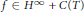$f\,\in \,{{H}^{\infty }}\,+\,C\left( T \right)$ through the compactness of the commutators 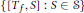$\left\{ \left[ {{T}_{f,}}\,S \right]\,:\,S\,\in \,\mathcal{S} \right\}$.

Keywords

46H1047B3547C05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 2 , 01 June 2002 , pp. 309 - 318
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Berger, C. and Coburn, L., On Voiculescu's double commutant theorem. Proc. Amer. Math. Soc. 124 (1996), 124–1996.Google Scholar
[2] Davidson, K., On operators commuting with Toeplitz operators modulo the compact operators. J. Funct. Anal. 24 (1977), 24–1977.Google Scholar
[3] Douglas, R., Banach algebra techniques in operator theory. Academic Press, New York, 1972.Google Scholar
[4] Hartman, P., On completely continuous Hankel matrices. Proc. Amer. Math. Soc. 9 (1958), 9–1958.Google Scholar
[5] Garnett, J., Bounded analytic functions. Academic Press, New York, 1981.Google Scholar
[6] Gohberg, I. and Krupnik, N., The algebra generated by Toeplitz matrices. Funct. Anal. Appl. 3 (1969), 3–1969.Google Scholar
[7] Gorkin, P. and Zheng, D., Essentially commuting Toeplitz operators. Pacific J. Math. 190 (1999), 190–1999.Google Scholar
[8] Johnson, B. and Parrot, S., Operators commuting with a von Neumann algebra modulo the set of compact operators. J. Funct. Anal. 11 (1972), 11–1972.Google Scholar
[9] Muhly, P. and Xia, J., Calderón-Zygmund operators, local mean oscillation and certain automorphisms of the Toeplitz algebra. Amer. J. Math. 117 (1995), 117–1995.Google Scholar
[10] Popa, S., The commutant modulo the set of compact operators of a von Neumann algebra. J. Funct. Anal. 71 (1981), 71–1981.Google Scholar
[11] Sarason, D., On products of Toeplitz operators. Acta Sci. Math. (Szeged) 35 (1973), 35–1973.Google Scholar
[12] Voiculescu, D., A non-commutative Weyl-von Neumann theorem. Rev. Roumaine Math. Pure Appl. 21 (1976), 21–1976.Google Scholar
[13] Xia, J., Joint mean oscillation and local ideals in the Toeplitz algebra. Proc. Amer. Math. Soc. 128 (2000), 128–2000.Google Scholar
[14] Xia, J., Coincidence of essential commutant and the double commutant relation in the Calkin algebra. Preprint, 2001.Google Scholar
[15] Zhu, K., Operator theory in function spaces. Marcel Dekker, New York, 1990.Google Scholar