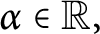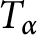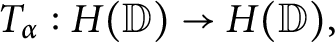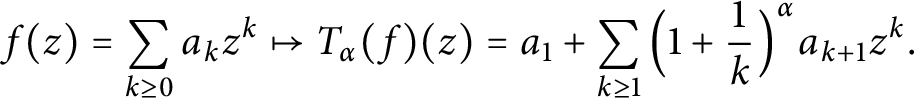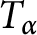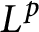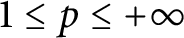1 Introduction
Let
![]() $\mathbb {D}$
denote the open unit disc
$\mathbb {D}$
denote the open unit disc
![]() $\{z\in \mathbb {C}:\vert z\vert <1\}$
of the complex plane. If
$\{z\in \mathbb {C}:\vert z\vert <1\}$
of the complex plane. If
![]() $0<r<1$
and f is an analytic function in
$0<r<1$
and f is an analytic function in
![]() $\mathbb {D}$
(i.e.,
$\mathbb {D}$
(i.e.,
![]() $f\in H(\mathbb {D})$
), we set
$f\in H(\mathbb {D})$
), we set
 $$ \begin{align*} M_p(r,f)&=\Big(\frac{1}{2\pi}\int_{0}^{2\pi}\vert f(re^{i\theta})\vert^{p}d\theta\Big)^{1/p} (1\leq p<\infty),\\ M_{\infty}(r,f)&=\mathop{\text{sup}}\limits_{0\leq t\leq 2\pi}\vert f(re^{it})\vert. \end{align*} $$
$$ \begin{align*} M_p(r,f)&=\Big(\frac{1}{2\pi}\int_{0}^{2\pi}\vert f(re^{i\theta})\vert^{p}d\theta\Big)^{1/p} (1\leq p<\infty),\\ M_{\infty}(r,f)&=\mathop{\text{sup}}\limits_{0\leq t\leq 2\pi}\vert f(re^{it})\vert. \end{align*} $$
In the same spirit, for any holomorphic polynomial
![]() $q,$
let us define, for all
$q,$
let us define, for all
![]() $p\geq 1,$
$p\geq 1,$
 $$\begin{align*}\Vert q\Vert_p=\Big(\frac{1}{2\pi}\int_{0}^{2\pi}\vert q(e^{i\theta})\vert^{p}d\theta\Big)^{1/p} \quad\mbox{ and }\quad \Vert q\Vert_{\infty}=\mathop{\mathrm{sup}}\limits_{0\leq t\leq 2\pi}\vert q(e^{it})\vert.\end{align*}$$
$$\begin{align*}\Vert q\Vert_p=\Big(\frac{1}{2\pi}\int_{0}^{2\pi}\vert q(e^{i\theta})\vert^{p}d\theta\Big)^{1/p} \quad\mbox{ and }\quad \Vert q\Vert_{\infty}=\mathop{\mathrm{sup}}\limits_{0\leq t\leq 2\pi}\vert q(e^{it})\vert.\end{align*}$$
Moreover, for all
![]() $p> 1, p'$
will stand for the exponent conjugate to p, i.e.,
$p> 1, p'$
will stand for the exponent conjugate to p, i.e.,
 $\frac {1}{p}+\frac {1}{p'}=1$
. For any f in
$\frac {1}{p}+\frac {1}{p'}=1$
. For any f in
![]() $H(\mathbb {D})$
and any z in
$H(\mathbb {D})$
and any z in
![]() $\mathbb {D},$
we will write
$\mathbb {D},$
we will write
![]() $f(z)=\sum _{k\geq 0}a_{k}z^{k}.$
For all
$f(z)=\sum _{k\geq 0}a_{k}z^{k}.$
For all
![]() $\alpha \in \mathbb {R},$
we consider the sequence
$\alpha \in \mathbb {R},$
we consider the sequence
![]() $(\omega _n(\alpha ))$
defined as follows:
$(\omega _n(\alpha ))$
defined as follows:
 $$\begin{align*}\omega_{0}(\alpha)=1\quad\text{ and }\quad \omega_{n}(\alpha)=\Big(1+\frac{1}{n}\Big)^{\alpha} \mbox{ for } n\geq 1.\end{align*}$$
$$\begin{align*}\omega_{0}(\alpha)=1\quad\text{ and }\quad \omega_{n}(\alpha)=\Big(1+\frac{1}{n}\Big)^{\alpha} \mbox{ for } n\geq 1.\end{align*}$$
We deal with the following (polynomial) weighted Taylor shifts acting on
![]() $H(\mathbb {D})$
endowed with the topology of uniform convergence on compact subsets:
$H(\mathbb {D})$
endowed with the topology of uniform convergence on compact subsets:
 $$\begin{align*}T_{\alpha}:H(\mathbb{D})\longrightarrow H(\mathbb{D}),\quad f(z)=\sum\limits_{k\geq 0}a_{k}z^{k}\longmapsto T_{\alpha}(f)(z)=\sum\limits_{k\geq 0}\omega_{k}(\alpha)a_{k+1}z^{k}.\end{align*}$$
$$\begin{align*}T_{\alpha}:H(\mathbb{D})\longrightarrow H(\mathbb{D}),\quad f(z)=\sum\limits_{k\geq 0}a_{k}z^{k}\longmapsto T_{\alpha}(f)(z)=\sum\limits_{k\geq 0}\omega_{k}(\alpha)a_{k+1}z^{k}.\end{align*}$$
Notice that
![]() $T_{0}$
is the classical Taylor shift acting on
$T_{0}$
is the classical Taylor shift acting on
![]() $H(\mathbb {D})$
[Reference Beise, Meyrath and Müller4]. In [Reference Thelen14], the author shows that the operator
$H(\mathbb {D})$
[Reference Beise, Meyrath and Müller4]. In [Reference Thelen14], the author shows that the operator
![]() $T_0$
is frequently hypercyclic. Actually, for any
$T_0$
is frequently hypercyclic. Actually, for any
![]() $\alpha \in \mathbb {R}, T_{\alpha }$
is frequently hypercyclic. Let us recall that an operator
$\alpha \in \mathbb {R}, T_{\alpha }$
is frequently hypercyclic. Let us recall that an operator
![]() $T:X\rightarrow X,$
where X is a Fréchet space, is said to be frequently hypercyclic if there is a vector
$T:X\rightarrow X,$
where X is a Fréchet space, is said to be frequently hypercyclic if there is a vector
![]() $x\in X$
such that for every non-empty open set
$x\in X$
such that for every non-empty open set
![]() $U\subset X,$
the lower density of the set
$U\subset X,$
the lower density of the set
![]() $N(x,U):=\{n\in \mathbb {N}:T^nx\in U\}$
is positive (i.e.,
$N(x,U):=\{n\in \mathbb {N}:T^nx\in U\}$
is positive (i.e.,
![]() $\underline {d}(N(x,U))=\liminf _{N\rightarrow +\infty }\#\{1\leq n\leq N:n\in N(x,U)\}/N>0$
). Such a vector x is called frequently hypercyclic. This natural new concept of hypercyclicity was introduced in 2004 by Bayart and Grivaux [Reference Bayart and Grivaux1, Reference Bayart and Grivaux2] and has been the subject of many developments since then. We refer the reader to [Reference Bayart and Matheron3] or [Reference Grosse Erdmann and Peris10] and the references therein. In particular, the following result is a crucial tool used to exhibit a lot of examples of frequently hypercyclic operators.
$\underline {d}(N(x,U))=\liminf _{N\rightarrow +\infty }\#\{1\leq n\leq N:n\in N(x,U)\}/N>0$
). Such a vector x is called frequently hypercyclic. This natural new concept of hypercyclicity was introduced in 2004 by Bayart and Grivaux [Reference Bayart and Grivaux1, Reference Bayart and Grivaux2] and has been the subject of many developments since then. We refer the reader to [Reference Bayart and Matheron3] or [Reference Grosse Erdmann and Peris10] and the references therein. In particular, the following result is a crucial tool used to exhibit a lot of examples of frequently hypercyclic operators.
Theorem 1.1 (Frequent hypercyclicity criterion)
Let T be an operator on a separable Fréchet space X. If there is a dense subset
![]() $X_0$
of X and a map
$X_0$
of X and a map
![]() $S:X_0\rightarrow X_0$
such that, for any
$S:X_0\rightarrow X_0$
such that, for any
![]() $x\in X_0,$
$x\in X_0,$
-
(i)
 $\sum _{n\geq 0}T^nx$
converges unconditionally,
$\sum _{n\geq 0}T^nx$
converges unconditionally, -
(ii)
 $\sum _{n\geq 0}S^nx$
converges unconditionally,
$\sum _{n\geq 0}S^nx$
converges unconditionally, -
(iii)
 $TSx=x$
,
$TSx=x$
,
then T is frequently hypercyclic.
In our context, a straightforward application of the frequent hypercyclicity criterion yields the frequent hypercyclicity of the operators
![]() $T_{\alpha }$
for all
$T_{\alpha }$
for all
![]() $\alpha \in \mathbb {R}$
. Indeed, let
$\alpha \in \mathbb {R}$
. Indeed, let
![]() $X_0$
be the set of polynomials with coefficients in
$X_0$
be the set of polynomials with coefficients in
![]() $\mathbb {Q}+i\mathbb {Q}$
. Clearly, the set
$\mathbb {Q}+i\mathbb {Q}$
. Clearly, the set
![]() $X_0$
is a countable and dense subset in
$X_0$
is a countable and dense subset in
![]() $H(\mathbb {D})$
. Now we apply Theorem 1.1. First observe that condition (i) is clearly satisfied, since for any polynomial f,
$H(\mathbb {D})$
. Now we apply Theorem 1.1. First observe that condition (i) is clearly satisfied, since for any polynomial f,
![]() $T_{\alpha }^nf=0$
if the integer n is strictly greater than the degree of f. Moreover, if we consider the map
$T_{\alpha }^nf=0$
if the integer n is strictly greater than the degree of f. Moreover, if we consider the map
![]() $S_{\alpha }:X_0\rightarrow X_0,$
given by
$S_{\alpha }:X_0\rightarrow X_0,$
given by
 $\sum _{k=0}^db_kz^k\mapsto \sum _{k=0}^{d} b_{k}(\omega _{k}(\alpha ))^{-1}z^{k+1},$
condition (iii) is obviously satisfied. Finally, for
$\sum _{k=0}^db_kz^k\mapsto \sum _{k=0}^{d} b_{k}(\omega _{k}(\alpha ))^{-1}z^{k+1},$
condition (iii) is obviously satisfied. Finally, for
 $f(z)=\sum _{k=0}^d b_kz^k,$
for all
$f(z)=\sum _{k=0}^d b_kz^k,$
for all
![]() $0<r<1,$
we easily get
$0<r<1,$
we easily get
 $$\begin{align*}\mathop{\mathrm{sup}}\limits_{\vert z\vert\leq r}\!\left\vert S_{\alpha}^nf (z)\right\vert \leq (n+1)^{\vert \alpha\vert}\frac{r^n}{1-r}\max_{j=0,\dots,d}\vert b_j\vert,\end{align*}$$
$$\begin{align*}\mathop{\mathrm{sup}}\limits_{\vert z\vert\leq r}\!\left\vert S_{\alpha}^nf (z)\right\vert \leq (n+1)^{\vert \alpha\vert}\frac{r^n}{1-r}\max_{j=0,\dots,d}\vert b_j\vert,\end{align*}$$
which gives condition (ii). Thus, the operators
![]() $T_{\alpha }$
are frequently hypercyclic for all
$T_{\alpha }$
are frequently hypercyclic for all
![]() $\alpha \in \mathbb {R}.$
$\alpha \in \mathbb {R}.$
Now we are interested in the growth of frequently hypercyclic functions for the Taylor shifts
![]() $T_{\alpha }, \alpha \in \mathbb {R}.$
Such results have been achieved in the case of frequently hypercyclic functions for the differentiation operator on
$T_{\alpha }, \alpha \in \mathbb {R}.$
Such results have been achieved in the case of frequently hypercyclic functions for the differentiation operator on
![]() $H(\mathbb {C})$
. We refer the reader to [Reference Blasco, Bonilla and Grosse Erdmann5, Reference Drasin and Saksman6] and the references therein. Recently, in [Reference Mouze and Munnier11], the authors obtained the optimal growth in terms of average
$H(\mathbb {C})$
. We refer the reader to [Reference Blasco, Bonilla and Grosse Erdmann5, Reference Drasin and Saksman6] and the references therein. Recently, in [Reference Mouze and Munnier11], the authors obtained the optimal growth in terms of average
![]() $L^p$
-norms of frequently hypercyclic functions
$L^p$
-norms of frequently hypercyclic functions
![]() $f\in H(\mathbb {D})$
for the Taylor shift
$f\in H(\mathbb {D})$
for the Taylor shift
![]() $T_0$
. The result is stated as follows.
$T_0$
. The result is stated as follows.
Theorem 1.2 ([Reference Mouze and Munnier11])
We have the following assertions.
-
(i) Given
 $2\leq p\leq +\infty $
, there is a frequently hypercyclic function
$2\leq p\leq +\infty $
, there is a frequently hypercyclic function
 $f\in H(\mathbb {D})$
for the Taylor shift
$f\in H(\mathbb {D})$
for the Taylor shift
 $T_0$
satisfying the following estimate: there exists
$T_0$
satisfying the following estimate: there exists
 $C>0$
such that for every
$C>0$
such that for every
 $0<r<1,$
This estimate is optimal: every frequently hypercyclic function
$0<r<1,$
This estimate is optimal: every frequently hypercyclic function $$\begin{align*}M_{p}(r,f)\leq\frac{C}{\sqrt{1-r}}.\end{align*}$$
$$\begin{align*}M_{p}(r,f)\leq\frac{C}{\sqrt{1-r}}.\end{align*}$$
 $f\in H(\mathbb {D})$
for the Taylor shift
$f\in H(\mathbb {D})$
for the Taylor shift
 $T_0$
satisfies
$T_0$
satisfies  $$\begin{align*}\liminf_{r\rightarrow 1}\!(\sqrt{1-r} M_{p}(r,f))>0.\end{align*}$$
$$\begin{align*}\liminf_{r\rightarrow 1}\!(\sqrt{1-r} M_{p}(r,f))>0.\end{align*}$$
-
(ii) Given
 $1<p<2$
, there is a frequently hypercyclic function
$1<p<2$
, there is a frequently hypercyclic function
 $f\in H(\mathbb {D})$
for the Taylor shift
$f\in H(\mathbb {D})$
for the Taylor shift
 $T_0$
satisfying the following estimate: there exists
$T_0$
satisfying the following estimate: there exists
 $C>0$
such that for every
$C>0$
such that for every
 $0<r<1,$
This estimate is optimal: every frequently hypercyclic function
$0<r<1,$
This estimate is optimal: every frequently hypercyclic function $$\begin{align*}M_{p}(r,f)\leq\frac{C}{(1-r)^{1/p'}}.\end{align*}$$
$$\begin{align*}M_{p}(r,f)\leq\frac{C}{(1-r)^{1/p'}}.\end{align*}$$
 $f\in H(\mathbb {D})$
for the Taylor shift
$f\in H(\mathbb {D})$
for the Taylor shift
 $T_0$
satisfies
$T_0$
satisfies  $$\begin{align*}\liminf_{r\rightarrow 1}((1-r)^{1/p'}M_{p}(r,f))>0.\end{align*}$$
$$\begin{align*}\liminf_{r\rightarrow 1}((1-r)^{1/p'}M_{p}(r,f))>0.\end{align*}$$
A version of this statement in the case
![]() $p=1$
was also given. A natural question that arises is the following: what is the slowest possible growth for a frequently hypercyclic vector f for the operator
$p=1$
was also given. A natural question that arises is the following: what is the slowest possible growth for a frequently hypercyclic vector f for the operator
![]() $T_{\alpha }$
? Here, we exhibit a critical exponent from which the growth of frequently hypercyclic functions changes from polynomial to logarithmic behavior, and then becomes bounded on the whole unit disc. Summing up, the following theorem is our main result.
$T_{\alpha }$
? Here, we exhibit a critical exponent from which the growth of frequently hypercyclic functions changes from polynomial to logarithmic behavior, and then becomes bounded on the whole unit disc. Summing up, the following theorem is our main result.
Theorem 1.3 Let
![]() $\alpha \in \mathbb {R}.$
The following assertions hold:
$\alpha \in \mathbb {R}.$
The following assertions hold:
-
(i) For any
 $2\leq p< +\infty ,$
there is a frequently hypercyclic function f in
$2\leq p< +\infty ,$
there is a frequently hypercyclic function f in
 $H(\mathbb {D})$
for
$H(\mathbb {D})$
for
 $T_{\alpha }$
satisfying the following estimates: there exists
$T_{\alpha }$
satisfying the following estimates: there exists
 $C>0$
such that for every
$C>0$
such that for every
 $0<r<1,$
These estimates are optimal: every frequently hypercyclic function f in
$0<r<1,$
These estimates are optimal: every frequently hypercyclic function f in $$\begin{align*}M_{p}(r,f)\leq \begin{cases} C(1-r)^{\alpha-\frac{1}{2}} &\text{if } \alpha<1/2,\\ C \sqrt{\vert \log(1-r) \vert } &\text{if } \alpha=1/2,\\ C &\text{if } \alpha>1/2. \end{cases}\end{align*}$$
$$\begin{align*}M_{p}(r,f)\leq \begin{cases} C(1-r)^{\alpha-\frac{1}{2}} &\text{if } \alpha<1/2,\\ C \sqrt{\vert \log(1-r) \vert } &\text{if } \alpha=1/2,\\ C &\text{if } \alpha>1/2. \end{cases}\end{align*}$$
 $H(\mathbb {D})$
for
$H(\mathbb {D})$
for
 $T_{\alpha }$
is bounded from below by the corresponding previous estimate depending on
$T_{\alpha }$
is bounded from below by the corresponding previous estimate depending on
 $\alpha .$
$\alpha .$
-
(ii) For any
 $1<p<2$
, there is a frequently hypercyclic function f in
$1<p<2$
, there is a frequently hypercyclic function f in
 $H(\mathbb {D})$
for
$H(\mathbb {D})$
for
 $T_{\alpha }$
satisfying the following estimates: there exists
$T_{\alpha }$
satisfying the following estimates: there exists
 $C>0$
such that for every
$C>0$
such that for every
 $0<r<1,$
These estimates are optimal: every frequently hypercyclic function f in
$0<r<1,$
These estimates are optimal: every frequently hypercyclic function f in $$\begin{align*}M_{p}(r,f)\leq \begin{cases} C(1-r)^{\alpha-\frac{1}{p'}} &\text{if } \alpha <1/p',\\ C \vert \log(1-r) \vert^{\frac{1}{p}} &\text{if } \alpha =1/p',\\ C &\text{if } \alpha>1/p'. \end{cases}\end{align*}$$
$$\begin{align*}M_{p}(r,f)\leq \begin{cases} C(1-r)^{\alpha-\frac{1}{p'}} &\text{if } \alpha <1/p',\\ C \vert \log(1-r) \vert^{\frac{1}{p}} &\text{if } \alpha =1/p',\\ C &\text{if } \alpha>1/p'. \end{cases}\end{align*}$$
 $H(\mathbb {D})$
for
$H(\mathbb {D})$
for
 $T_{\alpha }$
is bounded from below by the corresponding previous estimate depending on
$T_{\alpha }$
is bounded from below by the corresponding previous estimate depending on
 $\alpha .$
$\alpha .$
-
(iii) There is a frequently hypercyclic function f in
 $H(\mathbb {D})$
for
$H(\mathbb {D})$
for
 $T_{\alpha }$
satisfying the following estimates: there exists
$T_{\alpha }$
satisfying the following estimates: there exists
 $C>0$
such that for every
$C>0$
such that for every
 $0<r<1,$
For
$0<r<1,$
For $$\begin{align*}M_{\infty}(r,f)\leq \begin{cases} C(1-r)^{\alpha-\frac{1}{2}} &\text{if } \alpha<1/2,\\ C \vert\log(1-r)\vert &\text{if } \alpha=1/2,\\ C &\text{if } \alpha>1/2.\end{cases}\end{align*}$$
$$\begin{align*}M_{\infty}(r,f)\leq \begin{cases} C(1-r)^{\alpha-\frac{1}{2}} &\text{if } \alpha<1/2,\\ C \vert\log(1-r)\vert &\text{if } \alpha=1/2,\\ C &\text{if } \alpha>1/2.\end{cases}\end{align*}$$
 $\alpha \ne 1/2,$
these estimates are optimal: every frequently hypercyclic function f in
$\alpha \ne 1/2,$
these estimates are optimal: every frequently hypercyclic function f in
 $H(\mathbb {D})$
for
$H(\mathbb {D})$
for
 $T_{\alpha }$
is bounded from below by the corresponding previous estimate depending on
$T_{\alpha }$
is bounded from below by the corresponding previous estimate depending on
 $\alpha .$
$\alpha .$
Finally, we deal with the case
![]() $p=1$
to obtain a similar statement that extends the result for the Taylor shift
$p=1$
to obtain a similar statement that extends the result for the Taylor shift
![]() $T_0$
given in [Reference Mouze and Munnier11] to the weighted Taylor shifts
$T_0$
given in [Reference Mouze and Munnier11] to the weighted Taylor shifts
![]() $T_{\alpha }$
, for all
$T_{\alpha }$
, for all
![]() $\alpha \in \mathbb {R}$
. We refer the reader to Proposition 4.1 and Theorem 4.4.
$\alpha \in \mathbb {R}$
. We refer the reader to Proposition 4.1 and Theorem 4.4.
The paper is organized as follows: in Section 2, the minimum growth of frequently hypercyclic functions for
![]() $T_{\alpha }$
is established. To do this, we use several well-known inequalities, such as the Jensen inequality, the Hardy–Littlewood inequality, or the Hausdorff–Young inequality. In Section 3, inspired by the ideas of [Reference Drasin and Saksman6], using Rudin–Shapiro polynomials, we will show by a constructive proof that these minimum estimates of the growth of frequently hypercyclic functions are attained. In Section4, we deal with the case
$T_{\alpha }$
is established. To do this, we use several well-known inequalities, such as the Jensen inequality, the Hardy–Littlewood inequality, or the Hausdorff–Young inequality. In Section 3, inspired by the ideas of [Reference Drasin and Saksman6], using Rudin–Shapiro polynomials, we will show by a constructive proof that these minimum estimates of the growth of frequently hypercyclic functions are attained. In Section4, we deal with the case
![]() $p=1$
.
$p=1$
.
Throughout the paper, whenever A and B depend on some parameters, we will use the notation
![]() $A\lesssim B$
(resp.
$A\lesssim B$
(resp.
![]() $A\gtrsim B$
) to mean
$A\gtrsim B$
) to mean
![]() $A\leq CB$
(resp.
$A\leq CB$
(resp.
![]() $A\geq C B$
) for some constant
$A\geq C B$
) for some constant
![]() $C>0$
that does not depend on the involved parameters apart from p and
$C>0$
that does not depend on the involved parameters apart from p and
![]() $\alpha $
.
$\alpha $
.
2 On the Growth of the Frequently Hypercyclic Functions
Let
![]() $\alpha \in \mathbb {R}$
. We establish some results concerning the blowing-up in terms of
$\alpha \in \mathbb {R}$
. We establish some results concerning the blowing-up in terms of
![]() $L^p$
-norms of a frequently hypercyclic function in
$L^p$
-norms of a frequently hypercyclic function in
![]() $H(\mathbb {D})$
for the weighted shift operator
$H(\mathbb {D})$
for the weighted shift operator
![]() $T_{\alpha }.$
We begin with the case
$T_{\alpha }.$
We begin with the case
![]() $2\leq p\leq +\infty .$
$2\leq p\leq +\infty .$
Proposition 2.1 Let
![]() $2\leq p\leq +\infty $
,
$2\leq p\leq +\infty $
,
![]() $\alpha \in \mathbb {R}$
and
$\alpha \in \mathbb {R}$
and
![]() $f\in H(\mathbb {D})$
. Assume that f is a frequently hypercyclic vector for
$f\in H(\mathbb {D})$
. Assume that f is a frequently hypercyclic vector for
![]() $T_{\alpha }$
. Then, for all
$T_{\alpha }$
. Then, for all
![]() $0<r<1,$
the following estimates hold:
$0<r<1,$
the following estimates hold:
 $$\begin{align*}M_p(r,f)\gtrsim \begin{cases} (1-r)^{\alpha-\frac{1}{2}}&\text{if } \alpha<1/2,\\ \sqrt{\vert\log(1-r)\vert}&\text{if } \alpha=1/2,\\ 1&\text{if } \alpha>1/2. \end{cases}\end{align*}$$
$$\begin{align*}M_p(r,f)\gtrsim \begin{cases} (1-r)^{\alpha-\frac{1}{2}}&\text{if } \alpha<1/2,\\ \sqrt{\vert\log(1-r)\vert}&\text{if } \alpha=1/2,\\ 1&\text{if } \alpha>1/2. \end{cases}\end{align*}$$
Proof We write
![]() $f(z)=a_0+\sum _{k\geq 1}a_{k}k^{-\alpha }z^{k}$
. Since f is frequently hypercyclic, there exists an increasing subsequence
$f(z)=a_0+\sum _{k\geq 1}a_{k}k^{-\alpha }z^{k}$
. Since f is frequently hypercyclic, there exists an increasing subsequence
![]() $(n_{k})\subset \mathbb {N}$
with positive lower density such that, for all
$(n_{k})\subset \mathbb {N}$
with positive lower density such that, for all
![]() $k\geq 1, \vert T_{\alpha }^{n_k}f(0)-3/2\vert =\vert a_{n_k}-3/2\vert <1/2$
, which implies that
$k\geq 1, \vert T_{\alpha }^{n_k}f(0)-3/2\vert =\vert a_{n_k}-3/2\vert <1/2$
, which implies that
![]() $\vert a_{n_k}\vert \geq 1$
. Moreover, since the sequence
$\vert a_{n_k}\vert \geq 1$
. Moreover, since the sequence
![]() $(n_{k})$
has positive lower density, there exists
$(n_{k})$
has positive lower density, there exists
![]() $C>1$
such that
$C>1$
such that
![]() $k \leq n_{k}\leq Ck$
. Let us consider a positive integer
$k \leq n_{k}\leq Ck$
. Let us consider a positive integer
![]() $l\geq 1$
. For any
$l\geq 1$
. For any
![]() $r\in [1-2^{-l},1-2^{-(l+1)}],$
Jensen’s inequality and Parseval’s Theorem imply
$r\in [1-2^{-l},1-2^{-(l+1)}],$
Jensen’s inequality and Parseval’s Theorem imply
 $$\begin{align*}[M_p(r,f)]^{2}\geq \big[M_p(1-2^{-l},f)\big]^{2}\geq \sum_{k\geq 1}\frac{\vert a_{k}\vert ^{2}}{k^{2\alpha}} (1-2^{-l} )^{2k}.\end{align*}$$
$$\begin{align*}[M_p(r,f)]^{2}\geq \big[M_p(1-2^{-l},f)\big]^{2}\geq \sum_{k\geq 1}\frac{\vert a_{k}\vert ^{2}}{k^{2\alpha}} (1-2^{-l} )^{2k}.\end{align*}$$
Thus, we deduce
 $$ \begin{align*} [M_p(r,f)]^{2} &\geq \sum_{k\geq 1} \frac{\vert a_{n_{k}}\vert ^{2}}{n_{k}^{2\alpha}}\left(1-2^{-l}\right)^{2n_{k}} \geq \sum_{k\geq 1}\frac{\left(1-2^{-l}\right)^{2Ck}}{(Ck)^{2\alpha}} \gtrsim \sum_{k=1}^{2^l}k^{-2\alpha}\\ &\gtrsim \begin{cases} 1 &\text{if } \alpha>\frac{1}{2},\\ 2^{(1-2\alpha)l}&\text{if } \alpha<\frac{1}{2},\\ \log(2^l)&\text{if } \alpha=\frac{1}{2}. \end{cases} \end{align*} $$
$$ \begin{align*} [M_p(r,f)]^{2} &\geq \sum_{k\geq 1} \frac{\vert a_{n_{k}}\vert ^{2}}{n_{k}^{2\alpha}}\left(1-2^{-l}\right)^{2n_{k}} \geq \sum_{k\geq 1}\frac{\left(1-2^{-l}\right)^{2Ck}}{(Ck)^{2\alpha}} \gtrsim \sum_{k=1}^{2^l}k^{-2\alpha}\\ &\gtrsim \begin{cases} 1 &\text{if } \alpha>\frac{1}{2},\\ 2^{(1-2\alpha)l}&\text{if } \alpha<\frac{1}{2},\\ \log(2^l)&\text{if } \alpha=\frac{1}{2}. \end{cases} \end{align*} $$
To conclude, it suffices to observe that for all
![]() $l\geq 1,$
if we have
$l\geq 1,$
if we have
![]() $r\in [1-2^{-l},1-2^{-(l+1)}]$
, then
$r\in [1-2^{-l},1-2^{-(l+1)}]$
, then
![]() $1-r\leq 2^{-l}\leq 2(1-r).$
Thus, we deduce for any
$1-r\leq 2^{-l}\leq 2(1-r).$
Thus, we deduce for any
 $\frac {1}{2}<r<1,$
$\frac {1}{2}<r<1,$
 $$ \begin{align*} M_p(r,f) \gtrsim \begin{cases} 1 &\text{ if } \alpha>\frac{1}{2},\\ (1-r)^{\alpha-\frac{1}{2}} &\text{ if } \alpha<\frac{1}{2},\\ \sqrt{\vert \log(1-r)\vert} &\text{ if } \alpha=\frac{1}{2}. \end{cases} \end{align*} $$
$$ \begin{align*} M_p(r,f) \gtrsim \begin{cases} 1 &\text{ if } \alpha>\frac{1}{2},\\ (1-r)^{\alpha-\frac{1}{2}} &\text{ if } \alpha<\frac{1}{2},\\ \sqrt{\vert \log(1-r)\vert} &\text{ if } \alpha=\frac{1}{2}. \end{cases} \end{align*} $$
▪
Using a similar method, we obtain the following estimates for the case
![]() $p\in (1,2).$
$p\in (1,2).$
Proposition 2.2 Let
![]() $1<p<2$
,
$1<p<2$
,
![]() $\alpha \in \mathbb {R}$
and
$\alpha \in \mathbb {R}$
and
![]() $f\in H(\mathbb {D})$
. Assume that f is a frequently hypercyclic vector for
$f\in H(\mathbb {D})$
. Assume that f is a frequently hypercyclic vector for
![]() $T_{\alpha }$
. Then, for all
$T_{\alpha }$
. Then, for all
![]() $0<r<1,$
the following estimates hold:
$0<r<1,$
the following estimates hold:
 $$\begin{align*}M_p(r,f) \gtrsim \begin{cases} (1-r)^{\alpha-\frac{1}{p'}}&\mathrm{if }\,\alpha<1/p',\\ \vert\log(1-r)\vert^{\frac{1}{p}}&\mathrm{ if }\,\alpha=1/p',\\ 1&\mathrm{ if }\,\alpha>1/p', \end{cases}\end{align*}$$
$$\begin{align*}M_p(r,f) \gtrsim \begin{cases} (1-r)^{\alpha-\frac{1}{p'}}&\mathrm{if }\,\alpha<1/p',\\ \vert\log(1-r)\vert^{\frac{1}{p}}&\mathrm{ if }\,\alpha=1/p',\\ 1&\mathrm{ if }\,\alpha>1/p', \end{cases}\end{align*}$$
with
 $\frac {1}{p}+\frac {1}{p'}=1.$
$\frac {1}{p}+\frac {1}{p'}=1.$
Proof We write
![]() $f(z)=a_0+\sum _{k\geq 1}a_{k}k^{-\alpha }z^{k}$
. Since f is frequently hypercyclic, there exists an increasing subsequence
$f(z)=a_0+\sum _{k\geq 1}a_{k}k^{-\alpha }z^{k}$
. Since f is frequently hypercyclic, there exists an increasing subsequence
![]() $(n_{k})\subset \mathbb {N}$
with positive lower density such that, for all
$(n_{k})\subset \mathbb {N}$
with positive lower density such that, for all
![]() $k\geq 1, \vert T_{\alpha }^{n_k}f(0)-3/2\vert =\vert a_{n_k}-3/2\vert <1/2$
, which implies that
$k\geq 1, \vert T_{\alpha }^{n_k}f(0)-3/2\vert =\vert a_{n_k}-3/2\vert <1/2$
, which implies that
![]() $\vert a_{n_k}\vert \geq 1$
. Moreover, since the sequence
$\vert a_{n_k}\vert \geq 1$
. Moreover, since the sequence
![]() $(n_{k})$
has positive lower density, there exists
$(n_{k})$
has positive lower density, there exists
![]() $C>1$
such that
$C>1$
such that
![]() $k \leq n_{k}\leq Ck$
. Let us consider a positive integer
$k \leq n_{k}\leq Ck$
. Let us consider a positive integer
![]() $l\geq 1$
.
$l\geq 1$
.
Case
 $\alpha \ne \frac {1}{p'}$
: from the Hausdorff–Young inequality (we refer the reader to [Reference Duren7]), we get, for any r in
$\alpha \ne \frac {1}{p'}$
: from the Hausdorff–Young inequality (we refer the reader to [Reference Duren7]), we get, for any r in
![]() $[1-2^{-l},1-2^{-(l+1)}]$
,
$[1-2^{-l},1-2^{-(l+1)}]$
,
 $$ \begin{align*} [M_p(r,f)]^{p'} &\geq\big[M_p(1-2^{-l},f)\big]^{p'} \geq \sum_{k\geq 1}\frac{\vert a_{k}\vert ^{p'}}{k^{\alpha p'}} (1-2^{-l} )^{kp'}\\[-6pt] &\geq \sum_{k\geq 1}\frac{\vert a_{n_{k}}\vert ^{p'}}{n_{k}^{\alpha p'}} (1-2^{-l} )^{n_{k}p'}. \end{align*} $$
$$ \begin{align*} [M_p(r,f)]^{p'} &\geq\big[M_p(1-2^{-l},f)\big]^{p'} \geq \sum_{k\geq 1}\frac{\vert a_{k}\vert ^{p'}}{k^{\alpha p'}} (1-2^{-l} )^{kp'}\\[-6pt] &\geq \sum_{k\geq 1}\frac{\vert a_{n_{k}}\vert ^{p'}}{n_{k}^{\alpha p'}} (1-2^{-l} )^{n_{k}p'}. \end{align*} $$
Thus, we have
 $$\begin{align*}[M_p(r,f)]^{p'}\geq \sum_{k\geq 1}\frac{\left(1-2^{-l}\right)^{Ckp'}}{(Ck)^{\alpha p'}} \gtrsim \sum_{k=1}^{2^{l}}k^{-\alpha p'} \gtrsim \begin{cases} 1 &\text{ if } \alpha>\frac{1}{p'}\\ 2^{(1-\alpha p')l}&\text{ if } \alpha<\frac{1}{p'}. \end{cases}\end{align*}$$
$$\begin{align*}[M_p(r,f)]^{p'}\geq \sum_{k\geq 1}\frac{\left(1-2^{-l}\right)^{Ckp'}}{(Ck)^{\alpha p'}} \gtrsim \sum_{k=1}^{2^{l}}k^{-\alpha p'} \gtrsim \begin{cases} 1 &\text{ if } \alpha>\frac{1}{p'}\\ 2^{(1-\alpha p')l}&\text{ if } \alpha<\frac{1}{p'}. \end{cases}\end{align*}$$
Hence, we obtain
 $$\begin{align*}M_p(r,f)\gtrsim \begin{cases} 1 &\text{ if } p'\alpha>1,\\ {(1-r)}^{\alpha -\frac{1}{p'}} &\text{ if } p'\alpha<1. \end{cases}\end{align*}$$
$$\begin{align*}M_p(r,f)\gtrsim \begin{cases} 1 &\text{ if } p'\alpha>1,\\ {(1-r)}^{\alpha -\frac{1}{p'}} &\text{ if } p'\alpha<1. \end{cases}\end{align*}$$
Case
 $\alpha = \frac {1}{p'}$
: we use a Hardy–Littewood inequality [Reference Duren7, Theorem 6.2] to obtain for any
$\alpha = \frac {1}{p'}$
: we use a Hardy–Littewood inequality [Reference Duren7, Theorem 6.2] to obtain for any
![]() $r\in [1-2^{-l},1-2^{-(l+1)}],$
$r\in [1-2^{-l},1-2^{-(l+1)}],$
 $$\begin{align*}[M_p(r,f)]^{p}\geq \big[M_p(1-2^{-l},f)\big]^{p} \geq \sum_{k\geq 1}\vert a_{k}\vert ^{p}k^{-\frac{p}{p'}} (1+k)^{p-2}\left(1-2^{-l}\right)^{kp}.\end{align*}$$
$$\begin{align*}[M_p(r,f)]^{p}\geq \big[M_p(1-2^{-l},f)\big]^{p} \geq \sum_{k\geq 1}\vert a_{k}\vert ^{p}k^{-\frac{p}{p'}} (1+k)^{p-2}\left(1-2^{-l}\right)^{kp}.\end{align*}$$
Thus, we have
 $$ \begin{align*} \left[M_p(r,f)\right]^{p}&\geq \big[M_p(1-2^{-l},f)\big]^{p}\gtrsim \sum_{k\geq 1}\frac{\vert a_{n_{k}}\vert ^{p}}{n_{k}}\left(1-2^{-l}\right)^{n_{k}p} \\&\gtrsim \sum_{k\geq 1}\frac{\left(1-2^{-l}\right)^{Ckp}}{Ck} \gtrsim \displaystyle \sum_{k=1}^{2^l}\frac{1}{k} \gtrsim \log(2^l).\end{align*} $$
$$ \begin{align*} \left[M_p(r,f)\right]^{p}&\geq \big[M_p(1-2^{-l},f)\big]^{p}\gtrsim \sum_{k\geq 1}\frac{\vert a_{n_{k}}\vert ^{p}}{n_{k}}\left(1-2^{-l}\right)^{n_{k}p} \\&\gtrsim \sum_{k\geq 1}\frac{\left(1-2^{-l}\right)^{Ckp}}{Ck} \gtrsim \displaystyle \sum_{k=1}^{2^l}\frac{1}{k} \gtrsim \log(2^l).\end{align*} $$
Hence, we obtain
 $$ \begin{align*}M_p(r,f)\gtrsim \vert \log(1-r) \vert ^{\frac{1}{p}}.\end{align*} $$
$$ \begin{align*}M_p(r,f)\gtrsim \vert \log(1-r) \vert ^{\frac{1}{p}}.\end{align*} $$
▪
3 Proof of the Main Result
3.1 Definitions and Notation
The proof of Theorem 1.3 follows the construction given in [Reference Drasin and Saksman6]. In particular, we use the so-called Rudin–Shapiro polynomials (combined with the de la Vallée–Poussin polynomials), which have coefficients
![]() $\pm 1$
(or bounded by
$\pm 1$
(or bounded by
![]() $1$
) and an optimal growth of sup-norm (ultra-flat polynomials). Let us recall [Reference Drasin and Saksman6, Lemma 2.1], which records the result of Rudin–Shapiro [Reference Rudin12].
$1$
) and an optimal growth of sup-norm (ultra-flat polynomials). Let us recall [Reference Drasin and Saksman6, Lemma 2.1], which records the result of Rudin–Shapiro [Reference Rudin12].
-
(i) For each
 $N\geq 1$
, there is a trigonometric polynomial
$N\geq 1$
, there is a trigonometric polynomial
 $p_N=\sum _{k=0}^{N-1} \varepsilon _{N,k}e^{ik\theta }$
where
$p_N=\sum _{k=0}^{N-1} \varepsilon _{N,k}e^{ik\theta }$
where
 $\varepsilon _{N,k}=\pm 1$
for all
$\varepsilon _{N,k}=\pm 1$
for all
 $0\leq k\leq N-1,$
with at least half of the coefficients being
$0\leq k\leq N-1,$
with at least half of the coefficients being
 $+1$
and with
$+1$
and with  $$\begin{align*}\Vert p_{N}\Vert_{p}\leq 5\sqrt{N}\mbox{ for }p\in [2,+\infty].\end{align*}$$
$$\begin{align*}\Vert p_{N}\Vert_{p}\leq 5\sqrt{N}\mbox{ for }p\in [2,+\infty].\end{align*}$$
-
(ii) For each
 $N\geq 1$
, there is a trigonometric polynomial
$N\geq 1$
, there is a trigonometric polynomial
 $p_N^*=\sum _{k=0}^{N-1}a_{N,k}e^{ik\theta }$
where
$p_N^*=\sum _{k=0}^{N-1}a_{N,k}e^{ik\theta }$
where
 $\vert a_{N,k}\vert \leq 1$
for all
$\vert a_{N,k}\vert \leq 1$
for all
 $0\leq k\leq N-1,$
with at least
$0\leq k\leq N-1,$
with at least
 $\lfloor \frac {N}{4} \rfloor $
coefficients being
$\lfloor \frac {N}{4} \rfloor $
coefficients being
 $+1$
and with
$+1$
and with  $$\begin{align*}\|p^{*}_{N}\|_{p}\leq 3N^{1/p'}\mbox{ for }p\in [1,2].\end{align*}$$
$$\begin{align*}\|p^{*}_{N}\|_{p}\leq 3N^{1/p'}\mbox{ for }p\in [1,2].\end{align*}$$
We keep the notation adopted in [Reference Drasin and Saksman6]. For any given polynomial q with
 $q(z)=\sum _{j=0}^d bj z^j$
with
$q(z)=\sum _{j=0}^d bj z^j$
with
![]() $b_d\ne 0$
, we denote
$b_d\ne 0$
, we denote
![]() $d=\mbox {deg}(q)$
and
$d=\mbox {deg}(q)$
and
 $ \Vert q\Vert _{\ell ^1}=\sum _{j=0}^d\vert b_j\vert $
. We set
$ \Vert q\Vert _{\ell ^1}=\sum _{j=0}^d\vert b_j\vert $
. We set
![]() $ 2\mathbb {N}=\bigcup _{k\geq 1}\mathcal {A}_{k}$
where for any
$ 2\mathbb {N}=\bigcup _{k\geq 1}\mathcal {A}_{k}$
where for any
![]() $k\geq 1,$
$k\geq 1,$
 $ \mathcal {A}_{k}=\left \{2^{k}(2j-1);j\in \mathbb {N} \right \}.$
Denote by
$ \mathcal {A}_{k}=\left \{2^{k}(2j-1);j\in \mathbb {N} \right \}.$
Denote by
![]() $\mathcal {P}$
the countable set of polynomials with rational coefficients and let us also consider pairs
$\mathcal {P}$
the countable set of polynomials with rational coefficients and let us also consider pairs
![]() $(q,l)$
with
$(q,l)$
with
![]() $q\in \mathcal {P}$
and
$q\in \mathcal {P}$
and
![]() $l\in \mathbb {N}$
satisfying
$l\in \mathbb {N}$
satisfying
![]() $\Vert q\Vert _{\ell ^1}\leq l$
. Let us consider an enumeration
$\Vert q\Vert _{\ell ^1}\leq l$
. Let us consider an enumeration
![]() $(q_k)$
of
$(q_k)$
of
![]() $\mathcal {P}$
and a sequence
$\mathcal {P}$
and a sequence
![]() $(l_k)$
tending to
$(l_k)$
tending to
![]() $+\infty $
such that
$+\infty $
such that
![]() $\Vert q_k\Vert \leq l_k$
. Clearly,
$\Vert q_k\Vert \leq l_k$
. Clearly,
![]() $(q_k)$
is a dense set in
$(q_k)$
is a dense set in
![]() $H(\mathbb {D})$
. Hence, for any
$H(\mathbb {D})$
. Hence, for any
![]() $k\geq 1,$
we set
$k\geq 1,$
we set
![]() $d_k=\deg (q_k),$
and we have
$d_k=\deg (q_k),$
and we have
In our context, for any
![]() $\alpha \in \mathbb {R},$
we will also need to modify the family of polynomials
$\alpha \in \mathbb {R},$
we will also need to modify the family of polynomials
![]() $(q_{k})$
as follows: for any positive integer
$(q_{k})$
as follows: for any positive integer
![]() $k\geq 1,$
we set
$k\geq 1,$
we set
 $ \widetilde {q_{k}}(z)=\sum _{j=0}^{d_{k}}j^\alpha b_{j}^{(k)}z^{j}$
(we omit the dependance on
$ \widetilde {q_{k}}(z)=\sum _{j=0}^{d_{k}}j^\alpha b_{j}^{(k)}z^{j}$
(we omit the dependance on
![]() $\alpha $
in order to keep some readable notation).
$\alpha $
in order to keep some readable notation).
Let
![]() $\alpha $
be a real number and let
$\alpha $
be a real number and let
![]() $p\in (1,\infty ].$
For all integers
$p\in (1,\infty ].$
For all integers
![]() $n\geq 0,$
we set
$n\geq 0,$
we set
![]() $I_{n}=\{2^{n},\ldots ,2^{n+1}-1\}.$
Next, for
$I_{n}=\{2^{n},\ldots ,2^{n+1}-1\}.$
Next, for
![]() $k\geq 1,$
let us define the integers
$k\geq 1,$
let us define the integers
 $$ \begin{align*} \alpha_{k}&=1+ \big\lfloor \max\big(l_{k}^{2}d_{k}^{2\max(\alpha, 0)},d_{k}+ \max(3,3+\alpha)l_{k}^2+\max(\alpha, 0)l_{k}\log(1+d_{k})\big)\big\rfloor,\\ \alpha^{*}_{k}&=1+ \big\lfloor \max\big(l_{k}^{p'}d_{k}^{p'\max(\alpha, 0)},d_{k}+\max(3,3+\alpha)l_{k}^2+\max(\alpha, 0)l_{k}\log(1+d_{k}) \big)\big\rfloor. \end{align*} $$
$$ \begin{align*} \alpha_{k}&=1+ \big\lfloor \max\big(l_{k}^{2}d_{k}^{2\max(\alpha, 0)},d_{k}+ \max(3,3+\alpha)l_{k}^2+\max(\alpha, 0)l_{k}\log(1+d_{k})\big)\big\rfloor,\\ \alpha^{*}_{k}&=1+ \big\lfloor \max\big(l_{k}^{p'}d_{k}^{p'\max(\alpha, 0)},d_{k}+\max(3,3+\alpha)l_{k}^2+\max(\alpha, 0)l_{k}\log(1+d_{k}) \big)\big\rfloor. \end{align*} $$
We set
![]() $ f_{\alpha }=\sum _{n\geq 0}P_{n,\alpha }$
where the blocks
$ f_{\alpha }=\sum _{n\geq 0}P_{n,\alpha }$
where the blocks
![]() $(P_{n,\alpha })$
are polynomials defined as follows, using Rudin–Shapiro polynomials given by Lemma 3.1,
$(P_{n,\alpha })$
are polynomials defined as follows, using Rudin–Shapiro polynomials given by Lemma 3.1,
 $$ \begin{align} P_{n,\alpha}(z) = \begin{cases} 0 &\mbox{ if } n \mbox{ is odd, }\\ 0 &\mbox{ if } n\in \mathcal{A}_{k}\mbox{ and } 2^{n-1}<\alpha_{k},\\ z^{2^{n}}Q_{n}(z) &\mbox{ if } n\in \mathcal{A}_{k}\mbox{ and }2^{n-1}\geq \alpha_{k}, \end{cases} \end{align} $$
$$ \begin{align} P_{n,\alpha}(z) = \begin{cases} 0 &\mbox{ if } n \mbox{ is odd, }\\ 0 &\mbox{ if } n\in \mathcal{A}_{k}\mbox{ and } 2^{n-1}<\alpha_{k},\\ z^{2^{n}}Q_{n}(z) &\mbox{ if } n\in \mathcal{A}_{k}\mbox{ and }2^{n-1}\geq \alpha_{k}, \end{cases} \end{align} $$
with for
![]() $n\in \mathcal {A}_{k}$
,
$n\in \mathcal {A}_{k}$
,
 $$\begin{align*}Q_{n}(z)=\sum_{j\in I_{n}}j^{-\alpha}c_{j-2^{n}}^{(k)}z^{j-2^{n}},\end{align*}$$
$$\begin{align*}Q_{n}(z)=\sum_{j\in I_{n}}j^{-\alpha}c_{j-2^{n}}^{(k)}z^{j-2^{n}},\end{align*}$$
where the sequence
 $(c_{j}^{(k)})$
denotes the sequence of the coefficients of the polynomial given by
$(c_{j}^{(k)})$
denotes the sequence of the coefficients of the polynomial given by
 $z\mapsto p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor }(z^{\alpha _k})\tilde {q_{k}}(z)$
.
$z\mapsto p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor }(z^{\alpha _k})\tilde {q_{k}}(z)$
.
We also set
![]() $ f^{*}_{\alpha }=\sum _{n\geq 0}P^{*}_{n,\alpha }$
where the blocks
$ f^{*}_{\alpha }=\sum _{n\geq 0}P^{*}_{n,\alpha }$
where the blocks
![]() $(P^{*}_{n,\alpha })$
are polynomials defined as follows, using the de la Vallée–Poussin polynomials given by Lemma 3.1,
$(P^{*}_{n,\alpha })$
are polynomials defined as follows, using the de la Vallée–Poussin polynomials given by Lemma 3.1,
 $$ \begin{align} P^{*}_{n,\alpha}(z) = \begin{cases} 0 &\mbox{ if } n \mbox{ is odd, }\\ 0 &\mbox{ if } n\in \mathcal{A}_{k}\mbox{ and } 2^{n-1}<\alpha^{*}_{k},\\ \displaystyle z^{2^{n}}Q_{n}^{*}(z)&\mbox{ if } n\in \mathcal{A}_{k}\mbox{ and } 2^{n-1}\geq\alpha^{*}_{k}, \end{cases} \end{align} $$
$$ \begin{align} P^{*}_{n,\alpha}(z) = \begin{cases} 0 &\mbox{ if } n \mbox{ is odd, }\\ 0 &\mbox{ if } n\in \mathcal{A}_{k}\mbox{ and } 2^{n-1}<\alpha^{*}_{k},\\ \displaystyle z^{2^{n}}Q_{n}^{*}(z)&\mbox{ if } n\in \mathcal{A}_{k}\mbox{ and } 2^{n-1}\geq\alpha^{*}_{k}, \end{cases} \end{align} $$
with, for
![]() $n\in \mathcal {A}_{k}$
,
$n\in \mathcal {A}_{k}$
,
 $$\begin{align*}Q_{n}^{*}(z)=\sum\limits_{j\in I_{n}}j^{-\alpha}c_{j-2^{n}}^{(k)}z^{j-2^{n}},\end{align*}$$
$$\begin{align*}Q_{n}^{*}(z)=\sum\limits_{j\in I_{n}}j^{-\alpha}c_{j-2^{n}}^{(k)}z^{j-2^{n}},\end{align*}$$
where the sequence
 $(c_{j}^{(k)})$
denotes the sequence of the coefficients of the polynomial given by
$(c_{j}^{(k)})$
denotes the sequence of the coefficients of the polynomial given by
 $z\mapsto \displaystyle p^{*}_{\lfloor \frac {2^{n-1}}{\alpha ^{*}_{k}} \rfloor }(z^{\alpha ^{*}_{k}})\widetilde {q_{k}}(z)$
.
$z\mapsto \displaystyle p^{*}_{\lfloor \frac {2^{n-1}}{\alpha ^{*}_{k}} \rfloor }(z^{\alpha ^{*}_{k}})\widetilde {q_{k}}(z)$
.
A combination of Lemma 3.2 (resp. Lemma 3.3) below with the triangle inequality will ensure that the function
![]() $f_{\alpha }$
(resp.
$f_{\alpha }$
(resp.
![]() $f_{\alpha }^*$
) belongs to
$f_{\alpha }^*$
) belongs to
![]() $H(\mathbb {D})$
. Observe that, if we denote the polynomial
$H(\mathbb {D})$
. Observe that, if we denote the polynomial
 $z\mapsto p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor }(z^{\alpha _k})$
(resp.
$z\mapsto p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor }(z^{\alpha _k})$
(resp.
 $z\mapsto p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor }^*(z^{\alpha _k^*})$
) by
$z\mapsto p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor }^*(z^{\alpha _k^*})$
) by
![]() $g_k$
(resp.
$g_k$
(resp.
![]() $g_k^*$
), we have, for all
$g_k^*$
), we have, for all
 $1\leq p\leq +\infty , \Vert g_k \Vert _p= \Vert p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor }\Vert _p$
(resp.
$1\leq p\leq +\infty , \Vert g_k \Vert _p= \Vert p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor }\Vert _p$
(resp.
 $\Vert g_k^* \Vert _p=\Vert p_{\lfloor \frac {2^{n-1}}{\alpha _{k}^*} \rfloor }^*\Vert _p$
). Finally, for any integer n, let us denote
$\Vert g_k^* \Vert _p=\Vert p_{\lfloor \frac {2^{n-1}}{\alpha _{k}^*} \rfloor }^*\Vert _p$
). Finally, for any integer n, let us denote
![]() $(\phi _n(k))$
the sequence defined as follows
$(\phi _n(k))$
the sequence defined as follows
 $$\begin{align*}\phi_{n}(k)= \begin{cases}k^{-\alpha}&\mbox{ if }k\in I_n,\\ 0&\mbox{ otherwise.} \end{cases}\end{align*}$$
$$\begin{align*}\phi_{n}(k)= \begin{cases}k^{-\alpha}&\mbox{ if }k\in I_n,\\ 0&\mbox{ otherwise.} \end{cases}\end{align*}$$
3.2 Growth of Specific Functions: the
 $L^{p}-$
case for
$L^{p}-$
case for
 $1<p<+\infty $
$1<p<+\infty $
In this subsection, for all
![]() $1<p<+\infty $
, we are going to construct specific functions
$1<p<+\infty $
, we are going to construct specific functions
![]() $f\in H(\mathbb {D})$
and we shall study their growth. We will appeal to a strong form of the Marcinkiewicz Multiplier Theorem (we refer the reader to [Reference Edwards and Gaudry8]) to deal with all the cases except for the critical cases (i.e.,
$f\in H(\mathbb {D})$
and we shall study their growth. We will appeal to a strong form of the Marcinkiewicz Multiplier Theorem (we refer the reader to [Reference Edwards and Gaudry8]) to deal with all the cases except for the critical cases (i.e.,
 $\alpha =\frac {1}{2}$
when
$\alpha =\frac {1}{2}$
when
![]() $p\geq 2$
and
$p\geq 2$
and
 $\alpha =\frac {1}{p'}$
when
$\alpha =\frac {1}{p'}$
when
![]() $1<p<2$
) where we will use a Paley–Littlewood decomposition or a method of interpolation to conclude. We begin this section with some useful lemmas.
$1<p<2$
) where we will use a Paley–Littlewood decomposition or a method of interpolation to conclude. We begin this section with some useful lemmas.
Lemma 3.2 For any
![]() $2\leq p<+\infty ,$
any
$2\leq p<+\infty ,$
any
![]() $0<r<1$
and any
$0<r<1$
and any
![]() $n\in \mathbb {N},$
we have
$n\in \mathbb {N},$
we have
 $$\begin{align*}M_p(r,P_{n,\alpha})\lesssim 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}}.\end{align*}$$
$$\begin{align*}M_p(r,P_{n,\alpha})\lesssim 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}}.\end{align*}$$
Proof Let
![]() $2\leq p<+\infty .$
Let n be a positive integer. Without loss of generality, we can assume that n belongs to the set
$2\leq p<+\infty .$
Let n be a positive integer. Without loss of generality, we can assume that n belongs to the set
![]() $\mathcal {A}_{k}$
for some
$\mathcal {A}_{k}$
for some
![]() $k\geq 1$
. Let r be in
$k\geq 1$
. Let r be in
![]() $(0,1).$
Since
$(0,1).$
Since
![]() $\displaystyle r \mapsto M_p(r,\cdot )$
is increasing, we get
$\displaystyle r \mapsto M_p(r,\cdot )$
is increasing, we get
 $$\begin{align*}M_p(r,P_{n,\alpha})\leq r^{2^{n}}\|Q_{n}\|_{p}.\end{align*}$$
$$\begin{align*}M_p(r,P_{n,\alpha})\leq r^{2^{n}}\|Q_{n}\|_{p}.\end{align*}$$
Then the polynomial
![]() $Q_{n}$
can be viewed as a trigonometric polynomial obtained by an abstract convolution operator on
$Q_{n}$
can be viewed as a trigonometric polynomial obtained by an abstract convolution operator on
![]() $\mathbb {T},$
given by
$\mathbb {T},$
given by
 $(c_{k})_{k\geq 0} \mapsto (\phi _{n}(j)c_{j-2^{n}}^{(k)})_{j\geq 0}$
(where
$(c_{k})_{k\geq 0} \mapsto (\phi _{n}(j)c_{j-2^{n}}^{(k)})_{j\geq 0}$
(where
 $(c_{j}^{(k)})$
denotes the sequence of the coefficients of the polynomial
$(c_{j}^{(k)})$
denotes the sequence of the coefficients of the polynomial
 $ p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor }\widetilde {q_{k}}$
). Now, we are going to apply the Marcinkiewicz Multiplier Theorem [Reference Edwards and Gaudry8, Theorem 8.2 p. 148]. To do this, observe that we have, for any
$ p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor }\widetilde {q_{k}}$
). Now, we are going to apply the Marcinkiewicz Multiplier Theorem [Reference Edwards and Gaudry8, Theorem 8.2 p. 148]. To do this, observe that we have, for any
![]() $l\geq 1,$
$l\geq 1,$
 $$ \begin{align*}\mathop{\text{sup}}\limits_{j\in I_{l}}\vert \phi_{n}(j) \vert &\leq\mathop{\text{sup}}\limits_{j\in I_{n}}\vert \phi_{n}(j) \vert \lesssim 2^{-n\alpha},\\ \mathop{\text{sup}}\limits_{l}\sum_{j\in I_{l}}\vert \phi_{n}(j+1)-\phi_{n}(j)\vert &\leq \sum_{j\in I_{n}}\vert \phi_{n}(j+1)-\phi_{n}(j)\vert \lesssim 2^{-n\alpha}. \end{align*} $$
$$ \begin{align*}\mathop{\text{sup}}\limits_{j\in I_{l}}\vert \phi_{n}(j) \vert &\leq\mathop{\text{sup}}\limits_{j\in I_{n}}\vert \phi_{n}(j) \vert \lesssim 2^{-n\alpha},\\ \mathop{\text{sup}}\limits_{l}\sum_{j\in I_{l}}\vert \phi_{n}(j+1)-\phi_{n}(j)\vert &\leq \sum_{j\in I_{n}}\vert \phi_{n}(j+1)-\phi_{n}(j)\vert \lesssim 2^{-n\alpha}. \end{align*} $$
Hence, taking into account the choice of
![]() $\alpha _k$
and Lemma 3.1, we get
$\alpha _k$
and Lemma 3.1, we get
 $$ \begin{align*} \|Q_{n}\|_{p} & \lesssim 2^{-n\alpha} \Vert p_{\lfloor \frac{2^{n-1}}{\alpha_{k}}\rfloor}\Vert_{p} \|\tilde{q_{k}}\|_{\infty}\\ & \lesssim 2^{-n\alpha} \sqrt{\frac{2^{n}}{\alpha_{k}}}\ l_{k}(1+d_{k})^{\max(\alpha,0)}\\ & \lesssim 2^{n(\frac{1}{2}-\alpha)}.\end{align*} $$
$$ \begin{align*} \|Q_{n}\|_{p} & \lesssim 2^{-n\alpha} \Vert p_{\lfloor \frac{2^{n-1}}{\alpha_{k}}\rfloor}\Vert_{p} \|\tilde{q_{k}}\|_{\infty}\\ & \lesssim 2^{-n\alpha} \sqrt{\frac{2^{n}}{\alpha_{k}}}\ l_{k}(1+d_{k})^{\max(\alpha,0)}\\ & \lesssim 2^{n(\frac{1}{2}-\alpha)}.\end{align*} $$
Finally, we obtain the desired estimate
 $$ \begin{align*} M_p(r,P_{n,\alpha})\lesssim 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}}. \end{align*} $$
$$ \begin{align*} M_p(r,P_{n,\alpha})\lesssim 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}}. \end{align*} $$
▪
Lemma 3.3 For any
![]() $1<p<2,$
any
$1<p<2,$
any
![]() $0<r<1,$
and any
$0<r<1,$
and any
![]() $n\in \mathbb {N},$
we have
$n\in \mathbb {N},$
we have
 $$\begin{align*}M_p(r,P^{*}_{n,\alpha})\lesssim 2^{n(\frac{1}{p'}-\alpha)}r^{2^{n}}.\end{align*}$$
$$\begin{align*}M_p(r,P^{*}_{n,\alpha})\lesssim 2^{n(\frac{1}{p'}-\alpha)}r^{2^{n}}.\end{align*}$$
Proof The proof is similar to that of Lemma 3.2. Let
![]() $1<p<2$
and n be a positive integer. Without loss of generality, we can assume that n belongs to the set
$1<p<2$
and n be a positive integer. Without loss of generality, we can assume that n belongs to the set
![]() $\mathcal {A}_{k}$
for some
$\mathcal {A}_{k}$
for some
![]() $k\geq 1$
. Let r be in
$k\geq 1$
. Let r be in
![]() $(0,1).$
Again, combining the Marcinkiewicz Multiplier Theorem with Lemma 3.1 and the choice of
$(0,1).$
Again, combining the Marcinkiewicz Multiplier Theorem with Lemma 3.1 and the choice of
![]() $\alpha ^{*}_{k}$
, we obtain
$\alpha ^{*}_{k}$
, we obtain
 $$\begin{align*}\|Q_{n}^{*}\|_{p} \lesssim 2^{-n\alpha} \|p^{*}_{\lfloor \frac{2^{n-1}}{\alpha_{k}^*}\rfloor}\|_{p} \|\tilde{q_{k}}\|_{\infty} \lesssim 2^{-n\alpha} \Big(\frac{2^{n}}{\alpha^{*}_{k}}\Big)^{\frac{1}{p'}}l_{k}(1+d_{k})^{\max(\alpha, 0)} \lesssim 2^{n(\frac{1}{p'}-\alpha)}.\end{align*}$$
$$\begin{align*}\|Q_{n}^{*}\|_{p} \lesssim 2^{-n\alpha} \|p^{*}_{\lfloor \frac{2^{n-1}}{\alpha_{k}^*}\rfloor}\|_{p} \|\tilde{q_{k}}\|_{\infty} \lesssim 2^{-n\alpha} \Big(\frac{2^{n}}{\alpha^{*}_{k}}\Big)^{\frac{1}{p'}}l_{k}(1+d_{k})^{\max(\alpha, 0)} \lesssim 2^{n(\frac{1}{p'}-\alpha)}.\end{align*}$$
Finally, using (3.2), we deduce the desired estimate. ▪
Now we are ready to obtain the rate of growth of the aforementioned functions
![]() $f_{\alpha }$
and
$f_{\alpha }$
and
![]() $f^*_{\alpha }.$
We begin with the case
$f^*_{\alpha }.$
We begin with the case
![]() $2\leq p<+\infty $
.
$2\leq p<+\infty $
.
Lemma 3.4 Let
![]() $2\leq p<+\infty .$
For all
$2\leq p<+\infty .$
For all
![]() $0<r<1,$
the following estimates hold:
$0<r<1,$
the following estimates hold:
 $$\begin{align*}M_p(r,f_{\alpha})\lesssim \begin{cases} (1-r)^{\alpha-\frac{1}{2}}&\mbox{ if }\alpha<1/2,\\ \sqrt{\vert\log (1-r)\vert}&\mbox{ if }\alpha=1/2,\\ 1&\mbox{ if }\alpha>1/2.\end{cases}\end{align*}$$
$$\begin{align*}M_p(r,f_{\alpha})\lesssim \begin{cases} (1-r)^{\alpha-\frac{1}{2}}&\mbox{ if }\alpha<1/2,\\ \sqrt{\vert\log (1-r)\vert}&\mbox{ if }\alpha=1/2,\\ 1&\mbox{ if }\alpha>1/2.\end{cases}\end{align*}$$
Proof Let
![]() $2\leq p<+\infty .$
Let us recall that
$2\leq p<+\infty .$
Let us recall that
![]() $ f_{\alpha }=\sum _{n\geq 0}P_{n,\alpha }.$
First, we deal with the case
$ f_{\alpha }=\sum _{n\geq 0}P_{n,\alpha }.$
First, we deal with the case
 $\alpha>\frac {1}{2}.$
Combining Lemma 3.2 with the triangle inequality, we obtain, for any r in
$\alpha>\frac {1}{2}.$
Combining Lemma 3.2 with the triangle inequality, we obtain, for any r in
![]() $(0,1),$
$(0,1),$
 $$\begin{align*}M_p(r,f_{\alpha})\leq \sum\limits_{n\geq 0}M_p(r,P_{n,\alpha})\lesssim \sum\limits_{n\geq 0} 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}} \lesssim 1.\end{align*}$$
$$\begin{align*}M_p(r,f_{\alpha})\leq \sum\limits_{n\geq 0}M_p(r,P_{n,\alpha})\lesssim \sum\limits_{n\geq 0} 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}} \lesssim 1.\end{align*}$$
Then we treat the case
 $\alpha <\frac {1}{2}$
. Combining Lemma 3.2 with the triangle inequality and the integral comparison test, we get, for any r in
$\alpha <\frac {1}{2}$
. Combining Lemma 3.2 with the triangle inequality and the integral comparison test, we get, for any r in
![]() $(0,1),$
$(0,1),$
 $$\begin{align*}M_p(r,f_{\alpha}) \leq \sum\limits_{n\geq 0}M_p(r,P_{n,\alpha})\lesssim \sum\limits_{n\geq 0}2^{n(\frac{1}{2}-\alpha)}r^{2^{n}} \lesssim (1-r)^{\alpha-\frac{1}{2}}.\end{align*}$$
$$\begin{align*}M_p(r,f_{\alpha}) \leq \sum\limits_{n\geq 0}M_p(r,P_{n,\alpha})\lesssim \sum\limits_{n\geq 0}2^{n(\frac{1}{2}-\alpha)}r^{2^{n}} \lesssim (1-r)^{\alpha-\frac{1}{2}}.\end{align*}$$
Finally, for the case
 $\alpha =\frac {1}{2},$
we have by a corollary of the Paley–Littlewood decomposition (we refer the reader to [Reference Edwards and Gaudry8, Theorem 5.3.1]) and the integral comparison test
$\alpha =\frac {1}{2},$
we have by a corollary of the Paley–Littlewood decomposition (we refer the reader to [Reference Edwards and Gaudry8, Theorem 5.3.1]) and the integral comparison test
![]() $\forall 0<r<1$
,
$\forall 0<r<1$
,
 $$ \begin{align*} M_p(r,f_{\alpha}) &\lesssim \Big( \sum\limits_{n\geq 0} \left[M_p(r,P_{n,\alpha})\right]^{2} \Big)^{\frac{1}{2}} \lesssim \Big(\sum\limits_{n\geq 0}r^{2^{n}}\Big)^{\frac{1}{2}}\\&\lesssim \sqrt{\vert \log(1-r) \vert}.\end{align*} $$
$$ \begin{align*} M_p(r,f_{\alpha}) &\lesssim \Big( \sum\limits_{n\geq 0} \left[M_p(r,P_{n,\alpha})\right]^{2} \Big)^{\frac{1}{2}} \lesssim \Big(\sum\limits_{n\geq 0}r^{2^{n}}\Big)^{\frac{1}{2}}\\&\lesssim \sqrt{\vert \log(1-r) \vert}.\end{align*} $$
▪
Next we deal with the case
![]() $1<p<2$
. The following result holds.
$1<p<2$
. The following result holds.
Lemma 3.5 Let
![]() $1<p<2$
. For all
$1<p<2$
. For all
![]() $0<r<1,$
the following estimates hold:
$0<r<1,$
the following estimates hold:
 $$\begin{align*}M_p(r,f_{\alpha}^{*})\lesssim \begin{cases} (1-r)^{\alpha-\frac{1}{p'}}&\mbox{ if }\alpha<1/p',\\ \vert\log (1-r)\vert^{\frac{1}{p}}&\mbox{ if }\alpha=1/p',\\ 1&\mbox{ if }\alpha>1/p'.\end{cases}\end{align*}$$
$$\begin{align*}M_p(r,f_{\alpha}^{*})\lesssim \begin{cases} (1-r)^{\alpha-\frac{1}{p'}}&\mbox{ if }\alpha<1/p',\\ \vert\log (1-r)\vert^{\frac{1}{p}}&\mbox{ if }\alpha=1/p',\\ 1&\mbox{ if }\alpha>1/p'.\end{cases}\end{align*}$$
Proof Let
![]() $1<p<2$
. Let us recall that
$1<p<2$
. Let us recall that
![]() $ f^{*}_{\alpha }=\sum _{n\geq 0}P^{*}_{n,\alpha }.$
Then, applying Lemma 3.3, we obtain by the triangle inequality, for any
$ f^{*}_{\alpha }=\sum _{n\geq 0}P^{*}_{n,\alpha }.$
Then, applying Lemma 3.3, we obtain by the triangle inequality, for any
![]() $0<r<1,$
$0<r<1,$
 $$\begin{align*}M_p(r,f_{\alpha}^{*})\leq \sum\limits_{n\geq 0}M_p(r,P^{*}_{n,\alpha})\lesssim \sum\limits_{n\geq 0} 2^{n(\frac{1}{p'}-\alpha)}r^{2^{n}}.\end{align*}$$
$$\begin{align*}M_p(r,f_{\alpha}^{*})\leq \sum\limits_{n\geq 0}M_p(r,P^{*}_{n,\alpha})\lesssim \sum\limits_{n\geq 0} 2^{n(\frac{1}{p'}-\alpha)}r^{2^{n}}.\end{align*}$$
Therefore, using a straightforward estimate or the integral comparison test, we get, for any
![]() $0<r<1,$
$0<r<1,$
 $$\begin{align*}M_p(r,f_{\alpha}^{*})\lesssim \begin{cases} 1&\mbox{ if } p'\alpha>1,\\ (1-r)^{\alpha-\frac{1}{p'}}&\mbox{ if } p'\alpha<1. \end{cases}\end{align*}$$
$$\begin{align*}M_p(r,f_{\alpha}^{*})\lesssim \begin{cases} 1&\mbox{ if } p'\alpha>1,\\ (1-r)^{\alpha-\frac{1}{p'}}&\mbox{ if } p'\alpha<1. \end{cases}\end{align*}$$
Finally, we deal with the case
 $\alpha =\frac {1}{p'}$
: first we have by the classical
$\alpha =\frac {1}{p'}$
: first we have by the classical
![]() $L^{p}$
Bernstein inequality
$L^{p}$
Bernstein inequality
 $$\begin{align*}M_p(r,(P_{n,\alpha}^{*})') \lesssim 2^{n}M_p(r,P_{n,\alpha}^{*})\lesssim 2^{n}r^{2^{n}}.\end{align*}$$
$$\begin{align*}M_p(r,(P_{n,\alpha}^{*})') \lesssim 2^{n}M_p(r,P_{n,\alpha}^{*})\lesssim 2^{n}r^{2^{n}}.\end{align*}$$
By an easy calculation, we deduce
 $$\begin{align*}M_p(r,(f_{\alpha}^{*})')\lesssim \sum_{n\geq 0}2^{n}r^{2^{n}} \lesssim \frac{1}{1-r}.\end{align*}$$
$$\begin{align*}M_p(r,(f_{\alpha}^{*})')\lesssim \sum_{n\geq 0}2^{n}r^{2^{n}} \lesssim \frac{1}{1-r}.\end{align*}$$
Hence, [Reference Girela and Peláez9, Theorem 2] gives the following conclusion, for any
![]() $0<r<1,$
$0<r<1,$
 $$ \begin{align*}M_p(r,f_{\alpha}^{*})\lesssim \vert \log(1-r) \vert^{\frac{1}{p}}.\end{align*} $$
$$ \begin{align*}M_p(r,f_{\alpha}^{*})\lesssim \vert \log(1-r) \vert^{\frac{1}{p}}.\end{align*} $$
▪
3.3 Growth of Specific Functions: the
 $L^{\infty }$
case
$L^{\infty }$
case
This part is based on the use of a weighted Bernstein inequality for the case
![]() $\alpha \leq 0$
. Then we proceed to an induction based on a fine control of derivatives, since the multipliers we are dealing with are extremely localized for the case
$\alpha \leq 0$
. Then we proceed to an induction based on a fine control of derivatives, since the multipliers we are dealing with are extremely localized for the case
![]() $\alpha \geq 0$
. Nonetheless, to deal with the critical case given by
$\alpha \geq 0$
. Nonetheless, to deal with the critical case given by
 $\alpha =\frac {1}{2}$
, we need to exploit the flatness of the Rudin–Shapiro polynomials.
$\alpha =\frac {1}{2}$
, we need to exploit the flatness of the Rudin–Shapiro polynomials.
We begin this section with some useful estimates of the sup norm of the aforementioned polynomials
![]() $P_{n,\alpha }$
.
$P_{n,\alpha }$
.
Lemma 3.6 For any
![]() $\alpha \leq 0$
and any integer
$\alpha \leq 0$
and any integer
![]() $n\geq 0,$
we have
$n\geq 0,$
we have
 $$\begin{align*}M_{\infty}(r,P_{n,\alpha}) \lesssim 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}}.\end{align*}$$
$$\begin{align*}M_{\infty}(r,P_{n,\alpha}) \lesssim 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}}.\end{align*}$$
Proof Let
![]() $\alpha \leq 0.$
Let n be an integer such that n belongs to
$\alpha \leq 0.$
Let n be an integer such that n belongs to
![]() $\mathcal {A}_{k}$
for some
$\mathcal {A}_{k}$
for some
![]() $k\geq 1$
. Then, using the form of the polynomial
$k\geq 1$
. Then, using the form of the polynomial
![]() $P_{n,\alpha }$
, Lemma 3.1, and a fractional Bernstein’s inequality (see [Reference Samko, Kilbas and Marichev13, Theorem 19.10 and Remark 19.5]), we obtain
$P_{n,\alpha }$
, Lemma 3.1, and a fractional Bernstein’s inequality (see [Reference Samko, Kilbas and Marichev13, Theorem 19.10 and Remark 19.5]), we obtain
 $$\begin{align*}M_{\infty}(r,P_{n,\alpha}) \lesssim 2^{-n\alpha}r^{2^{n}} \sqrt{\frac{2^{n}}{\alpha_{k}}}l_{k}.\end{align*}$$
$$\begin{align*}M_{\infty}(r,P_{n,\alpha}) \lesssim 2^{-n\alpha}r^{2^{n}} \sqrt{\frac{2^{n}}{\alpha_{k}}}l_{k}.\end{align*}$$
Finally, the choice of
![]() $\alpha _k$
ensures that
$\alpha _k$
ensures that
 $$ \begin{align*}M_{\infty}(r,P_{n,\alpha})\lesssim 2^{-n(\alpha-\frac{1}{2})}r^{2^{n}}.\end{align*} $$
$$ \begin{align*}M_{\infty}(r,P_{n,\alpha})\lesssim 2^{-n(\alpha-\frac{1}{2})}r^{2^{n}}.\end{align*} $$
▪
Then we complete the previous proof to obtain the following lemma.
Lemma 3.7 For any
![]() $\alpha \in \mathbb {R}$
and any integer
$\alpha \in \mathbb {R}$
and any integer
![]() $n\geq 0,$
we have
$n\geq 0,$
we have
 $$\begin{align*}M_{\infty}(r,P_{n,\alpha}) \lesssim 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}}.\end{align*}$$
$$\begin{align*}M_{\infty}(r,P_{n,\alpha}) \lesssim 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}}.\end{align*}$$
Proof In the case
![]() $\alpha \leq 0,$
the proof comes from Lemma 3.6. Assume now that
$\alpha \leq 0,$
the proof comes from Lemma 3.6. Assume now that
![]() $\alpha>0.$
First, we deal with the case
$\alpha>0.$
First, we deal with the case
![]() $0<\alpha \leq 1.$
We keep the notation of Section 3.1. Let
$0<\alpha \leq 1.$
We keep the notation of Section 3.1. Let
![]() $n\geq 1$
be an integer and assume that n belongs to
$n\geq 1$
be an integer and assume that n belongs to
![]() $\mathcal {A}_{k}$
for some
$\mathcal {A}_{k}$
for some
![]() $k\geq 1$
. Then we write
$k\geq 1$
. Then we write
 $$\begin{align*}P_{n,\alpha}(z)=\sum_{j\in I_{n}}\frac{u_{j}}{j^{\alpha}}z^{j}\quad\text{ and }\quad P'_{n,\alpha}(z)=\sum_{j\in I_{n}}\frac{u_{j}}{j^{\alpha-1}}z^{j-1}.\end{align*}$$
$$\begin{align*}P_{n,\alpha}(z)=\sum_{j\in I_{n}}\frac{u_{j}}{j^{\alpha}}z^{j}\quad\text{ and }\quad P'_{n,\alpha}(z)=\sum_{j\in I_{n}}\frac{u_{j}}{j^{\alpha-1}}z^{j-1}.\end{align*}$$
Since
![]() $\alpha -1\leq 0$
, it follows from the proof of Lemma 3.6 that
$\alpha -1\leq 0$
, it follows from the proof of Lemma 3.6 that
 $$\begin{align*}M_{\infty}(r,P'_{n,\alpha})\lesssim 2^{-n((\alpha-1)-\frac{1}{2})}r^{2^{n}-1}.\end{align*}$$
$$\begin{align*}M_{\infty}(r,P'_{n,\alpha})\lesssim 2^{-n((\alpha-1)-\frac{1}{2})}r^{2^{n}-1}.\end{align*}$$
We deduce, for any
![]() $\theta \in \mathbb {R}$
and any
$\theta \in \mathbb {R}$
and any
![]() $0<r<1,$
$0<r<1,$
 $$ \begin{align*} \vert P_{n,\alpha}(re^{i\theta}) \vert& =\bigg\vert \int_{0}^{r} e^{i\theta} P_{n,\alpha}'(te^{i\theta}) dt\bigg\vert \leq \int_{0}^{r} \vert P_{n,\alpha}'(te^{i\theta}) \vert dt\\ & \lesssim 2^{-n((\alpha-1)-\frac{1}{2})}\int_{0}^{r}t^{2^{n}-1}dt\\ & \lesssim 2^{-n(\alpha-\frac{1}{2})}r^{2^{n}}. \end{align*} $$
$$ \begin{align*} \vert P_{n,\alpha}(re^{i\theta}) \vert& =\bigg\vert \int_{0}^{r} e^{i\theta} P_{n,\alpha}'(te^{i\theta}) dt\bigg\vert \leq \int_{0}^{r} \vert P_{n,\alpha}'(te^{i\theta}) \vert dt\\ & \lesssim 2^{-n((\alpha-1)-\frac{1}{2})}\int_{0}^{r}t^{2^{n}-1}dt\\ & \lesssim 2^{-n(\alpha-\frac{1}{2})}r^{2^{n}}. \end{align*} $$
Finally, we obtain
 $$\begin{align*}M_{\infty}(r,P_{n,\alpha})\lesssim 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}}.\end{align*}$$
$$\begin{align*}M_{\infty}(r,P_{n,\alpha})\lesssim 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}}.\end{align*}$$
The general case (given by
![]() $\alpha \geq 0$
) follows by a straightforward induction on
$\alpha \geq 0$
) follows by a straightforward induction on
![]() $l\geq 0,$
which is the order of differentiation with
$l\geq 0,$
which is the order of differentiation with
![]() $l< \alpha \leq l+1$
.▪
$l< \alpha \leq l+1$
.▪
Now we are ready to estimate the rate of growth of the aforementioned function
![]() $f_{\alpha }.$
$f_{\alpha }.$
Lemma 3.8 For all
![]() $0<r<1,$
the following estimates hold:
$0<r<1,$
the following estimates hold:
 $$\begin{align*}M_{\infty}(r,f_{\alpha})\lesssim \begin{cases} (1-r)^{\alpha-\frac{1}{2}}&\mbox{ if }\alpha<1/2,\\ \vert\log(1-r)\vert&\mbox{ if }\alpha=1/2,\\ 1&\mbox{ if }\alpha>1/2.\end{cases}\end{align*}$$
$$\begin{align*}M_{\infty}(r,f_{\alpha})\lesssim \begin{cases} (1-r)^{\alpha-\frac{1}{2}}&\mbox{ if }\alpha<1/2,\\ \vert\log(1-r)\vert&\mbox{ if }\alpha=1/2,\\ 1&\mbox{ if }\alpha>1/2.\end{cases}\end{align*}$$
Proof Let us recall that
![]() $ f_{\alpha }=\sum _{n\geq 0}P_{n,\alpha }.$
Taking into account Lemma 3.7, we obtain—along the same lines as the proof of Lemma 3.4— on one hand, for
$ f_{\alpha }=\sum _{n\geq 0}P_{n,\alpha }.$
Taking into account Lemma 3.7, we obtain—along the same lines as the proof of Lemma 3.4— on one hand, for
 $\alpha>\frac {1}{2}$
and for any r in
$\alpha>\frac {1}{2}$
and for any r in
![]() $(0,1),$
$(0,1),$
 $$\begin{align*}M_{\infty}(r,f_{\alpha})\leq \sum\limits_{n\geq 0}M_{\infty}(r,P_{n,\alpha})\lesssim \sum\limits_{n\geq 0} 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}} \lesssim 1,\end{align*}$$
$$\begin{align*}M_{\infty}(r,f_{\alpha})\leq \sum\limits_{n\geq 0}M_{\infty}(r,P_{n,\alpha})\lesssim \sum\limits_{n\geq 0} 2^{n(\frac{1}{2}-\alpha)}r^{2^{n}} \lesssim 1,\end{align*}$$
on the other hand, for
 $\alpha <\frac {1}{2}$
and for any r in
$\alpha <\frac {1}{2}$
and for any r in
![]() $(0,1),$
$(0,1),$
 $$\begin{align*}M_{\infty}(r,f_{\alpha})\leq \sum\limits_{n\geq 0}M_{\infty}(r,P_{n,\alpha})\lesssim \sum\limits_{n\geq 0}2^{n(\frac{1}{2}-\alpha)}r^{2^{n}} \lesssim (1-r)^{\alpha-\frac{1}{2}}.\end{align*}$$
$$\begin{align*}M_{\infty}(r,f_{\alpha})\leq \sum\limits_{n\geq 0}M_{\infty}(r,P_{n,\alpha})\lesssim \sum\limits_{n\geq 0}2^{n(\frac{1}{2}-\alpha)}r^{2^{n}} \lesssim (1-r)^{\alpha-\frac{1}{2}}.\end{align*}$$
Finally the case
![]() $\alpha =1/2$
is easy: Lemma 3.7 implies
$\alpha =1/2$
is easy: Lemma 3.7 implies
 $$\begin{align*}M_{\infty}(r,f_{\frac{1}{2}})\leq \sum\limits_{n\geq 0}M_{\infty}(r,P_{n,\frac{1}{2}})\lesssim \sum\limits_{n\geq 0} r^{2^{n}},\end{align*}$$
$$\begin{align*}M_{\infty}(r,f_{\frac{1}{2}})\leq \sum\limits_{n\geq 0}M_{\infty}(r,P_{n,\frac{1}{2}})\lesssim \sum\limits_{n\geq 0} r^{2^{n}},\end{align*}$$
and the estimate
 $\sum _{n\geq 0} r^{2^{n}}\lesssim \vert \log (1-r)\vert $
gives the conclusion. ▪
$\sum _{n\geq 0} r^{2^{n}}\lesssim \vert \log (1-r)\vert $
gives the conclusion. ▪
3.4 Frequent Hypercyclicity
In this subsection, we are going to prove that the functions
![]() $f_{\alpha }$
and
$f_{\alpha }$
and
![]() $f^{*}_{\alpha }$
given by Section 3.1 are frequently hypercyclic vectors for the weighted Taylor shift operator
$f^{*}_{\alpha }$
given by Section 3.1 are frequently hypercyclic vectors for the weighted Taylor shift operator
![]() $T_{\alpha }, \alpha \in \mathbb {R}$
. The construction of these elements and the proof of this crucial fact are an adaptation of the ideas given by Drasin and Saksman in the case of Mac–Lane differentiation operator [Reference Drasin and Saksman6].
$T_{\alpha }, \alpha \in \mathbb {R}$
. The construction of these elements and the proof of this crucial fact are an adaptation of the ideas given by Drasin and Saksman in the case of Mac–Lane differentiation operator [Reference Drasin and Saksman6].
Lemma 3.9 We keep the notation of Section 3.1. For
![]() $p\geq 2$
(resp.
$p\geq 2$
(resp.
![]() $1<p<2$
), the function
$1<p<2$
), the function
![]() $f_{\alpha }$
(resp.
$f_{\alpha }$
(resp.
![]() $f^{*}_{\alpha }$
) is a frequently hypercyclic vector for the operator
$f^{*}_{\alpha }$
) is a frequently hypercyclic vector for the operator
![]() $T_{\alpha }$
.
$T_{\alpha }$
.
Proof Since the proof for
![]() $f^{*}_{\alpha }$
is very similar, we only prove the frequent hypercyclicity of
$f^{*}_{\alpha }$
is very similar, we only prove the frequent hypercyclicity of
![]() $f_{\alpha }$
for the operator
$f_{\alpha }$
for the operator
![]() $T_{\alpha }$
. We do not repeat the details for
$T_{\alpha }$
. We do not repeat the details for
![]() $f^{*}_{\alpha }$
: it suffices to replace
$f^{*}_{\alpha }$
: it suffices to replace
![]() $\alpha _k$
and
$\alpha _k$
and
 $p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor } $
by
$p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor } $
by
![]() $\alpha _k^*$
and
$\alpha _k^*$
and
 $p_{\lfloor \frac {2^{n-1}}{\alpha _{k}^*} \rfloor }^* $
and to adapt the proof.
$p_{\lfloor \frac {2^{n-1}}{\alpha _{k}^*} \rfloor }^* $
and to adapt the proof.
Let k be a large enough integer. Let us consider
![]() $n\in \mathcal {A}_{k}$
such that
$n\in \mathcal {A}_{k}$
such that
![]() $2^{n-1}\geq \alpha _{k}.$
We consider
$2^{n-1}\geq \alpha _{k}.$
We consider
![]() $\mathcal {B}_{n}$
the set of s in
$\mathcal {B}_{n}$
the set of s in
![]() $[2^{n},2^{n+1}]\cap \mathbb {N}$
such that the coefficient
$[2^{n},2^{n+1}]\cap \mathbb {N}$
such that the coefficient
![]() $z^{s}$
in the polynomial
$z^{s}$
in the polynomial
 $z^{2^{n}}p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor }(z^{\alpha _{k}})$
is equal to
$z^{2^{n}}p_{\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor }(z^{\alpha _{k}})$
is equal to
![]() $1$
. We denote by
$1$
. We denote by
 $\displaystyle T_{k}=\left \{s: s\in \mathcal {B}_{n},\ n\in \mathcal {A}_{k}, \ 2^{n-1}\geq \alpha _{k}\right \}.$
According to Lemma 3.1, we have
$\displaystyle T_{k}=\left \{s: s\in \mathcal {B}_{n},\ n\in \mathcal {A}_{k}, \ 2^{n-1}\geq \alpha _{k}\right \}.$
According to Lemma 3.1, we have
 $$\begin{align*}\#\mathcal{B}_{n}\geq \frac{2^{n}}{10\alpha_{k}}=\frac{\#(\{2^{n},\ldots,2^{n+1}-1\})}{10\alpha_{k}}= \frac{\#(\{2^{n},\ldots,2^{n+2}-1\})}{30\alpha_{k}}.\end{align*}$$
$$\begin{align*}\#\mathcal{B}_{n}\geq \frac{2^{n}}{10\alpha_{k}}=\frac{\#(\{2^{n},\ldots,2^{n+1}-1\})}{10\alpha_{k}}= \frac{\#(\{2^{n},\ldots,2^{n+2}-1\})}{30\alpha_{k}}.\end{align*}$$
Since the elements of
![]() $\mathcal {A}_{k}$
are in arithmetic progression, we finally obtain that
$\mathcal {A}_{k}$
are in arithmetic progression, we finally obtain that
![]() $T_k$
has positive lower density.
$T_k$
has positive lower density.
Then let
![]() $\alpha $
be a real number and let k be in
$\alpha $
be a real number and let k be in
![]() $\mathbb {N}$
. Now let us consider
$\mathbb {N}$
. Now let us consider
![]() $s\in \mathcal {B}_{n}$
with
$s\in \mathcal {B}_{n}$
with
![]() $n\in \mathcal {A}_{k}$
satisfying
$n\in \mathcal {A}_{k}$
satisfying
![]() $2^{n-1}\geq \alpha _{k}.$
We are going to prove that
$2^{n-1}\geq \alpha _{k}.$
We are going to prove that
 $$\begin{align*}\mathop{\mathrm{sup}}\limits_{\vert z\vert = 1-\frac{1}{l_{k}}} \vert T_{\alpha}^{s}(f_{\alpha})(z)-q_{k}(z)\vert \lesssim \frac{1}{l_{k}},\end{align*}$$
$$\begin{align*}\mathop{\mathrm{sup}}\limits_{\vert z\vert = 1-\frac{1}{l_{k}}} \vert T_{\alpha}^{s}(f_{\alpha})(z)-q_{k}(z)\vert \lesssim \frac{1}{l_{k}},\end{align*}$$
provided that k is chosen large enough. This will allow us to obtain the frequent hypercyclicity property of
![]() $T_{\alpha }$
using the properties of the enumeration
$T_{\alpha }$
using the properties of the enumeration
![]() $(q_k,l_k)$
. Therefore, to do this, we choose an even integer
$(q_k,l_k)$
. Therefore, to do this, we choose an even integer
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $s\in \mathcal {B}_n$
. Let us write
$s\in \mathcal {B}_n$
. Let us write
![]() $s=2^{n}+m\alpha _{k}$
for some
$s=2^{n}+m\alpha _{k}$
for some
 $m\in \{0,\dots ,\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor \}$
with
$m\in \{0,\dots ,\lfloor \frac {2^{n-1}}{\alpha _{k}} \rfloor \}$
with
 $$\begin{align*}z^{2^{n}}p_{\lfloor \frac{2^{n-1}}{\alpha_{k}} \rfloor}(z^{\alpha_{k}})=\cdots+ \textbf{1}z^{s}+\cdots .\end{align*}$$
$$\begin{align*}z^{2^{n}}p_{\lfloor \frac{2^{n-1}}{\alpha_{k}} \rfloor}(z^{\alpha_{k}})=\cdots+ \textbf{1}z^{s}+\cdots .\end{align*}$$
By the choice of
![]() $\alpha _{k}$
, the next block of coefficients is dissociated from the present one because of the condition
$\alpha _{k}$
, the next block of coefficients is dissociated from the present one because of the condition
![]() $\displaystyle \alpha _{k}+d_{k}<2\alpha _{k}.$
Hence, using the form of the polynomials
$\displaystyle \alpha _{k}+d_{k}<2\alpha _{k}.$
Hence, using the form of the polynomials
![]() $\tilde {q_{k}}$
and the definition of
$\tilde {q_{k}}$
and the definition of
![]() $T_{\alpha }$
, we have that the first
$T_{\alpha }$
, we have that the first
![]() $d_{k}$
Taylor coefficients of
$d_{k}$
Taylor coefficients of
![]() $T_{\alpha }^{s}(f_{\alpha })$
are precisely those of
$T_{\alpha }^{s}(f_{\alpha })$
are precisely those of
![]() $q_{k}.$
Notice again by the choice of
$q_{k}.$
Notice again by the choice of
![]() $\alpha _{k}$
(or
$\alpha _{k}$
(or
![]() $\alpha ^{*}_{k}$
) that the Taylor coefficients of
$\alpha ^{*}_{k}$
) that the Taylor coefficients of
![]() $T_{\alpha }^{s}(f_{\alpha })$
of index j with
$T_{\alpha }^{s}(f_{\alpha })$
of index j with
![]() $\displaystyle s+d_{k}+1\leq j \leq s+\left (\max (3,3+\alpha )\right )l_{k}^2+\max (\alpha ,0)l_{k}\log (d_{k})$
are null. Moreover, since n is an even integer, by the construction of each block
$\displaystyle s+d_{k}+1\leq j \leq s+\left (\max (3,3+\alpha )\right )l_{k}^2+\max (\alpha ,0)l_{k}\log (d_{k})$
are null. Moreover, since n is an even integer, by the construction of each block
![]() $P_{n}$
, all the coefficients having indexes lying in
$P_{n}$
, all the coefficients having indexes lying in
![]() $[2^{n+1},2^{n+2}-1]$
are also null. Indeed, the last index that belongs to
$[2^{n+1},2^{n+2}-1]$
are also null. Indeed, the last index that belongs to
![]() $\mathcal {B}_n$
is bounded from above by
$\mathcal {B}_n$
is bounded from above by
![]() $2^n+2^{n-1}+d_k<2^{n+1}$
(by the choice of n such that
$2^n+2^{n-1}+d_k<2^{n+1}$
(by the choice of n such that
![]() $2^n\geq 2\alpha _k\geq 2d_k$
). Therefore, we can write
$2^n\geq 2\alpha _k\geq 2d_k$
). Therefore, we can write
 $$ \begin{align*} T_{\alpha}^{s}(f_{\alpha})(z)-q_{k}(z) =&\sum_{ j_k\leq j \leq 2^{n+1}-1}\frac{c_{j}^{(k)}}{(j-s)^{\alpha}}z^{j-s} \\&+ \sum_{j=2^{n+2}}^{+\infty}\frac{c_{j}^{(k)}}{(j-s)^{\alpha}}z^{j-s} :=S_{1}(z)+S_{2}(z), \end{align*} $$
$$ \begin{align*} T_{\alpha}^{s}(f_{\alpha})(z)-q_{k}(z) =&\sum_{ j_k\leq j \leq 2^{n+1}-1}\frac{c_{j}^{(k)}}{(j-s)^{\alpha}}z^{j-s} \\&+ \sum_{j=2^{n+2}}^{+\infty}\frac{c_{j}^{(k)}}{(j-s)^{\alpha}}z^{j-s} :=S_{1}(z)+S_{2}(z), \end{align*} $$
where
![]() $j_k= s+\left (\max (3,3+\alpha )\right )l_{k}^2+\max (\alpha , 0)l_{k}\log (1+d_{k}).$
By the construction of
$j_k= s+\left (\max (3,3+\alpha )\right )l_{k}^2+\max (\alpha , 0)l_{k}\log (1+d_{k}).$
By the construction of
![]() $f_{\alpha }$
, we observe for any
$f_{\alpha }$
, we observe for any
![]() $j\in \displaystyle [j_k,2^{n+1}-1]\cap \mathbb {N}$
that all the coefficients
$j\in \displaystyle [j_k,2^{n+1}-1]\cap \mathbb {N}$
that all the coefficients
 $c_{j}^{(k)}$
coincide with the coefficients of
$c_{j}^{(k)}$
coincide with the coefficients of
![]() $\tilde {q_{k}}$
possibly multiplied by some coefficient bounded by
$\tilde {q_{k}}$
possibly multiplied by some coefficient bounded by
![]() $1$
. Therefore, we obtain, for any
$1$
. Therefore, we obtain, for any
![]() $j\in \displaystyle [j_k,2^{n+1}-1]\cap \mathbb {N},$
the following estimate:
$j\in \displaystyle [j_k,2^{n+1}-1]\cap \mathbb {N},$
the following estimate:
 $$\begin{align*}\displaystyle \vert c_{j}^{(k)} \vert \leq \|\tilde{q_{k}}\|_{\ell_{1}}\leq d_{k}^{\max(\alpha, 0)}l_{k}.\end{align*}$$
$$\begin{align*}\displaystyle \vert c_{j}^{(k)} \vert \leq \|\tilde{q_{k}}\|_{\ell_{1}}\leq d_{k}^{\max(\alpha, 0)}l_{k}.\end{align*}$$
Hence, we get, by the triangle inequality and from the basic inequality
![]() $1-t\leq e^{-t}$
for
$1-t\leq e^{-t}$
for
![]() $t>0$
,
$t>0$
,
 $$ \begin{align*} \mathop{\text{sup}}\limits_{\vert z\vert=1-\frac{1}{l_{k}}}\vert S_{1}(z) \vert & \leq d_{k}^{\max(\alpha, 0)}l_{k}\sum\limits_{j\geq j_k}\max((j-s)^{-\alpha},1) \Big(1-\frac{1}{l_{k}}\Big)^{j-s}\\ & \leq d_{k}^{\max(\alpha, 0)}l_{k}\sum\limits_{j\geq j_k-s}\max(j^{-\alpha},1)e^{-\frac{j}{l_{k}}}. \end{align*} $$
$$ \begin{align*} \mathop{\text{sup}}\limits_{\vert z\vert=1-\frac{1}{l_{k}}}\vert S_{1}(z) \vert & \leq d_{k}^{\max(\alpha, 0)}l_{k}\sum\limits_{j\geq j_k}\max((j-s)^{-\alpha},1) \Big(1-\frac{1}{l_{k}}\Big)^{j-s}\\ & \leq d_{k}^{\max(\alpha, 0)}l_{k}\sum\limits_{j\geq j_k-s}\max(j^{-\alpha},1)e^{-\frac{j}{l_{k}}}. \end{align*} $$
For
![]() $\alpha>0$
, thanks to the inequality
$\alpha>0$
, thanks to the inequality
![]() $t/3\leq 1-e^{-t}$
, for
$t/3\leq 1-e^{-t}$
, for
![]() $0<t<1$
, we get
$0<t<1$
, we get
 $$\begin{align*}\mathop{\mathrm{sup}}\limits_{\vert z\vert=1-\frac{1}{l_{k}}}\vert S_{1}(z) \vert\leq d_k^{\alpha}l_k\sum\limits_{j\geq j_k-s}e^{-\frac{j}{l_{k}}}\leq \frac{d_k^{\alpha}l_k}{1-e^{-1/l_k}}e^{-(3+\alpha)l_k-\alpha\log(1+d_k)}\leq \frac{3}{l_k}.\end{align*}$$
$$\begin{align*}\mathop{\mathrm{sup}}\limits_{\vert z\vert=1-\frac{1}{l_{k}}}\vert S_{1}(z) \vert\leq d_k^{\alpha}l_k\sum\limits_{j\geq j_k-s}e^{-\frac{j}{l_{k}}}\leq \frac{d_k^{\alpha}l_k}{1-e^{-1/l_k}}e^{-(3+\alpha)l_k-\alpha\log(1+d_k)}\leq \frac{3}{l_k}.\end{align*}$$
In the same spirit, for
![]() $\alpha \leq 0$
, we get, for all k large enough,
$\alpha \leq 0$
, we get, for all k large enough,
 $$\begin{align*}\mathop{\mathrm{sup}}\limits_{\vert z\vert=1-\frac{1}{l_{k}}}\vert S_{1}(z) \vert \leq l_{k}\sum\limits_{j\geq j_k-s}j^{-\alpha}e^{-\frac{j}{l_{k}}} \lesssim l_k^2(3l_k^2)^{-\alpha}e^{-3l_k}\lesssim\frac{1}{l_{k}},\end{align*}$$
$$\begin{align*}\mathop{\mathrm{sup}}\limits_{\vert z\vert=1-\frac{1}{l_{k}}}\vert S_{1}(z) \vert \leq l_{k}\sum\limits_{j\geq j_k-s}j^{-\alpha}e^{-\frac{j}{l_{k}}} \lesssim l_k^2(3l_k^2)^{-\alpha}e^{-3l_k}\lesssim\frac{1}{l_{k}},\end{align*}$$
using an integral comparison test.
Now we deal with the sum
![]() $S_2(z).$
Combining the growth of
$S_2(z).$
Combining the growth of
![]() $f_{\alpha }$
given by Section 3.3 with Cauchy formula’s along the radii
$f_{\alpha }$
given by Section 3.3 with Cauchy formula’s along the radii
![]() $r=1-1/j,$
we get, for any
$r=1-1/j,$
we get, for any
![]() $j\geq 1,$
$j\geq 1,$
 $$\begin{align*}\vert c_{j}^{(k)} \vert \leq C_{p} j^{\alpha} \max(j^{\frac{1}{2}-\alpha+\varepsilon},1) \lesssim j^{\max(\frac{1}{2}+\varepsilon, \alpha)},\end{align*}$$
$$\begin{align*}\vert c_{j}^{(k)} \vert \leq C_{p} j^{\alpha} \max(j^{\frac{1}{2}-\alpha+\varepsilon},1) \lesssim j^{\max(\frac{1}{2}+\varepsilon, \alpha)},\end{align*}$$
where
![]() $C_p>0$
only depends on p and
$C_p>0$
only depends on p and
![]() $0<\varepsilon \ll 1$
(which allows us to take into account the logarithmic factor for the case
$0<\varepsilon \ll 1$
(which allows us to take into account the logarithmic factor for the case
 $\alpha =\frac {1}{2}$
). Since we have both
$\alpha =\frac {1}{2}$
). Since we have both
![]() $\displaystyle 2^{n+1}\geq 4\alpha _{k}\geq 4\max (3,3+\alpha )l_k^2,$
which implies
$\displaystyle 2^{n+1}\geq 4\alpha _{k}\geq 4\max (3,3+\alpha )l_k^2,$
which implies
![]() $2^{n+1}\geq 4\alpha _{k}\geq 4\max (1, \alpha )l_{k}^2$
, and
$2^{n+1}\geq 4\alpha _{k}\geq 4\max (1, \alpha )l_{k}^2$
, and
![]() $\displaystyle \{j-s:j\geq 2^{n+2}\}\subset \{j\geq 2^{n+1}\},$
we obtain, provided that k is large enough again,
$\displaystyle \{j-s:j\geq 2^{n+2}\}\subset \{j\geq 2^{n+1}\},$
we obtain, provided that k is large enough again,
 $$ \begin{align*} \mathop{\text{sup}}\limits_{\vert z\vert=1-\frac{1}{l_{k}}}\vert S_{2}(z) \vert & \lesssim \sum_{j\geq 2^{n+1}}j^{\max(-\alpha, 0)} (j+s)^{\max(\frac{1}{2}+\varepsilon, \alpha)}\Big(1-\frac{1}{l_{k}}\Big)^{j}\\ & \lesssim \sum_{j\geq 2^{n+1}}j^{\max(\frac{1}{2}+\varepsilon,\frac{1}{2}+\varepsilon-\alpha,\alpha)}e^{-\frac{j}{l_{k}}}\\ & \lesssim \int_{4\max(1, \alpha)l_{k}^2}^{+\infty}t^{\max(\frac{1}{2}+\varepsilon,\frac{1}{2}+\varepsilon-\alpha,\alpha)} e^{-\frac{t}{l_{k}}}dt. \end{align*} $$
$$ \begin{align*} \mathop{\text{sup}}\limits_{\vert z\vert=1-\frac{1}{l_{k}}}\vert S_{2}(z) \vert & \lesssim \sum_{j\geq 2^{n+1}}j^{\max(-\alpha, 0)} (j+s)^{\max(\frac{1}{2}+\varepsilon, \alpha)}\Big(1-\frac{1}{l_{k}}\Big)^{j}\\ & \lesssim \sum_{j\geq 2^{n+1}}j^{\max(\frac{1}{2}+\varepsilon,\frac{1}{2}+\varepsilon-\alpha,\alpha)}e^{-\frac{j}{l_{k}}}\\ & \lesssim \int_{4\max(1, \alpha)l_{k}^2}^{+\infty}t^{\max(\frac{1}{2}+\varepsilon,\frac{1}{2}+\varepsilon-\alpha,\alpha)} e^{-\frac{t}{l_{k}}}dt. \end{align*} $$
Taking into consideration the different cases, an easy calculation leads to the following inequality:
 $$\begin{align*}\mathop{\mathrm{sup}}\limits_{\vert z\vert=1-\frac{1}{l_{k}}}\vert S_{2}(z) \vert \lesssim l_{k}^{\beta(\alpha)+1}l_k^{\beta(\alpha)}e^{-4\max(1, \alpha)l_k}\lesssim \frac{1}{l_{k}},\end{align*}$$
$$\begin{align*}\mathop{\mathrm{sup}}\limits_{\vert z\vert=1-\frac{1}{l_{k}}}\vert S_{2}(z) \vert \lesssim l_{k}^{\beta(\alpha)+1}l_k^{\beta(\alpha)}e^{-4\max(1, \alpha)l_k}\lesssim \frac{1}{l_{k}},\end{align*}$$
with
![]() $\beta (\alpha )=\max \left (1/2+\varepsilon ,1/2+\varepsilon -\alpha , \alpha \right ).$
This finishes the proof. ▪
$\beta (\alpha )=\max \left (1/2+\varepsilon ,1/2+\varepsilon -\alpha , \alpha \right ).$
This finishes the proof. ▪
3.5 Final Step
Now we are ready to prove Theorem 1.3. To do this, it suffices to combine Lemma 3.9 with:
-
Proposition 2.1 and Lemma 3.4, in the case
 $2\leq p<+\infty $
;
$2\leq p<+\infty $
; -
Proposition 2.1 and Lemma 3.8, in the case
 $p=+\infty $
;
$p=+\infty $
; -
Proposition 2.2 and Lemma 3.5, in the case
 $1<p<2$
.
$1<p<2$
.
Remark 3.10 For
![]() $p=+\infty $
and
$p=+\infty $
and
 $\alpha =\frac {1}{2},$
there is still a question: what is the optimal growth of a frequently hypercyclic vector for
$\alpha =\frac {1}{2},$
there is still a question: what is the optimal growth of a frequently hypercyclic vector for
![]() $T_{\frac {1}{2}}$
? According to Proposition 2.1, such an element f satisfies, for any
$T_{\frac {1}{2}}$
? According to Proposition 2.1, such an element f satisfies, for any
 $0<r<1, M_{\infty }(r,f)\gtrsim \sqrt {\vert \log (1-r)\vert }$
. On the other hand, Lemmas 3.8 and 3.9 ensure that there exists frequently hypercyclic vector f for
$0<r<1, M_{\infty }(r,f)\gtrsim \sqrt {\vert \log (1-r)\vert }$
. On the other hand, Lemmas 3.8 and 3.9 ensure that there exists frequently hypercyclic vector f for
![]() $T_{\frac {1}{2}}$
such that, for any
$T_{\frac {1}{2}}$
such that, for any
![]() $0<r<1, M_{\infty }(r,f)\lesssim \vert \log (1-r)\vert $
.
$0<r<1, M_{\infty }(r,f)\lesssim \vert \log (1-r)\vert $
.
4 The Case
 $p=1$
$p=1$
To conclude, let us consider the case
![]() $p=1$
. First it is easy to obtain the following estimates. The proof follows the ideas of Proposition 2.1. The case
$p=1$
. First it is easy to obtain the following estimates. The proof follows the ideas of Proposition 2.1. The case
![]() $\alpha =0$
was already known [Reference Mouze and Munnier11].
$\alpha =0$
was already known [Reference Mouze and Munnier11].
Proposition 4.1 Let
![]() $\alpha \in \mathbb {R}$
and
$\alpha \in \mathbb {R}$
and
![]() $f\in H(\mathbb {D})$
. Assume that f is a frequently hypercyclic vector for
$f\in H(\mathbb {D})$
. Assume that f is a frequently hypercyclic vector for
![]() $T_{\alpha }$
. Then, for all
$T_{\alpha }$
. Then, for all
![]() $0<r<1,$
the following estimates hold:
$0<r<1,$
the following estimates hold:
 $$\begin{align*}M_1(r,f)\gtrsim \begin{cases}(1-r)^{\alpha}&\mathrm{ if }\,\alpha<0,\\ -\log(1-r)&\mathrm{ if }\,\alpha=0,\\ 1&\mathrm{ if }\,\alpha>0. \end{cases}\end{align*}$$
$$\begin{align*}M_1(r,f)\gtrsim \begin{cases}(1-r)^{\alpha}&\mathrm{ if }\,\alpha<0,\\ -\log(1-r)&\mathrm{ if }\,\alpha=0,\\ 1&\mathrm{ if }\,\alpha>0. \end{cases}\end{align*}$$
Proof We write
![]() $f(z)=a_0+\sum _{k\geq 1}a_{k}k^{-\alpha }z^{k}$
. We argue as in the beginning of the proof of Proposition 2.1 to find an increasing subsequence
$f(z)=a_0+\sum _{k\geq 1}a_{k}k^{-\alpha }z^{k}$
. We argue as in the beginning of the proof of Proposition 2.1 to find an increasing subsequence
![]() $(n_{k})\subset \mathbb {N}$
satisfying
$(n_{k})\subset \mathbb {N}$
satisfying
![]() $k \leq n_{k}\leq Ck$
with
$k \leq n_{k}\leq Ck$
with
![]() $C>1$
such that for all
$C>1$
such that for all
![]() $k,$
$k,$
![]() $\vert a_{n_k}\vert \geq 1$
. Let us consider a positive integer
$\vert a_{n_k}\vert \geq 1$
. Let us consider a positive integer
![]() $l\geq 1$
. For any
$l\geq 1$
. For any
![]() $r\in [1-2^{-l},1-2^{-(l+1)}],$
we apply Hardy’s inequality to obtain
$r\in [1-2^{-l},1-2^{-(l+1)}],$
we apply Hardy’s inequality to obtain
 $$ \begin{align*} M_1(r,f)&\geq M_1(1-2^{-l},f)\geq \sum\limits_{k\geq 1}\frac{\vert a_{k}\vert }{k^{\alpha+1}}\left(1-2^{-l}\right)^{k}\\ &\geq \sum\limits_{k\geq 1}\frac{\vert a_{n_{k}}\vert}{n_{k}^{\alpha+1}} \left(1-2^{-l}\right)^{n_{k}} \geq \sum\limits_{k\geq 1}\frac{\left(1-2^{-l}\right)^{Ck}}{(Ck)^{\alpha +1}}\\& \gtrsim \sum_{k=1}^{2^l}k^{-\alpha-1} \gtrsim \begin{cases} (1-r)^{\alpha}&\mbox{ if }\alpha<0,\\ -\log(1-r)&\mbox{ if }\alpha=0,\\ 1&\mbox{ if }\alpha>0. \end{cases} \end{align*} $$
$$ \begin{align*} M_1(r,f)&\geq M_1(1-2^{-l},f)\geq \sum\limits_{k\geq 1}\frac{\vert a_{k}\vert }{k^{\alpha+1}}\left(1-2^{-l}\right)^{k}\\ &\geq \sum\limits_{k\geq 1}\frac{\vert a_{n_{k}}\vert}{n_{k}^{\alpha+1}} \left(1-2^{-l}\right)^{n_{k}} \geq \sum\limits_{k\geq 1}\frac{\left(1-2^{-l}\right)^{Ck}}{(Ck)^{\alpha +1}}\\& \gtrsim \sum_{k=1}^{2^l}k^{-\alpha-1} \gtrsim \begin{cases} (1-r)^{\alpha}&\mbox{ if }\alpha<0,\\ -\log(1-r)&\mbox{ if }\alpha=0,\\ 1&\mbox{ if }\alpha>0. \end{cases} \end{align*} $$
▪
On the other hand, for
![]() $\alpha =0$
, we established the following result (see [Reference Mouze and Munnier11]), which gives in some sense the optimality of the estimate of Proposition 4.1. In the following, for any positive integer l, the notation
$\alpha =0$
, we established the following result (see [Reference Mouze and Munnier11]), which gives in some sense the optimality of the estimate of Proposition 4.1. In the following, for any positive integer l, the notation
![]() $\log _l$
will stand for the iterated function
$\log _l$
will stand for the iterated function
![]() $\log \circ \dots \circ \log $
where
$\log \circ \dots \circ \log $
where
![]() $\log $
appears l times.
$\log $
appears l times.
Theorem 4.2 ([Reference Mouze and Munnier11])
For any
![]() $l\geq 1$
, there is a frequently hypercyclic function
$l\geq 1$
, there is a frequently hypercyclic function
![]() $f\in H(\mathbb {D})$
for T satisfying the following estimate: there exists
$f\in H(\mathbb {D})$
for T satisfying the following estimate: there exists
![]() $C>0$
such that for every
$C>0$
such that for every
![]() $0<r<1$
sufficiently large,
$0<r<1$
sufficiently large,
 $$\begin{align*}M_1(r,f)\leq C\big\vert\log(1-r)\big\vert \log_{l}\big(-\log(1-r)\big).\end{align*}$$
$$\begin{align*}M_1(r,f)\leq C\big\vert\log(1-r)\big\vert \log_{l}\big(-\log(1-r)\big).\end{align*}$$
For
![]() $\alpha \ne 0,$
we are going to combine the ideas of [Reference Mouze and Munnier11] with those of Subsection 3.3 to obtain a similar result. Let
$\alpha \ne 0,$
we are going to combine the ideas of [Reference Mouze and Munnier11] with those of Subsection 3.3 to obtain a similar result. Let
![]() $l\geq 1$
. We also set
$l\geq 1$
. We also set
![]() $ f^{*}_{\alpha }=\sum _{n\geq 0}P^{*}_{n,\alpha }$
where the blocks
$ f^{*}_{\alpha }=\sum _{n\geq 0}P^{*}_{n,\alpha }$
where the blocks
![]() $(P^{*}_{n,\alpha })$
are polynomials defined as in (3.2), with
$(P^{*}_{n,\alpha })$
are polynomials defined as in (3.2), with
 $$\begin{align*}\alpha^{*}_{k}=1+ \left\lfloor \max\left(u_{k},d_{k}+\max(3,3+\alpha)l_{k}^2+\max(\alpha, 0)l_{k}\log(1+d_{k}) \right)\right\rfloor,\end{align*}$$
$$\begin{align*}\alpha^{*}_{k}=1+ \left\lfloor \max\left(u_{k},d_{k}+\max(3,3+\alpha)l_{k}^2+\max(\alpha, 0)l_{k}\log(1+d_{k}) \right)\right\rfloor,\end{align*}$$
where
![]() $u_{k}$
is chosen such that
$u_{k}$
is chosen such that
![]() $\log _{l+1}(\alpha _{k}^*)\geq l_{k}$
.
$\log _{l+1}(\alpha _{k}^*)\geq l_{k}$
.
Lemma 4.3 We have for any
![]() $\alpha \in \mathbb {R}$
, for all
$\alpha \in \mathbb {R}$
, for all
![]() $n\in \mathbb {N,}$
and for any
$n\in \mathbb {N,}$
and for any
![]() $r\in (0,1),$
$r\in (0,1),$
 $$\begin{align*}M_1(r,P^{*}_{n,\alpha})\lesssim r^{2^{n}}2^{-n\alpha} l_{k}.\end{align*}$$
$$\begin{align*}M_1(r,P^{*}_{n,\alpha})\lesssim r^{2^{n}}2^{-n\alpha} l_{k}.\end{align*}$$
Proof We argue as in the proof of Lemmas 3.6 and 3.7. First, let
![]() $\alpha \leq 0.$
Then, by the maximum principle, we can write
$\alpha \leq 0.$
Then, by the maximum principle, we can write
 $$ \begin{align} M_1(r,P_{n,\alpha}^*)&\leq \frac{r^{2^n}}{2\pi}\int_0^{2\pi}\big\vert Q_{n}^*(re^{it})\big\vert dt\nonumber\\ & = \frac{r^{2^n}}{2\pi}\int_0^{2\pi}\Big\vert \sum_{j\in I_n}j^{-\alpha}c_{j-2^n}^{(k)}(re^{it})^{j-2^n}\Big\vert dt. \end{align} $$
$$ \begin{align} M_1(r,P_{n,\alpha}^*)&\leq \frac{r^{2^n}}{2\pi}\int_0^{2\pi}\big\vert Q_{n}^*(re^{it})\big\vert dt\nonumber\\ & = \frac{r^{2^n}}{2\pi}\int_0^{2\pi}\Big\vert \sum_{j\in I_n}j^{-\alpha}c_{j-2^n}^{(k)}(re^{it})^{j-2^n}\Big\vert dt. \end{align} $$
Let us consider the trigonometric polynomials
 $$\begin{align*}U_{n,\alpha}(e^{i\theta})=\sum_{j\in I_n}j^{-\alpha}c_{j-2^n}^{(k)}r^{j-2^n} e^{ij\theta}\quad \mbox{ and }\quad V_{n}(e^{i\theta})=\sum_{j\in I_n}c_{j-2^n}^{(k)}r^{j-2^n} e^{ij\theta}.\end{align*}$$
$$\begin{align*}U_{n,\alpha}(e^{i\theta})=\sum_{j\in I_n}j^{-\alpha}c_{j-2^n}^{(k)}r^{j-2^n} e^{ij\theta}\quad \mbox{ and }\quad V_{n}(e^{i\theta})=\sum_{j\in I_n}c_{j-2^n}^{(k)}r^{j-2^n} e^{ij\theta}.\end{align*}$$
Observe that
 $$ \begin{align} \sum_{j\in I_n}j^{-\alpha}c_{j-2^n}^{(k)}(re^{i\theta})^{j-2^n} =e^{-i2^n\theta}U_{n,\alpha}(e^{i\theta})\quad\mbox{ and }\quad q_{n,k}^*(e^{i\theta})=e^{-i2^n\theta}V_{n}(e^{i\theta}). \end{align} $$
$$ \begin{align} \sum_{j\in I_n}j^{-\alpha}c_{j-2^n}^{(k)}(re^{i\theta})^{j-2^n} =e^{-i2^n\theta}U_{n,\alpha}(e^{i\theta})\quad\mbox{ and }\quad q_{n,k}^*(e^{i\theta})=e^{-i2^n\theta}V_{n}(e^{i\theta}). \end{align} $$
From (4.1), (4.2), and the fractional Bernstein’s inequality (see [Reference Samko, Kilbas and Marichev13, Theorem 19.10 and Remark 19.5]), we get
 $$\begin{align*}M_1(r,P_{n,\alpha}^*)\leq r^{2^n} \Vert U_{n,\alpha}\Vert_1 \lesssim r^{2^n} 2^{-(n+1)\alpha} \left\Vert V_{n}\right\Vert{}_1 =r^{2^n} 2^{-(n+1)\alpha}\Vert q_{n,k}^*\Vert_1.\end{align*}$$
$$\begin{align*}M_1(r,P_{n,\alpha}^*)\leq r^{2^n} \Vert U_{n,\alpha}\Vert_1 \lesssim r^{2^n} 2^{-(n+1)\alpha} \left\Vert V_{n}\right\Vert{}_1 =r^{2^n} 2^{-(n+1)\alpha}\Vert q_{n,k}^*\Vert_1.\end{align*}$$
Thus, using Lemma 3.1, we obtain
 $$ \begin{align} M_1(r,P_{n,\alpha}^*)\lesssim r^{2^n} 2^{-n\alpha}l_k. \end{align} $$
$$ \begin{align} M_1(r,P_{n,\alpha}^*)\lesssim r^{2^n} 2^{-n\alpha}l_k. \end{align} $$
Now let us consider the case
![]() $\alpha \in (0,1].$
Since we have, for any
$\alpha \in (0,1].$
Since we have, for any
![]() $r\in (0,1),$
$r\in (0,1),$
 $$ \begin{align*} \vert P^{*}_{n,\alpha}(re^{i\theta})\vert &= \Big\vert \int_{0}^{r}e^{i\theta}\left(P^{*}_{n,\alpha}\right)'(te^{i\theta})dt\Big\vert\\ &\leq \int_{0}^{r}\vert \left(P^{*}_{n,\alpha}\right)'(te^{i\theta})\vert dt=\int_{0}^{r} t^{-1}\vert P^{*}_{n,\alpha-1}(te^{i\theta})\vert dt,\end{align*} $$
$$ \begin{align*} \vert P^{*}_{n,\alpha}(re^{i\theta})\vert &= \Big\vert \int_{0}^{r}e^{i\theta}\left(P^{*}_{n,\alpha}\right)'(te^{i\theta})dt\Big\vert\\ &\leq \int_{0}^{r}\vert \left(P^{*}_{n,\alpha}\right)'(te^{i\theta})\vert dt=\int_{0}^{r} t^{-1}\vert P^{*}_{n,\alpha-1}(te^{i\theta})\vert dt,\end{align*} $$
we deduce, by integrating this inequality and using (4.3) with
![]() $\alpha -1\leq 0,$
$\alpha -1\leq 0,$
 $$\begin{align*}M_1(r,P^{*}_{n,\alpha})\lesssim \int_{0}^{r} t^{-1}M_1(t,P^{*}_{n,\alpha-1})dt \lesssim l_{k}2^{-n(\alpha-1)}\int_{0}^{r}t^{2^{n}-1}dt\lesssim r^{2^n}2^{-n\alpha}l_{k}.\end{align*}$$
$$\begin{align*}M_1(r,P^{*}_{n,\alpha})\lesssim \int_{0}^{r} t^{-1}M_1(t,P^{*}_{n,\alpha-1})dt \lesssim l_{k}2^{-n(\alpha-1)}\int_{0}^{r}t^{2^{n}-1}dt\lesssim r^{2^n}2^{-n\alpha}l_{k}.\end{align*}$$
The general case follows by an easy induction on m with
![]() $m<\alpha \leq m+1$
.▪
$m<\alpha \leq m+1$
.▪
We are ready to prove in a certain sense the optimality of Proposition 4.1.
Theorem 4.4 Let
![]() $\alpha \in \mathbb {R}$
. For any
$\alpha \in \mathbb {R}$
. For any
![]() $l\geq 1$
, there is a frequently hypercyclic function
$l\geq 1$
, there is a frequently hypercyclic function
![]() $f_{\alpha }^*\in H(\mathbb {D})$
for T satisfying the following estimate: there exists
$f_{\alpha }^*\in H(\mathbb {D})$
for T satisfying the following estimate: there exists
![]() $C>0$
such that for every
$C>0$
such that for every
![]() $0<r<1$
sufficiently large
$0<r<1$
sufficiently large
 $$\begin{align*}M_1(r,f)\leq \begin{cases} C (1-r)^{\alpha}\log_{l}(-\log(1-r))&\mbox{ if }\alpha<0,\\ C\left\vert\log(1-r)\right\vert \log_{l}(-\log(1-r))&\mbox{ if }\alpha=0,\\ C&\mbox{ if }\alpha>0.\\ \end{cases}\end{align*}$$
$$\begin{align*}M_1(r,f)\leq \begin{cases} C (1-r)^{\alpha}\log_{l}(-\log(1-r))&\mbox{ if }\alpha<0,\\ C\left\vert\log(1-r)\right\vert \log_{l}(-\log(1-r))&\mbox{ if }\alpha=0,\\ C&\mbox{ if }\alpha>0.\\ \end{cases}\end{align*}$$
Proof The case
![]() $\alpha =0$
is given by Theorem 4.2. In the following, for
$\alpha =0$
is given by Theorem 4.2. In the following, for
![]() $l\geq 1,$
we denote by
$l\geq 1,$
we denote by
![]() $A_l$
the smallest integer so that for all
$A_l$
the smallest integer so that for all
![]() $n\geq A_l, \log _l(n)\geq \log _{l+1}(\alpha _k)$
(with
$n\geq A_l, \log _l(n)\geq \log _{l+1}(\alpha _k)$
(with
![]() $2^{n-1}\geq \alpha _k$
). Then, for any j large enough, the use of Lemma 4.3 and the inequality
$2^{n-1}\geq \alpha _k$
). Then, for any j large enough, the use of Lemma 4.3 and the inequality
![]() $(1-t)\leq e^{-t}$
, for
$(1-t)\leq e^{-t}$
, for
![]() $0\leq t\leq 1$
, leads to
$0\leq t\leq 1$
, leads to
 $$ \begin{align*} M_1\left(1-\frac{1}{2^{j}},f^{*}_{\alpha}\right) &\leq \sum\limits_{n\geq 1}M_1\Big(1-\frac{1}{2^{j}},P^{*}_{n,\alpha}\Big)\\ &\lesssim \sum_{\substack{n\geq 0,\\ 2^{n-1}\geq \alpha_{k}^*}}\Big(1-\frac{1}{2^{j}}\Big)^{2^{n-1}}2^{-n\alpha}l_{k}\\ & \leq \log_{l+1}(\alpha_k^*)A_{l}2^{A_l\max(0,-\alpha)} +\sum\limits_{n\geq A_{l}}e^{-2^{n-j-1}}2^{-n\alpha}\log_l(n). \end{align*} $$
$$ \begin{align*} M_1\left(1-\frac{1}{2^{j}},f^{*}_{\alpha}\right) &\leq \sum\limits_{n\geq 1}M_1\Big(1-\frac{1}{2^{j}},P^{*}_{n,\alpha}\Big)\\ &\lesssim \sum_{\substack{n\geq 0,\\ 2^{n-1}\geq \alpha_{k}^*}}\Big(1-\frac{1}{2^{j}}\Big)^{2^{n-1}}2^{-n\alpha}l_{k}\\ & \leq \log_{l+1}(\alpha_k^*)A_{l}2^{A_l\max(0,-\alpha)} +\sum\limits_{n\geq A_{l}}e^{-2^{n-j-1}}2^{-n\alpha}\log_l(n). \end{align*} $$
For
![]() $\alpha>0$
, the last sum is bounded by
$\alpha>0$
, the last sum is bounded by
 $$\begin{align*}\sum\limits_{n\geq A_{l}}e^{-2^{n-j-1}}2^{-n\alpha}\log_l(n)\leq \sum\limits_{n\geq A_{l}}2^{-n\alpha}\log_l(n)\lesssim 1.\end{align*}$$
$$\begin{align*}\sum\limits_{n\geq A_{l}}e^{-2^{n-j-1}}2^{-n\alpha}\log_l(n)\leq \sum\limits_{n\geq A_{l}}2^{-n\alpha}\log_l(n)\lesssim 1.\end{align*}$$
For
![]() $\alpha <0,$
we can write
$\alpha <0,$
we can write
 $$ \begin{align*} \sum\limits_{n\geq A_{l}}e^{-2^{n-j-1}}2^{-n\alpha}\log_l(n)&\leq \sum\limits_{n= A_{l}}^{j+1}e^{-2^{n-j-1}}2^{-n\alpha}\log_l(n)\\&\quad+\sum\limits_{n\geq j+2}e^{-2^{n-j-1}}2^{-n\alpha}\log_l(n) \\&\leq \log_l(j+1)\sum_{n=1}^{j+1}2^{-n\alpha}\\& \quad +2^{-(j+1)\alpha}\sum_{m\geq 1}e^{-2^m}2^{-m\alpha}\log_l(m+j+1)\\ &\leq \log_l(j+1) 2^{-(j+1)\alpha}\\& \quad+2^{-(j+1)\alpha}\log_l(j+1)\sum_{m\geq 1}e^{-2^m}2^{-m\alpha}(m+1)\\ &\lesssim 2^{-j\alpha}\log_l(j). \end{align*} $$
$$ \begin{align*} \sum\limits_{n\geq A_{l}}e^{-2^{n-j-1}}2^{-n\alpha}\log_l(n)&\leq \sum\limits_{n= A_{l}}^{j+1}e^{-2^{n-j-1}}2^{-n\alpha}\log_l(n)\\&\quad+\sum\limits_{n\geq j+2}e^{-2^{n-j-1}}2^{-n\alpha}\log_l(n) \\&\leq \log_l(j+1)\sum_{n=1}^{j+1}2^{-n\alpha}\\& \quad +2^{-(j+1)\alpha}\sum_{m\geq 1}e^{-2^m}2^{-m\alpha}\log_l(m+j+1)\\ &\leq \log_l(j+1) 2^{-(j+1)\alpha}\\& \quad+2^{-(j+1)\alpha}\log_l(j+1)\sum_{m\geq 1}e^{-2^m}2^{-m\alpha}(m+1)\\ &\lesssim 2^{-j\alpha}\log_l(j). \end{align*} $$
We deduce
 $$\begin{align*}M_1(1-\frac{1}{2^{j}},f^{*}_{\alpha})\lesssim \begin{cases} \log_l(j)2^{-j\alpha} & \mbox{ if } \alpha< 0,\\ 1 & \mbox{ if } \alpha>0. \end{cases}\end{align*}$$
$$\begin{align*}M_1(1-\frac{1}{2^{j}},f^{*}_{\alpha})\lesssim \begin{cases} \log_l(j)2^{-j\alpha} & \mbox{ if } \alpha< 0,\\ 1 & \mbox{ if } \alpha>0. \end{cases}\end{align*}$$
Hence, we obtain for any
 $ 1-\frac {1}{2^{j}} \leq r<1-\frac {1}{2^{j+1}}$
(with j large enough),
$ 1-\frac {1}{2^{j}} \leq r<1-\frac {1}{2^{j+1}}$
(with j large enough),
 $$ \begin{align*} M_1(r,f^{*}_{\alpha}) &\leq M_1\Big(1-\frac{1}{2^{j+1}},f^{*}_{\alpha}\Big) \lesssim \begin{cases} \log_l(j)2^{-j\alpha} & \mbox{ if } \alpha<0,\\ 1 & \mbox{ if } \alpha>0. \end{cases} \\&\lesssim \begin{cases} \log_l\left(- \log(1-r) \right)(1-r)^{\alpha} & \mbox{ if } \alpha<0,\\ 1 & \mbox{ if } \alpha>0. \end{cases} \end{align*} $$
$$ \begin{align*} M_1(r,f^{*}_{\alpha}) &\leq M_1\Big(1-\frac{1}{2^{j+1}},f^{*}_{\alpha}\Big) \lesssim \begin{cases} \log_l(j)2^{-j\alpha} & \mbox{ if } \alpha<0,\\ 1 & \mbox{ if } \alpha>0. \end{cases} \\&\lesssim \begin{cases} \log_l\left(- \log(1-r) \right)(1-r)^{\alpha} & \mbox{ if } \alpha<0,\\ 1 & \mbox{ if } \alpha>0. \end{cases} \end{align*} $$
To obtain the frequent hypercyclicity of the vector
![]() $f_{\alpha }^*$
for the weighted Taylor shift
$f_{\alpha }^*$
for the weighted Taylor shift
![]() $T_{\alpha },$
it suffices to mimic the proof of Lemma 3.9. ▪
$T_{\alpha },$
it suffices to mimic the proof of Lemma 3.9. ▪
Remark 4.5 For
![]() $p=1$
and
$p=1$
and
![]() $\alpha \leq 0$
, the following problems remain open: does there exist a frequently hypercyclic function
$\alpha \leq 0$
, the following problems remain open: does there exist a frequently hypercyclic function
![]() $g_{\alpha }\in H(\mathbb {D})$
for the Taylor shift
$g_{\alpha }\in H(\mathbb {D})$
for the Taylor shift
![]() $T_{\alpha }$
such that
$T_{\alpha }$
such that
![]() $ \limsup _{r\rightarrow 1}\left ((1-r)^{-\alpha }M_1(r,g_{\alpha })\right )<+\infty $
if
$ \limsup _{r\rightarrow 1}\left ((1-r)^{-\alpha }M_1(r,g_{\alpha })\right )<+\infty $
if
![]() $\alpha <0$
or
$\alpha <0$
or
 $ \limsup _{r\rightarrow 1}\big (\frac {M_1(r,g_{0})}{-\log (1-r)}\big )<+\infty $
if
$ \limsup _{r\rightarrow 1}\big (\frac {M_1(r,g_{0})}{-\log (1-r)}\big )<+\infty $
if
![]() $\alpha =0$
?
$\alpha =0$
?