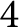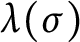1 Introduction
This is a companion paper to our earlier work [Reference Akhmedov, Hughes and Park1] with M. C. Hughes and addresses the geography problem for closed simply connected nonspin symplectic
![]() $4$
-manifolds with positive signature. For some background and history, we refer the reader to the introduction in [Reference Akhmedov, Hughes and Park1]. For the corresponding spin geography problem, we refer the reader to our papers [Reference Akhmedov and Park3, Reference Akhmedov and Park4].
$4$
-manifolds with positive signature. For some background and history, we refer the reader to the introduction in [Reference Akhmedov, Hughes and Park1]. For the corresponding spin geography problem, we refer the reader to our papers [Reference Akhmedov and Park3, Reference Akhmedov and Park4].
We start by setting up some basic notation. Given a closed smooth
![]() $4$
-manifold M, let
$4$
-manifold M, let
![]() $e(M)$
and
$e(M)$
and
![]() $\sigma (M)$
denote the Euler characteristic and the signature of M, respectively. We define
$\sigma (M)$
denote the Euler characteristic and the signature of M, respectively. We define
 $\chi _h(M) = \frac {1}{4}(e(M)+\sigma (M))$
and
$\chi _h(M) = \frac {1}{4}(e(M)+\sigma (M))$
and
![]() $c_1^2(M) = 2e(M)+3\sigma (M)$
. When M is a complex surface,
$c_1^2(M) = 2e(M)+3\sigma (M)$
. When M is a complex surface,
![]() $\chi _h(M)$
is the holomorphic Euler characteristic of
$\chi _h(M)$
is the holomorphic Euler characteristic of
![]() $M,$
while
$M,$
while
![]() $c_1^2(M)$
is the square of the first Chern class of M. Given an ordered pair of integers
$c_1^2(M)$
is the square of the first Chern class of M. Given an ordered pair of integers
![]() $(a,b)$
, the geography problem asks whether there exists a closed smooth
$(a,b)$
, the geography problem asks whether there exists a closed smooth
![]() $4$
-manifold M with the desired properties satisfying
$4$
-manifold M with the desired properties satisfying
![]() $\chi _h(M) =a$
and
$\chi _h(M) =a$
and
![]() $c_1^2(M)= b$
. We note that such M must satisfy
$c_1^2(M)= b$
. We note that such M must satisfy
![]() $b=8a+\sigma (M)$
.
$b=8a+\sigma (M)$
.
Given
![]() $x\in \mathbb {R}$
, we define the ceiling function as
$x\in \mathbb {R}$
, we define the ceiling function as
Next we recall the following definition from [Reference Akhmedov, Hughes and Park1, Definition 13].
Definition 1.1 Given an integer
![]() $\sigma \geq 0$
, let
$\sigma \geq 0$
, let
![]() $\lambda (\sigma )$
be the smallest positive integer with the following properties.
$\lambda (\sigma )$
be the smallest positive integer with the following properties.
-
(i)
 $\lambda (\sigma )\geq \lceil (\sigma +1)/2\rceil $
.
$\lambda (\sigma )\geq \lceil (\sigma +1)/2\rceil $
. -
(ii) Every integral point
 $(a,b)$
on the line
$(a,b)$
on the line
 $b = 8a + \sigma $
satisfying
$b = 8a + \sigma $
satisfying
 $a\geq \lambda (\sigma )$
is realized as
$a\geq \lambda (\sigma )$
is realized as
 $(\chi _h(M_i),c_1^2(M_i))$
, where
$(\chi _h(M_i),c_1^2(M_i))$
, where
 $\{M_i \mid i\in \mathbb {Z} \}$
is an infinite family of homeomorphic but pairwise nondiffeomorphic closed simply connected nonspin irreducible
$\{M_i \mid i\in \mathbb {Z} \}$
is an infinite family of homeomorphic but pairwise nondiffeomorphic closed simply connected nonspin irreducible
 $4$
-manifolds such that
$4$
-manifolds such that
 $M_i$
is symplectic for each
$M_i$
is symplectic for each
 $i\geq 0$
and
$i\geq 0$
and
 $M_i$
is nonsymplectic for each
$M_i$
is nonsymplectic for each
 $i<0$
.
$i<0$
.
We also recall the following definition from [Reference Akhmedov and Park3, Definition 1].
Definition 1.2 We say that a
![]() $4$
-manifold M has
$4$
-manifold M has
![]() $\infty ^2$
-property if there exist infinitely many pairwise nondiffeomorphic irreducible symplectic
$\infty ^2$
-property if there exist infinitely many pairwise nondiffeomorphic irreducible symplectic
![]() $4$
-manifolds and infinitely many pairwise nondiffeomorphic irreducible nonsymplectic
$4$
-manifolds and infinitely many pairwise nondiffeomorphic irreducible nonsymplectic
![]() $4$
-manifolds, all of which are homeomorphic to M.
$4$
-manifolds, all of which are homeomorphic to M.
Let
![]() $\mathbb {CP}^2$
be the complex projective plane, and let
$\mathbb {CP}^2$
be the complex projective plane, and let
![]() $\overline {\mathbb {CP}}{}^2$
be the underlying smooth
$\overline {\mathbb {CP}}{}^2$
be the underlying smooth
![]() $4$
-manifold
$4$
-manifold
![]() $\mathbb {CP}^2$
equipped with the opposite orientation. By Freedman’s classification theorem (cf. [Reference Freedman11]), if k is any odd integer satisfying
$\mathbb {CP}^2$
equipped with the opposite orientation. By Freedman’s classification theorem (cf. [Reference Freedman11]), if k is any odd integer satisfying
![]() $k\geq 2\lambda (\sigma )-1$
, then the nonspin
$k\geq 2\lambda (\sigma )-1$
, then the nonspin
![]() $4$
-manifold
$4$
-manifold
![]() $k\mathbb {CP}^2\#(k-\sigma )\overline {\mathbb {CP}}{}^2$
, the connected sum of k copies of
$k\mathbb {CP}^2\#(k-\sigma )\overline {\mathbb {CP}}{}^2$
, the connected sum of k copies of
![]() $\mathbb {CP}^2$
, and
$\mathbb {CP}^2$
, and
![]() $k-\sigma $
copies of
$k-\sigma $
copies of
![]() $\overline {\mathbb {CP}}{}^2$
, have
$\overline {\mathbb {CP}}{}^2$
, have
![]() $\infty ^2$
-property. The following conjecture from [Reference Akhmedov, Hughes and Park1] remains open.
$\infty ^2$
-property. The following conjecture from [Reference Akhmedov, Hughes and Park1] remains open.
Conjecture 1.3
![]() $\lambda (\sigma ) = \lceil (\sigma +1)/2\rceil $
for every integer
$\lambda (\sigma ) = \lceil (\sigma +1)/2\rceil $
for every integer
![]() $\sigma \geq 0$
. Equivalently, given any integer
$\sigma \geq 0$
. Equivalently, given any integer
![]() $\sigma \geq 0$
,
$\sigma \geq 0$
,
![]() $k\mathbb {CP}^2\#(k-\sigma )\overline {\mathbb {CP}}{}^2$
has
$k\mathbb {CP}^2\#(k-\sigma )\overline {\mathbb {CP}}{}^2$
has
![]() $\infty ^2$
-property for every odd integer k satisfying
$\infty ^2$
-property for every odd integer k satisfying
 $$ \begin{align*} k\geq \begin{cases} \sigma & \textrm{when}\ \sigma\ \textrm{is}\ \textrm{odd,}\ \\ \sigma+1 & \textrm{when}\ \sigma\ \textrm{is}\ \textrm{even.} \end{cases} \end{align*} $$
$$ \begin{align*} k\geq \begin{cases} \sigma & \textrm{when}\ \sigma\ \textrm{is}\ \textrm{odd,}\ \\ \sigma+1 & \textrm{when}\ \sigma\ \textrm{is}\ \textrm{even.} \end{cases} \end{align*} $$
We note that Conjecture 1.3 postulates that there would be no constraint on
![]() $k\mathbb {CP}^2\#(k-\sigma )\overline {\mathbb {CP}}{}^2$
having
$k\mathbb {CP}^2\#(k-\sigma )\overline {\mathbb {CP}}{}^2$
having
![]() $\infty ^2$
-property other than the positive integer k being odd, which is necessary for
$\infty ^2$
-property other than the positive integer k being odd, which is necessary for
![]() $k\mathbb {CP}^2\#(k-\sigma )\overline {\mathbb {CP}}{}^2$
to support a symplectic (and hence an almost complex) structure.
$k\mathbb {CP}^2\#(k-\sigma )\overline {\mathbb {CP}}{}^2$
to support a symplectic (and hence an almost complex) structure.
In [Reference Akhmedov, Hughes and Park1, Reference Akhmedov and Park2, Reference Akhmedov and Sakallı5], numerical upper bounds for
![]() $\lambda (\sigma )$
were given when
$\lambda (\sigma )$
were given when
![]() $0\leq \sigma \leq 100$
. In Section 3, we will present a new algorithm for constructing simply connected
$0\leq \sigma \leq 100$
. In Section 3, we will present a new algorithm for constructing simply connected
![]() $4$
-manifolds starting from a surface fibration over a surface with a section, which need not be a fiber bundle nor a Lefschetz fibration. Using this algorithm, we will construct two new infinite families of closed, simply connected, nonspin, irreducible, symplectic
$4$
-manifolds starting from a surface fibration over a surface with a section, which need not be a fiber bundle nor a Lefschetz fibration. Using this algorithm, we will construct two new infinite families of closed, simply connected, nonspin, irreducible, symplectic
![]() $4$
-manifolds of positive signature, many of which have a smaller value of
$4$
-manifolds of positive signature, many of which have a smaller value of
![]() $\chi _h$
than the currently known upper bounds on
$\chi _h$
than the currently known upper bounds on
![]() $\lambda (\sigma )$
. We cannot currently show that all of these
$\lambda (\sigma )$
. We cannot currently show that all of these
![]() $4$
-manifolds have
$4$
-manifolds have
![]() $\infty ^2$
-property, but we suspect that they all do (see Remark 3.4 and Corollary 3.6). The new building blocks in our construction are certain complex surfaces of general type found in [Reference Bauer and Catanese6, Reference Catanese and Dettweiler8, Reference Lee, Lönne and Rollenske16], and these will be reviewed in Section 2. In Section 4, we will also provide two explicit formulae for upper bounds on
$\infty ^2$
-property, but we suspect that they all do (see Remark 3.4 and Corollary 3.6). The new building blocks in our construction are certain complex surfaces of general type found in [Reference Bauer and Catanese6, Reference Catanese and Dettweiler8, Reference Lee, Lönne and Rollenske16], and these will be reviewed in Section 2. In Section 4, we will also provide two explicit formulae for upper bounds on
![]() $\lambda (\sigma )$
that work for every nonnegative integer
$\lambda (\sigma )$
that work for every nonnegative integer
![]() $\sigma $
(see Corollaries 4.2 and 4.4). Asymptotically as
$\sigma $
(see Corollaries 4.2 and 4.4). Asymptotically as
![]() $\sigma \rightarrow \infty $
, we will prove that
$\sigma \rightarrow \infty $
, we will prove that
 $$ \begin{align} \lambda(\sigma)\leq\frac{8}{5}\sigma +O(\sigma^{1/2}). \end{align} $$
$$ \begin{align} \lambda(\sigma)\leq\frac{8}{5}\sigma +O(\sigma^{1/2}). \end{align} $$
Such an asymptotic upper bound has been missing in the literature, and we hope that our bound provides a useful benchmark for future works. Our ultimate goal is to decrease the coefficient of
![]() $\sigma $
in (1.2) from
$\sigma $
in (1.2) from
![]() $1.6$
to a smaller number that is much closer to the coefficient
$1.6$
to a smaller number that is much closer to the coefficient
![]() $0.5$
in Conjecture 1.3.
$0.5$
in Conjecture 1.3.
2 Building Blocks
In this section, we will collect all the
![]() $4$
-manifold building blocks that we will need for our constructions later. Our first family of building blocks are the so-called
$4$
-manifold building blocks that we will need for our constructions later. Our first family of building blocks are the so-called
![]() $BCD$
surfaces constructed by Bauer, Catanese, and Dettweiler in [Reference Bauer and Catanese6, Reference Catanese and Dettweiler8].
$BCD$
surfaces constructed by Bauer, Catanese, and Dettweiler in [Reference Bauer and Catanese6, Reference Catanese and Dettweiler8].
Lemma 2.1 For each positive integer
![]() $n\geq 5$
that is coprime with
$n\geq 5$
that is coprime with
![]() $6$
, there exists a minimal complex surface
$6$
, there exists a minimal complex surface
![]() $S(n)$
of general type with
$S(n)$
of general type with
![]() $c_1^2(S(n))=5(n-2)^2$
,
$c_1^2(S(n))=5(n-2)^2$
,
![]() $e(S(n))=2n^2-10n+15$
, and
$e(S(n))=2n^2-10n+15$
, and
![]() $\sigma (S(n))=(n^2-10)/3$
. Each
$\sigma (S(n))=(n^2-10)/3$
. Each
![]() $S(n)$
admits a genus
$S(n)$
admits a genus
![]() $n-1$
fibration over a genus
$n-1$
fibration over a genus
![]() $(n-1)/2$
curve. Moreover,
$(n-1)/2$
curve. Moreover,
![]() $S(n)$
also contains four disjoint genus
$S(n)$
also contains four disjoint genus
![]() $(n-1)/2$
curves of self-intersection
$(n-1)/2$
curves of self-intersection
![]() $-1$
, one of which is a section of the fibration, and each of the other three is contained in a singular fiber and hence disjoint from regular fibers.
$-1$
, one of which is a section of the fibration, and each of the other three is contained in a singular fiber and hence disjoint from regular fibers.
Proof Recall from [Reference Catanese and Dettweiler8] that
![]() $S(n)$
arises as a
$S(n)$
arises as a
![]() $(\mathbb {Z}/n\mathbb {Z})^2$
Abelian Galois ramified cover (in the sense of [Reference Pardini18]) over a del Pezzo surface
$(\mathbb {Z}/n\mathbb {Z})^2$
Abelian Galois ramified cover (in the sense of [Reference Pardini18]) over a del Pezzo surface
![]() $\mathbb {CP}^2\#4\overline {\mathbb {CP}}{}^2$
of degree 5. The branch divisor of this covering is a sum of ten rational curves, four of which are the exceptional divisors of the blow-ups. We note that the preimages of the exceptional divisors under this
$\mathbb {CP}^2\#4\overline {\mathbb {CP}}{}^2$
of degree 5. The branch divisor of this covering is a sum of ten rational curves, four of which are the exceptional divisors of the blow-ups. We note that the preimages of the exceptional divisors under this
![]() $(\mathbb {Z}/n\mathbb {Z})^2$
covering map are disjoint genus
$(\mathbb {Z}/n\mathbb {Z})^2$
covering map are disjoint genus
![]() $(n-1)/2$
curves of self-intersection
$(n-1)/2$
curves of self-intersection
![]() $-1$
. The genus
$-1$
. The genus
![]() $n-1$
fibration structure on
$n-1$
fibration structure on
![]() $S(n)$
and its singular fibers are discussed in [Reference Catanese and Dettweiler8, Proposition 4.2]. We recall that this fibration is obtained by lifting a pencil of lines going through a point of blow-up, and thus a section of the fibration is given by the inclusion of the preimage of the corresponding exceptional divisor. The characteristic numbers
$S(n)$
and its singular fibers are discussed in [Reference Catanese and Dettweiler8, Proposition 4.2]. We recall that this fibration is obtained by lifting a pencil of lines going through a point of blow-up, and thus a section of the fibration is given by the inclusion of the preimage of the corresponding exceptional divisor. The characteristic numbers
![]() $c_1^2(S(n))$
and
$c_1^2(S(n))$
and
![]() $e(S(n))$
were computed in [Reference Catanese and Dettweiler8, Proposition 4.3]. We can readily compute the signature of
$e(S(n))$
were computed in [Reference Catanese and Dettweiler8, Proposition 4.3]. We can readily compute the signature of
![]() $S(n)$
using the well-known formula
$S(n)$
using the well-known formula
![]() $c_1^2=2e+3\sigma $
. ▪
$c_1^2=2e+3\sigma $
. ▪
Let
![]() $\Sigma _b$
denote a closed connected
$\Sigma _b$
denote a closed connected
![]() $2$
-manifold with genus
$2$
-manifold with genus
![]() $b\geq 0$
. Our second building block is a
$b\geq 0$
. Our second building block is a
![]() $\Sigma _7$
bundle over
$\Sigma _7$
bundle over
![]() $\Sigma _5$
that was constructed in [Reference Lee, Lönne and Rollenske16].
$\Sigma _5$
that was constructed in [Reference Lee, Lönne and Rollenske16].
Lemma 2.2 There exists a minimal complex surface Y of general type with
![]() $e(Y)=96$
and
$e(Y)=96$
and
![]() $\sigma (Y)=16$
such that Y is the total space of a surface bundle over a surface with base genus
$\sigma (Y)=16$
such that Y is the total space of a surface bundle over a surface with base genus
![]() $5$
and fiber genus
$5$
and fiber genus
![]() $7$
. Moreover, this surface bundle admits a section whose image in Y has self-intersection
$7$
. Moreover, this surface bundle admits a section whose image in Y has self-intersection
![]() $-8$
.
$-8$
.
Proof In [Reference Lee, Lönne and Rollenske16, Example 6.9], such Y was constructed as the double cover of
![]() $\Sigma _3\times \Sigma _3$
branched over
$\Sigma _3\times \Sigma _3$
branched over
![]() $4$
disjoint graphs of involutions on
$4$
disjoint graphs of involutions on
![]() $\Sigma _3$
. Each graph in the branch locus gives rise to a section of the bundle whose image in Y has self-intersection equal to
$\Sigma _3$
. Each graph in the branch locus gives rise to a section of the bundle whose image in Y has self-intersection equal to
![]() $2$
times the self-intersection of the graph in
$2$
times the self-intersection of the graph in
![]() $\Sigma _3\times \Sigma _3,$
which is
$\Sigma _3\times \Sigma _3,$
which is
![]() $-4$
. ▪
$-4$
. ▪
Our next family of building blocks are the homotopy elliptic surfaces constructed by Fintushel and Stern in [Reference Fintushel and Stern9]. Let
![]() $E(1)=\mathbb {CP}^2\#9\overline {\mathbb {CP}}{}^2$
denote a rational elliptic surface that is the complex projective plane blown up nine times. For a positive integer r, let
$E(1)=\mathbb {CP}^2\#9\overline {\mathbb {CP}}{}^2$
denote a rational elliptic surface that is the complex projective plane blown up nine times. For a positive integer r, let
![]() $E(r)$
denote the fiber sum of r copies of
$E(r)$
denote the fiber sum of r copies of
![]() $E(1)$
. Then
$E(1)$
. Then
![]() $E(r)$
is a simply connected elliptic surface without any multiple fiber. Let F be a smooth torus fiber of
$E(r)$
is a simply connected elliptic surface without any multiple fiber. Let F be a smooth torus fiber of
![]() $E(r)$
and let K be a knot of genus
$E(r)$
and let K be a knot of genus
![]() $g(K)$
in
$g(K)$
in
![]() $S^3$
. Let
$S^3$
. Let
![]() $E(r)_K$
denote the result of performing a knot surgery on
$E(r)_K$
denote the result of performing a knot surgery on
![]() $E(r)$
along F:
$E(r)$
along F:
 $$ \begin{align} E(r)_K = \big[ E(r)\backslash \nu(F) \big] \cup \big[ S^1\times(S^3\backslash\nu(K)) \big], \end{align} $$
$$ \begin{align} E(r)_K = \big[ E(r)\backslash \nu(F) \big] \cup \big[ S^1\times(S^3\backslash\nu(K)) \big], \end{align} $$
where the
![]() $\nu $
’s denote tubular neighborhoods. In (2.1), we glue the 3-torus boundaries in such a way that the meridians of F get identified with the longitudes of K.
$\nu $
’s denote tubular neighborhoods. In (2.1), we glue the 3-torus boundaries in such a way that the meridians of F get identified with the longitudes of K.
We recall that
![]() $E(r)_K$
is homeomorphic to
$E(r)_K$
is homeomorphic to
![]() $E(r),$
so we have
$E(r),$
so we have
![]() $\pi _1(E(r)_K)=1$
,
$\pi _1(E(r)_K)=1$
,
We also recall that
![]() $E(r)$
and
$E(r)$
and
![]() $E(r)_K$
are spin if and only if r is even. If K is a fibered knot, then
$E(r)_K$
are spin if and only if r is even. If K is a fibered knot, then
![]() $E(r)_K$
admits a symplectic structure, and a sphere section of
$E(r)_K$
admits a symplectic structure, and a sphere section of
![]() $E(r)$
and a Seifert surface of K can be glued together to form a symplectic submanifold
$E(r)$
and a Seifert surface of K can be glued together to form a symplectic submanifold
![]() $\Sigma _K$
of genus
$\Sigma _K$
of genus
![]() $g(K)$
and self-intersection
$g(K)$
and self-intersection
![]() $-r$
inside
$-r$
inside
![]() $E(r)_K$
. Given a nonnegative integer m, let
$E(r)_K$
. Given a nonnegative integer m, let
![]() $F_K^m$
be the genus
$F_K^m$
be the genus
![]() $g(K)+m$
symplectic submanifold of
$g(K)+m$
symplectic submanifold of
![]() $E(r)_K$
with self-intersection
$E(r)_K$
with self-intersection
![]() $2m-r$
that is obtained from the union of
$2m-r$
that is obtained from the union of
![]() $\Sigma _K$
and m copies of torus fiber by symplectically resolving their m intersection points. We note that
$\Sigma _K$
and m copies of torus fiber by symplectically resolving their m intersection points. We note that
![]() $F_K^0=\Sigma _K$
.
$F_K^0=\Sigma _K$
.
Lemma 2.3 Let
![]() $m\geq 0$
and
$m\geq 0$
and
![]() $r>0$
be integers, and let K be a fibered knot in
$r>0$
be integers, and let K be a fibered knot in
![]() $S^3$
. Let
$S^3$
. Let
![]() $\nu (F_K^m)$
denote a tubular neighborhood of
$\nu (F_K^m)$
denote a tubular neighborhood of
![]() $F_K^m$
in
$F_K^m$
in
![]() $E(r)_K$
. Then the complement
$E(r)_K$
. Then the complement
![]() $E(r)_K \backslash \nu (F_K^m)$
is simply connected. If
$E(r)_K \backslash \nu (F_K^m)$
is simply connected. If
![]() $r\geq 2$
, then write
$r\geq 2$
, then write
![]() $r=2\rho +\epsilon $
for integers
$r=2\rho +\epsilon $
for integers
![]() $\epsilon =0,1$
and
$\epsilon =0,1$
and
![]() $\rho \geq 1$
. Then
$\rho \geq 1$
. Then
![]() $E(r)_K\backslash \nu (F_K^m)$
contains
$E(r)_K\backslash \nu (F_K^m)$
contains
![]() $2\rho $
disjoint symplectic tori
$2\rho $
disjoint symplectic tori
![]() $T_j (j=1,\dots ,2\rho )$
of self-intersection
$T_j (j=1,\dots ,2\rho )$
of self-intersection
![]() $0$
such that
$0$
such that
 $\pi _1(E(r)_K\backslash (\nu (F_K^m) \cup (\cup _{j=1}^{2\rho } T_j)))=1$
.
$\pi _1(E(r)_K\backslash (\nu (F_K^m) \cup (\cup _{j=1}^{2\rho } T_j)))=1$
.
Proof Each surface
![]() $F_K^m$
transversely intersects once a topological sphere in
$F_K^m$
transversely intersects once a topological sphere in
![]() $E(r)_K$
coming from a cusp fiber of
$E(r)_K$
coming from a cusp fiber of
![]() $E(r)$
. Thus, any meridian of
$E(r)$
. Thus, any meridian of
![]() $F_K^m$
is nullhomotopic in
$F_K^m$
is nullhomotopic in
![]() $E(r)_K \backslash \nu (F_K^m)$
. Hence, we conclude that
$E(r)_K \backslash \nu (F_K^m)$
. Hence, we conclude that
![]() $\pi _{1}(E(r)_K \backslash \nu (F_K^m))=\pi _1(E(r)_K)=1$
. Next, we recall from [Reference Gompf and Mrowka13] that
$\pi _{1}(E(r)_K \backslash \nu (F_K^m))=\pi _1(E(r)_K)=1$
. Next, we recall from [Reference Gompf and Mrowka13] that
![]() $E(2)$
contains
$E(2)$
contains
![]() $3$
disjoint copies of the Gompf nucleus. If
$3$
disjoint copies of the Gompf nucleus. If
![]() $r\geq 2$
, then
$r\geq 2$
, then
![]() $E(r)$
can be viewed as the fiber sum of
$E(r)$
can be viewed as the fiber sum of
![]() $\rho $
copies of
$\rho $
copies of
![]() $E(2)$
and possibly a copy of
$E(2)$
and possibly a copy of
![]() $E(1)$
. In each copy of
$E(1)$
. In each copy of
![]() $E(2)$
, we have
$E(2)$
, we have
![]() $2$
copies of Gompf nuclei that are disjoint from the tori and sections used in the fiber sum, and thus
$2$
copies of Gompf nuclei that are disjoint from the tori and sections used in the fiber sum, and thus
![]() $E(r)_K$
contains
$E(r)_K$
contains
![]() $2\rho $
Gompf nuclei that are all disjoint from
$2\rho $
Gompf nuclei that are all disjoint from
![]() $\nu (F_K^m)$
. Let
$\nu (F_K^m)$
. Let
![]() $N_j$
denote one of these nuclei, and let
$N_j$
denote one of these nuclei, and let
![]() $T_j$
be a smooth torus fiber in
$T_j$
be a smooth torus fiber in
![]() $N_j$
(
$N_j$
(
![]() $j=1,\dots ,2\rho $
). By changing the symplectic form on the
$j=1,\dots ,2\rho $
). By changing the symplectic form on the
![]() $E(2)$
parts if necessary, we can arrange each
$E(2)$
parts if necessary, we can arrange each
![]() $T_j$
to be a symplectic submanifold of
$T_j$
to be a symplectic submanifold of
![]() $E(r)_K$
. Since
$E(r)_K$
. Since
![]() $T_j$
transversely intersects once a sphere section of
$T_j$
transversely intersects once a sphere section of
![]() $N_j$
with self-intersection
$N_j$
with self-intersection
![]() $-2$
, every meridian of
$-2$
, every meridian of
![]() $T_j$
is nullhomotopic. It follows that
$T_j$
is nullhomotopic. It follows that
 $\pi _1(E(r)_K\backslash (\nu (F_K^m) \cup (\cup _{j=1}^{2\rho } T_j)))=\pi _1(E(r)_K\backslash \nu (F_K^m))=1$
. ▪
$\pi _1(E(r)_K\backslash (\nu (F_K^m) \cup (\cup _{j=1}^{2\rho } T_j)))=\pi _1(E(r)_K\backslash \nu (F_K^m))=1$
. ▪
From the Seifert–Van Kampen theorem, we can also deduce that
 $$ \begin{align*} \pi_1(E(r)_K\backslash (\nu(F_K^m) \cup (\cup_{j=1}^{\tau} T_j)))=1 \end{align*} $$
$$ \begin{align*} \pi_1(E(r)_K\backslash (\nu(F_K^m) \cup (\cup_{j=1}^{\tau} T_j)))=1 \end{align*} $$
for any integer
![]() $\tau $
satisfying
$\tau $
satisfying
![]() $0\leq \tau \leq 2\rho $
, i.e., we can choose to take out less tori and still have the complement remain simply connected. Our final set of building blocks are certain families of symplectic
$0\leq \tau \leq 2\rho $
, i.e., we can choose to take out less tori and still have the complement remain simply connected. Our final set of building blocks are certain families of symplectic
![]() $4$
-manifolds that were studied in [Reference Akhmedov, Hughes and Park1].
$4$
-manifolds that were studied in [Reference Akhmedov, Hughes and Park1].
Lemma 2.4 For each positive integer u, there is a pair of closed simply connected nonspin irreducible symplectic
![]() $4$
-manifolds
$4$
-manifolds
![]() $Q(u)$
and
$Q(u)$
and
![]() $\tilde {Q}(u)$
satisfying
$\tilde {Q}(u)$
satisfying
 $$ \begin{align*} \sigma(Q(u))&=26u-2\lceil u/2\rceil -2,\\ \chi_h(Q(u))&=27u+32\lceil u/2\rceil -2,\\ \sigma(\tilde{Q}(u))&=25u^2+u-2\lceil u/2\rceil -2,\\ \chi_h(\tilde{Q}(u))&=25u^2+\lceil u/2\rceil(30u+2) +2u -2, \end{align*} $$
$$ \begin{align*} \sigma(Q(u))&=26u-2\lceil u/2\rceil -2,\\ \chi_h(Q(u))&=27u+32\lceil u/2\rceil -2,\\ \sigma(\tilde{Q}(u))&=25u^2+u-2\lceil u/2\rceil -2,\\ \chi_h(\tilde{Q}(u))&=25u^2+\lceil u/2\rceil(30u+2) +2u -2, \end{align*} $$
where
![]() $\lceil \ \rceil $
is given by (1.1). Let Q denote either
$\lceil \ \rceil $
is given by (1.1). Let Q denote either
![]() $Q(u)$
or
$Q(u)$
or
![]() $\tilde {Q}(u)$
. Then each Q contains a disjoint pair of symplectic tori
$\tilde {Q}(u)$
. Then each Q contains a disjoint pair of symplectic tori
![]() $T_1^{\prime }$
and
$T_1^{\prime }$
and
![]() $T_2^{\prime }$
of self-intersection
$T_2^{\prime }$
of self-intersection
![]() $0$
satisfying
$0$
satisfying
![]() $\pi _1(Q\backslash (T_1^{\prime } \cup T_2^{\prime }))=1$
.
$\pi _1(Q\backslash (T_1^{\prime } \cup T_2^{\prime }))=1$
.
Proof We let
![]() $Q(u)=Q_n^m(W^{p,v}_{u_1,u_2})$
in [Reference Akhmedov, Hughes and Park1, Example 12] with
$Q(u)=Q_n^m(W^{p,v}_{u_1,u_2})$
in [Reference Akhmedov, Hughes and Park1, Example 12] with
![]() $m=1$
,
$m=1$
,
![]() $p=5$
,
$p=5$
,
![]() $u_1=u$
,
$u_1=u$
,
![]() $u_2=1$
,
$u_2=1$
,
![]() $v=1$
,
$v=1$
,
![]() $t=\lceil u/2 \rceil $
, and
$t=\lceil u/2 \rceil $
, and
![]() $n=16\lceil u/2\rceil +u+1\geq 18$
. We let
$n=16\lceil u/2\rceil +u+1\geq 18$
. We let
![]() $\tilde {Q}(u)=Q_n^m(W^{p,v}_{u_1,u_2})$
in [Reference Akhmedov, Hughes and Park1, Example 12] with
$\tilde {Q}(u)=Q_n^m(W^{p,v}_{u_1,u_2})$
in [Reference Akhmedov, Hughes and Park1, Example 12] with
![]() $m=1$
,
$m=1$
,
![]() $p=5$
,
$p=5$
,
![]() $u_1=u$
,
$u_1=u$
,
![]() $u_2=u$
,
$u_2=u$
,
![]() $v=1$
,
$v=1$
,
![]() $t=\lceil u/2 \rceil $
, and
$t=\lceil u/2 \rceil $
, and
![]() $n=\lceil u/2\rceil (15u+1)+u+1\geq 18$
. The existence of
$n=\lceil u/2\rceil (15u+1)+u+1\geq 18$
. The existence of
![]() $T_1^{\prime }$
and
$T_1^{\prime }$
and
![]() $T_2^{\prime }$
follows from [Reference Akhmedov, Hughes and Park1, Theorem 9]. ▪
$T_2^{\prime }$
follows from [Reference Akhmedov, Hughes and Park1, Theorem 9]. ▪
3 New Symplectic
 $4$
-manifolds
$4$
-manifolds
We start the section with a general algorithm for producing simply connected
![]() $4$
-manifolds from a symplectic fibration. Let X be a closed symplectic
$4$
-manifolds from a symplectic fibration. Let X be a closed symplectic
![]() $4$
-manifold that is the total space of a fibration
$4$
-manifold that is the total space of a fibration
![]() $f: X\rightarrow \Sigma _b$
whose regular fiber is a
$f: X\rightarrow \Sigma _b$
whose regular fiber is a
![]() $2$
-manifold
$2$
-manifold
![]() $\Sigma _a$
with genus
$\Sigma _a$
with genus
![]() $a\geq 0$
. Assume that this fibration has a section
$a\geq 0$
. Assume that this fibration has a section
![]() $s:\Sigma _b \rightarrow X$
whose image
$s:\Sigma _b \rightarrow X$
whose image
![]() $s(\Sigma _b)$
has self-intersection equal to d in X. Next let t and
$s(\Sigma _b)$
has self-intersection equal to d in X. Next let t and
![]() $\delta $
be nonnegative integers. By symplectically resolving the double points of the union of
$\delta $
be nonnegative integers. By symplectically resolving the double points of the union of
![]() $s(\Sigma _b)$
and t copies of the fiber
$s(\Sigma _b)$
and t copies of the fiber
![]() $\Sigma _a$
, we obtain a symplectic submanifold
$\Sigma _a$
, we obtain a symplectic submanifold
![]() $\Sigma _{ta+b}$
in X with genus
$\Sigma _{ta+b}$
in X with genus
![]() $ta+b$
and self-intersection
$ta+b$
and self-intersection
![]() $2t+d$
. By symplectically blowing up
$2t+d$
. By symplectically blowing up
![]() $\delta $
points of
$\delta $
points of
![]() $\Sigma _{ta+b}$
in X, we obtain a genus
$\Sigma _{ta+b}$
in X, we obtain a genus
![]() $ta+b$
symplectic submanifold
$ta+b$
symplectic submanifold
![]() $\Sigma _{ta+b}^{\prime }$
in the blow-up
$\Sigma _{ta+b}^{\prime }$
in the blow-up
![]() $X\#\delta \overline {\mathbb {CP}}{}^2$
with self-intersection
$X\#\delta \overline {\mathbb {CP}}{}^2$
with self-intersection
![]() $2t+d-\delta $
.
$2t+d-\delta $
.
Let
![]() $E(r)_K$
and
$E(r)_K$
and
![]() $F_K^m$
be as in Section 2. Let
$F_K^m$
be as in Section 2. Let
 $E(X)_{K,m,r}^{t,\delta }$
denote the symplectic normal sum (cf. [Reference Gompf12, Reference McCarthy and Wolfson17]) of
$E(X)_{K,m,r}^{t,\delta }$
denote the symplectic normal sum (cf. [Reference Gompf12, Reference McCarthy and Wolfson17]) of
![]() $X\#\delta \overline {\mathbb {CP}}{}^2$
and
$X\#\delta \overline {\mathbb {CP}}{}^2$
and
![]() $E(r)_K$
along symplectic submanifolds
$E(r)_K$
along symplectic submanifolds
![]() $\Sigma _{ta+b}^{\prime }$
and
$\Sigma _{ta+b}^{\prime }$
and
![]() $F_K^m$
:
$F_K^m$
:
 $$ \begin{align*} E(X)_{K,m,r}^{t,\delta}=\big[(X\#\delta\overline{\mathbb{CP}}{}^2)\backslash\nu(\Sigma_{ta+b}^{\prime})\big]\cup\big[E(r)_K\backslash\nu(F_K^m)\big]. \end{align*} $$
$$ \begin{align*} E(X)_{K,m,r}^{t,\delta}=\big[(X\#\delta\overline{\mathbb{CP}}{}^2)\backslash\nu(\Sigma_{ta+b}^{\prime})\big]\cup\big[E(r)_K\backslash\nu(F_K^m)\big]. \end{align*} $$
For this symplectic normal sum to be well-defined, we require the genera of submanifolds to be equal and their self-intersections to have opposite signs, i.e.,
Theorem 3.1 Assume that both conditions in (3.1) hold. Then
 $E(X)_{K,m,r}^{t,\delta }$
is a closed symplectic
$E(X)_{K,m,r}^{t,\delta }$
is a closed symplectic
![]() $4$
-manifold with
$4$
-manifold with
 $$ \begin{align*} e(E(X)_{K,m,r}^{t,\delta})&=e(X)+\delta+12r+4ta+4b-4, \\ \sigma(E(X)_{K,m,r}^{t,\delta})&=\sigma(X)-\delta-8r, \\ \chi_h(E(X)_{K,m,r}^{t,\delta})&= \chi_h(X)+r+ta+b-1. \end{align*} $$
$$ \begin{align*} e(E(X)_{K,m,r}^{t,\delta})&=e(X)+\delta+12r+4ta+4b-4, \\ \sigma(E(X)_{K,m,r}^{t,\delta})&=\sigma(X)-\delta-8r, \\ \chi_h(E(X)_{K,m,r}^{t,\delta})&= \chi_h(X)+r+ta+b-1. \end{align*} $$
If
![]() $\delta>0$
, then
$\delta>0$
, then
 $E(X)_{K,m,r}^{t,\delta }$
is nonspin. If
$E(X)_{K,m,r}^{t,\delta }$
is nonspin. If
![]() $t>0$
, then
$t>0$
, then
 $E(X)_{K,m,r}^{t,\delta }$
is simply connected. If
$E(X)_{K,m,r}^{t,\delta }$
is simply connected. If
![]() $t>0$
and
$t>0$
and
![]() $r\geq 2$
, then
$r\geq 2$
, then
 $E(X)_{K,m,r}^{t,\delta }$
contains two disjoint symplectic tori,
$E(X)_{K,m,r}^{t,\delta }$
contains two disjoint symplectic tori,
![]() $T_1$
and
$T_1$
and
![]() $T_2,$
of self-intersection
$T_2,$
of self-intersection
![]() $0$
such that
$0$
such that
 $\pi _1(E(X)_{K,m,r}^{t,\delta } \backslash (T_1\cup T_2))=1$
.
$\pi _1(E(X)_{K,m,r}^{t,\delta } \backslash (T_1\cup T_2))=1$
.
Proof We compute that
 $e(E(X)_{K,m,r}^{t,\delta })=e(X\#\delta \overline {\mathbb {CP}}{}^2)+e(E(r)_K)-2e(\Sigma _{ta+b}^{\prime })$
and
$e(E(X)_{K,m,r}^{t,\delta })=e(X\#\delta \overline {\mathbb {CP}}{}^2)+e(E(r)_K)-2e(\Sigma _{ta+b}^{\prime })$
and
 $\sigma (E(X)_{K,m,r}^{t,\delta })=\sigma (X\#\delta \overline {\mathbb {CP}}{}^2)+\sigma (E(r)_K)$
. When
$\sigma (E(X)_{K,m,r}^{t,\delta })=\sigma (X\#\delta \overline {\mathbb {CP}}{}^2)+\sigma (E(r)_K)$
. When
![]() $\delta>0$
, we have a punctured
$\delta>0$
, we have a punctured
![]() $2$
-sphere in the
$2$
-sphere in the
 $[(X\#\delta \overline {\mathbb {CP}}{}^2)\backslash \nu (\Sigma _{ta+b}^{\prime })]$
half coming from an exceptional divisor of a blow-up. We can glue this disk to a punctured torus fiber in the
$[(X\#\delta \overline {\mathbb {CP}}{}^2)\backslash \nu (\Sigma _{ta+b}^{\prime })]$
half coming from an exceptional divisor of a blow-up. We can glue this disk to a punctured torus fiber in the
![]() $[E(r)_K\backslash \nu (F_K^m)]$
half and obtain a torus with self-intersection
$[E(r)_K\backslash \nu (F_K^m)]$
half and obtain a torus with self-intersection
![]() $-1$
, which implies that the intersection form of
$-1$
, which implies that the intersection form of
 $E(X)_{K,m,r}^{t,\delta }$
is not even.
$E(X)_{K,m,r}^{t,\delta }$
is not even.
Since we know from Lemma 2.3 that
the Seifert–Van Kampen theorem implies that
 $$ \begin{align} \pi_1(E(X)_{K,m,r}^{t,\delta}) \cong \frac{\pi_1((X\#\delta\overline{\mathbb{CP}}{}^2)\backslash \nu (\Sigma_{ta+b}^{\prime}))}{\langle\pi_1(\partial\nu(\Sigma_{ta+b}^{\prime}))\rangle}, \end{align} $$
$$ \begin{align} \pi_1(E(X)_{K,m,r}^{t,\delta}) \cong \frac{\pi_1((X\#\delta\overline{\mathbb{CP}}{}^2)\backslash \nu (\Sigma_{ta+b}^{\prime}))}{\langle\pi_1(\partial\nu(\Sigma_{ta+b}^{\prime}))\rangle}, \end{align} $$
where
![]() $\partial \nu (\Sigma _{ta+b}^{\prime })$
is the boundary of
$\partial \nu (\Sigma _{ta+b}^{\prime })$
is the boundary of
![]() $\nu (\Sigma _{ta+b}^{\prime })$
and
$\nu (\Sigma _{ta+b}^{\prime })$
and
![]() $\langle \pi _1(\partial \nu (\Sigma _{ta+b}^{\prime }))\rangle $
is the normal subgroup of
$\langle \pi _1(\partial \nu (\Sigma _{ta+b}^{\prime }))\rangle $
is the normal subgroup of
 $\pi _1((X\#\delta \overline {\mathbb {CP}}{}^2)\backslash \nu (\Sigma _{ta+b}^{\prime }))$
generated by the image of
$\pi _1((X\#\delta \overline {\mathbb {CP}}{}^2)\backslash \nu (\Sigma _{ta+b}^{\prime }))$
generated by the image of
![]() $\pi _1(\partial \nu (\Sigma _{ta+b}^{\prime }))$
under the inclusion induced homomorphism.
$\pi _1(\partial \nu (\Sigma _{ta+b}^{\prime }))$
under the inclusion induced homomorphism.
Note that
![]() $\partial \nu (\Sigma _{ta+b}^{\prime })$
is a circle bundle over
$\partial \nu (\Sigma _{ta+b}^{\prime })$
is a circle bundle over
![]() $\Sigma _{ta+b}^{\prime }$
with Euler number
$\Sigma _{ta+b}^{\prime }$
with Euler number
![]() $2t+d-\delta $
. It is well known (cf. [Reference Fomenko and Matveev10, Proposition 10.4]) that
$2t+d-\delta $
. It is well known (cf. [Reference Fomenko and Matveev10, Proposition 10.4]) that
 $$ \begin{align*} \pi_1(\partial\nu(\Sigma_{ta+b}^{\prime})) = \Big\langle \alpha_i, \beta_i, \mu \bigm| {\textstyle \prod\limits_{i=1}^{ta+b}}[\alpha_i,\beta_i]=\mu^{2t+d-\delta},\, \alpha_i \mu \alpha_i^{-1} = \mu,\, \beta_i\mu\beta_i^{-1} = \mu \Big\rangle, \end{align*} $$
$$ \begin{align*} \pi_1(\partial\nu(\Sigma_{ta+b}^{\prime})) = \Big\langle \alpha_i, \beta_i, \mu \bigm| {\textstyle \prod\limits_{i=1}^{ta+b}}[\alpha_i,\beta_i]=\mu^{2t+d-\delta},\, \alpha_i \mu \alpha_i^{-1} = \mu,\, \beta_i\mu\beta_i^{-1} = \mu \Big\rangle, \end{align*} $$
where the index i ranges over
![]() $1,\dots ,ta+b$
. Here,
$1,\dots ,ta+b$
. Here,
![]() $\mu $
is represented by a fiber circle that is a meridian of
$\mu $
is represented by a fiber circle that is a meridian of
![]() $\Sigma _{ta+b}^{\prime }$
, and
$\Sigma _{ta+b}^{\prime }$
, and
![]() $\alpha _i,\beta _i$
are the parallel push-offs of the standard generators of
$\alpha _i,\beta _i$
are the parallel push-offs of the standard generators of
![]() $\pi _1(\Sigma _{ta+b}^{\prime })$
.
$\pi _1(\Sigma _{ta+b}^{\prime })$
.
In (3.3), we have
![]() $\mu =1$
in the quotient group, since
$\mu =1$
in the quotient group, since
![]() $\mu \in \langle \pi _1(\partial \nu (\Sigma _{ta+b}^{\prime }))\rangle $
. Thus, we can write
$\mu \in \langle \pi _1(\partial \nu (\Sigma _{ta+b}^{\prime }))\rangle $
. Thus, we can write
 $$ \begin{align} \pi_1(E(X)_{K,m,r}^{t,\delta}) \cong \frac{\pi_1(X\#\delta\overline{\mathbb{CP}}{}^2)}{\langle\pi_1(\Sigma_{ta+b}^{\prime})\rangle} \cong \frac{\pi_1(X)}{\langle\pi_1(\Sigma_{ta+b})\rangle}. \end{align} $$
$$ \begin{align} \pi_1(E(X)_{K,m,r}^{t,\delta}) \cong \frac{\pi_1(X\#\delta\overline{\mathbb{CP}}{}^2)}{\langle\pi_1(\Sigma_{ta+b}^{\prime})\rangle} \cong \frac{\pi_1(X)}{\langle\pi_1(\Sigma_{ta+b})\rangle}. \end{align} $$
From the long exact sequence of the fibration, we have an exact sequence
where the first and second arrows are induced by the inclusion of a regular fiber and the fibration map, respectively. When
![]() $t>0$
, the image of
$t>0$
, the image of
![]() $\pi _1(\Sigma _{ta+b})$
in
$\pi _1(\Sigma _{ta+b})$
in
![]() $\pi _1(X)$
contains all the generators of the images of
$\pi _1(X)$
contains all the generators of the images of
![]() $\pi _1(\Sigma _a)$
and
$\pi _1(\Sigma _a)$
and
![]() $\pi _1(s(\Sigma _b))$
under the inclusion induced homomorphisms. Thus, we can conclude that the quotient group (3.4) is trivial.
$\pi _1(s(\Sigma _b))$
under the inclusion induced homomorphisms. Thus, we can conclude that the quotient group (3.4) is trivial.
When
![]() $r\geq 2$
, Lemma 2.3 tells us that the
$r\geq 2$
, Lemma 2.3 tells us that the
![]() $[E(r)_K\backslash \nu (F_K^m)]$
half contains (at least) two disjoint symplectic tori
$[E(r)_K\backslash \nu (F_K^m)]$
half contains (at least) two disjoint symplectic tori
![]() $T_1$
and
$T_1$
and
![]() $T_2$
of self-intersection
$T_2$
of self-intersection
![]() $0$
such that
$0$
such that
To show that
 $\pi _1(E(X)_{K,m,r}^{t,\delta } \backslash (T_1\cup T_2))=1$
, we can apply the above argument to show that
$\pi _1(E(X)_{K,m,r}^{t,\delta } \backslash (T_1\cup T_2))=1$
, we can apply the above argument to show that
 $\pi _1(E(X)_{K,m,r}^{t,\delta })=1$
with the only change being the replacement of (3.2) with (3.5). ▪
$\pi _1(E(X)_{K,m,r}^{t,\delta })=1$
with the only change being the replacement of (3.2) with (3.5). ▪
Next we apply Theorem 3.1 to the
![]() $BCD$
surface
$BCD$
surface
![]() $S(n)$
from Lemma 2.1, now viewed as a symplectic
$S(n)$
from Lemma 2.1, now viewed as a symplectic
![]() $4$
-manifold.
$4$
-manifold.
Corollary 3.2 For any positive integer
![]() $n\geq 5$
such that
$n\geq 5$
such that
![]() $n\equiv \pm 1\pmod {6}$
and any fibered knot
$n\equiv \pm 1\pmod {6}$
and any fibered knot
![]() $K\subset S^3$
of genus
$K\subset S^3$
of genus
![]() $3(n-1)/2$
, there is a simply connected irreducible symplectic
$3(n-1)/2$
, there is a simply connected irreducible symplectic
![]() $4$
-manifold
$4$
-manifold
![]() $M(n)_K$
that is homeomorphic to
$M(n)_K$
that is homeomorphic to
 $$ \begin{align} \bigg(\frac{7}{6}n^2-2n+\frac{11}{6}\bigg)\mathbb{CP}^2 \#\bigg(\frac{5}{6}n^2-2n+\frac{79}{6}\bigg)\overline{\mathbb{CP}}{}^2. \end{align} $$
$$ \begin{align} \bigg(\frac{7}{6}n^2-2n+\frac{11}{6}\bigg)\mathbb{CP}^2 \#\bigg(\frac{5}{6}n^2-2n+\frac{79}{6}\bigg)\overline{\mathbb{CP}}{}^2. \end{align} $$
Proof An integer n is coprime with
![]() $6$
if and only if
$6$
if and only if
![]() $n\equiv \pm 1\pmod {6}$
. We let
$n\equiv \pm 1\pmod {6}$
. We let
 $M(n)_K=E(X)_{K,m,r}^{t,\delta }$
with
$M(n)_K=E(X)_{K,m,r}^{t,\delta }$
with
![]() $X=S(n)$
,
$X=S(n)$
,
![]() $a=n-1$
,
$a=n-1$
,
![]() $b=(n-1)/2$
,
$b=(n-1)/2$
,
![]() $d=-1$
,
$d=-1$
,
![]() $t=1$
,
$t=1$
,
![]() $\delta =0$
,
$\delta =0$
,
![]() $g(K)=3(n-1)/2$
,
$g(K)=3(n-1)/2$
,
![]() $m=0$
, and
$m=0$
, and
![]() $r=1$
. We can easily check that both conditions in (3.1) are satisfied. We note that
$r=1$
. We can easily check that both conditions in (3.1) are satisfied. We note that
![]() $M(n)_K$
is nonspin, since it contains three curves of square
$M(n)_K$
is nonspin, since it contains three curves of square
![]() $-1$
in the
$-1$
in the
 $[(X\#\delta \overline {\mathbb {CP}}{}^2)\backslash \nu (\Sigma _{ta+b}^{\prime })]$
half by Lemma 2.1.
$[(X\#\delta \overline {\mathbb {CP}}{}^2)\backslash \nu (\Sigma _{ta+b}^{\prime })]$
half by Lemma 2.1.
Since
![]() $e(M(n)_K)=2n^2-4n+17$
and
$e(M(n)_K)=2n^2-4n+17$
and
![]() $\sigma (M(n)_K)=(n^2-34)/3$
, Freedman’s classification theorem (cf. [Reference Freedman11]) implies that
$\sigma (M(n)_K)=(n^2-34)/3$
, Freedman’s classification theorem (cf. [Reference Freedman11]) implies that
![]() $M(n)_K$
must be homeomorphic to (3.6). Since
$M(n)_K$
must be homeomorphic to (3.6). Since
![]() $S(n)$
is minimal, the symplectic normal sum
$S(n)$
is minimal, the symplectic normal sum
![]() $M(n)_K$
is also minimal by Usher’s theorem in [Reference Usher19]. We recall from [Reference Hamilton and Kotschick14, Reference Kotschick15] that any simply connected minimal symplectic
$M(n)_K$
is also minimal by Usher’s theorem in [Reference Usher19]. We recall from [Reference Hamilton and Kotschick14, Reference Kotschick15] that any simply connected minimal symplectic
![]() $4$
-manifold is irreducible. ▪
$4$
-manifold is irreducible. ▪
We note that
![]() $M(n)_K$
has positive signature except when
$M(n)_K$
has positive signature except when
![]() $n=5$
. For many values of n, Corollary 3.2 gives a new symplectic (and thus exotic) smooth structure on (3.6). For example, when
$n=5$
. For many values of n, Corollary 3.2 gives a new symplectic (and thus exotic) smooth structure on (3.6). For example, when
![]() $n=7,11,13,17$
, we get an exotic smooth structure on each of
$n=7,11,13,17$
, we get an exotic smooth structure on each of
![]() $45\mathbb {CP}^2\#40\overline {\mathbb {CP}}{}^2$
,
$45\mathbb {CP}^2\#40\overline {\mathbb {CP}}{}^2$
,
![]() $121\mathbb {CP}^2\#92\overline {\mathbb {CP}}{}^2$
,
$121\mathbb {CP}^2\#92\overline {\mathbb {CP}}{}^2$
,
![]() $173\mathbb {CP}^2\#128\overline {\mathbb {CP}}{}^2,$
and
$173\mathbb {CP}^2\#128\overline {\mathbb {CP}}{}^2,$
and
![]() $305\mathbb {CP}^2\#220\overline {\mathbb {CP}}{}^2$
. These
$305\mathbb {CP}^2\#220\overline {\mathbb {CP}}{}^2$
. These
![]() $4$
-manifolds have signature equal to
$4$
-manifolds have signature equal to
![]() $5$
,
$5$
,
![]() $29$
,
$29$
,
![]() $45,$
and
$45,$
and
![]() $85$
, and
$85$
, and
![]() $\chi _h$
equal to
$\chi _h$
equal to
![]() $23$
,
$23$
,
![]() $61$
,
$61$
,
![]() $87,$
and
$87,$
and
![]() $153$
, respectively. For comparison, we showed in [Reference Akhmedov, Hughes and Park1, Table 2] that
$153$
, respectively. For comparison, we showed in [Reference Akhmedov, Hughes and Park1, Table 2] that
![]() $\lambda (5)\leq 47$
,
$\lambda (5)\leq 47$
,
![]() $\lambda (29)\leq 87$
,
$\lambda (29)\leq 87$
,
![]() $\lambda (45)\leq 85$
and
$\lambda (45)\leq 85$
and
![]() $\lambda (85)\leq 166$
. Thus these exotic smooth structures are new solutions to the symplectic geography problem when
$\lambda (85)\leq 166$
. Thus these exotic smooth structures are new solutions to the symplectic geography problem when
![]() $n=7,11,17$
as far as we know.
$n=7,11,17$
as far as we know.
Similarly, we can apply Theorem 3.1 to the surface bundle Y from Lemma 2.2 and obtain the following corollary.
Corollary 3.3 For any fibered knot
![]() $K\subset S^3$
of genus
$K\subset S^3$
of genus
![]() $8$
, there is a simply connected irreducible symplectic
$8$
, there is a simply connected irreducible symplectic
![]() $4$
-manifold
$4$
-manifold
![]() $Z_K$
that is homeomorphic to
$Z_K$
that is homeomorphic to
![]() $79\mathbb {CP}^2\#72\overline {\mathbb {CP}}{}^2$
.
$79\mathbb {CP}^2\#72\overline {\mathbb {CP}}{}^2$
.
Proof We let
 $Z_K=E(X)_{K,m,r}^{t,\delta }$
with
$Z_K=E(X)_{K,m,r}^{t,\delta }$
with
![]() $X=Y$
,
$X=Y$
,
![]() $a=7$
,
$a=7$
,
![]() $b=5$
,
$b=5$
,
![]() $d=-8$
,
$d=-8$
,
![]() $t=1$
,
$t=1$
,
![]() $\delta =1$
,
$\delta =1$
,
![]() $g(K)\,{=}\,8$
,
$g(K)\,{=}\,8$
,
![]() $m=4$
, and
$m=4$
, and
![]() $r=1$
. We have
$r=1$
. We have
![]() $e(Z_K)=153$
and
$e(Z_K)=153$
and
![]() $\sigma (Z_K)=7$
. The rest of the proof is similar to that of Corollary 3.2 and is left to the reader. ▪
$\sigma (Z_K)=7$
. The rest of the proof is similar to that of Corollary 3.2 and is left to the reader. ▪
In [Reference Akhmedov, Hughes and Park1], we showed that
![]() $\lambda (7)\leq 49$
. Since
$\lambda (7)\leq 49$
. Since
![]() $\chi _h(Z_K)=40$
, the symplectic smooth structure in Corollary 3.3 is new.
$\chi _h(Z_K)=40$
, the symplectic smooth structure in Corollary 3.3 is new.
Remark 3.4 It is well known (cf. [Reference Burde7]) that for a fixed genus
![]() $g>1$
, there are infinitely many genus g fibered (and nonfibered) knots that are distinguished by their Alexander polynomials. By varying the knot K while fixing the genus
$g>1$
, there are infinitely many genus g fibered (and nonfibered) knots that are distinguished by their Alexander polynomials. By varying the knot K while fixing the genus
![]() $g(K)$
, we expect the resulting collection of
$g(K)$
, we expect the resulting collection of
![]() $M(n)_K$
’s and
$M(n)_K$
’s and
![]() $Z_K$
’s to provide infinitely many distinct smooth structures on (3.6) and
$Z_K$
’s to provide infinitely many distinct smooth structures on (3.6) and
![]() $79\mathbb {CP}^2\#72\overline {\mathbb {CP}}{}^2$
. At present, it is not clear to us how to compute the Seiberg–Witten invariants of these
$79\mathbb {CP}^2\#72\overline {\mathbb {CP}}{}^2$
. At present, it is not clear to us how to compute the Seiberg–Witten invariants of these
![]() $4$
-manifolds completely so as to distinguish their smooth structures.
$4$
-manifolds completely so as to distinguish their smooth structures.
We end this section by constructing another family of simply connected irreducible symplectic
![]() $4$
-manifolds.
$4$
-manifolds.
Corollary 3.5 For any positive integer
![]() $n\geq 5$
such that
$n\geq 5$
such that
![]() $n\equiv \pm 1\pmod {6}$
and any fibered knot
$n\equiv \pm 1\pmod {6}$
and any fibered knot
![]() $K\subset S^3$
of genus
$K\subset S^3$
of genus
 $\frac {3}{2}(n-1)-1$
, there is a simply connected irreducible symplectic
$\frac {3}{2}(n-1)-1$
, there is a simply connected irreducible symplectic
![]() $4$
-manifold
$4$
-manifold
![]() $X(n)_K$
that is homeomorphic to
$X(n)_K$
that is homeomorphic to
 $$ \begin{align} \bigg(\frac{7}{6}n^2-2n+\frac{23}{6}\bigg)\mathbb{CP}^2 \#\bigg(\frac{5}{6}n^2-2n+\frac{145}{6}\bigg)\overline{\mathbb{CP}}{}^2. \end{align} $$
$$ \begin{align} \bigg(\frac{7}{6}n^2-2n+\frac{23}{6}\bigg)\mathbb{CP}^2 \#\bigg(\frac{5}{6}n^2-2n+\frac{145}{6}\bigg)\overline{\mathbb{CP}}{}^2. \end{align} $$
Moreover, each
![]() $X(n)_K$
contains two disjoint symplectic tori,
$X(n)_K$
contains two disjoint symplectic tori,
![]() $T_1$
and
$T_1$
and
![]() $T_2,$
of self-intersection
$T_2,$
of self-intersection
![]() $0$
such that
$0$
such that
![]() $\pi _1(X(n)_K\backslash (T_1\cup T_2))=1$
.
$\pi _1(X(n)_K\backslash (T_1\cup T_2))=1$
.
Proof We let
 $X(n)_K=E(X)_{K,m,r}^{t,\delta }$
with
$X(n)_K=E(X)_{K,m,r}^{t,\delta }$
with
![]() $X=S(n)$
,
$X=S(n)$
,
![]() $a=n-1$
,
$a=n-1$
,
![]() $b=(n-1)/2$
,
$b=(n-1)/2$
,
![]() $d=-1$
,
$d=-1$
,
![]() $t=1$
,
$t=1$
,
![]() $\delta =1$
,
$\delta =1$
,
 $g(K)=\frac {3}{2}(n-1)-1$
,
$g(K)=\frac {3}{2}(n-1)-1$
,
![]() $m=1$
, and
$m=1$
, and
![]() $r=2$
. We have
$r=2$
. We have
![]() $e(X(n)_K)=2n^2-4n+30$
and
$e(X(n)_K)=2n^2-4n+30$
and
 $\sigma (X(n)_K)=\frac {1}{3}(n^2-61)$
. The rest of the proof is similar to the proof of Corollary 3.2 and is left to the reader. ▪
$\sigma (X(n)_K)=\frac {1}{3}(n^2-61)$
. The rest of the proof is similar to the proof of Corollary 3.2 and is left to the reader. ▪
We note that the signature of
![]() $X(n)_K$
is positive when
$X(n)_K$
is positive when
![]() $n\geq 11$
. By performing knot surgeries along
$n\geq 11$
. By performing knot surgeries along
![]() $T_1$
(and/or
$T_1$
(and/or
![]() $T_2$
) on
$T_2$
) on
![]() $X(n)_K$
, we can obtain infinitely many distinct smooth structures on (3.7).
$X(n)_K$
, we can obtain infinitely many distinct smooth structures on (3.7).
Corollary 3.6 For any positive integer
![]() $n\geq 5$
such that
$n\geq 5$
such that
![]() $n\equiv \pm 1\pmod {6}$
, the
$n\equiv \pm 1\pmod {6}$
, the
![]() $4$
-manifold (3.7) in Corollary 3.5 has
$4$
-manifold (3.7) in Corollary 3.5 has
![]() $\infty ^2$
-property (cf. Definition 1.2).
$\infty ^2$
-property (cf. Definition 1.2).
Proof This follows immediately from [Reference Akhmedov, Hughes and Park1, Theorem 16]. ▪
For example, when
![]() $n=17$
, we obtain infinitely many exotic smooth structures on
$n=17$
, we obtain infinitely many exotic smooth structures on
![]() $307\mathbb {CP}^2\#231\overline {\mathbb {CP}}{}^2$
, which have signature equal to
$307\mathbb {CP}^2\#231\overline {\mathbb {CP}}{}^2$
, which have signature equal to
![]() $76$
and
$76$
and
![]() $\chi _h$
equal to
$\chi _h$
equal to
![]() $154$
. For comparison, we only showed in [Reference Akhmedov, Hughes and Park1] that
$154$
. For comparison, we only showed in [Reference Akhmedov, Hughes and Park1] that
![]() $\lambda (76)\leq 167$
, so these exotic smooth structures are new (cf. Remark 4.5).
$\lambda (76)\leq 167$
, so these exotic smooth structures are new (cf. Remark 4.5).
4 Upper Bounds on
 $\lambda (\sigma )$
$\lambda (\sigma )$
The goal of this section is to exhibit concrete formulae for upper bounds on
![]() $\lambda (\sigma )$
that are valid for any nonnegative integer
$\lambda (\sigma )$
that are valid for any nonnegative integer
![]() $\sigma $
. First, we recall the following theorem, which was proved in [Reference Akhmedov, Hughes and Park1, Corollary 17].
$\sigma $
. First, we recall the following theorem, which was proved in [Reference Akhmedov, Hughes and Park1, Corollary 17].
Theorem 4.1 Let X be a closed, simply connected, nonspin, minimal, symplectic
![]() $4$
-manifold with
$4$
-manifold with
![]() $b_2^+(X)>1$
and
$b_2^+(X)>1$
and
![]() $\sigma (X)\geq 0$
. Assume that X contains disjoint symplectic tori
$\sigma (X)\geq 0$
. Assume that X contains disjoint symplectic tori
![]() $T_1$
and
$T_1$
and
![]() $T_2$
of self-intersection
$T_2$
of self-intersection
![]() $0$
such that
$0$
such that
![]() $\pi _1(X\backslash (T_1 \cup T_2))=1$
. Suppose
$\pi _1(X\backslash (T_1 \cup T_2))=1$
. Suppose
![]() $\sigma $
is a fixed integer satisfying
$\sigma $
is a fixed integer satisfying
![]() $0\leq \sigma \leq \sigma (X)$
. If
$0\leq \sigma \leq \sigma (X)$
. If
![]() $\lceil x\rceil =\min \{k\in \mathbb {Z} \mid k\geq x\}$
and if we define
$\lceil x\rceil =\min \{k\in \mathbb {Z} \mid k\geq x\}$
and if we define
 $$ \begin{align*} \ell(\sigma)=\Big\lceil \frac{\sigma(X)-\sigma}{8} -1 \Big\rceil , \end{align*} $$
$$ \begin{align*} \ell(\sigma)=\Big\lceil \frac{\sigma(X)-\sigma}{8} -1 \Big\rceil , \end{align*} $$
then
Now we apply Theorem 4.1 to the
![]() $4$
-manifolds
$4$
-manifolds
![]() $Q(u)$
in Lemma 2.4 and obtain the following corollary.
$Q(u)$
in Lemma 2.4 and obtain the following corollary.
Corollary 4.2 If
![]() $\lambda (\sigma )$
is as in Definition 1.1, then we have
$\lambda (\sigma )$
is as in Definition 1.1, then we have
 $$ \begin{align} \lambda(\sigma)< \frac{43}{25}\sigma+\frac{6813}{100} =1.72\sigma+68.13. \end{align} $$
$$ \begin{align} \lambda(\sigma)< \frac{43}{25}\sigma+\frac{6813}{100} =1.72\sigma+68.13. \end{align} $$
Proof Given a nonnegative integer
![]() $\sigma $
, let u be the smallest positive integer such that
$\sigma $
, let u be the smallest positive integer such that
![]() $\sigma \leq \sigma (Q(u))=26u-2\lceil u/2\rceil -2$
. It follows that when
$\sigma \leq \sigma (Q(u))=26u-2\lceil u/2\rceil -2$
. It follows that when
![]() $u>1$
,
$u>1$
,
 $$ \begin{align} \sigma(Q(u))-\sigma < \sigma(Q(u))-\sigma(Q(u-1)) = 26 -2\big(\lceil u/2\rceil -\lceil (u-1)/2\rceil\big) \leq 26, \end{align} $$
$$ \begin{align} \sigma(Q(u))-\sigma < \sigma(Q(u))-\sigma(Q(u-1)) = 26 -2\big(\lceil u/2\rceil -\lceil (u-1)/2\rceil\big) \leq 26, \end{align} $$
since
![]() $\lceil u/2\rceil -\lceil (u-1)/2\rceil $
is either
$\lceil u/2\rceil -\lceil (u-1)/2\rceil $
is either
![]() $0$
or
$0$
or
![]() $1$
depending on whether u is even or odd. Note that
$1$
depending on whether u is even or odd. Note that
![]() $\sigma (Q(1))=22$
so that we still have
$\sigma (Q(1))=22$
so that we still have
![]() $\sigma (Q(u))-\sigma < 26$
even when
$\sigma (Q(u))-\sigma < 26$
even when
![]() $u=1$
. Thus, we have
$u=1$
. Thus, we have
![]() $\ell (\sigma )<(\sigma (Q(u))-\sigma )/8 < 13/4$
. Since
$\ell (\sigma )<(\sigma (Q(u))-\sigma )/8 < 13/4$
. Since
by (4.2) and
![]() $2\lceil u/2\rceil $
is u or
$2\lceil u/2\rceil $
is u or
![]() $u+1$
depending on whether u is even or odd, we conclude that
$u+1$
depending on whether u is even or odd, we conclude that
![]() $\sigma>26u-(u+1)-28=25u-29$
. Thus, we have
$\sigma>26u-(u+1)-28=25u-29$
. Thus, we have
![]() $u<(\sigma +29)/25$
and
$u<(\sigma +29)/25$
and
 $$ \begin{align*} \lambda(\sigma)&\leq \chi_h(Q(u)) + \ell(\sigma) + 1 <27u+32\Big\lceil \frac{u}{2}\Big\rceil -2+\frac{13}{4}+1\\ &\leq 43u+\frac{73}{4} <\frac{43}{25}\sigma+\frac{6813}{100}, \end{align*} $$
$$ \begin{align*} \lambda(\sigma)&\leq \chi_h(Q(u)) + \ell(\sigma) + 1 <27u+32\Big\lceil \frac{u}{2}\Big\rceil -2+\frac{13}{4}+1\\ &\leq 43u+\frac{73}{4} <\frac{43}{25}\sigma+\frac{6813}{100}, \end{align*} $$
since
![]() $32\lceil u/2\rceil $
is
$32\lceil u/2\rceil $
is
![]() $16u$
or
$16u$
or
![]() $16u+16$
depending on whether u is even or odd. ▪
$16u+16$
depending on whether u is even or odd. ▪
Remark 4.3 For a specific value of
![]() $\sigma $
, (4.1) may not provide the optimal bound procured from
$\sigma $
, (4.1) may not provide the optimal bound procured from
![]() $Q(u)$
. For example, when
$Q(u)$
. For example, when
![]() $\sigma =76$
, we can apply Theorem 4.1 to
$\sigma =76$
, we can apply Theorem 4.1 to
![]() $Q(4)$
directly and obtain
$Q(4)$
directly and obtain
![]() $\lambda (76)\leq 173$
, which is better than the bound
$\lambda (76)\leq 173$
, which is better than the bound
![]() $\lambda (76)\leq 198$
coming from (4.1).
$\lambda (76)\leq 198$
coming from (4.1).
Similarly, we apply Theorem 4.1 to the
![]() $4$
-manifolds
$4$
-manifolds
![]() $\tilde {Q}(u)$
in Lemma 2.4 and obtain the following corollary.
$\tilde {Q}(u)$
in Lemma 2.4 and obtain the following corollary.
Corollary 4.4 If
![]() $\lambda (\sigma )$
is as in Definition 1.1, then we have
$\lambda (\sigma )$
is as in Definition 1.1, then we have
 $$ \begin{align} \lambda(\sigma)< \frac{8}{5}\sigma +\frac{417}{20}\sqrt{\sigma +4}+\frac{1353}{20} =1.6\sigma +20.85\sqrt{\sigma +4}+67.65. \end{align} $$
$$ \begin{align} \lambda(\sigma)< \frac{8}{5}\sigma +\frac{417}{20}\sqrt{\sigma +4}+\frac{1353}{20} =1.6\sigma +20.85\sqrt{\sigma +4}+67.65. \end{align} $$
Proof Given a nonnegative integer
![]() $\sigma $
, let u be the smallest positive integer such that
$\sigma $
, let u be the smallest positive integer such that
![]() $\sigma \leq \sigma (\tilde {Q}(u))= 25u^2+u-2\lceil u/2\rceil -2$
. Note that
$\sigma \leq \sigma (\tilde {Q}(u))= 25u^2+u-2\lceil u/2\rceil -2$
. Note that
 $$ \begin{align*} \sigma(\tilde{Q}(u))-\sigma(\tilde{Q}(u-1)) =50u-24-2\big(\lceil u/2\rceil -\lceil (u-1)/2\rceil\big) \leq 50u-24. \end{align*} $$
$$ \begin{align*} \sigma(\tilde{Q}(u))-\sigma(\tilde{Q}(u-1)) =50u-24-2\big(\lceil u/2\rceil -\lceil (u-1)/2\rceil\big) \leq 50u-24. \end{align*} $$
It follows that
Note that
![]() $\sigma (\tilde {Q}(1))=22$
so that (4.4) still holds when
$\sigma (\tilde {Q}(1))=22$
so that (4.4) still holds when
![]() $u=1$
. Thus, we have
$u=1$
. Thus, we have
 $\ell (\sigma )<(\sigma (\tilde {Q}(u))-\sigma )/8 < \frac {25}{4}u-3$
. Since
$\ell (\sigma )<(\sigma (\tilde {Q}(u))-\sigma )/8 < \frac {25}{4}u-3$
. Since
![]() $\lceil u/2\rceil \leq (u+1)/2$
, we get
$\lceil u/2\rceil \leq (u+1)/2$
, we get
 $$ \begin{align} \lambda(\sigma)&\leq \chi_h(\tilde{Q}(u))+\ell(\sigma)+1\nonumber \\ &< 25u^2+\lceil u/2\rceil(30u+2) +2u -2+\frac{25}{4}u-2\nonumber \\ &\leq 25u^2+(u+1)(15u+1)+\frac{33}{4}u-4 =40u^2+\frac{97}{4}u-3. \end{align} $$
$$ \begin{align} \lambda(\sigma)&\leq \chi_h(\tilde{Q}(u))+\ell(\sigma)+1\nonumber \\ &< 25u^2+\lceil u/2\rceil(30u+2) +2u -2+\frac{25}{4}u-2\nonumber \\ &\leq 25u^2+(u+1)(15u+1)+\frac{33}{4}u-4 =40u^2+\frac{97}{4}u-3. \end{align} $$
From (4.4), we also obtain
 $$ \begin{align*} \sigma &>\sigma(\tilde{Q}(u))-50u+24= 25u^2 -2\lceil u/2\rceil -49u+22\\ &\geq 25u^2 -(u+1) -49u+22 =25u^2-50u+21. \end{align*} $$
$$ \begin{align*} \sigma &>\sigma(\tilde{Q}(u))-50u+24= 25u^2 -2\lceil u/2\rceil -49u+22\\ &\geq 25u^2 -(u+1) -49u+22 =25u^2-50u+21. \end{align*} $$
Thus, we must have
 $u<1+\frac {1}{5}\sqrt {\sigma +4}$
, and plugging this into (4.5), we obtain (4.3). ▪
$u<1+\frac {1}{5}\sqrt {\sigma +4}$
, and plugging this into (4.5), we obtain (4.3). ▪
We observe that (4.1) is a better (i.e., lower) upper bound than (4.3) when
![]() $\sigma \leq 30185$
and (4.3) is better than (4.1) when
$\sigma \leq 30185$
and (4.3) is better than (4.1) when
![]() $\sigma \geq 30186$
.
$\sigma \geq 30186$
.
Remark 4.5 If we apply Theorem 4.1 to our
![]() $4$
-manifolds
$4$
-manifolds
![]() $X(n)_K$
in Corollary 3.5 with
$X(n)_K$
in Corollary 3.5 with
![]() $n\geq 11$
and argue as in the proof of Corollary 4.4, then we can deduce an upper bound
$n\geq 11$
and argue as in the proof of Corollary 4.4, then we can deduce an upper bound
 $$ \begin{align*} \lambda(\sigma)< \frac{7}{4}\sigma +4\sqrt{3\sigma+61}+45, \end{align*} $$
$$ \begin{align*} \lambda(\sigma)< \frac{7}{4}\sigma +4\sqrt{3\sigma+61}+45, \end{align*} $$
which is always worse than (4.1). However, we note that it is still possible to get a new and better upper bound for
![]() $\lambda (\sigma )$
from
$\lambda (\sigma )$
from
![]() $X(n)_K$
for individual
$X(n)_K$
for individual
![]() $\sigma $
. For example, by applying Theorem 4.1 to
$\sigma $
. For example, by applying Theorem 4.1 to
![]() $X(17)_K$
, we obtain
$X(17)_K$
, we obtain
which are better than the bounds
![]() $\lambda (75)\leq 197$
and
$\lambda (75)\leq 197$
and
![]() $\lambda (76)\leq 198$
coming from (4.1). The upper bounds in (4.6) are also better than the bound
$\lambda (76)\leq 198$
coming from (4.1). The upper bounds in (4.6) are also better than the bound
![]() $\lambda (\sigma )\leq 173$
for
$\lambda (\sigma )\leq 173$
for
![]() $\sigma =75,76$
that is obtained by applying Theorem 4.1 to
$\sigma =75,76$
that is obtained by applying Theorem 4.1 to
![]() $Q(4)$
(cf. Remark 4.3), and the bound
$Q(4)$
(cf. Remark 4.3), and the bound
![]() $\lambda (\sigma )\leq 167$
for
$\lambda (\sigma )\leq 167$
for
![]() $\sigma =75,76$
in [Reference Akhmedov, Hughes and Park1, Table 2], which was obtained by applying Theorem 4.1 to
$\sigma =75,76$
in [Reference Akhmedov, Hughes and Park1, Table 2], which was obtained by applying Theorem 4.1 to
![]() $\tilde {Q}(2)$
.
$\tilde {Q}(2)$
.
We finish our paper by observing that (4.1) does not give the least known upper bound on
![]() $\lambda (\sigma )$
for very low values of
$\lambda (\sigma )$
for very low values of
![]() $\sigma $
. For example, (4.1) gives
$\sigma $
. For example, (4.1) gives
![]() $\lambda (0)\leq 68$
, whereas we already know from [Reference Akhmedov and Sakallı5] that
$\lambda (0)\leq 68$
, whereas we already know from [Reference Akhmedov and Sakallı5] that
![]() $\lambda (0)\leq 12$
. We still hope that (4.1) and (4.3) provide baselines of comparison for future research.
$\lambda (0)\leq 12$
. We still hope that (4.1) and (4.3) provide baselines of comparison for future research.
Acknowledgment
The authors thank F. Catanese for valuable e-mail exchanges regarding the
![]() $BCD$
surfaces and S. Sakallı for her interest in this work.
$BCD$
surfaces and S. Sakallı for her interest in this work.