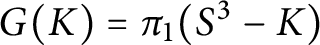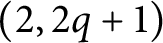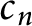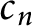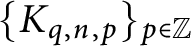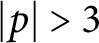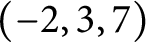1 Introduction
Let G be a group, and let g be a nontrivial element in G. If some nonempty finite product of conjugates of g equals the identity, then g is called a generalized torsion element. In particular, any nontrivial torsion element is a generalized torsion element.
A group G is said to be bi-orderable if G admits a strict total ordering
$<$
which is invariant under multiplication from the left and the right. That is, if
$g<h$
, then
$agb<ahb$
for any
$g,h,a,b\in G$
. In this paper, the trivial group
$\{1\}$
is considered to be bi-orderable.
It is easy to see that a bi-orderable group does not have a generalized torsion element. Thus, the existence of generalized torsion element is an obstruction for a group to be bi-orderable. It is known that the converse does not hold in general [Reference Mura and Rhemtulla16, Chapter 4]. However, among
$3$
-manifold groups (fundamental groups of
$3$
-manifolds), one may expect that the converse does hold, and the authors proposed the following conjecture [Reference Motegi and Teragaito15].
Conjecture 1.1 Let G be the fundamental group of a
$3$
-manifold. Then, G is bi-orderable if and only if G has no generalized torsion element.
Let us restrict our attention to a knot group
$G(K)$
, the fundamental group of the exterior
$E(K)$
of a knot K in
$S^3$
. Then,
$G(K)$
is known to be left-orderable, i.e., it has a strict total ordering
$<$
which is invariant under multiplication from the left [Reference Boyer, Rolfsen and Wiest2, Reference Howie and Short9]. On the other hand, little is known for having generalized torsion elements or being bi-orderable.
In what follows, for short, we often say that K has generalized torsion if its knot group
$G(K)$
has a generalized torsion element. Any nontrivial torus knot has generalized torsion [Reference Naylor and Rolfsen17], and hence any satellite of a nontrivial torus knot also has generalized torsion.
Using this simple fact, we may observe the following in ad hoc fashion.
Proposition 1.2 For a given knot K, there are infinitely many twisting circles c such that
$K_p$
, the knot obtained from K by p twisting about c, has generalized torsion.
Proof Let us take an unknotted solid torus V which contains K in its interior, so that K is not a core of V and not embedded in a
$3$
-ball in V. Note that there are infinitely many such solid tori. Then, let c be an unknotting circle on
$\partial V$
which wraps
$m\ (\ge $
2) times in the meridional direction and once in the longitudinal direction of V. If we perform p-twisting about c, then the core of V becomes a
$(m, pm+1)$
-torus knot. Thus,
$K_p$
is a satellite knot which has the torus knot
$T_{m, pm+1}$
as a companion knot. Recall that
$\pi _1(E(T_{m, pm+1}))$
has a generalized torsion element (see [Reference Naylor and Rolfsen17]; cf. [Reference Motegi and Teragaito15]). Because
$\pi _1(E(T_{m, pm+1}))$
injects into
$\pi _1(E(K_p))$
,
$\pi _1(E(K_p))$
also has a generalized torsion element.▪
By construction, the knots given in Proposition 1.2 are satellite knots. Turning to hyperbolic knots, Naylor and Rolfsen [Reference Naylor and Rolfsen17] discovered a generalized torsion element in the knot group of the hyperbolic knot
$5_2$
by using a computer. It is surprising that this is the first example of hyperbolic knot with generalized torsion. The knot
$5_2$
is the
$(-2)$
-twist knot, and the second-named author extends this example to all negative twist knots [Reference Teragaito19]. As far as we know, these twist knots are the only known hyperbolic knots with generalized torsion. We emphasize that all twist knots have genus one.
In this paper, applying twisting operation, we demonstrate the following theorem.
Theorem 1.3 Let
$K_q$
be a
$(2, 2q+1)$
-torus knot
$T_{2, 2q+1} (q \ge 1)$
. Then, there are infinitely many unknots
$c_n$
(indexed by positive integers) in
$S^3$
disjoint from
$K_q$
such that each
$c_n$
enjoys the following property. Let
$K_{q, n, p}$
be a knot obtained from
$K_q$
by p-twisting about
$c_n$
. Then, for each infinite family
$\{ K_{q, n, p}\}_{p \in \mathbb {Z}}$
,
$K_{q, n, p}$
is a hyperbolic knot with generalized torsion whenever
$|p|> 3$
.
Because the linking number between
$c_n$
and
$K_q$
is greater than 1, [Reference Baker and Motegi1, Theorem 2.1] shows that the genus of
$K_{q, n, p}$
tends to
$\infty $
as
$|p| \to \infty $
.
Corollary 1.4 There are infinitely many hyperbolic knots with arbitrarily high genus, each of which has generalized torsion.
Furthermore, we will show that some twisted torus knots, including the
$(-2, 3, 7)$
-pretzel knot, have generalized torsion. This implies the following.
Corollary 1.5 The knot group of the pretzel knot of type
$(-2,3,2s+5)$
is not bi-orderable for
$s\ge 0$
.
Lidman and Moore [Reference Lidman and Moore13] showed that the pretzel knots of type
$(-2,3,2s+1)$
are L-space knots which are not bi-orderable by [Reference Clay and Rolfsen4, Theorem 1.2]. Thus, our result gives an alternative proof, but the absence of bi-ordering does not imply the existence of generalized torsion.
2 Decomposition of commutators
We prepare a few useful facts which will be exploited to identify a generalized torsion element. Throughout this paper,
$[x, y]$
denotes the commutator
$x^{-1}y^{-1}xy$
, and
$x^g = g^{-1}x g$
in a group G.
Recall the well-known commutator identity which holds in a group.
Lemma 2.1
$[x, yz] = [x, z] [x, y]^z$
.
Proof
$[x, yz] = x^{-1}(yz)^{-1}x (yz) =(x^{-1}z^{-1}xz)z^{-1}(x^{-1}y^{-1}xy)z = [x, z][x, y]^z$
.▪
Lemma 2.2 In a group, let
$w(a^{\varepsilon _a}, b^{\varepsilon _b}) (\varepsilon _a$
and
$\varepsilon _b$
are either
$1$
or
$-1)$
be any word in which only
$a^{\varepsilon _a}$
and
$b^{\varepsilon _b}$
appear; neither
$a^{-\varepsilon _a}$
nor
$b^{-\varepsilon _b}$
appears. Then, the commutator
$[x,w(a^{\varepsilon _a}, b^{\varepsilon _b})]$
can be decomposed into a product of conjugates of
$[x, a^{\varepsilon _a}]$
and
$[x, b^{\varepsilon _b}]$
.
Proof The proof is done by the induction on the length of
$w(a^{\varepsilon _a}, b^{\varepsilon _b})$
. For simplicity, we assume
$\varepsilon _a = \varepsilon _b = 1$
. The other cases are similar.
If the length of
$w(a, b)$
is 1, then
$w(a, b) = a$
or b by the assumption, and
$[x, w(a, b)]$
is nothing but
$[x, a]$
or
$[x, b]$
.
Assume that for any word
$w'(a, b)$
with length
$n-1$
,
$[x, w'(a, b)]$
can be written as a product of conjugates of
$[x, a]$
and
$[x, b]$
. Then, we show that the same is true for
$[x, w(a, b)]$
for
$w(a, b)$
with length n. Here, we suppose that the initial letter of
$w(a, b)$
is a, i.e.,
$w(a, b) = aw'(a, b)$
. Then,
$[x, w(a, b)] = [x, aw'(a, b)]$
. Applying Lemma 2.1, we have
$[x, aw'(a, b)] = [x, w'(a, b)][x, a]^{w'(a, b)}$
. Because
$w'(a, b)$
has length
$n-1$
, we may write
$[x, w'(a, b)]$
as a product of conjugates of
$[x, a]$
and
$[x, b]$
, completing the proof.▪
Because
$[b,b]=[b,b^{-1}]=1$
, we have the following proposition.
Proposition 2.3 The commutator
$[b, w(a^{\varepsilon _a}, b^{\varepsilon _b})]$
can be decomposed into a product of conjugates of
$[b, a^{\varepsilon _a}]$
.
3 Generalized torsion which arises from twisting torus knots
$T_{2, 2q+1}$
The goal of this section is to prove the following theorem.
Theorem 1.3 Let
$K_q$
be a
$(2, 2q+1)$
-torus knot
$T_{2, 2q+1} (q \ge 1)$
. Then, there are infinitely many unknots
$c_n$
(indexed by positive integers) in
$S^3$
disjoint from
$K_q$
such that each
$c_n$
enjoys the following property. Let
$K_{q, n, p}$
be a knot obtained from
$K_q$
by p-twisting about
$c_n$
. Then, for each infinite family
$\{ K_{q, n, p}\}_{p \in \mathbb {Z}}$
,
$K_{q, n, p}$
is a hyperbolic knot with generalized torsion whenever
$|p|> 3$
.
Proof For integers
$q,\ n \ge 1$
, we consider the braid
$$ \begin{align*} (\sigma_1\sigma_2\cdots \sigma_{2q+n+1})(\sigma_1\sigma_2\cdots \sigma_{2q}) \end{align*} $$
of
$2q+n+2$
strands, where
$\sigma _i$
’s are the standard generators of the braid group. Figure 1 shows this braid and its axis
$c_n$
. Let
$K_q$
be its closure. Then,
$K_q \cup c_n$
is deformed as shown in Figures 2–5, where full twists are right-handed. Hence,
$K_q$
is the torus knot
$T_{2, 2q+1}$
.
Figure 1 A braid with an axis
$c_n$
.
Figure 2 Deform
$K_q \cup c_n$
.
Figure 3 Deform
$K_q \cup c_n$
.
Figure 4 Deform
$K_q \cup c_n$
.
Figure 5 The link
$K_q \cup c_n$
with unknotting tunnel
$\gamma $
.
Then, as shown in Figures 2–5, the link
$K_q \cup c_n$
is deformed into a link given in Figure 6.
Figure 6
$K_q \cup c_n$
.
We first claim that the link
$K_q \cup c_n$
is a hyperbolic link whose link group contains a generalized torsion element.
Claim 3.1
$K_q \cup c_n$
is hyperbolic.▪
Proof of Claim 3.1 The braid given by Figure 1 is the mirror image of the braid in [Reference Hironaka and Kin8, Figure 18(c)]. So, it is pseudo-Anosov by [Reference Hironaka and Kin8, Theorem 3.11]. (In [Reference Kin and Rolfsen12], Theorem 6.7 treats the case where
$n=1$
. Furthermore, in Figure 18(b) and (c) of [Reference Hironaka and Kin8], there is a mistake. The number
$2m-1$
of strands should be
$2m$
.) Hence, the link complement of
$K_q \cup c_n$
is hyperbolic. ▪
Claim 3.2 The link group of
$K_q \cup c_n$
contains a generalized torsion element.
Proof of Claim 3.2 The link
$K_q \cup c_n$
has tunnel number 1. Let
$\gamma $
be its unknotting tunnel as shown in Figure 5. This means that the outside of the regular neighborhood
$N(K_q \cup c_n \cup \gamma )$
is a genus-two handlebody. Let
$\ell $
be the co-core loop of
$N(\gamma )\subset N(K_q \cup c_n \cup \gamma )$
. We deform
$N=N(c_n \cup \gamma )$
with
$\ell $
as shown in Figure 7, where
$q+n+2$
full twists are expressed as
$-1/(q+n+2)$
-surgery along an unknotted circle. Figures 8, 9, and 10 show the deformation of N with
$\ell $
, where
$\ell $
is expressed as a band sum of two circles on
$\partial N$
as shown in Figure 7. Then, subsequently, deform N as shown in Figures 8 and 9. Finally, the q twists in Figure 9 are absorbed as illustrated in Figure 11.
Figure 7 Deform N with
$\ell $
.
Figure 8 Deform N with
$\ell $
.
Figure 9 Deform N with
$\ell $
.
Figure 10 Deform N with
$\ell $
;
$\ell $
is twisted in N as in the right-hand side of Figure 11.
Figure 11 Absorb q twists.
In the final form of Figure 10, it is obvious to see that the outside of
$N(K_q \cup c_n \cup \gamma )$
is a genus-two handlebody denoted by H. As shown in Figure 12, the loops
$\alpha $
and
$\beta $
, which lie on
$\partial N$
, bound mutually disjoint nonseparating meridian disks of H. If we take generators a and b of
$\pi _1(H)$
as duals of
$\alpha $
and
$\beta $
, then
$\pi _1(H)$
is a rank- 2 free group generated by a and b. The link exterior of
$K_q \cup c_n$
is obtained from H by attaching a
$2$
-handle along
$\ell $
. By following the intersection points of
$\ell $
with
$\alpha $
and
$\beta $
, we can represent
$\ell $
as a word w of a and b, in fact, by choosing the base point and an orientation for
$\ell $
as shown in Figure 11. Then, referring to Figure 12, we obtain
$$ \begin{align*} w_{q, n} &= a(b^{-1}a^{-1})^{q}b^{-1}(ab)^{q}a^{n+2}b(ab)^{q}(a^{-1}b^{-1})^{q}a^{-1}a^{-(n+2)} \\ &= a(b^{-1}a^{-1})^{q}b^{-1}(ab)^{q}a^{n+2}(ba)^{q}b(a^{-1}b^{-1})^{q}a^{-(n+3)}. \end{align*} $$
Hence, we have
$$ \begin{align*} \pi_1(S^3-K_q \cup c_n) &=\langle a, b \mid w_{q, n} = 1 \rangle\\ &=\langle a, b \mid (ab)^{q}a^{n+2}(ba)^{q}b=b(ab)^{q}a^{n+2}(ba)^{q} \rangle\\ &=\langle a, b \mid [b, (ab)^{q}a^{n+2}(ba)^{q}]=1 \rangle. \end{align*} $$
Figure 12 Two loops
$\alpha $
and
$\beta $
bound mutually disjoint meridian disks of the outside handlebody H.
Proposition 2.3 shows that the commutator
$[b, (ab)^{q}a^{n+2}(ba)^{q}]$
is decomposed into a product of conjugates of
$[b, a]$
. Hence,
$[b, a]$
is a generalized torsion element in
$\pi _1(S^3-K_q \cup c_n)$
if it is nontrivial. Assume for a contradiction that
$[b, a] = 1$
in
$\pi _1(S^3-K_q \cup c_n)$
. Then, because a and b generate
$\pi _1(S^3-K_q \cup c_n)$
,
$\pi _1(S^3-K_q \cup c_n)$
would be abelian. However, the unknot and the Hopf link are the only knot and link with abelian knot or link group, contradicting Claim 3.1. Thus,
$[b,a]$
is nontrivial and, hence, a generalized torsion element in
$\pi _1(S^3-K_q \cup c_n)$
.
Claim 3.3
$[b, a]$
is a generalized torsion element of
$G(K_{q, n, p})$
, provided if
$|p| \ne 1$
.
Proof We remark that
$E(K_{q, n, p})$
is obtained from
$S^3 - \mathrm {int}N(K_q \cup c_n)$
by
$(-\frac {1}{p})$
-Dehn filling along
$\partial N(c_n)$
. This gives us an epimorphism
$$ \begin{align*} \varphi \colon \pi_1(S^3 - \mathrm{int}N(K_q \cup c_n)) \to G(K_{q, n, p}) = \pi_1(E(K_{q, n, p})). \end{align*} $$
Recall that a and b generate
$\pi _1(S^3 - \mathrm {int}N(K_q \cup c_n))$
and satisfy
$[b, (ab)^q a^{n+2}(ba)^q] = 1$
. For notational simplicity, in the following, we use the same symbols a and b to denote
$\varphi (a)$
and
$\varphi (b)$
. Then,
$G(K_{q, n, p})$
is generated by a and b. Because
$[b, (ab)^q a^{n+2}(ba)^q] = 1 \in G(K_{q, n, p})$
, by Proposition 2.3,
$[b, a]$
is a generalized torsion element of
$G(K_{q, n, p})$
whenever it is nontrivial.
Let us assume that
$[b, a]$
is trivial in
$G(K_{q, n, p})$
. Then,
$G(K_{q, n, p})$
is abelian, and hence
$G(K_{q, n, p}) \cong \mathbb {Z}$
, i.e.,
$K_{q, n, p}$
is a trivial knot. If
$p = 0$
, then
$K_{q, n, 0} = K_{q}$
is a nontrivial torus knot
$T_{2, 2q+1}$
. Hence,
$p \ne 0$
. Note that the torus knot space
$E(K_{q}) = E(K_{q, n, 0}) = E(T_{2, 2q+1})$
is obtained from the solid torus
$V = S^3 - \mathrm {int}N(K_{q, n, p})$
by
$\frac {1}{p}$
-surgery on
$c_n$
. Furthermore,
$V- \mathrm {int}N(c_n)$
is homeomorphic to the exterior of the link
$K_q\cup c_n$
, so it is hyperbolic by Claim 3.1. Thus,
$c_n $
is not contained in a
$3$
-ball in V and, moreover, is neither a core of V nor a cable of a
$0$
-braid in V. Because
$E(K_{q})$
is a Seifert fiber space, we may apply [Reference Miyazaki and Motegi14, Theorem 1.2] to conclude that
$|p| = 1$
.▪
Remark 3.4 In Claim 3.3,
$K_{q, n, \pm 1}$
also has a generalized torsion element. We may observe that
$K_{q, n, 1}$
is a closure of a positive braid, and
$K_{q, n, -1}$
is a closure of a negative braid. Hence, [Reference Stallings18] shows that both have a positive genus. This implies that
$K_{q,n,\pm 1}$
is nontrivial.
Claim 3.5
$K_{q, n, p}$
is a hyperbolic knot if
$|p|> 3$
.
Proof Because
$K_{q, n}$
is a nontrivial torus knot
$T_{2, 2q+1}$
and
$S^3 - \mathrm {int}N(K_q \cup c_n)$
is hyperbolic (Claim 3.1), [Reference Deruelle, Miyazaki and Motegi6, Proposition 5.11] shows that
$K_{q, n, p}$
is hyperbolic if
$|p|> 3$
.▪
Claim 3.6
$K_q \cup c_n$
and
$K_q \cup c_{n'}$
are not isotopic when
$n \ne n'$
.
Proof As shown in Figure 1, the linking number between
$K_q$
and
$c_n$
is
$2q+n+2$
with a suitable orientation. Hence, if
$n \ne n'$
,
$K_q \cup c_n$
and
$K_q \cup c_{n'}$
are not isotopic.▪
Thus, we obtain infinitely many twisting circles
$c_n$
for
$K _q = T_{2, 2q+1}$
by varying n.
Now, the proof of Theorem 1.3 follows from Claims 3.3, 3.5, and 3.6.
Remark 3.7
-
(1) When
$q=0$
, the link
$K_0\cup c_n$
is equivalent to the pretzel link of type
$(-2,3,2n+6)$
. This special case is treated in [Reference Teragaito20]. -
(2) The generalized torsion element for
$K_{q,n,p}$
is derived from that of the link
$K_q\cup c_n$
. Hence, the element lies in the complement of
$K_q\cup c_n$
, and furthermore, the
$2$
-complex which realizes the triviality of the product of its conjugates also lies there. The word representing the element is
$[b,a]$
in common, but the generators a and b of
$\pi _1(S^3-\mathrm {int} N(K_q\cup c_n))$
depend on the parameters q and n.
As an application, we have the following corollary.
Corollary 1.4 There are infinitely many hyperbolic knots with arbitrarily high genus, each of which has generalized torsion.
Proof Let us take the twist family
$\{ K_{q, n, p} \}_{p \in \mathbb {Z}}$
given in Theorem 1.3. Then,
$K_{q, n, p}$
is a hyperbolic knot with a generalized torsion element whenever
$|p|> 3$
. Because the linking number between
$K_q$
and
$c_n$
is greater than 1, [Reference Baker and Motegi1, Theorem 2.1] shows that the genus of
$K_{q, n, p}$
tends to
$\infty $
as
$p \to \infty $
.▪
The next is a slight generalization of [Reference Kin and Rolfsen12, Theorem 6.7]. An n-strand braid naturally induces an automorphism of the free group
$F_n$
of rank n. It is well known that
$F_n$
is bi-orderable. The braid is said to be order-preserving if the corresponding automorphism preserves some bi-ordering of
$F_n$
. See [Reference Kin and Rolfsen12] for details.
Corollary 3.8 For an integer
$q\ge 1$
and
$n\ge 1$
, the braid
$$ \begin{align*} (\sigma_1\sigma_2\cdots \sigma_{2q +n+1})(\sigma_1\sigma_2\cdots \sigma_{2q}) \end{align*} $$
is not order-preserving.
Proof As shown in the proof of Theorem 1.3 (Claim 3.2), the link
$K_q \cup c_n$
has a generalized torsion element in its link group, so the group is not bi-orderable. By [Reference Kin and Rolfsen12, Proposition 4.1], this is equivalent to the conclusion.▪
4 Twisted torus knots
In this section, we give several families of twisted torus knots, whose knot groups have generalized torsion elements.
Let
$p\ge 2$
and
$m, s\ge 1$
, and let K be the twisted torus knot
$K(p(m+1)+1,pm+1; 2, s)$
.
Lemma 4.1 The knot group
$G(K)$
has a presentation
$$ \begin{align} \langle a, c \mid\ & a^{(p-1)(m+1)+1}( a^{-(p-2)(m+1)-1} c^{(p-2)m+1} )^s a^{m+1} \nonumber\\ & =c^{(p-1)m+1} ( a^{-(p-2)(m+1)-1} c^{(p-2)m+1} )^s c^{m} \rangle\,. \end{align} $$
Proof We follow the argument of [Reference Christianson, Goluboff, Hamann and Varadaraj3, Reference Clay and Watson5]. Let
$\Sigma $
be the standard genus-two Heegaard surface of
$S^3$
with the standard generators
$a, b, c, d$
of
$\pi _1(\Sigma )$
. Then, it bounds genus-two handlebodies U inside and V outside. Note that
$a, b$
generate
$\pi _1(U)$
and
$c, d$
generate
$\pi _1(V)$
. For convenience, we use the same symbols
$a, b$
to denote
$i_*(a), i_*(b) \in \pi _1(U)$
, where
$i \colon \Sigma \to U$
is the inclusion, and similarly use the same symbols
$c,d$
to denote
$j_*(c), j_*(d) \in \pi _1(V)$
, where
$j \,{\colon}\, \Sigma \to V$
is the inclusion.
We put
$K_0$
as illustrated in Figure 13. Then,
$\Sigma -K_0$
retracts to the wedge of three circles
$G_0$
,
$R_0$
, and
$P_0$
. Hence,
$G_0$
,
$R_0$
, and
$P_0$
represent generators of
$\pi _1(\Sigma -K_0)$
. We also note that
$G_0$
,
$R_0$
, and
$P_0$
represent b, d, and c, respectively.
Figure 13 The Heegaard surface
$\Sigma $
and the standard generators
$a, b, c, d$
of
$\pi _1(\Sigma )$
.
Let us take the circles
$C_1$
,
$C_2$
,
$C_3$
, and
$C_4$
on
$\Sigma $
, as shown in Figure 14, so that these curves are disjoint from the base point
$x_0$
of the fundamental group
$\pi _1(\Sigma )$
.
Figure 14
$K_0$
and the generators
$[G_0]$
,
$[R_0]$
,
$[P_0]$
of
$\pi _1(\Sigma -K_0)$
(left); the circles
$C_1$
,
$C_2$
,
$C_3$
, and
$C_4$
(right).
Let
$\varphi \colon \Sigma \to \Sigma $
be an automorphism which is obtained by composing Dehn twists along these curves in the following order:
-
(D1) 2 times along
$C_1$
to the left. -
(D2)
$p-2$
times along
$C_2$
to the left. -
(D3) m times along
$C_3$
to the right. -
(D4) Once along
$C_2$
to the left. -
(D5) s times along
$C_4$
to the right.
We may assume that each Dehn twist fixes a base point
$x_0 \in \Sigma $
, and hence so does
$\varphi $
. Then,
$K = \varphi (K_0)$
is our twisted torus knot
$K(p(m+1)+1,pm+1; 2, s)$
; we denote
$G = \varphi (G_0),\ R = \varphi (R_0)$
, and
$P = \varphi (P_0)$
. They represent generators of
$\pi _1(\Sigma - K)$
.
To give a presentation of
$G(K)$
, we consider the following decomposition:
$S^3 - K = (U-K) \cup (V-K)$
,
$(U-K) \cap (V-K) = \Sigma - K$
. Recall that
$\pi _1(U-K) \cong \pi _1(U)$
is generated by
$a, b$
, and
$\pi _1(V-K) \cong \pi _1(V)$
is generated by
$c, d$
. We also recall that
$\pi _1(\Sigma - K)$
is generated by
$[G], [R]$
, and
$[P]$
.
We express
$[G]$
,
$[R]$
, and
$[P]$
in
$\pi _1(\Sigma )$
using the standard generators
$a, b, c$
, and d, and then push them into
$\pi _1(U) = \pi _1(U-K)$
and
$\pi _1(V) = \pi _1(V-K)$
. To this end, for convenience, we collect the effect of the above Dehn twists (D1)–(D5) on generators
$a, b, c$
, and d.
Recall that
$[G] = b,\ [R] = d$
, and
$[P] = c$
. Following the table, for
$[G] = b$
, we have:
$$ \begin{align*} [G] = b \mapsto b \mapsto b \mapsto b \mapsto b \mapsto d^sb. \end{align*} $$
Thus,
$[G] = b \in \pi _1(U)$
(putting
$d = 1$
) and
$[G] = d^s \in \pi _1(V)$
(putting
$b = 1$
). Similarly, for
$[R] = d$
, we have
$$ \begin{align*} [R] = d \mapsto d(ab)^2 \mapsto d(ab)^2 \mapsto d\bigl((ac^m)b\bigr)^2 \mapsto d\bigl(a(ac)^mb\bigr)^2 \mapsto d\bigl(a(ac)^m(d^sb)\bigr)^2. \end{align*} $$
Thus,
$[R] = a^{m+1}ba^{m+1}b \in \pi _1(U)$
(putting
$c = d = 1$
) and
$[R] = dc^md^sc^m d^{s} \in \pi _1(V)$
(putting
$a = b = 1$
).
For
$[P] = c$
, we have
$$ \begin{align*} \begin{split} [P] = & c \mapsto c(ab)^2 \mapsto (a^{p-2}c)(ab)^2 \mapsto (ac^m)^{p-2}c\bigl((ac^m)b\bigr)^2 \\ & \mapsto \bigl(a(ac)^m\bigr)^{p-2}(ac)\bigl(a(ac)^mb\bigr)^2 \mapsto (a(ac)^m)^{p-2}ac\bigl(a(ac)^m(d^sb)\bigr)^2. \end{split} \end{align*} $$
Thus,
$[P] = a^{(m+1)(p-2)}a(a^{m+1}b)^2 = a^{(p-1)(m+1)+1} b a^{m+1}b \in \pi _1(U)$
(putting
$c = d = 1$
) and
$[P] = c^{(p-1)m+1}d^sc^md^s \in \pi _1(V)$
(putting
$a = b = 1$
) .
The results are summarized as follows.
By the Seifert–van Kampen theorem,
$G(K)$
has a presentation
$$ \begin{align*} \begin{split} G=\langle a,b,c,d \mid & \ b=d^s, a^{m+1}ba^{m+1}b=dc^md^sc^m d^{s} \\ &\qquad a^{(p-1)(m+1)+1}ba^{m+1}b=c^{(p-1)m+1}d^sc^{m}d^s \rangle. \end{split} \end{align*} $$
This is equivalent to
$$ \begin{align*} \langle a,c,d \mid a^{m+1}d^s a^{m+1}=dc^md^sc^m, a^{(p-1)(m+1)+1}d^sa^{m+1}=c^{(p-1)m+1}d^sc^m \rangle. \end{align*} $$
The second relation is changed to
$$ \begin{align*} a^{(p-2)(m+1)+1 }\cdot a^{m+1}d^s a^{m+1}=c^{(p-1)m+1}d^sc^{m}. \end{align*} $$
By using the first relation, this gives
$$ \begin{align*} a^{(p-2)(m+1)+1}\cdot dc^md^sc^m=c^{(p-1)m+1}d^sc^m. \end{align*} $$
So, we have
$$ \begin{align*} a^{(p-2)(m+1)+1}d=c^{(p-2)m+1}. \end{align*} $$
By deleting the generator d, we have
$$ \begin{align*} \langle a, c \mid\ & a^{m+1}( a^{-(p-2)(m+1)-1} c^{(p-2)m+1} )^s a^{m+1}= \\ &a^{-(p-2)(m+1)-1} c^{(p-2)m+1} c^m( a^{-(p-2)(m+1)-1} c^{(p-2)m+1} )^s c^{m} \rangle. \end{align*} $$
Finally, this is equivalent to
$$ \begin{align*} \langle a, c \mid\ & a^{(p-1)(m+1)+1}( a^{-(p-2)(m+1)-1} c^{(p-2)m+1} )^s a^{m+1}= \\ & c^{(p-1)m+1} ( a^{-(p-2)(m+1)-1} c^{(p-2)m+1} )^s c^{m} \rangle\,, \end{align*} $$
as desired.▪
Remark 4.2 The twisted torus knot
$K(p(m+1)+1,pm+1; 2, s)$
(
$p \ge 2, m, s \ge 1$
) is the closure of a positive braid with braid index
$p(m+1)+1$
and word length
$(p(m+1)+1 -1)(pm+1) + 2s = p(m+1)(pm+1) + 2s$
. Hence, the genus of
$K(p(m+1)+1,pm+1; 2, s)$
is given by
$\dfrac {1 - (p(m+1)+1) + p(m+1)(pm+1) + 2s}{2} = \dfrac {p^2m(m+1)}{2} + s$
(see [Reference Stallings18]).
Theorem 4.3 Let
$p\ge 2$
and
$m\ge 1$
. The knot group G of the twisted torus knot
$K(p(m+1)+1,pm+1; 2,1)$
admits a generalized torsion element.
Proof Putting
$s=1$
in (4.1) and rewriting the relation, G has a presentation
$$ \begin{align*} G=\langle a,c \mid\ & a^{(p-1)(m+1)+1}a^{-(p-2)(m+1)-1}c^{(p-2)m+1}a^{m+1}=\\ & c^{(p-1)m+1}a^{-(p-2)(m+1)-1}c^{(p-2)m+1}c^m \rangle \\ = \langle a,c \mid\ & a^{m+1}c^{(p-2)m+1}a^{m+1}= c^{(p-1)m+1}a^{-(p-2)(m+1)-1}c^{(p-1)m+1} \rangle. \end{align*} $$
The relation is changed to
$$ \begin{align*} c^{(p-2)m+1}=a^{-(m+1)}c^{(p-1)m+1}a^{-(p-2)(m+1)-1}c^{(p-1)m+1}a^{-(m+1)}. \end{align*} $$
Let
$w(a^{-1},c)$
be the right-hand side of this relation. Then, the commutator
$[c,w(a^{-1},c)]$
is the identity, and it is decomposed into a product of conjugates of
$[c,a^{-1}]$
(Proposition 2.3).
Once we know that
$[c,a^{-1}]\ne 1$
, this give a generalized torsion element in G. If
$[c,a^{-1}]=1$
in G, then G would be abelian. Hence, K must be trivial. However, this is impossible, because K is a closure of a positive braid, so a fibered knot of genus
$p^2m(m+1)/2+1$
.▪
In Theorem 4.3, for a technical reason, we assumed
$s = 1$
, while we may vary p and m. On the other hand, if we put
$p=2$
and
$m=1$
, then we may vary the twisting parameter
$s \ge 0$
.
Theorem 4.4 The knot group G of the twisted torus knot
$K(5,3; 2,s)$
admits a generalized torsion element for any
$s\ge 0$
.
Proof Applying Tietze transformations to the presentation (4.1), we have:
$$ \begin{align*} G&=\langle a, c \mid\ a^{3}( a^{-1} c )^s a^{2}= c^{2} ( a^{-1} c )^s c \rangle \\ &=\langle a, c, b \mid\ a^{3}b^s a^{2}= c^{2} b^s c, b=a^{-1}c \rangle \\ &=\langle a, b \mid\ a^{2}b^s a^{2}=bab^{s+1}ab \rangle \\ &=\langle a, b, x \mid a^{2}b^sa^{2}=ba b^{s+1} ab, x=ab^{s-1}\rangle \\ &=\langle b, x \mid (xb^{-(s-1)})^2 b^s (xb^{-(s-1)})^2=bxb^{-(s-1)}b^{s+1}xb^{-(s-1)}b\rangle\\ &=\langle b, x \mid xb^{-(s-1)}xbxb^{-(s-1)}x=bxb^2xb \rangle\\ &=\langle b, x, y \mid xb^{-(s-1)}xbxb^{-(s-1)}x=bxb^2xb, y=bxb \rangle\\ &=\langle b,x,y \mid xb^{-(s-1)}xbxb^{-(s-1)}x=y^2, y=bxb \rangle\\ &=\langle b, y \mid y^2=(b^{-1}yb^{-1}) b^{-(s-1)} (b^{-1}y b^{-1}) b ( b^{-1}yb^{-1} )b^{-(s-1)} (b^{-1}yb^{-1}) \rangle\\ &=\langle b, y \mid y^2=b^{-1}yb^{-(s+1)} y b^{-1}y b^{-(s+1)}y b^{-1}\rangle. \end{align*} $$
Let
$w(b^{-1},y)=b^{-1}yb^{-(s+1)} y b^{-1}y b^{-(s+1)}y b^{-1}$
. Then, the relation says
$y^2=w(b^{-1},y)$
. Consider the commutator
$[y,w(b^{-1},y)]$
, which is the identity. However, Proposition 2.3 shows that this commutator can be decomposed into a product of conjugates of
$[y, b^{-1}]$
only. Here,
$[y, b^{-1}]\ne 1$
, for otherwise
$K(5,3; 2,s)$
would be trivial. However,
$K(5,3;2,s)$
is a fibered knot of genus
$s+4$
as in the proof of Theorem 4.3. Thus,
$[y,w(b^{-1},y)]$
is a generalized torsion element in G.▪
We should remark that the twisted torus knot
$K(5,3;2,s)$
is the
$(-2,3,2s+5)$
-pretzel knot. In particular,
$(-2,3,7)$
-pretzel knot admits a generalized torsion element in its knot group. Moreover, as mentioned in the proof of Theorem 4.4, this knot has genus
$s+4$
. Furthermore, this is hyperbolic, except the torus knot
$K(5,3;2,0)$
[Reference Kawauchi11]. Thus, these pretzel knots give another examples of Corollary 1.4 realizing arbitrarily high genus.
Furthermore, Theorem 4.4 implies the following corollary.
Corollary 1.5 The knot group of the pretzel knot of type
$(-2,3,2n+5)$
is not bi-orderable for
$n\ge 0$
.
Because this pretzel knot is fibered, if the Alexander polynomial has no positive real root, then the knot group is not bi-orderable [Reference Clay and Rolfsen4]. In fact, the Alexander polynomial of the pretzel knot of type
$(-2,3,2n+5)$
is
$$ \begin{align*} \Delta(t)=t^{2n+8}-t^{2n+7}+(t^{2n+5}-t^{2n+4}+t^{2n+3}-t^{2n+2}+\dots-t^4+t^3)-t+1\,, \end{align*} $$
as given in [Reference Hironaka7]. It is easy to see that there is no positive real root (consider the cases
$t\ge 1$
and
$0\le t<1$
). Hence, this gives another proof of Corollary 1.5. (Note that the absence of bi-ordering does not imply the existence of generalized torsion elements.)
Recently, Johnson [Reference Johnson10] examines the bi-orderability for genus-one pretzel knots.
Remark 4.5 It should be interesting to compare twist families given in Theorem 1.3 and that given in Theorem 4.4. In the former, we may twist
$K_q$
about
$c_n$
in both positive and negative directions to obtain knots with generalized torsion. On the contrary, the latter family forces us to perform only positive twisting for a technical reason. We wonder if this condition is necessary in the latter. In other words, if
$s < 0$
, then does the knot obtained by s twisting have bi-ordering?
Acknowledgment
We would like to thank the referee for careful reading and suggestions. We would also like to thank Eiko Kin for helpful conversation.
