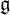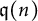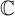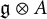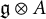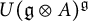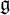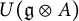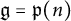1 Introduction
The theory of Lie superalgebras primarily arose from an attempt to understand the mathematical foundation of supersymmetry in theoretical physics. The literature has been developed substantially since then. Representation theory of Lie superalgebras plays a crucial role in quantum optics and many other areas of theoretical physics, notably in string theory. A comprehensive description of the mathematical theory of Lie superalgebras is given in [Reference Kac8], containing the complete classification of all finite-dimensional simple Lie superalgebras over an algebraically closed field of characteristic zero. For generalities of the theory of Lie superalgebras and supergeometry we refer to [Reference Musson11] and [Reference Deligne and Morgan5], respectively.
Loop (super)algebras are of great importance in the literature. Affine Kac Moody Lie (super)algebras can be realized by means of an affinization technique on Loop superalgebras. In superstring theory a particular type of Loop superalgebras, namely the superconformal algebras are invaluable tool. By definition, they are tensor product of finite dimensional simple Lie superalgebras with the algebra of Laurent polynomials. For a survey on finite dimensional representation theory of loop algebras we refer to [Reference Senesi17].
In this article we deal with Loop superalgebras associated with the superalgebras belong to the strange series in Kac’s classification, namely the queer and periplectic Lie superalgebras. By definition, a loop superalgebra is of the form
![]() $\operatorname {\mathfrak{g}}\otimes A$
, where
$\operatorname {\mathfrak{g}}\otimes A$
, where
![]() $\operatorname {\mathfrak{g}}$
is a Lie superalgebra and A is an associative commutative finitely generated
$\operatorname {\mathfrak{g}}$
is a Lie superalgebra and A is an associative commutative finitely generated
![]() $\mathbb C$
-algebra with identity. When
$\mathbb C$
-algebra with identity. When
![]() $\mathfrak{g}$
is a basic classical superalgebra and
$\mathfrak{g}$
is a basic classical superalgebra and
![]() $A=\mathbb C[t_1^{\pm 1}, \ldots ,t_d^{\pm 1}]$
, the Laurent polynomial algebra in d commuting variables, a complete classification of irreducible finite dimensional modules for
$A=\mathbb C[t_1^{\pm 1}, \ldots ,t_d^{\pm 1}]$
, the Laurent polynomial algebra in d commuting variables, a complete classification of irreducible finite dimensional modules for
![]() $\mathfrak{g} \otimes A$
is given in [Reference Senesi17] and [Reference Rao12]. They turn out to be evaluation modules at finitely many points except in types
$\mathfrak{g} \otimes A$
is given in [Reference Senesi17] and [Reference Rao12]. They turn out to be evaluation modules at finitely many points except in types
![]() $A(m,n)$
and
$A(m,n)$
and
![]() $C(n)$
. In [Reference Savage16], Savage classified irreducible finite-dimensional representations of equivariant map superalgebras in the case where
$C(n)$
. In [Reference Savage16], Savage classified irreducible finite-dimensional representations of equivariant map superalgebras in the case where
![]() $\mathfrak{g}$
is a basic classical Lie superalgebra. As a special case, his results give the classification of the irreducible finite-dimensional modules for the twisted loop superalgebras, and in particular generalize the classification results obtained in [Reference Rao and Zhao15] and [Reference Rao12]. In [Reference Calixto, Moura and Savage2], the authors classified finite-dimensional irreducible representations of equivariant map queer Lie superalgebras. While in the basic classical setting those irreducible modules were isomorphic to tensor products of generalized evaluation modules, in the queer case they are irreducible products of evaluation modules. In [Reference Calixto and Macedo1], the authors completed the classification of finite-dimensional irreducible modules of equivariant map superalgebras by describing these modules for the periplectic superalgebra.
$\mathfrak{g}$
is a basic classical Lie superalgebra. As a special case, his results give the classification of the irreducible finite-dimensional modules for the twisted loop superalgebras, and in particular generalize the classification results obtained in [Reference Rao and Zhao15] and [Reference Rao12]. In [Reference Calixto, Moura and Savage2], the authors classified finite-dimensional irreducible representations of equivariant map queer Lie superalgebras. While in the basic classical setting those irreducible modules were isomorphic to tensor products of generalized evaluation modules, in the queer case they are irreducible products of evaluation modules. In [Reference Calixto and Macedo1], the authors completed the classification of finite-dimensional irreducible modules of equivariant map superalgebras by describing these modules for the periplectic superalgebra.
In [Reference Rao14], Rao defined a set of operators for the Loop superalgebra
![]() $\operatorname {\mathfrak{g}}\otimes A$
, where
$\operatorname {\mathfrak{g}}\otimes A$
, where
![]() $\operatorname {\mathfrak{g}}$
is a contragredient Lie superalgebra, and called them the generalized Casimir operators, generalizing his work in [Reference Rao13] for Lie algebras. In particular, specializing to the case where
$\operatorname {\mathfrak{g}}$
is a contragredient Lie superalgebra, and called them the generalized Casimir operators, generalizing his work in [Reference Rao13] for Lie algebras. In particular, specializing to the case where
![]() $\operatorname {\mathfrak{g}}=\mathfrak{gl}(m|n)$
, he defined a set of central operators
$\operatorname {\mathfrak{g}}=\mathfrak{gl}(m|n)$
, he defined a set of central operators
![]() $T_k(a_1,\dots ,a_k)$
for
$T_k(a_1,\dots ,a_k)$
for
![]() $a_i\in A$
, in the universal enveloping algebra
$a_i\in A$
, in the universal enveloping algebra
![]() $U(\operatorname {\mathfrak{g}}\otimes A)$
of
$U(\operatorname {\mathfrak{g}}\otimes A)$
of
![]() $\operatorname {\mathfrak{g}} \otimes A$
, using the construction of the Gelfand invariants in the center of
$\operatorname {\mathfrak{g}} \otimes A$
, using the construction of the Gelfand invariants in the center of
![]() $U(\operatorname {\mathfrak{g}})$
and conjectured that these central operators generate the algebra of
$U(\operatorname {\mathfrak{g}})$
and conjectured that these central operators generate the algebra of
![]() $\operatorname {\mathfrak{g}}$
-invariants of
$\operatorname {\mathfrak{g}}$
-invariants of
![]() $U(\operatorname {\mathfrak{g}}\otimes A)$
. In [Reference Mukherjee, Pattanayak and Sharma10], the authors gave a proof of this conjecture and gave a spanning set for the space of invariants
$U(\operatorname {\mathfrak{g}}\otimes A)$
. In [Reference Mukherjee, Pattanayak and Sharma10], the authors gave a proof of this conjecture and gave a spanning set for the space of invariants
![]() $U(\mathfrak{osp}(m|2n) \otimes A)^{\mathrm{OSp}(m|2n)}$
where
$U(\mathfrak{osp}(m|2n) \otimes A)^{\mathrm{OSp}(m|2n)}$
where
![]() $\mathfrak{osp}(m|2n)$
is the orthosymplectic superalgebra and
$\mathfrak{osp}(m|2n)$
is the orthosymplectic superalgebra and
![]() $\mathrm{OSp}(m|2n)$
is the corresponding supergroup.
$\mathrm{OSp}(m|2n)$
is the corresponding supergroup.
In the current article, we study
![]() $U(\operatorname {\mathfrak{g}}\otimes A)^{\operatorname {\mathfrak{g}}}$
corresponding to the strange series of superalgebras, i.e.,
$U(\operatorname {\mathfrak{g}}\otimes A)^{\operatorname {\mathfrak{g}}}$
corresponding to the strange series of superalgebras, i.e.,
![]() $\operatorname {\mathfrak{g}}$
is either
$\operatorname {\mathfrak{g}}$
is either
![]() $\operatorname {\mathfrak{q}}(n)$
and
$\operatorname {\mathfrak{q}}(n)$
and
![]() $\operatorname {\mathfrak{p}}(n)$
. Using the Schur–Weyl–Sergeev duality, we first derive the tensor version of the first fundamental theorem (FFT) of invariant theory for
$\operatorname {\mathfrak{p}}(n)$
. Using the Schur–Weyl–Sergeev duality, we first derive the tensor version of the first fundamental theorem (FFT) of invariant theory for
![]() $\operatorname {\mathfrak{q}}(n)$
which gives a spanning set for
$\operatorname {\mathfrak{q}}(n)$
which gives a spanning set for
![]() $(V^{\otimes k} \otimes (V^*)^{\otimes k})^{\operatorname {\mathfrak{q}}(n)}$
,
$(V^{\otimes k} \otimes (V^*)^{\otimes k})^{\operatorname {\mathfrak{q}}(n)}$
,
![]() $k \geq 1$
, where
$k \geq 1$
, where
![]() $V=\mathbb C^n \oplus \mathbb C^n$
is the defining representation of
$V=\mathbb C^n \oplus \mathbb C^n$
is the defining representation of
![]() $\operatorname {\mathfrak{q}}(n)$
. Using this version of FFT, we give a spanning set for
$\operatorname {\mathfrak{q}}(n)$
. Using this version of FFT, we give a spanning set for
![]() $U(\operatorname {\mathfrak{q}}(n)\otimes A)^{\operatorname {\mathfrak{q}}(n)}$
. We define a set of central operator for
$U(\operatorname {\mathfrak{q}}(n)\otimes A)^{\operatorname {\mathfrak{q}}(n)}$
. We define a set of central operator for
![]() $U(\operatorname {\mathfrak{q}}(n) \otimes A)$
which are similar to the central operators defined by Rao in [Reference Rao14] in the case of
$U(\operatorname {\mathfrak{q}}(n) \otimes A)$
which are similar to the central operators defined by Rao in [Reference Rao14] in the case of
![]() $\mathfrak{gl}(m|n)$
. We show that these central operators generate
$\mathfrak{gl}(m|n)$
. We show that these central operators generate
![]() $U(\operatorname {\mathfrak{q}}(n)\otimes A)^{\operatorname {\mathfrak{q}}(n)}$
as an algebra. Specializing to
$U(\operatorname {\mathfrak{q}}(n)\otimes A)^{\operatorname {\mathfrak{q}}(n)}$
as an algebra. Specializing to
![]() $A=\mathbb C$
, these central operators give an algebra generating set for the center of the universal enveloping algebra of
$A=\mathbb C$
, these central operators give an algebra generating set for the center of the universal enveloping algebra of
![]() $\operatorname {\mathfrak{q}}(n)$
. We mention that a set of algebra generators of the center of
$\operatorname {\mathfrak{q}}(n)$
. We mention that a set of algebra generators of the center of
![]() $\operatorname {\mathfrak{q}}(n)$
is given in [Reference Sergeev18] without a proof. These operators are helpful to understand the tensor product decompositions of
$\operatorname {\mathfrak{q}}(n)$
is given in [Reference Sergeev18] without a proof. These operators are helpful to understand the tensor product decompositions of
![]() $\mathfrak{g}$
-modules. In fact these central operators when applied to a certain tensor product of
$\mathfrak{g}$
-modules. In fact these central operators when applied to a certain tensor product of
![]() $\operatorname {\mathfrak{q}}(n)$
-modules move one highest weight vector to another highest weight vector.
$\operatorname {\mathfrak{q}}(n)$
-modules move one highest weight vector to another highest weight vector.
The periplectic Lie superalgebra
![]() $\operatorname {\mathfrak{p}}(n)$
is a superanalog of the orthogonal or symplectic Lie algebra preserving an odd non-degenerate symmetric or skew-symmetric bilinear form. In [Reference Moon9], Moon proved a Schur–Weyl duality statement for
$\operatorname {\mathfrak{p}}(n)$
is a superanalog of the orthogonal or symplectic Lie algebra preserving an odd non-degenerate symmetric or skew-symmetric bilinear form. In [Reference Moon9], Moon proved a Schur–Weyl duality statement for
![]() $\operatorname {\mathfrak{p}}(n)$
by introducing an algebra called the periplectic Brauer algebra which plays the role of Brauer algebra as in the case of orthogonal and symplectic Lie algebra or in the case of the encompassing orthosymplectic Lie superalgebra. In [Reference Deligne, Lehrer and Zhang4], Deligne et al., proved the tensor version of the FFT for the periplectic Lie supergroup, hence thereby giving a spanning set for
$\operatorname {\mathfrak{p}}(n)$
by introducing an algebra called the periplectic Brauer algebra which plays the role of Brauer algebra as in the case of orthogonal and symplectic Lie algebra or in the case of the encompassing orthosymplectic Lie superalgebra. In [Reference Deligne, Lehrer and Zhang4], Deligne et al., proved the tensor version of the FFT for the periplectic Lie supergroup, hence thereby giving a spanning set for
![]() $(V^{\otimes 2k})^{Pe(V)}$
, where
$(V^{\otimes 2k})^{Pe(V)}$
, where
![]() $V=\mathbb C^n \oplus \mathbb C^n$
and
$V=\mathbb C^n \oplus \mathbb C^n$
and
![]() $Pe(V)$
is the periplectic supergroup which is by definition the subgroup of
$Pe(V)$
is the periplectic supergroup which is by definition the subgroup of
![]() $GL(V)$
preserving a non-degenerate odd symmetric form on V. Using these results, for an associative, commutative and finitely generated
$GL(V)$
preserving a non-degenerate odd symmetric form on V. Using these results, for an associative, commutative and finitely generated
![]() $\mathbb C$
-algebra A, we show that the only
$\mathbb C$
-algebra A, we show that the only
![]() $\mathfrak{p}(n)$
-invariants of
$\mathfrak{p}(n)$
-invariants of
![]() $U(\mathfrak{p}(n) \otimes A)$
are the elements of
$U(\mathfrak{p}(n) \otimes A)$
are the elements of
![]() $\mathbb C$
. We note that from the work of M. Gorelik it can also be derived that the centre of
$\mathbb C$
. We note that from the work of M. Gorelik it can also be derived that the centre of
![]() $\mathfrak{p}(n)$
is trivial (see [Reference Gorelik7]).
$\mathfrak{p}(n)$
is trivial (see [Reference Gorelik7]).
We briefly describe the contents of each sections. In Section 2, we give preliminaries of queer Lie superalgebra and recall the Schur–Weyl–Sergeev duality for
![]() $\mathfrak{q}(n)$
. In Section 3, we define loop superalgebras and describe a spanning (resp. algebra generating) set for
$\mathfrak{q}(n)$
. In Section 3, we define loop superalgebras and describe a spanning (resp. algebra generating) set for
![]() $U(\mathfrak{g} \otimes A)^{\mathfrak{g}}$
starting with a homogeneous basis (resp. a set of homogeneous algebra generators) of
$U(\mathfrak{g} \otimes A)^{\mathfrak{g}}$
starting with a homogeneous basis (resp. a set of homogeneous algebra generators) of
![]() $[T(\mathfrak{g})]^{\mathfrak{g}}$
. In Section 4, we prove the tensor FFT for the the queer superalgebra. In Section 5, we give a spanning set for
$[T(\mathfrak{g})]^{\mathfrak{g}}$
. In Section 4, we prove the tensor FFT for the the queer superalgebra. In Section 5, we give a spanning set for
![]() $U(\mathfrak{q}(n) \otimes A)^{\operatorname {\mathfrak{q}}(n)}$
, define a set of central operators in
$U(\mathfrak{q}(n) \otimes A)^{\operatorname {\mathfrak{q}}(n)}$
, define a set of central operators in
![]() $U(\mathfrak{q}(n) \otimes A)$
and show that these central operators generate the algebra
$U(\mathfrak{q}(n) \otimes A)$
and show that these central operators generate the algebra
![]() $U(\mathfrak{q}(n) \otimes A)^{\operatorname {\mathfrak{q}}(n)}$
. In Section 6, after recalling the definition of the periplectic Lie superalgebra
$U(\mathfrak{q}(n) \otimes A)^{\operatorname {\mathfrak{q}}(n)}$
. In Section 6, after recalling the definition of the periplectic Lie superalgebra
![]() $\operatorname {\mathfrak{p}}(n)$
, we show that the only
$\operatorname {\mathfrak{p}}(n)$
, we show that the only
![]() $\mathfrak{p}(n)$
-invariants of
$\mathfrak{p}(n)$
-invariants of
![]() $U(\mathfrak{p}(n) \otimes A)$
are the constants.
$U(\mathfrak{p}(n) \otimes A)$
are the constants.
Notation: Throughout this article, we work over the field of complex numbers
![]() $\mathbb C$
. All modules and algebras are defined over
$\mathbb C$
. All modules and algebras are defined over
![]() $\mathbb C$
and in addition all the modules are of finite dimension. We write
$\mathbb C$
and in addition all the modules are of finite dimension. We write
![]() $\mathbb Z_2=\{0,1\}$
and use its standard field structure. We put
$\mathbb Z_2=\{0,1\}$
and use its standard field structure. We put
![]() $(-1)^0=1$
and
$(-1)^0=1$
and
![]() $(-1)^1=-1$
.
$(-1)^1=-1$
.
2 Preliminaries
2.1 Queer superalgebra
For a positive integer n, we set
![]() $I_{n|n}:=\{-1,\ldots ,-n,1,2, \ldots ,n\}$
, on which we define the parity of
$I_{n|n}:=\{-1,\ldots ,-n,1,2, \ldots ,n\}$
, on which we define the parity of
![]() $i \in I_{n|n}$
to be
$i \in I_{n|n}$
to be
![]() $|i|=0$
if
$|i|=0$
if
![]() $i>0$
and
$i>0$
and
![]() $|i|=1$
if
$|i|=1$
if
![]() $i<0$
.
$i<0$
.
Let
![]() $V:=\mathbb C^n \oplus \mathbb C^n$
be the superspace with standard basis
$V:=\mathbb C^n \oplus \mathbb C^n$
be the superspace with standard basis
![]() $v_i$
of parity i for
$v_i$
of parity i for
![]() $i \in I_{n|n}$
. Its endomorphism ring
$i \in I_{n|n}$
. Its endomorphism ring
![]() $\operatorname {End}_{\mathbb C}(V)$
is an associative superalgebra with standard basis
$\operatorname {End}_{\mathbb C}(V)$
is an associative superalgebra with standard basis
![]() $E_{ij}$
of parity
$E_{ij}$
of parity
![]() $|i|+|j|$
for
$|i|+|j|$
for
![]() $i,j \in I_{n|n}$
. It is also a Lie superalgebra under the standard supercommutator
$i,j \in I_{n|n}$
. It is also a Lie superalgebra under the standard supercommutator
for all homogeneous
![]() $x,y \in \operatorname {End}_{\mathbb C}(V)$
. It is denoted by
$x,y \in \operatorname {End}_{\mathbb C}(V)$
. It is denoted by
![]() $\mathfrak{gl}(n|n)$
.
$\mathfrak{gl}(n|n)$
.
The queer superalgebra
![]() $\operatorname {\mathfrak{q}}(n)$
can be defined in two ways. The map
$\operatorname {\mathfrak{q}}(n)$
can be defined in two ways. The map
![]() $E_{ij} \mapsto E_{-i,-j}$
is an involutive automorphism of
$E_{ij} \mapsto E_{-i,-j}$
is an involutive automorphism of
![]() $\mathfrak{gl}(n|n)$
and we define
$\mathfrak{gl}(n|n)$
and we define
![]() $\operatorname {\mathfrak{q}}(n)$
to be the fixed point sub-superalgebra of this automorphism.
$\operatorname {\mathfrak{q}}(n)$
to be the fixed point sub-superalgebra of this automorphism.
Alternatively, we define
![]() $P:V\to V$
by
$P:V\to V$
by
![]() $Pv_i=(-1)^{|v_i|}v_{-i}$
and
$Pv_i=(-1)^{|v_i|}v_{-i}$
and
![]() $\mathfrak{q}(n):=\{f \in \operatorname {End}_{\mathbb C}(V): [f,P]=0\}$
. It is closed under the superbracket and we call it the queer superalgebra.
$\mathfrak{q}(n):=\{f \in \operatorname {End}_{\mathbb C}(V): [f,P]=0\}$
. It is closed under the superbracket and we call it the queer superalgebra.
With respect to the ordered basis
![]() $B:=B_1 \cup B_0=\{e_{-1},\dots e_{-n},e_1,\dots ,e_n\}$
, the operator P can be written in matrix form as
$B:=B_1 \cup B_0=\{e_{-1},\dots e_{-n},e_1,\dots ,e_n\}$
, the operator P can be written in matrix form as
 $$ \begin{align*}P=\begin{pmatrix} 0 & I \\ -I & 0 \end{pmatrix}\end{align*} $$
$$ \begin{align*}P=\begin{pmatrix} 0 & I \\ -I & 0 \end{pmatrix}\end{align*} $$
and
![]() $\mathfrak{q}(n)$
can be expressed in the matrix form as
$\mathfrak{q}(n)$
can be expressed in the matrix form as
 $$ \begin{align*}\mathfrak{q}(n)=\left\{\begin{pmatrix} A & B \\ B & A \end{pmatrix}: A, B \,\, \text{are arbitrary } n \times n \text{ matrices}\right\}.\end{align*} $$
$$ \begin{align*}\mathfrak{q}(n)=\left\{\begin{pmatrix} A & B \\ B & A \end{pmatrix}: A, B \,\, \text{are arbitrary } n \times n \text{ matrices}\right\}.\end{align*} $$
In terms of basis elements of
![]() $\mathfrak{gl}(n|n)$
we have
$\mathfrak{gl}(n|n)$
we have
![]() $P=E_{-n,n}+E_{-(n-1),n-1}+\cdots +E_{-1,1}-E_{1,-1}-\cdots -E_{n,-n}$
. Note that
$P=E_{-n,n}+E_{-(n-1),n-1}+\cdots +E_{-1,1}-E_{1,-1}-\cdots -E_{n,-n}$
. Note that
![]() $\mathfrak{q}(n)$
as the Lie sub-superalgebra of
$\mathfrak{q}(n)$
as the Lie sub-superalgebra of
![]() $\mathfrak{gl}(n|n)$
is spanned by
$\mathfrak{gl}(n|n)$
is spanned by
![]() $F_{ij}:=E_{ij}+E_{-i,-j}$
for
$F_{ij}:=E_{ij}+E_{-i,-j}$
for
![]() $i>0$
. Note that we have
$i>0$
. Note that we have
![]() $F_{ij}=F_{-i,-j}=F_{-j,-i}$
for all
$F_{ij}=F_{-i,-j}=F_{-j,-i}$
for all
![]() $i,j$
.
$i,j$
.
The superalgebra
![]() $\mathfrak{gl}(n|n)$
and hence
$\mathfrak{gl}(n|n)$
and hence
![]() $\mathfrak{q}(n)$
acts on V by matrix multiplication and on the k-fold tensor product
$\mathfrak{q}(n)$
acts on V by matrix multiplication and on the k-fold tensor product
![]() $V^{\otimes k}$
by
$V^{\otimes k}$
by
 $$ \begin{align} x\cdot(v_1 \otimes v_2 \otimes \cdots \otimes v_k)=\sum_{j=1}^k(-1)^{(|v_1|+\cdots +|v_{j-1}|)|v|}v_1 \otimes v_2 \otimes \cdots \otimes xv_j \otimes v_{j+1} \otimes \cdots \otimes v_k, \end{align} $$
$$ \begin{align} x\cdot(v_1 \otimes v_2 \otimes \cdots \otimes v_k)=\sum_{j=1}^k(-1)^{(|v_1|+\cdots +|v_{j-1}|)|v|}v_1 \otimes v_2 \otimes \cdots \otimes xv_j \otimes v_{j+1} \otimes \cdots \otimes v_k, \end{align} $$
where the elements
![]() $x \in \mathfrak{q}(n)$
and
$x \in \mathfrak{q}(n)$
and
![]() $v_i \in V$
are all homogeneous. We then extend to all of
$v_i \in V$
are all homogeneous. We then extend to all of
![]() $\mathfrak{q}(n)$
acting on all of
$\mathfrak{q}(n)$
acting on all of
![]() $V^{\otimes k}$
by linearity.
$V^{\otimes k}$
by linearity.
2.2 The Sergeev superalgebras
Let
![]() $S_k$
be the symmetric group on k letters. It is generated by the transpositions
$S_k$
be the symmetric group on k letters. It is generated by the transpositions
![]() $s_1,\dots ,s_{k-1}$
, where
$s_1,\dots ,s_{k-1}$
, where
![]() $s_i=(i,i+1)$
for all i.
$s_i=(i,i+1)$
for all i.
The Sergeev superalgebra
![]() $Ser_k$
is the associative superalgebra generated by
$Ser_k$
is the associative superalgebra generated by
![]() $s_1,\dots ,s_{k-1}$
and
$s_1,\dots ,s_{k-1}$
and
![]() $c_1,\dots ,c_{k-1},c_k$
with the following defining relations:
$c_1,\dots ,c_{k-1},c_k$
with the following defining relations:
-
•
 $s_i^2=1,\ s_is_{i+1}s_i=s_{i+1}s_is_{i+1},\ s_is_j=s_js_i \quad (|i-j|>1),$
$s_i^2=1,\ s_is_{i+1}s_i=s_{i+1}s_is_{i+1},\ s_is_j=s_js_i \quad (|i-j|>1),$
-
•
 $c_i^2=-1,\ c_ic_j=-c_jc_i,\quad (i \neq j)$
$c_i^2=-1,\ c_ic_j=-c_jc_i,\quad (i \neq j)$
-
•
 $s_ic_is_i=c_{i+1},\ s_ic_j=c_js_i,\quad j \neq i,i+1$
.
$s_ic_is_i=c_{i+1},\ s_ic_j=c_js_i,\quad j \neq i,i+1$
.
The generators
![]() $s_1,\dots ,s_{k-1}$
are regarded as even and the subalgebra generated by them is isomorphic to the group algebra
$s_1,\dots ,s_{k-1}$
are regarded as even and the subalgebra generated by them is isomorphic to the group algebra
![]() $\mathbb C[S_k]$
of
$\mathbb C[S_k]$
of
![]() $S_k$
; the generators
$S_k$
; the generators
![]() $c_1,\dots ,c_{k-1},c_k$
are called odd and the
$c_1,\dots ,c_{k-1},c_k$
are called odd and the
![]() $\mathbb C$
-subalgebra generated by them is isomorphic to the Clifford superalgebra
$\mathbb C$
-subalgebra generated by them is isomorphic to the Clifford superalgebra
![]() $\mathbf {C}l_k$
.
$\mathbf {C}l_k$
.
The Sergeev superalgebra
![]() $Ser_k$
is isomorphic to the superalgebra
$Ser_k$
is isomorphic to the superalgebra
![]() $\mathbb C[S_k] \ltimes \mathbf {C}l_k$
, which is
$\mathbb C[S_k] \ltimes \mathbf {C}l_k$
, which is
![]() $\mathbb C[S_k] \otimes \mathbf {C}l_k$
as a superspace with the multiplication given by
$\mathbb C[S_k] \otimes \mathbf {C}l_k$
as a superspace with the multiplication given by
where
![]() $1 \leq i_s, j_t \leq k$
.
$1 \leq i_s, j_t \leq k$
.
The superalgebra
![]() $Ser_k$
has as basis the elements which can be written in the form
$Ser_k$
has as basis the elements which can be written in the form
![]() $\sigma \otimes c_1^{\epsilon _1}\ldots c_k^{\epsilon _k}$
where
$\sigma \otimes c_1^{\epsilon _1}\ldots c_k^{\epsilon _k}$
where
![]() $\sigma \in S_k$
and
$\sigma \in S_k$
and
![]() $\epsilon _i \in \mathbb Z_2$
for all i.
$\epsilon _i \in \mathbb Z_2$
for all i.
2.3 Action of the Sergeev algebra and Schur–Weyl–Sergeev duality
The symmetric group
![]() $S_k$
acts on the k-fold tensor product
$S_k$
acts on the k-fold tensor product
![]() $V^{\otimes k}$
by
$V^{\otimes k}$
by
where
![]() $v_i$
’s are
$v_i$
’s are
![]() $\mathbb Z_2$
-homogeneous. We then extend the action to
$\mathbb Z_2$
-homogeneous. We then extend the action to
![]() $V^{\otimes k}$
by linearity.
$V^{\otimes k}$
by linearity.
More generally the action of
![]() $S_k$
on
$S_k$
on
![]() $V^{\otimes k}$
is defined as follows: for
$V^{\otimes k}$
is defined as follows: for
![]() $\sigma \in S_k$
and homogeneous
$\sigma \in S_k$
and homogeneous
![]() $\pmb {v}=v_1 \otimes v_2 \otimes \cdots \otimes v_k$
, the action of
$\pmb {v}=v_1 \otimes v_2 \otimes \cdots \otimes v_k$
, the action of
![]() $\sigma $
on
$\sigma $
on
![]() $\pmb {v}$
is given by:
$\pmb {v}$
is given by:
where
![]() $\gamma (\pmb {v},\sigma ^{-1})=\prod _{(i,j)\in \text {Inv}(\sigma )}{|v_i||v_j|}$
, with
$\gamma (\pmb {v},\sigma ^{-1})=\prod _{(i,j)\in \text {Inv}(\sigma )}{|v_i||v_j|}$
, with
![]() $\text {Inv}(\sigma )=\{(i,j)\colon i<j\text { and }\sigma (i)>\sigma (j)\}$
. It can be easily verified that
$\text {Inv}(\sigma )=\{(i,j)\colon i<j\text { and }\sigma (i)>\sigma (j)\}$
. It can be easily verified that
![]() $\gamma (\pmb {v},\sigma \tau )=\gamma (\sigma ^{-1}\pmb {v},\tau )+\gamma (\pmb {v},\sigma )$
for two permutations
$\gamma (\pmb {v},\sigma \tau )=\gamma (\sigma ^{-1}\pmb {v},\tau )+\gamma (\pmb {v},\sigma )$
for two permutations
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
.
$\tau $
.
The generators
![]() $c_j$
acts on
$c_j$
acts on
![]() $V^{\otimes k}$
by
$V^{\otimes k}$
by
where
![]() $v_1, \dots ,v_k \in V$
are homogeneous elements and we then extend the action to
$v_1, \dots ,v_k \in V$
are homogeneous elements and we then extend the action to
![]() $V^{\otimes k}$
by linearity.
$V^{\otimes k}$
by linearity.
More generally, for
![]() $\varepsilon _i\in \mathbb Z_2$
,
$\varepsilon _i\in \mathbb Z_2$
,
![]() $i=1,\ldots , k$
, we have
$i=1,\ldots , k$
, we have
The actions of
![]() $S_k$
and
$S_k$
and
![]() $\mathbf {C}l_k$
give rise to a left action of the Sergeev superalgebra
$\mathbf {C}l_k$
give rise to a left action of the Sergeev superalgebra
![]() $\operatorname {\mathrm{Ser}}_k$
on
$\operatorname {\mathrm{Ser}}_k$
on
![]() $V^{\otimes k}$
. So we get an algebra homomorphism
$V^{\otimes k}$
. So we get an algebra homomorphism
We record that for a basis element
![]() $\sigma ^{-1}\otimes c_1^{\varepsilon _1}\ldots c_k^{\varepsilon _k} \in Ser_k$
, we have
$\sigma ^{-1}\otimes c_1^{\varepsilon _1}\ldots c_k^{\varepsilon _k} \in Ser_k$
, we have
Let
![]() $\operatorname {End}_{\operatorname {\mathfrak{q}}(n)} (V^{\otimes k})$
be the centralizer algebra of the
$\operatorname {End}_{\operatorname {\mathfrak{q}}(n)} (V^{\otimes k})$
be the centralizer algebra of the
![]() $\operatorname {\mathfrak{q}}(n)$
-action on
$\operatorname {\mathfrak{q}}(n)$
-action on
![]() $V^{\otimes k}$
. That is
$V^{\otimes k}$
. That is
Let
![]() $\rho : \operatorname {\mathfrak{q}}(n) \rightarrow \operatorname {End}_{\mathbb C}(V^{\otimes k})$
be the superalgebra homomorphism induced from the action of
$\rho : \operatorname {\mathfrak{q}}(n) \rightarrow \operatorname {End}_{\mathbb C}(V^{\otimes k})$
be the superalgebra homomorphism induced from the action of
![]() $\operatorname {\mathfrak{q}}(n)$
on
$\operatorname {\mathfrak{q}}(n)$
on
![]() $V^{\otimes k}$
. In [Reference Savage16], Sergeev proved the following double centralizer theorem along the lines of the Schur–Weyl duality for the queer superalgebra.
$V^{\otimes k}$
. In [Reference Savage16], Sergeev proved the following double centralizer theorem along the lines of the Schur–Weyl duality for the queer superalgebra.
Theorem 2.1 Let
![]() $\rho : \operatorname {\mathfrak{q}}(n) \rightarrow \operatorname {End}_{\mathbb C}(V^{\otimes k})$
and
$\rho : \operatorname {\mathfrak{q}}(n) \rightarrow \operatorname {End}_{\mathbb C}(V^{\otimes k})$
and
![]() $\Psi _k: \operatorname {\mathrm{Ser}}_k \rightarrow \operatorname {End}_{\mathbb C}(V^{\otimes k})$
be the maps defined as above. Let A be the image of
$\Psi _k: \operatorname {\mathrm{Ser}}_k \rightarrow \operatorname {End}_{\mathbb C}(V^{\otimes k})$
be the maps defined as above. Let A be the image of
![]() $\Psi _k$
and let B be the subalgebra of
$\Psi _k$
and let B be the subalgebra of
![]() $\operatorname {End}_{\mathbb C}(V^{\otimes k})$
spanned by the image of
$\operatorname {End}_{\mathbb C}(V^{\otimes k})$
spanned by the image of
![]() $\rho $
. Then A and B are centralizers of each other.
$\rho $
. Then A and B are centralizers of each other.
Remark 2.2 It may be noted that in the statement of the above theorem we consider the left action of the Sergeev algebra whereas Sergeev considers the action from the right and uses
![]() $\operatorname {\mathrm{Ser}}_k^{op}$
instead.
$\operatorname {\mathrm{Ser}}_k^{op}$
instead.
3 Loop superalgebras
3.1
Let
![]() $\operatorname {\mathfrak{g}}$
be either a simple Lie superalgebra or
$\operatorname {\mathfrak{g}}$
be either a simple Lie superalgebra or
![]() $\mathfrak{gl}(m|n)$
, or any Lie superalgebra among
$\mathfrak{gl}(m|n)$
, or any Lie superalgebra among
![]() $\mathfrak{q}(n)$
or
$\mathfrak{q}(n)$
or
![]() $\mathfrak{p}(n)$
. Let A be an associative, commutative and finitely generated
$\mathfrak{p}(n)$
. Let A be an associative, commutative and finitely generated
![]() $\mathbb C$
-algebra with unity. Then
$\mathbb C$
-algebra with unity. Then
![]() $\mathfrak{g} \otimes A$
has a natural structure of Lie superalgebra:
$\mathfrak{g} \otimes A$
has a natural structure of Lie superalgebra:
With this the even part of
![]() $\mathfrak{g} \otimes A$
is
$\mathfrak{g} \otimes A$
is
![]() ${(\mathfrak{g})}_0 \otimes A$
and the odd part is
${(\mathfrak{g})}_0 \otimes A$
and the odd part is
![]() ${(\mathfrak{g})}_1 \otimes A$
. Let
${(\mathfrak{g})}_1 \otimes A$
. Let
![]() ${\mathfrak{g} = \mathfrak{n}^- \oplus \mathfrak h \oplus \mathfrak{n}^+}$
be the standard triangular decomposition of
${\mathfrak{g} = \mathfrak{n}^- \oplus \mathfrak h \oplus \mathfrak{n}^+}$
be the standard triangular decomposition of
![]() $\mathfrak{g}$
. Then
$\mathfrak{g}$
. Then
![]() $\mathfrak{g} \otimes A = (\mathfrak{n}^- \otimes A) \oplus (\mathfrak h \otimes A) \oplus (\mathfrak{n}^- \otimes A)$
is a triangular decomposition of
$\mathfrak{g} \otimes A = (\mathfrak{n}^- \otimes A) \oplus (\mathfrak h \otimes A) \oplus (\mathfrak{n}^- \otimes A)$
is a triangular decomposition of
![]() $\mathfrak{g} \otimes A$
.
$\mathfrak{g} \otimes A$
.
3.2
Let
![]() $T(\mathfrak{g} \otimes A)=\bigoplus _{k =0}^{\infty } T^k(\mathfrak{g} \otimes A)$
, where
$T(\mathfrak{g} \otimes A)=\bigoplus _{k =0}^{\infty } T^k(\mathfrak{g} \otimes A)$
, where
![]() $T^k(\mathfrak{g} \otimes A)=(\mathfrak{g} \otimes A)^{\otimes k}$
, be the tensor algebra of
$T^k(\mathfrak{g} \otimes A)=(\mathfrak{g} \otimes A)^{\otimes k}$
, be the tensor algebra of
![]() $\mathfrak{g} \otimes A$
and let
$\mathfrak{g} \otimes A$
and let
![]() $U(\mathfrak{g} \otimes A)$
be the enveloping algebra of
$U(\mathfrak{g} \otimes A)$
be the enveloping algebra of
![]() $\mathfrak{g} \otimes A$
. The universal enveloping algebra of
$\mathfrak{g} \otimes A$
. The universal enveloping algebra of
![]() $\mathfrak{g} \otimes A$
is a quotient of the tensor algebra
$\mathfrak{g} \otimes A$
is a quotient of the tensor algebra
![]() $T(\mathfrak{g} \otimes A)$
modulo the two-sided ideal I generated in
$T(\mathfrak{g} \otimes A)$
modulo the two-sided ideal I generated in
![]() $T(\mathfrak{g} \otimes A)$
by all elements of the form
$T(\mathfrak{g} \otimes A)$
by all elements of the form
![]() $x \otimes y-(-1)^{|x||y|} y \otimes x-[x,y]$
, where
$x \otimes y-(-1)^{|x||y|} y \otimes x-[x,y]$
, where
![]() $x,y \in \mathfrak{g} \otimes A$
. Note that
$x,y \in \mathfrak{g} \otimes A$
. Note that
![]() $T(\mathfrak{g} \otimes A)$
has a
$T(\mathfrak{g} \otimes A)$
has a
![]() $\mathbb Z_2$
-grading extending that on
$\mathbb Z_2$
-grading extending that on
![]() $\mathfrak{g} \otimes A$
. Since the ideal I is homogeneous,
$\mathfrak{g} \otimes A$
. Since the ideal I is homogeneous,
![]() $U(\mathfrak{g} \otimes A)$
is
$U(\mathfrak{g} \otimes A)$
is
![]() $\mathbb Z_2$
-graded.
$\mathbb Z_2$
-graded.
We have a natural surjective algebra homomorphism:
Let
be the subalgebra of
![]() $\mathfrak{g}$
-invariants. Note that it is naturally
$\mathfrak{g}$
-invariants. Note that it is naturally
![]() $\mathbb Z_2$
-graded.
$\mathbb Z_2$
-graded.
If we take
![]() $A=\mathbb C$
, then
$A=\mathbb C$
, then
![]() $U(\mathfrak{g} \otimes A)^{\mathfrak{g}}$
reduces to
$U(\mathfrak{g} \otimes A)^{\mathfrak{g}}$
reduces to
![]() $U(\mathfrak{g})^{\mathfrak{g}}$
. Using a PBW basis, we see that if an element of
$U(\mathfrak{g})^{\mathfrak{g}}$
. Using a PBW basis, we see that if an element of
![]() $U(\operatorname {\mathfrak{g}})$
supercommutes with all elements of
$U(\operatorname {\mathfrak{g}})$
supercommutes with all elements of
![]() $\operatorname {\mathfrak{g}}$
, it supercommutes with all elements of the PBW basis. So
$\operatorname {\mathfrak{g}}$
, it supercommutes with all elements of the PBW basis. So
![]() $U(\operatorname {\mathfrak{g}})^{\operatorname {\mathfrak{g}}}$
is the center of
$U(\operatorname {\mathfrak{g}})^{\operatorname {\mathfrak{g}}}$
is the center of
![]() $U(\mathfrak{g})$
, which we denote by
$U(\mathfrak{g})$
, which we denote by
![]() $Z(\mathfrak{g})$
.
$Z(\mathfrak{g})$
.
Let
![]() $\mathfrak h=\mathfrak h_0+\mathfrak h_1$
be a Cartan subalgebra of
$\mathfrak h=\mathfrak h_0+\mathfrak h_1$
be a Cartan subalgebra of
![]() $\mathfrak{g}$
and
$\mathfrak{g}$
and
![]() $\mathfrak{g}=\mathfrak n^- \oplus \mathfrak h \oplus \mathfrak n^+$
be a triangular decomposition of
$\mathfrak{g}=\mathfrak n^- \oplus \mathfrak h \oplus \mathfrak n^+$
be a triangular decomposition of
![]() $\mathfrak{g}$
. We note that for basic Lie superalgebras
$\mathfrak{g}$
. We note that for basic Lie superalgebras
![]() $\mathfrak h=\mathfrak h_0$
, whereas for
$\mathfrak h=\mathfrak h_0$
, whereas for
![]() $\operatorname {\mathfrak{g}}=\operatorname {\mathfrak{q}}(n)$
and
$\operatorname {\mathfrak{g}}=\operatorname {\mathfrak{q}}(n)$
and
![]() $\operatorname {\mathfrak{p}}(n)$
,
$\operatorname {\mathfrak{p}}(n)$
,
![]() $\mathfrak h_1 \neq 0$
. Let
$\mathfrak h_1 \neq 0$
. Let
![]() $\{x_1,x_2,\dots ,x_m\}$
,
$\{x_1,x_2,\dots ,x_m\}$
,
![]() $\{h_1,h_2,\dots ,h_n\}$
, and
$\{h_1,h_2,\dots ,h_n\}$
, and
![]() $\{y_1,y_2,\dots ,y_p\}$
be homogeneous bases for
$\{y_1,y_2,\dots ,y_p\}$
be homogeneous bases for
![]() $\mathfrak{n}^-$
,
$\mathfrak{n}^-$
,
![]() $\mathfrak{h}$
and
$\mathfrak{h}$
and
![]() $\mathfrak{n}^+$
respectively. Then the monomials
$\mathfrak{n}^+$
respectively. Then the monomials
![]() $x_1^{r_1}\dots x_m^{r_m}h_1^{s_1}\dots h_n^{s_n}y_1^{t_1}\dots y_p^{t_p}$
, where the exponents of the even elements runs through the set of all positive integers, and the exponents of odd elements ranges over
$x_1^{r_1}\dots x_m^{r_m}h_1^{s_1}\dots h_n^{s_n}y_1^{t_1}\dots y_p^{t_p}$
, where the exponents of the even elements runs through the set of all positive integers, and the exponents of odd elements ranges over
![]() $\{0,1\}$
, form a PBW basis of
$\{0,1\}$
, form a PBW basis of
![]() $U(\operatorname {\mathfrak{g}})$
. The monomials where
$U(\operatorname {\mathfrak{g}})$
. The monomials where
![]() $r_1=\dots =r_m=t_1=\dots =t_p=0$
form a basis of
$r_1=\dots =r_m=t_1=\dots =t_p=0$
form a basis of
![]() $U(\mathfrak{h})$
, while the set of all remaining monomials is a basis of
$U(\mathfrak{h})$
, while the set of all remaining monomials is a basis of
![]() $(\mathfrak n^- U(\mathfrak{g}) + U(\mathfrak{g})\mathfrak n^+)$
. This yields a decomposition of
$(\mathfrak n^- U(\mathfrak{g}) + U(\mathfrak{g})\mathfrak n^+)$
. This yields a decomposition of
![]() $U(\mathfrak{g})$
as
$U(\mathfrak{g})$
as
![]() ${U(\mathfrak{g})=U(\mathfrak h) \oplus (\mathfrak n^- U(\mathfrak{g}) + U(\mathfrak{g})\mathfrak n^+)}$
. The Harish Chandra homomorphism
${U(\mathfrak{g})=U(\mathfrak h) \oplus (\mathfrak n^- U(\mathfrak{g}) + U(\mathfrak{g})\mathfrak n^+)}$
. The Harish Chandra homomorphism
![]() $HC$
is the restriction to the center
$HC$
is the restriction to the center
![]() $Z(\operatorname {\mathfrak{g}})$
of the projection map
$Z(\operatorname {\mathfrak{g}})$
of the projection map
![]() $\pi \colon U(\operatorname {\mathfrak{g}})\to U(\mathfrak{h})$
with kernel
$\pi \colon U(\operatorname {\mathfrak{g}})\to U(\mathfrak{h})$
with kernel
![]() $(\mathfrak n^- U(\mathfrak{g}) + U(\mathfrak{g})\mathfrak n^+)$
. With the identification of
$(\mathfrak n^- U(\mathfrak{g}) + U(\mathfrak{g})\mathfrak n^+)$
. With the identification of
![]() $U(\mathfrak{h} )$
to the symmetric algebra
$U(\mathfrak{h} )$
to the symmetric algebra
![]() $S(\mathfrak{h} )$
, it is well known that for all basic Lie superalgebras and
$S(\mathfrak{h} )$
, it is well known that for all basic Lie superalgebras and
![]() $\mathfrak{q}(n) $
, the image of the Harish Chandra homomorphism is contained in the commutative algebra
$\mathfrak{q}(n) $
, the image of the Harish Chandra homomorphism is contained in the commutative algebra
![]() $S(\mathfrak{h}_0)$
(see [Reference Cheng and Wang3, Sections 2.2 and 2.3]). Since the Harish Chandra homomorphism is injective, it follows that the center
$S(\mathfrak{h}_0)$
(see [Reference Cheng and Wang3, Sections 2.2 and 2.3]). Since the Harish Chandra homomorphism is injective, it follows that the center
![]() $Z(\operatorname {\mathfrak{g}})=U(\operatorname {\mathfrak{g}})^{\operatorname {\mathfrak{g}}}$
comprises only even elements, hence
$Z(\operatorname {\mathfrak{g}})=U(\operatorname {\mathfrak{g}})^{\operatorname {\mathfrak{g}}}$
comprises only even elements, hence
![]() $U(\mathfrak{g} \otimes A)^{\mathfrak{g}}$
also contains only even elements. For an alternative proof of this fact, we refer to [Reference Wei, Zheng and Shu20, 3.2, Proposition]. It is known that the center of
$U(\mathfrak{g} \otimes A)^{\mathfrak{g}}$
also contains only even elements. For an alternative proof of this fact, we refer to [Reference Wei, Zheng and Shu20, 3.2, Proposition]. It is known that the center of
![]() $U(\mathfrak{p}(n))=\mathbb C$
(see [Reference Gorelik7]). We give an alternate proof of this fact in Section 6. Therefore, it now follows that the center of
$U(\mathfrak{p}(n))=\mathbb C$
(see [Reference Gorelik7]). We give an alternate proof of this fact in Section 6. Therefore, it now follows that the center of
![]() $U(\operatorname {\mathfrak{g}}\otimes A)$
contains only even elements for all basic Lie superalgebras,
$U(\operatorname {\mathfrak{g}}\otimes A)$
contains only even elements for all basic Lie superalgebras,
![]() $\operatorname {\mathfrak{q}}(n)$
and
$\operatorname {\mathfrak{q}}(n)$
and
![]() $\operatorname {\mathfrak{p}}(n)$
.
$\operatorname {\mathfrak{p}}(n)$
.
3.3
For any
![]() $\theta \in [\mathfrak{g} ^{\otimes k}]^{\mathfrak{g}}$
,
$\theta \in [\mathfrak{g} ^{\otimes k}]^{\mathfrak{g}}$
,
![]() $\theta =\sum _i x_1^i \otimes x_2^i \otimes \cdots \otimes x_k^i$
and for any
$\theta =\sum _i x_1^i \otimes x_2^i \otimes \cdots \otimes x_k^i$
and for any
![]() $a_1, a_2, \dots ,a_k \in A$
, we define
$a_1, a_2, \dots ,a_k \in A$
, we define
The element
![]() $\hat {\theta }(a_1,a_2, \dots ,a_k) := \sum _i (x_1^i \otimes a_1) \otimes (x_2^i \otimes a_2) \otimes \cdots \otimes (x_k^i \otimes a_k) \in T(\mathfrak{g} \otimes A)$
maps to
$\hat {\theta }(a_1,a_2, \dots ,a_k) := \sum _i (x_1^i \otimes a_1) \otimes (x_2^i \otimes a_2) \otimes \cdots \otimes (x_k^i \otimes a_k) \in T(\mathfrak{g} \otimes A)$
maps to
![]() $\theta (a_1,a_2, \dots ,a_k)$
under the surjective map
$\theta (a_1,a_2, \dots ,a_k)$
under the surjective map
![]() $\pi $
and since
$\pi $
and since
![]() $[x,\hat {\theta }(a_1,a_2, \ldots ,a_k)]=0$
for all
$[x,\hat {\theta }(a_1,a_2, \ldots ,a_k)]=0$
for all
![]() $x \in \mathfrak{g}$
, we get that
$x \in \mathfrak{g}$
, we get that
![]() $[x,\theta (a_1,a_2, \ldots ,a_k)]=0$
for all
$[x,\theta (a_1,a_2, \ldots ,a_k)]=0$
for all
![]() $x \in \mathfrak{g}$
. Hence, we have
$x \in \mathfrak{g}$
. Hence, we have
We then have the following proposition.
Proposition 3.1 Let
![]() $\operatorname {\mathfrak{g}}$
be a simple Lie superalgebra or
$\operatorname {\mathfrak{g}}$
be a simple Lie superalgebra or
![]() $\mathfrak{gl}(m|n)$
, or any Lie superalgebra among
$\mathfrak{gl}(m|n)$
, or any Lie superalgebra among
![]() $\mathfrak{q}(n) $
or
$\mathfrak{q}(n) $
or
![]() $\mathfrak{p}(n)$
. Then the subalgebra
$\mathfrak{p}(n)$
. Then the subalgebra
![]() $U(\operatorname {\mathfrak{g}} \otimes A)^{\operatorname {\mathfrak{g}}}$
is spanned by
$U(\operatorname {\mathfrak{g}} \otimes A)^{\operatorname {\mathfrak{g}}}$
is spanned by
![]() $\theta (a_1,a_2, \dots , a_k)$
,
$\theta (a_1,a_2, \dots , a_k)$
,
![]() $k \geq 0$
and
$k \geq 0$
and
![]() $a_i\in A$
for
$a_i\in A$
for
![]() $i=1,2,\dots ,k$
where
$i=1,2,\dots ,k$
where
![]() $\theta $
runs over a homogeneous basis of
$\theta $
runs over a homogeneous basis of
![]() $T(\operatorname {\mathfrak{g}})^{\operatorname {\mathfrak{g}}}$
.
$T(\operatorname {\mathfrak{g}})^{\operatorname {\mathfrak{g}}}$
.
Further, the subalgebra
![]() $U(\operatorname {\mathfrak{g}} \otimes A)^{\operatorname {\mathfrak{g}}}$
is generated as an algebra by
$U(\operatorname {\mathfrak{g}} \otimes A)^{\operatorname {\mathfrak{g}}}$
is generated as an algebra by
![]() $\theta (a_1,a_2, \dots , a_k)$
,
$\theta (a_1,a_2, \dots , a_k)$
,
![]() $k \geq 0$
and
$k \geq 0$
and
![]() $a_1, a_2, \dots ,a_k \in A$
, where
$a_1, a_2, \dots ,a_k \in A$
, where
![]() $\theta $
runs over a set of homogeneous algebra generators of
$\theta $
runs over a set of homogeneous algebra generators of
![]() $T(\operatorname {\mathfrak{g}})^{\operatorname {\mathfrak{g}}}$
.
$T(\operatorname {\mathfrak{g}})^{\operatorname {\mathfrak{g}}}$
.
Proof The map
is surjective. By using the PBW basis for
![]() $U(\operatorname {\mathfrak{g}} \otimes A)$
, we see that
$U(\operatorname {\mathfrak{g}} \otimes A)$
, we see that
![]() $\pi $
splits. So we have a surjective degree preserving algebra homomorphism
$\pi $
splits. So we have a surjective degree preserving algebra homomorphism
Note that
![]() $T(\operatorname {\mathfrak{g}} \otimes A)^{\operatorname {\mathfrak{g}}}$
is a graded algebra and the grading comes from the grading of
$T(\operatorname {\mathfrak{g}} \otimes A)^{\operatorname {\mathfrak{g}}}$
is a graded algebra and the grading comes from the grading of
![]() $T(\operatorname {\mathfrak{g}})^{\operatorname {\mathfrak{g}}}$
. Since
$T(\operatorname {\mathfrak{g}})^{\operatorname {\mathfrak{g}}}$
. Since
![]() $\operatorname {\mathfrak{g}} \otimes \mathbb Ca_1 \cong \operatorname {\mathfrak{g}}$
as
$\operatorname {\mathfrak{g}} \otimes \mathbb Ca_1 \cong \operatorname {\mathfrak{g}}$
as
![]() $\operatorname {\mathfrak{g}}$
-modules,
$\operatorname {\mathfrak{g}}$
-modules,
![]() $(\operatorname {\mathfrak{g}} \otimes \mathbb Ca_1) \otimes (\operatorname {\mathfrak{g}} \otimes \mathbb Ca_2) \otimes \cdots \otimes (\operatorname {\mathfrak{g}} \otimes \mathbb Ca_k)$
as a
$(\operatorname {\mathfrak{g}} \otimes \mathbb Ca_1) \otimes (\operatorname {\mathfrak{g}} \otimes \mathbb Ca_2) \otimes \cdots \otimes (\operatorname {\mathfrak{g}} \otimes \mathbb Ca_k)$
as a
![]() $\operatorname {\mathfrak{g}}$
-module is isomorphic to
$\operatorname {\mathfrak{g}}$
-module is isomorphic to
![]() $\operatorname {\mathfrak{g}} \otimes \operatorname {\mathfrak{g}} \otimes \cdots \otimes \operatorname {\mathfrak{g}}$
. Then the spanning (resp. algebra generating) set of
$\operatorname {\mathfrak{g}} \otimes \operatorname {\mathfrak{g}} \otimes \cdots \otimes \operatorname {\mathfrak{g}}$
. Then the spanning (resp. algebra generating) set of
![]() $T(\operatorname {\mathfrak{g}})^{\operatorname {\mathfrak{g}}}$
maps to a spanning (resp. algebra generating) set of
$T(\operatorname {\mathfrak{g}})^{\operatorname {\mathfrak{g}}}$
maps to a spanning (resp. algebra generating) set of
![]() $U(\operatorname {\mathfrak{g}} \otimes A)^{\operatorname {\mathfrak{g}}}$
.
$U(\operatorname {\mathfrak{g}} \otimes A)^{\operatorname {\mathfrak{g}}}$
.
4 Tensor FFT for Queer Lie superalgebra
In this section after listing out some isomorphisms that we require in this note, we prove the tensor version of the first fundamental theorem of the queer Lie superalgebra.
4.1 Isomorphisms
Let V be a super vector space over
![]() $\mathbb C$
.
$\mathbb C$
.
1. We have
![]() $V \otimes V^* \cong \operatorname {End}_{\mathbb C}(V)$
defined by
$V \otimes V^* \cong \operatorname {End}_{\mathbb C}(V)$
defined by
![]() $(v,\phi ) \mapsto T_{(v,\phi )}$
where
$(v,\phi ) \mapsto T_{(v,\phi )}$
where
![]() $T_{(v,\phi )}(w)=\phi (w)v$
for
$T_{(v,\phi )}(w)=\phi (w)v$
for
![]() $v,w \in V$
.
$v,w \in V$
.
This implies that
![]() $\operatorname {End}_{\mathbb C}(V)^{\otimes k} \cong (V \otimes V^*)^{\otimes k}$
for
$\operatorname {End}_{\mathbb C}(V)^{\otimes k} \cong (V \otimes V^*)^{\otimes k}$
for
![]() $k \geq 1$
.
$k \geq 1$
.
2. For two super vector spaces V and W, we have an isomorphism
![]() $V \otimes W \rightarrow W \otimes V$
defined by
$V \otimes W \rightarrow W \otimes V$
defined by
![]() $v\otimes w \mapsto (-1)^{|v||w|}w \otimes v$
, where v and w are homogeneous elements of V and W, respectively.
$v\otimes w \mapsto (-1)^{|v||w|}w \otimes v$
, where v and w are homogeneous elements of V and W, respectively.
3. Let V and W be two super vector spaces. For simple homogeneous tensors
![]() $\pmb {v}=v_1\otimes v_2\otimes \dots \otimes v_k \in V^{\otimes k}$
and
$\pmb {v}=v_1\otimes v_2\otimes \dots \otimes v_k \in V^{\otimes k}$
and
![]() $\pmb {w}=w_1\otimes w_2\otimes \dots \otimes w_k\in W^{\otimes k}$
, we define
$\pmb {w}=w_1\otimes w_2\otimes \dots \otimes w_k\in W^{\otimes k}$
, we define ![]() where
where ![]() , for
, for
![]() $1\leq j\leq k-1$
. We extend this definition by linearity to arbitrary tensors.
$1\leq j\leq k-1$
. We extend this definition by linearity to arbitrary tensors.
We have an evaluation map
![]() $(V^*)^{\otimes k} \times V^{\otimes k} \rightarrow \mathbb C$
defined by:
$(V^*)^{\otimes k} \times V^{\otimes k} \rightarrow \mathbb C$
defined by:
where
![]() $\pmb {f}=f_1\otimes f_2\otimes \cdots \otimes f_k$
, and
$\pmb {f}=f_1\otimes f_2\otimes \cdots \otimes f_k$
, and
![]() $\pmb {v}=v_1\otimes v_2\otimes \cdots \otimes v_k$
for homogeneous elements
$\pmb {v}=v_1\otimes v_2\otimes \cdots \otimes v_k$
for homogeneous elements
![]() $f_i \in V^*$
and
$f_i \in V^*$
and
![]() $v_i \in V$
. This evaluation map extends to a non-degenerate bilinear form and hence we get an isomorphism between
$v_i \in V$
. This evaluation map extends to a non-degenerate bilinear form and hence we get an isomorphism between
![]() $(V^*)^{\otimes k}$
and
$(V^*)^{\otimes k}$
and
![]() $(V^{\otimes k})^*$
.
$(V^{\otimes k})^*$
.
4. Let
![]() $\tau $
be the permutation which takes
$\tau $
be the permutation which takes
![]() $(1,2,\dots , k,k+1, \dots ,2k)$
to
$(1,2,\dots , k,k+1, \dots ,2k)$
to
![]() $(\tau (1), \tau (2), \dots ,\tau (k),\tau (k+1), \dots ,\tau (2k))=(1,3,5,\ldots ,2k-1, 2,4,6, \dots ,2k)$
. By applying the permutation
$(\tau (1), \tau (2), \dots ,\tau (k),\tau (k+1), \dots ,\tau (2k))=(1,3,5,\ldots ,2k-1, 2,4,6, \dots ,2k)$
. By applying the permutation
![]() $\tau $
to
$\tau $
to
![]() $(V \otimes V^*)^{\otimes k}=(V \otimes V^*) \otimes (V \otimes V^*) \otimes \cdots \otimes (V \otimes V^*)$
we get a
$(V \otimes V^*)^{\otimes k}=(V \otimes V^*) \otimes (V \otimes V^*) \otimes \cdots \otimes (V \otimes V^*)$
we get a
![]() $\operatorname {End}_{\mathbb C}(V)$
-module isomorphism between
$\operatorname {End}_{\mathbb C}(V)$
-module isomorphism between
![]() $(V \otimes V^*)^{\otimes k}$
and
$(V \otimes V^*)^{\otimes k}$
and
![]() $V^{\otimes k} \otimes (V^*)^{\otimes k}$
. We then have
$V^{\otimes k} \otimes (V^*)^{\otimes k}$
. We then have
Let
![]() $\pmb {v}=v_1 \otimes v_2 \otimes \cdots \otimes v_k$
and
$\pmb {v}=v_1 \otimes v_2 \otimes \cdots \otimes v_k$
and
![]() $\pmb {f}=f_1\otimes f_2\otimes \cdots \otimes f_k$
. Then the map in the reverse direction is defined by
$\pmb {f}=f_1\otimes f_2\otimes \cdots \otimes f_k$
. Then the map in the reverse direction is defined by
![]() $\pmb {v} \otimes \pmb {f} \mapsto (-1)^{p(\pmb {v},\pmb {f})}(v_1 \otimes f_1) \otimes (v_2 \otimes f_2) \otimes \cdots \otimes (v_k \otimes f_k)$
.
$\pmb {v} \otimes \pmb {f} \mapsto (-1)^{p(\pmb {v},\pmb {f})}(v_1 \otimes f_1) \otimes (v_2 \otimes f_2) \otimes \cdots \otimes (v_k \otimes f_k)$
.
Remark: All the isomorphisms mentioned above are in particular
![]() $\operatorname {\mathfrak{q}}(n)$
-equivariant.
$\operatorname {\mathfrak{q}}(n)$
-equivariant.
4.2 Tensor FFT
The tensor version of the first fundamental theorem (FFT) of invariant theory (see [Reference Goodman and Wallach6]) for
![]() $\mathfrak{q}(n) $
describes a spanning set for
$\mathfrak{q}(n) $
describes a spanning set for
![]() $(V^{\otimes k} \otimes V^{*{\otimes k}})^{\mathfrak{q}(n) }$
which can be derived from the Shur–Weyl–Sergeev duality described above.
$(V^{\otimes k} \otimes V^{*{\otimes k}})^{\mathfrak{q}(n) }$
which can be derived from the Shur–Weyl–Sergeev duality described above.
For
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $V=\mathbb {C}^n\oplus \mathbb {C}^n$
. Then
$V=\mathbb {C}^n\oplus \mathbb {C}^n$
. Then
![]() $\operatorname {End}_{\mathbb C}(V)=\mathfrak{gl}(n|n)$
. We take the standard basis of V as
$\operatorname {End}_{\mathbb C}(V)=\mathfrak{gl}(n|n)$
. We take the standard basis of V as
![]() $\{e_{-1},\dots ,e_{-n},e_1,\dots ,e_n\}$
and we denote the index set for this basis by B. Put
$\{e_{-1},\dots ,e_{-n},e_1,\dots ,e_n\}$
and we denote the index set for this basis by B. Put
![]() $|i|=0$
if
$|i|=0$
if
![]() $i>0$
and 1 otherwise. The
$i>0$
and 1 otherwise. The
![]() $\mathbb {Z}_2$
-gradation of V is defined by setting
$\mathbb {Z}_2$
-gradation of V is defined by setting
![]() $|e_i|=|i|$
. The standard basis of
$|e_i|=|i|$
. The standard basis of
![]() $\operatorname {End}_{\mathbb C}(V)$
consists of the matrix units
$\operatorname {End}_{\mathbb C}(V)$
consists of the matrix units
![]() $E_{ij}$
where
$E_{ij}$
where
![]() $E_{ij}e_k=\delta _{jk}e_i$
. Note that
$E_{ij}e_k=\delta _{jk}e_i$
. Note that
![]() $\operatorname {End}_{\mathbb C}(V)$
is also
$\operatorname {End}_{\mathbb C}(V)$
is also
![]() $\mathbb Z_2$
-graded by
$\mathbb Z_2$
-graded by
![]() $|E_{ij}|=|i|+|j|$
.
$|E_{ij}|=|i|+|j|$
.
To every basis element of the Sergeev algebra
![]() $\operatorname {\mathrm{Ser}}_k$
, we wish to associate an element of
$\operatorname {\mathrm{Ser}}_k$
, we wish to associate an element of
![]() $V^{\otimes k}\otimes V^{\ast \otimes k} $
. In order to avoid cumbersome notations, we let
$V^{\otimes k}\otimes V^{\ast \otimes k} $
. In order to avoid cumbersome notations, we let
![]() $\pmb {c}$
denote the element
$\pmb {c}$
denote the element
![]() $c_1^{\epsilon _1}\ldots c_k^{\epsilon _k}$
. Let
$c_1^{\epsilon _1}\ldots c_k^{\epsilon _k}$
. Let
![]() $\{i_1,\dots ,i_k\}$
be a multi-subset of B of cardinality k. The basis element of
$\{i_1,\dots ,i_k\}$
be a multi-subset of B of cardinality k. The basis element of
![]() $V^{\otimes k}$
which corresponds to I is
$V^{\otimes k}$
which corresponds to I is ![]() . We simply write
. We simply write
![]() $\gamma (I,\sigma )$
for
$\gamma (I,\sigma )$
for
![]() $\gamma (\pmb {e_I},\sigma )$
. For any two length-k multi-subsets of indices
$\gamma (\pmb {e_I},\sigma )$
. For any two length-k multi-subsets of indices
![]() $I=\{i_1, \ldots ,i_k\}$
and
$I=\{i_1, \ldots ,i_k\}$
and
![]() $J=\{j_1, \ldots ,j_k\}$
of B, we define
$J=\{j_1, \ldots ,j_k\}$
of B, we define ![]() .
.
Now we assign the element
![]() $\sigma ^{-1}\otimes \pmb {c} \in \operatorname {\mathrm{Ser}}_k$
to the following element:
$\sigma ^{-1}\otimes \pmb {c} \in \operatorname {\mathrm{Ser}}_k$
to the following element:
where
![]() $I=\{i_1,\dots ,i_k\}$
runs over all multi-subsets of B of cardinality k and
$I=\{i_1,\dots ,i_k\}$
runs over all multi-subsets of B of cardinality k and
With the notations just introduced, the first fundamental theorem for
![]() $\mathfrak{q}(n) $
is stated below.
$\mathfrak{q}(n) $
is stated below.
Theorem 4.1 For all
![]() $\sigma \in S_k$
,
$\sigma \in S_k$
,
![]() $\pmb {c} \in \mathbf {C}l_k$
, we have that
$\pmb {c} \in \mathbf {C}l_k$
, we have that
![]() $\xi ^{(k)}_{\sigma ^{-1},\pmb {c}} \in (V^{\otimes k} \otimes V^{*\otimes k})^{\mathfrak{q}(n)}$
, and the space
$\xi ^{(k)}_{\sigma ^{-1},\pmb {c}} \in (V^{\otimes k} \otimes V^{*\otimes k})^{\mathfrak{q}(n)}$
, and the space
![]() $(V^{\otimes k}\otimes V^{\ast \otimes k} )^{\mathfrak{q}(n) }$
is spanned by the set
$(V^{\otimes k}\otimes V^{\ast \otimes k} )^{\mathfrak{q}(n) }$
is spanned by the set
![]() $\{\xi ^{(k)}_{\sigma ^{-1},\pmb {c}} \colon \pmb {c}\in \mathbf {C}l_k,\ \sigma \in S_k\}$
.
$\{\xi ^{(k)}_{\sigma ^{-1},\pmb {c}} \colon \pmb {c}\in \mathbf {C}l_k,\ \sigma \in S_k\}$
.
Proof By the isomorphisms (1) and (3) in the previous subsection, we have an isomorphism
![]() $\Theta \colon V^{\otimes k}\otimes V^{\ast \otimes k} \to \operatorname {End}_{\mathbb C}(V^{\otimes k})$
.
$\Theta \colon V^{\otimes k}\otimes V^{\ast \otimes k} \to \operatorname {End}_{\mathbb C}(V^{\otimes k})$
.
Since the tensor product action of
![]() $\mathfrak{q}(n) $
on
$\mathfrak{q}(n) $
on
![]() $V\otimes V^*$
corresponds to the adjoint action on
$V\otimes V^*$
corresponds to the adjoint action on
![]() $\mathfrak{q}(n) $
,
$\mathfrak{q}(n) $
,
![]() $\Theta $
induces an isomorphism
$\Theta $
induces an isomorphism
![]() $\tilde {\Theta }$
to the subspace
$\tilde {\Theta }$
to the subspace
![]() $\mathfrak{q}(n) $
-invariants:
$\mathfrak{q}(n) $
-invariants:
By Schur–Weyl–Sergeev duality (Theorem 2.1), we have
![]() $\Psi _k(\operatorname {\mathrm{Ser}}_k)=\operatorname {End}_{\mathfrak{q}(n) }(V^{\otimes k})$
. We claim that
$\Psi _k(\operatorname {\mathrm{Ser}}_k)=\operatorname {End}_{\mathfrak{q}(n) }(V^{\otimes k})$
. We claim that
![]() $\Theta $
maps
$\Theta $
maps
![]() $\xi ^{(k)}_{\sigma ^{-1},\pmb {c}}$
to
$\xi ^{(k)}_{\sigma ^{-1},\pmb {c}}$
to
![]() $\Psi _k(\sigma ^{-1}\otimes \pmb {c})$
. To show this, we take
$\Psi _k(\sigma ^{-1}\otimes \pmb {c})$
. To show this, we take
![]() $J=\{j_1, j_2, \ldots ,j_k\}$
and then we have
$J=\{j_1, j_2, \ldots ,j_k\}$
and then we have
 $$ \begin{align*} \Theta(\xi^{(k)}_{\sigma^{-1},\pmb{c}})({e_{j_1}}\otimes\dots\otimes {e_{j_k}}) &= \begin{aligned}[t] \sum_{I} \varsigma(\pmb{c},I,\sigma) &({P^{\epsilon_{\sigma(1)}}e_{i_{\sigma(1)}}}\otimes\dots\otimes {P^{\epsilon_{\sigma(k)}}e_{i_{\sigma(k)}}})\\ \otimes &({e_{i_1}^*}\otimes\dots\otimes {e_{i_k}^*}) ({e_{j_1}}\otimes\dots\otimes {e_{j_k}}) \end{aligned}\\ &=\sum_{I} (-1)^{p(I,J)} \varsigma(\pmb{c},I,\sigma) [e_{i_1}^*(e_{j_1})\ldots e_{i_k}^*(e_{j_k})]\\ &=(-1)^{\gamma(J,\sigma)+\sum_{s>t}\epsilon_s|e_{j_t}|} ({P^{\epsilon_{\sigma(1)}}e_{j_{\sigma(1)}}}\otimes\dots\otimes {P^{\epsilon_{\sigma(k)}}e_{j_{\sigma(k)}}})\\&=\Psi_k(\sigma^{-1}\otimes\pmb{c}). \end{align*} $$
$$ \begin{align*} \Theta(\xi^{(k)}_{\sigma^{-1},\pmb{c}})({e_{j_1}}\otimes\dots\otimes {e_{j_k}}) &= \begin{aligned}[t] \sum_{I} \varsigma(\pmb{c},I,\sigma) &({P^{\epsilon_{\sigma(1)}}e_{i_{\sigma(1)}}}\otimes\dots\otimes {P^{\epsilon_{\sigma(k)}}e_{i_{\sigma(k)}}})\\ \otimes &({e_{i_1}^*}\otimes\dots\otimes {e_{i_k}^*}) ({e_{j_1}}\otimes\dots\otimes {e_{j_k}}) \end{aligned}\\ &=\sum_{I} (-1)^{p(I,J)} \varsigma(\pmb{c},I,\sigma) [e_{i_1}^*(e_{j_1})\ldots e_{i_k}^*(e_{j_k})]\\ &=(-1)^{\gamma(J,\sigma)+\sum_{s>t}\epsilon_s|e_{j_t}|} ({P^{\epsilon_{\sigma(1)}}e_{j_{\sigma(1)}}}\otimes\dots\otimes {P^{\epsilon_{\sigma(k)}}e_{j_{\sigma(k)}}})\\&=\Psi_k(\sigma^{-1}\otimes\pmb{c}). \end{align*} $$
Since the isomorphism
![]() $\Theta $
is
$\Theta $
is
![]() $\mathfrak{q}(n) $
-equivariant, for all
$\mathfrak{q}(n) $
-equivariant, for all
![]() $x\in \mathfrak{q}(n) $
, it follows that
$x\in \mathfrak{q}(n) $
, it follows that
The last equality is valid as
![]() $\Psi _k(\sigma ^{-1}\otimes \pmb {c})\in \operatorname {End}_{\mathfrak{q}(n) }(V^{\otimes k})$
. Since
$\Psi _k(\sigma ^{-1}\otimes \pmb {c})\in \operatorname {End}_{\mathfrak{q}(n) }(V^{\otimes k})$
. Since
![]() $\Theta $
is injective, we conclude that
$\Theta $
is injective, we conclude that
![]() $\xi ^{(k)}_{\sigma ^{-1},\pmb {c}} \in (V^{\otimes k} \otimes V^{*\otimes k})^{\mathfrak{q}(n)}$
, for all
$\xi ^{(k)}_{\sigma ^{-1},\pmb {c}} \in (V^{\otimes k} \otimes V^{*\otimes k})^{\mathfrak{q}(n)}$
, for all
![]() $\sigma \in S_k$
,
$\sigma \in S_k$
,
![]() $\pmb {c} \in \mathbf {C}l_k$
. Since
$\pmb {c} \in \mathbf {C}l_k$
. Since
![]() $\tilde {\Theta }$
is an isomorphism and the elements
$\tilde {\Theta }$
is an isomorphism and the elements
![]() $\sigma ^{-1}\otimes \pmb {c}$
span the Sergeev superalgebra
$\sigma ^{-1}\otimes \pmb {c}$
span the Sergeev superalgebra
![]() $\operatorname {\mathrm{Ser}}_k$
, it follows that the set
$\operatorname {\mathrm{Ser}}_k$
, it follows that the set
![]() $\{\xi ^{(k)}_{\sigma ^{-1},\pmb {c}} \colon \pmb {c}\in \mathbf {C}l_k,\ \sigma \in S_k\}$
spans
$\{\xi ^{(k)}_{\sigma ^{-1},\pmb {c}} \colon \pmb {c}\in \mathbf {C}l_k,\ \sigma \in S_k\}$
spans
![]() $(V^{\otimes k}\otimes V^{\ast \otimes k} )^{\mathfrak{q}(n) }$
.
$(V^{\otimes k}\otimes V^{\ast \otimes k} )^{\mathfrak{q}(n) }$
.
5 The
 $\mathfrak{q}(n) $
invariants of the universal enveloping algebra
$\mathfrak{q}(n) $
invariants of the universal enveloping algebra
Let V be the vector superspace
![]() $\mathbb {C}^n\oplus \mathbb {C}^n$
. Then
$\mathbb {C}^n\oplus \mathbb {C}^n$
. Then
![]() $\operatorname {End}_{\mathbb C}(V)=\mathfrak{gl}(n|n)$
. We have a
$\operatorname {End}_{\mathbb C}(V)=\mathfrak{gl}(n|n)$
. We have a
![]() $\mathfrak{q}(n) $
-equivariant epimorphism
$\mathfrak{q}(n) $
-equivariant epimorphism
![]() $\phi \colon \mathfrak{gl}(n|n)\to \mathfrak{q}(n) $
given by
$\phi \colon \mathfrak{gl}(n|n)\to \mathfrak{q}(n) $
given by
![]() $E_{i,j}\mapsto F_{i,j}$
. As
$E_{i,j}\mapsto F_{i,j}$
. As
![]() $\operatorname {End}_{\mathbb C}(V)\cong V\otimes V^*$
(
$\operatorname {End}_{\mathbb C}(V)\cong V\otimes V^*$
(
![]() $E_{i,j}$
identifies to
$E_{i,j}$
identifies to
![]() $e_i\otimes e_j^*$
),
$e_i\otimes e_j^*$
),
![]() $\phi $
induces a surjective map (also denoted by
$\phi $
induces a surjective map (also denoted by
![]() $\phi $
)
$\phi $
)
![]() $(V\otimes V^*)^{\otimes k}\to \mathfrak{q}(n) ^{\otimes k}$
.
$(V\otimes V^*)^{\otimes k}\to \mathfrak{q}(n) ^{\otimes k}$
.
Let A be an associative, commutative, and finitely generated
![]() $\mathbb C$
-algebra with unity. For
$\mathbb C$
-algebra with unity. For
![]() $k \in \mathbb N$
and
$k \in \mathbb N$
and
![]() $a_1,a_2, \dots ,a_k \in A$
, we define
$a_1,a_2, \dots ,a_k \in A$
, we define
 $$ \begin{align*}&C_n^{(k)}(a_1,\dots,a_k)\\&\quad:=\sum_{I} (-1)^{|i_2|+\dots+|i_k|}(F_{i_1,i_2}\otimes a_1)(F_{i_1,i_2}\otimes a_1) \ldots (F_{i_{k-1},i_k}\otimes a_{k-1})(F_{i_k,i_1}\otimes a_k),\end{align*} $$
$$ \begin{align*}&C_n^{(k)}(a_1,\dots,a_k)\\&\quad:=\sum_{I} (-1)^{|i_2|+\dots+|i_k|}(F_{i_1,i_2}\otimes a_1)(F_{i_1,i_2}\otimes a_1) \ldots (F_{i_{k-1},i_k}\otimes a_{k-1})(F_{i_k,i_1}\otimes a_k),\end{align*} $$
where the sum is over all the multi-subsets
![]() $I=\{i_1,i_2, \ldots ,i_k\}$
of B of cardinality k. Note that
$I=\{i_1,i_2, \ldots ,i_k\}$
of B of cardinality k. Note that
![]() $C_n^{(k)}(a_1,\dots ,a_k) \in U(\operatorname {\mathfrak{q}}(n) \otimes A)$
.
$C_n^{(k)}(a_1,\dots ,a_k) \in U(\operatorname {\mathfrak{q}}(n) \otimes A)$
.
It is easy to see that
![]() $[x, C_n^{(k)}(a_1,\dots ,a_k)]=0$
for all
$[x, C_n^{(k)}(a_1,\dots ,a_k)]=0$
for all
![]() $x \in \operatorname {\mathfrak{q}}(n)$
and
$x \in \operatorname {\mathfrak{q}}(n)$
and
![]() $a_1,a_2, \dots ,a_k \in A$
and so
$a_1,a_2, \dots ,a_k \in A$
and so
![]() $C_n^{(k)}(a_1,\dots ,a_k) \in U(\operatorname {\mathfrak{q}}(n) \otimes A)^{\mathfrak{q}(n) }$
. These central operators generalize the classical Gelfand invariants for the general linear Lie algebra. We call them the “generalized casimir operators” for
$C_n^{(k)}(a_1,\dots ,a_k) \in U(\operatorname {\mathfrak{q}}(n) \otimes A)^{\mathfrak{q}(n) }$
. These central operators generalize the classical Gelfand invariants for the general linear Lie algebra. We call them the “generalized casimir operators” for
![]() $\mathfrak{q}(n) $
. In fact, as in the classical case, in this section we show that these central operators generate
$\mathfrak{q}(n) $
. In fact, as in the classical case, in this section we show that these central operators generate
![]() $U(\operatorname {\mathfrak{q}}(n) \otimes A)^{\mathfrak{q}(n) }$
as an algebra. We proceed to describe a spanning set of
$U(\operatorname {\mathfrak{q}}(n) \otimes A)^{\mathfrak{q}(n) }$
as an algebra. We proceed to describe a spanning set of
![]() $U(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
. First we introduce few notations.
$U(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
. First we introduce few notations.
-
• For a k-length multi-subset
 $I=(i_1,\dots ,i_k)$
of B, we put
$I=(i_1,\dots ,i_k)$
of B, we put
 $J_I=(i_2,i_3,\dots ,i_k,i_1)$
.
$J_I=(i_2,i_3,\dots ,i_k,i_1)$
. -
• For
 $\sigma \in S_k$
and
$\sigma \in S_k$
and
 $\pmb {c}\in \mathbf {C}l_k$
, we set
$\pmb {c}\in \mathbf {C}l_k$
, we set  $$\begin{align*}{J_I}^{\sigma\otimes\pmb{c}}=((-1)^{\epsilon_{\sigma(k)}}i_{\sigma(k)},(-1)^{\epsilon_{\sigma(1)}}i_{\sigma(1)},\dots,(-1)^{\epsilon_{\sigma(k-1)}}i_{\sigma(k-1)}).\end{align*}$$
$$\begin{align*}{J_I}^{\sigma\otimes\pmb{c}}=((-1)^{\epsilon_{\sigma(k)}}i_{\sigma(k)},(-1)^{\epsilon_{\sigma(1)}}i_{\sigma(1)},\dots,(-1)^{\epsilon_{\sigma(k-1)}}i_{\sigma(k-1)}).\end{align*}$$
-
• Set
 , where
, where
 $\varsigma (\pmb {c},I,\sigma )$
is defined in Equation (4.1).
$\varsigma (\pmb {c},I,\sigma )$
is defined in Equation (4.1). -
• Let
 $\zeta ^{(k)}_{\sigma ^{-1},\pmb {c}}$
denote the following element in
$\zeta ^{(k)}_{\sigma ^{-1},\pmb {c}}$
denote the following element in
 $U(\mathfrak{q}(n) )$
: (5.1)where the sum is over all the multi-subsets
$U(\mathfrak{q}(n) )$
: (5.1)where the sum is over all the multi-subsets
 $I=\{i_1,i_2,\ldots ,i_k\}$
of B of cardinality k.
$I=\{i_1,i_2,\ldots ,i_k\}$
of B of cardinality k.
Theorem 5.1 The space
![]() $U(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
is spanned by the set described below:
$U(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
is spanned by the set described below:
Proof We have a canonical projection map
![]() $T(\mathfrak{q}(n) )\to U(\mathfrak{q}(n) )$
which respects the gradings of both the algebras. Since the grading of
$T(\mathfrak{q}(n) )\to U(\mathfrak{q}(n) )$
which respects the gradings of both the algebras. Since the grading of
![]() $T(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
is induced from that of
$T(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
is induced from that of
![]() $T(\mathfrak{q}(n) )$
, we obtain a degree preserving algebra epimorphism
$T(\mathfrak{q}(n) )$
, we obtain a degree preserving algebra epimorphism
![]() $T(\mathfrak{q}(n) )^{\mathfrak{q}(n) }\to U(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
. We claim that the kth-graded component of
$T(\mathfrak{q}(n) )^{\mathfrak{q}(n) }\to U(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
. We claim that the kth-graded component of
![]() $T(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
, i.e.,
$T(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
, i.e.,
![]() $(\mathfrak{q}(n) ^{\otimes k})^{\mathfrak{q}(n) }$
is spanned by the set
$(\mathfrak{q}(n) ^{\otimes k})^{\mathfrak{q}(n) }$
is spanned by the set
![]() $\{\eta ^{(k)}_{\sigma ^{-1},\pmb {c}} \colon \pmb {c}\in \mathbf {C}l_k,\ \sigma \in S_k\}$
with
$\{\eta ^{(k)}_{\sigma ^{-1},\pmb {c}} \colon \pmb {c}\in \mathbf {C}l_k,\ \sigma \in S_k\}$
with
 $$ \begin{align*} \begin{aligned} \eta^{(k)}_{\sigma^{-1},\pmb{c}}= \sum_{I} \nu(\pmb{c},I,\sigma) F_{(-1)^{\epsilon_{\sigma(k)}}i_{\sigma(k)},i_2}&\otimes F_{(-1)^{\epsilon_{\sigma(1)}}i_{\sigma(1)},i_3}\\ &\otimes\cdots\otimes F_{(-1)^{\epsilon_{\sigma(k-2)}}i_{\sigma(k-2)},i_k}\otimes F_{(-1)^{\epsilon_{\sigma(k-1)}}i_{\sigma(k-1)},i_1}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \eta^{(k)}_{\sigma^{-1},\pmb{c}}= \sum_{I} \nu(\pmb{c},I,\sigma) F_{(-1)^{\epsilon_{\sigma(k)}}i_{\sigma(k)},i_2}&\otimes F_{(-1)^{\epsilon_{\sigma(1)}}i_{\sigma(1)},i_3}\\ &\otimes\cdots\otimes F_{(-1)^{\epsilon_{\sigma(k-2)}}i_{\sigma(k-2)},i_k}\otimes F_{(-1)^{\epsilon_{\sigma(k-1)}}i_{\sigma(k-1)},i_1}. \end{aligned} \end{align*} $$
To prove the claim we note that by Theorem 4.1, the space
![]() $(V^{\otimes k}\otimes V^{\ast \otimes k} )^{\mathfrak{q}(n) }$
is spanned by the set
$(V^{\otimes k}\otimes V^{\ast \otimes k} )^{\mathfrak{q}(n) }$
is spanned by the set
![]() $\{\xi ^{(k)}_{\sigma ^{-1},\pmb {c}} \colon \pmb {c}\in \mathbf {C}l_k,\ \sigma \in S_k\}$
, where
$\{\xi ^{(k)}_{\sigma ^{-1},\pmb {c}} \colon \pmb {c}\in \mathbf {C}l_k,\ \sigma \in S_k\}$
, where
and the sum is over all the multi-subsets
![]() $I=\{i_1, i_2, \ldots ,i_k\}$
of B of cardinality k. Let
$I=\{i_1, i_2, \ldots ,i_k\}$
of B of cardinality k. Let
![]() $\tau \in S_{2k}$
be the permutation defined by:
$\tau \in S_{2k}$
be the permutation defined by:
 $$\begin{align*}&(\tau(1),\tau(2),\dots,\tau(k),\tau(k+1),\tau(k+2),\dots,\tau(2k))\\&\quad=(3,5,\dots,2k-1,1,2k,2\dots,2k-2).\end{align*}$$
$$\begin{align*}&(\tau(1),\tau(2),\dots,\tau(k),\tau(k+1),\tau(k+2),\dots,\tau(2k))\\&\quad=(3,5,\dots,2k-1,1,2k,2\dots,2k-2).\end{align*}$$
By applying
![]() $\tau $
to
$\tau $
to
![]() $(V\otimes V^*)^{\otimes k}=(V\otimes V^*)\otimes (V\otimes V^*)\otimes \dots \otimes (V\otimes V^*)$
, we get a
$(V\otimes V^*)^{\otimes k}=(V\otimes V^*)\otimes (V\otimes V^*)\otimes \dots \otimes (V\otimes V^*)$
, we get a
![]() $\mathfrak{q}(n) $
-module isomorphism between
$\mathfrak{q}(n) $
-module isomorphism between
![]() $(V\otimes V^*)^{\otimes k}$
and
$(V\otimes V^*)^{\otimes k}$
and
![]() $V^{\otimes k}\otimes V^{\ast \otimes k} $
. So we get
$V^{\otimes k}\otimes V^{\ast \otimes k} $
. So we get
![]() $((V\otimes V^*)^{\otimes k})^{\mathfrak{q}(n) }\cong (V^{\otimes k}\otimes V^{\ast \otimes k} )^{\mathfrak{q}(n) }$
. Under this isomorphism the element
$((V\otimes V^*)^{\otimes k})^{\mathfrak{q}(n) }\cong (V^{\otimes k}\otimes V^{\ast \otimes k} )^{\mathfrak{q}(n) }$
. Under this isomorphism the element
![]() $\xi ^{(k)}_{\sigma ^{-1},\pmb {c}} \in (V^{\otimes k}\otimes V^{\ast \otimes k} )^{\mathfrak{q}(n) }$
maps to
$\xi ^{(k)}_{\sigma ^{-1},\pmb {c}} \in (V^{\otimes k}\otimes V^{\ast \otimes k} )^{\mathfrak{q}(n) }$
maps to
![]() $\theta ^{(k)}_{\sigma ^{-1},\pmb {c}}$
in
$\theta ^{(k)}_{\sigma ^{-1},\pmb {c}}$
in
![]() $(\operatorname {End}_{\mathbb C}(V)^{\otimes k})^{\operatorname {\mathfrak{q}}(n)}$
, where
$(\operatorname {End}_{\mathbb C}(V)^{\otimes k})^{\operatorname {\mathfrak{q}}(n)}$
, where
 $$ \begin{align*} \begin{aligned} \theta^{(k)}_{\sigma^{-1},\pmb{c}}= \sum_{I} \varsigma(\pmb{c},I,\sigma)(-1)^{p({J_I}^{\sigma\otimes\pmb{c}},J_I)} (P^{\epsilon_{{\sigma(k)}}}e_{i_{\sigma(k)}}\otimes e_{i_2}^*) &\otimes (P^{\epsilon_{{\sigma(1)}}}e_{i_{\sigma(1)}}\otimes e_{i_3}^*)\\ &\otimes \cdots \otimes (P^{\epsilon_{{\sigma(k-1)}}}e_{\sigma(i_{k-1})} \otimes e_{i_1}^*). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \theta^{(k)}_{\sigma^{-1},\pmb{c}}= \sum_{I} \varsigma(\pmb{c},I,\sigma)(-1)^{p({J_I}^{\sigma\otimes\pmb{c}},J_I)} (P^{\epsilon_{{\sigma(k)}}}e_{i_{\sigma(k)}}\otimes e_{i_2}^*) &\otimes (P^{\epsilon_{{\sigma(1)}}}e_{i_{\sigma(1)}}\otimes e_{i_3}^*)\\ &\otimes \cdots \otimes (P^{\epsilon_{{\sigma(k-1)}}}e_{\sigma(i_{k-1})} \otimes e_{i_1}^*). \end{aligned} \end{align*} $$
Using the fact that
![]() $P^\epsilon e_i=(-1)^{\epsilon |e_i|}e_{-i}$
for each i and the identification
$P^\epsilon e_i=(-1)^{\epsilon |e_i|}e_{-i}$
for each i and the identification
![]() $E_{i,j}=e_i \otimes e_j^*$
, we get that
$E_{i,j}=e_i \otimes e_j^*$
, we get that
 $$ \begin{align} \begin{aligned} \theta^{(k)}_{\sigma^{-1},\pmb{c}} = \sum_{I} \nu(\pmb{c},I,\sigma) E_{(-1)^{\epsilon_{\sigma(k)}}i_{\sigma(k)},i_2} &\otimes E_{(-1)^{\epsilon_{\sigma(1)}}i_{\sigma(1)},i_3}\\ &\otimes\cdots\otimes E_{(-1)^{\epsilon_{\sigma(k-2)}}i_{\sigma(k-2)},i_k}\otimes E_{(-1)^{\epsilon_{\sigma(k-1)}}i_{\sigma(k-1)},i_1}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \theta^{(k)}_{\sigma^{-1},\pmb{c}} = \sum_{I} \nu(\pmb{c},I,\sigma) E_{(-1)^{\epsilon_{\sigma(k)}}i_{\sigma(k)},i_2} &\otimes E_{(-1)^{\epsilon_{\sigma(1)}}i_{\sigma(1)},i_3}\\ &\otimes\cdots\otimes E_{(-1)^{\epsilon_{\sigma(k-2)}}i_{\sigma(k-2)},i_k}\otimes E_{(-1)^{\epsilon_{\sigma(k-1)}}i_{\sigma(k-1)},i_1}. \end{aligned} \end{align} $$
Under
![]() $\phi $
the image of
$\phi $
the image of
![]() $\theta ^{(k)}_{\sigma ^{-1},\pmb {c}}$
in
$\theta ^{(k)}_{\sigma ^{-1},\pmb {c}}$
in
![]() $(\mathfrak{q}(n) ^{\otimes k})^{\mathfrak{q}(n) }$
is the following element:
$(\mathfrak{q}(n) ^{\otimes k})^{\mathfrak{q}(n) }$
is the following element:
 $$ \begin{align} \begin{aligned} \eta^{(k)}_{\sigma^{-1},\pmb{c}}=\sum_{I} \nu(\pmb{c},I,\sigma)F_{(-1)^{\epsilon_{\sigma(k)}}i_{\sigma(k)},i_2} &\otimes F_{(-1)^{\epsilon_{\sigma(1)}}i_{\sigma(1)},i_3}\\ &\otimes\cdots\otimes F_{(-1)^{\epsilon_{\sigma(k-2)}}i_{\sigma(k-2)},i_k}\otimes F_{(-1)^{\epsilon_{\sigma(k-1)}}i_{\sigma(k-1)},i_1}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \eta^{(k)}_{\sigma^{-1},\pmb{c}}=\sum_{I} \nu(\pmb{c},I,\sigma)F_{(-1)^{\epsilon_{\sigma(k)}}i_{\sigma(k)},i_2} &\otimes F_{(-1)^{\epsilon_{\sigma(1)}}i_{\sigma(1)},i_3}\\ &\otimes\cdots\otimes F_{(-1)^{\epsilon_{\sigma(k-2)}}i_{\sigma(k-2)},i_k}\otimes F_{(-1)^{\epsilon_{\sigma(k-1)}}i_{\sigma(k-1)},i_1}. \end{aligned} \end{align} $$
Since
![]() $\phi $
surjective, we get that
$\phi $
surjective, we get that
![]() $\{\eta ^{(k)}_{\sigma ^{-1},\pmb {c}} \colon \pmb {c}\in \mathbf {C}l_k,\ \sigma \in S_k\}$
spans
$\{\eta ^{(k)}_{\sigma ^{-1},\pmb {c}} \colon \pmb {c}\in \mathbf {C}l_k,\ \sigma \in S_k\}$
spans
![]() $(\mathfrak{q}(n) ^{\otimes k})^{\mathfrak{q}(n) }$
. This means that the images of these elements under the canonical map
$(\mathfrak{q}(n) ^{\otimes k})^{\mathfrak{q}(n) }$
. This means that the images of these elements under the canonical map
![]() $T(\mathfrak{q}(n) )^{\mathfrak{q}(n) }\to U(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
span the kth-graded component of
$T(\mathfrak{q}(n) )^{\mathfrak{q}(n) }\to U(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
span the kth-graded component of
![]() $U(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
. By definition, the image of
$U(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
. By definition, the image of
![]() $\eta ^{(k)}_{\sigma ^{-1},\pmb {c}}$
is the element
$\eta ^{(k)}_{\sigma ^{-1},\pmb {c}}$
is the element
![]() $\zeta ^{(k)}_{\sigma ^{-1},\pmb {c}}$
. Consequently, the result follows.
$\zeta ^{(k)}_{\sigma ^{-1},\pmb {c}}$
. Consequently, the result follows.
Let A be a finitely generated associative commutative
![]() $\mathbb C$
-algebra with identity. For
$\mathbb C$
-algebra with identity. For
![]() $a_1,\dots ,a_k\in A$
, we define:
$a_1,\dots ,a_k\in A$
, we define:

where the sum is over all the multi-subsets
![]() $I=\{i_1,i_2, \ldots ,i_k\}$
of B of cardinality k.
$I=\{i_1,i_2, \ldots ,i_k\}$
of B of cardinality k.
With this notation, we have the following corollary.
Corollary 5.2 Let A be a finitely generated associative commutative
![]() $\mathbb C$
-algebra with identity, and
$\mathbb C$
-algebra with identity, and ![]() be an arbitrary k-tuple. Then
be an arbitrary k-tuple. Then
![]() $U(\mathfrak{q}(n) \otimes A)^{\mathfrak{q}(n) }$
is spanned by the following set:
$U(\mathfrak{q}(n) \otimes A)^{\mathfrak{q}(n) }$
is spanned by the following set:
Proof By the above Theorem, we see that
![]() $U(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
is spanned by the set described in formula (5.1). Therefore, it follows from Proposition 3.1 that
$U(\mathfrak{q}(n) )^{\mathfrak{q}(n) }$
is spanned by the set described in formula (5.1). Therefore, it follows from Proposition 3.1 that
![]() $U(\mathfrak{q}(n) \otimes A)^{\mathfrak{q}(n) }$
is spanned by the elements given above.
$U(\mathfrak{q}(n) \otimes A)^{\mathfrak{q}(n) }$
is spanned by the elements given above.
5.1 Center of
 $\operatorname {\mathfrak{q}}(n)$
$\operatorname {\mathfrak{q}}(n)$
In this subsection, we describe a set of algebra generators of
![]() $Z(\mathfrak{q}(n) )=U(\operatorname {\mathfrak{q}}(n))^{\operatorname {\mathfrak{q}}(n)}$
. In what follows we denote the k-cycle
$Z(\mathfrak{q}(n) )=U(\operatorname {\mathfrak{q}}(n))^{\operatorname {\mathfrak{q}}(n)}$
. In what follows we denote the k-cycle
![]() $(12\ldots k)$
by
$(12\ldots k)$
by
![]() $\sigma _k$
and
$\sigma _k$
and
![]() $|e_i|$
by just
$|e_i|$
by just
![]() $|i|$
.
$|i|$
.
Theorem 5.3 The centre
![]() $Z(\mathfrak{q}(n) )$
is generated as an algebra by the following elements:
$Z(\mathfrak{q}(n) )$
is generated as an algebra by the following elements:
where k runs over the set of all odd positive integers and I over all multi-subsets of B of cardinality k.
Proof Choose an arbitrary basis element
![]() $\pmb {c}=c_1^{\epsilon _1}\ldots c_k^{\epsilon _k}$
of
$\pmb {c}=c_1^{\epsilon _1}\ldots c_k^{\epsilon _k}$
of
![]() $\mathbf {C}l_k$
. Then formula (5.3) shows that the invariant associated with
$\mathbf {C}l_k$
. Then formula (5.3) shows that the invariant associated with
![]() $\sigma _k^{-1}\otimes \pmb {c}$
in
$\sigma _k^{-1}\otimes \pmb {c}$
in
![]() $(\operatorname {\mathfrak{q}}(n)^{\otimes k})^{\operatorname {\mathfrak{q}}(n)}$
is given by
$(\operatorname {\mathfrak{q}}(n)^{\otimes k})^{\operatorname {\mathfrak{q}}(n)}$
is given by
We begin by calculating explicitly the element in Equation (5.6). In this case, the sign
![]() $\nu (\pmb {c},I,\sigma _k)$
is given by
$\nu (\pmb {c},I,\sigma _k)$
is given by
Since
![]() $\text {Inv}(\sigma _k)=\{(1,k),(2,k),\dots ,(k-1,k)\}$
, it follows that
$\text {Inv}(\sigma _k)=\{(1,k),(2,k),\dots ,(k-1,k)\}$
, it follows that
![]() $ \gamma (I,\sigma _k) = |i_1|(|i_2|+\cdots |i_k|).$
$ \gamma (I,\sigma _k) = |i_1|(|i_2|+\cdots |i_k|).$
By definition
We also have
Recall that
![]() ${J_I}^{\sigma \otimes \pmb {c}}=((-1)^{\epsilon _{\sigma (k)}}i_{\sigma (k)},(-1)^{\epsilon _{\sigma (1)}}i_{\sigma (1)},\dots ,(-1)^{\epsilon _{\sigma (k-1)}}i_{\sigma (k-1)})$
for
${J_I}^{\sigma \otimes \pmb {c}}=((-1)^{\epsilon _{\sigma (k)}}i_{\sigma (k)},(-1)^{\epsilon _{\sigma (1)}}i_{\sigma (1)},\dots ,(-1)^{\epsilon _{\sigma (k-1)}}i_{\sigma (k-1)})$
for
![]() $\sigma \in S_k$
where
$\sigma \in S_k$
where
![]() $J_I=(i_2,\dots ,i_k,i_1)$
. So for
$J_I=(i_2,\dots ,i_k,i_1)$
. So for
![]() $\sigma =\sigma _k$
, we get that
$\sigma =\sigma _k$
, we get that
 $$ \begin{align*} p({J_I}^{\sigma_k\otimes\pmb{c}},J_I) = {|i_2|}(|{(-1)^{\epsilon_2}i_2}|+\dots+|{(-1)^{\epsilon_k}i_k}|) +{|i_3|}(|{(-1)^{\epsilon_3}i_3}|+\dots+|{(-1)^{\epsilon_k}i_k}|) \\ +\dots+ |i_k||(-1)^{\epsilon_k}i_k|. \end{align*} $$
$$ \begin{align*} p({J_I}^{\sigma_k\otimes\pmb{c}},J_I) = {|i_2|}(|{(-1)^{\epsilon_2}i_2}|+\dots+|{(-1)^{\epsilon_k}i_k}|) +{|i_3|}(|{(-1)^{\epsilon_3}i_3}|+\dots+|{(-1)^{\epsilon_k}i_k}|) \\ +\dots+ |i_k||(-1)^{\epsilon_k}i_k|. \end{align*} $$
Since
![]() $|(-1)^\epsilon i|=\epsilon +|i|$
and
$|(-1)^\epsilon i|=\epsilon +|i|$
and
![]() $|i|^2=|i|$
, we get that
$|i|^2=|i|$
, we get that
 $$ \begin{align} p({J_I}^{\sigma_k\otimes\pmb{c}},J_I)\kern1.5pt{=}\kern1.5pt (|i_2|+|i_3|+\cdots +|i_k|)\kern1.5pt{+}\kern1.5pt|i_2|(\epsilon_2+\dots+\epsilon_k)+\dots+ & |i_{k-1}|(\epsilon_{k-1}\kern1.5pt{+}\kern1.5pt\epsilon_k)\kern1.5pt{+}\kern1.5pt|i_k|\epsilon_k \\ & +p(I,I)-\gamma(I,\sigma_k).\nonumber \end{align} $$
$$ \begin{align} p({J_I}^{\sigma_k\otimes\pmb{c}},J_I)\kern1.5pt{=}\kern1.5pt (|i_2|+|i_3|+\cdots +|i_k|)\kern1.5pt{+}\kern1.5pt|i_2|(\epsilon_2+\dots+\epsilon_k)+\dots+ & |i_{k-1}|(\epsilon_{k-1}\kern1.5pt{+}\kern1.5pt\epsilon_k)\kern1.5pt{+}\kern1.5pt|i_k|\epsilon_k \\ & +p(I,I)-\gamma(I,\sigma_k).\nonumber \end{align} $$
So
![]() $\nu (\pmb {c},I,\sigma _k)= (-1)^{(\epsilon _1+\dots +\epsilon _k)|i_1|+(|i_2|+\dots +|i_k|)}.$
$\nu (\pmb {c},I,\sigma _k)= (-1)^{(\epsilon _1+\dots +\epsilon _k)|i_1|+(|i_2|+\dots +|i_k|)}.$
In particular, if
![]() $\pmb {c}=c_{t_1}\ldots c_{t_m}$
with
$\pmb {c}=c_{t_1}\ldots c_{t_m}$
with
![]() $0\ne t_1>\dots >t_m$
, then
$0\ne t_1>\dots >t_m$
, then
![]() $\nu (\pmb {c},I,\sigma _k)= (-1)^{m|i_1|+|i_2|+\dots +|i_k|}$
. Using this information we can rewrite Equation (5.5) corresponding to
$\nu (\pmb {c},I,\sigma _k)= (-1)^{m|i_1|+|i_2|+\dots +|i_k|}$
. Using this information we can rewrite Equation (5.5) corresponding to
![]() $\sigma =\sigma _k$
, and
$\sigma =\sigma _k$
, and
![]() $\pmb {c}=c_{t_1}\ldots c_{t_m}$
as
$\pmb {c}=c_{t_1}\ldots c_{t_m}$
as
 $$ \begin{align} \sum_{I}(-1)^{m|i_1|+|i_2|+\dots+|i_k|} F_{i_1,i_2}&\otimes\cdots \otimes F_{i_{{t_1}-1},i_{t_1}}\otimes F_{-i_{t_1,i_{{t_1}+1}}} \\ &\otimes\dots\otimes F_{i_{{t_m}-1},i_{t_m}}\otimes{F_{-i_{t_m,i_{{t_m}+1}}}}\otimes\dots\otimes {F_{i_k,i_1}}.\nonumber \end{align} $$
$$ \begin{align} \sum_{I}(-1)^{m|i_1|+|i_2|+\dots+|i_k|} F_{i_1,i_2}&\otimes\cdots \otimes F_{i_{{t_1}-1},i_{t_1}}\otimes F_{-i_{t_1,i_{{t_1}+1}}} \\ &\otimes\dots\otimes F_{i_{{t_m}-1},i_{t_m}}\otimes{F_{-i_{t_m,i_{{t_m}+1}}}}\otimes\dots\otimes {F_{i_k,i_1}}.\nonumber \end{align} $$
In the sum (5.5a) we first replace
![]() $i_{t_1}$
by
$i_{t_1}$
by
![]() $-i_{t_1}$
, and then using the relation
$-i_{t_1}$
, and then using the relation
![]() $F_{i,j}=F_{-i,-j}$
, we replace the factor
$F_{i,j}=F_{-i,-j}$
, we replace the factor
![]() $F_{i_{{t_1}-1},i_{t_1}}\otimes F_{-i_{t_1,i_{{t_1}+1}}}$
in (5.5a) by
$F_{i_{{t_1}-1},i_{t_1}}\otimes F_{-i_{t_1,i_{{t_1}+1}}}$
in (5.5a) by
![]() $F_{-i_{{t_1}-1},i_{t_1}}\otimes F_{i_{t_1,i_{{t_1}+1}}}$
. Since for any
$F_{-i_{{t_1}-1},i_{t_1}}\otimes F_{i_{t_1,i_{{t_1}+1}}}$
. Since for any
![]() $1\leq q\leq k$
, we have
$1\leq q\leq k$
, we have
![]() $(-1)^{|i_q|}=-(-1)^{|-i_q|}$
, this replacement will have the sole effect of multiplication by
$(-1)^{|i_q|}=-(-1)^{|-i_q|}$
, this replacement will have the sole effect of multiplication by
![]() $-1$
. Performing the same operation inductively on
$-1$
. Performing the same operation inductively on
![]() $i_{{t_1}-1}$
and then up to on
$i_{{t_1}-1}$
and then up to on
![]() $i_2$
, we can bring the negative sign to
$i_2$
, we can bring the negative sign to
![]() $i_1$
while keeping the signs of all intermediate subscripts between
$i_1$
while keeping the signs of all intermediate subscripts between
![]() $i_2$
and
$i_2$
and
![]() $i_{t_1}$
positive. This implies that the sum (5.5a) is same as
$i_{t_1}$
positive. This implies that the sum (5.5a) is same as
 $$ \begin{align} (-1)^{t_1-1} \sum_I (-1)^{m|i_1|+|i_2|+\dots+|i_k|} F_{-i_1,i_2}&\otimes\cdots \otimes F_{i_{{t_1}-1},i_{t_1}}\otimes F_{i_{t_1,i_{{t_1}+1}}} \\&\otimes\dots\otimes F_{i_{{t_m}-1},i_{t_m}}\otimes{F_{-i_{t_m,i_{{t_m}+1}}}}\otimes\dots\otimes {F_{i_k,i_1}}.\nonumber \end{align} $$
$$ \begin{align} (-1)^{t_1-1} \sum_I (-1)^{m|i_1|+|i_2|+\dots+|i_k|} F_{-i_1,i_2}&\otimes\cdots \otimes F_{i_{{t_1}-1},i_{t_1}}\otimes F_{i_{t_1,i_{{t_1}+1}}} \\&\otimes\dots\otimes F_{i_{{t_m}-1},i_{t_m}}\otimes{F_{-i_{t_m,i_{{t_m}+1}}}}\otimes\dots\otimes {F_{i_k,i_1}}.\nonumber \end{align} $$
Now, we repeat the same procedure in the sum (5.5b) with
![]() $i_{t_2}$
and then inductively up to
$i_{t_2}$
and then inductively up to
![]() $i_{t_m}$
to obtain that the sum (5.5a) is same as:
$i_{t_m}$
to obtain that the sum (5.5a) is same as:
We denote by f the sum in (5.5c) without the sign
![]() $(-1)^{t_1+\dots +t_m-m}$
. When m is an even integer, we have
$(-1)^{t_1+\dots +t_m-m}$
. When m is an even integer, we have
![]() $f=C_n^{(k)}$
. If m is odd we show that
$f=C_n^{(k)}$
. If m is odd we show that
![]() $f=0$
.
$f=0$
.
When m is odd, we have
By changing the signs of all the subscripts and using
![]() $F_{i,j}=F_{-i,-j}$
, we get that
$F_{i,j}=F_{-i,-j}$
, we get that
![]() ${f=(-1)^k f}$
. Therefore,
${f=(-1)^k f}$
. Therefore,
![]() $f=0$
when k is odd. We have the following identity:
$f=0$
when k is odd. We have the following identity:
So, f can also be written as
Now we replace
![]() $i_2,\dots ,i_k$
by their negatives to obtain
$i_2,\dots ,i_k$
by their negatives to obtain
![]() $f=(-1)^{k-1}f$
. This implies that
$f=(-1)^{k-1}f$
. This implies that
![]() $f=0$
when k is even too.
$f=0$
when k is even too.
To sum up, we have obtained that for any positive integer k, the element in (5.5) corresponding to
![]() $(\sigma _k^{-1}\otimes c_{t_1}\ldots c_{t_m})$
is
$(\sigma _k^{-1}\otimes c_{t_1}\ldots c_{t_m})$
is
![]() $0$
when m is odd; and when m is even, it equals either
$0$
when m is odd; and when m is even, it equals either
![]() $C_n^{(k)}$
or
$C_n^{(k)}$
or
![]() $-C_n^{(k)}$
. Therefore, for each
$-C_n^{(k)}$
. Therefore, for each
![]() $k\geq 1$
, we associate to it the element
$k\geq 1$
, we associate to it the element
![]() $C_n^{(k)}$
.
$C_n^{(k)}$
.
Since the symmetric group
![]() $S_k$
is generated by the cycles
$S_k$
is generated by the cycles
![]() $(12)=\sigma _2$
, and
$(12)=\sigma _2$
, and
![]() $(12\ldots k)=\sigma _k$
, it follows that any element of
$(12\ldots k)=\sigma _k$
, it follows that any element of
![]() $\cup _{k\geq 1}S_k$
can be written as a product of various
$\cup _{k\geq 1}S_k$
can be written as a product of various
![]() $\sigma _k$
’s where
$\sigma _k$
’s where
![]() $k\in \mathbb {N}$
. The multiplication for the Sergeev algebra enables us to write
$k\in \mathbb {N}$
. The multiplication for the Sergeev algebra enables us to write
![]() $(\sigma _1\sigma _2\otimes \pmb {c})=(\sigma _1\otimes 1)\cdot (\sigma _2\otimes \pmb {c})$
, for any
$(\sigma _1\sigma _2\otimes \pmb {c})=(\sigma _1\otimes 1)\cdot (\sigma _2\otimes \pmb {c})$
, for any
![]() $\sigma _1,\sigma _2\in S_k$
. As
$\sigma _1,\sigma _2\in S_k$
. As
![]() $\Psi _k$
is an algebra homomorphism, we get that
$\Psi _k$
is an algebra homomorphism, we get that
![]() $\eta ^{(k)}_{\sigma ,\pmb {c}}=\eta ^{(k)}_{\sigma _1,\pmb {1}} \eta ^{(k)}_{\sigma _2,\pmb {c}}$
. From here we conclude that the elements
$\eta ^{(k)}_{\sigma ,\pmb {c}}=\eta ^{(k)}_{\sigma _1,\pmb {1}} \eta ^{(k)}_{\sigma _2,\pmb {c}}$
. From here we conclude that the elements
![]() $\{C_n^{k}\colon k\in \mathbb N\}$
generate
$\{C_n^{k}\colon k\in \mathbb N\}$
generate
![]() $Z(\mathfrak{q}(n) )$
as an algebra.
$Z(\mathfrak{q}(n) )$
as an algebra.
Corollary 5.4 Let A be a finitely generated associative commutative
![]() $\mathbb C$
-algebra with identity. Then
$\mathbb C$
-algebra with identity. Then
![]() $U(\mathfrak{q}(n) \otimes A)^{\mathfrak{q}(n) }$
is generated as an algebra by the following elements:
$U(\mathfrak{q}(n) \otimes A)^{\mathfrak{q}(n) }$
is generated as an algebra by the following elements:
where k runs over the set of all odd positive integers,
![]() $a_1,\dots ,a_k\in A$
are arbitrary, and I runs over all multi-subsets of B of cardinality k.
$a_1,\dots ,a_k\in A$
are arbitrary, and I runs over all multi-subsets of B of cardinality k.
Proof Follows directly from Proposition 3.1.
Remark: Let
![]() $V(\lambda _1),\dots , V(\lambda _m)$
be finite-dimensional irreducible modules for
$V(\lambda _1),\dots , V(\lambda _m)$
be finite-dimensional irreducible modules for
![]() $\operatorname {\mathfrak{q}}(n)$
. Let
$\operatorname {\mathfrak{q}}(n)$
. Let
![]() $A=\mathbb C[t,t^{-1}]$
be the algebra of Laurent polynomials in one variable, and
$A=\mathbb C[t,t^{-1}]$
be the algebra of Laurent polynomials in one variable, and
![]() $d_1,\dots ,d_m$
be m distinct nonzero complex numbers. We denote the m-tuples
$d_1,\dots ,d_m$
be m distinct nonzero complex numbers. We denote the m-tuples
![]() $(\lambda _1,\dots ,\lambda _m)$
, and
$(\lambda _1,\dots ,\lambda _m)$
, and
![]() $(d_1,\dots ,d_m)$
, respectively by
$(d_1,\dots ,d_m)$
, respectively by
![]() $\pmb {\lambda }$
and
$\pmb {\lambda }$
and
![]() $\pmb {d}$
. Then
$\pmb {d}$
. Then ![]() is a
is a
![]() $\mathfrak{q}(n) \otimes A$
-module, where the action is defined by
$\mathfrak{q}(n) \otimes A$
-module, where the action is defined by
 $$ \begin{align*} & (x\otimes f(t))\cdot ({v_1}\otimes\dots\otimes {v_m})=f(d_1) ({x\cdot v_1}\otimes\dots\otimes {v_m}) +(-1)^{|x||v_1|}f(d_2)( v_1\otimes{x\cdot v_2}\otimes\dots\otimes {v_m})\\ & +\dots+(-1)^{|x|(|v_1|+\dots+|v_{m-1}|}f(d_m)({v_1}\otimes\dots\otimes {x\cdot v_m}) \,\ \text{for} \,\, x\otimes f(t) \in \mathfrak{q}(n) \otimes A \,\, \text{and} \,\, v_i \in V(\lambda_i). \end{align*} $$
$$ \begin{align*} & (x\otimes f(t))\cdot ({v_1}\otimes\dots\otimes {v_m})=f(d_1) ({x\cdot v_1}\otimes\dots\otimes {v_m}) +(-1)^{|x||v_1|}f(d_2)( v_1\otimes{x\cdot v_2}\otimes\dots\otimes {v_m})\\ & +\dots+(-1)^{|x|(|v_1|+\dots+|v_{m-1}|}f(d_m)({v_1}\otimes\dots\otimes {x\cdot v_m}) \,\ \text{for} \,\, x\otimes f(t) \in \mathfrak{q}(n) \otimes A \,\, \text{and} \,\, v_i \in V(\lambda_i). \end{align*} $$
Then
![]() $V(\pmb {\lambda },\pmb {d})$
with the above action is called an evaluation module. A proof similar to the proof given in [Reference Rao14, Section IV, Part C] shows that the
$V(\pmb {\lambda },\pmb {d})$
with the above action is called an evaluation module. A proof similar to the proof given in [Reference Rao14, Section IV, Part C] shows that the
![]() $\mathfrak{q}(n) \otimes A$
-module
$\mathfrak{q}(n) \otimes A$
-module
![]() $V(\pmb {\lambda },\pmb {d})$
is irreducible. Moreover, if
$V(\pmb {\lambda },\pmb {d})$
is irreducible. Moreover, if
![]() $V(\pmb {\lambda },\pmb {d})=\bigoplus _{\mu \in \mathfrak{h} ^*}V(\pmb {\lambda },\pmb {d})_\mu $
is the weight space decomposition, where
$V(\pmb {\lambda },\pmb {d})=\bigoplus _{\mu \in \mathfrak{h} ^*}V(\pmb {\lambda },\pmb {d})_\mu $
is the weight space decomposition, where
![]() $V(\pmb {\lambda },\pmb {d})_\mu =\{v\in V(\pmb {\lambda },\pmb {d})\colon h\cdot v=\mu (h)v, \,\, \forall \,\, h \in \mathfrak{h} \}$
, then we have that
$V(\pmb {\lambda },\pmb {d})_\mu =\{v\in V(\pmb {\lambda },\pmb {d})\colon h\cdot v=\mu (h)v, \,\, \forall \,\, h \in \mathfrak{h} \}$
, then we have that
where
![]() $V(\pmb {\lambda },\pmb {d})_\mu ^+=\{v\in V(\pmb {\lambda },\pmb {d})_\mu \colon \mathfrak{q}(n) ^+ v=0\}$
,
$V(\pmb {\lambda },\pmb {d})_\mu ^+=\{v\in V(\pmb {\lambda },\pmb {d})_\mu \colon \mathfrak{q}(n) ^+ v=0\}$
,
![]() $\mathfrak{q}(n) ^+$
is the sum of all root spaces,
$\mathfrak{q}(n) ^+$
is the sum of all root spaces,
![]() $p_i$
is the Lagrange’s polynomial defined by
$p_i$
is the Lagrange’s polynomial defined by
![]() $p_i(t)=\prod _{k\ne i}(t-d_k)/(d_i-d_k)$
, for
$p_i(t)=\prod _{k\ne i}(t-d_k)/(d_i-d_k)$
, for
![]() $1\leq i\leq m$
,
$1\leq i\leq m$
,
![]() $i_1,\dots ,i_k\in \{1,\dots ,m\}$
, and
$i_1,\dots ,i_k\in \{1,\dots ,m\}$
, and
![]() $C_n^{(k)}(p_1,\dots ,p_k)=\sum _I (-1)^{|i_2|+\dots +|i_k|}F_{i_1,i_2}(p_1)\otimes \dots \otimes F_{i_k,i_1}(p_k),$
with
$C_n^{(k)}(p_1,\dots ,p_k)=\sum _I (-1)^{|i_2|+\dots +|i_k|}F_{i_1,i_2}(p_1)\otimes \dots \otimes F_{i_k,i_1}(p_k),$
with
![]() $F_{p,q}(p_i)=F_{p,q}\otimes p_i$
. This means that the central operators
$F_{p,q}(p_i)=F_{p,q}\otimes p_i$
. This means that the central operators
![]() $C_n^{(k)}(p_{i_1}(t),\dots ,p_{i_k}(t))$
send a highest weight vector to another highest weight vector. This is an effective method of producing new highest weight vectors from a given one. For details, we refer to [Reference Rao14, Section IV, Part D].
$C_n^{(k)}(p_{i_1}(t),\dots ,p_{i_k}(t))$
send a highest weight vector to another highest weight vector. This is an effective method of producing new highest weight vectors from a given one. For details, we refer to [Reference Rao14, Section IV, Part D].
6 Invariants of the periplectic Lie superalgebra
6.1 Periplectic Lie superalgebra
The periplectic Lie superalgebra is the Lie superalgebra preserving an odd non-degenerate symmetric or skew-symmetric bilinear form. It is thus a superanalog of the orthogonal or symplectic Lie algebra.
For
![]() $n \in \mathbb N$
, let
$n \in \mathbb N$
, let
![]() $V=\mathbb C^n \oplus \mathbb C^n$
equipped with a non-degenerate odd symmetric bilinear form
$V=\mathbb C^n \oplus \mathbb C^n$
equipped with a non-degenerate odd symmetric bilinear form
Then
![]() $\mathfrak{p}(V)$
is the Lie sub-superalgebra of
$\mathfrak{p}(V)$
is the Lie sub-superalgebra of
![]() $\operatorname {End}_{\mathbb C}(V)$
preserving
$\operatorname {End}_{\mathbb C}(V)$
preserving
![]() $\beta $
, i.e., satisfying
$\beta $
, i.e., satisfying
It can also be defined as the fixed point Lie sub-superalgebra of the involution
![]() $\sigma : \mathfrak{gl}(n|n) \rightarrow \mathfrak{gl}(n|n)$
by
$\sigma : \mathfrak{gl}(n|n) \rightarrow \mathfrak{gl}(n|n)$
by
![]() $E_{i,j} \mapsto -(-1)^{|i||j|+|i|}E_{n+j,n+i}$
.
$E_{i,j} \mapsto -(-1)^{|i||j|+|i|}E_{n+j,n+i}$
.
We note that
![]() $\mathfrak{p}(V)$
acts on V by matrix multiplication and on the r-fold tensor product
$\mathfrak{p}(V)$
acts on V by matrix multiplication and on the r-fold tensor product
![]() $V^{\otimes r}$
by the rule given in Equation (2.1).
$V^{\otimes r}$
by the rule given in Equation (2.1).
Since the bilinear form is nondegenerate on V, we can choose bases
![]() $v_1, v_2, \ldots ,v_n$
for
$v_1, v_2, \ldots ,v_n$
for
![]() $V_{0}$
and
$V_{0}$
and
![]() $v_{n+1},v_{n+2}, \ldots ,v_{2n}$
for
$v_{n+1},v_{n+2}, \ldots ,v_{2n}$
for
![]() $V_1$
such that
$V_1$
such that
![]() $\beta (v_{n+i},v_j)=\beta (v_j, v_{n+i})=\delta _{ij}$
and
$\beta (v_{n+i},v_j)=\beta (v_j, v_{n+i})=\delta _{ij}$
and
![]() $\beta (v_i,v_j)=\beta (v_{n+i},v_{n+j})=0$
for
$\beta (v_i,v_j)=\beta (v_{n+i},v_{n+j})=0$
for
![]() $i,j=1,2, \ldots ,n$
. The basis elements
$i,j=1,2, \ldots ,n$
. The basis elements
![]() $v_i$
and
$v_i$
and
![]() $v_{n+i}$
are dual to each other with respect to the bilinear form. This form enables us to identify V and
$v_{n+i}$
are dual to each other with respect to the bilinear form. This form enables us to identify V and
![]() $V^*$
. An element
$V^*$
. An element
![]() $f\in V^*$
is identified with
$f\in V^*$
is identified with
![]() $v_f\in V$
such that
$v_f\in V$
such that
![]() $f(u)=\beta (u,v_f)$
for every
$f(u)=\beta (u,v_f)$
for every
![]() $u\in V$
. The matrix of
$u\in V$
. The matrix of
![]() $\beta $
with respect to this basis is
$\beta $
with respect to this basis is
 $$ \begin{align*}\begin{pmatrix} 0 & I_n \\ I_n & 0 \end{pmatrix}\end{align*} $$
$$ \begin{align*}\begin{pmatrix} 0 & I_n \\ I_n & 0 \end{pmatrix}\end{align*} $$
We use the notation
![]() $v_{i+n}^*:=v_i$
and
$v_{i+n}^*:=v_i$
and
![]() $v_i^*:=v_{i+n}$
.
$v_i^*:=v_{i+n}$
.
With respect to the above basis an element
![]() $X \in \mathfrak{p}(V)$
can be represented in matrix form as
$X \in \mathfrak{p}(V)$
can be represented in matrix form as
 $$ \begin{align*}X=\begin{pmatrix} A & B \\ C & -A^T \end{pmatrix},\end{align*} $$
$$ \begin{align*}X=\begin{pmatrix} A & B \\ C & -A^T \end{pmatrix},\end{align*} $$
where
![]() $A, B,C$
are
$A, B,C$
are
![]() $n \times n$
matrices such that
$n \times n$
matrices such that
![]() $B=B^T$
and
$B=B^T$
and
![]() $C=-C^T$
. We identify
$C=-C^T$
. We identify
![]() $\mathfrak{p}(V)$
with the space
$\mathfrak{p}(V)$
with the space
![]() $\mathfrak{p}(n)$
of matrices in the above form. The elements
$\mathfrak{p}(n)$
of matrices in the above form. The elements
![]() $E_{i,j}-E_{j+n, i+n}, E_{i,j+n}+E_{j,i+n}, E_{i+n,j}-E_{j+n,i}, \text { for } 1 \leq i,j \leq n$
form a basis for
$E_{i,j}-E_{j+n, i+n}, E_{i,j+n}+E_{j,i+n}, E_{i+n,j}-E_{j+n,i}, \text { for } 1 \leq i,j \leq n$
form a basis for
![]() $\mathfrak{p}(n)$
.
$\mathfrak{p}(n)$
.
There is a grading
![]() $\mathfrak{p}(n)=\mathfrak{p}(n)_{-1} \oplus \mathfrak{p}(n)_0\oplus \mathfrak{p}(n)_1$
, where
$\mathfrak{p}(n)=\mathfrak{p}(n)_{-1} \oplus \mathfrak{p}(n)_0\oplus \mathfrak{p}(n)_1$
, where
![]() $\mathfrak{p}(n)_0 \cong \mathfrak{gl}_n$
,
$\mathfrak{p}(n)_0 \cong \mathfrak{gl}_n$
,
![]() $\mathfrak{p}(n)_{-1} \cong \wedge ^2((\mathbb C^n)^*)$
and
$\mathfrak{p}(n)_{-1} \cong \wedge ^2((\mathbb C^n)^*)$
and
![]() $\mathfrak{p}(n)_{1} \cong Sym^2(\mathbb C^{n})$
as
$\mathfrak{p}(n)_{1} \cong Sym^2(\mathbb C^{n})$
as
![]() $\mathfrak{p}(n)_0$
-modules. It is well known that the derived superalgebra
$\mathfrak{p}(n)_0$
-modules. It is well known that the derived superalgebra
![]() $\mathfrak{sp}(n)=\mathfrak{p}(n) \cap \mathfrak{sl}(n,n)=[\mathfrak{p}(n), \mathfrak{p}(n)]$
is simple for
$\mathfrak{sp}(n)=\mathfrak{p}(n) \cap \mathfrak{sl}(n,n)=[\mathfrak{p}(n), \mathfrak{p}(n)]$
is simple for
![]() $n \geq 3$
. We have
$n \geq 3$
. We have
![]() $\mathfrak{p}(n)=\mathbb CI' \oplus \mathfrak{sp}(n)$
, where
$\mathfrak{p}(n)=\mathbb CI' \oplus \mathfrak{sp}(n)$
, where
![]() $I'=\left (\begin {smallmatrix} I_n & 0 \\ 0 & -I_n \end {smallmatrix}\right )$
.
$I'=\left (\begin {smallmatrix} I_n & 0 \\ 0 & -I_n \end {smallmatrix}\right )$
.
6.2
We note that the following element
 $$\begin{align*} c=\sum_{i=1}^{2n}(-1)^{|i|}v_i\otimes v_i^*, \end{align*}$$
$$\begin{align*} c=\sum_{i=1}^{2n}(-1)^{|i|}v_i\otimes v_i^*, \end{align*}$$
where
![]() $v_i^*=v_{i+n}$
for
$v_i^*=v_{i+n}$
for
![]() $1\leq i\leq n$
, and
$1\leq i\leq n$
, and
![]() $v_i^*=v_{i-n}$
when
$v_i^*=v_{i-n}$
when
![]() $n<i\leq 2n$
, is
$n<i\leq 2n$
, is
![]() $\mathfrak{p}(V)$
-invariant [Reference Moon9]. Then we have that
$\mathfrak{p}(V)$
-invariant [Reference Moon9]. Then we have that
where the sum runs over all
![]() $2k$
-multi-subsets
$2k$
-multi-subsets
![]() $I=(i_1,i_2,\dots ,i_{2k})$
of the index set
$I=(i_1,i_2,\dots ,i_{2k})$
of the index set
![]() $\{1,2,\dots ,2n\}$
with the property that
$\{1,2,\dots ,2n\}$
with the property that
![]() $|i_1-i_2|=|i_3-i_4|=\dots =|i_{2k-1}-i_{2k}|=n$
. As the action of
$|i_1-i_2|=|i_3-i_4|=\dots =|i_{2k-1}-i_{2k}|=n$
. As the action of
![]() $\operatorname {\mathfrak{p}}(V)$
on
$\operatorname {\mathfrak{p}}(V)$
on
![]() $V^{\otimes 2k}$
commutes with the action of
$V^{\otimes 2k}$
commutes with the action of
![]() $S_{2k}$
, all the
$S_{2k}$
, all the
![]() $2k$
-tensors
$2k$
-tensors
![]() ${\theta _\sigma :=\sigma \circ c^{\otimes k}}$
are also
${\theta _\sigma :=\sigma \circ c^{\otimes k}}$
are also
![]() $\operatorname {\mathfrak{p}}(V)$
invariants for every
$\operatorname {\mathfrak{p}}(V)$
invariants for every
![]() $\sigma \in S_{2k}$
. We have that
$\sigma \in S_{2k}$
. We have that
 $$ \begin{align*} \begin{aligned} \theta_{\sigma^{-1}}=\sum_I (-1)^{\gamma(I,\sigma)+(|i_1|+|i_3|+\dots+|i_{2k-1}|)}(v_{i_{\sigma(1)}}\otimes v_{i_{\sigma(2)}}) &\otimes (v_{i_{\sigma(3)}}\otimes v_{i_{\sigma(4)}})\\ &\otimes\dots\otimes (v_{i_{\sigma(2k-1)}}\otimes v_{i_{\sigma(2k)}}), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \theta_{\sigma^{-1}}=\sum_I (-1)^{\gamma(I,\sigma)+(|i_1|+|i_3|+\dots+|i_{2k-1}|)}(v_{i_{\sigma(1)}}\otimes v_{i_{\sigma(2)}}) &\otimes (v_{i_{\sigma(3)}}\otimes v_{i_{\sigma(4)}})\\ &\otimes\dots\otimes (v_{i_{\sigma(2k-1)}}\otimes v_{i_{\sigma(2k)}}), \end{aligned} \end{align*} $$
where I is as described above, and
![]() $\gamma (I,\sigma )$
is the sign resulting from the action of
$\gamma (I,\sigma )$
is the sign resulting from the action of
![]() $\sigma ^{-1}$
on
$\sigma ^{-1}$
on
![]() $v_I=v_{i_1}\otimes \dots \otimes v_{i_{2k}}$
. It is known that the space
$v_I=v_{i_1}\otimes \dots \otimes v_{i_{2k}}$
. It is known that the space
![]() $(V^{\otimes 2k})^{\operatorname {\mathfrak{p}}(V)}$
is spanned by the set
$(V^{\otimes 2k})^{\operatorname {\mathfrak{p}}(V)}$
is spanned by the set
![]() $\{\theta _\sigma \colon \sigma \in S_{2k}\}$
(see [Reference Deligne, Lehrer and Zhang4],[Reference Sergeev19]).
$\{\theta _\sigma \colon \sigma \in S_{2k}\}$
(see [Reference Deligne, Lehrer and Zhang4],[Reference Sergeev19]).
We have a
![]() $\operatorname {\mathrm{\mathfrak{p}}}(V)$
-module isomorphism
$\operatorname {\mathrm{\mathfrak{p}}}(V)$
-module isomorphism
![]() $\phi _1\colon V\otimes V\cong \mathfrak{gl}(V)$
which sends
$\phi _1\colon V\otimes V\cong \mathfrak{gl}(V)$
which sends
![]() $v_i\otimes v_{i+n}$
to
$v_i\otimes v_{i+n}$
to
![]() $(-1)^{|i|}E_{i,i}$
and
$(-1)^{|i|}E_{i,i}$
and
![]() $v_{i+n}\otimes v_i$
to
$v_{i+n}\otimes v_i$
to
![]() $(-1)^{|i+n|}E_{i+n,i+n}$
for
$(-1)^{|i+n|}E_{i+n,i+n}$
for
![]() $1\leq i\leq n$
. There is a surjective homomorphism
$1\leq i\leq n$
. There is a surjective homomorphism
![]() $\phi _2\colon \mathfrak{gl}(V)\to \mathfrak{p}(V)$
, that sends a basis vector
$\phi _2\colon \mathfrak{gl}(V)\to \mathfrak{p}(V)$
, that sends a basis vector
![]() $E_{i,j}$
of
$E_{i,j}$
of
![]() $\mathfrak{gl}(V) $
to a certain basis vector of
$\mathfrak{gl}(V) $
to a certain basis vector of
![]() $\operatorname {\mathrm{\mathfrak{p}}}(V)$
by the following rule:
$\operatorname {\mathrm{\mathfrak{p}}}(V)$
by the following rule:
 $$ \begin{align} \phi_2(E_{i,j})&= \begin{cases} E_{i,j}-E_{j+n,i+n} \quad&\text{for}\quad 1\le i,j\le n\\ E_{i,j}-E_{j-n,i-n} \quad&\text{for}\quad n< i,j\le 2n\\ E_{i,j}+E_{j-n,i+n} \quad&\text{for}\quad 1\le i\le n\quad\text{and}\quad n<j\le 2n\\ E_{i,j}-E_{j+n,i-n} \quad&\text{for}\quad n< i\le 2n\quad\text{and}\quad 1\le j\le n. \end{cases} \end{align} $$
$$ \begin{align} \phi_2(E_{i,j})&= \begin{cases} E_{i,j}-E_{j+n,i+n} \quad&\text{for}\quad 1\le i,j\le n\\ E_{i,j}-E_{j-n,i-n} \quad&\text{for}\quad n< i,j\le 2n\\ E_{i,j}+E_{j-n,i+n} \quad&\text{for}\quad 1\le i\le n\quad\text{and}\quad n<j\le 2n\\ E_{i,j}-E_{j+n,i-n} \quad&\text{for}\quad n< i\le 2n\quad\text{and}\quad 1\le j\le n. \end{cases} \end{align} $$
We denote the composition
![]() $\phi _2\circ \phi _1\colon V\otimes V\to \operatorname {\mathrm{\mathfrak{p}}}(V)$
by
$\phi _2\circ \phi _1\colon V\otimes V\to \operatorname {\mathrm{\mathfrak{p}}}(V)$
by
![]() $\phi $
. Then,
$\phi $
. Then,
 $$ \begin{align} \phi(v_i\otimes v_j)&= \begin{cases} (-1)^{|i|}E_{i,j+n}+E_{j,i+n}\quad&\text{for}\quad 1\le i,j\le n\\ (-1)^{|i|}E_{i,j-n}-E_{j,i-n}\quad&\text{for}\quad n< i,j\le 2n\\ (-1)^{|i|}E_{i,j-n}-E_{j,i+n} \quad&\text{for}\quad 1\le i\le n\quad\text{and}\quad n<j\le 2n\\ (-1)^{|i|}E_{i,j+n}-E_{j,i-n} \quad&\text{for}\quad n<i\le 2n\quad\text{and}\quad 1\le j\le n. \end{cases} \end{align} $$
$$ \begin{align} \phi(v_i\otimes v_j)&= \begin{cases} (-1)^{|i|}E_{i,j+n}+E_{j,i+n}\quad&\text{for}\quad 1\le i,j\le n\\ (-1)^{|i|}E_{i,j-n}-E_{j,i-n}\quad&\text{for}\quad n< i,j\le 2n\\ (-1)^{|i|}E_{i,j-n}-E_{j,i+n} \quad&\text{for}\quad 1\le i\le n\quad\text{and}\quad n<j\le 2n\\ (-1)^{|i|}E_{i,j+n}-E_{j,i-n} \quad&\text{for}\quad n<i\le 2n\quad\text{and}\quad 1\le j\le n. \end{cases} \end{align} $$
The map
![]() $\phi $
induces an epimorphism
$\phi $
induces an epimorphism
![]() $\phi ^{\otimes k}\colon (V\otimes V)^{\otimes k}=V^{\otimes 2k}\to \operatorname {\mathrm{\mathfrak{p}}}(V)^{\otimes k}$
defined by
$\phi ^{\otimes k}\colon (V\otimes V)^{\otimes k}=V^{\otimes 2k}\to \operatorname {\mathrm{\mathfrak{p}}}(V)^{\otimes k}$
defined by
which further induces a surjective map
![]() $\eta $
on the
$\eta $
on the
![]() $\operatorname {\mathrm{\mathfrak{p}}}(V)$
-invariants:
$\operatorname {\mathrm{\mathfrak{p}}}(V)$
-invariants:
We now calculate the image of the element
![]() $c\in V\otimes V$
under
$c\in V\otimes V$
under
![]() $\phi $
. Using formula (6.3), we find that
$\phi $
. Using formula (6.3), we find that
 $$ \begin{align*} \phi(c)&= \phi\Big(\sum_{i=1}^n(-1)^{|i|}v_i\otimes v_{i+n}\Big)+\phi\Big(\sum_{j=1}^n (-1)^{|j+n|}v_{j+n}\otimes v_j\Big)\\ &=\sum_{i=1}^n(E_{i,i}-E_{n+i,n+i})+\sum_{j=1}^n(E_{n+j,n+j}-E_{j,j})=0. \end{align*} $$
$$ \begin{align*} \phi(c)&= \phi\Big(\sum_{i=1}^n(-1)^{|i|}v_i\otimes v_{i+n}\Big)+\phi\Big(\sum_{j=1}^n (-1)^{|j+n|}v_{j+n}\otimes v_j\Big)\\ &=\sum_{i=1}^n(E_{i,i}-E_{n+i,n+i})+\sum_{j=1}^n(E_{n+j,n+j}-E_{j,j})=0. \end{align*} $$
Therefore,
![]() $\eta (c^{\otimes k})=\phi ^{\otimes k}(c^{\otimes k})=0$
. Since the action of
$\eta (c^{\otimes k})=\phi ^{\otimes k}(c^{\otimes k})=0$
. Since the action of
![]() $\operatorname {\mathrm{\mathfrak{p}}}(V)$
is compatible with the action of the symmetric group
$\operatorname {\mathrm{\mathfrak{p}}}(V)$
is compatible with the action of the symmetric group
![]() $S_{2k}$
on
$S_{2k}$
on
![]() $V^{\otimes 2k}$
we conclude that
$V^{\otimes 2k}$
we conclude that
![]() $\eta (\theta _{\sigma ^{-1}})=0$
for every
$\eta (\theta _{\sigma ^{-1}})=0$
for every
![]() $\sigma \in S_{2k}$
. This means
$\sigma \in S_{2k}$
. This means
![]() $(\operatorname {\mathrm{\mathfrak{p}}}(V)^{\otimes k})^{\operatorname {\mathrm{\mathfrak{p}}}(V)}=0$
, for every positive integer k, and consequently,
$(\operatorname {\mathrm{\mathfrak{p}}}(V)^{\otimes k})^{\operatorname {\mathrm{\mathfrak{p}}}(V)}=0$
, for every positive integer k, and consequently,
![]() $T(\operatorname {\mathrm{\mathfrak{p}}}(V))^{\operatorname {\mathrm{\mathfrak{p}}}(V)}=\mathbb C$
. Thus by Proposition 3.1, we obtain the following.
$T(\operatorname {\mathrm{\mathfrak{p}}}(V))^{\operatorname {\mathrm{\mathfrak{p}}}(V)}=\mathbb C$
. Thus by Proposition 3.1, we obtain the following.
Proposition 6.1 Let A be an associative commutative finitely generated
![]() $\mathbb C$
-algebra with identity. Then
$\mathbb C$
-algebra with identity. Then
![]() $U(\operatorname {\mathrm{\mathfrak{p}}}(V)\otimes A)^{\operatorname {\mathrm{\mathfrak{p}}}(V)}=\mathbb C$
. In particular, for
$U(\operatorname {\mathrm{\mathfrak{p}}}(V)\otimes A)^{\operatorname {\mathrm{\mathfrak{p}}}(V)}=\mathbb C$
. In particular, for
![]() $A=\mathbb C$
, we get that the center of
$A=\mathbb C$
, we get that the center of
![]() $U(\mathfrak{p}(V))$
consists only of scalars.
$U(\mathfrak{p}(V))$
consists only of scalars.
Acknowledgements
We would like to thank Preena Samuel for some useful discussions. We would also like to thank the referee for many valuable comments and suggestions on this article.