Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-06T16:05:14.132Z Has data issue: false hasContentIssue false
  • English
  • Français

Galois Groups of Even Sextic Polynomials

Part of: Computational number theory Field extensions

Published online by Cambridge University Press:  12 December 2019

Chad Awtrey  and
Peter Jakes
Chad Awtrey
Affiliation:
Department of Mathematics and Statistics, Elon University, Campus Box 2320, Elon, NC 27244 Email: cawtrey@elon.edupjakes@elon.edu
Peter Jakes
Affiliation:
Department of Mathematics and Statistics, Elon University, Campus Box 2320, Elon, NC 27244 Email: cawtrey@elon.edupjakes@elon.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 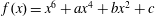$f(x)=x^{6}+ax^{4}+bx^{2}+c$ be an irreducible sextic polynomial with coefficients from a field 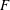$F$ of characteristic 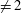$\neq 2$, and let $g(x)=x^{3}+ax^{2}+bx+c$. We show how to identify the conjugacy class in 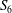$S_{6}$ of the Galois group of 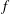$f$ over 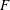$F$ using only the discriminants of 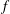$f$ and 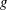$g$ and the reducibility of a related sextic polynomial. We demonstrate that our method is useful for producing one-parameter families of even sextic polynomials with a specified Galois group.

Keywords

even polynomialssexticGalois group

MSC classification

Primary: 11Y40: Algebraic number theory computations
Secondary: 12F10: Separable extensions, Galois theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 3 , September 2020 , pp. 670 - 676
Check for updates
Copyright
© Canadian Mathematical Society 2019

References

Butler, G. and McKay, J., The transitive groups of degree up to eleven. Comm. Algebra 11(1983), no. 8, 863–911. https://doi.org/10.1080/00927878308822884CrossRefGoogle Scholar
Cohen, H., A course in computational algebraic number theory. Graduate Texts in Mathematics, 138, Springer-Verlag, Berlin, 1993. https://doi.org/10.1007/978-3-662-02945-9CrossRefGoogle Scholar
Eloff, D., Spearman, B. K., and Williams, K. S., A 4-sextic fields with a power basis. Missouri J. Math. Sci. 19(2007), no. 3, 188–194.10.35834/mjms/1316032976Google Scholar
Harrington, J. and Jones, L., The irreducibility of power compositional sextic polynomials and their Galois groups. Math. Scand. 120(2017), no. 2, 181–194. https://doi.org/10.7146/math.scand.a-25850CrossRefGoogle Scholar
Ide, J. and Jones, L., Infinite families of A 4-sextic polynomials. Canad. Math. Bull. 57(2014), no. 3, 538–545. https://doi.org/10.4153/CMB-2014-008-1CrossRefGoogle Scholar
Kappe, L.-C. and Warren, B., An elementary test for the Galois group of a quartic polynomial. Amer. Math. Monthly 96(1989), no. 2, 133–137. https://doi.org/10.2307/2323198CrossRefGoogle Scholar
Smith, G. W., Some polynomials over Q (t) and their Galois groups. Math. Comp. 69(2000), no. 230, 775–796. https://doi.org/10.1090/S0025-5718-99-01160-6CrossRefGoogle Scholar
Soicher, L., The computation of Galois groups. Master’s thesis, Concordia University, Montreal, 1981.Google Scholar