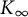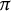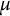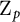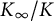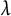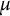1 Introduction
Let p be a prime, and let F be a finite extension of
$\mathbb {Q}_p$
, with ring of integers
$\mathcal {O}$
and uniformizing element
$\pi $
. Suppose that
$V_1$
and
$V_2$
denote two F-representations of the absolute Galois group of a fixed number field K, and that
$T_1 \subseteq V_1$
and
$T_2 \subseteq V_2$
are two Galois stable sublattices. We let
$A_1 = V_1/T_1$
and
$A_2 = V_2/T_2$
and we assume that
$A_1[\pi ^l]$
and
$A_2[\pi ^l]$
are isomorphic as Galois modules for some
$l \in \mathbb {N}$
. In this article, we study the Pontryagin duals of the fine Selmer groups of
$A_1$
and
$A_2$
over (strongly) admissible p-adic Lie extensions, and we compare their ranks and Iwasawa invariants.
By an admissible p-adic Lie extension, we mean a normal extension
$K_\infty /K$
such that only finitely many primes of K ramify in
$K_\infty $
and such that
${G = \textrm {Gal}(K_\infty /K)}$
is a compact, pro-p, p-adic Lie group without p-torsion. For any finite set
$\Sigma $
of primes of K, an admissible p-adic Lie extension
$K_\infty /K$
shall be called strongly
$\Sigma $
-admissible if
$K_\infty $
contains a
$\mathbb {Z}_p$
-extension L of K such that no prime
$v \in \Sigma $
and no prime of K which ramifies in
$K_\infty $
is completely split in L (see also Section 2; in the literature usually only the case of the cyclotomic
$\mathbb {Z}_p$
-extension
$L = K_\infty ^c$
of K is considered, see for example [Reference LimLim17a]—in this article, we typically focus on complementary cases).
The comparison of Selmer groups of congruent p-adic representations goes back to the seminal work of Greenberg and Vatsal (see [Reference Greenberg and VatsalGV00]), who considered elliptic curves defined over
$\mathbb {Q}$
with good and ordinary reduction at some odd prime p (in fact the Selmer groups were studied more generally in the context of Galois representations). The main issue dealt with in the article [Reference Greenberg and VatsalGV00] is the relation between algebraically and analytically ( i.e., via p-adic L-functions) defined Iwasawa invariants. Roughly speaking, Greenberg and Vatsal treated the
$\mu = 0$
case and only considered the cyclotomic
$\mathbb {Z}_p$
-extension.
Over the last years, the results in [Reference Greenberg and VatsalGV00] have been generalized in many different ways and we only mention a few exemplary results. For the comparison of analytical invariants of congruent elliptic curves defined over
$\mathbb {Q}$
, we refer to [Reference HatleyHat17]; in the present article, we stick to the algebraic side. Most authors have focused on the
$\mu = 0$
setting from [Reference Greenberg and VatsalGV00]: if
$\mu = 0$
for the Selmer group of
$A_1$
, then the same holds true for the Selmer group of
$A_2$
. Moreover, over
$\mathbb {Z}_p$
-extensions one can then often prove equality of
$\lambda $
-invariants (we refer to Section 2 for the definition of the Iwasawa invariants). Analogous results have been obtained for Selmer groups of Galois representations over the anticyclotomic
$\mathbb {Z}_p$
-extension of an imaginary quadratic base field K (see [Reference Hatley and LeiHL19]) and for signed Selmer groups of Galois representations over the cyclotomic
$\mathbb {Z}_p$
-extension of a number field in the non-ordinary setting (see, e.g., [Reference PonsinetPon20, Section 3]). Moreover, there exist vast generalisations to Selmer groups attached to families of modular forms (see, e.g., [Reference Emerton, Pollack and WestonEPW06, Reference SharmaSha09, Reference BarthBar13]).
Situations where
$\mu \ne 0$
have been studied, for example, in [Reference Ahmed and ShekharAS15, Reference Barman and SaikiaBS10]. In these articles, the authors considered congruent elliptic curves
$E_1$
and
$E_2$
over
$\mathbb {Q}$
at primes
$p> 2$
of good ordinary reduction. Under the additional assumption that
$E_j(\mathbb {Q})[p^\infty ] = \{0\}$
for
$j \in \{ 1,2 \}$
, the authors deduced the equality of
$\lambda $
-invariants (see [Reference Ahmed and ShekharAS15]), respectively
$\mu $
-invariants (see [Reference Barman and SaikiaBS10]) from a sufficiently high congruence relation
$E_1[p^l] \cong E_2[p^l]$
. Much more generally, Lim studied the Selmer groups of Galois representations over admissible p-adic Lie extensions in [Reference LimLim17a]. In particular, he obtained the following result: if
$A_1$
and
$A_2$
are attached to two p-adic Galois representations and
$A_1[\pi ^l] \cong A_2[\pi ^l]$
for some sufficiently large l, then the
$\pi $
-primary submodules of the Pontryagin duals of the associated Selmer groups are pseudo-isomorphic. This comparison statement is much stronger than the previous results. We are able to prove a similar result for fine Selmer groups (see Theorem 1.1). Lim also studied strict Selmer groups, as introduced by Greenberg in [Reference GreenbergGre89]. These strict Selmer groups of p-adic Galois representations have also been studied by Hachimori in [Reference HachimoriHac11].
In the present article, our main objective is the comparison of fine Selmer groups of congruent p-adic Galois representations over admissible p-adic Lie extensions. These objects have previously been investigated by Lim and Sujatha in [Reference Lim and SujathaLS18], who obtained a comparison result in the
$\mu = 0$
setting under a stronger condition on the decomposition of primes in
$K_\infty /K$
(see [Reference Lim and SujathaLS18, Theorem 3.5]). Moreover, Jha studied in [Reference JhaJha12] the invariance of several arithmetic properties of fine Selmer groups of modular forms in a branch of a Hida family in the
$\mu = 0$
setting.
Our first main result is an analogue of the strong result of Lim in [Reference LimLim17a] for fine Selmer groups over strongly admissible p-adic Lie extensions, which is not restricted to the case
$\mu = 0$
. We note that it is conjectured that the
$\mu $
-invariant of fine Selmer groups over the cyclotomic
$\mathbb {Z}_p$
-extension of any number field should vanish (see [Reference Coates and SujathaCS05, Conjecture A]), and this propagates to p-adic Lie extensions containing the cyclotomic
$\mathbb {Z}_p$
-extension (cf. e.g., [Reference LimLim15]). On the other hand, fine Selmer groups with nonzero
$\mu $
-invariant do occur naturally. For example, let K be an imaginary-quadratic number field, and let
$K_\infty ^a$
be the anticyclotomic
$\mathbb {Z}_p$
-extension of K. Choose at least
$t = 2 (p-1)+1$
primes
$\mathfrak {q}_1, \ldots , \mathfrak {q}_{t}$
of K which do not split in
$K/\mathbb {Q}$
, and let
$\alpha \in K$
be divisible by each of theses primes exactly once. Then Iwasawa proved that the classical Iwasawa
$\mu $
-invariant of the shifted anticyclotomic
$\mathbb {Z}_p$
-extension
$K_\infty ' = K_\infty ^a \cdot K'$
of
$K' := K(\mu _p, \sqrt [p]{\alpha })$
is nonzero (see [Reference LangLan90, Theorems 13.5.1 and 13.5.2]). Now let A be any abelian variety defined over K such that each prime of bad reduction is coprime with p and splits in
$K/\mathbb {Q}$
. Then each of these primes is finitely split in
$K_\infty '/K'$
by work of Brink (see [Reference BrinkBri07, Theorem 2]), and the same holds for the primes above p. Now, we enlarge the base field further and let
$L = K'(A[p])$
and
$L_\infty = K_\infty ' L$
. It then follows from work of Lim and Murty (see [Reference Lim and Kumar MurtyLKM16, Theorem 5.1]) that the
$\mu $
-invariant of the fine Selmer group of A over
$L_\infty $
is nontrivial. In fact, with a little more work, one can produce examples with arbitrarily large
$\mu $
-invariant (see [Reference KunduKun21, Sections 3 and 4]).
For an admissible p-adic Lie extension
$K_\infty $
of K and an F-representation V of the absolute Galois group of K, we let T denote a Galois stable
$\mathcal {O}$
-lattice in V and set
${A =V/T}$
. Let
$\Sigma $
be a finite set of primes of K containing all the primes above p and each prime where V is ramified. Then
$Y_{A, \Sigma }^{(K_\infty )}$
shall denote the Pontryagin dual of the
$\Sigma $
-fine Selmer group of A over
$K_\infty $
(see Section 2.2 for the precise definition).
Theorem 1.1 Let
$A_1$
and
$A_2$
be associated with two F-representations
$V_1$
and
$V_2$
of the absolute Galois group of the number field K. If
$p = 2$
, then we assume that K is totally imaginary. Let
$\Sigma $
be a finite set of primes of K which contains the primes above p and the sets of primes of K where either
$V_1$
or
$V_2$
is ramified. Let
$K_\infty /K$
be a strongly
$\Sigma $
-admissible p-adic Lie extension, and let
$G = \textrm {Gal}(K_\infty /K)$
.
We let
$r_j = \textrm {rank}_{\mathcal {O}[[G]]}\left (Y_{A_j, \Sigma }^{(K_\infty )}\right )$
,
$1 \le j \le 2$
. Let l be the minimal integer such that
$\left (\pi ^l Y_{A_1, \Sigma }^{(K_\infty )}\right )[\pi ]$
is pseudo-null over
$\mathcal {O}[[G]]$
in the sense of Section
2.1
. Then the following statements hold.
-
(a) If
$A_1[\pi ^l]\cong A_2[\pi ^l]$
as
$G_{K}$
-modules and
$r_2 \le r_1$
, then
$\mu \left (Y_{A_1, \Sigma }^{(K_\infty )}\right )\le \mu \left (Y_{A_2, \Sigma }^{(K_\infty )}\right )$
. -
(b) If
$A_1[\pi ^{l+1}]\cong A_2[\pi ^{l+1}]$
, then
$r_2 \le r_1$
. If moreover
$r_2 = r_1$
, then and the modules
$$\begin{align*}\mu\left(Y_{A_1, \Sigma}^{(K_\infty)}\right) = \mu\left(Y_{A_2, \Sigma}^{(K_\infty)}\right)\\[-15pt]\end{align*}$$
$Y_{A_1, \Sigma }^{(K_\infty )}[\pi ^{\infty }]$
and
$Y_{A_2, \Sigma }^{(K_\infty )}[\pi ^{\infty }]$
are pseudo-isomorphic in the sense of Section
2.1
.
-
(c) In particular, if
$A_1[\pi ]\cong A_2[\pi ]$
and
$r_2 = r_1$
, then
${\mu \left (Y_{A_1, \Sigma }^{(K_\infty )}\right )=0}$
holds if and only if
$\mu \left (Y_{A_2, \Sigma }^{(K_\infty )}\right )=0$
. -
(d) If
$A_1[\pi ^{l+1}] \cong A_2[\pi ^{l+1}]$
for some integer l such that both
$\left (\pi ^l Y_{A_j, \Sigma }^{(K_\infty )}\right )[\pi ]$
,
${1 \le j \le 2}$
, are pseudo-null, then
$r_2 = r_1$
and
${\mu \left (Y_{A_1, \Sigma }^{(K_\infty )}\right ) = \mu \left (Y_{A_2, \Sigma }^{(K_\infty )}\right )}$
.
Note that
$Y_{A,\Sigma }^{(K_\infty )}$
may contain quite complicated pseudo-null submodules and it may be difficult in practice to determine the right value for l and to prove the isomorphisms
$A_1[\pi ^l] \cong A_2[\pi ^l]$
needed in Theorem 1.1 (see [Reference Barman and SaikiaBS10, Section 3] for a concrete example for 9-congruent elliptic curves)—if we want to apply Theorem 1.1 in a non-cyclotomic setting, then the additional problem occurs of how to determine or at least estimate one of the two
$\mu $
-invariants in order to derive information about the second one.
The weak Leopoldt conjecture for A over
$K_\infty $
holds if and only if
$Y_{A, \Sigma }^{(K_\infty )}$
is a torsion
$\mathcal {O}[[G]]$
-module (see also [Reference LimLim17b, Lemma 7.1]). The authors are not aware of any example where this conjecture is known to fail. Nevertheless, we paid attention to proving Theorem 1.1 also in the higher rank setting, since this allows a formulation which is unconditional.
Theorem 1.1 will be proved in Section 3.1. The basic idea of the proof is to relate the
$\pi ^k$
-torsion subgroups of the fine Selmer groups of
$A_j$
,
$k \in \mathbb {N}$
, to certain
$\pi ^k$
-fine Selmer groups (defined in Section 2) which depend only on
$A_j[\pi ^k]$
. In the case of admissible p-adic Lie extensions
$K_\infty /K$
which are not strongly admissible, we can derive similar results under the hypothesis that
$A_j(K_v)[\pi ]=\{0\}$
for every
$v \in \Sigma $
and
$j \in \{1,2\}$
(see Theorem 3.7). In order to obtain this result, we use an argument which goes back to the paper of Greenberg and Vatsal (see [Reference Greenberg and VatsalGV00, Proposition 2.8]). It also appears in work of Mazur and Rubin (see [Reference Mazur and RubinMR04, Lemma 3.5.3]) and has been used in, e.g., [Reference Barman and SaikiaBS10, Reference PonsinetPon20]. This approach is of particular interest if one wants to treat
$\mathbb {Z}_p$
-extensions
$K_\infty $
of K in which some prime above p or a ramified prime is completely split. In the special case of
$\mathbb {Z}_p$
-extensions, and under the additional hypotheses on the
$\pi $
-torsion which have been mentioned above, we can in fact go one step further and obtain results on the
$\lambda $
-invariants, provided that the
$\mathcal {O}[[G]]$
-modules
$Y_{A_i, \Sigma }^{(K_\infty )}$
both are torsion:
Theorem 1.2 In the setting of Theorem
3.7
, suppose that
$G \cong \mathbb {Z}_p$
and that both ranks
$r_1$
and
$r_2$
are zero. Then, in addition to the assertions of Theorem
3.7
, the following two statements hold:
-
(a) If
$l \in \mathbb {N}$
is large enough such that
$\left (\pi ^l Y_{A_1, \Sigma }^{(K_\infty )}\right )[\pi ] = \{0\}$
and
${A_1[\pi ^{l+1}] \cong A_2[\pi ^{l+1}]}$
, then
${\lambda \left (Y_{A_2, \Sigma }^{(K_\infty )}\right ) \le \lambda \left (Y_{A_1, \Sigma }^{(K_\infty )}\right )}$
. -
(b) If
$A_1[\pi ^{l+1}] \cong A_2[\pi ^{l+1}]$
for some l such that both
$\left (\pi ^l Y_{A_j, \Sigma }^{(K_\infty )}\right )[\pi ] = \{0\}$
,
${1 \le j \le 2}$
, then
${\lambda \left (Y_{A_1, \Sigma }^{(K_\infty )}\right ) = \lambda \left (Y_{A_2, \Sigma }^{(K_\infty )}\right )}$
.
We remark that we do not have to assume that the
$\mu $
-invariants vanish in Theorem 1.2.
Finally, in Section 4, we consider certain abelian non-p-extensions
$K_\infty $
of K. In two different settings (inspired by the two different cases treated in Section 3), we compare the
$\mathcal {O}$
-ranks of
$Y_{A_1, \Sigma }^{(K_\infty )}$
and
$Y_{A_2, \Sigma }^{(K_\infty )}$
and derive (in-)equalities analogous to those in Theorem 1.2. We also remark that the group ring
$\mathcal {O}[[\textrm {Gal}(K_\infty /K)]]$
is not well-behaved in this situation and the
$\mathcal {O}$
-rank is the natural substitute for the notion of Iwasawa
$\lambda $
-invariants.
2 Background and notation
2.1 Admissible p-adic Lie extensions and Iwasawa modules
We fix once and for all a rational prime p. Let F be a finite extension of
$\mathbb {Q}_p$
. We denote its ring of integers by
$\mathcal {O}$
and a generator of its maximal ideal by
$\pi $
. Note that
$\mathcal {O}/(\pi )$
is a finite field with
$q = p^f$
elements, where f is the inertia degree of p in
$F/\mathbb {Q}_p$
. For any Noetherian
$\mathcal {O}$
-module G, we denote by
$G[\pi ^\infty ]$
the subgroup of
$\pi $
-power torsion elements; for any
$i \in \mathbb {N}$
,Footnote
1
$G[\pi ^i]$
shall denote the subgroup of elements which are annihilated by
$\pi ^i$
.
In this article, an admissible p-adic Lie extension
$K_\infty $
of a number field K will always be a normal extension
$K_\infty /K$
such that
-
•
$G := \textrm {Gal}(K_\infty /K)$
is a compact pro-
$p, p$
-adic Lie group, -
•
$G[p^\infty ] = \{0\}$
, i.e., G does not contain any p-torsion elements, and -
• the set
$S_{\textrm {ram}}(K_\infty /K)$
of primes of K ramifying in
$K_\infty $
is finite.
Let
$\Sigma $
be a finite set of finite primes of K. The pro-p-extension
$K_\infty /K$
is called strongly
$\Sigma $
-admissible if it is admissible and moreover contains a
$\mathbb {Z}_p$
-extension L of K such that no prime in
$\Sigma \cup S_{\textrm {ram}}(K_{\infty }/K)$
is completely split in L. In this case, we fix L and denote by
$H \subseteq G$
the subgroup fixing L. Note that any strongly
$\Sigma $
-admissible p-adic Lie extension
$K_\infty /K$
is strongly
$\Sigma \cup S_{\textrm {ram}}(K_{\infty }/K)$
-admissible. By abuse of notation, we always assume that
$\Sigma $
contains
$S_{\textrm {ram}}(K_{\infty }/K)$
if
$K_{\infty }/K$
is a strongly
$\Sigma $
-admissible p-adic Lie extension.
An admissible p-adic Lie extension
$K_\infty /K$
is called strongly admissible if it contains the cyclotomic
$\mathbb {Z}_p$
-extension of K. Since no prime of K splits completely in the cyclotomic
$\mathbb {Z}_p$
-extension, a strongly admissible p-adic Lie extension is strongly
$\Sigma $
-admissible for every finite set
$\Sigma $
.
If
$K_\infty /K$
is an admissible p-adic Lie extension, then the completed group ring
${\mathcal {O}[[G]] = \mathcal {O} \otimes _{\mathbb {Z}_p} \mathbb {Z}_p[[G]]}$
is a Noetherian domain (see [Reference Coates and HowsonCH01, Theorem 2.3]), and we can define the
$\mathcal {O}[[G]]$
-rank of a finitely generated
$\mathcal {O}[[G]]$
-module X by
$$ \begin{align*} \textrm{rank}_{\mathcal{O}[[G]]}(X) = \dim_{\mathcal{F}(G)}(\mathcal{F}(G) \otimes_{\mathcal{O}[[G]]} X), \end{align*} $$
where
$\mathcal {F}(G)$
denotes the skew field of fractions of
$\mathcal {O}[[G]]$
(see [Reference Goodearl and WarfieldGW04, Chapter 10]).
A finitely generated
$\mathcal {O}[[G]]$
-module X is called pseudo-null if X is torsion and
$\textrm {Ext}_{\mathcal {O}[[G]]}^1(X, \mathcal {O}[[G]]) = \{0\}$
. Moreover, following Howson (see [Reference HowsonHow02, (33)]), we define the
$\mu $
-invariant of a finitely generated
$\mathcal {O}[[G]]$
-module X as
$$ \begin{align} \mu(X) = \sum_{i \ge 0} \textrm{rank}_{\mathbb{F}_q[[G]]}(\pi^i X[\pi^\infty]/\pi^{i+1} X[\pi^\infty]); \end{align} $$
this is a finite sum as X is Noetherian.
Remark 2.1 Let X be a Noetherian
$\pi $
-primary
$\mathcal {O}[[G]]$
-module. Then there exists an integer m such that
$\pi ^mX=\{0\}$
. Suppose now that
${\textrm {rank}_{\mathbb {F}_q[[G]]}( X[\pi ])=0}$
. Then there exists an annihilator
${f\in \mathcal {O}[[G]]\setminus \pi \mathcal {O}[[G]]}$
of
$X[\pi ]$
. In particular,
$$\begin{align*}\pi^{m-1}fX=\{0\} \quad \text{ and } \quad \pi^{m-2}fX\subseteq X[\pi]. \end{align*}$$
Thus, we inductively obtain that
${f^mX=\{0\}}$
. Therefore
${\textrm {rank}_{\mathbb {F}_q[[G]]}(X/\pi X)=0}$
.
Lemma 2.2 (Lim)
Let G be a compact pro-
$p p$
-adic Lie group without p-torsion, and let X be a finitely generated
$\mathcal {O}[[G]]$
-module. Then
$$ \begin{align*} \textrm{rank}_{\mathbb{F}_q[[G]]}(X/\pi X) = \textrm{rank}_{\mathbb{F}_q[[G]]}(X[\pi]) + \textrm{rank}_{\mathcal{O}[[G]]}(X). \end{align*} $$
Proof. This is [Reference LimLim17b, Proposition 4.12].▪
Corollary 2.3 Let G be as in Lemma
2.2
, and let X be a finitely generated
$\mathcal {O}[[G]]$
-module of rank r. Then
$$\begin{align*}\textrm{rank}_{\mathbb{F}_q[[G]]}(\pi^i X[\pi^\infty]/\pi^{i+1}X[\pi^\infty]) = \textrm{rank}_{\mathbb{F}_q[[G]]}(\pi^iX/\pi^{i+1}X) - r\end{align*}$$
for each
$i \in \mathbb {N}$
.
Proof. By applying Lemma 2.2 to the
$\mathcal {O}[[G]]$
-modules
$\pi ^i X$
and
$\pi ^i X[\pi ^\infty ]$
, we obtain that
$$\begin{align*}\textrm{rank}_{\mathbb{F}_q[[G]]}(\pi^iX/\pi^{i+1}X) = \textrm{rank}_{\mathbb{F}_q[[G]]}((\pi^iX)[\pi]) + \textrm{rank}_{\mathcal{O}[[G]]}(\pi^i X)\end{align*}$$
and
$$\begin{align*}\textrm{rank}_{\mathbb{F}_q[[G]]}(\pi^iX[\pi^\infty]/\pi^{i+1}X[\pi^\infty]) &= \textrm{rank}_{\mathbb{F}_q[[G]]}((\pi^iX[\pi^\infty])[\pi])\\ &\quad + \textrm{rank}_{\mathcal{O}[[G]]}(\pi^i X[\pi^\infty]). \end{align*}$$
Now
$(\pi ^i X)[\pi ] = (\pi ^i X[\pi ^\infty ])[\pi ]$
,
$\textrm {rank}_{\mathcal {O}[[G]]}(\pi ^iX) = r$
and
$\textrm {rank}_{\mathcal {O}[[G]]}(\pi ^iX[\pi ^\infty ]) = 0$
, and therefore, starting from the second equation,
$$ \begin{align*} \textrm{rank}_{\mathbb{F}_q[[G]]}(\pi^iX[\pi^\infty]/\pi^{i+1}X[\pi^\infty]) & = \textrm{rank}_{\mathbb{F}_q[[G]]}((\pi^iX[\pi^\infty])[\pi]) \\ & = \textrm{rank}_{\mathbb{F}_q[[G]]}((\pi^iX)[\pi]) \\ & = \textrm{rank}_{\mathbb{F}_q[[G]]}(\pi^iX/\pi^{i+1}X) - r.\\[-36pt] \end{align*} $$
▪
The most important class of admissible p-adic Lie extensions are the
$\mathbb {Z}_p$
-extensions. A
$\mathbb {Z}_p$
-extension
$K_\infty /K$
is a normal extension such that
$G = \textrm {Gal}(K_\infty /K)$
is isomorphic to the additive group of p-adic integers. In this special case, the theory of finitely generated
$\mathcal {O}[[G]]$
-modules is well understood: the completed group ring
$\mathcal {O}[[G]]$
is isomorphic to the ring
$\Lambda :=\mathcal {O}[[T]]$
of formal power series in one variable. Each finitely generated
$\Lambda $
-module X is pseudo-isomorphic to an elementary
$\Lambda $
-module of the form
$$\begin{align*}E_X = \Lambda^r \oplus \bigoplus_{i=1}^s \Lambda/(\pi^{e_i}) \oplus \bigoplus_{j = 1}^t \Lambda/(h_j), \end{align*}$$
where
$h_1, \ldots , h_t \in \Lambda $
are so-called distinguished polynomials. Here, pseudo-isomorphic means that there exists a
$\Lambda $
-module homomorphism
$\varphi : X \longrightarrow E_X$
with finite kernel and cokernel. One defines the (classical) Iwasawa invariants of X by
${\mu (X) := \sum _{i=1}^s e_i}$
and
${\lambda (X) := \sum _{j=1}^t \deg (h_j)}$
. This notation is well-defined since the classical
$\mu $
-invariant coincides with the invariant
$\mu (X)$
given in (2.1) in the special case of
$\mathbb {Z}_p$
-extensions:
Lemma 2.4 Let X be a finitely generated
$\Lambda $
-module. Then the classical Iwasawa
$\mu $
-invariant is equal to
$$ \begin{align*}\sum_{i=0}^{\infty} \textrm{rank}_{\mathbb{F}_q[[T]]}(\pi^i X[\pi^\infty] /\pi^{i+1}X[\pi^\infty]). \end{align*} $$
Proof. This proof is well-known (see, e.g., [Reference VenjakobVen02, Section 3.4]), but we recall it for the convenience of the reader. Let
$E_X$
be an elementary
$\Lambda $
-module that is pseudo-isomorphic to X. Then, we can write
$ E_X=\Lambda ^r \oplus \bigoplus _{i=1}^s\Lambda /(\pi ^{e_i})\oplus E_{\lambda }$
for a torsion
$\Lambda $
-module
$E_{\lambda }$
which is a finitely generated free
$\mathcal {O}$
-module. Therefore, the classical Iwasawa invariants can be computed as
$$ \begin{align*} \mu(X)=\mu( E_X)= \sum_{i=0}^{\infty}\vert \{k\mid e_k \ge i+1\}\vert=\sum_{i=0}^{\infty} \textrm{rank}_{\mathbb{F}_q[[T]]}(\pi^{i}X[\pi^\infty]/\pi^{i+1}X[\pi^\infty])\end{align*} $$
because
$$ \begin{align*} \textrm{rank}_{\mathbb{F}_q[[T]]}(\pi^iX[\pi^\infty]/\pi^{i+1}X[\pi^\infty]) & = \textrm{rank}_{\mathbb{F}_q[[T]]}(\pi^i E_X[\pi^\infty]/\pi^{i+1} E_X[\pi^\infty]) \\ & = \vert \{k \mid e_k \ge i+1\} \vert\end{align*} $$
for every
$i \in \mathbb {N}$
▪.
2.2 Fine Selmer groups
For any discrete
$\mathbb {Z}_p$
-module M, we define the Pontryagin dual of M as
$$ \begin{align*} M^\vee = \textrm{Hom}_{\textrm{cont}}(M, \mathbb{Q}_p/\mathbb{Z}_p) \end{align*} $$
(i.e., the set of continuous homomorphisms).
If K is a number field and v denotes any prime of K, then
$K_v$
will always denote the completion of K at v. We denote by
$G_K$
the Galois group
$\textrm {Gal}(\overline {K}/K)$
, where
$\overline {K}$
denotes a fixed algebraic closure of K. If M is any
$G_K$
-module, then we let
${H^i(K,M) := H^i(G_K,M)}$
denote the corresponding Galois cohomology groups,
$i \in \mathbb {N}$
. Moreover, if
$L/K$
is an algebraic extension, then we write
${H^i(L/K,M) = H^i(\textrm {Gal}(L/K),M)}$
for brevity.
Now fix a number field K. Let V be a finite dimensional F-vector space with a continuous action of
$\textrm {Gal}(\overline {K}/K)$
for some fixed algebraic closure
$\overline {K}$
of K. Let T be a Galois stable
$\mathcal {O}$
-lattice in V and write
$A=V/T$
. Note that, as an
$\mathcal {O}$
-module, A is isomorphic to
$(F/\mathcal {O})^d$
for some non-negative integer
$d=\textrm {dim}(V)$
. In particular,
$A = A[\pi ^\infty ]$
is
$\pi $
-primary, i.e., each element of the
$\mathcal {O}$
-module A is annihilated by some power of
$\pi $
. By abuse of terminology we will also refer to d as the dimension of A.
We denote by
$S_p$
and
$S_{\textrm {ram}}(A)$
the set of primes of K over p and the set of primes of K where V is ramified. For any algebraic extension
$L \supseteq K$
we denote by
$A(L)$
the maximal submodule of A on which
$\textrm {Gal}(\overline {K}/L)$
acts trivially. If
$L_v$
is the completion of a number field
$L\supseteq K$
at some prime v, then we denote by
$A(L_v)$
the maximal submodule of A on which the local absolute Galois group
$G_{L_v}$
acts trivially (here
$G_{L_v}$
is embedded canonically into the absolute Galois group
$G_L$
).
We mention an important and classical special case: let A be an abelian variety defined over the number field K. We assume that
$F = \mathbb {Q}_p$
, i.e.,
$\mathcal {O} = \mathbb {Z}_p$
. Let
${T = T_p(A) = \varprojlim _n A[p^n]}$
be the Tate module of A and
${V = T_p(A) \otimes _{\mathbb {Z}_p} \mathbb {Q}_p}$
; then
${V/T \cong A[p^\infty ]}$
. In this setting, for any field L as above, the group
$A(L)[p^\infty ]$
is the usual group of L-rational p-power torsion points on A. Moreover, the ramified primes correspond to the primes of K where A has bad reduction, by the criterion of Néron–Ogg–Shafarevich (see [Reference LangLan97, Theorem IV.4.1]).
For the number field K,
$A = V/T$
as above and a prime number p, we define, following [Reference Coates and SujathaCS05], the (
$\pi $
-primary part of the) fine Selmer group of A over K as
$$ \begin{align*} \textrm{Sel}_{0,A}(K) = \ker \left( H^1(K, A) \longrightarrow \prod_v H^1(K_{v}, A) \right).\end{align*} $$
In our applications, it will be more convenient to work with the following definition:
$$ \begin{align*} \textrm{Sel}_{0,A,\Sigma}(K) = \ker \left( H^1(K_\Sigma/K, A) \longrightarrow \prod_{v \in \Sigma} H^1(K_v, A) \right) \end{align*} $$
for suitable (usually finite) sets
$\Sigma $
of primes of K containing all the ramified primes of the representation V and all primes above p. Here, we let
$K_{\Sigma }$
be the maximal algebraic extension of K unramified outside the primes in
$\Sigma $
. If
$L\subseteq K_{\Sigma }$
is any, non-necessarily finite, extension, then we define
$$ \begin{align*}\textrm{Sel}_{0,A,\Sigma}(L)=\varinjlim_{K\subseteq L'\subseteq L}\textrm{Sel}_{0,A,\Sigma}(L'), \end{align*} $$
where
$L'$
runs through all finite subextensions
$K\subseteq L'\subseteq L$
. Here, we note that
$K_\Sigma = L^{\prime }_\Sigma $
, since
$L/K$
is unramified outside of
$\Sigma $
, and therefore each
$\textrm {Sel}_{0,A,\Sigma }(L')$
is a subgroup of
$H^1(K_\Sigma /K, A)$
.
A priori, this definition depends on the choice of
$\Sigma $
. But if the cyclotomic
$\mathbb {Z}_p$
-extension of K, denoted by
$K_{\infty }^c$
, is contained in L, then the definition becomes independent of the set
$\Sigma $
by a result of Sujatha and Witte (see [Reference Sujatha and WitteSW18, Section 3]). They also show that in this case the two definitions of the Selmer group given above coincide. In fact, their proof depends only on the fact that none of the primes in
$\Sigma $
is totally split in
$K^c_{\infty }/K$
. Therefore, the definition of the fine Selmer group does not depend on the choice of
$\Sigma $
if we consider strongly
$\Sigma $
-admissible extensions
$K_{\infty }/K$
.
Finally, we define
$\pi ^i$
-fine Selmer groups,
$i \in \mathbb {N}$
, as
$$ \begin{align*} \textrm{Sel}_{0,A[\pi^i],\Sigma}(K) = \ker \left( H^1(K_\Sigma/K, A[\pi^i]) \longrightarrow \prod_{v \in \Sigma} H^1(K_{v}, A[\pi^i]) \right),\end{align*} $$
where
$\Sigma $
is as above. Note: these
$\pi ^i$
-fine Selmer groups may depend on the choice of
$\Sigma $
even for algebraic extensions L of K which contain the cyclotomic
$\mathbb {Z}_p$
-extension
$K_\infty ^c$
(see [Reference Lim and Kumar MurtyLKM16, proof of Theorem 5.1] for an example for abelian varieties).
Now let
$K_\infty /K$
be an admissible p-adic Lie extension, and let
$\Sigma $
be a finite set of primes of K which contains
${S_{\textrm {ram}}(K_\infty /K) \cup S_p \cup S_{\textrm {ram}}(A)}$
(if
$p = 2$
, then we assume that K is totally imaginary). Then we can define fine Selmer groups of A over each number field
$L \subseteq K_\infty $
containing K. We denote the corresponding Pontryagin duals by
$$ \begin{align*} Y_{A,\Sigma}^{(L)} = \textrm{Sel}_{0,A,\Sigma}(L)^\vee, \end{align*} $$
and we define the projective limit
$$ \begin{align*} Y_{A,\Sigma}^{(K_\infty)} = \varprojlim_{K \subseteq L \subseteq K_\infty} Y_{A,\Sigma}^{(L)}\end{align*} $$
with respect to the corestriction maps (where L runs over the finite subextensions of
$K_\infty /K$
).
3 Fine Selmer groups of congruent representations
The aim of this section is to study the relation between the Iwasawa invariants of the fine Selmer groups associated with two representations
$V_1$
and
$V_2$
defined over the same number field K. The representations we consider will always satisfy a congruence condition, meaning that
$A_1[\pi ^l]$
and
$A_2[\pi ^l]$
are isomorphic as
$G_K$
-modules for some integer l (where
$A_i = V_i/T_i$
as usual). Note that this implies that the two representations have the same dimension d. We will always fix a set
$\Sigma $
of primes in K containing all ramified places for
$A_1$
and
$A_2$
, and all places above p. Let
$K_{\infty }/K$
be an admissible p-adic Lie extension. We consider two cases:
-
i)
$K_{\infty }/K$
is strongly
$\Sigma $
-admissible (Section 3.1). -
ii)
$K_{\infty }/K$
is admissible and
$A(K_v)[\pi ]=0$
for all
$v\in \Sigma $
(Section 3.2).
Note that case ii) only becomes relevant if a prime of
$\Sigma $
is completely split in
$K_{\infty }/K$
.
3.1 The generic case
In this section, we prove Theorem 1.1. The main ingredient in the proof is a relation between
$\textrm {Sel}_{0,A}(L)[\pi ^l]$
and
$\textrm {Sel}_{0,A[\pi ^l]}(L)$
for any finite subextension
$K\subseteq L\subseteq K_{\infty }$
of the p-adic Lie extension
$K_{\infty }/K$
.
Lemma 3.1 Let A be associated with a representation of
$G_K$
of dimension d and let
$\Sigma $
be a finite set of primes of K containing
$S_p$
and
$S_{{\rm ram}}(A)$
. If
$p = 2$
, then we assume that K is totally imaginary. Let
$L/K$
be a finite extension which is contained in
$K_\Sigma $
. Then
$$ \begin{align*}\vert v_p(|\textrm{Sel}_{0,A,\Sigma}(L))[\pi^k]|)-v_p(|\textrm{Sel}_{0,A[\pi^k],\Sigma}(L)|)\vert \le fdk(1+|\Sigma(L)|) \end{align*} $$
for each integer
$k \ge 1$
, where
$\Sigma (L)$
denotes the set of primes of L above
$\Sigma $
and f is the inertia degree of p in
$F/\mathbb {Q}_p$
.
Remark 3.2 Note that if A is the p-primary part of an abelian variety of dimension d then the corresponding representation has dimension
$2d$
.
Proof. We start with the following commutative diagram
Consider the exact sequence
$$ \begin{align*}0\longrightarrow A[\pi^k]\longrightarrow A \stackrel{\cdot \pi^k}{\longrightarrow} A\longrightarrow 0.\end{align*} $$
The surjectivity follows from the fact that A is divisible as
$\mathcal {O}$
-module. Note further that the representation V is unramified outside
$\Sigma $
. Thus, there is a well-defined action of
$\textrm {Gal}(K_{\Sigma }/L)$
on A and we can take
$K_{\Sigma }/L$
-cohomology of the exact sequence in order to see that the map h is surjective. Moreover,
$$ \begin{align*} \ker(h) & \cong \mathrm{coker}(\pi^k\colon H^0(K_{\Sigma}/L,A)\longrightarrow H^0(K_{\Sigma}/L,A)) \\ & = A(L)/\pi^k A(L). \end{align*} $$
The last equality is due to the fact that all ramified primes are contained in
$\Sigma $
. Analogously, we see that g is surjective and that
$$\begin{align*}\ker(g)\cong \bigoplus_{v\in \Sigma(L)}A(L_{v})/\pi^k A(L_{v}). \end{align*}$$
We obtain the bounds
$v_p(|\ker (h)|) \le dkf$
and
$v_p(|\ker (g)|)\le dkf|\Sigma (L)|$
. Using the exact sequence
$$ \begin{align} 0\longrightarrow \ker(s)\longrightarrow \textrm{Sel}_{0,A[\pi^k],\Sigma}(L)\longrightarrow \textrm{Sel}_{0,A,\Sigma}(L)[\pi^k]\longrightarrow \mathrm{coker}(s)\longrightarrow 0,\end{align} $$
we may conclude that
$\vert v_p(|\textrm {Sel}_{0,A[\pi ^k],\Sigma }(L)|)- v_p(|\textrm {Sel}_{0,A,\Sigma }(L)[\pi ^k]|)\vert $
is bounded by
$$ \begin{align*} v_p(|\ker(s)|)+v_p(|\mathrm{coker}(s)|)&\le v_p(|\ker(h)|)+v_p(|\ker(g)|)\\&\le fdk+dfk|\Sigma(L)|.\\[-32pt]\end{align*} $$
▪
Corollary 3.3 Let A be associated with a representation of
$G_K$
, and let
$\Sigma $
be a finite set of primes of K containing
$S_p$
and
$S_{\textrm {ram}}(A)$
. If
$p = 2$
, then we assume that K is totally imaginary. Let
$K_\infty /K$
be a strongly
$\Sigma $
-admissible p-adic Lie extension. Then
$\textrm {rank}_{\mathbb {F}_q[[G]]}(\pi ^i Y_{A,\Sigma }^{(K_\infty )}/\pi ^{i+1}Y_{A,\Sigma }^{(K_\infty )})$
equals
$$ \begin{align*}\textrm{rank}_{\mathbb{F}_q[[G]]}\left(\varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A[\pi^{i+1}],\Sigma}(L)^\vee / \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A[\pi^{i}],\Sigma}(L)^\vee\right)\end{align*} $$
for every
$i \in \mathbb {N}$
, where L runs over the finite subfields of
$K_\infty /K$
.
Proof. Let
$k \in \mathbb {N}$
. For every finite subextension
$L \subseteq K_\infty $
of K, we consider the exact sequence
$$ \begin{align*} 0 \longrightarrow M^{(L)} \longrightarrow \textrm{Sel}_{0,A,\Sigma}(L)[\pi^k]^\vee \longrightarrow \textrm{Sel}_{0,A[\pi^k],\Sigma}(L)^\vee \longrightarrow N^{(L)} \longrightarrow 0,\end{align*} $$
which is obtained from (3.1) by taking Pontryagin duals. In particular,
$N^{(L)}$
is a finite abelian group of order at most
$p^{dkf}$
, and
$M^{(L)} = \bigoplus _{v \in \Sigma (L)} G_v^{(L)}$
, where each
$G_v^{(L)}$
is a finite abelian group of order at most
$p^{dkf}$
.
Taking the projective limits along the
$L \subseteq K_\infty $
, we obtain an exact sequence
$$ \begin{align} 0 \longrightarrow M \longrightarrow Y_{A,\Sigma}^{(K_\infty)}/\pi^k Y_{A,\Sigma}^{(K_\infty)} \longrightarrow \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A[\pi^k],\Sigma}(L)^\vee \longrightarrow N \longrightarrow 0, \end{align} $$
where N is a finite abelian group and where M is finitely generated over
$\mathcal {O}[[H]]$
because no prime
$v \in \Sigma $
splits completely in the
$\mathbb {Z}_p$
-extension
$K_\infty ^H$
of K which is fixed by
$H \subseteq G$
. In fact, replacing K by a finite subextension of
$K_\infty ^H$
if necessary (this does not affect the projective limit), we may assume that actually the primes
$v \in \Sigma $
do not split at all in
$K_\infty ^H/K$
.
Letting
$\Gamma := G/H \cong \mathbb {Z}_p$
, the group ring
$\mathcal {O}[[\Gamma ]]$
can be identified with the ring
$\Lambda = \mathcal {O}[[T]]$
. Since M is finitely generated over
$\mathcal {O}[[H]]$
, there exists a nonconstant annihilator of M in
${\mathcal {O}[[G]] \cong \mathcal {O}[[H]][[T]]}$
by [Reference Coates, Fukaya, Kato, Sujatha and VenjakobCFK+ 05, Proposition 2.3 and Theorem 2.4]; in particular, the annihilator is not a power of
$\pi $
(note: the result in [Reference Coates, Fukaya, Kato, Sujatha and VenjakobCFK+ 05] is formulated for the case
$\mathcal {O} = \mathbb {Z}_p$
, but the proof goes through in our more general setting).
Considering now
$k = i$
and
$k = i+1$
, we may conclude that there exists a nonconstant annihilator in
$\mathcal {O}[[G]]$
of the cokernels and kernels of both maps
$$ \begin{align*}Y_{A,\Sigma}^{(K_\infty)}/ \pi^i Y_{A,\Sigma}^{(K_\infty)} \longrightarrow \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A[\pi^{i}],\Sigma}(L)^\vee\end{align*} $$
and
$$ \begin{align*}Y_{A,\Sigma}^{(K_\infty)} / \pi^{i+1} Y_{A,\Sigma}^{(K_\infty)} \longrightarrow \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A[\pi^{i+1}],\Sigma}(L)^\vee. \end{align*} $$
Taking quotients proves the assertion of the corollary.▪
We need one final auxiliary
Lemma 3.4 Let
$A_1$
and
$A_2$
be associated with two representations
$V_1$
and
$V_2$
of
$G_K$
, and let
$\Sigma $
be a finite set of primes of K which contains
${S_p \cup S_{\textrm {ram}}(A_1) \cup S_{\textrm {ram}}(A_2)}$
. If
$p = 2$
, then we assume that K is totally imaginary. We assume that
$A_1[\pi ^i]$
and
$A_2[\pi ^i]$
are isomorphic as
$G_K$
-modules for some
$i \in \mathbb {N}$
,
$i \ge 1$
.
Then
$\textrm {Sel}_{0,A_1[\pi ^i],\Sigma }(L)\cong \textrm {Sel}_{0,A_2[\pi ^i],\Sigma }(L)$
for every finite extension
$L \subseteq K_\Sigma $
of K.
Proof. Let
$\phi \colon A_1[\pi ^i] \longrightarrow A_2[\pi ^i]$
be a
$G_K$
-module homomorphism. As
$V_1$
and
$V_2$
are unramified outside of
$\Sigma $
, the group
$\textrm {Gal}(\overline {K}/K_{\Sigma })$
acts trivially on
$A_1$
and
$A_2$
and we can interpret
$\phi $
as a
$\textrm {Gal}(K_{\Sigma }/K)$
-isomorphism. Then
$\phi $
induces an isomorphism
$$ \begin{align*} \phi \colon H^1(K_\Sigma/L, A_1[\pi^i]) \longrightarrow H^1(K_\Sigma/L, A_2[\pi^i])\end{align*} $$
of
$G_K$
-modules.
For any prime v of L, the inclusion
$ G_{L_v} \hookrightarrow G_{L}$
of the local absolute Galois group at the completion
$L_v$
of L at v induces an isomorphism
$$ \begin{align*}H^1(L_v, A_1[\pi^i]) \longrightarrow H^1(L_v, A_2[\pi^i]). \end{align*} $$
The corresponding isomorphism between fine Selmer groups is now immediate.▪
Now we turn to the proof of our first main result.
Proof of Theorem 1.1
Let l be such that
$(\pi ^lY_{A_1,\Sigma }^{(K_{\infty })})[\pi ]$
is pseudo-null. By definition of the
$\mu $
-invariant (see (2.1)) and Corollary 2.3, we have
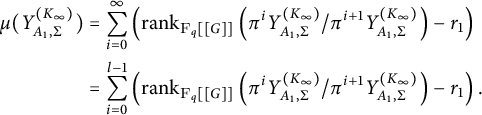$$ \begin{align} \mu(Y_{A_1,\Sigma}^{(K_\infty)})&=\sum_{i=0}^{\infty} \left(\textrm{rank}_{\mathbb{F}_q[[G]]}\left(\pi^iY_{A_1,\Sigma}^{(K_\infty)}/\pi^{i+1}Y_{A_1,\Sigma}^{(K_\infty)}\right) - r_1\right) \nonumber \\&=\sum_{i=0}^{l-1} \left(\textrm{rank}_{\mathbb{F}_q[[G]]}\left(\pi^iY_{A_1,\Sigma}^{(K_\infty)}/\pi^{i+1}Y_{A_1,\Sigma}^{(K_\infty)}\right) - r_1\right).\end{align} $$
Now Corollary 3.3 implies that for both
$j = 1$
and
$j = 2$
and every
$i \in \mathbb {N}$
, the
$\mathbb {F}_q[[G]]$
-rank of
$\pi ^iY_{A_j,\Sigma }^{(K_{\infty })}/\pi ^{i+1}Y_{A_j,\Sigma }^{(K_{\infty })}$
equals
$$ \begin{align*} \textrm{rank}_{\mathbb{F}_q[[G]]}\left(\varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A_j[\pi^{i+1}],\Sigma}(L)^\vee/ \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A_j[\pi^i],\Sigma}(L)^\vee\right). \end{align*} $$
Using that
$A_1[\pi ^l]\cong A_2[\pi ^l]$
, Lemma 3.4 implies that
$$\begin{align*}\textrm{Sel}_{0,A_1[\pi^i],\Sigma}(L)\cong \textrm{Sel}_{0,A_2[\pi^i],\Sigma}(L)\end{align*}$$
for every
$i \le l$
. By (3.3), we may conclude that
$$ \begin{align*} \mu(Y_{A_1,\Sigma}^{(K_\infty)})&=\sum_{i=0}^{l-1} \left(\textrm{rank}_{\mathbb{F}_q[[G]]}\left(\pi^iY_{A_1,\Sigma}^{(K_\infty)}/\pi^{i+1}Y_{A_1,\Sigma}^{(K_\infty)}\right) - r_1\right)\\ &=\sum_{i=0}^{l-1} \left(\textrm{rank}_{\mathbb{F}_q[[G]]}\left(\pi^iY_{A_2,\Sigma}^{(K_\infty)}/\pi^{i+1}Y_{A_2,\Sigma}^{(K_\infty)}\right) - r_1\right)\\ &\le \sum_{i=0}^{\infty} \left(\textrm{rank}_{\mathbb{F}_q[[G]]}\left(\pi^iY_{A_2,\Sigma}^{(K_\infty)}/\pi^{i+1}Y_{A_2,\Sigma}^{(K_\infty)}\right) - r_2\right) = \mu\left(Y_{A_2,\Sigma}^{(K_\infty)}\right). \end{align*} $$
Here, we used the hypothesis
$r_2 \le r_1$
, i.e.,
$-r_1 \le -r_2$
.
Now we prove assertion (b). In the following, we abbreviate
$\textrm {rank}_{\mathbb {F}_q[[G]]}$
to r. If
$A_1[\pi ^{l+1}]\cong A_2[\pi ^{l+1}]$
then
$$ \begin{align*} r\left(\pi^{l} Y_{A_1,\Sigma}^{(K_{\infty})}/\pi^{l+1}Y_{A_1,\Sigma}^{(K_{\infty})}\right) & = r\left(\varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A_1[\pi^{l+1}],\Sigma}(L)^\vee / \varprojlim_{K \subseteq L \subseteq K_\infty}\textrm{Sel}_{0,A_1[\pi^{l}],\Sigma}(L)^\vee\right)\\ & = r\left(\varprojlim_{K \subseteq L \subseteq K_\infty}\textrm{Sel}_{0,A_2[\pi^{l+1}],\Sigma}(L)^\vee / \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A_2[\pi^{l}],\Sigma}(L)^\vee\right)\\ & = r\left(\pi^{l}Y_{A_2,\Sigma}^{(K_{\infty})}/\pi^{l+1}Y_{A_2,\Sigma}^{(K_{\infty})}\right).\end{align*} $$
Using Lemma 2.2 and the definition of l, we obtain
$$ \begin{align*} r\left(\pi^l Y_{A_1,\Sigma}^{(K_\infty)}/\pi^{l+1}Y_{A_1,\Sigma}^{(K_\infty)}\right) & = r\left(\left(\pi^lY_{A_1,\Sigma}^{(K_\infty)}\right)[\pi]\right) + \textrm{rank}_{\mathbb{Z}_q[[G]]}\left(\pi^l Y_{A_1,\Sigma}^{(K_\infty)}\right) \\ & = 0 + r_1, \end{align*} $$
and similarly
$$\begin{align*}r\left(\pi^l Y_{A_2,\Sigma}^{(K_\infty)}/\pi^{l+1}Y_{A_2,\Sigma}^{(K_\infty)}\right) \ge r_2. \end{align*}$$
This proves the first claim of (b).
If
$r_2 = r_1$
, then it follows from the above that
${\textrm {rank}_{\mathbb {F}_q[[G]]}((\pi ^lY_{A_2,\Sigma }^{(K_\infty )})[\pi ]) = 0}$
. In view of Remark 2.1 this implies that
$$\begin{align*}\mu\left(Y_{A_2,\Sigma}^{(K_\infty)}\right) = \sum_{i=0}^{l-1} \left(\textrm{rank}_{\mathbb{F}_q[[G]]}\left(\pi^i Y_{A_2,\Sigma}^{(K_\infty)}/\pi^{i+1}Y_{A_2,\Sigma}^{(K_\infty)}\right) - r_2\right) = \mu\left(Y_{A_1,\Sigma}^{(K_\infty)}\right), \end{align*}$$
proving the second claim of (b). Using the equality of ranks derived above we obtain that
$$ \begin{align*}\textrm{rank}_{\mathbb{F}_q[[G]]}\left(\pi^iY_{A_1,\Sigma}^{(K_{\infty})}/\pi^{i+1}Y_{A_1,\Sigma}^{(K_{\infty})}\right) = \textrm{rank}_{\mathbb{F}_q[[G]]}\left(\pi^iY_{A_2,\Sigma}^{(K_{\infty})}/\pi^{i+1}Y_{A_2,\Sigma}^{(K_{\infty})}\right)\end{align*} $$
for all
$0\le i\le l$
. Let
$E_j = \bigoplus _{i=1}^{s_j} \mathcal {O}[[G]]/(\pi ^{e_i^j})$
be the elementary
$\mathcal {O}[[G]]$
-module associated to
$Y_{A_j,\Sigma }^{(K_{\infty })}[\pi ^{\infty }]$
via [Reference VenjakobVen02, Theorem 3.40] (Venjakob’s result is proven only for
$\mathcal {O} = \mathbb {Z}_p$
, but it is valid in our more general setting) and define
$$\begin{align*}f_i^{j}= \vert \{k\mid e_k^j>i\}\vert.\end{align*}$$
Since
$r_1=r_2 =:r$
we obtain
$$ \begin{align*}\textrm{rank}_{\mathbb{F}_q[[G]]}\left(\pi^iY_{A_j,\Sigma}^{(K_{\infty})}/\pi^{i+1}Y_{A_j,\Sigma}^{(K_{\infty})}\right) = r+f^j_i \end{align*} $$
by Corollary 2.3. Therefore,
$f^1_i=f^2_i$
for all
$0\le i\le l$
and thus
$E_1=E_2$
from which the claim is immediate.
The assertion (c) is a special case of (b). Finally, if
$(\pi ^l Y_{A_2,\Sigma }^{(K_\infty )})[\pi ]$
is also pseudo-null, then we can exchange the roles of
$A_1$
and
$A_2$
and obtain equality of
$\mu $
-invariants.▪
3.2 The completely split case
Now we treat admissible p-adic Lie extensions
$K_\infty /K$
such that some
$v \in \Sigma $
may be completely split in
$K_\infty /K$
. In this case, we work under the restrictive assumption that
$A_j(K_v)[\pi ] = \{0\}$
for every
$v \in \Sigma $
and
$j\in \{1,2\}$
(meaning that the subgroup of
$A_j[\pi ]$
fixed by
$G_{K_v} \subseteq G_K$
is trivial). First, we derive several auxiliary results, starting with a lemma which will serve as a substitute for Lemma 3.1.
Lemma 3.5 Let A be associated with a p-adic
$G_K$
-representation V and let
$\Sigma $
be a finite set of primes of K containing
$S_p \cup S_{\textrm {ram}}(A)$
. If
$p = 2$
, then we assume that K is totally imaginary. Assume that
$A(K_v)[p] = \{0\}$
for every
$v \in \Sigma $
. Then
$$ \begin{align*}\textrm{Sel}_{0,A,\Sigma}(L)[\pi^i]\cong \textrm{Sel}_{0,A[\pi^i],\Sigma}(L) \end{align*} $$
for every finite normal p-extension
$L \subseteq K_\Sigma $
of K and each
$i \in \mathbb {N}$
,
$i \ge 1$
.
Proof. The assumptions imply that
$A(K)[\pi ]=\{ 0 \}$
. Since
$L/K$
is a p-extension, it follows from [Reference Neukirch, Schmidt and WingbergNSW08, Corollary (1.6.13)] that also
${H^0(L, A[\pi ]) = A(L)[\pi ]=\{0\}}$
. Hence,
$H^0(L,A)= \{ 0 \}$
. As V is unramified outside of
$\Sigma $
we obtain that
${H^0(K_{\Sigma }/L, A)=0}$
. Now consider the exact sequence
$$ \begin{align*}0\longrightarrow A[\pi^i]\longrightarrow A\stackrel{ \cdot \pi^i}{\longrightarrow} A\longrightarrow 0.\end{align*} $$
Taking
$K_{\Sigma }/L$
-cohomology we obtain a second exact sequence
$$ \begin{align*}0\longrightarrow H^1(K_{\Sigma}/L,A[\pi^i])\longrightarrow H^1(K_{\Sigma}/L, A)\longrightarrow H^1(K_{\Sigma}/L,A), \end{align*} $$
where the last homomorphism is multiplication by
$\pi ^i$
. Hence, we obtain the isomorphism
$$ \begin{align*}H^1(K_{\Sigma}/L,A[\pi^i])\cong H^1(K_{\Sigma}/L,A)[\pi^i].\end{align*} $$
Let now w be a place in L above a prime
$v \in \Sigma $
. Using analogous arguments, we can derive from the hypothesis
$A(K_v)[\pi ] = \{0\}$
that
$$ \begin{align*}H^1(L_{w},A[\pi^i])\cong H^1(L_{w},A)[\pi^i].\\[-36pt]\end{align*} $$
▪
Corollary 3.6 Let A be as above, let
$K_\infty /K$
be an admissible p-adic Lie extension, and let
$\Sigma $
be a finite set of primes of K containing
${S_{\textrm {ram}}(K_\infty /K) \cup S_p \cup S_{\textrm {ram}}(A)}$
. If
$p = 2$
, then we assume that K is totally imaginary. Assume that
$A(K_v)[\pi ] = \{0\}$
for every
$v \in \Sigma $
. Then
$$ \begin{align*} Y_{A,\Sigma}^{(K_\infty)} / \pi^i Y_{A,\Sigma}^{(K_\infty)} \cong \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A[\pi^i],\Sigma}(L)^\vee \end{align*} $$
for every
$i \in \mathbb {N}$
,
$i \ge 1$
, where the projective limit is taken over the finite normal subextensions L of
$K_\infty /K$
.
Proof. In view of Lemma 3.5, we have isomorphisms
$$ \begin{align*} \textrm{Sel}_{0,A,\Sigma}(L)[\pi^i]\cong \textrm{Sel}_{0,A[\pi^i],\Sigma}(L)\end{align*} $$
for each L. By duality,
$\pi ^{i}Y_{A,\Sigma }^{(L)}$
is precisely the group acting trivially on
$\textrm {Sel}_{0,A,\Sigma }(L)[\pi ^i]$
. Therefore,
$$ \begin{align*} Y_{A,\Sigma}^{(L)} / \pi^i Y_{A,\Sigma}^{(L)} \cong (\textrm{Sel}_{0,A,\Sigma}(L)[\pi^i])^\vee \cong \textrm{Sel}_{0,A[\pi^i],\Sigma}(L)^\vee. \end{align*} $$
The result now follows since
$$ \begin{align*} Y_{A,\Sigma}^{(K_\infty)} / \pi^i Y_{A,\Sigma}^{(K_\infty)} \cong \varprojlim_{K \subseteq L \subseteq K_\infty} Y_{A,\Sigma}^{(L)} / \pi^i Y_{A,\Sigma}^{(L)}. \\[-40pt]\end{align*} $$
▪
We can now prove an analogon of Theorem 1.1:
Theorem 3.7 Let
$A_1$
and
$A_2$
be associated with two representations
$V_1$
and
$V_2$
of
$G_K$
. Let
$K_\infty /K$
be an admissible p-adic Lie extension, and let
$G = \textrm {Gal}(K_\infty /K)$
. Let
$\Sigma $
be a finite set of primes of K which contains
$S_{\text {ram}}(K_\infty /K)$
,
$S_p$
and the sets of primes of K where either
$V_1$
or
$V_2$
is ramified. If
$p = 2$
, then we assume that K is totally imaginary.
Suppose that
$A_j(K_v)[\pi ] = \{0\}$
for every
$v \in \Sigma $
and
$j\in \{1,2\}$
. We let
$r_j = \textrm {rank}_{\mathcal {O}[[G]]} (Y_{A_j,\Sigma }^{(K_\infty )})$
,
${1 \le j \le 2}$
. Let l be minimal such that
${(\pi ^l Y_{A_1,\Sigma }^{(K_\infty )})[\pi ]}$
is pseudo-null.
Then the statements from Theorem 1.1 hold.
Proof. Suppose that
$A_1[\pi ^l] \cong A_2[\pi ^l]$
as
$G_K$
-modules. Then
$$ \begin{align*} \pi^{i} Y_{A_1,\Sigma}^{(K_{\infty})}/\pi^{i+1}Y_{A_1,\Sigma}^{(K_{\infty})} & \cong \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A_1[\pi^{i+1}],\Sigma}(L)^\vee / \varprojlim_{K \subseteq L \subseteq K_\infty}\textrm{Sel}_{0,A_1[\pi^{i}],\Sigma}(L)^\vee \\ & \cong \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A_2[\pi^{i+1}],\Sigma}(L)^\vee / \varprojlim_{K \subseteq L \subseteq K_\infty}\textrm{Sel}_{0,A_2[\pi^{i}],\Sigma}(L)^\vee \\ & \cong \pi^{i} Y_{A_2,\Sigma}^{(K_{\infty})}/\pi^{i+1}Y_{A_2,\Sigma}^{(K_{\infty})} \end{align*} $$
for every
$i < l$
, by Corollary 3.6 and Lemma 3.4. In particular, both
$\mathbb {F}_q[[G]]$
-modules have the same rank. Therefore, we can proceed as in the proof of Theorem 1.1.▪
Proof of Theorem 1.2
The hypothesis in (a) implies that
$\pi ^l Y_{A_1,\Sigma }^{(K_\infty )}$
is
$\mathcal {O}$
-free. Let E be an elementary
$\Lambda $
-module pseudo-isomorphic to
$\pi ^l Y_{A_1,\Sigma }^{(K_\infty )}$
. For any finitely generated
$\mathcal {O}$
-module M, we denote by
$\textrm {rank}_q(M)$
the dimension of
$M/\pi M$
as
$\mathbb {F}_q$
-vector space. The following auxiliary lemma follows by using an argument given in the proof of [Reference KleineKle17, Proposition 3.4(i)].
Lemma 3.8 We have
${\textrm {rank}_q(\pi ^l Y_{A_1, \Sigma }^{(K_\infty )}) = \textrm {rank}_q(E)}$
.▪
Proof. Since
$\pi ^l Y_{A_1,\Sigma }^{(K_\infty )}$
is
$\mathcal {O}$
-free, the maximal finite submodule of
$Y_{A_1,\Sigma }^{(K_\infty )}$
is annihilated by
$\pi ^l$
. Therefore, we have an injection
${\varphi \colon \pi ^l Y_{A_1,\Sigma }^{(K_\infty )} \longrightarrow E}$
with finite cokernel. Moreover, since multiplication by
$\pi $
is injective on E, the quotients
$E/\textrm {im}(\varphi )$
and
$\pi E / \pi \textrm {im}(\varphi )$
are isomorphic, proving that
$$\begin{align*}\textrm{rank}_q(\pi^l Y_{A_1, \Sigma}^{(K_\infty)}) = \textrm{rank}_q(\textrm{im}(\varphi))\end{align*}$$
indeed equals
$\textrm {rank}_q(E)$
.▪
Therefore,
$$ \begin{align*} |\pi^{l} Y_{A_1,\Sigma}^{(K_{\infty})}/\pi^{l+1}Y_{A_1,\Sigma}^{(K_{\infty)}}| = q^{\textrm{rank}_q(\pi^lY_{A_1,\Sigma}^{(K_\infty)})} = q^{\textrm{rank}_q(E)} = q^{\lambda(E)} = q^{\lambda(Y_{A_1,\Sigma}^{(K_\infty)})}. \end{align*} $$
On the other hand, the maximal finite
$\Lambda $
-submodule of
$Y_{A_2,\Sigma }^{(K_\infty )}$
need not be annihilated by
$\pi ^l$
; therefore
$$ \begin{align*} |\pi^{l} Y_{A_2,\Sigma}^{(K_{\infty})}/\pi^{l+1}Y_{A_2, \Sigma},\Sigma^{(K_{\infty)}}| \ge q^{\lambda( Y_{A_2,\Sigma}^{(K_\infty)})}. \end{align*} $$
This concludes the proof of (a). If both
$\pi ^l Y_{A_1,\Sigma }^{(K_\infty )}$
and
$\pi ^l Y_{A_2,\Sigma }^{(K_\infty )}$
are
$\mathcal {O}$
-free, then we can exchange the roles of
$A_1$
and
$A_2$
and obtain equality of
$\lambda $
-invariants.
4 Non p-extensions
In this final section, we study the growth of fine Selmer groups of congruent Galois representations over normal algebraic extensions of K which are the compositum of finite r-extensions for suitable primes
$r \ne p$
. If
$p = 2$
, then we always assume that K is totally imaginary. Similarly as in Sections 3.1 and 3.2, we distinguish between two different settings, starting with one resembling the case which has been studied in Section 3.2.
Theorem 4.1 Let p be a fixed prime, let
$A_1$
and
$A_2$
be associated with two representations of
$G_K$
, and let
$K_\infty /K$
be a normal algebraic extension. Let
$\mathcal {P}$
be the set of primes r such that
$K_\infty /K$
contains a finite subextension of degree r over K. Let
$\Sigma $
be a finite set of primes of K which contains
$S_p$
,
$S_{ram}(K_\infty /K)$
and
$S_{\textrm {ram}}(A_j)$
,
$j \in \{ 1,2\}$
.
We assume that
${\dim (A_1) = \dim (A_2) =: d}$
, that
$r \ge q^{d}$
for each
$r \in \mathcal {P}$
, and that
${A_j(K_v)[\pi ] = \{0\}}$
for
$j \in \{ 1,2\}$
and every
$v \in \Sigma $
. Then the following statements hold:
-
(a) If
$A_1[\pi ] \cong A_2[\pi ]$
as
$G_K$
-modules, then
$Y_{A_1, \Sigma }^{(K_\infty )}$
is a finitely generated
$\mathcal {O}$
-module if and only if
$Y_{A_2,\Sigma }^{(K_\infty )}$
is finitely generated over
$\mathcal {O}$
. -
(b) Suppose that both
$Y_{A_j,\Sigma }^{(K_\infty )}$
,
$j \in \{ 1,2\}$
, are finitely generated over
$\mathcal {O}$
. Let
$l \in \mathbb {N}$
be large enough such that
$(\pi ^l Y_{A_1, \Sigma }^{(K_\infty )})[\pi ] = \{0\}$
. If
$A_1[\pi ^{l+1}] \cong A_2[\pi ^{l+1}]$
as
$G_K$
-modules, then
$\textrm {rank}_{\mathcal {O}}(Y_{A_2,\Sigma }^{(K_\infty )}) \le \textrm {rank}_{\mathcal {O}}(Y_{A_1,\Sigma }^{(K_\infty )})$
. -
(c) In the setting of (b), suppose that
$A_1[\pi ^{l+1}] \cong A_2[\pi ^{l+1}]$
for some l such that both
$(\pi ^l Y_{A_j,\Sigma }^{(K_\infty )})[\pi ]$
are trivial. Then
$\textrm {rank}_{\mathcal {O}}(Y_{A_2,\Sigma }^{(K_\infty )}) = \textrm {rank}_{\mathcal {O}}(Y_{A_1,\Sigma }^{(K_\infty )})$
.
Proof. The proof is analogous to the proofs of Theorems 3.7 and 1.2. Note that
$Y^{(K_\infty )}_{A_j,\Sigma }$
is a finitely generated
$\mathcal {O}$
-module if and only if
$Y^{(K_\infty )}_{A_j,\Sigma }/\pi Y^{(K_\infty )}_{A_j,\Sigma }$
is finite. Recall that
$Y^{(K_\infty )}_{A_j,\Sigma }/\pi Y^{(K_\infty )}_{A_j,\Sigma }=\varprojlim _{K \subseteq L \subseteq K_\infty } \textrm {Sel}_{0,A_j,\Sigma }(L)[\pi ]^\vee $
. Claim (a) now follows from the fact that
$A_1[\pi ]\cong A_2[\pi ]$
, by using the following
Lemma 4.2 Let A be associated with a
$G_K$
-representation of dimension d, let
$\Sigma $
be a finite set of primes of K containing
${S_p \cup S_{\textrm {ram}}(A)}$
. If
$p = 2$
, then we assume that K is totally imaginary. Assume that
$A(K_v)[\pi ] = \{0\}$
for every
$v \in \Sigma $
.
Let
$L \subseteq K_\Sigma $
be a finite normal extension of K such that each prime number r dividing
$[L:K]$
satisfies
$r \ge q^{d}$
. Then
$$ \begin{align*}\textrm{Sel}_{0,A,\Sigma}(L)[\pi^i]\cong \textrm{Sel}_{0,A[\pi^i],\Sigma}(L) \end{align*} $$
for each
$i \in \mathbb {N}$
,
$i \ge 1$
.▪
Proof. By assumption
$A(K)[\pi ]=\{ 0 \}$
. We mimic the proof of [Reference Neukirch, Schmidt and WingbergNSW08, Corollary (1.6.13)] and show that also
$H^0(L, A[\pi ]) = A(L)[\pi ]=\{0\}$
. Let r be the smallest prime number dividing
$[L:K]$
. Since
$A(L)[\pi ] \setminus A(K)[\pi ]$
is the disjoint union of
$\textrm {Gal}(L/K)$
-orbits with more than one element, the cardinality of each such orbit is divisible by some prime
$r' \ge r$
. Thus, if there exists at least one orbit containing more than one element, then
$$\begin{align*}|A(L)[\pi]| \ge |A(K)[\pi]|+r'\ge |A(K)[\pi]|+r. \end{align*}$$
On the other hand,
$|A(L)[\pi ]| \le q^{d}$
. Since
$r \ge q^{d}$
by assumption, we obtain that such a nontrivial orbit cannot exist. Therefore,
$A(L)[\pi ]=\{0\}$
. Now we can proceed as in the proof of Lemma 3.5.▪
For points (b) and (c), we note that
$\pi ^lY^{(K_\infty )}_{A_1,\Sigma }$
is a free
$\mathcal {O}$
-module with the property that
$\vert \pi ^lY^{(K_\infty )}_{A_1,\Sigma }/\pi ^{l+1}Y^{(K_\infty )}_{A_1,\Sigma }\vert =q^{\textrm {rank}_q(\pi ^lY^{(K_\infty )}_{A_1,\Sigma })}=q^{\textrm {rank}_{\mathcal {O}}(Y^{(K_\infty )}_{A_1,\Sigma })}$
, where
$\textrm {rank}_q$
is defined as in the proof of Theorem 1.2. As the maximal finite submodule of
$Y^{(K_\infty )}_{A_2,\Sigma }$
is not necessarily annihilated by
$\pi ^l$
, claim (b) follows. In the situation of claim (c), we can interchange the roles of
$A_1$
and
$A_2$
in order to obtain equality.
Now we turn to the second result for non-p-extensions. As in Theorem 4.1, we let
$\mathcal {P} = \mathcal {P}(K_\infty )$
be the set of prime numbers r such that
$K_\infty $
contains an extension of K of degree r.
Theorem 4.3 Let p be a fixed prime, let
$A_1$
and
$A_2$
be associated with two
$G_K$
-representations, and let
$K_\infty /K$
be an abelian algebraic extension such that
${p \not \in \mathcal {P}(K_\infty )}$
. Let
$\Sigma $
be a finite set of primes of K which contains
$S_p$
,
$S_{ram}(K_\infty /K)$
and
$S_{\textrm {ram}}(A_j)$
,
$j \in \{1,2\}$
.
We assume that each prime
$v \in \Sigma $
is finitely split in
$K_\infty /K$
.
-
(a) If
$A_1[\pi ] \cong A_2[\pi ]$
as
$G_K$
-modules, then
$Y_{A_1,\Sigma }^{(K_\infty )}$
is a finitely generated
$\mathcal {O}$
-module if and only if
$Y_{A_2,\Sigma }^{(K_\infty )}$
is finitely generated over
$\mathcal {O}$
.
Suppose now that for each
$j\in \{1,2\}$
and every
$w \in \Sigma (K_\infty )$
, the group
$A_j(K_{\infty ,w})[\pi ^\infty ]$
is finite. Then also the following statements hold:
-
(b) Suppose that both
$Y_{A_j,\Sigma }^{(K_\infty )}$
,
$j \in \{ 1,2\}$
, are finitely generated over
$\mathcal {O}$
. Let
${l \in \mathbb {N}}$
be large enough such that
$(\pi ^l Y_{A_1,\Sigma }^{(K_\infty )})[\pi ] = \{0\}$
and
${\pi ^l A_1(K_{\infty ,w})[\pi ^\infty ] = \{0\}}$
for every
$w \in \Sigma (K_\infty )$
. If
$A_1[\pi ^{l+1}] \cong A_2[\pi ^{l+1}]$
as
$G_K$
-modules, then
$\textrm {rank}_{\mathcal {O}}(Y_{A_2,\Sigma }^{(K_\infty )}) \le \textrm {rank}_{\mathcal {O}}(Y_{A_1,\Sigma }^{(K_\infty )})$
. -
(c) In the setting of (b), if
$A_1[\pi ^{l+1}] \cong A_2[\pi ^{l+1}]$
for some l such that both
$(\pi ^l Y_{A_j,\Sigma }^{(K_\infty )})[\pi ]$
and all the groups
$\pi ^l A_j(K_{\infty ,w})[\pi ^\infty ]$
,
$j \in \{1,2\}$
, are trivial, then
$$\begin{align*}\textrm{rank}_{\mathcal{O}}\left(Y_{A_2,\Sigma}^{(K_\infty)}\right) = \textrm{rank}_{\mathcal{O}}\left(Y_{A_1,\Sigma}^{(K_\infty)}\right). \end{align*}$$
Proof. We first note that
$Y_{A_j,\Sigma }^{(K_\infty )}$
is finitely generated over
$\mathcal {O}$
if and only if the quotient
$Y_{A_j,\Sigma }^{(K_\infty )}/\pi Y_{A_j,\Sigma }^{(K_\infty )}$
is finite. The exact sequence (3.2) from the proof of Corollary 3.3 implies that the kernels and cokernels of the maps
$$ \begin{align*} Y_{A_j,\Sigma}^{(K_\infty)}/\pi Y_{A_j,\Sigma}^{(K_\infty)} \longrightarrow \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A_j[\pi],\Sigma}(L)^\vee\end{align*} $$
are finite for both
$j = 1$
and
$j = 2$
(here, we use the hypothesis that each
$v \in \Sigma $
is finitely split in
$K_\infty /K$
). The assertion (a) therefore follows from the isomorphism
$A_1[\pi ]\cong A_2[\pi ]$
.
More generally, we have exact sequences
$$ \begin{align*} 0 \longrightarrow M_k \longrightarrow Y_{A_j,\Sigma}^{(K_\infty)}/\pi^k Y_{A_j,\Sigma}^{(K_\infty)} \longrightarrow \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A_j[\pi^k],\Sigma}(L)^\vee \longrightarrow N_k \longrightarrow 0 \end{align*} $$
for finite abelian groups
$M_k$
and
$N_k$
,
$k \in \mathbb {N}$
. Moreover, from the proof of Lemma 3.1, we obtain exact sequences
$$ \begin{align} \begin{split} & 0 \longrightarrow N_k \longrightarrow A_j(K_\infty)[\pi^\infty]/\pi^k A_j(K_\infty)[\pi^\infty] \longrightarrow C_k \longrightarrow 0, \\ & 0 \longrightarrow C_k \longrightarrow\bigoplus_{w \in \Sigma(K_\infty)} A_j(K_{\infty,w})[\pi^\infty]/\pi^k A_j(K_{\infty,w})[\pi^\infty] \longrightarrow M_k \longrightarrow 0 \end{split} \end{align} $$
for every
$k \in \mathbb {N}$
and
$j \in \{ 1,2\}$
(note that
$M_k \cong M_k^\vee $
and
$N_k \cong N_k^\vee $
). Using the assumption that
$A_j(K_{\infty ,w})[\pi ^\infty ]$
is finite, we can deduce from (4.1) the following equality:
$$ \begin{align*} \vert N_k\vert =\frac{\vert A_j(K_\infty)[\pi^\infty]/\pi^k A_j(K_\infty)[\pi^\infty]\vert}{\vert\bigoplus_{w \in \Sigma(K_\infty)} A_j(K_{\infty,w})[\pi^\infty]/\pi^k A_j(K_{\infty,w})[\pi^\infty]\vert}\vert M_k\vert. \end{align*} $$
To simplify notation we write
$B_k=\bigoplus _{w \in \Sigma (K_\infty )} A_j(K_{\infty ,w})[\pi ^\infty ]/\pi ^k A_j(K_{\infty ,w})[\pi ^\infty ]$
and
$C_k=A_j(K_\infty )[\pi ^\infty ]/\pi ^k A_j(K_\infty )[\pi ^\infty ]$
. Clearly,
$C_k$
can be seen as a subgroup of each direct term of
$B_k$
. Hence,
$$ \begin{align*}\frac{\vert N_{k+1}\vert }{\vert N_k\vert}=\frac{\vert M_{k+1}\vert }{\vert M_k\vert}\frac{\vert C_{k+1}\vert\vert B_k\vert}{\vert C_k\vert \vert B_{k+1}\vert}\le \frac{\vert M_{k+1}\vert}{\vert M_k\vert}.\end{align*} $$
Therefore,
$|\pi ^k Y_{A_j, \Sigma }^{(K_\infty )}/\pi ^{k+1}Y_{A_j, \Sigma }^{(K_\infty )}|$
differs from
$$ \begin{align*}|\varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A_j[\pi^{k+1}],\Sigma}(L)^\vee / \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A_j[\pi^k],\Sigma}(L)^\vee|\end{align*} $$
by a factor
$\frac {|M_k| |N_{k+1}|}{|N_k||M_{k+1}|}$
which is smaller than or equal to 1. In fact, for
$k = l$
and
$j = 1$
, this factor is 1 by our hypotheses. Therefore,
$$ \begin{align*} |\pi^l Y_{A_1,\Sigma}^{(K_\infty)}/\pi^{l+1}Y_{A_1,\Sigma}^{(K_\infty)}| = |\varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A_2[\pi^{l+1}],\Sigma}(L)^\vee / \varprojlim_{K \subseteq L \subseteq K_\infty} \textrm{Sel}_{0,A_2[\pi^l],\Sigma}(L)^\vee|\end{align*} $$
because
$A_1[\pi ^{l+1}] \cong A_2[\pi ^{l+1}]$
. Note that the factor
$\frac {|M_k| |N_{k+1}|}{|N_k||M_{k+1}|}$
can be strictly smaller than 1 for
$A_2$
. This happens if
$\pi ^l$
does not annihilate the
$\pi $
-primary subgroups of the
$A_2(K_{\infty ,w}$
). We have thus shown that
$$\begin{align*}\textrm{rank}_q\left(\pi^l Y_{A_2,\Sigma}^{(K_\infty)}\right) \le \textrm{rank}_q\left(\pi^l Y_{A_1,\Sigma}^{(K_\infty)}\right),\end{align*}$$
where
$\textrm {rank}_q$
is defined as in the proof of Theorem 1.2. The assertion (b) follows since
$$ \begin{align*} |\pi^l Y_{A_1,\Sigma}^{(K_\infty)}/\pi^{l+1}Y_{A_1,\Sigma}^{(K_\infty)}| = q^{\textrm{rank}_{\mathcal{O}}(Y_{A_1,\Sigma}^{(K_\infty)})} \end{align*} $$
because
$(\pi ^l Y_{A_1,\Sigma }^{(K_\infty )})[\pi ] = \{0\}$
by assumption; the
$\mathcal {O}$
-rank of
$Y_{A_2,\Sigma }^{(K_\infty )}$
can be strictly smaller than the corresponding q-rank, as in the proof of Theorem 1.2.
Finally, (c) follows by interchanging the roles of
$A_1$
and
$A_2$
in the previous proof.▪
Remark 4.4 Going through the proof of the theorem, one sees that actually the finiteness of
$A_2(K_{\infty ,w})[\pi ^\infty ]$
is needed only for at least one
$w \in \Sigma (K_\infty )$
. Moreover, if one assumes that
$A(K_{\infty })[\pi ]=\{0\}$
, then one can drop completely the condition that the group
$A_2(K_{\infty ,w})[\pi ^\infty ]$
is finite for every
$w \in \Sigma (K_\infty )$
in point (b) of the above theorem.
Remark 4.5 In order to give some evidence for the finiteness assumptions in the last two parts of Theorem 4.3, we mention some known results in the special setting of abelian varieties. In the following, we let A be an abelian variety defined over the number field K, and we consider
$\mathcal {O} = \mathbb {Z}_p$
.
Actually the following conditions are sufficient for ensuring finite torsion groups, i.e., not only finite p-torsion for some fixed prime p.
-
(i) If
$K_\infty /K$
is a finite extension, then the torsion subgroup of
$A(K_{\infty ,w})$
is finite for each prime w by the theorem of Mattuck (see [Reference MattuckMat55]). -
(ii) If A has potentially good and ordinary reduction at some prime q, then the torsion subgroup of
$A(K_{\infty ,w})$
is finite for each
$w \mid q$
if
$K_\infty $
is a finite extension of the cyclotomic
$\mathbb {Z}_q$
-extension of K (see [Reference ImaiIma75]). -
(iii) For global fields, more is known: let
$\Omega $
be the field obtained from K by adjoining all roots of unity in some fixed algebraic closure of K (i.e.,
$\Omega $
contains the cyclotomic
$\mathbb {Z}_q$
-extensions for all primes q). Then it follows from results of Ribet (see [Reference Katz and LangKL81, Appendix, Theorem 1]) that the torsion group of
$\Omega (A)$
is finite.
We conclude by mentioning a special setting, namely of an elliptic curve
$A = E$
defined over K, in which
$Y_{A, \Sigma }^{(K_\infty )}$
is known to be finitely generated over
$\mathcal {O} = \mathbb {Z}_p$
for an infinite non-p-extension
$K_\infty $
of K.
Example 4.6 Let N be an imaginary quadratic number field, and let E be an elliptic curve defined over N with complex multiplication by the ring of integers
$\mathcal {O}_N$
of N. Let
$q> 3$
be a prime of good reduction which splits in N,
$q \mathcal {O}_N = \mathfrak {q} \overline {\mathfrak {q}}$
. Let K be an abelian extension of N which is tamely ramified at
$\mathfrak {q}$
, and let
$K_\infty = K \cdot N(E[\mathfrak {q}^\infty ])$
.
Now suppose that
$p \ne q$
is a prime number which is co-prime with
$6 [K:N]$
. We assume that p splits in
$N/\mathbb {Q}$
, does not ramify in
$K/N$
and that E has good reduction at the primes of N above p. Let
$\Sigma $
be a finite set of primes of K which contains
$S_{\textrm {ram}}(K_\infty /K)$
,
$S_p$
and
$S_{\textrm {ram}}(E)$
. If
$E(K)[p] = \{0\}$
and
$E(K_v)[p] = \{0\}$
for every
$v \in \Sigma $
, then
$\textrm {rank}_{\mathbb {Z}_p}(Y_{E',\Sigma }^{(K_\infty )})$
is finite for every elliptic curve
$E'$
which is defined over K and satisfies
$S_{\textrm {ram}}(E') \subseteq \Sigma $
and
$E'[p] \cong E[p]$
as
$G_K$
-modules.
Indeed, by [Reference LamplughLam15, Theorem 1.2], the hypotheses of the above example imply that in fact the Pontryagin dual
$X_E^{(K_\infty )}$
of the (ordinary) Selmer group over
$K_\infty $
is finitely generated over
$\mathbb {Z}_p$
. Now we can apply Theorem 4.1.
Acknowledgment
We thank Dominik Bullach and Antonio Lei for their valuable comments on an earlier draft of this article. Moreover, we are grateful to the anonymous referees for suggesting several improvements.
