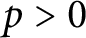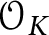1 Introduction
1.1
Let K be a complete discrete valuation field of characteristic
![]() $0$
, with residue field k of characteristic
$0$
, with residue field k of characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $\overline {K}$
be an algebraic closure of K, let
$\overline {K}$
be an algebraic closure of K, let
![]() $G_K$
be the Galois group of
$G_K$
be the Galois group of
![]() $\overline {K}$
over K, let C be the p-adic completion of
$\overline {K}$
over K, let C be the p-adic completion of
![]() $\overline {K}$
. We denote by
$\overline {K}$
. We denote by
![]() $C(r)$
the r-th Tate twist. For an abelian variety X over K, we denote its Tate module by
$C(r)$
the r-th Tate twist. For an abelian variety X over K, we denote its Tate module by
![]() $T_p(X)$
. When k is perfect and X has good reduction, Tate [Reference TateTat67] constructed a canonical
$T_p(X)$
. When k is perfect and X has good reduction, Tate [Reference TateTat67] constructed a canonical
![]() $G_K$
-equivariant exact sequence
$G_K$
-equivariant exact sequence
 $$ \begin{align} 0&\longrightarrow H^1(X,\mathcal{O}_X)\otimes_KC(1)\longrightarrow \operatorname{Hom}_{\mathbb{Z}_p}\big(T_p(X),C(1)\big) \\&\longrightarrow H^0(X,\Omega_{X/K}^1)\otimes_KC\longrightarrow 0.\nonumber \end{align} $$
$$ \begin{align} 0&\longrightarrow H^1(X,\mathcal{O}_X)\otimes_KC(1)\longrightarrow \operatorname{Hom}_{\mathbb{Z}_p}\big(T_p(X),C(1)\big) \\&\longrightarrow H^0(X,\Omega_{X/K}^1)\otimes_KC\longrightarrow 0.\nonumber \end{align} $$
In the same paper, Tate also computed the Galois cohomology groups of
![]() $C(r)$
. He proved in particular that
$C(r)$
. He proved in particular that
![]() $H^1(G_K,C(r))=0$
for any
$H^1(G_K,C(r))=0$
for any
![]() $r\neq 0$
, which implies that the sequence (1.1.1) has a
$r\neq 0$
, which implies that the sequence (1.1.1) has a
![]() $G_K$
-equivariant splitting, and that
$G_K$
-equivariant splitting, and that
![]() $H^0(G_K,C(r))=0$
for any
$H^0(G_K,C(r))=0$
for any
![]() $r\neq 0$
, which implies that the splitting is unique. Tate conjectured that for any proper smooth scheme X over K, there is a canonical
$r\neq 0$
, which implies that the splitting is unique. Tate conjectured that for any proper smooth scheme X over K, there is a canonical
![]() $G_K$
-equivariant decomposition (called the Hodge–Tate decomposition)
$G_K$
-equivariant decomposition (called the Hodge–Tate decomposition)
 $$\begin{align*}H^n_{\acute{\mathrm{e}}\mathrm{t}}(X_{\overline{K}},\mathbb{Q}_p)\otimes_{\mathbb{Q}_p}C=\bigoplus_{i=0}^n H^{i}(X,\Omega_{X/K}^{n-i})\otimes_K C(i-n). \end{align*}$$
$$\begin{align*}H^n_{\acute{\mathrm{e}}\mathrm{t}}(X_{\overline{K}},\mathbb{Q}_p)\otimes_{\mathbb{Q}_p}C=\bigoplus_{i=0}^n H^{i}(X,\Omega_{X/K}^{n-i})\otimes_K C(i-n). \end{align*}$$
Then subsequently, Raynaud used the semistable reduction theorem to show that any abelian variety over K admits a Hodge–Tate decomposition ([Reference Deligne, Raynaud, Rim and Grothendiecksga72, IX 3.6, 5.6]). Afterwards, Fontaine [Reference FontaineFon82] gave a new proof for general abelian varieties. He constructed a canonical map
 $H^0(X,\Omega _{X/K}^1)\to \mathrm {Hom}_{\mathbb {Z}_p[G_K]}(T_p(X),C(1))$
, by computing
$H^0(X,\Omega _{X/K}^1)\to \mathrm {Hom}_{\mathbb {Z}_p[G_K]}(T_p(X),C(1))$
, by computing
 $\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1$
and pulling back differentials. The conjecture of Tate was finally settled by Faltings [Reference FaltingsFal88, Reference FaltingsFal02] and Tsuji [Reference TsujiTsu99, Reference TsujiTsu02] independently.
$\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1$
and pulling back differentials. The conjecture of Tate was finally settled by Faltings [Reference FaltingsFal88, Reference FaltingsFal02] and Tsuji [Reference TsujiTsu99, Reference TsujiTsu02] independently.
When k is not necessarily perfect, Hyodo proved that there is still an exact sequence (1.1.1) for abelian varieties with good reduction, following the same argument as in [Reference TateTat67] ([Reference HyodoHyo86, Remark 1]). But the sequence does not split in general ([Reference HyodoHyo86, Theorem 3]). In this paper, we will construct the exact sequence (1.1.1) for general abelian varieties by generalizing Fontaine’s method to the imperfect residue field case.
We remark that Scholze [Reference ScholzeSch13] has generalized the conjecture of Tate to any proper smooth rigid-analytic variety X over C. He proved that there is a canonical filtration (called the Hodge–Tate filtration)
![]() $\operatorname {Fil}^\bullet $
on
$\operatorname {Fil}^\bullet $
on
![]() $H^{n}_{{\acute {\mathrm {e}}\mathrm {t}}}(X,\mathbb {Q}_p)\otimes _{\mathbb {Q}_p}C$
, such that
$H^{n}_{{\acute {\mathrm {e}}\mathrm {t}}}(X,\mathbb {Q}_p)\otimes _{\mathbb {Q}_p}C$
, such that
 $$\begin{align*}\operatorname{Fil}^i(H^{n}_{{\acute{\mathrm{e}}\mathrm{t}}}(X,\mathbb{Q}_p)\otimes_{\mathbb{Q}_p}C)/\operatorname{Fil}^{i+1} (H^{n}_{{\acute{\mathrm{e}}\mathrm{t}}}(X,\mathbb{Q}_p)\otimes_{\mathbb{Q}_p}C)=H^i(X,\Omega_{X/C}^{n-i})\otimes_CC(i-n). \end{align*}$$
$$\begin{align*}\operatorname{Fil}^i(H^{n}_{{\acute{\mathrm{e}}\mathrm{t}}}(X,\mathbb{Q}_p)\otimes_{\mathbb{Q}_p}C)/\operatorname{Fil}^{i+1} (H^{n}_{{\acute{\mathrm{e}}\mathrm{t}}}(X,\mathbb{Q}_p)\otimes_{\mathbb{Q}_p}C)=H^i(X,\Omega_{X/C}^{n-i})\otimes_CC(i-n). \end{align*}$$
1.2 For any abelian group M, we set
In Section 4, we construct a Faltings extension of
![]() $\mathcal {O}_K$
over
$\mathcal {O}_K$
over
![]() $\mathbb {Z}_p$
. It is a canonical exact sequence of C-
$\mathbb {Z}_p$
. It is a canonical exact sequence of C-
![]() $G_K$
-modules that splits as a sequence of C-modules (cf. Theorem 4.4),
$G_K$
-modules that splits as a sequence of C-modules (cf. Theorem 4.4),
 $$ \begin{align} 0\longrightarrow C(1)\stackrel{\iota}{\longrightarrow} V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1) \stackrel{\nu}{\longrightarrow}C\otimes_{\mathcal{O}_C}(\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K} \Omega_{\mathcal{O}_{K}/\mathbb{Z}_p}^1)^\wedge\longrightarrow 0, \end{align} $$
$$ \begin{align} 0\longrightarrow C(1)\stackrel{\iota}{\longrightarrow} V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1) \stackrel{\nu}{\longrightarrow}C\otimes_{\mathcal{O}_C}(\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K} \Omega_{\mathcal{O}_{K}/\mathbb{Z}_p}^1)^\wedge\longrightarrow 0, \end{align} $$
where
![]() $(-)^\wedge $
denotes the p-adic completion. Based on Hyodo’s computation of Galois cohomology (cf. Theorem 3.8), we will show that the connecting map of the above sequence
$(-)^\wedge $
denotes the p-adic completion. Based on Hyodo’s computation of Galois cohomology (cf. Theorem 3.8), we will show that the connecting map of the above sequence
 $$ \begin{align} \delta: \big(C\otimes_{\mathcal{O}_C}(\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K} \Omega_{\mathcal{O}_{K}/\mathbb{Z}_p}^1)^\wedge\big)^{G_K}\longrightarrow H^1(G_K,C(1)) \end{align} $$
$$ \begin{align} \delta: \big(C\otimes_{\mathcal{O}_C}(\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K} \Omega_{\mathcal{O}_{K}/\mathbb{Z}_p}^1)^\wedge\big)^{G_K}\longrightarrow H^1(G_K,C(1)) \end{align} $$
is an isomorphism (cf. Corollary 4.5).
Following Fontaine, we deduce from the above sequence and its cohomological properties a canonical K-linear injective homomorphism (cf. Theorem 5.6)
 $$ \begin{align} \rho:H^0(X,\Omega_{X/K}^1)\longrightarrow \operatorname{Hom}_{\mathbb{Z}_p[G_K]}(T_p(X),V_p (\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)). \end{align} $$
$$ \begin{align} \rho:H^0(X,\Omega_{X/K}^1)\longrightarrow \operatorname{Hom}_{\mathbb{Z}_p[G_K]}(T_p(X),V_p (\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)). \end{align} $$
The arguments are essentially the same as in [Reference FontaineFon82].
Our main result can be stated as follows (cf. Theorem 7.4 and Paragraphs, ).
Theorem 1.3 For any abelian variety X over K, there is a canonical exact sequence of C-
![]() $G_K$
-modules
$G_K$
-modules
 $$ \begin{align} 0\longrightarrow H^1(X,\mathcal{O}_X)\otimes_KC(1) & \stackrel{\psi}{\longrightarrow} \operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),C(1))\\ & \stackrel{\phi}{\longrightarrow} H^0(X,\Omega_{X/K}^1) \otimes_KC\longrightarrow 0 \nonumber \end{align} $$
$$ \begin{align} 0\longrightarrow H^1(X,\mathcal{O}_X)\otimes_KC(1) & \stackrel{\psi}{\longrightarrow} \operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),C(1))\\ & \stackrel{\phi}{\longrightarrow} H^0(X,\Omega_{X/K}^1) \otimes_KC\longrightarrow 0 \nonumber \end{align} $$
satisfying the following properties:
-
(i) Any C-linear retraction of
 $\iota $
in (1.2.1) induces a C-linear section of
$\iota $
in (1.2.1) induces a C-linear section of
 $\phi $
. More precisely, we have a commutative diagram
$\phi $
. More precisely, we have a commutative diagram
 where
where
 $\rho $
is induced by the map (1.2.3), and
$\rho $
is induced by the map (1.2.3), and
 $\pi $
is induced by any retraction of
$\pi $
is induced by any retraction of
 $\iota $
in (1.2.1).
$\iota $
in (1.2.1). -
(ii) The connecting map
 $\delta '$
associated with (1.3.1) fits into a commutative diagram
$\delta '$
associated with (1.3.1) fits into a commutative diagram
 where
where
 $\rho $
is the map (1.2.3),
$\rho $
is the map (1.2.3),
 $\pi '$
is induced by
$\pi '$
is induced by
 $-\nu $
of (1.2.1), and the unlabeled arrow is induced by
$-\nu $
of (1.2.1), and the unlabeled arrow is induced by
 $\delta ^{-1}$
(1.2.2) and
$\delta ^{-1}$
(1.2.2) and
 $\psi $
of (1.3.1).
$\psi $
of (1.3.1).
Corollary 1.4 For any abelian variety X over K, sequence (1.3.1) splits if and only if the image of
![]() $\rho $
(1.2.3) lies in
$\rho $
(1.2.3) lies in
![]() $\operatorname {Hom}_{\mathbb {Z}_p[G_K]}(T_p(X),C(1))$
. In fact, when it splits, the splitting is unique.
$\operatorname {Hom}_{\mathbb {Z}_p[G_K]}(T_p(X),C(1))$
. In fact, when it splits, the splitting is unique.
Remark 1.5 Caraiani and Scholze [Reference Caraiani and ScholzeCS17] constructed a relative version of Hodge–Tate filtration for proper smooth morphisms of adic spaces. And recently, Abbes and Gros [Reference Abbes and GrosAG20] constructed a relative version of Hodge–Tate spectral sequence for projective smooth morphisms of logarithmic schemes. Unlike these works that rely on advanced theories and results, our proof for abelian varieties uses only basic algebraic geometry and p-adic Galois cohomology computation of Tate and Hyodo. For instance, we do not use Faltings’ almost purity theorem.
2 Notation
2.1
Let K be a complete discrete valuation field of characteristic
![]() $0$
, with residue field k of characteristic
$0$
, with residue field k of characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $\overline {K}$
be an algebraic closure of K, let
$\overline {K}$
be an algebraic closure of K, let
![]() $G_K$
be the Galois group of
$G_K$
be the Galois group of
![]() $\overline {K}$
over K. Let C be the p-adic completion of
$\overline {K}$
over K. Let C be the p-adic completion of
![]() $\overline {K}$
,
$\overline {K}$
,
![]() $v_p$
the valuation on C such that
$v_p$
the valuation on C such that
![]() $v_p(p)=1$
,
$v_p(p)=1$
,
![]() $|\ |_p$
the absolute value on C such that
$|\ |_p$
the absolute value on C such that
![]() $|p|_p=1/p$
. We fix a complete discrete valuation subfield
$|p|_p=1/p$
. We fix a complete discrete valuation subfield
![]() $K_0$
of K such that
$K_0$
of K such that
![]() $\mathcal {O}_{K_0}/p\mathcal {O}_{K_0}=k$
(by Cohen structure theorem, cf. [Reference GrothendieckGro64,
$\mathcal {O}_{K_0}/p\mathcal {O}_{K_0}=k$
(by Cohen structure theorem, cf. [Reference GrothendieckGro64,
![]() ${0}_{IV}$
19.8.6]). We remark that
${0}_{IV}$
19.8.6]). We remark that
![]() $K/K_0$
is a totally ramified finite extension. We fix elements
$K/K_0$
is a totally ramified finite extension. We fix elements
![]() $(u_i)_{i\in I}$
of
$(u_i)_{i\in I}$
of
![]() $\mathcal {O}_{K_0}$
such that the reductions
$\mathcal {O}_{K_0}$
such that the reductions
![]() $(\overline {u_i})_{i\in I}$
form a p-base of k. For each
$(\overline {u_i})_{i\in I}$
form a p-base of k. For each
![]() $i\in I$
, we fix elements
$i\in I$
, we fix elements
![]() $(w_{im})_{m\geq 0}$
of
$(w_{im})_{m\geq 0}$
of
![]() $\mathcal {O}_{\overline {K}}$
such that
$\mathcal {O}_{\overline {K}}$
such that
 $w_{i,m+1}^p=w_{i,m}$
and
$w_{i,m+1}^p=w_{i,m}$
and
![]() $w_{i,0}=u_i$
. We denote by
$w_{i,0}=u_i$
. We denote by
![]() $(e_i)_{i\in I}$
the standard basis of
$(e_i)_{i\in I}$
the standard basis of
![]() $\oplus _{i\in I} \mathbb {Z}$
.
$\oplus _{i\in I} \mathbb {Z}$
.
2.2
For any discrete valuation field L of characteristic
![]() $0$
, with residue field of characteristic p, we denote by
$0$
, with residue field of characteristic p, we denote by
 $$\begin{align*}\hat{\Omega}_{\mathcal{O}_L}^1=(\Omega_{\mathcal{O}_{L}/\mathbb{Z}_p}^1)^\wedge \end{align*}$$
$$\begin{align*}\hat{\Omega}_{\mathcal{O}_L}^1=(\Omega_{\mathcal{O}_{L}/\mathbb{Z}_p}^1)^\wedge \end{align*}$$
the p-adic completion of the module of differentials of
![]() $\mathcal {O}_L$
over
$\mathcal {O}_L$
over
![]() $\mathbb {Z}_p$
.
$\mathbb {Z}_p$
.
For any algebraic extension
![]() $L'$
over L, we set
$L'$
over L, we set
 $$\begin{align*}\hat{\Omega}_{\mathcal{O}_{L}}^1(\mathcal{O}_{L'})=\mathop{\mathrm{colim}}_{L_1/L}\ \hat{\Omega}_{\mathcal{O}_{L_1}}^1, \end{align*}$$
$$\begin{align*}\hat{\Omega}_{\mathcal{O}_{L}}^1(\mathcal{O}_{L'})=\mathop{\mathrm{colim}}_{L_1/L}\ \hat{\Omega}_{\mathcal{O}_{L_1}}^1, \end{align*}$$
where
![]() $L_1$
runs through all finite subextensions of
$L_1$
runs through all finite subextensions of
![]() $L'/L$
. We remark that
$L'/L$
. We remark that
 $\hat {\Omega }_{\mathcal {O}_{L}}^1(\mathcal {O}_{L'})=\hat {\Omega }_{\mathcal {O}_{L_1}}^1(\mathcal {O}_{L'})$
for any finite subextension
$\hat {\Omega }_{\mathcal {O}_{L}}^1(\mathcal {O}_{L'})=\hat {\Omega }_{\mathcal {O}_{L_1}}^1(\mathcal {O}_{L'})$
for any finite subextension
![]() $L_1$
of
$L_1$
of
![]() $L'/L$
, and that
$L'/L$
, and that
 $\hat {\Omega }_{\mathcal {O}_{L}}^1(\mathcal {O}_{L})=\hat {\Omega }_{\mathcal {O}_L}^1$
.
2.3
For any abelian group M, we define
$\hat {\Omega }_{\mathcal {O}_{L}}^1(\mathcal {O}_{L})=\hat {\Omega }_{\mathcal {O}_L}^1$
.
2.3
For any abelian group M, we define
 $$ \begin{align*} T_p(M)&=\varprojlim_{x\mapsto px} M[p^n]=\operatorname{Hom}_{\mathbb{Z}}(\mathbb{Z}[1/p]/\mathbb{Z},M),\nonumber\\ V_p(M)&=\varprojlim_{x\mapsto px} M=\operatorname{Hom}_{\mathbb{Z}}(\mathbb{Z}[1/p],M). \end{align*} $$
$$ \begin{align*} T_p(M)&=\varprojlim_{x\mapsto px} M[p^n]=\operatorname{Hom}_{\mathbb{Z}}(\mathbb{Z}[1/p]/\mathbb{Z},M),\nonumber\\ V_p(M)&=\varprojlim_{x\mapsto px} M=\operatorname{Hom}_{\mathbb{Z}}(\mathbb{Z}[1/p],M). \end{align*} $$
Being an inverse limit of
![]() $\mathbb {Z}$
-modules each killed by some power of p,
$\mathbb {Z}$
-modules each killed by some power of p,
![]() $T_p(M)$
is a p-adically complete
$T_p(M)$
is a p-adically complete
![]() $\mathbb {Z}_p$
-module ([Reference JannsenJan88, 4.4]). If M is p-primary torsion, then
$\mathbb {Z}_p$
-module ([Reference JannsenJan88, 4.4]). If M is p-primary torsion, then
![]() $V_p(M)=T_p(M)\otimes _{\mathbb {Z}_p}\mathbb {Q}_p$
, and thus it has a natural
$V_p(M)=T_p(M)\otimes _{\mathbb {Z}_p}\mathbb {Q}_p$
, and thus it has a natural
![]() $\mathbb {Q}_p$
-module structure. If M is a
$\mathbb {Q}_p$
-module structure. If M is a
![]() $\mathbb {Z}_p$
-module, then
$\mathbb {Z}_p$
-module, then
![]() $T_p(M)=\operatorname {Hom}_{\mathbb {Z}_p}(\mathbb {Q}_p/\mathbb {Z}_p,M)$
,
$T_p(M)=\operatorname {Hom}_{\mathbb {Z}_p}(\mathbb {Q}_p/\mathbb {Z}_p,M)$
,
![]() $V_p(M)=\operatorname {Hom}_{\mathbb {Z}_p}(\mathbb {Q}_p,M)$
. We set
$V_p(M)=\operatorname {Hom}_{\mathbb {Z}_p}(\mathbb {Q}_p,M)$
. We set
 $\mathbb {Z}_p(1)=T_p(\mathcal {O}_{\overline {K}}^\times )$
, a free
$\mathbb {Z}_p(1)=T_p(\mathcal {O}_{\overline {K}}^\times )$
, a free
![]() $\mathbb {Z}_p$
-module of rank
$\mathbb {Z}_p$
-module of rank
![]() $1$
with continuous
$1$
with continuous
![]() $G_K$
-action. For any
$G_K$
-action. For any
![]() $\mathbb {Z}_p$
-module M and
$\mathbb {Z}_p$
-module M and
![]() $r\in \mathbb {Z}$
, we set
$r\in \mathbb {Z}$
, we set
![]() $M(r)=M\otimes _{\mathbb {Z}_p}\mathbb {Z}_p(1)^{\otimes r}$
, the r-th Tate twist of M. Let X be an abelian variety over K. We set
$M(r)=M\otimes _{\mathbb {Z}_p}\mathbb {Z}_p(1)^{\otimes r}$
, the r-th Tate twist of M. Let X be an abelian variety over K. We set
 $T_p(X)=T_p(X(\overline {K}))$
and
$T_p(X)=T_p(X(\overline {K}))$
and
 $V_p(X)=V_p(X(\overline {K}))$
.
$V_p(X)=V_p(X(\overline {K}))$
.
3 Review of Hyodo’s Computation of Galois Cohomology Groups of
 $C(r)$
$C(r)$
Lemma 3.1 Let
![]() $B/A$
be a finite extension of discrete valuation rings, whose fraction field extension and residue field extension are both separable. We assume that A is henselian, or that
$B/A$
be a finite extension of discrete valuation rings, whose fraction field extension and residue field extension are both separable. We assume that A is henselian, or that
![]() $B/A$
is totally ramified. Let R be a subring of A. Then the canonical map
$B/A$
is totally ramified. Let R be a subring of A. Then the canonical map
 $B\otimes _A \Omega _{A/R}^1\to \Omega _{B/R}^1$
is injective.
$B\otimes _A \Omega _{A/R}^1\to \Omega _{B/R}^1$
is injective.
Proof After replacing A by its maximal unramified extension in B, we can assume that B is totally ramified over A. Hence, B is of the form
![]() $A[X]/(f(X))$
for some irreducible polynomial
$A[X]/(f(X))$
for some irreducible polynomial
![]() $f\in A[X]$
. Let x be the image of X in B. Then we have
$f\in A[X]$
. Let x be the image of X in B. Then we have
 $$\begin{align*}\Omega_{B/R}^1=(B\otimes_A\Omega_{A/R}^1\oplus B\mathrm{d} X)/B(\mathrm{d}_Af(x)+f'(x)\mathrm{d} X), \end{align*}$$
$$\begin{align*}\Omega_{B/R}^1=(B\otimes_A\Omega_{A/R}^1\oplus B\mathrm{d} X)/B(\mathrm{d}_Af(x)+f'(x)\mathrm{d} X), \end{align*}$$
where
 $\mathrm {d}_A f\in A[X]\otimes _A \Omega _{A/R}^1$
is obtained by differentiating the coefficients of f. Since
$\mathrm {d}_A f\in A[X]\otimes _A \Omega _{A/R}^1$
is obtained by differentiating the coefficients of f. Since
![]() $f'(x)\neq 0$
, the canonical map
$f'(x)\neq 0$
, the canonical map
 $B\otimes _A\Omega _{A/R}^1\to \Omega _{B/R}^1$
is injective. ▪
$B\otimes _A\Omega _{A/R}^1\to \Omega _{B/R}^1$
is injective. ▪
Lemma 3.2 ([Reference HyodoHyo86, 4-4])
There is an isomorphism of
![]() $\mathcal {O}_{K_0}$
-modules
$\mathcal {O}_{K_0}$
-modules
 $$\begin{align*}(\oplus_{i\in I}\mathcal{O}_{K_0})^\wedge\stackrel{\sim}{\longrightarrow} \hat{\Omega}_{\mathcal{O}_{K_0}}^1 ,\quad e_i\longmapsto \mathrm{d}\log u_i,\quad \forall i\in I. \end{align*}$$
$$\begin{align*}(\oplus_{i\in I}\mathcal{O}_{K_0})^\wedge\stackrel{\sim}{\longrightarrow} \hat{\Omega}_{\mathcal{O}_{K_0}}^1 ,\quad e_i\longmapsto \mathrm{d}\log u_i,\quad \forall i\in I. \end{align*}$$
Proof As
![]() $(\overline {u_i})_{i\in I}$
form a p-base of the residue field of
$(\overline {u_i})_{i\in I}$
form a p-base of the residue field of
![]() $\mathcal {O}_{K_0}$
, we have
$\mathcal {O}_{K_0}$
, we have
 $\Omega _{\mathcal {O}_{K_0}/\mathbb {Z}_p}^1\otimes _{\mathbb {Z}_p}\mathbb {Z}_p/p\mathbb {Z}_p=\Omega _{k/\mathbb {F}_p}^1= \oplus _{i\in I}k$
, where
$\Omega _{\mathcal {O}_{K_0}/\mathbb {Z}_p}^1\otimes _{\mathbb {Z}_p}\mathbb {Z}_p/p\mathbb {Z}_p=\Omega _{k/\mathbb {F}_p}^1= \oplus _{i\in I}k$
, where
![]() $e_i$
corresponds to
$e_i$
corresponds to
![]() $\mathrm {d}\log \overline {u_i}$
. Since
$\mathrm {d}\log \overline {u_i}$
. Since
![]() $\mathcal {O}_{K_0}$
is flat over
$\mathcal {O}_{K_0}$
is flat over
![]() $\mathbb {Z}_p$
and k is formally smooth over
$\mathbb {Z}_p$
and k is formally smooth over
![]() $\mathbb {F}_p$
,
$\mathbb {F}_p$
,
![]() $\mathcal {O}_{K_0}/p^n\mathcal {O}_{K_0}$
is formally smooth over
$\mathcal {O}_{K_0}/p^n\mathcal {O}_{K_0}$
is formally smooth over
![]() $\mathbb {Z}_p/p^n\mathbb {Z}_p$
for each
$\mathbb {Z}_p/p^n\mathbb {Z}_p$
for each
![]() $n\geq 1$
([Reference GrothendieckGro64,
$n\geq 1$
([Reference GrothendieckGro64,
![]() ${0}_{IV}$
19.7.1], [Sta20, 031L]). In particular,
${0}_{IV}$
19.7.1], [Sta20, 031L]). In particular,
 $\Omega _{\mathcal {O}_{K_0}/\mathbb {Z}_p}^1\otimes \mathbb {Z}_p/p^n\mathbb {Z}_p$
is a projective
$\Omega _{\mathcal {O}_{K_0}/\mathbb {Z}_p}^1\otimes \mathbb {Z}_p/p^n\mathbb {Z}_p$
is a projective
![]() $\mathcal {O}_{K_0}/p^n\mathcal {O}_{K_0}$
-module. Hence, we have an exact sequence
$\mathcal {O}_{K_0}/p^n\mathcal {O}_{K_0}$
-module. Hence, we have an exact sequence
 $$ \begin{align*} 0\longrightarrow \Omega_{\mathcal{O}_{K_0}/\mathbb{Z}_p}^1\otimes\mathbb{Z}_p/p\mathbb{Z}_p & \stackrel{\cdot p^{n-1}}{\longrightarrow} \Omega_{\mathcal{O}_{K_0}/\mathbb{Z}_p}^1 \otimes\mathbb{Z}_p/p^n\mathbb{Z}_p \\ & \longrightarrow \Omega_{\mathcal{O}_{K_0}/\mathbb{Z}_p}^1\otimes\mathbb{Z}_p/p^{n-1}\mathbb{Z}_p\longrightarrow 0, \end{align*} $$
$$ \begin{align*} 0\longrightarrow \Omega_{\mathcal{O}_{K_0}/\mathbb{Z}_p}^1\otimes\mathbb{Z}_p/p\mathbb{Z}_p & \stackrel{\cdot p^{n-1}}{\longrightarrow} \Omega_{\mathcal{O}_{K_0}/\mathbb{Z}_p}^1 \otimes\mathbb{Z}_p/p^n\mathbb{Z}_p \\ & \longrightarrow \Omega_{\mathcal{O}_{K_0}/\mathbb{Z}_p}^1\otimes\mathbb{Z}_p/p^{n-1}\mathbb{Z}_p\longrightarrow 0, \end{align*} $$
from which we get isomorphisms
 $\oplus _{i\in I}\mathcal {O}_{K_0}/p^n\mathcal {O}_{K_0}\stackrel {\sim }{\to }\Omega _{\mathcal {O}_{K_0}/\mathbb {Z}_p}^1\otimes \mathbb {Z}_p/p^n\mathbb {Z}_p$
by induction. The conclusion follows by taking limit over n.▪
$\oplus _{i\in I}\mathcal {O}_{K_0}/p^n\mathcal {O}_{K_0}\stackrel {\sim }{\to }\Omega _{\mathcal {O}_{K_0}/\mathbb {Z}_p}^1\otimes \mathbb {Z}_p/p^n\mathbb {Z}_p$
by induction. The conclusion follows by taking limit over n.▪
Proposition 3.3 ([Reference HyodoHyo86, 4-2-1])
There is an exact sequence of
![]() $\mathcal {O}_K$
-modules
$\mathcal {O}_K$
-modules
 $$\begin{align*}0\longrightarrow (\oplus_{i\in I}\mathcal{O}_K)^\wedge\stackrel{\theta}{\longrightarrow} \hat{\Omega}_{\mathcal{O}_K}^1\longrightarrow \Omega_{\mathcal{O}_K/\mathcal{O}_{K_0}}^1\longrightarrow 0, \end{align*}$$
$$\begin{align*}0\longrightarrow (\oplus_{i\in I}\mathcal{O}_K)^\wedge\stackrel{\theta}{\longrightarrow} \hat{\Omega}_{\mathcal{O}_K}^1\longrightarrow \Omega_{\mathcal{O}_K/\mathcal{O}_{K_0}}^1\longrightarrow 0, \end{align*}$$
where
![]() $\theta (e_i)=\mathrm {d}\log u_i$
for any
$\theta (e_i)=\mathrm {d}\log u_i$
for any
![]() $i\in I$
.
$i\in I$
.
Proof The sequence of modules of differentials of
![]() $\mathcal {O}_K/\mathcal {O}_{K_0}/\mathbb {Z}_p$
,
$\mathcal {O}_K/\mathcal {O}_{K_0}/\mathbb {Z}_p$
,
 $$\begin{align*}0\longrightarrow \mathcal{O}_K\otimes_{\mathcal{O}_{K_0}}\Omega_{\mathcal{O}_{K_0}/\mathbb{Z}_p}^1\longrightarrow \Omega_{\mathcal{O}_{K}/\mathbb{Z}_p}^1\longrightarrow \Omega_{\mathcal{O}_K/\mathcal{O}_{K_0}}^1\longrightarrow 0, \end{align*}$$
$$\begin{align*}0\longrightarrow \mathcal{O}_K\otimes_{\mathcal{O}_{K_0}}\Omega_{\mathcal{O}_{K_0}/\mathbb{Z}_p}^1\longrightarrow \Omega_{\mathcal{O}_{K}/\mathbb{Z}_p}^1\longrightarrow \Omega_{\mathcal{O}_K/\mathcal{O}_{K_0}}^1\longrightarrow 0, \end{align*}$$
is exact by Lemma 3.1. Passing to p-adic completions, as
 $\Omega _{\mathcal {O}_K/\mathcal {O}_{K_0}}^1$
is killed by a power of p, we still get an exact sequence [Sta20, 0BNG]. The conclusion follows from Lemma 3.2, and the isomorphism
$\Omega _{\mathcal {O}_K/\mathcal {O}_{K_0}}^1$
is killed by a power of p, we still get an exact sequence [Sta20, 0BNG]. The conclusion follows from Lemma 3.2, and the isomorphism
 $\mathcal {O}_K\otimes _{\mathcal {O}_{K_0}} (\oplus _{i\in I}\mathcal {O}_{K_0})^\wedge \stackrel {\sim }{\to } (\oplus _{i\in I}\mathcal {O}_{K})^\wedge $
as
$\mathcal {O}_K\otimes _{\mathcal {O}_{K_0}} (\oplus _{i\in I}\mathcal {O}_{K_0})^\wedge \stackrel {\sim }{\to } (\oplus _{i\in I}\mathcal {O}_{K})^\wedge $
as
![]() $\mathcal {O}_K$
is finite free over
$\mathcal {O}_K$
is finite free over
![]() $\mathcal {O}_{K_0}$
.▪
$\mathcal {O}_{K_0}$
.▪
Lemma 3.4 ([Reference HyodoHyo86, 4-4])
Let
![]() $M_0=\bigcup _{i\in I,m\geq 0}K_0(w_{im})\subseteq \overline {K}$
. Then there is an isomorphism of
$M_0=\bigcup _{i\in I,m\geq 0}K_0(w_{im})\subseteq \overline {K}$
. Then there is an isomorphism of
![]() $\mathcal {O}_{M_0}$
-modules
$\mathcal {O}_{M_0}$
-modules
 $$\begin{align*}M_0\otimes_{\mathcal{O}_{K_0}}(\oplus_{i\in I}\mathcal{O}_{K_0})^\wedge\stackrel{\sim}{\longrightarrow} \hat{\Omega}_{\mathcal{O}_{K_0}}^1(\mathcal{O}_{M_0}),\quad p^{-m}\otimes e_i\longmapsto \mathrm{d}\log w_{im},\ \forall i\in I,m\in \mathbb{N}. \end{align*}$$
$$\begin{align*}M_0\otimes_{\mathcal{O}_{K_0}}(\oplus_{i\in I}\mathcal{O}_{K_0})^\wedge\stackrel{\sim}{\longrightarrow} \hat{\Omega}_{\mathcal{O}_{K_0}}^1(\mathcal{O}_{M_0}),\quad p^{-m}\otimes e_i\longmapsto \mathrm{d}\log w_{im},\ \forall i\in I,m\in \mathbb{N}. \end{align*}$$
Proof For an integer
![]() $N>0$
and a finite subset
$N>0$
and a finite subset
![]() $J\subseteq I$
, let
$J\subseteq I$
, let
![]() $L_0=\bigcup _{i\in J}K_0(w_{iN})$
. Then by Lemma 3.2,
$L_0=\bigcup _{i\in J}K_0(w_{iN})$
. Then by Lemma 3.2,
![]() $(\oplus _{i\in I}\mathcal {O}_{L_0})^\wedge $
is isomorphic to
$(\oplus _{i\in I}\mathcal {O}_{L_0})^\wedge $
is isomorphic to
 $\hat {\Omega }_{\mathcal {O}_{L_0}}^1$
by sending
$\hat {\Omega }_{\mathcal {O}_{L_0}}^1$
by sending
![]() $e_i$
to
$e_i$
to
![]() $\mathrm {d}\log w_{iN}$
if
$\mathrm {d}\log w_{iN}$
if
![]() $i\in J$
, and to
$i\in J$
, and to
![]() $\mathrm {d}\log u_i$
if
$\mathrm {d}\log u_i$
if
![]() $i\notin J$
. The conclusion follows by taking colimit over J and N. ▪
$i\notin J$
. The conclusion follows by taking colimit over J and N. ▪
Lemma 3.5 ([Reference HyodoHyo86, 4-7])
With the same notation as in Lemma 3.4, let M be a finite extension of
![]() $M_0$
. Then there is a canonical exact sequence of
$M_0$
. Then there is a canonical exact sequence of
![]() $\mathcal {O}_M$
-modules
$\mathcal {O}_M$
-modules
 $$\begin{align*}0\longrightarrow \mathcal{O}_{M}\otimes_{\mathcal{O}_{M_0}}\hat{\Omega}_{\mathcal{O}_{K_0}}^1(\mathcal{O}_{M_0}) \longrightarrow \hat{\Omega}_{\mathcal{O}_{K_0}}^1(\mathcal{O}_{M})\longrightarrow \Omega_{\mathcal{O}_M/\mathcal{O}_{M_0}}^1 \longrightarrow 0. \end{align*}$$
$$\begin{align*}0\longrightarrow \mathcal{O}_{M}\otimes_{\mathcal{O}_{M_0}}\hat{\Omega}_{\mathcal{O}_{K_0}}^1(\mathcal{O}_{M_0}) \longrightarrow \hat{\Omega}_{\mathcal{O}_{K_0}}^1(\mathcal{O}_{M})\longrightarrow \Omega_{\mathcal{O}_M/\mathcal{O}_{M_0}}^1 \longrightarrow 0. \end{align*}$$
Proof We notice that
![]() $\mathcal {O}_{M_0}$
is a henselian discrete valuation ring with perfect residue field. Let
$\mathcal {O}_{M_0}$
is a henselian discrete valuation ring with perfect residue field. Let
![]() $M_{\operatorname {ur}}$
be the maximal unramified subextension of
$M_{\operatorname {ur}}$
be the maximal unramified subextension of
![]() $M/M_0$
, and let
$M/M_0$
, and let
![]() $f\in \mathcal {O}_{M_{\operatorname {ur}}}[X]$
be the monic minimal polynomial of a uniformizer
$f\in \mathcal {O}_{M_{\operatorname {ur}}}[X]$
be the monic minimal polynomial of a uniformizer
![]() $\varpi $
of
$\varpi $
of
![]() $\mathcal {O}_M$
. Then we have
$\mathcal {O}_M$
. Then we have
![]() $\mathcal {O}_M=\mathcal {O}_{M_{\operatorname {ur}}}[X]/(f(X))$
. For a sufficiently large finite subextension
$\mathcal {O}_M=\mathcal {O}_{M_{\operatorname {ur}}}[X]/(f(X))$
. For a sufficiently large finite subextension
![]() $L_1$
of
$L_1$
of
![]() $M_{\operatorname {ur}}/K_0$
such that
$M_{\operatorname {ur}}/K_0$
such that
![]() $f\in \mathcal {O}_{L_1}[X]$
,
$f\in \mathcal {O}_{L_1}[X]$
,
![]() $L_2=L_1(\varpi )$
is totally ramified over
$L_2=L_1(\varpi )$
is totally ramified over
![]() $L_1$
. The same argument as in Proposition 3.3 gives us a canonical exact sequence
$L_1$
. The same argument as in Proposition 3.3 gives us a canonical exact sequence
 $$\begin{align*}0\longrightarrow \mathcal{O}_{L_2}\otimes_{\mathcal{O}_{L_1}}\hat{\Omega}_{\mathcal{O}_{L_1}}^1 \longrightarrow \hat{\Omega}_{\mathcal{O}_{L_2}}^1\longrightarrow \Omega_{\mathcal{O}_{L_2}/\mathcal{O}_{L_1}}^1 \longrightarrow 0. \end{align*}$$
$$\begin{align*}0\longrightarrow \mathcal{O}_{L_2}\otimes_{\mathcal{O}_{L_1}}\hat{\Omega}_{\mathcal{O}_{L_1}}^1 \longrightarrow \hat{\Omega}_{\mathcal{O}_{L_2}}^1\longrightarrow \Omega_{\mathcal{O}_{L_2}/\mathcal{O}_{L_1}}^1 \longrightarrow 0. \end{align*}$$
By taking colimit over
![]() $L_1$
, we get an exact sequence
$L_1$
, we get an exact sequence
 $$ \begin{align} 0\longrightarrow\mathcal{O}_{M}\otimes_{\mathcal{O}_{M_{\operatorname{ur}}}}\hat{\Omega}_{\mathcal{O}_{K_0}}^1(\mathcal{O}_{M_{\operatorname{ur}}}) \longrightarrow\hat{\Omega}_{\mathcal{O}_{K_0}}^1(\mathcal{O}_{M})\longrightarrow \Omega_{\mathcal{O}_M/\mathcal{O}_{M_{\operatorname{ur}}}}^1\longrightarrow 0. \end{align} $$
$$ \begin{align} 0\longrightarrow\mathcal{O}_{M}\otimes_{\mathcal{O}_{M_{\operatorname{ur}}}}\hat{\Omega}_{\mathcal{O}_{K_0}}^1(\mathcal{O}_{M_{\operatorname{ur}}}) \longrightarrow\hat{\Omega}_{\mathcal{O}_{K_0}}^1(\mathcal{O}_{M})\longrightarrow \Omega_{\mathcal{O}_M/\mathcal{O}_{M_{\operatorname{ur}}}}^1\longrightarrow 0. \end{align} $$
A similar colimit argument shows that
 $\hat {\Omega }_{\mathcal {O}_{K_0}}^1(\mathcal {O}_{M_{\operatorname {ur}}})=\mathcal {O}_{M_{\operatorname {ur}}}\otimes _{\mathcal {O}_{M_0}}\hat {\Omega }_{\mathcal {O}_{K_0}}^1(\mathcal {O}_{M_{0}})$
. The conclusion follows from (3.5.1). ▪
$\hat {\Omega }_{\mathcal {O}_{K_0}}^1(\mathcal {O}_{M_{\operatorname {ur}}})=\mathcal {O}_{M_{\operatorname {ur}}}\otimes _{\mathcal {O}_{M_0}}\hat {\Omega }_{\mathcal {O}_{K_0}}^1(\mathcal {O}_{M_{0}})$
. The conclusion follows from (3.5.1). ▪
Proposition 3.6 ([Reference HyodoHyo86, 4-2-2])
There is an exact sequence of
![]() $\mathcal {O}_{\overline {K}}$
-
$\mathcal {O}_{\overline {K}}$
-
![]() $G_K$
-modules that splits as a sequence of
$G_K$
-modules that splits as a sequence of
![]() $\mathcal {O}_{\overline {K}}$
-modules,
$\mathcal {O}_{\overline {K}}$
-modules,
 $$ \begin{align} 0\longrightarrow \overline{K}/\mathfrak{a}(1)\stackrel{\vartheta}{\longrightarrow} \hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})\longrightarrow \overline{K}\otimes_{\mathcal{O}_K}(\oplus_{i\in I}\mathcal{O}_K)^\wedge\longrightarrow 0, \end{align} $$
$$ \begin{align} 0\longrightarrow \overline{K}/\mathfrak{a}(1)\stackrel{\vartheta}{\longrightarrow} \hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})\longrightarrow \overline{K}\otimes_{\mathcal{O}_K}(\oplus_{i\in I}\mathcal{O}_K)^\wedge\longrightarrow 0, \end{align} $$
where
 $\mathfrak {a}=\{x\in \overline {K}\ |\ v_p(x)\geq -1/(p-1)\}$
, and
$\mathfrak {a}=\{x\in \overline {K}\ |\ v_p(x)\geq -1/(p-1)\}$
, and
![]() $\vartheta (p^{-k}\otimes (\zeta _n)_n)=\mathrm {d}\log \zeta _k$
for any
$\vartheta (p^{-k}\otimes (\zeta _n)_n)=\mathrm {d}\log \zeta _k$
for any
![]() $k\in \mathbb {N}$
and any
$k\in \mathbb {N}$
and any
![]() $(\zeta _n)_n\in \mathbb {Z}_p(1)$
. The map
$(\zeta _n)_n\in \mathbb {Z}_p(1)$
. The map
 $\overline {K}\otimes _{\mathcal {O}_K}(\oplus _{i\in I}\mathcal {O}_K)^\wedge \to \hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}})$
, sending
$\overline {K}\otimes _{\mathcal {O}_K}(\oplus _{i\in I}\mathcal {O}_K)^\wedge \to \hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}})$
, sending
![]() $p^{-m}\otimes e_i$
to
$p^{-m}\otimes e_i$
to
![]() $\mathrm {d}\log w_{im}$
for any
$\mathrm {d}\log w_{im}$
for any
![]() $i\in I$
and
$i\in I$
and
![]() $m\in \mathbb {N}$
, gives a splitting of the sequence.
$m\in \mathbb {N}$
, gives a splitting of the sequence.
Proof With the same notation as in Lemma 3.4, let M run through all finite subextensions of
![]() $\overline {K}/M_0$
. We get from Lemma 3.5 an exact sequence of
$\overline {K}/M_0$
. We get from Lemma 3.5 an exact sequence of
![]() $\mathcal {O}_{\overline {K}}$
-modules
$\mathcal {O}_{\overline {K}}$
-modules
 $$ \begin{align} 0\longrightarrow\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_{M_0}}\hat{\Omega}_{\mathcal{O}_{K_0}}^1(\mathcal{O}_{M_0}) \longrightarrow\hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})\longrightarrow \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_{M_0}}^1 \longrightarrow 0. \end{align} $$
$$ \begin{align} 0\longrightarrow\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_{M_0}}\hat{\Omega}_{\mathcal{O}_{K_0}}^1(\mathcal{O}_{M_0}) \longrightarrow\hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})\longrightarrow \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_{M_0}}^1 \longrightarrow 0. \end{align} $$
We identify its first term with
![]() $\overline {K}\otimes _{\mathcal {O}_K}(\oplus _{i\in I}\mathcal {O}_K)^\wedge $
by Lemma 3.4. Let
$\overline {K}\otimes _{\mathcal {O}_K}(\oplus _{i\in I}\mathcal {O}_K)^\wedge $
by Lemma 3.4. Let
 $\overline {\mathbb {Q}_p}$
be the algebraic closure of
$\overline {\mathbb {Q}_p}$
be the algebraic closure of
![]() $\mathbb {Q}_p$
in
$\mathbb {Q}_p$
in
![]() $\overline {K}$
,
$\overline {K}$
,
![]() $\overline {\mathbb {Z}_p}$
the integral closure of
$\overline {\mathbb {Z}_p}$
the integral closure of
![]() $\mathbb {Z}_p$
in
$\mathbb {Z}_p$
in
 $\overline {\mathbb {Q}_p}$
. By Fontaine’s computation [Reference FontaineFon82, Théorème 1′], we have an isomorphism of
$\overline {\mathbb {Q}_p}$
. By Fontaine’s computation [Reference FontaineFon82, Théorème 1′], we have an isomorphism of
![]() $\overline {\mathbb {Z}_p}$
-modules
$\overline {\mathbb {Z}_p}$
-modules
 $$\begin{align*}\overline{\mathbb{Q}_p}/\mathfrak{a}_0(1)\stackrel{\sim}{\longrightarrow} \Omega_{\overline{\mathbb{Z}_p}/\mathbb{Z}_p}^1,\quad p^{-k}\otimes (\zeta_n)_n\longmapsto \mathrm{d}\log \zeta_k,\quad \forall k\in \mathbb{N},\quad \forall (\zeta_n)_n\in \mathbb{Z}_p(1), \end{align*}$$
$$\begin{align*}\overline{\mathbb{Q}_p}/\mathfrak{a}_0(1)\stackrel{\sim}{\longrightarrow} \Omega_{\overline{\mathbb{Z}_p}/\mathbb{Z}_p}^1,\quad p^{-k}\otimes (\zeta_n)_n\longmapsto \mathrm{d}\log \zeta_k,\quad \forall k\in \mathbb{N},\quad \forall (\zeta_n)_n\in \mathbb{Z}_p(1), \end{align*}$$
where
 $\mathfrak {a}_0=\{x\in \overline {\mathbb {Q}_p}\ |\ v_p(x)\geq -1/(p-1)\}$
, and we have an isomorphism of
$\mathfrak {a}_0=\{x\in \overline {\mathbb {Q}_p}\ |\ v_p(x)\geq -1/(p-1)\}$
, and we have an isomorphism of
![]() $\mathcal {O}_{\overline {K}}$
-modules
$\mathcal {O}_{\overline {K}}$
-modules
 $$\begin{align*}\overline{K}/\mathfrak{a}(1)\stackrel{\sim}{\longrightarrow}\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_{M_0}}^1,\quad p^{-k}\otimes (\zeta_n)_n\longmapsto \mathrm{d}\log \zeta_k,\quad \forall k\in \mathbb{N},\quad \forall (\zeta_n)_n\in \mathbb{Z}_p(1), \end{align*}$$
$$\begin{align*}\overline{K}/\mathfrak{a}(1)\stackrel{\sim}{\longrightarrow}\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_{M_0}}^1,\quad p^{-k}\otimes (\zeta_n)_n\longmapsto \mathrm{d}\log \zeta_k,\quad \forall k\in \mathbb{N},\quad \forall (\zeta_n)_n\in \mathbb{Z}_p(1), \end{align*}$$
where
 $\mathfrak {a}=\{x\in \overline {K}\ |\ v_p(x)\geq -1/(p-1)\}$
. Hence, the composition of
$\mathfrak {a}=\{x\in \overline {K}\ |\ v_p(x)\geq -1/(p-1)\}$
. Hence, the composition of
 $$\begin{align*}\overline{K}/\mathfrak{a}(1)\stackrel{\sim}{\longrightarrow}\mathcal{O}_{\overline{K}}\otimes_{\overline{\mathbb{Z}_p}} \Omega_{\overline{\mathbb{Z}_p}/\mathbb{Z}_p}^1\longrightarrow \Omega_{\mathcal{O}_{\overline{K}}/\mathbb{Z}_p}^1 \longrightarrow \hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}}) \end{align*}$$
$$\begin{align*}\overline{K}/\mathfrak{a}(1)\stackrel{\sim}{\longrightarrow}\mathcal{O}_{\overline{K}}\otimes_{\overline{\mathbb{Z}_p}} \Omega_{\overline{\mathbb{Z}_p}/\mathbb{Z}_p}^1\longrightarrow \Omega_{\mathcal{O}_{\overline{K}}/\mathbb{Z}_p}^1 \longrightarrow \hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}}) \end{align*}$$
gives a splitting of (3.6.2). Thus, we obtain the splitting sequence (3.6.1) of
![]() $\mathcal {O}_{\overline {K}}$
-modules. We notice that the Galois conjugates of
$\mathcal {O}_{\overline {K}}$
-modules. We notice that the Galois conjugates of
![]() $\zeta _n, w_{im}$
are of the form
$\zeta _n, w_{im}$
are of the form
![]() $\zeta _n^a,\zeta _m^bw_{im,}$
respectively, which implies that (3.6.1) is
$\zeta _n^a,\zeta _m^bw_{im,}$
respectively, which implies that (3.6.1) is
![]() $G_K$
-equivariant.▪
$G_K$
-equivariant.▪
3.7
As
 $\hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}})$
is p-divisible, we have an exact sequence
$\hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}})$
is p-divisible, we have an exact sequence
 $0\to T_p(\hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}})) \to V_p(\hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}}))\to \hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}})\to 0$
. After inverting p, we get an exact sequence
$0\to T_p(\hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}})) \to V_p(\hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}}))\to \hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}})\to 0$
. After inverting p, we get an exact sequence
 $$ \begin{align} 0\longrightarrow C(1) & \longrightarrow \overline{K}\otimes_{\mathcal{O}_{\overline{K}}} V_p(\hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})) \\ & \longrightarrow\overline{K}\otimes_{\mathcal{O}_{\overline{K}}}\hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})\longrightarrow 0, \nonumber \end{align} $$
$$ \begin{align} 0\longrightarrow C(1) & \longrightarrow \overline{K}\otimes_{\mathcal{O}_{\overline{K}}} V_p(\hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})) \\ & \longrightarrow\overline{K}\otimes_{\mathcal{O}_{\overline{K}}}\hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})\longrightarrow 0, \nonumber \end{align} $$
where we identified
 $\overline {K}\otimes _{\mathcal {O}_{\overline {K}}}T_p(\hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}}))$
with
$\overline {K}\otimes _{\mathcal {O}_{\overline {K}}}T_p(\hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}}))$
with
![]() $C(1)$
by (3.6.1).
$C(1)$
by (3.6.1).
Theorem 3.8 ([Reference HyodoHyo86, Theorem 1 and Remark 3])
-
(i) The composition of
(3.8.1)where $$ \begin{align} K\otimes_{\mathcal{O}_K}\hat{\Omega}_{\mathcal{O}_K}^1\stackrel{\epsilon}{\longrightarrow} (\overline{K}\otimes_{\mathcal{O}_{\overline{K}}}\hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}}))^{G_K}\stackrel{\delta}{\longrightarrow} H^1(G_K,C(1)), \end{align} $$
$$ \begin{align} K\otimes_{\mathcal{O}_K}\hat{\Omega}_{\mathcal{O}_K}^1\stackrel{\epsilon}{\longrightarrow} (\overline{K}\otimes_{\mathcal{O}_{\overline{K}}}\hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}}))^{G_K}\stackrel{\delta}{\longrightarrow} H^1(G_K,C(1)), \end{align} $$
 $\epsilon $
is the canonical map and
$\epsilon $
is the canonical map and
 $\delta $
is the connecting map associated with (3.7.1), is an isomorphism. Moreover, for any integer q, the cup product induces an isomorphism
$\delta $
is the connecting map associated with (3.7.1), is an isomorphism. Moreover, for any integer q, the cup product induces an isomorphism  $$\begin{align*}(\wedge^q H^1(G_K,C(1)))^\wedge\stackrel{\sim}{\longrightarrow} H^q(G_K,C(q)). \end{align*}$$
$$\begin{align*}(\wedge^q H^1(G_K,C(1)))^\wedge\stackrel{\sim}{\longrightarrow} H^q(G_K,C(q)). \end{align*}$$
-
(ii) The K-module
 $H^1(G_K,C)$
is free of rank
$H^1(G_K,C)$
is free of rank
 $1$
. Moreover, for any integer q, the cup product induces an isomorphism
$1$
. Moreover, for any integer q, the cup product induces an isomorphism  $$\begin{align*}H^1(G_K,C)\otimes_K (\wedge^{q-1} H^1(G_K,C(1)))^\wedge\stackrel{\sim}{\longrightarrow} H^q(G_K,C(q-1)). \end{align*}$$
$$\begin{align*}H^1(G_K,C)\otimes_K (\wedge^{q-1} H^1(G_K,C(1)))^\wedge\stackrel{\sim}{\longrightarrow} H^q(G_K,C(q-1)). \end{align*}$$
-
(iii) For any integers r and q such that
 $r\neq q$
or
$r\neq q$
or
 $q-1$
, we have
$q-1$
, we have
 $H^q(G_K,C(r))=0$
.
$H^q(G_K,C(r))=0$
.
Remark 3.9 By Proposition 3.3, we have an isomorphism
 $$ \begin{align} \qquad K\otimes_{\mathcal{O}_K} (\oplus_{i\in I}\mathcal{O}_K)^\wedge\stackrel{\sim}{\longrightarrow} K\otimes_{\mathcal{O}_K}\hat{\Omega}_{\mathcal{O}_K}^1,\quad 1\otimes e_i\longmapsto 1\otimes \mathrm{d}\log u_i,\quad \forall i\in I. \end{align} $$
$$ \begin{align} \qquad K\otimes_{\mathcal{O}_K} (\oplus_{i\in I}\mathcal{O}_K)^\wedge\stackrel{\sim}{\longrightarrow} K\otimes_{\mathcal{O}_K}\hat{\Omega}_{\mathcal{O}_K}^1,\quad 1\otimes e_i\longmapsto 1\otimes \mathrm{d}\log u_i,\quad \forall i\in I. \end{align} $$
By composing it with (3.8.1), we get an isomorphism
where
![]() $f_i$
is a
$f_i$
is a
![]() $1$
-cocycle sending each
$1$
-cocycle sending each
![]() $\sigma \in G_K$
to
$\sigma \in G_K$
to
![]() $\sigma (1\otimes (\mathrm {d}\log w_{im})_m)-1\otimes (\mathrm {d}\log w_{im})_m$
in view of (3.7.1).
$\sigma (1\otimes (\mathrm {d}\log w_{im})_m)-1\otimes (\mathrm {d}\log w_{im})_m$
in view of (3.7.1).
4 Faltings Extension
Lemma 4.1 Let
![]() $M=\bigcup _{i\in I,m\geq 0}K(w_{im})\subseteq \overline {K}$
. Then there is an isomorphism of
$M=\bigcup _{i\in I,m\geq 0}K(w_{im})\subseteq \overline {K}$
. Then there is an isomorphism of
![]() $\mathcal {O}_M$
-modules
$\mathcal {O}_M$
-modules
 $$\begin{align*}\oplus_{i\in I} M/\mathcal{O}_M\stackrel{\sim}{\longrightarrow} \Omega_{\mathcal{O}_M/\mathcal{O}_K}^1 ,\quad p^{-m}e_i\longmapsto \mathrm{d}\log w_{im},\quad \forall i\in I,m\in \mathbb{N}. \end{align*}$$
$$\begin{align*}\oplus_{i\in I} M/\mathcal{O}_M\stackrel{\sim}{\longrightarrow} \Omega_{\mathcal{O}_M/\mathcal{O}_K}^1 ,\quad p^{-m}e_i\longmapsto \mathrm{d}\log w_{im},\quad \forall i\in I,m\in \mathbb{N}. \end{align*}$$
Proof For any
![]() $N\geq 0$
, we set
$N\geq 0$
, we set
![]() $M_N=\bigcup _{i\in I}K(w_{iN})$
. Since
$M_N=\bigcup _{i\in I}K(w_{iN})$
. Since
![]() $(\overline {u_i})$
form a p-base of the residue field k, the elements of the form
$(\overline {u_i})$
form a p-base of the residue field k, the elements of the form
 $\prod _{i\in I} \overline {w_{iN}}^{k_i}$
where
$\prod _{i\in I} \overline {w_{iN}}^{k_i}$
where
![]() $0\leq k_i<p^N$
with finitely many nonvanishing, are linearly independent over k. Therefore,
$0\leq k_i<p^N$
with finitely many nonvanishing, are linearly independent over k. Therefore,
 $\mathcal {O}_{M_N}=\mathcal {O}_K[T_i]_{i\in I}/ (T_i^{p^N}-u_i)$
, where
$\mathcal {O}_{M_N}=\mathcal {O}_K[T_i]_{i\in I}/ (T_i^{p^N}-u_i)$
, where
![]() $T_i$
maps to
$T_i$
maps to
![]() $w_{iN}$
. Hence,
$w_{iN}$
. Hence,
 $$\begin{align*}\Omega_{\mathcal{O}_{M_N}/\mathcal{O}_K}^1=\oplus_{i\in I}\mathcal{O}_{M_N}/p^N\mathcal{O}_{M_N}=\oplus_{i\in I}p^{-N}\mathcal{O}_{M_N}/\mathcal{O}_{M_N}, \end{align*}$$
$$\begin{align*}\Omega_{\mathcal{O}_{M_N}/\mathcal{O}_K}^1=\oplus_{i\in I}\mathcal{O}_{M_N}/p^N\mathcal{O}_{M_N}=\oplus_{i\in I}p^{-N}\mathcal{O}_{M_N}/\mathcal{O}_{M_N}, \end{align*}$$
where
![]() $p^{-N}e_i$
corresponds to
$p^{-N}e_i$
corresponds to
![]() $\mathrm {d}\log w_{iN}$
. The conclusion follows by taking colimit over N.▪
$\mathrm {d}\log w_{iN}$
. The conclusion follows by taking colimit over N.▪
Proposition 4.2 With the same notation as in Lemma 4.1, there is an exact sequence of
![]() $\mathcal {O}_{\overline {K}}$
-modules
$\mathcal {O}_{\overline {K}}$
-modules
 $$\begin{align*}0\longrightarrow \oplus_{i\in I} \overline{K}/\mathcal{O}_{\overline{K}}\stackrel{\theta}{\longrightarrow} \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1\longrightarrow \overline{K}/\mathfrak{b}(1)\longrightarrow 0, \end{align*}$$
$$\begin{align*}0\longrightarrow \oplus_{i\in I} \overline{K}/\mathcal{O}_{\overline{K}}\stackrel{\theta}{\longrightarrow} \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1\longrightarrow \overline{K}/\mathfrak{b}(1)\longrightarrow 0, \end{align*}$$
where
![]() $\theta (p^{-m} e_i)=\mathrm {d}\log w_{im}$
for any
$\theta (p^{-m} e_i)=\mathrm {d}\log w_{im}$
for any
![]() $i\in I$
and
$i\in I$
and
![]() $m\in \mathbb {N}$
, and
$m\in \mathbb {N}$
, and
 $\mathfrak {b}=\{x\in \overline {K}\ |\ v_p(x)\geq -v_p(\mathfrak {D}_{M/M_1})-1/(p-1)\}$
, where
$\mathfrak {b}=\{x\in \overline {K}\ |\ v_p(x)\geq -v_p(\mathfrak {D}_{M/M_1})-1/(p-1)\}$
, where
![]() $M_1$
is the fraction field of the Witt ring with coefficients in the residue field of M, and
$M_1$
is the fraction field of the Witt ring with coefficients in the residue field of M, and
![]() $\mathfrak {D}_{M/M_1}$
is the different ideal of
$\mathfrak {D}_{M/M_1}$
is the different ideal of
![]() $M/M_1$
.
$M/M_1$
.
Proof We notice that
![]() $\mathcal {O}_M$
is a henselian discrete valuation ring with perfect residue field. Thus, the sequence of modules of differentials of
$\mathcal {O}_M$
is a henselian discrete valuation ring with perfect residue field. Thus, the sequence of modules of differentials of
![]() $\mathcal {O}_{\overline {K}}/\mathcal {O}_M/\mathcal {O}_K$
,
$\mathcal {O}_{\overline {K}}/\mathcal {O}_M/\mathcal {O}_K$
,
 $$ \begin{align} 0\longrightarrow \mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_M}\Omega_{\mathcal{O}_M/\mathcal{O}_K}^1 \longrightarrow \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1\longrightarrow \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_M}^1\longrightarrow 0, \end{align} $$
$$ \begin{align} 0\longrightarrow \mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_M}\Omega_{\mathcal{O}_M/\mathcal{O}_K}^1 \longrightarrow \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1\longrightarrow \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_M}^1\longrightarrow 0, \end{align} $$
is exact by Lemma 3.1. We identify its first term with
 $\oplus _{i\in I} \overline {K}/\mathcal {O}_{\overline {K}}$
by Lemma 4.1. By Fontaine’s computation ([Reference FontaineFon82, Théorème
$\oplus _{i\in I} \overline {K}/\mathcal {O}_{\overline {K}}$
by Lemma 4.1. By Fontaine’s computation ([Reference FontaineFon82, Théorème
![]() ${1}^{\prime }$
]), we have an isomorphism of
${1}^{\prime }$
]), we have an isomorphism of
![]() $\mathcal {O}_{\overline {K}}$
-modules
$\mathcal {O}_{\overline {K}}$
-modules
 $$ \begin{align*} \overline{K}/\mathfrak{b}(1)\stackrel{\sim}{\longrightarrow} \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_M}^1,\quad p^{-k}\otimes (\zeta_n)_n\longmapsto \mathrm{d}\log \zeta_k,\quad \forall k\in \mathbb{N},\quad \forall (\zeta_n)_n\in \mathbb{Z}_p(1). \end{align*} $$
$$ \begin{align*} \overline{K}/\mathfrak{b}(1)\stackrel{\sim}{\longrightarrow} \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_M}^1,\quad p^{-k}\otimes (\zeta_n)_n\longmapsto \mathrm{d}\log \zeta_k,\quad \forall k\in \mathbb{N},\quad \forall (\zeta_n)_n\in \mathbb{Z}_p(1). \end{align*} $$
The conclusion follows from (4.2.1). ▪
Lemma 4.3 The canonical map
is an isomorphism.
Proof It follows from the following descriptions
 $$ \begin{align} &C\otimes_{\mathcal{O}_C}(\oplus_{i\in I}\mathcal{O}_C)^\wedge\nonumber\\&\qquad=\Big\{(x_i) \in\prod_{i\in I}C\mid \forall N>0,\ \exists \text{ finite }J\subseteq I, |x_i|_p<1/N,\ \forall i\notin J\Big\}, \end{align} $$
$$ \begin{align} &C\otimes_{\mathcal{O}_C}(\oplus_{i\in I}\mathcal{O}_C)^\wedge\nonumber\\&\qquad=\Big\{(x_i) \in\prod_{i\in I}C\mid \forall N>0,\ \exists \text{ finite }J\subseteq I, |x_i|_p<1/N,\ \forall i\notin J\Big\}, \end{align} $$
 $$ \begin{align} & K\otimes_{\mathcal{O}_K}(\oplus_{i\in I}\mathcal{O}_K)^\wedge\nonumber\\&\qquad = \Big\{(x_i)\in\prod_{i\in I}K\mid \forall N>0,\ \exists \text{ finite }J\subseteq I, |x_i|_p<1/N,\ \forall i\notin J\Big\}.\blacksquare \end{align} $$
$$ \begin{align} & K\otimes_{\mathcal{O}_K}(\oplus_{i\in I}\mathcal{O}_K)^\wedge\nonumber\\&\qquad = \Big\{(x_i)\in\prod_{i\in I}K\mid \forall N>0,\ \exists \text{ finite }J\subseteq I, |x_i|_p<1/N,\ \forall i\notin J\Big\}.\blacksquare \end{align} $$
Theorem 4.4 There is a canonical exact sequence of C-
![]() $G_K$
-modules that splits as a sequence of C-modules,
$G_K$
-modules that splits as a sequence of C-modules,
 $$ \begin{align} 0\longrightarrow C(1)\stackrel{\iota}{\longrightarrow} V_p (\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\stackrel{\nu}{\longrightarrow} C\otimes_{\mathcal{O}_C}(\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K} \Omega_{\mathcal{O}_K/\mathbb{Z}_p}^1)^\wedge\longrightarrow 0, \end{align} $$
$$ \begin{align} 0\longrightarrow C(1)\stackrel{\iota}{\longrightarrow} V_p (\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\stackrel{\nu}{\longrightarrow} C\otimes_{\mathcal{O}_C}(\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K} \Omega_{\mathcal{O}_K/\mathbb{Z}_p}^1)^\wedge\longrightarrow 0, \end{align} $$
where
![]() $\iota (1\otimes (\zeta _n)_n)=(\mathrm {d}\log \zeta _n)_n$
for any
$\iota (1\otimes (\zeta _n)_n)=(\mathrm {d}\log \zeta _n)_n$
for any
![]() $(\zeta _n)_n\in \mathbb {Z}_p(1)$
. There is an isomorphism of C-
$(\zeta _n)_n\in \mathbb {Z}_p(1)$
. There is an isomorphism of C-
![]() $G_K$
-modules
$G_K$
-modules
 $$ \begin{align} C\otimes_{\mathcal{O}_C}(\oplus_{i\in I}\mathcal{O}_C)^\wedge &\stackrel{\sim}{\longrightarrow} C\otimes_{\mathcal{O}_C}(\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K} \Omega_{\mathcal{O}_K/\mathbb{Z}_p}^1)^\wedge, \\ 1\otimes e_i&\longmapsto 1\otimes 1\otimes \mathrm{d}\log u_i,\quad \forall i\in I, \nonumber \end{align} $$
$$ \begin{align} C\otimes_{\mathcal{O}_C}(\oplus_{i\in I}\mathcal{O}_C)^\wedge &\stackrel{\sim}{\longrightarrow} C\otimes_{\mathcal{O}_C}(\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K} \Omega_{\mathcal{O}_K/\mathbb{Z}_p}^1)^\wedge, \\ 1\otimes e_i&\longmapsto 1\otimes 1\otimes \mathrm{d}\log u_i,\quad \forall i\in I, \nonumber \end{align} $$
and the map
 $C\otimes _{\mathcal {O}_C}(\oplus _{i\in I}\mathcal {O}_C)^\wedge \to V_p(\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1)$
, sending
$C\otimes _{\mathcal {O}_C}(\oplus _{i\in I}\mathcal {O}_C)^\wedge \to V_p(\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1)$
, sending
![]() $1\otimes e_i$
to
$1\otimes e_i$
to
![]() $(\mathrm {d}\log w_{im})_m$
for any
$(\mathrm {d}\log w_{im})_m$
for any
![]() $i\in I$
, gives a C-linear section of
$i\in I$
, gives a C-linear section of
![]() $\nu $
.
$\nu $
.
Proof We consider the sequence of modules of differentials of
![]() $\mathcal {O}_L/\mathcal {O}_K/\mathbb {Z}_p$
, where
$\mathcal {O}_L/\mathcal {O}_K/\mathbb {Z}_p$
, where
![]() $L/K$
is a finite subextension of
$L/K$
is a finite subextension of
![]() $\overline {K}/K$
, and pass to p-adic completions. Since
$\overline {K}/K$
, and pass to p-adic completions. Since
 $\Omega _{\mathcal {O}_{L}/\mathcal {O}_K}^1$
is killed by a power of p, we still get an exact sequence [Sta20, 0315, 0BNG]
$\Omega _{\mathcal {O}_{L}/\mathcal {O}_K}^1$
is killed by a power of p, we still get an exact sequence [Sta20, 0315, 0BNG]
 $$\begin{align*}\mathcal{O}_L\otimes_{\mathcal{O}_K}\hat{\Omega}_{\mathcal{O}_K}^1\longrightarrow \hat{\Omega}_{\mathcal{O}_L}^1\longrightarrow \Omega_{\mathcal{O}_{L}/\mathcal{O}_K}^1\longrightarrow 0. \end{align*}$$
$$\begin{align*}\mathcal{O}_L\otimes_{\mathcal{O}_K}\hat{\Omega}_{\mathcal{O}_K}^1\longrightarrow \hat{\Omega}_{\mathcal{O}_L}^1\longrightarrow \Omega_{\mathcal{O}_{L}/\mathcal{O}_K}^1\longrightarrow 0. \end{align*}$$
By taking colimit over all such L, we get an exact sequence
 $$ \begin{align} \mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K}\hat{\Omega}_{\mathcal{O}_K}^1 \stackrel{\alpha}{\longrightarrow} \hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})\stackrel{\beta}{\longrightarrow} \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1\longrightarrow 0. \end{align} $$
$$ \begin{align} \mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K}\hat{\Omega}_{\mathcal{O}_K}^1 \stackrel{\alpha}{\longrightarrow} \hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})\stackrel{\beta}{\longrightarrow} \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1\longrightarrow 0. \end{align} $$
Combining with Propositions 3.3, 3.6, and 4.2, we get a commutative diagram:
 where the rows and columns are exact, and the middle column splits. We set
where the rows and columns are exact, and the middle column splits. We set
![]() $D=\operatorname {Ker}(\beta )=\operatorname {Im}(\alpha )$
. We see that
$D=\operatorname {Ker}(\beta )=\operatorname {Im}(\alpha )$
. We see that
![]() $\mathcal {O}_{\overline {K}}\otimes _{\mathcal {O}_K}(\oplus _{i\in I}\mathcal {O}_K)^\wedge \to D$
is injective, whose cokernel is killed by a power of p. Now for any
$\mathcal {O}_{\overline {K}}\otimes _{\mathcal {O}_K}(\oplus _{i\in I}\mathcal {O}_K)^\wedge \to D$
is injective, whose cokernel is killed by a power of p. Now for any
![]() $n>0$
, by applying
$n>0$
, by applying
![]() $\operatorname {Hom}_{\mathbb {Z}_p}(\mathbb {Z}_p/p^n\mathbb {Z}_p,-)$
to (4.4.3), we get an exact sequence of
$\operatorname {Hom}_{\mathbb {Z}_p}(\mathbb {Z}_p/p^n\mathbb {Z}_p,-)$
to (4.4.3), we get an exact sequence of
![]() $\mathcal {O}_{\overline {K}}/p^n\mathcal {O}_{\overline {K}}$
-modules
$\mathcal {O}_{\overline {K}}/p^n\mathcal {O}_{\overline {K}}$
-modules
 $$ \begin{align} 0\longrightarrow D[p^n]\longrightarrow \hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})[p^n]&\longrightarrow \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1[p^n]\longrightarrow D/p^nD \\ & \longrightarrow \hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})/p^n\hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})=0. \nonumber \end{align} $$
$$ \begin{align} 0\longrightarrow D[p^n]\longrightarrow \hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})[p^n]&\longrightarrow \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1[p^n]\longrightarrow D/p^nD \\ & \longrightarrow \hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})/p^n\hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})=0. \nonumber \end{align} $$
We notice that the inverse system
![]() $(D[p^n])_n$
is Artin–Rees null, and that
$(D[p^n])_n$
is Artin–Rees null, and that
 $(\hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}}) [p^n])_n$
satisfies Mittag–Leffler condition. Therefore, by taking the inverse limit of (4.4.5), we get an exact sequence of
$(\hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}}) [p^n])_n$
satisfies Mittag–Leffler condition. Therefore, by taking the inverse limit of (4.4.5), we get an exact sequence of
![]() $\mathcal {O}_{C}$
-modules
$\mathcal {O}_{C}$
-modules
 $$ \begin{align} 0\longrightarrow T_p(\hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})) \longrightarrow T_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\longrightarrow D^\wedge\longrightarrow 0. \end{align} $$
$$ \begin{align} 0\longrightarrow T_p(\hat{\Omega}_{\mathcal{O}_{K}}^1(\mathcal{O}_{\overline{K}})) \longrightarrow T_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\longrightarrow D^\wedge\longrightarrow 0. \end{align} $$
By applying
![]() $T_p(-)$
to the middle column of (4.4.4), we get
$T_p(-)$
to the middle column of (4.4.4), we get
 $T_p(\hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}}))=\widehat {\mathfrak {a}}(1)$
. On the other hand, we notice that
$T_p(\hat {\Omega }_{\mathcal {O}_{K}}^1(\mathcal {O}_{\overline {K}}))=\widehat {\mathfrak {a}}(1)$
. On the other hand, we notice that
 $\oplus _{i\in I}\overline {K}/\mathcal {O}_{\overline {K}}$
is p-divisible, and that
$\oplus _{i\in I}\overline {K}/\mathcal {O}_{\overline {K}}$
is p-divisible, and that
 $((\oplus _{i\in I}\overline {K}/\mathcal {O}_{\overline {K}})[p^n])_n$
satisfies the Mittag–Leffler condition. Therefore, by applying
$((\oplus _{i\in I}\overline {K}/\mathcal {O}_{\overline {K}})[p^n])_n$
satisfies the Mittag–Leffler condition. Therefore, by applying
![]() $T_p(-)$
to the right column of (4.4.4), we get an exact sequence of
$T_p(-)$
to the right column of (4.4.4), we get an exact sequence of
![]() $\mathcal {O}_C$
-modules
$\mathcal {O}_C$
-modules
 $$ \begin{align} 0\longrightarrow (\oplus_{i\in I}\mathcal{O}_C)^\wedge\longrightarrow T_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\longrightarrow \widehat{\mathfrak{b}}(1) \longrightarrow 0. \end{align} $$
$$ \begin{align} 0\longrightarrow (\oplus_{i\in I}\mathcal{O}_C)^\wedge\longrightarrow T_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\longrightarrow \widehat{\mathfrak{b}}(1) \longrightarrow 0. \end{align} $$
As
 $\Omega _{\mathcal {O}_K/\mathcal {O}_{K_0}}^1$
is killed by a power of p, the map
$\Omega _{\mathcal {O}_K/\mathcal {O}_{K_0}}^1$
is killed by a power of p, the map
 $(\mathcal {O}_{\overline {K}}\otimes _{\mathcal {O}_K}\hat {\Omega }_{\mathcal {O}_K}^1)^\wedge \to D^\wedge $
becomes an isomorphism after inverting p. Afterwards, we get from (4.4.6) a canonical exact sequence of C-modules
$(\mathcal {O}_{\overline {K}}\otimes _{\mathcal {O}_K}\hat {\Omega }_{\mathcal {O}_K}^1)^\wedge \to D^\wedge $
becomes an isomorphism after inverting p. Afterwards, we get from (4.4.6) a canonical exact sequence of C-modules
 $$ \begin{align} 0\longrightarrow C(1)\to V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1) \longrightarrow C\otimes_{\mathcal{O}_C}(\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K} \hat{\Omega}_{\mathcal{O}_K}^1)^\wedge\longrightarrow 0, \end{align} $$
$$ \begin{align} 0\longrightarrow C(1)\to V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1) \longrightarrow C\otimes_{\mathcal{O}_C}(\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K} \hat{\Omega}_{\mathcal{O}_K}^1)^\wedge\longrightarrow 0, \end{align} $$
and from (4.4.7) an exact sequence of C-modules
 $$ \begin{align} 0\longrightarrow C\otimes_{\mathcal{O}_C}(\oplus_{i\in I}\mathcal{O}_C)^\wedge \longrightarrow V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\longrightarrow C(1)\longrightarrow 0. \end{align} $$
$$ \begin{align} 0\longrightarrow C\otimes_{\mathcal{O}_C}(\oplus_{i\in I}\mathcal{O}_C)^\wedge \longrightarrow V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\longrightarrow C(1)\longrightarrow 0. \end{align} $$
The latter gives a splitting of (4.4.8) and an isomorphism
 $C\otimes _{\mathcal {O}_C}(\oplus _{i\in I}\mathcal {O}_C)^\wedge \stackrel {\sim }{\to } C\otimes _{\mathcal {O}_C}(\mathcal {O}_{\overline {K}}\otimes _{\mathcal {O}_K} \hat {\Omega }_{\mathcal {O}_K}^1)^\wedge $
by sending
$C\otimes _{\mathcal {O}_C}(\oplus _{i\in I}\mathcal {O}_C)^\wedge \stackrel {\sim }{\to } C\otimes _{\mathcal {O}_C}(\mathcal {O}_{\overline {K}}\otimes _{\mathcal {O}_K} \hat {\Omega }_{\mathcal {O}_K}^1)^\wedge $
by sending
![]() $1\otimes e_i$
to
$1\otimes e_i$
to
![]() $1\otimes 1\otimes \mathrm {d}\log u_i$
by diagram chasing. We notice that the Galois conjugates of
$1\otimes 1\otimes \mathrm {d}\log u_i$
by diagram chasing. We notice that the Galois conjugates of
![]() $\zeta _n, w_{im}$
are of the form
$\zeta _n, w_{im}$
are of the form
![]() $\zeta _n^a,\zeta _m^bw_{im}$
respectively, which implies that (4.4.8) is
$\zeta _n^a,\zeta _m^bw_{im}$
respectively, which implies that (4.4.8) is
![]() $G_K$
-equivariant. Hence, (4.4.8) gives us the exact sequence (4.4.1) of C-
$G_K$
-equivariant. Hence, (4.4.8) gives us the exact sequence (4.4.1) of C-
![]() $G_K$
-modules that splits as a sequence of C-modules.▪
$G_K$
-modules that splits as a sequence of C-modules.▪
Corollary 4.5 The canonical map
 $K\otimes _{\mathcal {O}_K}\hat {\Omega }_{\mathcal {O}_K}^1\to (C\otimes _{\mathcal {O}_C}(\mathcal {O}_{\overline {K}}\otimes _{\mathcal {O}_K} \Omega _{\mathcal {O}_K/\mathbb {Z}_p}^1)^\wedge )^{G_K}$
is an isomorphism, and the connecting map of the sequence (4.4.1)
$K\otimes _{\mathcal {O}_K}\hat {\Omega }_{\mathcal {O}_K}^1\to (C\otimes _{\mathcal {O}_C}(\mathcal {O}_{\overline {K}}\otimes _{\mathcal {O}_K} \Omega _{\mathcal {O}_K/\mathbb {Z}_p}^1)^\wedge )^{G_K}$
is an isomorphism, and the connecting map of the sequence (4.4.1)
 $$ \begin{align} \delta: K\otimes_{\mathcal{O}_K}\hat{\Omega}_{\mathcal{O}_K}^1\longrightarrow H^1(G_K,C(1)) \end{align} $$
$$ \begin{align} \delta: K\otimes_{\mathcal{O}_K}\hat{\Omega}_{\mathcal{O}_K}^1\longrightarrow H^1(G_K,C(1)) \end{align} $$
is an isomorphism that coincides with (3.8.1). In particular,
 $$ \begin{align} V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)^{G_K}=0. \end{align} $$
$$ \begin{align} V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)^{G_K}=0. \end{align} $$
Proof By (3.9.1), (4.4.2), and 4.3, we see that the canonical map
 $K\otimes _{\mathcal {O}_K}\hat {\Omega }_{\mathcal {O}_K}^1\to (C\otimes _{\mathcal {O}_C}(\mathcal {O}_{\overline {K}}\otimes _{\mathcal {O}_K} \hat {\Omega }_{\mathcal {O}_K}^1)^\wedge )^{G_K}$
is an isomorphism. Now (4.5.1) follows from Theorem 3.8(i) and Remark 3.9. And (4.5.2) follows from the fact that
$K\otimes _{\mathcal {O}_K}\hat {\Omega }_{\mathcal {O}_K}^1\to (C\otimes _{\mathcal {O}_C}(\mathcal {O}_{\overline {K}}\otimes _{\mathcal {O}_K} \hat {\Omega }_{\mathcal {O}_K}^1)^\wedge )^{G_K}$
is an isomorphism. Now (4.5.1) follows from Theorem 3.8(i) and Remark 3.9. And (4.5.2) follows from the fact that
![]() $C(1)^{G_K}=0$
. ▪
$C(1)^{G_K}=0$
. ▪
Definition 4.6. We call sequence (4.4.1) the Faltings extension of
![]() $\mathcal {O}_K$
over
$\mathcal {O}_K$
over
![]() $\mathbb {Z}_p$
.
$\mathbb {Z}_p$
.
5 Fontaine’s Injection
5.1
For any proper model
![]() $\mathfrak {X}$
of the abelian variety X over
$\mathfrak {X}$
of the abelian variety X over
![]() $\mathcal {O}_K$
(i.e., a proper
$\mathcal {O}_K$
(i.e., a proper
![]() $\mathcal {O}_K$
-scheme whose generic fiber is X), we identify
$\mathcal {O}_K$
-scheme whose generic fiber is X), we identify
![]() $\mathfrak {X}(\mathcal {O}_{\overline {K}})$
with
$\mathfrak {X}(\mathcal {O}_{\overline {K}})$
with
![]() $X(\overline {K})$
by valuative criterion. Pullback of Kähler differentials defines a map
$X(\overline {K})$
by valuative criterion. Pullback of Kähler differentials defines a map
 $$ \begin{align} H^0(\mathfrak{X},\Omega_{\mathfrak{X}/\mathcal{O}_K}^1)\longrightarrow \operatorname{Map}_{G_K}(X(\overline{K}), \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1),\quad \omega\longmapsto (u\longmapsto u^*\omega). \end{align} $$
$$ \begin{align} H^0(\mathfrak{X},\Omega_{\mathfrak{X}/\mathcal{O}_K}^1)\longrightarrow \operatorname{Map}_{G_K}(X(\overline{K}), \Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1),\quad \omega\longmapsto (u\longmapsto u^*\omega). \end{align} $$
We notice that
 $H^0(X,\Omega _{X/K}^1)=K\otimes _{\mathcal {O}_K}H^0(\mathfrak {X},\Omega _{\mathfrak {X}/\mathcal {O}_K}^1)$
, and that any differential form over X is invariant under translations. Hence, we can take an integer
$H^0(X,\Omega _{X/K}^1)=K\otimes _{\mathcal {O}_K}H^0(\mathfrak {X},\Omega _{\mathfrak {X}/\mathcal {O}_K}^1)$
, and that any differential form over X is invariant under translations. Hence, we can take an integer
![]() $r>0$
big enough, such that for any
$r>0$
big enough, such that for any
 $\omega \in p^r H^0(\mathfrak {X},\Omega _{\mathfrak {X}/\mathcal {O}_K}^1)$
and
$\omega \in p^r H^0(\mathfrak {X},\Omega _{\mathfrak {X}/\mathcal {O}_K}^1)$
and
![]() $u_1,u_2\in \mathfrak {X}(\mathcal {O}_{\overline {K}})$
,
$u_1,u_2\in \mathfrak {X}(\mathcal {O}_{\overline {K}})$
,
![]() $(u_1+u_2)^*\omega =u_1^* \omega +u_2^*\omega $
(cf. [Reference FontaineFon82, Proposition 3]). Therefore, (5.1.1) induces a homomorphism of
$(u_1+u_2)^*\omega =u_1^* \omega +u_2^*\omega $
(cf. [Reference FontaineFon82, Proposition 3]). Therefore, (5.1.1) induces a homomorphism of
![]() $\mathcal {O}_K$
-modules
$\mathcal {O}_K$
-modules
 $$\begin{align*}\rho_1:p^rH^0(\mathfrak{X},\Omega_{\mathfrak{X}/\mathcal{O}_K}^1)\longrightarrow \operatorname{Hom}_{\mathbb{Z}[G_K]}(X(\overline{K}),\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1),\ \quad \omega\longmapsto (u\longmapsto u^*\omega). \end{align*}$$
$$\begin{align*}\rho_1:p^rH^0(\mathfrak{X},\Omega_{\mathfrak{X}/\mathcal{O}_K}^1)\longrightarrow \operatorname{Hom}_{\mathbb{Z}[G_K]}(X(\overline{K}),\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1),\ \quad \omega\longmapsto (u\longmapsto u^*\omega). \end{align*}$$
We can also assume that
 $p^rH^0(\mathfrak {X},\Omega _{\mathfrak {X}/\mathcal {O}_K}^1)$
has no p-torsion for further use.
$p^rH^0(\mathfrak {X},\Omega _{\mathfrak {X}/\mathcal {O}_K}^1)$
has no p-torsion for further use.
5.2
The functor
![]() $V_p(-)$
gives us an injective homomorphism
$V_p(-)$
gives us an injective homomorphism
 $$ \begin{align} \rho_2:\operatorname{Hom}_{\mathbb{Z}[G_K]}(X(\overline{K}),\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\longrightarrow \operatorname{Hom}_{\mathbb{Z}[G_K]}\big(V_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big), \end{align} $$
$$ \begin{align} \rho_2:\operatorname{Hom}_{\mathbb{Z}[G_K]}(X(\overline{K}),\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\longrightarrow \operatorname{Hom}_{\mathbb{Z}[G_K]}\big(V_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big), \end{align} $$
since
![]() $X(\overline {K})$
is p-divisible (cf. [Reference FontaineFon82, 3.5, Lemme 1]).
$X(\overline {K})$
is p-divisible (cf. [Reference FontaineFon82, 3.5, Lemme 1]).
5.3
The composition
![]() $\rho _2\circ \rho _1$
induces a homomorphism of K-modules
$\rho _2\circ \rho _1$
induces a homomorphism of K-modules
 $$ \begin{align} H^0(X,\Omega_{X/K}^1) & = K\otimes_{\mathcal{O}_K}p^rH^0 (\mathfrak{X},\Omega_{\mathfrak{X}/\mathcal{O}_K}^1) \\ & \quad \longrightarrow \operatorname{Hom}_{\mathbb{Z}[G_K]}(V_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)). \nonumber\end{align} $$
$$ \begin{align} H^0(X,\Omega_{X/K}^1) & = K\otimes_{\mathcal{O}_K}p^rH^0 (\mathfrak{X},\Omega_{\mathfrak{X}/\mathcal{O}_K}^1) \\ & \quad \longrightarrow \operatorname{Hom}_{\mathbb{Z}[G_K]}(V_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)). \nonumber\end{align} $$
As the category of
![]() $\mathcal {O}_K$
-proper models of X is connected, this composition does not depend on the choice of the model and number r (cf. [Reference FontaineFon82, Proposition 4]). We conclude by the following lemma that (5.3.1) is injective.
$\mathcal {O}_K$
-proper models of X is connected, this composition does not depend on the choice of the model and number r (cf. [Reference FontaineFon82, Proposition 4]). We conclude by the following lemma that (5.3.1) is injective.
Lemma 5.4 ([Reference FontaineFon82, 3.5, Lemme 1])
There is a proper model
![]() $\mathfrak {X}$
of X such that
$\mathfrak {X}$
of X such that
![]() $\rho _1$
is injective.
$\rho _1$
is injective.
Proof We follow closely the proof of [Reference FontaineFon82, 3.5, Lemme 1], which does not essentially use the assumption that the residue field k is perfect. We briefly sketch how to adapt Fontaine’s proof.
-
(a) Let u be the origin of X and let d be the dimension of X. We first take a closed immersion
 $X\to \mathbb {P}^n_K$
, and then we take an open immersion
$X\to \mathbb {P}^n_K$
, and then we take an open immersion
 $\mathbb {P}^n_K\to \mathbb {P}^n_{\mathcal {O}_K}$
described later (all the morphisms are over
$\mathbb {P}^n_K\to \mathbb {P}^n_{\mathcal {O}_K}$
described later (all the morphisms are over
 $\mathcal {O}_K$
). Let
$\mathcal {O}_K$
). Let
 $\mathfrak {X}$
be the scheme theoretic image of the composition
$\mathfrak {X}$
be the scheme theoretic image of the composition
 $X\to \mathbb {P}^n_{\mathcal {O}_K}$
, which is thus a proper model of X. Let
$X\to \mathbb {P}^n_{\mathcal {O}_K}$
, which is thus a proper model of X. Let
 $\overline {u}$
be the special point of the scheme theoretic image of u. It is a k-point. After a linear transformation of coordinates, we can at first choose an open immersion
$\overline {u}$
be the special point of the scheme theoretic image of u. It is a k-point. After a linear transformation of coordinates, we can at first choose an open immersion
 $\mathbb {P}^n_K\to \mathbb {P}^n_{\mathcal {O}_K}$
such that
$\mathbb {P}^n_K\to \mathbb {P}^n_{\mathcal {O}_K}$
such that
 $\mathcal {O}_{\mathfrak {X},\overline {u}}$
is a
$\mathcal {O}_{\mathfrak {X},\overline {u}}$
is a
 $(d+1)$
-dimensional regular local ring (cf. [Reference FontaineFon82, 3.6, Lemme 3]).
$(d+1)$
-dimensional regular local ring (cf. [Reference FontaineFon82, 3.6, Lemme 3]). -
(b) The
 $\mathfrak {m}_{\mathfrak {X},\overline {u}}$
-adic completion of the local ring
$\mathfrak {m}_{\mathfrak {X},\overline {u}}$
-adic completion of the local ring
 $\mathcal {O}_{\mathfrak {X},\overline {u}}$
is isomorphic to
$\mathcal {O}_{\mathfrak {X},\overline {u}}$
is isomorphic to
 $\mathcal {O}_K [\!\![T_1,\dots ,T_d]\!\!]$
, denoted by
$\mathcal {O}_K [\!\![T_1,\dots ,T_d]\!\!]$
, denoted by
 $\widehat {\mathcal {O}}_{\mathfrak {X},\overline {u}}$
. The
$\widehat {\mathcal {O}}_{\mathfrak {X},\overline {u}}$
. The
 $\mathfrak {m}_{\mathfrak {X},\overline {u}}$
-adic completion of
$\mathfrak {m}_{\mathfrak {X},\overline {u}}$
-adic completion of
 $\Omega _{\mathcal {O}_{\mathfrak {X},\overline {u}}/\mathcal {O}_K}^{1}$
is a free
$\Omega _{\mathcal {O}_{\mathfrak {X},\overline {u}}/\mathcal {O}_K}^{1}$
is a free
 $\widehat {\mathcal {O}}_{\mathfrak {X},\overline {u}}$
-module of rank d, denoted by
$\widehat {\mathcal {O}}_{\mathfrak {X},\overline {u}}$
-module of rank d, denoted by
 $\hat {\Omega }_{\mathcal {O}_{\mathfrak {X},\overline {u}}/\mathcal {O}_K}^{1}$
. The invariance of differential forms over X and the fact that
$\hat {\Omega }_{\mathcal {O}_{\mathfrak {X},\overline {u}}/\mathcal {O}_K}^{1}$
. The invariance of differential forms over X and the fact that
 $p^rH^0(\mathfrak {X},\Omega _{\mathfrak {X}/\mathcal {O}_K}^1)\subseteq H^0(X,\Omega _{X/K}^1)$
imply that the canonical map
$p^rH^0(\mathfrak {X},\Omega _{\mathfrak {X}/\mathcal {O}_K}^1)\subseteq H^0(X,\Omega _{X/K}^1)$
imply that the canonical map
 $p^rH^0(\mathfrak {X},\Omega _{\mathfrak {X}/\mathcal {O}_K}^1)\to {\Omega }_{\mathcal {O}_{\mathfrak {X},\overline {u}}/\mathcal {O}_K}^{1}$
is injective (cf. [Reference FontaineFon82, 3.7]). We remark that the canonical map
$p^rH^0(\mathfrak {X},\Omega _{\mathfrak {X}/\mathcal {O}_K}^1)\to {\Omega }_{\mathcal {O}_{\mathfrak {X},\overline {u}}/\mathcal {O}_K}^{1}$
is injective (cf. [Reference FontaineFon82, 3.7]). We remark that the canonical map
 ${\Omega }_{\mathcal {O}_{\mathfrak {X},\overline {u}}/\mathcal {O}_K}^{1}\to \hat {\Omega }_{\mathcal {O}_{\mathfrak {X},\overline {u}}/\mathcal {O}_K}^{1}$
is injective, as
${\Omega }_{\mathcal {O}_{\mathfrak {X},\overline {u}}/\mathcal {O}_K}^{1}\to \hat {\Omega }_{\mathcal {O}_{\mathfrak {X},\overline {u}}/\mathcal {O}_K}^{1}$
is injective, as
 ${\Omega }_{\mathcal {O}_{\mathfrak {X},\overline {u}}/\mathcal {O}_K}^{1}$
is of finite type over the Noetherian local ring
${\Omega }_{\mathcal {O}_{\mathfrak {X},\overline {u}}/\mathcal {O}_K}^{1}$
is of finite type over the Noetherian local ring
 $\mathcal {O}_{\mathfrak {X},\overline {u}}$
.
$\mathcal {O}_{\mathfrak {X},\overline {u}}$
. -
(c) We have the following commutative diagram
 where we identify the set of continuous
where we identify the set of continuous
 $\mathcal {O}_K$
-algebra homomorphisms from
$\mathcal {O}_K$
-algebra homomorphisms from
 $\widehat {\mathcal {O}}_{\mathfrak {X},\overline {u}}$
to
$\widehat {\mathcal {O}}_{\mathfrak {X},\overline {u}}$
to
 $\mathcal {O}_{\overline {K}}$
with a subset of
$\mathcal {O}_{\overline {K}}$
with a subset of
 $\mathfrak {X}(\mathcal {O}_{\overline {K}})=X(\overline {K})$
. To show the injectivity of
$\mathfrak {X}(\mathcal {O}_{\overline {K}})=X(\overline {K})$
. To show the injectivity of
 $\rho _1,$
it suffices to show that of
$\rho _1,$
it suffices to show that of
 $\rho _1'$
. More precisely, we need to show that for any nonzero formal differential form
$\rho _1'$
. More precisely, we need to show that for any nonzero formal differential form
 $\sum _{i=1}^d\alpha _i(T_1,\dots ,T_d)\mathrm {d} T_i$
where
$\sum _{i=1}^d\alpha _i(T_1,\dots ,T_d)\mathrm {d} T_i$
where
 $\alpha _i\in \mathcal {O}_K [\!\![T_1,\dots ,T_d]\!\!]$
, there are
$\alpha _i\in \mathcal {O}_K [\!\![T_1,\dots ,T_d]\!\!]$
, there are
 $x_1,\dots ,x_d\in \mathfrak {m}_{\overline {K}}$
such that
$x_1,\dots ,x_d\in \mathfrak {m}_{\overline {K}}$
such that
 $\sum _{i=1}^d\alpha _i(x_1,\dots ,x_d)\mathrm {d} x_i$
is not zero in
$\sum _{i=1}^d\alpha _i(x_1,\dots ,x_d)\mathrm {d} x_i$
is not zero in
 $\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1$
.
$\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1$
. -
(d) For
 $d=1$
, suppose
$d=1$
, suppose
 $\alpha (T)=\sum _{k\geq 0}a_kT^k$
where
$\alpha (T)=\sum _{k\geq 0}a_kT^k$
where
 $a_k\in \mathcal {O}_K$
not all zero. Let
$a_k\in \mathcal {O}_K$
not all zero. Let
 $k_0$
be the minimal number such that
$k_0$
be the minimal number such that
 $v_p(a_{k_0})$
is minimal. For a sufficiently large integer N, we take
$v_p(a_{k_0})$
is minimal. For a sufficiently large integer N, we take
 $x=\varpi ^{1/p^N}\in \mathfrak {m}_{\overline {K}}$
, where
$x=\varpi ^{1/p^N}\in \mathfrak {m}_{\overline {K}}$
, where
 $\varpi $
is a uniformizer of
$\varpi $
is a uniformizer of
 $\mathcal {O}_K$
, such that
$\mathcal {O}_K$
, such that
 $v_p(a_{k_0}x^{k_0})<v_p(a_kx^k)$
for any
$v_p(a_{k_0}x^{k_0})<v_p(a_kx^k)$
for any
 $k\neq k_0$
. Let
$k\neq k_0$
. Let
 $M=\bigcup _{i\in I,m\geq 0}K(w_{im})\subseteq \overline {K}$
. The annihilator of
$M=\bigcup _{i\in I,m\geq 0}K(w_{im})\subseteq \overline {K}$
. The annihilator of
 $\mathrm {d} x$
in
$\mathrm {d} x$
in
 $\Omega _{\mathcal {O}_{M(x)}/\mathcal {O}_M}^1$
is generated by
$\Omega _{\mathcal {O}_{M(x)}/\mathcal {O}_M}^1$
is generated by
 $p^Nx^{p^N-1}$
. As
$p^Nx^{p^N-1}$
. As
 $\mathcal {O}_M$
is a henselian discrete valuation ring with perfect residue field, Lemma 3.1 implies that the annihilator of
$\mathcal {O}_M$
is a henselian discrete valuation ring with perfect residue field, Lemma 3.1 implies that the annihilator of
 $\mathrm {d} x$
in
$\mathrm {d} x$
in
 $\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_M}^1$
is also generated by
$\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_M}^1$
is also generated by
 $p^Nx^{p^N-1}$
. When N is big enough,
$p^Nx^{p^N-1}$
. When N is big enough,
 $\alpha (x)\mathrm {d} x$
is not zero in
$\alpha (x)\mathrm {d} x$
is not zero in
 $\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1$
(cf. [Reference FontaineFon82, 3.7, Lemme 4]).
$\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1$
(cf. [Reference FontaineFon82, 3.7, Lemme 4]). -
(e) As
 $\mathcal {O}_K$
is an infinite domain, there are formal series
$\mathcal {O}_K$
is an infinite domain, there are formal series
 $\beta _1,\dots ,\beta _d\in \mathcal {O}_K [\!\![T]\!\!]$
without constant term, such that
$\beta _1,\dots ,\beta _d\in \mathcal {O}_K [\!\![T]\!\!]$
without constant term, such that
 $\sum _{i=1}^d \alpha _i(\beta _1,\dots ,\beta _d)\cdot \beta _i'\in \mathcal {O}_K [\!\![T]\!\!]$
is still nonzero. Hence, the general case reduces to the case
$\sum _{i=1}^d \alpha _i(\beta _1,\dots ,\beta _d)\cdot \beta _i'\in \mathcal {O}_K [\!\![T]\!\!]$
is still nonzero. Hence, the general case reduces to the case
 $d=1$
(cf. [Reference FontaineFon82, 3.7, Lemme 5]).▪
$d=1$
(cf. [Reference FontaineFon82, 3.7, Lemme 5]).▪
5.5
As
![]() $X(\overline {K})$
is p-divisible, we have a canonical exact sequence
$X(\overline {K})$
is p-divisible, we have a canonical exact sequence
 $$ \begin{align*} 0\longrightarrow T_p(X)\longrightarrow V_p(X)\longrightarrow X(\overline{K})\longrightarrow 0. \end{align*} $$
$$ \begin{align*} 0\longrightarrow T_p(X)\longrightarrow V_p(X)\longrightarrow X(\overline{K})\longrightarrow 0. \end{align*} $$
After applying the functor
 $\operatorname {Hom}_{\mathbb {Z}[G_K]}(-,V_p(\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1))$
, we get an exact sequence
$\operatorname {Hom}_{\mathbb {Z}[G_K]}(-,V_p(\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1))$
, we get an exact sequence
 $$ \begin{align*} 0\longrightarrow\operatorname{Hom}_{\mathbb{Z}[G_K]}\big(X(\overline{K}),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big) & \longrightarrow\operatorname{Hom}_{\mathbb{Z}[G_K]}\big(V_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big) \\ & \longrightarrow \operatorname{Hom}_{\mathbb{Z}[G_K]}\big(T_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big). \end{align*} $$
$$ \begin{align*} 0\longrightarrow\operatorname{Hom}_{\mathbb{Z}[G_K]}\big(X(\overline{K}),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big) & \longrightarrow\operatorname{Hom}_{\mathbb{Z}[G_K]}\big(V_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big) \\ & \longrightarrow \operatorname{Hom}_{\mathbb{Z}[G_K]}\big(T_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big). \end{align*} $$
Let
 $f:X(\overline {K})\to V_p(\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1)$
be a
$f:X(\overline {K})\to V_p(\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1)$
be a
![]() $G_K$
-equivariant homomorphism. For any finite extension
$G_K$
-equivariant homomorphism. For any finite extension
![]() $L/K$
, we denote by
$L/K$
, we denote by
![]() $G_L=\operatorname {Gal}(\overline {K}/L)$
the absolute Galois group of L. Then f maps
$G_L=\operatorname {Gal}(\overline {K}/L)$
the absolute Galois group of L. Then f maps
![]() $X(L)$
to
$X(L)$
to
 $V_p(\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1)^{G_L}$
. We notice that the kernel of the surjection
$V_p(\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1)^{G_L}$
. We notice that the kernel of the surjection
 $\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1\to \Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_L}^1$
is killed by a power of p, which indicates that the map
$\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1\to \Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_L}^1$
is killed by a power of p, which indicates that the map
 $V_p(\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1)\to V_p(\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_L}^1)$
is an isomorphism. Now, by applying (4.5.2) to L, we get
$V_p(\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_K}^1)\to V_p(\Omega _{\mathcal {O}_{\overline {K}}/\mathcal {O}_L}^1)$
is an isomorphism. Now, by applying (4.5.2) to L, we get
 $$ \begin{align*} V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)^{G_L}=V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_L}^1)^{G_L}=0. \end{align*} $$
$$ \begin{align*} V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)^{G_L}=V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_L}^1)^{G_L}=0. \end{align*} $$
Hence,
 $f(X(\overline {K}))=\bigcup _{L/K}f(X(L))=0$
, which indicates that we have an injective map (cf. [Reference FontaineFon82, 3.5, Lemme 2])
$f(X(\overline {K}))=\bigcup _{L/K}f(X(L))=0$
, which indicates that we have an injective map (cf. [Reference FontaineFon82, 3.5, Lemme 2])
 $$ \begin{align*} \rho_3:\operatorname{Hom}_{\mathbb{Z}[G_K]}\big(V_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big)\longrightarrow \operatorname{Hom}_{\mathbb{Z}[G_K]}\big(T_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big). \end{align*} $$
$$ \begin{align*} \rho_3:\operatorname{Hom}_{\mathbb{Z}[G_K]}\big(V_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big)\longrightarrow \operatorname{Hom}_{\mathbb{Z}[G_K]}\big(T_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big). \end{align*} $$
Remark that any element in the image of
![]() $\rho _3\circ \rho _2\circ \rho _1$
is
$\rho _3\circ \rho _2\circ \rho _1$
is
![]() $\mathbb {Z}_p$
-linear. All in all, we have generalized Fontaine’s injection ([Reference FontaineFon82, Théorème
$\mathbb {Z}_p$
-linear. All in all, we have generalized Fontaine’s injection ([Reference FontaineFon82, Théorème
![]() ${2}^{\prime }$
]) to the imperfect residue field case.
${2}^{\prime }$
]) to the imperfect residue field case.
Theorem 5.6 There is a canonical K-linear injective homomorphism
 $$ \begin{align} \rho:H^0(X,\Omega_{X/K}^1)\longrightarrow \operatorname{Hom}_{\mathbb{Z}_p[G_K]} \big(T_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big). \end{align} $$
$$ \begin{align} \rho:H^0(X,\Omega_{X/K}^1)\longrightarrow \operatorname{Hom}_{\mathbb{Z}_p[G_K]} \big(T_p(X),V_p(\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1)\big). \end{align} $$
6 Weak Hodge–Tate Representations
Definition 6.1 For any C-
![]() $G_K$
-module V of finite dimension, let
$G_K$
-module V of finite dimension, let
be a composition series of V, i.e.,
![]() $V_{i+1}/V_i$
is an irreducible C-
$V_{i+1}/V_i$
is an irreducible C-
![]() $G_K$
-module for any i. The set of factors
$G_K$
-module for any i. The set of factors
![]() $\{V_{i+1}/V_i\}_{0\leq i<n}$
does not depend on the choice of the composition series by Schreier refinement theorem. We call the multiset
$\{V_{i+1}/V_i\}_{0\leq i<n}$
does not depend on the choice of the composition series by Schreier refinement theorem. We call the multiset
 $$ \begin{align} \operatorname{wt}(V)=\big\{r_i\mid V_{i+1}/V_i\cong C(r_i),\ 0\leq i<n\big\} \end{align} $$
$$ \begin{align} \operatorname{wt}(V)=\big\{r_i\mid V_{i+1}/V_i\cong C(r_i),\ 0\leq i<n\big\} \end{align} $$
the multiset of weak Hodge–Tate weights of V. If all the factors are Tate twists of C, i.e.,
![]() $\dim _C V$
equals the cardinality of
$\dim _C V$
equals the cardinality of
![]() $\operatorname {wt}(V)$
, then we call V a weak Hodge–Tate C-representation of
$\operatorname {wt}(V)$
, then we call V a weak Hodge–Tate C-representation of
![]() $G_K$
. We denote by
$G_K$
. We denote by
![]() $\mathscr {C}$
the full subcategory of finite-dimensional C-
$\mathscr {C}$
the full subcategory of finite-dimensional C-
![]() $G_K$
-modules formed by weak Hodge–Tate representations.
$G_K$
-modules formed by weak Hodge–Tate representations.
Proposition 6.2 Let V be a finite-dimensional C-
![]() $G_K$
-module.
$G_K$
-module.
-
(i) For any short exact sequence of finite-dimensional C-
 $G_K$
-modules
$G_K$
-modules
 $0\to V'\to V\to V''\to 0$
, we have
$0\to V'\to V\to V''\to 0$
, we have
 $\operatorname {wt}(V)=\operatorname {wt}(V')\sqcup \operatorname {wt}(V'')$
. In particular,
$\operatorname {wt}(V)=\operatorname {wt}(V')\sqcup \operatorname {wt}(V'')$
. In particular,
 $\mathscr {C}$
is a closed under taking subrepresentation, quotient and extension.
$\mathscr {C}$
is a closed under taking subrepresentation, quotient and extension. -
(ii) For the dual representation
 $V^*=\operatorname {Hom}_C(V,C)$
, we have
$V^*=\operatorname {Hom}_C(V,C)$
, we have
 $\operatorname {wt}(V^*)=-\operatorname {wt}(V)$
.
$\operatorname {wt}(V^*)=-\operatorname {wt}(V)$
.
Proof The first assertion follows from the basic properties of composition series. The second assertion follows from the basic fact
![]() $C(r)^*=C(-r)$
. ▪
$C(r)^*=C(-r)$
. ▪
Proposition 6.3 For
![]() $s\in \mathbb {N}$
and
$s\in \mathbb {N}$
and
![]() $r\in \mathbb {Z}$
, the subrepresentations and quotients of
$r\in \mathbb {Z}$
, the subrepresentations and quotients of
![]() $C(r)^{\oplus s}$
in
$C(r)^{\oplus s}$
in
![]() $\mathscr {C}$
are direct summands of
$\mathscr {C}$
are direct summands of
![]() $C(r)^{\oplus s}$
of the form
$C(r)^{\oplus s}$
of the form
![]() $C(r)^{\oplus t}$
for some
$C(r)^{\oplus t}$
for some
![]() $t\in \mathbb {N}$
.
$t\in \mathbb {N}$
.
Proof After twisting by
![]() $-r$
, we can assume that
$-r$
, we can assume that
![]() $r=0$
. For any subrepresentation V of
$r=0$
. For any subrepresentation V of
![]() $C^{\oplus s}$
, we set
$C^{\oplus s}$
, we set
![]() $W=C^{\oplus s}/V$
. Consider the following commutative diagram
$W=C^{\oplus s}/V$
. Consider the following commutative diagram We see that the first and third vertical maps are injective, because K-linearly independent
We see that the first and third vertical maps are injective, because K-linearly independent
![]() $G_K$
-invariant elements are also C-linearly independent. But the middle map is identity, which shows that
$G_K$
-invariant elements are also C-linearly independent. But the middle map is identity, which shows that
![]() $V=V^{G_K}\otimes _KC$
,
$V=V^{G_K}\otimes _KC$
,
![]() $W=W^{G_K}\otimes _KC$
. Then any splitting of
$W=W^{G_K}\otimes _KC$
. Then any splitting of
![]() $0\to V^{G_K}\to K^{\oplus s}\to W^{G_K}\to 0$
induces a splitting of
$0\to V^{G_K}\to K^{\oplus s}\to W^{G_K}\to 0$
induces a splitting of
![]() $0\to V\to C^{\oplus s}\to W\to 0$
, which completes our proof. ▪
$0\to V\to C^{\oplus s}\to W\to 0$
, which completes our proof. ▪
Proposition 6.4 For
![]() $s,t\in \mathbb {N}$
and integers
$s,t\in \mathbb {N}$
and integers
![]() $r_1, r_2$
such that
$r_1, r_2$
such that
![]() $r_1-r_2\neq 1$
or
$r_1-r_2\neq 1$
or
![]() $0$
, any extension of
$0$
, any extension of
![]() $C(r_2)^{\oplus s}$
by
$C(r_2)^{\oplus s}$
by
![]() $C(r_1)^{\oplus t}$
in
$C(r_1)^{\oplus t}$
in
![]() $\mathscr {C}$
is trivial.
$\mathscr {C}$
is trivial.
Proof After twisting by
![]() $-r_2$
, we can assume that
$-r_2$
, we can assume that
![]() $r_2=0$
and
$r_2=0$
and
![]() $r_1=r\neq 1$
or
$r_1=r\neq 1$
or
![]() $0$
. Given an exact sequence
$0$
. Given an exact sequence
![]() $0\to C(r)^{\oplus t}\to V\to C^{\oplus s}\to 0$
, take
$0\to C(r)^{\oplus t}\to V\to C^{\oplus s}\to 0$
, take
![]() $G_K$
-invariants; then we obtain an exact sequence
$G_K$
-invariants; then we obtain an exact sequence
 $$ \begin{align*} 0=\big(C(r)^{\oplus t}\big)^{G_K}\longrightarrow V^{G_K}\longrightarrow K^{\oplus s}\longrightarrow H^1\big(G_K,C(r)^{\oplus t}\big)=0, \end{align*} $$
$$ \begin{align*} 0=\big(C(r)^{\oplus t}\big)^{G_K}\longrightarrow V^{G_K}\longrightarrow K^{\oplus s}\longrightarrow H^1\big(G_K,C(r)^{\oplus t}\big)=0, \end{align*} $$
from which we get an isomorphism
![]() $V^{G_K}\stackrel {\sim }{\to } K^{\oplus s}$
. Hence,
$V^{G_K}\stackrel {\sim }{\to } K^{\oplus s}$
. Hence,
![]() $V=C(r)^{\oplus t}\oplus C^{\oplus s}$
.▪
$V=C(r)^{\oplus t}\oplus C^{\oplus s}$
.▪
7 Hodge–Tate Filtration for Abelian Varieties
7.1 We keep the following simplified notation in this section:
 $$ \begin{align*} G&=G_K,\ \Omega=\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1;\\ K_I&=K\otimes_{\mathcal{O}_K} \hat{\Omega}_{\mathcal{O}_K}^1\stackrel{\sim}{\longleftarrow} K\otimes_{\mathcal{O}_K}(\oplus_{i\in I}\mathcal{O}_K)^\wedge\ (\text{by }(3.9.1));\\ C_I&=C\otimes_{\mathcal{O}_C}(\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K} \Omega_{\mathcal{O}_K/\mathbb{Z}_p}^1)^\wedge\stackrel{\sim}{\longleftarrow} C\otimes_{\mathcal{O}_C}(\oplus_{i\in I}\mathcal{O}_C)^\wedge\ (\text{by }(4.4.2));\\ E&=\operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),C),\ E^{G}(1)=\operatorname{Hom}_{\mathbb{Z}_p[G]}(T_p(X),C)\otimes_KC(1)\subseteq E(1). \end{align*} $$
$$ \begin{align*} G&=G_K,\ \Omega=\Omega_{\mathcal{O}_{\overline{K}}/\mathcal{O}_K}^1;\\ K_I&=K\otimes_{\mathcal{O}_K} \hat{\Omega}_{\mathcal{O}_K}^1\stackrel{\sim}{\longleftarrow} K\otimes_{\mathcal{O}_K}(\oplus_{i\in I}\mathcal{O}_K)^\wedge\ (\text{by }(3.9.1));\\ C_I&=C\otimes_{\mathcal{O}_C}(\mathcal{O}_{\overline{K}}\otimes_{\mathcal{O}_K} \Omega_{\mathcal{O}_K/\mathbb{Z}_p}^1)^\wedge\stackrel{\sim}{\longleftarrow} C\otimes_{\mathcal{O}_C}(\oplus_{i\in I}\mathcal{O}_C)^\wedge\ (\text{by }(4.4.2));\\ E&=\operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),C),\ E^{G}(1)=\operatorname{Hom}_{\mathbb{Z}_p[G]}(T_p(X),C)\otimes_KC(1)\subseteq E(1). \end{align*} $$
We remark that the Tate module
![]() $T_p(X)$
of the abelian variety X is a finite free
$T_p(X)$
of the abelian variety X is a finite free
![]() $\mathbb {Z}_p$
-module. By applying the functor
$\mathbb {Z}_p$
-module. By applying the functor
![]() $\operatorname {Hom}_{\mathbb {Z}_p}(T_p(X),-)=E\otimes _C-$
to the Faltings extension (4.4.1), we get an exact sequence of C-
$\operatorname {Hom}_{\mathbb {Z}_p}(T_p(X),-)=E\otimes _C-$
to the Faltings extension (4.4.1), we get an exact sequence of C-
![]() $G_K$
-modules
$G_K$
-modules
 $$ \begin{align} 0\longrightarrow \operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),C(1)) & \longrightarrow \operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),V_p(\Omega)) \\ & \longrightarrow \operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),C_I)\longrightarrow 0. \nonumber \end{align} $$
$$ \begin{align} 0\longrightarrow \operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),C(1)) & \longrightarrow \operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),V_p(\Omega)) \\ & \longrightarrow \operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),C_I)\longrightarrow 0. \nonumber \end{align} $$
We also write it as
![]() $0\to E(1)\to E\otimes _CV_p(\Omega ) \to E\otimes _CC_I\to 0$
.
$0\to E(1)\to E\otimes _CV_p(\Omega ) \to E\otimes _CC_I\to 0$
.
We choose a C-linear retraction of
![]() $\iota $
in (4.4.1) and denote by
$\iota $
in (4.4.1) and denote by
 $$ \begin{align} \pi:\operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),V_p(\Omega))\longrightarrow \operatorname{Hom}_{\mathbb{Z}_p}\big(T_p(X),C(1)\big) \end{align} $$
$$ \begin{align} \pi:\operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),V_p(\Omega))\longrightarrow \operatorname{Hom}_{\mathbb{Z}_p}\big(T_p(X),C(1)\big) \end{align} $$
the induced C-linear homomorphism.
We denote by
![]() $\tilde {\rho }$
the composition of
$\tilde {\rho }$
the composition of
 $$ \begin{align*} H^0(X,\Omega_{X/K}^1)\stackrel{\rho}{\longrightarrow} \operatorname{Hom}_{\mathbb{Z}_p[G]}(T_p(X),V_p(\Omega))\stackrel{\pi}{\longrightarrow} E(1)\longrightarrow E(1)/E^{G}(1), \end{align*} $$
$$ \begin{align*} H^0(X,\Omega_{X/K}^1)\stackrel{\rho}{\longrightarrow} \operatorname{Hom}_{\mathbb{Z}_p[G]}(T_p(X),V_p(\Omega))\stackrel{\pi}{\longrightarrow} E(1)\longrightarrow E(1)/E^{G}(1), \end{align*} $$
where
![]() $\rho $
is the Fontaine’s injection (5.6.1).
$\rho $
is the Fontaine’s injection (5.6.1).
Lemma 7.2 The canonical map
is an isomorphism.
Proof Since E is a finite-dimensional C-vector space, the complete absolute value on C extends to a complete absolute value on E uniquely up to equivalence. We fix such an absolute value and still denote it by
![]() $|\ |_p$
. Following (4.3.2) and (4.3.3), the conclusion follows from the following descriptions
$|\ |_p$
. Following (4.3.2) and (4.3.3), the conclusion follows from the following descriptions
 $$ \begin{align*} E\otimes_C C_I&=\Big\{(x_i)\in\prod_{i\in I}E\ |\ \forall N>0,\ \exists \text{ finite }J\subseteq I, |x_i|_p<1/N,\ \forall i\notin J\Big\},\\ E^G\otimes_K K_I&=\Big\{(x_i)\in\prod_{i\in I}E^G\ |\ \forall N>0,\ \exists \text{ finite }J\subseteq I, |x_i|_p<1/N,\ \forall i\notin J\Big\}. \blacksquare \end{align*} $$
$$ \begin{align*} E\otimes_C C_I&=\Big\{(x_i)\in\prod_{i\in I}E\ |\ \forall N>0,\ \exists \text{ finite }J\subseteq I, |x_i|_p<1/N,\ \forall i\notin J\Big\},\\ E^G\otimes_K K_I&=\Big\{(x_i)\in\prod_{i\in I}E^G\ |\ \forall N>0,\ \exists \text{ finite }J\subseteq I, |x_i|_p<1/N,\ \forall i\notin J\Big\}. \blacksquare \end{align*} $$
Lemma 7.3 The map
![]() $\tilde {\rho }$
is injective, and its image lies in the G-invariants of
$\tilde {\rho }$
is injective, and its image lies in the G-invariants of
![]() $E(1)/E^{G}(1)$
. Moreover,
$E(1)/E^{G}(1)$
. Moreover,
![]() $\tilde {\rho }$
does not depend on the choice of
$\tilde {\rho }$
does not depend on the choice of
![]() $\pi $
. Hence, we have a canonical K-linear injective homomorphism
$\pi $
. Hence, we have a canonical K-linear injective homomorphism
 $$ \begin{align*} \tilde{\rho}:H^0(X,\Omega_{X/K}^1)\longrightarrow \big(E(1)/E^{G}(1)\big)^{G}. \end{align*} $$
$$ \begin{align*} \tilde{\rho}:H^0(X,\Omega_{X/K}^1)\longrightarrow \big(E(1)/E^{G}(1)\big)^{G}. \end{align*} $$
Proof We take a K-basis
![]() $\{h_l\}$
of
$\{h_l\}$
of
![]() $E^G$
. For any
$E^G$
. For any
 $\omega \in H^0(X,\Omega _{X/K}^1)$
, thanks to Lemma 7.2, we denote by
$\omega \in H^0(X,\Omega _{X/K}^1)$
, thanks to Lemma 7.2, we denote by
![]() $\sum h_l\otimes \alpha _l\in E^G\otimes _K K_I$
the image of
$\sum h_l\otimes \alpha _l\in E^G\otimes _K K_I$
the image of
![]() $\omega $
in
$\omega $
in
![]() $\operatorname {Hom}_{\mathbb {Z}_p}(T_p(X),C_I)$
via Fontaine’s injection
$\operatorname {Hom}_{\mathbb {Z}_p}(T_p(X),C_I)$
via Fontaine’s injection
![]() $\rho $
(5.6.1) and (7.1.1). Take any lifting
$\rho $
(5.6.1) and (7.1.1). Take any lifting
![]() $\beta _l\in V_p(\Omega )$
of
$\beta _l\in V_p(\Omega )$
of
![]() $\alpha _l$
in the Faltings extension (4.4.1). Consider the element
$\alpha _l$
in the Faltings extension (4.4.1). Consider the element
 $$ \begin{align*} \rho(\omega)-\sum h_l\otimes \beta_l\in \operatorname{Hom}_{\mathbb{Z}_p} \big(T_p(X),V_p(\Omega)\big)=E\otimes_C V_p(\Omega). \end{align*} $$
$$ \begin{align*} \rho(\omega)-\sum h_l\otimes \beta_l\in \operatorname{Hom}_{\mathbb{Z}_p} \big(T_p(X),V_p(\Omega)\big)=E\otimes_C V_p(\Omega). \end{align*} $$
In fact, it lies in
![]() $E(1)$
. For any
$E(1)$
. For any
![]() $\sigma \in G$
,
$\sigma \in G$
,
 $$ \begin{align*} \sigma(\rho(\omega)-\sum h_l\otimes \beta_l)-(\rho(\omega)-\sum h_l\otimes \beta_l)=\sum h_l\otimes (\beta_l-\sigma(\beta_l))\in E^G(1). \end{align*} $$
$$ \begin{align*} \sigma(\rho(\omega)-\sum h_l\otimes \beta_l)-(\rho(\omega)-\sum h_l\otimes \beta_l)=\sum h_l\otimes (\beta_l-\sigma(\beta_l))\in E^G(1). \end{align*} $$
Therefore,
![]() $\rho (\omega )-\sum h_l\otimes \beta _l$
is G-invariant modulo
$\rho (\omega )-\sum h_l\otimes \beta _l$
is G-invariant modulo
![]() $E^G(1)$
; i.e., it defines an element in
$E^G(1)$
; i.e., it defines an element in
![]() $(E(1)/E^G(1))^G$
. Moreover, this element does not depend on the choice of the lifting
$(E(1)/E^G(1))^G$
. Moreover, this element does not depend on the choice of the lifting
![]() $\beta _l$
. Indeed, suppose
$\beta _l$
. Indeed, suppose
![]() $\beta _l$
and
$\beta _l$
and
![]() $\beta _l'$
two liftings of
$\beta _l'$
two liftings of
![]() $\alpha _l$
, then
$\alpha _l$
, then
![]() $\beta _l'-\beta _l\in C(1),$
which shows that
$\beta _l'-\beta _l\in C(1),$
which shows that
![]() $(\rho (\omega )-\sum h_l\otimes \beta _l)-(\rho (\omega )-\sum h_l\otimes \beta _l')\in E^G(1)$
. In particular,
$(\rho (\omega )-\sum h_l\otimes \beta _l)-(\rho (\omega )-\sum h_l\otimes \beta _l')\in E^G(1)$
. In particular,
![]() $\tilde {\rho }$
does not depend on the choice of
$\tilde {\rho }$
does not depend on the choice of
![]() $\pi $
.
$\pi $
.
Now we show the injectivity of
![]() $\tilde {\rho }$
. Suppose that
$\tilde {\rho }$
. Suppose that
![]() $\rho (\omega )-\sum h_l\otimes \beta _l=\sum h_l\otimes \gamma _l\in E^G(1)$
. Then for any
$\rho (\omega )-\sum h_l\otimes \beta _l=\sum h_l\otimes \gamma _l\in E^G(1)$
. Then for any
![]() $\sigma \in G$
,
$\sigma \in G$
,
which implies that
 $\beta _l+\gamma _l\in V_p(\Omega )^G$
=0 by (4.5.2). Hence,
$\beta _l+\gamma _l\in V_p(\Omega )^G$
=0 by (4.5.2). Hence,
![]() $\rho (\omega )=0$
, which forces
$\rho (\omega )=0$
, which forces
![]() $\omega $
to be zero, since
$\omega $
to be zero, since
![]() $\rho $
is injective. ▪
$\rho $
is injective. ▪
Theorem 7.4 There is a canonical exact sequence of C-
![]() $G_K$
-modules
$G_K$
-modules
 $$ \begin{align} 0\longrightarrow H^1(X,\mathcal{O}_X)\otimes_KC(1)\stackrel{\psi}{\longrightarrow} \operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),C(1)) \stackrel{\phi}{\longrightarrow} H^0(X,\Omega_{X/K}^1)\otimes_KC\longrightarrow 0. \end{align} $$
$$ \begin{align} 0\longrightarrow H^1(X,\mathcal{O}_X)\otimes_KC(1)\stackrel{\psi}{\longrightarrow} \operatorname{Hom}_{\mathbb{Z}_p}(T_p(X),C(1)) \stackrel{\phi}{\longrightarrow} H^0(X,\Omega_{X/K}^1)\otimes_KC\longrightarrow 0. \end{align} $$
Proof We set
 $d=\dim X=\dim _K H^0(X,\Omega _{X/K}^1)$
. Then
$d=\dim X=\dim _K H^0(X,\Omega _{X/K}^1)$
. Then
![]() $T_p(X)$
is a free
$T_p(X)$
is a free
![]() $\mathbb {Z}_p$
-module of rank
$\mathbb {Z}_p$
-module of rank
![]() $2d$
. Lemma 7.3 implies that the weak Hodge–Tate weight
$2d$
. Lemma 7.3 implies that the weak Hodge–Tate weight
![]() $0$
of
$0$
of
![]() $E(1)$
has multiplicity
$E(1)$
has multiplicity
![]() $\geq d$
. Let
$\geq d$
. Let
![]() $X'$
be the dual abelian variety of X, and we set
$X'$
be the dual abelian variety of X, and we set
![]() $E'=\operatorname {Hom}_{\mathbb {Z}_p}(T_p(X'),C)$
. Due to the fact that
$E'=\operatorname {Hom}_{\mathbb {Z}_p}(T_p(X'),C)$
. Due to the fact that
![]() $E'=E(1)^*$
(by Weil pairing) and Proposition 6.2, the weak Hodge–Tate weight
$E'=E(1)^*$
(by Weil pairing) and Proposition 6.2, the weak Hodge–Tate weight
![]() $1$
of
$1$
of
![]() $E(1)$
has multiplicity
$E(1)$
has multiplicity
![]() $\geq d$
. But
$\geq d$
. But
![]() $\dim _C E(1)=2d$
, which forces these inequalities to be equalities. In particular,
$\dim _C E(1)=2d$
, which forces these inequalities to be equalities. In particular,
 $\tilde {\rho }:H^0(X,\Omega _{X/K}^1)\to (E(1)/E^{G}(1))^{G}$
is an isomorphism. Since
$\tilde {\rho }:H^0(X,\Omega _{X/K}^1)\to (E(1)/E^{G}(1))^{G}$
is an isomorphism. Since
![]() $C(1)$
has only trivial extension by
$C(1)$
has only trivial extension by
![]() $C^{\oplus d}$
(Proposition 6.4), we see that
$C^{\oplus d}$
(Proposition 6.4), we see that
![]() $C^{\oplus d}$
is a quotient representation of
$C^{\oplus d}$
is a quotient representation of
![]() $E(1)$
. By duality again, we see that
$E(1)$
. By duality again, we see that
![]() $C(1)^{\oplus d}$
is a subrepresentation of
$C(1)^{\oplus d}$
is a subrepresentation of
![]() $E(1)$
, and thus the canonical injection
$E(1)$
, and thus the canonical injection
![]() $(E(1)/E^G(1))^G\otimes _K C\to E(1)/E^G(1)$
is an isomorphism. Therefore, we have a canonical surjection
$(E(1)/E^G(1))^G\otimes _K C\to E(1)/E^G(1)$
is an isomorphism. Therefore, we have a canonical surjection
 $$ \begin{align*} E(1)\longrightarrow H^0(X,\Omega_{X/K}^1)\otimes_KC. \end{align*} $$
$$ \begin{align*} E(1)\longrightarrow H^0(X,\Omega_{X/K}^1)\otimes_KC. \end{align*} $$
By duality,
 $H^1(X,\mathcal {O}_X)\otimes _KC(1)=H^0(X',\Omega _{X'/K}^1)^*\otimes _KC(1)$
canonically identifies with a subrepresentation of
$H^1(X,\mathcal {O}_X)\otimes _KC(1)=H^0(X',\Omega _{X'/K}^1)^*\otimes _KC(1)$
canonically identifies with a subrepresentation of
![]() $E(1)$
. Now (7.4.1) follows from the avoidance of
$E(1)$
. Now (7.4.1) follows from the avoidance of
![]() $C(1)^{\oplus d}$
and
$C(1)^{\oplus d}$
and
![]() $C^{\oplus d}$
.▪
$C^{\oplus d}$
.▪
7.5
Let us complete the proof of the Main Theorem 1.3. We choose a retraction of
![]() $\iota $
in the Faltings extension (4.4.1). By our construction, we have the following commutative diagram
$\iota $
in the Faltings extension (4.4.1). By our construction, we have the following commutative diagram
 where
where
![]() $\phi $
is the surjection in the Hodge–Tate filtration (7.4.1),
$\phi $
is the surjection in the Hodge–Tate filtration (7.4.1),
![]() $\pi $
is induced by the chosen retraction, and
$\pi $
is induced by the chosen retraction, and
![]() $\rho $
is the Fontaine’s injection (5.6.1). Consider the following diagram:
$\rho $
is the Fontaine’s injection (5.6.1). Consider the following diagram:
 where
where
![]() $\delta '$
is the connecting map associated to (7.4.1), where
$\delta '$
is the connecting map associated to (7.4.1), where
![]() $-\pi '$
is the surjection in (7.1.1), and where we identify
$-\pi '$
is the surjection in (7.1.1), and where we identify
![]() $H^1(X,\mathcal {O}_X)$
with
$H^1(X,\mathcal {O}_X)$
with
![]() $\operatorname {Hom}_{\mathbb {Z}_p[G]}(T_p(X),C)$
by (7.4.1) and identify
$\operatorname {Hom}_{\mathbb {Z}_p[G]}(T_p(X),C)$
by (7.4.1) and identify
![]() $H^1(G,C(1))$
with
$H^1(G,C(1))$
with
![]() $K_I$
by (4.5.1), which gives the right vertical arrow. Let
$K_I$
by (4.5.1), which gives the right vertical arrow. Let
![]() $\{h_l\}$
be a K-basis of
$\{h_l\}$
be a K-basis of
![]() $H^1(X,\mathcal {O}_X)$
. For any
$H^1(X,\mathcal {O}_X)$
. For any
 $\omega \in H^0(X,\Omega _{X/K}^1)$
, we write
$\omega \in H^0(X,\Omega _{X/K}^1)$
, we write
![]() $-\pi '(\rho (\omega ))=\sum h_l\otimes \alpha _l$
by 7.2, where
$-\pi '(\rho (\omega ))=\sum h_l\otimes \alpha _l$
by 7.2, where
![]() $\alpha _l\in K_I$
. Let
$\alpha _l\in K_I$
. Let
![]() $\beta _l\in V_p(\Omega )$
be the lifting of
$\beta _l\in V_p(\Omega )$
be the lifting of
![]() $\alpha _l$
via the chosen splitting of the Faltings extension. We see by the diagram (7.5.1) that
$\alpha _l$
via the chosen splitting of the Faltings extension. We see by the diagram (7.5.1) that
![]() $\rho (\omega )-\sum h_l\otimes \beta _l$
is a lifting of
$\rho (\omega )-\sum h_l\otimes \beta _l$
is a lifting of
![]() $\omega $
via
$\omega $
via
![]() $\phi $
. Thus,
$\phi $
. Thus,
![]() $\delta '(\omega )$
is represented by the following
$\delta '(\omega )$
is represented by the following
![]() $1$
-cocycle:
$1$
-cocycle:
 $$ \begin{align*} \sigma\longmapsto \sum h_l\otimes \big(\beta_l-\sigma(\beta_l)\big),\quad \forall \sigma\in G. \end{align*} $$
$$ \begin{align*} \sigma\longmapsto \sum h_l\otimes \big(\beta_l-\sigma(\beta_l)\big),\quad \forall \sigma\in G. \end{align*} $$
We notice that
![]() $\alpha _l\in K_I$
corresponds to a class in
$\alpha _l\in K_I$
corresponds to a class in
![]() $H^1(G,C(1))$
represented by the following
$H^1(G,C(1))$
represented by the following
![]() $1$
-cocycle:
$1$
-cocycle:
In conclusion, diagram (7.5.2) is commutative.
7.6
Now we can prove Corollary 1.4 to the main theorem. If the sequence (7.4.1) splits, then the
![]() $\phi $
in (7.5.2) is surjective. Hence,
$\phi $
in (7.5.2) is surjective. Hence,
![]() $\delta '$
is zero map, and so is
$\delta '$
is zero map, and so is
![]() $\pi '\circ \rho $
. Thus, the image of the Fontaine’s injection
$\pi '\circ \rho $
. Thus, the image of the Fontaine’s injection
![]() $\rho $
lies in
$\rho $
lies in
![]() $\operatorname {Hom}_{\mathbb {Z}_p}(T_p(X),C(1))$
. We easily see that, conversely, if the image of the Fontaine’s injection
$\operatorname {Hom}_{\mathbb {Z}_p}(T_p(X),C(1))$
. We easily see that, conversely, if the image of the Fontaine’s injection
![]() $\rho $
lies in
$\rho $
lies in
![]() $\operatorname {Hom}_{\mathbb {Z}_p}(T_p(X),C(1))$
, then sequence (7.4.1) splits. Moreover, the splitting is unique by the avoidance of
$\operatorname {Hom}_{\mathbb {Z}_p}(T_p(X),C(1))$
, then sequence (7.4.1) splits. Moreover, the splitting is unique by the avoidance of
![]() $C(1)^{\oplus d}$
and
$C(1)^{\oplus d}$
and
![]() $C^{\oplus d}$
.
$C^{\oplus d}$
.
Acknowledgment
I would like to express my sincere gratitude to my advisor Ahmed Abbes. He led me to this topic and spent a lot of time discussing it with me. He gave me plenty of helpful advice on both studying and writing. I would like to thank the referee for improving some statements and many other helpful comments. This work was done while I was a master’s student at Département de Mathématiques d’Orsay, Université Paris-Saclay, supported by Fondation Mathématique Jacques Hadamard (FMJH).