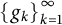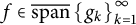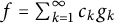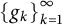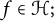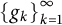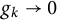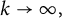1 Introduction
Let
${\cal H}$
denote a separable infinite-dimensional Hilbert space, and suppose that a given sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
in
${\cal H}$
has the expansion property, i.e., that each
$f\in \overline {\text {span}} \left \{g_k\right \}_{k=1}^{\infty }$
has a representation
$$ \begin{align} f= \sum_{k=1}^{\infty} c_k g_k \end{align} $$
for certain coefficients
$c_k\in \mathbb C$
. Our goal is to address the following question: when and how can we perform small norm-perturbations on the sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
and hereby obtain a sequence
$\{\psi _k\}_{k=1}^{\infty }$
such that arbitrary elements
$f\in {\cal H}$
have an expansion
$ f= \sum _{k=1}^{\infty } c_k \psi _k$
for certain coefficients
$c_k\in \mathbb C?$
Formulated as above, the question is clearly a completion problem. We will show that the completion problem has an affirmative answer for the so-called Riesz sequences and frame sequences, but not for general basic sequences; along the way, we also consider a number of other completion problems. Interestingly, the insight gained from the above analysis can be used to address a somewhat dual question: when and how can a redundant system
$\left \{g_k\right \}_{k=1}^{\infty }$
be turned into a complete but nonredundant system
$\{\psi _k\}_{k=1}^{\infty }$
by small norm-perturbations? We will provide a positive answer to this question for a number of frames, in particular, for the so-called near-Riesz bases introduced by Holub in [Reference Holub13]. Additional motivation for this particular question will be provided at the end of the paper.
The paper is organized as follows. In the rest of the introduction, we set the stage by providing a number of definitions and results from the literature. In Section 2, we present the results about the completion problem; the dual problem concerning removal of redundancy is considered in Section 3.
A sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
in the Hilbert space
${\cal H}$
is called a frame for
${\cal H}$
if there exist constants
$A,B>0$
such that
$$ \begin{align} A \, ||f||^2 \le \sum_{k=1}^{\infty} | \langle f, g_k\rangle|^2\le B\, ||f||^2, \, \forall f \in {\cal H}; \end{align} $$
suitable numbers
$A,B$
are called lower, resp. upper frame bounds. The sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
is called a Bessel sequence if at least the right-hand inequality in (1.2) holds. A frame which is at the same time a basis is called a Riesz basis. Note that several other characterizations of frames and Riesz bases exist, e.g., in terms of operator theory. For example, if
$\{e_k\}_{k=1}^{\infty }$
is a given orthonormal basis for
${\cal H},$
frames for
${\cal H}$
are precisely the sequences
$\{Ve_k\}_{k=1}^{\infty }$
where
$V: {\cal H} \to {\cal H}$
is a bounded surjective operator; Riesz bases correspond precisely to the case where the operator V also is injective. Finally, a sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
which is a frame for the (sub)space
${\cal K}:= \overline {\text {span}} \left \{g_k\right \}_{k=1}^{\infty }$
is called a frame sequence; Riesz sequences are defined in the analogue way.
One of the key reasons for the interest in frames is that a frame has the expansion property: in fact, given any frame
$\left \{g_k\right \}_{k=1}^{\infty },$
there exists a so-called dual frame
$\{f_k\}_{k=1}^{\infty }$
such that
$$ \begin{align*} f= \sum_{k=1}^{\infty} \langle f, f_k\rangle g_k, \, \forall f\in {\cal H}. \end{align*} $$
In general, the dual frame
$\{f_k\}_{k=1}^{\infty }$
is not unique: indeed, the case where
$\left \{g_k\right \}_{k=1}^{\infty }$
is a Riesz basis is characterized precisely by the existence of a unique dual. We refer to [Reference Christensen9] for more information about frames and Riesz bases, also about their history and applications.
The following lemma collects a number of well-known results concerning norm-perturbations of various sequences with the expansion property.
Lemma 1.1 Consider two sequences
$\left \{g_k\right \}_{k=1}^{\infty }, \{h_k\}_{k=1}^{\infty }$
in
${\cal H},$
satisfying that
$$ \begin{align*} \sum_{k=1}^{\infty} ||g_k-h_k||^2 < A, \end{align*} $$
for a value of A as specified below. Then, the following holds:
-
(i) [Reference Christensen7] If
$\left \{g_k\right \}_{k=1}^{\infty }$
is a frame for
${\cal H}$
with lower bound
$A,$
then
$\{h_k\}_{k=1}^{\infty }$
is a frame for
${\cal H}.$
-
(ii) [Reference Christensen8] If
$\left \{g_k\right \}_{k=1}^{\infty }$
is a Riesz sequence with lower bound
$A,$
then
$\{h_k\}_{k=1}^{\infty }$
is a Riesz sequence; furthermore,
$\text {codim}( \overline {\text {span}} \left \{g_k\right \}_{k=1}^{\infty })= \text {codim}( \overline {\text {span}} \{h_k\}_{k=1}^{\infty }).$
Alternative norm-perturbation conditions are formulated in [Reference Chen, Li and Zheng6]; however, they need that we have access to information about a dual frame, which is not the case in the current paper. Note also that a number of classical results about norm-perturbation (typically for orthonormal sequences) are collected in [Reference Young17]. Observe that more general perturbation results are available in the literature, typically formulated in terms of certain operators rather than norm-perturbations (see, e.g., [Reference Christensen9] and the references therein).
2 Completion via norm-perturbation
Our main interest is to consider the completion problem for sequences
$\left \{g_k\right \}_{k=1}^{\infty }$
having the expansion property. However, we first state a number of other completion properties, some of which will be needed in latter proofs. Given any sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
in
${\cal H},$
we define its excess
${\cal E}(\left \{g_k\right \}_{k=1}^{\infty })$
as the maximal number of elements that can be removed without changing the spanned space, i.e.,
$$ \begin{align} {\cal E}(\left\{g_k\right\}_{k=1}^{\infty}):= \max \sharp \{J \subset \mathbb N \, \big| \, \overline{\text{span}} \{g_k\}_{k\in \mathbb N \setminus J}= \overline{\text{span}} \left\{g_k\right\}_{k=1}^{\infty} \}. \end{align} $$
Furthermore, we will use the standard convention and say that a sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
in
${\cal H}$
is norm-bounded below if there exists a constant
$C>0$
such that
$||g_k|| \ge C$
for all
$k\in \mathbb N$
.
Proposition 2.1 Let
$\left \{g_k\right \}_{k=1}^{\infty }$
be a sequence in
${\cal H}.$
Then, the following hold:
-
(i) If
$\left \{g_k\right \}_{k=1}^{\infty }$
is not norm-bounded below, there exists a complete sequence
$\{\psi _k\}_{k=1}^{\infty }$
in
${\cal H}$
such that (2.2)
$$ \begin{align} || g_k-\psi_k|| \to 0 \, \text{as } \, k\to \infty; \end{align} $$
-
(ii) If
${\cal E}(\left \{g_k\right \}_{k=1}^{\infty }) \ge \mbox {codim}(\overline {\text {span}} \left \{g_k\right \}_{k=1}^{\infty })$
, there exists a complete sequence
$\{\psi _k\}_{k=1}^{\infty }$
in
${\cal H}$
such that (2.2) holds. -
(iii) If
$\left \{g_k\right \}_{k=1}^{\infty }$
is convergent, there exists a complete sequence
$\{\psi _k\}_{k=1}^{\infty }$
in
${\cal H}$
such that (2.2) holds; in particular,
$\{\psi _k\}_{k=1}^{\infty }$
converges to the same limit as
$\left \{g_k\right \}_{k=1}^{\infty }.$
In all the stated cases, given any
$\delta>0,$
the sequence
$\{\psi _k\}_{k=1}^{\infty }$
can be chosen such that additionally
$|| g_k-\psi _k|| \le \delta $
for all
$k\in \mathbb N.$
Proof. For the proof of (i), given
$\delta>0,$
choose a frame
$\{f_k\}_{k=1}^{\infty }$
for
${\cal H}$
such that
$||f_k|| \le \delta $
for all
$k\in \mathbb N$
and
$||f_k|| \to 0$
as
$k\to \infty ;$
for example, letting
$\{e_k\}_{k=1}^{\infty }$
denote any orthonormal basis, we can take
$$ \begin{align*} \{f_k\}_{k=1}^{\infty} = \left\{\delta\, e_1, \frac{\delta}{\sqrt{2}}\, e_2, \frac{\delta}{\sqrt{2}}\, e_2, \frac{\delta}{\sqrt{3}}\, e_3,\frac{\delta}{\sqrt{3}}\, e_3,\frac{\delta}{\sqrt{3}}\, e_3, \dots\right\}.\end{align*} $$
Denote the lower frame bound for the frame
$\{ f_k \}_{k=1}^{\infty }$
by
$A.$
Choose now a subsequence
$\{g_{k_n}\}_{n=1}^{\infty } $
of
$\left \{g_k\right \}_{k=1}^{\infty }$
such that
$ ||g_{k_n}||^2 \le \frac {3 A}{\pi ^2 n^2}, \, n\in \mathbb N;$
then,
$$ \begin{align*} \sum_{n=1}^{\infty} || f_n- \left( f_n+g_{k_n}\right)||^2 = \sum_{n=1}^{\infty} ||g_{k_n}||^2 \le \frac{A}{2}.\end{align*} $$
Using Lemma 1.1(i), this implies that
$\{ f_n+g_{k_n}\}_{n=1}^{\infty }$
is a frame for
${\cal H}$
and hence complete. Thus, the sequence
$\{\psi _k\}_{k=1}^{\infty }$
formed from
$\left \{g_k\right \}_{k=1}^{\infty }$
by replacing the elements
$\{g_{k_n}\}_{n=1}^{\infty } $
by
$\{f_n+g_{k_n}\}_{n=1}^{\infty }$
will satisfy the requirements.
For the proof of (ii), we first assume additionally that
$M:=\mbox {codim}(\overline {\text {span}} \left \{g_k\right \}_{k=1}^{\infty })$
is finite. Without loss of generality and only for notational convenience, assume that the sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
is ordered such that
$g_1, \dots , g_M\in \overline {\text {span}}\{g_k\}_{k=M+1}^{\infty },$
and take an orthonormal basis
$\{e_k\}_{k=1}^M$
for the orthogonal complement
$(\overline {\text {span}} \left \{g_k\right \}_{k=1}^{\infty })^{\bot }.$
Then, the sequence
$$ \begin{align*} \{\psi_k\}_{k=1}^{\infty} = \left\{g_1+ \delta e_1, g_2+ \frac{\delta}{2}\, e_2,\dots, g_M+ \frac{\delta}{M} e_M, g_{M+1}, g_{M+2}, \dots\right\}\end{align*} $$
satisfies the requirements. The case where
${\cal E}(\left \{g_k\right \}_{k=1}^{\infty })= \mbox {codim}(\overline {\text {span}} \left \{g_k\right \}_{k=1}^{\infty })=\infty $
is similar and only requires minor notational modifications.
For the proof of (iii), assume that the sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
converges to
$f\in {\cal H}.$
Given
$\delta>0,$
choose
$K\in \mathbb N$
such that
$||f-g_k|| \le \delta /2$
for
$k\ge K.$
Let
$\{e_k\}_{k=1}^{\infty }$
denote an orthonormal basis for
${\cal H}$
, and define
$\{\psi _k\}_{k=1}^{\infty }$
by
$$ \begin{align*} \psi_k:= \begin{cases} g_k, &\mbox{if } \, k=1, \dots, K-1; \\ f, &\mbox{if } \, k=K; \\ f+ \frac{\delta}{2^{k-K}}e_{k-K}, &\mbox{if } \, k>K.\end{cases} \end{align*} $$
Then,
$\text {span} \{e_k\}_{k=1}^{\infty } \subseteq \text {span} \{\psi _k\}_{k=1}^{\infty },$
so
$\text {span} \{\psi _k\}_{k=1}^{\infty }$
is clearly complete. Furthermore, for
$k\ge K,$
$$ \begin{align*} || g_k-\psi_k|| \le ||g_k-f|| + ||f-\psi_k|| \le\delta,\end{align*} $$
and
$|| g_k-\psi _k||\to 0$
as
$k\to \infty .$
▪
We are now ready to consider the completion problem for Riesz sequences and frame sequences. The proofs rely on an interesting result proved recently by Olevskii.
Lemma 2.2 [Reference Olevskii15, Reference Olevskii16]
If
$\{e_k\}_{k=1}^{\infty }$
is an orthonormal sequence in
${\cal H},$
there exists an orthonormal basis
$\{ \chi _k\}_{k=1}^{\infty }$
for
${\cal H}$
such that
$$ \begin{align*} || e_k-\chi_k || \to 0 \, \mbox{as } \, k\to \infty.\end{align*} $$
In addition, given any
$\delta>0,$
the sequence
$\{ \chi _k\}_{k=1}^{\infty }$
can be chosen such that
$|| e_k-\chi _k || \le \delta $
for all
$k\in \mathbb N.$
Theorem 2.3 Let
$\left \{g_k\right \}_{k=1}^{\infty }$
be a sequence in
${\cal H}.$
Then, the following hold:
-
(i) If
$\left \{g_k\right \}_{k=1}^{\infty }$
is a Riesz sequence, there exists a Riesz basis
$\{\psi _k\}_{k=1}^{\infty }$
for
${\cal H}$
such that (2.3)
$$ \begin{align} || g_k-\psi_k|| \to 0 \, \mbox{as } \, k\to \infty.\end{align} $$
-
(ii) If
$\left \{g_k\right \}_{k=1}^{\infty }$
is a frame sequence, there exists a frame
$\{\psi _k\}_{k=1}^{\infty }$
for
${\cal H}$
such that (2.3) holds. -
(iii) If
$\left \{g_k\right \}_{k=1}^{\infty }$
is a Bessel sequence, there exists a complete Bessel sequence
$\{\psi _k\}_{k=1}^{\infty }$
such that (2.3) holds.
In all the stated cases, given any
$\delta>0,$
the sequence
$\{\psi _k\}_{k=1}^{\infty }$
can be chosen such that
$|| g_k-\psi _k|| \le \delta $
for all
$k\in \mathbb N.$
Proof. We first prove (iii). Thus, let
$\left \{g_k\right \}_{k=1}^{\infty }$
be a Bessel sequence in
${\cal H},$
and let
${\cal K}:= \overline {\text {span}} \left \{g_k\right \}_{k=1}^{\infty };$
we can assume that
${\cal K}^{\bot } \neq \{0\}.$
Furthermore, if
${\cal K}$
is finite-dimensional, clearly
${\cal E}(\left \{g_k\right \}_{k=1}^{\infty }) = \infty $
, and thus the results follow from Proposition 2.1(ii). Therefore, we now assume that
${\cal K}$
is infinite-dimensional. Now, by the standard properties of a Bessel sequence [Reference Christensen9], choose an orthonormal basis
$\{e_k\}_{k=1}^{\infty }$
for
${\cal K}$
and a bounded operator
$U: {\cal K} \to {\cal K}$
such that
$g_k=Ue_k, \, k\in \mathbb N.$
Associated with the orthonormal sequence
$\{e_k\}_{k=1}^{\infty }$
, choose the orthonormal basis
$\{ \chi _k\}_{k=1}^{\infty }$
for
${\cal H}$
as in Lemma 2.2, and define a bounded operator
$V: {\cal H} \to {\cal H}$
by
$$ \begin{align} V=U \mbox{ on } {\cal K}, \, \, V=I \mbox{ on } {\cal K}^{\bot}.\end{align} $$
Because the range of the operator U contains the vectors
$\left \{g_k\right \}_{k=1}^{\infty },$
it is dense in
${\cal K}.$
Thus, the range of the operator V is dense in
${\cal H};$
this implies that the sequence
$\{\psi _k\}_{k=1}^{\infty }:=\{ V\chi _k\}_{k=1}^{\infty }$
is complete in
${\cal H}.$
A direct calculation reveals that
$\{\psi _k\}_{k=1}^{\infty }$
is a Bessel sequence. Furthermore, for all
$k\in \mathbb N,$
$$ \begin{align*} ||g_k-\psi_k||= ||Ue_k - V \chi_k|| = ||Ve_k- V\chi_k|| \le ||V||\, || e_k- \chi_k||.\end{align*} $$
Because the operator V only depends on the sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
(and the fixed choice of
$\{e_k\}_{k=1}^{\infty }$
), this proves (iii). This also gives the proof of (i) and (ii). Indeed, if
$\left \{g_k\right \}_{k=1}^{\infty }$
is a frame sequence, the range of the operator U equals
${\cal K},$
which implies that the range of the operator V equals
${\cal H},$
and hence
$\{\psi _k\}_{k=1}^{\infty }$
is a frame for
${\cal H};$
and if
$\{f_k\}_{k=1}^{\infty }$
is a Riesz sequence, the operator
$U:{\cal K} \to {\cal K}$
is bijective, implying that
$V:{\cal H} \to {\cal H}$
is bijective, and hence that
$\{\psi _k\}_{k=1}^{\infty }$
is a Riesz sequence.▪
Remark 2.4 Despite the fact that
$\delta>0$
can be chosen arbitrarily small in Theorem 2.3, there is a restriction on how “close” the sequence
$\{\psi _k\}_{k=1}^{\infty }$
can be to the sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
. Indeed, if
$\left \{g_k\right \}_{k=1}^{\infty }$
is a (noncomplete) Riesz sequence with lower bound
$A,$
then the sequence
$\{\psi _k\}_{k=1}^{\infty }$
in Theorem 2.3(i) must satisfy that
$$ \begin{align} \sum_{k=1}^{\infty} ||g_k-\psi_k||^2 \ge A; \end{align} $$
otherwise, Lemma 1.1(ii) would imply that
$\{\psi _k\}_{k=1}^{\infty }$
is noncomplete as well. A similar result holds for frame sequences, although the lower bound on the infinite sum in (2.5) will involve the gap between two particular subspaces of
${\cal H}$
(see [Reference Christensen8, Reference Christensen, deFlicht and Lennard10] for more detailed information).
Theorem 2.3 makes it natural to ask whether a basic sequence (i.e., a Schauder basis for a subspace) also can be extended to a Schauder basis for
${\cal H}$
by small norm-perturbations of the elements. The following example shows that the answer is no, in general, unless additional assumptions are added.
Example 2.5 Let
$\{e_k\}_{k=1}^{\infty }$
denote an orthonormal basis for
${\cal H}$
, and consider the sequence
$$ \begin{align*} \left\{g_k\right\}_{k=1}^{\infty}= \{2e_2, 4e_4, 6e_6, \dots\}=\{2k e_{2k}\}_{k=1}^{\infty}.\end{align*} $$
Clearly,
$\left \{g_k\right \}_{k=1}^{\infty }$
is a basic sequence. Now, given any
$\delta \in ]0, 2\sqrt {6}\pi ^{-1}[,$
consider a sequence
$\{\psi _k\}_{k=1}^{\infty } $
in
${\cal H}$
such that
$|| g_k- \psi _k|| \le \delta $
for all
$k\in \mathbb N.$
Then,
$$ \begin{align*} \sum_{k=1}^{\infty} || e_{2k} - \frac1{2k}\, \psi_k||^2 = \sum_{k=1}^{\infty} \frac1{4k^2}\, || g_k- \psi_k||^2 \le \frac{\pi^2 \delta^2}{24} <1.\end{align*} $$
Because
$\{e_{2k}\}_{k=1}^{\infty }$
forms a Riesz sequence with lower bound
$A=1,$
Lemma 1.1(ii) implies that
$\{(2k)^{-1} \psi _k\}_{k=1}^{\infty }$
also forms a Riesz sequence, spanning a space of the same codimension as
$\{e_{2k}\}_{k=1}^{\infty };$
in particular,
$\{ \psi _k\}_{k=1}^{\infty }$
cannot be complete in
${\cal H},$
and hence is not a Schauder basis for
${\cal H}.$
3 Removal of redundancy via norm-perturbations
In this section, the focus is on sequences
$\left \{g_k\right \}_{k=1}^{\infty }$
having the expansion property on the entire underlying Hilbert space
${\cal H}.$
Such expansions might be redundant, i.e., a given
$f\in {\cal H}$
might have expansions
$f= \sum _{k=1}^{\infty } c_k g_k$
for more than one choice of the scalar coefficients
$\{c_k\}_{k=1}^{\infty }.$
A typical example of a redundant sequence is a frame
$\left \{g_k\right \}_{k=1}^{\infty }$
which is not a Riesz basis. Our goal is to show that for certain frames
$\left \{g_k\right \}_{k=1}^{\infty }$
, the redundancy can be removed via small norm-perturbations of the vectors
$g_k.$
Our first observation, stated next, does not even need the frame assumption or any other expansion property.
Theorem 3.1 Consider any sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
in
${\cal H}$
such that
$g_k\to 0$
as
$k\to \infty .$
Then, given any
$\delta>0,$
there exists a Riesz basis
$\{\psi _k\}_{k=1}^{\infty }$
for
${\cal H}$
such that
$$ \begin{align*} ||g_k- \psi_k || \le \delta, \, \forall k\in \mathbb N.\end{align*} $$
Proof. First, given any
$\delta>0,$
choose
$K\in \mathbb N$
such that
$||g_k|| < \delta /2$
for
$k\ge K.$
We will now construct
$\{\psi _k\}_{k=1}^{\infty }$
recursively, of the form
$\psi _k:= g_k + \varphi _k$
with the vectors
$\varphi _k$
chosen as described next. First, take
$\varphi _1\in {\cal H}$
such that
$|| \varphi _1|| \le \delta $
and
$\psi _1 \neq 0.$
Then, choose
$\varphi _2\in {\cal H}$
such that
$|| \varphi _2|| \le \delta $
and
$\{\psi _1, \psi _2\}$
is linearly independent. Continuing recursively, we finally choose
$\varphi _K\in {\cal H}$
such that
$|| \varphi _K|| \le \delta $
and
$\{\psi _1, \psi _2, \dots , \psi _K\}$
is linearly independent. Then,
$\{\psi _1, \psi _2, \dots , \psi _K\}$
is a Riesz basis for the subspace
$V:=\text {span}\{\psi _1, \psi _2, \dots , \psi _K\}.$
Now, choose an orthonormal basis
$\{e_k\}_{k=1}^{\infty }$
for
$V^{\bot }$
and define
$\psi _k$
for
$k>K$
by
$\psi _k:= \frac {\delta }{2}e_k.$
Then,
$\{\psi _k\}_{k=1}^{\infty }$
is a Riesz basis for
${\cal H}$
and
$||g_k-\psi _k|| \le \delta $
for all
$k\in \mathbb N.$
▪
The result in Theorem 3.1 immediately applies to a number of well-known frames in the literature.
Example 3.2 We state a number of examples of frames
$\left \{g_k\right \}_{k=1}^{\infty }$
such that
$g_k\to 0$
as
$k\to {\infty}$
:
-
(i) Given any orthonormal basis
$\{e_k\}_{k=1}^{\infty }$
for
${\cal H},$
the family is a frame for
$$ \begin{align*} \left\{g_k\right\}_{k=1}^{\infty}:= \left\{e_1, \frac1{\sqrt{2}}\,e_2,\frac1{\sqrt{2}}\,e_2, \frac1{\sqrt{3}}\,e_3, \frac1{\sqrt{3}}\,e_3, \frac1{\sqrt{3}}\,e_3, \dots \right\}\end{align*} $$
${\cal H}.$
Clearly,
$g_k\to 0$
as
$k\to \infty .$
Note that this particular frame was used in the proof of Proposition 2.1.
-
(ii) Let again
$\{e_k\}_{k=1}^{\infty }$
be an orthonormal basis for
${\cal H}$
, and fix any
$\alpha \in ]0,1[.$
Let
$\lambda _{\ell }:= 1- \alpha ^{-\ell }$
for
$\ell \in \mathbb N,$
and define the vectors Then,
$$ \begin{align*} g_k:= \sum_{\ell=1}^{\infty} \lambda_{\ell}^k \sqrt{1- \lambda_{\ell}^2} e_{\ell}, \, k\in \mathbb N.\end{align*} $$
$\left \{g_k\right \}_{k=1}^{\infty }$
is a frame (the so-called Carleson frame), a result proved by Aldroubi et al. in [Reference Aldroubi, Cabrelli, Molter and Tang1, Reference Aldroubi, Cabrelli, Çakmak, Molter and Petrosyan2]. It is easy to see that
$g_k \to 0$
as
$k\to \infty .$
Note that
$\left \{g_k\right \}_{k=1}^{\infty }$
is heavily redundant: it can be proved that for any
$N\in \mathbb N,$
any subfamily
$\{g_{Nk}\}_{k\in \mathbb N}$
of
$\left \{g_k\right \}_{k=1}^{\infty }$
is a redundant frame as well. From this point of view, it is surprising that
$\left \{g_k\right \}_{k=1}^{\infty }$
can be approximated by a Riesz basis, as stated in Theorem 3.1.
-
(iii) More generally than (ii), it was proved in [Reference Christensen, Hasannasab and Philipp12] that any redundant frame that can be represented as an operator orbit
$\left \{g_k\right \}_{k=1}^{\infty }= \{T^k \varphi \}_{k=1}^{\infty }$
for a bounded operator
$T:{\cal H} \to {\cal H}$
and some
$\varphi \in {\cal H}$
will have the property that
$g_k\to 0$
as
$k\to \infty .$
In order to reach the next result, we need the following lemma. Recall that the deficit of a sequence
$\left \{g_k\right \}_{k=1}^{\infty }$
is defined as the codimension of the vector space
$\overline {\text {span}} \left \{g_k\right \}_{k=1}^{\infty }.$
Lemma 3.3 Let
$\{e_k\}_{k=1}^{\infty }$
be an orthonormal basis for
${\cal H}.$
Given any
$\delta>0$
and any
$N\in \mathbb N,$
there exists an orthonormal system
$\{\varepsilon _k\}_{k=1}^{\infty }$
with deficit N such that
$||e_k-\varepsilon _k||\le \delta $
for all
$k\in \mathbb N.$
Proof. Take any orthonormal system
$\{\varphi _k\}_{k=1}^{\infty }$
with deficit
$N,$
and choose via Lemma 2.2 an orthonormal basis
$\{\chi _k\}_{k=1}^{\infty }$
for
${\cal H}$
such that
$||\varphi _k - \chi _k||\le \delta $
for all
$k\in \mathbb N.$
Then, choose the unitary operator
$U: {\cal H} \to {\cal H}$
such that
$e_k= U\chi _k,$
and let
$\varepsilon _k:=U\varphi _k, k\in \mathbb N.$
Then,
$\{\varepsilon _k\}_{k=1}^{\infty }$
is an orthonormal system with deficit
$N,$
and
$|| e_k-\varepsilon _k||=||U\chi _k-U\varphi _k|| = ||\chi _k-\varphi _k|| \le \delta $
for all
$k\in \mathbb N,$
as desired.▪
Theorem 3.4 Consider a frame of the form
$\left \{g_k\right \}_{k=1}^{\infty }= \{g_k\}_{k=1}^N \cup \{g_k\}_{k=N+1}^{\infty },$
where
$N\in \mathbb N$
and
$\{g_k\}_{k=N+1}^{\infty }$
is a Riesz basis for
${\cal H}.$
Then, given any
$\delta>0,$
there exists a Riesz basis
$\{\psi _k\}_{k=1}^{\infty } $
such that
$||g_k-\psi _k||\le \delta $
for all
$k\in \mathbb N.$
Proof. First, consider an orthonormal basis for
${\cal H}$
indexed as
$\{e_k\}_{k=N+1}^{\infty }$
, and choose the bounded bijective operator
$V:{\cal H} \to {\cal H}$
such that
$g_k=Ve_k$
for
$k=N+1, N+2, \dots .$
Using Lemma 3.3, choose an orthonormal system
$\{\varepsilon _k\}_{k=N+1}^{\infty }$
with deficit N such that
$||e_k-\varepsilon _k||\le \delta /{||V||}$
for
$k=N+1, N+2, \dots .$
Then, letting
$\psi _k:= V\varepsilon _k, k=N+1, N+2, \dots ,$
the family
$\{\psi _k\}_{k=N+1}^{\infty }$
is a Riesz sequence with deficit
$N,$
and
$||g_k-\psi _k|| = || Ve_k-V\varepsilon _k|| \le \delta $
for
$k=N+1, N+2, \dots .$
Now, consider the vector
$g_N.$
If
$g_N \notin \overline {\text {span}} \{\psi _k\}_{k=N+1}^{\infty },$
let
$\psi _N:=g_N;$
then,
$\{\psi _k\}_{k=N}^{\infty }$
is a Riesz sequence with deficit
$N-1.$
On the other hand, if
$g_N \in \overline {\text {span}} \{\psi _k\}_{k=N+1}^{\infty },$
choose any normalized vector
$\varphi _N \notin \overline {\text {span}} \{\psi _k\}_{k=N+1}^{\infty },$
and let
$\psi _N:= g_N+ \delta \varphi _N;$
then, again
$\{\psi _k\}_{k=N}^{\infty }$
is a Riesz sequence with deficit
$N-1,$
and
$||g_k-\psi _k|| \le \delta $
for
$k=N,N+1, N+2, \dots .$
Applying now the same procedure on
$g_{N-1},g_{N-2}, \dots ,g_1,$
we arrive at the desired Riesz basis
$\{\psi _k\}_{k=1}^{\infty }$
in a finite number of steps.▪
Interestingly, frames of the type considered in Theorem 3.4 were called near-Riesz bases by Holub in the paper [Reference Holub13]; the above result provides an additional reason for this name being very appropriate.
Remark 3.5 Despite the fact that
$\delta>0$
can be chosen arbitrarily small in Theorem 3.4, the Riesz basis
$\{\psi _k\}_{k=1}^{\infty }$
must satisfy that
$\sum _{k=1}^{\infty } ||g_k-\psi _k||^2 \ge A,$
where A is the lower frame bound for
$\left \{g_k\right \}_{k=1}^{\infty };$
otherwise, the results in [Reference Casazza and Christensen5] show that
$\{\psi _k\}_{k=1}^{\infty }$
would be a frame with the same excess as
$\left \{g_k\right \}_{k=1}^{\infty }.$
We want to point out that the proof of Theorem 3.4 somewhat hides the fact that it is highly nontrivial to get direct access to the Riesz basis
$\{\psi _k\}_{k=1}^{\infty },$
especially due to the intriguing and deep construction by Olevskii playing a key role in the argument. The next example illustrates this by a concrete construction.
Example 3.6 Let again
$\{e_k\}_{k=1}^{\infty }$
be an orthonormal basis for
${\cal H}$
, and consider the frame
$$ \begin{align*} \left\{g_k\right\}_{k=1}^{\infty}:= \{e_1, e_1, e_2, e_3, e_4, \dots\}, \end{align*} $$
consisting of the orthonormal basis and a single extra element. A natural way to try to remove the redundancy would be to fix a small
$\epsilon>0$
and let
$\psi _1:=e_1$
and for
$k>1, \psi _k:= \frac 12 e_{k-1} + ( \frac 12 + \epsilon ) e_k.$
Then, for any finite sequence
$\{c_k\}_{k=2}^{\infty },$
$$ \begin{align*} \left|\left| \sum_{k=2}^{\infty} c_k\left( \left(\frac12 + \epsilon\right)e_k-\psi_k\right) \right|\right|{}^2= \frac14 \left|\left| \sum_{k=2}^{\infty} c_ke_{k-1} \right|\right|{}^2 = \frac14 \sum_{k=2}^{\infty} |c_k|^2.\end{align*} $$
Observe that
$\{e_1\}\cup \{(\frac 12 + \epsilon )e_k\}_{k=2}^{\infty }$
is a Riesz basis with lower bound
$\frac 12 + \epsilon .$
Considering
$\{\psi _k\}_{k=1}^{\infty }$
as a perturbation of this Riesz basis, it now follows from the results in [Reference Casazza and Christensen5] that
$\{\psi _k\}_{k=1}^{\infty }$
is a Riesz basis for
${\cal H}.$
Note that
$$ \begin{align*} || g_k-\psi_k||= \sqrt{\frac 14 + \left(\frac12 + \epsilon\right)^2};\end{align*} $$
however, this construction does not allow us to obtain
$|| g_k - \psi _k|| \le \delta $
when
$\delta < 2^{-1/2}\approx 0.7.$
In fact, in order to obtain the result in Theorem 3.4 for smaller values of
$\delta ,$
it would be necessary to consider much more complicated perturbations
$\{\psi _k\}_{k=1}^{\infty }$
of
$\left \{g_k\right \}_{k=1}^{\infty},$
making it highly nontrivial to do this in practice.
Remark 3.7 The question of removal of redundancy is partly motivated by the research topic dynamical sampling, introduced in the papers [Reference Aldroubi, Cabrelli, Çakmak, Molter and Petrosyan2, Reference Aldroubi, Davis and Krishtal3]. One of the key issues in dynamical sampling is the construction of frames as orbits
$\{T^k \varphi \}_{k=0}^{\infty }$
of a bounded operator
$T:{\cal H} \to {\cal H},$
for some
$\varphi \in {\cal H};$
we encountered such frames already in Example 3.2(ii,iii). Unfortunately, it is very difficult to construct such frames, and the only concrete examples available in the literature are indeed Riesz bases [Reference Christensen and Hasannasab11] and the Carleson frame [Reference Aldroubi, Cabrelli, Çakmak, Molter and Petrosyan2] considered in Example 3.2(ii). Furthermore, it was proved in [Reference Christensen and Hasannasab11] that a near-Riesz basis never has this property. This raises the natural question whether a near-Riesz basis can be approximated by a Riesz basis, and hence by an orbit of a bounded operator; Theorem 3.4 confirms that this indeed is possible. We will phrase this consequence of Theorem 3.4 as a separate result, where we index the given near-Riesz basis by
$\{g_k\}_{k=0}^{\infty }$
for notational convenience.
Corollary 3.8 Consider any near-Riesz basis
$\{g_k\}_{k=0}^{\infty }.$
Then, given any
$\delta>0,$
there exists
$\varphi \in {\cal H}$
and a bounded operator
$T:{\cal H} \to {\cal H}$
such that
$$ \begin{align*} ||g_k-T^k \varphi|| \le \delta, \, \forall k\in \mathbb N_0.\end{align*} $$
The results in Theorems 3.1 and 3.4 do not cover the standard (regular) redundant Gabor frames and wavelet frames: they consist of vectors with equal norm, and they have infinite excess [Reference Balan, Casazza, Heil and Landau4]. Due to the complications discussed in Example 3.1 and the preceding text, it seems to be very difficult to answer the question whether all frames indeed can be approximated by a Riesz basis. At least for Gabor frames and wavelet frames, we can apply the following adaption of the Feichtinger theorem (finally proved in one of its equivalent formulations in [Reference Marcus, Spielman and Srivastava14]), showing that any frame which is norm-bounded below can be approximated by a finite collection of Riesz bases.
Theorem 3.9 Let
$\left \{g_k\right \}_{k=1}^{\infty }$
be a frame which is norm-bounded below. Then, there exists a finite partition
$\left \{g_k\right \}_{k=1}^{\infty } = \bigcup _{j=1}^J \{g_k\}_{k\in I_j}$
with the property that for each
$\delta>0$
, there exist Riesz bases
$\{\psi _k\}_{k\in I_j}, j=1, \dots , J,$
for
${\cal H}$
such that
$||g_k-\psi _k||\le \delta $
for all
$k\in \mathbb N.$
Proof. Choose according to the Feichtinger theorem a finite partition
$\left \{g_k\right \}_{k=1}^{\infty } = \bigcup _{j=1}^J \{g_k\}_{k\in I_j}$
such that each sequence
$\{g_k\}_{k\in I_j}, j=1, \dots ,J$
, is a Riesz sequence; using Theorem 2.1 in [Reference Christensen and Hasannasab11], we can shuffle the elements around to ensure that each of the index sets
$I_j$
is infinite. Now, the result follows directly from Theorem 2.3(i).▪
The result in Theorem 3.9 can be formulated as an operator-theoretic result, similarly to Corollary 3.8; we leave the precise formulation to the interested reader.
Acknowledgment
We would like to express our sincere gratitude for the anonymous reviewer for helpful comments, which improved the presentation of the results.
