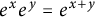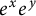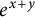1 Introduction
Throughout this paper, A will be assumed to be a complex and unital Banach algebra with the unit denoted by
${\mathbf 1}$
. The group of invertible elements, and the center of A modulo the radical, are denoted respectively by
$G(A)$
and
$Z(A)$
. We shall use
$\sigma _A$
and
$\rho _A$
to denote, respectively, the spectrum
$$ \begin{align*} \sigma_A(x):=\{\lambda\in{\mathbb C}:\lambda{\mathbf 1}-x\notin G(A)\}, \end{align*} $$
and the spectral radius
$$ \begin{align*} \rho_A(x):=\sup\{|\lambda|:\lambda\in\sigma_A(x)\} \end{align*} $$
of an element
$x\in A$
(and agree to omit the subscript if the underlying algebra is clear from the context). If
$K\subset {\mathbb C}$
, then
$\#K$
denotes the number of elements in K; so either
$\#K<\infty $
or
$\#K=\infty $
. For each
$x\in A$
, completeness of A gives the existence of an element
$e^x$
, either via the Holomorphic Functional Calculus, or equivalently, by the direct series expansion
$e^x:=\sum _{n=0}^{\infty } \frac {x^n}{n!}$
. As is evident from the literature on algebras of operators, and more generally Banach algebras, the utility of the complex exponential function extends to the more general settings. If x and y commute, then, as in the complex case, the exponential formula
$e^xe^y=e^{x+y}$
holds, and if the exponential formula holds for all
$x,y\in A$
then A is commutative. We should point out that it is possible, for some
$x,y\in A$
, that
$e^xe^y=e^{x+y}$
even though x and y do not commute. In fact, the first study of this phenomena goes back to Fréchet [Reference Fréchet6] and was very quickly followed by [Reference Huff8–Reference Morinaga and Nôno11]. For a more recent development on this matter, see [Reference de Seguins Pazzis14]. The aim of the current paper is to compare
$e^xe^y$
and
$e^{x+y}$
with respect to the spectral parameters
$\rho $
and
$\#\sigma $
, but on a larger scale than for single elements x and y. In particular, we are able to characterize commutative
$C^\star $
-algebras in this way (see Theorem 2.1 and Corollary 2.2). In Theorem 3.2, we use similar ideas to characterize semisimple commutative Banach algebras in general.
The most familiar spectral characterization of semisimple commutative Banach algebras is probably the following: If A is semisimple, then A is commutative if and only if there exists
$K>0$
such that
$\|x\|\leq K\rho (x)$
for all
$x\in A$
. We should note that the easiest proof of this uses exponentials together with the fact that, for any Banach algebra A, the spectral radius is cyclic i.e.,
$\rho (xy)=\rho (yx)$
holds for all
$x,y\in A$
. More interesting spectral characterizations of commutativity appeared later during the 1970s; in a rather intriguing series of three papers, Aupetit [Reference Aupetit1] on the one hand, and Zemánek [Reference Zemánek16] and Zemánek and Pták [Reference Pták and Zemánek12] on the other hand, obtained, independently, but at the same time, a number of striking results where spectral conditions imposed on the algebra imply commutativity. The methods employed by Aupetit and those used by Zemánek, and Zemánek and Pták, differ greatly with the latter mentioned authors relying mostly on connections with classical complex analysis, and Aupetit on subharmonic techniques, the origin of which goes back to Vesentini’s theorem [Reference Vesentini15]. Most notably, they established the following equivalences:
-
(i) A is commutative.
-
(ii)
$\rho $
is uniformly continuous on A. -
(iii)
$\rho $
is Lipschitz continuous on A. -
(iv)
$\rho $
is subadditive on A. -
(iv)
$\rho $
is submultiplicative on A.
The following two results, due to Aupetit, will be crucial in our arguments and are stated for the sake of convenience.
Theorem 1.1 (Scarcity Principle, [Reference Aupetit2, Theorem 3.4.25])
If f is an analytic function from a domain
$D\subseteq {\mathbb C}$
into a Banach algebra A, then either
$$ \begin{align*} D_F=\{\lambda\in D:\sigma(f(\lambda))\mbox{ is finite}\} \end{align*} $$
is a Borel set with zero capacity, or there is
$n\in \mathbb N$
and a closed, discrete subset
$E\subset D$
such that
$\#\sigma (f(\lambda ))=n$
for
$\lambda \in D\backslash E$
and
$\#\sigma (f(\lambda ))<n$
for
$\lambda \in E$
. In the latter case, the n points of
$\sigma (f(\lambda ))$
(as
$\lambda $
varies) are locally holomorphic functions on
$D\backslash E$
.
Theorem 1.2 (Spectral Characterization of Central Elements, [Reference Aupetit1, Lemma 4])
If
$a\in A$
satisfies
$\#\sigma (ax-xa)=1 \mbox { for all }x\in A,$
then
$a\in Z(A).$
We shall also make use of the following standard application of Gelfand theory:
Lemma 1.3 ([Reference Rudin13, Theorem 11.23])
Suppose that a and b are commuting elements of A. Then
$\sigma (a+b) \subseteq \sigma (a) + \sigma (b) \mbox { and }\sigma (ab) \subseteq \sigma (a)\sigma (b)$
.
2 Algebraic elements and
$C^\star $
-algebras
In our first main result, Theorem 2.1, we show that if A is a semisimple noncommutative Banach algebra containing noncentral algebraic elements, then there must be some degree to which the terms
$e^xe^y$
exert dominance over the terms
$e^{x+y}$
with respect to the spectral radius as well as the number of elements in the respective spectra. Further, we are inclined to believe that the condition (i) implies that A itself is commutative, although this may be hard to prove. On the other hand, we show, in Example 2.3, that condition (ii) is too weak to establish this.
Theorem 2.1 Let A be a semisimple Banach algebra. Then every algebraic element of A belongs to
$Z(A)$
if any one of the following conditions holds:
-
(i) There exists some
$K>0$
such that
$\rho (e^xe^y)\leq K\rho (e^{x+y})\mbox { for all }x,y\in A.$
-
(ii) There exists
$\epsilon>0$
such that
$\#\sigma (e^xe^y)\leq \#\sigma (e^{x+y})\mbox { for all }x,y\in B(0,\epsilon ).$
Proof. (i) We shall first prove that zero is the only nilpotent element of A. Since an algebra which contains nonzero nilpotent elements must necessarily also contain elements with nilpotency degree
$2$
it suffices to show that
$q^2=0\Rightarrow q=0$
. Let
$x\in A$
be arbitrary but fixed. From the assumption we then have that
$$ \begin{align*}\rho(e^{\lambda x}e^{\lambda q-\lambda x})\leq K\rho (e^{\lambda q})=K\mbox{ for all }\lambda\in{\mathbb C}.\end{align*} $$
Since the map
$\lambda \mapsto e^{\lambda x}e^{\lambda q-\lambda x}$
is an entire function from
${\mathbb C}$
to A it follows by Liouville’s Spectral Theorem [Reference Aupetit2, Theorem 3.4.14] that the polynomially convex hull of
$\sigma (e^{\lambda x}e^{\lambda q-\lambda x})$
is constant on
${\mathbb C}$
. By setting
$\lambda =0$
we deduce that
$$ \begin{align*} \sigma(e^{\lambda x}e^{\lambda q-\lambda x}-{\mathbf 1})=\{0\}\mbox{ for all }\lambda\in{\mathbb C}. \end{align*} $$
In a similar fashion, we have that
$$ \begin{align*} \sigma(e^{\lambda x-\lambda q}e^{-\lambda x}-{\mathbf 1})=\{0\}\mbox{ for all }\lambda\in{\mathbb C}. \end{align*} $$
Since
$e^{\lambda x-\lambda q}e^{-\lambda x}$
and
$e^{\lambda x}e^{\lambda q-\lambda x}$
commute it follows from Lemma 1.3 that
$$ \begin{align} \sigma(e^{\lambda x}e^{\lambda q-\lambda x} + e^{\lambda x-\lambda q}e^{-\lambda x} -\mathbf 2)=\{0\}\mbox{ for all }\lambda\in{\mathbb C}. \end{align} $$
Using the fact that
$q^2=0,$
we now have
$$ \begin{align*} &e^{\lambda x} e^{\lambda q-\lambda x} + e^{\lambda x-\lambda q}e^{-\lambda x} -\mathbf 2\\ &\quad =\left(\sum_{j=0}^{\infty}\frac{(\lambda x)^j}{j!}\right)\left(\sum_{j=0}^{\infty}\frac{(\lambda q-\lambda x)^j}{j!}\right)+\left(\sum_{j=0}^{\infty}\frac{(\lambda x-\lambda q)^j}{j!}\right)\left(\sum_{j=0}^{\infty}\frac{(-\lambda x)^j}{j!}\right)-\mathbf 2\\ &\quad =q^2\lambda^2+\left(\frac{x^2q^2}{2}-\frac{q^2x}{2}\right)\lambda^3 +\bigg(\frac{q^4}{12}+\frac{q^2x^2}{6} + \frac{q^3x}{12} + \frac{xq^2}{12} + \frac{x^2q^2}{6}-\frac{qxq^2}{12}\\ &\qquad +\frac{qx^2q}{12}-\frac{q^2xq}{12}-\frac{xq^2x}{4}-\frac{qxqx}{12}-\frac{xqxq}{12}\bigg)\lambda^4+\cdots\\ &\quad =\left(\frac{qx^2q}{12}-\frac{qxqx}{12}-\frac{xqxq}{12}\right)\lambda^4+\cdots\\ &\quad =-\frac{1}{12}(qx-xq)^2\lambda^4+\cdots. \end{align*} $$
Next, define an entire function from
${\mathbb C}$
into A by
$$ \begin{align*} f(\lambda) = \left\{\begin{array}{ll} \left(e^{\lambda x}e^{\lambda q-\lambda x} + e^{\lambda x-\lambda q} e^{-\lambda x} - {\mathbf 2}\right)/{\lambda^4}, & \lambda\not=0, \\ -(qx-xq)^2/12, & \lambda=0.\end{array}\right. \end{align*} $$
For all
$0\not =\lambda \in {\mathbb C}$
it follows that the subharmonic function
$\lambda \mapsto \rho (f(\lambda ))$
satisfies
$\rho (f(\lambda ))=0$
, and hence, by the Maximum Principle for subharmonic functions [Reference Aupetit2, Theorem A.1.3] that
$\rho (f(0))=0$
. From this, we deduce, from the Spectral Mapping Theorem, that
$\sigma (qx-xq)=\{0\}$
for all
$x\in A$
, and so, by Theorem 1.2, we obtain
$q\in Z(A)$
. Consequently, from Lemma 1.3 it follows that
$\sigma (qx) = \{0\}$
for all
$x \in A$
. Hence, we conclude that q belongs to the radical of A, and so, since A is semisimple, it follows that
$q=0$
as required. The next step is to show that every idempotent of A belongs to
$Z(A)$
. Let
$p\in A$
be a nontrivial idempotent. For each
$x\in A,$
we have that
$px({\mathbf 1}-p)$
is nilpotent and hence by the first part of the proof
$pxp=px$
. Similarly,
$({\mathbf 1}-p)xp$
is nilpotent and so
$pxp=xp$
. This shows that
$p\in Z(A)$
. Finally, if a is an algebraic element, then, by the Holomorphic Functional Calculus, a can be written as
$a=\lambda _1p_1+\cdots \lambda _kp_k+q$
where each
$\lambda _i\in {\mathbb C}$
,
$p_i$
is an idempotent, and q is a nilpotent element. Since
$q=0$
and
$p_i\in Z(A)$
it follows that
$a\in Z(A)$
.
(ii) Suppose, as the first of two cases, that
$\dim A=\infty $
. Let
$q\in A$
be nilpotent of degree
$2$
and
$0\not =x\in A$
arbitrary. Then, by the hypothesis, there is
$\delta>0$
such that
$$ \begin{align} \#\sigma(e^{\lambda x}e^{\lambda q-\lambda x})\leq\#\sigma(e^{\lambda q})=1\mbox{ for all }\lambda\in B(0,\delta). \end{align} $$
If we recall that the function
$\lambda \mapsto e^{\lambda x}e^{\lambda q-\lambda x}$
is entire, then, since the spectrum is nonempty, it follows from (2.2) and Theorem 1.1 that
$$ \begin{align*} \#\sigma(e^{\lambda x}e^{\lambda q-\lambda x})=1\mbox{ for all }\lambda\in{\mathbb C}. \end{align*} $$
Observe then that, for each
$\lambda $
,
$e^{\lambda x-\lambda q}e^{-\lambda x}$
is the inverse of
$e^{\lambda x}e^{\lambda q-\lambda x}$
when we also have
$\#\sigma \left (e^{\lambda x-\lambda q}e^{-\lambda x}\right )=1\mbox { for all }\lambda \in {\mathbb C}.$
So together, using Lemma 1.3, we can deduce that
$$ \begin{align*} \#\sigma\left(e^{\lambda x}e^{\lambda q-\lambda x} + e^{\lambda x-\lambda q}e^{-\lambda x} -\mathbf 2\right)=1\mbox{ for all }\lambda\in{\mathbb C}. \end{align*} $$
With f as in the proof of (i) above, Theorem 1.1 yields
$\#\sigma ((qx-xq)^2)=1$
. This implies that, for each
$x\in A$
, we have one of the following:
-
(a)
$\#\sigma (qx-xq)=1$
or -
(b)
$\#\sigma (qx-xq)=2.$
If (b) holds for some
$y\in A$
, then, since
$\#\sigma ((qy-yq)^2)=1$
, we are forced to conclude that
$qy-yq\in G(A)$
. Further, since the map
$D:x\to qx-xq$
is an inner derivation on A satisfying
$\#\sigma (D(x))\leq 2$
for each
$x\in A$
, it follows that, for each x,
$D(x)$
belongs to the socle of A [Reference Brešar and Šemrl4, Theorem 3.2]. However, this would mean that the socle contains an invertible element of A, and so, since the socle is an ideal, it must be all of A. Since every element of the socle has a finite spectrum, the Hirschfeld–Johnson Criterion [Reference Hirschfeld and Johnson7, p. 19] now implies that A is finite-dimensional. But this contradicts the assumption that
$\dim A=\infty $
. So it follows that (a) holds for each
$x\in A$
, and the remaining part of the proof follows as in (i).
Suppose now that
$\dim A<\infty $
. With the cardinality assumption on the spectrum, we first establish the result for
$A=M_n({\mathbb C})$
, that is, we show that the assumption forces
$n=1$
. Suppose to the contrary that
$n\geq 2$
. Then
$A=M_n({\mathbb C})$
has a subalgebra, say B, which contains
${\mathbf 1}\in A$
and
$$ \begin{align*}B\cong M_2({\mathbb C})\oplus\underbrace{{\mathbb C}\oplus\cdots\oplus{\mathbb C}}_{n-2\text{ factors}}.\end{align*} $$
Of course, if
$x\in B$
, then
$\sigma _B(x)=\sigma _A(x)=\sigma (x)$
. Let
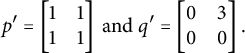$$ \begin{align*} p^{\prime}=\begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}\mbox{ and }q^{\prime}=\begin{bmatrix} 0 & 3 \\ 0 & 0 \end{bmatrix}. \end{align*} $$
Then, with
$x^{\prime }=-p^{\prime }$
and
$y^{\prime }=p^{\prime }+q^{\prime }$
it follows that
$$ \begin{align*} e^{x^{\prime}}=\begin{bmatrix} \frac{e^2+1}{2e^2}&\frac{-e^2+1}{2e^2}\\[1ex] \frac{-e^2+1}{2e^2}&\frac{e^2+1}{2e^2} \end{bmatrix}\mbox{ and }\ e^{y^{\prime}}=\begin{bmatrix} \frac{e^4+1}{2e}&\frac{e^4-1}{e}\\[1ex] \frac{e^4-1}{4e}&\frac{e^4+1}{2e} \end{bmatrix}, \end{align*} $$
so that
$$ \begin{align*} e^{x^{\prime}}e^{y^{\prime}}=\begin{bmatrix} \frac{e^6+3e^4+3e^2+1}{8e^3}&\frac{e^6+3e^4-3e^2-1}{4e^3}\\[1ex] \frac{-e^6+3e^4-3e^2+1}{8e^3}&\frac{-e^6+3e^4+3e^2-1}{4e^3}\end{bmatrix}\mbox{ and }\ e^{x^{\prime}+y^{\prime}}=\begin{bmatrix} 1 & 3 \\ 0 & 1 \end{bmatrix}. \end{align*} $$
Now let
$$ \begin{align*} x=(x^{\prime},0,\dots,0)\mbox{ and }y=(y^{\prime},0,\dots,0)\in B. \end{align*} $$
Then there exists
$\delta>0,$
such that
$\lambda \in B(0,\delta )\subseteq {\mathbb C}$
implies that
$\lambda x,\lambda y\in B(0,\epsilon )\subseteq A$
. Since for all
$\lambda \in {\mathbb C}$
, we have that
$\sigma (e^{\lambda (x+y)})=\{1\}$
it follows, by our assumption, that
$$ \begin{align*}\#\sigma(e^{\lambda x}e^{\lambda y})\leq\#\sigma(e^{\lambda(x+y)})=1\mbox{ for all }\lambda\in B(0,\delta).\end{align*} $$
Since the spectrum is nonempty, it follows by Theorem 1.1 that
$\#\sigma (e^{\lambda x}e^{\lambda y})=1$
for all
$\lambda \in {\mathbb C}$
. If we observe that the matrices
$x^{\prime },y^{\prime }\in M_2({\mathbb C})$
satisfy
$$ \begin{align*}\operatorname{\mathrm{tr}}\left(e^{x^{\prime}}e^{y^{\prime}}\right)=\frac{-e^6+9e^4+9e^2-1}{8e^3}\mbox{ and }\det\left(e^{x^{\prime}}e^{y^{\prime}}\right)=1,\end{align*} $$
then
$$ \begin{align*}\operatorname{\mathrm{tr}}^2\left(e^{x^{\prime}}e^{y^{\prime}}\right)-4\det\left(e^{x^{\prime}}e^{y^{\prime}}\right)\not=0\Rightarrow \#\sigma_{M_2({\mathbb C})}\left(e^{x^{\prime}}e^{y^{\prime}}\right)=2\end{align*} $$
from which it follows that
$\#\sigma (e^{x}e^{y})\geq 2$
thereby contradicting the fact that
$\#\sigma (e^{\lambda x}e^{\lambda y})=1$
for all
$\lambda \in {\mathbb C}$
. This means that n cannot be greater or equal to
$2$
, and so
$A={\mathbb C}$
. If A is an arbitrary semisimple finite dimensional Banach algebra, then the Wedderburn–Artin representation, together with the preceding result, imply that
$A\cong {\mathbb C}^n$
for some
$n\in \mathbb N$
, and thus that A is commutative.▪
Corollary 2.2 If A is a
$C^\star $
-algebra, and if either of the conditions (i) or (ii) in the statement of Theorem 2.1 holds, then A is commutative.
Proof. An old theorem of Kaplansky’s [Reference Blackadar3, Proposition 6.4.14, p. 110] says that any noncommutative
$C^\star $
-algebra contains nonzero nilpotent elements. So the result follows from Theorem 2.1.▪
Example 2.3 There exists a noncommutative semisimple Banach algebra A such that
$\#\sigma (e^xe^y)\leq \#\sigma (e^{x+y})$
for all
$x,y\in A$
.
Proof. We consider the first exposition [Reference Duncan and Tullo5, Theorem 9] of a noncommutative Banach algebra which contains no nonzero quasinilpotent elements; the first part of our proof is essentially Duncan and Tullo’s argument. Let
$\{u,v\}$
be an alphabet of two letters, and denote by
$$ \begin{align*} \mathcal W=\{u,v, u^2, uv, vu, v^2, \dots\} \end{align*} $$
the standard enumeration of words, formed by juxtaposition, from the alphabet. The length of a word is the number of letters that comprises the word (counting repetition). From this, we may construct the Banach algebra B consisting of all infinite series
$$ \begin{align*} x=\alpha_1u+\alpha_2v+\alpha_3u^2+\alpha_4uv+\alpha_5vu+\alpha_6v^2+\cdots \end{align*} $$
such that
$$ \begin{align*} \|x\|:=\sum_{n=1}^{\infty}|\alpha_n|<\infty. \end{align*} $$
Of course, a zero coefficient in the representation of x deletes the corresponding word from the representation. In the usual manner, we adjoin an identity element
${\mathbf 1}$
to B to obtain the unital Banach algebra A with norm
$\|\alpha {\mathbf 1}+x\|=|\alpha |+\|x\|$
for
$\alpha \in {\mathbb C}$
and
$x\in B$
. Now let
$0\not =\alpha {\mathbf 1}+x\in A$
be arbitrary. Notice that, if
$\alpha \not =0$
, then
$$ \begin{align*} \|(\alpha{\mathbf 1}+x)^n\|\geq|\alpha|^n\Rightarrow\rho(\alpha{\mathbf 1}+x)\geq|\alpha|. \end{align*} $$
If
$\alpha =0$
, then let
$s(u,v)$
be any one of the (finite collection of) shortest words which appears in the representation of x, and let
$\beta $
be its coefficient. It follows that, for each
$n\in \mathbb N$
, the coefficient of
$[s(u,v)]^n$
in the representation of
$x^n$
is
$\beta ^n$
. By definition of the norm on B, we have that
$$ \begin{align*} \|x^n\|\geq |\beta|^n\Rightarrow \rho(x)\geq |\beta|. \end{align*} $$
This proves that A contains no nonzero quasinilpotent elements. Suppose next that
$\alpha {\mathbf 1}+x$
(
$x\in B$
) is a nontrivial idempotent of A. Then either x or
$-x$
is an idempotent; therefore if A has a nontrivial idempotent then B has a nontrivial idempotent. But, by comparison of the lengths of the shortest words in x and
$x^2$
, this is clearly impossible. Thus the only idempotents of A are trivial. Further, if
$a\in A$
has finite spectrum then, from the Holomorphic Functional Calculus, we know that
$a=\lambda_1 p_1 + \cdots + \lambda _k p_k + q$
where
$\lambda _i\in {\mathbb C}$
,
$p_i$
is an idempotent, and q is a quasinilpotent element. This proves that
${\mathbb C}{\mathbf 1}$
are the only elements in A which have finite spectra. If for some
$x,y\in A$
,
$\sigma (e^{x+y})$
is a finite set, then, since the spectrum is compact and the complex exponential function has period
$2\pi $
, the Spectral Mapping Theorem implies that
$\sigma (x+y)$
is also finite. It then follows that
$x=\alpha {\mathbf 1}-y$
for some
$\alpha \in {\mathbb C}$
, and thus that x and y commute. This is sufficient to deduce that
$\#\sigma (e^xe^y)\leq \#\sigma (e^{x+y})$
for all
$x,y\in A$
. Observe further that if some
$x\in A$
has countably infinite spectrum, then one could separate
$\sigma (x)$
, and use the Holomorphic Functional Calculus to construct a nontrivial idempotent in A which leads to a contradiction. We therefore actually have the stronger result:
$\operatorname {\mathrm {Card}}\sigma (e^xe^y)\leq \operatorname {\mathrm {Card}}\sigma (e^{x+y})$
for all
$x,y\in A$
.▪
Remark 2.4 To see that Theorem 2.1 (i) cannot be localized, consider the following: Let
$A=M_2({\mathbb C})$
, let
$r>0$
be arbitrary, and take
$K=e^{4r}$
. For any
$x,y\in B(0,r)$
observe that
$$ \begin{align*} \sigma (x+y)&\subseteq \{\lambda\in{\mathbb C}:{-2r}\leq\operatorname{\mathrm{Re}}{\lambda}\leq {2r}\}\\ &\Rightarrow\sigma(e^{x+y})=e^{\sigma(x+y)}\subseteq \{\lambda\in{\mathbb C}:e^{-2r}\leq|\lambda|\leq e^{2r}\}\\ &\Rightarrow e^{-2r}\leq \rho (e^{x+y}). \end{align*} $$
Then, for each
$x,y\in B(0,r)$
, it follows that
$$ \begin{align*} \rho(e^xe^y)\leq e^{\|x\|}e^{\|y\|}\leq e^{2r}\leq K \rho(e^{x+y}). \end{align*} $$
Thus the hypothesis in Theorem 2.1 (i) is satisfied in the ball
$B(0,r)$
, but not all the algebraic elements of A can belong to
$Z(A)$
since every element of A is algebraic.
To see that Theorem 2.1 (ii) cannot be generalized to arbitrary open balls in A, consider the following: Let
$A=M_2({\mathbb C})$
and pick
$z\in A$
such that
$\sigma (z)=\{\lambda _1,\lambda _2\}\subset \mathbb R$
and
$\lambda _1\not =\lambda _2$
. By spectral mapping
$\sigma (e^{2z} )= \{e^{2\lambda _1},e^{2\lambda _2}\}\subset \mathbb R$
. If we take disjoint discs
$B(e^{2\lambda _1},\epsilon )$
and
$B(e^{2\lambda _2},\epsilon )$
then, by continuity of the spectrum and continuity of the map
$x\mapsto e^{x}$
, it follows that there exists
$r>0$
such that
$$ \begin{align*} w\in B(2z,r)\Rightarrow \#\sigma(e^w)\cap B(e^{2\lambda_1},\epsilon)=1\mbox{ and }\ \#\sigma(e^w)\cap B(e^{2\lambda_2},\epsilon)=1, \end{align*} $$
so that
$w\in B(2z,r)\Rightarrow \#\sigma (e^w)=2$
. If
$x,y\in B(z,r/2)$
then, by the triangle inequality, we have that
$x+y\in B(2z,r)$
whence the preceding calculation shows that
$$ \begin{align*}\#\sigma(e^{x+y})=2.\end{align*} $$
Since the spectral cardinality of any element in A is at most
$2,$
we have
$$ \begin{align*}\#\sigma (e^xe^y )\leq\#\sigma (e^{x+y})=2\mbox{ for all }x,y\in B(z,r/2).\end{align*} $$
But, as in the first example,
$A\not =Z(A)$
.
3 General commutativity
We start with the following simple result the proof of which follows along the same lines as the standard argument which gives
$$ \begin{align*}A\mbox{ is commutative }\Leftrightarrow \|xy\|=\|yx\|\mbox{ for all }x,y\in A.\end{align*} $$
Proposition 3.1 A complex Banach algebra A is commutative if and only if there exists some
$K>0$
such that
$$ \begin{align*} \|e^xe^y\|\leq K\|e^{x+y}\|\mbox{ for all }x,y\in A. \end{align*} $$
Proof. Let
$x,y\in A$
. By the hypothesis, we have
$$ \begin{align*} \|e^{\lambda x+y}e^{-\lambda x}\|\leq K\|e^y\|\mbox{ for all }\lambda\in{\mathbb C}. \end{align*} $$
Define
$\phi :{\mathbb C}\to A$
by
$$ \begin{align*} \phi(\lambda)=e^{\lambda x+y}e^{-\lambda x}, \end{align*} $$
and let
$f\in A^{\prime }$
be arbitrary. Then
$f\circ \phi $
is an entire function satisfying
$$ \begin{align*} |f(\phi(\lambda))|\leq\|f\|\|\phi(\lambda)\|\leq\|f\|\|e^y\|\mbox{ for all }\lambda\in{\mathbb C}. \end{align*} $$
Thus, by Liouville’s theorem,
$f(\phi (\lambda ))=f(e^y)$
for all
$\lambda \in {\mathbb C}$
. Since
$f\in A^{\prime }$
was arbitrary it follows, from the Hahn–Banach theorem, that
$\phi (\lambda )=e^y$
for all
$\lambda \in {\mathbb C},$
and hence, with
$\lambda =1$
, we get that
$e^{x+y}=e^ye^x\mbox { for all }x,y\in A.$
So, by symmetry, any two exponentials of A commute. If
$x,y\in A$
are arbitrary, then choose
$n\in \mathbb N$
sufficiently large so that both
$\sigma ({\mathbf 1}+x/n)$
and
$\sigma ({\mathbf 1}+y/n)$
do not separate
$0$
from infinity. By the Holomorphic Calculus, there exist
$a,b\in A$
such that
${\mathbf 1}+x/n=e^a$
and
${\mathbf 1}+y/n=e^b$
. Then
${\mathbf 1}+x/n$
and
${\mathbf 1}+y/n$
commute, which implies that x and y commute.▪
Theorem 3.2 A semisimple Banach algebra A is commutative if and only if there exists an open set
$U\subset A$
such that any one of the following conditions holds:
-
(i)
$\#\sigma (e^{x+y}-e^xe^y)=1\mbox { for all }x,y\in U$
. -
(ii)
$\#\sigma (e^{x+y}e^{-x}e^{-y})=1\mbox { for all }x,y\in U$
.
Proof. (i) Let
$x\in U$
and
$y\in A$
be arbitrary, and define
$g:{\mathbb C}\to A$
by
$$ \begin{align*}g(\lambda)=(1-\lambda)x+\lambda y.\end{align*} $$
Then there exists
$\epsilon>0,$
such that
$g(\lambda )\in U$
for all
$\lambda \in B(0,\epsilon )$
. By assumption, we have that
$$ \begin{align} \#\sigma(e^{x+g(\lambda)}-e^xe^{g(\lambda)})=1\mbox{ for all }\lambda\in B(0,\epsilon). \end{align} $$
If we observe that the map
$\lambda \mapsto e^{x+g(\lambda )}-e^xe^{g(\lambda )}$
is analytic from
${\mathbb C}$
into A, then, since the spectrum is nonempty, it follows from Theorem 1.1 that (3.1) holds for all
$\lambda \in {\mathbb C}$
. By taking
$\lambda =1$
it follows that the hypothesis in (i) holds for all
$x\in U$
,
$y\in A$
. From this, it then further follows that there exists
$\delta>0,$
such that
$$ \begin{align} \#\sigma\left(e^{\lambda(x+y)}-e^{\lambda x}e^{\lambda y}\right)=1\mbox{ for all }\lambda\in B(1,\delta). \end{align} $$
Another application of Theorem 1.1 shows that (3.2) is in fact valid for all
$\lambda \in {\mathbb C}$
. From the power series expansion
$$ \begin{align*}e^{\lambda(x+y)}-e^{\lambda x}e^{\lambda y}=\frac{yx-xy}{2}\lambda^2+a_3\lambda^3+a_4\lambda^4+\cdots \end{align*} $$
for some
$a_i\in A$
,
$i\geq 3$
(the particulars of which are of no importance to us), we observe that the function
$$ \begin{align*} \lambda\mapsto \left(e^{\lambda(x+y)}-e^{\lambda x}e^{\lambda y}\right)/\lambda^2 \end{align*} $$
has a removable singularity at
$\lambda =0$
. Hence the function
$$ \begin{align*} f(\lambda)=\left\{\begin{array}{cc} (e^{\lambda(x+y)}-e^{\lambda x}e^{\lambda y})/\lambda^2, & \lambda\not=0,\\ (yx-xy)/2, & \lambda=0.\end{array}\right. \end{align*} $$
is an entire function from
${\mathbb C}$
to A. Notice then that
$\#\sigma (f(\lambda ))=1$
for each
$0\not =\lambda \in {\mathbb C}$
from which Theorem 1.1 again gives
$\#\sigma (f(\lambda ))=1$
for all
$\lambda \in {\mathbb C}$
. In particular, with
$\lambda =0$
, we see that
$\#\sigma (yx-xy)=1$
. Since
$y\in A$
was arbitrary Theorem 1.2 says that
$x\in Z(A)$
and therefore that
$U\subset Z(A)$
. But this is obviously sufficient to establish that
$A\subset Z(A)$
which completes the proof.
(ii) The proof is very similar to the proof of (i); with the same arguments we obtain that, for any
$x\in U$
and
$y\in A$
,
$\#\sigma (e^{\lambda (x+y)}e^{-\lambda x}e^{-\lambda y})=1\mbox { for all }\lambda \in {\mathbb C}$
which, by translation implies that
$\#\sigma (e^{\lambda (x+y)}e^{-\lambda x}e^{-\lambda y}-\mathbf 1)=1\mbox { for all }\lambda \in {\mathbb C}$
. If we consider the power series expansion
$$ \begin{align*} e^{\lambda(x+y)}e^{-\lambda x}e^{-\lambda y}-{\mathbf 1}=\frac{xy-yx}{2}\lambda^2+b_3\lambda^3+b_4\lambda^4+\cdots, \end{align*} $$
where
$b_i\in A$
,
$i\geq 3$
, then the same argument as in the proof of (i) is valid with f replaced by
$$ \begin{align*} h(\lambda):= \left\{\begin{array}{cc} (e^{\lambda(x+y)}e^{-\lambda x}e^{-\lambda y}-{\mathbf 1})/\lambda^2, & \lambda\not=0, \\ (xy-yx)/2, & \lambda=0.\end{array}\right. \end{align*} $$
▪
