2 The proof

We will work in a modification of the model of van Douwen (see [Reference van Douwen8] or [Reference Howard and Rubin1, Model $\mathbf{\mathcal{N}}2\left(\textit{LO}\right)$ ]). We let $\mathcal {M}$ be a model of $\textbf {ZFA} + \textbf {AC}$ with set A of atoms such that $|A| = \aleph _1$ . Write A as a disjoint union $A = \bigcup _{\alpha < \aleph _1} A_{\alpha }$ with each $A_{\alpha }$ being countably infinite and endowed with a total order $<_{\alpha }$ which makes $A_{\alpha }$ order isomorphic to $\mathbb {Z}$ . Let $\Gamma $ be the set of bijections $\tau $ on A for which $\tau \upharpoonright A_{\alpha } \in \operatorname {Aut}(A_{\alpha }, <_{\alpha })$ for all $\alpha < \aleph _1$ . Let $\mathcal {F}$ be the normal filter on $\Gamma $ given by the ideal of countable subsets of A. Let $\mathcal {N} \subseteq \mathcal {M}$ denote the permutation model of hereditarily $\mathcal {F}$ -symmetric objects in $\mathcal {M}$ . For each $B \subseteq A$ we let $\operatorname {fix}(B) = \{\tau \in \Gamma \mid (\forall a\in B)\tau (a) = a\}$ and for an object $x \in \mathcal {M}$ we let $\operatorname {stab}(x) = \{\tau \in \Gamma \mid \tau (x) = x\}$ . For each $a\in A$ we let $s(a)$ denote the next largest element under $<_{\alpha }$ in $A_{\alpha }$ , where $a \in A_{\alpha }$ .

That the model $\mathcal {N}$ satisfies the principle of dependent choices follows from the fact that the ideal defining the filter $\mathcal {F}$ is closed under taking countable unions (see [Reference Howard and Rubin1, Note 144]). It is not difficult to see that the existence of the claimed groups in Theorem 1.1 is boundable in the sense of Pincus [Reference Pincus5]. Thus, our main result will follow from the transfer principle [Reference Pincus6, Theorem 4] (or see [Reference Howard and Rubin1, p. 286]) provided that we can establish the existence of the claimed groups in the model $\mathcal {N}$ .

Let $J = A\times \{0, 1\}$ and $\mathbb {F}(J) = (W_J, \circ _J, ^{-1}, 1_{W_J})$ denote the free group on the set J, with $W_J$ denoting the set of reduced words over the alphabet $J^{\pm 1}$ , $\circ _J$ and $^{-1}$ denoting the group multiplication and group inversion operations, and $1_{W_J}$ denoting the trivial element. This group, which we have defined in $\mathcal {M}$ , is clearly in $\mathcal {N}$ as well; moreover, $\operatorname {stab}(W_J) = \operatorname {stab}(\circ _J) = \operatorname {stab}(^{-1}) = \Gamma $ . Notice that the subset $X_J = \{(s(a), 0)(a, 1)(s(a), 0)^{-1}(s(a), 1)\}_{a\in A} \subseteq W_J$ is also in $\mathcal {N}$ and also supported by $\emptyset \subseteq A$ . Therefore, the normal subgroup $N_J = \langle \langle X_J \rangle \rangle \unlhd \mathbb {F}(J)$ is in $\mathcal {N}$ and supported by $\emptyset $ , and the similar claims hold for the quotient $\mathcal {G} = \mathbb {F}(J)/N_J$ . We emphasize that the identity element $N_J$ of $\mathcal {G}$ , which we will denote $1_{\mathcal {G}}$ , is supported by $\emptyset $ .

$\mathcal {G}$ is locally free. For each $\alpha < \aleph _1$ , let $J_{\alpha } = (\bigcup _{\beta \leq \alpha } A_{\beta }) \times \{0, 1\}$ . Similarly, define the free group $\mathbb {F}(J_{\alpha })$ and notice that $\mathbb {F}(J_{\alpha })$ is in $\mathcal {N}$ and the set of reduced words in $J_{\alpha }^{\pm 1}$ , the group multiplication operation and the inverse operation are supported by $\emptyset $ . Let $r_{\alpha }: \mathbb {F}(J) \rightarrow \mathbb {F}(J_{\alpha })$ denote the retraction map given by deleting all letters in $J^{\pm 1} \setminus J_{\alpha }^{\pm 1}$ and freely reducing, and notice that $r_{\alpha }$ is in $\mathcal {N}$ and supported by $\emptyset $ . Letting $\mathcal {G}_{\alpha } = F(J_{\alpha })N_J$ , we see that $\mathcal {G}_{\alpha }$ is also in $\mathcal {N}$ and supported by $\emptyset $ . Also, $r_{\alpha }(X_J) \subseteq X_J \cup \{1_{W_J}\}$ and so $r_{\alpha }(N_J) \subseteq N_J$ . Then the retraction homomorphism $\mathcal {G} \rightarrow \mathcal {G}_n$ given by taking a coset K of $N_J$ to $r_n(K)N_J$ is in $\mathcal {N}$ and is similarly invariant under $\Gamma $ .

We will show that each $\mathcal {G}_{\alpha }$ is locally free and this is sufficient since any finitely generated subgroup of $\mathcal {G}$ includes into some $\mathcal {G}_{\alpha }$ . Fix $\alpha < \aleph _1$ . Let $T_{\alpha }$ denote the group

$$ \begin{align*}\mathbb{F}(J_{\alpha})/\langle\langle \{(s(a), 0)(a, 1)(s(a), 0)^{-1}(s(a), 1)\}_{a\in \bigcup_{\beta \leq \alpha}A_{\beta}}\rangle\rangle.\end{align*} $$

It is easy to see that $T_{\alpha }$ is in $\mathcal {N}$ and that the identity map on the generators induces an isomorphism with $\mathcal {G}_{\alpha }$ (and this isomorphism is also in $\mathcal {N}$ ). We establish that $T_{\alpha }$ is locally free.

By selecting $a_{\beta } \in A_{\beta }$ for each $\beta \leq \alpha $ , we have $\operatorname {fix}(\{a_{\beta }\}_{\beta \leq \alpha }) = \operatorname {fix}(\bigcup _{\beta \leq \alpha }A_{\beta })$ . Since the object $T_{\alpha }$ is hereditarily supported by $\operatorname {fix}(\{a_{\beta }\}_{\beta \leq \alpha })$ and $\mathcal {M}$ is a model of $\textbf {ZFA} + \textbf {AC}$ , we may use $\textbf {AC}$ in arguing that $T_{\alpha }$ is locally free. It is clear that $T_{\alpha }$ is the free product of $|\alpha | + 1$ copies of the group H given by presentation.

(1) $$ \begin{align} \begin{array}{ll} \langle \{x_m\}_{m\in \mathbb{Z}} \cup \{y_n\}_{n\in \mathbb{Z}}\mid \{y_n = x_{n+1}^{-1}y_{n+1}^{-1}x_{n+1}\}_{n\in \mathbb{Z}}\rangle. \end{array} \end{align} $$

Since the class of locally free groups is closed under taking free products, we now need to show that H is locally free.

Proof. Notice that for a fixed $N \in \mathbb {Z}$ , the presentation defining H does not require the relators $\{y_n = x_{n+1}^{-1}y_{n+1}^{-1}x_{n+1}\}_{n<N}$ and the generators $\{y_n\}_{n<N}$ since the relators $\{y_n = x_{n+1}^{-1}y_{n+1}^{-1}x_{n+1}\}_{n<N}$ are only used in giving names to the elements $\{y_n\}_{n<N}$ . This is because for any positive $k\in \omega $ we can write

$$ \begin{align*} y_{N-k} = x_{N - k + 1}^{-1}x_{N - k + 2}^{-1}\cdots x_N^{-1} y_N^{(-1)^k} x_N \cdots x_{N - k + 2} x_{N - k + 1.} \end{align*} $$

In particular, for any fixed $N\in \mathbb {Z}$ , we know that H is isomorphic to the group $H_N$ with presentation

(2) $$ \begin{align}\begin{array}{ll} \langle \{x_m\}_{m\in \mathbb{Z}} \cup \{y_n\}_{n\geq N}\mid \{y_n = x_{n+1}^{-1}y_{n+1}^{-1}x_{n+1}\}_{n\geq N}\rangle \end{array} \end{align} $$

via the map $\rho _N$ determined by

$$ \begin{align*} \begin{array}{c} x_m \mapsto x_m \mbox{ for all }n\in\mathbb{Z}\\ y_n \mapsto y_n \mbox{ for }n\geq N\\ y_{N - k} \mapsto x_{N - k + 1}^{-1}x_{N - k + 2}^{-1}\cdots x_N^{-1} y_N^{(-1)^k} x_N \cdots x_{N - k + 2} x_{N - k + 1} \mbox{ for } k \geq 1. \end{array} \end{align*} $$

Consider the normal subgroup $K = \langle \langle \{x_n\}_{n>N}\rangle \rangle \unlhd H_N$ . The quotient $H_N/K$ has presentation

$$ \begin{align*}\begin{array}{ll} \langle \{x_m\}_{m\leq N} \cup \{y_n\}_{n\geq N}\mid \{y_n = y_{n+1}^{-1}\}_{n\geq N}\rangle \end{array} \end{align*} $$

and this group is simply the free group in the generators $\{x_m\}_{m\leq N} \cup \{y_N\}$ . This implies that for each $N\in \mathbb {Z}$ the set $\{x_m\}_{m \leq N} \cup \{y_N\}$ freely generates a subgroup of  $H_N$ .

For any finite set of words $\{w_0, \ldots , w_r\}$ in the letters $\{x_m\}_{m\in \mathbb {Z}}^{\pm 1} \cup \{y_n\}_{n\in \mathbb {Z}}^{\pm 1}$ , there exists some N for which each of the words $w_0, \ldots , w_r$ is written in the letters $\{x_m\}_{m\leq N}^{\pm 1} \cup \{y_n\}_{n\leq N}^{\pm 1}$ . Then applying $\rho _N$ to the group elements represented by $w_0, \ldots , w_r$ places this set within the subgroup $\langle \{x_m\}_{m\leq N} \cup \{y_N\}\rangle \leq H_N$ , and since this subgroup is free, we have that H is locally free. The second claim follows immediately from our proof since we showed that for each $N\in \mathbb {Z}$ the set $\{x_m\}_{m\leq N}\cup \{y_N\}$ freely generates a subgroup of H.▪

$\mathcal {G}$ can be given a total order. Toward producing a total order on $\mathcal {G}$ , we produce, in $\mathcal {M}$ , a normal form for $\mathcal {G}$ . Since $\textbf {AC}$ holds in $\mathcal {M}$ , we shall freely use choices in this construction, and the fact that the normal form is also in $\mathcal {N}$ will become apparent. Recall that a word rewriting system on a free monoid $\operatorname {Mon}(X)$ on set X is a set of rules $\mathcal {R}$ whose inputs and outputs are words in the monoid (see [Reference Sapir7, Section 1.7]). We define binary relation $\rightarrow _{\mathcal {R}}$ on $\operatorname {Mon}(X)$ by letting $w_0 \rightarrow _{\mathcal {R}} w_1$ if there exist $v_0, v_1, v_1', v_2 \in \operatorname {Mon}(X)$ with $w_0 \equiv v_0v_1v_2$ and $w_1 \equiv v_0v_1'v_2$ and $(v_1, v_1')\in \mathcal {R}$ . Let $\rightarrow _{\mathcal {R}}^*$ be the smallest transitive binary relation including $\rightarrow _{\mathcal {R}}$ and let $\leftrightarrow _{\mathcal {R}}^*$ denote the smallest equivalence class including $\rightarrow _{\mathcal {R}}^*$ . Rewriting system $\mathcal {R}$ is confluent if whenever $w_0 \rightarrow _{\mathcal {R}}^*w_1$ and $w_0 \rightarrow _{\mathcal {R}}^* w_2$ , there exists $w_3$ for which $w_1 \rightarrow _{\mathcal {R}}^* w_3$ and $w_2 \rightarrow _{\mathcal {R}}^* w_3$ . It is locally confluent if whenever $w_0 \rightarrow _{\mathcal {R}} w_1$ and $w_0 \rightarrow _{\mathcal {R}} w_2$ , there exists $w_3$ for which $w_1 \rightarrow _{\mathcal {R}}^* w_3$ and ${w_2 \rightarrow _{\mathcal {R}}^* w_3}$ .

Rewriting system $\mathcal {R}$ is terminating if each sequence $w_0 \rightarrow _{\mathcal {R}} w_1 \rightarrow _{\mathcal {R}} w_2 \cdots \rightarrow _{\mathcal {R}} w_n$ must eventually stabilize. A word w is a terminus of $\mathcal {R}$ if $w \rightarrow _{\mathcal {R}} v$ implies $w \equiv v$ . If $\mathcal {R}$ is terminating and locally confluent, then it is confluent, and if $\mathcal {R}$ is terminating and confluent then each equivalence class in $\leftrightarrow _{\mathcal {R}}^*$ contains a unique terminus (see [Reference Sapir7, Section 1.7]).

We let $\operatorname {Mon}(J^{\pm 1})$ denote the free monoid on the set $\{(a, 0)\}_{a\in A} \cup \{(a, 1)\}_{a\in A} \cup \{(a, 0)^{-1}\}_{a\in A}\cup \{(a,1)^{-1}\}_{a\in A}$ , and let e denote the empty word. Consider the rewriting system $\mathcal {R}$ under which for all $a\in A$ we have rules

1. (1) $(a, 0)(a, 0)^{-1}\mapsto e$

2. (2) $(a, 0)^{-1}(a, 0) \mapsto e$

3. (3) $(a, 1)(a, 1)^{-1}\mapsto e$

4. (4) $(a, 1)^{-1}(a, 1)\mapsto e$

5. (5) $(s(a), 0)(a, 1) \mapsto (s(a), 1)^{-1}(s(a), 0)$

6. (6) $(s(a), 0)(a, 1)^{-1} \mapsto (s(a), 1)(s(a), 0)$

7. (7) $(s(a), 0)^{-1}(s(a), 1) \mapsto (a, 1)^{-1}(s(a), 0)^{-1}$

8. (8) $(s(a), 0)^{-1}(s(a), 1)^{-1} \mapsto (a, 1)(s(a), 0)^{-1}$

The idea of this system is to both freely reduce and to move the $(a, 0)^{\pm 1}$ letters to the right.

Proof. We will argue in cases. It is easy to see that if rules are applied independently to nonoverlapping subwords then the order of application makes no difference. More explicitly if we have a word $w \equiv u_0u_1$ and consider an application of a rule to $u_0$ to obtain $w \rightarrow _{\mathcal {R}} u_0'u_1$ , and consider the application of a possibly different rule to $u_1$ to obtain $w \rightarrow _{\mathcal {R}}u_0u_1'$ then clearly $u_0'u_1 \rightarrow _{\mathcal {R}}u_0'u_1'$ and $u_0u_1' \rightarrow _{\mathcal {R}} u_0'u_1'$ and so there can be no obstruction to local confluence in this setting. Thus, it will only be necessary to consider cases where rule applications are to overlapping subwords.

If $w \rightarrow _{\mathcal {R}} w_0$ and $w \rightarrow _{\mathcal {R}} w_1$ are each obtained by an application of a free reduction rule (i.e., each is obtained by one of (i)–(iv)) then by applying free reductions to each of $w_0$ and $w_1$ , we obtain a unique freely reduced word $w_2$ , so that $w_0 \rightarrow _{\mathcal {R}}^* w_2$ and $w_1 \rightarrow _{\mathcal {R}}^* w_2$ . Next, if $w \rightarrow _{\mathcal {R}} w_0$ and $w \rightarrow _{\mathcal {R}} w_1$ and each of these was given by an application of possibly different rules among (v)–(viii) then either $w_0 \equiv w_1$ or these rules were applied on distinct nonoverlapping subwords, and this latter case was considered above.

Next, we suppose that $w \equiv v_0(s(a), 0)(a, 1)(a, 1)^{-1}v_1$ . By applying (iii), one has $w \rightarrow _{\mathcal {R}} v_0(s(a), 0)v_1$ . By instead applying (v) to w we see that

$$ \begin{align*}w \rightarrow_{\mathcal{R}} v_0 (s(a), 1)^{-1}(s(a), 0)(a, 1)^{-1}v_1\end{align*} $$

and by applying (vi) and then (iv), we see that

$$ \begin{align*}v_0 (\kern-0.1pt s(\kern-0.1pt a\kern-0.1pt), 1\kern-0.1pt)^{\kern0.1pt -1}(\kern-0.1pt s(\kern-0.1pt a\kern-0.1pt), 0\kern-0.1pt)\kern0.1pt(\kern-0.1pt a, 1\kern-0.1pt)^{\kern0.1pt -1}v_1 \kern-1.5pt\rightarrow_{\mathcal{R}}\kern-2.5pt v_0(\kern-0.1pt s(\kern-0.1pt a\kern-0.1pt), 1\kern-0.1pt)^{\kern-0.1pt -1}(\kern-0.1pt s(\kern-0.1pt a\kern-0.1pt), 1\kern-0.1pt)\kern0.1pt (\kern-0.1pt s(\kern-0.1pt a\kern-0.1pt), 0\kern-0.1pt)v_1 \kern-1.5pt\rightarrow_{\mathcal{R}}\kern-2.5pt v_0(\kern-0.2pt s(\kern-0.2pt a\kern-0.2pt), 0\kern-0.2pt)v_1.\end{align*} $$

The cases where w is of form

$$ \begin{align*} \begin{aligned} w &\equiv v_0(s(a), 0)(a, 1)^{-1}(a, 1)v_1;\\ w &\equiv v_0(s(a), 0)^{-1} (s(a), 1)(s(a), 1)^{-1}v_1; \mbox{ or}\\ w &\equiv v_0(s(a), 0)^{-1}(s(a), 1)^{-1}(s(a), 1)v_1 \end{aligned} \end{align*} $$

are each handled similarly.

Suppose that we have a word $w \equiv v_0(s(a), 0)^{-1}(s(a), 0)(a, 1)v_1$ . If one applies (ii), then one has $w \rightarrow _{\mathcal {R}} v_0(a, 1)v_1$ . If we instead apply (v), then we get $w\rightarrow _{\mathcal {R}} v_0(s(a), 0)^{-1}(s(a), 1)^{-1}(s(a), 0)v_1$ , and applying rule (viii) and then (ii), we get

$$ \begin{align*} v_0(s(a), 0)^{-1}(s(a), 1)^{-1}(s(a), 0)v_1\rightarrow_{\mathcal{R}} v_0(a, 1)(s(a), 0)^{-1}(s(a), 0) v_1 \rightarrow_{\mathcal{R}} v_0(a, 1)v_1. \end{align*} $$

The check in case w is of form

$$ \begin{align*} \begin{aligned} w &\equiv v_0(s(a), 0)^{-1}(s(a), 0)(a, 1)^{-1}v_1;\\ w &\equiv v_0(s(a), 0)(s(a), 0)^{-1}(s(a), 1)v_1; \mbox{ or}\\ w &\equiv v_0(s(a), 0)(s(a), 0)^{-1}(s(a), 1)^{-1}v_1 \end{aligned} \end{align*} $$

is similar. Thus local confluence holds. ▪

We note also that the rewriting system is terminating. To see this, given a word w we consider the function

$$ \begin{align*} j(w) = \sum_{0 \leq i <\operatorname{Len}(w), w(i) \in \{(a, 0)^{\pm 1}\}_{a\in A} } |\{i < k < \operatorname{Len}(w)\mid w(k) \in \{(a', 1)^{\pm 1}\}_{a'\in A}\}| \end{align*} $$

which counts the total number of times that a letter of form $(a', 1)^{\pm 1}$ appears in the word somewhere to the right of a letter of form $(a, 0)^{\pm 1}$ . Each application of a rule will lower the value of the function $\operatorname {Len}(w) + j(w)$ (where $\operatorname {Len}(\cdot )$ denotes the length of the word) and so the fact that the system is terminating follows. Thus, each equivalence class under $\leftrightarrow _{\mathcal {R}}^*$ contains a unique terminus.

All elements of the set R of words which are the terminus of a word in $\operatorname {Mon}(J^{\pm 1})$ under $\mathcal {R}$ are freely reduced. The set R is also obviously in $\mathcal {N}$ (notice that the rules are themselves invariant under the action of $\Gamma $ ) and supported by $\emptyset $ . Furthermore, it is straightforward to see that each element in R is a unique representative of an element in $\mathcal {G}$ . We give an order $<^l$ to the letters in $J^{\pm 1}$ as follows:

$$ \begin{align*} (a, 0)^{-1} <^l (a, 0) <^l (a, 1)^{-1} <^l (a, 1) <^l (a', 0)^{-1} <^l (a', 0) <^l (a', 1)^{-1} <^l (a', 1), \end{align*} $$

where either $a, a'\in A_{\alpha }$ with $a <_{\alpha } a'$ or $a\in A_{\alpha }$ and $a'\in A_{\alpha '}$ with $\alpha < \alpha '$ . Endow the elements of R with the shortlex order $<^o$ : $w_0 <^o w_1$ if either $\operatorname {Len}(w_0) < \operatorname {Len}(w_1)$ , or $\operatorname {Len}(w_0) = \operatorname {Len}(w_1)$ and for the least $0 \leq i <\operatorname {Len}(w_0)$ at which $w_0(i) \neq w_1(i)$ we have $w_0(i) <^l w_1(i)$ . It is clear that both $<^l$ and $<^o$ are in $\mathcal {N}$ , and more particularly they are supported by $\emptyset $ .

$\mathcal {G}$ is not bi-orderable. To see that $\mathcal {G}$ is not bi-orderable, we suppose for contradiction that $<_{\mathcal {G}}$ is a bi-order on $\mathcal {G}$ in $\mathcal {N}$ . Select countable $B \subseteq A$ for which ${\operatorname {fix}(B) \leq \operatorname {stab}(<_{\mathcal {G}})}$ . Select $\alpha < \aleph _1$ such that $A_{\alpha } \cap B = \emptyset $ . Let $\tau \in \Gamma $ be given by

$$ \begin{align*} \tau(a) = \begin{cases}a \mbox{ if } a\notin A_{\alpha}\\ s(a) \mbox{ if } a\in A_{\alpha.} \end{cases} \end{align*} $$

Let $a\in A_{\alpha }$ be given. By Lemma 2.1, we know that $(a, 1)N_J$ is nontrivial. If $1_{\mathcal {G}} <_{\mathcal {G}} (a, 1)N_J$ then $1_{\mathcal {G}} <_{\mathcal {G}} (s(a), 0)(a, 1)(s(a), 0)^{-1}N_J = (s(a), 1)^{-1}N_J$ , from which we see that $(s(a), 1)N_J <_{\mathcal {G}} 1_{\mathcal {G}}$ , but on the other hand

$$ \begin{align*} 1_{\mathcal{G}} = \tau(1_{\mathcal{G}}) <_{\mathcal{G}} \tau((a, 1))N_J = (s(a), 1)N_J \end{align*} $$

which is a contradiction. The proof in case $(a, 1)N_J <_{\mathcal {G}} 1_{\mathcal {G}}$ is symmetric.

The group $\mathcal {A}$ and its properties. We construct the group $\mathcal {A}$ which is claimed to be in the model $\mathcal {N}$ . In checking its various properties, we will simply sketch over the aspects of the proofs which are nearly identical to those in the case of $\mathcal {G}$ . We take $\mathbb {F}(A)$ to be the free group on the set A of atoms. Consider the subset $X_A = \{[a, a']\}_{a, a'\in A} \cup \{a(s(a))^2\}_{a\in A}$ , where $[a, a']$ denotes the commutator $aa'a^{-1}(a')^{-1}$ . This set is in $\mathcal {N}$ and supported by $\emptyset $ , and similarly for the normal subgroup $N_A = \langle \langle X_A\rangle \rangle $ and relevant group operations and underlying set of $\mathcal {A} = \mathbb {F}(A)/N_A$ . Letting $0_{\mathcal {A}}$ denote the identity element, we emphasize that $0_{\mathcal {A}}$ is supported by $\emptyset $ . Let $B_{\alpha } = \bigcup _{\beta \leq \alpha } A_{\beta }$ and $r_{\alpha }: \mathbb {F}(A) \rightarrow \mathbb {F}(B_{\alpha })$ be the retraction. Let $\mathcal {A}_{\alpha } = \mathbb {F}(B_{\alpha })N_A$ . Since $r_{\alpha }(Y) \subseteq Y \cup \{1\}$ we have $r_n(N_A) \subseteq N_A$ . Thus, we have a retraction map $\mathcal {A} \rightarrow \mathcal {A}_{\alpha }$ given by $K \mapsto r_{\alpha }(K) N_A$ which is in $\mathcal {N}$ and supported by $\emptyset $ .

Let $L_{\alpha }$ denote the group $\mathbb {F}(B_{\alpha })/\langle \langle \{[a, a']\}_{a, a'\in B_{\alpha }} \cup \{a(s(a))^2\}_{a\in B_{\alpha }} \rangle \rangle $ . Notice that $L_n \simeq \mathcal {A}_n$ via the identity map on the generators (and this isomorphism is in $\mathcal {N}$ ). Taking $a_{\beta } \in A_{\beta }$ for each $\beta \leq \alpha $ we have again that $\operatorname {fix}(\{a_{\beta }\}_{\beta \leq \alpha }) = \operatorname {fix}(B_{\alpha })$ . Thus, we may utilize $\textbf {AC}$ , which holds in $\mathcal {M}$ , in analyzing $L_{\alpha }$ . It is easy to see that $L_{\alpha }$ is isomorphic to a direct sum of $|\alpha |+1$ copies of the additive group 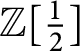$\mathbb {Z}[\frac {1}{2}]$ . Thus $\mathcal {A}_{\alpha }$ , and therefore all of $\mathcal {A}$ , is torsion-free abelian and for each $a\in A$ we have $aN_A$ nontrivial in $\mathcal {A}$ .

A normal form on $\mathcal {A}$ is given by words of the form

$$ \begin{align*} a_0^{z_0}a_1^{z_1}\cdots a_m^{z_m}, \end{align*} $$

where for each $ 0\leq i \leq m$ we have $z_i \in \mathbb {Z} \setminus 2\mathbb {Z}$ and $a_i\in A_{j_i}$ with $j_0 < j_1 < \cdots < j_m$ . The set of all such words is in $\mathcal {N}$ and supported by $\emptyset $ . Order the letters $A^{\pm 1}$ by order $<^l$ given by

$$ \begin{align*} a^{-1} <^l a <^l (a')^{-1} <^l a', \end{align*} $$

where $a, a'\in A_{\alpha }$ for some $\alpha < \aleph _1$ and $a <_{\alpha } a'$ , or $a\in A_{\alpha }$ and $a'\in A_{\alpha '}$ with $\alpha < \alpha '$ . This order $<^l$ is invariant under $\Gamma $ . Order $\mathcal {A}$ using shortlex on the normal form.

Now suppose that $<_{\mathcal {A}}$ is a bi-order on $\mathcal {A}$ . Let $B \subseteq A$ be countable with $\operatorname {fix}(B) \leq \operatorname {stab}(<_{\mathcal {A}})$ . Select $\alpha \in \omega $ such that $A_{\alpha } \cap B = \emptyset $ . Let $\tau \in \Gamma $ be given by

$$ \begin{align*} \tau(a) = \begin{cases} a \mbox{ if } a\in A \setminus A_{\alpha,}\\ s(a) \mbox{ if } a\in A_{\alpha}. \end{cases} \end{align*} $$

Let $a\in A_{\alpha }$ . Suppose that $0_{\mathcal {A}} <_{\mathcal {A}} aN_A$ . On one hand, we have that $0_{\mathcal {A}} = \tau (0_{\mathcal {A}}) <_{\mathcal {A}} \tau (aN_A) = s(a)N_A$ , but on the other hand, we have $s(a)^2N_A = a^{-1}N_A <_{\mathcal {A}} 0_{\mathcal {A}}$ , a contradiction. The proof in case $aN_A <_{\mathcal {A}} 0_{\mathcal {A}}$ is symmetric.