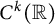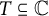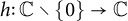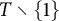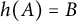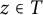1 Introduction
The Barth–Schneider theorem [Reference Barth and Schneider1] states that whenever
![]() $A,B$
are countable dense subsets of
$A,B$
are countable dense subsets of
![]() $\mathbb {R}$
, there is an entire function f which restricts to an order-isomorphism of A onto B. This generalizes Cantor’s theorem which gives an order-isomorphism of A onto B which then extends uniquely to an order-isomorphism of
$\mathbb {R}$
, there is an entire function f which restricts to an order-isomorphism of A onto B. This generalizes Cantor’s theorem which gives an order-isomorphism of A onto B which then extends uniquely to an order-isomorphism of
![]() $\mathbb {R}$
onto itself. P. M. Gauthier noted (private communication) that if A and B are countable dense subsets of the unit circle
$\mathbb {R}$
onto itself. P. M. Gauthier noted (private communication) that if A and B are countable dense subsets of the unit circle
![]() $T\subseteq \mathbb {C}$
, then there is a diffeomorphism
$T\subseteq \mathbb {C}$
, then there is a diffeomorphism
![]() $T\to T$
mapping A onto B and asked whether this diffeomorphism can be taken to be analytic.
$T\to T$
mapping A onto B and asked whether this diffeomorphism can be taken to be analytic.
It is a standard exercise (cf. [Reference Rudin4, Exercise 4, p. 264 and Exercise 25, p. 295]) that the entire functions that map the unit circle T into itself are the functions
![]() $f(z) = az^n$
,
$f(z) = az^n$
,
![]() $|a|=1$
,
$|a|=1$
,
![]() $n=0,1,2,\dots $
. These map T bijectively onto itself only when they are rotations, i.e., when
$n=0,1,2,\dots $
. These map T bijectively onto itself only when they are rotations, i.e., when
![]() $n=1$
. Thus they give a bijection satisfying
$n=1$
. Thus they give a bijection satisfying
![]() $f(A)=B$
only when B is the image of A under a rotation.
$f(A)=B$
only when B is the image of A under a rotation.
We will prove a version (Theorem 3.6) of the Barth–Schneider theorem for sets A, B which are invariant under a translation
![]() ${\sigma }(x)=x+t$
and use it to show (Theorem 4.1) that if A and B are countable dense subsets of
${\sigma }(x)=x+t$
and use it to show (Theorem 4.1) that if A and B are countable dense subsets of
![]() $T\setminus \{1\}$
, where
$T\setminus \{1\}$
, where
![]() $T\subseteq \mathbb {C}$
is the unit circle
$T\subseteq \mathbb {C}$
is the unit circle
![]() $|z|=1$
, then there is an analytic function
$|z|=1$
, then there is an analytic function
![]() $h\colon \mathbb {C}\setminus \{0\}\to \mathbb {C}$
that restricts to an order isomorphism of the arc
$h\colon \mathbb {C}\setminus \{0\}\to \mathbb {C}$
that restricts to an order isomorphism of the arc
![]() $T\setminus \{1\}$
onto itself
$T\setminus \{1\}$
onto itself
![]() $T\setminus \{1\}$
and satisfies
$T\setminus \{1\}$
and satisfies
![]() $h(A)=B$
and
$h(A)=B$
and
![]() $h'(z)\not =0$
when
$h'(z)\not =0$
when
![]() $z\in T$
. The proof uses a version (Theorem 3.3 and Corollary 3.5) of Theorem 3.2 of [Reference Burke2], adapted to produce functions which commute with a translation. In this paper, we fix a positive real number t, and the translation
$z\in T$
. The proof uses a version (Theorem 3.3 and Corollary 3.5) of Theorem 3.2 of [Reference Burke2], adapted to produce functions which commute with a translation. In this paper, we fix a positive real number t, and the translation
![]() ${\sigma }$
given by
${\sigma }$
given by
![]() ${\sigma }(z)=z+t$
. Note that
${\sigma }(z)=z+t$
. Note that
![]() $f{\sigma }=f$
says that f is periodic with period t, where
$f{\sigma }=f$
says that f is periodic with period t, where
![]() $f{\sigma }$
denotes the composition
$f{\sigma }$
denotes the composition
![]() $f\circ {\sigma }$
.
$f\circ {\sigma }$
.
2 Preliminary results
In this section, we prove two technical facts needed in the next section. The first is an analog of a result of Walsh (cf. [Reference Deutsch3, Corollaries 1.2 and 1.3]). This is likely known, but we have not found it in the literature except for
![]() $k=0$
, so we give a proof. The second is adapting Proposition 2.1 of [Reference Burke2] to our present context.
$k=0$
, so we give a proof. The second is adapting Proposition 2.1 of [Reference Burke2] to our present context.
Theorem 2.1 Let k be a nonnegative integer,
![]() ${\sigma }(z)=z+t$
. If
${\sigma }(z)=z+t$
. If
![]() $f\colon \mathbb {R}\to \mathbb {R}$
is a
$f\colon \mathbb {R}\to \mathbb {R}$
is a
![]() $C^k$
function which satisfies
$C^k$
function which satisfies
![]() $f{\sigma }=f$
, and
$f{\sigma }=f$
, and
![]() $F\subseteq \mathbb {R}$
is finite, then there is an entire function g such that
$F\subseteq \mathbb {R}$
is finite, then there is an entire function g such that
-
(a)
 $g(\mathbb {R})\subseteq \mathbb {R}$
and
$g(\mathbb {R})\subseteq \mathbb {R}$
and
 $g{\sigma }=g$
$g{\sigma }=g$
-
(b)
 $|D^ig(x)-D^if(x)|<{\varepsilon }$
,
$|D^ig(x)-D^if(x)|<{\varepsilon }$
,
 $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
 $i=0,\dots ,k$
$i=0,\dots ,k$
-
(c)
 $D^ig(x)=D^if(x)$
for
$D^ig(x)=D^if(x)$
for
 $x\in F$
,
$x\in F$
,
 $i=0,\dots ,k$
$i=0,\dots ,k$
Proof If we can arrange (a) and (b), then it follows that we can also arrange (c) by Theorem 0 of [Reference Deutsch3] applied to the space
![]() $X_k=\{f\in C^k(\mathbb {R}):f{\sigma }=f\}$
with the norm
$X_k=\{f\in C^k(\mathbb {R}):f{\sigma }=f\}$
with the norm
![]() $\|f\|=\sum _{i=0}^k\|D^if\|_\infty $
. (Cf. [Reference Deutsch3, Example (1), p. 1183, and Corollary 1.3]) So we need only arrange (a) and (b).
$\|f\|=\sum _{i=0}^k\|D^if\|_\infty $
. (Cf. [Reference Deutsch3, Example (1), p. 1183, and Corollary 1.3]) So we need only arrange (a) and (b).
It is standard that in
![]() $X_0$
the functions
$X_0$
the functions
![]() $g(2\pi z/t)$
, where g is a trigonometric polynomial with real coefficients, are dense (e.g., see [Reference Deutsch3, Example (2), p. 1183] or [Reference Sohrab5, Remark 9.4.24 (2)]).
$g(2\pi z/t)$
, where g is a trigonometric polynomial with real coefficients, are dense (e.g., see [Reference Deutsch3, Example (2), p. 1183] or [Reference Sohrab5, Remark 9.4.24 (2)]).
For the general case, we proceed by induction on k. When
![]() $k>0$
, fix
$k>0$
, fix
![]() $f\in X_k$
and apply the induction hypothesis to
$f\in X_k$
and apply the induction hypothesis to
![]() $Df$
to get an entire function
$Df$
to get an entire function
![]() $g_1$
satisfying
$g_1$
satisfying
![]() $g_1(\mathbb {R})\subseteq \mathbb {R}$
,
$g_1(\mathbb {R})\subseteq \mathbb {R}$
,
![]() $g_1{\sigma }=g_1$
and
$g_1{\sigma }=g_1$
and
![]() $|D^{i-1}g_1(x)-D^if(x)|<\delta =\min ({\varepsilon }/2,{\varepsilon }/(2t))$
for
$|D^{i-1}g_1(x)-D^if(x)|<\delta =\min ({\varepsilon }/2,{\varepsilon }/(2t))$
for
![]() $x\in \mathbb {R}$
and
$x\in \mathbb {R}$
and
![]() $i=1,\dots ,k$
. Define an entire function g by
$i=1,\dots ,k$
. Define an entire function g by
where
![]() $c=(1/t)\int _0^t g_1(s)\,ds$
is the average value of
$c=(1/t)\int _0^t g_1(s)\,ds$
is the average value of
![]() $g_1$
over
$g_1$
over
![]() $[0,t]$
. Since
$[0,t]$
. Since
![]() $\int _0^tDf = 0$
by periodicity, we have
$\int _0^tDf = 0$
by periodicity, we have
To verify that
![]() $g{\sigma }=g$
, it suffices to check that
$g{\sigma }=g$
, it suffices to check that
![]() $g(x+t)=g(x)$
when x is real, and that follows by the following calculation.
$g(x+t)=g(x)$
when x is real, and that follows by the following calculation.
For
![]() $x\in [0,t]$
, we also have
$x\in [0,t]$
, we also have
 $$ \begin{align*} |g(x)-f(x)| & = \Bigl|\int_{0}^x (g_1(s)-Df(s))\,ds - cx\Bigr| \\ & \leq \int_{0}^x |g_1(s)-Df(s)|\,ds + |c|x \\ & \leq t\delta + t\delta = 2t\delta < {\varepsilon}, \end{align*} $$
$$ \begin{align*} |g(x)-f(x)| & = \Bigl|\int_{0}^x (g_1(s)-Df(s))\,ds - cx\Bigr| \\ & \leq \int_{0}^x |g_1(s)-Df(s)|\,ds + |c|x \\ & \leq t\delta + t\delta = 2t\delta < {\varepsilon}, \end{align*} $$
and so, by periodicity,
![]() $|g(x)-f(x)| <{\varepsilon }$
for all
$|g(x)-f(x)| <{\varepsilon }$
for all
![]() $x\in \mathbb {R}$
. This takes care of the bound on
$x\in \mathbb {R}$
. This takes care of the bound on
![]() $|D^ig(x)-D^if(x)|$
,
$|D^ig(x)-D^if(x)|$
,
![]() $x\in \mathbb {R}$
, when
$x\in \mathbb {R}$
, when
![]() $i=0$
. When
$i=0$
. When
![]() $i=1$
we have
$i=1$
we have
and when
![]() $2\leq i\leq k$
,
$2\leq i\leq k$
,
![]() $|D^ig(x)-D^if(x)|=|D^{i-1}g_1(x)-D^if(x)|<\delta <{\varepsilon }$
. ▪
$|D^ig(x)-D^if(x)|=|D^{i-1}g_1(x)-D^if(x)|<\delta <{\varepsilon }$
. ▪
Lemma 2.2 Let
![]() ${\varepsilon }>0$
. Let k be a nonnegative integer and let
${\varepsilon }>0$
. Let k be a nonnegative integer and let
![]() $F\subseteq [0,t]$
be a finite set such that
$F\subseteq [0,t]$
be a finite set such that
![]() $\{0,t\}\subseteq F$
or
$\{0,t\}\subseteq F$
or
![]() $\{0,t\}\cap F=\emptyset $
. For each
$\{0,t\}\cap F=\emptyset $
. For each
![]() $p\in F$
and
$p\in F$
and
![]() $i=0,\dots k$
, let
$i=0,\dots k$
, let
![]() $k_{p,i}\in \{-1,0,1\}$
with
$k_{p,i}\in \{-1,0,1\}$
with
![]() $k_{0,i}=k_{t,i}$
if
$k_{0,i}=k_{t,i}$
if
![]() $0\in F$
. Then there is an entire function
$0\in F$
. Then there is an entire function
![]() $f\colon \mathbb {C}\to \mathbb {C}$
such that
$f\colon \mathbb {C}\to \mathbb {C}$
such that
![]() $f{\sigma }=f$
,
$f{\sigma }=f$
,
![]() $f(\mathbb {R})\subseteq \mathbb {R}$
and for
$f(\mathbb {R})\subseteq \mathbb {R}$
and for
![]() $i=0,\dots ,k$
and
$i=0,\dots ,k$
and
![]() $x\in \mathbb {R}$
, we have
$x\in \mathbb {R}$
, we have
![]() $|(D^i f)(x)| < {\varepsilon }$
and for
$|(D^i f)(x)| < {\varepsilon }$
and for
![]() $p\in F$
,
$p\in F$
,
![]() $(D^i f)(p)$
is
$(D^i f)(p)$
is
![]() $<0$
,
$<0$
,
![]() $=0$
,
$=0$
,
![]() $>0$
when
$>0$
when
![]() $k_{p,i}=-1,0,1$
, respectively.
$k_{p,i}=-1,0,1$
, respectively.
Proof For
![]() $r>0$
and
$r>0$
and
![]() $p\in \mathbb {R}$
, write
$p\in \mathbb {R}$
, write
![]() $I_r(p)=(p-r,p+r)$
. For each
$I_r(p)=(p-r,p+r)$
. For each
![]() $p\in F$
, choose
$p\in F$
, choose
![]() $0<r_p<1$
, so that the intervals
$0<r_p<1$
, so that the intervals
![]() $I_{r_p}(p)$
are contained in
$I_{r_p}(p)$
are contained in
![]() $(0,t)$
when
$(0,t)$
when
![]() $0<p<t$
,
$0<p<t$
,
![]() $I_{r_t}(t) = I_{r_0}(0) + t$
if
$I_{r_t}(t) = I_{r_0}(0) + t$
if
![]() $0\in F$
, and the intervals
$0\in F$
, and the intervals
![]() $I_{r_p}(p)$
for
$I_{r_p}(p)$
for
![]() $p\in F$
and have closures which are disjoint from each other. For each
$p\in F$
and have closures which are disjoint from each other. For each
![]() $p\in F$
, choose a
$p\in F$
, choose a
![]() $C^\infty $
bump function
$C^\infty $
bump function
![]() $\varphi _p$
with support equal to the closure of
$\varphi _p$
with support equal to the closure of
![]() $I_{r_p}(p)$
, so that
$I_{r_p}(p)$
, so that
![]() $0\leq \varphi _p\leq 1$
,
$0\leq \varphi _p\leq 1$
,
![]() $\varphi _p(p)=1$
,
$\varphi _p(p)=1$
,
![]() $\varphi _p$
has a flat point at p (i.e.,
$\varphi _p$
has a flat point at p (i.e.,
![]() $(D^i \varphi _p)(p)=0$
for all nonzero i), taking
$(D^i \varphi _p)(p)=0$
for all nonzero i), taking
![]() $\varphi _t(x)=\varphi _0(x-t)$
if
$\varphi _t(x)=\varphi _0(x-t)$
if
![]() $0\in F$
. Let
$0\in F$
. Let
![]() $\theta _p$
be a
$\theta _p$
be a
![]() $C^\infty $
function whose derivatives at p follow the requisite pattern, with
$C^\infty $
function whose derivatives at p follow the requisite pattern, with
![]() $\theta _t(x)=\theta _0(x-t)$
if
$\theta _t(x)=\theta _0(x-t)$
if
![]() $0\in F$
, for example, take
$0\in F$
, for example, take
![]() $\theta _p(x)=\sum _{i=0}^kk_{p,i}(x-p)^i$
. For suitably chosen positive constants
$\theta _p(x)=\sum _{i=0}^kk_{p,i}(x-p)^i$
. For suitably chosen positive constants
![]() $\lambda _p$
, we set
$\lambda _p$
, we set
![]() $g(x) = \sum _{p\in F}\lambda _p\theta _p(x)\varphi _p(x)$
,
$g(x) = \sum _{p\in F}\lambda _p\theta _p(x)\varphi _p(x)$
,
![]() $0\leq x\leq t$
, and extend g by periodicity to all of
$0\leq x\leq t$
, and extend g by periodicity to all of
![]() $\mathbb {R}$
so that
$\mathbb {R}$
so that
![]() $g{\sigma }=g$
. This function g is
$g{\sigma }=g$
. This function g is
![]() $C^\infty $
and its derivatives have the requisite pattern at the points
$C^\infty $
and its derivatives have the requisite pattern at the points
![]() $p\in F$
since for
$p\in F$
since for
![]() $i=0,\dots ,k$
we have
$i=0,\dots ,k$
we have
![]() $(D^i g)(p) = \lambda _p(D^i (\varphi _p\theta _p))(p) = \lambda _p D^{i}\theta _p(p)$
. Choose the constants
$(D^i g)(p) = \lambda _p(D^i (\varphi _p\theta _p))(p) = \lambda _p D^{i}\theta _p(p)$
. Choose the constants
![]() $\lambda _p$
,
$\lambda _p$
,
![]() $p\in F$
, small enough so that for each
$p\in F$
, small enough so that for each
![]() $i=0,\dots ,k$
,
$i=0,\dots ,k$
,
Then g is a
![]() $C^\infty $
function which satisfies the conclusion in the place of f and with
$C^\infty $
function which satisfies the conclusion in the place of f and with
![]() ${\varepsilon }$
replaced by
${\varepsilon }$
replaced by
![]() ${\varepsilon }/2$
. Get the desired entire function f by applying Theorem 2.1 to g with
${\varepsilon }/2$
. Get the desired entire function f by applying Theorem 2.1 to g with
![]() ${\varepsilon }/2$
in the place of
${\varepsilon }/2$
in the place of
![]() ${\varepsilon }$
. ▪
${\varepsilon }$
. ▪
3 Barth–Schneider for periodic functions
Definition 3.1 A fiber-preserving local homeomorphism of
![]() $\mathbb {R}^{2}\cong \mathbb {R}\times \mathbb {R}$
is a homeomorphism
$\mathbb {R}^{2}\cong \mathbb {R}\times \mathbb {R}$
is a homeomorphism
![]() $h\colon G^1_h\to G^2_h$
between two open sets
$h\colon G^1_h\to G^2_h$
between two open sets
![]() $G^1_h,G^2_h\subseteq \mathbb {R}^{2}$
such that h has the form
$G^1_h,G^2_h\subseteq \mathbb {R}^{2}$
such that h has the form
![]() $h(x,y)=(x,h^*(x,y))$
for some continuous map
$h(x,y)=(x,h^*(x,y))$
for some continuous map
![]() $h^*\colon G^1_h\to \mathbb {R}$
. We write
$h^*\colon G^1_h\to \mathbb {R}$
. We write
![]() $k_h$
for the inverse of h.
$k_h$
for the inverse of h.
We can identify a fiber-preserving homeomorphism h with the family
![]() $\{(h^*)_x\}$
of vertical sections of
$\{(h^*)_x\}$
of vertical sections of
![]() $h^*$
, given by
$h^*$
, given by
![]() $(h^*)_x(y)=h^*(x,y)$
. These are homeomorphisms
$(h^*)_x(y)=h^*(x,y)$
. These are homeomorphisms
![]() $(h^*)_x\colon (G^1_h)^{\,}_x\to (G^2_h)^{\,}_x$
, where
$(h^*)_x\colon (G^1_h)^{\,}_x\to (G^2_h)^{\,}_x$
, where
![]() $(G^1_h)^{\,}_x$
,
$(G^1_h)^{\,}_x$
,
![]() $(G^2_h)^{\,}_x$
are the vertical sections at x of
$(G^2_h)^{\,}_x$
are the vertical sections at x of
![]() $G^1_h$
,
$G^1_h$
,
![]() $G^2_h$
.
$G^2_h$
.

It is separate continuity rather than joint continuity that we require for these fiber-preserving maps. In our context, however, this is not a weaker property as the following proposition shows.
Proposition 3.1 Let X be any topological space,
![]() $G\subseteq X\times \mathbb {R}$
an open set, and let
$G\subseteq X\times \mathbb {R}$
an open set, and let
![]() $h\colon G\to X\times \mathbb {R}$
. Assume that for each
$h\colon G\to X\times \mathbb {R}$
. Assume that for each
![]() $x\in X$
,
$x\in X$
,
![]() $h(G_x)\subseteq \{x\}\times \mathbb {R}$
, h is one-to-one and h is separately continuous, i.e., the functions
$h(G_x)\subseteq \{x\}\times \mathbb {R}$
, h is one-to-one and h is separately continuous, i.e., the functions
![]() $x\mapsto h(x,y)$
,
$x\mapsto h(x,y)$
,
![]() $y\mapsto h(x,y)$
are continuous on their domains. Then h is continuous.
$y\mapsto h(x,y)$
are continuous on their domains. Then h is continuous.
Taking
![]() $h(x,y)=(x,h^*(x,y))$
on
$h(x,y)=(x,h^*(x,y))$
on
![]() $\mathbb {R}\times \mathbb {R}$
with
$\mathbb {R}\times \mathbb {R}$
with
![]() $h^*(x,y)=xy/(x^2+y^2)$
when
$h^*(x,y)=xy/(x^2+y^2)$
when
![]() $(x,y)\not =(0,0)$
,
$(x,y)\not =(0,0)$
,
![]() $h^*(0,0)=0$
, shows that the assumption that h is one-to-one cannot be omitted.
$h^*(0,0)=0$
, shows that the assumption that h is one-to-one cannot be omitted.
Proof Write
![]() $h(x,y)=(x,h^*(x,y))$
. The continuity of h is equivalent to that of
$h(x,y)=(x,h^*(x,y))$
. The continuity of h is equivalent to that of
![]() $h^*$
. Also note that because h is one-to-one, so is
$h^*$
. Also note that because h is one-to-one, so is
![]() $y\mapsto h^*(x,y)$
for each fixed x. Let
$y\mapsto h^*(x,y)$
for each fixed x. Let
![]() $a\in X$
,
$a\in X$
,
![]() $b,c\in \mathbb {R}$
with
$b,c\in \mathbb {R}$
with
![]() $(a,b)\in G$
and
$(a,b)\in G$
and
![]() $h^*(a,b)=c$
. Fix an open neighborhood U of a and an open interval V containing b such that
$h^*(a,b)=c$
. Fix an open neighborhood U of a and an open interval V containing b such that
![]() $U\times V\subseteq G$
. Choose an open interval W with
$U\times V\subseteq G$
. Choose an open interval W with
![]() $c\in W$
. Since
$c\in W$
. Since
![]() $y\mapsto h^*(a,y)$
is continuous, there is a
$y\mapsto h^*(a,y)$
is continuous, there is a
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $|y-b|\leq \delta $
implies
$|y-b|\leq \delta $
implies
![]() $y\in V$
and
$y\in V$
and
![]() $h^*(a,y)\in W$
. The two functions
$h^*(a,y)\in W$
. The two functions
![]() $x\mapsto h^*(x,b\pm \delta )$
are continuous at a and hence there is an open neighborhood
$x\mapsto h^*(x,b\pm \delta )$
are continuous at a and hence there is an open neighborhood
![]() $U'\subseteq U$
of a such that
$U'\subseteq U$
of a such that
![]() $x\in U'$
implies
$x\in U'$
implies
![]() $h^*(x,b\pm \delta )\in W$
. For
$h^*(x,b\pm \delta )\in W$
. For
![]() $x\in U'$
,
$x\in U'$
,
![]() $y\mapsto h^*(x,y)$
is a continuous one-to-one function on the interval
$y\mapsto h^*(x,y)$
is a continuous one-to-one function on the interval
![]() $[b-\delta ,b+\delta ]$
, so that the image of this interval is an interval with endpoints
$[b-\delta ,b+\delta ]$
, so that the image of this interval is an interval with endpoints
![]() $h^*(x,b\pm \delta )$
, and hence is contained in W. Thus,
$h^*(x,b\pm \delta )$
, and hence is contained in W. Thus,
![]() $h^*(U'\times (b-\delta ,b+\delta ))\subseteq W$
and therefore
$h^*(U'\times (b-\delta ,b+\delta ))\subseteq W$
and therefore
![]() $h^*$
is continuous at
$h^*$
is continuous at
![]() $(a,b)$
. ▪
$(a,b)$
. ▪
Remark 3.2 The inverse
![]() $k_h$
of a fiber-preserving local homeomorphism h is also a fiber-preserving local homeomorphism and is related to h by the fact that
$k_h$
of a fiber-preserving local homeomorphism h is also a fiber-preserving local homeomorphism and is related to h by the fact that
![]() $(x,y)\in G^1_h$
and
$(x,y)\in G^1_h$
and
![]() $h^*(x,y)=z$
if and only if
$h^*(x,y)=z$
if and only if
![]() $(x,z)\in G^2_h$
and
$(x,z)\in G^2_h$
and
![]() $k^*_h(x,z)=y$
. As pointed out in the proof of Proposition 3.1, the vertical sections of
$k^*_h(x,z)=y$
. As pointed out in the proof of Proposition 3.1, the vertical sections of
![]() $h^*$
are one-to-one since h is one-to-one. The main examples for our purposes are
$h^*$
are one-to-one since h is one-to-one. The main examples for our purposes are
![]() $h=\operatorname {id}_{\mathbb {R}^2}$
, the identity map on
$h=\operatorname {id}_{\mathbb {R}^2}$
, the identity map on
![]() $\mathbb {R}^{2}$
(for which
$\mathbb {R}^{2}$
(for which
![]() $(h^*)_x(y)=y$
is the identity map for each
$(h^*)_x(y)=y$
is the identity map for each
![]() $x\in \mathbb {R}$
), and for a given a continuous map
$x\in \mathbb {R}$
), and for a given a continuous map
![]() $g\colon \mathbb {R}\to \mathbb {R}$
,
$g\colon \mathbb {R}\to \mathbb {R}$
,
![]() $h^*(x,y)=g(x)+y$
. Both of these have
$h^*(x,y)=g(x)+y$
. Both of these have
![]() $G^1_h=G^2_h=\mathbb {R}^{2}$
.
$G^1_h=G^2_h=\mathbb {R}^{2}$
.
We shall prove our main results using the following version of Theorem 3.2 of [Reference Burke2]. The proof is similar to that of the original version, but we repeat the argument with the necessary changes in order to be clear.
Theorem 3.3 Let
![]() $E_i\subseteq [0,t]$
,
$E_i\subseteq [0,t]$
,
![]() $i=0,\dots ,k$
, be countable sets with
$i=0,\dots ,k$
, be countable sets with
![]() $\{0,t\}\subseteq E_i$
or
$\{0,t\}\subseteq E_i$
or
![]() $E_i\cap \{0,t\}=\emptyset $
. Let
$E_i\cap \{0,t\}=\emptyset $
. Let
![]() $F\subseteq [0,t]$
be a finite set disjoint from
$F\subseteq [0,t]$
be a finite set disjoint from
![]() $\bigcup _{i=0}^k E_i$
with
$\bigcup _{i=0}^k E_i$
with
![]() $\{0,t\}\subseteq F$
or
$\{0,t\}\subseteq F$
or
![]() $F\cap \{0,t\}=\emptyset $
. For each
$F\cap \{0,t\}=\emptyset $
. For each
![]() $p\in E_i$
, let
$p\in E_i$
, let
![]() $A_{p,i}\subseteq \mathbb {R}$
be a countable dense set, with
$A_{p,i}\subseteq \mathbb {R}$
be a countable dense set, with
![]() $A_{0,i}=A_{t,i}$
if
$A_{0,i}=A_{t,i}$
if
![]() $\{0,t\}\subseteq A$
. Let
$\{0,t\}\subseteq A$
. Let
![]() ${\varepsilon }>0$
. Let
${\varepsilon }>0$
. Let
![]() $\mathscr {H}$
be a countable family of fiber-preserving local homeomorphisms of
$\mathscr {H}$
be a countable family of fiber-preserving local homeomorphisms of
![]() $\mathbb {R}^2$
. There exists an entire function
$\mathbb {R}^2$
. There exists an entire function
![]() $f\colon \mathbb {C}\to \mathbb {C}$
such that
$f\colon \mathbb {C}\to \mathbb {C}$
such that
![]() $f(\mathbb {R})\subseteq \mathbb {R}$
,
$f(\mathbb {R})\subseteq \mathbb {R}$
,
![]() $f{\sigma }=f$
and for all
$f{\sigma }=f$
and for all
![]() $x\in \mathbb {R}$
and
$x\in \mathbb {R}$
and
![]() $i=0,\dots ,k$
,
$i=0,\dots ,k$
,
-
(a)
 $|(D^{i}f)(x)|<{\varepsilon }$
, and if
$|(D^{i}f)(x)|<{\varepsilon }$
, and if
 $x\in F$
then
$x\in F$
then
 $D^if(x)=0$
.
$D^if(x)=0$
. -
(b) for each
 $p\in E_i$
,
$p\in E_i$
,
 $(D^i f)(p)\in A_{p,i}$
.
$(D^i f)(p)\in A_{p,i}$
. -
(c) for every
 $q\in \mathbb {R}$
,
$q\in \mathbb {R}$
,
 $h\in \mathscr {H}$
and every open interval
$h\in \mathscr {H}$
and every open interval
 $U\subseteq \mathbb {R}\setminus F$
, if for some
$U\subseteq \mathbb {R}\setminus F$
, if for some $$ \begin{align*} (x,(D^i f)(x))\in G^1_h\quad \text{and}\quad q = h^*(x,(D^i f)(x)) \end{align*} $$
$$ \begin{align*} (x,(D^i f)(x))\in G^1_h\quad \text{and}\quad q = h^*(x,(D^i f)(x)) \end{align*} $$
 $x\in U\cap \operatorname {cl} Y_{h,q,i}$
, where
$x\in U\cap \operatorname {cl} Y_{h,q,i}$
, where
 $Y_{h,q,i} = \{p\in E_i:$
for some
$Y_{h,q,i} = \{p\in E_i:$
for some
 $q'\in A_{p,i}$
,
$q'\in A_{p,i}$
,
 $(p,q')\in G^1_h$
and
$(p,q')\in G^1_h$
and
 $q=h^*(p,q')\}$
, then
$q=h^*(p,q')\}$
, then
 $q = h^*(p,(D^i f)(p))$
for some
$q = h^*(p,(D^i f)(p))$
for some
 $p\in U\cap E_i$
.
$p\in U\cap E_i$
.
Remark 3.4 (i) For the hypothesis in (c) to be nonvacuous, there must be a point
![]() $x\in U\cap \operatorname {cl} E_i\subseteq U\cap [0,t]$
, so only intervals which intersect
$x\in U\cap \operatorname {cl} E_i\subseteq U\cap [0,t]$
, so only intervals which intersect
![]() $[0,t]$
are relevant.
$[0,t]$
are relevant.
(ii) It is sometimes useful to reword clause (c) in an equivalent form. The criterion for
![]() $p\in Y_{h,q,i}$
is that
$p\in Y_{h,q,i}$
is that
![]() $p\in E_i$
and
$p\in E_i$
and
![]() $q\in (h^*)_p(A_{p,i})$
. Clause (c) says equivalently that for
$q\in (h^*)_p(A_{p,i})$
. Clause (c) says equivalently that for
![]() $x\in [0,t]\setminus F$
, if
$x\in [0,t]\setminus F$
, if
![]() $q=(h^*)_x((D^i f)(x))$
and arbitrarily close to x there are points
$q=(h^*)_x((D^i f)(x))$
and arbitrarily close to x there are points
![]() $p\in E_i$
such that
$p\in E_i$
such that
![]() $q\in (h^*)_p(A_{p,i})$
, then arbitrarily close to x there are points
$q\in (h^*)_p(A_{p,i})$
, then arbitrarily close to x there are points
![]() $p\in E_i$
such that
$p\in E_i$
such that
![]() $q=(h^*)_p((D^i f)(p))$
.
$q=(h^*)_p((D^i f)(p))$
.
(iii) If we require
![]() $\operatorname {id}_{\mathbb {R}^2}\in \mathscr {H}$
then this ensures that either f is constant or for
$\operatorname {id}_{\mathbb {R}^2}\in \mathscr {H}$
then this ensures that either f is constant or for
![]() $x\in [0,t]\setminus F$
,
$x\in [0,t]\setminus F$
,
![]() $i=0,\dots ,k$
, if
$i=0,\dots ,k$
, if
![]() $q=(D^i f)(x)$
and arbitrarily close to x there are points
$q=(D^i f)(x)$
and arbitrarily close to x there are points
![]() $p\in E_i$
such that
$p\in E_i$
such that
![]() $q\in A_{p,i}$
, then
$q\in A_{p,i}$
, then
![]() $x\in E_i$
. To see why, apply the reworded clause (c) in (ii) with h being the identity map to get that if
$x\in E_i$
. To see why, apply the reworded clause (c) in (ii) with h being the identity map to get that if
![]() $q=(D^i f)(x)$
and arbitrarily close to x there are points
$q=(D^i f)(x)$
and arbitrarily close to x there are points
![]() $p\in E_i$
such that
$p\in E_i$
such that
![]() $q\in A_{p,i}$
, then arbitrarily close to x there are points
$q\in A_{p,i}$
, then arbitrarily close to x there are points
![]() $p\in E_i$
such that
$p\in E_i$
such that
![]() $q=(D^i f)(p)$
. If x itself does not belong to
$q=(D^i f)(p)$
. If x itself does not belong to
![]() $E_i$
, then since
$E_i$
, then since
![]() $D^if$
is entire,
$D^if$
is entire,
![]() $D^if$
is constant with value q and hence f is a polynomial. Since f is periodic, it then follows that f is constant.
$D^if$
is constant with value q and hence f is a polynomial. Since f is periodic, it then follows that f is constant.
Proof We may assume that
![]() $\bigcup _{i=0}^k E_i\not =\emptyset $
(otherwise take
$\bigcup _{i=0}^k E_i\not =\emptyset $
(otherwise take
![]() $f=0$
) and that
$f=0$
) and that
![]() ${\varepsilon }\leq 1$
. Let
${\varepsilon }\leq 1$
. Let
![]() $\mathscr {B}=\{U_r:r=1,2,\dots \}$
be a one-to-one enumeration of a base of bounded open intervals for
$\mathscr {B}=\{U_r:r=1,2,\dots \}$
be a one-to-one enumeration of a base of bounded open intervals for
![]() $\mathbb {R}\setminus F$
. For each r, write
$\mathbb {R}\setminus F$
. For each r, write
![]() $U_r=\bigcup _{n=1}^\infty U_{r,n}$
, the union of an increasing sequence of concentric intervals so that
$U_r=\bigcup _{n=1}^\infty U_{r,n}$
, the union of an increasing sequence of concentric intervals so that
![]() $\operatorname {cl} U_{r,n}\subseteq U_{r,n+1}$
. Let
$\operatorname {cl} U_{r,n}\subseteq U_{r,n+1}$
. Let
![]() $\{(i_n,s_n):n=1,2,\dots \}$
list all pairs
$\{(i_n,s_n):n=1,2,\dots \}$
list all pairs
![]() $(i,s)$
consisting of an
$(i,s)$
consisting of an
![]() $i=0,\dots ,k$
and a point
$i=0,\dots ,k$
and a point
![]() $s\in E_i$
. Let
$s\in E_i$
. Let
![]() $Q=\{h^*(p,q'):h\in \mathscr {H},\, p\in E_i,\, q'\in A_{p,i},\, (p,q')\in G^1_h,\, i=0,\dots ,k\}$
. List the quadruples
$Q=\{h^*(p,q'):h\in \mathscr {H},\, p\in E_i,\, q'\in A_{p,i},\, (p,q')\in G^1_h,\, i=0,\dots ,k\}$
. List the quadruples
![]() $(h,j,q,V)$
consisting of an
$(h,j,q,V)$
consisting of an
![]() $h\in \mathscr {H}$
, a
$h\in \mathscr {H}$
, a
![]() $j=0,\dots ,k$
and elements
$j=0,\dots ,k$
and elements
![]() $q\in Q$
,
$q\in Q$
,
![]() $V\in \mathscr {B}$
as
$V\in \mathscr {B}$
as
![]() $\{(h_m,j_m,q_m,V_m):m=1,2,\dots \}$
with each quadruple listed infinitely many times. As with the
$\{(h_m,j_m,q_m,V_m):m=1,2,\dots \}$
with each quadruple listed infinitely many times. As with the
![]() $U_r$
above, we write
$U_r$
above, we write
![]() $V_m=\bigcup _{n=1}^\infty V_{m,n}$
where if
$V_m=\bigcup _{n=1}^\infty V_{m,n}$
where if
![]() $V_m=U_r$
then
$V_m=U_r$
then
![]() $V_{m,n}=U_{r,n}$
. We will write
$V_{m,n}=U_{r,n}$
. We will write
![]() $G^1_m$
,
$G^1_m$
,
![]() $G^2_m$
,
$G^2_m$
,
![]() $k_m$
for
$k_m$
for
![]() $G^1_{h_m}$
,
$G^1_{h_m}$
,
![]() $G^2_{h_m}$
,
$G^2_{h_m}$
,
![]() $k_{h_m}$
, respectively.
$k_{h_m}$
, respectively.
We will build the required function as
![]() $f=\sum _{n=1}^\infty \lambda _n u_n$
, where for each
$f=\sum _{n=1}^\infty \lambda _n u_n$
, where for each
![]() $n\in {\mathbb N}$
,
$n\in {\mathbb N}$
,
![]() $\lambda _n\in \mathbb {R}$
satisfies
$\lambda _n\in \mathbb {R}$
satisfies
![]() $|\lambda _n|\leq 1$
and
$|\lambda _n|\leq 1$
and
![]() $u_n\colon \mathbb {C}\to \mathbb {C}$
is an entire function such that
$u_n\colon \mathbb {C}\to \mathbb {C}$
is an entire function such that
![]() $u_n(\mathbb {R})\subseteq \mathbb {R}$
. We recursively define the following.
$u_n(\mathbb {R})\subseteq \mathbb {R}$
. We recursively define the following.
-
(i)
 $\lambda _n$
and
$\lambda _n$
and
 $u_n$
.
$u_n$
. -
(ii) An increasing sequence of finite sets
 $\emptyset =K_0\subseteq K_1\subseteq \dots $
of pairs
$\emptyset =K_0\subseteq K_1\subseteq \dots $
of pairs
 $(w,p)$
consisting of a
$(w,p)$
consisting of a
 $w=0,\dots ,k$
and a point
$w=0,\dots ,k$
and a point
 $p\in E_w$
.
$p\in E_w$
. -
(iii) A decreasing sequence of positive numbers
 $1=\delta _0>\delta _1>\dots $
.
$1=\delta _0>\delta _1>\dots $
.
We will arrange that the following properties hold for
![]() $n=1,2,\dots $
. In this list,
$n=1,2,\dots $
. In this list,
![]() $f_n$
denotes the sum
$f_n$
denotes the sum
![]() $\sum _{k=1}^n \lambda _k u_k$
, and
$\sum _{k=1}^n \lambda _k u_k$
, and
![]() $f_0=0$
.
$f_0=0$
.
-
(1)
 $u_n{\sigma }=u_n$
and
$u_n{\sigma }=u_n$
and
 $|(D^{i}u_n)(x)| < 2^{-n-1}\delta _{n-1}{\varepsilon }$
for
$|(D^{i}u_n)(x)| < 2^{-n-1}\delta _{n-1}{\varepsilon }$
for
 $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
 $i=0,\dots ,k$
.
$i=0,\dots ,k$
. -
(2)
 $(D^{w}u_n)(p) = 0$
for
$(D^{w}u_n)(p) = 0$
for
 $(w,p)\in K_{n-1}$
.
$(w,p)\in K_{n-1}$
. -
(3)
 $(D^{i}u_n)(x) = 0$
whenever
$(D^{i}u_n)(x) = 0$
whenever
 $x\in F$
,
$x\in F$
,
 $i=0,\dots ,k$
.
$i=0,\dots ,k$
. -
(4)
 $|u_n(z)| < 2^{-n}$
, for
$|u_n(z)| < 2^{-n}$
, for
 $|z|\leq n$
.
$|z|\leq n$
. -
(5) For each
 $(w,p)\in K_n$
,
$(w,p)\in K_n$
,
 $(D^w f_n)(p)\in A_{p,w}$
.
$(D^w f_n)(p)\in A_{p,w}$
. -
(6) If n is odd then
 $K_n = K_{n-1}\cup \{(i_\ell ,s_\ell )\}$
for the least
$K_n = K_{n-1}\cup \{(i_\ell ,s_\ell )\}$
for the least
 $\ell $
such that
$\ell $
such that
 $(i_\ell ,s_\ell )\not \in K_{n-1}$
. We have
$(i_\ell ,s_\ell )\not \in K_{n-1}$
. We have
 $(D^{i_\ell }u_n)(s_\ell ) \not = 0$
.
$(D^{i_\ell }u_n)(s_\ell ) \not = 0$
. -
(7) If
 $n=2m$
is even, we have the following. Suppose that
$n=2m$
is even, we have the following. Suppose that  $$ \begin{align*} (x,(D^{j_m}f_{n-1})(x))\in G^1_{m}\ \text{and}\ (x,q_m)\in G^2_{m}\ \text{whenever}\ x\in V_m. \end{align*} $$
$$ \begin{align*} (x,(D^{j_m}f_{n-1})(x))\in G^1_{m}\ \text{and}\ (x,q_m)\in G^2_{m}\ \text{whenever}\ x\in V_m. \end{align*} $$
-
(a) If
 $q_m=h^*_m(x,(D^{j_m}f_{n-1})(x))$
for some
$q_m=h^*_m(x,(D^{j_m}f_{n-1})(x))$
for some
 $x\in V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m}$
then for some
$x\in V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m}$
then for some
 $p\in V_m\cap Y_{h_m,q_m,j_m}$
,
$p\in V_m\cap Y_{h_m,q_m,j_m}$
,
 $h^*_m(p,(D^{j_m}f_{n})(p))=q_m$
and
$h^*_m(p,(D^{j_m}f_{n})(p))=q_m$
and
 $K_n = K_{n-1}\cup \{(j_m,p)\}$
.
$K_n = K_{n-1}\cup \{(j_m,p)\}$
. -
(b) If
 $q_m\not =h^*_m(x,(D^{j_m}f_{n-1})(x))$
for all
$q_m\not =h^*_m(x,(D^{j_m}f_{n-1})(x))$
for all
 $x\in V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m}$
then
$x\in V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m}$
then
 $u_n=0$
,
$u_n=0$
,
 $K_n = K_{n-1}$
and
$K_n = K_{n-1}$
and
 $\delta _n<\inf \{|k^*_m(x,q_m) - (D^{j_m}f_{n-1})(x)|:x\in V_{m,n}\cap \operatorname {cl} Y_{h_m,q_m,j_m}\}$
.
$\delta _n<\inf \{|k^*_m(x,q_m) - (D^{j_m}f_{n-1})(x)|:x\in V_{m,n}\cap \operatorname {cl} Y_{h_m,q_m,j_m}\}$
.
-
We now explain how to carry out the construction at odd stages and at even stages.
First suppose n is odd. This stage includes the initial step
![]() $n=1$
. Set
$n=1$
. Set
![]() $K_n = K_{n-1}\cup \{(i_\ell ,s_\ell )\}$
for the least
$K_n = K_{n-1}\cup \{(i_\ell ,s_\ell )\}$
for the least
![]() $\ell $
such that
$\ell $
such that
![]() $(i_\ell ,s_\ell )\not \in K_{n-1}$
. Apply Lemma 2.2 to get an entire function
$(i_\ell ,s_\ell )\not \in K_{n-1}$
. Apply Lemma 2.2 to get an entire function
![]() $u_n\colon \mathbb {C}\to \mathbb {C}$
satisfying (1), (2), (3), and (6). Arrange (4) by replacing
$u_n\colon \mathbb {C}\to \mathbb {C}$
satisfying (1), (2), (3), and (6). Arrange (4) by replacing
![]() $u_n$
by a smaller positive multiple of itself if necessary. Since
$u_n$
by a smaller positive multiple of itself if necessary. Since
![]() $(D^{i_\ell }u_n)(s_\ell )\not =0$
by (6), and
$(D^{i_\ell }u_n)(s_\ell )\not =0$
by (6), and
![]() $A_{s_\ell ,i_\ell }$
is dense in
$A_{s_\ell ,i_\ell }$
is dense in
![]() $\mathbb {R}$
, we may choose
$\mathbb {R}$
, we may choose
![]() $\lambda _n$
so that
$\lambda _n$
so that
![]() $0<\lambda _n<1$
and
$0<\lambda _n<1$
and
![]() $(D^{i_\ell }f_n)(s_\ell ) = (D^{i_\ell }f_{n-1})(s_\ell ) + \lambda _n (D^{i_\ell }u_n)(s_\ell )\in A_{s_\ell ,i_\ell }$
. This gives (5) because if
$(D^{i_\ell }f_n)(s_\ell ) = (D^{i_\ell }f_{n-1})(s_\ell ) + \lambda _n (D^{i_\ell }u_n)(s_\ell )\in A_{s_\ell ,i_\ell }$
. This gives (5) because if
![]() $(w,p)\in K_{n-1}$
then
$(w,p)\in K_{n-1}$
then
![]() $(D^w u_n)(p)=0$
by (2), so
$(D^w u_n)(p)=0$
by (2), so
![]() $(D^w f_n)(p) = (D^w f_{n-1})(p)$
which by (5) for
$(D^w f_n)(p) = (D^w f_{n-1})(p)$
which by (5) for
![]() $n-1$
belongs to
$n-1$
belongs to
![]() $A_{p,w}$
. For
$A_{p,w}$
. For
![]() $\delta _n$
, choose any positive number satisfying
$\delta _n$
, choose any positive number satisfying
![]() $\delta _n<\delta _{n-1}$
.
$\delta _n<\delta _{n-1}$
.
Now suppose that
![]() $n=2m$
is even. If the assumption of (7) fails, take
$n=2m$
is even. If the assumption of (7) fails, take
![]() $u_n=0$
,
$u_n=0$
,
![]() $\lambda _n=0$
,
$\lambda _n=0$
,
![]() $K_n=K_{n-1}$
, and let
$K_n=K_{n-1}$
, and let
![]() $\delta _n$
be any number such that
$\delta _n$
be any number such that
![]() $0<\delta _n<\delta _{n-1}$
. Clearly (1)–(7) hold. Now suppose that the assumption is satisfied, i.e.,
$0<\delta _n<\delta _{n-1}$
. Clearly (1)–(7) hold. Now suppose that the assumption is satisfied, i.e.,
![]() $(x,(D^{j_m}f_{n-1})(x))\in G^1_{m}$
and
$(x,(D^{j_m}f_{n-1})(x))\in G^1_{m}$
and
![]() $(x,q_m)\in G^2_{m}$
whenever
$(x,q_m)\in G^2_{m}$
whenever
![]() $x\in V_m$
.
$x\in V_m$
.
Case 1.
![]() $q_m\not = h^*_m(x,(D^{j_m}f_{n-1})(x))$
for all
$q_m\not = h^*_m(x,(D^{j_m}f_{n-1})(x))$
for all
![]() $x\in V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m} $
.
$x\in V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m} $
.
Let
![]() $u_n=0$
,
$u_n=0$
,
![]() $\lambda _n=0$
,
$\lambda _n=0$
,
![]() $K_n=K_{n-1}$
. Clearly (1)– (5) hold. For (7), choose any positive number
$K_n=K_{n-1}$
. Clearly (1)– (5) hold. For (7), choose any positive number
![]() $\delta _n<\delta _{n-1}$
so that
$\delta _n<\delta _{n-1}$
so that
![]() $\delta _n<\inf \{|k^*_m(x,q_m) - (D^{j_m}f_{n-1})(x)|:x\in V_{m,n}\cap \operatorname {cl} Y_{h_m,q_m,j_m}\}$
where the right-hand side is positive because
$\delta _n<\inf \{|k^*_m(x,q_m) - (D^{j_m}f_{n-1})(x)|:x\in V_{m,n}\cap \operatorname {cl} Y_{h_m,q_m,j_m}\}$
where the right-hand side is positive because
![]() $\operatorname {cl}(V_{m,n})\cap \operatorname {cl} (Y_{h_m,q_m,j_m})$
is compact and contained in
$\operatorname {cl}(V_{m,n})\cap \operatorname {cl} (Y_{h_m,q_m,j_m})$
is compact and contained in
![]() $V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m}$
.
$V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m}$
.
Case 2.
![]() $h^*_m(p,(D^{j_m}f_{n-1})(p))=q_m$
for some
$h^*_m(p,(D^{j_m}f_{n-1})(p))=q_m$
for some
![]() $p\in V_m\cap Y_{h_m,q_m,j_m}$
.
$p\in V_m\cap Y_{h_m,q_m,j_m}$
.
By definition,
![]() $p\in Y_{h_m,q_m,j_m}$
means that
$p\in Y_{h_m,q_m,j_m}$
means that
![]() $p\in E_{j_m}$
and there is a (unique)
$p\in E_{j_m}$
and there is a (unique)
![]() $q'\in A_{p,j_m}$
such that
$q'\in A_{p,j_m}$
such that
![]() $(p,q')\in G^1_m$
and
$(p,q')\in G^1_m$
and
![]() $q_m=h^*_m(p,q')$
. Since the vertical sections of
$q_m=h^*_m(p,q')$
. Since the vertical sections of
![]() $h^*_m$
are one-to-one, we must have
$h^*_m$
are one-to-one, we must have
![]() $(D^{j_m}f_{n-1})(p)=q'$
and hence
$(D^{j_m}f_{n-1})(p)=q'$
and hence
![]() $(D^{j_m}f_{n-1})(p)\in A_{p,j_m}$
. Let
$(D^{j_m}f_{n-1})(p)\in A_{p,j_m}$
. Let
![]() $u_n=0$
,
$u_n=0$
,
![]() $\lambda _n=0$
,
$\lambda _n=0$
,
![]() $K_n=K_{n-1}\cup \{(j_m,p)\}$
. Clearly (1)–(5) and (7) hold. For
$K_n=K_{n-1}\cup \{(j_m,p)\}$
. Clearly (1)–(5) and (7) hold. For
![]() $\delta _n$
, choose any positive number satisfying
$\delta _n$
, choose any positive number satisfying
![]() $\delta _n<\delta _{n-1}$
.
$\delta _n<\delta _{n-1}$
.
Case 3.
![]() $h^*_m(x,(D^{j_m}f_{n-1})(x))\not =q_m$
for all
$h^*_m(x,(D^{j_m}f_{n-1})(x))\not =q_m$
for all
![]() $x\in V_m\cap Y_{h_m,q_m,j_m}$
, but
$x\in V_m\cap Y_{h_m,q_m,j_m}$
, but
for some
![]() $p\in V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m}$
.
$p\in V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m}$
.
The assumptions give
![]() $h^*_m(p,(D^{j_m}f_{n-1})(p)) = q_m$
and
$h^*_m(p,(D^{j_m}f_{n-1})(p)) = q_m$
and
![]() $p\not \in V_m\cap Y_{h_m,q_m,j_m}$
, and since
$p\not \in V_m\cap Y_{h_m,q_m,j_m}$
, and since
![]() $p\in V_m$
this gives
$p\in V_m$
this gives
![]() $p\not \in Y_{h_m,q_m,j_m}$
. It follows from (5) that
$p\not \in Y_{h_m,q_m,j_m}$
. It follows from (5) that
![]() $(j_m,p)\not \in K_{n-1}$
because if
$(j_m,p)\not \in K_{n-1}$
because if
![]() $(j_m,p)\in K_{n-1}$
then
$(j_m,p)\in K_{n-1}$
then
![]() $p\in E_{j_m}$
and by (5) we have
$p\in E_{j_m}$
and by (5) we have
which together with
![]() $h^*_m(p,(D^{j_m}f_{n-1})(p))=q_m$
gives
$h^*_m(p,(D^{j_m}f_{n-1})(p))=q_m$
gives
![]() $p\in Y_{h_m,q_m,j_m}$
, contradiction. Apply Lemma 2.2 to get an entire function
$p\in Y_{h_m,q_m,j_m}$
, contradiction. Apply Lemma 2.2 to get an entire function
![]() $u_n\colon \mathbb {C}\to \mathbb {C}$
satisfying (1), (2), (3) and
$u_n\colon \mathbb {C}\to \mathbb {C}$
satisfying (1), (2), (3) and
![]() $(D^{j_m} u_n)(p)>0$
. Arrange (4) by replacing
$(D^{j_m} u_n)(p)>0$
. Arrange (4) by replacing
![]() $u_n$
by a smaller positive multiple of itself if necessary. The function
$u_n$
by a smaller positive multiple of itself if necessary. The function
![]() $x\mapsto (k^*_m(x,q_m) - (D^{j_m}f_{n-1})(x))/(D^{j_m}u_n)(x)$
is continuous at p with value
$x\mapsto (k^*_m(x,q_m) - (D^{j_m}f_{n-1})(x))/(D^{j_m}u_n)(x)$
is continuous at p with value
![]() $0$
there, and
$0$
there, and
![]() $p\in V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m}$
, so we can pick an element
$p\in V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m}$
, so we can pick an element
![]() $p'$
of
$p'$
of
![]() $V_m\cap Y_{h_m,q_m,j_m}$
so close to p that the number
$V_m\cap Y_{h_m,q_m,j_m}$
so close to p that the number
 $$ \begin{align*} \lambda_n = \frac{k^*_m(p',q_m) - (D^{j_m}f_{n-1})(p')}{(D^{j_m}u_n)(p')} \end{align*} $$
$$ \begin{align*} \lambda_n = \frac{k^*_m(p',q_m) - (D^{j_m}f_{n-1})(p')}{(D^{j_m}u_n)(p')} \end{align*} $$
satisfies
![]() $|\lambda _n|<1$
. With this value of
$|\lambda _n|<1$
. With this value of
![]() $\lambda _n$
, we have
$\lambda _n$
, we have
![]() $k^*_m(p',q_m)=(D^{j_m}f_n)(p')$
and therefore
$k^*_m(p',q_m)=(D^{j_m}f_n)(p')$
and therefore
and hence (7) holds if we take
![]() $K_n=K_{n-1}\cup \{(j_m,p')\}$
. Note that (5) is satisfied. For
$K_n=K_{n-1}\cup \{(j_m,p')\}$
. Note that (5) is satisfied. For
![]() $\delta _n$
, choose any positive number satisfying
$\delta _n$
, choose any positive number satisfying
![]() $\delta _n<\delta _{n-1}$
.
$\delta _n<\delta _{n-1}$
.
This completes the construction. Property (4) ensures that the formula
![]() $f = \sum _{n=1}^\infty \lambda _nu_n$
defines an entire function and that
$f = \sum _{n=1}^\infty \lambda _nu_n$
defines an entire function and that
 $$ \begin{align*} (D^{i}f)(z) = \sum_{n=1}^\infty \lambda_n(D^{i}u_n)(z) \end{align*} $$
$$ \begin{align*} (D^{i}f)(z) = \sum_{n=1}^\infty \lambda_n(D^{i}u_n)(z) \end{align*} $$
for all
![]() $i=0,\dots ,k$
and
$i=0,\dots ,k$
and
![]() $z\in \mathbb {C}$
. Clearly
$z\in \mathbb {C}$
. Clearly
![]() $f(\mathbb {R})\subseteq \mathbb {R}$
and by (1), we have
$f(\mathbb {R})\subseteq \mathbb {R}$
and by (1), we have
![]() $f{\sigma }=\sum _{n=1}^\infty \lambda _nu_n{\sigma }=f$
. We now verify (a)–(c).
$f{\sigma }=\sum _{n=1}^\infty \lambda _nu_n{\sigma }=f$
. We now verify (a)–(c).
(a) When
![]() $i=0,\dots ,k$
,
$i=0,\dots ,k$
,
![]() $x\in \mathbb {R}$
, we have using (1) that
$x\in \mathbb {R}$
, we have using (1) that
![]() $|(D^{i}f)(x)| \leq \sum _{i=1}^\infty |(D^{i}u_i)(x)| < \sum _{i=1}^\infty 2^{-i-1}{\varepsilon } = {\varepsilon }$
and, using (3), when
$|(D^{i}f)(x)| \leq \sum _{i=1}^\infty |(D^{i}u_i)(x)| < \sum _{i=1}^\infty 2^{-i-1}{\varepsilon } = {\varepsilon }$
and, using (3), when
![]() $x\in F$
we have
$x\in F$
we have
![]() $(D^{i}f)(x) = 0$
.
$(D^{i}f)(x) = 0$
.
(b) When
![]() $p\in E_i$
,
$p\in E_i$
,
![]() $i=0,\dots ,k$
, (6) ensures that
$i=0,\dots ,k$
, (6) ensures that
![]() $(i,p)\in K_n$
if n is sufficiently large. Then (5) gives
$(i,p)\in K_n$
if n is sufficiently large. Then (5) gives
![]() $(D^{i}f_n)(p) \in A_{p,i}$
. From (2), we get that
$(D^{i}f_n)(p) \in A_{p,i}$
. From (2), we get that
![]() $(D^{i}u_j)(p)=0$
,
$(D^{i}u_j)(p)=0$
,
![]() $j\geq n+1$
, and hence
$j\geq n+1$
, and hence
![]() $(D^{i}f)(p) = (D^{i}f_n)(p) \in A_{p,i}$
.
$(D^{i}f)(p) = (D^{i}f_n)(p) \in A_{p,i}$
.
(c) Suppose
![]() $i=0,\dots ,k$
,
$i=0,\dots ,k$
,
![]() $q\in \mathbb {R}$
,
$q\in \mathbb {R}$
,
![]() $U\subseteq \mathbb {R}\setminus F$
is an open interval, and we have
$U\subseteq \mathbb {R}\setminus F$
is an open interval, and we have
![]() $(p,(D^i f)(p))\in G^1_h$
, and
$(p,(D^i f)(p))\in G^1_h$
, and
![]() $q = h^*(p,(D^i f)(p))$
for some
$q = h^*(p,(D^i f)(p))$
for some
![]() $p\in U\cap \operatorname {cl} Y_{h,q,i}$
. We wish to show that
$p\in U\cap \operatorname {cl} Y_{h,q,i}$
. We wish to show that
![]() $q = h^*(\bar {p},(D^i f)(y))$
for some
$q = h^*(\bar {p},(D^i f)(y))$
for some
![]() $y\in U\cap E_i$
. We may assume that
$y\in U\cap E_i$
. We may assume that
![]() $U\in \mathscr {B}$
and for some open intervals
$U\in \mathscr {B}$
and for some open intervals
![]() $W_1,W_2\subseteq \mathbb {R}$
, for all
$W_1,W_2\subseteq \mathbb {R}$
, for all
![]() $x\in U$
,
$x\in U$
,
-
•
 $(D^i f)(x)\in W_1\subseteq \operatorname {cl} W_1\subseteq W_2$
, and
$(D^i f)(x)\in W_1\subseteq \operatorname {cl} W_1\subseteq W_2$
, and
 $U\times W_2\subseteq G^1_h$
and
$U\times W_2\subseteq G^1_h$
and -
•
 $(x,q)\in G^2_h$
.
$(x,q)\in G^2_h$
.
Since
![]() $D^i f_n\to D^i f$
uniformly on compact sets, for large enough n we have for
$D^i f_n\to D^i f$
uniformly on compact sets, for large enough n we have for
![]() $x\in U$
that
$x\in U$
that
![]() $(D^i f_n)(x)\in W_2$
and hence
$(D^i f_n)(x)\in W_2$
and hence
![]() $(x,(D^i f_n)(x))\in G^1_h$
. By assumption,
$(x,(D^i f_n)(x))\in G^1_h$
. By assumption,
![]() $p\in \operatorname {cl} Y_{h,q,i}$
, so
$p\in \operatorname {cl} Y_{h,q,i}$
, so
![]() $Y_{h,q,i}\not =\emptyset $
and hence
$Y_{h,q,i}\not =\emptyset $
and hence
![]() $q\in Q$
. Fix r such that
$q\in Q$
. Fix r such that
![]() $U=U_r$
. Choose an even
$U=U_r$
. Choose an even
![]() $n=2m$
with
$n=2m$
with
![]() $(h_m,j_m,q_m,V_m)=(h,i,q,U_r)$
, n large enough so that
$(h_m,j_m,q_m,V_m)=(h,i,q,U_r)$
, n large enough so that
![]() $p\in U_{r,n}=V_{m,n}$
and
$p\in U_{r,n}=V_{m,n}$
and
![]() $(x,(D^i f_{n-1})(x))\in G^1_h$
for all
$(x,(D^i f_{n-1})(x))\in G^1_h$
for all
![]() $x\in U$
.
$x\in U$
.
Claim.
![]() $q = h^*(x,(D^i f_{n-1})(x))$
for some
$q = h^*(x,(D^i f_{n-1})(x))$
for some
![]() $x\in U\cap \operatorname {cl} Y_{h,q,i}$
.
$x\in U\cap \operatorname {cl} Y_{h,q,i}$
.
If not, then by (7),
![]() $\delta _n<\inf \{|k^*_m(x,q_m) - (D^{j_m}f_{n-1})(x)|:x\in V_{m,n}\cap \operatorname {cl} Y_{h_m,q_m,j_m}\}$
and
$\delta _n<\inf \{|k^*_m(x,q_m) - (D^{j_m}f_{n-1})(x)|:x\in V_{m,n}\cap \operatorname {cl} Y_{h_m,q_m,j_m}\}$
and
![]() $u_n=0$
, so that
$u_n=0$
, so that
![]() $f_n=f_{n-1}$
. We have that for
$f_n=f_{n-1}$
. We have that for
![]() $j>n$
,
$j>n$
,
![]() $|(D^{i}u_j)(p)| < 2^{-j-1}\delta _{n}$
. This gives
$|(D^{i}u_j)(p)| < 2^{-j-1}\delta _{n}$
. This gives
 $$ \begin{align*} |(D^i f)(p) - (D^i f_{n-1})(p)|\leq \sum_{j=n}^{\infty} 2^{-j-1}\delta_{n} < \delta_{n} < |k^*_m(p,q) - (D^{i}f_{n-1})(p)|. \end{align*} $$
$$ \begin{align*} |(D^i f)(p) - (D^i f_{n-1})(p)|\leq \sum_{j=n}^{\infty} 2^{-j-1}\delta_{n} < \delta_{n} < |k^*_m(p,q) - (D^{i}f_{n-1})(p)|. \end{align*} $$
This contradicts
![]() $h^*(p,(D^i f)(p))=q$
(which is equivalent to
$h^*(p,(D^i f)(p))=q$
(which is equivalent to
![]() $k^*_h(p,q)=(D^i f)(p)$
). This completes the proof of the claim.
$k^*_h(p,q)=(D^i f)(p)$
). This completes the proof of the claim.
The claim says that
![]() $q_m=h^*_m(x,(D^{j_m}f_{n-1})(x))$
for some
$q_m=h^*_m(x,(D^{j_m}f_{n-1})(x))$
for some
![]() $x\in V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m}$
, so by (7), for some
$x\in V_m\cap \operatorname {cl} Y_{h_m,q_m,j_m}$
, so by (7), for some
![]() $y\in V_m\cap Y_{h_m,q_m,j_m}$
,
$y\in V_m\cap Y_{h_m,q_m,j_m}$
,
![]() $h^*_m(y,(D^{j_m}f_{n})(y))=q_m$
and
$h^*_m(y,(D^{j_m}f_{n})(y))=q_m$
and
![]() $K_n = K_{n-1}\cup \{(j_m,y)\}$
. But then by (2),
$K_n = K_{n-1}\cup \{(j_m,y)\}$
. But then by (2),
![]() $(D^{j_m}u_k)(y) = 0$
if
$(D^{j_m}u_k)(y) = 0$
if
![]() $k>n$
, so
$k>n$
, so
![]() $h^*_m(y,(D^{j_m}f)(y)) = h^*_m(y,(D^{j_m}f_{n})(y))=q_m$
. ▪
$h^*_m(y,(D^{j_m}f)(y)) = h^*_m(y,(D^{j_m}f_{n})(y))=q_m$
. ▪
The next corollary incorporates into the theorem the ability to approximate a given function g such that either
![]() $g{\sigma }=g$
or
$g{\sigma }=g$
or
![]() $g{\sigma }={\sigma } g$
. These two types of functions are related by the fact that for a function g, if we write
$g{\sigma }={\sigma } g$
. These two types of functions are related by the fact that for a function g, if we write
![]() $g=g_1+\operatorname {id}$
, i.e.,
$g=g_1+\operatorname {id}$
, i.e.,
![]() $g(x)=g_1(x)+x$
, then
$g(x)=g_1(x)+x$
, then
![]() ${\sigma } g=g{\sigma }$
if and only if
${\sigma } g=g{\sigma }$
if and only if
![]() $g_1{\sigma }=g_1$
. Also note that if either
$g_1{\sigma }=g_1$
. Also note that if either
![]() $g{\sigma }=g$
or
$g{\sigma }=g$
or
![]() $g{\sigma }={\sigma } g$
then
$g{\sigma }={\sigma } g$
then
![]() $(D^ig){\sigma }=D^ig$
for
$(D^ig){\sigma }=D^ig$
for
![]() $i>0$
when the derivatives exist.
$i>0$
when the derivatives exist.
Corollary 3.5 (A) Let
![]() $g\in C^k(\mathbb {R})$
satisfy
$g\in C^k(\mathbb {R})$
satisfy
![]() $g{\sigma }=g$
. Let
$g{\sigma }=g$
. Let
![]() $E_i\subseteq [0,t]$
,
$E_i\subseteq [0,t]$
,
![]() $i=0,\dots ,k$
, be countable sets with
$i=0,\dots ,k$
, be countable sets with
![]() $\{0,t\}\subseteq E_i$
or
$\{0,t\}\subseteq E_i$
or
![]() $E_i\cap \{0,t\}=\emptyset $
. Let
$E_i\cap \{0,t\}=\emptyset $
. Let
![]() $F\subseteq [0,t]$
be a finite set disjoint from
$F\subseteq [0,t]$
be a finite set disjoint from
![]() $\bigcup _{i=0}^k E_i$
with
$\bigcup _{i=0}^k E_i$
with
![]() $\{0,t\}\subseteq F$
or
$\{0,t\}\subseteq F$
or
![]() $F\cap \{0,t\}=\emptyset $
. For each
$F\cap \{0,t\}=\emptyset $
. For each
![]() $p\in E_i$
, let
$p\in E_i$
, let
![]() $A_{p,i}\subseteq \mathbb {R}$
be a countable dense set, with
$A_{p,i}\subseteq \mathbb {R}$
be a countable dense set, with
![]() $A_{0,i}=A_{t,i}$
if
$A_{0,i}=A_{t,i}$
if
![]() $\{0,t\}\subseteq E_i$
. Let
$\{0,t\}\subseteq E_i$
. Let
![]() ${\varepsilon }>0$
. Let
${\varepsilon }>0$
. Let
![]() $\mathscr {H}$
be a countable family of fiber-preserving local homeomorphisms of
$\mathscr {H}$
be a countable family of fiber-preserving local homeomorphisms of
![]() $\mathbb {R}^2$
. There exists an entire function
$\mathbb {R}^2$
. There exists an entire function
![]() $f\colon \mathbb {C}\to \mathbb {C}$
such that
$f\colon \mathbb {C}\to \mathbb {C}$
such that
![]() $f(\mathbb {R})\subseteq \mathbb {R}$
,
$f(\mathbb {R})\subseteq \mathbb {R}$
,
![]() $f{\sigma }=f$
and for all
$f{\sigma }=f$
and for all
![]() $x\in \mathbb {R}$
and
$x\in \mathbb {R}$
and
![]() $i=0,\dots ,k$
,
$i=0,\dots ,k$
,
-
(a)
 $|(D^{i}f)(x)-(D^{i}g)(x)|<{\varepsilon }$
, and if
$|(D^{i}f)(x)-(D^{i}g)(x)|<{\varepsilon }$
, and if
 $x\in F$
then
$x\in F$
then
 $D^if(x)=D^ig(x)$
.
$D^if(x)=D^ig(x)$
. -
(b) for each
 $p\in E_i$
,
$p\in E_i$
,
 $(D^i f)(p)\in A_{p,i}$
.
$(D^i f)(p)\in A_{p,i}$
. -
(c) for every
 $q\in \mathbb {R}$
,
$q\in \mathbb {R}$
,
 $h\in \mathscr {H}$
and every open interval
$h\in \mathscr {H}$
and every open interval
 $U\subseteq \mathbb {R}\setminus F$
, if for some
$U\subseteq \mathbb {R}\setminus F$
, if for some $$ \begin{align*} (x,(D^i f)(x))\in G^1_h\ \text{and}\ q = h^*(x,(D^i f)(x)) \end{align*} $$
$$ \begin{align*} (x,(D^i f)(x))\in G^1_h\ \text{and}\ q = h^*(x,(D^i f)(x)) \end{align*} $$
 $x\in U\cap \operatorname {cl} Y_{h,q,i}$
, where
$x\in U\cap \operatorname {cl} Y_{h,q,i}$
, where
 $Y_{h,q,i} = \{p\in E_i:$
for some
$Y_{h,q,i} = \{p\in E_i:$
for some
 $q'\in A_{p,i}$
,
$q'\in A_{p,i}$
,
 $(p,q')\in G^1_h$
and
$(p,q')\in G^1_h$
and
 $q=h^*(p,q')\}$
, then
$q=h^*(p,q')\}$
, then
 $q = h^*(p,(D^i f)(p))$
for some
$q = h^*(p,(D^i f)(p))$
for some
 $p\in U\cap E_i$
.
$p\in U\cap E_i$
.
(B) The same statement is true with
![]() $g{\sigma }=g$
,
$g{\sigma }=g$
,
![]() $f{\sigma }=f$
replaced by
$f{\sigma }=f$
replaced by
![]() $g{\sigma }={\sigma } g$
,
$g{\sigma }={\sigma } g$
,
![]() $f{\sigma }={\sigma } f$
, respectively, and the condition
$f{\sigma }={\sigma } f$
, respectively, and the condition
![]() $A_{t,i}=A_{0,i} ($
when
$A_{t,i}=A_{0,i} ($
when
![]() $\{0,t\}\subseteq E_i)$
replaced by
$\{0,t\}\subseteq E_i)$
replaced by
![]() $A_{t,i}=A_{0,i}$
when
$A_{t,i}=A_{0,i}$
when
![]() $i\not =0$
,
$i\not =0$
,
![]() $A_{t,0}=A_{0,0}+t$
.
$A_{t,0}=A_{0,0}+t$
.
Proof (A) Using Theorem 2.1, we can approximate g by an entire function
![]() $g_0$
so that
$g_0$
so that
![]() $g_0(\mathbb {R})\subseteq \mathbb {R}$
,
$g_0(\mathbb {R})\subseteq \mathbb {R}$
,
![]() $g_0{\sigma }=g_0$
, and for
$g_0{\sigma }=g_0$
, and for
![]() $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
![]() $i=0,\dots ,k$
,
$i=0,\dots ,k$
,
![]() $|D^ig_0(x)-D^ig(x)|<{\varepsilon }/2$
and if
$|D^ig_0(x)-D^ig(x)|<{\varepsilon }/2$
and if
![]() $x\in F$
then
$x\in F$
then
![]() $D^ig_0(x)=D^ig(x)$
. If we approximate
$D^ig_0(x)=D^ig(x)$
. If we approximate
![]() $g_0$
as in Corollary 3.5, replacing
$g_0$
as in Corollary 3.5, replacing
![]() ${\varepsilon }$
by
${\varepsilon }$
by
![]() ${\varepsilon }/2$
, we get the desired function f. Hence, we may assume that g is entire.
${\varepsilon }/2$
, we get the desired function f. Hence, we may assume that g is entire.
For
![]() $p\in E_i$
, define
$p\in E_i$
, define
![]() $B_{p,i}=A_{p,i}-(D^i g)(p)$
. Writing
$B_{p,i}=A_{p,i}-(D^i g)(p)$
. Writing
![]() $\xi _i$
for the fiber-preserving homeomorphism of
$\xi _i$
for the fiber-preserving homeomorphism of
![]() $\mathbb {R}^{2}$
given by
$\mathbb {R}^{2}$
given by
![]() $\xi _i(x,y)=(x,y+(D^i g)(x))$
, take
$\xi _i(x,y)=(x,y+(D^i g)(x))$
, take
![]() $\mathscr {H}_i=\{h\circ \xi _i:h\in \mathscr {H}\}$
and apply Theorem 3.3 with
$\mathscr {H}_i=\{h\circ \xi _i:h\in \mathscr {H}\}$
and apply Theorem 3.3 with
![]() $A_{p,i}$
replaced by
$A_{p,i}$
replaced by
![]() $B_{p,i}$
and
$B_{p,i}$
and
![]() $\mathscr {H}$
replaced by
$\mathscr {H}$
replaced by
![]() $\overline {\mathscr {H}}=\bigcup _i\mathscr {H}_i$
. (Here,
$\overline {\mathscr {H}}=\bigcup _i\mathscr {H}_i$
. (Here,
![]() $h\circ \xi _i\colon \xi _i^{-1}(G^1_h)\to G^2_h$
.) If
$h\circ \xi _i\colon \xi _i^{-1}(G^1_h)\to G^2_h$
.) If
![]() $f_1$
is the resulting entire function, the function
$f_1$
is the resulting entire function, the function
![]() $f=g+f_1$
is as desired. We have
$f=g+f_1$
is as desired. We have
![]() $f{\sigma }=g{\sigma }+f_1{\sigma }=g+f_1=f$
. Clauses (a) and (b) are immediate from the corresponding clauses of Theorem 3.3 and the definition of
$f{\sigma }=g{\sigma }+f_1{\sigma }=g+f_1=f$
. Clauses (a) and (b) are immediate from the corresponding clauses of Theorem 3.3 and the definition of
![]() $B_{p,i}$
.
$B_{p,i}$
.
For (c), fix an
![]() $i=0,\dots ,k$
,
$i=0,\dots ,k$
,
![]() $q\in \mathbb {R}$
,
$q\in \mathbb {R}$
,
![]() $h\in \mathscr {H}$
, an open interval
$h\in \mathscr {H}$
, an open interval
![]() $U\subseteq \mathbb {R}\setminus F$
, and assume that
$U\subseteq \mathbb {R}\setminus F$
, and assume that
![]() $(x,(D^i f)(x))\in G^1_h$
and
$(x,(D^i f)(x))\in G^1_h$
and
![]() $q = h^*(x,(D^i f)(x))$
for some
$q = h^*(x,(D^i f)(x))$
for some
![]() $x\in U\cap \operatorname {cl} Y_{h,q,i}$
. Then
$x\in U\cap \operatorname {cl} Y_{h,q,i}$
. Then
![]() $\xi _i(x,(D^i f_1)(x))\in G^1_h$
, so
$\xi _i(x,(D^i f_1)(x))\in G^1_h$
, so
![]() $(x,(D^i f_1)(x))\in \xi _i^{-1}(G^1_h)$
, and
$(x,(D^i f_1)(x))\in \xi _i^{-1}(G^1_h)$
, and
![]() $q = (h^*\circ \xi _i)(x,(D^i f_1)(x))$
.
$q = (h^*\circ \xi _i)(x,(D^i f_1)(x))$
.
Claim.
![]() $Y_{h,q,i}\subseteq Y_{h\circ \xi _i,q,i}$
where the set
$Y_{h,q,i}\subseteq Y_{h\circ \xi _i,q,i}$
where the set
![]() $Y_{h\circ \xi _i,q,i}$
is defined using the
$Y_{h\circ \xi _i,q,i}$
is defined using the
![]() $B_{p,i}$
instead of the
$B_{p,i}$
instead of the
![]() $A_{p,i}$
.
$A_{p,i}$
.
Let
![]() $p\in Y_{h,q,i}$
. Then
$p\in Y_{h,q,i}$
. Then
![]() $p\in E_i$
and for some
$p\in E_i$
and for some
![]() $q'\in A_{p,i}$
,
$q'\in A_{p,i}$
,
![]() $(p,q')\in G^1_h$
and
$(p,q')\in G^1_h$
and
![]() $q=h^*(p,q')$
. We then have
$q=h^*(p,q')$
. We then have
![]() $q'-(D^i g)(p)\in B_{p,i}$
,
$q'-(D^i g)(p)\in B_{p,i}$
,
![]() $(p,q'-(D^i g)(p)) = \xi _i^{-1}(p,q')\in \xi _i^{-1}(G^1_h)$
and
$(p,q'-(D^i g)(p)) = \xi _i^{-1}(p,q')\in \xi _i^{-1}(G^1_h)$
and
![]() $q=(h^*\circ \xi _i)(p,q'-(D^i g)(p)) = (h\circ \xi _i)^*(p,q'-(D^i g)(p))$
. Thus,
$q=(h^*\circ \xi _i)(p,q'-(D^i g)(p)) = (h\circ \xi _i)^*(p,q'-(D^i g)(p))$
. Thus,
![]() $p\in Y_{h\circ \xi _i,q,i}$
, which proves the claim.
$p\in Y_{h\circ \xi _i,q,i}$
, which proves the claim.
By the claim,
![]() $x\in \operatorname {cl} Y_{h\circ \xi _i,q,i}$
and hence by (c) of Theorem 3.3,
$x\in \operatorname {cl} Y_{h\circ \xi _i,q,i}$
and hence by (c) of Theorem 3.3,
![]() $q = (h\circ \xi _i)^*(p,(D^i f_1)(p)) = (h^*\circ \xi _i)(p,(D^i f_1)(p))$
for some
$q = (h\circ \xi _i)^*(p,(D^i f_1)(p)) = (h^*\circ \xi _i)(p,(D^i f_1)(p))$
for some
![]() $p\in U\cap E_i$
. Then
$p\in U\cap E_i$
. Then
![]() $h^*(p,(D^i f)(p)) = (h^*\circ \xi _i)(p,(D^i f_1)(p))=q$
.
$h^*(p,(D^i f)(p)) = (h^*\circ \xi _i)(p,(D^i f_1)(p))=q$
.
(B) This part follows from (A) by an argument similar to that used for (A). Given
![]() $g\in C^k(\mathbb {R})$
satisfying
$g\in C^k(\mathbb {R})$
satisfying
![]() $g{\sigma }={\sigma } g$
, write
$g{\sigma }={\sigma } g$
, write
![]() $g=g_1+\operatorname {id}$
. As pointed out above, we have
$g=g_1+\operatorname {id}$
. As pointed out above, we have
![]() $g_1{\sigma }=g_1$
. For
$g_1{\sigma }=g_1$
. For
![]() $p\in E_i$
, define
$p\in E_i$
, define
![]() $B_{p,i}=A_{p,i}-(D^i \operatorname {id})(p)$
. (So
$B_{p,i}=A_{p,i}-(D^i \operatorname {id})(p)$
. (So
![]() $B_{p,0}=A_{p,0}-p$
,
$B_{p,0}=A_{p,0}-p$
,
![]() $B_{p,1}=A_{p,1}-1$
,
$B_{p,1}=A_{p,1}-1$
,
![]() $B_{p,i}=A_{p,i} (i>1)$
.) Writing
$B_{p,i}=A_{p,i} (i>1)$
.) Writing
![]() $\xi _i$
for the fiber-preserving homeomorphism of
$\xi _i$
for the fiber-preserving homeomorphism of
![]() $\mathbb {R}^{2}$
given by
$\mathbb {R}^{2}$
given by
![]() $\xi _i(x,y)=(x,y+(D^i \operatorname {id})(x))$
, take
$\xi _i(x,y)=(x,y+(D^i \operatorname {id})(x))$
, take
![]() $\mathscr {H}_i=\{h\circ \xi _i:h\in \mathscr {H}\}$
and apply part (A) to
$\mathscr {H}_i=\{h\circ \xi _i:h\in \mathscr {H}\}$
and apply part (A) to
![]() $g_1$
with
$g_1$
with
![]() $A_{p,i}$
replaced by
$A_{p,i}$
replaced by
![]() $B_{p,i}$
and
$B_{p,i}$
and
![]() $\mathscr {H}$
replaced by
$\mathscr {H}$
replaced by
![]() $\overline {\mathscr {H}}=\bigcup _i\mathscr {H}_i$
. (Here,
$\overline {\mathscr {H}}=\bigcup _i\mathscr {H}_i$
. (Here,
![]() $h\circ \xi _i\colon \xi _i^{-1}(G^1_h)\to G^2_h$
.) If
$h\circ \xi _i\colon \xi _i^{-1}(G^1_h)\to G^2_h$
.) If
![]() $f_1$
is the resulting entire function, the function
$f_1$
is the resulting entire function, the function
![]() $f=\operatorname {id}+f_1$
is as desired. Since
$f=\operatorname {id}+f_1$
is as desired. Since
![]() $f_1$
satisfies
$f_1$
satisfies
![]() $f_1{\sigma }=f_1$
, it follows that f satisfies
$f_1{\sigma }=f_1$
, it follows that f satisfies
![]() $f{\sigma }={\sigma } f$
. Clauses (a) and (b) of part (B) are immediate from the corresponding clauses of part (A) and the definition of
$f{\sigma }={\sigma } f$
. Clauses (a) and (b) of part (B) are immediate from the corresponding clauses of part (A) and the definition of
![]() $B_{p,i}$
. For (c), as in part (A), fix an
$B_{p,i}$
. For (c), as in part (A), fix an
![]() $i=0,\dots ,k$
,
$i=0,\dots ,k$
,
![]() $q\in \mathbb {R}$
,
$q\in \mathbb {R}$
,
![]() $h\in \mathscr {H}$
, an open interval
$h\in \mathscr {H}$
, an open interval
![]() $U\subseteq \mathbb {R}\setminus F$
, and assume that
$U\subseteq \mathbb {R}\setminus F$
, and assume that
![]() $(x,(D^i f)(x))\in G^1_h$
and
$(x,(D^i f)(x))\in G^1_h$
and
![]() $q = h^*(x,(D^i f)(x))$
for some
$q = h^*(x,(D^i f)(x))$
for some
![]() $x\in U\cap \operatorname {cl} Y_{h,q,i}$
. Then
$x\in U\cap \operatorname {cl} Y_{h,q,i}$
. Then
![]() $\xi _i(x,(D^i f_1)(x))\in G^1_h$
, so
$\xi _i(x,(D^i f_1)(x))\in G^1_h$
, so
![]() $(x,(D^i f_1)(x))\in \xi _i^{-1}(G^1_h)$
, and
$(x,(D^i f_1)(x))\in \xi _i^{-1}(G^1_h)$
, and
![]() $q = (h^*\circ \xi _i)(x,(D^i f_1)(x))$
. As in the proof of (A), we get
$q = (h^*\circ \xi _i)(x,(D^i f_1)(x))$
. As in the proof of (A), we get
![]() $Y_{h,q,i}\subseteq Y_{h\circ \xi _i,q,i}$
where the set
$Y_{h,q,i}\subseteq Y_{h\circ \xi _i,q,i}$
where the set
![]() $Y_{h\circ \xi _i,q,i}$
is defined using the
$Y_{h\circ \xi _i,q,i}$
is defined using the
![]() $B_{p,i}$
instead of the
$B_{p,i}$
instead of the
![]() $A_{p,i}$
. (In the proof of the claim in part (A), replace the four g’s by
$A_{p,i}$
. (In the proof of the claim in part (A), replace the four g’s by
![]() $\operatorname {id}$
.) Then finish exactly as in part (A), reading “by (c) of part (A)” instead of “by (c) of Theorem 3.3.” ▪
$\operatorname {id}$
.) Then finish exactly as in part (A), reading “by (c) of part (A)” instead of “by (c) of Theorem 3.3.” ▪
Theorem 3.6 Let
![]() $(A^i_n,B^i_n)$
,
$(A^i_n,B^i_n)$
,
![]() $i=0,\dots ,k$
,
$i=0,\dots ,k$
,
![]() $n\in {\mathbb N}$
, be pairs of countable dense subsets of
$n\in {\mathbb N}$
, be pairs of countable dense subsets of
![]() $\mathbb {R}$
invariant under
$\mathbb {R}$
invariant under
![]() ${\sigma }$
such that for each fixed i, the
${\sigma }$
such that for each fixed i, the
![]() $A^i_n$
are pairwise disjoint. Assume also that the
$A^i_n$
are pairwise disjoint. Assume also that the
![]() $B^0_n$
are pairwise disjoint. Let
$B^0_n$
are pairwise disjoint. Let
![]() $F\subseteq \mathbb {R}$
be a finite set disjoint from each
$F\subseteq \mathbb {R}$
be a finite set disjoint from each
![]() $A^i_n$
. Fix
$A^i_n$
. Fix
![]() ${\varepsilon }>0$
. Then for each
${\varepsilon }>0$
. Then for each
![]() $g\in C^k(\mathbb {R})$
with
$g\in C^k(\mathbb {R})$
with
![]() $k\geq 1$
such that
$k\geq 1$
such that
![]() $g{\sigma }={\sigma } g$
,
$g{\sigma }={\sigma } g$
,
![]() $Dg>0$
, and
$Dg>0$
, and
![]() $g(F)\cap B^0_n=\emptyset $
for all
$g(F)\cap B^0_n=\emptyset $
for all
![]() $n\in {\mathbb N}$
, there is an entire function f such that for
$n\in {\mathbb N}$
, there is an entire function f such that for
![]() $i=0,\dots ,k$
,
$i=0,\dots ,k$
,
![]() $n\in {\mathbb N}$
, and
$n\in {\mathbb N}$
, and
![]() $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
-
(a)
 $f(\mathbb {R})\subseteq \mathbb {R}$
,
$f(\mathbb {R})\subseteq \mathbb {R}$
,
 $f{\sigma }={\sigma } f$
,
$f{\sigma }={\sigma } f$
,
 $Df(x)>0$
$Df(x)>0$
-
(b)
 $|(D^{i}f)(x)-(D^{i}g)(x)|<{\varepsilon }$
, and if
$|(D^{i}f)(x)-(D^{i}g)(x)|<{\varepsilon }$
, and if
 $x\in F$
then
$x\in F$
then
 $D^if(x)=D^ig(x)$
$D^if(x)=D^ig(x)$
-
(c)
 $D^if(A^i_n)\subseteq B^i_n$
,
$D^if(A^i_n)\subseteq B^i_n$
,
 $f(A^0_n)=B^0_n$
$f(A^0_n)=B^0_n$
Proof For
![]() $i=0,\dots ,k$
, let
$i=0,\dots ,k$
, let
![]() $E_i=[0,t]\cap \bigcup _{n=1}^\infty A^i_n$
. For pairs
$E_i=[0,t]\cap \bigcup _{n=1}^\infty A^i_n$
. For pairs
![]() $(p,i)$
with
$(p,i)$
with
![]() $p\in E_i$
, for some unique n we have
$p\in E_i$
, for some unique n we have
![]() $p\in A^i_n$
. Define
$p\in A^i_n$
. Define
![]() $A_{p,i}=B^i_n$
. If
$A_{p,i}=B^i_n$
. If
![]() $0,t\in E_i$
, then for some n we have
$0,t\in E_i$
, then for some n we have
![]() $0,t\in A^i_n$
. Then
$0,t\in A^i_n$
. Then
![]() $A_{0,i}=A_{t,i}=B^i_n$
and therefore also
$A_{0,i}=A_{t,i}=B^i_n$
and therefore also
![]() ${\sigma }(A_{0,i})=A_{t,i}$
by invariance of
${\sigma }(A_{0,i})=A_{t,i}$
by invariance of
![]() $B^i_n$
. The orbit of each point has at most two points in
$B^i_n$
. The orbit of each point has at most two points in
![]() $[0,t]$
, so
$[0,t]$
, so
![]() $F_1=[0,t]\cap \bigcup _{\ell \in {\mathbb Z}}{\sigma }^\ell (F)$
is finite. We have
$F_1=[0,t]\cap \bigcup _{\ell \in {\mathbb Z}}{\sigma }^\ell (F)$
is finite. We have
![]() $E_i\cap F_1=\emptyset $
for each i, because
$E_i\cap F_1=\emptyset $
for each i, because
![]() $E_i\cap F_1 \subseteq (\bigcup _{n=1}^\infty A^i_n)\cap (\bigcup _{\ell =1}^\infty {\sigma }^\ell (F))$
and for all
$E_i\cap F_1 \subseteq (\bigcup _{n=1}^\infty A^i_n)\cap (\bigcup _{\ell =1}^\infty {\sigma }^\ell (F))$
and for all
![]() $n,\ell $
,
$n,\ell $
,
![]() $A^i_n\cap {\sigma }^\ell (F) = {\sigma }^{\ell }(A^i_n\cap F) = \emptyset $
. Similarly,
$A^i_n\cap {\sigma }^\ell (F) = {\sigma }^{\ell }(A^i_n\cap F) = \emptyset $
. Similarly,
![]() $g(F_1)\cap B^0_n =\emptyset $
because
$g(F_1)\cap B^0_n =\emptyset $
because
![]() $g({\sigma }^\ell (F))\cap B^0_n = {\sigma }^{\ell }(g(F)\cap B^0_n) = \emptyset $
for all
$g({\sigma }^\ell (F))\cap B^0_n = {\sigma }^{\ell }(g(F)\cap B^0_n) = \emptyset $
for all
![]() $n,\ell $
. Take
$n,\ell $
. Take
![]() ${\varepsilon }'=\min ({\varepsilon },\inf \{Dg(x):x\in \mathbb {R}\})$
which is positive by periodicity of
${\varepsilon }'=\min ({\varepsilon },\inf \{Dg(x):x\in \mathbb {R}\})$
which is positive by periodicity of
![]() $Dg$
and since
$Dg$
and since
![]() $Dg>0$
. Corollary 3.5 (B) with
$Dg>0$
. Corollary 3.5 (B) with
![]() $\mathscr {H}=\{\operatorname {id}_{\mathbb {R}^2}\}$
gives
$\mathscr {H}=\{\operatorname {id}_{\mathbb {R}^2}\}$
gives
![]() $f $
such that
$f $
such that
![]() $f (\mathbb {R})\subseteq \mathbb {R}$
,
$f (\mathbb {R})\subseteq \mathbb {R}$
,
![]() $f {\sigma }={\sigma } f $
and for all
$f {\sigma }={\sigma } f $
and for all
![]() $x\in \mathbb {R}$
and
$x\in \mathbb {R}$
and
![]() $i=0,\dots ,k$
,
$i=0,\dots ,k$
,
-
(i)
 $|(D^{i}f )(x)-(D^{i}g )(x)|<{\varepsilon }'$
, and if
$|(D^{i}f )(x)-(D^{i}g )(x)|<{\varepsilon }'$
, and if
 $x\in F_1$
then
$x\in F_1$
then
 $D^if (x)=D^ig (x)$
.
$D^if (x)=D^ig (x)$
. -
(ii) for each
 $p\in E_i$
,
$p\in E_i$
,
 $(D^i f )(p)\in A_{p,i}$
.
$(D^i f )(p)\in A_{p,i}$
. -
(iii) for any
 $q\in \mathbb {R}$
, if
$q\in \mathbb {R}$
, if
 $q = f(x)$
for some
$q = f(x)$
for some
 $x\in \operatorname {cl} \{p\in E_0: q\in A_{p,0}\}$
,
$x\in \operatorname {cl} \{p\in E_0: q\in A_{p,0}\}$
,
 $x\notin F_1$
, then
$x\notin F_1$
, then
 $q = f(p)$
for some
$q = f(p)$
for some
 $p\in E_0$
. (Since f is injective, necessarily
$p\in E_0$
. (Since f is injective, necessarily
 $x=p$
.)
$x=p$
.)
From (i) we get (b). From (i) we also get for
![]() $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
![]() $|Df(x)-Dg(x)| <{\varepsilon }'\leq Dg(x)$
, so
$|Df(x)-Dg(x)| <{\varepsilon }'\leq Dg(x)$
, so
![]() $Df(x)>0$
giving (a). For (c), fix
$Df(x)>0$
giving (a). For (c), fix
![]() $i=0,\dots ,k$
,
$i=0,\dots ,k$
,
![]() $n\in {\mathbb N}$
. We want to show that
$n\in {\mathbb N}$
. We want to show that
![]() $D^if(A^i_n)\subseteq B^i_n$
, and when
$D^if(A^i_n)\subseteq B^i_n$
, and when
![]() $i=0$
,
$i=0$
,
![]() $f(A^0_n)=B^0_n$
. For
$f(A^0_n)=B^0_n$
. For
![]() $p\in A^i_n$
we have for some
$p\in A^i_n$
we have for some
![]() $\ell $
that
$\ell $
that
![]() ${\sigma }^\ell (p)\in [0,t]$
. When
${\sigma }^\ell (p)\in [0,t]$
. When
![]() $i=0$
, we get, using (ii),
$i=0$
, we get, using (ii),
![]() $f (p) = {\sigma }^{-\ell }f ({\sigma }^\ell (p))\in {\sigma }^{-\ell }A_{{\sigma }^\ell (p),0} = B^0_n$
. When
$f (p) = {\sigma }^{-\ell }f ({\sigma }^\ell (p))\in {\sigma }^{-\ell }A_{{\sigma }^\ell (p),0} = B^0_n$
. When
![]() $i>0$
, we get similarly
$i>0$
, we get similarly
![]() $D^if (p) = D^if ({\sigma }^\ell (p)) \in A_{{\sigma }^\ell (p),i} = B^i_n$
.
$D^if (p) = D^if ({\sigma }^\ell (p)) \in A_{{\sigma }^\ell (p),i} = B^i_n$
.
There remains to show that
![]() $B^0_n\subseteq f(A^0_n)$
. Let
$B^0_n\subseteq f(A^0_n)$
. Let
![]() $q\in B^0_n$
. Since
$q\in B^0_n$
. Since
![]() $f(t)=f(0)+t$
, for some
$f(t)=f(0)+t$
, for some
![]() $\ell $
,
$\ell $
,
![]() ${\sigma }^\ell (q)\in [f(0),f(t)]$
and therefore, for some
${\sigma }^\ell (q)\in [f(0),f(t)]$
and therefore, for some
![]() $x\in [0,t]$
,
$x\in [0,t]$
,
![]() $f(x)={\sigma }^\ell (q)$
. We have
$f(x)={\sigma }^\ell (q)$
. We have
![]() $x\notin F_1$
because otherwise
$x\notin F_1$
because otherwise
![]() $g(x)=f(x)={\sigma }^\ell (q)\in B^0_n$
, contradicting the fact that
$g(x)=f(x)={\sigma }^\ell (q)\in B^0_n$
, contradicting the fact that
![]() $g(F_1)\cap B^0_n = \emptyset $
. Since
$g(F_1)\cap B^0_n = \emptyset $
. Since
![]() $A^0_n$
is dense, arbitrarily close to x there are
$A^0_n$
is dense, arbitrarily close to x there are
![]() $p\in A^0_n\cap [0,t]$
and these satisfy
$p\in A^0_n\cap [0,t]$
and these satisfy
![]() ${\sigma }^\ell (q)\in B^0_n = A_{p,0}$
, so by (iii), there is a
${\sigma }^\ell (q)\in B^0_n = A_{p,0}$
, so by (iii), there is a
![]() $p\in E_0$
such that
$p\in E_0$
such that
![]() ${\sigma }^\ell (q) = f(p)$
and therefore
${\sigma }^\ell (q) = f(p)$
and therefore
![]() $f({\sigma }^{-\ell }(p))=q$
. This gives
$f({\sigma }^{-\ell }(p))=q$
. This gives
![]() $q\in f(A^0_n)$
as long as
$q\in f(A^0_n)$
as long as
![]() $p\in A^0_n$
. Let m be such that
$p\in A^0_n$
. Let m be such that
![]() $p\in A^0_m$
. Then
$p\in A^0_m$
. Then
![]() ${\sigma }^\ell (q)=f (p)\in f (A^0_m)\subseteq B^0_m$
. Since
${\sigma }^\ell (q)=f (p)\in f (A^0_m)\subseteq B^0_m$
. Since
![]() $B^0_m$
and
$B^0_m$
and
![]() $B^0_n$
are disjoint, it follows that
$B^0_n$
are disjoint, it follows that
![]() $m=n$
. ▪
$m=n$
. ▪
4 Order-isomorphisms of the arc
 $\boldsymbol{T\setminus \{1\}}$
$\boldsymbol{T\setminus \{1\}}$
Applying Theorem 3.6 we can transfer the Barth–Schneider theorem for the real line to the following analog for the arc
![]() $T\setminus \{1\}$
.
$T\setminus \{1\}$
.
Theorem 4.1 Let
![]() $(A_n,B_n)$
,
$(A_n,B_n)$
,
![]() $n\in {\mathbb N}$
, be countable dense subsets of
$n\in {\mathbb N}$
, be countable dense subsets of
![]() $T\setminus \{1\}$
. Assume that
$T\setminus \{1\}$
. Assume that
![]() $A_n\cap A_m=\emptyset $
and
$A_n\cap A_m=\emptyset $
and
![]() $B_n\cap B_m=\emptyset $
when
$B_n\cap B_m=\emptyset $
when
![]() $n\not =m$
. Let
$n\not =m$
. Let
![]() $g\colon T\to T$
satisfy
$g\colon T\to T$
satisfy
![]() $g(e^{i\theta })=e^{i\beta (\theta )}$
,
$g(e^{i\theta })=e^{i\beta (\theta )}$
,
![]() $0\leq \theta \leq 2\pi $
, where
$0\leq \theta \leq 2\pi $
, where
![]() $\beta \colon [0,2\pi ]\to [0,2\pi ]$
is a
$\beta \colon [0,2\pi ]\to [0,2\pi ]$
is a
![]() $C^1$
bijection such that
$C^1$
bijection such that
![]() $D\beta>0$
and
$D\beta>0$
and
![]() $D\beta (0)=D\beta (2\pi )$
. Let
$D\beta (0)=D\beta (2\pi )$
. Let
![]() $F\subseteq T\setminus \{1\}$
be a finite set so that F is disjoint from each
$F\subseteq T\setminus \{1\}$
be a finite set so that F is disjoint from each
![]() $A_n$
and
$A_n$
and
![]() $g(F)$
is disjoint from each
$g(F)$
is disjoint from each
![]() $B_n$
. Then there is an analytic function
$B_n$
. Then there is an analytic function
![]() $h\colon \mathbb {C}\setminus \{0\}\to \mathbb {C}$
that restricts to an order-preserving bijection of the arc
$h\colon \mathbb {C}\setminus \{0\}\to \mathbb {C}$
that restricts to an order-preserving bijection of the arc
![]() $T\setminus \{1\}$
onto itself and satisfies the following.
$T\setminus \{1\}$
onto itself and satisfies the following.
-
(a)
 $|h(z)-g(z)|<{\varepsilon }$
for
$|h(z)-g(z)|<{\varepsilon }$
for
 $z\in T$
and
$z\in T$
and
 $h(z)=g(z)$
for
$h(z)=g(z)$
for
 $z\in F$
.
$z\in F$
. -
(b)
 $h(A_n)=B_n (n\in {\mathbb N})$
.
$h(A_n)=B_n (n\in {\mathbb N})$
. -
(c)
 $Dh(z)\not =0$
when
$Dh(z)\not =0$
when
 $z\in T$
.
$z\in T$
.
Remark 4.2 (i) It will be apparent from the proof that we can require that
![]() $h(e^{i\theta })=e^{i\alpha (\theta )}$
where
$h(e^{i\theta })=e^{i\alpha (\theta )}$
where
![]() $\alpha \colon [0,2\pi ]\to [0,2\pi ]$
is a bijection which is the restriction of an entire function, and
$\alpha \colon [0,2\pi ]\to [0,2\pi ]$
is a bijection which is the restriction of an entire function, and
![]() $D\alpha (\theta )>0$
and
$D\alpha (\theta )>0$
and
![]() $|D\alpha (\theta )-D\beta (\theta )|<{\varepsilon }$
for
$|D\alpha (\theta )-D\beta (\theta )|<{\varepsilon }$
for
![]() $\theta \in [0,2\pi ]$
.
$\theta \in [0,2\pi ]$
.
(ii) We take the ordering on the arc
![]() $T\setminus \{1\}$
to be counterclockwise. We could replace “order-preserving” by “order-reversing.” In this context,
$T\setminus \{1\}$
to be counterclockwise. We could replace “order-preserving” by “order-reversing.” In this context,
![]() $D\beta>0$
should be replaced by
$D\beta>0$
should be replaced by
![]() $D\beta <0$
. To get the desired conclusion, define
$D\beta <0$
. To get the desired conclusion, define
![]() $\bar {A}_n = \{\bar {z}:z\in A_n\}$
,
$\bar {A}_n = \{\bar {z}:z\in A_n\}$
,
![]() $\bar {F}= \{\bar {z}:z\in F\}$
. Then define
$\bar {F}= \{\bar {z}:z\in F\}$
. Then define
![]() $\tilde {\beta }(\theta ) = \beta (2\pi -\theta )$
,
$\tilde {\beta }(\theta ) = \beta (2\pi -\theta )$
,
![]() $\tilde {g}(z)=g(1/z)=e^{i\tilde {\beta }(\theta )}$
. Note that
$\tilde {g}(z)=g(1/z)=e^{i\tilde {\beta }(\theta )}$
. Note that
![]() $\bar {F}\cap \bar {A}_n = \overline {F\cap A}_n = \emptyset $
and
$\bar {F}\cap \bar {A}_n = \overline {F\cap A}_n = \emptyset $
and
![]() $\tilde {g}(\bar {F})\cap B_n = g(F)\cap B_n=\emptyset $
. From Theorem 4.1, get
$\tilde {g}(\bar {F})\cap B_n = g(F)\cap B_n=\emptyset $
. From Theorem 4.1, get
![]() $\tilde {h}$
satisfying (a)–(c) with respect to
$\tilde {h}$
satisfying (a)–(c) with respect to
![]() $\tilde {g}$
,
$\tilde {g}$
,
![]() $\bar {F}$
, and the pairs
$\bar {F}$
, and the pairs
![]() $(\bar {A}_n,B_n)$
. Then
$(\bar {A}_n,B_n)$
. Then
![]() $h(z)=\tilde {h}(1/z)$
gives the desired order-reversing bijection of the arc
$h(z)=\tilde {h}(1/z)$
gives the desired order-reversing bijection of the arc
![]() $T\setminus \{1\}$
.
$T\setminus \{1\}$
.
(iii) The order-preserving bijection from the arc
![]() $T\setminus \{1\}$
to itself can be replaced by an order-preserving bijection
$T\setminus \{1\}$
to itself can be replaced by an order-preserving bijection
![]() $T\setminus \{p\}\to T\setminus \{q\}$
(where
$T\setminus \{p\}\to T\setminus \{q\}$
(where
![]() $p\in T\setminus A_n$
,
$p\in T\setminus A_n$
,
![]() $q\in T\setminus B_n$
) by considering the rotated sets
$q\in T\setminus B_n$
) by considering the rotated sets
![]() $\bar {p}A_n$
and
$\bar {p}A_n$
and
![]() $\bar {q}B_n$
.
$\bar {q}B_n$
.
Proof Define
![]() $F'=\{0\}\cup \{\theta \in (0,2\pi ):e^{i\theta }\in F\}$
, and define
$F'=\{0\}\cup \{\theta \in (0,2\pi ):e^{i\theta }\in F\}$
, and define
The assumption on
![]() $\beta $
ensures that it extends to a
$\beta $
ensures that it extends to a
![]() $C^1$
function on
$C^1$
function on
![]() $\mathbb {R}$
satisfying
$\mathbb {R}$
satisfying
![]() ${\sigma }\beta =\beta {\sigma }$
. The sets
${\sigma }\beta =\beta {\sigma }$
. The sets
![]() $A^{\prime }_n$
,
$A^{\prime }_n$
,
![]() $B^{\prime }_n$
are countable, dense, and invariant under translation by
$B^{\prime }_n$
are countable, dense, and invariant under translation by
![]() $t=2\pi $
. The
$t=2\pi $
. The
![]() $A^{\prime }_n$
are pairwise disjoint, as are the
$A^{\prime }_n$
are pairwise disjoint, as are the
![]() $B^{\prime }_n$
, and the conditions
$B^{\prime }_n$
, and the conditions
![]() $F\cap A_n=\emptyset $
,
$F\cap A_n=\emptyset $
,
![]() $g(F)\cap B_n=\emptyset $
,
$g(F)\cap B_n=\emptyset $
,
![]() $1\notin A_n,B_n$
imply the conditions
$1\notin A_n,B_n$
imply the conditions
![]() $F'\cap A^{\prime }_n=\emptyset $
,
$F'\cap A^{\prime }_n=\emptyset $
,
![]() $\beta (F')\cap B^{\prime }_n=\emptyset $
. Choose
$\beta (F')\cap B^{\prime }_n=\emptyset $
. Choose
![]() $\delta>0$
so that
$\delta>0$
so that
![]() $D\beta (\theta )>\delta $
,
$D\beta (\theta )>\delta $
,
![]() $\theta \in \mathbb {R}$
, and
$\theta \in \mathbb {R}$
, and
![]() $|\theta _1-\theta _2|<\delta $
implies
$|\theta _1-\theta _2|<\delta $
implies
![]() $|e^{i\theta _1} - e^{i\theta _2}|<{\varepsilon }$
. Apply Theorem 3.6 to get an entire function
$|e^{i\theta _1} - e^{i\theta _2}|<{\varepsilon }$
. Apply Theorem 3.6 to get an entire function
![]() $\alpha $
such that such that
$\alpha $
such that such that
![]() $\alpha (\mathbb {R})\subseteq \mathbb {R}$
,
$\alpha (\mathbb {R})\subseteq \mathbb {R}$
,
![]() $\alpha {\sigma }={\sigma } \alpha $
, and
$\alpha {\sigma }={\sigma } \alpha $
, and
-
(i)
 $|\alpha (\theta )-\beta (\theta )|<\delta $
for
$|\alpha (\theta )-\beta (\theta )|<\delta $
for
 $\theta \in \mathbb {R}$
and
$\theta \in \mathbb {R}$
and
 $\alpha (\theta )=\beta (\theta )$
for
$\alpha (\theta )=\beta (\theta )$
for
 $\theta \in F'$
.
$\theta \in F'$
. -
(ii)
 $|D\alpha (\theta )-D\beta (\theta )|<\delta $
for
$|D\alpha (\theta )-D\beta (\theta )|<\delta $
for
 $\theta \in \mathbb {R}$
.
$\theta \in \mathbb {R}$
. -
(iii)
 $\alpha (A^{\prime }_n)=B^{\prime }_n (n\in {\mathbb N})$
.
$\alpha (A^{\prime }_n)=B^{\prime }_n (n\in {\mathbb N})$
. -
(iv)
 $D\alpha>0$
.
$D\alpha>0$
.
(Note that (iv) follows from (ii) and the choice of
![]() $\delta $
.) From (i) we get
$\delta $
.) From (i) we get
![]() $\alpha (0)=\beta (0)=0$
. For the function
$\alpha (0)=\beta (0)=0$
. For the function
![]() $\gamma (z)=\alpha (z)-z$
we have
$\gamma (z)=\alpha (z)-z$
we have
![]() $\gamma (z+2\pi )=\gamma (z)$
,
$\gamma (z+2\pi )=\gamma (z)$
,
![]() $\alpha (z)=z+\gamma (z)$
. Consider the branches of
$\alpha (z)=z+\gamma (z)$
. Consider the branches of
![]() $\log $
$\log $
We have
![]() $\operatorname {Log} z = \log z$
when
$\operatorname {Log} z = \log z$
when
![]() $\operatorname {Im} z> 0$
and
$\operatorname {Im} z> 0$
and
![]() $\log z = \operatorname {Log} z + 2\pi i$
when
$\log z = \operatorname {Log} z + 2\pi i$
when
![]() $\operatorname {Im} z < 0$
. By the periodicity of
$\operatorname {Im} z < 0$
. By the periodicity of
![]() $\gamma $
we have
$\gamma $
we have
Define
for
![]() $z\not =0$
not a positive real number. We have
$z\not =0$
not a positive real number. We have
Similarly, if we set
![]() $H(z)=e^{i\alpha (-i\operatorname {Log} z)}$
when
$H(z)=e^{i\alpha (-i\operatorname {Log} z)}$
when
![]() $z\not =0$
is not a negative real number, we get
$z\not =0$
is not a negative real number, we get
![]() $H(z) = ze^{i\gamma (-i\operatorname {Log} z)}$
, and by (4.1),
$H(z) = ze^{i\gamma (-i\operatorname {Log} z)}$
, and by (4.1),
![]() $h(z)=H(z)$
for
$h(z)=H(z)$
for
![]() $\operatorname {Im} z\not =0$
. Thus, h extends to an analytic function defined on
$\operatorname {Im} z\not =0$
. Thus, h extends to an analytic function defined on
![]() $\mathbb {C}\setminus \{0\}$
by setting
$\mathbb {C}\setminus \{0\}$
by setting
![]() $h(z)=H(z)$
when z is a positive real number.
$h(z)=H(z)$
when z is a positive real number.
When
![]() $z=e^{i\theta }$
,
$z=e^{i\theta }$
,
![]() $0<\theta <2\pi $
, we have
$0<\theta <2\pi $
, we have
![]() $-i\log z = \theta $
, so
$-i\log z = \theta $
, so
![]() $h(z)=e^{i\alpha (\theta )}$
. As
$h(z)=e^{i\alpha (\theta )}$
. As
![]() $\theta $
runs over
$\theta $
runs over
![]() $(0,2\pi )$
from
$(0,2\pi )$
from
![]() $0$
to
$0$
to
![]() $2\pi $
,
$2\pi $
,
![]() $\alpha (\theta )$
does the same since
$\alpha (\theta )$
does the same since
![]() $\alpha (0)=0$
and
$\alpha (0)=0$
and
![]() $\alpha (2\pi ) = \alpha (0)+2\pi =2\pi $
, so
$\alpha (2\pi ) = \alpha (0)+2\pi =2\pi $
, so
![]() $h(z)=h(e^{i\theta })=e^{i\alpha (\theta )}$
runs over the arc
$h(z)=h(e^{i\theta })=e^{i\alpha (\theta )}$
runs over the arc
![]() $T\setminus \{1\}$
counterclockwise from
$T\setminus \{1\}$
counterclockwise from
![]() $1$
to
$1$
to
![]() $1$
. From (i) and the choice of
$1$
. From (i) and the choice of
![]() $\delta $
we get
$\delta $
we get
and this implies the first part of (a). If
![]() $\theta \in F'$
then
$\theta \in F'$
then
![]() $h(e^{i\theta }) = e^{i\alpha (\theta )} = e^{i\beta (\theta )} = g(e^{i\theta })$
and this implies the second part of (a).
$h(e^{i\theta }) = e^{i\alpha (\theta )} = e^{i\beta (\theta )} = g(e^{i\theta })$
and this implies the second part of (a).
Also, for
![]() $0<\theta <2\pi $
and
$0<\theta <2\pi $
and
![]() $n\in {\mathbb N}$
,
$n\in {\mathbb N}$
,
so that for
![]() $z\in T\setminus \{1\}$
, we have
$z\in T\setminus \{1\}$
, we have
![]() $z\in A_n$
if and only if
$z\in A_n$
if and only if
![]() $h(z)\in B_n$
. Hence h restricts to an order-isomorphism of
$h(z)\in B_n$
. Hence h restricts to an order-isomorphism of
![]() $T\setminus \{1\}$
mapping
$T\setminus \{1\}$
mapping
![]() $A_n$
onto
$A_n$
onto
![]() $B_n$
.
$B_n$
.
There remains to verify that
![]() $Dh(z)\not =0$
when
$Dh(z)\not =0$
when
![]() $|z|=1$
. When
$|z|=1$
. When
![]() $|z|=1$
,
$|z|=1$
,
![]() $z\not =1$
, we have
$z\not =1$
, we have
which is nonzero since
![]() $-i\log z$
is real when
$-i\log z$
is real when
![]() $|z|=1$
and
$|z|=1$
and
![]() $D\alpha (\theta )\not =0$
for
$D\alpha (\theta )\not =0$
for
![]() $\theta \in \mathbb {R}$
. Writing
$\theta \in \mathbb {R}$
. Writing
![]() $\operatorname {Log}$
instead of
$\operatorname {Log}$
instead of
![]() $\log $
we have the analogous computation when
$\log $
we have the analogous computation when
![]() $|z|=1$
,
$|z|=1$
,
![]() $z\not =-1$
. ▪
$z\not =-1$
. ▪
Acknowledgment
The author thanks P. M. Gauthier for suggesting the problem and for helpful correspondence. The author also thanks the referee for a very careful reading of the paper and helpful suggestions for improving it.