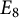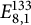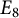Tits in [Reference Tits24] proposed a general construction of exceptional Lie algebras over an arbitrary field of characteristic not 2 or 3, now called the Tits construction. The inputs are an alternative algebra and a Jordan algebra, and the result is a simple Lie algebra of type
$F_4$
,
$E_6$
,
$E_7$
, or
$E_8$
, depending on the dimensions of the algebras. The construction produces, say, all real forms of the exceptional Lie algebras, and a natural question is if all Tits indices can be obtained this way. Garibaldi and Petersson in [Reference Garibaldi and Petersson12] showed that it is not the case for type
$E_6$
, namely that Lie algebras of Tits index
${}^2E_{6,1}^{35}$
do not appear as a result of the Tits construction. We show a similar result for type
$E_8$
, namely that Lie algebras of Tits index
$E_{8,1}^{133}$
cannot be obtained by means of the Tits construction, provided that the base field has no odd degree extensions. The proof uses the theory of symmetric spaces and the first author’s result with Semenov and Garibaldi about isotropy of groups of type
$E_7$
in terms of the Rost invariant [Reference Garibaldi, Petrov and Semenov13].
We prefer to use a more symmetric version of Tits construction due to Allison and Faulkner. Here, the input is a so-called structurable algebra with an involution (say, the tensor product of two octonion algebras) and three constants. The Lie algebra is given by some Chevalley-like relations. The Tits construction and the Allison–Faulkner construction have a large overlap but, strictly speaking, neither one is more general than the other. The Tits construction is capable of producing Lie algebras of type
$E_8$
whose Rost invariant has a nonzero three-torsion part (necessarily using a Jordan division algebra as input), but the Allison–Faulkner construction of
$E_8$
cannot do this—at least when the input is a form of the tensor product of two octonion algebras, because these can always be split by a two-extension of the base field. On the other hand, the Allison–Faulkner construction is capable of producing Lie algebras of type
$E_8$
with the property that the two-torsion part of their Rost invariant has symbol length 3, and this is impossible for the Tits construction (see [Reference Garibaldi, Baeza, Chan, Hoffmann and Schulze-Pillot8, 11.6]). An
$E_8$
with this property would necessarily come from what we call an indecomposable bi-octonion algebra, and these are related to some unusual examples of 14-dimensional quadratic forms discovered by Izhboldin and Karpenko [Reference Izhboldin and Karpenko16].
We produce two new cohomological invariants, one in degree
$6$
and one in degree
$8$
, and show that these invariants can be used to detect the isotropy rank of either the Tits or the Allison–Faulkner construction (but unlike the results of [Reference Garibaldi and Petersson12] for groups of type
$E_6$
, we give necessary conditions only). The main tool for constructing these invariants is a calculation of the Killing form of an Allison–Faulkner construction which, under a mild condition on the base field, is near to an eight-Pfister form (a so-called Pfister neighbour).
We are grateful to the referee for many comments on the exposition, especially for stating Lemma 3.2.
1 Preliminaries
Let K be a field of characteristic not 2 or 3. If q is a quadratic form, we write
$q(x,y) = q(x+y)-q(x)-q(y)$
for the associated symmetric bilinear form. Conversely, if b is a symmetric bilinear form, then
$q(x) = \frac {1}{2}b(x,x)$
is the associated quadratic form. This convention agrees with [Reference Springer and Veldkamp22] but differs from, say, [Reference Jacobson17, Section VII.6]. If A is an algebra and
$a \in A$
, we denote by
$L_a, R_a \in \operatorname {\textrm {End}}(A)$
the left- and right-multiplication operators, respectively.
1.1 Bi-octonion algebras
A K-algebra with involution
$(A,-)$
is called a decomposable bi-octonion algebra if it has two octonion subalgebras
$C_1$
and
$C_2$
that are stabilised by the involution, such that
$A = C_1 \otimes _K C_2$
. A bi-octonion algebra is an algebra with involution
$(A,-)$
that becomes isomorphic to a decomposable bi-octonion algebra over some field extension. These are important examples of central simple structurable algebras, as defined by Allison in [Reference Allison1], and they are instrumental in constructing Lie algebras of type
$E_8$
(see Section 1.5).
Any bi-octonion algebra
$(A,-)$
is either decomposable or it decomposes over a unique quadratic field extension
$E/K$
. In the latter case, there exists an octonion algebra C over E, unique up to K-isomorphism, from which
$(A,-)$
can be reconstructed as follows. Let
$\iota $
be the nonidentity automorphism of
$E/K$
, and let
${}^\iota C$
be a copy of C as a K-algebra, but with a different E-algebra structure given by
$e \cdot z = \iota (e)z$
. Then
$(A,-)$
is precisely the fixed point set of
${}^\iota C \otimes _E C$
under the K-automorphism
$x \otimes y \mapsto y \otimes x$
, with the involution being the restriction of the tensor product of the canonical involutions on
$^\iota C$
and C [Reference Allison2, Theorem 2.1]. We denote this algebra by
$(A,-) = N_{E/K}(C)$
.
To unify the description of both decomposable and nondecomposable bi-octonion algebras, if we consider
$C=C_1 \times C_2$
as an octonion algebra over the split quadratic étale extension
$K\times K$
, then
$N_{K\times K/K}(C)$
as defined above is just isomorphic to
$C_1\otimes _K C_2$
.
1.2 Additive and multiplicative transfer of quadratic forms
Let
$E/K$
be a quadratic étale extension and
$(q,V)$
an n-dimensional quadratic space over E. The additive transfer of
$(q,V)$
(also known as the trace or Scharlau transfer) is the
$2n$
-dimensional K-quadratic space
$(\operatorname {\textrm {tr}}_{E/K}(q),V)$
defined by
$\operatorname {\textrm {tr}}_{E/K}(q)(v) = \operatorname {\textrm {tr}}_{E/K}(q(v))$
for all
$v \in V$
.
Rost defined a multiplicative transfer for quadratic forms, and it has been studied by him and his students (e.g., in [Reference Rost18, Reference Wittkop26]) and used before to define cohomological invariants. The multiplicative transfer also appeared (independently, it seems) in an old paper of Tignol [Reference Tignol23].
If
$(q,V)$
is an n-dimensional quadratic space over a quadratic étale extension
$E/K$
, one defines the quadratic space
$({}^\iota q,{}^\iota V)$
where
$\iota $
is the nontrivial automorphism of
$E/K$
,
$^{\iota } V$
is a copy of V as a K-vector space but with the action of E modified by
$\iota $
, and
$^\iota q (v) = \iota (q(v))$
. The multiplicative transfer
$N_{E/K}(q)$
of q is the
$n^2$
-dimensional K-quadratic form obtained by restricting
${^\iota }q\otimes _E q$
to the K-subspace of tensors in
${^\iota V} \otimes _E V$
fixed by the switch map
$x \otimes y \mapsto y \otimes x$
.
In the case of a split quadratic étale extension, a quadratic form over
$K\times K$
is just a pair
$(q_1, q_2)$
where
$q_1, q_2$
are quadratic forms over K of the same dimension, and we have
$\operatorname {\textrm {tr}}_{E/K}(q_1, q_2) = q_1 \perp q_2$
and
$N_{K\times K/K}(q_1, q_2) = q_1 \otimes q_2$
.
Lemma 1.1 Let
$(A,-) = N_{E/K}(C)$
for an octonion algebra C over a quadratic étale extension
$E/K$
, and let n be the norm of C. Then
$N_{E/K}(n)$
equals the normalised trace form
$(x,y) \mapsto \frac {1}{64}\operatorname {\textrm {tr}}(L_{x \bar y + y \bar x})$
.
Proof Both
$N_{E/K}(n)$
and the normalised trace form are invariant symmetric bilinear forms on
$(A,-)$
in the sense that Allison defined (see [Reference Allison1, Theorem 17] and [Reference Allison2, Proposition 2.2]). By a theorem of Schafer [Reference Schafer19], a central simple structurable algebra has at most one such bilinear form, up to a scalar multiple. (As discussed in [Reference Schafer19, pp. 116–117], these facts are valid in characteristic 0 or
$p \ge 5$
, despite some of the original references being limited to characteristic 0.)▪
1.3 Lie-related triples
Let
$(A,-)$
be a central simple structurable algebra over K. A Lie related triple (in the sense of [Reference Allison and Faulkner4, Section 3]) is a triple
$T = (T_1, T_2, T_3)$
where
$T_i \in \operatorname {\textrm {End}}(A)$
and
$$\begin{align*}\overline{T_i\big(\ \overline{xy}\ \big)} = T_j(x)y + xT_k(t)\\[-15pt] \end{align*}$$
for all
$x, y \in A$
and all
$(i\ j\ k)$
that are cyclic permutations of
$(1\ 2\ 3)$
. Define
$\mathcal {T}$
to be the Lie subalgebra of
$\mathfrak {gl}(A) \times \mathfrak {gl}(A) \times \mathfrak {gl}(A)$
spanned by the set of related triples.
For
$a, b \in A$
and
$1 \le i \le 3$
, define
$$\begin{align*}T_{a,b}^{i} = (T_1, T_2, T_3),\\[-15pt] \end{align*}$$
where (taking indices mod 3):
$$ \begin{align*} T_i & = L_{\bar b} L_a - L_{\bar a } L_b,\\ T_{i+1} &= R_{\bar b} R_a - R_{\bar a} R_b, \\ T_{i+2} &= R_{\bar a b - \bar b a} + L_{b}L_{\bar a} - L_a L_{\bar b}. \end{align*} $$
Let
$\mathcal {T}_I$
be the subspace of
$\operatorname {\textrm {End}}(A)^3$
spanned by
$\{T_{a,b}^i \mid a, b \in A, 1 \le i \le 3\}$
. Since
$(A,-)$
is structurable,
$\mathcal {T}_I$
is a Lie subalgebra of
$\mathcal {T}$
[Reference Allison and Faulkner4, Lemma 5.4]. Finally, denote by
$\operatorname {\textrm {Skew}}(A,-)\subset A$
the
$(-1)$
-eigenspace of the involution, and let
$\mathcal {T}'$
be the subspace of
$\operatorname {\textrm {End}}(A)^3$
spanned by triples of the form
$$ \begin{align} (D,D,D) + (L_{s_2}-R_{s_3}, L_{s_3} -R_{s_1}, L_{s_1} - R_{s_2}), \end{align} $$
where
$D \in \operatorname {\textrm {Der}}(A,-)$
and
$s_i \in \operatorname {\textrm {Skew}}(A,-)$
with
$s_1 + s_2 + s_3 = 0$
.
Example 1.2 Let
$(C,-)$
be an octonion algebra with norm n. The principle of local triality holds in
$\mathcal {T}_I$
in the sense that each of the projections
$\mathcal {T}_I \to \mathfrak {gl}(C)$
,
$(T_1, T_2, T_3) \mapsto T_i$
, for
$1 \le i \le 3$
, is injective [Reference Springer and Veldkamp22, Theorem 3.5.5]. The Lie algebra
$\mathcal {T}_I$
is isomorphic to
$\mathfrak {so}(n)$
[Reference Springer and Veldkamp22, Lemma 3.5.2]. The
$(i+2)$
th entry of the triple
$T_{a,b}^i$
is
$R_{\bar a b - \bar b a} + L_{b}L_{\bar a} - L_a L_{\bar b}$
, and by [Reference Springer and Veldkamp22, pp. 51, 54] this is the map
$C \to C$
that sends
$$ \begin{align} x \mapsto 2n(x,a)b - 2n(x,b)a. \end{align} $$
Proposition 1.3 If
$(A,-)$
is a bi-octonion algebra of the form
$(A,-) = N_{E/K}(C)$
for some quadratic étale extension
$E/K$
and some octonion algebra C over E, then
$\mathcal {T}_I = \mathcal {T}_0 = \mathcal {T}' \simeq \operatorname {\mathrm{Lie}}(R_{E/K}(\mathbf{Spin}(n)))$
, where n is the norm of C.
Proof We have that
$\mathcal {T}_I \subset \mathcal {T} \subset \mathcal {T}'$
and
$\dim \mathcal {T}' = \dim \operatorname {\textrm {Der}}(A,-) + 2 \dim \operatorname {\textrm {Skew}}(A,-) = 28 + 28 = 56$
by [Reference Allison and Faulkner4, Corollary 3.5]. On the other hand,
$\mathcal {T}_I$
(as an E-module) is precisely
$\operatorname {\textrm {Lie}}(\textbf {Spin}(n))$
[Reference Springer and Veldkamp22, Theorem 3.5.5] and so
$\mathcal {T}_I$
(as a K-vector space) is 56-dimensional and isomorphic to
$\operatorname {\textrm {Lie}}(R_{E/K}(\textbf {Spin}(n)))$
.▪
1.4 Local triality
In the context of Proposition 1.3, the Lie algebra
$\mathcal {T}_I$
is of type
$D_4 + D_4$
. Local triality holds here too: the projections
$\mathcal {T}_I \to \mathfrak {gl}(A), (T_1, T_2,T_3) \mapsto T_i$
are injective for any
$1 \le i \le 3$
, and the symmetric group
$S_3$
acts on
$\mathcal {T}_I$
by E-automorphisms, where E is the centroid of
$\mathcal {T}_I$
(compare with [Reference Springer and Veldkamp22, Section 3.5]).
1.5 The Allison–Faulkner construction [Reference Allison and Faulkner4, Section 4]
Let
$(A,-)$
be a central simple structurable algebra and let
$\gamma = (\gamma _1, \gamma _2, \gamma _3) \in K^{\times }\times K^\times \times K^\times $
. For
$1 \le i,j \le 3$
and
$i \ne j$
, define
$A[ij] = \{a[ij] \mid a \in A \}$
to be a copy of A, and identify
$A[ij]$
with
$A[ji]$
by setting
$a[ij] = -\gamma _i \gamma _j^{-1} \overline {a}[ji]$
. Define the vector space
$$\begin{align*}K(A,-,\gamma) = \mathcal{T}_I \oplus A[12] \oplus A[23] \oplus A[31] \end{align*}$$
and equip it with an algebra structure defined by the multiplication:
$$ \begin{align*} [a[ij], b[jk]] &= -[b[jk],a[ij]] = ab[ik],\\ [T, a[ij]] &= - [a[ij],T] = T_k(a)[ij]\\ [a[ij],b[ij]] &= \gamma_i \gamma_j^{-1} T^i_{a,b} \end{align*} $$
for all
$a, b \in A$
,
$T = (T_1, T_2, T_3) \in \mathcal {T}_I$
, and
$(i\ j\ k)$
a cyclic permutation of
$(1\ 2\ 3)$
. Then
$K(A,-,\gamma )$
is clearly a
$\mathbb {Z}/2\mathbb {Z}\times \mathbb {Z}/2\mathbb {Z}$
-graded algebra, and it is in fact a central simple Lie algebra [Reference Allison and Faulkner4, Theorems 4.1, 4.3, 4.4, and 5.5].
1.6 Relation to the Tits–Kantor–Koecher construction
If the quadratic form
$\langle \gamma _1,\gamma _2,\gamma _3 \rangle $
is isotropic then
$K(A,-,\gamma ) \simeq K(A,-)$
where
$$ \begin{align} K(A,-) = \operatorname{\textrm{Skew}}(A) \oplus A \oplus V_{A,A} \oplus A \oplus \operatorname{\textrm{Skew}}(A)\end{align} $$
is the Tits–Kantor–Koecher construction [Reference Allison3, Corollary 4.7]. An isomorphism and its inverse are determined explicitly in [Reference Allison3, Theorem 2.2] in the case where
$-\gamma _1\gamma _2^{-1}$
is a square. More generally, if
$\langle \gamma _1,\gamma _2,\gamma _3 \rangle $
and
$\langle \gamma _1',\gamma _2',\gamma _3'\rangle $
are similar quadratic forms, then
$K(A,-,\gamma ) \simeq K(A,-,\gamma ')$
[Reference Allison3, Proposition 4.1]. In particular, if
$(A,-)$
is a bi-octonion algebra, then
$K(A,-,\gamma )$
is a central simple Lie algebra of type
$E_8$
.
The range of Lie algebras of type
$E_8$
that are of the form
$K(A,-)$
includes those with Tits index
$E_{8}^{91}$
,
$E_{8}^{66}$
,
$E_{8}^{28}$
, or
$E_{8}^0$
, and only those. We formulate a statement to this effect:
Proposition 1.4 Let L be a Lie algebra of type
$E_8$
corresponding to a class
$\varepsilon \in H^1(K, E_8)$
. Then
$L \simeq K(A,-)$
for some bi-octonion algebra
$(A,-)$
if and only if
$\varepsilon $
is in the image of
$H^1(K,\mathbf{Spin}_{14}) \to H^1(K, E_8)$
.
Proof Let
$L = \bigoplus _{i = -2}^2 L_{i}$
be the split
$E_8$
Lie algebra with the
$\mathbb {Z}$
-grading indicated by (1.3). The subalgebra
$L_0$
is reductive of type
$D_7$
; it is generated by a Cartan subalgebra and the root spaces of roots with
$\alpha _1$
-coordinate equal to zero (the dimensions of the components in the
$\mathbb {Z}$
-grading preclude anything else). If
$(A,-)$
is an arbitrary bi-octonion algebra, then
$K(A,-)$
has the same
$\mathbb {Z}$
-grading as L so it must have been twisted by a cocycle coming from
$H^1(K,\textbf {Spin}_{14})$
. This proves the “only if” part of the statement.
For the “if” part of the statement, we prefer to make an argument using the Levi subgroup
$H \subset E_8$
whose Lie algebra is
$L_0$
, rather than its semisimple subgroup
$\textbf {Spin}_{14}$
. Nothing is gained or lost this way, because
$H^1(K, H)$
and
$H^1(K, \textbf {Spin}_{14})$
have the same image in
$H^1(K, E_8)$
; see [Reference Tits25, p. 657]. Specifically, H is the group generated by a maximal torus of
$E_8$
and the root groups
$U_\beta $
where
$\beta $
has
$\alpha _1$
-coordinate equal to zero. It acts faithfully on L by graded automorphisms, its representation on
$L_1$
has a unique open orbit, and this orbit contains 1 (the identity in the split bi-octonions); see [Reference Garibaldi and Guralnick10, p. 547]. The stabilizer of 1 is the automorphism group G of the split bi-octonion algebra [Reference Allison and Hein5, Corollary 8.6]. The map
$H^1(K, G) \to H^1(K, H)$
is surjective by the open orbit theorem from [Reference Garibaldi9, pp. 28–29]. Consequently, any cocycle in the image of
$H^1(K,H) \to H^1(K,E_8)$
is also in the image of the map
$H^1(K,G) \to H^1(K,E_8)$
that sends the class of
$(A,-)$
to the class of
$K(A,-)$
.▪
1.7 Relation to the Tits construction
Tits in [Reference Tits24] defined the following construction of Lie algebras. Let C be an alternative algebra and J be a Jordan algebra. Denote by
$C^\circ $
and
$J^\circ $
the subspaces of elements of generic trace zero and define operations
$\circ $
and bilinear forms
$(-,-)$
on
$C^\circ $
and
$J^\circ $
by the formula
$$ \begin{align*}ab=a\circ b+(a,b)1. \end{align*} $$
Two elements
$a,b$
in J and C define an inner derivation
$\langle a,b\rangle $
of the respective algebra, namely:
$$\begin{align*}\langle a,b \rangle (x) = \tfrac{1}{4}[[a,b],x]- \tfrac{3}{4}[a,b,x]. \end{align*}$$
Then there is a Lie algebra structure on the vector space
$\operatorname {\textrm {Der}}(J)\oplus J^\circ \otimes C^\circ \oplus \operatorname {\textrm {Der}}(C)$
defined by the formulas
$$ \begin{align*} &[\operatorname{\textrm{Der}}(J),\operatorname{\textrm{Der}}(C)]=0;\\ &[B+D,a\otimes c]=B(a)\otimes c+a\otimes D(c);\\ &[a\otimes c,a'\otimes c']=(c,c')\langle a,a'\rangle+(a\circ a')\otimes(c\circ c')+(a,a')\langle c,c'\rangle \end{align*} $$
for all
$B \in \operatorname {\textrm {Der}}(J)$
,
$D \in \operatorname {\textrm {Der}}(C)$
,
$a,a' \in J^\circ $
, and
$c,c' \in C^\circ $
. If
$(A,-) = C_1 \otimes C_2$
is a decomposable bi-octonion algebra, then
$K(A,-,\gamma )$
is isomorphic to the Lie algebra obtained via the Tits construction from the composition algebra
$C_1$
and the reduced Albert algebra
$\mathcal {H}_3(C_2,\gamma )$
[Reference Allison3, Remark 1.9 (c)].
Proposition 1.5 Let
$(A,-) = C_1 \otimes C_2$
be a decomposable bi-octonion algebra. Then
$$\begin{align*}\mathcal{T}_I \oplus A[ij] \simeq \mathfrak{so}(\langle \gamma_i\rangle n_1 \perp \langle -\gamma_j^{-1} \rangle n_2),\end{align*}$$
where
$n_\ell $
is the norm of
$C_\ell $
.
Proof Consider the quadratic form
$Q = \langle \gamma _i \rangle n_1 \perp \langle - \gamma _j^{-1} \rangle n_2$
on the vector space
$C_1 \oplus C_2$
. The Lie algebra
$\mathfrak {so}(Q)$
can be embedded into the Clifford algebra
$C(Q)$
as the subspace spanned by elements of the form
$$ \begin{align*} [u,v]_{c}, &\quad u, v \in C_1 \oplus C_2, \end{align*} $$
where
$[-,-]_c$
denotes the commutator in the Clifford algebra (to avoid confusion with the commutators in
$C_1$
and
$C_2$
). These generators satisfy the relations [Reference Jacobson17, p. 232 (30)]:
$$ \begin{align*} [[u,v]_c,[u',v']_c]_c = &-2Q(u,u')[v,v']_c + 2Q(u,v')[v,u']_c \\&+ 2Q(v,u')[u,v']_c-2Q(v,v')[u,u']_c. \end{align*} $$
If
$z,z' \in C_1$
and
$w,w' \in C_2$
, this becomes
$$ \begin{align} [[z,w]_c,[z',w']_c]_c = -2\gamma_in_1(z,z')[w,w']_c + 2\gamma_j^{-1}n_2(w,w')[z,z']_c. \end{align} $$
This implies that the 64-dimensional subspace spanned by
$$ \begin{align*} [z,w]_c, &\quad z \in C_1, w \in C_2 \end{align*} $$
generates the Lie algebra
$\mathfrak {so}(Q)$
. Now define a linear bijection
$\theta : \mathfrak {so}(Q) \to \mathcal {T}_I \oplus A[ij]$
by
$$ \begin{align*} [z,z']_c &\mapsto \gamma_iT^i_{z,z'},\\ [w,w']_c &\mapsto -\gamma_j^{-1}T^i_{w,w'},\\ [z,w]_c &\mapsto zw[ij] \end{align*} $$
for all
$z,z' \in C_1$
and
$w, w' \in C_2$
. By [Reference Jacobson17, p. 232 (31)] and (1.2), the restriction of
$\theta $
to the subalgebra
$[C_1,C_1]_c \oplus [C_2,C_2]_c\simeq \mathfrak {so}(\langle \gamma _i \rangle n_1)\times \mathfrak {so}(\langle -\gamma _j^{-1} \rangle n_2)$
is a homomorphism.
Now we calculate using (1.4) that
$$ \begin{align} \theta([[z,w]_c,[z',w']_c]_c) &= \theta(-2\gamma_i n_1(z,z')[w,w']_c+2\gamma_j^{-1} n_2(w,w')[z,z']_c) \notag \\ &= -2\gamma_i n_1(z,z') \theta([w,w']_c)+2\gamma_j^{-1} n_2(w,w')\theta([z,z']_c) \notag \\ &= 2\gamma_i\gamma_j^{-1} \big(n_1(z,z') T_{w, w'}^i + n_2(w,w')T^i_{z,z'}\big). \end{align} $$
Meanwhile, we have
$$ \begin{align} [\theta([z,w]_c),\theta([z',w']_c)] = [zw[ij],z'w'[ij]] = \gamma_i\gamma_j^{-1} T_{zw,z'w'}^i. \end{align} $$
To complete the proof that
$\theta $
is an isomorphism, we show that the triples (1.5) and (1.6) are equal. It suffices to compare the ith entries of each triple (by §1.4). After recalling that
$$\begin{align*}L_{x}L_{\overline{x'}} + L_{x'}L_{\overline{x}} = L_{\overline x} L_{x'} + L_{\overline{ x'}}L_x = n_i(x,x') \operatorname{\textrm{id}}\end{align*}$$
for all
$x \in C_\ell $
[Reference Springer and Veldkamp22, Lemma 1.3.3 (iii)], the ith entry of (1.5) is
$$ \begin{align*} &~2\gamma_i\gamma_j^{-1}\big(n_1(z,z')(L_{\overline{w'}}L_w - L_{\overline{w}}L_{w'})+n_2(w,w')(L_{\overline{z'}}L_z - L_{\overline{z}}L_{z'})\big) \\ = &~2\gamma_i\gamma_j^{-1}\big((L_{\overline{z}}L_{z'} + L_{\overline{z'}}L_{{z}})(L_{\overline{w'}}L_w - L_{\overline{w}}L_{w'}) + (L_{\overline{w}}L_{w'} + L_{\overline{w'}}L_{w}) (L_{\overline{z'}}L_z - L_{\overline{z}}L_{z'})\big)\\ =&~2\gamma_i\gamma_j^{-1}(2L_{\overline{z'}}L_zL_{\overline{w'}}L_w - 2 L_{\overline{z}}L_{z'}L_{\overline{w}}L_{w'}) =4 \gamma_i\gamma_j^{-1}(L_{\overline{z'}}L_z L_{\overline{w'}} L_w - L_{\overline{z}}L_{z'}L_{\overline{w}} L_{w'}). \end{align*} $$
In the last line, we have used (multiple times) the fact that
$C_1$
and
$C_2$
commute and associate with each other in A. Using this fact a few more times, the ith entry of (1.6) is just
$$ \begin{align*} 4\gamma_i\gamma_j^{-1}(L_{\overline{z'w'}}L_{zw} - L_{\overline{zw}}L_{z'w'}) &= 4\gamma_i\gamma_j^{-1} (L_{\overline{z'}}L_z L_{\overline{w'}}L_w - L_{\overline{z}}L_{z'}L_{\overline{w}}L_{w'}). \\[-36pt]\end{align*} $$
▪
2 The Killing form of
$K(A,-,\gamma )$
By our convention, the Killing form (as a quadratic form) on a Lie algebra L is the form
$x \mapsto \frac {1}{2}\operatorname {\textrm {tr}}({\operatorname {\textrm {ad}}_x}^2)$
. For any quadratic form
$q = \langle x_1, \dots , x_n\rangle $
, the Killing form of
$\mathfrak {so}(q)$
is
$$ \begin{align} \langle 2-n \rangle \lambda^2(q), \end{align} $$
where
[Reference Garibaldi9, Exercise 19.2].
Lemma 2.1 Let
$A = N_{E/K}(C)$
as before, and let
$\rho _{ij}: R_{E/K}({\mathbf{Spin}}(n)) \to \operatorname {\mathrm{GL}}(A[ij])$
be the representation lifted from the representation of
$\mathcal {T}_I$
in
$A[ij]$
. Every quadratic form q on A invariant under this action of
$R_{E/K}({\mathbf{Spin}}(n))$
is a scalar multiple of the multiplicative transfer
$N_{E/K}(n)$
(equivalently, a scalar multiple of the trace form
$(x,y)\mapsto \operatorname {\textrm {tr}}(L_{x \bar y +y \bar x})$
).
Proof We can extend scalars from K to E, and then
$q_E$
is a quadratic form on
$A_E = C \otimes _E {{}^\iota C}$
which is invariant under the action of
$R_{E/K}(\textbf {Spin}(n))\times _K E = \textbf {Spin}(n) \times \textbf {Spin}({}^{\iota } n)$
. Then clearly
$q_E$
decomposes as
$q_1 \otimes q_2$
for some
$\textbf {Spin}(n)$
-invariant form
$q_1$
on C and some
$\textbf {Spin}({{}^\iota n})$
-invariant form
$q_2$
on
${{}^\iota C}$
. This implies
$q_1 \simeq \langle \lambda _1 \rangle n$
and
$q_2 \simeq \langle \lambda _2 \rangle {{}^\iota n}$
for certain scalars
$\lambda _i \in E^\times $
, and therefore,
$q_E = \langle \lambda _1\lambda _2 \rangle n \otimes {{}^\iota n}$
. However, since
$(q_E, A_E)$
is extended from
$(q,A)$
and
$n\otimes {{}^\iota n}(1\otimes 1) =1$
, we have
$\lambda _1 \lambda _2 \in K^\times $
. Therefore,
$q = q_E|_A = \langle \lambda _1 \lambda _2 \rangle N_{E/K}(n)$
.▪
We can now calculate the Killing form of
$K(A,-,\gamma )$
in the case where
$(A,-)$
is a bi-octonion algebra.
Proposition 2.2 If
$(A,-)=N_{E/K}(C)$
, then the Killing form on
$K(A,-,\gamma )$
is
$$ \begin{align} \langle-30\rangle\big(\operatorname{\textrm{tr}}_{E/K}(\lambda^2(n)) \perp\langle \gamma_1\gamma_2^{-1},\gamma_2\gamma_3^{-1},\gamma_3\gamma_1^{-1} \rangle N_{E/K}(n)\big). \end{align} $$
Proof Let
$\kappa $
be the Killing form of
$K(A,-,\gamma )$
. If
$x, y \in K(A,-,\gamma )$
are from different homogeneous components in the
$\mathbb {Z}/2\mathbb {Z}\times \mathbb {Z}/2\mathbb {Z}$
-grading, then
$\operatorname {\textrm {ad}}_x \operatorname {\textrm {ad}}_y$
shifts the grading and consequently
$\kappa (x,y) =\operatorname {\textrm {tr}}(\operatorname {\textrm {ad}}_x \operatorname {\textrm {ad}}_y) = 0$
.
Let
$\tau $
be the Killing form of
$\mathcal {T}_I$
. The Killing form of
$\operatorname {\textrm {Lie}}(\textbf {Spin}(n))$
is
$\langle -6 \rangle \lambda ^2(n)$
; see (2.1). Since
$\mathcal {T}_I \simeq \operatorname {\textrm {Lie}}(R_{E/K}(\textbf {Spin}(n))$
by Proposition 1.3, we have
$$\begin{align*}\tau = \operatorname{\textrm{tr}}_{E/K}(\langle -6 \rangle \lambda^2(n)) = \langle-6\rangle \operatorname{\textrm{tr}}_{E/K}(\lambda^2(n)).\end{align*}$$
There is an automorphism of
$K(A,-,\gamma )\otimes _K K^{\textrm {alg}}$
that swaps the two simple subalgebras of
$\mathcal {T}_I\otimes _K K^{\textrm {alg}}$
, and this implies
$\kappa |_{\mathcal {T}_I}$
is a scalar multiple of
$\tau $
; say
$\kappa |_{\mathcal {T}_I} = \langle \phi _0\rangle \langle -6 \rangle \operatorname {\textrm {tr}}_{E/K}(\lambda ^2(n))$
for some
$\phi _0\in K^\times $
.
Let us determine
$\phi _0$
. The grading on
$K(A,-,\gamma )$
makes it a sum of four
$\mathcal {T}_I$
-modules. For
$T, S \in \mathcal {T}_I$
and
$a \in A$
,
$$\begin{align*}[T,[S,a[ij]]] = T_k(S_k(a))[ij]. \end{align*}$$
Therefore,
$$\begin{align*}\kappa(T,S) = \operatorname{\textrm{tr}}(\operatorname{\textrm{ad}}_T \operatorname{\textrm{ad}}_S) = \tau(T,S)+ \operatorname{\textrm{tr}}(T_1S_1) + \operatorname{\textrm{tr}}(T_2S_2)+\operatorname{\textrm{tr}}(T_3S_3).\end{align*}$$
The trace forms of the irreducible representations
$\mathcal {T}_I \to \mathfrak {gl}(A)$
,
$T \mapsto T_\ell $
for
$1 \le \ell \le 3$
are all equal (despite them being inequivalent representations) and so
$\operatorname {\textrm {tr}}(T_1S_1) = \operatorname {\textrm {tr}}(T_2S_2) = \operatorname {\textrm {tr}}(T_3S_3)$
for all
$T,S \in \mathcal {T}_I$
. Moreover,
$\operatorname {\textrm {tr}}(T_1S_1)$
is a scalar multiple of
$\tau (T,S)$
.
To determine the ratio between
$\operatorname {\textrm {tr}}(T_1 S_1)$
and
$\tau (T,S)$
, we can assume
$A = C_1 \otimes C_2$
is decomposable, and consider the subalgebra
$\mathfrak {so}(n_1)\subset \mathfrak {so}(n_1)\times \mathfrak {so}(n_2) \simeq \operatorname {\textrm {Lie}}(R_{E/K}(\textbf {Spin}(n))$
, where
$n_\ell $
is the norm on
$C_\ell $
. It is well-known that the Killing form
$\kappa _1$
on
$\mathfrak {so}(n_1)$
is
$6\ (=8-2)$
times the trace form of its vector representation
$\mathfrak {so}(n_1)\to \mathfrak {gl}(C_1)$
, while the trace form of the representation
$\mathfrak {so}(n_1) \to \mathfrak {gl}(C_1\otimes C_2)$
is clearly eight times the trace form of the vector representation. But
$\kappa _1$
is equal to the restriction of the Killing form
$\tau $
on
$\mathfrak {so}(n_1)\times \mathfrak {so}(n_2)$
, so this means that (if
$T \in \mathcal {T}_I$
belongs to the
$\mathfrak {so}(n_1)$
subalgebra) we have
$\operatorname {\textrm {tr}}(T_1^2) = 8\operatorname {\textrm {tr}}({T_1|_{C_1}}^2) = \frac {8}{6}\kappa _1(T) = \frac {8}{6}\tau (T)$
. In conclusion,
$\phi _0 =5$
, so
$\kappa |_{\mathcal {T}_I} = \langle -30\rangle \operatorname {\textrm {tr}}_{E/K}(\lambda ^2(n))$
.
The restriction
$\kappa |_{A[ij]}$
is an invariant form under the action of
$R_{E/K}(\textbf {Spin}(n))$
, which means it is proportional to
$N_{E/K}(n)$
, by Lemma 2.1. Say
$\kappa |_{A[ij]} = \langle \phi _{ij}\rangle N_{E/K}(n)$
. To determine the
$\phi _{ij}$
, it suffices to calculate
$\kappa (1[ij])$
, since
$\kappa (1[ij]) = \phi _{ij}N_{E/K}(n)(1)= \phi _{ij}$
. By definition
$\kappa (1[ij])$
is half the trace of
${\operatorname {\textrm {ad}}_{1[ij]}}^2$
. The graded components of
$K(A,-,\gamma )$
are invariant under
${\operatorname {\textrm {ad}}_{1[ij]}}^2$
, so we work out the trace separately for each of these components.
For all
$b \in A$
, we have
$$ \begin{align*} [1[ij],[1[ij],b[jk]]] &= [1[ij],b[ik]] = -\gamma_i\gamma_j^{-1}[1[ji],b[ik]] = -\gamma_i\gamma_j^{-1}b[jk], \end{align*} $$
so
${\operatorname {\textrm {ad}}_{1[ij]}}^2|_{A[jk]} = -\gamma _i\gamma _j^{-1}\operatorname {\textrm {id}}$
, and
$\operatorname {\textrm {tr}}({\operatorname {\textrm {ad}}_{1[ij]}}^2|_{A[jk]}) = -64\gamma _i\gamma _j^{-1}$
. Similarly, for all
$b \in A$
,
$$ \begin{align*} [1[ij],[1[ij],b[ki]]] &= (-\gamma_i\gamma_j^{-1})(-\gamma_k\gamma_i^{-1})[1[ij],[1[ji],\bar{b}[ik]]] \\&= (-\gamma_i\gamma_j^{-1})(-\gamma_k\gamma_i^{-1})[1[ij],\bar{b}[jk]] \\ &= (-\gamma_i\gamma_j^{-1})(-\gamma_k\gamma_i^{-1})[\bar{b}[ik]] = (-\gamma_i\gamma_j^{-1})(-\gamma_k\gamma_i^{-1})(-\gamma_i\gamma_k^{-1})b[ki]\\ &= -\gamma_i\gamma_j^{-1}b[ki], \end{align*} $$
so
${\operatorname {\textrm {ad}}_{1[ij]}}^2|_{A[ki]} = -\gamma _i \gamma _j^{-1}\operatorname {\textrm {id}}$
, and
$\operatorname {\textrm {tr}}({\operatorname {\textrm {ad}}_{1[ij]}}^2|_{A[ki]}) = -64\gamma _i\gamma _j^{-1}$
. In contrast, for all
$b \in A$
,
$$ \begin{align*} [1[ij],[1[ij],b[ij]]] &= [1[ij],\gamma_i\gamma_j^{-1}T_{1,b}^i] = -\gamma_i\gamma_j^{-1}(T_{1,b}^i)_k(1)\\ &= -\gamma_i\gamma_j^{-1}(R_{b-\bar b}+L_b-L_{\bar b})(1) = -2\gamma_i\gamma_j^{-1}(b-\bar b). \end{align*} $$
Therefore,
${\operatorname {\textrm {ad}}_{1[ij]}}^2|_{A[ij]}$
has a 50-dimensional kernel
$\{a[ij] \mid \bar a =a \}$
and a 14-dimensional eigenspace
$\{a[ij] \mid \bar a = -a \}$
with eigenvalue
$-4\gamma _i\gamma _j^{-1}$
. This proves that
$\operatorname {\textrm {tr}}({\operatorname {\textrm {ad}}_{1[ij]}}^2|_{A[ij]}) = -56\gamma _i\gamma _j^{-1}$
.
Now if
$T = (T_1, T_2, T_3) \in \mathcal {T}_I$
, then
$$\begin{align*}[1[ij], [1[ij],T]] = [1[ij],-T_k(1)[ij]] = -\gamma_i\gamma_j^{-1} T^i_{1,T_k(1)}. \end{align*}$$
We can use (1.1) to write
$T = (D,D,D) + (L_{s_2}-R_{s_3}, L_{s_3}-R_{s_1}, L_{s_1} - R_{s_2})$
for some unique
$D \in \operatorname {\textrm {Der}}(A,-)$
and
$s_i \in \operatorname {\textrm {Skew}}(A,-)$
such that
$s_1 + s_2 + s_3 = 0$
. Note that the kth entry of T is
$L_{s_i}-R_{s_j}$
. Then
$T_k(1) = D(1) + L_{s_i}(1)-R_{s_j}(1) = s_i - s_j$
, so
${\operatorname {\textrm {ad}}_{1[ij]}}^2(T) = -\gamma _i\gamma _j^{-1}T^i_{1,T_k(1)}$
is the triple whose kth entry is
$$ \begin{align*} -\gamma_i\gamma_j^{-1} (R_{1T_k(1) - \overline{T_k(1)}1} + L_{T_k(1)}L_1 - L_1L_{\overline{T_k(1)}}) &= -\gamma_i\gamma_j^{-1}(R_{2(s_i-s_j)}+L_{2(s_i-s_j)}) \\&= -2\gamma_i\gamma_j^{-1}\big((L_{s_i}-R_{s_j}) - (L_{s_j}-R_{s_i})\big). \end{align*} $$
This shows
$\ker ({\operatorname {\textrm {ad}}_{1[ij]}}^2|_{\mathcal {T}_I})$
is the 42-dimensional subspace of
$\mathcal {T}_I$
whose kth projection is
$$\begin{align*}\{D + L_s - R_s \mid D \in \operatorname{\textrm{Der}}(A,-), s \in \operatorname{\textrm{Skew}}(A,-)\}. \end{align*}$$
And the subspace of
$\mathcal {T}_I$
whose kth projection is
$$\begin{align*}\{L_s + R_s \mid s \in \operatorname{\textrm{Skew}}(A,-)\} \end{align*}$$
is a 14-dimensional eigenspace of
${\operatorname {\textrm {ad}}_{1[ij]}}^2|_{\mathcal {T}_I}$
with eigenvalue
$-4\gamma _i\gamma _j^{-1}$
. This proves that
$\operatorname {\textrm {tr}}({\operatorname {\textrm {ad}}_{1[ij]}}^2|_{\mathcal {T}_I}) = -56\gamma _i\gamma _j^{-1}$
. Therefore,
$$\begin{align*}\phi_{ij} {\,=\,} \kappa(1[ij]) {\,=\,} \tfrac{1}{2}\operatorname{\textrm{tr}}({\operatorname{\textrm{ad}}_{1[ij]}}^2) = -32\gamma_i\gamma_j^{-1} - 32\gamma_i\gamma_j^{-1} -28\gamma_i\gamma_j^{-1} -28\gamma_i\gamma_j^{-1} {\,=\,} -120\gamma_i\gamma_j^{-1}, \end{align*}$$
and we can simplify to get (2.2) because 30 is in the same square class as 120.▪
If
$\operatorname {\textrm {char}}(K) = 5$
, then the Killing form on
$E_8$
is zero. However, if
$(A,-) = N_{E/K}(C)$
then the symmetric bilinear form on
$K(A,-,\gamma )$
associated to
$$ \begin{align} \operatorname{\textrm{tr}}_{E/K}(\lambda^2(n)) \perp\langle \gamma_1\gamma_2^{-1},\gamma_2\gamma_3^{-1},\gamma_3\gamma_1^{-1} \rangle N_{E/K}(n)\end{align} $$
is nondegenerate and Lie invariant. This can be proved in at least two ways: one can factor out
$\langle -30 \rangle $
in the Killing form of the Chevalley Lie algebra of type
$E_8$
defined over
$\mathbb {Z}$
, extend the new bilinear form to the split
$E_8$
over K, and then twist it to get the form (2.3) on
$K(A,-,\gamma )$
. This form is clearly invariant and nondegenerate (its radical is a nonzero ideal and
$E_8$
is a simple Lie algebra in all characteristics). Alternatively, one use the hint from [Reference Garibaldi, Merkurjev and Serre11, Exercise 27.21 (2)]: lift the Killing form of
$K(A,-,\gamma )$
to the ring of Witt vectors, divide by
$-30$
up there, and reduce modulo 5 to get (2.3).
Lemma 2.3 Let
$(A,-) = N_{E/K}(C)$
, and let
$\kappa '$
be a nondegenerate Lie invariant bilinear form on
$K(A,-,\gamma )$
. If
$-1$
is a sum of two squares in K, then
$\kappa ' \in I^6(K)$
and there is a unique
$64$
-dimensional form
$q \in I^6(K)$
such that
$q+ \kappa ' \in I^8(K)$
.
Proof Since
$\kappa '$
is unique up to a scalar multiple, we can assume without loss of generality that
$$\begin{align*}\kappa' = \operatorname{\textrm{tr}}_{E/K}(\lambda^2(n)) \perp\langle \gamma_1\gamma_2^{-1},\gamma_2\gamma_3^{-1},\gamma_3\gamma_1^{-1} \rangle N_{E/K}(n).\end{align*}$$
The assumption that
$-1$
is a sum of two squares is equivalent to the identity
$4 = 0$
in the Witt ring
$W(K)$
. This assumption implies that
$\operatorname {\textrm {tr}}_{E/K}(\lambda ^2(n)) = 0$
[Reference Garibaldi9, Lemma 19.8] and also that
$N_{E/K}(n) \in I^6(K)$
[Reference Rost18, Reference Wittkop26, Satz 2.16 (ii)], hence
$\kappa ' \in I^6(K)$
. Setting
$q = N_{E/K}(n)$
yields
$$\begin{align*}q + \kappa' = \langle 1, \gamma_1\gamma_2^{-1}, \gamma_2\gamma_3^{-1}, \gamma_3\gamma_1^{-1} \rangle N_{E/K}(n) = \langle\!\!\;\!\langle -\gamma_1\gamma_2^{-1}, -\gamma_2\gamma_3^{-1} \rangle\!\!\;\!\rangle N_{E/K}(n) \in I^8(K). \end{align*}$$
The uniqueness of q follows from the Arason–Pfister Hauptsatz.▪
Let
$Q(*) \subset R(*) \subset H^1(*,E_8)$
be the functors
$\mathsf {Fields}_{/K} \to \mathsf {Sets}$
such that for all fields
$F/K$
:
-
(1)
$Q(F)$
is the set of isomorphism classes of Lie algebras of type
$E_8$
that are isomorphic to
$K(A,-,\gamma )$
for some bi-octonion algebra
$(A,-)$
over F and some
$\gamma = (\gamma _1, \gamma _2, \gamma _3) \in (K^\times )^3$
; i.e.
$Q(F)$
is the image of the Allison–Faulkner construction
$$\begin{align*}H^1(F,(G_2\times G_2\rtimes \mathbb{Z}/2\mathbb{Z})\times (\mathbb{Z}/2\mathbb{Z})^3) \to H^1(F,E_8).\end{align*}$$
-
(2)
$R(F)$
is the set of isomorphism classes of Lie algebras L of type
$E_8$
such that the class of L is contained in
$Q(F')$
for some odd-degree extension
$F'/F$
.
Recall from 1.7 that
$Q(*)$
contains all Lie algebras of type
$E_8$
that are obtainable using the Tits construction from a reduced Albert algebra and an octonion algebra. Whereas,
$R(*)$
strictly contains all Lie algebras of type
$E_8$
that are obtainable using the Tits construction from an Albert algebra (even a division algebra) and an octonion algebra. Any cohomological invariant
$Q(*) \to \bigoplus _{i \ge 0} H^i(*,\mathbb {Z}/2\mathbb {Z})$
can be extended uniquely to a cohomological invariant
$R(*) \to \bigoplus _{i \ge 0} H^i(*,\mathbb {Z}/2\mathbb {Z})$
[Reference Garibaldi9, Section 7].
By applying the quadratic form invariants
$e_n: I^n(*) \to H^n(*,\mathbb {Z}/2\mathbb {Z})$
for
$n = 6$
and
$8$
, we obtain cohomological invariants of the Tits construction and the Allison–Faulkner construction.
Corollary 2.4 If
$-1$
is a sum of two squares in K, then there exist nontrivial cohomological invariants
$$ \begin{align*} h_6: R(*) &\to H^6(*,\mathbb{Z}/2\mathbb{Z}),\\ h_8: R(*) &\to H^8(*,\mathbb{Z}/2\mathbb{Z}), \\[-15pt]\end{align*} $$
such that if
$(A,-) = N_{E/F}(C)$
, then
$$ \begin{align*} h_6(K(A,-,\gamma)) &= e_6(N_{E/F}(n)),\\ h_8(K(A,-,\gamma)) &= (-\gamma_1\gamma_2^{-1}) \cup (-\gamma_2\gamma_3^{-1}) \cup e_6(N_{E/F}(n)). \\[-15pt]\end{align*} $$
2.1 Comparison with invariants of
$G_2\times F_4$
Since
$R(K)$
contains the image of the Tits construction
$H^1(K, G_2 \times F_4) \to H^1(K, E_8)$
, there are unique cohomological invariants
$$ \begin{align*}h_i^*: H^1(*, G_2 \times F_4) \to H^i(*,\mathbb{Z}/2\mathbb{Z}) &\quad i = 6,8,\\[-15pt]\end{align*} $$
such that
$h_i^*(C,J) = h_i(L)$
where L is the Lie algebra of type
$E_8$
constructed from the octonion algebra C and Albert algebra J. The cohomological invariants of
$G_2$
and
$F_4$
are classified [Reference Garibaldi, Merkurjev and Serre11]. The unique nontrivial invariant
$e_3$
of
$G_2$
assigns an octonion algebra C to the class
$e_3(C) = (\alpha _1)\cup (\alpha _2) \cup (\alpha _3)$
, where
$\langle \!\!\;\!\langle \alpha _1, \alpha _2, \alpha _3 \rangle \!\!\;\!\rangle $
is the norm of C. The unique nontrivial mod 2 invariants
$f_3, f_5$
of
$F_4$
assign a reduced Jordan algebra
$\mathcal {H}_3(C,\gamma )$
to the classes
$f_3(\mathcal {H}_3(C,\gamma )) = e_3(C)$
and
$f_5(\mathcal {H}_3(C,\gamma )) = (-\gamma _1 \gamma _2^{-1}) \cup (-\gamma _2 \gamma _3^{-1})\cup e_3(C)$
, respectively (see [Reference Garibaldi, Merkurjev and Serre11, Section 22] and [Reference Springer and Veldkamp22, p. 118]). Comparing with Corollary 2.4 and using the fact that
$e_6(N_{K\times K/K}(n_1, n_2)) = e_6(n_1\otimes n_2) = e_3(n_1)\cup e_3(n_2)$
yields
$$\begin{align*}h_i^*(C_1,\mathcal{H}_3(C_2,\gamma)) = h_i(K(C_1 \otimes C_2,-,\gamma)) = e_3(C_1)\cup f_{i-3}(\mathcal{H}_3(C_2,\gamma))\\[-15pt]\end{align*}$$
for all pairs of octonion algebras
$C_1, C_2$
and scalars
$\gamma _1, \gamma _2, \gamma _3$
. If two invariants with values in
$H^i(*,\mathbb {Z}/2\mathbb {Z})$
agree up to odd-degree extensions, then they are equal, so it follows that
$$ \begin{align*} h_6^*(C,J) &= e_3(C) \cup f_3(J),\\ h_8^*(C,J) &= e_3(C) \cup f_5(J) \end{align*} $$
for all octonion algebras C and Albert algebras J.
3 Isotropy of Tits construction
In this section, we continue to assume that the base field K is of characteristic not
$2$
or
$3$
.
3.1 Generalities on symmetric spaces
We use the basics of the theory of symmetric spaces over arbitrary fields; we refer to [Reference Helminck and Wang15] for the generalities.
Let G be a (connected) split reductive algebraic group over a field K and
$\sigma $
be an involution on G (that is an automorphism of order
$2$
). Then the fixed point subgroup
$H=G^\sigma $
has a reductive connected component
$H^\circ $
; in the case when
$\sigma $
is from
$G(K)$
and the commutator subgroup of G is simply connected, H is connected and has the same rank as G (see [Reference Gille14, Théorème 3.1.5]). We state some facts about its normalizer in the lemma below.
Lemma 3.1
-
(1)
$N_G(H)=N_G(H^\circ )$
; -
(2)
$g\in G$
belongs to
$N_G(H)$
if and only if
$\sigma (g)g^{-1}$
belongs to the center of G; -
(3) If
$\sigma $
is from
$G(K)$
and T is a
$\sigma $
-stable split maximal torus in G, then the map is surjective.
$$ \begin{align*}N_H(T)/T\to H/H^\circ \end{align*} $$
Proof The first two items are from [Reference Helminck and Wang15, Corollary 1.3], and the third is [Reference Gille14, Lemme 3.1.4]. Note that T as above always exists by [Reference Helminck and Wang15, Proposition 2.3].▪
A torus S in G (not necessary maximal) is called
$\sigma $
-split if
$\sigma (t)=t^{-1}$
for all
$t\in S$
. In the particular case
$S=\mathbb {G}_m$
, S defines two opposite parabolic subgroups in G; they are also called
$\sigma $
-split and are characterized by the fact that
$\sigma $
sends a
$\sigma $
-split parabolic subgroup to an opposite parabolic subgroup. Possible types of
$\sigma $
-split maximal parabolic subgroups correspond to the white vertices on the Satake diagram of
$(G,\sigma )$
, see [Reference Springer21, Lemma 2.9 and 2.11].
The quotient variety
$G/H$
is called a symmetric space. It is known to be spherical, that is for any parabolic subgroup P in G, H acts on
$G/P$
with a finite number of orbits. In particular, there is an open orbit; it consists of all
$\sigma $
-split parabolic subgroups of the same type as P (provided they exist).
Let us state a general lemma that will be applied to the case of
$E_8$
below.
Lemma 3.2 Let G be a split adjoint semisimple group over an infinite field K of characteristic not
$2$
,
$H=G^\sigma $
be the fixed point subgroup of an involution
$\sigma $
on G, P be a parabolic subgroup of G, C be the stabilizer of a point from the open orbit of the action of H on
$G/P$
,
$[\xi ]$
be an element from
$H^1(K,G)$
. Assume that the twisted form
${}_\xi G$
contains (over the base field K) a parabolic subgroup
$P'$
of the same type as P and a subgroup
$H'$
that is conjugate to H over a separable closure of K. Then
$[\xi ]$
comes from some
$[\zeta ]\in H^1(K,C)$
such that
${}_\zeta H$
is isomorphic to
$H'$
.
Proof By Lemma 3.1 (ii)
$N_G(H)=H$
, since the center of G is trivial. Note that
$H'$
corresponds to a rational point on
${}_\xi (G/H)$
, and by [Reference Serre20, Proposition 37]
$[\xi ]$
comes from some
$[\xi ']\in H^1(K,N_G(H))$
with
${}_{\xi '}H=H'$
.
Now
${}_\xi (G/P)$
is a smooth compactification of its open subvariety
$U={}_{\xi '}(H/C)$
and by the assumption has a rational point. The unipotent radical of a parabolic subgroup opposite to
$P'$
defines an open subvariety in
${}_\xi (G/P)$
isomorphic to the affine space
${\mathbb A}^N$
for some N. Since the base field is infinite, there is a rational point in
${\mathbb A}^N\cap U$
. Applying [Reference Serre20, Proposition 37] to
${}_{\xi '}(H/C)$
we obtain the claim.▪
3.2
$E_8/P_8$
as a compactification of
$D_8/N(A_7)$
Let G be the split group of type
$E_8$
over K and
$\sigma $
be the involution whose fixed point subgroup is
$D_8$
obtained by erasing vertex
$1$
from the extended Dynkin diagram:
More precisely,
$\sigma $
is the inner automorphism defined by
$\omega _1^\vee (-1)$
, where
$\alpha _i$
are the fundamental roots and
$\omega _j^\vee $
are coweights defined by
$\omega _j^\vee (\alpha _i)=\delta _{ij}$
.
All vertices of the Satake diagram for the symmetric space
$E_8/D_8$
are white; in particular, there is a parabolic subgroup P of type
$P_8$
such that
$\sigma (P)$
is opposite to P. It is not difficult to construct such a parabolic subgroup directly: it is defined by
$S=\mathbb {G}_m$
which is the image of
$\alpha _1^\vee $
in the maximal torus T (note that
$\alpha _1^\vee $
is Weyl-conjugate to
$\omega _8^\vee $
and so it has type
$P_8$
indeed).
Lemma 3.3 The stabilizer of a point from the open orbit of the action of
$D_8$
on
$E_8/P_8$
is
$N(A_7)$
, the normalizer of the maximal subgroup of type
$A_7$
in the simply connected group of type
$E_7$
.
Proof To check the claim we may pass to the algebraic closure of K. The stabilizer of the point corresponding to P is
$L^\sigma $
, where
$L=P\cap \sigma (P)$
. It contains the
$A_7$
subgroup generated by root subgroups corresponding to
$\pm \alpha _2$
,
$\pm \alpha _4,\ldots ,\pm \alpha _8$
and
$\pm \alpha _0$
(where
$\alpha _0$
stands for the negative maximal root). Since
$A_7$
is maximal in the commutator subgroup
$E_7$
of L and L is an almost direct product of
$E_7$
and the
$\sigma $
-split torus S, we see that the connected component of
$L^\sigma $
is
$A_7$
.
It is known (and can be deduced from Lemma 3.1) that
$A_7$
has index
$2$
in
$N(A_7)$
, so it remains to present an element from
$L^\sigma $
not lying in
$A_7$
. Consider any lifting
$\tilde w_0$
of the longest element in the Weyl group of
$E_7$
. Note that
$\tilde w_0$
normalizes
$A_7$
but cannot belong to
$L^\sigma $
, otherwise the fixed point subgroup
$E_7^\sigma $
would be not connected. Lemma 3.1 implies that
$\sigma (\tilde w_0)=\tilde w_0\alpha _1^{\vee }(-1)$
, for the second factor is the only nontrivial element in the center of
$E_7$
. Now
$\tilde w_0\alpha _1^{\vee }(i)$
, where i is a square root of
$-1$
, is an element from
$L^\sigma \cap N(A_7)$
not belonging to
$A_7$
.▪
One can show that
$N(A_7)$
is an extension of
$\mathbb {Z}/2\mathbb {Z}$
by
$\operatorname {\textrm {SL}}_8/\mu _2$
, which is split if and only if
$-1$
is a square in K.
Lemma 3.4 Let
$[\xi ]\in H^1(K,\operatorname {\textrm {PGO}}_{2n})$
be in the image of
$H^1(K,\operatorname {\textrm {GL}}_n/\mu _2\rtimes \mathbb {Z}/2\mathbb {Z})$
. Then there exists a quadratic field extension
$E/K$
such that the orthogonal involution corresponding to
$\xi _E$
is hyperbolic.
Proof Consider the following short exact sequence:
$$ \begin{align*}H^1(K,\operatorname{\textrm{GL}}_n/\mu_2)\to H^1(K,\operatorname{\textrm{GL}}_n/\mu_2\rtimes\mathbb{Z}/2\mathbb{Z})\to H^1(K,\mathbb{Z}/2\mathbb{Z}), \end{align*} $$
and take
$E/K$
corresponding to the image in
$H^1(K,\mathbb {Z}/2\mathbb {Z})$
of
$[\zeta ]$
in
$H^1(K,\operatorname {\textrm {GL}}_n/\mu _2\rtimes \mathbb {Z}/2\mathbb {Z})$
whose image in
$H^1(K,\operatorname {\textrm {PGO}}_{2n})$
is
$[\xi ]$
. Passing to E we see that
$[\xi _E]$
comes from
$H^1(E,\operatorname {\textrm {GL}}_n/\mu _2)$
and so produces a hyperbolic involution.▪
Theorem 3.5 Let K be a two-special (that is with no odd degree extensions) field of characteristic not
$2$
and
$3$
, L be a Lie algebra of type
$E_8$
over K obtained via the Tits construction. Then the group corresponding to L is not of Tits index
$E_{8,1}^{133}$
.
Proof Assume the contrary. Obviously the base field is infinite, for there are only split groups of type
$E_8$
over finite fields. Let L be obtained via the Tits construction from
$C_1$
and
$\mathcal {H}_3(C_2,\gamma )$
for some octonion algebras
$C_1$
and
$C_2$
, i.e., is
$K(A,-,\gamma )$
for
$(A,-) =C_1\otimes C_2$
. Denote by
$[\xi ]$
the class corresponding to L in
$H^1(K,E_8)$
. By Proposition 1.5 L contains a Lie subalgebra of type
$D_8$
, namely
$\mathfrak {so}(\langle \gamma _i\rangle n_1 \perp \langle -\gamma _j^{-1} \rangle n_2)$
, and so the corresponding group contains a subgroup
$H'$
of type
$D_8$
with the same Lie algebra (see [Reference Demazure and Grothendieck7, Exposé XXII, Corollaire 5.3.4]), that is corresponding to the quadratic form
$\langle \gamma _i\rangle n_1 \perp \langle -\gamma _j^{-1} \rangle n_2$
.
Applying Lemma 3.2 to the case
$G=E_8$
,
$H=D_8$
and
$H'$
as above, we see that
$[\xi ]$
comes from some
$[\zeta ]\in H^1(K,N(A_7))$
such that
$H'$
is isomorphic to
${}_\zeta D_8$
. Now the image of
$N(A_7)$
in
$\operatorname {\textrm {PGO}}_{16}^+$
normalizes
$\operatorname {\textrm {SL}}_8/\mu _2$
and so is contained in
$\operatorname {\textrm {GL}}_8/\mu _2\rtimes \mathbb {Z}/2\mathbb {Z}$
. Applying Lemma 3.4, we see that the quadratic form
$\langle \gamma _i\rangle n_1 \perp \langle -\gamma _j^{-1} \rangle n_2$
becomes hyperbolic over a quadratic field extension
$E/K$
. It follows that
$e_3(n_1)+e_3(n_2)$
is trivial over E, hence
$n_1-n_2$
belongs to
$I^4$
and so is hyperbolic over E. Now
$n_1-n_2$
is divisible by the discriminant of E and so
$e_3(n_1)+e_3(n_2)$
is a sum of two symbols with a common slot. But the Rost invariant of the anisotropic kernel of type
$E_7$
is
$e_3(n_1)+e_3(n_2)$
, and applying [Reference Garibaldi, Petrov and Semenov13, Theorem 10.18] we see that this group must be isotropic, a contradiction.▪
Note that [Reference Garibaldi9, Appendix A] provides an example of a strongly inner group of type
$E_7$
over a two-special field, hence an example of a group of Tits index
$E_{8,1}^{133}$
over such a field, which is not obtained via the Tits construction.
Corollary 3.6 Suppose K is a field such that
$-1$
is a sum of two squares, and let L be a Lie algebra over K of type
$E_8$
obtained via the Tits construction.
-
(1) If
$h_8(L)\ne 0$
then L is anisotropic. -
(2) If
$-1$
is a square in K and
$h_6(L) \ne 0$
then L has K-rank
$\le 1$
.
Proof It suffices to prove both items in case K is two-special.
(i) Suppose L is isotropic. We can assume that L does not have Tits index
$E_{8,1}^{133}$
by Theorem 3.5. Using [Reference De Clercq and Garibaldi6, Table 10] we see that L corresponds to a class in the image of
$H^1(K,\textbf {Spin}_{14}) \to H^1(K,E_8)$
, which implies by Proposition 1.4 that it is isomorphic to
$K(A,-) \simeq K(A,-,(1,-1,1))$
for some bi-octonion algebra A. Then clearly
$h_8(L) = 0$
.
(ii) Suppose L has K-rank
$\ge 2$
. Then L corresponds to a class in the image of
$H^1(K,\textbf {Spin}_{12}) \to H^1(K,E_8)$
. Its anisotropic kernel is a subgroup of
$\textbf {Spin}(q)$
for some
$12$
-dimensional form q belonging to
$I^3(K)$
, and by a well-known theorem of Pfister (see [Reference Garibaldi9, Theorem 17.13]) q is similar to
$n_1 - n_2$
for a pair of three-Pfister forms
$n_i$
with a common slot, say
$n_i = \langle \!\!\;\!\langle x, y_i,z_i \rangle \!\!\;\!\rangle $
. If
$C_i$
is the octonion algebra corresponding to
$n_i$
then we have
$L \simeq K(C_1 \otimes C_2,-)$
, and since
$-1$
is a square,
$$\begin{align*}h_6(L) = e_6(\langle\!\!\;\!\langle x,y_1,z_1, x, y_2,z_2\rangle\!\!\;\!\rangle) = (-1) \cup (x) \cup (y_1)\cup (y_2) \cup (z_1)\cup (z_2) = 0. \\[-34pt]\end{align*}$$
▪
