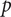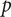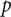1. The argument for the TP thesis based on the nominal reading

Greimann (Reference Greimann2008, 409) argues that if we can formulate Tarskian T-sentences with “… is the True,” we can take the predicate as a metalinguistic truth-predicate. Greimann claims that it is possible to construct T-sentences with “… is the True”: “the truth-value of ‘Grass is green’ is the True iff grass is green.” For Frege, however, sentences are true or false only derivatively, i.e., only in the sense that the thoughts expressed by them are true or false. So the relevant kind of (quasi) T-sentences would be something like this:

Griemann (Reference Greimann2008, 410) claims that we can construct a schema for the relevant kind of T-sentences out of “… is the True”:

Hence, there is no problem with taking “… is the True” as a truth-predicate in the relevant sense. Or so argues Greimann.

An immediate objection, however, would be that (FSch) uses the operator “the truth-value of.” Frege never uses such an operator in his explanations of logical laws. It rather seems as if Frege is using “… is the True” simply as the identity predicate “ $ x $ = the True,” so to speak, as in

(S) 2 + 2 = 4 is the True.

If so, we cannot confirm that Frege is using “… is the True” like a truth-predicate in the relevant sense (Greimann Reference Greimann2008, 410).

As a response to this objection, Greimann appeals to the nominal reading of Frege’s conception of sentence (Greimann Reference Greimann2007, Reference Greimann2008; Klement Reference Klement2001; Landini Reference Landini1996; Pedriali Reference Pedriali2017), according to which the sense of any sentence “ $ p $ ” is identical with the sense of the phrase “the truth-value of: (the thought) that $ p $ ” in Frege. If so, then even sentences such as (S) are in fact instances of (FSch). But why do we have to accept the nominal reading?Footnote ⁶

In Grundgesetze, Frege writes:

What Frege says here is related to the point that a sentence refers to a truth-value. In a sentence, or an equation in this case, we have a predicate: a word that refers to a concept, i.e., a function whose value is always a truth-value. For instance, in the above equations, we find the predicate “ $ {\xi}^2=4 $ .” Now, e.g., “ $ {2}^2=4 $ ” refers to the value of the concept $ {x}^2=4 $ saturated with the argument 2. Thus, it refers to the True. Because the value of a function is an object, truth-values are objects, and so the reference of a sentence, or an equation, is an object. Now, equations as such express thoughts. In Frege’s Begriffsschrift, however, writing an equation down is not asserting that the thought it expresses is true. By writing it down, we only designate a truth-value. For asserting, a special sign is necessary:

Expressions like (B) are well-formed sentences of Begriffsschrift (Begriffsschriftsatz).

If (B) is a sentence, then a question is raised. The reference of a sentence is always a truth-value. Hence, (B) is also the name of a truth-value. Now, say ├ $ {\xi}^2=4 $ is a concept such that it gives the True as its value if 2 is given as an argument and the False otherwise. Then, it follows that (B) also designates a truth-value as the equations in the earlier passage do. However, Frege clearly denies it:

This raises the question of how (B) can be a name of a truth-value while ├ $ {\xi}^2=4 $ is not a concept.

Greimann maintains that Frege distinguishes sentences from (mere) singular terms for truth-values. Only expressions such as (B) are sentences. Equations such as “ $ {2}^2=4 $ ” are not sentences but singular terms for truth values. Both sentences and singular terms for truth-values are of course proper names of truth-values; they “denote (bedeuten)” (Reference Greimann2008, 414) truth-values. However, singular terms for truth-values differ from sentences in that only the former can be used for the speech-act of reference qua a proper part of the speech act of assertion; only singular terms for truth-values “designate (bezeichnen)” (Reference Greimann2008, 414) in this sense.

Then, the sense of an equation such as “ $ {2}^2=4 $ ,” which would be taken as a sentence, must be that of an expression that can be used as a part of a sentence like (B) for the sake of the speech-act of reference qua a proper part of assertion. Indeed, Greimann argues, Frege is paraphrasing the sentence in the ordinary sense “(2 + 3 = 5) = (2 = 2)” into the nonsentential phrase: “the truth-value of: that “2 + 3 = 5” refers to the same as “2 = 2”’. Greimann insists that, in general, the sense of a singular truth-value term “ $ p $ ” is identical with that of “the truth-value of: that $ p $ .” Therefore, even “2 + 2 = 4 is the True” is indeed equivalent to the (quasi) T-sentence “The truth-value of: that 2 + 2 = 4 is the True.”Footnote ⁷ Greimann concludes: “… is the True” is a truth-predicate in the relevant sense.

2. Criticism: The nominal reading can’t be justified

The argument for the TP thesis heavily depends on the nominal reading according to which in Frege “2 + 2 = 4” can be paraphrased into “the truth-value of: that 2 + 2 is 4.” Consider the following objection to this interpretation. In a number of places, Frege says that the sense of a sentence in the usual sense is a thought. Since “2 + 2 = 4” is a sentence in the usual sense, its sense must be a thought, i.e., the thought that 2 + 2 is 4 or 〈2 + 2 is 4〉. On the contrary, “the truth-value of: that 2 + 2 is 4” is not a sentence in the usual sense. So its sense is not a thought. Thoughts differ from senses of nonsentential singular terms. For an arbitrary thought $ \left\langle p\right\rangle $ , it is always identical with 〈 $ \left\langle p\right\rangle $ is true〉 (Frege Reference Frege1892, Reference Frege1897, Reference Frege1906a, Reference Frege1914, Reference Frege1915, etc.). But the same point is not applied to a nonsentential singular term. A case in point: “the truth-value of: that 2 + 2 is 4.” Its sense differs from 〈The truth-value of: that 2 + 2 is 4 is true〉.Footnote ⁸ If “the truth-value of: that 2 + 2 is 4” and “2 + 2 is 4” have different senses, then one cannot be the paraphrase of the other.

Of course, as we have seen, Frege takes expressions such as “(2 + 3 = 5) = (2 = 2)” to be legitimate, and thus he considers “2 + 3 = 5” to be a proper name such as “the truth-value of: that 2 + 3 is 5” in the syntactical level. One might object that this syntactic assimilation of a sentence to a proper name strongly suggests that he also semantically assimilates a sentence to a proper name like “the truth-value of: that … .” However, there is no textual evidence for this claim. Moreover, Frege’s text rather seems to show that this syntactic assimilation does not lead to the suggested semantic assimilation. In “On Sense and Reference,” immediately after Frege classifies sentences as proper names (Reference Frege1892, 63), he says that 〈〈2 + 3 is 5〉 is true〉 is identical with 〈2 + 3 is 5〉 (64). As we have just said, the sense of “the truth-value of that 2 + 3 is 5” is not identical with 〈The truth-value of: that 2 + 3 is 5 is true〉. We will come back to this issue at the end of this section.

What is important is that Greimann has a different response to the above objection against the nominal reading, which does not depend on the controversial claim that Frege’s syntactic assimilation of sentences to proper names implies that he semantically assimilates sentences to the phrases like “the truth-value of: that $ p $ .” According to Greimann, the nominal reading does not reject that a thought as the sense of a sentence differs from the sense of a singular term like “the truth-value of: that 2 + 2 is 4.” When the nominal reading says that “the truth-value of: that 2 + 2 is 4” is a paraphrase of “2 + 2 = 4,” Greimann says, it is arguing that the latter as an expression of Begriffsschrift is “not to be considered as a sentence but as a complex singular term” (Reference Greimann2008, 411). Let me explain further. According to Greimann, it is not the case that Frege “wants to defend the absurd view that in natural languages an expression like ‘ $ {2}^2=4 $ ’ is used as a singular [truth-value] term [like ‘the truth-value of: that $ {2}^2 $ equals 4’]” (412). In natural language, it certainly expresses 〈 $ {2}^2 $ equals 4〉 and, as such, “can be used to assert something, but not to designate something” (412).Footnote ⁹ The point of Greimann’s defense of the nominal reading is thus that Frege turns what we regard as sentences in natural languages into singular truth-value terms in Begriffsschrift because he makes a clear distinction between a mere entertainment of a thought, i.e., what he calls “predication,” and assertion. With ordinary language sentences like “2 + 2 is equal to 4,” however, we cannot clearly mark the distinction. For we can use ordinary language sentences to perform both predication—entertainment of a thought—and assertion (412). The nominal reading claims that in order to make the distinction clearly shown, Frege regards “2 + 2 = 4” qua an expression of his formal language to mean “the truth-value of: that 2 + 2 equals 4,” which alone cannot be used for the act of assertion because it is not a sentence. A sentence is constructed and assertion is performed only if we write “├,” a special truth-predicate or truth-operator that can be translated into “… is the True” (Greimann Reference Greimann2004, Reference Greimann2007), in front of such a term.

Several clarifications are necessary here. First, Greimann claims that while “… is the True” in “The truth-value of: that grass is green is the True” is a truth-predicate, it does not function as a truth-predicate when it is “applied to a singular term that does not express a thought, as in ‘5 is the True’” (Reference Greimann2008, 414). This shows that Greimann takes the phrase “the truth-value of: that grass is green”—unlike “5”—to express a thought. If he does so, there is a conflict between Greimann’s terminology and mine. I use “thought” in order to refer to the sense of a sentence like “2 + 2 equals 4” in English. I also say that a term expresses $ S $ just in case a term has $ S $ as its sense—following Frege’s own terminology (Reference Frege1892, 61).Footnote ¹⁰ In my terminology, “the truth-value of: that 2 + 2 equals 4” does not express a thought because it is not a sentence and so its sense is not a thought. Recall that Greimann accepts that “2 + 2 is 4” and “the truth-value of: that 2 + 2 is 4” have different senses in English and that only expressions like the former count as sentences in it. Hence, he would accept that only “2 + 2 is 4” expresses a thought in my sense. Thus, when Greimann says that “the truth-value of: that $ p $ ” expresses a thought, he must be using “express a thought” in a different sense. Perhaps, he takes such a phrase to express a thought in the sense that it includes the name of a thought. What is important is that while following my terminology, we can still capture Greimann’s point safely as follows: “ $ 2+2=4 $ ” in Frege’s formal language does not have 〈2 + 2 is 4〉—the sense of “2 + 2 is 4” in English—as its sense. In fact, Greimann’s whole point is that no expression other than the ones prefixed with “├” can have a thought—the sense of a sentence—as its sense. Given this clarification, keeping my own terminology in the following discussion with care will not distort Greimann’s reading.

Secondly, one might think that saying that Greimann considers “├” to be a formal counterpart of “… is the True” is misleading because he says that the horizontal—the short horizontal stroke attached to the judgment-stroke—is such a formal counterpart (Reference Greimann2008, 418). Frege indeed takes the horizontal to refer to a concept such that it yields the True if the True is given as an argument and the False otherwise (Frege Reference Frege1893, sec. 5)—the concept being identical with the True. However, we need to note that by Greimann’s own light, “— $ 2+3=5 $ ,” which is a legitimate expression of Begriffsschrift, does not correspond to the sentence “2 + 3 = 5 is the True.” Because it does not have the judgment-stroke, it can only correspond to “the truth-value of: that 2 + 3 = 5 is the True.” An expression that corresponds to the sentence “2 + 3 = 5 is the True” is made only when we add the judgment-stroke at the left side of the horizontal. Greimann does not further explain how the judgment-stroke and the horizontal interact with each other to construct such a sentential expression. In any event, what is important to our purpose is that the predicate “… is the True” qua an expression that can produce a sentence of the form “ $ p $ is the True” only corresponds to “├,” not the horizontal. That appears to be why Greimann (Reference Greimann2008, 418) regards the sign “├” including the judgment-stroke, but not the horizontal alone, as a truth-operator. In the remainder of this paper, “… is the True” is a predicate as a part of the sentence of the form “ $ p $ is the True.” Again, “├” is a formal counterpart of “… is the True” as such.

Lastly, it is not Greimann’s point that just as Begriffsschrift needs “├” to construct a sentence and make an assertion, we need “… is the True” in order to do so in natural language. According to Greimann, for Frege, we perform sentence-construction/assertion in natural language with “the syntactic mood of assertoric sentences” (Reference Greimann2000, 219), not with such a predicate. Therefore, the functional counterpart of “├” in natural language is the syntactic mood of assertoric sentences in Greimann’s reading. However, as we have seen, precisely because in natural language we need to perform sentence-construction/assertion with the syntactic mood of assertoric sentences, natural language blurs the distinction between assertion and mere predication. For that reason, Greimann says, Frege makes a clear division between mere predication and assertion by interpreting “├ $ \hskip0.1em p $ ” as a combination of a nonsentential expression such as “the truth-value of: that $ p $ ”—which does not express truth—and the truth-predicate “… is the True,” i.e., the judgment-stroke.

To recap the emerging explanation of Begriffsschrift, say—following Greimann—“— 2 + 2 equals 4_E” is an English sentence and “2 + 2 = 4_F” is a corresponding singular term in Begriffsschrift. “2 + 2 equals 4_E” expresses 〈2 + 2 equals 4〉, and is a sentence in the sense that it can be used to assert, but not to designate, an object. But “2 + 2 = 4_F” does not express such a thought; it only expresses the sense of a singular term. Therefore, it is not a sentence in the same sense. We come to have a sentence in this sense only if we put “├” in front of it. Now, “├ $ \hskip0.1em 2+2=4 $ ” does express a thought, namely, 〈The truth-value of: that 2 + 2 equals 4 is the True〉. Hence, “├” is a formal version of “… is the True” as a part of a sentence like “2 + 3 = 5 is the True” and is the only genuine predicate—which is also a truth-predicate or -operator—of Begriffsschrift in the sense that only with “├” can we have a sentence.Footnote ¹¹

One problem with taking “├” to be a truth-predicate is that “├ $ \hskip0.1em 2 $ “ can also count as a Begriffsschriftsatz. Greimann ought to accept that, in such a case, “├” is not a truth-predicate, but a mere identity predicate. Then, why don’t we say that it is merely such an identity predicate? This leads to a doubt against his reading of “… is the True” because “2 is the True” seems to be a perfectly legitimate. But Greimann does not seem to take this issue seriously. He simply admits that, in such a case, “… is the True” fails to work as a truth-predicate. Greimann’s idea seems to be that as long as the predicate produces all instances of (FSch), the fact that it can play a different role does not prevent us from regarding it as a truth-predicate. That idea still seems controversial.Footnote ¹² However, this is not the major issue I would like to raise here.

According to the suggested interpretation of Begriffsschrift, we do not have a sentence that expresses a thought without “├” in Begriffsschrift. To put it in a different way, the sense of “├” contributes to the formation of the thought 〈… is the True〉. At the same time, “├” stands for assertoric force. Therefore, here, “├” (i) contributes to the formation of a thought and (ii) indicates assertoric force. In a significant sense, this explanation takes assertoric force to contribute to the formation of a thought. However, this is what Frege emphatically rejects in many places (e.g., Frege Reference Frege1892, Reference Frege1897, Reference Frege1906a, Reference Frege1914, Reference Frege1915). For instance, Frege writes in “On Schoenflies”:

In fact, the main logical defect of natural language concerning assertoric force—and assertion—is that it leads us to believe that assertoric force comes as a part of thought. In “My Basic Logical Insights,” Frege writes:

“This attempt miscarries,” Frege says, because

He is pointing to his claim that “ $ p $ ” and “The thought that $ p $ is true” have the same thought. Now, Frege writes:

We can see what Frege is getting at only if we take into account what he says about judgment and assertion in the first half of this short manuscript:

The truth-predication that occurs in “The thought that $ p $ is true” gives an expression to the nature of assertion because it does not add anything to the thought of which truth is predicated just as assertion does not alter the asserted thought.Footnote ¹⁴ The point here is not that the truth-predicate of a natural language is defective because it fails to make the assertoric force contribute to the formation of a thought. It is instead that to attempt to make the assertoric force be a part of a thought is defective because the assertoric force is not a part of a thought. It is hard to believe that Frege would let his logic commit the mistake he himself points out.

One might object that my argument depends on my terminology of “thought.” Specifically one might insist that “thought” in the above passages refers to the sense of “the truth-value of: that $ p $ .” However, that is not the case. In the above passages, Frege is analyzing natural language and diagnosing its problem. As Greimann himself admits, a sentence of natural language has the sense of a sentence, i.e., a thought in my terminology. Note: the thought that $ p $ in the above passages is identical with the thought that the thought that $ p $ is true. As we have already seen, the sense of “the truth-value of: that $ p $ ” cannot be said to be identical with 〈the truth-value of: that $ p $ is true〉. Therefore, Frege is talking about a thought in my terminology, i.e., a thought qua the sense of a natural language sentence. His point in the above passages is that the thought expressed by a sentence of natural language does not contain assertoric force in itself because assertoric force is not something expressed by a component of a sentence.

I believe that Greimann is right when he argues that (i) Frege needs a category of “expressions that are supposed to express a thought without simultaneously asserting its truth” (Greimann Reference Greimann2008, 412) and that (ii) “2 + 2 = 4_F” falls under such a category. The problem is, I believe, that from those true claims, he proceeds to the conclusion that “2 + 2 = 4_F” must correspond something like “the truth-value of: that 2 + 2 is 4” in English.Footnote ¹⁵ It is not clear at all why Frege ought to turn “2 + 2 = 4_F” into a nonsentential term in order to deprive assertoric force of it. Why can’t he simply regard “2 + 2 = 4_F” as corresponding to “2 + 2 is 4” in English to which assertoric force is not added, e.g., the sentence uttered by an actor on a stage (cf. Frege Reference Frege1892)? Is that because as soon as we form a sentence and thereby express a thought, we come to make an assertion, i.e., because sentences or thoughts contain assertoric force in themselves? But, as we have seen, that is just what Frege rejects. It does not appear that in order to detach assertoric force from “2 + 2 = 4_F” we ought to turn it into a nonsentential term. All we need to do is to realize that assertoric force is not its semantic component. If we realize it, then we can take “2 + 2 = 4_F” to be a sentence that expresses 〈2 + 2 is 4〉 but is not asserted. Assertoric force is added to the thought by “├.”

Indeed, “2 + 2 = 4_F” or what Greimann calls “singular truth-value term” in general is a sentence that expresses a thought. After introducing eight primitive functions, Frege writes:

First, note that Frege takes a Begriffsscrhfitsatz like

to be the combination of the judgment-stroke (the vertical stroke) and a name of a truth-value. Therefore, what Frege calls “name of a truth-value” is not a Begriffsschriftsatz. Rather, something like the following is an instance of such a truth-value name:

By the stipulations given for the functions involved in (N), we can specify when it refers to the True. Frege’s point entails that (N)’s sense is 〈Those conditions are met〉, i.e., 〈The value-range of the concept referred by the horizontal falls under the concept〉.Footnote ¹⁶ (N) is a typical case of what Greimann takes as a singular truth-value term: it certainly refers to a truth-value though it is not a Begriffsschriftsatz. Frege’s remarks are explicit enough to affirm that such a singular truth-value term “ $ p $ ” in general expresses $ \left\langle p\right\rangle $ , not the sense of “the truth-value of: that $ p $ .” One might object that because “ $ p $ ” and “the truth-value of: that $ p $ ” have the same condition for referring to the True, they should be taken to be equivalent. However, this objection is refuted by Frege’s remarks here. Though both “ $ p $ ” and “the truth-value of: that $ p $ ” refer to the True under exactly the same condition, only $ \left\langle p\right\rangle $ but not the sense of “the truth-value of: that $ p $ ” says that the condition is met. Again, singular truth-value terms express thoughts. A thought is the sense of a sentence. It follows that Frege takes singular truth-value terms to be sentences. Then a singular truth-value term “ $ p $ ” cannot be translated into a nonsentential term such as “the truth-value: that $ p $ .” The argument for the TP thesis based on the nominal reading must be rejected because the nominal reading is incorrect.

3. The remaining problem and the lesson about Begriffsschrift

The following still needs to be explained: only expressions like (B) count as sentences in Frege’s Begriffsschrift by means of which we can assert but cannot designate a truth-value, while expressions such as “2 + 2 = 4” only designate a truth-value. If our discussion is along the right lines, an expression cannot be used alone for asserting even if it expresses a thought. We need the sign “├” in front of such an expression. Why do we need such a sign in addition to a term that expresses a thought? The answer is in one of the passages from Grundgesetze we’ve already seen:

Designating a truth-value corresponds to writing down a name of a truth-value such as “2 + 3 = 5” without saying whether it refers to the True or the False. Then, to assert that 2 + 3 is 5, i.e., to write down “├ 2 + 3 = 5” is to “say” that 2 + 3 = 5 is the True.

To this end [of asserting] I make use of a vertical stroke at the left end of the horizontal, so that, e.g., by writing

├ 2 + 3 = 5

we assert that 2 + 3 equals 5. Thus here we are not just writing down a truth-value, as in

$$ 2+3=5, $$

but also at the same time saying that it is the True (Frege Reference Frege1891, 34; italics mine).

To assert that 2 + 3 equals 5 is to identify 2 + 3 = 5 with the True. We now have a neat explanation of the point in question. Assertion as such identification is distinguished from designation of a truth-value. Thus, to write down “├ 2 + 3 = 5,” i.e., to assert that 2 + 3 equals 5, is not to designate a truth-value. Writing down “2 + 3 = 5” cannot be asserting that 2 + 3 is 5 because it is not identifying the Truth with 2 + 3 = 5.

I believe that it is in Frege’s assimilation of assertion with identification that the standard interpretation of assertion (judgment) in Frege (Burge Reference Burge, Haaparanta and Hintikka1986; Dummett Reference Dummett1993; Heck and May Reference Heck, May and Glanzberg2018; Heck Reference Heck2012) is grounded. For instance, Heck (Reference Heck2012, sec. 2.3) says that we can understand asserting that $ p $ in Frege as referring the True via $ \left\langle p\right\rangle $ or by the sentence “ $ p $ .” Note that when we refer to an object $ o $ by the name “N”—as we refer to the True by the sentence “ $ p $ ”—we thereby identify $ o $ with the reference of “N.” We can take Heck to be trying to make sense of Frege’s assimilation of assertion with identification by way of the notion of the speech-act of referring to an object by a name.

One might object that because an act of identifying an object $ {O}_1 $ as $ {O}_2 $ is an act of assertively predicating “ $ x={O}_2 $ ” of “ $ {O}_1 $ ,” “├” is a formal version of “… is the True” as Greimann argues. But again that cannot be correct. Return to another passage we have seen:

What Frege wants to point out is that one cannot “say” that $ p $ is the True even by predicating the identity predicate “ $ x= $ T” of “ $ p $ “ where “T” is the most obvious name of the True.Footnote ¹⁷ This shows that to assert that $ p $ , i.e., to “say” that $ p $ is the True, cannot be done by predicating “… is the True” of “ $ p $ .” Thus, “├,” the device for asserting, cannot be such a predicate.

Then how do we have to understand “├”? Recall that the horizontal is a predicate that refers to the concept being the True. Thus, the horizontal is indeed “… is the True” (as in “ $ p $ is the True”). Then, one can argue that the judgment-stroke marks assertoric force attached to this predicate and thus that by writing down “├ 2 + 3 = 5” we assert that 2 + 3 = 5 is the True—identifying 2 + 3 = 5 with the True. This reading seems to fit what Frege says in Grundgesetze.

Although this reading is tempting, our discussion in section 2 casts doubt on it. Recall that Frege repeatedly claims that assertoric force does not belong to any predicate. However, if the judgment-stroke really marks assertoric force, there is a significant sense in which assertoric force belongs to a particular predicate, i.e., the horizontal. That is because the judgment-stroke must always be attached to the horizontal. “ $ \mid \hskip.8em 2+3=5 $ ” is not even a legitimate expression of Begriffsschrift although there is a legitimate predicate—the identity sign—and the judgment-stroke as a marker of assertoric force. We can make an assertion only by “├ $ \hskip0.1em 2+3=5 $ ,” i.e., only when we attach the judgment-stroke to the horizontal. If the judgment-stroke marks assertoric force, then the horizontal monopolizes assertoric force in Begriffsschrift and there is a substantive sense in which assertoric force belongs to it. Moreover, Frege maintains that because assertoric force is not a component of thoughts, “we do not need a special predicate” (Reference Frege1914, 233) in order to assert. However, if the above reading is correct, and so asserting that $ p $ is asserting that $ p $ is the True, then we need a special predicate for asserting—the identity predicate “… is the True” or the horizontal. Thus the above reading of “├” goes against Frege’s repeated claims about assertion.Footnote ¹⁸

Then, is there an alternative? One alternative is to take “├” to be a pure performative for performing a nonassertive act of identification. We are not unfamiliar with the nonassertoric conception of identification. According to Millikan (Reference Millikan1998, Reference Millikan2000) or Camp (Reference Camp2002), the act of identifying is neither an act of predicating an identity predicate nor asserting an identity. Identification is an activity of its own kind that cannot be explained in terms of predication or assertion. I believe that Frege is appealing to such a conception of identification when he elucidates that asserting that p is taking a step from $ \left\langle p\right\rangle $ to its truth-value in “On Sense and Reference” (Frege Reference Frege1892).Footnote ¹⁹ To go into the detail of this seminal article goes beyond the scope of this paper. What is important is that, given all his remarks we have seen, Frege would rather understand “├” as a performative for such a nonassertoric identification if he indeed takes the act of asserting that $ p $ to be that of identifying the True with $ p $ . Now, the remaining question is how we can understand the compositionality of “├” if it is such a performative. The reading I suggest is to regard the judgment-stroke as a performative generator that produces a performative for relevant nonassertive identification when it is combined with an identity predicate. Thus, when the judgment-stroke is combined with the horizontal, we have a performative for nonassertive identification of the True. If we understand the compostionality of “├” in this way, Begriffsschrift does not imply that we do not need the horizontal in order to assert. Of course, we need the horizontal to acquire the performative. However, that does not imply that we need the horizontal to assert. What we need for making an assertion is the act marked by “├,” not the components of the sign. The compositionality of the sign is only for making explicit the nature of the action we perform. The horizontal marks the point that what we affirm by our action is the identity with the True, and the judgment-stroke marks the point that what we perform is not assertion of identity. Also, assertoric force does not belong to the horizontal anymore in this interpretation. For the judgment-stroke is not a marker of assertoric force. Furthermore, we can say that the act of assertion is only contained in the judgment-stroke because it is a performative generator while the horizontal is a mere predicate.

The expressions like “├ $ \hskip0.1em {\xi}^2=4 $ ” are not functional expressions, because “├” is not a functor at all. What we have by putting “2” in the position of “ $ \xi $ ” is not a truth-value, but an act of asserting that $ {2}^2 $ equals 4, i.e., “saying” that $ {2}^2=4 $ is the True. Begriffsschriftsätze are not names of truth-values. Thus, they do not designate truth-values.Footnote ²⁰