Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-21T23:11:49.398Z Has data issue: false hasContentIssue false
  • English
  • Français

Recurrent Transformation Groups

Published online by Cambridge University Press:  20 November 2018

R. A. Christiansen
R. A. Christiansen*
Affiliation:
Grinnell College, Grinnell, Iowa
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (X, T, π) denote a flow, where X is a compact topological space metrizable by d, and T is a closed non-trivial subgroup of the reals under addition. T is recurrent if and only if for each 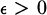and s > 0, there exists t > s such that x ∈ X implies 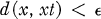. If T is almost-periodic, then T is both recurrent and distal. In §§ 4 and 5, it is shown that, under more stringent hypotheses, the recurrence of T is neither a necessary nor a sufficient condition for T to be distal. Let S be a closed non-trivial subgroup of T. It is shown in § 3 that T is recurrent if and only if S is recurrent. From this result, we obtain a solution to a problem posed by Nemyckiĭ (16, p. 492, Problem 6).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 564 - 575
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Auslander, L., Green, L., and Hahn, F., Flows on homogeneous spaces, Annals of Mathematical Studies No. 53 (Princeton Univ. Press, Princeton, N.J., 1963).Google Scholar
2. Bohr, H., On the definition of almost periodicity, J. Analyse Math. 1 (1951), 11–27.Google Scholar
3. Bourbaki, N., Éléments de mathématique. Fasc. X. Première partie. Livre III: Topologie générale. Chapitre 10: Espaces fonctionnels, 2e éd., Actualités Sci. Indu st., No. 1084 (Hermann, Paris, 1961).Google Scholar
4. Ellis, R., Distal transformation groups, Pacific J. Math. 8 (1958), 401–405.Google Scholar
5. Ellis, R., Locally compact transformation groups, Duke Math. J. 24 (1957), 119–125.Google Scholar
6. Furstenberg, H., Strict ergodicity and transformation of the torus, Amer. J. Math. 83 (1961), 573–601.Google Scholar
7. Furstenberg, H., The structure of distal flows, Amer. J. Math. 85 (1963), 477–515.Google Scholar
8. Gorman, C., A note on recurrent flows, Proc. Amer. Math. Soc. 7 (1956), 142–143.Google Scholar
9. Gottschalk, W. H., Characterizations of almost periodic transformation groups, Proc. Amer. Math. Soc. 7 (1956), 709–712.Google Scholar
10. Gottschalk, W. H., Transitivity and equicontinuity, Bull. Amer. Math. Soc. 54 (1948), 982–984.Google Scholar
11. Gottschalk, W. H. and Hedlund, G. A., Topological dynamics, Amer. Math. Soc. Colloq. PubL, Vol. 36 (Amer. Math. Soc, Providence, R. I., 1955).Google Scholar
12. Hewitt, E. and Ross, K. A., Abstract harmonic analysis, Vol. 1 (Academic Press, New York, 1963).Google Scholar
13. Hocking, J. G. and Young, G. S., Topology (Addison-Wesley, Reading, Mass., 1961).Google Scholar
14. Kelley, J. L., General topology (Van Nostrand, Princeton, N. J., 1955).Google Scholar
15. Morse, M. and Hedlund, G. A., Unending chess, symbolic dynamics, and a problem in semigroups, Duke Math. J. 11 (1944), 1–7.Google Scholar
16. Nemyckiï, V. V., Topological problems of the theory of dynamical systems, Amer. Math. Soc. Transi., Ser. 1, Vol. 5, No. 103 (Amer. Math. Soc, Providence, R. I., 1962).Google Scholar