No CrossRef data available.
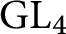 $ \operatorname {{\mathrm {GL}}}_4$
$ \operatorname {{\mathrm {GL}}}_4$Published online by Cambridge University Press: 23 November 2020
Let 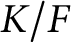 $K/F$
be an unramified quadratic extension of a non-Archimedean local field. In a previous work [1], we proved a formula for the intersection number on Lubin–Tate spaces. The main result of this article is an algorithm for computation of this formula in certain special cases. As an application, we prove the linear Arithmetic Fundamental Lemma for
$K/F$
be an unramified quadratic extension of a non-Archimedean local field. In a previous work [1], we proved a formula for the intersection number on Lubin–Tate spaces. The main result of this article is an algorithm for computation of this formula in certain special cases. As an application, we prove the linear Arithmetic Fundamental Lemma for 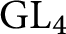 $ \operatorname {{\mathrm {GL}}}_4$
with the unit element in the spherical Hecke Algebra.
$ \operatorname {{\mathrm {GL}}}_4$
with the unit element in the spherical Hecke Algebra.