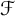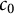1 Introduction
The study of the dynamical properties of weighted shift operators on sequence spaces of trees has been an active research topic in recent years. Martínez-Avendaño [Reference Martínez-Avendaño27], Rivera-Guasco and Martínez-Avendaño [Reference Martínez-Avendaño and Rivera-Guasco28], and Grosse-Erdmann and Papathanasiou [Reference Grosse-Erdmann and Papathanasiou22, Reference Grosse-Erdmann and Papathanasiou23] have made significant contributions in this field. See also [Reference Ángeles-Romero and Martínez-Avendaño6, Reference Baranov, Lishanskii and Papathanasiou7] for some further related research. Jblónski, Jung, and Stochel [Reference Jblónski, Jung and Stochel26] introduced and studied weighted forward shift operators on trees, while backward shift operators were introduced in [Reference Martínez-Avendaño27]. In [Reference Grosse-Erdmann and Papathanasiou22, Theorems 4.3 and 5.2], the authors provided a complete characterization of the hypercyclicity of backward shift operators on weighted
![]() $\ell ^p$
-spaces and
$\ell ^p$
-spaces and
![]() $c_0$
-spaces on directed trees.
$c_0$
-spaces on directed trees.
Recall that a bounded linear operator is hypercyclic if it has dense orbit. More precisely, let us consider X to be a Banach space and let
![]() $\mathcal {L}(X)$
be the space of bounded linear operators from X into itself. An operator
$\mathcal {L}(X)$
be the space of bounded linear operators from X into itself. An operator
![]() $T\in \mathcal {L}(X)$
is said to be hypercyclic if there exists a vector
$T\in \mathcal {L}(X)$
is said to be hypercyclic if there exists a vector
![]() $x\in X$
such that its orbit under T, denoted by
$x\in X$
such that its orbit under T, denoted by
is dense in X, where
![]() $\mathbb {N}_0=\{0,1,2,\ldots \}$
and
$\mathbb {N}_0=\{0,1,2,\ldots \}$
and
![]() $\mathbb {N}=\mathbb {N}_0\setminus \{0\}$
. Hypercyclicity is a well-studied concept in linear dynamics, see [Reference Bayart and Matheron8, Reference Grosse-Erdmann and Peris24]. In [Reference Salas29], Salas provided a description of hypercyclic weighted backward shift operators on
$\mathbb {N}=\mathbb {N}_0\setminus \{0\}$
. Hypercyclicity is a well-studied concept in linear dynamics, see [Reference Bayart and Matheron8, Reference Grosse-Erdmann and Peris24]. In [Reference Salas29], Salas provided a description of hypercyclic weighted backward shift operators on
![]() $\ell ^p$
-spaces, which was later extended by Grosse–Erdmann to backward shift operators defined on Fréchet sequence spaces [Reference Grosse-Erdmann21]. Additionally, Chan and Seceleanu proved that the hypercyclicity of backward shift operators is equivalent to the existence of an orbit with a nonzero limit point [Reference Chan and Seceleanu18]. Some recent improvements to these results have been achieved in [Reference Abakumov and Abbar1, Reference Bonilla, Cardeccia, Grosse-Erdmann and Muro11, Reference He, Huang and Yin25]. An immediate consequence of Chan and Seceleanu’s result is that the notions of recurrence and hypercyclicity coincide for backward shift operators on weighted
$\ell ^p$
-spaces, which was later extended by Grosse–Erdmann to backward shift operators defined on Fréchet sequence spaces [Reference Grosse-Erdmann21]. Additionally, Chan and Seceleanu proved that the hypercyclicity of backward shift operators is equivalent to the existence of an orbit with a nonzero limit point [Reference Chan and Seceleanu18]. Some recent improvements to these results have been achieved in [Reference Abakumov and Abbar1, Reference Bonilla, Cardeccia, Grosse-Erdmann and Muro11, Reference He, Huang and Yin25]. An immediate consequence of Chan and Seceleanu’s result is that the notions of recurrence and hypercyclicity coincide for backward shift operators on weighted
![]() $\ell ^p$
-spaces of sequences indexed by
$\ell ^p$
-spaces of sequences indexed by
![]() $\mathbb {Z}$
. A vector
$\mathbb {Z}$
. A vector
![]() $x\in X$
is called recurrent vector for an operator
$x\in X$
is called recurrent vector for an operator
![]() $T\in \mathcal {L}(X)$
if there exists a strictly increasing sequence of integers
$T\in \mathcal {L}(X)$
if there exists a strictly increasing sequence of integers
![]() $(n_k)_{k\in \mathbb {N}_0}$
such that
$(n_k)_{k\in \mathbb {N}_0}$
such that
The operator T is called recurrent if its set of recurrent vectors is dense in X, or equivalently (see [Reference Costakis, Manoussos and Parissis15, Proposition 2.1]), for every nonempty open set U of X, there exists an integer
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
The study of recurrence for linear operators was initiated by Costakis and Parissis [Reference Costakis and Parissis16] and later developed further by Costakis, Manoussos, and Parissis [Reference Costakis, Manoussos and Parissis15]. For recent contributions, see also [Reference Amouch, Bachir, Benchiheb and Mecheri4, Reference Bonilla, Grosse-Erdmann, López-Martínez and Peris12, Reference Grivaux and López-Martínez19, Reference Grivaux, López-Martínez and Peris20]. For any nonempty open subsets U and V of X, the return set (or, time set) from U to V will be denoted as
When there is no ambiguity, the index T will be omitted. Several topological notions in linear dynamics can be expressed by using return sets. The operator T is said to be topologically transitive if for any nonempty open subsets
![]() $U,V$
of X, the return set
$U,V$
of X, the return set
![]() $N(U,V)$
is nonempty (or, equivalently, infinite). Birkhoff’s transitivity theorem says that hypercyclicity and transitivity coincide, see [Reference Bayart and Matheron8, Theorem 1.2]. Moreover, T is said to be topologically mixing (resp., weakly mixing, ergodic) if for any nonempty open subsets
$N(U,V)$
is nonempty (or, equivalently, infinite). Birkhoff’s transitivity theorem says that hypercyclicity and transitivity coincide, see [Reference Bayart and Matheron8, Theorem 1.2]. Moreover, T is said to be topologically mixing (resp., weakly mixing, ergodic) if for any nonempty open subsets
![]() $U,V$
of X, the return set
$U,V$
of X, the return set
![]() $N(U,V)$
is cofinite (resp., thick, syndetic). Recall that a subset A of
$N(U,V)$
is cofinite (resp., thick, syndetic). Recall that a subset A of
![]() $\mathbb {N}_0$
is called
$\mathbb {N}_0$
is called
-
• thick if it contains arbitrarily long intervals, i.e., for every
 $n\in \mathbb {N}_0$
, there exists
$n\in \mathbb {N}_0$
, there exists
 $m\in A$
such that
$m\in A$
such that
 $[\![m,m+n]\!]:=\{k\in \mathbb {N}_0:\, m\leq k\leq m+n\}\subset A$
.
$[\![m,m+n]\!]:=\{k\in \mathbb {N}_0:\, m\leq k\leq m+n\}\subset A$
. -
• syndetic if it has bounded gaps, i.e., there exists an integer
 $n\in \mathbb {N}$
such that for all
$n\in \mathbb {N}$
such that for all
 $m\in \mathbb {N}_0$
, we have
$m\in \mathbb {N}_0$
, we have
 $[\![m,m+n]\!]\cap A\neq \emptyset $
.
$[\![m,m+n]\!]\cap A\neq \emptyset $
.
Furstenberg families, as defined in Section 2.3, serve to generalize the concepts of topological transitivity, mixing, weakly mixing, and ergodicity in terms of
![]() $\mathcal {F}$
-transitivity, see [Reference Bès, Menet, Peris and Puig9]. Let
$\mathcal {F}$
-transitivity, see [Reference Bès, Menet, Peris and Puig9]. Let
![]() $\mathcal {F}$
be a Furstenberg family of subsets of
$\mathcal {F}$
be a Furstenberg family of subsets of
![]() $\mathbb {N}_0$
. The operator T is called
$\mathbb {N}_0$
. The operator T is called
![]() $\mathcal {F}$
-transitive if, for any pair of nonempty open subsets U and V in X, the set
$\mathcal {F}$
-transitive if, for any pair of nonempty open subsets U and V in X, the set
![]() $N(U,V)$
belongs to
$N(U,V)$
belongs to
![]() $\mathcal {F}$
. Moreover, T is said to be topologically
$\mathcal {F}$
. Moreover, T is said to be topologically
![]() $\mathcal {F}$
-recurrent if, for any nonempty open subset U in X, the set
$\mathcal {F}$
-recurrent if, for any nonempty open subset U in X, the set
![]() $N(U,U)$
belongs to
$N(U,U)$
belongs to
![]() $\mathcal {F}$
(see [Reference Bonilla, Grosse-Erdmann, López-Martínez and Peris12, Remark 8.2]). In [Reference Bès, Menet, Peris and Puig9], the authors provided a characterization of
$\mathcal {F}$
(see [Reference Bonilla, Grosse-Erdmann, López-Martínez and Peris12, Remark 8.2]). In [Reference Bès, Menet, Peris and Puig9], the authors provided a characterization of
![]() $\mathcal {F}$
-transitive weighted bilateral backward shift operators on the spaces
$\mathcal {F}$
-transitive weighted bilateral backward shift operators on the spaces
![]() $\ell ^p(\mathbb {Z})$
and
$\ell ^p(\mathbb {Z})$
and
![]() $c_0(\mathbb {Z})$
, as well as
$c_0(\mathbb {Z})$
, as well as
![]() $\mathcal {F}$
-transitive weighted unilateral backward shift operators.
$\mathcal {F}$
-transitive weighted unilateral backward shift operators.
This article is devoted to studying
![]() $\mathcal {F}$
-transitive and topological
$\mathcal {F}$
-transitive and topological
![]() $\mathcal {F}$
-recurrence backward shift operators on trees, which extends the results obtained in [Reference Bès, Menet, Peris and Puig9, Reference Grosse-Erdmann and Papathanasiou22]. Additionally, we investigate the concept of
$\mathcal {F}$
-recurrence backward shift operators on trees, which extends the results obtained in [Reference Bès, Menet, Peris and Puig9, Reference Grosse-Erdmann and Papathanasiou22]. Additionally, we investigate the concept of
![]() $\Gamma $
-supercyclicity, introduced in [Reference Charpentier, Ernst and Menet14], for these operators. The structure of this article is outlined as follows:
$\Gamma $
-supercyclicity, introduced in [Reference Charpentier, Ernst and Menet14], for these operators. The structure of this article is outlined as follows:
In Section 2, we introduce the necessary notations and definitions for our analysis, including Furstenberg families and a review of backward shift operators on weighted
![]() $\ell ^p$
-spaces and
$\ell ^p$
-spaces and
![]() $c_0$
-spaces on trees.
$c_0$
-spaces on trees.
In Section 3, we give a variant of the
![]() $\mathcal {F}$
-transitivity criterion that we will specifically use to describe
$\mathcal {F}$
-transitivity criterion that we will specifically use to describe
![]() $\mathcal {F}$
-transitive backward shift operators on unrooted directed trees (see Theorem 3.1).
$\mathcal {F}$
-transitive backward shift operators on unrooted directed trees (see Theorem 3.1).
Section 4 focuses on characterizing
![]() $\mathcal {F}$
-transitive backward shift operators on weighted
$\mathcal {F}$
-transitive backward shift operators on weighted
![]() $\ell ^p$
-spaces and
$\ell ^p$
-spaces and
![]() $c_0$
-spaces defined on rooted directed trees. We demonstrate that
$c_0$
-spaces defined on rooted directed trees. We demonstrate that
![]() $\mathcal {F}$
-transitivity is equivalent to a property weaker than topological
$\mathcal {F}$
-transitivity is equivalent to a property weaker than topological
![]() $\mathcal {F}$
-recurrence (see Theorem 4.1). Additionally, we derive a corollary indicating that hypercyclicity of a backward shift operator B on a weighted
$\mathcal {F}$
-recurrence (see Theorem 4.1). Additionally, we derive a corollary indicating that hypercyclicity of a backward shift operator B on a weighted
![]() $\ell ^p$
-space or
$\ell ^p$
-space or
![]() $c_0$
-space defined on a rooted directed tree is equivalent to the existence of a bounded subset whose orbit under B is weakly dense in the underlying space (see Corollary 4.3).
$c_0$
-space defined on a rooted directed tree is equivalent to the existence of a bounded subset whose orbit under B is weakly dense in the underlying space (see Corollary 4.3).
In Section 5, we provide a characterization of
![]() $\mathcal {F}$
-transitivity and establish its equivalence with topological
$\mathcal {F}$
-transitivity and establish its equivalence with topological
![]() $\mathcal {F}$
-recurrence for backward shift operators on weighted
$\mathcal {F}$
-recurrence for backward shift operators on weighted
![]() $\ell ^p$
-spaces and
$\ell ^p$
-spaces and
![]() $c_0$
-spaces defined on unrooted directed trees (see Theorem 5.1).
$c_0$
-spaces defined on unrooted directed trees (see Theorem 5.1).
In Section 6, we discuss the concept of
![]() $\Gamma $
-supercyclicity for backward shift operators on trees (see Theorem 6.1). This enables us to recover the characterization of hypercyclicity for these operators, as established in [Reference Grosse-Erdmann and Papathanasiou22], and also to provide a characterization of their supercyclicity.
$\Gamma $
-supercyclicity for backward shift operators on trees (see Theorem 6.1). This enables us to recover the characterization of hypercyclicity for these operators, as established in [Reference Grosse-Erdmann and Papathanasiou22], and also to provide a characterization of their supercyclicity.
Finally, in the last section, we demonstrate that unlike the cases of the trees
![]() $\mathbb {N}_0$
or
$\mathbb {N}_0$
or
![]() $\mathbb {Z}$
, there exist backward shift operators on weighted spaces on trees that are not hypercyclic but possess orbits with a nonzero limit point (see Examples 7.2 and 7.4). Theorem 7.1 characterizes backward shifts that have an orbit with a nonzero limit point in the case of rooted trees. For unrooted cases, we provide a characterization of backward shifts that have an orbit of some nonnegative function with a nonzero limit point (see Proposition 7.3).
$\mathbb {Z}$
, there exist backward shift operators on weighted spaces on trees that are not hypercyclic but possess orbits with a nonzero limit point (see Examples 7.2 and 7.4). Theorem 7.1 characterizes backward shifts that have an orbit with a nonzero limit point in the case of rooted trees. For unrooted cases, we provide a characterization of backward shifts that have an orbit of some nonnegative function with a nonzero limit point (see Proposition 7.3).
2 Preliminaries
2.1 Directed trees
In what follows, we will recall the necessary terminology related to trees, for more information we refer to [Reference Grosse-Erdmann and Papathanasiou22, Reference Jblónski, Jung and Stochel26] and the references therein. A (directed) graph is a pair
![]() $\mathcal {G}=(V,E)$
which satisfies the two conditions:
$\mathcal {G}=(V,E)$
which satisfies the two conditions:
-
(1) V is a nonempty set, its elements are called vertices.
-
(2) E is a subset of
 $\lbrace (u,v): u,v\in V, u\neq v\rbrace $
, its elements are called edges.
$\lbrace (u,v): u,v\in V, u\neq v\rbrace $
, its elements are called edges.
An undirected edge of
![]() $\mathcal {G}$
means an element of the set
$\mathcal {G}$
means an element of the set
If
![]() $\lbrace u,v\rbrace \in \tilde {E}$
, we say that u and v are adjacent and we denote that by
$\lbrace u,v\rbrace \in \tilde {E}$
, we say that u and v are adjacent and we denote that by
![]() $u\backsim v$
.
$u\backsim v$
.
-
• The graph
 $\mathcal {G}$
is connected if any two distinct vertices
$\mathcal {G}$
is connected if any two distinct vertices
 $u\neq v\in V$
are related by an undirected path, i.e., there exist
$u\neq v\in V$
are related by an undirected path, i.e., there exist
 $v_1,\ldots ,v_n\in V$
such that
$v_1,\ldots ,v_n\in V$
such that
 $u=v_1\backsim v_2\backsim \cdots \backsim v_n=v$
.
$u=v_1\backsim v_2\backsim \cdots \backsim v_n=v$
. -
• A circuit of
 $\mathcal {G}$
is a sequence
$\mathcal {G}$
is a sequence
 $\lbrace v_j\rbrace _{j=1}^{n}$
of distinct vertices (
$\lbrace v_j\rbrace _{j=1}^{n}$
of distinct vertices (
 $n\geqslant 2$
) such that, for all
$n\geqslant 2$
) such that, for all
 $j\in \{ 1,\ldots ,n-1\}$
,
$j\in \{ 1,\ldots ,n-1\}$
,  $$ \begin{align*}(v_j,v_{j+1})\in E \quad \text{and} \quad (v_n,v_1)\in E.\end{align*} $$
$$ \begin{align*}(v_j,v_{j+1})\in E \quad \text{and} \quad (v_n,v_1)\in E.\end{align*} $$
Definition 2.1 (Directed trees)
A directed tree
![]() $\mathcal {T}=(V,E)$
is a directed graph such that
$\mathcal {T}=(V,E)$
is a directed graph such that
-
(1)
 $(V,E)$
is connected.
$(V,E)$
is connected. -
(2) The set E of edges has no circuits.
-
(3) For any vertex
 $v\in E$
, there exists at most one vertex
$v\in E$
, there exists at most one vertex
 $u\in V$
such that
$u\in V$
such that
 $(u,v)\in E$
.
$(u,v)\in E$
. -
(4) The set V of vertices is countable.
In what follows, let us assume that
![]() $(V,E)$
is a directed tree.
$(V,E)$
is a directed tree.
-
• A parent of a vertex
 $v\in V$
is a vertex
$v\in V$
is a vertex
 $u\in V$
such that
$u\in V$
such that
 $(u,v)\in E$
; we denote such vertex by
$(u,v)\in E$
; we denote such vertex by
 $\mathrm {par}(v)$
. Moreover, for any
$\mathrm {par}(v)$
. Moreover, for any
 $n\geq 2$
and
$n\geq 2$
and
 $v\in V$
,
$v\in V$
,
 $\mathrm{par}^n(v):=\mathrm{par}(\mathrm{par}^{n-1}(v))$
, whenever this is well-defined. Furthermore, for any
$\mathrm{par}^n(v):=\mathrm{par}(\mathrm{par}^{n-1}(v))$
, whenever this is well-defined. Furthermore, for any
 $F\subset V$
and
$F\subset V$
and
 $n\geq 1$
,
$n\geq 1$
,
 $\mathrm{par}^n(F)$
represents the set of all vertices
$\mathrm{par}^n(F)$
represents the set of all vertices
 $\mathrm{par}^{n}(v)$
(when well-defined) for
$\mathrm{par}^{n}(v)$
(when well-defined) for
 $v\in F$
.
$v\in F$
. -
• A child of a vertex
 $v\in V$
is a vertex
$v\in V$
is a vertex
 $u\in V$
whose parent is v. We denote by
$u\in V$
whose parent is v. We denote by
 $\mathrm {Chi}(v)$
the set of children of v, that is, Moreover, for every
$\mathrm {Chi}(v)$
the set of children of v, that is, Moreover, for every $$ \begin{align*}\mathrm{Chi}(v)=\lbrace u\in V: \, \mathrm{par}(u)=v\rbrace.\end{align*} $$
$$ \begin{align*}\mathrm{Chi}(v)=\lbrace u\in V: \, \mathrm{par}(u)=v\rbrace.\end{align*} $$
 $n\geqslant 2$
, we denote where
$n\geqslant 2$
, we denote where $$ \begin{align*}\mathrm{Chi}^n(v):=\bigcup_{u\in \mathrm{Chi}(v)}\mathrm{Chi}^{n-1}(u),\end{align*} $$
$$ \begin{align*}\mathrm{Chi}^n(v):=\bigcup_{u\in \mathrm{Chi}(v)}\mathrm{Chi}^{n-1}(u),\end{align*} $$
 $\mathrm {Chi}^{1}(v)=\mathrm {Chi}(v)$
and
$\mathrm {Chi}^{1}(v)=\mathrm {Chi}(v)$
and
 $\mathrm {Chi}^{0}(v)=\lbrace v\rbrace $
. Furthermore, for any
$\mathrm {Chi}^{0}(v)=\lbrace v\rbrace $
. Furthermore, for any
 $F\subset V$
and
$F\subset V$
and
 $n\in\mathbb{N}_0$
, we define
$n\in\mathbb{N}_0$
, we define  $$ \begin{align*}\mathrm{Chi}^n(F):=\bigcup_{v\in F}\mathrm{Chi}^{n}(v).\end{align*} $$
$$ \begin{align*}\mathrm{Chi}^n(F):=\bigcup_{v\in F}\mathrm{Chi}^{n}(v).\end{align*} $$
-
• A root of
 $(V,E)$
is a vertex without a parent. Any directed tree has at most one root, if such an element exists, it will be denoted simply by
$(V,E)$
is a vertex without a parent. Any directed tree has at most one root, if such an element exists, it will be denoted simply by
 $\texttt {r}$
.
$\texttt {r}$
. -
• A leaf of
 $(V,E)$
is a vertex without children.
$(V,E)$
is a vertex without children.
2.2 Backward shift on sequences spaces on directed trees
Let
![]() $(V,E)$
be a directed tree, let
$(V,E)$
be a directed tree, let
![]() $\mu =(\mu _v)_{v\in V}$
be a weight on V, that is, a sequence of nonzero numbers and let
$\mu =(\mu _v)_{v\in V}$
be a weight on V, that is, a sequence of nonzero numbers and let
![]() $\mathbb {K}$
denote the set of real or complex numbers. For
$\mathbb {K}$
denote the set of real or complex numbers. For
![]() $1\leqslant p<+\infty $
, the weighted
$1\leqslant p<+\infty $
, the weighted
![]() $\ell ^p$
-space of V is defined by
$\ell ^p$
-space of V is defined by
and equipped with the norm
 $$ \begin{align*}\|f\|_{p,\mu}:=\Big(\sum_{v\in V}|f(v)\,\mu_v|^p\Big)^{1/p},\end{align*} $$
$$ \begin{align*}\|f\|_{p,\mu}:=\Big(\sum_{v\in V}|f(v)\,\mu_v|^p\Big)^{1/p},\end{align*} $$
is a Banach space. As usual,
![]() $\ell ^\infty (V,\mu )$
is the Banach space of functions
$\ell ^\infty (V,\mu )$
is the Banach space of functions
![]() $f\in \mathbb {K}^{V}$
such that
$f\in \mathbb {K}^{V}$
such that
Finally, the weighted
![]() $c_0$
-space on V is defined by
$c_0$
-space on V is defined by
endowed with the norm
![]() $\|.\|_{\infty ,\mu }$
is a closed subspace of
$\|.\|_{\infty ,\mu }$
is a closed subspace of
![]() $\ell ^\infty (V,\mu )$
. For
$\ell ^\infty (V,\mu )$
. For
![]() $v\in V$
, let
$v\in V$
, let
![]() $e_v=\chi _{\lbrace v\rbrace }$
be the characteristic function of
$e_v=\chi _{\lbrace v\rbrace }$
be the characteristic function of
![]() $\lbrace v\rbrace $
. Note that the space
$\lbrace v\rbrace $
. Note that the space
![]() $\mathrm {span}\lbrace e_v:\, v\in V\rbrace $
is dense in
$\mathrm {span}\lbrace e_v:\, v\in V\rbrace $
is dense in
![]() $X=\ell ^p(V,\mu )$
,
$X=\ell ^p(V,\mu )$
,
![]() $1 \leq p<+\infty $
or
$1 \leq p<+\infty $
or
![]() $X=c_0(V,\mu )$
. The support of a function
$X=c_0(V,\mu )$
. The support of a function
![]() $f\in \mathbb {K}^{V}$
is the set
$f\in \mathbb {K}^{V}$
is the set
According to [Reference Martínez-Avendaño27], the backward shift B on
![]() $\mathbb {K}^V$
is defined by:
$\mathbb {K}^V$
is defined by:
where an empty sum is zero. It can be seen as the adjoint of the forward shift operator S on trees, which is naturally defined on
![]() $\mathbb {K}^V$
as follows, for any
$\mathbb {K}^V$
as follows, for any
![]() $f\in \mathbb {K}^V$
and
$f\in \mathbb {K}^V$
and
![]() $v\in V$
:
$v\in V$
:

Under the following pairing of duality:
the dual of
![]() $\ell ^p(V,\mu )$
, for
$\ell ^p(V,\mu )$
, for
![]() $1\leq p<+\infty $
, is
$1\leq p<+\infty $
, is
![]() $\ell ^{p^\ast }(V,1/\overline{\mu})$
, where
$\ell ^{p^\ast }(V,1/\overline{\mu})$
, where
![]() $p^\ast $
is the conjugate exponent of p. Moreover, the dual of
$p^\ast $
is the conjugate exponent of p. Moreover, the dual of
![]() $c_0(V,\mu )$
is
$c_0(V,\mu )$
is
![]() $\ell ^1(V,1/\overline{\mu})$
. Now, if B or S defines a bounded linear operator on
$\ell ^1(V,1/\overline{\mu})$
. Now, if B or S defines a bounded linear operator on
![]() $X=\ell ^p(V,\mu )$
,
$X=\ell ^p(V,\mu )$
,
![]() $1\leq p <+\infty $
, or
$1\leq p <+\infty $
, or
![]() $X=c_0(V,\mu )$
then
$X=c_0(V,\mu )$
then
and this is why B has been named the backward shift. Alternatively, we can define the backward shift B as the unique bounded linear operator that satisfies
 $$ \begin{align*}Be_v=\begin{cases} e_{\mathrm{par}(v)}&\text{ if } v\neq \texttt{r} \\ 0 &\text{ if } v=\texttt{r} \end{cases},\qquad v\in V. \end{align*} $$
$$ \begin{align*}Be_v=\begin{cases} e_{\mathrm{par}(v)}&\text{ if } v\neq \texttt{r} \\ 0 &\text{ if } v=\texttt{r} \end{cases},\qquad v\in V. \end{align*} $$
In the following proposition, we will recall the necessary and sufficient conditions for the boundedness of the backward shift on weighted
![]() $\ell ^p$
-spaces or
$\ell ^p$
-spaces or
![]() $c_0$
-spaces on trees, see [Reference Grosse-Erdmann and Papathanasiou22, Proposition 2.3].
$c_0$
-spaces on trees, see [Reference Grosse-Erdmann and Papathanasiou22, Proposition 2.3].
Proposition 2.2 Let
![]() $(V,E)$
be a directed tree, let
$(V,E)$
be a directed tree, let
![]() $\mu =(\mu _v)_{v\in V}$
be a weight on V, and let B be the backward shift on
$\mu =(\mu _v)_{v\in V}$
be a weight on V, and let B be the backward shift on
![]() $\mathbb {K}^V$
.
$\mathbb {K}^V$
.
-
(a) B is a bounded linear operator on
 $\ell ^1(V,\mu )$
if and only if
$\ell ^1(V,\mu )$
if and only if  $$ \begin{align*}\sup_{v\in V\setminus\lbrace\texttt{r}\rbrace}\Big|\frac{\mu_{\mathrm{par}(v)}}{\mu_v}\Big|<+\infty.\end{align*} $$
$$ \begin{align*}\sup_{v\in V\setminus\lbrace\texttt{r}\rbrace}\Big|\frac{\mu_{\mathrm{par}(v)}}{\mu_v}\Big|<+\infty.\end{align*} $$
In this case,
 $\|B\|=\underset {v\in V\setminus \lbrace \texttt {r}\rbrace }{\sup } \big |\frac {\mu _{\mathrm {par}(v)}}{\mu _v}\big |$
.
$\|B\|=\underset {v\in V\setminus \lbrace \texttt {r}\rbrace }{\sup } \big |\frac {\mu _{\mathrm {par}(v)}}{\mu _v}\big |$
. -
(b) Let
 $1<p<+\infty $
. B is a bounded linear operator on
$1<p<+\infty $
. B is a bounded linear operator on
 $\ell ^p(V,\mu )$
if and only if
$\ell ^p(V,\mu )$
if and only if  $$ \begin{align*}\underset{v\in V}{\sup}\, \sum_{u\in \mathrm{Chi}(v)} \Big|\frac{\mu_v}{\mu_u }\Big|^{p^\ast}<+\infty.\end{align*} $$
$$ \begin{align*}\underset{v\in V}{\sup}\, \sum_{u\in \mathrm{Chi}(v)} \Big|\frac{\mu_v}{\mu_u }\Big|^{p^\ast}<+\infty.\end{align*} $$
In this case,
 $\|B\|=\underset {v\in V}{\sup } \, \Big (\underset {{u\in \mathrm {Chi}(v)}}{\sum } \big |\frac {\mu _v}{\mu _u }\big |^{p^\ast }\Big )^{1/p^{\ast }}$
.
$\|B\|=\underset {v\in V}{\sup } \, \Big (\underset {{u\in \mathrm {Chi}(v)}}{\sum } \big |\frac {\mu _v}{\mu _u }\big |^{p^\ast }\Big )^{1/p^{\ast }}$
. -
(c) B is a bounded linear operator on
 $c_0(V,\mu )$
if and only if
$c_0(V,\mu )$
if and only if  $$ \begin{align*}\underset{v\in V}{\sup}\, \sum_{u\in \mathrm{Chi}(v)} \Big|\frac{\mu_v}{\mu_u }\Big|<+\infty.\end{align*} $$
$$ \begin{align*}\underset{v\in V}{\sup}\, \sum_{u\in \mathrm{Chi}(v)} \Big|\frac{\mu_v}{\mu_u }\Big|<+\infty.\end{align*} $$
In this case,
 $\|B\|=\underset {v\in V}{\sup }\, \underset {u\in \mathrm {Chi}(v)}{\sum } \big |\frac {\mu _v}{\mu _u}\big |$
.
$\|B\|=\underset {v\in V}{\sup }\, \underset {u\in \mathrm {Chi}(v)}{\sum } \big |\frac {\mu _v}{\mu _u}\big |$
.
As mentioned previously, K. Grosse-Erdmann and D. Papathanasiou provided a comprehensive characterization of hypercyclicity for backward shift operators on weighted
![]() $\ell ^p$
-spaces and
$\ell ^p$
-spaces and
![]() $c_0$
-spaces. In the cases of rooted directed trees, they obtained the following theorem, see [Reference Grosse-Erdmann and Papathanasiou22, Theorem 4.3].
$c_0$
-spaces. In the cases of rooted directed trees, they obtained the following theorem, see [Reference Grosse-Erdmann and Papathanasiou22, Theorem 4.3].
Theorem 2.3 Let
![]() $(V, E)$
be a rooted directed tree and let
$(V, E)$
be a rooted directed tree and let
![]() $\mu =(\mu _v)_{v\in V}$
be a weight on V. Let
$\mu =(\mu _v)_{v\in V}$
be a weight on V. Let
![]() $X=\ell ^p(V,\mu )$
,
$X=\ell ^p(V,\mu )$
,
![]() $1\leq p <+\infty $
, or
$1\leq p <+\infty $
, or
![]() $X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. Then the following assertions are equivalent:
$X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. Then the following assertions are equivalent:
-
(1) B is hypercyclic.
-
(2) B is weakly mixing.
-
(3) There is an increasing sequence
 $(n_k)_{k\in \mathbb {N}}$
of positive integers such that, for each
$(n_k)_{k\in \mathbb {N}}$
of positive integers such that, for each
 $v \in V$
, we have
$v \in V$
, we have  $$ \begin{align*}\begin{cases} \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty,\\ &\\ \underset{u\in\mathrm{Chi}^{n_{k}}(v)}{\inf}\,|\mu_u|\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu), \\ &\\ \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{1}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu). \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty,\\ &\\ \underset{u\in\mathrm{Chi}^{n_{k}}(v)}{\inf}\,|\mu_u|\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu), \\ &\\ \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{1}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu). \end{cases}\end{align*} $$
For the case of unrooted directed trees, we refer to [Reference Grosse-Erdmann and Papathanasiou22, Theorem 5.2]. In what follows, we will require the following lemma, which played a crucial role in establishing the results in [Reference Grosse-Erdmann and Papathanasiou22].
Lemma 2.4 [Reference Grosse-Erdmann and Papathanasiou22, Lemma 4.2]
Let J be a finite or countable set and let
![]() $\mu =(\mu _j)_{j\in J}\in (\mathbb {K}\setminus \lbrace 0\rbrace )^{J}$
. Then
$\mu =(\mu _j)_{j\in J}\in (\mathbb {K}\setminus \lbrace 0\rbrace )^{J}$
. Then
 $$ \begin{align*}\underset{\|x\|_1=1}{\inf}\Big(\sum_{j\in J}|x_j\mu_j|^p\Big)^{1/p}=\Big(\underset{j\in J}{\sum}\,\frac{1}{|\mu_j|^{p^\ast}}\Big)^{-1/p^{\ast}},\quad 1<p<+\infty, \text{ and } p^{\ast}=\frac{p}{p-1},\end{align*} $$
$$ \begin{align*}\underset{\|x\|_1=1}{\inf}\Big(\sum_{j\in J}|x_j\mu_j|^p\Big)^{1/p}=\Big(\underset{j\in J}{\sum}\,\frac{1}{|\mu_j|^{p^\ast}}\Big)^{-1/p^{\ast}},\quad 1<p<+\infty, \text{ and } p^{\ast}=\frac{p}{p-1},\end{align*} $$
 $$ \begin{align*}\underset{\|x\|_1=1}{\inf}\sup_{j\in J}|x_j\mu_j|=\Big(\underset{j\in J}{\sum}\,\frac{1}{|\mu_j|}\Big)^{-1},\end{align*} $$
$$ \begin{align*}\underset{\|x\|_1=1}{\inf}\sup_{j\in J}|x_j\mu_j|=\Big(\underset{j\in J}{\sum}\,\frac{1}{|\mu_j|}\Big)^{-1},\end{align*} $$
where
![]() $x\in \mathbb {K}^J$
,
$x\in \mathbb {K}^J$
,
![]() $\|x\|_{1}=\sum _{j\in J}|x_j|$
and
$\|x\|_{1}=\sum _{j\in J}|x_j|$
and
![]() $\infty ^{-1}=0$
. The same holds when the sequences x are required, in addition, to be of finite support.
$\infty ^{-1}=0$
. The same holds when the sequences x are required, in addition, to be of finite support.
2.3 Furstenberg families
We devote this subsection to recalling the necessary definitions related to Furstenberg families. A nonempty family
![]() $\mathcal {F}$
of subsets of
$\mathcal {F}$
of subsets of
![]() $\mathbb {N}_0$
is a Furstenberg family, if for all
$\mathbb {N}_0$
is a Furstenberg family, if for all
![]() $A \in \mathcal {F}$
it holds
$A \in \mathcal {F}$
it holds
-
• A is infinite;
-
• If
 $A \subset B \subset \mathbb {N}_0$
, then
$A \subset B \subset \mathbb {N}_0$
, then
 $B\in \mathcal {F}$
.
$B\in \mathcal {F}$
.
Let
![]() $\mathcal {F}\subset \mathcal {P}(\mathbb {N}_0)$
be a Furstenberg family. Following [Reference Bès, Menet, Peris and Puig9], we denote by
$\mathcal {F}\subset \mathcal {P}(\mathbb {N}_0)$
be a Furstenberg family. Following [Reference Bès, Menet, Peris and Puig9], we denote by
![]() $\mathcal {\widetilde {F}}$
(resp.,
$\mathcal {\widetilde {F}}$
(resp.,
![]() $\mathcal {\widetilde {F}}_{+}$
) the Furstenberg family consisting of subsets
$\mathcal {\widetilde {F}}_{+}$
) the Furstenberg family consisting of subsets
![]() $A\subset \mathbb {N}_0$
such that for every
$A\subset \mathbb {N}_0$
such that for every
![]() $N\in \mathbb {N}_0$
, there exists
$N\in \mathbb {N}_0$
, there exists
![]() $B\in \mathcal {F}$
satisfying
$B\in \mathcal {F}$
satisfying
It is clear that
![]() $\mathcal {\widetilde {F}}\subset \mathcal {\widetilde {F}}_{+}\subset \mathcal {F}$
; thus, any
$\mathcal {\widetilde {F}}\subset \mathcal {\widetilde {F}}_{+}\subset \mathcal {F}$
; thus, any
![]() $\mathcal {\widetilde {F}}$
-transitive operator is
$\mathcal {\widetilde {F}}$
-transitive operator is
![]() $\mathcal {F}$
-transitive.
$\mathcal {F}$
-transitive.
A filter on
![]() $\mathbb {N}_0$
is a Furstenberg family
$\mathbb {N}_0$
is a Furstenberg family
![]() $\mathcal {F}$
of subsets of
$\mathcal {F}$
of subsets of
![]() $\mathbb {N}_0$
that satisfies the property
$\mathbb {N}_0$
that satisfies the property
![]() $A \cap B \in \mathcal {F}$
whenever
$A \cap B \in \mathcal {F}$
whenever
![]() $A, B \in \mathcal {F}$
. A nonempty collection
$A, B \in \mathcal {F}$
. A nonempty collection
![]() $\mathcal {B}$
of subsets of
$\mathcal {B}$
of subsets of
![]() $\mathbb {N}_0$
is called a filter base if the following conditions hold:
$\mathbb {N}_0$
is called a filter base if the following conditions hold:
-
• Every set in
 $\mathcal {B}$
is infinite.
$\mathcal {B}$
is infinite. -
• The intersection of any two sets in
 $\mathcal {B}$
contains a set in
$\mathcal {B}$
contains a set in
 $\mathcal {B}$
.
$\mathcal {B}$
.
It is worth noting that every filter is a filter base. Conversely, if
![]() $\mathcal {B}$
is a filter base of subsets of
$\mathcal {B}$
is a filter base of subsets of
![]() $\mathbb {N}_0$
, then the collection of sets
$\mathbb {N}_0$
, then the collection of sets
forms a filter, called the filter generated by
![]() $\mathcal {B}$
. For a more detailed discussion on filters and filter bases, see [Reference Bourbaki13, Chapter I, Section 6]. See also [Reference Bès, Menet, Peris and Puig9, Reference Grivaux, López-Martínez and Peris20] for further examples of Furstenberg families and filters.
$\mathcal {B}$
. For a more detailed discussion on filters and filter bases, see [Reference Bourbaki13, Chapter I, Section 6]. See also [Reference Bès, Menet, Peris and Puig9, Reference Grivaux, López-Martínez and Peris20] for further examples of Furstenberg families and filters.
3
 $\mathcal {F}$
-transitivity criterion
$\mathcal {F}$
-transitivity criterion
In [Reference Bès, Menet, Peris and Puig9, Theorem 2.4], Bès, Menet, Peris, and Puig established an
![]() $\mathcal {F}$
-transitivity criterion. This criterion uses the concept of a limit along the family
$\mathcal {F}$
-transitivity criterion. This criterion uses the concept of a limit along the family
![]() $\mathcal {F}$
. Let
$\mathcal {F}$
. Let
![]() $(x_n)_n$
be a sequence in X, and let
$(x_n)_n$
be a sequence in X, and let
![]() $x \in X$
. We say that
$x \in X$
. We say that
if
![]() $\{n\in \mathbb {N}_0:\, x_n\in U\}\in \mathcal {F}$
holds for every neighborhood U of x. In our analysis, we will require a variant of this criterion, combined with the hypercyclicity criterion [Reference Grosse-Erdmann and Papathanasiou22, Proposition 5.1]. For the sake of completeness, we will include its proof, which is an adaptation of the proof provided in [Reference Bès, Menet, Peris and Puig9, Theorem 2.4].
$\{n\in \mathbb {N}_0:\, x_n\in U\}\in \mathcal {F}$
holds for every neighborhood U of x. In our analysis, we will require a variant of this criterion, combined with the hypercyclicity criterion [Reference Grosse-Erdmann and Papathanasiou22, Proposition 5.1]. For the sake of completeness, we will include its proof, which is an adaptation of the proof provided in [Reference Bès, Menet, Peris and Puig9, Theorem 2.4].
Theorem 3.1 (
 $\mathcal {F}$
-Transitivity Criterion)
$\mathcal {F}$
-Transitivity Criterion)
Let X be an infinite-dimensional Banach space,
![]() $T\in \mathcal {L}(X)$
and let
$T\in \mathcal {L}(X)$
and let
![]() $\mathcal {F}$
be a Furstenberg family on
$\mathcal {F}$
be a Furstenberg family on
![]() $\mathbb {N}_0$
such that
$\mathbb {N}_0$
such that
![]() $\widetilde {\mathcal {F}}$
is a filter. Suppose that there exist two dense subsets
$\widetilde {\mathcal {F}}$
is a filter. Suppose that there exist two dense subsets
![]() $X_0$
and
$X_0$
and
![]() $Y_0$
in X and maps
$Y_0$
in X and maps
![]() $I_n:X_0\to X$
and
$I_n:X_0\to X$
and
![]() $S_n: Y_0\to X$
,
$S_n: Y_0\to X$
,
![]() $n\in \mathbb {N}_0$
, such that, for any
$n\in \mathbb {N}_0$
, such that, for any
![]() $x\in X_0$
and any
$x\in X_0$
and any
![]() $y\in Y_0$
, the following conditions hold:
$y\in Y_0$
, the following conditions hold:
-
(1)
 $\mathcal {F}\text {-}\underset {n}{\lim }\,(I_nx,T^nI_nx)=(x,0)$
;
$\mathcal {F}\text {-}\underset {n}{\lim }\,(I_nx,T^nI_nx)=(x,0)$
; -
(2)
 $\mathcal {F}\text {-}\underset {n}{\lim }\,(S_ny,T^nS_ny)=(0,y)$
.
$\mathcal {F}\text {-}\underset {n}{\lim }\,(S_ny,T^nS_ny)=(0,y)$
.
Then T is
![]() $\widetilde {\mathcal {F}}$
-transitive.
$\widetilde {\mathcal {F}}$
-transitive.
Proof Note that, according to condition
![]() $(2)$
, T has dense range in X. Now, let
$(2)$
, T has dense range in X. Now, let
![]() $U,V$
be nonempty open subsets of X. There exist nonempty open subsets
$U,V$
be nonempty open subsets of X. There exist nonempty open subsets
![]() $U',V'$
of X and a
$U',V'$
of X and a
![]() $0$
-neighborhood W such that
$0$
-neighborhood W such that
Since
![]() $\widetilde {\mathcal {F}}$
is a filter and
$\widetilde {\mathcal {F}}$
is a filter and
it is enough to show that
![]() $N(U',W)\in \widetilde {\mathcal {F}}$
and
$N(U',W)\in \widetilde {\mathcal {F}}$
and
![]() $N(W,V')\in \widetilde {\mathcal {F}}$
. Let
$N(W,V')\in \widetilde {\mathcal {F}}$
. Let
![]() $N\in \mathbb {N}_0$
. Since T has dense range, the sets
$N\in \mathbb {N}_0$
. Since T has dense range, the sets
![]() $T^{-N}U'$
and
$T^{-N}U'$
and
![]() $T^{-N}V'$
are nonempty open sets. Choose
$T^{-N}V'$
are nonempty open sets. Choose
![]() $x\in X_0\cap T^{-N}U'$
and
$x\in X_0\cap T^{-N}U'$
and
![]() $y\in Y_0\cap T^{-N}V'$
. We start by showing that
$y\in Y_0\cap T^{-N}V'$
. We start by showing that
![]() $N(T^{-N}U',W)\in \widetilde {\mathcal {F}}_{+}$
. For any
$N(T^{-N}U',W)\in \widetilde {\mathcal {F}}_{+}$
. For any
![]() $M\in \mathbb {N}_0$
, by
$M\in \mathbb {N}_0$
, by
![]() $(1)$
, there exists
$(1)$
, there exists
![]() $A_M\in \mathcal {F}$
such that, for every
$A_M\in \mathcal {F}$
such that, for every
![]() $n\in A_M$
,
$n\in A_M$
,
 $$ \begin{align*}I_nx\in T^{-N}U' \quad \text{and} \quad T^nI_nx\in \bigcap_{k=0}^{M}T^{-k}W.\end{align*} $$
$$ \begin{align*}I_nx\in T^{-N}U' \quad \text{and} \quad T^nI_nx\in \bigcap_{k=0}^{M}T^{-k}W.\end{align*} $$
Note that, for any
![]() $n\in A_M+[\![0,M]\!]$
, there exists
$n\in A_M+[\![0,M]\!]$
, there exists
![]() $k\in [\![0,M]\!]$
such that
$k\in [\![0,M]\!]$
such that
![]() $n-k\in A_M$
, hence
$n-k\in A_M$
, hence
therefore,
![]() $I_{n-k}x \in T^{-N}U'$
and
$I_{n-k}x \in T^{-N}U'$
and
![]() $T^{n}I_{n-k}x\in W$
, so
$T^{n}I_{n-k}x\in W$
, so
![]() $n\in N(T^{-N}U',W)$
. Thus,
$n\in N(T^{-N}U',W)$
. Thus,
![]() $A_M+[\![0,M]\!]\subset N(T^{-N}U',W)$
holds for any arbitrary
$A_M+[\![0,M]\!]\subset N(T^{-N}U',W)$
holds for any arbitrary
![]() $M\in \mathbb {N}_0$
. Consequently,
$M\in \mathbb {N}_0$
. Consequently,
![]() $N(T^{-N}U',W) \in \widetilde {\mathcal {F}}_{+}$
. Thus, there is
$N(T^{-N}U',W) \in \widetilde {\mathcal {F}}_{+}$
. Thus, there is
![]() $B\in \mathcal {F}$
such that
$B\in \mathcal {F}$
such that
![]() $B+[\![0,2N]\!]\subset N(T^{-N}U',W)$
. Therefore,
$B+[\![0,2N]\!]\subset N(T^{-N}U',W)$
. Therefore,
and, since N was arbitrary, we deduce that
![]() $N(U',W)\in \widetilde {\mathcal {F}}$
.
$N(U',W)\in \widetilde {\mathcal {F}}$
.
On the other hand, by
![]() $(2)$
, there is
$(2)$
, there is
![]() $B\in \mathcal {F}$
such that, for every
$B\in \mathcal {F}$
such that, for every
![]() $n\in B$
,
$n\in B$
,
 $$ \begin{align*}S_n y\in \bigcap_{k=0}^{2N}T^{-k}W \quad\text{and}\quad T^n S_n(y)\in T^{-N}V'.\end{align*} $$
$$ \begin{align*}S_n y\in \bigcap_{k=0}^{2N}T^{-k}W \quad\text{and}\quad T^n S_n(y)\in T^{-N}V'.\end{align*} $$
In particular, for any
![]() $n\in (B+[\![-N,N]\!])\cap \mathbb {N}_0$
, there exists
$n\in (B+[\![-N,N]\!])\cap \mathbb {N}_0$
, there exists
![]() $k\in [\![-N,N]\!]$
such that
$k\in [\![-N,N]\!]$
such that
![]() $n-k\in B$
and
$n-k\in B$
and
![]() $N-k\in [\![0,2N]\!]$
, thus
$N-k\in [\![0,2N]\!]$
, thus
hence
from which we deduce that
![]() $n\in N(W,V')$
. Therefore,
$n\in N(W,V')$
. Therefore,
Since N was arbitrary, we obtain that
![]() $N(W,V')\in \widetilde {\mathcal {F}}$
. This finishes the proof.
$N(W,V')\in \widetilde {\mathcal {F}}$
. This finishes the proof.
4
 $\mathcal {F}$
-transitivity - rooted case
$\mathcal {F}$
-transitivity - rooted case
Our first main result provides a characterization of
![]() $\mathcal {F}$
-transitivity for backward shifts on rooted directed trees and establishes its equivalence with certain weak properties.
$\mathcal {F}$
-transitivity for backward shifts on rooted directed trees and establishes its equivalence with certain weak properties.
Theorem 4.1 Let
![]() $(V,E)$
be a rooted directed tree, let
$(V,E)$
be a rooted directed tree, let
![]() $\mu =(\mu _v)_{v\in V}$
be a weight on V, and let
$\mu =(\mu _v)_{v\in V}$
be a weight on V, and let
![]() $\mathcal {F}$
be a Furstenberg family on
$\mathcal {F}$
be a Furstenberg family on
![]() $\mathbb {N}_0$
. Let
$\mathbb {N}_0$
. Let
![]() $X=\ell ^p(V,\mu )$
,
$X=\ell ^p(V,\mu )$
,
![]() $1\leq p <+\infty $
, or
$1\leq p <+\infty $
, or
![]() $X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. The following assertions are equivalent:
$X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. The following assertions are equivalent:
-
(1) B is
 $\widetilde {\mathcal {F}}$
-transitive.
$\widetilde {\mathcal {F}}$
-transitive. -
(2) B is
 $\mathcal {F}$
-transitive.
$\mathcal {F}$
-transitive. -
(3) There exists a bounded subset
 $C\subset X\setminus \{0\}$
such that for every nonempty weakly open subset
$C\subset X\setminus \{0\}$
such that for every nonempty weakly open subset
 $W\subset X$
,
$W\subset X$
,
 $N(C,W)\in \mathcal {F}$
.
$N(C,W)\in \mathcal {F}$
. -
(4) For every
 $N\in \mathbb {N}$
and every finite subset
$N\in \mathbb {N}$
and every finite subset
 $F\subset V$
, we have
$F\subset V$
, we have  $$ \begin{align*}\bigcap_{v\in F}\Big\{n\in\mathbb{N}_0:\, \underset{u\in\mathrm{Chi}^n(v)}{\sup}\dfrac{1}{|\mu_u|}>N\Big\}\in\mathcal{F},\quad \text{if } X=\ell^1(V,\mu);\end{align*} $$
$$ \begin{align*}\bigcap_{v\in F}\Big\{n\in\mathbb{N}_0:\, \underset{u\in\mathrm{Chi}^n(v)}{\sup}\dfrac{1}{|\mu_u|}>N\Big\}\in\mathcal{F},\quad \text{if } X=\ell^1(V,\mu);\end{align*} $$
 $$ \begin{align*}\bigcap_{v\in F}\Big\{n\in\mathbb{N}_0:\, \Big(\underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\}\in\mathcal{F},\quad \text{if }X=\ell^p(V,\mu),\, 1<p<+\infty;\end{align*} $$
$$ \begin{align*}\bigcap_{v\in F}\Big\{n\in\mathbb{N}_0:\, \Big(\underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\}\in\mathcal{F},\quad \text{if }X=\ell^p(V,\mu),\, 1<p<+\infty;\end{align*} $$
 $$ \begin{align*}\bigcap_{v\in F}\Big\{n\in\mathbb{N}_0:\, \underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|}>N\Big\}\in\mathcal{F},\quad \text{if }X=c_0(V,\mu).\end{align*} $$
$$ \begin{align*}\bigcap_{v\in F}\Big\{n\in\mathbb{N}_0:\, \underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|}>N\Big\}\in\mathcal{F},\quad \text{if }X=c_0(V,\mu).\end{align*} $$
If
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $A\cap [n,+\infty [ \in \mathcal {F}$
whenever
$A\cap [n,+\infty [ \in \mathcal {F}$
whenever
![]() $A\in \mathcal {F}$
and
$A\in \mathcal {F}$
and
![]() $n\in \mathbb {N}$
, then the above conditions are equivalent to
$n\in \mathbb {N}$
, then the above conditions are equivalent to
-
(5) For every
 $g\in X$
, for every open neighborhood U of g, for every weakly open neighborhood W of g,
$g\in X$
, for every open neighborhood U of g, for every weakly open neighborhood W of g,
 $N(U,W)\in \mathcal {F}$
.
$N(U,W)\in \mathcal {F}$
.
If
![]() $\mathcal {F}$
is a filter, then the conditions
$\mathcal {F}$
is a filter, then the conditions
![]() $(1)\text {-}(4)$
are equivalent to
$(1)\text {-}(4)$
are equivalent to
-
(6) For every
 $N\in \mathbb {N}$
and every
$N\in \mathbb {N}$
and every
 $v\in V$
, we have
$v\in V$
, we have  $$ \begin{align*}\Big\{n\in\mathbb{N}_0:\, \underset{u\in\mathrm{Chi}^n(v)}{\sup}\dfrac{1}{|\mu_u|}>N\Big\}\in\mathcal{F},\quad \text{if } X=\ell^1(V,\mu);\end{align*} $$
$$ \begin{align*}\Big\{n\in\mathbb{N}_0:\, \underset{u\in\mathrm{Chi}^n(v)}{\sup}\dfrac{1}{|\mu_u|}>N\Big\}\in\mathcal{F},\quad \text{if } X=\ell^1(V,\mu);\end{align*} $$
 $$ \begin{align*}\Big\{n\in\mathbb{N}_0:\, \Big(\underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\}\in\mathcal{F},\quad \text{if }X=\ell^p(V,\mu),\, 1<p<+\infty;\end{align*} $$
$$ \begin{align*}\Big\{n\in\mathbb{N}_0:\, \Big(\underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\}\in\mathcal{F},\quad \text{if }X=\ell^p(V,\mu),\, 1<p<+\infty;\end{align*} $$
 $$ \begin{align*}\Big\{n\in\mathbb{N}_0:\, \underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|}>N\Big\}\in\mathcal{F},\quad \text{if }X=c_0(V,\mu).\end{align*} $$
$$ \begin{align*}\Big\{n\in\mathbb{N}_0:\, \underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|}>N\Big\}\in\mathcal{F},\quad \text{if }X=c_0(V,\mu).\end{align*} $$
Proof We will only prove the equivalences in the case where
![]() $X = \ell ^p(V,\mu )$
with
$X = \ell ^p(V,\mu )$
with
![]() $1 < p < +\infty $
. A similar argument can be made to deduce the cases where
$1 < p < +\infty $
. A similar argument can be made to deduce the cases where
![]() $X = \ell ^1(V,\mu )$
and
$X = \ell ^1(V,\mu )$
and
![]() $X = c_0(V,\mu )$
. It is clear that
$X = c_0(V,\mu )$
. It is clear that
![]() $(2)\Rightarrow (3)$
and
$(2)\Rightarrow (3)$
and
![]() $(2)\Rightarrow (5)$
. Moreover,
$(2)\Rightarrow (5)$
. Moreover,
![]() $(1)\Rightarrow (2)$
since
$(1)\Rightarrow (2)$
since
![]() $\widetilde {\mathcal {F}} \subset \mathcal {F}$
. Suppose that B is
$\widetilde {\mathcal {F}} \subset \mathcal {F}$
. Suppose that B is
![]() $\mathcal {F}$
-transitive; thus, it is transitive (equivalently, hypercyclic). Using [Reference Grosse-Erdmann and Papathanasiou22, Theorem 4.3], we can conclude that B is weakly mixing. Thus, B is both
$\mathcal {F}$
-transitive; thus, it is transitive (equivalently, hypercyclic). Using [Reference Grosse-Erdmann and Papathanasiou22, Theorem 4.3], we can conclude that B is weakly mixing. Thus, B is both
![]() $\mathcal {F}$
-transitive and weakly mixing, which is equivalent to saying that B is
$\mathcal {F}$
-transitive and weakly mixing, which is equivalent to saying that B is
![]() $\widetilde {\mathcal {F}}$
-transitive, according to [Reference Bès, Menet, Peris and Puig9, Lemma 2.3]. Hence,
$\widetilde {\mathcal {F}}$
-transitive, according to [Reference Bès, Menet, Peris and Puig9, Lemma 2.3]. Hence,
![]() $(2)\Rightarrow (1)$
. Moreover, it clear that
$(2)\Rightarrow (1)$
. Moreover, it clear that
![]() $(4)\Leftrightarrow (6)$
when
$(4)\Leftrightarrow (6)$
when
![]() $\mathcal {F}$
is a filter.
$\mathcal {F}$
is a filter.
![]() $(3)\Rightarrow (4)$
. Let C be a bounded subset of
$(3)\Rightarrow (4)$
. Let C be a bounded subset of
![]() $\ell ^p(V,\mu )\setminus \{0\}$
such that
$\ell ^p(V,\mu )\setminus \{0\}$
such that
![]() $N(W,C)\in \mathcal {F}$
, for every nonempty weakly open subset W of
$N(W,C)\in \mathcal {F}$
, for every nonempty weakly open subset W of
![]() $\ell ^p(V,\mu )$
. Set
$\ell ^p(V,\mu )$
. Set
![]() $M:=\sup \{\|f\|_{p,\mu }:\, f\in C\}<+\infty $
. Let
$M:=\sup \{\|f\|_{p,\mu }:\, f\in C\}<+\infty $
. Let
![]() $N\in \mathbb {N}$
and let
$N\in \mathbb {N}$
and let
![]() $F\subset V$
be a finite subset. Then
$F\subset V$
be a finite subset. Then
is a weakly open neighborhood of
![]() $(MN+1)\sum _{u\in F}e_u$
. By the hypothesis,
$(MN+1)\sum _{u\in F}e_u$
. By the hypothesis,
![]() $N(C,W)\in \mathcal {F}$
. Since
$N(C,W)\in \mathcal {F}$
. Since
![]() $\mathcal {F}$
is a Furstenberg family, we need only to prove that
$\mathcal {F}$
is a Furstenberg family, we need only to prove that
 $$ \begin{align} N(C,W)\subset \bigcap_{v\in F}\Big\{n\in\mathbb{N}_0:\, \Big(\underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\}. \end{align} $$
$$ \begin{align} N(C,W)\subset \bigcap_{v\in F}\Big\{n\in\mathbb{N}_0:\, \Big(\underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\}. \end{align} $$
Let
![]() $n\in N(C,W)$
. There exists then
$n\in N(C,W)$
. There exists then
![]() $f\in C$
such that
$f\in C$
such that
![]() $B^{n}f\in W$
, thus for every
$B^{n}f\in W$
, thus for every
![]() $v\in F$
$v\in F$
hence, by using Hölder’s inequality, we obtain
 $$ \begin{align*} MN&<\sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)|\\ &\leq \Big( \sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)\mu_u|^p\Big)^{1/p}\Big( \sum_{u\in\mathrm{Chi}^{n}(v)}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}\\ &\leq \|f\|_{p,\mu}\Big( \sum_{u\in\mathrm{Chi}^{n}(v)}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}\\ &\leq M\,\Big( \sum_{u\in\mathrm{Chi}^{n}(v)}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast},\\ \end{align*} $$
$$ \begin{align*} MN&<\sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)|\\ &\leq \Big( \sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)\mu_u|^p\Big)^{1/p}\Big( \sum_{u\in\mathrm{Chi}^{n}(v)}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}\\ &\leq \|f\|_{p,\mu}\Big( \sum_{u\in\mathrm{Chi}^{n}(v)}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}\\ &\leq M\,\Big( \sum_{u\in\mathrm{Chi}^{n}(v)}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast},\\ \end{align*} $$
therefore
 $$ \begin{align*}\Big( \sum_{u\in\mathrm{Chi}^{n}(v)}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N,\quad \forall v\in F,\end{align*} $$
$$ \begin{align*}\Big( \sum_{u\in\mathrm{Chi}^{n}(v)}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N,\quad \forall v\in F,\end{align*} $$
and so (4.1) holds.
Let us show that
![]() $(4)\Rightarrow (2)$
. Assume that
$(4)\Rightarrow (2)$
. Assume that
![]() $(4)$
holds, that is, for every
$(4)$
holds, that is, for every
![]() $N>0$
and every finite subset
$N>0$
and every finite subset
![]() $F\subset V$
, we have
$F\subset V$
, we have
 $$ \begin{align*}I(F,N):= \bigcap_{v\in F}\Big\{n\in\mathbb{N}_0:\, \Big(\underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\}\in\mathcal{F}.\end{align*} $$
$$ \begin{align*}I(F,N):= \bigcap_{v\in F}\Big\{n\in\mathbb{N}_0:\, \Big(\underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\}\in\mathcal{F}.\end{align*} $$
Let
![]() $\mathcal {B}$
be the filter base consisting of all subsets
$\mathcal {B}$
be the filter base consisting of all subsets
![]() $I(F,N)$
of
$I(F,N)$
of
![]() $\mathbb {N}_0$
, where
$\mathbb {N}_0$
, where
![]() $N>0$
and
$N>0$
and
![]() $F\subset V$
is finite. We define
$F\subset V$
is finite. We define
In other words,
![]() $\mathcal {F}_{\mathcal {B}}$
is the filter generated by
$\mathcal {F}_{\mathcal {B}}$
is the filter generated by
![]() $\mathcal {B}$
. We will show that B satisfies the
$\mathcal {B}$
. We will show that B satisfies the
![]() $\mathcal {F}_{\mathcal {B}}$
-transitivity criterion, which implies that B is
$\mathcal {F}_{\mathcal {B}}$
-transitivity criterion, which implies that B is
![]() $\mathcal {F}$
-transitive since
$\mathcal {F}$
-transitive since
![]() $\mathcal {F}_{\mathcal {B}}\subset \mathcal {F}$
. Set
$\mathcal {F}_{\mathcal {B}}\subset \mathcal {F}$
. Set
![]() $\mathcal {D}=\mathrm {span}\{e_v:\, v \in V\}$
. Note that
$\mathcal {D}=\mathrm {span}\{e_v:\, v \in V\}$
. Note that
![]() $\mathcal {D}$
is dense in
$\mathcal {D}$
is dense in
![]() $\ell ^p(V,\mu )$
. Let
$\ell ^p(V,\mu )$
. Let
![]() $f=\sum _{u\in F}f(u) e_u\in \mathcal {D}$
, with
$f=\sum _{u\in F}f(u) e_u\in \mathcal {D}$
, with
![]() $F\subset V$
finite. Let
$F\subset V$
finite. Let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\mathcal {U}:=B(0,\varepsilon )$
be the open ball of center
$\mathcal {U}:=B(0,\varepsilon )$
be the open ball of center
![]() $0$
and radius
$0$
and radius
![]() $\varepsilon $
in
$\varepsilon $
in
![]() $\ell ^p(V,\mu )$
. Let us start by proving that
$\ell ^p(V,\mu )$
. Let us start by proving that
To achieve this, it is enough to find a number
![]() $N\geq 1$
such that
$N\geq 1$
such that
![]() $I(F,N) \subset N(f,\mathcal {U})$
. First, select an integer
$I(F,N) \subset N(f,\mathcal {U})$
. First, select an integer
![]() $n_0\in \mathbb {N}$
large enough such that
$n_0\in \mathbb {N}$
large enough such that
![]() $\mathrm {Chi}^{n}(V)\cap F=\emptyset $
for every integer
$\mathrm {Chi}^{n}(V)\cap F=\emptyset $
for every integer
![]() $n\geq n_0$
. Then, we set
$n\geq n_0$
. Then, we set
 $$ \begin{align*}N:=1+\underset{v\in F}{\max}\,\underset{0\leq k<n_0}{\max}\Big(\underset{u\in\mathrm{Chi}^k(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}.\end{align*} $$
$$ \begin{align*}N:=1+\underset{v\in F}{\max}\,\underset{0\leq k<n_0}{\max}\Big(\underset{u\in\mathrm{Chi}^k(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}.\end{align*} $$
Note that, by using Proposition 2.2 and the boundedness of
![]() $B^{k}$
for every
$B^{k}$
for every
![]() $0\leq k<n_0$
, N is finite. Now, suppose that
$0\leq k<n_0$
, N is finite. Now, suppose that
![]() $n\in I(F,N)$
. This implies that
$n\in I(F,N)$
. This implies that
![]() $n\geq n_0$
. Thus, for every
$n\geq n_0$
. Thus, for every
![]() $v\in V$
, we have
$v\in V$
, we have
![]() $\mathrm {Chi}^n(v)\cap F=\emptyset $
, hence,
$\mathrm {Chi}^n(v)\cap F=\emptyset $
, hence,
![]() $(B^{n} f)(v)=0$
. This implies that
$(B^{n} f)(v)=0$
. This implies that
![]() $n\in N(f,\mathcal {U})$
. Therefore, we have shown that
$n\in N(f,\mathcal {U})$
. Therefore, we have shown that
![]() $I(F,N) \subset N(f,\mathcal {U})$
, and consequently,
$I(F,N) \subset N(f,\mathcal {U})$
, and consequently,
![]() $N(f,\mathcal {U})\in \mathcal {F}_{\mathcal {B}}$
since
$N(f,\mathcal {U})\in \mathcal {F}_{\mathcal {B}}$
since
![]() $\mathcal {F}_{\mathcal {B}}$
is a Furstenberg family. Hence, the first condition of the
$\mathcal {F}_{\mathcal {B}}$
is a Furstenberg family. Hence, the first condition of the
![]() $\mathcal {F}_{\mathcal {B}}$
-transitivity criterion holds, where the maps
$\mathcal {F}_{\mathcal {B}}$
-transitivity criterion holds, where the maps
![]() $I_n$
correspond to the identity map.
$I_n$
correspond to the identity map.
Now, for every
![]() $v\in V$
, let
$v\in V$
, let
![]() $(\delta _{v,n})_n$
be a decreasing sequence of positive real numbers tending to zero. For all
$(\delta _{v,n})_n$
be a decreasing sequence of positive real numbers tending to zero. For all
![]() $v\in V$
and
$v\in V$
and
![]() $n\in \mathbb {N}_0$
, by Lemma 2.4, we have
$n\in \mathbb {N}_0$
, by Lemma 2.4, we have
 $$ \begin{align*}\underset{\|x\|_1=1}{\inf}\Big(\underset{u \in \mathrm{Chi}^{n}(v)}{\sum}|x_u\mu_u|^p\Big)^{1/p}=\Big(\underset{u \in \mathrm{Chi}^{n}(v)}{\sum}\,\frac{1}{|\mu_u|^{p^\ast}}\Big)^{-1/p^{\ast}}.\end{align*} $$
$$ \begin{align*}\underset{\|x\|_1=1}{\inf}\Big(\underset{u \in \mathrm{Chi}^{n}(v)}{\sum}|x_u\mu_u|^p\Big)^{1/p}=\Big(\underset{u \in \mathrm{Chi}^{n}(v)}{\sum}\,\frac{1}{|\mu_u|^{p^\ast}}\Big)^{-1/p^{\ast}}.\end{align*} $$
There exists then
![]() $g_{v,n}\in \mathbb {K}^V$
nonnegative, of support in
$g_{v,n}\in \mathbb {K}^V$
nonnegative, of support in
![]() $\mathrm {Chi}^{n}(v)$
, such that
$\mathrm {Chi}^{n}(v)$
, such that
 $$ \begin{align} & \sum_{u\in \mathrm{Chi}^{n}(v)}g_{v,n}(u)=1 \quad \text{and} \quad \nonumber\\&\quad\Big(\sum_{u\in \mathrm{Chi}^{n}(v)}|g_{v,n}(u)\,\mu_u|^p\Big)^{1/p}<\Big(\underset{u \in \mathrm{Chi}^{n}(v)}{\sum}\,\frac{1}{|\mu_u|^{p^\ast}}\Big)^{-1/p^{\ast}}+\delta_{v,n}. \end{align} $$
$$ \begin{align} & \sum_{u\in \mathrm{Chi}^{n}(v)}g_{v,n}(u)=1 \quad \text{and} \quad \nonumber\\&\quad\Big(\sum_{u\in \mathrm{Chi}^{n}(v)}|g_{v,n}(u)\,\mu_u|^p\Big)^{1/p}<\Big(\underset{u \in \mathrm{Chi}^{n}(v)}{\sum}\,\frac{1}{|\mu_u|^{p^\ast}}\Big)^{-1/p^{\ast}}+\delta_{v,n}. \end{align} $$
Note that
![]() $g_{v,n}\in \ell ^p(V,\mu )$
. Let us define the maps
$g_{v,n}\in \ell ^p(V,\mu )$
. Let us define the maps
![]() $S_k:\mathcal {D}\to \ell ^p(V,\mu )$
linearly, for
$S_k:\mathcal {D}\to \ell ^p(V,\mu )$
linearly, for
![]() $k\geq 0$
, by
$k\geq 0$
, by
Let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $g=\sum _{u\in F} g(a) e_a\in \mathcal {D}$
, where F is the support of g. Set again
$g=\sum _{u\in F} g(a) e_a\in \mathcal {D}$
, where F is the support of g. Set again
![]() $\mathcal {U}:=B(0,\varepsilon )$
and
$\mathcal {U}:=B(0,\varepsilon )$
and
![]() $\mathcal {V}:=B(g,\varepsilon )$
. We want to show that
$\mathcal {V}:=B(g,\varepsilon )$
. We want to show that
Let
![]() $n_0\in \mathbb {N}$
be large enough so that
$n_0\in \mathbb {N}$
be large enough so that
![]() $\frac {\varepsilon }{|g(a)| |F|}-\delta _{a,n_0}>0$
, for every
$\frac {\varepsilon }{|g(a)| |F|}-\delta _{a,n_0}>0$
, for every
![]() $a\in F$
(where
$a\in F$
(where
![]() $|F|$
stands for the cardinality of the finite set F). Set
$|F|$
stands for the cardinality of the finite set F). Set
 $$ \begin{align*}N=\max\Bigg\{1+\underset{v\in F}{\max}\,\underset{0\leq k<n_0}{\max}\Big(\underset{u\in\mathrm{Chi}^k(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}, \dfrac{1}{ \underset{a\in F}{\min}\big\{\frac{\varepsilon}{|g(a)| |F|}-\delta_{a,n_0}\big\}} \Bigg\}.\end{align*} $$
$$ \begin{align*}N=\max\Bigg\{1+\underset{v\in F}{\max}\,\underset{0\leq k<n_0}{\max}\Big(\underset{u\in\mathrm{Chi}^k(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}, \dfrac{1}{ \underset{a\in F}{\min}\big\{\frac{\varepsilon}{|g(a)| |F|}-\delta_{a,n_0}\big\}} \Bigg\}.\end{align*} $$
We will show that
![]() $I(F,N)\subset A$
. Note that
$I(F,N)\subset A$
. Note that
![]() $B^nS_ne_v=B^ng_{v,n}=e_v$
, for every integer
$B^nS_ne_v=B^ng_{v,n}=e_v$
, for every integer
![]() $n\geq 0$
. Indeed, by (4.2), we have
$n\geq 0$
. Indeed, by (4.2), we have
 $$ \begin{align*} (B^ng_{v,n})(a)&=\sum_{b\in \mathrm{Chi}^n(a)}g_{v,n}(b)\\ &=\begin{cases} 1 & \text{ if } a=v \\ 0 & \text{ if } a\neq v \end{cases}\\ &=e_v(a). \end{align*} $$
$$ \begin{align*} (B^ng_{v,n})(a)&=\sum_{b\in \mathrm{Chi}^n(a)}g_{v,n}(b)\\ &=\begin{cases} 1 & \text{ if } a=v \\ 0 & \text{ if } a\neq v \end{cases}\\ &=e_v(a). \end{align*} $$
Thus,
![]() $B^nS_ng=g\in \mathcal {V}$
, for every integer
$B^nS_ng=g\in \mathcal {V}$
, for every integer
![]() $n\geq 0$
. Let
$n\geq 0$
. Let
![]() $n\in I(F,N)$
, so as above and by the definition of N, we have
$n\in I(F,N)$
, so as above and by the definition of N, we have
![]() $n\geq n_0$
and
$n\geq n_0$
and
 $$ \begin{align*}\Big(\underset{u \in \mathrm{Chi}^{n}(a)}{\sum}\,\frac{1}{|\mu_u|^{p^\ast}}\Big)^{-1/p^{\ast}}<\dfrac{1}{N}, \, \forall a\in F,\end{align*} $$
$$ \begin{align*}\Big(\underset{u \in \mathrm{Chi}^{n}(a)}{\sum}\,\frac{1}{|\mu_u|^{p^\ast}}\Big)^{-1/p^{\ast}}<\dfrac{1}{N}, \, \forall a\in F,\end{align*} $$
thus, by using (4.2), we obtain:
 $$ \begin{align*}\Big(\sum_{u\in \mathrm{Chi}^{n}(a)}|g_{a,n}(u)\,\mu_u|^p\Big)^{1/p}<\dfrac{1}{N}+\delta_{a,n}, \, \forall a\in F,\end{align*} $$
$$ \begin{align*}\Big(\sum_{u\in \mathrm{Chi}^{n}(a)}|g_{a,n}(u)\,\mu_u|^p\Big)^{1/p}<\dfrac{1}{N}+\delta_{a,n}, \, \forall a\in F,\end{align*} $$
by using again the definition of N, we deduce
 $$ \begin{align*}\Big(\sum_{u\in \mathrm{Chi}^{n}(a)}|g_{a,n}(u)\,\mu_u|^p\Big)^{1/p}<\dfrac{\varepsilon}{|g(a)| |F|}, \, \forall a\in F,\end{align*} $$
$$ \begin{align*}\Big(\sum_{u\in \mathrm{Chi}^{n}(a)}|g_{a,n}(u)\,\mu_u|^p\Big)^{1/p}<\dfrac{\varepsilon}{|g(a)| |F|}, \, \forall a\in F,\end{align*} $$
therefore
 $$ \begin{align*} \|S_ng\|_{p,\mu} \leq \sum_{a\in F} |g(a)| \|g_{a,n}\|_{p,\mu} =\sum_{a\in F} |g(a)| \Big( \sum_{b\in\mathrm{Chi}^n(a)}|g_{a,n}(b)\mu_b|^p\Big)^{1/p} <\varepsilon, \end{align*} $$
$$ \begin{align*} \|S_ng\|_{p,\mu} \leq \sum_{a\in F} |g(a)| \|g_{a,n}\|_{p,\mu} =\sum_{a\in F} |g(a)| \Big( \sum_{b\in\mathrm{Chi}^n(a)}|g_{a,n}(b)\mu_b|^p\Big)^{1/p} <\varepsilon, \end{align*} $$
hence
![]() $S_ng\in \mathcal {U}$
. We have shown that
$S_ng\in \mathcal {U}$
. We have shown that
![]() $n\in A$
and so
$n\in A$
and so
![]() $I(F,N)\subset A$
. Consequently,
$I(F,N)\subset A$
. Consequently,
![]() $A\in \mathcal {F}_{\mathcal {B}}$
. This provides the second condition of the
$A\in \mathcal {F}_{\mathcal {B}}$
. This provides the second condition of the
![]() $\mathcal {F}_{\mathcal {B}}$
-transitivity criterion. Hence, B is
$\mathcal {F}_{\mathcal {B}}$
-transitivity criterion. Hence, B is
![]() $\mathcal {F}$
-transitive and statement
$\mathcal {F}$
-transitive and statement
![]() $(2)$
holds.
$(2)$
holds.
![]() $(5)\Rightarrow (4)$
. Let us assume that
$(5)\Rightarrow (4)$
. Let us assume that
![]() $(5)$
holds. Let F be a finite subset of V and let
$(5)$
holds. Let F be a finite subset of V and let
![]() $N\in \mathbb {N}$
. We want to show that
$N\in \mathbb {N}$
. We want to show that
 $$ \begin{align*}I(F,N):= \bigcap_{v\in F}\Big\{n\in\mathbb{N}_0:\, \Big(\underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\}\in\mathcal{F}.\end{align*} $$
$$ \begin{align*}I(F,N):= \bigcap_{v\in F}\Big\{n\in\mathbb{N}_0:\, \Big(\underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\}\in\mathcal{F}.\end{align*} $$
Set
![]() $g=\sum _{v\in F} e_v\in \ell ^p(V,\mu )$
. Let
$g=\sum _{v\in F} e_v\in \ell ^p(V,\mu )$
. Let
![]() $U=\{f\in \ell ^p(V,\mu ):\, \|f-g\|_{p,\mu }<1/(2N)\}$
and
$U=\{f\in \ell ^p(V,\mu ):\, \|f-g\|_{p,\mu }<1/(2N)\}$
and
![]() $W=\{f\in \ell ^p(V,\mu ):\, |\langle f- g, e_{v}\rangle |<1/(2N),\, \forall v\in F\}$
. By the hypothesis, we have
$W=\{f\in \ell ^p(V,\mu ):\, |\langle f- g, e_{v}\rangle |<1/(2N),\, \forall v\in F\}$
. By the hypothesis, we have
![]() $N(U,W)\in \mathcal {F}$
an so
$N(U,W)\in \mathcal {F}$
an so
![]() $N(U,W)\cap [n,+\infty [\in \mathcal {F}$
for all
$N(U,W)\cap [n,+\infty [\in \mathcal {F}$
for all
![]() $n\in \mathbb {N}$
. Let
$n\in \mathbb {N}$
. Let
![]() $n_0\in \mathbb {N}$
big enough so that
$n_0\in \mathbb {N}$
big enough so that
![]() $\mathrm {Chi}^{n}(F)\cap F=\emptyset $
, for all
$\mathrm {Chi}^{n}(F)\cap F=\emptyset $
, for all
![]() $n\geq n_0$
. We will show that
$n\geq n_0$
. We will show that
Let
![]() $n\in N(U,W)\cap [n_0,+\infty [$
. Thus,
$n\in N(U,W)\cap [n_0,+\infty [$
. Thus,
![]() $\mathrm {Chi}^{n}(F)\cap F=\emptyset $
and there exists
$\mathrm {Chi}^{n}(F)\cap F=\emptyset $
and there exists
![]() $f\in \ell ^p(V,\mu )$
such that
$f\in \ell ^p(V,\mu )$
such that
Fix now
![]() $v\in F$
. Then the rightmost inequality in (4.3) gives
$v\in F$
. Then the rightmost inequality in (4.3) gives
 $$ \begin{align*} 0<\dfrac{1}{2}\leq 1- \dfrac{1}{2N} < \sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)|. \end{align*} $$
$$ \begin{align*} 0<\dfrac{1}{2}\leq 1- \dfrac{1}{2N} < \sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)|. \end{align*} $$
Since
![]() $\mathrm {Chi}^{n}(v)\cap F=\emptyset $
, by using the leftmost inequality in (4.3), we obtain
$\mathrm {Chi}^{n}(v)\cap F=\emptyset $
, by using the leftmost inequality in (4.3), we obtain
 $$ \begin{align*} \sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)\mu_u|^p<\dfrac{1}{(2N)^p}. \end{align*} $$
$$ \begin{align*} \sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)\mu_u|^p<\dfrac{1}{(2N)^p}. \end{align*} $$
Using Hölder’s inequality (for
![]() $p>1$
) and the last two inequalities, we can conclude that:
$p>1$
) and the last two inequalities, we can conclude that:
 $$ \begin{align*} \dfrac{1}{2N}&> \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)\mu_u|^p\Big)^{1/p}\\ &\geq \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)|\Big) \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|\mu_u|^{-p^{\ast}}\Big)^{-1/p^{\ast}}\\ &>\dfrac{1}{2} \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|\mu_u|^{-p^{\ast}}\Big)^{-1/p^{\ast}}, \end{align*} $$
$$ \begin{align*} \dfrac{1}{2N}&> \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)\mu_u|^p\Big)^{1/p}\\ &\geq \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)|\Big) \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|\mu_u|^{-p^{\ast}}\Big)^{-1/p^{\ast}}\\ &>\dfrac{1}{2} \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|\mu_u|^{-p^{\ast}}\Big)^{-1/p^{\ast}}, \end{align*} $$
thus
 $$ \begin{align*}\Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|\mu_u|^{-p^{\ast}}\Big)^{1/p^{\ast}}>N.\end{align*} $$
$$ \begin{align*}\Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|\mu_u|^{-p^{\ast}}\Big)^{1/p^{\ast}}>N.\end{align*} $$
This holds for all
![]() $v\in F$
. Therefore,
$v\in F$
. Therefore,
![]() $n\in I(F,N)$
, hence
$n\in I(F,N)$
, hence
![]() $N(U,W)\cap [n_0,+\infty [\subset I(F,N)$
. Consequently,
$N(U,W)\cap [n_0,+\infty [\subset I(F,N)$
. Consequently,
![]() $I(F,N)\in \mathcal {F}$
.
$I(F,N)\in \mathcal {F}$
.
The following example shows that the equivalence between conditions
![]() $(4)$
and
$(4)$
and
![]() $(6)$
in Theorem 4.1 does not hold for Frustenberg families which are not filters.
$(6)$
in Theorem 4.1 does not hold for Frustenberg families which are not filters.
Example 4.2 Let
![]() $(V,E)$
be the following rooted directed tree.
$(V,E)$
be the following rooted directed tree.

Let
![]() $(m_{k})_{k\geq 1}$
be a strictly increasing sequence of nonnegative integers and
$(m_{k})_{k\geq 1}$
be a strictly increasing sequence of nonnegative integers and
![]() $\mu =(\mu _v)_{v\in V}$
be the weight defined by
$\mu =(\mu _v)_{v\in V}$
be the weight defined by
![]() $\mu _{\texttt {r}}=1$
and, for every
$\mu _{\texttt {r}}=1$
and, for every
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $\mu _{u_k}=1/\mu _{v_k}$
, where
$\mu _{u_k}=1/\mu _{v_k}$
, where
 $$ \begin{align*}(\mu_{v_k})_{k\geq1}=\Big(\underset{2m_1}{\underbrace{\dfrac{1}{2},\ldots, \dfrac{1}{2^{m_1}},\dfrac{2}{2^{m_1}},\ldots,\dfrac{1}{2},1}},\underset{2m_2}{\underbrace{2,\ldots, 2^{m_2},\dfrac{2^{m_2}}{2},\ldots,2,1}},\ldots\Big).\end{align*} $$
$$ \begin{align*}(\mu_{v_k})_{k\geq1}=\Big(\underset{2m_1}{\underbrace{\dfrac{1}{2},\ldots, \dfrac{1}{2^{m_1}},\dfrac{2}{2^{m_1}},\ldots,\dfrac{1}{2},1}},\underset{2m_2}{\underbrace{2,\ldots, 2^{m_2},\dfrac{2^{m_2}}{2},\ldots,2,1}},\ldots\Big).\end{align*} $$
Let B be the backward shift on
![]() $\ell ^p(V,\mu )$
,
$\ell ^p(V,\mu )$
,
![]() $1<p<+\infty $
. By Proposition 2.2, B is bounded and
$1<p<+\infty $
. By Proposition 2.2, B is bounded and
![]() $\|B\|=(2^{p^\ast }+1/2^{p^\ast })^{1/p^\ast }$
. Let
$\|B\|=(2^{p^\ast }+1/2^{p^\ast })^{1/p^\ast }$
. Let
![]() $\mathcal {J}$
be the Furstenberg family of infinite subsets of
$\mathcal {J}$
be the Furstenberg family of infinite subsets of
![]() $\mathbb {N}_0$
. Note that
$\mathbb {N}_0$
. Note that
![]() $\mathcal {J}$
is not a filter. By the definition of the weight, for any
$\mathcal {J}$
is not a filter. By the definition of the weight, for any
![]() $N\in \mathbb {N}$
and
$N\in \mathbb {N}$
and
![]() $k\in \mathbb {N}$
, we have
$k\in \mathbb {N}$
, we have
However,
![]() $I(u_k,N)\cap I(v_k,N)=\emptyset $
, so
$I(u_k,N)\cap I(v_k,N)=\emptyset $
, so
![]() $I(u_k,N)\cap I(v_k,N)\notin \mathcal {J}.$
$I(u_k,N)\cap I(v_k,N)\notin \mathcal {J}.$
A bounded linear operator T defined on a Banach space X is said to be weakly hypercyclic if there exists a vector
![]() $x \in X$
such that its orbit
$x \in X$
such that its orbit
![]() $\mathrm {Orb}(x,T)$
is dense in X with respect to the weak topology.
$\mathrm {Orb}(x,T)$
is dense in X with respect to the weak topology.
When the Furstenberg family
![]() $\mathcal {F}$
in the previous theorem is chosen as the collection of syndetic subsets of
$\mathcal {F}$
in the previous theorem is chosen as the collection of syndetic subsets of
![]() $\mathbb {N}_0$
, we can derive a characterization of topologically ergodic backward shift operators on rooted directed trees. Furthermore, when
$\mathbb {N}_0$
, we can derive a characterization of topologically ergodic backward shift operators on rooted directed trees. Furthermore, when
![]() $\mathcal {F}$
represents the family of infinite subsets,
$\mathcal {F}$
represents the family of infinite subsets,
![]() $\mathcal {F}$
-transitivity coincides with hypercyclicity. This allows us to deduce the following corollary.
$\mathcal {F}$
-transitivity coincides with hypercyclicity. This allows us to deduce the following corollary.
Corollary 4.3 Let
![]() $(V,E)$
be a rooted directed tree and let
$(V,E)$
be a rooted directed tree and let
![]() $\mu =(\mu _v)_{v\in V}$
be a weight on V. Let
$\mu =(\mu _v)_{v\in V}$
be a weight on V. Let
![]() $X=\ell ^p(V,\mu )$
,
$X=\ell ^p(V,\mu )$
,
![]() $1\leq p <+\infty $
, or
$1\leq p <+\infty $
, or
![]() $X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. Then the following assertions are equivalent:
$X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. Then the following assertions are equivalent:
-
(1) B is hypercyclic.
-
(2) B is weakly hypercyclic.
-
(3) There exists a bounded subset C of
 $X\setminus \{0\}$
such that
$X\setminus \{0\}$
such that
 $\mathrm {Orb}(C,B)$
is weakly dense in X.
$\mathrm {Orb}(C,B)$
is weakly dense in X. -
(4) For every
 $g\in X$
, for every open neighborhood U of g, for every weakly open neighborhood W of g, there exists an integer
$g\in X$
, for every open neighborhood U of g, for every weakly open neighborhood W of g, there exists an integer
 $n\geq 1$
such that
$n\geq 1$
such that  $$ \begin{align*}B^n(U)\cap W\neq\emptyset.\end{align*} $$
$$ \begin{align*}B^n(U)\cap W\neq\emptyset.\end{align*} $$
Note that the implication
![]() $(2)\Rightarrow (4)$
in the previous corollary holds for any operator (see [Reference Chan and Sanders17, p. 42]). Furthermore, it is worth mentioning that if there exists an integer n satisfying condition
$(2)\Rightarrow (4)$
in the previous corollary holds for any operator (see [Reference Chan and Sanders17, p. 42]). Furthermore, it is worth mentioning that if there exists an integer n satisfying condition
![]() $(4)$
, then the return set from U to W is infinite.
$(4)$
, then the return set from U to W is infinite.
Remark 4.4 Let X be a Banach space and
![]() $T\in \mathcal {L}(X)$
be a linear operator. If for any nonempty weakly open subset U of X, there exists an integer
$T\in \mathcal {L}(X)$
be a linear operator. If for any nonempty weakly open subset U of X, there exists an integer
![]() $n\geq 1$
such that
$n\geq 1$
such that
then there are infinitely many integers that satisfy this property. To see this, note that the range of T is weakly dense in X since it meets any nonempty weakly open subset of X. By Mazur’s theorem, the weak and norm closures of the range of T coincide, which implies that T has dense range.
Now, let U be a nonempty weakly open subset of X,
![]() $x\in U$
, and let
$x\in U$
, and let
![]() $n\geq 1$
be an integer such that
$n\geq 1$
be an integer such that
![]() $T^n x\in U$
. Then, the set
$T^n x\in U$
. Then, the set
![]() $W=U\cap T^{-n}(U)$
is a nonempty weakly open subset of X. By the hypothesis, there exists an integer
$W=U\cap T^{-n}(U)$
is a nonempty weakly open subset of X. By the hypothesis, there exists an integer
![]() $m\geq 1$
such that
$m\geq 1$
such that
![]() $T^m(W)\cap W\neq \emptyset $
, and so we have
$T^m(W)\cap W\neq \emptyset $
, and so we have
Repeating this argument, we conclude that there exist infinitely many integers
![]() $k\geq 1$
such that
$k\geq 1$
such that
![]() $T^k(U)\cap U\neq \emptyset $
.
$T^k(U)\cap U\neq \emptyset $
.
In the case of rooted trees, by the previous corollary, recurrence and hypercyclicity coincide for backward shifts. This equivalence, in fact, holds for any bounded linear operator
![]() $T \in \mathcal {L}(X)$
whose generalized kernel (or, more generally, the set of vectors
$T \in \mathcal {L}(X)$
whose generalized kernel (or, more generally, the set of vectors
![]() $x \in X$
such that
$x \in X$
such that
![]() $T^nx\longrightarrow 0$
as
$T^nx\longrightarrow 0$
as
![]() $n\longrightarrow +\infty $
) is dense in the underlying space (see [Reference Bonilla, Grosse-Erdmann, López-Martínez and Peris12, Theorem 2.12]). Now, we will establish a similar result for
$n\longrightarrow +\infty $
) is dense in the underlying space (see [Reference Bonilla, Grosse-Erdmann, López-Martínez and Peris12, Theorem 2.12]). Now, we will establish a similar result for
![]() $\mathcal {F}$
-transitivity.
$\mathcal {F}$
-transitivity.
Proposition 4.5 Let X be a Banach space,
![]() $T\in \mathcal {L}(X)$
and let
$T\in \mathcal {L}(X)$
and let
![]() $\mathcal {F}$
be a Furstenberg family on
$\mathcal {F}$
be a Furstenberg family on
![]() $\mathbb {N}_0$
such that
$\mathbb {N}_0$
such that
![]() $A\cap [n, +\infty [\in \mathcal {F}$
whenever
$A\cap [n, +\infty [\in \mathcal {F}$
whenever
![]() $A\in \mathcal {F}$
and
$A\in \mathcal {F}$
and
![]() $n\in \mathbb {N}$
. Suppose that the set
$n\in \mathbb {N}$
. Suppose that the set
is dense in X. Then the following statements are equivalent:
-
(1) T is
 $\mathcal {F}$
-transitive.
$\mathcal {F}$
-transitive. -
(2) T is topologically
 $\mathcal {F}$
-recurrent.
$\mathcal {F}$
-recurrent.
Proof It is clear that
![]() $(1)\Rightarrow (2)$
. Assume that
$(1)\Rightarrow (2)$
. Assume that
![]() $(2)$
holds. Let
$(2)$
holds. Let
![]() $U,V$
be nonempty open subsets of X. There exist a nonempty open subset
$U,V$
be nonempty open subsets of X. There exist a nonempty open subset
![]() $V'$
of X and a
$V'$
of X and a
![]() $0$
-neighborhood W such that
$0$
-neighborhood W such that
![]() $W+V' \subset V$
. Assume that
$W+V' \subset V$
. Assume that
![]() $U\neq V'$
, otherwise there is nothing to prove. Let
$U\neq V'$
, otherwise there is nothing to prove. Let
![]() $y\in (U-V')\cap X_0$
. Then there exists a nonnegative integer N such that
$y\in (U-V')\cap X_0$
. Then there exists a nonnegative integer N such that
![]() $T^ny\in W$
, for all
$T^ny\in W$
, for all
![]() $n\geq N$
. By the hypothesis, we have
$n\geq N$
. By the hypothesis, we have
![]() $N(V',V')\in \mathcal {F}$
and so
$N(V',V')\in \mathcal {F}$
and so
![]() $N(V',V')\cap [N,+\infty [\in \mathcal {F}$
. Now, we will show that
$N(V',V')\cap [N,+\infty [\in \mathcal {F}$
. Now, we will show that
Let
![]() $n\in N(V',V')\cap [N,+\infty [$
. Thus,
$n\in N(V',V')\cap [N,+\infty [$
. Thus,
![]() $T^nV'\cap V'\neq \emptyset $
and
$T^nV'\cap V'\neq \emptyset $
and
![]() $T^ny\in W$
. Then there exists
$T^ny\in W$
. Then there exists
![]() $z\in V'$
such that
$z\in V'$
such that
![]() $T^nz\in V'$
. Hence
$T^nz\in V'$
. Hence
![]() $x=y+z\in U$
and
$x=y+z\in U$
and
therefore,
![]() $n\in N(U,V)$
. Consequently,
$n\in N(U,V)$
. Consequently,
![]() $N(V',V')\cap [N,+\infty [\subset N(U,V)$
and so
$N(V',V')\cap [N,+\infty [\subset N(U,V)$
and so
![]() $N(U,V)\in \mathcal {F}$
. This finishes the proof.
$N(U,V)\in \mathcal {F}$
. This finishes the proof.
5
 $\mathcal {F}$
-transitivity - unrooted case
$\mathcal {F}$
-transitivity - unrooted case
We will now present our second main result, which characterizes
![]() $\mathcal {F}$
-transitivity for backward shifts on unrooted directed trees and establishes its equivalence with topological
$\mathcal {F}$
-transitivity for backward shifts on unrooted directed trees and establishes its equivalence with topological
![]() $\mathcal {F}$
-recurrence.
$\mathcal {F}$
-recurrence.
Theorem 5.1 Let
![]() $(V,E)$
be an unrooted directed tree, let
$(V,E)$
be an unrooted directed tree, let
![]() $\mu =(\mu _v)_{v\in V}$
be a weight on V, and let
$\mu =(\mu _v)_{v\in V}$
be a weight on V, and let
![]() $\mathcal {F}$
be a Furstenberg family on
$\mathcal {F}$
be a Furstenberg family on
![]() $\mathbb {N}_0$
. Let
$\mathbb {N}_0$
. Let
![]() $X=\ell ^p(V,\mu )$
,
$X=\ell ^p(V,\mu )$
,
![]() $1\leq p <+\infty $
, or
$1\leq p <+\infty $
, or
![]() $X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. The following assertions are equivalent:
$X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. The following assertions are equivalent:
-
(1) B is
 $\widetilde {\mathcal {F}}$
-transitive.
$\widetilde {\mathcal {F}}$
-transitive. -
(2) B is
 $\mathcal {F}$
-transitive.
$\mathcal {F}$
-transitive. -
(3) For every
 $N\in \mathbb {N}$
and every finite subset
$N\in \mathbb {N}$
and every finite subset
 $F\subset V$
, we have
$F\subset V$
, we have
 $I(F,N)\cap J(F,N)\in \mathcal {F}$
, where and
$I(F,N)\cap J(F,N)\in \mathcal {F}$
, where and $$\begin{align*}& I(F,N):= \\ & \begin{cases} \underset{v\in F}{ \bigcap}\Big\{n\in\mathbb{N}_0:\, \underset{u\in\mathrm{Chi}^n(v)}{\sup}\dfrac{1}{|\mu_u|}>N\Big\} & \text{if } X=\ell^1(V,\mu);\\ \underset{v\in F}{ \bigcap}\Big\{n\in\mathbb{N}_0:\, \Big(\underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\} & \text{if }X=\ell^p(V,\mu),\, 1<p<+\infty;\\ \underset{v\in F}{ \bigcap}\Big\{n\in\mathbb{N}_0:\, \underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|}>N\Big\} & \text{if }X=c_0(V,\mu); \end{cases}\end{align*}$$
$$\begin{align*}& I(F,N):= \\ & \begin{cases} \underset{v\in F}{ \bigcap}\Big\{n\in\mathbb{N}_0:\, \underset{u\in\mathrm{Chi}^n(v)}{\sup}\dfrac{1}{|\mu_u|}>N\Big\} & \text{if } X=\ell^1(V,\mu);\\ \underset{v\in F}{ \bigcap}\Big\{n\in\mathbb{N}_0:\, \Big(\underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\} & \text{if }X=\ell^p(V,\mu),\, 1<p<+\infty;\\ \underset{v\in F}{ \bigcap}\Big\{n\in\mathbb{N}_0:\, \underset{u\in\mathrm{Chi}^n(v)}{\sum}\dfrac{1}{|\mu_u|}>N\Big\} & \text{if }X=c_0(V,\mu); \end{cases}\end{align*}$$
 $$\begin{align*} & J(F,N):=\\ &\begin{cases} \underset{v\in F}{ \bigcap}\Big\{n\in\mathbb{N}_0:\, \min\big(|\mu_{\mathrm{par}^{n}(v)}|,\underset{u\in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\inf}\,|\mu_u|\big)<\frac{1}{N}\Big\} & \text{if } X=\ell^1(V,\mu);\\ \underset{v\in F}{ \bigcap}\Big\{n\in\mathbb{N}_0:\, \dfrac{1}{|\mu_{\mathrm{par}^{n}(v)}|^{p^\ast}}+\underset{u \in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}>N^{p^\ast}\Big\} & \text{if }X=\ell^p(V,\mu),\, 1<p<+\infty;\\ \underset{v\in F}{ \bigcap}\Big\{n\in\mathbb{N}_0:\, \dfrac{1}{|\mu_{\mathrm{par}^{n}(v)}|}+\underset{u \in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\sum}\dfrac{1}{|\mu_u|}>N\Big\} & \text{if }X=c_0(V,\mu). \end{cases}\end{align*}$$
$$\begin{align*} & J(F,N):=\\ &\begin{cases} \underset{v\in F}{ \bigcap}\Big\{n\in\mathbb{N}_0:\, \min\big(|\mu_{\mathrm{par}^{n}(v)}|,\underset{u\in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\inf}\,|\mu_u|\big)<\frac{1}{N}\Big\} & \text{if } X=\ell^1(V,\mu);\\ \underset{v\in F}{ \bigcap}\Big\{n\in\mathbb{N}_0:\, \dfrac{1}{|\mu_{\mathrm{par}^{n}(v)}|^{p^\ast}}+\underset{u \in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}>N^{p^\ast}\Big\} & \text{if }X=\ell^p(V,\mu),\, 1<p<+\infty;\\ \underset{v\in F}{ \bigcap}\Big\{n\in\mathbb{N}_0:\, \dfrac{1}{|\mu_{\mathrm{par}^{n}(v)}|}+\underset{u \in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\sum}\dfrac{1}{|\mu_u|}>N\Big\} & \text{if }X=c_0(V,\mu). \end{cases}\end{align*}$$
If
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $A\cap [n,+\infty [ \in \mathcal {F}$
whenever
$A\cap [n,+\infty [ \in \mathcal {F}$
whenever
![]() $A\in \mathcal {F}$
and
$A\in \mathcal {F}$
and
![]() $n\in \mathbb {N}$
, then the above conditions are equivalent to
$n\in \mathbb {N}$
, then the above conditions are equivalent to
-
(4) B is topologically
 $\mathcal {F}$
-recurrent.
$\mathcal {F}$
-recurrent.
Proof We will only prove the equivalences in the case where
![]() $X = \ell ^p(V,\mu )$
with
$X = \ell ^p(V,\mu )$
with
![]() $1 < p < +\infty $
. A similar argument can be made to deduce the cases where
$1 < p < +\infty $
. A similar argument can be made to deduce the cases where
![]() $X = \ell ^1(V,\mu )$
and
$X = \ell ^1(V,\mu )$
and
![]() $X = c_0(V,\mu )$
. As in the proof of Theorem 4.1 and by using [Reference Grosse-Erdmann and Papathanasiou22, Theorem 5.2], we obtain that
$X = c_0(V,\mu )$
. As in the proof of Theorem 4.1 and by using [Reference Grosse-Erdmann and Papathanasiou22, Theorem 5.2], we obtain that
![]() $(1)\Longleftrightarrow (2)$
. Note that it is clear that
$(1)\Longleftrightarrow (2)$
. Note that it is clear that
![]() $(2)\Rightarrow (4)$
.
$(2)\Rightarrow (4)$
.
Let us show that
![]() $(4)\Rightarrow (3)$
. Let F be a finite subset of V and let
$(4)\Rightarrow (3)$
. Let F be a finite subset of V and let
![]() $N\in \mathbb {N}$
. Set
$N\in \mathbb {N}$
. Set
![]() $g=\sum _{v\in F} e_v\in \ell ^p(V,\mu )$
. Let
$g=\sum _{v\in F} e_v\in \ell ^p(V,\mu )$
. Let
![]() $U=\{f\in \ell ^p(V,\mu ):\, \|f-g\|_{p,\mu }<\frac {1}{2N}\}$
. Let
$U=\{f\in \ell ^p(V,\mu ):\, \|f-g\|_{p,\mu }<\frac {1}{2N}\}$
. Let
![]() $n_0\in \mathbb {N}$
be big enough so that
$n_0\in \mathbb {N}$
be big enough so that
![]() $\mathrm {Chi}^{n}(F)\cap F=\emptyset $
and
$\mathrm {Chi}^{n}(F)\cap F=\emptyset $
and
![]() $\mathrm {par}^{n}(F)\cap F=\emptyset $
, for all
$\mathrm {par}^{n}(F)\cap F=\emptyset $
, for all
![]() $n\geq n_0$
. By the hypothesis,
$n\geq n_0$
. By the hypothesis,
![]() $N(U,U)\in \mathcal {F}$
and so
$N(U,U)\in \mathcal {F}$
and so
![]() $N(U,U)\cap [n_0,+\infty [\in \mathcal {F}$
. Since
$N(U,U)\cap [n_0,+\infty [\in \mathcal {F}$
. Since
![]() $\mathcal {F}$
is a Furstenberg family, it is enough to prove that
$\mathcal {F}$
is a Furstenberg family, it is enough to prove that
We can assume that N is sufficiently large such that
![]() $1<|\mu _v|N$
,
$1<|\mu _v|N$
,
![]() $\forall v \in F$
. Let
$\forall v \in F$
. Let
![]() $n\in N(U,U)\cap [n_0,+\infty [$
. Then there then a function f in
$n\in N(U,U)\cap [n_0,+\infty [$
. Then there then a function f in
![]() $\ell ^p(V,\mu )$
such that
$\ell ^p(V,\mu )$
such that
Fix now
![]() $v\in F$
. By the rightmost inequality above, we have
$v\in F$
. By the rightmost inequality above, we have
 $$ \begin{align} 0<\dfrac{1}{2}<1-\dfrac{1}{2N|\mu_v|}< \sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)|. \end{align} $$
$$ \begin{align} 0<\dfrac{1}{2}<1-\dfrac{1}{2N|\mu_v|}< \sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)|. \end{align} $$
Since
![]() $\mathrm {Chi}^{n}(v)\cap F=\emptyset $
and
$\mathrm {Chi}^{n}(v)\cap F=\emptyset $
and
![]() $F=\operatorname {\mathrm {supp}}(g)$
, by the leftmost inequality in (5.1), we obtain
$F=\operatorname {\mathrm {supp}}(g)$
, by the leftmost inequality in (5.1), we obtain
 $$ \begin{align} \sum_{u\in \mathrm{Chi}^{n}(v) } |f(u)\,\mu_u|^p<\dfrac{1}{(2N)^p}. \end{align} $$
$$ \begin{align} \sum_{u\in \mathrm{Chi}^{n}(v) } |f(u)\,\mu_u|^p<\dfrac{1}{(2N)^p}. \end{align} $$
By Hölder’s inequality (
![]() $p>1$
) and (5.2), we get
$p>1$
) and (5.2), we get
 $$ \begin{align*} \sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)\mu_u|^p &\geqslant \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)|\Big)^{p} \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|\mu_u|^{\frac{p}{1-p}}\Big)^{1-p}\\ &\geqslant \dfrac{1}{2^p} \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|\mu_u|^{\frac{p}{1-p}}\Big)^{1-p}, \end{align*} $$
$$ \begin{align*} \sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)\mu_u|^p &\geqslant \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|f(u)|\Big)^{p} \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|\mu_u|^{\frac{p}{1-p}}\Big)^{1-p}\\ &\geqslant \dfrac{1}{2^p} \Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|\mu_u|^{\frac{p}{1-p}}\Big)^{1-p}, \end{align*} $$
combining this with (5.3), we get
 $$ \begin{align*}\Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|\mu_u|^{-p^{\ast}}\Big)^{1/p^{\ast}}>N;\end{align*} $$
$$ \begin{align*}\Big(\sum_{u\in\mathrm{Chi}^{n}(v)}|\mu_u|^{-p^{\ast}}\Big)^{1/p^{\ast}}>N;\end{align*} $$
this holds for any fixed
![]() $v\in F$
, hence
$v\in F$
, hence
![]() $n\in I(F,N)$
. Let us also show that
$n\in I(F,N)$
. Let us also show that
![]() $n\in J(F,N)$
. By contradiction, suppose that there is a
$n\in J(F,N)$
. By contradiction, suppose that there is a
![]() $v\in F$
for which it holds
$v\in F$
for which it holds
 $$ \begin{align} \dfrac{1}{|\mu_{\mathrm{par}^{n}(v)}|^{p^\ast}}+\underset{u \in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\leq N^{p^\ast}. \end{align} $$
$$ \begin{align} \dfrac{1}{|\mu_{\mathrm{par}^{n}(v)}|^{p^\ast}}+\underset{u \in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\leq N^{p^\ast}. \end{align} $$
Thus,
![]() $\frac {1}{N}\leqslant |\mu _{\mathrm {par}^{n}(v)}|$
. Set
$\frac {1}{N}\leqslant |\mu _{\mathrm {par}^{n}(v)}|$
. Set
One has
Note now that we have
where
![]() $d_n:=\big |\mathrm {Chi}^{n}(\mathrm {par}^{n}(v))\cap F\big |\geq 1$
, where
$d_n:=\big |\mathrm {Chi}^{n}(\mathrm {par}^{n}(v))\cap F\big |\geq 1$
, where
![]() $|\cdot |$
stands for the cardinality. Since
$|\cdot |$
stands for the cardinality. Since
![]() $\mathrm {par}^{n}(v)\in V\setminus F$
, by using the rightmost inequality in (5.1), we get
$\mathrm {par}^{n}(v)\in V\setminus F$
, by using the rightmost inequality in (5.1), we get
 $$ \begin{align*} \dfrac{1}{2N} &>|(B^{n}f)(\mathrm{par}^{n}(v))\,\mu_{\mathrm{par}^{n}(v)}|\\ &\geq \Big(d_n-\big|\sum_{u\in\mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}h(u)\big|\Big)|\mu_{\mathrm{par}^{n}(v)}|\\ & \geq \dfrac{1}{N}\Big(1-|\sum_{u\in\mathrm{Chi}^{n_k}(\mathrm{par}^{n_k}(v))}h_k(u)|\Big), \end{align*} $$
$$ \begin{align*} \dfrac{1}{2N} &>|(B^{n}f)(\mathrm{par}^{n}(v))\,\mu_{\mathrm{par}^{n}(v)}|\\ &\geq \Big(d_n-\big|\sum_{u\in\mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}h(u)\big|\Big)|\mu_{\mathrm{par}^{n}(v)}|\\ & \geq \dfrac{1}{N}\Big(1-|\sum_{u\in\mathrm{Chi}^{n_k}(\mathrm{par}^{n_k}(v))}h_k(u)|\Big), \end{align*} $$
hence
 $$ \begin{align*}\dfrac{1}{2}<\sum_{u\in\mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}|h(u)|.\end{align*} $$
$$ \begin{align*}\dfrac{1}{2}<\sum_{u\in\mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}|h(u)|.\end{align*} $$
By Hölder’s inequality and (5.5), we have
 $$ \begin{align*} \dfrac{1}{2N}&> \Big(\sum_{u\in\mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}|h(u)|\Big) \Big(\sum_{u\in\mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}|\mu_u|^{-p^\ast}\Big)^{-1/p^{\ast}}\\ &> \dfrac{1}{2} \Big(\sum_{u\in\mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}|\mu_u|^{-p^\ast}\Big)^{-1/p^{\ast}}, \end{align*} $$
$$ \begin{align*} \dfrac{1}{2N}&> \Big(\sum_{u\in\mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}|h(u)|\Big) \Big(\sum_{u\in\mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}|\mu_u|^{-p^\ast}\Big)^{-1/p^{\ast}}\\ &> \dfrac{1}{2} \Big(\sum_{u\in\mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}|\mu_u|^{-p^\ast}\Big)^{-1/p^{\ast}}, \end{align*} $$
then
 $$ \begin{align*}\underset{u \in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}>N^{p^\ast}.\end{align*} $$
$$ \begin{align*}\underset{u \in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}>N^{p^\ast}.\end{align*} $$
This contradicts (5.4). Therefore,
![]() $n\in J(F,N)$
. Consequently,
$n\in J(F,N)$
. Consequently,
![]() $N(U,U)\cap [n_0,+\infty [\subset I(F,N)\cap J(F,N)$
, and so
$N(U,U)\cap [n_0,+\infty [\subset I(F,N)\cap J(F,N)$
, and so
![]() $I(F,N)\cap J(F,N)\in \mathcal {F}$
.
$I(F,N)\cap J(F,N)\in \mathcal {F}$
.
Note that a minor adjustment to the proof of the implication
![]() $(4)\Rightarrow (3)$
allows us to deduce
$(4)\Rightarrow (3)$
allows us to deduce
![]() $(2)\Rightarrow (3)$
. Let us show now that
$(2)\Rightarrow (3)$
. Let us show now that
![]() $(3)\Rightarrow (2)$
. Let
$(3)\Rightarrow (2)$
. Let
![]() $\mathcal {B}$
be the filter base consisting of all subsets
$\mathcal {B}$
be the filter base consisting of all subsets
![]() $I(F,N)\cap J(F,N)$
of
$I(F,N)\cap J(F,N)$
of
![]() $\mathbb {N}_0$
, where
$\mathbb {N}_0$
, where
![]() $N>0$
and
$N>0$
and
![]() $F\subset V$
is finite. Let
$F\subset V$
is finite. Let
![]() $\mathcal {F}_{\mathcal {B}}$
be the filter generated by
$\mathcal {F}_{\mathcal {B}}$
be the filter generated by
![]() $\mathcal {B}$
, that is,
$\mathcal {B}$
, that is,
We will show that B satisfies the
![]() $\mathcal {F}_{\mathcal {B}}$
-transitivity criterion, which implies that B is
$\mathcal {F}_{\mathcal {B}}$
-transitivity criterion, which implies that B is
![]() $\mathcal {F}$
-transitive since
$\mathcal {F}$
-transitive since
![]() $\mathcal {F}_{\mathcal {B}}\subset \mathcal {F}$
. Set
$\mathcal {F}_{\mathcal {B}}\subset \mathcal {F}$
. Set
![]() $\mathcal {D}=\mathrm {span}\{e_v:\, v\in V\}$
, which is dense in
$\mathcal {D}=\mathrm {span}\{e_v:\, v\in V\}$
, which is dense in
![]() $\ell ^p(V,\mu )$
. For every
$\ell ^p(V,\mu )$
. For every
![]() $v\in V$
and
$v\in V$
and
![]() $n\in \mathbb {N}$
, by the continuity of
$n\in \mathbb {N}$
, by the continuity of
![]() $B^{n}$
, we have
$B^{n}$
, we have
 $$ \begin{align*}M_{v,n}:=\dfrac{1}{|\mu_{\mathrm{par}^{n}(v)}|^{p^\ast}}+\underset{u \in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}<+\infty,\end{align*} $$
$$ \begin{align*}M_{v,n}:=\dfrac{1}{|\mu_{\mathrm{par}^{n}(v)}|^{p^\ast}}+\underset{u \in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}<+\infty,\end{align*} $$
then either
 $$ \begin{align} \dfrac{1}{|\mu_{\mathrm{par}^{n}(v)}|^{p^\ast}}\geq \dfrac{M_{v,n}}{2}, \end{align} $$
$$ \begin{align} \dfrac{1}{|\mu_{\mathrm{par}^{n}(v)}|^{p^\ast}}\geq \dfrac{M_{v,n}}{2}, \end{align} $$
or
 $$ \begin{align} \underset{u \in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}>\dfrac{M_{v,n}}{2}. \end{align} $$
$$ \begin{align} \underset{u \in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}>\dfrac{M_{v,n}}{2}. \end{align} $$
In the case where (5.6) holds, we set
and then
 $$ \begin{align} \|I_{n}e_v-e_v\|_{p,\mu}=0 \quad \text{and} \quad\|B^{n}I_{n} e_v\|_{p,\mu}=\|e_{\mathrm{par}^{n}(v)}\|_{p,\mu}=| \mu_{\mathrm{par}^{n}(v)}|\leq \Big(\dfrac{2}{M_{v,n}}\Big)^{1/p^\ast}. \end{align} $$
$$ \begin{align} \|I_{n}e_v-e_v\|_{p,\mu}=0 \quad \text{and} \quad\|B^{n}I_{n} e_v\|_{p,\mu}=\|e_{\mathrm{par}^{n}(v)}\|_{p,\mu}=| \mu_{\mathrm{par}^{n}(v)}|\leq \Big(\dfrac{2}{M_{v,n}}\Big)^{1/p^\ast}. \end{align} $$
In the case where (5.7) holds, by Lemma 2.4, there exists
![]() $h_{v,n}\in \mathbb {K}^V$
nonnegative, of support in
$h_{v,n}\in \mathbb {K}^V$
nonnegative, of support in
![]() $\mathrm {Chi}^{n}(\mathrm {par}^{n}(v))$
such that
$\mathrm {Chi}^{n}(\mathrm {par}^{n}(v))$
such that
 $$ \begin{align} \sum_{u\in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}h_{v,n}(u)=1 \quad \text{and} \quad \Big(\sum_{u\in\mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}|h_{v,n}(u)\,\mu_u|^p\Big)^{1/p}\leq \Big(\dfrac{2}{M_{v,n}}\Big)^{1/p^\ast}. \end{align} $$
$$ \begin{align} \sum_{u\in \mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}h_{v,n}(u)=1 \quad \text{and} \quad \Big(\sum_{u\in\mathrm{Chi}^{n}(\mathrm{par}^{n}(v))}|h_{v,n}(u)\,\mu_u|^p\Big)^{1/p}\leq \Big(\dfrac{2}{M_{v,n}}\Big)^{1/p^\ast}. \end{align} $$
Hence,
![]() $h_{v,n}\in \ell ^p(V,\mu )$
, and by setting
$h_{v,n}\in \ell ^p(V,\mu )$
, and by setting
we obtain
 $$ \begin{align} \|I_{n}e_v-e_v\|_{p,\mu}\leq \Big(\dfrac{2}{M_{v,n}}\Big)^{1/p^\ast} \quad \text{and} \quad B^{n}I_{n} e_v=0. \end{align} $$
$$ \begin{align} \|I_{n}e_v-e_v\|_{p,\mu}\leq \Big(\dfrac{2}{M_{v,n}}\Big)^{1/p^\ast} \quad \text{and} \quad B^{n}I_{n} e_v=0. \end{align} $$
In both cases, we extend linearly on
![]() $\mathcal {D}$
the maps
$\mathcal {D}$
the maps
![]() $I_{n}$
. Let
$I_{n}$
. Let
![]() $g=\sum _{a\in F}g(a) e_a\in \mathcal {D}$
, where
$g=\sum _{a\in F}g(a) e_a\in \mathcal {D}$
, where
![]() $F\subset V$
is its support. We will show that
$F\subset V$
is its support. We will show that
![]() $\mathcal {F}_{\mathcal {B}}\text {-}\underset {n}{\lim }(I_ng,B^nI_ng)=(g,0)$
. Let
$\mathcal {F}_{\mathcal {B}}\text {-}\underset {n}{\lim }(I_ng,B^nI_ng)=(g,0)$
. Let
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $\mathcal {U}:=\{f\in \ell ^p(V,\mu ):\, \|f-g\|_{p,\mu }<\varepsilon \}$
and
$\mathcal {U}:=\{f\in \ell ^p(V,\mu ):\, \|f-g\|_{p,\mu }<\varepsilon \}$
and
![]() $\mathcal {V}:=\{f\in \ell ^p(V,\mu ):\, \|f\|_{p,\mu }<\varepsilon \}$
. Let us check that
$\mathcal {V}:=\{f\in \ell ^p(V,\mu ):\, \|f\|_{p,\mu }<\varepsilon \}$
. Let us check that
where
Let
![]() $n\in J(F,N)$
. We have then
$n\in J(F,N)$
. We have then
![]() $M_{a,n}>N^{p^\ast }$
, for all
$M_{a,n}>N^{p^\ast }$
, for all
![]() $a\in F$
. By the definition of N, (5.8) and (5.10), we obtain
$a\in F$
. By the definition of N, (5.8) and (5.10), we obtain
 $$ \begin{align*} \max \Big\{\|I_{n}g-g\|,\|B^{n}I_{n}g\|_{p,\mu} \Big\} &\leq \sum_{a\in F}|g(a)| \Big(\dfrac{2}{M_{a,n}}\Big)^{1/p^\ast}\\ &< \sum_{a\in F}|g(a)| \dfrac{2^{1/p^\ast}}{N}\\ &< \varepsilon, \end{align*} $$
$$ \begin{align*} \max \Big\{\|I_{n}g-g\|,\|B^{n}I_{n}g\|_{p,\mu} \Big\} &\leq \sum_{a\in F}|g(a)| \Big(\dfrac{2}{M_{a,n}}\Big)^{1/p^\ast}\\ &< \sum_{a\in F}|g(a)| \dfrac{2^{1/p^\ast}}{N}\\ &< \varepsilon, \end{align*} $$
hence
![]() $I_ng\in \mathcal {U}$
and
$I_ng\in \mathcal {U}$
and
![]() $B^nI_ng\in \mathcal {V}$
. Therefore, (5.11) holds and so
$B^nI_ng\in \mathcal {V}$
. Therefore, (5.11) holds and so
Consequently, the first statement of the
![]() $\mathcal {F}_{\mathcal {B}}$
-transitivity criterion holds. As for the second statement, we can define the maps
$\mathcal {F}_{\mathcal {B}}$
-transitivity criterion holds. As for the second statement, we can define the maps
![]() $S_n$
as in the proof of Theorem 4.1. By employing the same arguments, we can deduce that
$S_n$
as in the proof of Theorem 4.1. By employing the same arguments, we can deduce that
This shows that the second statement of the
![]() $\mathcal {F}_{\mathcal {B}}$
-transitivity criterion holds. Hence, B is
$\mathcal {F}_{\mathcal {B}}$
-transitivity criterion holds. Hence, B is
![]() $\mathcal {F}$
-transitive and statement
$\mathcal {F}$
-transitive and statement
![]() $(2)$
holds.
$(2)$
holds.
Once again, if the Furstenberg family
![]() $\mathcal {F}$
in the previous theorem represents the collection of syndetic subsets, we can derive a characterization of topologically ergodic backward shift operators on unrooted directed trees. Additionally, in the case where
$\mathcal {F}$
in the previous theorem represents the collection of syndetic subsets, we can derive a characterization of topologically ergodic backward shift operators on unrooted directed trees. Additionally, in the case where
![]() $\mathcal {F}$
represents the family of infinite subsets, we deduce the following corollary.
$\mathcal {F}$
represents the family of infinite subsets, we deduce the following corollary.
Corollary 5.2 Let
![]() $(V, E)$
be an unrooted directed tree and
$(V, E)$
be an unrooted directed tree and
![]() $\mu =(\mu _v)_{v\in V}$
a weight on V. Let
$\mu =(\mu _v)_{v\in V}$
a weight on V. Let
![]() $X=\ell ^p(V,\mu )$
,
$X=\ell ^p(V,\mu )$
,
![]() $1\leq p <+\infty $
, or
$1\leq p <+\infty $
, or
![]() $X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. Then B is hypercyclic if and only if B is recurrent.
$X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. Then B is hypercyclic if and only if B is recurrent.
In the upcoming section, we will generalize this corollary by using the concept of
![]() $\Gamma $
-supercyclicity.
$\Gamma $
-supercyclicity.
6
 $\Gamma $
-supercyclicity
$\Gamma $
-supercyclicity
Supercyclicity is a weaker notion than hypercyclicity, which requires the density of a projective orbit instead of an orbit, see [Reference Bayart and Matheron8]. We can study both these notions by considering the notion of
![]() $\Gamma $
-supercyclicity, see [Reference Charpentier, Ernst and Menet14]. Let X be a complex Banach space and
$\Gamma $
-supercyclicity, see [Reference Charpentier, Ernst and Menet14]. Let X be a complex Banach space and
![]() $\Gamma $
be a subset of
$\Gamma $
be a subset of
![]() $\mathbb {C}$
. An operator
$\mathbb {C}$
. An operator
![]() $T\in \mathcal {L}(X)$
is called
$T\in \mathcal {L}(X)$
is called
![]() $\Gamma $
-supercyclic if there exists some vector
$\Gamma $
-supercyclic if there exists some vector
![]() $x\in X$
such that the set
$x\in X$
such that the set
is dense in X. In particular,
![]() $\mathbb {C}$
-supercyclicity is simply called supercyclicity, and
$\mathbb {C}$
-supercyclicity is simply called supercyclicity, and
![]() $\{1\}$
-supercyclicity coincides with hypercyclicity. This notion has been studied for bilateral backward shifts in [Reference Abbar3], and more generally for a family of translation operators on weighted
$\{1\}$
-supercyclicity coincides with hypercyclicity. This notion has been studied for bilateral backward shifts in [Reference Abbar3], and more generally for a family of translation operators on weighted
![]() $L^p$
-spaces on locally compact groups in [Reference Abbar and Kuznetsova2].
$L^p$
-spaces on locally compact groups in [Reference Abbar and Kuznetsova2].
In the same way, we can extend the notion of recurrence as follows: a vector
![]() $x\in X$
is said to be
$x\in X$
is said to be
![]() $\Gamma $
-recurrent vector for T if there exist a strictly increasing sequence
$\Gamma $
-recurrent vector for T if there exist a strictly increasing sequence
![]() $(n_k)_{k\geq 1}$
of positive integers and a sequence
$(n_k)_{k\geq 1}$
of positive integers and a sequence
![]() $(\lambda _k)_{k\geq 1}$
in
$(\lambda _k)_{k\geq 1}$
in
![]() $\Gamma $
such that
$\Gamma $
such that
The operator T is called
![]() $\Gamma $
-recurrent if its set of
$\Gamma $
-recurrent if its set of
![]() $\Gamma $
-recurrent vectors, denoted by
$\Gamma $
-recurrent vectors, denoted by
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {Rec}(T)$
, is dense in X. This notion coincides with the so-called super-recurrence when
$\mathrm {Rec}(T)$
, is dense in X. This notion coincides with the so-called super-recurrence when
![]() $\Gamma $
is equal to the complex plane [Reference Amouch and Benchiheb5].
$\Gamma $
is equal to the complex plane [Reference Amouch and Benchiheb5].
In the following theorem, we provide a characterization of
![]() $\Gamma $
-supercyclicity for backward shift operators on unrooted directed trees and give its equivalence with
$\Gamma $
-supercyclicity for backward shift operators on unrooted directed trees and give its equivalence with
![]() $\Gamma $
-recurrence. The proof of this theorem is omitted, as it follows a similar approach to that of Theorem 5.1, specifically when considering the Furstenberg family
$\Gamma $
-recurrence. The proof of this theorem is omitted, as it follows a similar approach to that of Theorem 5.1, specifically when considering the Furstenberg family
![]() $\mathcal {F}$
as the collection of infinite subsets of
$\mathcal {F}$
as the collection of infinite subsets of
![]() $\mathbb {N}_0$
. Furthermore, instead of using the
$\mathbb {N}_0$
. Furthermore, instead of using the
![]() $\mathcal {F}$
-transitivity criterion, we employ the
$\mathcal {F}$
-transitivity criterion, we employ the
![]() $\Gamma $
-supercyclicity criterion described below.
$\Gamma $
-supercyclicity criterion described below.
Theorem 6.1 Let
![]() $(V, E)$
be an unrooted directed tree,
$(V, E)$
be an unrooted directed tree,
![]() $\mu =(\mu _v)_{v\in V}$
a weight on V and let
$\mu =(\mu _v)_{v\in V}$
a weight on V and let
![]() $\Gamma\subset\mathbb{C}$
be such that
$\Gamma\subset\mathbb{C}$
be such that
![]() $\Gamma\setminus\{0\}$
is nonempty. Let
$\Gamma\setminus\{0\}$
is nonempty. Let
![]() $X=\ell ^p(V,\mu )$
,
$X=\ell ^p(V,\mu )$
,
![]() $1\leq p <+\infty $
, or
$1\leq p <+\infty $
, or
![]() $X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. Then the following conditions are equivalent:
$X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. Then the following conditions are equivalent:
-
(1) B is
 $\Gamma $
-supercyclic.
$\Gamma $
-supercyclic. -
(2) B is
 $\Gamma $
-recurrent.
$\Gamma $
-recurrent. -
(3) There are an increasing sequence of positive integers
 $(n_k)_{k\geq 1}$
and a sequence
$(n_k)_{k\geq 1}$
and a sequence
 $(\lambda _k)_{\geq 1}$
in
$(\lambda _k)_{\geq 1}$
in
 $\Gamma \setminus \{0\}$
such that, for every
$\Gamma \setminus \{0\}$
such that, for every
 $v\in V$
, we have
$v\in V$
, we have  $$ \begin{align*}\begin{cases} \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{|\lambda_k|^{p^{\ast}}}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty;\\ &\\ \underset{u\in \mathrm{Chi}^{n_k}(v)}{\inf}\,\dfrac{|\mu_u|}{|\lambda_k|}\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu);\\ &\\ \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{|\lambda_k|}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu), \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{|\lambda_k|^{p^{\ast}}}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty;\\ &\\ \underset{u\in \mathrm{Chi}^{n_k}(v)}{\inf}\,\dfrac{|\mu_u|}{|\lambda_k|}\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu);\\ &\\ \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{|\lambda_k|}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu), \end{cases}\end{align*} $$
and
 $$ \begin{align*}\begin{cases} \dfrac{1}{|\lambda_k\,\mu_{\mathrm{par}^{n_k}(v)}|^{p^\ast}}+\underset{u \in \mathrm{Chi}^{n_k}(\mathrm{par}^{n_k}(v))}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty;\\ &\\ \min\Big(|\lambda_k\,\mu_{\mathrm{par}^{n_k}(v)}|,\underset{u\in \mathrm{Chi}^{n_k}(\mathrm{par}^{n_k}(v))}{\inf}\,|\mu_u|\Big)\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu);\\ &\\ \dfrac{1}{|\lambda_k\, \mu_{\mathrm{par}^{n_k}(v)}|}+\underset{u \in \mathrm{Chi}^{n_k}(\mathrm{par}^{n_k}(v))}{\sum}\dfrac{1}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu) \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} \dfrac{1}{|\lambda_k\,\mu_{\mathrm{par}^{n_k}(v)}|^{p^\ast}}+\underset{u \in \mathrm{Chi}^{n_k}(\mathrm{par}^{n_k}(v))}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty;\\ &\\ \min\Big(|\lambda_k\,\mu_{\mathrm{par}^{n_k}(v)}|,\underset{u\in \mathrm{Chi}^{n_k}(\mathrm{par}^{n_k}(v))}{\inf}\,|\mu_u|\Big)\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu);\\ &\\ \dfrac{1}{|\lambda_k\, \mu_{\mathrm{par}^{n_k}(v)}|}+\underset{u \in \mathrm{Chi}^{n_k}(\mathrm{par}^{n_k}(v))}{\sum}\dfrac{1}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu) \end{cases}\end{align*} $$
The proof of the
![]() $\Gamma $
-supercyclicity criterion presented below is a straightforward adaptation of the proof of the supercyclicity criterion given in [Reference Bayart and Matheron8, Theorem 1.14].
$\Gamma $
-supercyclicity criterion presented below is a straightforward adaptation of the proof of the supercyclicity criterion given in [Reference Bayart and Matheron8, Theorem 1.14].
Theorem 6.2 (
 $\Gamma $
-supercyclicity Criterion)
$\Gamma $
-supercyclicity Criterion)
Let X be an infinite-dimensional Banach space,
![]() $T\in \mathcal {L}(X)$
and let
$T\in \mathcal {L}(X)$
and let
![]() $\Gamma \subset \mathbb {C}$
be such that
$\Gamma \subset \mathbb {C}$
be such that
![]() $\Gamma \setminus \{0\}$
is nonempty. Assume that there exists an increasing sequence of positive integers
$\Gamma \setminus \{0\}$
is nonempty. Assume that there exists an increasing sequence of positive integers
![]() $(n_k)_{k\geq 1}$
, a sequence
$(n_k)_{k\geq 1}$
, a sequence
![]() $(\lambda _k)_{k\geq 1}$
in
$(\lambda _k)_{k\geq 1}$
in
![]() $\Gamma \setminus \{0\}$
, two dense subsets
$\Gamma \setminus \{0\}$
, two dense subsets
![]() $X_0$
and
$X_0$
and
![]() $Y_0$
in X, and two families of applications
$Y_0$
in X, and two families of applications
![]() $I_{n_k}:X_0\to X$
and
$I_{n_k}:X_0\to X$
and
![]() $S_{n_k}:Y_0\to X$
such that, for any
$S_{n_k}:Y_0\to X$
such that, for any
![]() $x\in X_0$
and any
$x\in X_0$
and any
![]() $y\in Y_0$
, the following conditions hold:
$y\in Y_0$
, the following conditions hold:
-
(a)
 $I_{n_k}x\underset {k\to +\infty }{\longrightarrow } x$
;
$I_{n_k}x\underset {k\to +\infty }{\longrightarrow } x$
; -
(b)
 $\lambda _k T^{n_k} I_{n_k}x\underset {k\to +\infty }{\longrightarrow } 0$
;
$\lambda _k T^{n_k} I_{n_k}x\underset {k\to +\infty }{\longrightarrow } 0$
; -
(c)
 $\dfrac {1}{\lambda _k} S_{n_k} y\underset {k\to +\infty }{\longrightarrow } 0$
;
$\dfrac {1}{\lambda _k} S_{n_k} y\underset {k\to +\infty }{\longrightarrow } 0$
; -
(d)
 $T^{n_k}S_{n_k} y\underset {k\to +\infty }{\longrightarrow } y$
.
$T^{n_k}S_{n_k} y\underset {k\to +\infty }{\longrightarrow } y$
.
Then
![]() $T\oplus T$
is
$T\oplus T$
is
![]() $\Gamma $
-supercyclic.
$\Gamma $
-supercyclic.
In the case of rooted trees, we can deduce from Corollary 4.3 that for any bounded subset
![]() $\Gamma $
of
$\Gamma $
of
![]() $\mathbb {C}\setminus \{0\}$
, a backward shift operator B is hypercyclic if and only if it is
$\mathbb {C}\setminus \{0\}$
, a backward shift operator B is hypercyclic if and only if it is
![]() $\Gamma $
-supercyclic. In addition, in the case where
$\Gamma $
-supercyclic. In addition, in the case where
![]() $\Gamma $
is an unbounded subset of
$\Gamma $
is an unbounded subset of
![]() $\mathbb {C}$
, B is always
$\mathbb {C}$
, B is always
![]() $\Gamma $
-supercyclic, because in this case B has dense generalized kernel and dense range, see Proposition 6.3 below.
$\Gamma $
-supercyclic, because in this case B has dense generalized kernel and dense range, see Proposition 6.3 below.
The generalized kernel of a bounded linear operator T defined on some Banach space X is the subspace
In [Reference Bermúdez, Bonilla and Peris10, Corollary 3.3], it was proven that an operator with dense generalized kernel is supercyclic if and only if it has dense range.
Proposition 6.3 Let X be a separable infinite-dimensional Banach space, and let
![]() $T\in \mathcal {L}(X)$
have a dense generalized kernel. Then the following assertions are equivalent:
$T\in \mathcal {L}(X)$
have a dense generalized kernel. Then the following assertions are equivalent:
-
(1) For any unbounded subset
 $\Gamma $
of
$\Gamma $
of
 $\mathbb {C}$
, T is
$\mathbb {C}$
, T is
 $\Gamma $
-supercyclic.
$\Gamma $
-supercyclic. -
(2) There exists an unbounded subset
 $\Gamma $
of
$\Gamma $
of
 $\mathbb {C}$
such that T is
$\mathbb {C}$
such that T is
 $\Gamma $
-supercyclic.
$\Gamma $
-supercyclic. -
(3) T has dense range.
Proof It is clear that
![]() $(1)\Rightarrow (2)\Rightarrow (3)$
. Let us show that
$(1)\Rightarrow (2)\Rightarrow (3)$
. Let us show that
![]() $(3)\Rightarrow (1)$
. Assume that T has dense range. Let
$(3)\Rightarrow (1)$
. Assume that T has dense range. Let
![]() $\Gamma $
be an unbounded subset of
$\Gamma $
be an unbounded subset of
![]() $\mathbb {C}$
. We will show that
$\mathbb {C}$
. We will show that
![]() $T\oplus T$
is
$T\oplus T$
is
![]() $\Gamma $
-supercyclic. Let
$\Gamma $
-supercyclic. Let
![]() $U_1$
,
$U_1$
,
![]() $U_2$
,
$U_2$
,
![]() $V_1$
,
$V_1$
,
![]() $V_2$
be nonempty open subsets of X. Since
$V_2$
be nonempty open subsets of X. Since
![]() $\ker ^\ast (T)$
is dense in X, there exists
$\ker ^\ast (T)$
is dense in X, there exists
![]() $(x_1,x_2)\in U_1\times U_2$
such that
$(x_1,x_2)\in U_1\times U_2$
such that
![]() $T^nx_1=T^nx_2=0$
for some
$T^nx_1=T^nx_2=0$
for some
![]() $n\in \mathbb {N}$
. Since T has dense range,
$n\in \mathbb {N}$
. Since T has dense range,
![]() $T^n$
also does; therefore, there exist
$T^n$
also does; therefore, there exist
![]() $y_1,y_2\in X$
such that
$y_1,y_2\in X$
such that
![]() $(T^ny_1,T^ny_2)\in V_1\times V_2$
. By the unboundedness of
$(T^ny_1,T^ny_2)\in V_1\times V_2$
. By the unboundedness of
![]() $\Gamma $
, there exists
$\Gamma $
, there exists
![]() $\lambda \in \Gamma $
such that
$\lambda \in \Gamma $
such that
and
Hence,
![]() $T\oplus T$
is
$T\oplus T$
is
![]() $\Gamma $
-supercyclic.
$\Gamma $
-supercyclic.
7 Zero-one law limit point
In [Reference Chan and Seceleanu18], Chan and Seceleanu showed that any weighted unilateral/bilateral backward shift that has an orbit with a nonzero limit point is hypercyclic. However, comparing the characterization of hypercyclicity for backward shift operators on rooted directed trees with the following theorem, we deduce that Chan and Seceleanu’s result does not hold for rooted directed trees.
Theorem 7.1 Let
![]() $(V,E)$
be a rooted directed tree and let
$(V,E)$
be a rooted directed tree and let
![]() $\mu =(\mu _v)_{v\in V}$
be a weight on V. Let
$\mu =(\mu _v)_{v\in V}$
be a weight on V. Let
![]() $X=\ell ^p(V,\mu )$
,
$X=\ell ^p(V,\mu )$
,
![]() $1\leq p <+\infty $
, or
$1\leq p <+\infty $
, or
![]() $X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. The following conditions are equivalent:
$X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. The following conditions are equivalent:
-
(1) B has an orbit with a nonzero limit point.
-
(2) B has an orbit with a nonzero weak limit point.
-
(3) B has an orbit with
 $e_{\texttt {r}}$
as a limit point.
$e_{\texttt {r}}$
as a limit point. -
(4) B has an orbit with
 $e_{\texttt {r}}$
as a weak limit point.
$e_{\texttt {r}}$
as a weak limit point. -
(5) There are an increasing sequence
 $(n_k)_{k}$
of positive integers and a vertex
$(n_k)_{k}$
of positive integers and a vertex
 $v\in V$
such that
$v\in V$
such that  $$ \begin{align*}\begin{cases} \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty;\\ &\\ \underset{u\in\mathrm{Chi}^{n_{k}}(v)}{\inf}\,|\mu_u|\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu); \\ &\\ \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{1}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu). \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty;\\ &\\ \underset{u\in\mathrm{Chi}^{n_{k}}(v)}{\inf}\,|\mu_u|\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu); \\ &\\ \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{1}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu). \end{cases}\end{align*} $$
-
(6) There is an increasing sequence
 $(n_k)_{k}$
of positive integers such that
$(n_k)_{k}$
of positive integers such that  $$ \begin{align*}\begin{cases} \underset{u \in \mathrm{Chi}^{n_k}(\texttt{r})}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty;\\ &\\ \underset{u\in\mathrm{Chi}^{n_{k}}(\texttt{r})}{\inf}\,|\mu_u|\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu); \\ &\\ \underset{u \in \mathrm{Chi}^{n_k}(\texttt{r})}{\sum}\dfrac{1}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu),\, \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} \underset{u \in \mathrm{Chi}^{n_k}(\texttt{r})}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty;\\ &\\ \underset{u\in\mathrm{Chi}^{n_{k}}(\texttt{r})}{\inf}\,|\mu_u|\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu); \\ &\\ \underset{u \in \mathrm{Chi}^{n_k}(\texttt{r})}{\sum}\dfrac{1}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu),\, \end{cases}\end{align*} $$
-
(7) There exist an increasing sequence
 $(n_k)_{k\in \mathbb {N}}$
of positive integers and a vertex
$(n_k)_{k\in \mathbb {N}}$
of positive integers and a vertex
 $v\in V$
such that, for any
$v\in V$
such that, for any
 $l\in \mathbb {N}_0$
,
$l\in \mathbb {N}_0$
,  $$ \begin{align*}\begin{cases} \underset{u \in \mathrm{Chi}^{n_k+l}(v)}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty;\\ &\\ \underset{u\in\mathrm{Chi}^{n_{k}+l}(v)}{\inf}\,|\mu_u|\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu); \\ &\\ \underset{u \in \mathrm{Chi}^{n_k+l}(v)}{\sum}\dfrac{1}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu). \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} \underset{u \in \mathrm{Chi}^{n_k+l}(v)}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty;\\ &\\ \underset{u\in\mathrm{Chi}^{n_{k}+l}(v)}{\inf}\,|\mu_u|\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu); \\ &\\ \underset{u \in \mathrm{Chi}^{n_k+l}(v)}{\sum}\dfrac{1}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu). \end{cases}\end{align*} $$
Proof It is enough to prove that
![]() $(2) \Rightarrow (5) \Rightarrow (6) \Rightarrow (3)$
and
$(2) \Rightarrow (5) \Rightarrow (6) \Rightarrow (3)$
and
![]() $(5)\Rightarrow (7)$
. We will prove these implications when
$(5)\Rightarrow (7)$
. We will prove these implications when
![]() $X=\ell ^p(V,\mu )$
, with
$X=\ell ^p(V,\mu )$
, with
![]() $1<p<+\infty $
, the same reasoning works for the other cases. Let us show that
$1<p<+\infty $
, the same reasoning works for the other cases. Let us show that
![]() $(2)$
implies
$(2)$
implies
![]() $(5)$
. Let
$(5)$
. Let
![]() $f,g\in \ell ^p(V,\mu )$
be nonzero vectors. Let
$f,g\in \ell ^p(V,\mu )$
be nonzero vectors. Let
![]() $v_0\in V$
such that
$v_0\in V$
such that
![]() $g(v_0)\neq 0$
. Let
$g(v_0)\neq 0$
. Let
![]() $(\delta _k)_{k}$
be a decreasing sequence of positive numbers such that
$(\delta _k)_{k}$
be a decreasing sequence of positive numbers such that
![]() $2\delta _k<|g(v_0)|$
. Let
$2\delta _k<|g(v_0)|$
. Let
![]() $(n_k)_{k}$
be an increasing sequence of nonnegative integers such that
$(n_k)_{k}$
be an increasing sequence of nonnegative integers such that
that is
thus
 $$ \begin{align} 0<\dfrac{|g(v_0)|}{2}<|g(v_0)|-\delta_k< \sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|f(u)|. \end{align} $$
$$ \begin{align} 0<\dfrac{|g(v_0)|}{2}<|g(v_0)|-\delta_k< \sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|f(u)|. \end{align} $$
Since
![]() $\|f\|_{p,\mu }<+\infty $
, we obtain
$\|f\|_{p,\mu }<+\infty $
, we obtain
hence
By Hölder’s inequality (
![]() $p>1$
), we get
$p>1$
), we get
 $$ \begin{align*} \sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|f(u)\mu_u|^p &\geqslant \Big(\sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|f(u)|\Big)^{p} \Big(\sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|\mu_u|^{\frac{p}{1-p}}\Big)^{1-p}\\ &\overset{(7.1)}{\geqslant} \dfrac{|g(v_0)|^p}{2^p} \Big(\sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|\mu_u|^{\frac{p}{1-p}}\Big)^{1-p} \end{align*} $$
$$ \begin{align*} \sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|f(u)\mu_u|^p &\geqslant \Big(\sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|f(u)|\Big)^{p} \Big(\sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|\mu_u|^{\frac{p}{1-p}}\Big)^{1-p}\\ &\overset{(7.1)}{\geqslant} \dfrac{|g(v_0)|^p}{2^p} \Big(\sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|\mu_u|^{\frac{p}{1-p}}\Big)^{1-p} \end{align*} $$
hence
 $$ \begin{align*}\Big(\sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|\mu_u|^{-p^{\ast}}\Big)^{-1/p^{\ast}}\leqslant \dfrac{2}{|g(v_0)|} \Big(\sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|f(u)\mu_u|^p\Big)^{1/p},\end{align*} $$
$$ \begin{align*}\Big(\sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|\mu_u|^{-p^{\ast}}\Big)^{-1/p^{\ast}}\leqslant \dfrac{2}{|g(v_0)|} \Big(\sum_{u\in\mathrm{Chi}^{n_k}(v_0)}|f(u)\mu_u|^p\Big)^{1/p},\end{align*} $$
combining this with (7.2), we get
 $$ \begin{align*}\sum_{u \in \mathrm{Chi}^{n_k}(v_0)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty.\end{align*} $$
$$ \begin{align*}\sum_{u \in \mathrm{Chi}^{n_k}(v_0)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty.\end{align*} $$
Let us show now that
![]() $(5)$
implies
$(5)$
implies
![]() $(6)$
. Suppose that
$(6)$
. Suppose that
![]() $(5)$
holds for some sequence
$(5)$
holds for some sequence
![]() $(n_k)_k$
and
$(n_k)_k$
and
![]() $v\in V$
. Let
$v\in V$
. Let
![]() $m\in \mathbb {N}$
be such that
$m\in \mathbb {N}$
be such that
![]() $v\in \mathrm {Chi}^{m}(\texttt {r})$
. Set
$v\in \mathrm {Chi}^{m}(\texttt {r})$
. Set
![]() $m_k=n_k+m$
. Thus,
$m_k=n_k+m$
. Thus,
![]() $\mathrm {Chi}^{n_k}(v)\subset \mathrm {Chi}^{m_k}(\texttt {r})$
and hence
$\mathrm {Chi}^{n_k}(v)\subset \mathrm {Chi}^{m_k}(\texttt {r})$
and hence
 $$ \begin{align*}\sum_{u \in \mathrm{Chi}^{n_k}(v)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\leqslant \sum_{u \in \mathrm{Chi}^{m_k}(\texttt{r})}\dfrac{1}{|\mu_u|^{p^{\ast}}},\end{align*} $$
$$ \begin{align*}\sum_{u \in \mathrm{Chi}^{n_k}(v)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\leqslant \sum_{u \in \mathrm{Chi}^{m_k}(\texttt{r})}\dfrac{1}{|\mu_u|^{p^{\ast}}},\end{align*} $$
since the term at the left goes to infinity, as
![]() $k \to +\infty $
, we get
$k \to +\infty $
, we get
 $$ \begin{align*}\sum_{u \in \mathrm{Chi}^{m_k}(\texttt{r})}\dfrac{1}{|\mu_u|^{p^{\ast}}} \underset{k\to+\infty}{\longrightarrow}+\infty.\end{align*} $$
$$ \begin{align*}\sum_{u \in \mathrm{Chi}^{m_k}(\texttt{r})}\dfrac{1}{|\mu_u|^{p^{\ast}}} \underset{k\to+\infty}{\longrightarrow}+\infty.\end{align*} $$
Let us show that
![]() $(6)$
implies
$(6)$
implies
![]() $(3)$
. Let
$(3)$
. Let
![]() $(n_k)_{k\geq 0}$
be an increasing sequence of positive integers such that
$(n_k)_{k\geq 0}$
be an increasing sequence of positive integers such that
 $$ \begin{align*}\sum_{u \in \mathrm{Chi}^{n_k}(\texttt{r})}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty.\end{align*} $$
$$ \begin{align*}\sum_{u \in \mathrm{Chi}^{n_k}(\texttt{r})}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty.\end{align*} $$
Set
![]() $J_k=\mathrm {Chi}^{n_k}(\texttt {r})$
, for
$J_k=\mathrm {Chi}^{n_k}(\texttt {r})$
, for
![]() $k\in \mathbb {N}$
. By Lemma 2.4, we obtain
$k\in \mathbb {N}$
. By Lemma 2.4, we obtain
 $$ \begin{align*}\underset{\|x\|_1=1}{\inf}\Big(\sum_{u\in J_k}|x_u\mu_u|^p\Big)^{1/p}\underset{k\to+\infty}{\longrightarrow}0\end{align*} $$
$$ \begin{align*}\underset{\|x\|_1=1}{\inf}\Big(\sum_{u\in J_k}|x_u\mu_u|^p\Big)^{1/p}\underset{k\to+\infty}{\longrightarrow}0\end{align*} $$
There exists then an increasing sequence
![]() $(k_j)_{j\geq 0}$
of positive integers such that, for each
$(k_j)_{j\geq 0}$
of positive integers such that, for each
![]() $j\in \mathbb {N}_0$
, we have
$j\in \mathbb {N}_0$
, we have
 $$ \begin{align*}\underset{\|x\|_1=1}{\inf}\Big(\sum_{u\in J_{k_j}}|x_u\mu_u|^p\Big)^{1/p}\leqslant\dfrac{1}{2^{j+1}c_j}, \quad\text{ where } \quad c_j=\max\lbrace 1; \|B^{n_{k_l}}\|, 0\leqslant l\leqslant j-1\rbrace,\end{align*} $$
$$ \begin{align*}\underset{\|x\|_1=1}{\inf}\Big(\sum_{u\in J_{k_j}}|x_u\mu_u|^p\Big)^{1/p}\leqslant\dfrac{1}{2^{j+1}c_j}, \quad\text{ where } \quad c_j=\max\lbrace 1; \|B^{n_{k_l}}\|, 0\leqslant l\leqslant j-1\rbrace,\end{align*} $$
hence, there exists
![]() $f_{k_j}\in \mathbb {K}^{V}$
, of support in
$f_{k_j}\in \mathbb {K}^{V}$
, of support in
![]() $J_{k_j}=\mathrm {Chi}^{n_{k_j}}(\texttt {r})$
such that
$J_{k_j}=\mathrm {Chi}^{n_{k_j}}(\texttt {r})$
such that
and
 $$ \begin{align} \Big(\sum_{u\in J_{k_j}}|f_{k_j}(u)\mu_u|^p\Big)^{1/p}\leqslant\dfrac{1}{2^{j}c_j}. \end{align} $$
$$ \begin{align} \Big(\sum_{u\in J_{k_j}}|f_{k_j}(u)\mu_u|^p\Big)^{1/p}\leqslant\dfrac{1}{2^{j}c_j}. \end{align} $$
For each
![]() $u\in V$
, set
$u\in V$
, set
 $$ \begin{align*}f(u)=\begin{cases} g_j(u) &\text{ if } u\in \mathrm{Chi}^{n_{k_j}}(\texttt{r}) \text{ for some } j\\ 0 &\text{ otherwise } \end{cases},\quad \text{where } g_j=|f_{k_j}|. \end{align*} $$
$$ \begin{align*}f(u)=\begin{cases} g_j(u) &\text{ if } u\in \mathrm{Chi}^{n_{k_j}}(\texttt{r}) \text{ for some } j\\ 0 &\text{ otherwise } \end{cases},\quad \text{where } g_j=|f_{k_j}|. \end{align*} $$
By (7.4), we obtain
 $$ \begin{align*}\|f\|_{p,\mu}^{p}=\sum_{u\in V}|f(u)\mu_u|^p=\sum_{j\in\mathbb{N}_0}\sum_{u\in \mathrm{Chi}^{n_{k_j}}(\texttt{r})}|f_{k_j}(u)\mu_u|^p \leqslant \sum_{j\in\mathbb{N}_0}\dfrac{1}{2^{pj}}<+\infty, \end{align*} $$
$$ \begin{align*}\|f\|_{p,\mu}^{p}=\sum_{u\in V}|f(u)\mu_u|^p=\sum_{j\in\mathbb{N}_0}\sum_{u\in \mathrm{Chi}^{n_{k_j}}(\texttt{r})}|f_{k_j}(u)\mu_u|^p \leqslant \sum_{j\in\mathbb{N}_0}\dfrac{1}{2^{pj}}<+\infty, \end{align*} $$
thus
![]() $f\in \ell ^p(V,\mu )$
. Moreover, we have
$f\in \ell ^p(V,\mu )$
. Moreover, we have
 $$ \begin{align*} \| B^{n_{k_j}}f-e_{\texttt{r}}\|_{p,\mu}&\leq \| B^{n_{k_j}}g_j-e_{\texttt{r}}\|_{p,\mu}+\sum_{ l=j+1} \| B^{n_{k_j}}g_l\|_{p,\mu}\\ &=\sum_{ l=j+1} \| B^{n_{k_j}}g_l\|_{p,\mu}\qquad (\text{by } (7.3))\\ &\leqslant \sum_{ l=j+1} \| B^{n_{k_j}}\| \|f_{k_l}\|_{p,\mu}\\ &< \sum_{ l=j+1}\dfrac{\| B^{n_{k_j}}\|}{2^{l}c_{l}} \qquad (\text{by } (7.4))\\ &\leqslant \sum_{ l=j+1}\dfrac{1}{2^{l}}\underset{j\to+\infty}{\longrightarrow}0, \end{align*} $$
$$ \begin{align*} \| B^{n_{k_j}}f-e_{\texttt{r}}\|_{p,\mu}&\leq \| B^{n_{k_j}}g_j-e_{\texttt{r}}\|_{p,\mu}+\sum_{ l=j+1} \| B^{n_{k_j}}g_l\|_{p,\mu}\\ &=\sum_{ l=j+1} \| B^{n_{k_j}}g_l\|_{p,\mu}\qquad (\text{by } (7.3))\\ &\leqslant \sum_{ l=j+1} \| B^{n_{k_j}}\| \|f_{k_l}\|_{p,\mu}\\ &< \sum_{ l=j+1}\dfrac{\| B^{n_{k_j}}\|}{2^{l}c_{l}} \qquad (\text{by } (7.4))\\ &\leqslant \sum_{ l=j+1}\dfrac{1}{2^{l}}\underset{j\to+\infty}{\longrightarrow}0, \end{align*} $$
hence condition
![]() $(3)$
holds.
$(3)$
holds.
Let us show that
![]() $(5)$
implies
$(5)$
implies
![]() $(7)$
. Set
$(7)$
. Set
![]() $C=\max \lbrace 2, \|B\|\rbrace $
. By assuming that
$C=\max \lbrace 2, \|B\|\rbrace $
. By assuming that
![]() $(5)$
holds, there exist an increasing sequence
$(5)$
holds, there exist an increasing sequence
![]() $(n_{k})_{k\in \mathbb {N}}$
of positive integers and a vertex
$(n_{k})_{k\in \mathbb {N}}$
of positive integers and a vertex
![]() $v\in V$
such that
$v\in V$
such that
 $$ \begin{align} \Big(\sum_{u \in \mathrm{Chi}^{n_{k}+k}(v)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\Big)^{-1/p^{\ast}}<C^{-2k}. \end{align} $$
$$ \begin{align} \Big(\sum_{u \in \mathrm{Chi}^{n_{k}+k}(v)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\Big)^{-1/p^{\ast}}<C^{-2k}. \end{align} $$
For every
![]() $u\in V\setminus \lbrace \texttt {r}\rbrace $
, by Proposition 2.2, we obtain
$u\in V\setminus \lbrace \texttt {r}\rbrace $
, by Proposition 2.2, we obtain
 $$ \begin{align*}C\geqslant \Big(\sum_{v\in \mathrm{Chi}(\mathrm{par}(u))} \left|\frac{\mu_{\mathrm{par}(u)}}{\mu_v }\right|{}^{p^\ast}\Big)^{1/p^{\ast}}\geqslant \left|\frac{\mu_{\mathrm{par}(u)}}{\mu_u }\right|,\end{align*} $$
$$ \begin{align*}C\geqslant \Big(\sum_{v\in \mathrm{Chi}(\mathrm{par}(u))} \left|\frac{\mu_{\mathrm{par}(u)}}{\mu_v }\right|{}^{p^\ast}\Big)^{1/p^{\ast}}\geqslant \left|\frac{\mu_{\mathrm{par}(u)}}{\mu_u }\right|,\end{align*} $$
that is, for every
![]() $u\in V\setminus \lbrace \texttt {r}\rbrace $
,
$u\in V\setminus \lbrace \texttt {r}\rbrace $
,
 $$ \begin{align} \left|\frac{\mu_u }{\mu_{\mathrm{par}(u)}}\right|\geqslant C^{-1}. \end{align} $$
$$ \begin{align} \left|\frac{\mu_u }{\mu_{\mathrm{par}(u)}}\right|\geqslant C^{-1}. \end{align} $$
Fix now
![]() $l\in \mathbb {N}_0$
. Let
$l\in \mathbb {N}_0$
. Let
![]() $k\in \mathbb {N}$
be such that
$k\in \mathbb {N}$
be such that
![]() $k>l$
. Note that
$k>l$
. Note that
and for every
![]() $u\in \mathrm {Chi}^{n_{k}+k}(v)$
, we have
$u\in \mathrm {Chi}^{n_{k}+k}(v)$
, we have
 $$ \begin{align*}\mu_{u}=\dfrac{\mu_u}{\mu_{\mathrm{par}(u)}}\times \dfrac{\mu_{\mathrm{par}(u)}}{\mu_{\mathrm{par}^2(u)}} \times \cdots\times \dfrac{\mu_{\mathrm{par}^{k-l-1}(u)}}{\mu_{\mathrm{par}^{k-l}(u)}}\times \mu_{\mathrm{par}^{k-l}(u)}.\end{align*} $$
$$ \begin{align*}\mu_{u}=\dfrac{\mu_u}{\mu_{\mathrm{par}(u)}}\times \dfrac{\mu_{\mathrm{par}(u)}}{\mu_{\mathrm{par}^2(u)}} \times \cdots\times \dfrac{\mu_{\mathrm{par}^{k-l-1}(u)}}{\mu_{\mathrm{par}^{k-l}(u)}}\times \mu_{\mathrm{par}^{k-l}(u)}.\end{align*} $$
By (7.6), we obtain
 $$ \begin{align*}\dfrac{1}{|\mu_{\mathrm{par}^{k-l}(u)}|^{p^{\ast}}}\geqslant C^{(l-k)p^{\ast}}\dfrac{1}{|\mu_{u}|^{p^{\ast}}}.\end{align*} $$
$$ \begin{align*}\dfrac{1}{|\mu_{\mathrm{par}^{k-l}(u)}|^{p^{\ast}}}\geqslant C^{(l-k)p^{\ast}}\dfrac{1}{|\mu_{u}|^{p^{\ast}}}.\end{align*} $$
Combining this with (7.7), we obtain
 $$ \begin{align*}\Big(\sum_{u \in \mathrm{Chi}^{n_{k}+l}(v)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\Big)^{1/p^{\ast}}\geqslant C^{l-k} \Big(\sum_{u \in \mathrm{Chi}^{n_{k}+k}(v)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\Big)^{1/p^{\ast}}.\end{align*} $$
$$ \begin{align*}\Big(\sum_{u \in \mathrm{Chi}^{n_{k}+l}(v)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\Big)^{1/p^{\ast}}\geqslant C^{l-k} \Big(\sum_{u \in \mathrm{Chi}^{n_{k}+k}(v)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\Big)^{1/p^{\ast}}.\end{align*} $$
Thus,
 $$ \begin{align*} \Big(\sum_{u \in \mathrm{Chi}^{n_{k}+l}(v)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\Big)^{-1/p^{\ast}}&\leqslant C^{k-l} \Big(\sum_{u \in \mathrm{Chi}^{n_{k}+k}(v)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\Big)^{-1/p^{\ast}}\\ &\overset{(7.5)}{\leqslant} C^{k-l} C^{-2k}\leqslant C^{-k} \underset{k\to+\infty}{\longrightarrow}0. \end{align*} $$
$$ \begin{align*} \Big(\sum_{u \in \mathrm{Chi}^{n_{k}+l}(v)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\Big)^{-1/p^{\ast}}&\leqslant C^{k-l} \Big(\sum_{u \in \mathrm{Chi}^{n_{k}+k}(v)}\dfrac{1}{|\mu_u|^{p^{\ast}}}\Big)^{-1/p^{\ast}}\\ &\overset{(7.5)}{\leqslant} C^{k-l} C^{-2k}\leqslant C^{-k} \underset{k\to+\infty}{\longrightarrow}0. \end{align*} $$
We now provide an example of a backward shift operator on a rooted directed tree that is not hypercyclic, but it has an orbit with a nonzero limit point.
Example 7.2 Let B be the backward shift operator given in Example 4.2. It is clear that, by using Theorem 4.1, B is not hypercyclic. For every
![]() $N\in \mathbb {N}$
, we have
$N\in \mathbb {N}$
, we have
 $$ \begin{align*}I(\texttt{r},N):=\Big\{n\in\mathbb{N}_0:\, \Big(\sum_{u\in\mathrm{Chi}^n(\texttt{r})} \dfrac{1}{|\mu_{u}|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\}\in\mathcal{J},\end{align*} $$
$$ \begin{align*}I(\texttt{r},N):=\Big\{n\in\mathbb{N}_0:\, \Big(\sum_{u\in\mathrm{Chi}^n(\texttt{r})} \dfrac{1}{|\mu_{u}|^{p^\ast}}\Big)^{1/p^\ast}>N\Big\}\in\mathcal{J},\end{align*} $$
hence, by using Theorem 7.1, we deduce that B has an orbit with a nonzero limit point.
The following proposition provides a characterization of backward shift operators that have an orbit of a non-negative function with a nonzero limit point, specifically in the context of unrooted directed trees. We omit the proof as it can be derived through straightforward modifications of the arguments presented in the proofs of the preceding theorems.
Proposition 7.3 Let
![]() $(V,E)$
be an unrooted directed tree and let
$(V,E)$
be an unrooted directed tree and let
![]() $\mu =(\mu _v)_{v\in V}$
be a weight on V. Let
$\mu =(\mu _v)_{v\in V}$
be a weight on V. Let
![]() $X=\ell ^p(V,\mu )$
,
$X=\ell ^p(V,\mu )$
,
![]() $1\leq p <+\infty $
, or
$1\leq p <+\infty $
, or
![]() $X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. The following conditions are equivalent:
$X=c_0(V,\mu )$
and suppose that the backward shift B is a bounded operator on X. The following conditions are equivalent:
-
(1) There exists a nonnegative vector in X whose orbit under B has a nonzero limit point.
-
(2) There exist a vertex
 $v\in V$
and a nonnegative vector in X whose orbit under B has
$v\in V$
and a nonnegative vector in X whose orbit under B has
 $e_{v}$
as a limit point.
$e_{v}$
as a limit point. -
(3) There exist an increasing sequence
 $(n_k)_{k}$
of positive integers and a vertex
$(n_k)_{k}$
of positive integers and a vertex
 $v\in V$
such that
$v\in V$
such that  $$ \begin{align*}\begin{cases} \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty;\\ &\\ \underset{u\in\mathrm{Chi}^{n_{k}}(v)}{\inf}\,|\mu_u|\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu); \\ &\\ \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{1}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu), \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{1}{|\mu_u|^{p^{\ast}}}\underset{k\to+\infty}{\longrightarrow}+\infty & \text{ if } X=\ell^p(V,\mu),\, 1< p<+\infty;\\ &\\ \underset{u\in\mathrm{Chi}^{n_{k}}(v)}{\inf}\,|\mu_u|\underset{k\to+\infty}{\longrightarrow}0 &\text{ if } X=\ell^1(V,\mu); \\ &\\ \underset{u \in \mathrm{Chi}^{n_k}(v)}{\sum}\dfrac{1}{|\mu_u|}\underset{k\to+\infty}{\longrightarrow}+\infty&\text{ if } X=c_0(V,\mu), \end{cases}\end{align*} $$
and, for every
 $i\in \mathbb {N}$
, we have
$i\in \mathbb {N}$
, we have  $$ \begin{align*}\mu_{\mathrm{par}^{n_k-n_i}(v)}\underset{k\to+\infty}{\longrightarrow}0.\end{align*} $$
$$ \begin{align*}\mu_{\mathrm{par}^{n_k-n_i}(v)}\underset{k\to+\infty}{\longrightarrow}0.\end{align*} $$
In the following example, we provide a nonhypercyclic bounded backward shift on an unrooted directed tree that has an orbit with a nonzero limit point, but it does not possess an orbit of a nonnegative function with a nonzero limit point.
Example 7.4 Let
![]() $(V,E)$
be the following unrooted directed tree:
$(V,E)$
be the following unrooted directed tree:

that is
Let
![]() $\mu =(\mu _v)_{v\in V}$
be the weight on V defined by
$\mu =(\mu _v)_{v\in V}$
be the weight on V defined by
Let B be the backward shift on
![]() $\ell ^p(V,\mu )$
,
$\ell ^p(V,\mu )$
,
![]() $1<p<+\infty $
. By Proposition 2.2, it is clear that B is bounded and
$1<p<+\infty $
. By Proposition 2.2, it is clear that B is bounded and
![]() $\|B\|=2^{2-\frac {1}{p}}$
. Now, consider any vertex
$\|B\|=2^{2-\frac {1}{p}}$
. Now, consider any vertex
![]() $v\in V$
, any increasing sequence
$v\in V$
, any increasing sequence
![]() $(n_k)_{k\in \mathbb {N}}$
of positive integers, and
$(n_k)_{k\in \mathbb {N}}$
of positive integers, and
![]() $i\in \mathbb {N}$
, we have
$i\in \mathbb {N}$
, we have
thus, the condition
![]() $(3)$
of Proposition 7.3 does not hold. Consequently, B does not possess an orbit of a nonnegative function with a nonzero limit point. Moreover, for any vertex
$(3)$
of Proposition 7.3 does not hold. Consequently, B does not possess an orbit of a nonnegative function with a nonzero limit point. Moreover, for any vertex
![]() $v\in V$
and any increasing sequence
$v\in V$
and any increasing sequence
![]() $(n_k)_{k\in \mathbb {N}}$
of positive integers, we have
$(n_k)_{k\in \mathbb {N}}$
of positive integers, we have

thus, by using Theorem 5.1 (when
![]() $\mathcal {F}$
is the Furstenberg family of infinite subsets of
$\mathcal {F}$
is the Furstenberg family of infinite subsets of
![]() $\mathbb {N}_0$
), we deduce that B is not hypercyclic.
$\mathbb {N}_0$
), we deduce that B is not hypercyclic.
Let
![]() $f:V\longrightarrow \mathbb {C}$
be the function defined by
$f:V\longrightarrow \mathbb {C}$
be the function defined by
We have
![]() $f\in \ell ^p(V,\mu )$
, since
$f\in \ell ^p(V,\mu )$
, since
Let us show that
![]() $B^{2^k-1}f\underset {k\to +\infty }{\longrightarrow }e_{u_1}-e_{v_1}$
. One has
$B^{2^k-1}f\underset {k\to +\infty }{\longrightarrow }e_{u_1}-e_{v_1}$
. One has
 $$ \begin{align*} \| B^{2^k-1}f-e_{u_1}+e_{v_1}\|_{p,\mu}^p&=\sum_{j\geq0}|(B^{2^k-1}f)(o_j)|^p\mu_{o_j}^p \\ &\quad +|(B^{2^k-1}f)(u_1)-1|^p\mu_{u_1}^{p}+ \sum_{j\geq2}|(B^{2^k-1}f)(u_j)|^p\mu_{u_j}^p\\ &\quad +|(B^{2^k-1}f)(v_1)+1|^p\mu_{v_1}^{p}+ \sum_{j\geq2}|(B^{2^k-1}f)(v_j)|^p\mu_{v_j}^p. \end{align*} $$
$$ \begin{align*} \| B^{2^k-1}f-e_{u_1}+e_{v_1}\|_{p,\mu}^p&=\sum_{j\geq0}|(B^{2^k-1}f)(o_j)|^p\mu_{o_j}^p \\ &\quad +|(B^{2^k-1}f)(u_1)-1|^p\mu_{u_1}^{p}+ \sum_{j\geq2}|(B^{2^k-1}f)(u_j)|^p\mu_{u_j}^p\\ &\quad +|(B^{2^k-1}f)(v_1)+1|^p\mu_{v_1}^{p}+ \sum_{j\geq2}|(B^{2^k-1}f)(v_j)|^p\mu_{v_j}^p. \end{align*} $$
We will show now that all these terms converge to
![]() $0$
, as k goes to
$0$
, as k goes to
![]() $+\infty $
.
$+\infty $
.
-
• Let
 $k,j\in \mathbb {N}$
. If
$k,j\in \mathbb {N}$
. If
 $2^{k}-1\leq j$
, then
$2^{k}-1\leq j$
, then
 $\mathrm {Chi}^{2^k-1}(o_j)=\{o_{j-2^k+1}\}$
, hence. If
$\mathrm {Chi}^{2^k-1}(o_j)=\{o_{j-2^k+1}\}$
, hence. If $$ \begin{align*}(B^{2^k-1}f)(o_j)=f(o_{j-2^k+1})=0.\end{align*} $$
$$ \begin{align*}(B^{2^k-1}f)(o_j)=f(o_{j-2^k+1})=0.\end{align*} $$
 $2^{k}-1>j$
, then
$2^{k}-1>j$
, then
 $\mathrm {Chi}^{2^k-1}(o_j)=\{u_{2^k-1-j},v_{2^k-1-j}\}$
, hence Thus
$\mathrm {Chi}^{2^k-1}(o_j)=\{u_{2^k-1-j},v_{2^k-1-j}\}$
, hence Thus $$ \begin{align*}(B^{2^k-1}f)(o_j)=f(u_{2^k-1-j})+f(v_{2^k-1-j})=0.\end{align*} $$
$$ \begin{align*}(B^{2^k-1}f)(o_j)=f(u_{2^k-1-j})+f(v_{2^k-1-j})=0.\end{align*} $$
 $$ \begin{align*}\sum_{j\geq0}|(B^{2^k-1}f)(o_j)|^p\mu_{o_j}^p=0.\end{align*} $$
$$ \begin{align*}\sum_{j\geq0}|(B^{2^k-1}f)(o_j)|^p\mu_{o_j}^p=0.\end{align*} $$
-
• Let
 $k\in \mathbb {N}$
. We have and
$k\in \mathbb {N}$
. We have and $$ \begin{align*}(B^{2^k-1}f)(u_1)=\sum_{v\in \mathrm{Chi}^{2^{k}-1}(u_1)}f(v)=f(u_{2^k})=1,\end{align*} $$
$$ \begin{align*}(B^{2^k-1}f)(u_1)=\sum_{v\in \mathrm{Chi}^{2^{k}-1}(u_1)}f(v)=f(u_{2^k})=1,\end{align*} $$
 $$ \begin{align*}(B^{2^k-1}f)(v_1)=\sum_{v\in \mathrm{Chi}^{2^{k}-1}(v_1)}f(v)=f(v_{2^k})=-1.\end{align*} $$
$$ \begin{align*}(B^{2^k-1}f)(v_1)=\sum_{v\in \mathrm{Chi}^{2^{k}-1}(v_1)}f(v)=f(v_{2^k})=-1.\end{align*} $$
-
• Let
 $k\in \mathbb {N}$
. We have since, for every
$k\in \mathbb {N}$
. We have since, for every $$ \begin{align*} \sum_{j\geq2}|(B^{2^k-1}f)(u_j)|^p\mu_{u_j}^p&=\sum_{j\geq2}|f(u_{2^k-1+j})|^p\mu_{u_j}^p\\ &=\sum_{l\geq k+1}|f(u_{2^l})|^p\mu_{u_{2^l-2^k+1}}^p\\ &=\dfrac{1}{2^p}\sum_{l\geq k+1}\dfrac{1}{2^{p(2^l-2^k)}}, \end{align*} $$
$$ \begin{align*} \sum_{j\geq2}|(B^{2^k-1}f)(u_j)|^p\mu_{u_j}^p&=\sum_{j\geq2}|f(u_{2^k-1+j})|^p\mu_{u_j}^p\\ &=\sum_{l\geq k+1}|f(u_{2^l})|^p\mu_{u_{2^l-2^k+1}}^p\\ &=\dfrac{1}{2^p}\sum_{l\geq k+1}\dfrac{1}{2^{p(2^l-2^k)}}, \end{align*} $$
 $l\geq k+1$
,
$l\geq k+1$
,
 $2^l-2^k\geq l$
, we get
$2^l-2^k\geq l$
, we get  $$ \begin{align*}\sum_{j\geq2}|(B^{2^k-1}f)(u_j)|^p\mu_{u_j}^p \leqslant \dfrac{1}{2}\sum_{l\geq k+1}\dfrac{1}{2^{l}}\underset{k\to+\infty}{\longrightarrow}0.\end{align*} $$
$$ \begin{align*}\sum_{j\geq2}|(B^{2^k-1}f)(u_j)|^p\mu_{u_j}^p \leqslant \dfrac{1}{2}\sum_{l\geq k+1}\dfrac{1}{2^{l}}\underset{k\to+\infty}{\longrightarrow}0.\end{align*} $$
-
• Similarly, for each
 $k\in \mathbb {N}$
, we have
$k\in \mathbb {N}$
, we have  $$ \begin{align*}\sum_{j\geq2}|(B^{2^k-1}f)(v_j)|^p\mu_{v_j}^p=\dfrac{1}{2^p}\sum_{l\geq k+1}\dfrac{1}{2^{p(2^l-2^k)}}\underset{k\to+\infty}{\longrightarrow}0.\end{align*} $$
$$ \begin{align*}\sum_{j\geq2}|(B^{2^k-1}f)(v_j)|^p\mu_{v_j}^p=\dfrac{1}{2^p}\sum_{l\geq k+1}\dfrac{1}{2^{p(2^l-2^k)}}\underset{k\to+\infty}{\longrightarrow}0.\end{align*} $$
Hence,
Therefore, B has an orbit with a nonzero limit point. Note that the above computations also work when considering the backward shift operator B as an operator acting on
![]() $\ell ^1(V,\mu )$
or
$\ell ^1(V,\mu )$
or
![]() $c_0(V,\mu )$
.
$c_0(V,\mu )$
.