Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-06T08:42:06.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Newforms of Half-integral Weight: The Minus Space Counterpart

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  31 October 2019

Ehud Moshe Baruch  and
Soma Purkait
Ehud Moshe Baruch
Affiliation:
Department of Mathematics, Technion, Haifa, 32000, Israel Email: embaruch@math.technion.ac.il
Soma Purkait
Affiliation:
Department of Mathematics, Tokyo Institute of Technology, Japan Email: somapurkait@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study genuine local Hecke algebras of the Iwahori type of the double cover of 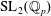$\operatorname{SL}_{2}(\mathbb{Q}_{p})$ and translate the generators and relations to classical operators on the space 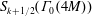$S_{k+1/2}(\unicode[STIX]{x1D6E4}_{0}(4M))$, 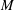$M$ odd and square-free. In [9] Manickam, Ramakrishnan, and Vasudevan defined the new space of 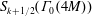$S_{k+1/2}(\unicode[STIX]{x1D6E4}_{0}(4M))$ that maps Hecke isomorphically onto the space of newforms of $S_{2k}(\unicode[STIX]{x1D6E4}_{0}(2M))$. We characterize this newspace as a common 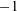$-1$-eigenspace of a certain pair of conjugate operators that come from local Hecke algebras. We use the classical Hecke operators and relations that we obtain to give a new proof of the results in [9] and to prove our characterization result.

Keywords

Hecke algebrahalf-integral weight formNiwa isomorphismKohnen plus space

MSC classification

Primary: 11F37: Forms of half-integer weight; nonholomorphic modular forms
Secondary: 11F12: Automorphic forms, one variable 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 2 , April 2020 , pp. 326 - 372
Copyright
© Canadian Mathematical Society 2019

References

Atkin, A. O. L. and Lehner, J., Hecke operators on 𝛤0(m). Math. Ann. 185(1970), 134–160. https://doi.org/10.1007/BF01359701Google Scholar
Baruch, E. M. and Purkait, S., Hecke algebras, new vectors and newforms on 𝛤0(m). Math. Zeit. 287(2017), 705–733. https://doi.org/10.1007/s00209-017-1842-yGoogle Scholar
Baruch, E. M. and Purkait, S., Newforms of half-integral weight: the minus space of S k+1/2(𝛤0(8M)). Israel J. Math. 232(2019), 41–73. https://doi.org/10.1007/s11856-019-1873-7Google Scholar
Gelbart, S., Weil’s representation and the spectrum of the metaplectic group. Lecture Notes in Mathematics, 530, Springer-Verlag, Berlin, 1976.Google Scholar
Kohnen, W., Modular forms of half-integral weight on 𝛤0(4). Math. Ann. 248(1980), 249–266. https://doi.org/10.1007/BF01420529Google Scholar
Kohnen, W., Newforms of half-integral weight. J. Reine Angew. Math. 333(1982), 32–72. https://doi.org/10.1515/crll.1982.333.32Google Scholar
Kumar, N. and Purkait, S., A note on the Fourier coefficients of half-integral weight modular forms. Arch. Math. (Basel) 102(2014), no. 4, 369–378. https://doi.org/10.1007/s00013-014-0622-8Google Scholar
Loke, H. Y. and Savin, G., Representations of the two-fold central extension of [[()[]mml:mo lspace="1em" rspace="0em"[]()]]SL[[()[]/mml:mo[]()]]2(ℚ2). Pacific J. Math. 247(2010), 435–454. https://doi.org/10.2140/pjm.2010.247.435Google Scholar
Manickam, M., Ramakrishnan, B., and Vasudevan, T., On the theory of newforms of half-integral weight. J. Number Theory 34(1990), 210–224. https://doi.org/10.1016/0022-314X(90)90151-GGoogle Scholar
Niwa, S., On Shimura’s trace formula. Nagoya Math. J. 66(1977), 183–202.Google Scholar
Purkait, S., On Shimura’s decomposition. Int. J. Number Theory 9(2013), 1431–1445. https://doi.org/10.1142/S179304211350036XGoogle Scholar
Purkait, S., Hecke operators in half-integral weight. J. Théor. Nombres Bordeaux 26(2014), 233–251.Google Scholar
Savin, G., On unramified representations of covering groups. J. Reine Angew. Math. 566(2004), 111–134. https://doi.org/10.1515/crll.2004.001Google Scholar
Shimura, G., On modular forms of half integral weight. Ann. of Math. 97(1973), 440–481. https://doi.org/10.2307/1970831Google Scholar
Shimura, G., The critical values of certain zeta functions associated with modular forms of half-integral weight. J. Math. Soc. Japan 33(1981), 649–672. https://doi.org/10.2969/jmsj/03340649Google Scholar
Ueda, M., On twisting operators and newforms of half-integral weight. Nagoya Math J. 131(1993), 135–205. https://doi.org/10.1017/S002776300000458XGoogle Scholar
Ueda, M. and Yamana, S., On newforms for Kohnen plus spaces. Math. Z. 264(2010), 1–13. https://doi.org/10.1007/s00209-008-0449-8Google Scholar
Waldspurger, J.-L., Sur les coefficients de Fourier des formes modulaires de poids demi-entier. J. Math. Pures Appl. (9) 60(1981), 375–484.Google Scholar