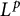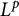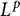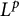1 Introduction
1.1 Main result
Let
![]() $n\geq 2$
, and for each
$n\geq 2$
, and for each
![]() $1\leq j \leq n$
, let
$1\leq j \leq n$
, let
![]() $b^j=(b^j_1,\dots , b^j_n)\in \mathbb {Q}^n$
be an n-tuple of rational numbers. Let
$b^j=(b^j_1,\dots , b^j_n)\in \mathbb {Q}^n$
be an n-tuple of rational numbers. Let
![]() $\mathscr {U}\subset {\mathbb {C}}^n$
be a bounded domain (open connected subset) of the form
$\mathscr {U}\subset {\mathbb {C}}^n$
be a bounded domain (open connected subset) of the form
 $$ \begin{align} \mathscr{U}=\left\{z\in{\mathbb{C}}^n: \text{ for } 1\leq j \leq n,\quad \prod_{k=1}^n\left\vert z_k\right\vert{{\hspace{-0.0001pt}}}^{b^j_k} <1 \right\}, \end{align} $$
$$ \begin{align} \mathscr{U}=\left\{z\in{\mathbb{C}}^n: \text{ for } 1\leq j \leq n,\quad \prod_{k=1}^n\left\vert z_k\right\vert{{\hspace{-0.0001pt}}}^{b^j_k} <1 \right\}, \end{align} $$
where it is understood that a point
![]() $z\in {\mathbb {C}}^n$
does not belong to
$z\in {\mathbb {C}}^n$
does not belong to
![]() $\mathscr {U}$
if for some
$\mathscr {U}$
if for some
![]() $1\leq j \leq n$
, the quantity
$1\leq j \leq n$
, the quantity
![]() $ \prod _{k=1}^n\left \vert z_k\right \vert {{\hspace{-0.0001pt}}}^{b^j_k}$
is not defined due to division by zero. We call a domain such as
$ \prod _{k=1}^n\left \vert z_k\right \vert {{\hspace{-0.0001pt}}}^{b^j_k}$
is not defined due to division by zero. We call a domain such as
![]() $\mathscr {U}$
a monomial polyhedron.
$\mathscr {U}$
a monomial polyhedron.
We refer the reader to Section 1.2 for a discussion of the significance of monomial polyhedra in complex analysis. Our main result is the following:
Theorem 1.2 Suppose that the monomial polyhedron
![]() $\mathscr {U}$
of (
1.1
) is bounded. Then there is a positive integer
$\mathscr {U}$
of (
1.1
) is bounded. Then there is a positive integer
![]() $\kappa (\mathscr {U})$
(the complexity of
$\kappa (\mathscr {U})$
(the complexity of
![]() $\mathscr {U}$
, whose computation is described below) such that the Bergman projection on
$\mathscr {U}$
, whose computation is described below) such that the Bergman projection on
![]() $\mathscr {U}$
is bounded on
$\mathscr {U}$
is bounded on
![]() $L^p(\mathscr {U})$
if and only if
$L^p(\mathscr {U})$
if and only if
 $$ \begin{align} \frac{2\kappa(\mathscr{U})}{\kappa(\mathscr{U})+1}<p< \frac{2\kappa(\mathscr{U})}{\kappa(\mathscr{U})-1}. \end{align} $$
$$ \begin{align} \frac{2\kappa(\mathscr{U})}{\kappa(\mathscr{U})+1}<p< \frac{2\kappa(\mathscr{U})}{\kappa(\mathscr{U})-1}. \end{align} $$
To compute
![]() $\kappa (\mathscr {U})$
, first define for a vector
$\kappa (\mathscr {U})$
, first define for a vector
![]() $x\in \mathbb {Q}^n\setminus \{0\}$
, the positive integer
$x\in \mathbb {Q}^n\setminus \{0\}$
, the positive integer
![]() $\mathsf {h}(x)$
(the projective height of x) as follows. If we think of x as the homogeneous coordinates of a point
$\mathsf {h}(x)$
(the projective height of x) as follows. If we think of x as the homogeneous coordinates of a point
![]() $[x]$
in the rational projective space
$[x]$
in the rational projective space
![]() $\mathbb {P}^{n-1}(\mathbb {Q})$
, there is clearly an integer vector
$\mathbb {P}^{n-1}(\mathbb {Q})$
, there is clearly an integer vector
![]() $y\in \mathbb {Z}^n$
such that
$y\in \mathbb {Z}^n$
such that
![]() $[y]=[x]$
(i.e., there is a
$[y]=[x]$
(i.e., there is a
![]() $\lambda \in \mathbb {Q}\setminus \{0\}$
such that
$\lambda \in \mathbb {Q}\setminus \{0\}$
such that
![]() $y=\lambda x$
), and we have additionally that
$y=\lambda x$
), and we have additionally that
![]() $\gcd (y_1,\dots , y_n)=1$
. We then set
$\gcd (y_1,\dots , y_n)=1$
. We then set
 $$ \begin{align} \mathsf{h}(x)=\sum_{j=1}^n \left\vert y_j\right\vert. \end{align} $$
$$ \begin{align} \mathsf{h}(x)=\sum_{j=1}^n \left\vert y_j\right\vert. \end{align} $$
We can think of
![]() $\mathsf {h}$
as a height function on
$\mathsf {h}$
as a height function on
![]() $\mathbb {P}^{n-1}(\mathbb {Q})$
in the sense of Diophantine geometry, uniformly comparable to the standard multiplicative height function (see [Reference Hindry and SilvermanHS00, pp. 174 ff.]).
$\mathbb {P}^{n-1}(\mathbb {Q})$
in the sense of Diophantine geometry, uniformly comparable to the standard multiplicative height function (see [Reference Hindry and SilvermanHS00, pp. 174 ff.]).
Let B be the
![]() $n\times n$
matrix whose entry in the jth row and kth column is
$n\times n$
matrix whose entry in the jth row and kth column is
![]() $b^j_k$
, i.e., the jth row of B is the multi-index
$b^j_k$
, i.e., the jth row of B is the multi-index
![]() $b^j$
in (1.1). It will follow from our work below (Proposition 3.2) that the matrix
$b^j$
in (1.1). It will follow from our work below (Proposition 3.2) that the matrix
![]() $B\in M_n(\mathbb {Q})$
is invertible. We define
$B\in M_n(\mathbb {Q})$
is invertible. We define
where
![]() $e_k$
denotes the
$e_k$
denotes the
![]() $n\times 1$
column vector all whose entries are zero, except the kth, which is 1. Notice that
$n\times 1$
column vector all whose entries are zero, except the kth, which is 1. Notice that
![]() $B^{-1}e_k$
is simply the kth column of the matrix
$B^{-1}e_k$
is simply the kth column of the matrix
![]() $B^{-1}$
, that is, the arithmetic complexity of the monomial polyhedron
$B^{-1}$
, that is, the arithmetic complexity of the monomial polyhedron
![]() $\mathscr {U}$
is the maximum projective height of the columns of
$\mathscr {U}$
is the maximum projective height of the columns of
![]() $B^{-1}$
, where B is the rational matrix whose rows are the multi-indices occurring in the n inequalities that define
$B^{-1}$
, where B is the rational matrix whose rows are the multi-indices occurring in the n inequalities that define
![]() $\mathscr {U}$
in (1.1). It will be shown below in Proposition 3.5 that the integer
$\mathscr {U}$
in (1.1). It will be shown below in Proposition 3.5 that the integer
![]() $\kappa (\mathscr {U})$
is determined only by the domain
$\kappa (\mathscr {U})$
is determined only by the domain
![]() $\mathscr {U}$
and not the particular representation on the right hand side of (1.1).
$\mathscr {U}$
and not the particular representation on the right hand side of (1.1).
1.2 Singular Reinhardt domains in complex analysis
Except in the degenerate case when it reduces to a polydisc (e.g., when
![]() $b^j=e_j$
, the jth natural basis vector of
$b^j=e_j$
, the jth natural basis vector of
![]() $\mathbb {Q}^n$
), the domain
$\mathbb {Q}^n$
), the domain
![]() $\mathscr {U}$
is a Reinhardt pseudoconvex domain (with center of symmetry at the origin) such that the origin is a boundary point. These singular Reinhardt domains (their boundaries are not Lipschitz at 0) display pathological holomorphic extension phenomena: the best-known example is that of the Hartogs triangle
$\mathscr {U}$
is a Reinhardt pseudoconvex domain (with center of symmetry at the origin) such that the origin is a boundary point. These singular Reinhardt domains (their boundaries are not Lipschitz at 0) display pathological holomorphic extension phenomena: the best-known example is that of the Hartogs triangle
![]() $\{\left \vert z_1\right \vert <\left \vert z_2\right \vert <1\}\subset {\mathbb {C}}^2$
, corresponding to a
$\{\left \vert z_1\right \vert <\left \vert z_2\right \vert <1\}\subset {\mathbb {C}}^2$
, corresponding to a
![]() $\mathscr {U}$
with
$\mathscr {U}$
with
![]() $b^1=(1,-1), b^2=(0,1)$
(see [Reference BehnkeBeh33, Reference SibonySib75]). For example, on a singular Reinhardt domain, each holomorphic function smooth up to the closure extends holomorphically to a fixed neighborhood of the closure (see [Reference ChakrabartiCha19]), something which is impossible for smoothly bounded pseudoconvex domains [Reference Hakim and SibonyHS80, Reference CatlinCat80]. Therefore, a profound understanding of function theory on these domains is an important step in extending classical results on the regularity of the
$b^1=(1,-1), b^2=(0,1)$
(see [Reference BehnkeBeh33, Reference SibonySib75]). For example, on a singular Reinhardt domain, each holomorphic function smooth up to the closure extends holomorphically to a fixed neighborhood of the closure (see [Reference ChakrabartiCha19]), something which is impossible for smoothly bounded pseudoconvex domains [Reference Hakim and SibonyHS80, Reference CatlinCat80]. Therefore, a profound understanding of function theory on these domains is an important step in extending classical results on the regularity of the
![]() $\overline \partial $
-problem (and associated operators such as the Bergman projection) to new and more general settings (see [Reference Jarnicki and PflugJP08]). Monomial polyhedra are an interesting class of such singular Reinhardt pseudoconvex domains with tractable geometry and some very interesting properties. They can be compared to analytic polyhedra in the classical theory of pseudoconvex domains: model exhausting domains where explicit computations are possible (see [Reference VladimirovVla66, Section 24]).
$\overline \partial $
-problem (and associated operators such as the Bergman projection) to new and more general settings (see [Reference Jarnicki and PflugJP08]). Monomial polyhedra are an interesting class of such singular Reinhardt pseudoconvex domains with tractable geometry and some very interesting properties. They can be compared to analytic polyhedra in the classical theory of pseudoconvex domains: model exhausting domains where explicit computations are possible (see [Reference VladimirovVla66, Section 24]).
The striking phenomenon observed in Theorem 1.2 was first noticed (see [Reference Edholm and McNealEM17]) in the setting of the so-called generalized Hartogs triangles, defined for coprime positive integers
![]() $k_1,k_2$
as
$k_1,k_2$
as
which corresponds to
![]() $b^1=\left (\frac {k_1}{k_2},-1\right )$
and
$b^1=\left (\frac {k_1}{k_2},-1\right )$
and
![]() $b^2=(0,1)$
. It is striking that the range (1.3) should depend, not on the shape of the domain as a subset of
$b^2=(0,1)$
. It is striking that the range (1.3) should depend, not on the shape of the domain as a subset of
![]() ${\mathbb {C}}^2$
(which is determined in the case of
${\mathbb {C}}^2$
(which is determined in the case of
![]() $H_{k_1/k_2}$
by the “fatness exponent”
$H_{k_1/k_2}$
by the “fatness exponent”
![]() $\frac {k_1}{k_2}$
), but on the complexity (which, for,
$\frac {k_1}{k_2}$
), but on the complexity (which, for,
![]() $H_{k_1/k_2}$
is
$H_{k_1/k_2}$
is
![]() $k_1+k_2$
) , the range becoming narrower as the complexity rises. As a limiting case, if
$k_1+k_2$
) , the range becoming narrower as the complexity rises. As a limiting case, if
![]() $\gamma>0$
is irrational, on the domain
$\gamma>0$
is irrational, on the domain
![]() $\{\left \vert z_1\right \vert {{\hspace{-0.0001pt}}}^\gamma <\left \vert z_2\right \vert <1\}\subset {\mathbb {C}}^2$
(a domain of infinite complexity!), the Bergman projection is bounded in the
$\{\left \vert z_1\right \vert {{\hspace{-0.0001pt}}}^\gamma <\left \vert z_2\right \vert <1\}\subset {\mathbb {C}}^2$
(a domain of infinite complexity!), the Bergman projection is bounded in the
![]() $L^p$
-norm, only if
$L^p$
-norm, only if
![]() $p=2$
. The proofs of the precise range of
$p=2$
. The proofs of the precise range of
![]() $L^p$
-boundedness of the Bergman projection on
$L^p$
-boundedness of the Bergman projection on
![]() $H_{k_1/k_2}$
and its generalizations in earlier work [Reference Edholm and McNealEM17, Reference ChenChe17, Reference HuoHuo18, Reference ZhangZha20, Reference ZhangZha19] consist of an explicit computation of the Bergman kernel, followed by an application of Schur’s theorem on
$H_{k_1/k_2}$
and its generalizations in earlier work [Reference Edholm and McNealEM17, Reference ChenChe17, Reference HuoHuo18, Reference ZhangZha20, Reference ZhangZha19] consist of an explicit computation of the Bergman kernel, followed by an application of Schur’s theorem on
![]() $L^p$
boundedness of operators defined by integral kernels to determine the range of
$L^p$
boundedness of operators defined by integral kernels to determine the range of
![]() $L^p$
-boundedness. Other authors have used techniques of classical harmonic analysis, such as weak-type endpoint estimates along with interpolation in
$L^p$
-boundedness. Other authors have used techniques of classical harmonic analysis, such as weak-type endpoint estimates along with interpolation in
![]() $L^p$
-spaces, Muckenhoupt
$L^p$
-spaces, Muckenhoupt
![]() $A_p$
weights etc. to study related questions. See [Reference Chakrabarti and ZeytuncuCZ16, Reference EdholmEdh16, Reference Edholm and McNealEM16, Reference Chakrabarti, Edholm and McNealCEM19, Reference Huo and WickHW19, Reference Chen, Krantz and YuanCKY20, Reference Edholm and McNealEM20, Reference Chen, Jin and YuanCJY20] for other results in this circle of ideas.
$A_p$
weights etc. to study related questions. See [Reference Chakrabarti and ZeytuncuCZ16, Reference EdholmEdh16, Reference Edholm and McNealEM16, Reference Chakrabarti, Edholm and McNealCEM19, Reference Huo and WickHW19, Reference Chen, Krantz and YuanCKY20, Reference Edholm and McNealEM20, Reference Chen, Jin and YuanCJY20] for other results in this circle of ideas.
Theorem 1.2 not only encompasses the known examples of domains on which the relation between the regularity of the Bergman projection and arithmetic complexity has been observed, but also substantially extends this class of domains. Its proof is based on an understanding of the geometry of monomial polyhedra as quotient domains. It is hoped that this will eventually lead to a deeper understanding of this mysterious notion of complexity, and its extension to other contexts.
1.3 Ingredients in the proof of Theorem 1.2
The range of
![]() $L^p$
-boundedness of the Bergman projection on a domain is a function theoretic property determined by its Hermitian geometry, but the full extent of this relationship is yet to be understood. This article brings to bear a new perspective on this problem in the case of monomial polyhedra: one in which the domain is realized as a quotient of a simpler domain under the action of a group of biholomorphic automorphisms
$L^p$
-boundedness of the Bergman projection on a domain is a function theoretic property determined by its Hermitian geometry, but the full extent of this relationship is yet to be understood. This article brings to bear a new perspective on this problem in the case of monomial polyhedra: one in which the domain is realized as a quotient of a simpler domain under the action of a group of biholomorphic automorphisms
![]() $\Gamma $
(Theorem 3.12 below).
$\Gamma $
(Theorem 3.12 below).
Our approach to the geometry of
![]() $\mathscr {U}$
in Section 3 is inspired by the observation that in the “log-absolute coordinates”
$\mathscr {U}$
in Section 3 is inspired by the observation that in the “log-absolute coordinates”
![]() $\xi _k=\log \left \vert z_k\right \vert $
, it is represented as
$\xi _k=\log \left \vert z_k\right \vert $
, it is represented as
 $$ \begin{align} \sum_{k=1}^n b^j_k\xi_k<0,\quad \text{ for each } 1\leq j \leq n, \end{align} $$
$$ \begin{align} \sum_{k=1}^n b^j_k\xi_k<0,\quad \text{ for each } 1\leq j \leq n, \end{align} $$
which is an open polyhedral cone (intersection of open half-spaces) in the sense of convex geometry. By a classical result (see [Reference ZieglerZie95, Theorem 1.3, p. 30], also [Reference GrünbaumGrü03, Section 3.1]), such a polyhedral cone can also be represented as the cone generated by its extreme points, i.e., it is the image of an orthant (in a possibly higher dimensional Euclidean space) under a linear map. In Section 3, we prove an analogous statement for
![]() $\mathscr {U}$
: there is a domain
$\mathscr {U}$
: there is a domain
![]() $\mathbb {D}^n_{\mathsf {L}(B)}\subset {\mathbb {C}}^n$
, which is the product of a certain number of unit discs with a certain number of punctured unit discs, and a proper holomorphic map
$\mathbb {D}^n_{\mathsf {L}(B)}\subset {\mathbb {C}}^n$
, which is the product of a certain number of unit discs with a certain number of punctured unit discs, and a proper holomorphic map
![]() $\Phi _A:\mathbb {D}^n_{\mathsf {L}(B)}\to \mathscr {U}$
which is of the “quotient type” (see Definition 3.10), i.e., off some small analytic sets in the source and target, it is essentially a quotient map by a group
$\Phi _A:\mathbb {D}^n_{\mathsf {L}(B)}\to \mathscr {U}$
which is of the “quotient type” (see Definition 3.10), i.e., off some small analytic sets in the source and target, it is essentially a quotient map by a group
![]() $\Gamma $
of automorphisms of the source. It turns out that the map
$\Gamma $
of automorphisms of the source. It turns out that the map
![]() $\Phi _A$
is of “monomial type” in the sense of [Reference Nagel and PramanikNP20], i.e., an n-dimensional analog of the branched covering map from the disc to itself given by
$\Phi _A$
is of “monomial type” in the sense of [Reference Nagel and PramanikNP20], i.e., an n-dimensional analog of the branched covering map from the disc to itself given by
![]() $z\mapsto z^a$
for an integer
$z\mapsto z^a$
for an integer
![]() $a>0$
. This fact has several pleasant consequences and facilitates computations.
$a>0$
. This fact has several pleasant consequences and facilitates computations.
One of the consequences of the existence of the map
![]() $\Phi _A$
is that it allows us to compute the Bergman kernel of
$\Phi _A$
is that it allows us to compute the Bergman kernel of
![]() $\mathscr {U}$
explicitly. This has been a crucial step in the study of the Bergman projection on such domains in all prior investigations. In this paper, however, we avoid computing Bergman kernels and directly study the transformation properties of
$\mathscr {U}$
explicitly. This has been a crucial step in the study of the Bergman projection on such domains in all prior investigations. In this paper, however, we avoid computing Bergman kernels and directly study the transformation properties of
![]() $L^p$
-Bergman spaces. However, we do show in Proposition 3.22, using Theorem 3.12, that the Bergman kernel of
$L^p$
-Bergman spaces. However, we do show in Proposition 3.22, using Theorem 3.12, that the Bergman kernel of
![]() $\mathscr {U}$
is a rational function.
$\mathscr {U}$
is a rational function.
In Section 4, we study how
![]() $L^p$
-Bergman spaces and the Bergman projection acting on
$L^p$
-Bergman spaces and the Bergman projection acting on
![]() $L^p$
-Bergman spaces transform under proper holomorphic maps of quotient type. This point of view leads to a transformation law (Theorem 4.15 below) relating the
$L^p$
-Bergman spaces transform under proper holomorphic maps of quotient type. This point of view leads to a transformation law (Theorem 4.15 below) relating the
![]() $L^p$
-Bergman spaces and Bergman projections of the source and target—one that is closely connected to the well-known Bell’s transformation law relating the Bergman kernels. One new ingredient here is the use of subspaces invariant under the action of the deck transformation group of the proper holomorphic map, which allows us to state a sharp result which can be used in the Proof of Theorem 1.2. We believe that the considerations of Section 4 have an independent interest beyond their application here.
$L^p$
-Bergman spaces and Bergman projections of the source and target—one that is closely connected to the well-known Bell’s transformation law relating the Bergman kernels. One new ingredient here is the use of subspaces invariant under the action of the deck transformation group of the proper holomorphic map, which allows us to state a sharp result which can be used in the Proof of Theorem 1.2. We believe that the considerations of Section 4 have an independent interest beyond their application here.
The transformation law Theorem 4.15 can be used to pull back the problem from
![]() $\mathscr {U}$
to the well-understood domain
$\mathscr {U}$
to the well-understood domain
![]() $\mathbb {D}^n_{\mathsf {L}(B)}$
, which is the polydisc, except for a missing analytic hypersurface. The pulled-back problem can be solved using classical estimates on the polydisc. This is achieved in Sections 5 and 6, completing the proof of Theorem 1.2.
$\mathbb {D}^n_{\mathsf {L}(B)}$
, which is the polydisc, except for a missing analytic hypersurface. The pulled-back problem can be solved using classical estimates on the polydisc. This is achieved in Sections 5 and 6, completing the proof of Theorem 1.2.
The germ of the idea of relating the
![]() $L^p$
-regularity of the Bergman projection with the properties of a “uniformizing” map from a simpler domain may already be found in [Reference Chakrabarti and ZeytuncuCZ16, Reference Chen, Krantz and YuanCKY20]. The sharper version of this technique presented in this paper may be thought of as a step toward a unified understanding of the way in which boundary singularities affect the mapping properties of the Bergman projection.
$L^p$
-regularity of the Bergman projection with the properties of a “uniformizing” map from a simpler domain may already be found in [Reference Chakrabarti and ZeytuncuCZ16, Reference Chen, Krantz and YuanCKY20]. The sharper version of this technique presented in this paper may be thought of as a step toward a unified understanding of the way in which boundary singularities affect the mapping properties of the Bergman projection.
1.4 Examples in
 ${\mathbb {C}}^2$
${\mathbb {C}}^2$
It is not difficult to see that a monomial polyhedron in
![]() ${\mathbb {C}}^n$
is bounded by n Levi-flat “faces” (in the log-absolute representation (1.7), these faces are linear hyperplanes; see the proof of Proposition 3.5). The generalized Hartogs triangles of (1.6) are special in that one of the faces is a “coordinate face”, i.e., represented by a coordinate hyperplane in log-absolute coordinates. In (1.6), this is,
${\mathbb {C}}^n$
is bounded by n Levi-flat “faces” (in the log-absolute representation (1.7), these faces are linear hyperplanes; see the proof of Proposition 3.5). The generalized Hartogs triangles of (1.6) are special in that one of the faces is a “coordinate face”, i.e., represented by a coordinate hyperplane in log-absolute coordinates. In (1.6), this is,
![]() $\{\left \vert z_2\right \vert =1\}$
which corresponds to
$\{\left \vert z_2\right \vert =1\}$
which corresponds to
![]() $\{\xi _2=0\}$
in the log-absolute representation. In two dimensions, the generic monomial polyhedron has two noncoordinate faces, and can be thought of as an intersections of two generalized Hartogs triangles. The Reinhardt shadows in
$\{\xi _2=0\}$
in the log-absolute representation. In two dimensions, the generic monomial polyhedron has two noncoordinate faces, and can be thought of as an intersections of two generalized Hartogs triangles. The Reinhardt shadows in
![]() ${\mathbb {R}}^2$
(the image of
${\mathbb {R}}^2$
(the image of
![]() $z\mapsto (\left \vert z_1\right \vert , \left \vert z_2\right \vert )$
) of three monomial polyhedra in
$z\mapsto (\left \vert z_1\right \vert , \left \vert z_2\right \vert )$
) of three monomial polyhedra in
![]() ${\mathbb {C}}^2$
can be seen in Figure 1. The domains corresponding to
${\mathbb {C}}^2$
can be seen in Figure 1. The domains corresponding to
![]() $(a), (b),$
and
$(a), (b),$
and
![]() $(c)$
are respectively given by:
$(c)$
are respectively given by:

Figure 1: Reinhardt shadows of some monomial polyhedra.
1.5
 $L^p$
-theory of the Bergman projection
$L^p$
-theory of the Bergman projection
We collect here some general information about the Bergman projection, and set up notation for later use.
Let
![]() $\Omega $
be a domain (an open connected set) in
$\Omega $
be a domain (an open connected set) in
![]() ${\mathbb {C}}^n$
. The Bergman space
${\mathbb {C}}^n$
. The Bergman space
![]() $A^2(\Omega )$
is the Hilbert space of holomorphic functions on
$A^2(\Omega )$
is the Hilbert space of holomorphic functions on
![]() $\Omega $
which are square integrable with respect to the Lebesgue measure; see [Reference KrantzKra13] for a modern treatment. The space
$\Omega $
which are square integrable with respect to the Lebesgue measure; see [Reference KrantzKra13] for a modern treatment. The space
![]() $A^2(\Omega )$
is a closed subspace of
$A^2(\Omega )$
is a closed subspace of
![]() $L^2(\Omega )$
, the usual Hilbert space of measurable functions square integrable with respect to the Lebesgue measure. The Bergman projection is the orthogonal projection
$L^2(\Omega )$
, the usual Hilbert space of measurable functions square integrable with respect to the Lebesgue measure. The Bergman projection is the orthogonal projection
The construction of Bergman spaces has a contravariant functorial character. If
![]() $\phi :\Omega _1\to \Omega _2$
is a suitable holomorphic map of domains, we can associate a continuous linear mapping of Hilbert spaces
$\phi :\Omega _1\to \Omega _2$
is a suitable holomorphic map of domains, we can associate a continuous linear mapping of Hilbert spaces
![]() $\phi ^\sharp : L^2(\Omega _2)\to L^2(\Omega _1)$
defined for each
$\phi ^\sharp : L^2(\Omega _2)\to L^2(\Omega _1)$
defined for each
![]() $f\in L^2(\Omega _2)$
by
$f\in L^2(\Omega _2)$
by
where
![]() $\phi '(z):{\mathbb {C}}^n\to {\mathbb {C}}^n$
is the complex derivative of the map
$\phi '(z):{\mathbb {C}}^n\to {\mathbb {C}}^n$
is the complex derivative of the map
![]() $\phi $
at
$\phi $
at
![]() $z\in \Omega _1$
. It is clear that
$z\in \Omega _1$
. It is clear that
![]() $\phi ^\sharp $
restricts to a map
$\phi ^\sharp $
restricts to a map
![]() $A^2(\Omega _2) \to A^2(\Omega _1)$
. We will refer to
$A^2(\Omega _2) \to A^2(\Omega _1)$
. We will refer to
![]() $\phi ^\sharp $
as the pullback induced by
$\phi ^\sharp $
as the pullback induced by
![]() $\phi $
. It is not difficult to see that if
$\phi $
. It is not difficult to see that if
![]() $\phi $
is a biholomorphism, then the pullback
$\phi $
is a biholomorphism, then the pullback
![]() $\phi ^\sharp $
is an isometric isomorphism of Hilbert spaces
$\phi ^\sharp $
is an isometric isomorphism of Hilbert spaces
![]() $L^2(\Omega _2)\cong L^2(\Omega _1)$
, and restricts to an isometric isomorphism
$L^2(\Omega _2)\cong L^2(\Omega _1)$
, and restricts to an isometric isomorphism
![]() $A^2(\Omega _2) \cong A^2(\Omega _1)$
. This biholomorphic invariance of Bergman spaces can be understood intrinsically by interpreting the Bergman space as a space of top-degree holomorphic forms (see [Reference KobayashiKob59] or [Reference KrantzKra13, p. 178 ff.]), and the map
$A^2(\Omega _2) \cong A^2(\Omega _1)$
. This biholomorphic invariance of Bergman spaces can be understood intrinsically by interpreting the Bergman space as a space of top-degree holomorphic forms (see [Reference KobayashiKob59] or [Reference KrantzKra13, p. 178 ff.]), and the map
![]() $\phi ^\sharp $
as the pullback map of forms induced by the holomorphic map
$\phi ^\sharp $
as the pullback map of forms induced by the holomorphic map
![]() $\phi $
. This invariance can be extended to proper holomorphic mappings via Bell’s transformation formula, and lies at the heart of classical applications of Bergman theory to the boundary regularity of holomorphic maps; see [Reference BellBel81, Reference BellBel82, Reference Diederich and FornaessDF82, Reference Bell and CatlinBC82].
$\phi $
. This invariance can be extended to proper holomorphic mappings via Bell’s transformation formula, and lies at the heart of classical applications of Bergman theory to the boundary regularity of holomorphic maps; see [Reference BellBel81, Reference BellBel82, Reference Diederich and FornaessDF82, Reference Bell and CatlinBC82].
For
![]() $0<p<\infty $
, define
$0<p<\infty $
, define
![]() $L^p$
-Bergman spaces
$L^p$
-Bergman spaces
![]() $A^p(\Omega )$
of pth power integrable holomorphic functions on
$A^p(\Omega )$
of pth power integrable holomorphic functions on
![]() $\Omega $
. For
$\Omega $
. For
![]() $p\ge 1$
, these are Banach spaces when equipped with the
$p\ge 1$
, these are Banach spaces when equipped with the
![]() $L^p$
-norm. An extensive theory of these spaces on the unit disc has been developed, in analogy with the theory of Hardy spaces (cf. [Reference Duren and SchusterDS04, Reference Hedenmalm, Korenblum and ZhuHKZ00]). Unlike the
$L^p$
-norm. An extensive theory of these spaces on the unit disc has been developed, in analogy with the theory of Hardy spaces (cf. [Reference Duren and SchusterDS04, Reference Hedenmalm, Korenblum and ZhuHKZ00]). Unlike the
![]() $L^2$
-Bergman space, the general
$L^2$
-Bergman space, the general
![]() $L^p$
-Bergman space is not invariantly determined by the complex structure alone, but also depends on the Hermitian structure of the domain as a subset of
$L^p$
-Bergman space is not invariantly determined by the complex structure alone, but also depends on the Hermitian structure of the domain as a subset of
![]() ${\mathbb {C}}^n$
. An important question about these spaces is the boundedness of the Bergman projection in the
${\mathbb {C}}^n$
. An important question about these spaces is the boundedness of the Bergman projection in the
![]() $L^p$
-norm. After initial results were obtained for discs and balls ([Reference Zaharjuta and JudovicZJ64, Reference Forelli and RudinFR75]) the problem was studied on various classes of smoothly bounded pseudoconvex domains using estimates on the kernel (e.g., [Reference Phong and SteinPS77, Reference McNeal and SteinMS94]). On these domains the Bergman projection is bounded in
$L^p$
-norm. After initial results were obtained for discs and balls ([Reference Zaharjuta and JudovicZJ64, Reference Forelli and RudinFR75]) the problem was studied on various classes of smoothly bounded pseudoconvex domains using estimates on the kernel (e.g., [Reference Phong and SteinPS77, Reference McNeal and SteinMS94]). On these domains the Bergman projection is bounded in
![]() $L^p$
for
$L^p$
for
![]() $1<p<\infty $
. Many examples have been given which show that there are domains on which the Bergman projection fails to be bounded in
$1<p<\infty $
. Many examples have been given which show that there are domains on which the Bergman projection fails to be bounded in
![]() $L^p$
for certain p. See [Reference BarrettBar84, Reference Barrett and ŞahutoğluBŞ12, Reference Krantz and PelosoKP08, Reference HedenmalmHed02], in addition to the singular Reinhardt domains already mentioned in [Reference Chakrabarti and ZeytuncuCZ16, Reference Edholm and McNealEM16, Reference Edholm and McNealEM17, Reference ChenChe17, Reference Chen, Krantz and YuanCKY20, Reference HuoHuo18, Reference Huo and WickHW19]. This paper proves sharp
$L^p$
for certain p. See [Reference BarrettBar84, Reference Barrett and ŞahutoğluBŞ12, Reference Krantz and PelosoKP08, Reference HedenmalmHed02], in addition to the singular Reinhardt domains already mentioned in [Reference Chakrabarti and ZeytuncuCZ16, Reference Edholm and McNealEM16, Reference Edholm and McNealEM17, Reference ChenChe17, Reference Chen, Krantz and YuanCKY20, Reference HuoHuo18, Reference Huo and WickHW19]. This paper proves sharp
![]() $L^p$
-regularity results on a large class of singular Reinhardt domains.
$L^p$
-regularity results on a large class of singular Reinhardt domains.
1.6 Two examples of Theorem 1.2
We illustrate the application of Theorem 1.2 to two families of domains generalizing the Hartogs triangle to higher dimensions, recapturing the results of [Reference ZhangZha20, Reference ZhangZha19].
Let
![]() $k = (k_1, \ldots , k_n)$
be an n-tuple of positive integers. The domain
$k = (k_1, \ldots , k_n)$
be an n-tuple of positive integers. The domain
 $$ \begin{align} \mathscr{H}_{k}=\left\{z\in \mathbb{D}^n: \left\vert z_1\right\vert{{\hspace{-0.0001pt}}}^{k_1} < \prod_{j=2}^n \left\vert z_j\right\vert{{\hspace{-0.0001pt}}}^{k_j}\right\}, \end{align} $$
$$ \begin{align} \mathscr{H}_{k}=\left\{z\in \mathbb{D}^n: \left\vert z_1\right\vert{{\hspace{-0.0001pt}}}^{k_1} < \prod_{j=2}^n \left\vert z_j\right\vert{{\hspace{-0.0001pt}}}^{k_j}\right\}, \end{align} $$
was introduced in [Reference Chakrabarti, Konkel, Mainkar and MillerCKMM20] where it was called an elementary Reinhardt domain of signature 1, and its Bergman kernel was computed explicitly. We see that
![]() $\mathscr {H}_{k}$
is a monomial polyhedron as in (1.1), since
$\mathscr {H}_{k}$
is a monomial polyhedron as in (1.1), since
The matrix B whose rows are multi-indices occurring in the inequalities in (1.10) is then given by

where
![]() ${I}_{n-1}$
is the identity matrix of size
${I}_{n-1}$
is the identity matrix of size
![]() $n-1$
. The projective height of the first column of
$n-1$
. The projective height of the first column of
![]() $B^{-1}$
is 1, and for
$B^{-1}$
is 1, and for
![]() $2\leq j\leq n$
that of the jth column is
$2\leq j\leq n$
that of the jth column is
 $\dfrac {k_1+k_j}{\gcd (k_1,k_j)}$
, using (1.4). Therefore, we get the complexity of
$\dfrac {k_1+k_j}{\gcd (k_1,k_j)}$
, using (1.4). Therefore, we get the complexity of
![]() $\mathscr {H}_{k}$
as (see (1.5)):
$\mathscr {H}_{k}$
as (see (1.5)):
 $$ \begin{align*}\displaystyle{\kappa({\mathscr{H}_{k}}) = \max \left\{ 1, \frac{k_1+k_2}{\mathrm{gcd}(k_1, k_2)}, \ldots, \frac{k_1+k_n}{\mathrm{gcd}(k_1, k_n)} \right\}}= \max_{2\leq j \leq n} \left\{\frac{k_1+k_j}{\mathrm{gcd}(k_1, k_j)}\right\}. \end{align*} $$
$$ \begin{align*}\displaystyle{\kappa({\mathscr{H}_{k}}) = \max \left\{ 1, \frac{k_1+k_2}{\mathrm{gcd}(k_1, k_2)}, \ldots, \frac{k_1+k_n}{\mathrm{gcd}(k_1, k_n)} \right\}}= \max_{2\leq j \leq n} \left\{\frac{k_1+k_j}{\mathrm{gcd}(k_1, k_j)}\right\}. \end{align*} $$
Noting that the function
![]() $x\mapsto \frac {x}{x-1}$
is decreasing for
$x\mapsto \frac {x}{x-1}$
is decreasing for
![]() $x>1$
, and the function
$x>1$
, and the function
![]() $x\mapsto \frac {x}{x+1}$
is increasing, by Theorem 1.2, the Bergman projection on
$x\mapsto \frac {x}{x+1}$
is increasing, by Theorem 1.2, the Bergman projection on
![]() $\mathscr {H}_{k}$
is bounded on
$\mathscr {H}_{k}$
is bounded on
![]() $L^p(\mathscr {H}_{k})$
if and only if
$L^p(\mathscr {H}_{k})$
if and only if
 $$ \begin{align*} \max_{2\leq j \leq n}\, \frac{2(k_1+k_j)}{k_1+k_j+\mathrm{gcd}(k_1, k_j)} < p < \min_{2\leq j \leq n}\, \frac{2(k_1 +k_j)}{k_1+k_j- \mathrm{gcd}(k_1, k_j)}, \end{align*} $$
$$ \begin{align*} \max_{2\leq j \leq n}\, \frac{2(k_1+k_j)}{k_1+k_j+\mathrm{gcd}(k_1, k_j)} < p < \min_{2\leq j \leq n}\, \frac{2(k_1 +k_j)}{k_1+k_j- \mathrm{gcd}(k_1, k_j)}, \end{align*} $$
in consonance with the result of [Reference ZhangZha19].
The second family of domains, which we denote by
![]() $\mathscr {S}_{k}$
, gives a different type of generalization of the Hartogs triangle. For an n-tuple of positive integers
$\mathscr {S}_{k}$
, gives a different type of generalization of the Hartogs triangle. For an n-tuple of positive integers
![]() $(k_1,\dots , k_n)$
we define:
$(k_1,\dots , k_n)$
we define:
In [Reference ParkPar18], the Bergman kernel of
![]() $\mathscr {S}_{k}$
was explicitly computed for
$\mathscr {S}_{k}$
was explicitly computed for
![]() $n=3$
, and in [Reference ChenChe17] the special case
$n=3$
, and in [Reference ChenChe17] the special case
![]() $k=(1,1,\dots , 1)$
was considered and it was shown that the Bergman projection is
$k=(1,1,\dots , 1)$
was considered and it was shown that the Bergman projection is
![]() $L^p$
-bounded on
$L^p$
-bounded on
![]() $\mathscr {S}_{(1,1,\dots ,1)}$
if and only if
$\mathscr {S}_{(1,1,\dots ,1)}$
if and only if
![]() $\frac {2n}{n+1}<p< \frac {2n}{n-1}$
. In [Reference ZhangZha20] the Bergman kernel of
$\frac {2n}{n+1}<p< \frac {2n}{n-1}$
. In [Reference ZhangZha20] the Bergman kernel of
![]() $\mathscr {S}_{k}$
was computed in general, and the range of
$\mathscr {S}_{k}$
was computed in general, and the range of
![]() $L^p$
-boundedness of the Bergman projection was determined. Since
$L^p$
-boundedness of the Bergman projection was determined. Since
![]() $\mathscr {S}_{k}$
is a monomial polyhedron given by
$\mathscr {S}_{k}$
is a monomial polyhedron given by
the matrix B in the definition of complexity and its inverse
![]() $B^{-1}$
are given as below:
$B^{-1}$
are given as below:
 $$ \begin{align*}B = \begin{pmatrix} k_1 & -k_2 & 0 & 0 & \cdots& 0 \\ 0& \phantom{-} k_2 & -k_3 & 0& \cdots & 0\\ \vdots & \phantom{k_2} & \ddots & \ddots & \phantom{0} &\vdots \\ \vdots & \phantom{k_2} & \phantom{k_2} & \ddots & \ddots& \vdots \\ 0 & 0& \cdots & 0 & k_{n-1} & - k_n \\ 0 & 0 & 0 & \cdots& 0 & \phantom{-} k_n \end{pmatrix}, \quad \ B^{-1} = \frac{1}{K} \begin{pmatrix} \ell_1 & \ell_1 & \ell_1 & \cdots& \cdots & \ell_1 \\ 0& \ell_2 & \ell_2 & \cdots & \cdots & \ell_2\\ 0 & 0 & \ell_3 & \cdots & \cdots& \ell_3 \\ \vdots & \vdots & \phantom{k_2} & \ddots & \phantom{k_2} & \vdots \\ 0 & 0 & \cdots& \cdots& 0 & \ell_n \end{pmatrix},\end{align*} $$
$$ \begin{align*}B = \begin{pmatrix} k_1 & -k_2 & 0 & 0 & \cdots& 0 \\ 0& \phantom{-} k_2 & -k_3 & 0& \cdots & 0\\ \vdots & \phantom{k_2} & \ddots & \ddots & \phantom{0} &\vdots \\ \vdots & \phantom{k_2} & \phantom{k_2} & \ddots & \ddots& \vdots \\ 0 & 0& \cdots & 0 & k_{n-1} & - k_n \\ 0 & 0 & 0 & \cdots& 0 & \phantom{-} k_n \end{pmatrix}, \quad \ B^{-1} = \frac{1}{K} \begin{pmatrix} \ell_1 & \ell_1 & \ell_1 & \cdots& \cdots & \ell_1 \\ 0& \ell_2 & \ell_2 & \cdots & \cdots & \ell_2\\ 0 & 0 & \ell_3 & \cdots & \cdots& \ell_3 \\ \vdots & \vdots & \phantom{k_2} & \ddots & \phantom{k_2} & \vdots \\ 0 & 0 & \cdots& \cdots& 0 & \ell_n \end{pmatrix},\end{align*} $$
where
![]() $K = \prod _{j=1}^n k_j$
and
$K = \prod _{j=1}^n k_j$
and
![]() $\ell _j =\frac {K}{k_j} $
for
$\ell _j =\frac {K}{k_j} $
for
![]() $1 \leq j \leq n.$
Note that the height of the mth column of
$1 \leq j \leq n.$
Note that the height of the mth column of
![]() $B^{-1}$
is
$B^{-1}$
is
 $$ \begin{align*} h_m= \frac{\sum_{j=1}^m \ell_j}{\mathrm{gcd}(\ell_1, \ldots, \ell_m)}. \end{align*} $$
$$ \begin{align*} h_m= \frac{\sum_{j=1}^m \ell_j}{\mathrm{gcd}(\ell_1, \ldots, \ell_m)}. \end{align*} $$
As m increases, the numerator
![]() $\sum _{j=1}^m \ell _j$
of
$\sum _{j=1}^m \ell _j$
of
![]() $h_m$
increases and the denominator
$h_m$
increases and the denominator
![]() $\gcd (\ell _1, \ldots , \ell _m)$
decreases, so
$\gcd (\ell _1, \ldots , \ell _m)$
decreases, so
![]() $h_m$
increases with m. Therefore, the complexity of
$h_m$
increases with m. Therefore, the complexity of
![]() $\mathscr {S}_{k}$
is
$\mathscr {S}_{k}$
is
 $$ \begin{align*}\kappa(\mathscr{S}_{k}) = \max_{1\leq m\leq n} h_m =h_n= \frac{\sum_{j=1}^n \ell_j}{\mathrm{gcd}(\ell_1, \ldots, \ell_n)} .\end{align*} $$
$$ \begin{align*}\kappa(\mathscr{S}_{k}) = \max_{1\leq m\leq n} h_m =h_n= \frac{\sum_{j=1}^n \ell_j}{\mathrm{gcd}(\ell_1, \ldots, \ell_n)} .\end{align*} $$
Therefore, Theorem 1.2 shows that the Bergman projection on
![]() $\mathscr {S}_{k}$
is bounded on
$\mathscr {S}_{k}$
is bounded on
![]() $L^p(\mathscr {S}_{k})$
if and only if
$L^p(\mathscr {S}_{k})$
if and only if
 $$ \begin{align*} \frac{2 \sum_{j=1}^n \ell_j}{ \sum_{j=1}^n \ell_j + \gcd (\ell_1, \ldots, \ell_n)} < p < \frac{2 \sum_{j=1}^n \ell_j}{ \sum_{j=1}^n \ell_j - \gcd (\ell_1, \ldots, \ell_n)},\end{align*} $$
$$ \begin{align*} \frac{2 \sum_{j=1}^n \ell_j}{ \sum_{j=1}^n \ell_j + \gcd (\ell_1, \ldots, \ell_n)} < p < \frac{2 \sum_{j=1}^n \ell_j}{ \sum_{j=1}^n \ell_j - \gcd (\ell_1, \ldots, \ell_n)},\end{align*} $$
recapturing the main result of [Reference ZhangZha20].
2 Notation
2.1 Elementwise operations on matrices
Let A be an
![]() $m\times n$
matrix. We denote the entry of A at the jth row and kth column by
$m\times n$
matrix. We denote the entry of A at the jth row and kth column by
![]() $a^j_k$
, where
$a^j_k$
, where
![]() $1\leq j \leq m, 1\leq k \leq n$
. We use two kinds of products of matrices: one is the standard matrix multiplication, denoted by simple juxtaposition
$1\leq j \leq m, 1\leq k \leq n$
. We use two kinds of products of matrices: one is the standard matrix multiplication, denoted by simple juxtaposition
![]() $AB$
, or sometimes a dot for clarity:
$AB$
, or sometimes a dot for clarity:
![]() $A\cdot B$
.
$A\cdot B$
.
We also need a second type of multiplication, the elementwise, or Hadamard–Schur product, in which the product of two
![]() $m\times n$
matrices
$m\times n$
matrices
![]() $A=(a^j_k)$
and
$A=(a^j_k)$
and
![]() $B=(b^j_k)$
is the
$B=(b^j_k)$
is the
![]() $m\times n$
matrix C, for which we have
$m\times n$
matrix C, for which we have
![]() $c^j_k=a^j_kb^j_k$
, i.e., the element at a certain position of the product is the product of the corresponding entries of the factors. We denote this by
$c^j_k=a^j_kb^j_k$
, i.e., the element at a certain position of the product is the product of the corresponding entries of the factors. We denote this by
It will be important to distinguish between column and row vectors. We denote the R-module of
![]() $n\times 1$
column vectors by
$n\times 1$
column vectors by
![]() $R^n$
, where R can be one of
$R^n$
, where R can be one of
![]() $\mathbb {Z},\mathbb {Q},{\mathbb {R}}, {\mathbb {C}}$
. The R-module of
$\mathbb {Z},\mathbb {Q},{\mathbb {R}}, {\mathbb {C}}$
. The R-module of
![]() $1\times n$
row vectors is denoted by
$1\times n$
row vectors is denoted by
![]() $(R^n)^\dagger $
. We write the entries of the row vector a (resp. the column vector b) as
$(R^n)^\dagger $
. We write the entries of the row vector a (resp. the column vector b) as
![]() $(a_1,\dots , a_n)$
(resp. as
$(a_1,\dots , a_n)$
(resp. as
![]() $(b_1,\dots ,b_n)^T$
). We let
$(b_1,\dots ,b_n)^T$
). We let
![]() denote a
denote a
![]() $1\times n$
row vector, all whose entries are 1. The positive integer n will be clear from the context:
$1\times n$
row vector, all whose entries are 1. The positive integer n will be clear from the context:
Similarly,
![]() is the
is the
![]() $n\times 1$
column vector, all whose entries are 1. Notice that these are identity elements for the elementwise multiplication of row and column vectors.
$n\times 1$
column vector, all whose entries are 1. Notice that these are identity elements for the elementwise multiplication of row and column vectors.
For real matrices of the same size
![]() $A,B$
, the notations
$A,B$
, the notations
stand for the natural elementwise order, e.g.,
![]() $A \succ B$
denotes that
$A \succ B$
denotes that
![]() $a^j_k> b^j_k.$
Note that this elementwise ordering of matrices is distinct from other notions of matrix ordering, such as positive (semi-)definiteness.
$a^j_k> b^j_k.$
Note that this elementwise ordering of matrices is distinct from other notions of matrix ordering, such as positive (semi-)definiteness.
2.2 Vector and matrix powers
If
![]() $\alpha $
is a row vector of size n, and z is column vector of the same size, we will denote
$\alpha $
is a row vector of size n, and z is column vector of the same size, we will denote
 $$ \begin{align*}z^\alpha =z_1^{\alpha_1}\dots z_n^{\alpha_n}=\prod_{j=1}^n z_j^{\alpha_j},\end{align*} $$
$$ \begin{align*}z^\alpha =z_1^{\alpha_1}\dots z_n^{\alpha_n}=\prod_{j=1}^n z_j^{\alpha_j},\end{align*} $$
whenever the powers
![]() $z_j^{\alpha _j}$
make sense, and where we use the convention
$z_j^{\alpha _j}$
make sense, and where we use the convention
![]() $0^0=1.$
For example, we could have
$0^0=1.$
For example, we could have
![]() $\alpha \in (\mathbb {Z}^n)^\dagger $
and
$\alpha \in (\mathbb {Z}^n)^\dagger $
and
![]() $z\in {\mathbb {C}}^n$
such that for each j such that
$z\in {\mathbb {C}}^n$
such that for each j such that
![]() $\alpha _j<0$
, we have
$\alpha _j<0$
, we have
![]() $z_j\not =0$
. In this context
$z_j\not =0$
. In this context
![]() $\alpha $
is typically called a multi-index and
$\alpha $
is typically called a multi-index and
![]() $z^\alpha $
a (Laurent) monomial. We also set
$z^\alpha $
a (Laurent) monomial. We also set
Informally, we think of a monomial function as a “vector power” of a vector variable.
We will also use “matrix powers.” Recall from the previous subsection that for an
![]() $n\times n$
matrix A, we denote the element at the jth row and kth column of A by
$n\times n$
matrix A, we denote the element at the jth row and kth column of A by
![]() $a_k^j$
. Let
$a_k^j$
. Let
![]() $a^j$
denote the jth row of A, so that each row can be thought of as a multi-index. We then define for a column vector z of size n,
$a^j$
denote the jth row of A, so that each row can be thought of as a multi-index. We then define for a column vector z of size n,
 $$ \begin{align} z^A=\begin{pmatrix} z^{a^1}\\\vdots\\ z^{a^n} \end{pmatrix}= \begin{pmatrix} z_1^{a^1_1}z_2^{a^1_2}\cdots z_n^{a^1_n}\\\vdots\\ z_1^{a^n_1}z_2^{a^n_2}\cdots z_n^{a^n_n} \end{pmatrix} \end{align} $$
$$ \begin{align} z^A=\begin{pmatrix} z^{a^1}\\\vdots\\ z^{a^n} \end{pmatrix}= \begin{pmatrix} z_1^{a^1_1}z_2^{a^1_2}\cdots z_n^{a^1_n}\\\vdots\\ z_1^{a^n_1}z_2^{a^n_2}\cdots z_n^{a^n_n} \end{pmatrix} \end{align} $$
provided each of the monomials is defined. We will also set
which is called a monomial map.
For row vectors
![]() $\alpha , \beta $
, square matrices
$\alpha , \beta $
, square matrices
![]() $A,B$
and column vectors
$A,B$
and column vectors
![]() $z,w$
such that the vector and matrix powers are well-defined, the following simple algebraic properties of monomials and monomial mappings can be easily verified. Not unexpectedly, these mirror familiar rules of elementary algebra for exponents.
$z,w$
such that the vector and matrix powers are well-defined, the following simple algebraic properties of monomials and monomial mappings can be easily verified. Not unexpectedly, these mirror familiar rules of elementary algebra for exponents.
2.3 Two other maps
-
(1) The (elementwise) exponential map
(2.8)can be thought of as the exponential map associated to the abelian Lie group $$ \begin{align} \exp: {\mathbb{C}}^n \to ({\mathbb{C}}^*)^n, \quad \exp(z)=(e^{z_1},\dots, e^{z_n})^T \end{align} $$
$$ \begin{align} \exp: {\mathbb{C}}^n \to ({\mathbb{C}}^*)^n, \quad \exp(z)=(e^{z_1},\dots, e^{z_n})^T \end{align} $$
 $({\mathbb {C}}^*)^n$
. Notice that for
$({\mathbb {C}}^*)^n$
. Notice that for
 $\alpha \in (\mathbb {Z}^n)^\dagger $
and
$\alpha \in (\mathbb {Z}^n)^\dagger $
and
 $A\in M_n(\mathbb {Z})$
we have: (2.9)
$A\in M_n(\mathbb {Z})$
we have: (2.9) $$ \begin{align} \exp(z)^\alpha=e^{\alpha z}\text{ and } \exp(z)^A=\exp(Az). \end{align} $$
$$ \begin{align} \exp(z)^\alpha=e^{\alpha z}\text{ and } \exp(z)^A=\exp(Az). \end{align} $$
-
(2) The multi-radius map
(2.10)restricts to a surjective group homomorphism $$ \begin{align} \rho : {\mathbb{C}}^n\to {\mathbb{R}}^n \quad z\mapsto(\left\vert z_1\right\vert, \dots , \left\vert z_n\right\vert )^T \end{align} $$
$$ \begin{align} \rho : {\mathbb{C}}^n\to {\mathbb{R}}^n \quad z\mapsto(\left\vert z_1\right\vert, \dots , \left\vert z_n\right\vert )^T \end{align} $$
 $({\mathbb {C}}^*)^n \to ({\mathbb {R}}^+)^n$
, and satisfies, for
$({\mathbb {C}}^*)^n \to ({\mathbb {R}}^+)^n$
, and satisfies, for
 $\alpha \in (\mathbb {Z}^n)^\dagger $
and
$\alpha \in (\mathbb {Z}^n)^\dagger $
and
 $A\in M_n(\mathbb {Z})$
(2.11)
$A\in M_n(\mathbb {Z})$
(2.11) $$ \begin{align} \rho(z)^\alpha=\left\vert z^\alpha\right\vert \text{ and } \rho(z)^A=\rho(z^A). \end{align} $$
$$ \begin{align} \rho(z)^\alpha=\left\vert z^\alpha\right\vert \text{ and } \rho(z)^A=\rho(z^A). \end{align} $$
3 Geometry of monomial polyhedra
The main goal of this section is Theorem 3.12, which gives a “uniformization” of a monomial polyhedron by a proper holomorphic monomial map. This construction is crucial for everything that follows. We also show that the Bergman kernel of a monomial polyhedron is rational, although this fact is not used in the sequel.
3.1 The matrix B
The definition of the domain
![]() $\mathscr {U}$
as given in (1.1) can be succinctly rewritten, using the notation introduced in the previous Section 2 as
$\mathscr {U}$
as given in (1.1) can be succinctly rewritten, using the notation introduced in the previous Section 2 as
where
![]() $B\in M_n(\mathbb {Q})$
is the matrix whose jth row is
$B\in M_n(\mathbb {Q})$
is the matrix whose jth row is
![]() $b^j$
. In the next proposition, we show that the matrix B in the definition of
$b^j$
. In the next proposition, we show that the matrix B in the definition of
![]() $\mathscr {U}$
can always be taken to be an integer matrix which is monotone in the sense of Collatz (see [Reference CollatzCol66, p. 376 ff.]):
$\mathscr {U}$
can always be taken to be an integer matrix which is monotone in the sense of Collatz (see [Reference CollatzCol66, p. 376 ff.]):
Proposition 3.2 In the representation (
3.1
) of the bounded monomial polyhedron
![]() $\mathscr {U}$
of Theorem 1.2, we may assume without loss of generality (after switching two rows, if necessary) that
$\mathscr {U}$
of Theorem 1.2, we may assume without loss of generality (after switching two rows, if necessary) that
Proof Let
![]() $B\in M_n(\mathbb {Q})$
be the matrix whose rows are
$B\in M_n(\mathbb {Q})$
be the matrix whose rows are
![]() $b^1,\dots ,b^n$
, where for
$b^1,\dots ,b^n$
, where for
![]() $1\leq j \leq n$
, the vector
$1\leq j \leq n$
, the vector
![]() $b^j\in (\mathbb {Q}^n)^\dagger $
,
$b^j\in (\mathbb {Q}^n)^\dagger $
,
![]() $b^j=(b^j_1,\dots , b^j_n)$
is as in (1.1), which can be written in the form (3.1) using the notation introduced above. Notice that if any one of the vectors
$b^j=(b^j_1,\dots , b^j_n)$
is as in (1.1), which can be written in the form (3.1) using the notation introduced above. Notice that if any one of the vectors
![]() $b^j$
is 0, then
$b^j$
is 0, then
![]() $\mathscr {U}$
is empty, since the inequality
$\mathscr {U}$
is empty, since the inequality
![]() $\rho (z)^{b^j}<1$
becomes
$\rho (z)^{b^j}<1$
becomes
![]() $1<1$
.
$1<1$
.
If
![]() $\delta _j>0$
is a common denominator for the rational numbers
$\delta _j>0$
is a common denominator for the rational numbers
![]() $b^j_1,\dots , b^j_n$
, then notice that for a
$b^j_1,\dots , b^j_n$
, then notice that for a
![]() $z\in {\mathbb {C}}^n$
, the quantity
$z\in {\mathbb {C}}^n$
, the quantity
![]() $\rho (z)^{b^j}$
is defined and less than 1 if and only if
$\rho (z)^{b^j}$
is defined and less than 1 if and only if
![]() $\rho (z)^{\delta _j b^j}$
is defined and less than 1. Therefore, we can assume without loss of generality that the matrix B has integer entries. Note also that interchanging the rows of B simply corresponds renumbering the equations in (1.1), so we can further assume without loss of generality that
$\rho (z)^{\delta _j b^j}$
is defined and less than 1. Therefore, we can assume without loss of generality that the matrix B has integer entries. Note also that interchanging the rows of B simply corresponds renumbering the equations in (1.1), so we can further assume without loss of generality that
![]() $\det B\geq 0$
.
$\det B\geq 0$
.
Now, assuming that
![]() $B\in M_n(\mathbb {Z})$
and
$B\in M_n(\mathbb {Z})$
and
![]() $\det B\geq 0$
, suppose for a contradiction that
$\det B\geq 0$
, suppose for a contradiction that
![]() $\det B=0$
. We will show that
$\det B=0$
. We will show that
![]() $\mathscr {U}$
is unbounded, which will contradict the hypothesis of Theorem 1.2. Since
$\mathscr {U}$
is unbounded, which will contradict the hypothesis of Theorem 1.2. Since
![]() $\det B=0$
, there is a nonzero vector
$\det B=0$
, there is a nonzero vector
![]() $x\in {\mathbb {R}}^n$
such that
$x\in {\mathbb {R}}^n$
such that
![]() $Bx=0$
. Let
$Bx=0$
. Let
![]() $r\in \mathscr {U}$
be such that
$r\in \mathscr {U}$
be such that
![]() $r \succ 0$
(such an r exists since
$r \succ 0$
(such an r exists since
![]() $\mathscr {U}$
is nonempty, open, and Reinhardt). Consider the curve
$\mathscr {U}$
is nonempty, open, and Reinhardt). Consider the curve
![]() $f : {\mathbb {R}} \to {\mathbb {C}}^n$
parametrized by
$f : {\mathbb {R}} \to {\mathbb {C}}^n$
parametrized by
where
![]() $\exp $
is as in (2.8). Observe that
$\exp $
is as in (2.8). Observe that
since
![]() $Bx=0$
. Therefore,
$Bx=0$
. Therefore,
But since
![]() $r \in \mathscr {U}$
, it follows that
$r \in \mathscr {U}$
, it follows that
![]() , so in fact f is a curve in
, so in fact f is a curve in
![]() $\mathscr {U}$
. As
$\mathscr {U}$
. As
![]() $x \in {\mathbb {R}}^n $
is nonzero, some component
$x \in {\mathbb {R}}^n $
is nonzero, some component
![]() $x_k$
of x is nonzero, so that the kth component of the curve f, given by
$x_k$
of x is nonzero, so that the kth component of the curve f, given by
![]() $f_k(t)= r_k e^{tx_k}$
is unbounded as
$f_k(t)= r_k e^{tx_k}$
is unbounded as
![]() $t\to \pm \infty $
. Thus,
$t\to \pm \infty $
. Thus,
![]() $\mathscr {U}$
contains the unbounded image of the curve f, showing that
$\mathscr {U}$
contains the unbounded image of the curve f, showing that
![]() $\mathscr {U}$
is unbounded if
$\mathscr {U}$
is unbounded if
![]() $\det B=0$
. Since by assumption
$\det B=0$
. Since by assumption
![]() $\mathscr {U}$
is bounded, we have
$\mathscr {U}$
is bounded, we have
![]() $\det B\neq 0$
. So
$\det B\neq 0$
. So
![]() $\det B>0$
.
$\det B>0$
.
To show that
![]() $B^{-1}\succeq 0$
, we let A be the adjugate of B, i.e.,
$B^{-1}\succeq 0$
, we let A be the adjugate of B, i.e.,
![]() $A = \operatorname {\mathrm {adj}} B$
, and we show that
$A = \operatorname {\mathrm {adj}} B$
, and we show that
where
![]() $\Phi _A$
is the monomial map as in (2.6), and
$\Phi _A$
is the monomial map as in (2.6), and
![]() $(\mathbb {D}^*)^n$
is the product of n punctured unit disks. Since
$(\mathbb {D}^*)^n$
is the product of n punctured unit disks. Since
![]() $\mathscr {U}$
is bounded this implies that
$\mathscr {U}$
is bounded this implies that
![]() $\Phi _A((\mathbb {D}^*)^n)$
is bounded. Let
$\Phi _A((\mathbb {D}^*)^n)$
is bounded. Let
![]() $w \in \Phi _A((\mathbb {D}^*)^n)$
and let
$w \in \Phi _A((\mathbb {D}^*)^n)$
and let
![]() $z \in (\mathbb {D}^*)^n$
be such that
$z \in (\mathbb {D}^*)^n$
be such that
![]() $z^A=w$
. Notice that
$z^A=w$
. Notice that
![]() $z \in (\mathbb {D}^*)^n$
is equivalent to
$z \in (\mathbb {D}^*)^n$
is equivalent to
![]() , and we also have
, and we also have
![]() $z^A=w \in ({\mathbb {C}}^*)^n$
. By applying (2.11) and Cramer’s rule, we find
$z^A=w \in ({\mathbb {C}}^*)^n$
. By applying (2.11) and Cramer’s rule, we find
As
![]() $\det B> 0$
we find that
$\det B> 0$
we find that
![]() , i.e.,
, i.e.,
![]() $w \in \mathscr {U}$
, yielding the desired inclusion
$w \in \mathscr {U}$
, yielding the desired inclusion
![]() $\Phi _A((\mathbb {D}^*)^n) \subset \mathscr {U}$
.
$\Phi _A((\mathbb {D}^*)^n) \subset \mathscr {U}$
.
If
![]() $A \not \succeq 0$
then there exist some
$A \not \succeq 0$
then there exist some
![]() $1 \leq j,k \leq n$
such that
$1 \leq j,k \leq n$
such that
![]() $a^j_k < 0$
. Let
$a^j_k < 0$
. Let
![]() $z\in (\mathbb {D}^*)^n$
be such that all its components, except the kth, are
$z\in (\mathbb {D}^*)^n$
be such that all its components, except the kth, are
![]() $1/2$
. Then the jth component of
$1/2$
. Then the jth component of
![]() $\Phi _A(z)$
is given by
$\Phi _A(z)$
is given by
 $$ \begin{align*} z^{a^j} = {z_k^{a^j_k}}\cdot \frac{1}{2^m},\quad \text{where }\quad m= \sum_{\substack{1 \leq \ell \leq n \\ \ell \neq k}} a^j_\ell. \end{align*} $$
$$ \begin{align*} z^{a^j} = {z_k^{a^j_k}}\cdot \frac{1}{2^m},\quad \text{where }\quad m= \sum_{\substack{1 \leq \ell \leq n \\ \ell \neq k}} a^j_\ell. \end{align*} $$
As
![]() $a^j_k < 0$
we see that as
$a^j_k < 0$
we see that as
![]() $z_k\to 0$
, the monomial
$z_k\to 0$
, the monomial
![]() $z^{a^j}$
is unbounded, showing that
$z^{a^j}$
is unbounded, showing that
![]() $\Phi _A((\mathbb {D}^*)^n)$
is unbounded. Therefore, the boundedness of
$\Phi _A((\mathbb {D}^*)^n)$
is unbounded. Therefore, the boundedness of
![]() $\mathscr {U}$
guarantees that
$\mathscr {U}$
guarantees that
![]() $A = \operatorname {\mathrm {adj}} B \succeq 0$
.
$A = \operatorname {\mathrm {adj}} B \succeq 0$
.
To complete the proof note that
![]() $A \succeq 0$
implies that
$A \succeq 0$
implies that
![]() $B^{-1}=(\det B)^{-1} \operatorname {\mathrm {adj}} B\succeq 0$
. ▪
$B^{-1}=(\det B)^{-1} \operatorname {\mathrm {adj}} B\succeq 0$
. ▪
Due to Proposition 3.2, we can easily establish a more concrete bound on monomial polyhedra:
Corollary 3.4 A bounded monomial polyhedron is contained in the unit polydisc
![]() $\mathbb {D}^n$
and its boundary contains the unit torus
$\mathbb {D}^n$
and its boundary contains the unit torus
![]() $\mathbb {T}^n=\{\left \vert z_j\right \vert =1, 1\leq j\leq n\}$
.
$\mathbb {T}^n=\{\left \vert z_j\right \vert =1, 1\leq j\leq n\}$
.
Proof For a bounded monomial polyhedron
![]() $\mathscr {U}$
, let
$\mathscr {U}$
, let
![]() $z\in \mathscr {U}$
so that
$z\in \mathscr {U}$
so that
![]() $\rho (z)^B\prec 1$
, where B is as in Proposition 3.2. Since
$\rho (z)^B\prec 1$
, where B is as in Proposition 3.2. Since
![]() $B^{-1}\succeq 0$
, we have for any
$B^{-1}\succeq 0$
, we have for any
![]() $r\in {\mathbb {R}}^n$
with,
$r\in {\mathbb {R}}^n$
with,
![]() $0\preceq r \prec 1$
that
$0\preceq r \prec 1$
that
![]() $r^{B^{-1}}\prec 1$
. Therefore, we have
$r^{B^{-1}}\prec 1$
. Therefore, we have
![]() $(\rho (z)^{B})^{B^{-1}}=\rho (z)\prec 1$
, i.e.,
$(\rho (z)^{B})^{B^{-1}}=\rho (z)\prec 1$
, i.e.,
![]() $z\in \mathbb {D}^n$
. The second assertion follows on noting that in the log absolute representation (1.7) of
$z\in \mathbb {D}^n$
. The second assertion follows on noting that in the log absolute representation (1.7) of
![]() $\mathscr {U}$
, the origin (which corresponds to the unit torus of
$\mathscr {U}$
, the origin (which corresponds to the unit torus of
![]() ${\mathbb {C}}^n$
) is a boundary point. ▪
${\mathbb {C}}^n$
) is a boundary point. ▪
In the Definition (3.1), it is clear that the matrix B is not unique: permuting the order of inequalities, does not change to domain
![]() $\mathscr {U}$
, and multiplying for each j the row
$\mathscr {U}$
, and multiplying for each j the row
![]() $b^j$
by the same rational
$b^j$
by the same rational
![]() $\delta _j>0$
also gives exactly the same
$\delta _j>0$
also gives exactly the same
![]() $\mathscr {U}$
. Therefore, for any permutation matrix P and any positive diagonal matrix D with rational entries, the domains corresponding to B and
$\mathscr {U}$
. Therefore, for any permutation matrix P and any positive diagonal matrix D with rational entries, the domains corresponding to B and
![]() $DPB$
are the same. The following proposition shows that the complexity
$DPB$
are the same. The following proposition shows that the complexity
![]() $\kappa (\mathscr {U})$
is independent of the matrix B and depends only on
$\kappa (\mathscr {U})$
is independent of the matrix B and depends only on
![]() $\mathscr {U}$
.
$\mathscr {U}$
.
Proposition 3.5 The complexity
![]() $\kappa (\mathscr {U})$
is independent of the choice of the representing matrix B in (
3.1
).
$\kappa (\mathscr {U})$
is independent of the choice of the representing matrix B in (
3.1
).
Proof Notice that switching two rows of B does not change the complexity of
![]() $\mathscr {U}$
, we can assume that the conditions (3.3) hold for the representing matrix. In the log-absolute coordinates
$\mathscr {U}$
, we can assume that the conditions (3.3) hold for the representing matrix. In the log-absolute coordinates
![]() $\xi _k=\log \left \vert z_k\right \vert $
the domain
$\xi _k=\log \left \vert z_k\right \vert $
the domain
![]() $\mathscr {U}$
is represented by the equations (1.7), which define the open polyhedral cone
$\mathscr {U}$
is represented by the equations (1.7), which define the open polyhedral cone
![]() $\mathscr {C}_{\mathscr {U}}=\{B\xi \prec 0\}\subset {\mathbb {R}}^n$
. We claim that for each
$\mathscr {C}_{\mathscr {U}}=\{B\xi \prec 0\}\subset {\mathbb {R}}^n$
. We claim that for each
![]() $1\leq j\leq n$
, the hyperplane
$1\leq j\leq n$
, the hyperplane
![]() $H_j=\{ b^j \xi = 0 \}$
determined by the jth row of the matrix B is a face of
$H_j=\{ b^j \xi = 0 \}$
determined by the jth row of the matrix B is a face of
![]() $\mathscr {C}_{\mathscr {U}}$
, i.e., the intersection
$\mathscr {C}_{\mathscr {U}}$
, i.e., the intersection
![]() $\overline {\mathscr {C}_{\mathscr {U}}}\cap H_j\not =\emptyset $
. Indeed, since by Proposition 3.2,
$\overline {\mathscr {C}_{\mathscr {U}}}\cap H_j\not =\emptyset $
. Indeed, since by Proposition 3.2,
![]() $B^{-1}\succ 0$
and B is a linear automorphism of
$B^{-1}\succ 0$
and B is a linear automorphism of
![]() $\mathbb {Q}^n$
, it is easy to verify that the image
$\mathbb {Q}^n$
, it is easy to verify that the image
![]() $B^{-1}(\mathscr {C}_{\mathscr {U}})$
is precisely the negative orthant
$B^{-1}(\mathscr {C}_{\mathscr {U}})$
is precisely the negative orthant
![]() $\{\eta \prec 0\}\subset {\mathbb {R}}^n$
. But the negative orthant clearly has faces
$\{\eta \prec 0\}\subset {\mathbb {R}}^n$
. But the negative orthant clearly has faces
![]() $\{\eta _j=0\}, j=1,\dots , n$
, which corresponds to the faces
$\{\eta _j=0\}, j=1,\dots , n$
, which corresponds to the faces
![]() $H_j$
of
$H_j$
of
![]() $\mathscr {C}_{\mathscr {U}}$
.
$\mathscr {C}_{\mathscr {U}}$
.
Now, if
![]() $C\in M_n(\mathbb {Q})$
is another matrix (satisfying (3.3)) such that
$C\in M_n(\mathbb {Q})$
is another matrix (satisfying (3.3)) such that
then the faces of
![]() $\mathscr {C}_{\mathscr {U}}$
are also given by
$\mathscr {C}_{\mathscr {U}}$
are also given by
![]() $\{ c^j \xi = 0 \}, 1\leq j\leq n$
, so that there exists a permutation
$\{ c^j \xi = 0 \}, 1\leq j\leq n$
, so that there exists a permutation
![]() $\sigma \in S_n$
such that
$\sigma \in S_n$
such that
for each
![]() $1 \leq j \leq n$
. Then the transposes
$1 \leq j \leq n$
. Then the transposes
![]() $(c^j)^T$
and
$(c^j)^T$
and
![]() $(b^{\sigma (j)})^T$
are both normal to
$(b^{\sigma (j)})^T$
are both normal to
![]() $H_{\sigma (j)}$
, so that there is a
$H_{\sigma (j)}$
, so that there is a
![]() $\delta _j \in \mathbb {Q}\setminus \{0\}$
such that
$\delta _j \in \mathbb {Q}\setminus \{0\}$
such that
![]() $c^j = \delta _j b^{\sigma (j)}$
. Therefore,
$c^j = \delta _j b^{\sigma (j)}$
. Therefore,
![]() $C=DPB$
, where D is the diagonal matrix
$C=DPB$
, where D is the diagonal matrix
![]() $\mathrm {diag}(\delta _1,\dots ,\delta _n)$
and P is the permutation matrix whose jth column is
$\mathrm {diag}(\delta _1,\dots ,\delta _n)$
and P is the permutation matrix whose jth column is
![]() $e_{\sigma (j)}$
. Note that
$e_{\sigma (j)}$
. Note that
![]() $P^{-1}$
is also a permutation matrix, and hence
$P^{-1}$
is also a permutation matrix, and hence
![]() $P^{-1} \succ 0$
. Therefore, since
$P^{-1} \succ 0$
. Therefore, since
![]() $C^{-1}=B^{-1}P^{-1}D^{-1}$
and we have
$C^{-1}=B^{-1}P^{-1}D^{-1}$
and we have
![]() $C^{-1}\succ 0, B^{-1}\succ 0$
by Proposition 3.2, we have
$C^{-1}\succ 0, B^{-1}\succ 0$
by Proposition 3.2, we have
![]() $D\succ 0$
since
$D\succ 0$
since
![]() $B^{-1}P^{-1}\succ 0$
. Therefore,
$B^{-1}P^{-1}\succ 0$
. Therefore,
 $$ \begin{align*} \max_{1 \leq j \leq n} \mathsf{h}(C^{-1}e_j) &= \max_{1 \leq j \leq n} \mathsf{h}(B^{-1}P^{-1}D^{-1}e_j) = \max_{1 \leq j \leq n} \mathsf{h}(\frac{1}{\delta_j}B^{-1}e_{\sigma(j)}) \\ &=\max_{1 \leq j \leq n} \mathsf{h}(B^{-1}e_{\sigma(j)}) =\max_{1 \leq j \leq n} \mathsf{h}(B^{-1}e_j). \end{align*} $$
$$ \begin{align*} \max_{1 \leq j \leq n} \mathsf{h}(C^{-1}e_j) &= \max_{1 \leq j \leq n} \mathsf{h}(B^{-1}P^{-1}D^{-1}e_j) = \max_{1 \leq j \leq n} \mathsf{h}(\frac{1}{\delta_j}B^{-1}e_{\sigma(j)}) \\ &=\max_{1 \leq j \leq n} \mathsf{h}(B^{-1}e_{\sigma(j)}) =\max_{1 \leq j \leq n} \mathsf{h}(B^{-1}e_j). \end{align*} $$
This shows that
![]() $\kappa (\mathscr {U})$
as in 1.5 is well-defined, being independent of the matrix B. ▪
$\kappa (\mathscr {U})$
as in 1.5 is well-defined, being independent of the matrix B. ▪
3.2 The Jacobian determinant of
 $\Phi _A$
$\Phi _A$
For a subset
![]() $E \subseteq \{1 ,\dots , n \}$
, define
$E \subseteq \{1 ,\dots , n \}$
, define
 $$ \begin{align} {\mathbb{C}}^n_E := \{z \in {\mathbb{C}}^n : z_k \neq 0 \text{ for all } k \in E \} = \prod_{k=1}^n \Omega_k, \end{align} $$
$$ \begin{align} {\mathbb{C}}^n_E := \{z \in {\mathbb{C}}^n : z_k \neq 0 \text{ for all } k \in E \} = \prod_{k=1}^n \Omega_k, \end{align} $$
where
![]() $\Omega _k = {\mathbb {C}}$
if
$\Omega _k = {\mathbb {C}}$
if
![]() $k \not \in E$
and
$k \not \in E$
and
![]() $\Omega _k = {\mathbb {C}}^*$
if
$\Omega _k = {\mathbb {C}}^*$
if
![]() $k \in E$
. Then for
$k \in E$
. Then for
![]() $P \in M_n(\mathbb {Q})$
define
$P \in M_n(\mathbb {Q})$
define
that is,
![]() $\mathsf {K}(P)$
is the set of indices of those columns of P which have at least one negative entry. Notice that if
$\mathsf {K}(P)$
is the set of indices of those columns of P which have at least one negative entry. Notice that if
![]() $P\in M_n(\mathbb {Z})$
the matrix power
$P\in M_n(\mathbb {Z})$
the matrix power
![]() $z^P$
is defined for
$z^P$
is defined for
![]() $z\in {\mathbb {C}}^n$
if and only if
$z\in {\mathbb {C}}^n$
if and only if
![]() $z\in {\mathbb {C}}^n_{\mathsf {K}(P)}$
, i.e., in computing
$z\in {\mathbb {C}}^n_{\mathsf {K}(P)}$
, i.e., in computing
![]() $z^P$
we do not raise zero to a negative power. Similarly, for
$z^P$
we do not raise zero to a negative power. Similarly, for
![]() $P\in M_n(\mathbb {Q})$
and a vector
$P\in M_n(\mathbb {Q})$
and a vector
![]() $r\in {\mathbb {R}}^n$
with
$r\in {\mathbb {R}}^n$
with
![]() $r_j\geq 0$
, the rational power
$r_j\geq 0$
, the rational power
![]() $r^P$
is defined provided
$r^P$
is defined provided
![]() $r \in {\mathbb {R}}^n_{\mathsf {K}(P)} $
for exactly the same reason.
$r \in {\mathbb {R}}^n_{\mathsf {K}(P)} $
for exactly the same reason.
The following analog of the calculus formula
![]() $\frac {d}{dx}x^n=nx^{n-1}$
may be found in [Reference Nagel and PramanikNP09, Lemma 4.2], and will be needed frequently in the sequel.
$\frac {d}{dx}x^n=nx^{n-1}$
may be found in [Reference Nagel and PramanikNP09, Lemma 4.2], and will be needed frequently in the sequel.
Lemma 3.8 For any
![]() $A \in M_n (\mathbb {Z})$
and any
$A \in M_n (\mathbb {Z})$
and any
![]() $z \in {\mathbb {C}}^n_{\mathsf {K}(A)}$
we have
$z \in {\mathbb {C}}^n_{\mathsf {K}(A)}$
we have
where
![]() $\Phi _A(z)=z^A$
and
$\Phi _A(z)=z^A$
and
![]() $\Phi _A'(z):{\mathbb {C}}^n\to {\mathbb {C}}^n$
is the complex derivative of
$\Phi _A'(z):{\mathbb {C}}^n\to {\mathbb {C}}^n$
is the complex derivative of
![]() $\Phi _A$
at the point
$\Phi _A$
at the point
![]() $z\in {\mathbb {C}}^n_{\mathsf {K}(A)}$
.
$z\in {\mathbb {C}}^n_{\mathsf {K}(A)}$
.
Proof First assume that z is such that
![]() $z_k{\neq }0$
for each k. For
$z_k{\neq }0$
for each k. For
![]() $1\leq j,k \leq n$
, the entry in the jth row and kth column of the complex derivative matrix
$1\leq j,k \leq n$
, the entry in the jth row and kth column of the complex derivative matrix
![]() $\Phi _A'(z)$
is
$\Phi _A'(z)$
is
![]() $\dfrac {\partial z^{a^j}}{\partial z_k}$
, where recall that
$\dfrac {\partial z^{a^j}}{\partial z_k}$
, where recall that
![]() $a^j$
denotes the multi-index in
$a^j$
denotes the multi-index in
![]() $(\mathbb {Z}^n)^\dagger $
whose entries constitute the jth row of A. If
$(\mathbb {Z}^n)^\dagger $
whose entries constitute the jth row of A. If
![]() $a_k^j \neq 0$
then
$a_k^j \neq 0$
then
 $$ \begin{align*}\frac{\partial z^{a^j}}{\partial z_k}=a_k^j z_k^{a_k^j-1} \prod_{\substack{\ell=1 \\ \ell\neq k}}^n z_\ell^{a_\ell^j} = a_k^j\cdot \frac{z^{a^j}}{z_k}.\end{align*} $$
$$ \begin{align*}\frac{\partial z^{a^j}}{\partial z_k}=a_k^j z_k^{a_k^j-1} \prod_{\substack{\ell=1 \\ \ell\neq k}}^n z_\ell^{a_\ell^j} = a_k^j\cdot \frac{z^{a^j}}{z_k}.\end{align*} $$
If
![]() $a_k^j=0$
, then
$a_k^j=0$
, then
 $\dfrac {\partial z^{a^j}}{\partial z_k}=0$
, so in fact the above formula holds for all
$\dfrac {\partial z^{a^j}}{\partial z_k}=0$
, so in fact the above formula holds for all
![]() $j,k$
. Now, by the representation of a determinant as an explicit polynomial in the matrix entries, we find
$j,k$
. Now, by the representation of a determinant as an explicit polynomial in the matrix entries, we find

where we have used the fact that

Also,

Therefore,
for z such that
![]() $z_k{\neq }0$
for each k. The result follows by analytic continuation. ▪
$z_k{\neq }0$
for each k. The result follows by analytic continuation. ▪
3.3 A branched covering of the domain
 $\mathscr {U}$
$\mathscr {U}$
In this section, we will construct a quotient map under a group action from a domain with simple geometry (a product of some copies of discs with some copies of punctured discs) to the domain
![]() $\mathscr {U}$
, and this construction will be fundamental in the proof of Theorem 1.2. We first specify what we mean by a quotient map.
$\mathscr {U}$
, and this construction will be fundamental in the proof of Theorem 1.2. We first specify what we mean by a quotient map.
Definition 3.10 Let
![]() $\Omega _1, \Omega _2\subset {\mathbb {C}}^n$
be domains, let
$\Omega _1, \Omega _2\subset {\mathbb {C}}^n$
be domains, let
![]() $\Phi : \Omega _1\to \Omega _2$
be a proper holomorphic mapping. Let
$\Phi : \Omega _1\to \Omega _2$
be a proper holomorphic mapping. Let
![]() $\Gamma \subset \mathrm {Aut}(\Omega _1)$
be a group of biholomorphic automorphisms of
$\Gamma \subset \mathrm {Aut}(\Omega _1)$
be a group of biholomorphic automorphisms of
![]() $\Omega _1$
. We will say that
$\Omega _1$
. We will say that
![]() $\Phi $
is of quotient type with group
$\Phi $
is of quotient type with group
![]() $\Gamma $
if there exist closed lower-dimensional complex-analytic subvarieties
$\Gamma $
if there exist closed lower-dimensional complex-analytic subvarieties
![]() $Z_j\subset \Omega _j, j=1,2$
such that
$Z_j\subset \Omega _j, j=1,2$
such that
![]() $\Phi $
restricts to a covering map
$\Phi $
restricts to a covering map
and for each
![]() $z\in \Omega _2\setminus Z_2$
, the action of
$z\in \Omega _2\setminus Z_2$
, the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Omega _1$
restricts to a transitive action on the fiber
$\Omega _1$
restricts to a transitive action on the fiber
![]() $\Phi ^{-1}(z)$
. Other names in the literature for such proper maps include regular and Galois proper maps. The group
$\Phi ^{-1}(z)$
. Other names in the literature for such proper maps include regular and Galois proper maps. The group
![]() $\Gamma $
will be referred to as the group of deck transformations of
$\Gamma $
will be referred to as the group of deck transformations of
![]() $\Phi $
(sometimes called the Galois group).
$\Phi $
(sometimes called the Galois group).
Notice that the restricted map
![]() $\Phi :\Omega _1\setminus Z_1 \to \Omega _2\setminus Z_2$
becomes a so called regular covering map (see [Reference MasseyMas91, p. 135 ff.]), i.e., the covering map gives rise to a biholomorphism between
$\Phi :\Omega _1\setminus Z_1 \to \Omega _2\setminus Z_2$
becomes a so called regular covering map (see [Reference MasseyMas91, p. 135 ff.]), i.e., the covering map gives rise to a biholomorphism between
![]() $\Omega _2\setminus Z_2$
and the quotient
$\Omega _2\setminus Z_2$
and the quotient
![]() $(\Omega _1\setminus Z_1)/\Gamma $
, where it can be shown that
$(\Omega _1\setminus Z_1)/\Gamma $
, where it can be shown that
![]() $\Gamma $
acts properly and discontinuously on
$\Gamma $
acts properly and discontinuously on
![]() $ \Omega _1\setminus Z_1$
. Further, it follows that
$ \Omega _1\setminus Z_1$
. Further, it follows that
![]() $\Gamma $
is in fact the full group of deck transformations of the covering map
$\Gamma $
is in fact the full group of deck transformations of the covering map
![]() $\Phi :\Omega _1\setminus Z_1 \to \Omega _2\setminus Z_2$
, and that this covering map has exactly
$\Phi :\Omega _1\setminus Z_1 \to \Omega _2\setminus Z_2$
, and that this covering map has exactly
![]() $\left \vert \Gamma \right \vert $
sheets. Notice that by analytic continuation, the relation
$\left \vert \Gamma \right \vert $
sheets. Notice that by analytic continuation, the relation
![]() $\Phi \circ \sigma =\Phi $
holds for each
$\Phi \circ \sigma =\Phi $
holds for each
![]() $\sigma $
in
$\sigma $
in
![]() $\Gamma $
on all of
$\Gamma $
on all of
![]() $\Omega _1$
.
$\Omega _1$
.
Now let B be a matrix, let the set
![]() $\mathsf {K}(B)\subset \{1,\dots , n\}$
be as in (3.7), the set of indices of those columns of B which have at least one negative entry. Define a subset
$\mathsf {K}(B)\subset \{1,\dots , n\}$
be as in (3.7), the set of indices of those columns of B which have at least one negative entry. Define a subset
![]() $\mathsf {L}(B) \subset \{1,\dots , n\}$
by setting
$\mathsf {L}(B) \subset \{1,\dots , n\}$
by setting
We define the domain
![]() $\mathbb {D}^n_{\mathsf {L}(B)} =\mathbb {D}^n \cap {\mathbb {C}}^n_{\mathsf {L}(B)} $
, i.e.,
$\mathbb {D}^n_{\mathsf {L}(B)} =\mathbb {D}^n \cap {\mathbb {C}}^n_{\mathsf {L}(B)} $
, i.e.,
Notice that
![]() $\mathbb {D}^n_{\mathsf {L}(B)}$
is the product of some copies of the unit disc with some copies of the punctured unit disc.
$\mathbb {D}^n_{\mathsf {L}(B)}$
is the product of some copies of the unit disc with some copies of the punctured unit disc.
Theorem 3.12 Let
![]() $\mathscr {U}$
be the domain of Theorem 1.2, and assume (without loss of generality) that
$\mathscr {U}$
be the domain of Theorem 1.2, and assume (without loss of generality) that
![]() $\mathscr {U}$
is represented as in (
3.1
), where the matrix
$\mathscr {U}$
is represented as in (
3.1
), where the matrix
![]() $B=(b^j_k)$
satisfies the conditions (
3.3
), and let
$B=(b^j_k)$
satisfies the conditions (
3.3
), and let
![]() $A = \operatorname {\mathrm {adj}} B.$
Then the mononial map
$A = \operatorname {\mathrm {adj}} B.$
Then the mononial map
![]() $\Phi _A$
of (
2.6
) maps
$\Phi _A$
of (
2.6
) maps
![]() $\mathbb {D}^n_{\mathsf {L}(B)}$
onto
$\mathbb {D}^n_{\mathsf {L}(B)}$
onto
![]() $\mathscr {U}$
, and the map so defined
$\mathscr {U}$
, and the map so defined
is a proper holomorphic map of quotient type with group
![]() $\Gamma $
consisting of the automorphisms
$\Gamma $
consisting of the automorphisms
![]() $\sigma _\nu : \mathbb {D}^n_{\mathsf {L}(B)} \to \mathbb {D}^n_{\mathsf {L}(B)}$
given by
$\sigma _\nu : \mathbb {D}^n_{\mathsf {L}(B)} \to \mathbb {D}^n_{\mathsf {L}(B)}$
given by
for
![]() $\nu \in \mathbb {Z}^n$
. Further, the group
$\nu \in \mathbb {Z}^n$
. Further, the group
![]() $\Gamma $
has exactly
$\Gamma $
has exactly
![]() $\det A$
elements.
$\det A$
elements.
Some related results may be found in [Reference Nagel and PramanikNP20, Reference ZwonekZwo99].
Proof By the conditions (3.3), we have
![]() $A =(\det B)B^{-1} \succeq 0$
, so
$A =(\det B)B^{-1} \succeq 0$
, so
![]() $\Phi _A$
is defined on all of
$\Phi _A$
is defined on all of
![]() $\mathbb {D}^n_{\mathsf {L}(B)}$
. We first claim that the image
$\mathbb {D}^n_{\mathsf {L}(B)}$
. We first claim that the image
![]() $\Phi _A(\mathbb {D}^n_{\mathsf {L}(B)})$
is contained in
$\Phi _A(\mathbb {D}^n_{\mathsf {L}(B)})$
is contained in
![]() ${\mathbb {C}}^n_{\mathsf {K}(B)}$
. Indeed, if
${\mathbb {C}}^n_{\mathsf {K}(B)}$
. Indeed, if
![]() $z\in \Phi _A(\mathbb {D}^n_{\mathsf {L}(B)})$
, then
$z\in \Phi _A(\mathbb {D}^n_{\mathsf {L}(B)})$
, then
![]() $z_\ell {\neq }0$
if
$z_\ell {\neq }0$
if
![]() $a^k_\ell {\neq }0$
for some
$a^k_\ell {\neq }0$
for some
![]() $k\in \mathsf {K}(B)$
. Therefore the kth element of the vector
$k\in \mathsf {K}(B)$
. Therefore the kth element of the vector
![]() $z^A$
, i.e.,
$z^A$
, i.e.,
is nonzero, so
![]() $z^A\in {\mathbb {C}}^n_{\mathsf {K}(B)}.$
Now notice that
$z^A\in {\mathbb {C}}^n_{\mathsf {K}(B)}.$
Now notice that
since
![]() $\rho (z)^B$
(and
$\rho (z)^B$
(and
![]() $z^B$
) are defined if and only if
$z^B$
) are defined if and only if
![]() $z\in {\mathbb {C}}^n_{\mathsf {K}(B)}.$
Therefore, as in the proof of Proposition 3.2, we have
$z\in {\mathbb {C}}^n_{\mathsf {K}(B)}.$
Therefore, as in the proof of Proposition 3.2, we have
for each point
![]() $z\in \mathbb {D}^n_{\mathsf {L}(B)} $
since
$z\in \mathbb {D}^n_{\mathsf {L}(B)} $
since
![]() $\det B>0$
. This shows that
$\det B>0$
. This shows that
![]() $\Phi _A : \mathbb {D}^n_{\mathsf {L}(B)} \to \mathscr {U}$
is a well defined holomorphic map.
$\Phi _A : \mathbb {D}^n_{\mathsf {L}(B)} \to \mathscr {U}$
is a well defined holomorphic map.
We now show that, if we think of
![]() $\Phi _A$
as a map from
$\Phi _A$
as a map from
![]() ${\mathbb {C}}^n$
to itself (recall that
${\mathbb {C}}^n$
to itself (recall that
![]() $A\succeq 0$
), then we have
$A\succeq 0$
), then we have
If
![]() $z\in {\mathbb {C}}^n$
is such that
$z\in {\mathbb {C}}^n$
is such that
![]() $\Phi _A(z)=z^A\in \mathscr {U}$
, then
$\Phi _A(z)=z^A\in \mathscr {U}$
, then
![]() $\rho (z^A)^B$
is well defined and
$\rho (z^A)^B$
is well defined and
. The fact that
![]() $\rho (z^A)^B$
is well defined is equivalent to
$\rho (z^A)^B$
is well defined is equivalent to
![]() $z^A\in {\mathbb {C}}^n_{\mathsf {K}(B)}$
, i.e., for each
$z^A\in {\mathbb {C}}^n_{\mathsf {K}(B)}$
, i.e., for each
![]() $k\in \mathsf {K}(B)$
we have the entry
$k\in \mathsf {K}(B)$
we have the entry
![]() $z^{a^k}{\neq }0.$
Now from (3.15), we see that whenever
$z^{a^k}{\neq }0.$
Now from (3.15), we see that whenever
![]() $a^k_\ell {\neq }0$
(so
$a^k_\ell {\neq }0$
(so
![]() $a^k_\ell \geq 1$
since
$a^k_\ell \geq 1$
since
![]() $A\succeq 0$
), we must have
$A\succeq 0$
), we must have
![]() $z_\ell {\neq }0$
, i.e.,
$z_\ell {\neq }0$
, i.e.,
![]() $z\in {\mathbb {C}}^n_{\mathsf {L}(B)}$
. The other condition
$z\in {\mathbb {C}}^n_{\mathsf {L}(B)}$
. The other condition
on the point z shows that
Since
![]() $\det B>0$
, this shows that
$\det B>0$
, this shows that
, i.e.,
![]() $z\in \mathbb {D}^n$
. Together these conditions show that
$z\in \mathbb {D}^n$
. Together these conditions show that
![]() $z\in \mathbb {D}^n_{\mathsf {L}(B)}$
, proving the desired inclusion of (3.16).
$z\in \mathbb {D}^n_{\mathsf {L}(B)}$
, proving the desired inclusion of (3.16).
We can now show that
![]() $\Phi _A:\mathbb {D}^n_{\mathsf {L}(B)}\to \mathscr {U}$
is a proper holomorphic map. Let
$\Phi _A:\mathbb {D}^n_{\mathsf {L}(B)}\to \mathscr {U}$
is a proper holomorphic map. Let
![]() $K \subset \mathscr {U}$
be compact. Since the topology induced on K from
$K \subset \mathscr {U}$
be compact. Since the topology induced on K from
![]() $\mathscr {U}$
is the same as that induced from
$\mathscr {U}$
is the same as that induced from
![]() ${\mathbb {C}}^n$
, it follows that K is closed in
${\mathbb {C}}^n$
, it follows that K is closed in
![]() ${\mathbb {C}}^n$
(and bounded). As
${\mathbb {C}}^n$
(and bounded). As
![]() $\Phi _A$
is continuous,
$\Phi _A$
is continuous,
![]() $\Phi _A^{-1} (K)$
is closed in
$\Phi _A^{-1} (K)$
is closed in
![]() ${\mathbb {C}}^n$
and in fact
${\mathbb {C}}^n$
and in fact
![]() $\Phi _A^{-1} (K) \subseteq \mathbb {D}^n_{\mathsf {L}(B)}$
by (3.16), so that it is bounded as well. Thus,
$\Phi _A^{-1} (K) \subseteq \mathbb {D}^n_{\mathsf {L}(B)}$
by (3.16), so that it is bounded as well. Thus,
![]() $\Phi _A^{-1} (K)$
is compact for every compact
$\Phi _A^{-1} (K)$
is compact for every compact
![]() $K \subset \mathscr {U}$
, which is to say
$K \subset \mathscr {U}$
, which is to say
![]() $\Phi _A$
is proper.
$\Phi _A$
is proper.
Now we want to verify that the proper holomorphic map
![]() $\Phi _A:\mathbb {D}^n_{\mathsf {L}(B)} \to \mathscr {U}$
is of quotient type in the sense of Definition 3.10 with group
$\Phi _A:\mathbb {D}^n_{\mathsf {L}(B)} \to \mathscr {U}$
is of quotient type in the sense of Definition 3.10 with group
![]() $\Gamma = \{\sigma _\nu : \nu \in \mathbb {Z}^n \},$
with
$\Gamma = \{\sigma _\nu : \nu \in \mathbb {Z}^n \},$
with
![]() $\sigma _\nu $
as in (3.14) above. Let
$\sigma _\nu $
as in (3.14) above. Let

be the union of the coordinate hyperplanes, which is an analytic variety in
![]() ${\mathbb {C}}^n$
of codimension one. Notice that the formula (3.9) shows that the set of regular points of the map
${\mathbb {C}}^n$
of codimension one. Notice that the formula (3.9) shows that the set of regular points of the map
![]() $\Phi _A$
(i.e., the set of points
$\Phi _A$
(i.e., the set of points
![]() $\{z\in \mathbb {D}^n_{\mathsf {L}(B)}: \det \Phi _A'(z){\neq }0 \}$
) contains
$\{z\in \mathbb {D}^n_{\mathsf {L}(B)}: \det \Phi _A'(z){\neq }0 \}$
) contains
![]() $\mathbb {D}^n_{\mathsf {L}(B)}\setminus Z_1$
, and from the fact that
$\mathbb {D}^n_{\mathsf {L}(B)}\setminus Z_1$
, and from the fact that
![]() $\Phi _A(z)=z^A$
, we see that the regular values of
$\Phi _A(z)=z^A$
, we see that the regular values of
![]() $\Phi _A$
contains the open set
$\Phi _A$
contains the open set
![]() $\mathscr {U}\setminus Z_2$
. Notice that both
$\mathscr {U}\setminus Z_2$
. Notice that both
![]() $\mathbb {D}^n_{\mathsf {L}(B)}\setminus Z_1$
and
$\mathbb {D}^n_{\mathsf {L}(B)}\setminus Z_1$
and
![]() $\mathscr {U}\setminus Z_2$
are open subsets of the “algebraic torus”
$\mathscr {U}\setminus Z_2$
are open subsets of the “algebraic torus”
![]() $({\mathbb {C}}^*)^n$
, and it is clear that
$({\mathbb {C}}^*)^n$
, and it is clear that
![]() $\Phi _A$
maps
$\Phi _A$
maps
![]() $({\mathbb {C}}^*)^n$
into itself (and is even a group homomorphism, if
$({\mathbb {C}}^*)^n$
into itself (and is even a group homomorphism, if
![]() $({\mathbb {C}}^*)^n$
is given the group structure from the elementwise multiplication operation
$({\mathbb {C}}^*)^n$
is given the group structure from the elementwise multiplication operation
![]() $\odot $
). Since a proper holomorphic map is a covering map restricted to its regular points, it now follows that
$\odot $
). Since a proper holomorphic map is a covering map restricted to its regular points, it now follows that
![]() $\Phi _A: \mathbb {D}^n_{\mathsf {L}(B)}\setminus Z_1\to \mathscr {U}\setminus Z_2 $
is a holomorphic covering map. We need to show that it is regular.
$\Phi _A: \mathbb {D}^n_{\mathsf {L}(B)}\setminus Z_1\to \mathscr {U}\setminus Z_2 $
is a holomorphic covering map. We need to show that it is regular.
Let
![]() $w\in \mathscr {U}\setminus Z_2$
have polar representation
$w\in \mathscr {U}\setminus Z_2$
have polar representation
![]() $w=\rho (w)\odot \exp (i\theta )$
, where
$w=\rho (w)\odot \exp (i\theta )$
, where
![]() $\theta \in {\mathbb {R}}^n$
. Let
$\theta \in {\mathbb {R}}^n$
. Let
![]() $z\in \mathbb {D}^n_{\mathsf {L}(B)}$
be such that
$z\in \mathbb {D}^n_{\mathsf {L}(B)}$
be such that
![]() $\Phi _A(z)=z^A=w$
. Comparing the radial and angular parts, one such preimage is
$\Phi _A(z)=z^A=w$
. Comparing the radial and angular parts, one such preimage is
Now notice that the angular vector
![]() $\theta $
is known only up to an additive ambiguity of
$\theta $
is known only up to an additive ambiguity of
![]() $2\pi \mathbb {Z}^n$
, i.e., two values of
$2\pi \mathbb {Z}^n$
, i.e., two values of
![]() $\theta $
corresponding to the same w differ by
$\theta $
corresponding to the same w differ by
![]() $2\pi \nu $
for some integer vector
$2\pi \nu $
for some integer vector
![]() $\nu \in \mathbb {Z}^n$
. Therefore two different preimages
$\nu \in \mathbb {Z}^n$
. Therefore two different preimages
![]() $z,z'$
of the point w (corresponding to the choices
$z,z'$
of the point w (corresponding to the choices
![]() $\theta $
and
$\theta $
and
![]() $\theta +2\pi \nu $
of the angular vector in the polar representation of w) are related by
$\theta +2\pi \nu $
of the angular vector in the polar representation of w) are related by
 $$ \begin{align*} z' &= \rho(w)^{A^{-1}}\odot \exp\left( i A^{-1}(\theta+2\pi\nu)\right) = \rho(w)^{A^{-1}}\odot \exp\left( i A^{-1}\theta\right)\odot \exp\left(2\pi i A^{-1}\nu\right)\\ &= \exp\left(2\pi i A^{-1}\nu\right)\odot z =\sigma_\nu(z), \end{align*} $$
$$ \begin{align*} z' &= \rho(w)^{A^{-1}}\odot \exp\left( i A^{-1}(\theta+2\pi\nu)\right) = \rho(w)^{A^{-1}}\odot \exp\left( i A^{-1}\theta\right)\odot \exp\left(2\pi i A^{-1}\nu\right)\\ &= \exp\left(2\pi i A^{-1}\nu\right)\odot z =\sigma_\nu(z), \end{align*} $$
which shows that the group
![]() $\Gamma $
acts transitively on the fiber
$\Gamma $
acts transitively on the fiber
![]() $\Phi ^{-1}(w)$
.
$\Phi ^{-1}(w)$
.
Now we want to show that the group
![]() $\Gamma $
has exactly
$\Gamma $
has exactly
![]() $\det A$
elements. Consider the map
$\det A$
elements. Consider the map
![]() $\psi : \mathbb {Z}^n\to \Gamma $
given by
$\psi : \mathbb {Z}^n\to \Gamma $
given by
![]() $\psi (\nu )= \sigma _\nu . $
For any
$\psi (\nu )= \sigma _\nu . $
For any
![]() $\nu , \mu \in \mathbb {Z}^n$
and any
$\nu , \mu \in \mathbb {Z}^n$
and any
![]() $z \in \mathbb {D}^n_{\mathsf {L}(B)}$
we find that
$z \in \mathbb {D}^n_{\mathsf {L}(B)}$
we find that
 $$ \begin{align*} \psi(\nu+\mu)(z)=\sigma_{\nu + \mu}(z) &=\exp \left(2 \pi i A^{-1}(\nu + \mu) \right) \odot z \\ &= \exp \left(2 \pi i A^{-1}\nu \right)\odot \left( \exp\left(2 \pi i A^{-1} \mu \right) \odot z \right) \\ &= \sigma_\nu \circ \sigma_\mu (z)\\ &=\psi(\nu) \circ \psi(\mu) (z). \end{align*} $$
$$ \begin{align*} \psi(\nu+\mu)(z)=\sigma_{\nu + \mu}(z) &=\exp \left(2 \pi i A^{-1}(\nu + \mu) \right) \odot z \\ &= \exp \left(2 \pi i A^{-1}\nu \right)\odot \left( \exp\left(2 \pi i A^{-1} \mu \right) \odot z \right) \\ &= \sigma_\nu \circ \sigma_\mu (z)\\ &=\psi(\nu) \circ \psi(\mu) (z). \end{align*} $$
Hence,
![]() $\psi : \mathbb {Z}^n \to \Gamma $
is a surjective group homomorphism, and so we have an isomorphism
$\psi : \mathbb {Z}^n \to \Gamma $
is a surjective group homomorphism, and so we have an isomorphism
given by
![]() $\psi ([\nu ])=\sigma _\nu $
where
$\psi ([\nu ])=\sigma _\nu $
where
![]() $[\nu ] \in \mathbb Z^n/ \ker \psi $
is the class of
$[\nu ] \in \mathbb Z^n/ \ker \psi $
is the class of
![]() $\nu \in \mathbb Z^n$
. Notice that
$\nu \in \mathbb Z^n$
. Notice that
![]() $\nu \in \ker \psi $
if and only if
$\nu \in \ker \psi $
if and only if
![]() . This means that
. This means that
![]() $A^{-1}\nu \in \mathbb {Z}^n$
, so it follows that
$A^{-1}\nu \in \mathbb {Z}^n$
, so it follows that
![]() $\ker \psi = A(\mathbb Z^n)$
. Therefore, the group
$\ker \psi = A(\mathbb Z^n)$
. Therefore, the group
![]() $\Gamma $
is isomorphic to the quotient
$\Gamma $
is isomorphic to the quotient
![]() $\mathbb {Z}^n/A(\mathbb {Z}^n)$
by the isomorphism
$\mathbb {Z}^n/A(\mathbb {Z}^n)$
by the isomorphism
![]() $ \overline {\psi }: \mathbb {Z}^n/A(\mathbb {Z}^n)\to \Gamma $
$ \overline {\psi }: \mathbb {Z}^n/A(\mathbb {Z}^n)\to \Gamma $
To complete the proof, it is sufficient to recall that for any matrix
![]() $A\in M_n(\mathbb {Z})$
with
$A\in M_n(\mathbb {Z})$
with
![]() $\det A{\neq }0$
we have
$\det A{\neq }0$
we have
For completeness, we give two proofs of (3.17), neither of which unfortunately avoids high technology. The first (see [Reference Nagel and PramanikNP20] and [Reference ZwonekZwo99, Theorem 2.1]) is based on the Smith Canonical Form of an integer matrix (see [Reference MunkresMun84, p. 53 ff.]): for any
![]() $A \in M_n (\mathbb Z)$
there exist
$A \in M_n (\mathbb Z)$
there exist
![]() $P,Q \in GL_n(\mathbb Z)$
and a diagonal matrix
$P,Q \in GL_n(\mathbb Z)$
and a diagonal matrix
![]() $D \in M_n(\mathbb Z)$
, say
$D \in M_n(\mathbb Z)$
, say
![]() $D = \mathrm {diag}(\delta _1 ,\dots ,\delta _n)$
, such that
$D = \mathrm {diag}(\delta _1 ,\dots ,\delta _n)$
, such that
![]() $A = PDQ$
. Consider the automorphism of
$A = PDQ$
. Consider the automorphism of
![]() $\mathbb {Z}^n$
given by
$\mathbb {Z}^n$
given by
![]() $x\mapsto P^{-1}x$
. This maps
$x\mapsto P^{-1}x$
. This maps
![]() $A(\mathbb {Z}^n)$
to
$A(\mathbb {Z}^n)$
to
![]() $D(\mathbb {Z}^n)$
isomorphically, and therefore leads to an isomorphism
$D(\mathbb {Z}^n)$
isomorphically, and therefore leads to an isomorphism
![]() $\mathbb {Z}^n/A(\mathbb {Z}^n)$
with
$\mathbb {Z}^n/A(\mathbb {Z}^n)$
with
![]() $\mathbb {Z}^n/D(\mathbb {Z}^n)$
, but
$\mathbb {Z}^n/D(\mathbb {Z}^n)$
, but
![]() $\mathbb {Z}^n/D(\mathbb {Z}^n)$
is isomorphic to the product abelian group
$\mathbb {Z}^n/D(\mathbb {Z}^n)$
is isomorphic to the product abelian group
![]() $\prod _{j=1}^n\mathbb {Z}/\delta _j\mathbb {Z}$
, which has exactly
$\prod _{j=1}^n\mathbb {Z}/\delta _j\mathbb {Z}$
, which has exactly
![]() $\prod _{j=1}^n\left \vert \delta _j\right \vert $
elements. On the other hand note that
$\prod _{j=1}^n\left \vert \delta _j\right \vert $
elements. On the other hand note that
 $$ \begin{align*}&\left\vert\det A\right\vert=\left\vert \det(PDQ)\right\vert= \left\vert\det P\det D\det Q\right\vert= \left\vert\pm 1\cdot \prod_{j=1}^n \delta_j \cdot \pm 1\right\vert,\\[-6pt]\end{align*} $$
$$ \begin{align*}&\left\vert\det A\right\vert=\left\vert \det(PDQ)\right\vert= \left\vert\det P\det D\det Q\right\vert= \left\vert\pm 1\cdot \prod_{j=1}^n \delta_j \cdot \pm 1\right\vert,\\[-6pt]\end{align*} $$
which completes the first proof.
The second proof of (3.17) is geometric, and based on noticing that the inclusion of abelian groups
![]() $A(\mathbb {Z}^n)\hookrightarrow \mathbb {Z}^n$
gives rise to a covering map of tori
$A(\mathbb {Z}^n)\hookrightarrow \mathbb {Z}^n$
gives rise to a covering map of tori
given by
![]() $x+A(\mathbb {Z}^n)\mapsto x+\mathbb {Z}^n$
. If we endow
$x+A(\mathbb {Z}^n)\mapsto x+\mathbb {Z}^n$
. If we endow
![]() ${\mathbb {R}}^n$
with the Euclidean metric (thought of as a Riemannian metric), we obtain quotient (flat) Riemannian structures on both
${\mathbb {R}}^n$
with the Euclidean metric (thought of as a Riemannian metric), we obtain quotient (flat) Riemannian structures on both
![]() ${\mathbb {R}}^n/A(\mathbb {Z}^n)$
and
${\mathbb {R}}^n/A(\mathbb {Z}^n)$
and
![]() ${\mathbb {R}}^n/\mathbb {Z}^n$
, so that the covering map (3.18) is actually a local isometry. Therefore, the number of sheets of this covering map coincides with the ratio
${\mathbb {R}}^n/\mathbb {Z}^n$
, so that the covering map (3.18) is actually a local isometry. Therefore, the number of sheets of this covering map coincides with the ratio
![]() $\mathrm {vol}({\mathbb {R}}^n/A(\mathbb {Z}^n))/\mathrm {vol}( {\mathbb {R}}^n/\mathbb {Z}^n)$
. But we know that
$\mathrm {vol}({\mathbb {R}}^n/A(\mathbb {Z}^n))/\mathrm {vol}( {\mathbb {R}}^n/\mathbb {Z}^n)$
. But we know that
![]() $\mathrm {vol}( {\mathbb {R}}^n/\mathbb {Z}^n)$
is 1, being also the volume of the unit parallelepiped, and similarly
$\mathrm {vol}( {\mathbb {R}}^n/\mathbb {Z}^n)$
is 1, being also the volume of the unit parallelepiped, and similarly
![]() $\mathrm {vol}({\mathbb {R}}^n/A(\mathbb {Z}^n))$
is the volume of the image of the unit parallelepiped under the action of A, which is therefore
$\mathrm {vol}({\mathbb {R}}^n/A(\mathbb {Z}^n))$
is the volume of the image of the unit parallelepiped under the action of A, which is therefore
![]() $\left \vert \det A\right \vert $
. On the other hand, by covering space theory, we see that the number of sheets is equal to the order of the group of deck transformations of the covering p, which is in turn isomorphic to
$\left \vert \det A\right \vert $
. On the other hand, by covering space theory, we see that the number of sheets is equal to the order of the group of deck transformations of the covering p, which is in turn isomorphic to
![]() $\pi _1({\mathbb {R}}^n/\mathbb {Z}^n)/p_*\pi _1({\mathbb {R}}^n/A(\mathbb {Z}^n))=\mathbb {Z}^n/A(\mathbb {Z}^n)$
. ▪
$\pi _1({\mathbb {R}}^n/\mathbb {Z}^n)/p_*\pi _1({\mathbb {R}}^n/A(\mathbb {Z}^n))=\mathbb {Z}^n/A(\mathbb {Z}^n)$
. ▪
3.4 Rationality of the Bergman kernel of
 $\mathscr {U}$
$\mathscr {U}$
For a domain
![]() $\Omega \subset {\mathbb {C}}^n$
, denote by
$\Omega \subset {\mathbb {C}}^n$
, denote by
![]() $\mathrm {Rat}\left (\Omega \right )$
the rational functions of
$\mathrm {Rat}\left (\Omega \right )$
the rational functions of
![]() ${\mathbb {C}}^n$
restricted to
${\mathbb {C}}^n$
restricted to
![]() $\Omega $
. An element f of
$\Omega $
. An element f of
![]() $\Omega $
is defined on
$\Omega $
is defined on
![]() $\Omega \setminus Z_f$
, where
$\Omega \setminus Z_f$
, where
![]() $Z_f$
is an affine algebraic variety in
$Z_f$
is an affine algebraic variety in
![]() ${\mathbb {C}}^n$
. Algebraically,
${\mathbb {C}}^n$
. Algebraically,
![]() $\mathrm {Rat}\left (\Omega \right )$
is a field, and is isomorphic to the field of rational functions
$\mathrm {Rat}\left (\Omega \right )$
is a field, and is isomorphic to the field of rational functions
![]() ${\mathbb {C}}(z_1,\dots ,z_n)$
in n indeterminates. The map
${\mathbb {C}}(z_1,\dots ,z_n)$
in n indeterminates. The map
![]() $\Phi _A:\mathbb {D}^n_{\mathsf {L}(B)}\to \mathscr {U}$
of (3.13) induces a mapping of fields
$\Phi _A:\mathbb {D}^n_{\mathsf {L}(B)}\to \mathscr {U}$
of (3.13) induces a mapping of fields
given by
![]() $\Phi _A^*(f)= f\circ \Phi _A$
. Denote by k the image
$\Phi _A^*(f)= f\circ \Phi _A$
. Denote by k the image
Then k is clearly a subfield of
![]() $\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
. The following lemma records a special case of a very general phenomenon:
$\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
. The following lemma records a special case of a very general phenomenon:
Lemma 3.20 The field extension
![]() $\mathrm {Rat} (\mathbb {D}^n_{\mathsf {L}(B)})/k$
is Galois, and the map
$\mathrm {Rat} (\mathbb {D}^n_{\mathsf {L}(B)})/k$
is Galois, and the map
where
![]() $f\in \mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)}), \sigma \in \Gamma $
, is an isomorphism of the group of deck transformations of the proper map
$f\in \mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)}), \sigma \in \Gamma $
, is an isomorphism of the group of deck transformations of the proper map
![]() $\Phi _A$
with the Galois group of the extension.
$\Phi _A$
with the Galois group of the extension.
Proof Denote by
![]() $w_j$
the jth component of the map
$w_j$
the jth component of the map
![]() $\Phi _A$
, where
$\Phi _A$
, where
![]() $1\leq j \leq n$
. Notice that
$1\leq j \leq n$
. Notice that
![]() $w_j$
can be identified with the function
$w_j$
can be identified with the function
![]() $\Phi _A^*(\pi _j)=\pi _j\circ \Phi _A$
where
$\Phi _A^*(\pi _j)=\pi _j\circ \Phi _A$
where
![]() $\pi _j$
is the jth coordinate function on
$\pi _j$
is the jth coordinate function on
![]() $\mathscr {U}$
. Since
$\mathscr {U}$
. Since
![]() $\mathrm {Rat}(\mathscr {U})={\mathbb {C}}(\pi _1,\dots , \pi _n)$
, the field k is generated over
$\mathrm {Rat}(\mathscr {U})={\mathbb {C}}(\pi _1,\dots , \pi _n)$
, the field k is generated over
![]() ${\mathbb {C}}$
by the functions
${\mathbb {C}}$
by the functions
![]() $w_1,\dots , w_n$
, i.e.,
$w_1,\dots , w_n$
, i.e.,
![]() $k={\mathbb {C}}(w_1,\dots , w_n)$
. Denoting the coordinate functions on
$k={\mathbb {C}}(w_1,\dots , w_n)$
. Denoting the coordinate functions on
![]() $\mathbb {D}^n_{\mathsf {L}(B)}$
by
$\mathbb {D}^n_{\mathsf {L}(B)}$
by
![]() $z_1,\dots , z_n$
, we see that
$z_1,\dots , z_n$
, we see that
![]() $\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})= k(z_1,\dots , z_n)$
. To show that
$\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})= k(z_1,\dots , z_n)$
. To show that
![]() $\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})/k$
is Galois, we need to show that each
$\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})/k$
is Galois, we need to show that each
![]() $z_j$
is algebraic over k, and all the conjugates of
$z_j$
is algebraic over k, and all the conjugates of
![]() $z_j$
over k are already present in
$z_j$
over k are already present in
![]() $\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)}).$
$\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)}).$
Notice that by definition for each
![]() $1\leq j \leq n$
, we have
$1\leq j \leq n$
, we have
![]() $w_j=z_1^{a^j_1}\dots z_n^{a^j_n}=z^{a^j}$
, which follows from the fact that
$w_j=z_1^{a^j_1}\dots z_n^{a^j_n}=z^{a^j}$
, which follows from the fact that
![]() $w=\Phi _A(z)=z^A$
. Therefore we have
$w=\Phi _A(z)=z^A$
. Therefore we have
Denoting the jth row of the integer matrix
![]() $ \operatorname {\mathrm {adj}} A$
by
$ \operatorname {\mathrm {adj}} A$
by
![]() $c^j$
we see that
$c^j$
we see that
![]() $z_j^{\det A} = w^{c^j}\in k,$
so that
$z_j^{\det A} = w^{c^j}\in k,$
so that
![]() $z_j$
is a root of the polynomial
$z_j$
is a root of the polynomial
![]() $t^{\det A}-w^{c^j}\in k[t]$
. Further, all the roots of this polynomial (which are of the form
$t^{\det A}-w^{c^j}\in k[t]$
. Further, all the roots of this polynomial (which are of the form
![]() $\omega \cdot z_j $
for a
$\omega \cdot z_j $
for a
![]() $(\det A)$
th root of unity,
$(\det A)$
th root of unity,
![]() $\omega \in {\mathbb {C}}$
) are clearly in
$\omega \in {\mathbb {C}}$
) are clearly in
![]() $\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
. It follows that
$\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
. It follows that
![]() $\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
is Galois over the subfield k.
$\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
is Galois over the subfield k.
For each
![]() $\sigma \in \Gamma $
, it is clear that
$\sigma \in \Gamma $
, it is clear that
![]() $\Theta (\sigma )$
is an automorphism of the field
$\Theta (\sigma )$
is an automorphism of the field
![]() $\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
. We need to show that it fixes k. But for
$\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
. We need to show that it fixes k. But for
![]() $h=\Phi _A^*g\in k$
, where
$h=\Phi _A^*g\in k$
, where
![]() $g\in \mathrm {Rat}\left (\mathscr {U}\right )$
, we have
$g\in \mathrm {Rat}\left (\mathscr {U}\right )$
, we have
since
![]() $\sigma $
is a deck transformation of
$\sigma $
is a deck transformation of
![]() $\Phi _A$
. It follows that
$\Phi _A$
. It follows that
![]() $\Theta (\sigma )\in \mathrm {Gal}(\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})/k)$
. It is easily verified by direct computation that
$\Theta (\sigma )\in \mathrm {Gal}(\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})/k)$
. It is easily verified by direct computation that
![]() $\Theta $
is an injective group homomorphism. To show that
$\Theta $
is an injective group homomorphism. To show that
![]() $\Theta $
is surjective, for
$\Theta $
is surjective, for
![]() $\gamma \in \mathrm {Gal}(\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})/k)$
, we find a deck transformation
$\gamma \in \mathrm {Gal}(\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})/k)$
, we find a deck transformation
![]() $\theta \in \Gamma $
such that
$\theta \in \Gamma $
such that
![]() $\gamma (f)=f\circ \theta $
, so that
$\gamma (f)=f\circ \theta $
, so that
![]() $\gamma =\Theta ( \theta ^{-1})$
. Let
$\gamma =\Theta ( \theta ^{-1})$
. Let
![]() $\theta _j\in \mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
be the function
$\theta _j\in \mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
be the function
![]() $\theta _j=\gamma (z_j)$
, where
$\theta _j=\gamma (z_j)$
, where
![]() $z_j\in \mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
is the jth coordinate function. As we saw above, we have
$z_j\in \mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
is the jth coordinate function. As we saw above, we have
![]() $\theta _j=\omega _j\cdot z_j$
, where
$\theta _j=\omega _j\cdot z_j$
, where
![]() $\omega _j$
is a
$\omega _j$
is a
![]() $(\det A)$
th root of unity. Then
$(\det A)$
th root of unity. Then
![]() $\theta =(\theta _1,\dots ,\theta _n)$
defines a diagonal unitary mapping of
$\theta =(\theta _1,\dots ,\theta _n)$
defines a diagonal unitary mapping of
![]() ${\mathbb {C}}^n$
and therefore maps
${\mathbb {C}}^n$
and therefore maps
![]() $\mathbb {D}^n_{\mathsf {L}(B)}$
(a product of discs and punctured discs) into itself. Also, the jth component of
$\mathbb {D}^n_{\mathsf {L}(B)}$
(a product of discs and punctured discs) into itself. Also, the jth component of
![]() $\Phi _A\circ \theta $
is given by
$\Phi _A\circ \theta $
is given by
which is precisely the jth component of
![]() $\Phi _A$
. Therefore,
$\Phi _A$
. Therefore,
![]() $\Phi _A\circ \theta =\Phi _A$
, and
$\Phi _A\circ \theta =\Phi _A$
, and
![]() $\theta \in \Gamma $
. Finally, for a rational function
$\theta \in \Gamma $
. Finally, for a rational function
![]() $f=f(z_1,\dots ,z_n)\in \mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
, we have
$f=f(z_1,\dots ,z_n)\in \mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
, we have
▪
Proposition 3.22 The Bergman kernel of
![]() $\mathscr {U}$
is a rational function.
$\mathscr {U}$
is a rational function.
Proof Choosing a local continuous branch
![]() $\theta _j$
of
$\theta _j$
of
![]() $\arg w_j$
for each coordinate of
$\arg w_j$
for each coordinate of
![]() $w\in \mathscr {U}$
, we can write
$w\in \mathscr {U}$
, we can write
![]() $w=\rho (w)\odot \exp (i\theta )$
for
$w=\rho (w)\odot \exp (i\theta )$
for
![]() $\theta \in {\mathbb {R}}^n$
. Then
$\theta \in {\mathbb {R}}^n$
. Then
![]() $\psi (w)= w^{A^{-1}}=\rho (w)^{A^{-1}}\odot \exp (iA^{-1}\theta )$
is a local inverse to the proper holomorphic map
$\psi (w)= w^{A^{-1}}=\rho (w)^{A^{-1}}\odot \exp (iA^{-1}\theta )$
is a local inverse to the proper holomorphic map
![]() $\Phi _A:\mathbb {D}^n_{\mathsf {L}(B)}\to \mathscr {U}$
. Since
$\Phi _A:\mathbb {D}^n_{\mathsf {L}(B)}\to \mathscr {U}$
. Since
![]() $\Phi _A$
is of the quotient type, it follows that the local branches of
$\Phi _A$
is of the quotient type, it follows that the local branches of
![]() $\Phi ^{-1}_A$
are
$\Phi ^{-1}_A$
are
![]() $ \{\sigma \circ \psi : \sigma \in \Gamma \}.$
By Theorem 3.12, the map
$ \{\sigma \circ \psi : \sigma \in \Gamma \}.$
By Theorem 3.12, the map
![]() $\sigma :\mathbb {D}^n_{\mathsf {L}(B)}\to \mathbb {D}^n_{\mathsf {L}(B)}$
is the restriction of a unitary linear map on
$\sigma :\mathbb {D}^n_{\mathsf {L}(B)}\to \mathbb {D}^n_{\mathsf {L}(B)}$
is the restriction of a unitary linear map on
![]() ${\mathbb {C}}^n$
, so, noting that the argument behind the proof of (3.9) also applies for (locally defined) rational matrix powers, we have
${\mathbb {C}}^n$
, so, noting that the argument behind the proof of (3.9) also applies for (locally defined) rational matrix powers, we have

Therefore, by the Bell transformation formula, for
![]() $z\in \mathbb {D}^n_{\mathsf {L}(B)}$
and
$z\in \mathbb {D}^n_{\mathsf {L}(B)}$
and
![]() $w\in \mathscr {U}$
, the Bergman kernels
$w\in \mathscr {U}$
, the Bergman kernels
![]() $K_{\mathscr {U}}$
and
$K_{\mathscr {U}}$
and
![]() $K_{\mathbb {D}^n_{\mathsf {L}(B)}}=K_{\mathbb {D}^n}$
are related by
$K_{\mathbb {D}^n_{\mathsf {L}(B)}}=K_{\mathbb {D}^n}$
are related by

For a fixed
![]() $z\in \mathbb {D}^n_{\mathsf {L}(B)}$
, consider the function L on
$z\in \mathbb {D}^n_{\mathsf {L}(B)}$
, consider the function L on
![]() $\mathbb {D}^n_{\mathsf {L}(B)}$
given by
$\mathbb {D}^n_{\mathsf {L}(B)}$
given by
where
![]() $\overline {z}=(\overline {z_1},\dots , \overline {z_n})\in \mathbb {D}^n_{\mathsf {L}(B)} $
. Recalling that
$\overline {z}=(\overline {z_1},\dots , \overline {z_n})\in \mathbb {D}^n_{\mathsf {L}(B)} $
. Recalling that
 $$ \begin{align} K_{\mathbb{D}^n}(z,w)= \frac{1}{\pi^n}\prod_{j=1}^n \frac{1}{(1-z_j\overline{w_j})^2}, \end{align} $$
$$ \begin{align} K_{\mathbb{D}^n}(z,w)= \frac{1}{\pi^n}\prod_{j=1}^n \frac{1}{(1-z_j\overline{w_j})^2}, \end{align} $$
we see that
![]() $L\in \mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
, and
$L\in \mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
, and

We now claim that
![]() $L\in k$
, where
$L\in k$
, where
![]() $k\subset \mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
is as in (3.19). Since the extension
$k\subset \mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})$
is as in (3.19). Since the extension
![]() $\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})/k$
is Galois, it suffices to show that for each field-automorphism
$\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})/k$
is Galois, it suffices to show that for each field-automorphism
![]() $\tau \in \mathrm {Gal}(\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})/k)$
, we have
$\tau \in \mathrm {Gal}(\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})/k)$
, we have
![]() $\tau (L)=L$
. But by Lemma 3.20, for each
$\tau (L)=L$
. But by Lemma 3.20, for each
![]() $\tau \in \mathrm {Gal}(\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})/k)$
there is a
$\tau \in \mathrm {Gal}(\mathrm {Rat}(\mathbb {D}^n_{\mathsf {L}(B)})/k)$
there is a
![]() $\theta \in \Gamma $
such that
$\theta \in \Gamma $
such that
![]() $\tau (L)=L\circ \theta $
. Notice that thanks to (3.14), we can think of the map
$\tau (L)=L\circ \theta $
. Notice that thanks to (3.14), we can think of the map
![]() $\theta :\mathbb {D}^n_{\mathsf {L}(B)}\to \mathbb {D}^n_{\mathsf {L}(B)}$
as a linear map of
$\theta :\mathbb {D}^n_{\mathsf {L}(B)}\to \mathbb {D}^n_{\mathsf {L}(B)}$
as a linear map of
![]() ${\mathbb {C}}^n$
represented by a diagonal matrix. Therefore, we have
${\mathbb {C}}^n$
represented by a diagonal matrix. Therefore, we have
Consequently

establishing the claim.
Now since
![]() $L\in k$
, there is a function
$L\in k$
, there is a function
![]() $R(z,\cdot )\in \mathrm {Rat}(\mathscr {U})$
such that
$R(z,\cdot )\in \mathrm {Rat}(\mathscr {U})$
such that
![]() $L=\Phi _A^* R(z,\cdot )$
, i,e,
$L=\Phi _A^* R(z,\cdot )$
, i,e,
Therefore, we have

which shows that for each fixed
![]() $z\in \mathbb {D}^n_{\mathsf {L}(B)}$
, the function
$z\in \mathbb {D}^n_{\mathsf {L}(B)}$
, the function
![]() $K_{\mathscr {U}}(z,\cdot )$
is rational. By the Reinhardt symmetry of
$K_{\mathscr {U}}(z,\cdot )$
is rational. By the Reinhardt symmetry of
![]() $K_{\mathscr {U}}$
, there is a function
$K_{\mathscr {U}}$
, there is a function
![]() $\widetilde {K}$
such that
$\widetilde {K}$
such that
Since for a fixed z, the function
![]() $w\mapsto \widetilde {K}(z\odot \overline {w})$
is rational, it follows that the function
$w\mapsto \widetilde {K}(z\odot \overline {w})$
is rational, it follows that the function
![]() $t\mapsto \widetilde {K}(t)=\widetilde {K}(t_1,\dots , t_n)$
is also rational. Therefore, the function
$t\mapsto \widetilde {K}(t)=\widetilde {K}(t_1,\dots , t_n)$
is also rational. Therefore, the function
![]() $K_{\mathscr {U}}$
is rational on
$K_{\mathscr {U}}$
is rational on
![]() $\mathscr {U}\times \mathscr {U}$
. ▪
$\mathscr {U}\times \mathscr {U}$
. ▪
4 Transformation of
 $L^p$
-Bergman spaces under quotient maps
$L^p$
-Bergman spaces under quotient maps
4.1 Definitions
In order to state our results, we introduce some terminology:
Definition 4.1 We say that a linear map T between Banach spaces
![]() $(E_1, \left \Vert \cdot \right \Vert {{\hspace{-0.0001pt}}}_1)$
and
$(E_1, \left \Vert \cdot \right \Vert {{\hspace{-0.0001pt}}}_1)$
and
![]() $(E_2, \left \Vert \cdot \right \Vert {{\hspace{-0.0001pt}}}_2)$
is a homothetic isomorphism if it is a continuous bijection (and therefore has a continuous inverse) and there is a constant
$(E_2, \left \Vert \cdot \right \Vert {{\hspace{-0.0001pt}}}_2)$
is a homothetic isomorphism if it is a continuous bijection (and therefore has a continuous inverse) and there is a constant
![]() $C>0$
such that for each
$C>0$
such that for each
![]() $x\in E_1$
we have
$x\in E_1$
we have
Remark If T is a homothetic isomorphism between Banach spaces, then
![]() $\tfrac {1}{\left \Vert T\right \Vert }\cdot T$
is an isometric isomorphism of Banach spaces, so a homothetic isomorphism is simply the product of an isometric isomorphism and a scalar operator. In particular, a homothetic isomorphism between Hilbert spaces preserves angles, and in particular orthogonality of vectors.
$\tfrac {1}{\left \Vert T\right \Vert }\cdot T$
is an isometric isomorphism of Banach spaces, so a homothetic isomorphism is simply the product of an isometric isomorphism and a scalar operator. In particular, a homothetic isomorphism between Hilbert spaces preserves angles, and in particular orthogonality of vectors.
The following definition and facts are standard:
Definition 4.2 Let
![]() $\Omega \subset {\mathbb {C}}^n$
be a domain, let
$\Omega \subset {\mathbb {C}}^n$
be a domain, let
![]() $\lambda>0$
be a continuous function (the weight), and let
$\lambda>0$
be a continuous function (the weight), and let
![]() $0<p<\infty $
. Then we define
$0<p<\infty $
. Then we define
and
where the latter is called a weighted Bergman space. If
![]() $p\geq 1$
, then each of
$p\geq 1$
, then each of
![]() $L^p(\Omega ,\lambda )$
and
$L^p(\Omega ,\lambda )$
and
![]() $A^p(\Omega , \lambda )$
is a Banach space with the natural weighted norm, and
$A^p(\Omega , \lambda )$
is a Banach space with the natural weighted norm, and
![]() $A^p(\Omega ,\lambda )$
is a closed subspace of
$A^p(\Omega ,\lambda )$
is a closed subspace of
![]() $L^p(\Omega ,\lambda )$
.
$L^p(\Omega ,\lambda )$
.
We will make extensive use of the following notion:
Definition 4.3 Given a group G of biholomorphic automorphisms of a domain
![]() $\Omega \subset {\mathbb {C}}^n$
, and a space
$\Omega \subset {\mathbb {C}}^n$
, and a space
![]() $\mathfrak {F}$
of functions on
$\mathfrak {F}$
of functions on
![]() $\Omega $
, we denote by
$\Omega $
, we denote by
![]() $[ \mathfrak {F}]^G$
the subspace of
$[ \mathfrak {F}]^G$
the subspace of
![]() $\mathfrak {F}$
consisting of functions which are G-invariant in the following sense
$\mathfrak {F}$
consisting of functions which are G-invariant in the following sense
where
![]() $\sigma ^\sharp $
is the pullback induced by
$\sigma ^\sharp $
is the pullback induced by
![]() $\sigma $
as in (1.8).
$\sigma $
as in (1.8).
Remark Interpreting
![]() $\mathfrak {F}$
as a space of holomorphic forms on
$\mathfrak {F}$
as a space of holomorphic forms on
![]() $\Omega $
by associating
$\Omega $
by associating
![]() $f\in \mathfrak {F}$
with the form
$f\in \mathfrak {F}$
with the form
![]() $fdz_1\wedge \dots \wedge dz_n$
, this simply says that the forms in
$fdz_1\wedge \dots \wedge dz_n$
, this simply says that the forms in
![]() $[\mathfrak {F}]^G$
are invariant under pullback by elements of G.
$[\mathfrak {F}]^G$
are invariant under pullback by elements of G.
4.2 Transformation of Bergman spaces
With the above definitions, we are ready to state and prove the following elementary facts. For completeness, we give details of the proofs.
Proposition 4.5 Let
![]() $\Omega _1,\Omega _2$
be domains in
$\Omega _1,\Omega _2$
be domains in
![]() ${\mathbb {C}}^n$
, and let
${\mathbb {C}}^n$
, and let
![]() $\Phi :\Omega _1\to \Omega _2$
be a proper holomorphic map of quotient type with group
$\Phi :\Omega _1\to \Omega _2$
be a proper holomorphic map of quotient type with group
![]() $\Gamma \subset \mathrm {Aut}(\Omega _1)$
. Then for
$\Gamma \subset \mathrm {Aut}(\Omega _1)$
. Then for
![]() $1<p<\infty $
, the pullback map
$1<p<\infty $
, the pullback map
![]() $\Phi ^\sharp $
gives rise to a homothetic isomorphism
$\Phi ^\sharp $
gives rise to a homothetic isomorphism
This restricts to a homothetic isomorphism
Proof Let f be a function on
![]() $\Omega _2$
, and let
$\Omega _2$
, and let
![]() $g=\Phi ^\sharp f$
be its pullback to
$g=\Phi ^\sharp f$
be its pullback to
![]() $\Omega _1$
, then we have for each
$\Omega _1$
, then we have for each
![]() $\sigma \in \Gamma $
that
$\sigma \in \Gamma $
that
where we have used the contravariance of the pullback
![]() $(\Phi \circ \sigma )^\sharp =\sigma ^\sharp \circ \Phi ^\sharp $
and the fact that
$(\Phi \circ \sigma )^\sharp =\sigma ^\sharp \circ \Phi ^\sharp $
and the fact that
![]() $\Phi \circ \sigma =\Phi $
which follows since the action of
$\Phi \circ \sigma =\Phi $
which follows since the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Omega _2$
restricts to actions on each of the fibers. This shows that the range of
$\Omega _2$
restricts to actions on each of the fibers. This shows that the range of
![]() $\Phi ^\sharp $
consists of
$\Phi ^\sharp $
consists of
![]() $\Gamma $
-invariant functions. Special cases of this invariance were already noticed [Reference Misra, Roy and ZhangMSRZ13, Reference Chen, Krantz and YuanCKY20].
$\Gamma $
-invariant functions. Special cases of this invariance were already noticed [Reference Misra, Roy and ZhangMSRZ13, Reference Chen, Krantz and YuanCKY20].
To complete the proof of (4.6) we must show that
-
(i) for each
 $f\in L^p(\Omega _2)$
, (4.8)
$f\in L^p(\Omega _2)$
, (4.8) $$ \begin{align} \left\Vert\Phi^\sharp f\right\Vert{{\hspace{-0.0001pt}}}^p_{L^p\left(\Omega_1, \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p}\right)}= \left\vert\Gamma\right\vert\cdot \left\Vert f\right\Vert{{\hspace{-0.0001pt}}}^p_{L^p(\Omega_2)}, \end{align} $$
$$ \begin{align} \left\Vert\Phi^\sharp f\right\Vert{{\hspace{-0.0001pt}}}^p_{L^p\left(\Omega_1, \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p}\right)}= \left\vert\Gamma\right\vert\cdot \left\Vert f\right\Vert{{\hspace{-0.0001pt}}}^p_{L^p(\Omega_2)}, \end{align} $$
-
(ii) The image
 $\Phi ^\sharp (L^p(\Omega _2))$
is precisely
$\Phi ^\sharp (L^p(\Omega _2))$
is precisely
 $\left [L^p\left (\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p}\right )\right ]^\Gamma $
.
$\left [L^p\left (\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p}\right )\right ]^\Gamma $
.
Let
![]() $Z_1, Z_2$
be as in the Definition 3.10 of proper holomorphic maps of quotient type, i.e.,
$Z_1, Z_2$
be as in the Definition 3.10 of proper holomorphic maps of quotient type, i.e.,
![]() $\Phi $
is a regular covering map from
$\Phi $
is a regular covering map from
![]() $\Omega _1\setminus Z_1$
to
$\Omega _1\setminus Z_1$
to
![]() $\Omega _2\setminus Z_2$
. Let U be an open set in
$\Omega _2\setminus Z_2$
. Let U be an open set in
![]() $\Omega _2\setminus Z_2$
which is evenly covered by
$\Omega _2\setminus Z_2$
which is evenly covered by
![]() $\Phi $
, and let V be an open set of
$\Phi $
, and let V be an open set of
![]() $\Omega _1\setminus Z_1$
which is mapped biholomorphically by
$\Omega _1\setminus Z_1$
which is mapped biholomorphically by
![]() $\Phi $
onto U. Then the inverse image
$\Phi $
onto U. Then the inverse image
![]() $\Phi ^{-1}(U)$
is the finite disjoint union
$\Phi ^{-1}(U)$
is the finite disjoint union
![]() $\bigcup _{\sigma \in \Gamma } \sigma V$
. Therefore, if
$\bigcup _{\sigma \in \Gamma } \sigma V$
. Therefore, if
![]() $f\in L^p(\Omega _2)$
is supported in U, then
$f\in L^p(\Omega _2)$
is supported in U, then
![]() $\Phi ^\sharp f$
is supported in
$\Phi ^\sharp f$
is supported in
![]() $\bigcup _{\sigma \in \Gamma } \sigma V$
, and we have
$\bigcup _{\sigma \in \Gamma } \sigma V$
, and we have
 $$ \begin{align*} &\left\Vert\Phi^\sharp f\right\Vert{{\hspace{-0.0001pt}}}^p_{L^p\left(\Omega_1, \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p}\right)}\\[10pt]&\quad =\int_{\Omega_1} \left\vert f\circ \Phi \cdot \det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{p} \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p} dV \\[10pt]&\quad =\sum_{\sigma \in \Gamma}\int_{\sigma V} \left\vert f\circ \Phi\right\vert{{\hspace{-0.0001pt}}}^p \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^2 dV= \sum_{\sigma\in \Gamma }\int_{U} \left\vert f\right\vert{{\hspace{-0.0001pt}}}^p dV = \left\vert\Gamma\right\vert\cdot\left\Vert f\right\Vert{{\hspace{-0.0001pt}}}_{L^p(\Omega_2)}^p, \end{align*} $$
$$ \begin{align*} &\left\Vert\Phi^\sharp f\right\Vert{{\hspace{-0.0001pt}}}^p_{L^p\left(\Omega_1, \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p}\right)}\\[10pt]&\quad =\int_{\Omega_1} \left\vert f\circ \Phi \cdot \det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{p} \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p} dV \\[10pt]&\quad =\sum_{\sigma \in \Gamma}\int_{\sigma V} \left\vert f\circ \Phi\right\vert{{\hspace{-0.0001pt}}}^p \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^2 dV= \sum_{\sigma\in \Gamma }\int_{U} \left\vert f\right\vert{{\hspace{-0.0001pt}}}^p dV = \left\vert\Gamma\right\vert\cdot\left\Vert f\right\Vert{{\hspace{-0.0001pt}}}_{L^p(\Omega_2)}^p, \end{align*} $$
where we have used the change of variables formula applied to the biholomorphic map
![]() $\Phi |_{\sigma V}$
along with the fact that the real Jacobian determinant of the map
$\Phi |_{\sigma V}$
along with the fact that the real Jacobian determinant of the map
![]() $\Phi $
is equal to
$\Phi $
is equal to
![]() $\left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^2$
.
$\left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^2$
.
For a general
![]() $f\in L^p(\Omega _2)$
, modify the proof as follows. There is clearly a collection of pairwise disjoint open sets
$f\in L^p(\Omega _2)$
, modify the proof as follows. There is clearly a collection of pairwise disjoint open sets
![]() $\{U_j\}_{j\in J}$
in
$\{U_j\}_{j\in J}$
in
![]() $\Omega _2\setminus Z_2$
such that each
$\Omega _2\setminus Z_2$
such that each
![]() $U_j$
is evenly covered by
$U_j$
is evenly covered by
![]() $\Phi $
and
$\Phi $
and
![]() $\Omega _2 \setminus \bigcup _{j\in J} U_j$
has measure zero. Set
$\Omega _2 \setminus \bigcup _{j\in J} U_j$
has measure zero. Set
![]() $f_j = f\cdot \chi _j$
, where
$f_j = f\cdot \chi _j$
, where
![]() $\chi _j$
is the indicator function of
$\chi _j$
is the indicator function of
![]() $U_j$
, so that each
$U_j$
, so that each
![]() $f_j\in L^p(\Omega _2)$
and
$f_j\in L^p(\Omega _2)$
and
![]() $f=\sum _{j}f_j$
. Also, the functions
$f=\sum _{j}f_j$
. Also, the functions
![]() $\Phi ^\sharp f_j$
have pairwise disjoint supports in
$\Phi ^\sharp f_j$
have pairwise disjoint supports in
![]() $\Omega _1$
. Therefore we have
$\Omega _1$
. Therefore we have
 $$ \begin{align*} \left\Vert\Phi^\sharp f\right\Vert{{\hspace{-0.0001pt}}}^p_{L^p\left(\Omega_1, \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p}\right)}&= \sum_{j\in J} \left\Vert\Phi^\sharp f_j\right\Vert{{\hspace{-0.0001pt}}}^p_{L^p\left(\Omega_1, \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p}\right)} \\[10pt]&= \left\vert\Gamma\right\vert \sum_{j\in J} \left\Vert f_j\right\Vert{{\hspace{-0.0001pt}}}_{L^p(\Omega_2)}^p = \left\vert\Gamma\right\vert \left\Vert f\right\Vert{{\hspace{-0.0001pt}}}_{L^p(\Omega_2)}^p. \end{align*} $$
$$ \begin{align*} \left\Vert\Phi^\sharp f\right\Vert{{\hspace{-0.0001pt}}}^p_{L^p\left(\Omega_1, \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p}\right)}&= \sum_{j\in J} \left\Vert\Phi^\sharp f_j\right\Vert{{\hspace{-0.0001pt}}}^p_{L^p\left(\Omega_1, \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p}\right)} \\[10pt]&= \left\vert\Gamma\right\vert \sum_{j\in J} \left\Vert f_j\right\Vert{{\hspace{-0.0001pt}}}_{L^p(\Omega_2)}^p = \left\vert\Gamma\right\vert \left\Vert f\right\Vert{{\hspace{-0.0001pt}}}_{L^p(\Omega_2)}^p. \end{align*} $$
To complete the proof, we need to show that
![]() $\Phi ^\sharp $
is surjective in both (4.6) and (4.7). Let
$\Phi ^\sharp $
is surjective in both (4.6) and (4.7). Let
![]() $g\in \left [L^p\left (\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p}\right )\right ]^{\Gamma } $
. Let
$g\in \left [L^p\left (\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p}\right )\right ]^{\Gamma } $
. Let
![]() $\{U_j\}_{j\in J}$
be as in the previous paragraph, and set
$\{U_j\}_{j\in J}$
be as in the previous paragraph, and set
![]() $g_j= g\cdot \chi _{\Phi ^{-1}(U_j)}$
, where
$g_j= g\cdot \chi _{\Phi ^{-1}(U_j)}$
, where
![]() $\chi _{\Phi ^{-1}(U_j)}$
is the indicator function of
$\chi _{\Phi ^{-1}(U_j)}$
is the indicator function of
![]() $\Phi ^{-1}(U_j)$
. Notice that
$\Phi ^{-1}(U_j)$
. Notice that
![]() $g_j\in \left [L^p\left (\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p}\right )\right ]^{\Gamma }$
. Let
$g_j\in \left [L^p\left (\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p}\right )\right ]^{\Gamma }$
. Let
![]() $V_j\subset \Phi ^{-1}(U_j)$
be such that
$V_j\subset \Phi ^{-1}(U_j)$
be such that
![]() $\Phi $
maps
$\Phi $
maps
![]() $V_j$
biholomorphically to
$V_j$
biholomorphically to
![]() $U_j$
, and let
$U_j$
, and let
![]() $\Psi : U_j\to V_j$
be the local inverse of
$\Psi : U_j\to V_j$
be the local inverse of
![]() $\Phi $
onto
$\Phi $
onto
![]() $V_j$
. Define
$V_j$
. Define
We claim that
![]() $f_j$
is defined independently of the choice of
$f_j$
is defined independently of the choice of
![]() $V_j$
. Indeed, any other choice is of the form
$V_j$
. Indeed, any other choice is of the form
![]() $\sigma V_j$
for some
$\sigma V_j$
for some
![]() $\sigma \in \Gamma $
and the corresponding local inverse is
$\sigma \in \Gamma $
and the corresponding local inverse is
![]() $\sigma \circ \Psi $
. But we have
$\sigma \circ \Psi $
. But we have
where we have used the fact that
![]() $ \sigma ^\sharp g_j=g_j$
since since
$ \sigma ^\sharp g_j=g_j$
since since
![]() $g_j\in [L^p(\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p})]^{\Gamma }$
.
$g_j\in [L^p(\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p})]^{\Gamma }$
.
Now we define
![]() $f=\sum _{j}f_j$
. Notice that the
$f=\sum _{j}f_j$
. Notice that the
![]() $f_j$
have pairwise disjoint support, and it is easily checked that
$f_j$
have pairwise disjoint support, and it is easily checked that
![]() $\Phi ^\sharp f =g$
. This establishes that (4.6) is a homothetic isomorphism.
$\Phi ^\sharp f =g$
. This establishes that (4.6) is a homothetic isomorphism.
It is clear that if f is holomorphic on
![]() $\Omega _2$
, then
$\Omega _2$
, then
![]() $\Phi ^\sharp f$
is holomorphic on
$\Phi ^\sharp f$
is holomorphic on
![]() $\Omega _1$
, therefore,
$\Omega _1$
, therefore,
![]() $\Phi ^\sharp $
maps
$\Phi ^\sharp $
maps
![]() $A^p(\Omega _2)$
into
$A^p(\Omega _2)$
into
![]() $[A^p(\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p})]^{\Gamma }$
. Now, in the argument in the previous paragraph showing that the image
$[A^p(\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p})]^{\Gamma }$
. Now, in the argument in the previous paragraph showing that the image
![]() $\Phi ^\sharp (L^p(\Omega _2))$
is
$\Phi ^\sharp (L^p(\Omega _2))$
is
![]() $[L^p(\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p})]^{\Gamma }$
, local definition of the inverse map (4.9) shows that if
$[L^p(\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p})]^{\Gamma }$
, local definition of the inverse map (4.9) shows that if
![]() $g\in [A^p(\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p})]^{\Gamma }$
, then the f constructed by this procedure is holomorphic, and therefore lies in
$g\in [A^p(\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p})]^{\Gamma }$
, then the f constructed by this procedure is holomorphic, and therefore lies in
![]() $A^p(\Omega _2)$
. This completes the proof of the proposition. ▪
$A^p(\Omega _2)$
. This completes the proof of the proposition. ▪
4.3 Bell transformation law for quotient maps
The following is a refinement (for the class of proper holomorphic maps of quotient type) of a classic result of Bell (see [Reference BellBel81, Theorem 1], [Reference BellBel82, Equation 2.2]).
Proposition 4.10 Let
![]() $\Omega _1,\Omega _2$
be domains in
$\Omega _1,\Omega _2$
be domains in
![]() ${\mathbb {C}}^n$
and let
${\mathbb {C}}^n$
and let
![]() $\Phi :\Omega _1\to \Omega _2$
be a proper holomorphic map of quotient type with group
$\Phi :\Omega _1\to \Omega _2$
be a proper holomorphic map of quotient type with group
![]() $\Gamma \subset \mathrm {Aut}(\Omega _1)$
. Then the following diagram commutes:
$\Gamma \subset \mathrm {Aut}(\Omega _1)$
. Then the following diagram commutes:

In order to prove the proposition, we need the following simple lemma, which shows that the Bergman projection interacts well with the action of automorphisms:
Lemma 4.12 Let
![]() $\Omega \subset {\mathbb {C}}^n$
be a domain, and let
$\Omega \subset {\mathbb {C}}^n$
be a domain, and let
![]() $\boldsymbol {B}_\Omega $
be its Bergman projection operator.
$\boldsymbol {B}_\Omega $
be its Bergman projection operator.
-
(1) If
 $\sigma \in \mathrm {Aut}(\Omega )$
is a biholomorphic automorphism, then (4.13)
$\sigma \in \mathrm {Aut}(\Omega )$
is a biholomorphic automorphism, then (4.13) $$ \begin{align} \boldsymbol{B}_{\Omega}\circ \sigma^\sharp = \sigma^\sharp \circ \boldsymbol{B}_{\Omega}. \end{align} $$
$$ \begin{align} \boldsymbol{B}_{\Omega}\circ \sigma^\sharp = \sigma^\sharp \circ \boldsymbol{B}_{\Omega}. \end{align} $$
-
(2) If
 $G\subset \operatorname {\mathrm {Aut}}(\Omega )$
is a group of biholomorphic automorphisms, then
$G\subset \operatorname {\mathrm {Aut}}(\Omega )$
is a group of biholomorphic automorphisms, then
 $\boldsymbol {B}_{\Omega }$
restricts to the orthogonal projection operator from
$\boldsymbol {B}_{\Omega }$
restricts to the orthogonal projection operator from
 $[L^2(\Omega )]^G$
onto
$[L^2(\Omega )]^G$
onto
 $[A^2(\Omega )]^G$
.
$[A^2(\Omega )]^G$
.
Proof For (1), note that
![]() $\sigma ^\sharp $
is a unitary operator on
$\sigma ^\sharp $
is a unitary operator on
![]() $L^2(\Omega )$
and
$L^2(\Omega )$
and
![]() $\boldsymbol {B}_{\Omega }$
is an orthogonal projection on
$\boldsymbol {B}_{\Omega }$
is an orthogonal projection on
![]() $L^2(\Omega )$
, therefore the unitarily similar operator
$L^2(\Omega )$
, therefore the unitarily similar operator
![]() $Q=\sigma ^\sharp \circ \boldsymbol {B}_{\Omega }\circ (\sigma ^\sharp )^{-1}$
is also an orthogonal projection. Since
$Q=\sigma ^\sharp \circ \boldsymbol {B}_{\Omega }\circ (\sigma ^\sharp )^{-1}$
is also an orthogonal projection. Since
![]() $ \sigma ^\sharp $
(and therefore its inverse) leaves
$ \sigma ^\sharp $
(and therefore its inverse) leaves
![]() $A^2(\Omega )$
invariant, it follows that the range of Q is
$A^2(\Omega )$
invariant, it follows that the range of Q is
![]() $A^2(\Omega )$
. Therefore,
$A^2(\Omega )$
. Therefore,
![]() $Q=\boldsymbol {B}_{\Omega }$
.
$Q=\boldsymbol {B}_{\Omega }$
.
For (2), let
![]() $f\in [L^2(\Omega )]^G$
. Then using (4.13), we have for
$f\in [L^2(\Omega )]^G$
. Then using (4.13), we have for
![]() $\sigma \in G$
$\sigma \in G$
which shows that
![]() $\boldsymbol {B}_{\Omega }f\in [A^2(\Omega )]^G$
, so that
$\boldsymbol {B}_{\Omega }f\in [A^2(\Omega )]^G$
, so that
![]() $\boldsymbol {B}_{\Omega }$
maps the G-invariant functions
$\boldsymbol {B}_{\Omega }$
maps the G-invariant functions
![]() $[L^2(\Omega )]^G$
into the G-invariant holomorphic functions
$[L^2(\Omega )]^G$
into the G-invariant holomorphic functions
![]() $[A^2(\Omega )]^G$
. Since
$[A^2(\Omega )]^G$
. Since
![]() $\boldsymbol {B}_\Omega $
restricts to the identity on
$\boldsymbol {B}_\Omega $
restricts to the identity on
![]() $[A^2(\Omega )]^G$
, it follows that the range of
$[A^2(\Omega )]^G$
, it follows that the range of
![]() $\boldsymbol {B}_{\Omega }$
is
$\boldsymbol {B}_{\Omega }$
is
![]() $[A^2(\Omega )]^G$
. Observe that
$[A^2(\Omega )]^G$
. Observe that
which shows that kernel of the restriction of
![]() $\boldsymbol {B}_{\Omega }$
to
$\boldsymbol {B}_{\Omega }$
to
![]() $[L^2(\Omega )]^G$
is orthogonal to its range, and therefore an orthogonal projection. ▪
$[L^2(\Omega )]^G$
is orthogonal to its range, and therefore an orthogonal projection. ▪
Proof of Proposition 4.10 By Proposition 4.5, the
![]() $\Phi ^\sharp $
represented by the top (resp. bottom) horizontal arrow is a homothetic isomorphism from the Hilbert space
$\Phi ^\sharp $
represented by the top (resp. bottom) horizontal arrow is a homothetic isomorphism from the Hilbert space
![]() $ {L}^2(\Omega _2)$
(resp.
$ {L}^2(\Omega _2)$
(resp.
![]() $ {A}^2(\Omega _2)$
) onto the Hilbert space
$ {A}^2(\Omega _2)$
) onto the Hilbert space
![]() $[{L}^2(\Omega _1)]^\Gamma $
(resp.
$[{L}^2(\Omega _1)]^\Gamma $
(resp.
![]() $[{A}^2(\Omega _1)]^\Gamma $
). Therefore,
$[{A}^2(\Omega _1)]^\Gamma $
). Therefore,
![]() $\Phi ^\sharp $
preserves angles and in particular orthogonality. Now consider the map
$\Phi ^\sharp $
preserves angles and in particular orthogonality. Now consider the map
![]() $ P: [{L}^2(\Omega _1)]^\Gamma \to [{A}^2(\Omega _1)]^\Gamma $
defined by
$ P: [{L}^2(\Omega _1)]^\Gamma \to [{A}^2(\Omega _1)]^\Gamma $
defined by
which, being a composition of continuous linear maps, is a continuous linear mapping of Hilbert spaces. Notice that
so P is a projection in
![]() $[{L}^2(\Omega _1)]^\Gamma $
, with range contained in
$[{L}^2(\Omega _1)]^\Gamma $
, with range contained in
![]() $[{A}^2(\Omega _1)]^\Gamma $
. Since
$[{A}^2(\Omega _1)]^\Gamma $
. Since
![]() $(\Phi ^\sharp )^{-1}$
and
$(\Phi ^\sharp )^{-1}$
and
![]() $\Phi ^\sharp |_{A^2(\Omega )}$
are isomorphisms, and
$\Phi ^\sharp |_{A^2(\Omega )}$
are isomorphisms, and
![]() $\boldsymbol {B}_{\Omega _2}$
is surjective, it follows that P is a projection onto
$\boldsymbol {B}_{\Omega _2}$
is surjective, it follows that P is a projection onto
![]() $[{A}^2(\Omega _1)]^\Gamma $
. We claim that P is in fact the orthogonal projection on to
$[{A}^2(\Omega _1)]^\Gamma $
. We claim that P is in fact the orthogonal projection on to
![]() $[{A}^2(\Omega _1)]^\Gamma $
, i.e., the kernel of P is
$[{A}^2(\Omega _1)]^\Gamma $
, i.e., the kernel of P is
![]() $\left ([{A}^2(\Omega _1)]^\Gamma \right )^\perp $
, the orthogonal complement of
$\left ([{A}^2(\Omega _1)]^\Gamma \right )^\perp $
, the orthogonal complement of
![]() $[{A}^2(\Omega _1)]^\Gamma $
in
$[{A}^2(\Omega _1)]^\Gamma $
in
![]() $[{L}^2(\Omega _1)]^\Gamma $
. Since in formula (4.14), the maps
$[{L}^2(\Omega _1)]^\Gamma $
. Since in formula (4.14), the maps
![]() $(\Phi ^\sharp )^{-1}$
and
$(\Phi ^\sharp )^{-1}$
and
![]() $\Phi ^\sharp $
are isomorphisms, it follows that
$\Phi ^\sharp $
are isomorphisms, it follows that
![]() $f\in \ker P$
if and only if
$f\in \ker P$
if and only if
![]() $(\Phi ^\sharp )^{-1}f\in \ker \boldsymbol {B}_{\Omega _2}$
. But
$(\Phi ^\sharp )^{-1}f\in \ker \boldsymbol {B}_{\Omega _2}$
. But
![]() $\ker \boldsymbol {B}_{\Omega _2}= A^2(\Omega _2)^\perp $
, since the Bergman projection is orthogonal. It follows that
$\ker \boldsymbol {B}_{\Omega _2}= A^2(\Omega _2)^\perp $
, since the Bergman projection is orthogonal. It follows that
![]() $\ker P = \Phi ^\sharp (A^2(\Omega _2)^\perp )$
. Notice that
$\ker P = \Phi ^\sharp (A^2(\Omega _2)^\perp )$
. Notice that
![]() $\Phi ^\sharp $
, being a homothetic isomorphism of Hilbert spaces, preserves orthogonality, and maps
$\Phi ^\sharp $
, being a homothetic isomorphism of Hilbert spaces, preserves orthogonality, and maps
![]() $A^2(\Omega _2)$
to
$A^2(\Omega _2)$
to
![]() $[{A}^2(\Omega _1)]^\Gamma $
isomorphically, therefore,
$[{A}^2(\Omega _1)]^\Gamma $
isomorphically, therefore,
![]() $\Phi ^\sharp ( (A^2(\Omega _2))^\perp )= \left ([{A}^2(\Omega _1)]^\Gamma \right )^\perp $
, which establishes the claim.
$\Phi ^\sharp ( (A^2(\Omega _2))^\perp )= \left ([{A}^2(\Omega _1)]^\Gamma \right )^\perp $
, which establishes the claim.
Therefore, we have shown that
![]() $P=\Phi ^\sharp \circ \boldsymbol {B}_{\Omega _2}\circ (\Phi ^\sharp )^{-1}$
is the orthogonal projection from
$P=\Phi ^\sharp \circ \boldsymbol {B}_{\Omega _2}\circ (\Phi ^\sharp )^{-1}$
is the orthogonal projection from
![]() $ [{L}^2(\Omega _1)]^\Gamma $
to the subspace
$ [{L}^2(\Omega _1)]^\Gamma $
to the subspace
![]() $[{A}^2(\Omega _1)]^\Gamma $
. To complete the proof, we only need to show that the restriction of the Bergman projection
$[{A}^2(\Omega _1)]^\Gamma $
. To complete the proof, we only need to show that the restriction of the Bergman projection
![]() $\boldsymbol {B}_{\Omega _1}$
to the
$\boldsymbol {B}_{\Omega _1}$
to the
![]() $\Gamma $
-invariant subspace
$\Gamma $
-invariant subspace
![]() $[{L}^2(\Omega _1)]^\Gamma $
is also the orthogonal projection from
$[{L}^2(\Omega _1)]^\Gamma $
is also the orthogonal projection from
![]() $[{L}^2(\Omega _1)]^\Gamma $
onto
$[{L}^2(\Omega _1)]^\Gamma $
onto
![]() $[{A}^2(\Omega _1)]^\Gamma $
. But this follows from Lemma 4.12 above.
$[{A}^2(\Omega _1)]^\Gamma $
. But this follows from Lemma 4.12 above.
Thus
![]() $P=\boldsymbol {B}_{\Omega _1}|_{[L^2(\Omega _1)]^\Gamma }$
, and the commutativity of (4.11) follows. ▪
$P=\boldsymbol {B}_{\Omega _1}|_{[L^2(\Omega _1)]^\Gamma }$
, and the commutativity of (4.11) follows. ▪
4.4 Transformation of the Bergman projection in
 $L^p$
-spaces
$L^p$
-spaces
The following result will be our main tool on studying
![]() $L^p$
-regularity of the Bergman projection in the domain
$L^p$
-regularity of the Bergman projection in the domain
![]() $\mathscr {U}$
:
$\mathscr {U}$
:
Theorem 4.15 Let
![]() $\Omega _1,\Omega _2$
be bounded domains in
$\Omega _1,\Omega _2$
be bounded domains in
![]() ${\mathbb {C}}^n$
, let
${\mathbb {C}}^n$
, let
![]() $\Phi :\Omega _1\to \Omega _2$
be a proper holomorphic map of quotient type with group
$\Phi :\Omega _1\to \Omega _2$
be a proper holomorphic map of quotient type with group
![]() $\Gamma \subset \mathrm {Aut}(\Omega _1)$
. Let
$\Gamma \subset \mathrm {Aut}(\Omega _1)$
. Let
![]() $p\geq 1$
. The following two assertions are equivalent:
$p\geq 1$
. The following two assertions are equivalent:
-
(1) The Bergman projection
 $\boldsymbol {B}_{\Omega _2}$
gives rise to a bounded operator mapping
$\boldsymbol {B}_{\Omega _2}$
gives rise to a bounded operator mapping  $$ \begin{align*}L^p(\Omega_2) \to A^p(\Omega_2).\end{align*} $$
$$ \begin{align*}L^p(\Omega_2) \to A^p(\Omega_2).\end{align*} $$
-
(2) The Bergman projection
 $\boldsymbol {B}_{\Omega _1}$
gives rise to a bounded operator mapping
$\boldsymbol {B}_{\Omega _1}$
gives rise to a bounded operator mapping  $$ \begin{align*}\left[L^p\left(\Omega_1, \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p}\right)\right]^{\Gamma} \to \left[A^p\left(\Omega_1, \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p}\right)\right]^{\Gamma}.\end{align*} $$
$$ \begin{align*}\left[L^p\left(\Omega_1, \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p}\right)\right]^{\Gamma} \to \left[A^p\left(\Omega_1, \left\vert\det \Phi'\right\vert{{\hspace{-0.0001pt}}}^{2-p}\right)\right]^{\Gamma}.\end{align*} $$
If one of the conditions (
1
) or (
2
) holds (and therefore both hold), then the following diagram commutes, where
![]() $\boldsymbol {B}_{\Omega _j}, j=1,2$
denote the extension by continuity of the Bergman projections:
$\boldsymbol {B}_{\Omega _j}, j=1,2$
denote the extension by continuity of the Bergman projections:

Remark Statement (1) in Theorem 4.15 means the following: the restriction of the Bergman projection to a dense subspace of
![]() $L^p(\Omega _2)$
given by
$L^p(\Omega _2)$
given by
is bounded in the
![]() $L^p$
-norm, i.e., there is a
$L^p$
-norm, i.e., there is a
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $f\in L^2(\Omega _2)\cap L^p(\Omega _2)$
,
$f\in L^2(\Omega _2)\cap L^p(\Omega _2)$
,
By continuity
![]() $\boldsymbol {B}_{\Omega _2}$
extends to a bounded linear operator from
$\boldsymbol {B}_{\Omega _2}$
extends to a bounded linear operator from
![]() $L^p(\Omega _2)$
to
$L^p(\Omega _2)$
to
![]() $A^p(\Omega _2)$
.
$A^p(\Omega _2)$
.
Similarly, Statement (2) means the following: the restriction of the Bergman projection to the dense subspace of
![]() $\left [L^p\left (\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p}\right )\right ]^{\Gamma }$
given by
$\left [L^p\left (\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p}\right )\right ]^{\Gamma }$
given by
is bounded in the
![]() $L^p\left (\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p}\right )$
-norm, i.e., there is a
$L^p\left (\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p}\right )$
-norm, i.e., there is a
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $f\in [L^2(\Omega _1)]^\Gamma \cap \left [L^p\left (\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p}\right )\right ]^{\Gamma }$
,
$f\in [L^2(\Omega _1)]^\Gamma \cap \left [L^p\left (\Omega _1, \left \vert \det \Phi '\right \vert {{\hspace{-0.0001pt}}}^{2-p}\right )\right ]^{\Gamma }$
,
We now see by Lemma 4.12 that
where we have used continuity to extend the operator.
Proof Proposition 4.5 says that
![]() $\Phi ^\sharp $
is a homothetic isomorphism, mapping
$\Phi ^\sharp $
is a homothetic isomorphism, mapping
and that it restricts to a homothetic isomorphism on the holomorphic subspaces. Similarly,
![]() $(\Phi ^\sharp )^{-1}$
has the same properties with the domains and ranges switched.
$(\Phi ^\sharp )^{-1}$
has the same properties with the domains and ranges switched.
First assume Statement (2). From the diagram (4.11), we write
By hypothesis,
![]() $\boldsymbol {B}_{\Omega _1}$
is a bounded linear operator mapping
$\boldsymbol {B}_{\Omega _1}$
is a bounded linear operator mapping
Consequently, this composition maps
![]() $L^p(\Omega _2)$
boundedly into
$L^p(\Omega _2)$
boundedly into
![]() $A^p(\Omega _2)$
, giving statement (1). A similar argument shows that (1) implies (2).
$A^p(\Omega _2)$
, giving statement (1). A similar argument shows that (1) implies (2).
For the commutativity of the diagram, rewrite (4.17) and see that on the subspace
![]() $L^p(\Omega _2)\cap L^2(\Omega _2)$
of
$L^p(\Omega _2)\cap L^2(\Omega _2)$
of
![]() $L^p(\Omega _2)$
we have the relation
$L^p(\Omega _2)$
we have the relation
Using the hypothesis (for the
![]() $\boldsymbol {B}_{\Omega _j}$
) and Proposition 4.5 (for
$\boldsymbol {B}_{\Omega _j}$
) and Proposition 4.5 (for
![]() $\Phi ^\sharp $
), we see that each of the four maps in the diagram (4.16) extends to the respective domain in that diagram and is continuous. By continuity, (4.18) continues to hold for the extended maps. This shows that the diagram (4.16) is commutative. ▪
$\Phi ^\sharp $
), we see that each of the four maps in the diagram (4.16) extends to the respective domain in that diagram and is continuous. By continuity, (4.18) continues to hold for the extended maps. This shows that the diagram (4.16) is commutative. ▪
Remark Diagram (4.11) is a special case of diagram (4.16) for
![]() $p=2$
.
$p=2$
.
5 The unboundedness of the Bergman projection on
 $\mathscr {U}$
$\mathscr {U}$
Using Proposition 5.1 and the results of Section 4, we will prove in this section the following partial form of Theorem 1.2:
Proposition 5.1 The Bergman projection is not bounded in
![]() $L^p(\mathscr {U})$
, provided
$L^p(\mathscr {U})$
, provided
 $$ \begin{align} p \geq \frac{2\kappa(\mathscr{U})}{\kappa(\mathscr{U})-1}, \end{align} $$
$$ \begin{align} p \geq \frac{2\kappa(\mathscr{U})}{\kappa(\mathscr{U})-1}, \end{align} $$
where
![]() $\kappa (\mathscr {U})\in \mathbb {N}$
is the complexity of the domain
$\kappa (\mathscr {U})\in \mathbb {N}$
is the complexity of the domain
![]() $\mathscr {U}$
, as defined in Section 1.1.
$\mathscr {U}$
, as defined in Section 1.1.
5.1 Reinhardt domains
Recall some elementary facts about holomorphic function theory on Reinhardt domains (which are always assumed to be centered at the origin). Let
![]() $\Omega \subset \mathbb {C}^n$
be a Reinhardt domain. Every holomorphic function
$\Omega \subset \mathbb {C}^n$
be a Reinhardt domain. Every holomorphic function
![]() $f\in \mathcal {O}(\Omega )$
admits a unique Laurent expansion
$f\in \mathcal {O}(\Omega )$
admits a unique Laurent expansion
where for
![]() $\alpha \in (\mathbb {Z}^n)^\dagger $
,
$\alpha \in (\mathbb {Z}^n)^\dagger $
,
![]() $\varphi _\alpha (z)$
is the Laurent monomial
$\varphi _\alpha (z)$
is the Laurent monomial
![]() $z^\alpha $
as in (2.4), and where
$z^\alpha $
as in (2.4), and where
![]() $a_\alpha (f) \in \mathbb C$
is the
$a_\alpha (f) \in \mathbb C$
is the
![]() $\alpha $
th Laurent coefficient. The Laurent series of f converges absolutely and uniformly to f on every compact subset of
$\alpha $
th Laurent coefficient. The Laurent series of f converges absolutely and uniformly to f on every compact subset of
![]() $\Omega $
.
$\Omega $
.
When f lies in the Bergman space
![]() $A^2(\Omega )$
, we can say more about the series (5.3): it is actually an orthogonal series converging in the Hilbert space
$A^2(\Omega )$
, we can say more about the series (5.3): it is actually an orthogonal series converging in the Hilbert space
![]() $A^2(\Omega )$
, and the family of monomials
$A^2(\Omega )$
, and the family of monomials
 $$ \begin{align} {\left\{\dfrac{\varphi_\alpha}{\left\Vert\varphi_\alpha\right\Vert{{\hspace{-0.0001pt}}}_{L^2}}: \varphi_\alpha\in L^2(\Omega)\right\}} \end{align} $$
$$ \begin{align} {\left\{\dfrac{\varphi_\alpha}{\left\Vert\varphi_\alpha\right\Vert{{\hspace{-0.0001pt}}}_{L^2}}: \varphi_\alpha\in L^2(\Omega)\right\}} \end{align} $$
forms an orthonormal basis of
![]() $A^2(\Omega )$
. In particular, if
$A^2(\Omega )$
. In particular, if
![]() $f\in A^2(\Omega )$
then the Laurent series (5.3) can have
$f\in A^2(\Omega )$
then the Laurent series (5.3) can have
![]() $a_\alpha (f){\neq }0$
only when
$a_\alpha (f){\neq }0$
only when
![]() $\varphi _\alpha \in L^2(\Omega )$
. It is possible to generalize some of these results to the spaces
$\varphi _\alpha \in L^2(\Omega )$
. It is possible to generalize some of these results to the spaces
![]() $A^p(\Omega )$
; see [Reference Chakrabarti, Edholm and McNealCEM19].
$A^p(\Omega )$
; see [Reference Chakrabarti, Edholm and McNealCEM19].
5.2 A criterion for unboundedness of the Bergman projection
We now give an easily checkable condition which shows
![]() $L^p$
-Bergman unboundedness on any Reinhardt domain.
$L^p$
-Bergman unboundedness on any Reinhardt domain.
Lemma 5.5 Let
![]() $\Omega $
be a bounded Reinhardt domain in
$\Omega $
be a bounded Reinhardt domain in
![]() ${\mathbb {C}}^n$
, and let
${\mathbb {C}}^n$
, and let
![]() $p\geq 2$
. Suppose that there is a multi-index
$p\geq 2$
. Suppose that there is a multi-index
![]() $\beta \in (\mathbb {Z}^n)^\dagger $
such that
$\beta \in (\mathbb {Z}^n)^\dagger $
such that
Then the Bergman projection
![]() $\boldsymbol {B}_\Omega $
fails to map
$\boldsymbol {B}_\Omega $
fails to map
![]() $L^p(\Omega ) \to L^p(\Omega )$
.
$L^p(\Omega ) \to L^p(\Omega )$
.
Proof Define subsets
![]() $\mathcal {J}_\beta , \mathcal {K}_\beta \subset \{1,2,\cdots ,n \}$
with
$\mathcal {J}_\beta , \mathcal {K}_\beta \subset \{1,2,\cdots ,n \}$
with
and let
 $$ \begin{align*} f(w)= \prod_{j\in \mathcal{J}_\beta} w_j^{\beta_j} \times \prod_{k\in \mathcal{K}_\beta } \left(\overline{w_k}\right)^{-\beta_k}. \end{align*} $$
$$ \begin{align*} f(w)= \prod_{j\in \mathcal{J}_\beta} w_j^{\beta_j} \times \prod_{k\in \mathcal{K}_\beta } \left(\overline{w_k}\right)^{-\beta_k}. \end{align*} $$
Then f is a bounded function on
![]() $\Omega $
, and therefore
$\Omega $
, and therefore
![]() $f \in L^p(\Omega )$
. We now show that
$f \in L^p(\Omega )$
. We now show that
![]() $\boldsymbol {B}_\Omega f = C \varphi _\beta $
for some
$\boldsymbol {B}_\Omega f = C \varphi _\beta $
for some
![]() $C{\neq }0$
. Since
$C{\neq }0$
. Since
![]() $\varphi _\beta \not \in L^p(\Omega )$
, this will show that
$\varphi _\beta \not \in L^p(\Omega )$
, this will show that
![]() $\boldsymbol {B}_\Omega $
fails to map the element
$\boldsymbol {B}_\Omega $
fails to map the element
![]() $f\in L^p(\Omega )$
to a function in
$f\in L^p(\Omega )$
to a function in
![]() $L^p(\Omega )$
. This will imply that
$L^p(\Omega )$
. This will imply that
![]() $ \boldsymbol {B}_\Omega $
is not bounded in the
$ \boldsymbol {B}_\Omega $
is not bounded in the
![]() $L^p$
-norm, since if it were so, it would extend to a map from the dense subspace
$L^p$
-norm, since if it were so, it would extend to a map from the dense subspace
![]() $L^p(\Omega )\cap L^2(\Omega )$
to the whole of
$L^p(\Omega )\cap L^2(\Omega )$
to the whole of
![]() $L^p(\Omega )$
.
$L^p(\Omega )$
.
Let
![]() $\gamma =(\left \vert \beta _1\right \vert , \dots , \left \vert \beta _n\right \vert )\in \mathbb {N}^n$
be the multi-index obtained by replacing each entry of
$\gamma =(\left \vert \beta _1\right \vert , \dots , \left \vert \beta _n\right \vert )\in \mathbb {N}^n$
be the multi-index obtained by replacing each entry of
![]() $\beta $
by its absolute value. Write the polar form of w as
$\beta $
by its absolute value. Write the polar form of w as
![]() $w=\rho (w)\odot \exp (i\theta )$
for a
$w=\rho (w)\odot \exp (i\theta )$
for a
![]() $\theta \in {\mathbb {R}}^n$
. Then
$\theta \in {\mathbb {R}}^n$
. Then
![]() $ f(w) = \rho (w)^\gamma e^{i \beta \theta }, $
and for
$ f(w) = \rho (w)^\gamma e^{i \beta \theta }, $
and for
![]() $\alpha \in (\mathbb {Z}^n)^\dagger $
, we have
$\alpha \in (\mathbb {Z}^n)^\dagger $
, we have
Further, denote by
![]() $\left \vert \Omega \right \vert =\{\rho (z):z\in \Omega \}\subset {\mathbb {R}}^n$
the Reinhardt shadow of
$\left \vert \Omega \right \vert =\{\rho (z):z\in \Omega \}\subset {\mathbb {R}}^n$
the Reinhardt shadow of
![]() $\Omega $
, and let
$\Omega $
, and let
![]() $\mathbb {T}^n$
be the unit torus of n dimensions. Then, for each
$\mathbb {T}^n$
be the unit torus of n dimensions. Then, for each
![]() $\alpha \in \mathbb {Z}^n $
, we have
$\alpha \in \mathbb {Z}^n $
, we have

Since (5.4) is an orthonormal basis of
![]() $A^2(\Omega )$
it follows that all the Fourier coefficients of
$A^2(\Omega )$
it follows that all the Fourier coefficients of
![]() $\boldsymbol {B}_\Omega f$
with respect this basis vanish, except the
$\boldsymbol {B}_\Omega f$
with respect this basis vanish, except the
![]() $\beta $
th coefficient, which is nonzero. Therefore,
$\beta $
th coefficient, which is nonzero. Therefore,
![]() $\boldsymbol {B}_\Omega f = C \varphi _\beta \notin L^p(\Omega ), $
for some constant
$\boldsymbol {B}_\Omega f = C \varphi _\beta \notin L^p(\Omega ), $
for some constant
![]() $C{\neq }0$
. ▪
$C{\neq }0$
. ▪
5.3 Preliminaries
In this section (and the following Section 6), we will use the following default notation and conventions:
-
(1)
 $B\in M_n(\mathbb {Z})$
is a matrix such that the domain
$B\in M_n(\mathbb {Z})$
is a matrix such that the domain
 $\mathscr {U}$
is represented as in (3.1),
$\mathscr {U}$
is represented as in (3.1), -
(2) B satisfies the properties (3.3), which is not a loss of generality by Proposition 3.2.
-
(3) We have
 $A= \operatorname {\mathrm {adj}} B$
.
$A= \operatorname {\mathrm {adj}} B$
.
Observe that then by Theorem 3.12, the monomial map
![]() $\Phi _A$
is a proper holomorphic map of quotient type.
$\Phi _A$
is a proper holomorphic map of quotient type.
We note the following computation:
Proposition 5.7 The upper bound in ( 1.3 ) is given by

where, as usual,
![]() $a_j$
is the jth column of the matrix A, where notation is as above.
$a_j$
is the jth column of the matrix A, where notation is as above.
Proof Recall the definition of the projective height function as in (1.4). Then we have, by projective invariance, for each
![]() $1\leq j \leq n$
:
$1\leq j \leq n$
:
Since
![]() $A\succ 0$
, it follows that
$A\succ 0$
, it follows that
![]() $a_j$
is a vector of non-negative integers, and the vector
$a_j$
is a vector of non-negative integers, and the vector
![]() $\frac {1}{\gcd (a_j)}a_j$
is such that its entries are coprime non-negative integers. Therefore,
$\frac {1}{\gcd (a_j)}a_j$
is such that its entries are coprime non-negative integers. Therefore,

So

Since the function
![]() $x\mapsto \dfrac {2x}{x-1}$
is strictly decreasing for
$x\mapsto \dfrac {2x}{x-1}$
is strictly decreasing for
![]() $x>1$
, we have
$x>1$
, we have

▪
5.4 p-allowable multi-indices
Let
![]() $\beta \in (\mathbb {Z}^n)^\dagger $
be a multi-index. We say that
$\beta \in (\mathbb {Z}^n)^\dagger $
be a multi-index. We say that
![]() $\beta $
is p-allowable on a Reinhardt domain
$\beta $
is p-allowable on a Reinhardt domain
![]() $\Omega $
if we have that the monomial
$\Omega $
if we have that the monomial
![]() $\varphi _\beta \in L^p(\Omega )$
, i.e.,
$\varphi _\beta \in L^p(\Omega )$
, i.e.,
We denote the collection of p-allowable multi-indices on
![]() $\Omega $
by
$\Omega $
by
![]() $\mathscr {S}_p(\Omega )$
. We first compute the p-allowable multi-indices on the domain
$\mathscr {S}_p(\Omega )$
. We first compute the p-allowable multi-indices on the domain
![]() $\mathscr {U}$
. Recall that the conventions introduced in Section 5.3 are in force.
$\mathscr {U}$
. Recall that the conventions introduced in Section 5.3 are in force.
Proposition 5.9 Let
![]() $\beta \in (\mathbb {Z}^n)^\dagger $
and
$\beta \in (\mathbb {Z}^n)^\dagger $
and
![]() $p>0$
. Then
$p>0$
. Then
![]() $\beta \in \mathscr {S}_p(\mathscr {U})$
if and only if
$\beta \in \mathscr {S}_p(\mathscr {U})$
if and only if
Proof By Theorem 3.12,
![]() $\Phi _A:\mathbb {D}^n_{\mathsf {L}(B)}\to \mathscr {U}$
is a proper holomorphic map of quotient type with
$\Phi _A:\mathbb {D}^n_{\mathsf {L}(B)}\to \mathscr {U}$
is a proper holomorphic map of quotient type with
![]() $\det A$
sheets. Therefore, by Proposition 4.5 (in particular (4.8)) we see that
$\det A$
sheets. Therefore, by Proposition 4.5 (in particular (4.8)) we see that

where
![]() $a_j \in \mathbb Z^n$
is the jth column of A. It is clear that
$a_j \in \mathbb Z^n$
is the jth column of A. It is clear that
![]() $\int _{\mathscr {U}} \left \vert \varphi _\beta \right \vert {{\hspace{-0.0001pt}}}^p dV<\infty $
if and only if
$\int _{\mathscr {U}} \left \vert \varphi _\beta \right \vert {{\hspace{-0.0001pt}}}^p dV<\infty $
if and only if
for each
![]() $1\leq j \leq n$
. This completes the proof. ▪
$1\leq j \leq n$
. This completes the proof. ▪
Remark The above proposition can be seen as a special case of [Reference ZwonekZwo00, Lemma 2.2.1].
We now consider the important case
![]() $p=2$
, so that
$p=2$
, so that
![]() $\mathscr {S}_2(\Omega )$
corresponds to the monomials in the Bergman space. For a matrix
$\mathscr {S}_2(\Omega )$
corresponds to the monomials in the Bergman space. For a matrix
![]() $A\in M_n(\mathbb {Z})$
, none of whose columns are zero, denote by
$A\in M_n(\mathbb {Z})$
, none of whose columns are zero, denote by
![]() $\gcd (a_j)$
the greatest common divisor of the entries in the jth column of A. We then let
$\gcd (a_j)$
the greatest common divisor of the entries in the jth column of A. We then let
be the integer row vector whose jth entry is the greatest common divisor of the jth column of A.
-
(1) Let
 $\beta \in (\mathbb {Z}^n)^\dagger $
. Then
$\beta \in (\mathbb {Z}^n)^\dagger $
. Then
 $\beta \in \mathscr {S}_2(\mathscr {U})$
if and only if (5.13)
$\beta \in \mathscr {S}_2(\mathscr {U})$
if and only if (5.13)
-
(2) For
 $1\leq j \leq n$
let
$1\leq j \leq n$
let
 $\Pi _j$
be the integer hypersurface determined by equality in the jth entry of (5.13), that is (5.14)Then we have
$\Pi _j$
be the integer hypersurface determined by equality in the jth entry of (5.13), that is (5.14)Then we have
 $$ \begin{align*} \Pi_j\cap \mathscr{S}_2(\mathscr{U}){\neq}\emptyset.\end{align*} $$
$$ \begin{align*} \Pi_j\cap \mathscr{S}_2(\mathscr{U}){\neq}\emptyset.\end{align*} $$
The following Lemma will be needed in the proof of part (2) of the proposition.
Lemma 5.15 Let P be an
![]() $m\times n$
integer matrix of rank m for positive integers
$m\times n$
integer matrix of rank m for positive integers
![]() $n\geq m$
, and let
$n\geq m$
, and let
![]() $q\in (\mathbb {Z}^n)^\dagger $
. Then there is an
$q\in (\mathbb {Z}^n)^\dagger $
. Then there is an
![]() $x\in (\mathbb {Z}^m)^\dagger $
such that
$x\in (\mathbb {Z}^m)^\dagger $
such that
![]() $xP\succeq q$
.
$xP\succeq q$
.
Proof Let
![]() $\mathcal {O}=\{x\in ({\mathbb {R}}^m)^\dagger :xP\succeq q \} .$
Then
$\mathcal {O}=\{x\in ({\mathbb {R}}^m)^\dagger :xP\succeq q \} .$
Then
![]() $\mathcal {O}$
is an unbounded convex set, so at least one of the coordinates
$\mathcal {O}$
is an unbounded convex set, so at least one of the coordinates
![]() $x_1,\dots , x_m$
is unbounded on
$x_1,\dots , x_m$
is unbounded on
![]() $\mathcal {O}$
. Rename the coordinates so that
$\mathcal {O}$
. Rename the coordinates so that
![]() $x_1$
is unbounded. It follows that the projection
$x_1$
is unbounded. It follows that the projection
of
![]() $\mathcal {O}$
on the coordinate axis
$\mathcal {O}$
on the coordinate axis
![]() $x_1$
is an unbounded convex set, and therefore a ray or the whole of
$x_1$
is an unbounded convex set, and therefore a ray or the whole of
![]() ${\mathbb {R}}$
. For an integer N let
${\mathbb {R}}$
. For an integer N let
![]() $C_N=\{x_1=N\}\cap \mathcal {O}$
, which is naturally thought of as a subset of
$C_N=\{x_1=N\}\cap \mathcal {O}$
, which is naturally thought of as a subset of
![]() $({\mathbb {R}}^{m-1})^\dagger $
. Therefore, either there is an
$({\mathbb {R}}^{m-1})^\dagger $
. Therefore, either there is an
![]() $N_1$
such that
$N_1$
such that
![]() $C_N$
is nonempty if
$C_N$
is nonempty if
![]() $N\geq N_1$
or there is an
$N\geq N_1$
or there is an
![]() $N_2$
such that
$N_2$
such that
![]() $C_N$
is nonempty if
$C_N$
is nonempty if
![]() $N\leq N_2$
. Assuming the former, we see that the sets
$N\leq N_2$
. Assuming the former, we see that the sets
![]() $C_N$
are convex subsets of
$C_N$
are convex subsets of
![]() $({\mathbb {R}}^{m-1})^\dagger $
and similar to each other, i.e., they are dilations of the same set. As the size of each
$({\mathbb {R}}^{m-1})^\dagger $
and similar to each other, i.e., they are dilations of the same set. As the size of each
![]() $C_N$
becomes infinite as
$C_N$
becomes infinite as
![]() $N\to \infty $
, for large N, the set
$N\to \infty $
, for large N, the set
![]() $C_N$
contains cubes of arbitrarily large size, where a cube is a product of intervals of the same size in each coordinate. As soon as
$C_N$
contains cubes of arbitrarily large size, where a cube is a product of intervals of the same size in each coordinate. As soon as
![]() $C_N$
contains a cube of side
$C_N$
contains a cube of side
![]() $(1+\epsilon )$
for some
$(1+\epsilon )$
for some
![]() $\epsilon>0$
, we see that there is a point
$\epsilon>0$
, we see that there is a point
![]() $M\in (\mathbb {Z}^{m-1})^\dagger $
that belongs to
$M\in (\mathbb {Z}^{m-1})^\dagger $
that belongs to
![]() $C_N$
. It follows that the point
$C_N$
. It follows that the point
![]() $(N,M)\in \mathbb {Z}\times (\mathbb {Z}^{m-1})^\dagger $
belongs to
$(N,M)\in \mathbb {Z}\times (\mathbb {Z}^{m-1})^\dagger $
belongs to
![]() $\mathcal {O}$
. ▪
$\mathcal {O}$
. ▪
Proof of Proposition 5.12 (1) If
![]() $p=2$
, the condition (5.10) becomes
$p=2$
, the condition (5.10) becomes
, which is equivalent to
Now the jth entry of the row vector on the left of the above equation is given by
which is a positive integer divisible by
![]() $\gcd (a_j)=\gcd (a^1_j,\dots , a^n_j).$
It follows that (5.16) holds if and only if
$\gcd (a_j)=\gcd (a^1_j,\dots , a^n_j).$
It follows that (5.16) holds if and only if
which is precisely the content of (5.13).
(2) Fix
![]() $1\leq j \leq n$
. By the Euclidean algorithm,
$1\leq j \leq n$
. By the Euclidean algorithm,
![]() $\Pi _j {\neq }\emptyset $
. Choose
$\Pi _j {\neq }\emptyset $
. Choose
![]() $y \in \Pi _j$
. Define a
$y \in \Pi _j$
. Define a
![]() $\mathbb {Z}$
-module homomorphism
$\mathbb {Z}$
-module homomorphism
![]() $\phi : (\mathbb {Z}^n)^\dagger \to \mathbb {Z}$
by setting
$\phi : (\mathbb {Z}^n)^\dagger \to \mathbb {Z}$
by setting
![]() $\phi (x)=xa_j$
, i.e.,
$\phi (x)=xa_j$
, i.e.,
 $$ \begin{align*} \phi(x_1, \ldots, x_n) = \sum_{k=1}^n x_k a^k_j.\end{align*} $$
$$ \begin{align*} \phi(x_1, \ldots, x_n) = \sum_{k=1}^n x_k a^k_j.\end{align*} $$
We then see that
![]() $\Pi _j = y + \ker \phi $
. Since
$\Pi _j = y + \ker \phi $
. Since
![]() $\mathbb {Z}$
is a principal ideal domain,
$\mathbb {Z}$
is a principal ideal domain,
![]() $\ker \phi $
is a free
$\ker \phi $
is a free
![]() $\mathbb {Z}$
-submodule of
$\mathbb {Z}$
-submodule of
![]() $(\mathbb {Z}^n)^\dagger $
of rank
$(\mathbb {Z}^n)^\dagger $
of rank
![]() $\leq n$
(see [Reference Dummit and FooteDF04, Theorem 4, Chapter 12 (p. 460)]). Moreover as
$\leq n$
(see [Reference Dummit and FooteDF04, Theorem 4, Chapter 12 (p. 460)]). Moreover as
![]() $\phi $
is surjective, the quotient
$\phi $
is surjective, the quotient
![]() $\mathbb {Z}$
-module
$\mathbb {Z}$
-module
![]() $(\mathbb {Z}^n)^\dagger /\ker \phi $
is isomorphic to
$(\mathbb {Z}^n)^\dagger /\ker \phi $
is isomorphic to
![]() $\mathbb {Z}$
. It can be seen, by tensoring with
$\mathbb {Z}$
. It can be seen, by tensoring with
![]() $\mathbb Q$
for example, that the rank of
$\mathbb Q$
for example, that the rank of
![]() $\ker \phi $
is
$\ker \phi $
is
![]() $n-1$
. Let D be an
$n-1$
. Let D be an
![]() $(n-1)\times n$
integer matrix whose rows are a
$(n-1)\times n$
integer matrix whose rows are a
![]() $\mathbb {Z}$
-basis of
$\mathbb {Z}$
-basis of
![]() $\ker \phi $
. Then the map
$\ker \phi $
. Then the map
![]() $f:(\mathbb {Z}^{n-1})^\dagger \to (\mathbb {Z}^n)^\dagger $
given by
$f:(\mathbb {Z}^{n-1})^\dagger \to (\mathbb {Z}^n)^\dagger $
given by
![]() $ f(t)=y+tD$
is a parametrization of
$ f(t)=y+tD$
is a parametrization of
![]() $\Pi _j$
, i.e., it is one-to-one and its range is precisely
$\Pi _j$
, i.e., it is one-to-one and its range is precisely
![]() $\Pi _j$
. To complete the proof of the result, it is sufficient to show that
$\Pi _j$
. To complete the proof of the result, it is sufficient to show that
![]() $f^{-1}(\mathscr {S}_2(\mathscr {U}))$
is a nonempty subset of
$f^{-1}(\mathscr {S}_2(\mathscr {U}))$
is a nonempty subset of
![]() $(\mathbb {Z}^{n-1})^\dagger $
. Notice now that an integer vector
$(\mathbb {Z}^{n-1})^\dagger $
. Notice now that an integer vector
![]() $t\in f^{-1}(\mathscr {S}_2(\mathscr {U}))$
, i.e.,
$t\in f^{-1}(\mathscr {S}_2(\mathscr {U}))$
, i.e.,
![]() $f(t)\in \mathscr {S}_2(\mathscr {U})\cap \Pi _j$
if and only if
$f(t)\in \mathscr {S}_2(\mathscr {U})\cap \Pi _j$
if and only if
By Lemma 5.15, there is an integer vector
![]() $t\in (\mathbb {Z}^{n-1})^\dagger $
that satisfies the above system of inequalities. This concludes the proof of part (2) ▪
$t\in (\mathbb {Z}^{n-1})^\dagger $
that satisfies the above system of inequalities. This concludes the proof of part (2) ▪
5.5 Proof of Proposition 5.1
Recall that p satisfies (5.2). Now by (5.8),

so that there is a J with
![]() $1\leq J \leq n$
such that
$1\leq J \leq n$
such that
By part 2 of Proposition 5.12, there is an
![]() $\beta \in (\mathbb {Z}^n)^\dagger $
which lies in
$\beta \in (\mathbb {Z}^n)^\dagger $
which lies in
![]() $\mathscr {S}_2(\mathscr {U})\cap \Pi _J$
. Such a
$\mathscr {S}_2(\mathscr {U})\cap \Pi _J$
. Such a
![]() $\beta $
satisfies:
$\beta $
satisfies:
and also
with
![]() $g(A)$
as in (5.11). By construction,
$g(A)$
as in (5.11). By construction,
![]() $\beta \in \mathscr {S}_2(\mathscr {U})$
. We now claim that
$\beta \in \mathscr {S}_2(\mathscr {U})$
. We now claim that
![]() $\beta \not \in \mathscr {S}_p(\mathscr {U})$
. By Lemma 5.5 this shows that the Bergman projection is not bounded in
$\beta \not \in \mathscr {S}_p(\mathscr {U})$
. By Lemma 5.5 this shows that the Bergman projection is not bounded in
![]() $L^p(\mathscr {U})$
. To establish the claim we note that the Jth entry of the row vector
$L^p(\mathscr {U})$
. To establish the claim we note that the Jth entry of the row vector
is

where in the second line we have used (5.18). Thanks to the inequality (5.17) it follows that the quantity in (5.20) is not positive. It follows by Proposition 5.9 that
![]() $\beta $
is not in
$\beta $
is not in
![]() $L^p(\mathscr {U})$
, which establishes the claim and completes the proof.
$L^p(\mathscr {U})$
, which establishes the claim and completes the proof.
6 Boundedness of the Bergman projection
In this section, we obtain the following part of Theorem 1.2:
Proposition 6.1 Let
 $$ \begin{align} 2\leq p < \frac{2\kappa(\mathscr{U})}{\kappa(\mathscr{U})-1}, \end{align} $$
$$ \begin{align} 2\leq p < \frac{2\kappa(\mathscr{U})}{\kappa(\mathscr{U})-1}, \end{align} $$
then the Bergman projection is bounded on
![]() $L^p(\mathscr {U})$
.
$L^p(\mathscr {U})$
.
We begin by recalling the following fact, which will be the main “hard analysis” ingredient of the proof:
Proposition 6.3 The Bergman projection on the polydisc
![]() $\mathbb {D}^n$
gives rise to a bounded operator
$\mathbb {D}^n$
gives rise to a bounded operator
![]() $\boldsymbol {B}_{\mathbb {D}^n}:L^p(\mathbb {D}^n) \to A^p(\mathbb {D}^n)$
for all
$\boldsymbol {B}_{\mathbb {D}^n}:L^p(\mathbb {D}^n) \to A^p(\mathbb {D}^n)$
for all
![]() $1<p<\infty $
.
$1<p<\infty $
.
Proof For the polydisc
![]() $\mathbb {D}^n$
, the Bergman projection has the well-known integral representation
$\mathbb {D}^n$
, the Bergman projection has the well-known integral representation
where K is the Bergman kernel of the polydisc, which is easily shown to be given by the well-known formula (3.23).
The case
![]() $n=1$
of Propsition 6.3 is by now a staple result in Bergman theory, going back to [Reference Zaharjuta and JudovicZJ64], where it was proved using the
$n=1$
of Propsition 6.3 is by now a staple result in Bergman theory, going back to [Reference Zaharjuta and JudovicZJ64], where it was proved using the
![]() $L^p$
-boundedness of a Calderón–Zygmund singular integral operator. Another approach, based on Schur’s test for
$L^p$
-boundedness of a Calderón–Zygmund singular integral operator. Another approach, based on Schur’s test for
![]() $L^p$
-boundedness of an integral operator, was used in [Reference Forelli and RudinFR75]. An alternative proof of the main estimate needed in this method can be found in [Reference AxlerAxl88] and in the monograph [Reference Duren and SchusterDS04].
$L^p$
-boundedness of an integral operator, was used in [Reference Forelli and RudinFR75]. An alternative proof of the main estimate needed in this method can be found in [Reference AxlerAxl88] and in the monograph [Reference Duren and SchusterDS04].
Since
![]() $\mathbb {D}^n$
is a product domain, the theorem in higher dimensions follows from a textbook application of Fubini’s theorem to the case
$\mathbb {D}^n$
is a product domain, the theorem in higher dimensions follows from a textbook application of Fubini’s theorem to the case
![]() $n=1$
. ▪
$n=1$
. ▪
6.1 Two lemmas
The following two simple lemmas will be used to deduce monomially weighted estimates starting from Proposition 6.3:
Lemma 6.4 Let
![]() $1\leq p<\infty $
, let
$1\leq p<\infty $
, let
![]() $n\geq 1$
, and let
$n\geq 1$
, and let
![]() $\gamma \in ({\mathbb {R}}^n)^\dagger $
be such that
$\gamma \in ({\mathbb {R}}^n)^\dagger $
be such that
![]() . Then there is a
. Then there is a
![]() $C>0$
such that for any
$C>0$
such that for any
![]() $f\in A^p(\mathbb {D}^n)$
we have
$f\in A^p(\mathbb {D}^n)$
we have
where as usual,
![]() $\rho (z)^\gamma = \prod _{j=1}^n \left \vert z_j\right \vert {{\hspace{-0.0001pt}}}^{\gamma _j}$
.
$\rho (z)^\gamma = \prod _{j=1}^n \left \vert z_j\right \vert {{\hspace{-0.0001pt}}}^{\gamma _j}$
.
Proof Throughout this proof, C will denote a constant that depends only on p and
![]() $\gamma $
. The actual value of C may change from line to line.
$\gamma $
. The actual value of C may change from line to line.
Proceed by induction on the dimension n. First consider the base case
![]() $n=1$
. We have, by the Bergman inequality (cf. [Reference Duren and SchusterDS04, Theorem 1]) that there is a
$n=1$
. We have, by the Bergman inequality (cf. [Reference Duren and SchusterDS04, Theorem 1]) that there is a
![]() $C>0$
such that
$C>0$
such that
for all
![]() $f\in A^p(\mathbb {D})$
. Therefore, for
$f\in A^p(\mathbb {D})$
. Therefore, for
![]() $f\in A^p(\mathbb {D})$
we have the estimate
$f\in A^p(\mathbb {D})$
we have the estimate
 $$ \begin{align} \int_{\left\vert z\right\vert<\frac{1}{2}}\left\vert f(z)\right\vert{{\hspace{-0.0001pt}}}^p \left\vert z\right\vert{{\hspace{-0.0001pt}}}^\gamma dV(z)\leq \mathop{\mathrm{sup}}\limits_{\left\vert z\right\vert< \frac{1}{2}} \left\vert f(z)\right\vert{{\hspace{-0.0001pt}}}^p \cdot \int_{\left\vert z\right\vert<\frac{1}{2}} \left\vert z\right\vert{{\hspace{-0.0001pt}}}^\gamma dV(z) < C \cdot\left\Vert f\right\Vert{{\hspace{-0.0001pt}}}_{L^p(\mathbb{D})}^p, \end{align} $$
$$ \begin{align} \int_{\left\vert z\right\vert<\frac{1}{2}}\left\vert f(z)\right\vert{{\hspace{-0.0001pt}}}^p \left\vert z\right\vert{{\hspace{-0.0001pt}}}^\gamma dV(z)\leq \mathop{\mathrm{sup}}\limits_{\left\vert z\right\vert< \frac{1}{2}} \left\vert f(z)\right\vert{{\hspace{-0.0001pt}}}^p \cdot \int_{\left\vert z\right\vert<\frac{1}{2}} \left\vert z\right\vert{{\hspace{-0.0001pt}}}^\gamma dV(z) < C \cdot\left\Vert f\right\Vert{{\hspace{-0.0001pt}}}_{L^p(\mathbb{D})}^p, \end{align} $$
where we have used the fact that since
![]() $\gamma>-2$
we have
$\gamma>-2$
we have
 $$ \begin{align*}\int_{\left\vert z\right\vert<\frac{1}{2}} \left\vert z\right\vert{{\hspace{-0.0001pt}}}^\gamma dV(z)=2\pi\int_0^{\frac{1}{2}} r^{\gamma+1}dr <\infty. \end{align*} $$
$$ \begin{align*}\int_{\left\vert z\right\vert<\frac{1}{2}} \left\vert z\right\vert{{\hspace{-0.0001pt}}}^\gamma dV(z)=2\pi\int_0^{\frac{1}{2}} r^{\gamma+1}dr <\infty. \end{align*} $$
On the other hand,
where we have used the fact that
![]() $\displaystyle { \mathop {\mathrm {sup}}\limits _{\frac {1}{2}\leq \left \vert z\right \vert <1} \left \vert z\right \vert {{\hspace{-0.0001pt}}}^\gamma <\infty . }$
$\displaystyle { \mathop {\mathrm {sup}}\limits _{\frac {1}{2}\leq \left \vert z\right \vert <1} \left \vert z\right \vert {{\hspace{-0.0001pt}}}^\gamma <\infty . }$
Adding (6.6) and (6.7), the estimate (6.5) follows in the case
![]() $n=1$
.
$n=1$
.
For the general case, assume the result established in
![]() $n-1$
dimensions. Write the coordinates of
$n-1$
dimensions. Write the coordinates of
![]() ${\mathbb {C}}^n$
as
${\mathbb {C}}^n$
as
![]() $z=(z',z_{n})\in {\mathbb {C}}^{n-1}\times {\mathbb {C}}$
, and
$z=(z',z_{n})\in {\mathbb {C}}^{n-1}\times {\mathbb {C}}$
, and
![]() $\gamma =(\gamma ',\gamma _n)\in {\mathbb {R}}^{n-1}\times {\mathbb {R}}$
. Then, using Fubini’s theorem
$\gamma =(\gamma ',\gamma _n)\in {\mathbb {R}}^{n-1}\times {\mathbb {R}}$
. Then, using Fubini’s theorem
 $$ \begin{align*} \int_{\mathbb{D}^n}\left\vert f\right\vert{{\hspace{-0.0001pt}}}^p \rho^{\gamma} dV& = \int_{\mathbb{D}^{n-1}}\rho(z')^{\gamma'}\left(\int_{\mathbb{D}} \left\vert f(z',z_n)\right\vert{{\hspace{-0.0001pt}}}^p\left\vert z_n\right\vert{{\hspace{-0.0001pt}}}^{\gamma_n}dV(z_n)\right)dV(z')\\ &\leq C \int_{\mathbb{D}^{n-1}}\rho(z')^{\gamma'}\left(\int_{\mathbb{D}} \left\vert f(z',z_n)\right\vert{{\hspace{-0.0001pt}}}^p dV(z_n)\right)dV(z')\\ &\leq C \int_{\mathbb{D}}\left(\int_{\mathbb{D}^{n-1}}\left\vert f(z',z_n)\right\vert{{\hspace{-0.0001pt}}}^p \rho(z')^{\gamma'} dV(z')\right)dV(z_n)\\ &\leq C \int_{\mathbb{D}}\left(\int_{\mathbb{D}^{n-1}}\left\vert f(z',z_n)\right\vert{{\hspace{-0.0001pt}}}^p dV(z')\right)dV(z_n)\\ &=C \int_{\mathbb{D}^n}\left\vert f(z',z_n)\right\vert{{\hspace{-0.0001pt}}}^p dV(z',z_n), \end{align*} $$
$$ \begin{align*} \int_{\mathbb{D}^n}\left\vert f\right\vert{{\hspace{-0.0001pt}}}^p \rho^{\gamma} dV& = \int_{\mathbb{D}^{n-1}}\rho(z')^{\gamma'}\left(\int_{\mathbb{D}} \left\vert f(z',z_n)\right\vert{{\hspace{-0.0001pt}}}^p\left\vert z_n\right\vert{{\hspace{-0.0001pt}}}^{\gamma_n}dV(z_n)\right)dV(z')\\ &\leq C \int_{\mathbb{D}^{n-1}}\rho(z')^{\gamma'}\left(\int_{\mathbb{D}} \left\vert f(z',z_n)\right\vert{{\hspace{-0.0001pt}}}^p dV(z_n)\right)dV(z')\\ &\leq C \int_{\mathbb{D}}\left(\int_{\mathbb{D}^{n-1}}\left\vert f(z',z_n)\right\vert{{\hspace{-0.0001pt}}}^p \rho(z')^{\gamma'} dV(z')\right)dV(z_n)\\ &\leq C \int_{\mathbb{D}}\left(\int_{\mathbb{D}^{n-1}}\left\vert f(z',z_n)\right\vert{{\hspace{-0.0001pt}}}^p dV(z')\right)dV(z_n)\\ &=C \int_{\mathbb{D}^n}\left\vert f(z',z_n)\right\vert{{\hspace{-0.0001pt}}}^p dV(z',z_n), \end{align*} $$
which proves the result. ▪
Lemma 6.8 Let
![]() $1\leq p<\infty $
, let
$1\leq p<\infty $
, let
![]() $n\geq 1$
and let
$n\geq 1$
and let
![]() $\lambda \in \mathbb {N}^n$
be a multi-index of non-negative integers. Then there is a
$\lambda \in \mathbb {N}^n$
be a multi-index of non-negative integers. Then there is a
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $f\in A^p(\mathbb {D}^n)$
we have the estimate:
$f\in A^p(\mathbb {D}^n)$
we have the estimate:
where
![]() $\varphi _\lambda (z)=z^\lambda $
is as in (
2.4
).
$\varphi _\lambda (z)=z^\lambda $
is as in (
2.4
).
Proof We need only to prove the case in which
![]() $\lambda =(1,0,\dots ,0)$
, so that
$\lambda =(1,0,\dots ,0)$
, so that
![]() $\varphi _\lambda (z)=z_1$
. Once this special case is established, the general result follows by repeatedly applying it and permuting the coordinates.
$\varphi _\lambda (z)=z_1$
. Once this special case is established, the general result follows by repeatedly applying it and permuting the coordinates.
In what follows, C will denote some positive constant that depends only on p and
![]() $\lambda $
, where the actual value of C may change from line to line. First, consider the one dimensional case, so that we have to show that for a holomorphic function f on the disc we have
$\lambda $
, where the actual value of C may change from line to line. First, consider the one dimensional case, so that we have to show that for a holomorphic function f on the disc we have
where the left hand side is assumed to be finite (and therefore the right hand side is finite.) First note that we obviously have
On the other hand, if
![]() $\left \vert z\right \vert =\frac {1}{2}$
, we have
$\left \vert z\right \vert =\frac {1}{2}$
, we have
 $$ \begin{align*} \left\vert f(z)\right\vert{{\hspace{-0.0001pt}}}^p &= 2^p \left\vert z f(z)\right\vert{{\hspace{-0.0001pt}}}^p\\ &\leq 2^p \mathop{\mathrm{sup}}\limits_{\left\vert w\right\vert\leq \frac{1}{2}} \left\vert w f(w)\right\vert{{\hspace{-0.0001pt}}}^p& \text{(maximum principle)}\\ &\leq C \int_{\mathbb{D}}\left\vert w f(w)\right\vert{{\hspace{-0.0001pt}}}^p dV(w) &\text{(Bergman's inequality)} \end{align*} $$
$$ \begin{align*} \left\vert f(z)\right\vert{{\hspace{-0.0001pt}}}^p &= 2^p \left\vert z f(z)\right\vert{{\hspace{-0.0001pt}}}^p\\ &\leq 2^p \mathop{\mathrm{sup}}\limits_{\left\vert w\right\vert\leq \frac{1}{2}} \left\vert w f(w)\right\vert{{\hspace{-0.0001pt}}}^p& \text{(maximum principle)}\\ &\leq C \int_{\mathbb{D}}\left\vert w f(w)\right\vert{{\hspace{-0.0001pt}}}^p dV(w) &\text{(Bergman's inequality)} \end{align*} $$
The maximum principle now implies
 $$ \begin{align*} \mathop{\mathrm{sup}}\limits_{\left\vert z\right\vert\leq \frac{1}{2}} \left\vert f(z)\right\vert{{\hspace{-0.0001pt}}}^p \leq C \int_{\mathbb{D}}\left\vert z f(z)\right\vert{{\hspace{-0.0001pt}}}^p dV(z), \end{align*} $$
$$ \begin{align*} \mathop{\mathrm{sup}}\limits_{\left\vert z\right\vert\leq \frac{1}{2}} \left\vert f(z)\right\vert{{\hspace{-0.0001pt}}}^p \leq C \int_{\mathbb{D}}\left\vert z f(z)\right\vert{{\hspace{-0.0001pt}}}^p dV(z), \end{align*} $$
so that we have
Combining (6.10) and (6.11) the result follows for
![]() $n=1$
.
$n=1$
.
For the higher-dimensional case, denote the coordinates of
![]() ${\mathbb {C}}^n$
as
${\mathbb {C}}^n$
as
![]() $(z_1, z')$
where
$(z_1, z')$
where
![]() $z'=(z_2,\dots , z_n)$
. Then for
$z'=(z_2,\dots , z_n)$
. Then for
![]() $f\in A^p(\mathbb {D}^n)$
we have
$f\in A^p(\mathbb {D}^n)$
we have
 $$ \begin{align*} \int_{\mathbb{D}^n} \left\vert f(z_1, z')\right\vert{{\hspace{-0.0001pt}}}^pdV(z_1, z')& = \int_{\mathbb{D}^{n-1}} \left(\int_{\mathbb{D}} \left\vert f(z_1,z')\right\vert{{\hspace{-0.0001pt}}}^p dV(z_1)\right)dV(z')\\ &\leq C \int_{\mathbb{D}^{n-1}} \left(\int_{\mathbb{D}} \left\vert z_1f(z_1,z')\right\vert{{\hspace{-0.0001pt}}}^p dV(z_1)\right)dV(z')\\ &= C\int_{\mathbb{D}^{n}} \left\vert z_1f(z_1,z')\right\vert{{\hspace{-0.0001pt}}}^p dV(z_1,z'). \end{align*} $$
$$ \begin{align*} \int_{\mathbb{D}^n} \left\vert f(z_1, z')\right\vert{{\hspace{-0.0001pt}}}^pdV(z_1, z')& = \int_{\mathbb{D}^{n-1}} \left(\int_{\mathbb{D}} \left\vert f(z_1,z')\right\vert{{\hspace{-0.0001pt}}}^p dV(z_1)\right)dV(z')\\ &\leq C \int_{\mathbb{D}^{n-1}} \left(\int_{\mathbb{D}} \left\vert z_1f(z_1,z')\right\vert{{\hspace{-0.0001pt}}}^p dV(z_1)\right)dV(z')\\ &= C\int_{\mathbb{D}^{n}} \left\vert z_1f(z_1,z')\right\vert{{\hspace{-0.0001pt}}}^p dV(z_1,z'). \end{align*} $$
▪
6.2 Determination of
 $\Gamma $
-invariant subspaces
$\Gamma $
-invariant subspaces
In this section and Section 6.3, we use the notation established in Section 5.3 above, so that B and A have the same meaning as there. The group
![]() $\Gamma $
is as in Theorem 3.12: the deck transformation group associated to the map
$\Gamma $
is as in Theorem 3.12: the deck transformation group associated to the map
![]() $\Phi _A$
. We will now determine the
$\Phi _A$
. We will now determine the
![]() $\Gamma $
-invariant subspaces of holomorphic functions, in the sense of (4.4):
$\Gamma $
-invariant subspaces of holomorphic functions, in the sense of (4.4):
Proposition 6.12 Let
![]() $\alpha \in (\mathbb {Z}^n)^\dagger $
. Then the monomial
$\alpha \in (\mathbb {Z}^n)^\dagger $
. Then the monomial
![]() $\varphi _\alpha (z)=z^\alpha $
belongs to the space
$\varphi _\alpha (z)=z^\alpha $
belongs to the space
![]() $\left [\mathcal {O}\left ((\mathbb {D}^*)^n\right )\right ]^\Gamma $
of
$\left [\mathcal {O}\left ((\mathbb {D}^*)^n\right )\right ]^\Gamma $
of
![]() $\Gamma $
-invariant holomorphic functions on
$\Gamma $
-invariant holomorphic functions on
![]() $(\mathbb {D}^*)^n$
if and only if there is a
$(\mathbb {D}^*)^n$
if and only if there is a
![]() $\beta \in (\mathbb {Z}^n)^\dagger $
such that
$\beta \in (\mathbb {Z}^n)^\dagger $
such that
Proof Recall that, by definition, the monomial
![]() $\varphi _\alpha $
is invariant under the group action of
$\varphi _\alpha $
is invariant under the group action of
![]() $\Gamma $
if and only if
$\Gamma $
if and only if
![]() $\sigma _\nu ^\sharp (\varphi _\alpha )= (\varphi _\alpha \circ \sigma _\nu ) \det \sigma _\nu ' = \varphi _\alpha $
for all
$\sigma _\nu ^\sharp (\varphi _\alpha )= (\varphi _\alpha \circ \sigma _\nu ) \det \sigma _\nu ' = \varphi _\alpha $
for all
![]() $\sigma _\nu \in \Gamma $
, where for
$\sigma _\nu \in \Gamma $
, where for
![]() $\nu \in \mathbb {Z}^n$
, the automorphism
$\nu \in \mathbb {Z}^n$
, the automorphism
![]() $\sigma _\nu \in \Gamma $
is as in (3.14). Denote the rows of
$\sigma _\nu \in \Gamma $
is as in (3.14). Denote the rows of
![]() $A^{-1}$
by
$A^{-1}$
by
![]() $c^1, \ldots , c^n$
. By the linearity of
$c^1, \ldots , c^n$
. By the linearity of
![]() $\sigma _\nu $
$\sigma _\nu $

for
![]() $\nu \in \mathbb {Z}^n$
. Also, for
$\nu \in \mathbb {Z}^n$
. Also, for
![]() $z \in (\mathbb {D}^*)^n$
and
$z \in (\mathbb {D}^*)^n$
and
![]() $ \nu \in \mathbb {Z}^n$
,
$ \nu \in \mathbb {Z}^n$
,
Therefore,
Hence,
![]() $\varphi _\alpha \in [\mathcal {O} ({\mathbb {D}^n_{\mathsf {L}(B)}})]^\Gamma $
if and only if
$\varphi _\alpha \in [\mathcal {O} ({\mathbb {D}^n_{\mathsf {L}(B)}})]^\Gamma $
if and only if
![]() $\sigma _\nu ^\sharp (\varphi _\alpha )=\varphi _\alpha $
for all
$\sigma _\nu ^\sharp (\varphi _\alpha )=\varphi _\alpha $
for all
![]() $\nu \in \mathbb {Z}^n$
, i.e.,
$\nu \in \mathbb {Z}^n$
, i.e.,
for all
![]() $z \in (\mathbb {D}^*)^n$
and
$z \in (\mathbb {D}^*)^n$
and
![]() $ \nu \in \mathbb {Z}^n, $
i.e., if and only if
$ \nu \in \mathbb {Z}^n, $
i.e., if and only if
Now if there is
![]() $\beta \in (\mathbb {Z}^n)^\dagger $
such that
$\beta \in (\mathbb {Z}^n)^\dagger $
such that
![]() , then clearly,
, then clearly,
![]() for all
for all
![]() $\nu \in \mathbb {Z}^n$
. Conversely, assume that
$\nu \in \mathbb {Z}^n$
. Conversely, assume that
![]() for all
for all
![]() $\nu \in \mathbb {Z}^n$
and let
$\nu \in \mathbb {Z}^n$
and let
![]() $e_1,\dots , e_n$
be the standard basis of
$e_1,\dots , e_n$
be the standard basis of
![]() $\mathbb {Z}^n$
. Then the jth column of
$\mathbb {Z}^n$
. Then the jth column of
![]() (where I is the
(where I is the
![]() $n\times n$
identity matrix) is
$n\times n$
identity matrix) is
![]() which is therefore in
which is therefore in
![]() $\mathbb {Z}$
. Therefore, we have
$\mathbb {Z}$
. Therefore, we have
![]() . It follows that
. It follows that
![]() as desired. ▪
as desired. ▪
Corollary 6.14 Let
![]() $f\in \left [\mathcal {O}(\mathbb {D}^n)\right ]^\Gamma $
. Then there is an
$f\in \left [\mathcal {O}(\mathbb {D}^n)\right ]^\Gamma $
. Then there is an
![]() $h\in \mathcal {O}(\mathbb {D}^n)$
such that
$h\in \mathcal {O}(\mathbb {D}^n)$
such that
with
![]() $g(A)$
as in (5.11).
$g(A)$
as in (5.11).
Proof Let
![]() $\displaystyle { f(z)=\sum _{\alpha \succeq 0}a_\alpha z^\alpha }$
, be the Taylor expansion of f. If f is
$\displaystyle { f(z)=\sum _{\alpha \succeq 0}a_\alpha z^\alpha }$
, be the Taylor expansion of f. If f is
![]() $\Gamma $
invariant, then we claim that for each
$\Gamma $
invariant, then we claim that for each
![]() $\alpha $
such that
$\alpha $
such that
![]() $a_\alpha {\neq }0$
, we have that
$a_\alpha {\neq }0$
, we have that
![]() $z^\alpha $
is
$z^\alpha $
is
![]() $\Gamma $
-invariant. Indeed using (6.13) we have
$\Gamma $
-invariant. Indeed using (6.13) we have

comparing this with the Taylor expansion of f and equating coefficients the claim follows. Therefore, the Taylor expansion of f is of the form

Notice that

. The integer
![]() $\beta a_j=\sum _{k=1}^n\beta _k a_j^k$
which occurs in the exponent is divisible by
$\beta a_j=\sum _{k=1}^n\beta _k a_j^k$
which occurs in the exponent is divisible by
![]() $\gcd (a_j)$
. Further since
$\gcd (a_j)$
. Further since
![]() $\sum _{k=1}^n\beta _k a_j^k\geq 1$
it follows that
$\sum _{k=1}^n\beta _k a_j^k\geq 1$
it follows that
![]() $\beta a_j\geq \gcd (a_j).$
It follows that the monomial
$\beta a_j\geq \gcd (a_j).$
It follows that the monomial
is of the form
, where
![]() $\gamma \succeq 0$
. The corollary follows from (6.15). ▪
$\gamma \succeq 0$
. The corollary follows from (6.15). ▪
6.3 Proof of Proposition 6.1
By Theorem 3.12,
![]() $\Phi _A: \mathbb {D}^n_{\mathsf {L}(B)}\to \mathscr {U} $
is a proper holomorphic map of quotient type with group
$\Phi _A: \mathbb {D}^n_{\mathsf {L}(B)}\to \mathscr {U} $
is a proper holomorphic map of quotient type with group
![]() $\Gamma $
. Therefore, thanks to Theorem 4.15, the Bergman projection
$\Gamma $
. Therefore, thanks to Theorem 4.15, the Bergman projection
is bounded if and only if
is bounded. We therefore show that the map (6.16) is bounded if
![]() $2\leq p < \frac {2\kappa (\mathscr {U})}{\kappa (\mathscr {U})-1}$
.
$2\leq p < \frac {2\kappa (\mathscr {U})}{\kappa (\mathscr {U})-1}$
.
To do this we express the map of (6.16) as a composition of three maps, and show that each of these three maps is continuous:
-
(1) We first show that we have an inclusion of Banach spaces
and that the inclusion map $$ \begin{align*} \left[L^p(\mathbb{D}^n_{\mathsf{L}(B)} , \left\vert\det \Phi_A'\right\vert{{\hspace{-0.0001pt}}}^{2-p}) \right]^{\Gamma} \subseteq \left[L^p(\mathbb{D}^n_{\mathsf{L}(B)})\right]^\Gamma,\end{align*} $$
(6.17)is bounded.
$$ \begin{align*} \left[L^p(\mathbb{D}^n_{\mathsf{L}(B)} , \left\vert\det \Phi_A'\right\vert{{\hspace{-0.0001pt}}}^{2-p}) \right]^{\Gamma} \subseteq \left[L^p(\mathbb{D}^n_{\mathsf{L}(B)})\right]^\Gamma,\end{align*} $$
(6.17)is bounded. $$ \begin{align} \imath: \left[ L^p(\mathbb{D}^n , \left\vert\det \Phi_A'\right\vert{{\hspace{-0.0001pt}}}^{2-p}) \right]^{\Gamma} \hookrightarrow \left[L^p(\mathbb{D}^n)\right]^\Gamma \end{align} $$
$$ \begin{align} \imath: \left[ L^p(\mathbb{D}^n , \left\vert\det \Phi_A'\right\vert{{\hspace{-0.0001pt}}}^{2-p}) \right]^{\Gamma} \hookrightarrow \left[L^p(\mathbb{D}^n)\right]^\Gamma \end{align} $$
It is clearly sufficient to show that there is a continuous inclusion of the full space
 $ L^p(\mathbb {D}^n_{\mathsf {L}(B)} , \left \vert \det \Phi _A'\right \vert {{\hspace{-0.0001pt}}}^{2-p}) $
into
$ L^p(\mathbb {D}^n_{\mathsf {L}(B)} , \left \vert \det \Phi _A'\right \vert {{\hspace{-0.0001pt}}}^{2-p}) $
into
 $L^p(\mathbb {D}^n_{\mathsf {L}(B)})$
. For
$L^p(\mathbb {D}^n_{\mathsf {L}(B)})$
. For
 $z\in \mathbb {D}^n$
we have for
$z\in \mathbb {D}^n$
we have for
 $p\geq 2$
where we use the fact that the exponent of
$p\geq 2$
where we use the fact that the exponent of
 $\rho (z)$
is nonpositive, since A has non-negative integer entries and
$\rho (z)$
is nonpositive, since A has non-negative integer entries and
 $p\geq 2$
. Thus for any
$p\geq 2$
. Thus for any
 $p \geq 2$
and any
$p \geq 2$
and any
 $f \in L^p(\mathbb {D}^n_{\mathsf {L}(B)} , \left \vert \det \Phi _A'\right \vert {{\hspace{-0.0001pt}}}^{2-p}) $
we have (6.18)which proves the inclusion and its continuity.
$f \in L^p(\mathbb {D}^n_{\mathsf {L}(B)} , \left \vert \det \Phi _A'\right \vert {{\hspace{-0.0001pt}}}^{2-p}) $
we have (6.18)which proves the inclusion and its continuity. $$ \begin{align} \int_{\mathbb{D}^n_{\mathsf{L}(B)}} \left\vert f\right\vert{{\hspace{-0.0001pt}}}^p dV \leq \frac{1}{\left\vert \det A\right\vert{{\hspace{-0.0001pt}}}^{2-p}} \int_{\mathbb{D}^n_{\mathsf{L}(B)}} \left\vert f\right\vert{{\hspace{-0.0001pt}}}^p \left\vert \det \Phi_A'\right\vert{{\hspace{-0.0001pt}}}^{2-p} dV, \end{align} $$
$$ \begin{align} \int_{\mathbb{D}^n_{\mathsf{L}(B)}} \left\vert f\right\vert{{\hspace{-0.0001pt}}}^p dV \leq \frac{1}{\left\vert \det A\right\vert{{\hspace{-0.0001pt}}}^{2-p}} \int_{\mathbb{D}^n_{\mathsf{L}(B)}} \left\vert f\right\vert{{\hspace{-0.0001pt}}}^p \left\vert \det \Phi_A'\right\vert{{\hspace{-0.0001pt}}}^{2-p} dV, \end{align} $$
-
(2) Let
 $P_\Gamma = \left .\boldsymbol {B}_{\mathbb {D}^n_{\mathsf {L}(B)}}\right |{{\hspace{-0.0001pt}}}_{\left [ L^p(\mathbb {D}^n_{\mathsf {L}(B)}) \right ]^{\Gamma } }$
be the restriction of the Bergman projection operator to the
$P_\Gamma = \left .\boldsymbol {B}_{\mathbb {D}^n_{\mathsf {L}(B)}}\right |{{\hspace{-0.0001pt}}}_{\left [ L^p(\mathbb {D}^n_{\mathsf {L}(B)}) \right ]^{\Gamma } }$
be the restriction of the Bergman projection operator to the
 $\Gamma $
-invariant functions. We claim that the operator of Banach spaces(6.19)is bounded. Indeed, we have that
$\Gamma $
-invariant functions. We claim that the operator of Banach spaces(6.19)is bounded. Indeed, we have that $$ \begin{align} P_\Gamma: \left[ L^p(\mathbb{D}^n_{\mathsf{L}(B)}) \right]^{\Gamma} \to \left[ A^p(\mathbb{D}^n_{\mathsf{L}(B)}) \right]^{\Gamma} \end{align} $$
$$ \begin{align} P_\Gamma: \left[ L^p(\mathbb{D}^n_{\mathsf{L}(B)}) \right]^{\Gamma} \to \left[ A^p(\mathbb{D}^n_{\mathsf{L}(B)}) \right]^{\Gamma} \end{align} $$
 $L^p(\mathbb {D}^n_{\mathsf {L}(B)})=L^p(\mathbb {D}^n)$
(since
$L^p(\mathbb {D}^n_{\mathsf {L}(B)})=L^p(\mathbb {D}^n)$
(since
 $\mathbb {D}^n_{\mathsf {L}(B)}$
is obtained from
$\mathbb {D}^n_{\mathsf {L}(B)}$
is obtained from
 $\mathbb {D}^n$
by removing an analytic set Z, which is of measure zero) and
$\mathbb {D}^n$
by removing an analytic set Z, which is of measure zero) and
 $ A^p(\mathbb {D}^n_{\mathsf {L}(B)})= A^p(\mathbb {D}^n)$
, in the sense that the analytic set Z is a removable singularity of functions integrable in the pth power,
$ A^p(\mathbb {D}^n_{\mathsf {L}(B)})= A^p(\mathbb {D}^n)$
, in the sense that the analytic set Z is a removable singularity of functions integrable in the pth power,
 $p\geq 2$
(see [Reference BellBel82, p. 687]). By Proposition 6.3, the Bergman projection maps
$p\geq 2$
(see [Reference BellBel82, p. 687]). By Proposition 6.3, the Bergman projection maps
 $L^p(\mathbb {D}^n)$
to
$L^p(\mathbb {D}^n)$
to
 $A^p(\mathbb {D}^n)$
boundedly. Finally, by part (2) of Lemma 4.12, the Bergman projection maps
$A^p(\mathbb {D}^n)$
boundedly. Finally, by part (2) of Lemma 4.12, the Bergman projection maps
 $\Gamma $
-invariant functions to
$\Gamma $
-invariant functions to
 $\Gamma $
-invariant functions. The boundedness of
$\Gamma $
-invariant functions. The boundedness of
 $P_\Gamma $
follows.
$P_\Gamma $
follows.
-
(3) Finally, we show that there is an inclusion
 $ [A^p(\mathbb {D}^n_{\mathsf {L}(B)})]^\Gamma \subset [ A^p (\mathbb {D}^n_{\mathsf {L}(B)}, \left \vert \det \Phi _A'\right \vert {{\hspace{-0.0001pt}}}^{2-p})]^\Gamma $
, and the inclusion map so determined is bounded. As noted above
$ [A^p(\mathbb {D}^n_{\mathsf {L}(B)})]^\Gamma \subset [ A^p (\mathbb {D}^n_{\mathsf {L}(B)}, \left \vert \det \Phi _A'\right \vert {{\hspace{-0.0001pt}}}^{2-p})]^\Gamma $
, and the inclusion map so determined is bounded. As noted above
 $A^p(\mathbb {D}^n_{\mathsf {L}(B)})=A^p(\mathbb {D}^n)$
, so it will suffice to show that there is a continuous inclusion (6.20)Let
$A^p(\mathbb {D}^n_{\mathsf {L}(B)})=A^p(\mathbb {D}^n)$
, so it will suffice to show that there is a continuous inclusion (6.20)Let $$ \begin{align} \jmath :\left[A^p(\mathbb{D}^n)\right]^\Gamma \hookrightarrow{} \left[ A^p (\mathbb{D}^n, \left\vert \det \Phi_A'\right\vert{{\hspace{-0.0001pt}}}^{2-p}) \right]^\Gamma. \end{align} $$
$$ \begin{align} \jmath :\left[A^p(\mathbb{D}^n)\right]^\Gamma \hookrightarrow{} \left[ A^p (\mathbb{D}^n, \left\vert \det \Phi_A'\right\vert{{\hspace{-0.0001pt}}}^{2-p}) \right]^\Gamma. \end{align} $$
 $f \in \left [A^p(\mathbb {D}^n)\right ]^\Gamma $
, so by Corollary 6.14, there exists
$f \in \left [A^p(\mathbb {D}^n)\right ]^\Gamma $
, so by Corollary 6.14, there exists
 $h \in \mathcal {O}(\mathbb {D}^n)$
such that (6.21)In fact,
$h \in \mathcal {O}(\mathbb {D}^n)$
such that (6.21)In fact,
 $h\in A^p(\mathbb {D}^n)$
, since where the first of the two integrals is clearly finite and the second integral is
$h\in A^p(\mathbb {D}^n)$
, since where the first of the two integrals is clearly finite and the second integral is

Now we have that
(6.22)Combining Hypotheses (6.2) and (5.8), so for each
so for each
 $1\leq j \leq n$
, Therefore, the jth component of the exponent of
$1\leq j \leq n$
, Therefore, the jth component of the exponent of
 $\rho $
in (6.22) is where we have used the obvious fact that
$\rho $
in (6.22) is where we have used the obvious fact that
 . Therefore, we have and so we have, for constants
. Therefore, we have and so we have, for constants
 $C_1, C_2$
independent of the function f: It follows that the inclusion
$C_1, C_2$
independent of the function f: It follows that the inclusion
 $\jmath $
of (6.20) is continuous.
$\jmath $
of (6.20) is continuous.
Therefore, the map
![]() $\boldsymbol {B}_{\mathbb {D}^n_{\mathsf {L}(B)}}$
of Banach spaces in (6.16) can be represented as a composition
$\boldsymbol {B}_{\mathbb {D}^n_{\mathsf {L}(B)}}$
of Banach spaces in (6.16) can be represented as a composition
where
![]() $\imath $
,
$\imath $
,
![]() $P_\Gamma $
and
$P_\Gamma $
and
![]() $\jmath $
are as in (6.17), (6.19) and (6.20), respectively and each of which has already been shown to be continuous. The proof of Proposition 6.1 is complete.
$\jmath $
are as in (6.17), (6.19) and (6.20), respectively and each of which has already been shown to be continuous. The proof of Proposition 6.1 is complete.
7 Conclusion
7.1 End of proof of Theorem 1.2
Recall that, as a consequence of the self-adjointness of the Bergman projection on
![]() $L^2$
, the set of p for which the Bergman projection on a domain is
$L^2$
, the set of p for which the Bergman projection on a domain is
![]() $L^p$
-bounded is Hölder-symmetric (see [Reference Edholm and McNealEM16, Reference Chakrabarti and ZeytuncuCZ16]), i.e., p belongs to this set if and only if the conjugate index
$L^p$
-bounded is Hölder-symmetric (see [Reference Edholm and McNealEM16, Reference Chakrabarti and ZeytuncuCZ16]), i.e., p belongs to this set if and only if the conjugate index
![]() $p'$
also belongs to it, where
$p'$
also belongs to it, where
![]() $\frac {1}{p'}+\frac {1}{p}=1$
. Notice now that the index conjugate to
$\frac {1}{p'}+\frac {1}{p}=1$
. Notice now that the index conjugate to
![]() $\frac {2\kappa (\mathscr {U})}{\kappa (\mathscr {U})-1}$
is
$\frac {2\kappa (\mathscr {U})}{\kappa (\mathscr {U})-1}$
is
![]() $\frac {2\kappa (\mathscr {U})}{\kappa (\mathscr {U})+1}$
. Now by combining Propositions 6.1 and 5.1, we see that for
$\frac {2\kappa (\mathscr {U})}{\kappa (\mathscr {U})+1}$
. Now by combining Propositions 6.1 and 5.1, we see that for
![]() $p\geq 2$
, the Bergman projection on
$p\geq 2$
, the Bergman projection on
![]() $\mathscr {U}$
is bounded if and only if
$\mathscr {U}$
is bounded if and only if
![]() $p\in \left [2, \frac {2\kappa (\mathscr {U})}{\kappa (\mathscr {U})-1} \right ).$
By Hölder symmetry, for
$p\in \left [2, \frac {2\kappa (\mathscr {U})}{\kappa (\mathscr {U})-1} \right ).$
By Hölder symmetry, for
![]() $p\leq 2$
, the Bergman projection is bounded if and only if
$p\leq 2$
, the Bergman projection is bounded if and only if
![]() $p\in \left (\frac {2\kappa (\mathscr {U})}{\kappa (\mathscr {U})+1},2\right ] $
. The bounds claimed in (1.3) are proved, and therefore Theorem 1.2 holds.
$p\in \left (\frac {2\kappa (\mathscr {U})}{\kappa (\mathscr {U})+1},2\right ] $
. The bounds claimed in (1.3) are proved, and therefore Theorem 1.2 holds.
7.2 Comments and questions
The methods used to prove Theorem 1.2 are more general than the result itself, and apply to the Bergman projection on various quotient domains of simple domains with known Bergman kernels, provided the quotient type proper holomorphic map is a monomial map. For example, we may deduce using a modification of our arguments, the range of p for which the Bergman projection is bounded in
![]() $L^p$
on the domain
$L^p$
on the domain
where
![]() $k_1,k_2$
are positive integers.
$k_1,k_2$
are positive integers.
Thanks to Theorem 1.2, the Bergman projection is no longer bounded in
![]() $L^p(\mathscr {U})$
if
$L^p(\mathscr {U})$
if
![]() $p\geq \frac {2\kappa (\mathscr {U})}{\kappa (\mathscr {U})-1}$
. It is natural to ask if there is an alternate projection from
$p\geq \frac {2\kappa (\mathscr {U})}{\kappa (\mathscr {U})-1}$
. It is natural to ask if there is an alternate projection from
![]() $L^p(\mathscr {U})$
to
$L^p(\mathscr {U})$
to
![]() $A^p(\mathscr {U})$
for such p. In the special case
$A^p(\mathscr {U})$
for such p. In the special case
![]() $\mathscr {U}=H_{m/n}$
, the generalized Hartogs triangle of (1.6), it is possible to construct for each
$\mathscr {U}=H_{m/n}$
, the generalized Hartogs triangle of (1.6), it is possible to construct for each
![]() $p\geq 2$
a sub-Bergman projection which gives rise to a bounded projection on
$p\geq 2$
a sub-Bergman projection which gives rise to a bounded projection on
![]() $L^p$
. It would be interesting to see whether a similar statement holds for the monomial polyhedra considered in this paper.
$L^p$
. It would be interesting to see whether a similar statement holds for the monomial polyhedra considered in this paper.
Finally, we would like to understand the precise geometric significance of the arithmetic complexity of
![]() $\mathscr {U}$
without reference to the representation in terms of the matrix B. Such a description will pave the way of generalizing the results of this paper to wider classes of domains.
$\mathscr {U}$
without reference to the representation in terms of the matrix B. Such a description will pave the way of generalizing the results of this paper to wider classes of domains.
Acknowledgments
We would like to thank Yuan Yuan for very interesting discussions with DC and LE about this problem and the results of [Reference Chen, Krantz and YuanCKY20] during the 2019 Midwest Several Complex Variables Conference at Dearborn, MI, and Steven Krantz for comments on the same paper made to LE during a visit to Washington University at St. Louis, MO, in the same year. DC would like to thank the mathematics department of the University of Michigan, Ann Arbor for its hospitality in Fall 2019. We also thank Shuo Zhang for pointing out his work in [Reference ZhangZha20, Reference ZhangZha19], and Włodzimierz Zwonek for pointing out his work in [Reference ZwonekZwo99, Reference ZwonekZwo00].