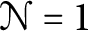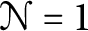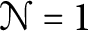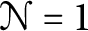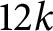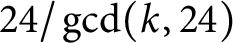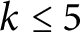The motivation for this note comes from an attempt to construct two-dimensional superconformal field theories (SCFTs) that would explain some features of the generalized cohomology theory known as topological modular forms (TMF). The connection between SCFTs and TMF is predicted by conjectures of Stolz and Teichner [Reference Stolz and TeichnerST11] proposing a geometric model of TMF in terms of (not necessarily conformal) two-dimensional supersymmetric field theory. In particular, as we explain in Section 5, each holomorphic vertex operator algebra (VOA) of central charge c equipped with
$\mathcal N=1$
supersymmetry should determine a class in
$\textrm{TMF}_{2c} = \pi _{2c}\textrm{TMF}(\textrm{pt})$
. Let
$\textrm{MF}_c$
denote the space of integral modular forms of weight c. There is an edge map
$\textrm{TMF}_{2c} \to \textrm{MF}_c$
, which in the proposed model should take an SCFT to its supersymmetric index, multiplied by
$\eta ^{2c} = \Delta ^{c/12}$
. A curious feature of
$\textrm{TMF}$
is that the smallest multiple of
$\Delta ^k$
in the image of
$\textrm{TMF}_{24k} \to \textrm{MF}_{12k}$
is
$\frac {24}{\gcd (k,24)}\Delta ^k$
. Our goal is to construct holomorphic
$\mathcal N=1$
VOAs realizing these values. We pose this goal as our Main Question:
Main Question For each k, does there exist a holomorphic
$\mathcal N=1$
VOA with central charge
$c=12k$
and supersymmetric index
$\frac {24}{\gcd (k,24)}$
?
In order to answer the Main Question, and to explore TMF more generally, it is useful to have a source for holomorphic
$\mathcal N=1$
VOAs. As described in Section 2, every linear ternary self-dual, also called “Type III,” code determines a VOA equipped with
$\mathcal N=1$
structure; it is a lattice VOA for what in [Reference Harada and MunemasaHM09] is called a “three-framed lattice,” and so we will refer to the result as a “three-framed VOA.” Further
$\mathcal N=1$
VOAs can be constructed by orbifolding three-framed VOAs by nonanomalous symmetries. We study the supersymmetry-preserving automorphisms of three-framed VOAs in Section 3. The theory of fermionic orbifolds is studied in Section 4, where we clarify the role of the ’t Hooft anomaly and of its trivializations. Among the
$\mathcal N=1$
VOAs that arise as orbifolds of three-framed VOAs are the “supermoonshine” model of [Reference DuncanDun07] (Examples 2.3 and 3.2) and of the “beauty and the beast” model of [Reference Dixon, Ginsparg and HarveyDGH88] (Example 4.5).
The supersymmetric index of the three-framed VOA and of its orbifolds can be computed directly from the code (Proposition 2.4 and Theorem 5.6). This suggests that one study the “index” of self-dual ternary codes for their own sake. Our results and conjectures lead to the following divisibility statement (Theorem 1.3 and Conjecture 1.4): the index of a self-dual ternary code is always divisible by
$24$
. Our proof requires nontrivial divisibility results about modular forms. Section 1 contains some elementary background on ternary codes and explains the definition of the index of a code without reference to supersymmetric field theory.
All together, one way to affirmatively answer the Main Question is to construct self-dual ternary codes with index
$24$
(and an appropriate orbifoldable symmetry). For small c, the complete classification of self-dual ternary codes of length c is known [Reference Harada and MunemasaHM09], but for large c the best approach available is an exponential-time computer search. With help from Noam D. Elkies implementing such a search, we succeeded at finding
$\mathcal N=1$
VOAs of central charge
$c = 12k$
and supersymmetric index
$\frac {24}{\gcd (k,24)}$
for
$k\leq 5$
.
This work suggests several interesting future directions of inquiry:
Question 0.1 Is there a systematic construction of self-dual ternary codes of index
$24$
which would avoid the use of intensive computation? Such a construction could provide a systematic construction of
$\mathcal N=1$
VOAs realizing the modular forms
$\frac {24}{\gcd (k,24)}\Delta ^k$
.
Question 0.2 After
$\frac {24}{\gcd (k,24)}\Delta ^k$
, the next most interesting modular forms in the image of
$\textrm{TMF} \to \textrm{MF}$
are the Theta functions of even unimodular lattices. These will not come from holomorphic VOAs, but might come from full CFTs with
$\mathcal N=(0,1)$
supersymmetry. Is there a systematic construction that inputs an even unimodular lattice
$\Lambda $
of rank r and produces a
$\mathcal N=(0,1)$
full CFT of total central charge
$c_R - c_L = r$
and Ramond–Ramond partition function
$\Theta _{\Lambda } / \eta ^r$
?
Question 0.3 Does the Stolz–Teichner proposal generalize to involve supersymmetric field theories equipped with discrete symmetry group actions of specified ’t Hooft anomaly? It would be nice to find what the corresponding “equivariant” TMF theory should look like. The holomorphic SCFTs we build have large discrete symmetry groups and should have interesting images under such a conjectural correspondence.
Question 0.4 What is the physical meaning of TMF classes, especially of torsion type? Which physical relation between two theories implies that they represent the same class in TMF?
1 The index of a ternary code
Let
denote the field of order
$3$
. By definition, a ternary code of length c is a linear subspace
. The ambient space
has a standard “Cartesian” inner product
, and so given a code
one can construct its dual code
. A ternary code is self-dual if
$C^\perp = C$
.
Elements of
are called words, and if a code C is fixed, elements of C are called code words. The Hamming weight of a word is its number of nonzero entries. A word is maximal if its Hamming weight is c. In a self-dual ternary code, every code word is self-orthogonal, and so in particular has Hamming weight divisible by
$3$
. It is well-known that self-dual ternary codes of length c can occur only when c is divisible by
$4$
, and so a self-dual ternary code can contain maximal codewords only when
$c = 12k$
for some
.
Suppose
is a maximal word. Let us say that w is even or odd according to the number of
$1$
s among its entries, mod
$2$
.
Definition 1.1 Suppose C is a self-dual ternary code. The index of C is
$$ \begin{align*} \operatorname{\textrm{Index}}(C) = \# \{\text{even maximal codewords}\} - \#\{\text{odd maximal codewords}\}.\end{align*} $$
Remark 1.2 The index is the value at
$(x,y,z) = (0,1,-1)$
of the complete weight enumerator defined as
$$ \begin{align*} \operatorname{\textrm{CWE}}_C(x,y,z) = \sum_{w\in C} x^{n_0(w)} y^{n_1(w)} z^{n_{-1}(w)} = \sum_{w \in C} \prod_{i=1}^c x_{w(i)},\end{align*} $$
where
$n_i(w)$
is the number of is among the coordinates of w,
$(x_0,x_1,x_{-1}) = (x,y,z)$
, and
is the ith coordinate of w.
The first main result of this paper is:
Theorem 1.3 If C is a self-dual ternary code of length divisible by
$24$
, then
$ \operatorname {\textrm{Index}}(C)$
is divisible by
$24$
. If the length of C is merely divisible by
$12$
, then
$ \operatorname {\textrm{Index}}(C)$
is divisible by
$12$
.
If the length of C is not divisible by
$12$
, then
$ \operatorname {\textrm{Index}}(C)$
vanishes, as there are simply no maximal codewords. The second sentence in the Theorem follows immediately from the first together with the easy observation that
$ \operatorname {\textrm{Index}}(C' \oplus C'') = \operatorname {\textrm{Index}}(C') \operatorname {\textrm{Index}}(C'')$
(and the even easier observation that if
$24$
divides
$n^2$
, then
$12$
divides n). We will prove the first sentence in the next section, after Remark 2.5. Our proof relies on some nontrivial facts about Theta functions of lattices, and we do not know if there is an elementary proof. Furthermore, we expect that:
Conjecture 1.4 The index of any self-dual ternary code is divisible by
$24$
, even if the length is merely divisibly by
$12$
. For all lengths
$c = 12k$
, there exists a self-dual ternary code of index
$24$
.
Conjecture 1.4 follows from the deeper Conjecture 5.5, which, together with Proposition 2.4, implies that
$ \operatorname {\textrm{Index}}(C)$
is divisibly by
$8$
whenever C is a self-dual ternary code of length
$c = 12 \bmod {24}$
.
Example 1.5 Up to signed coordinate permutations, there are only three self-dual ternary codes of length
$c=12$
:
-
(1) First is the direct sum of three copies of the unique code of length
$4$
. It can be generated by (i.e., spanned by the rows of) the matrix: This code has no maximal codewords, hence index
$$ \begin{align*} \left( \begin{array}{cccccccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 & -1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & -1 \\ \end{array} \right). \end{align*} $$
$0$
.
-
(2) Second, there is a self-dual ternary code of length
$c=12$
with eight even and eight odd maximal codewords, hence index
$0$
. A generating matrix is:
$$ \begin{align*} \left( \begin{array}{cccccccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 1&0&-1&1&-1&1 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1&0&1&-1&1&-1 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0&1&-1&1&1&-1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0&1&1&-1&-1&1 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0&0&1&1&0&0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0&0&0&0&1&1 \\ \end{array} \right). \end{align*} $$
-
(3) Finally, there is the Ternary Golay code from [Reference GolayGol49], which has 24 even and no odd maximal codewords, hence index
$24$
. It can be generated by the matrix:
$$ \begin{align*} \left( \begin{array}{cccccccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1\\ 0 & 1 & 0 & 0 & 0 & 0 & -1 & 0 & 1 & -1 & -1 & 1\\ 0 & 0 & 1 & 0 & 0 & 0 & -1 & 1 & 0 & 1 & -1 & -1\\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & -1 & 1 & 0 & 1 & -1\\ 0 & 0 & 0 & 0 & 1 & 0 & -1 & -1 & -1 & 1 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 1 & -1 & 1 & -1 & -1 & 1 & 0 \end{array} \right). \end{align*} $$
In particular, Conjecture 1.4 holds for
$c=12$
.
Example 1.6 For
$c=24$
, we may confirm Conjecture 1.4 by appealing to the classification of self-dual ternary codes from [Reference Harada and MunemasaHM09]. The first step of their classification is to convert each self-dual ternary code C of length c into an odd unimodular lattice
$\Lambda (C)$
of rank c; we will review that construction in the next section. Odd unimodular lattices of rank
$\leq 24$
were classified by Borcherds and listed in [Reference Conway, Sloane, Bannai, Borcherds, Leech, Norton, Odlyzko, Parker, Queen and VenkovCS99, Chapter 17]. As we will explain during the proof of Theorem 1.3, when
$c=24$
the index of C is precisely the difference between the numbers of roots of the two “even neighbors” of
$\Lambda (C)$
. Inspecting the list, we find that of the
$338$
inequivalent self-dual ternary codes of length
$24$
,
$30$
have index
$24$
.
Conjecture 1.4 is further supported by the following experimental evidence. Together with Noam D. Elkies, we randomly generated self-dual codes and calculated their indexes. (The runtime of this calculation grows exponentially with the length c.) A random sampling of hundreds of self-dual ternary codes of length
$c=36$
and of dozens of self-dual ternary codes of lengths
$c=48$
and
$c=60$
always produced codes of index divisible by
$24$
. Codes of index precisely
$24$
appeared fairly often. A coarse estimate predicts that the expected value of
$ \operatorname {\textrm{Index}}(C)^2$
grows slowly with c, contributing to the difficulty of finding codes of index
$24$
by random search, but the total number of codes grows very quickly with c, so the existence of a code of index
$24$
remains likely.
2 From ternary codes to SCFTs
Suppose
is a ternary code of length c such that
$C \subset C^\perp $
. One can construct an integral lattice
$\Lambda (C)$
from C as follows. Consider the lattice
, i.e., the rank-1 lattice with basis vector of square-length
$3$
, and its dual lattice
. Choose an identification of (the additive group of)
with the quotient group
. (There are two such identifications, and the choice does not affect the final answer.) Then
$\Lambda (C)$
is defined by the following pullback:
This lattice is integral because
$C \subset C^\perp $
. It is unimodular exactly when C is self-dual. Note that one automatically has an injection
. Following [Reference Harada and MunemasaHM09], we will call a rank-c lattice
$\Lambda $
equipped with an injection
three-framed. Each three-framed lattice arises from a unique ternary code
.
There is a well-known construction that produces from each integral lattice
$\Lambda $
of rank c a vertex operator algebra
$V_{\Lambda }$
of central charge c. For the definition of “vertex operator algebra” and for details of the construction, we refer the reader to the standard textbooks [Reference KacKac98, Reference Frenkel and Ben-ZviFBZ04]. In outline, the construction of
$V_{\Lambda }$
goes as follows. One begins with a “free boson” VOA
$ \operatorname {\textrm{Bos}}(\mathfrak {h})$
built functorially from the vector space
. The irreducible vertex modules for
$ \operatorname {\textrm{Bos}}(\mathfrak {h})$
are naturally indexed by the points in
$\mathfrak {h}$
: given
$\lambda \in \mathfrak {h}$
, there is a module
$M_{\lambda }$
generated over
$ \operatorname {\textrm{Bos}}(\mathfrak {h})$
by an element
$\Gamma _{\lambda } \in M_{\lambda }$
; as a vector space,
, where
is the one-dimensional space with basis
$\Gamma _{\lambda }$
. The element
$\Gamma _{\lambda }$
has conformal dimension
$\lambda ^2/2$
. Finally, we set
$$ \begin{align*} V_{\Lambda} = \bigoplus_{\lambda \in \Lambda} (-1)^{\lambda^2} M_{\lambda},\end{align*} $$
where the notation “
$(-1)^{\lambda ^2}$
” denotes that the summands corresponding to vectors of odd square-length are considered to be fermionic, and those of even square-length are bosonic. If
$\Lambda $
is an integral lattice, then
$V_{\Lambda }$
is naturally a VOA [Reference Frenkel, Lepowsky and MeurmanFLM88, Theorem 8.10.2]. It is holomorphic (i.e., it has only one irreducible module) exactly when
$\Lambda $
is unimodular.
The above description of
$V_{\Lambda }$
can be made quite explicit when
$\Lambda = \Lambda (C)$
for a ternary code
. Consider first the case
$c=1$
and
$C=\{0\}$
, so that
. Then
is generated by a “free boson at level 3”
$\alpha $
together with fermionic operators
$\Gamma _{\pm \sqrt 3}$
. The operator product expansions are
$$ \begin{align*} \alpha(z)\,\alpha(w) &\sim \frac3{(z-w)^2}, \\ \alpha(z)\,\Gamma_{\pm\sqrt3}(w) &\sim \frac{\pm 3 \Gamma_{\pm\sqrt3}(w)}{z-w} ,\\ \Gamma_{\pm\sqrt3}(z)\,\Gamma_{\pm\sqrt3}(w) &\sim 0 \quad \text{(same sign)},\\ \Gamma_{+\sqrt3}(z)\,\Gamma_{-\sqrt3}(w) & \sim \frac1{(z-w)^3} + \frac{\alpha(w)}{(z-w)^2} + \frac{\frac12 {:} \alpha^2(w) {:} + \frac12\partial\alpha(w)}{z-w}. \end{align*} $$
The subalgebra
is generated by
$\alpha $
alone. For general
with
$n\geq 0$
, we have
$\Gamma _{\pm n\sqrt 3} = {{:} \Gamma _{\pm \sqrt 3}^n {:}}$
.
When c is arbitrary and
$C=\{0\}$
, we set
The irreps of
are naturally indexed by
[Reference DongDon93], and for arbitrary
we set
The VOA
is also called “
$U(1)$
at level
$3$
.” It is well known to be an
$\mathcal N=2$
minimal model: the boson
$\alpha $
generates the R-symmetry, and the polarized supersymmetry generators are
$\Gamma _{\pm \sqrt 3}$
. It follows that
has the structure of
$\mathcal N=2$
supersymmetric VOA. We will focus on the induced
$\mathcal N=1$
structure. The generator of
$\mathcal N=1$
supersymmetry on
is
$G = \Gamma _{+\sqrt 3} + \Gamma _{-\sqrt 3}$
. Letting
, with the G in the ith spot, the generator of
$\mathcal N=1$
supersymmetry on
$V_{\Lambda (C)}$
is
$\sum _{i=1}^c G_i$
. Based on the lattice notion from [Reference Harada and MunemasaHM09], we will use the term three-framed VOA for a VOA V of central charge
equipped with an injection
. A three-framed VOA V is necessarily of the form
$V_{\Lambda (C)}$
for some ternary code
$C \subset C^\perp $
.
Example 2.1 Consider the non-self-dual code
$C_3$
of length
$3$
spanned by the vector
. The corresponding lattice is
, where
$A_2$
denotes the root lattice of
$\mathfrak {sl}(3)$
. Indeed,
has two vectors of length
$1$
, namely
$\pm \frac 1{\sqrt 3}(1,1,1)$
; orthogonal to these are six vectors of square-length
$2$
, namely the cyclic permutations of
$\pm \frac 1{\sqrt 3}(1,1,-2)$
. We therefore find an isomorphism
. The famous “boson-fermion correspondence” identifies the lattice VOA
with the VOA
$ \operatorname {\textrm{Fer}}(2)$
of two Majorana fermions, and so
$V_{\Lambda (C_3)} \cong V_{A_2} \times \operatorname {\textrm{Fer}}(2)$
.
For any rank-r integral lattice
$\Lambda $
, the VOA
$V_{\Lambda } \otimes \operatorname {\textrm{Fer}}(r)$
can be equipped with an
$\mathcal N=1$
supersymmetry that simply exchanges the r free fermions generating
$ \operatorname {\textrm{Fer}}(r)$
with the r free bosons generating
[Reference Heluani and KacHK07]. In the basis, we are working in, the
$\mathcal N=1$
supersymmetry on
$V_{\Lambda (C_3)}\cong V_{A_2} \times \operatorname {\textrm{Fer}}(2)$
is not this one. However, we claim that there is an automorphism of
$V_{\Lambda (C_3)}$
intertwining the two
$\mathcal N=1$
structures. In general, to write a rational VOA V of central charge
as a lattice VOA, one must choose a subalgebra
$ \operatorname {\textrm{Bos}}(c) \subset V$
, i.e., one must choose c many commuting fields of conformal weight
$1$
; the lattice is then the lattice of weights of the action of
$ \operatorname {\textrm{Bos}}(c)$
on V [Reference Li and XuLX95]. (The choice of
$ \operatorname {\textrm{Bos}}(c) \subset V$
is analogous to a choice of Cartan subalgebra of a semisimple Lie algebra.) Starting with
, we choose to keep the free boson pointing in the
$(1,1,1)$
-direction, but to replace the other two bosons (spanning the
-plane inside
) with
$X = \Gamma _{\frac 1{\sqrt 3}(1,1,-2)} + \Gamma _{\frac 1{\sqrt 3}(1,-2,1)} + \Gamma _{\frac 1{\sqrt 3}(-2,1,1)}$
and
$Y = \Gamma _{\frac 1{\sqrt 3}(-1,-1,2)} + \Gamma _{\frac 1{\sqrt 3}(-1,2,-1)} + \Gamma _{\frac 1{\sqrt 3}(2,-1,-1)}$
. One may check that X and Y commute, and that the supersymmetry
$G = \Gamma _{(\sqrt 3,0,0)} + \dots + \Gamma _{(0,0,-\sqrt 3)}$
exchanges X and Y with the free fermion fields
$\Gamma _{\frac 1{\sqrt 3}(1,1,1)}$
and
$\Gamma _{-\frac 1{\sqrt 3}(1,1,1)}$
respectively. Thus for this new Cartan we find the
$\mathcal N=1$
structure on
$V_{A_2} \otimes \operatorname {\textrm{Fer}}(2)$
of [Reference Heluani and KacHK07].
Example 2.2 Let
denote the unique self-dual ternary code of length
$4$
, which has generator matrix
$$ \begin{align*} \left( \begin{array}{cccc} 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & -1 \end{array} \right).\end{align*} $$
Then
, and so
$V_{\Lambda (C_4)} \cong \operatorname {\textrm{Fer}}(8)$
by the boson-fermion correspondence.
$\mathcal N=1$
supersymmetry structures on
$ \operatorname {\textrm{Fer}}(n)$
were classified in [Reference Goddard and OliveGO85], and correspond to n-dimensional semisimple Lie algebras. There is a unique semisimple Lie algebra of dimension eight, namely
$\mathfrak {su}(3)$
, and so we must have an isomorphism of
$\mathcal N=1$
VOAs
$V_{\Lambda (C_4)} \cong \operatorname {\textrm{Fer}}(\mathfrak {su}(3))$
.
Example 2.3 Let us work out the VOAs corresponding to the three self-dual ternary codes of length
$12$
from Example 1.5.
-
(1) The first code from Example 1.5 was
$C_4^{\oplus 3}$
, where
$C_4$
is the unique self-dual ternary code of length
$4$
from Example 2.2. The
$\mathcal N=1$
structure on
$V_{\Lambda (C_4 \oplus C_4 \oplus C_4)} \cong V_{\Lambda (C_4)}^{\otimes 3} \cong \operatorname {\textrm{Fer}}(8)^{\otimes 3} \cong \operatorname {\textrm{Fer}}(24)$
is the one coming from the Lie algebra
$\mathfrak {su}(3)^3$
. -
(2) Let
$C_3$
denote the nonself-dual code of length
$3$
from Example 2.1, and let C denote the second self-dual ternary code C in Example 1.5. Then C is an extension of
$C_3^{\oplus 4}$
, and so
$V_{\Lambda (C)}$
is an extension of
$V_{\Lambda (C_3)}^{\otimes 4} = V_{A_2^4} \otimes \operatorname {\textrm{Fer}}(8)$
. The lattice
$A_2^4$
has only one unimodular extension, namely the
$E_8$
lattice. After changing bases as in Example 2.1, we find an isomorphism of
$\mathcal N=1$
SCFTs between
$V_{\Lambda (C)}$
and
$V_{E_8} \otimes \operatorname {\textrm{Fer}}(8)$
made into an
$\mathcal N=1$
SCFT as in [Reference Heluani and KacHK07]. -
(3) Finally, consider the Ternary Golay code, listed third in Example 1.5. The lattice
$\Lambda (\text {Golay})$
turns out to be isomorphic to the
$D_{12}^+$
lattice, i.e., the
$D_{12}$
root lattice together with its coset containing the highest weight of the (positive) half-spin representation of
$\operatorname {Spin}(24)$
. (Indeed,
$\Lambda [\text {Golay}]$
contains no vectors of length
$1$
, and
$D_{12}^+$
is the unique unimodular lattice of rank
$12$
with this property.) The corresponding VOA
$V_{D_{12}^+}$
is isomorphic to the Duncan’s “supermoonshine” VOA
$V^{f\natural }$
from [Reference DuncanDun07]. One of the main results of that paper is that
$V^{f\natural }$
carries a unique-up-to-isomorphism
$\mathcal N=1$
supersymmetry structure (and is the unique
$c=12$
and
$\mathcal N=1$
SCFT with no fields of conformal dimension
$1/2$
). See also Example 3.2.
Suppose V is a holomorphic
$\mathcal N=1$
VOA of central charge c, and let
$V_R$
denote its Ramond sector, i.e., the Hilbert space assigned by V to the circle with nonbounding spin structure. Consider the Ramond–Ramond partition function
$Z_{RR}(V) = \textrm{tr}_{V_R} (-1)^f q^{L_0 - c/24}$
, i.e., the partition function of V evaluated on elliptic curves with spin structure induced from the Lie group framing of the elliptic curve. If V were merely a nonsupersymmetric holomorphic VOA, then
$Z_{RR}(V)$
would be merely a (level one, meromorphic) modular function in q. But the supersymmetry generator determines an odd endomorphism of
$V_R$
whose square is
$L_0 - \frac {c}{24}$
, and so all contributions to
$Z_{RR}(V)$
with
$L_0 - \frac {c}{24} \neq 0$
cancel. Thus
merely counts (with signs) the Ramond-sector ground states, i.e., the Ramond-sector states of conformal dimension
$c/24$
. This count is called the (supersymmetric) index of V.
When
$V = V_{\Lambda }$
for an odd self-dual lattice
$\Lambda $
, the Ramond sector
$(V_{\Lambda })_R$
can be constructed analogously to the construction of
$V_{\Lambda }$
above. Indeed, call a vector
$\chi \in \Lambda $
characteristic if
$\langle \chi ,\lambda \rangle = \langle \lambda ,\lambda \rangle\ \mod 2$
for all
$\lambda \in \Lambda $
. It is easy to see, using unimodularity, that a characteristic vector exists. The coset
$\Lambda + \frac \chi 2$
of
$\Lambda $
does not depend on the choice of characteristic vector, and
$V_R$
is the sum of
$ \operatorname {\textrm{Bos}}(\mathfrak {h})$
-modules indexed by vectors in
$\Lambda + \frac \chi 2$
. Actually, “the” Ramond sector of a holomorphic VOA is well-defined only up to an overall fermion parity. The choice of characteristic vector
$\chi $
determines this parity operator: one sets
$$ \begin{align*} (V_{\Lambda})_R = \bigoplus_{\lambda \in \Lambda} (-1)^{\langle \chi,\lambda\rangle} M_{\lambda+\frac\chi2}.\end{align*} $$
As in the construction of
$V_{\Lambda }$
from the beginning of this section, “
$(-1)^{\langle \chi ,\lambda \rangle }$
” indicates the fermion parity to use for the
$ \operatorname {\textrm{Bos}}(\mathfrak {h})$
-module
$M_{\lambda +\frac \chi 2}$
.
Proposition 2.4 Suppose C is a self-dual ternary code. Then
$Z_{RR}(V_{\Lambda (C)}) = \operatorname {\textrm{Index}}(C)$
.
Proof By the remarks above,
$Z_{RR}(V_{\Lambda (C)})$
merely counts states in
$(V_{\Lambda (C)})_R$
of conformal dimension
$c/24$
: the contributions from all other states cancel. The states of minimal conformal dimension are the
$\Gamma _{\lambda + \frac \chi 2}$
where
$\frac 12(\lambda + \frac \chi 2)^2$
is as small as possible. Since
, as our characteristic vector we may take
$\chi = \sqrt 3(1,1,\dots ,1)$
. Then
, and so
$\frac 12(\lambda + \frac \chi 2)^2$
is bounded below by
$\frac 12 \bigl ( \frac 1{\sqrt 3}(\frac 12,\frac 12,\dots ,\frac 12)\bigr )^2 = c/{24}$
, with equality only when
$\lambda + \frac \chi 2 \in \frac 1{\sqrt 3}\{ \pm \frac 12 \}^c$
. This, in turn, forces
$\lambda + \frac \chi 2 = \frac 1{2\sqrt 3} \iota (w)$
, where
$w \in C$
is a maximal codeword and
is the canonical injection. So Ramond-sector ground states of
$V_{\Lambda (C)}$
are in natural bijection with maximal codewords in C, and their signed count is precisely the index of C. ▪
Remark 2.5 One can alternately prove Proposition 2.4 by formula. (The following argument was pointed out to us by Noam D. Elkies.) Let
$\eta (q) = q^{1/24} \prod _{n=1}^\infty (1-q^n)$
denote Dedekind’s eta function. For an arbitrary odd unimodular lattice
$\Lambda $
, it follows easily from the construction of the Ramond sector of
$V_{\Lambda }$
indicated above that
$$ \begin{align*} Z_{RR}(V_{\Lambda}) = \eta(q)^{-c} \sum_{\lambda \in \Lambda} (-1)^{\langle\lambda,\chi\rangle} q^{\frac12(\lambda + \frac\chi2)^2}. \end{align*} $$
Set
$\Lambda = \Lambda (C)$
, choose the characteristic vector
$\chi = \sqrt 3(1,1,\dots ,1)$
, and let
denote the natural injection. Then
Expand each vector
and each codeword
in coordinates:
$v = (v_1,\dots ,v_c)$
,
$w = (w_1,\dots ,w_c)$
. Note that
$\langle \sqrt 3 v + \frac 1{\sqrt 3}\iota (w), \chi \rangle = \sum _{i=1}^c \left ( v_i + \iota (w_i) \right ) \bmod 2$
. Then
Here,
$ \operatorname {\textrm{CWE}}_C$
is the complete weight enumerator mentioned in Remark 1.2. Similar formulas present the ordinary Theta function of
$\Lambda (C)$
in terms of
$ \operatorname {\textrm{CWE}}_C$
; see for example the last section of [Reference ElkiesElk00].
But
because the nth summand cancels with the
$(1-n)$
th summand. Furthermore, the Euler identity implies
All together, we find
$$ \begin{align*} Z_{RR}(V_{\Lambda(C)}) = \eta(q)^{-c} \operatorname{\textrm{CWE}}_C(0,\eta(q),-\eta(q)) = \operatorname{\textrm{CWE}}_C(0,1,-1) = \operatorname{\textrm{Index}}(C)\end{align*} $$
since
$ \operatorname {\textrm{CWE}}_C$
is homogeneous of degree c.
We may now prove Theorem 1.3, which asserts that if C is a self-dual ternary code of length divisible by
$24$
, then
$ \operatorname {\textrm{Index}}(C)$
is divisible by
$24$
.
Proof of Theorem 1.3
Let
$\Lambda $
be an odd unimodular lattice of rank c and, as in the proof of Proposition 2.4, choose a characteristic vector
$\chi \in \Lambda $
. Decompose
$\Lambda = \Lambda _{\textrm{ev}} \sqcup \Lambda _{\textrm{odd}}$
, where
$\Lambda _{\textrm{ev}}$
, resp.
$\Lambda _{\textrm{odd}}$
, is the set of vectors in
$\Lambda $
of even, resp. odd, square-length. Consider the sets
$$ \begin{align*} \Lambda^+ & = \Lambda_{\textrm{ev}} \sqcup \left(\Lambda_{\textrm{ev}} + \frac\chi2\right), \\ \Lambda^- & = \Lambda_{\textrm{ev}} \sqcup \left(\Lambda_{\textrm{odd}} + \frac\chi2\right). \end{align*} $$
When c is divisible by
$4$
,
$\Lambda _\pm $
are unimodular lattices, called the neighbors of
$\Lambda $
. They are even lattices when c is divisible by
$8$
. (A different choice of characteristic vector might exchange
$\Lambda _+ \leftrightarrow \Lambda _-$
.) Recall that the Theta function of a lattice
$\Lambda $
is
$$ \begin{align*} \Theta_L(q) = \sum_{\lambda \in \Lambda} q^{\lambda^2/2}.\end{align*} $$
Then, when c is divisible by
$4$
, we find
$$ \begin{align*} Z_{RR}(V_{\Lambda}) = \eta^{-c} (\Theta_{\Lambda^+} - \Theta_{\Lambda^-}).\end{align*} $$
Suppose now that C is a self-dual ternary code of length
$c=24k$
, and take
$\Lambda = \Lambda (C)$
. Since
$\Lambda ^\pm $
is even unimodular of rank
$24k$
,
$\Theta _{\Lambda ^\pm }$
is an integral modular form of weight
$12k$
, and so has an expansion of the form
$$ \begin{align*} \Theta_{\Lambda^\pm} = a^\pm_0 \Delta^k + a^\pm_1 \Delta^{k-1} c_4^3 + \dots + a^\pm_k c_4^{3k}, \end{align*} $$
where
$c_4$
denotes the weight-4 Eisenstein series and
$\Delta = \eta ^{24}$
is the discriminant. Since
$ \operatorname {\textrm{Index}}(C) = \Delta ^{-k} ( \Theta _{\Lambda ^+} - \Theta _{\Lambda ^-})$
is a supersymmetric index, it is an integer, and so
$a^+_i = a^-_i$
for
$i>0$
and the index is
$ \operatorname {\textrm{Index}}(C) = a^+_0 - a^-_0$
. But by [Reference BorcherdsBor95, Theorem 12.1] (see also [Reference HopkinsHop02, Theorem 5.10]),
$a^\pm _0$
is divisible by
$24$
. ▪
3 Automorphisms of 3-framed SCFTs
The standard definition of automorphism of a self-dual ternary code
is the following. Consider the group
$2^c{:}S_c$
. (The notation follows that of the ATLAS [Reference Conway, Curtis, Norton, Parker, Wilson and ThackrayCCN+85]. In particular, the colon denotes a semidirect product,
$p^n$
denotes an elementary abelian group of that order, and
$S_n$
denotes the symmetric group.) It acts by signed coordinate permutations on
, and
$$ \begin{align*} \textrm{Aut}(C) = \{ g \in 2^c{:}S_c\ \text{s.t.}\ g(C) = C \text{ as a set}\}.\end{align*} $$
The signed coordinate permutation action of
$2^c{:}S_c$
on
lifts to actions on
and on
, and so
$\textrm{Aut}(C)$
acts naturally on the lattice
$\Lambda (C)$
built from C.
In general, the automorphism group
$\textrm{Aut}(\Lambda )$
of a lattice
$\Lambda $
does not act on the corresponding vertex algebra
$V_{\Lambda }$
. Indeed, the modules
$M_{\lambda }$
, or equivalently their generators
$\Gamma _{\lambda }$
, are defined only up to phase, and so the action of
$\textrm{Aut}(\Lambda )$
suffers from a phase ambiguity. Let
$\widehat {\Lambda } = \hom (\Lambda ,\textrm U(1))$
denote the Pontryagin dual torus to
$\Lambda $
. Then
$\textrm{Aut}(V_{\Lambda })$
contains a subgroup of shape
$\widehat {\Lambda } .\textrm{Aut}(\Lambda )$
, where the dot denotes an extension which might or might not split. This subgroup, in turn, contains a subgroup of shape
$\widehat {\Lambda } [2].\textrm{Aut}(\Lambda )$
, where
$\widehat {\Lambda } [2] = \hom (\Lambda ,2)$
is the two-torsion subgroup of
$\widehat {\Lambda } $
; if
$\Lambda $
has rank c, then
$\widehat {\Lambda } [2] \cong 2^c$
. (The subgroup
$\widehat {\Lambda } [2].\textrm{Aut}(\Lambda ) \subset \widehat {\Lambda } .\textrm{Aut}(\Lambda )$
is not canonical, but it is canonical up to conjugation by an element of
$\widehat {\Lambda }$
. Said another way, the phase ambiguity in defining
$\Gamma _{\lambda }$
can be resolved to a sign ambiguity. That sign ambiguity cannot be resolved in general.) The subgroups
$\widehat {\Lambda } [2].\textrm{Aut}(\Lambda ) \subset \widehat {\Lambda } .\textrm{Aut}(\Lambda ) \subset \textrm{Aut}(V_{\Lambda })$
were first studied in [Reference LepowskyLep85], and the complete calculation of
$\textrm{Aut}(V_{\Lambda })$
is due to [Reference Dong and NagatomoDN99]. These results are nicely surveyed in [Reference MöllerMöl16, Section 5.3].
In spite of the fact that, in general, the extension
$\widehat {\Lambda } [2].\textrm{Aut}(\Lambda ) \subset \textrm{Aut}(V_{\Lambda })$
might not split, we claim:
Theorem 3.1 Let
be a self-dual ternary code of length c. Then
$\textrm{Aut}(C) \subset \textrm{Aut}(\Lambda (C))$
acts on
$V_{\Lambda (C)}$
— the extension
$\widehat {\Lambda (C)} [2].\textrm{Aut}(C)$
splits. The group
$\textrm{Aut}_{\mathcal N=1}(V_{\Lambda (C)})$
of automorphisms of
$V_{\Lambda (C)}$
preserving the
$\mathcal N=1$
supersymmetry contains a subgroup of shape
${C^*}{:}\textrm{Aut}(C)$
, where
. The group
$\textrm{Aut}_{\mathcal N=2}(V_{\Lambda (C)})$
of automorphisms preserving the
$\mathcal N=2$
structure contains a subgroup of shape
$C^* {:} (\textrm{Aut}(C) \cap S_c)$
.
Proof We first observe that the signed permutation action of
$2^c{:}S_c$
on
lifts to an action on
. Indeed,
carries a permutation action by
$S_c$
, and the reflections
$2^c$
also act since the automorphism
$n \sqrt 3 \leftrightarrow -n\sqrt 3$
of
lifts to an order-2 automorphism
$\Gamma _{+\sqrt 3} \leftrightarrow \Gamma _{-\sqrt 3}$
of
. Note further that this automorphism preserves the
$\mathcal N=1$
supersymmetry generator
$G = \Gamma _{+\sqrt 3} + \Gamma _{-\sqrt 3}$
on
, and so
. The reflections
$\Gamma _{+\sqrt 3} \leftrightarrow \Gamma _{-\sqrt 3}$
do not preserve the
$\mathcal N=2$
structure, but the permutations do:
.
The action of the group
$\widehat {\Lambda (C)}[2].\textrm{Aut}(C)$
on
$V_{\Lambda (C)}$
preserves (as a set) the subalgebra
, and so we have a map
extending the map
(dual to the inclusion
) and covering the map
$\textrm{Aut}(C) \hookrightarrow 2^c{:}S_c$
. But the remarks in the previous paragraph imply that the latter extension
splits. Since
has odd index in
$\Lambda (C)$
, the map
is an isomorphism. Thus the extension
$\widehat {\Lambda (C)}[2].\textrm{Aut}(C)$
splits. The subgroup
$\textrm{Aut}(C)$
manifestly preserves the
$\mathcal N=1$
structure, and
$\textrm{Aut}(C) \cap S_c$
preserves the
$\mathcal N=2$
structure.
Not all of the torus
$\widehat {\Lambda (C)} \subset \textrm{Aut}(V_{\Lambda (C)})$
preserves the supersymmetry, but the subgroup that acts trivially on the subalgebra
does. This subgroup is the kernel of the map
, and so is Pontryagin dual to the cokernel of the inclusion
. But there is a canonical isomorphism
, and its Pontryagin dual is canonically isomorphic to
$C^*$
. ▪
Example 3.2 Let
$c=12$
and consider the Ternary Golay code mentioned in Example 2.3, so that
$V_{\Lambda (\text {Golay})} \cong V^{f\natural }$
is the “supermoonshine” module of [Reference DuncanDun07]. According to [Reference DuncanDun07],
$\textrm{Aut}_{\mathcal N=1}(V^{f\natural }) \cong \textrm{Co}_1$
, Conway’s largest simple sporadic group. Since
$\textrm{Aut}(\text {Golay}) \cong 2M_{12}$
, our construction makes manifest the maximal subgroup
$3^6{:}2M_{12} \subset \textrm{Co}_1$
, which contains the three-Sylow subgroup. For comparison, the construction from [Reference DuncanDun07] makes manifest the two-Sylow-containing maximal subgroup of shape
$2^{11}{:}M_{24}$
. (The groups
$M_n$
are those of Mathieu. The “
$2$
” in
$2M_{12}$
denotes the Schur cover, called
$2.M_{12}$
in [Reference Conway, Curtis, Norton, Parker, Wilson and ThackrayCCN+85].)
The Ternary Golay code is unique up to signed permutations, but it is not unique if one uses only unsigned coordinate permutations, and different choices produce different
$\mathcal N=2$
structures. By adjusting the signs of the coordinates, one may find a copy of the Ternary Golay code which contains the all-
$1$
s word
$(1,1,\dots ,1)$
; the version given in Example 1.5 has this property. For this choice of Ternary Golay code,
$\textrm{Aut}(\text {Golay}) \cap S_c \cong M_{11}$
, and so for this
$\mathcal N=2$
structure,
$\textrm{Aut}_{\mathcal N=2}(V^{f\natural }) \supset 3^6{:}M_{11}$
. According to [Reference Cheng, Dong, Duncan, Harrison, Kachru and WraseCDD+15], a choice of
$\mathcal N=2$
structure on
$V^{f\natural }$
corresponds to a choice of oriented two-plane inside the real span of the Leech lattice, and its group of automorphisms is the subgroup of
$\textrm{Co}_1$
whose lift to
$\textrm{Co}_0=2\textrm{Co}_1$
(the Schur cover of
$\textrm{Co}_1$
) preserves this two-plane. There is only one two-plane, up to isomorphism, whose automorphism group contains a group of shape
$3^6{:}M_{11}$
. In the notation of [Reference Conway, Sloane, Bannai, Borcherds, Leech, Norton, Odlyzko, Parker, Queen and VenkovCS99, Chapter 10], it is the two-plane spanned by a simplex of “type 333,” and its full automorphism group is
$*333 \cong 3^6{:}M_{11}$
.
4 Orbifolds of 3-framed SCFTs
Let V be a holomorphic, possibly fermionic, VOA and
$G \subset \textrm{Aut}(V)$
a finite group of automorphisms of V. A typical question in conformal field theory is to “gauge” the action of G on V, to produce a new holomorphic VOA
—in the language of VOAs, the result of such a gauging procedure is the called “twisted orbifold” of V by G. One expects on physical grounds that there might be choices involved when gauging a symmetry group, and that the problem might be obstructed. Specifically, one expects to encounter an ’t Hooft anomaly living in some cohomology group of G such that trivializations of the anomaly correspond to choices of
. (In particular, if the anomaly is trivializable, then there are as many choices of orbifold
as there are elements in the cohomology group of one lower degree.) The bosonic case is well studied in the VOA literature: the ’t Hooft anomaly is an ordinary cohomology class
[Reference Dijkgraaf, Vafa, Verlinde and VerlindeDVVV89, Reference KirillovKir02, Reference MügerMüg10], and is known to exist when G is solvable [Reference Carnahan and MiyamotoCM16] and expected to exist in general.
We will need the fermionic generalization, which has been only partially explored in the VOA literature. The main complication is that the anomalies do not live in ordinary
-valued cohomology, but rather in a generalized cohomology theory called “supercohomology.” There are two versions of this cohomology theory, a “restricted” version
$ \operatorname {\textrm{rSH}}^\bullet $
introduced in the condensed matter literature in [Reference Gu and WenGW14] and an “extended” version
$ \operatorname {\textrm{SH}}^\bullet $
introduced in [Reference Wang and GuWG18]. (These objects have been introduced earlier in the mathematics literature. For example,
$ \operatorname {\textrm{rSH}}^\bullet $
is isomorphic to the cohomology theory called “E-theory” in [Reference FreedFre08].)
These cohomology theories can be constructed in various ways. The quickest description is the following.
First, consider the symmetric monoidal category
of complex super vector spaces. It has a symmetric monoidal subcategory
of
$\otimes $
-invertible objects and morphisms: up to isomorphism,
has two objects (the bosonic and fermionic lines
and
); all morphisms in
are isomorphisms, and the automorphism group of any object is
. Any category
$\mathcal C$
has a classifying space
$|\mathcal C|$
built as a simplicial complex: each object in
$\mathcal C$
provides a point in
$|\mathcal C|$
; each one-morphism in
$\mathcal C$
provides a one-simplex in
$|\mathcal C|$
; each composable pair
$X \overset f \to Y \overset g \to Z$
provides a two-simplex with sides f, g, and
$gf$
; and so on. This construction is simplest when starting with a groupoid like
, as one can immediately read off the homotopy groups:
,
for any basepoint, and all other homotopy groups are trivial. In other words, at the level of spaces there is a homotopy equivalence
— but we will equip
with more structure that does not factor as a product. Specifically, the symmetric monoidal structure on
restricts to a symmetric monoidal structure on
, and this induces an infinite loop space structure on
which does not factor as a product.
The same construction can be applied to the the symmetric monoidal bicategory
of complex super algebras and super bimodules (so that equivalences in
are super Morita equivalences). One first restricts attention to its sub-bicategory
of
$\otimes $
-invertible objects and morphisms; it is a symmetric monoidal two-groupoid. Then one constructs the classifying space
, which is an infinite loop space because of the symmetric monoidal structure. Its homotopy groups are
,
, and
.
Any infinite loop space determines a generalized cohomology theory. When starting with a symmetric monoidal n-groupoid
$\mathcal C$
, it is convenient to index the degrees so that the degree-k cohomology of a point is
$\pi _{n-k} |\mathcal C|$
; in this way, the cohomology of all spaces is supported in nonnegative degrees. With this convention, we define:
Definition 4.1 The generalized cohomology theory
$ \operatorname {\textrm{rSH}}^\bullet $
of restricted supercohomology is the cohomology theory determined by the infinite loop space
, with degrees indexed so that
and
(and the other cohomology groups of a point vanish). Its values on a space X are:
In this formula, the space
is the k-fold delooping of
, witnessing it as an infinite loop space, with homotopy groups
$\pi _{k+i} \textrm B^k = \pi _i$
. The use of
$\pi _1$
is because
is a one-category.
The generalized cohomology theory
$ \operatorname {\textrm{SH}}^\bullet $
of extended supercohomology is the cohomology theory determined by the infinite loop space
, with degrees indexed to that
,
, and
(and the other cohomology groups of a point vanish). Its values on a space X are:
The fibre sequences
and
of infinite loop spaces lead to long exact sequences
In the first of these, the connecting map
, also called the k-invariant of
, is
$(-1)^{ \operatorname {\textrm{Sq}}^2}$
, where
$ \operatorname {\textrm{Sq}}^2$
is the degree-2 Steenrod square. This arises directly from (indeed, it encodes) the Koszul sign rules in
. This long exact sequence can be used to compute the restricted supercohomology of any space, and, together with the general construction of [Reference Kock, Kristensen and MadsenKKM67], it determines a cocycle model of
$ \operatorname {\textrm{rSH}}^\bullet $
that exactly matches the cocycle model from [Reference Gu and WenGW14]. The second long exact sequence is more complicated and we do not know a complete formula for its connecting map; discussion of the k-invariants in
$ \operatorname {\textrm{SH}}^\bullet $
can be found for example in [Reference Gaiotto and Johnson-FreydGJF19, Section 5.4].
Given a class in
$ \operatorname {\textrm{SH}}^\bullet (X)$
, its image in
is called its Majorana layer. Given a class in
$ \operatorname {\textrm{rSH}}^\bullet (X)$
, its image in
is called its Gu–Wen layer. The connecting maps in the above long exact sequences are stable cohomology operations, and so vanish in very low degrees. In particular, for
$\bullet =3$
, we have inclusions
When G is a finite group and
$\textrm H^\bullet (-)$
a cohomology theory, we will write
$\textrm H^\bullet _{\textrm{gp}}(G)$
in place of
$\textrm H^\bullet (\textrm B G)$
. We will denote reduced cohomology by
$\widetilde {\textrm H}{}$
,
$\widetilde { \operatorname {\textrm{SH}}}{}$
, etc; for instance,
$\widetilde { \operatorname {\textrm{SH}}}_{\textrm{gp}}^\bullet (G)$
is by definition the kernel of the restriction map
$ \operatorname {\textrm{SH}}^\bullet _{\textrm{gp}}(G) \to \operatorname {\textrm{SH}}^\bullet _{\textrm{gp}}(\textrm{pt})$
, so that there is a canonical direct sum decomposition
$ \operatorname {\textrm{SH}}^\bullet _{\textrm{gp}}(G) \cong \widetilde { \operatorname {\textrm{SH}}}_{\textrm{gp}}^\bullet (G) \oplus \operatorname {\textrm{SH}}^\bullet _{\textrm{gp}}(\textrm{pt})$
. (In particular,
$ \operatorname {\textrm{SH}}^\bullet $
and
$\widetilde { \operatorname {\textrm{SH}}}^\bullet $
agree except for in degrees
$\bullet \leq 2$
.) Recall that a VOA is regular if its category of admissible modules is finite semisimple.
Theorem 4.2 Let V be a holomorphic, possibly fermionic, VOA and G a finite group acting faithfully on (the NS sector of) V. Assume that the G-fixed sub-VOA
$V^G$
is regular. Then there is a well-defined ’t Hooft anomaly
$\alpha \in \widetilde { \operatorname {\textrm{SH}}}^3_{\textrm{gp}}(G)$
. Each trivialization of
$\alpha $
determines an orbifold VOA
. In particular, there are
$\widetilde { \operatorname {\textrm{SH}}}^2_{\textrm{gp}}(G)$
-many orbifolds.
When V is bosonic, the ’t Hooft anomaly
$\alpha $
lives in
. Trivializations in
give bosonic orbifolds.
Note that if G is solvable, then regularity of
$V^G$
follows from the main result of [Reference Carnahan and MiyamotoCM16]. (That paper discusses the bosonic case, but the fermionic case follows immediately by passing to the bosonic subalgebra of V.)
Proof The bosonic statement is the main result of [Reference KirillovKir02]. The proof of the fermionic version is essentially the same, replacing everywhere the word “category” with “supercategory”—a
-linear supercategory is a category enriched and tensored over
. Details on supercategories, as well the analytic steps to identify categorical constructions inside modular tensor (super)categories with vertex operator (super)algebraic constructions, can be found in [Reference Creutzig, Kanade and McRaeCKM17]. One version of the proof goes as follows.
For each
$g \in G$
, consider the supercategory
of g-twisted V-modules. It is nonempty, and regularity of
$V^G$
provides a fusion product
. Thus the direct sum
is a G-graded “superfusion category.” Its neutral component
is a copy of
since V is holomorphic. The tensor product of nonzero objects in a (super) fusion category never vanishes. (Indeed, let
$X,Y \in \mathcal C$
be nonzero. Then
$\operatorname {id}_Y \neq 0 \in \hom (Y,Y)$
, which by adjunction says that the coevaluation map
$\operatorname {coev}_Y : \textbf {1}_{\mathcal C} \to Y \otimes Y^*$
is nonzero, hence an injection since the unit object
$\textbf {1}_{\mathcal C}$
is simple. But then
$\operatorname {id}_X \otimes \operatorname {coev}_Y : X \to X \otimes Y \otimes Y^*$
is an injection, and so
$X \otimes Y$
cannot vanish.) Fix g, and suppose
. Then
is nonzero, and so
$\hom (Y,X) = \hom (\textbf {1}_{\mathcal C},X \otimes Y^*)$
is a nonzero super vector space. It follows that for each g,
has only one (up to possibly odd isomorphism) simple object, with endomorphism algebra either
or
.
There is a natural “Deligne” tensor product
$\boxtimes $
of supercategories. Consider the assignment
. The previous paragraph shows that
is
$\boxtimes $
-invertible, and the fusion
turns the assignment
into a monoidal functor
$$ \begin{align*} G \to \{\boxtimes\text{-invertible supercategories}\},\end{align*} $$
where G is considered a monoidal bicategory with only identity one- and two-morphisms. The functor that to each superalgebra assigns its supercategory of modules provides an equivalence
of (symmetric) monoidal bicategories. All together, we have constructed a monoidal map
, which is precisely the data of a class
$\alpha \in \operatorname {\textrm{SH}}^3_{\textrm{gp}}(G)$
. Going the other way, a class
$\alpha \in \operatorname {\textrm{SH}}^3_{\textrm{gp}}(G)$
determines a super fusion category
, and the construction is arranged to produce an equivalence
.
Following [Reference KirillovKir02], we can identify
with the Drinfeld center of
, understood of course in the super sense. Trivializations of
$\alpha $
determine algebra objects in
with certain nice properties (in particular, they are “Lagrangian”), and hence extensions of
$V^G$
to holomorphic VOAs. These extensions are the orbifolds
. ▪
Example 4.3 Suppose V is a holomorphic VOA with a nonanomalous action by the Klein-4 group
. We will work out all possible orbifolds of V by subgroups of G.
First, suppose that V is bosonic—what are its bosonic orbifolds? There are three copies of
, each nonanomalous, and so we find three VOAs
. There are also two ways to orbifold V by all of G, since
. Anticipating the answer, we rename
$V = V_1$
, and call the two orbifolds
by the names
$V_2$
and
$V_3$
. One can form
$V_2$
from
$V_1$
in two steps. First, orbifold one of the
s inside G, say the first one
$\langle g \rangle \subset G$
, resulting in the VOA
$W_1$
. Then
$W_1$
has a new
acting on it by changing the sign of the twist field. It also has an “old”
symmetry. Actually, to define this “old”
action requires the data of the trivialization of the anomaly
$\alpha $
:
$W_1$
has two canonical “old”
actions, differing by the action of the “new”
. After choosing the trivialization of
$\alpha $
, we can build
$V_2$
by orbifolding
$W_1$
by this old
action. If we had used the other trivialization of
$\alpha $
, hence the other “old”
, we would land not at
$V_2$
but at
$V_3$
. If instead we had orbifolded
$W_1$
by the “new”
that changed the sign of the twist field, we would return to
$V_1$
. All together we find that our six VOAs
$V_1,V_2,V_3,W_1,W_2,W_3$
form a
$K_{3,3}$
graph, where the edges denote possible
-orbifolds:
Consider now to the situation that
$V=V_1$
is still bosonic, but allow fermionic orbifolds. For each
, there is a unique bosonic orbifold
, since
, but there is also a fermionic one, since
. Note that since V is bosonic and holomorphic, its central charge, hence the central charge of all of its orbifolds, is divisible by
$8$
. Now suppose F is any actually-fermionic holomorphic VOA of central charge divisible by
$8$
—by “actually fermionic” we mean that F is not bosonic. Then F has two bosonic neighbors, defined as the two bosonic holomorphic VOAs containing the even subalgebra of F, or equivalently the two results of gauging the fermion parity operator
$(-1)^f$
on F. (Only when the central charge is divisible by
$8$
is
$(-1)^f$
is nonanomalous with
bosonic.) These two neighbors
$V,W$
of F are related by a (bosonic)
-orbifold. In this way actually-fermionic holomorphic VOAs of central charge divisible by
$8$
are identified with pairs of bosonic VOAs related by
orbifold. This identification is a VOA analog of the “even neighbors” of an odd unimodular lattice of rank divisible by
$8$
.
Returning to our question, we find that the actually-fermionic orbifolds of
$V = V_1$
by subgroups of
are in bijection with the edges of the above
$K_{3,3}$
graph. For
$i,j \in \{1,2,3\}$
, we will let
$F_{ij}$
denote the fermionic VOA whose neighbors are
$V_i$
and
$W_j$
. The orbifolds of
$V_1$
by a single
are the
$W_j$
s and the
$F_{1j}$
s. (There are three
s, and each gives
many orbifolds.) The remaining
$V_2,V_3,F_{2j},F_{3j}$
are the results of orbifolding
$V_1$
by all of
. To check that we have not missed any, note that there should be precisely
such orbifolds.
Just as in the bosonic case, the fermionic orbifolds
$F_{ij}$
each come with an action of a Klein-4 group
, which now contains the fermion parity operator
$(-1)^f$
. Each of the other
s provides two orbifolds, which are themselves related by a
-orbifold: in the fermionic world,
-orbifolds always come in trios (for example, an actually-fermionic VOA together with its even neighbors). All together, we find that the above
$K_{3,3}$
graph expands to the following:
Finally, in the case where there is no bosonic theory in sight, one finds the same graph of possible orbifolds, with the only difference being that there is no way to distinguish which vertices are “V,” “F,” or “
$W.$
” This graph has a more symmetrical description. (We thank David Treumann for helping to understand this point.) The vertices correspond to Lagrangian two-planes inside symplectic
(equivalently Lagrangian algebras in
). The edges correspond to pairs of planes intersecting in a line. Every isotropic line is contained in precisely three Lagrangian planes, hence the triangles. The symmetry group of the graph is the symplectic group
.
The construction of
$\alpha \in \operatorname {\textrm{SH}}^3_{\textrm{gp}}(G)$
in the proof of Theorem 4.2 identifies its layers as follows. Choose, for each
$g\in G$
, a simple object
. The object
$V(g)$
is “the” g-twisted sector—the word “the” is in quotes because
$V(g)$
is unique only up to possibly-odd isomorphism. The Majorana layer
records whether
$V(g)$
is “ordinary” with
or “Majorana” with
. Suppose that the Majorana layer vanishes, and let
denote the Gu–Wen layer of
$\alpha $
. Then
$\alpha ^{(2)}(g_1,g_2)$
records whether the isomorphism
$V(g_1) \otimes V(g_2) \cong V(g_1g_2)$
is even or odd. Finally, the “ordinary cohomology” layer of
$\alpha $
provides the associator on
$\mathcal C$
, just as in the bosonic case.
There is another description of the Majorana and Gu–Wen layers of
$\alpha $
that is more useful for computation. (One can show the two descriptions agree by studying the “bosonic shadow” of the super fusion category
of G-twisted V-modules; see [Reference Bhardwaj, Gaiotto and KapustinBGK17].) Consider the action of
$g\in G$
on “the” Ramond sector
$V_R$
of V. Again the word “the” is in quotes because
$V_R$
is defined only up to possibly-odd isomorphism. In particular, the action of g on
$V_R$
might be even or odd, determined by the Majorana layer
$\alpha ^{(1)}(g)$
. Suppose that the Majorana layer vanishes, so that the anomaly
$\alpha $
lives in restricted supercohomology. Then G acts by even automorphisms of
$V_R$
, but the action may still be projective (since
$V_R$
is determined only up to isomorphism). The projectivity of the action is precisely the Gu–Wen layer
.
In this paper we care most about the case when
is a cyclic group. The abelian group structure of extended supercohomology can be hard to understand—formulas for it in [Reference Bhardwaj, Gaiotto and KapustinBGK17] require the quaternion group
$Q_8$
. Restricted supercohomology is easier. In particular, if
is a cyclic group of order m with generator g, then
generated by the ’t Hooft anomaly of the action of
on
$ \operatorname {\textrm{Fer}}(2)$
in which g acts by
$\frac {2\pi }m$
-rotation of the two fermions.
Suppose
acts on V with trivial Majorana layer. Consider the character of g, defined as
$$ \begin{align*}Z_{NS,NS}^{1,g}(V) = \textrm{tr}_V(g q^{L_0 - c/24}).\end{align*} $$
Since V is holomorphic, this character will have good modularity properties. In particular, it will be a meromorphic level-m modular function, perhaps with multiplier, when m is even. When m is odd, the spin structures get rearranged by the modular transformation
$T^m$
, and so
$Z_{NS,NS}^{1,g}(V)$
will have level
$2m$
. In both cases, if the action were nonanomalous, the multiplier would agree with the multiplier of
$Z_{NS,NS}^{1,1}(V) = \textrm{tr}_V(q^{L_0 - c/24})$
. By studying the
$\frac {2\pi }m$
-rotation of two free fermions, one finds that when m is odd and
acts on V with anomaly
, then
$ST^{2m}S^{-1}$
will act on
$Z_{NS,NS}^{1,g}(V)/Z_{NS,NS}^{1,1}(V)$
with eigenvalue
$\exp (\alpha \frac {2\pi i}m)$
. If m is even and
acts on V with anomaly
, then
$ST^{m}S^{-1}$
will act on
$Z_{NS,NS}^{1,g}(V)/Z_{NS,NS}^{1,1}(V)$
with eigenvalue
$\exp (\alpha \frac {2\pi i}{2m})$
. Thus, when G is cyclic and the Majorana layer vanishes, the multiplier fully determines the ’t Hooft anomaly (compare [Reference Gaberdiel, Persson, Ronellenfitsch and VolpatoGPRV13, Section 3]).
Example 4.4 Let
$\Lambda $
be a (possibly odd) unimodular lattice, and
$g \in \textrm{Aut}(\Lambda )$
an automorphism of order m. Choose a lift
$\tilde {g}$
of g to
$\widehat {\Lambda }.\textrm{Aut}(\Lambda ) \subset \textrm{Aut}(V_{\Lambda })$
. Choose also a characteristic vector
$\chi \in \Lambda $
, so that the Ramond sector is built from the states
$\Gamma _{\lambda + \frac \chi 2}$
for
$\lambda \in \Lambda $
. Then
$\tilde {g}$
acts on the Ramond sector by
$\tilde {g}(\Gamma _{\lambda + \frac \chi 2}) \propto \Gamma _{g(\lambda ) + \frac {g(\chi )}2}$
, where the proportionality factor has not been determined. In particular,
$\tilde {g}$
is even or odd depending only on the relative parity of the vectors
$\lambda + \frac \chi 2$
and
$g(\lambda ) + \frac {g(\chi )}2$
. Since
$\chi $
is characteristic, this relative parity is
$$ \begin{align*} & \left\langle \chi, \left(\lambda + \frac\chi2\right) - \left(g(\lambda) + \frac{g(\chi)}2\right)\right\rangle\\ &\quad= \langle \chi, (1-g)\lambda\rangle + \left\langle \chi, (1-g)\frac\chi2\right\rangle = \frac12 \langle \chi, (1-g)\chi\rangle\ \ \ \,\mod 2.\end{align*} $$
The second equality follows from the fact that
$\langle \chi ,g\lambda \rangle = (g\lambda )^2 = \lambda ^2 = \langle \chi ,\lambda \rangle \bmod 2$
, for any
$\lambda \in \Lambda $
. In particular,
, and we find that the Majorana layer of the ’t Hooft anomaly of the
$\tilde {g}$
action vanishes if and only if
.
Suppose that this Majorana layer does vanish, and suppose further that g has no (nonzero) fixed points. Then all lifts
$\tilde {g}$
of g are conjugate. Since conjugate automorphisms have the same ’t Hooft anomaly, we will drop the tilde, writing
$g \in \textrm{Aut}(V_{\Lambda })$
for any lift of
$g \in \Lambda $
. Let us assume that this lift still has order m. This is automatic when m is odd; when m is even, it happens if and only if
for all
$\lambda $
.
Since the action of g on
$\Lambda $
has no fixed points, the character of
${g}$
is easy to compute. Since g is a lattice automorphism, its characteristic polynomial factors as
$$ \begin{align*} \det(g-x) = \prod_{k|m} (1-x^k)^{d_k} \end{align*} $$
for some integers
$d_k$
. The corresponding formal expression
$\prod k^{d_k}$
is the Frame shape of g, introduced by Frame in [Reference FrameFra70]. Define the corresponding eta product to be
$$ \begin{align*} \eta_g(q) = \prod_{k|m} \eta(q^k)^{d_k}. \end{align*} $$
Then standard formulas give
$$ \begin{align*} Z_{NS,NS}^{1,g} = \frac1{\eta_g(q)}.\end{align*} $$
Noting that
$\eta $
itself has a multiplier of
$\exp (\frac {2\pi i}{24})$
under the action of T, we find that
$ST^{m}S^{-1}$
(or
$ST^{2m}S^{-1}$
, if m is odd) acts on
$Z_{NS,NS}^{1,g}/Z_{NS,NS}^{1,1}$
with eigenvalue
$$ \begin{align*} \exp\left( \frac{2\pi i}{24} \sum_{k|m} d_k \frac m k (k^2-1)\right). \end{align*} $$
It is a basic fact that if k is coprime to
$6$
, then
$k^2-1$
is divisible by
$24$
. (Conway and Norton in [Reference Conway and NortonCN79] call this fact “the defining property of the number
$24$
.”) In particular, lattice automorphisms of order coprime to
$6$
always have vanishing ’t Hooft anomaly. Assuming the Majorana layer vanishes, the ’t Hooft anomaly of an arbitrary fixed-point-free lattice automorphism always has order dividing
$24$
, and is determined by the Frame shape of the automorphism:
$\alpha $
“
$=$
”
$\sum _{k|m} d_k \frac m k (k^2-1) \bmod 24$
.
If g had fixed a sublattice
$\Lambda ^g \subset \Lambda $
, then the character would have a numerator of the form
$\sum _{\lambda \in \Lambda ^g} \phi (\lambda ) q^{\lambda ^2/2}$
for some phases
$\phi (\lambda )$
, and the lift of g would not be unique up to conjugation. There is always a “standard” lift [Reference LepowskyLep85], for which these phases are trivial. In this case the ’t Hooft anomaly is again determined the the Frame shape (provided the Majorana layer vanishes); compare [Reference MöllerMöl16, Chapter 5]. We warn the reader, however, that, when
$\Lambda $
is odd and m is even, the most natural lift might not be the “standard” one, and encourage the interested reader to consider the case of
$g = \bigl ( \begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix}\bigr )$
acting on the
lattice.
Example 4.5 There are precisely two self-dual ternary codes of length
$c=24$
with minimal Hamming weight
$9$
[Reference Leon, Pless and SloaneLPS81]: the quadratic residue code
$Q_{23}$
and Pless’s code
$P_{11}$
from [Reference PlessPle69]. Letting C be either of these codes, the corresponding lattice
$\Lambda (C)$
will be a rank-
$24$
lattice whose shortest vectors have square-length
$3$
. There is a unique such lattice, the “odd Leech lattice”
$\textrm{OddLeech}$
discovered in [Reference O’Connor and PallOP44]. The automorphism group of
$\textrm{OddLeech}$
has shape
$2^{12}{:}M_{24}$
; the codes
$Q_{23}$
and
$P_{11}$
make visible the subgroups
and
respectively.
Each of these codes C equips
$V_{\textrm{OddLeech}} = V_{\Lambda (C)}$
with an
$\mathcal N=1$
supersymmetry. These two supersymmetries are not related by an automorphism of
$V_{\textrm{OddLeech}}$
. Indeed, since the shortest vectors in
$\textrm{OddLeech}$
have square-length
$3$
, the connected component of
$\textrm{Aut}(V_{\textrm{OddLeech}})$
is merely the dual torus
$\widehat {\textrm{OddLeech}}$
, and so the action of
$\widehat {\textrm{OddLeech}}$
on
$V_{\textrm{OddLeech}}$
is canonical (and not just canonical up to isomorphism). Decompose the supersymmetry generator coming from the self-dual ternary code C into
$\widehat {\textrm{OddLeech}}$
-eigenvectors. Its “support” (i.e., those eigenvalues appearing with nonzero coefficient in the decomposition) generates the sublattice
. Since the only automorphisms of
are signed coordinate permutations, the embedding
, which was determined by the supersymmetry generator, determines C up to isomorphism.
Consider the automorphism
$g : \lambda \mapsto -\lambda $
of
$\textrm{OddLeech}$
of order
$m=2$
. As with all lattices, g lifts to an order-2 automorphism of
$V_{\textrm{OddLeech}}$
, unique up to conjugation. As with all lattices built from self-dual ternary codes, we may choose the characteristic vector
, and calculate
. So the Majorana layer of the ’t Hooft anomaly of g vanishes. The full anomaly may be calculated as in Example 4.4: the Frame shape of g is
$1^{-24}2^{24}$
, and
$\sum _{k|m} d_k \frac m k (k^2-1) = (-12)\frac 21 (1^2-1) + (24)\frac 22 (2^2-1) = 72 = 0 \bmod 24$
. Thus the action of g on
$V_{\textrm{OddLeech}}$
is nonanomalous.
We claim that both orbifolds
are isomorphic to the “beauty and the beast” odd VOA from [Reference Dixon, Ginsparg and HarveyDGH88], which we will call
$V^\sharp $
(it is not given a name in [Reference Dixon, Ginsparg and HarveyDGH88]). Recall the usual construction of the Moonshine VOA
$V^\natural $
from [Reference Frenkel, Lepowsky and MeurmanFLM88]:
, where implicitly the bosonic orbifold is chosen. One can instead choose the fermionic orbifold, with bosonic neighbors
$V_{\textrm{Leech}}$
and
$V^\natural $
. That fermionic orbifold is precisely
$V^\sharp $
.
To explain the isomorphism
, let us first recall some of the standard Moonshine story from [Reference Frenkel, Lepowsky and MeurmanFLM88]. The presentation
makes visible the maximal subgroup of shape
$2^{1+24}.\textrm{Co}_1$
of the Monster group
; to see the whole Monster group, one must make visible one further automorphism, and this is done in [Reference Frenkel, Lepowsky and MeurmanFLM88] by starting not with the Leech lattice but with the Niemeier lattice
${\operatorname {Nie}(A_1^{24})}$
with root system
$A_1^{24}$
. The connected component of the automorphism group of
$V_{{\operatorname {Nie}(A_1^{24})}}$
is isomorphic to the quotient
$\textrm{SU}(2)^{24} / 2^{12}$
, where the normal subgroup
$2^{12} \subset \textrm{Center}(\textrm{SU}(2)^{24}) = 2^{24}$
is a copy of the binary Golay code, and in particular contains the element
$(-I,-I,\dots ,-I)$
, where
$I \in \textrm{SU}(2)$
is the identity matrix. Consider the Klein-4 subgroup of
$\textrm{SU}(2)^{24} / 2^{12}$
generated by the elements
$g = (S,\dots ,S)$
and
$h = (H,\dots ,H)$
, where
$S = \bigl (\begin {smallmatrix} 0 & 1 \\ -1 & 0 \end {smallmatrix}\bigr )$
and
$H = \bigl ( \begin {smallmatrix} i & 0 \\ 0 & -i \end {smallmatrix}\bigr )$
. The orbifold
is manifestly isomorphic to
$V_{\textrm{Leech}}$
, since h is the lattice momentum vector picking out the lattice neighborship relating
${\operatorname {Nie}(A_1^{24})}$
and
$\textrm{Leech}$
, whereas g is a lift of the lattice involution
$\lambda \mapsto -\lambda $
. For either trivialization of the anomaly, the action of
$\langle g \rangle $
on
is a lift of
$\lambda \mapsto -\lambda $
. Thus, we find that, for either trivialization,
. But g and h are conjugate in
$\textrm{SU}(2)^{24} / 2^{12}$
, and this symmetry survives to
$V^\natural $
, providing the extra automorphism desired.
In terms of the bosonic
$K_{3,3}$
diagram from Example 4.3, we have
$V_1 \cong V_{\operatorname {Nie}(A_1^{24})}$
,
$W_1 \cong W_2 \cong W_3 \cong V_{\textrm{Leech}}$
, and
$V_2 \cong V_3 \cong V^\natural $
. From this we can fill in the fermionic theories:
$F_{1j} \cong V_{\textrm{OddLeech}}$
for all j, and
$F_{2j} \cong F_{3j} \cong V^\sharp $
. Identifying
$F_{11} = V_{\textrm{OddLeech}}$
with the fermionic orbifold
, we find that the other
actions on
$F_{11}$
—the groups
$\langle g \rangle $
and
$\langle gh \rangle $
—both lift the lattice involution
$\lambda \mapsto -\lambda $
. Inspecting the fermionic diagram from Example 4.3, we find that the possible orbifolds
are the theories called
$F_{ij}$
with
$i,j\in \{2,3\}$
, which are all isomorphic to
$V^\sharp $
.
The main result of the paper [Reference Dixon, Ginsparg and HarveyDGH88] is that
$V^\sharp $
admits
$\mathcal N=1$
supersymmetry. Their proof is nonconstructive (and we were unable to follow certain important steps in it). By instead realizing
$V^\sharp $
as
for a self-dual ternary code C, we have made the supersymmetry explicit. Indeed, the two different codes
$P_{11}$
and
$Q_{23}$
provide, a priori, two different
$\mathcal N=1$
supersymmetries to
$V^\sharp $
. We do not know if they are in fact isomorphic.
5 Topological modular forms
TMF are a fairly mysterious object from stable homotopy theory that refines the usual ring of modular forms (see e.g., [Reference HopkinsHop02, Reference Douglas, Francis, Henriques and HillDFHH14]). TMF is a “chromatic height two” analog of oriented K-theory: “chromatic height” in stable homotopy theory is roughly the same as “category number” and so one expects that, whereas the K-theory of a manifold measures its one-category of vector bundles, the TMF of that manifold measures some two-category. TMF owes its origins to Witten’s work connecting supersymmetric string theory to the K-theory of loop spaces [Reference WittenWit87, Reference WittenWit88]; see also Segal’s early survey [Reference SegalSeg88], in which he suggests a model of TMF in terms of his then-recent axiomatization of conformal field theory. Building on those ideas, Stolz and Teichner proposed a conjectural geometric description of TMF [Reference Stolz and TeichnerST04, Reference Stolz and TeichnerST11]. Translated into more physical language, their description is:
Conjecture 5.1 (Stolz–Teichner)
Let X be a manifold. The degree-n TMF of X is
$$ \begin{align*} \mathrm{TMF}^n(X) = \pi_0 \left\{ \begin{array}{c} \mathcal N=(0,1)\mbox{ boundary conditions for the}\ n\mbox{th power} \\ \mbox{of the}\ c=\frac12\ \mbox{invertible fermionic (2+1)d TFT} \\ \mbox{which couple to a background scalar field valued in }X \end{array} \right\}. \end{align*} $$
By “the nth power of the
$c=\frac 12$
invertible fermionic (2+1)d TFT,” we mean the invertible topological order admitting n antichiral Majorana fermions as a boundary condition. Take any
$\mathcal N=(0,1)$
boundary condition for this bulk theory. Up to minor ambiguities (see Remark 5.3), we can identify the boundary condition with an
$\mathcal N=(0,1)$
SQFT with gravitational anomaly
$n/2$
. Taking X to be a point, we have:
Conjecture 5.2 (Stolz–Teichner, simplified)
$$ \begin{align*}\pi_n \mathrm{TMF} = \pi_0 \{\mathcal N=(0,1) \mbox{ SQFTs with gravitational anomaly } n/2\}.\end{align*} $$
Remark 5.3 Recall that for an SCFT, the gravitational anomaly is
$c_R - c_L$
; the notion of “gravitational anomaly” makes sense even when the SQFT is not conformal. The relationship between gravitational anomalies and boundary theories is explored, among other places, in [Reference Freed and TelemanFT14].
Conjecture 5.2 should not be taken too literally because of a minor sign ambiguity stemming, ultimately, from the choice of fermion parity of “the” Ramond sector. This leads to a sign ambiguity in defining the Ramond–Ramond partition function. Changing that sign corresponds to stacking the theory with an invertible fermionic (1+1)d TFT.
There is an alternate way to relate the Conjectures. By employing the reference Majorana fermions boundary condition, one can map the
$\mathcal N=(0,1)$
boundary condition to an
$\mathcal N=(0,1)$
SQFT with no gravitational anomaly and a decoupled subsector consisting of n left-moving Majorana fermions, acted upon trivially by the
$\mathcal N=(0,1)$
supercharge. Conversely, one can rephrase Conjecture 5.1 to avoid any mention of (2+1)d TFTs by instead using the moduli space of nonanomalous SQFTs equipped with such a subsector. The coset of the subsector is the gravitationally-anomalous SQFT in Conjecture 5.2.
A basic property of topological modular forms is that there is a map from TMF to ordinary cohomology with coefficients in the ring
$\textrm{MF}$
of ordinary integral modular forms. (The homotopy theorists’ convention is to think of
$\textrm{MF}$
as a graded-commutative ring concentrated entirely in even degrees, so that weight-c modular forms are in homotopical degree
$n=2c$
.) When the primes
$2$
and
$3$
are inverted, this map
$\textrm{TMF} \to \textrm{MF}$
is an isomorphism, but it has interesting kernel and cokernel at the primes
$2$
and
$3$
. The map has been computed on homotopy. In particular, the image of
$\pi _n \textrm{TMF} \to \textrm{MF}_{n/2}$
is fully understood [Reference HopkinsHop02, Proposition 4.6]. It is not a surjection. Its most interesting feature is that
$m \Delta ^k$
is in the image of
$\pi _n \textrm{TMF} \to \textrm{MF}_{n/2}$
when and only when
$24$
divides
$mk$
.
In terms of Conjecture 5.2, the map
$\textrm{TMF} \to \textrm{MF}$
should take an
$\mathcal N=(0,1)$
SQFT V to its Ramond-Ramond partition function
$Z_{RR}(V)$
, multiplied by
$\eta ^n$
. The supersymmetry plays two roles: it protects
$Z_{RR}(V)$
to be invariant under deformations, and in particular under RG flow; it makes
$Z_{RR}(V)$
, which for a general QFT would be a function of both q and
$\bar {q}$
, into a function of q alone. As a special case, Conjecture 5.1 predicts:
Conjecture 5.4 Each holomorphic VOA V of central charge c equipped with
$\mathcal N=1$
supersymmetry determines a class in
$\pi _{2c}\textrm{TMF}$
. Its image in
$\textrm{MF}$
is
$Z_{RR}(V) \eta ^{2c}$
, where
denotes the supersymmetric index of V.
Conjecture 5.5 In particular, if V is a holomorphic
$\mathcal N=1$
SCFT of central charge
$c=12k$
, then
$Z_{RR}(V)$
is divisible by
$\frac {24}{\gcd (k,24)}$
.
One may prove this Conjecture when
$k\leq 2$
by inspecting the classification of holomorphic VOAs of small central charge:
Proof of Conjecture 5.5 for k ≤ 2
When
$k=1$
, the only holomorphic
$\mathcal N=1$
VOA of central charge
$c=12$
and nonzero index is Duncan’s supermoonshine SCFT
$V^{f\natural }$
[Reference DuncanDun07]; see Examples 2.3 and 3.2. Its index is
$24$
.
When
$k=2$
, Conjecture 5.5 holds even when there is no supersymmetry. Indeed, suppose V is an actually-fermionic holomorphic VOA of central charge
$c=24$
. Its bosonic neighbors
$V^\pm $
are the two results of gauging the fermion parity operator
$(-1)^f$
on V. This symmetry is nonanomalous, and the results of gauging it are bosonic, because the central charge is divisible by
$8$
. (This generalizes the “even neighbors” of an odd lattice; c.f. [Reference Conway, Sloane, Bannai, Borcherds, Leech, Norton, Odlyzko, Parker, Queen and VenkovCS99, Chapter 17].) Just as in the proof of Theorem 1.3, we find
$Z_{RR}(V) = Z(V^+) - Z(V^-)$
, where
$Z(V^\pm )$
denotes the ordinary partition function of
$V^\pm $
. Being holmorphic VOAs of central charge
$c=24$
, these
$V^\pm $
are highly constrained [Reference SchellekensSch93]. In particular, their partition functions are of the form
$Z(V^\pm ) = J + \dim (V^\pm _1)$
where
$J(q) = q^{-1} + O(q) = c_4^3\Delta ^{-1} - 744$
is the normalized
hauptmodule and
$\dim (V^\pm _1)$
are the dimensions of the horizontal Lie algebras in
$V^\pm $
. By inspecting Schellekens’ list [Reference SchellekensSch93], we find that
$\dim (V^\pm _1)$
, hence
$Z_{RR}$
, is always divisible by
$12$
. ▪
The converse of Conjecture 5.5 is our Main Question, restated here:
Main Question For each k, does there exist a holomorphic
$\mathcal N=1$
VOA with central charge
$c=12k$
and index
$\frac {24}{\gcd (k,24)}$
?
Our ternary code methods answer the Main Question in the affirmative for
$k\leq 5$
:
Theorem 5.6 Let C be a self-dual ternary code of length
$c=12k$
and index
$24$
which admits an automorphism
$g\in \textrm{Aut}(C) \subset 2^c{:}S_c$
of order
$m=\gcd (24,k)$
. Suppose that:
-
(1) If m is even, then
$g^{m/2} = -1 \in \textrm{Aut}(C)$
is the central element. -
(2) If m is divisible by
$3$
, then
$g^{m/3}$
fixes the same number of even and odd maximal codewords, and the image of
$g^{m/3}$
in
$S_c$
has cycle shape
$3^{c/3}$
.
Lift g to an automorphism of
$V_{\Lambda (C)}$
via Theorem 3.1. Then
answers the Main Question: its index is
$\frac {24}m$
. In particular, the codes listed in Example 5.7 provide answers to the Main Question for
$k\leq 5$
.
Proof We first check that the action of
$\langle g \rangle $
on
$V_{\Lambda (C)}$
is nonanomalous. We will do so by following Example 4.4.
When m is even, we must first check that the anomaly has no Majorana layer, i.e. we must check that
, where
$\chi = \sqrt 3(1,1,\dots ,1)$
. Condition (5.6) says that the
$(m/2)$
th power of g is
$-1 \in \textrm{Aut}(C) \subset 2^c{:}S_c$
. Together with condition (5.6) when
$m = 2^a\times 3$
, we find that the image of g in
$S_c$
consists entirely of blocks of size
$m/2$
, and each block changes an odd number of signs. There are
$c/(m/2) = 2c/m = 24k/m$
blocks, each contributing
$3(m/2) - 2\times \text {odd}$
to
$\langle \chi , (1-g)\chi \rangle $
. The claim follows.
Let us continue the case when m is even. Then g acts without fixed points on
$\Lambda (C)$
, and so we may apply Example 4.4. The previous paragraph identifies the Frame shape of g: it is
$(m/2)^{-24k/m} m^{24k/m}$
. Noting that m divides k, we see that the ’t Hooft anomaly of the action of g is
$24$
times that of an automorphism of Frame shape
$(m/2)^{-k/m} m^{k/m}$
, and so vanishes.
The final case to check is when
$m=3$
. Then g preserves a sublattice, and so there are multiple lifts of
$g \in \textrm{Aut}(\Lambda (C))$
to an automorphism of
$V_{\Lambda (C)}$
. The lift we are using is standard in the sense that it commutes with a choice of lift of
$-1 \in \textrm{Aut}(\Lambda (C))$
, and so the Frame shape formula from Example 4.4 applies [Reference MöllerMöl16, Chapter 5]. The Frame shape of g is
$3^{12k/m}$
, and k is divisible by m, completing the verification that the anomaly vanishes.
It remains to actually calculate
.
Let V be any holomorphic VOA and
$G \subset \textrm{Aut}(V)$
a nonanomalous finite subgroup, with chosen trivialization of the anomaly, so that the orbifold
is defined. The Ramond–Ramond partition function
can be computed as a sum over “twisted-twined” partition functions of the action of G on V:
The notation means the following. One takes the “
$g'$
-twisted Ramond-sector” V-module, and computes the super (i.e., signed) trace of the action of
$g''$
thereon. The choice of trivialization of the anomaly is hidden in the notation: it is used to define the action of
$g''$
on the
$g'$
-twisted Ramond sector (a priori the action of
$g''$
is defined only projectively) and to assign fermion parities to the twisted sectors.
We now take
$V = V_{\Lambda (C)}$
and
$G = \langle g \rangle $
of order
$|G| = n$
. The “untwisted” contribution to
is
Thus it suffices to show that the “twisted” terms all vanish.
Suppose that
$g',g''\in \langle g\rangle $
are not both the identity. The subgroup of
$\langle g\rangle $
generated by
$g',g''$
is a cyclic group; let h denote a choice of generator. Then
is related by a modular transformation to
. So it suffices to show that
for
$h \neq 1$
.
By construction, the action of h commutes with the supersymmetry, and so, just as for
$Z_{RR}(V)$
, the contributions to
from non-ground states cancel:
is simply the trace of
$(-1)^fh$
acting on the Ramond-sector ground states. In the proof of Proposition 2.4 we identified the Ramond-sector ground states with maximal code words in C. Thus the action of h on the Ramond-sector ground states lifts the permutation action of h on the maximal codewords. In particular,
$\textrm{tr}_{\text {ground states}}\left ((-1)^fh\right )$
receives contributions only from the fixed points of the permutation action of h on
$\{\text {maximal codewords}\}$
.
If h has even order, then, by the first condition, some power of h acts by the central element
$-1 \in \textrm{Aut}(C)$
, and so h has no fixed points. If h has odd order, then there is no sign ambiguity when lifting the action of h from
$\textrm{Aut}(C)$
to
$\textrm{Aut}(V_{\Lambda })$
, and
$\textrm{tr}_{\text {ground states}}\left ((-1)^fh\right )$
is simply a signed count of h-fixed maximal codewords. The second condition assures that this signed count vanishes. ▪
Example 5.7 We end by listing codes satisfying the conditions of Theorem 5.6 for
$k\leq 5$
. They were found by randomly generating self-dual codes with an appropriate automorphism and then calculating the index, repeating the search until one with index
$24$
turned up. We received significant help from Noam D. Elkies. In particular, he explained to us how to run such a search in a reasonable amount of time, and provided the
$k=5$
solution.
-
(1) The only, up to signed permutations of the coordinates, self-dual ternary code of length
$12$
and non-zero index is the (extended) Ternary Golay code from [Reference GolayGol49]. Its index is
$24$
. It can be presented by the generator matrix:
$$ \begin{align*} \left( \begin{array}{cccccccccccc} 1 & . & . & . & . & . & . & 1 & 1 & 1 & 2 & 1\\ . & 1 & . & . & . & . & 2 & 1 & . & 2 & 1 & 1\\ . & . & 1 & . & . & . & 1 & 2 & 1 & 2 & . & 1\\ . & . & . & 1 & . & . & 1 & . & 2 & 1 & 1 & 1\\ . & . & . & . & 1 & . & 1 & 1 & 2 & 2 & 2 & .\\ . & . & . & . & . & 1 & 1 & 1 & 1 & . & 1 & 2\\ \end{array} \right). \end{align*} $$
-
(2) The following generator matrix spans a code of length
$24$
and index
$24$
: We set
$$ \begin{align*} \left( \begin{array}{c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c@{\hspace{7pt}}c} 1 & . & . & . & . & . & . & . & . & . & . & . & 1 & 2 & . & . & 2 & 1 & 1 & 1 & 2 & 1 & . & .\\ . & 1 & . & . & . & . & . & . & . & . & . & . & . & . & . & 1 & 1 & 1 & 1 & 1 & . & 1 & 2 & 1\\ . & . & 1 & . & . & . & . & . & . & . & . & . & 1 & 2 & . & 1 & 1 & . & 2 & . & 1 & 1 & 2 & .\\ . & . & . & 1 & . & . & . & . & . & . & . & . & 1 & 1 & 2 & . & 1 & 2 & . & 2 & 1 & 1 & . & .\\ . & . & . & . & 1 & . & . & . & . & . & . & . & . & 2 & 1 & 1 & . & . & 2 & 2 & . & 1 & 1 & 1\\ . & . & . & . & . & 1 & . & . & . & . & . & . & 1 & 1 & 1 & 2 & 2 & 1 & 1 & . & 2 & 2 & 1 & 2\\ . & . & . & . & . & . & 1 & . & . & . & . & . & . & 2 & 2 & 1 & 1 & . & . & . & 1 & 1 & 2 & 2\\ . & . & . & . & . & . & . & 1 & . & . & . & . & 2 & . & 1 & 2 & 2 & . & 2 & 2 & . & 2 & . & 2\\ . & . & . & . & . & . & . & . & 1 & . & . & . & 2 & 1 & 1 & 1 & 1 & 2 & 1 & . & 1 & 1 & 1 & 1\\ . & . & . & . & . & . & . & . & . & 1 & . & . & 2 & . & . & . & . & 1 & 1 & 2 & 2 & 2 & 2 & 2\\ . & . & . & . & . & . & . & . & . & . & 1 & . & 2 & 2 & 1 & . & . & 1 & . & 2 & . & . & . & .\\ . & . & . & . & . & . & . & . & . & . & . & 1 & . & . & 1 & 1 & . & 1 & . & 2 & 2 & 2 & 2 & 2 \end{array} \right). \end{align*} $$
$g = -1 \in \textrm{Aut}(C)$
.
-
(3) The following generator matrix spans a self-dual ternary code of length
$36$
and index
$24$
. This code is invariant under the permutation
$$ \begin{align*} \hspace{-1.2in} \left( \begin{array}{c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}c@{\hspace{6.3pt}}} 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 2\!\! & 2\!\! & .\!\! & 2\!\! & 2\!\! & 2\!\! & 1\!\! & .\!\! & .\!\! & 2\!\! & .\!\! & 1\!\! & 1\!\! & 1\!\! & 1\!\! & 1\!\! & 2\!\! & .\!\! & 2\\ .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & 2\!\! & .\!\! & .\!\! & 2\!\! & .\!\! & .\!\! & 2\!\! & .\!\! & .\!\! & .\!\! & 2\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & 1\!\! & .\\ .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & 2\!\! & 1\!\! & .\!\! & 1\!\! & 2\!\! & 2\!\! & .\!\! & 1\!\! & .\!\! & 2\!\! & 1\!\! & .\!\! & 1\!\! & 2\!\! & .\\ .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & 2\!\! & 1\!\! & 1\!\! & 1\!\! & .\!\! & 1\!\! & 2\!\! & 2\!\! & .\!\! & 2\!\! & 1\!\! & .\\ .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 2\!\! & .\!\! & 1\!\! & 2\!\! & 2\!\! & 1\!\! & .\!\! & 2\!\! & 2\!\! & 2\!\! & .\!\! & 2\!\! & .\!\! & 1\!\! & 1\!\! & 1\!\! & 1\!\! & 1\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 2\!\! & .\!\! & 2\!\! & .\!\! & 2\!\! & 2\!\! & 2\!\! & .\!\! & .\!\! & 2\!\! & .\!\! & 2\!\! & 1\!\! & 1\!\! & .\!\! & 2\!\! & .\!\! & 1\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & 1\!\! & 1\!\! & .\!\! & 2\!\! & 1\!\! & 1\!\! & 2\!\! & 1\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & 2\!\! & .\!\! & .\!\! & .\!\! & 2\!\! & 2\!\! & 2\!\! & .\!\! & 1\!\! & 2\!\! & .\!\! & .\!\! & 1\!\! & 2\!\! & .\!\! & 2\!\! & 1\!\! & .\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 2\!\! & 1\!\! & .\!\! & 2\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & 1\!\! & 1\!\! & 2\!\! & 1\!\! & 1\!\! & 1\!\! & 2\!\! & 1\!\! & .\!\! & 2\!\! & 1\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 2\!\! & 1\!\! & .\!\! & 1\!\! & .\!\! & 1\!\! & 1\!\! & 1\!\! & 1\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & 2\!\! & 1\!\! & 2\!\! & 2\!\! & 1\!\! & 2\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & 2\!\! & .\!\! & .\!\! & 2\!\! & .\!\! & 1\!\! & 1\!\! & .\!\! & 2\!\! & 2\!\! & 2\!\! & 1\!\! & 1\!\! & 1\!\! & 2\!\! & 1\!\! & 1\!\! & .\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & 1\!\! & 2\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & 1\!\! & 1\!\! & 2\!\! & .\!\! & .\!\! & .\!\! & 2\!\! & .\!\! & .\!\! & .\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 2\!\! & 2\!\! & 1\!\! & 1\!\! & 1\!\! & 1\!\! & 1\!\! & 2\!\! & .\!\! & 2\!\! & 2\!\! & 2\!\! & 1\!\! & .\!\! & 1\!\! & 2\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & .\!\! & 2\!\! & 2\!\! & .\!\! & .\!\! & 2\!\! & 1\!\! & 1\!\! & 2\!\! & 1\!\! & 2\!\! & .\!\! & 2\!\! & 1\!\! & 2\!\! & 2\!\! & 1\!\! & .\!\! & 2\!\! & .\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & 2\!\! & .\!\! & .\!\! & .\!\! & 2\!\! & 1\!\! & .\!\! & 1\!\! & 1\!\! & .\!\! & 1\!\! & .\!\! & 1\!\! & .\!\! & .\!\! & 1\!\! & 1\!\! & 2\!\! & 2\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & .\!\! & 2\!\! & 2\!\! & .\!\! & 2\!\! & 2\!\! & 2\!\! & 2\!\! & 1\!\! & .\!\! & 2\!\! & 2\!\! & 1\!\! & 1\!\! & 2\!\! & 2\!\! & 1\!\! & 2\!\! & 1\!\! & 1\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & 2\!\! & 1\!\! & .\!\! & 1\!\! & .\!\! & 1\!\! & 2\!\! & .\!\! & 1\!\! & 1\!\! & 1\!\! & 1\!\! & 2\!\! & 2\!\! & 1\!\! & .\!\! & .\!\! & 1\!\! & 2\\ .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & .\!\! & 1\!\! & 2\!\! & 1\!\! & 1\!\! & 2\!\! & .\!\! & 1\!\! & 2\!\! & 1\!\! & 2\!\! & 1\!\! & 1\!\! & 1\!\! & 1\!\! & .\!\! & 2\!\! & 2 \end{array} \right). \hspace{-1in} \end{align*} $$
$g : e_i \mapsto e_{i + 12}$
of the coordinates, where the coordinates are
$e_1,\dots ,e_{36}$
and the sum is considered mod
$36$
. The fixed subcode, when considered as a code inside
, has the following generator matrix: This is a copy of the self-dual ternary code of length
$$ \begin{align*} \left(\begin{array}{cccccccccccc} . & . & . & . & . & 2 & 2 & . & 1 & 1 & 1 & 1\\ . & 1 & . & . & . & 2 & 1 & . & 2 & 2 & 2 & .\\ . & . & 1 & . & . & . & . & . & 2 & 1 & . & .\\ 1 & . & . & 1 & . & . & 1 & . & 1 & 1 & 2 & .\\ 1 & . & . & . & 1 & . & 2 & . & 2 & 2 & 1 & .\\ . & . & . & . & . & . & 1 & 1 & . & . & 1 & . \end{array}\right).\end{align*} $$
$12$
with 8 even and 8 odd maximal codewords, and so this pair
$(C,g)$
satisfies condition (2) of Theorem 5.6.
-
(4) The following generator matrix spans a self-dual ternary code of length
$48$
and index
$24$
. It is invariant under the signed permutation
$$ \begin{align*} \hspace{-1.2in} \left(\begin{array}{c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}c@{\hspace{6.8pt}}} 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\\ .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\\ .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & 2\\ .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 1\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & 2\!\!\!\! & .\!\!\!\! & .\!\!\!\! & 1\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 2\!\!\!\! & 1 \end{array}\right). \hspace{-1in} \end{align*} $$
$$ \begin{align*} e_i \mapsto \begin{cases} e_{i+24}, & i \leq 24, \\ - e_{i-24}, & i> 24. \end{cases}\end{align*} $$
-
(5) The following generator matrix spans a self-dual ternary code of length
$60$
and index
$24$
: Since
$$ \begin{align*} \hspace{-1.2in} \left(\begin{array}{c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}c@{\hspace{5.7pt}}} 1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\\ .\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\\ .\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&.\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\\ .\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&2\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&1\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&.\!\!\!\!&1\!\!\!\!&2\!\!\!\!&2\!\!\!\!&.\!\!\!\!&.\!\!\!\!&. \end{array} \right).\hspace{-1in} \end{align*} $$
$5$
is coprime to
$24$
, we do not need any automorphism.
