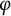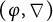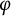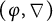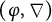1 Introduction
Let p be a prime number and q a power of p. Let K be a complete nonarchimedean discretely valued field of characteristic
![]() $0$
equipped with an automorphism
$0$
equipped with an automorphism
![]() $\varphi $
, the Frobenius, inducing the q-power map on the residue field
$\varphi $
, the Frobenius, inducing the q-power map on the residue field
![]() $\kappa \supseteq \mathbb {F}_q$
. We also require K to be unramified over the fixed subfield F under
$\kappa \supseteq \mathbb {F}_q$
. We also require K to be unramified over the fixed subfield F under
![]() $\varphi $
. See Hypothesis 2.1 for a concrete example.
$\varphi $
. See Hypothesis 2.1 for a concrete example.
The Robba ring
![]() $\mathcal {R}=\mathcal {R}(K,t)$
is the ring of bidirectional power series
$\mathcal {R}=\mathcal {R}(K,t)$
is the ring of bidirectional power series
![]() $\sum \limits _{i\in \mathbb {Z}}c_it^i$
in one variable t with coefficients in K which converge in an annulus
$\sum \limits _{i\in \mathbb {Z}}c_it^i$
in one variable t with coefficients in K which converge in an annulus
![]() $[\alpha ,1)$
for some series-dependent
$[\alpha ,1)$
for some series-dependent
![]() $0<\alpha <1$
. The Robba ring
$0<\alpha <1$
. The Robba ring
![]() $\mathcal {R}$
is endowed with an absolute Frobenius lift
$\mathcal {R}$
is endowed with an absolute Frobenius lift
![]() $\varphi $
which extends the Frobenius on K and lifts the q-power map on
$\varphi $
which extends the Frobenius on K and lifts the q-power map on
![]() $\kappa (\!( t )\!)$
, and with the derivation
$\kappa (\!( t )\!)$
, and with the derivation
![]() $\partial =d/dt$
.
$\partial =d/dt$
.
A
![]() $(\varphi ,\nabla )$
-module over
$(\varphi ,\nabla )$
-module over
![]() $\mathcal {R}$
is a triple
$\mathcal {R}$
is a triple
![]() $(M,\Phi ,\nabla )$
, where M is a finite free
$(M,\Phi ,\nabla )$
, where M is a finite free
![]() $\mathcal {R}$
-module,
$\mathcal {R}$
-module,
![]() $\Phi $
is a Frobenius, i.e., a
$\Phi $
is a Frobenius, i.e., a
![]() $\varphi $
-linear endomorphism of M whose image spans M over
$\varphi $
-linear endomorphism of M whose image spans M over
![]() $\mathcal {R}$
, and
$\mathcal {R}$
, and
![]() $\nabla \colon M\to M\bigotimes _{\mathcal {R}} \mathcal {R} dt$
is a connection. Moreover,
$\nabla \colon M\to M\bigotimes _{\mathcal {R}} \mathcal {R} dt$
is a connection. Moreover,
![]() $\Phi $
and
$\Phi $
and
![]() $\nabla $
should satisfy the gauge compatibility condition, which says that, after choosing an
$\nabla $
should satisfy the gauge compatibility condition, which says that, after choosing an
![]() $\mathcal {R}$
-basis for M, the actions
$\mathcal {R}$
-basis for M, the actions
![]() $\Phi $
and
$\Phi $
and
![]() $\nabla $
are given by matrices A and N, respectively, and these matrices should satisfy
$\nabla $
are given by matrices A and N, respectively, and these matrices should satisfy
![]() $N=\operatorname {\mathrm {\boldsymbol \mu }}\cdot A(\varphi (N))A^{-1}-\partial (A)A^{-1}$
, where
$N=\operatorname {\mathrm {\boldsymbol \mu }}\cdot A(\varphi (N))A^{-1}-\partial (A)A^{-1}$
, where
![]() $\operatorname {\mathrm {\boldsymbol \mu }}:= \partial (\varphi (t))$
.
$\operatorname {\mathrm {\boldsymbol \mu }}:= \partial (\varphi (t))$
.
The
![]() $(\varphi ,\nabla )$
-modules, also known as the overconvergent
$(\varphi ,\nabla )$
-modules, also known as the overconvergent
![]() $\mathrm {F}$
-isocrystals in the literature, are closely related to p-adic local systems on
$\mathrm {F}$
-isocrystals in the literature, are closely related to p-adic local systems on
![]() $\operatorname {\mathrm {Spec}} \kappa (\!( t )\!)$
(for a summary, we refer to [Reference Kedlaya13]), for which the correct monodromy theorem is the p-adic local monodromy theorem (pLMT), conjectured by Crew [Reference Crew5], and proved independently by André [Reference André1], Kedlaya [Reference Kedlaya9], and Mebkhout [Reference Mebkhout17]. It states that every
$\operatorname {\mathrm {Spec}} \kappa (\!( t )\!)$
(for a summary, we refer to [Reference Kedlaya13]), for which the correct monodromy theorem is the p-adic local monodromy theorem (pLMT), conjectured by Crew [Reference Crew5], and proved independently by André [Reference André1], Kedlaya [Reference Kedlaya9], and Mebkhout [Reference Mebkhout17]. It states that every
![]() $(\varphi ,\nabla )$
-module over
$(\varphi ,\nabla )$
-module over
![]() $\mathcal {R}$
is quasi-unipotent. Concretely, a
$\mathcal {R}$
is quasi-unipotent. Concretely, a
![]() $(\varphi ,\nabla )$
-module M over
$(\varphi ,\nabla )$
-module M over
![]() $\mathcal {R}$
, after an étale extension to
$\mathcal {R}$
, after an étale extension to
![]() $\mathcal {R}_L$
(the Robba ring canonically associated to some finite separable extension L of
$\mathcal {R}_L$
(the Robba ring canonically associated to some finite separable extension L of
![]() $\kappa (\!( t )\!)$
), admits a filtration by
$\kappa (\!( t )\!)$
), admits a filtration by
![]() $(\varphi ,\nabla )$
-submodules such that the connections induced on the gradiation are trivial. A matricial description of the theorem is given as follows. Let d be the rank of M over
$(\varphi ,\nabla )$
-submodules such that the connections induced on the gradiation are trivial. A matricial description of the theorem is given as follows. Let d be the rank of M over
![]() $\mathcal {R}$
, and let
$\mathcal {R}$
, and let
![]() $A\in \operatorname {\mathrm {GL}}_d(\mathcal {R})$
(resp.
$A\in \operatorname {\mathrm {GL}}_d(\mathcal {R})$
(resp.
![]() $N\in \operatorname {\mathrm {Mat}}_{d,d}(\mathcal {R})$
) be the matrix of
$N\in \operatorname {\mathrm {Mat}}_{d,d}(\mathcal {R})$
) be the matrix of
![]() $\Phi $
(resp.
$\Phi $
(resp.
![]() $\nabla $
) in some basis. Then, there exists
$\nabla $
) in some basis. Then, there exists
![]() $B\in \operatorname {\mathrm {GL}}_d(\mathcal {R}_L)$
such that
$B\in \operatorname {\mathrm {GL}}_d(\mathcal {R}_L)$
such that
![]() $BNB^{-1}-\partial (B)B^{-1}$
is an upper-triangular block matrix with zero blocks in the diagonal.
$BNB^{-1}-\partial (B)B^{-1}$
is an upper-triangular block matrix with zero blocks in the diagonal.
We mention two applications of the pLMT in p-adic Hodge theory.
-
• In [Reference Berger3], Berger associated to every p-adic de Rham representation V a
 $(\varphi ,\nabla )$
-module
$(\varphi ,\nabla )$
-module
 $\mathrm {N}_{\operatorname {\mathrm {dR}}}(V)$
over a Robba ring. He showed that V is potentially semistable if and only if
$\mathrm {N}_{\operatorname {\mathrm {dR}}}(V)$
over a Robba ring. He showed that V is potentially semistable if and only if
 $\mathrm {N}_{\operatorname {\mathrm {dR}}}(V)$
is quasi-unipotent. Using the pLMT, he could prove the p-adic monodromy theorem (previously a conjecture of Fontaine): every p-adic de Rham representation is potentially semistable.
$\mathrm {N}_{\operatorname {\mathrm {dR}}}(V)$
is quasi-unipotent. Using the pLMT, he could prove the p-adic monodromy theorem (previously a conjecture of Fontaine): every p-adic de Rham representation is potentially semistable. -
• In [Reference Marmora16], Marmora used the pLMT to construct a functor from the category of
 $(\varphi ,\nabla )$
-modules over
$(\varphi ,\nabla )$
-modules over
 $\mathcal {R}$
to that of
$\mathcal {R}$
to that of
 $K^{\operatorname {\mathrm {nr}}}$
-valued Weil–Deligne representations of the Weil group
$K^{\operatorname {\mathrm {nr}}}$
-valued Weil–Deligne representations of the Weil group
 $\mathcal {W}_{\kappa (\!( t )\!)}$
, where
$\mathcal {W}_{\kappa (\!( t )\!)}$
, where
 $K^{\operatorname {\mathrm {nr}}}$
is the maximal unramified extension of K in a fixed algebraic closure of K.
$K^{\operatorname {\mathrm {nr}}}$
is the maximal unramified extension of K in a fixed algebraic closure of K.
Rather than the general linear group, a Galois representation may take value in some connected reductive group G, such as a special linear group or a symplectic group. In order to have appropriate formulations of the above results in this context, it is helpful to establish a G-version of the pLMT, which is the main motivation of our present paper.
In this paper, we introduce the notion of G-
![]() $\varphi $
-modules over
$\varphi $
-modules over
![]() $\mathcal {R}$
(resp. G-
$\mathcal {R}$
(resp. G-
![]() $(\varphi ,\nabla )$
-modules over
$(\varphi ,\nabla )$
-modules over
![]() $\mathcal {R}$
), which are exact faithful F-linear tensor functors from the category
$\mathcal {R}$
), which are exact faithful F-linear tensor functors from the category
![]() $\operatorname {\mathrm {\textbf {Rep}}}_F(G)$
of G-representations on finite-dimensional F-vector spaces to the category
$\operatorname {\mathrm {\textbf {Rep}}}_F(G)$
of G-representations on finite-dimensional F-vector spaces to the category
![]() $\operatorname {\mathrm {\textbf {Mod}^{\varphi }_{\mathcal {R}}}}$
of
$\operatorname {\mathrm {\textbf {Mod}^{\varphi }_{\mathcal {R}}}}$
of
![]() $\varphi $
-modules over
$\varphi $
-modules over
![]() $\mathcal {R}$
(resp. to the category
$\mathcal {R}$
(resp. to the category
![]() $\operatorname {\mathrm {\textbf {Mod}^{\varphi ,\nabla }_{\mathcal {R}}}}$
of
$\operatorname {\mathrm {\textbf {Mod}^{\varphi ,\nabla }_{\mathcal {R}}}}$
of
![]() $(\varphi ,\nabla )$
-modules over
$(\varphi ,\nabla )$
-modules over
![]() $\mathcal {R}$
), commuting with the respective fiber functors. These constructions are inspired by that of G-isocrystals introduced in [Reference Dat, Orlik and Rapoport6, Section IX.1].
$\mathcal {R}$
), commuting with the respective fiber functors. These constructions are inspired by that of G-isocrystals introduced in [Reference Dat, Orlik and Rapoport6, Section IX.1].
Before coming to the main theorem, we first explain the group-theoretic gauge compatibility condition (Definition 4.6). Let G be an affine algebraic F-group, and let
![]() $\mathfrak {g}$
be its Lie algebra. For any
$\mathfrak {g}$
be its Lie algebra. For any
![]() $y\in G(\mathcal {R})$
and
$y\in G(\mathcal {R})$
and
![]() $Y\in \mathfrak {g}\bigotimes _F \mathcal {R}$
, we define
$Y\in \mathfrak {g}\bigotimes _F \mathcal {R}$
, we define
![]() $\Gamma _y(Y) := \operatorname {\mathrm {Ad}}(y)(Y)-\operatorname {\mathrm {dlog}}(y)$
, where
$\Gamma _y(Y) := \operatorname {\mathrm {Ad}}(y)(Y)-\operatorname {\mathrm {dlog}}(y)$
, where
![]() $\operatorname {\mathrm {Ad}} \colon G \to \operatorname {\mathrm {GL}}_{\mathfrak {g}}$
is the adjoint representation, and
$\operatorname {\mathrm {Ad}} \colon G \to \operatorname {\mathrm {GL}}_{\mathfrak {g}}$
is the adjoint representation, and
![]() $\operatorname {\mathrm {dlog}} \colon G(\mathcal {R}) \to \mathfrak {g}\bigotimes _F\mathcal {R}$
is defined in Construction 4.4. We say
$\operatorname {\mathrm {dlog}} \colon G(\mathcal {R}) \to \mathfrak {g}\bigotimes _F\mathcal {R}$
is defined in Construction 4.4. We say
![]() $g\in G(\mathcal {R})$
and
$g\in G(\mathcal {R})$
and
![]() $X\in \mathfrak {g}\bigotimes _F\mathcal {R}$
satisfy the gauge compatibility condition if
$X\in \mathfrak {g}\bigotimes _F\mathcal {R}$
satisfy the gauge compatibility condition if
![]() $X=\Gamma _g\big (\operatorname {\mathrm {\boldsymbol \mu }}\varphi (X) \big )$
. When
$X=\Gamma _g\big (\operatorname {\mathrm {\boldsymbol \mu }}\varphi (X) \big )$
. When
![]() $G=\operatorname {\mathrm {GL}}_d$
, we have
$G=\operatorname {\mathrm {GL}}_d$
, we have
![]() $\operatorname {\mathrm {Ad}}(y)(Y)=yYy^{-1}$
and
$\operatorname {\mathrm {Ad}}(y)(Y)=yYy^{-1}$
and
![]() $\operatorname {\mathrm {dlog}}(y)=\partial (y)y^{-1}$
. In this context, the group-theoretic gauge compatibility condition coincides with the aforementioned matrical one.
$\operatorname {\mathrm {dlog}}(y)=\partial (y)y^{-1}$
. In this context, the group-theoretic gauge compatibility condition coincides with the aforementioned matrical one.
Our main theorem is the following G-version of the pLMT.
Theorem 1.1 (Theorem 4.21)
Let G be a connected reductive F-group, and let
![]() $\mathfrak {g}$
be its Lie algebra. If
$\mathfrak {g}$
be its Lie algebra. If
![]() $g\in G(\mathcal {R})$
and
$g\in G(\mathcal {R})$
and
![]() $X\in \mathfrak {g}\bigotimes _F\mathcal {R}$
satisfy
$X\in \mathfrak {g}\bigotimes _F\mathcal {R}$
satisfy
![]() $X=\Gamma _g\big (\operatorname {\mathrm {\boldsymbol \mu }}\varphi (X) \big )$
, then there exists a finite separable extension L over
$X=\Gamma _g\big (\operatorname {\mathrm {\boldsymbol \mu }}\varphi (X) \big )$
, then there exists a finite separable extension L over
![]() $\kappa (\!( t )\!)$
and an element
$\kappa (\!( t )\!)$
and an element
![]() $b\in G(\mathcal {R}_L)$
such that
$b\in G(\mathcal {R}_L)$
such that
![]() $\Gamma _b(X)\in \operatorname {\mathrm {Lie}} \big (U_{G_{\mathcal {R}}}(-\lambda _g)\big )\bigotimes _{\mathcal {R}} {\mathcal {R}_L}$
.
$\Gamma _b(X)\in \operatorname {\mathrm {Lie}} \big (U_{G_{\mathcal {R}}}(-\lambda _g)\big )\bigotimes _{\mathcal {R}} {\mathcal {R}_L}$
.
Here,
![]() $\lambda _g \colon \mathbb {G}_{m,\mathcal {R}} \to G_{\mathcal {R}}$
is a cocharacter associated to g whose reciprocal is denoted by
$\lambda _g \colon \mathbb {G}_{m,\mathcal {R}} \to G_{\mathcal {R}}$
is a cocharacter associated to g whose reciprocal is denoted by
![]() $-\lambda _g$
, and
$-\lambda _g$
, and
![]() $U_{G_{\mathcal {R}}}(-\lambda _g)$
denotes the unipotent radical of the parabolic subgroup of
$U_{G_{\mathcal {R}}}(-\lambda _g)$
denotes the unipotent radical of the parabolic subgroup of
![]() $G_{\mathcal {R}}$
associated to
$G_{\mathcal {R}}$
associated to
![]() $-\lambda _g$
. When
$-\lambda _g$
. When
![]() $G=\operatorname {\mathrm {GL}}_d$
, g (resp. X) should be thought as the matrix of the Frobenius (resp. the matrix of the connection), and
$G=\operatorname {\mathrm {GL}}_d$
, g (resp. X) should be thought as the matrix of the Frobenius (resp. the matrix of the connection), and
![]() $\Gamma _b(\rule {2mm}{0.15mm})$
as the matrix of a connection under the change-of-basis via
$\Gamma _b(\rule {2mm}{0.15mm})$
as the matrix of a connection under the change-of-basis via
![]() $b^{-1}$
. Moreover,
$b^{-1}$
. Moreover,
![]() $\operatorname {\mathrm {Lie}} \big (U_{G_{\mathcal {R}}}(-\lambda _g)\big )\bigotimes _{\mathcal {R}} {\mathcal {R}_L}$
consists of upper-triangular matrices over
$\operatorname {\mathrm {Lie}} \big (U_{G_{\mathcal {R}}}(-\lambda _g)\big )\bigotimes _{\mathcal {R}} {\mathcal {R}_L}$
consists of upper-triangular matrices over
![]() $\mathcal {R}_L$
with zero blocks (of certain sizes) in the diagonal. As such, Theorem 1.1 recovers the matricial pLMT described above.
$\mathcal {R}_L$
with zero blocks (of certain sizes) in the diagonal. As such, Theorem 1.1 recovers the matricial pLMT described above.
In Proposition 4.9, we show that G-
![]() $(\varphi ,\nabla )$
-modules over
$(\varphi ,\nabla )$
-modules over
![]() $\mathcal {R}$
are indeed pairs
$\mathcal {R}$
are indeed pairs
![]() $(g,X)$
subject to the gauge compatibility condition in the theorem. In this sense, the theorem can be interpreted as saying that G-
$(g,X)$
subject to the gauge compatibility condition in the theorem. In this sense, the theorem can be interpreted as saying that G-
![]() $(\varphi ,\nabla )$
-modules over
$(\varphi ,\nabla )$
-modules over
![]() $\mathcal {R}$
are “G-quasi-unipotent.” In Examples 4.10 and 4.11, we give examples of the existence of such pairs for G a special linear group and a symplectic group, respectively.
$\mathcal {R}$
are “G-quasi-unipotent.” In Examples 4.10 and 4.11, we give examples of the existence of such pairs for G a special linear group and a symplectic group, respectively.
More examples of G-
![]() $(\varphi ,\nabla )$
-modules are expected from Berger’s functor
$(\varphi ,\nabla )$
-modules are expected from Berger’s functor
![]() $\mathrm {N}_{\operatorname {\mathrm {dR}}}$
mentioned previously. Explicitly, we hope to show in a future work that if a p-adic de Rham representation V takes value in a connected reductive group G, then
$\mathrm {N}_{\operatorname {\mathrm {dR}}}$
mentioned previously. Explicitly, we hope to show in a future work that if a p-adic de Rham representation V takes value in a connected reductive group G, then
![]() $\mathrm {N}_{\operatorname {\mathrm {dR}}}(V)$
is a G-
$\mathrm {N}_{\operatorname {\mathrm {dR}}}(V)$
is a G-
![]() $(\varphi ,\nabla )$
-module. As another future work, we intend to use Theorem 1.1 to formulate a G-version of Marmora’s functor, namely, to construct a functor from the category of G-
$(\varphi ,\nabla )$
-module. As another future work, we intend to use Theorem 1.1 to formulate a G-version of Marmora’s functor, namely, to construct a functor from the category of G-
![]() $(\varphi ,\nabla )$
-modules over
$(\varphi ,\nabla )$
-modules over
![]() $\mathcal {R}$
to that of Weil–Deligne representations of the Weil group
$\mathcal {R}$
to that of Weil–Deligne representations of the Weil group
![]() $\mathcal {W}_{\kappa (\!( t )\!)}$
taking value in
$\mathcal {W}_{\kappa (\!( t )\!)}$
taking value in
![]() $G(K^{\operatorname {\mathrm {nr}}})$
.
$G(K^{\operatorname {\mathrm {nr}}})$
.
Our approach to the theorem closely follows that of the pLMT in [Reference Kedlaya9] for absolute Frobenius lifts, wherein the author used his slope filtration theorem (along with applying the pushforward functor and twisting to each quotient of the filtration) to reduce the problem to the unit-root case, and then apply the unit-root pLMT attributed to Tsuzuki [Reference Tsuzuki23] to finish. More precisely, we use Kedlaya’s slope filtration theorem to construct a
![]() $\mathbb {Q}$
-filtered fiber functor
$\mathbb {Q}$
-filtered fiber functor
![]() $\operatorname {\mathrm {{HN}}}_g$
from
$\operatorname {\mathrm {{HN}}}_g$
from
![]() $\operatorname {\mathrm {\textbf {Rep}}}_F(G)$
to
$\operatorname {\mathrm {\textbf {Rep}}}_F(G)$
to
![]() $ \mathbb {Q}$
-
$ \mathbb {Q}$
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_{\mathcal {R}}$
, the category of
$\operatorname {\mathrm {\textbf {Fil}}}_{\mathcal {R}}$
, the category of
![]() $\mathbb {Q}$
-filtered modules over
$\mathbb {Q}$
-filtered modules over
![]() $\mathcal {R}$
(see Theorem 3.4). We then reduce
$\mathcal {R}$
(see Theorem 3.4). We then reduce
![]() $\operatorname {\mathrm {{HN}}}_g$
to a
$\operatorname {\mathrm {{HN}}}_g$
to a
![]() $\mathbb {Z}$
-filtered fiber functor
$\mathbb {Z}$
-filtered fiber functor
![]() $\operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
from
$\operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
from
![]() $\operatorname {\mathrm {\textbf {Rep}}}_F(G)$
to
$\operatorname {\mathrm {\textbf {Rep}}}_F(G)$
to
![]() $\mathbb {Z}$
-
$\mathbb {Z}$
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_{\mathcal {R}}$
, the category of
$\operatorname {\mathrm {\textbf {Fil}}}_{\mathcal {R}}$
, the category of
![]() $\mathbb {Z}$
-filtered modules over
$\mathbb {Z}$
-filtered modules over
![]() $\mathcal {R}$
(see Lemma 3.10). Then, a result of Ziegler (Theorem 2.12) immediately implies that
$\mathcal {R}$
(see Lemma 3.10). Then, a result of Ziegler (Theorem 2.12) immediately implies that
![]() $\operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
is splittable, i.e., factors through a
$\operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
is splittable, i.e., factors through a
![]() $\mathbb {Z}$
-graded fiber functor (see Proposition 3.11). In particular, for any splitting of
$\mathbb {Z}$
-graded fiber functor (see Proposition 3.11). In particular, for any splitting of
![]() $\operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
, we construct a morphism
$\operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
, we construct a morphism
![]() $\lambda _g\colon \mathbb {G}_{m,\mathcal {R}} \to G_{\mathcal {R}}$
of
$\lambda _g\colon \mathbb {G}_{m,\mathcal {R}} \to G_{\mathcal {R}}$
of
![]() $\mathcal {R}$
-groups in Section 3.4, which is called the
$\mathcal {R}$
-groups in Section 3.4, which is called the
![]() $\mathbb {Z}$
-slope morphism of g. With this, we can reduce the G-
$\mathbb {Z}$
-slope morphism of g. With this, we can reduce the G-
![]() $(\varphi ,\nabla )$
-module
$(\varphi ,\nabla )$
-module
![]() $(g,X)$
over
$(g,X)$
over
![]() $\mathcal {R}$
, involving the (generalized) pushforward functor and twisting, to a unit-root one (see Corollary 4.20). Theorem 1.1 then follows from the unit-root pLMT and a Tannakian argument.
$\mathcal {R}$
, involving the (generalized) pushforward functor and twisting, to a unit-root one (see Corollary 4.20). Theorem 1.1 then follows from the unit-root pLMT and a Tannakian argument.
The paper is organized as follows. In Section 2, we set up basic notation and conventions, and then recall some necessary background on the theory of slopes and Tannakian formalism. In Section 3, we study G-
![]() $\varphi $
-modules over the Robba ring, and construct slope morphisms. In Section 4, we consider G-
$\varphi $
-modules over the Robba ring, and construct slope morphisms. In Section 4, we consider G-
![]() $(\varphi ,\nabla )$
-modules over the Robba ring, and prove our main result, Theorem 1.1, in the last subsection.
$(\varphi ,\nabla )$
-modules over the Robba ring, and prove our main result, Theorem 1.1, in the last subsection.
2 Preliminaries
2.1 Notation and conventions
When k is a field, we denote by
![]() $\operatorname {\mathrm {\textbf {Vec}}}_k$
the category of finite-dimensional k-vector spaces. When R is a k-algebra,Footnote
1
we denote by
$\operatorname {\mathrm {\textbf {Vec}}}_k$
the category of finite-dimensional k-vector spaces. When R is a k-algebra,Footnote
1
we denote by
![]() $\operatorname {\mathrm {\textbf {Mod}}}_R$
the category of R-modules, and by
$\operatorname {\mathrm {\textbf {Mod}}}_R$
the category of R-modules, and by
![]() $\operatorname {\mathrm {\textbf {Alg}}}_R$
the category of R-algebras. When
$\operatorname {\mathrm {\textbf {Alg}}}_R$
the category of R-algebras. When
![]() $V,W \in \operatorname {\mathrm {\textbf {Vec}}}_k$
, we write
$V,W \in \operatorname {\mathrm {\textbf {Vec}}}_k$
, we write
![]() $V_R$
for
$V_R$
for
![]() $V\bigotimes _k R$
, and write
$V\bigotimes _k R$
, and write
![]() $\alpha _R:= \alpha \otimes R$
, the R-linear extension of
$\alpha _R:= \alpha \otimes R$
, the R-linear extension of
![]() $\alpha $
, for all k-linear maps
$\alpha $
, for all k-linear maps
![]() $\alpha \colon V\to W$
. When G is an affine algebraic k-group, we denote by
$\alpha \colon V\to W$
. When G is an affine algebraic k-group, we denote by
![]() $k[G]$
the Hopf algebra of G, by
$k[G]$
the Hopf algebra of G, by
![]() $G_R:= G \times _{\operatorname {\mathrm {Spec}} k} \operatorname {\mathrm {Spec}} R$
the base extension, by
$G_R:= G \times _{\operatorname {\mathrm {Spec}} k} \operatorname {\mathrm {Spec}} R$
the base extension, by
![]() $H^1(k,G):= H^1 \big (\operatorname {\mathrm {Gal}}(k^{\operatorname {\mathrm {sep}}}/k),G(k^{\operatorname {\mathrm {sep}}}) \big )$
the first Galois cohomology set, and by
$H^1(k,G):= H^1 \big (\operatorname {\mathrm {Gal}}(k^{\operatorname {\mathrm {sep}}}/k),G(k^{\operatorname {\mathrm {sep}}}) \big )$
the first Galois cohomology set, and by
![]() $\operatorname {\mathrm {\textbf {Rep}}}_k(G)$
the category of representations of G on finite-dimensional k-vector spaces.
$\operatorname {\mathrm {\textbf {Rep}}}_k(G)$
the category of representations of G on finite-dimensional k-vector spaces.
By a reductive k-group, we mean a (not necessarily connected) affine algebraic k-group G such that every smooth connected unipotent normal subgroup of
![]() $G_{\bar k}$
is trivial, where
$G_{\bar k}$
is trivial, where
![]() $\bar {k}$
is an algebraic closure of k.
$\bar {k}$
is an algebraic closure of k.
For the rest of this paper, we work under the following hypothesis.
Hypothesis 2.1 Let p be a prime number and
![]() $q=p^f$
an integral power of p. Let F be a finite extension of
$q=p^f$
an integral power of p. Let F be a finite extension of
![]() $\mathbb {Q}_p$
with the ring of integers
$\mathbb {Q}_p$
with the ring of integers
![]() $\mathcal {O}_F$
, a fixed uniformizer
$\mathcal {O}_F$
, a fixed uniformizer
![]() $\varpi _F$
and the residue field
$\varpi _F$
and the residue field
![]() $\mathbb {F}_q$
of q elements. Let
$\mathbb {F}_q$
of q elements. Let
![]() $\kappa $
be a perfect field containing
$\kappa $
be a perfect field containing
![]() $\mathbb {F}_q$
. Let
$\mathbb {F}_q$
. Let
![]() $\mathcal {O}_K=\mathcal {O}_F\bigotimes _{W(\mathbb {F}_q)} W(\kappa )$
, where
$\mathcal {O}_K=\mathcal {O}_F\bigotimes _{W(\mathbb {F}_q)} W(\kappa )$
, where
![]() $W(\mathbb {F}_q)$
(resp.
$W(\mathbb {F}_q)$
(resp.
![]() $W(\kappa )$
) denotes the ring of Witt vectors with coefficients in
$W(\kappa )$
) denotes the ring of Witt vectors with coefficients in
![]() $\mathbb {F}_q$
(resp. in
$\mathbb {F}_q$
(resp. in
![]() $\kappa $
). Then,
$\kappa $
). Then,
![]() $K:= \operatorname {\mathrm {Frac}}(\mathcal {O}_K)\cong F\bigotimes _{W(\mathbb {F}_q)} W(\kappa )$
is a complete discretely valued field with ring of integers
$K:= \operatorname {\mathrm {Frac}}(\mathcal {O}_K)\cong F\bigotimes _{W(\mathbb {F}_q)} W(\kappa )$
is a complete discretely valued field with ring of integers
![]() $\mathcal {O}_K$
, a uniformizer
$\mathcal {O}_K$
, a uniformizer
![]() $\varpi := \varpi _F\otimes 1$
and residue field
$\varpi := \varpi _F\otimes 1$
and residue field
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $\operatorname {\mathrm {Frob}}$
be the ring endomorphism of
$\operatorname {\mathrm {Frob}}$
be the ring endomorphism of
![]() $W(\kappa )$
induced by the p-power map on
$W(\kappa )$
induced by the p-power map on
![]() $\kappa $
, and let
$\kappa $
, and let
be the Frobenius automorphism on K relative to F. Then,
![]() $\varphi $
reduces to the q-power map on
$\varphi $
reduces to the q-power map on
![]() $\kappa $
, and the fixed field of
$\kappa $
, and the fixed field of
![]() $\varphi $
on K is
$\varphi $
on K is
![]() $F\bigotimes _{W(\mathbb {F}_q)} W(\mathbb {F}_q) \cong F$
.
$F\bigotimes _{W(\mathbb {F}_q)} W(\mathbb {F}_q) \cong F$
.
2.2 The Robba ring and its variants
For
![]() $\alpha \in (0,1)$
, we put
$\alpha \in (0,1)$
, we put
For any
![]() $\rho \in [\alpha ,1)$
, we define the
$\rho \in [\alpha ,1)$
, we define the
![]() $\rho $
-Gauss norm on
$\rho $
-Gauss norm on
![]() $\mathcal {R}_\alpha $
by setting
$\mathcal {R}_\alpha $
by setting
![]() $\big |\sum \limits _i c_it^i \big |_\rho :=\sup _i\{|c_i|\rho ^i\}$
. The Robba ring is defined to be the union
$\big |\sum \limits _i c_it^i \big |_\rho :=\sup _i\{|c_i|\rho ^i\}$
. The Robba ring is defined to be the union
![]() $\mathcal {R} := \mathcal {R}(K,t):= \bigcup \limits _{\alpha \in (0,1)}\mathcal {R}_\alpha $
. For any
$\mathcal {R} := \mathcal {R}(K,t):= \bigcup \limits _{\alpha \in (0,1)}\mathcal {R}_\alpha $
. For any
![]() $\sum \limits _i c_it^i\in \mathcal {R}$
, we define
$\sum \limits _i c_it^i\in \mathcal {R}$
, we define
![]() $\big |\sum \limits _i c_it^i\big |_1:=\sup _i\{|c_i|\}\in \mathbb {R}_{\geq 0}\cup \{\infty \}$
, the
$\big |\sum \limits _i c_it^i\big |_1:=\sup _i\{|c_i|\}\in \mathbb {R}_{\geq 0}\cup \{\infty \}$
, the
![]() $1$
-Gauss norm.
$1$
-Gauss norm.
The bounded Robba ring
![]() $\mathcal {E}^{\dagger }=\mathcal {E}^{\dagger }(K,t)$
is the subring of
$\mathcal {E}^{\dagger }=\mathcal {E}^{\dagger }(K,t)$
is the subring of
![]() $\mathcal {R}$
consisting of bounded elements (i.e., elements with finite
$\mathcal {R}$
consisting of bounded elements (i.e., elements with finite
![]() $1$
-Gauss norm), which is actually a Henselian discretely valued field w.r.t. the
$1$
-Gauss norm), which is actually a Henselian discretely valued field w.r.t. the
![]() $1$
-Gauss norm with residue field
$1$
-Gauss norm with residue field
![]() $\kappa (\!( t)\!)$
.
$\kappa (\!( t)\!)$
.
Let
![]() $R\in \{\mathcal {R}, \mathcal {E}^{\dagger }\}$
. An absolute q-power Frobenius lift on R is a ring endomorphism
$R\in \{\mathcal {R}, \mathcal {E}^{\dagger }\}$
. An absolute q-power Frobenius lift on R is a ring endomorphism
![]() $\varphi \colon R\to R$
given by
$\varphi \colon R\to R$
given by
![]() $\sum \limits _{i\in \mathbb {Z}} c_it^i \longmapsto \sum \limits _{i\in \mathbb {Z}} \varphi (c_i)u^i$
for
$\sum \limits _{i\in \mathbb {Z}} c_it^i \longmapsto \sum \limits _{i\in \mathbb {Z}} \varphi (c_i)u^i$
for
![]() $u=\varphi (t)\in R$
such that
$u=\varphi (t)\in R$
such that
![]() $|u-t^q|_1<1$
.
$|u-t^q|_1<1$
.
For any
![]() $\alpha \in (0,1)$
, we define
$\alpha \in (0,1)$
, we define
![]() $\tilde {\mathcal {R}}_\alpha $
to be the ring of formal sums
$\tilde {\mathcal {R}}_\alpha $
to be the ring of formal sums
![]() $\operatorname *{\mathrm {\sum }}\limits _{i\in \mathbb {Q}} c_it^i$
with
$\operatorname *{\mathrm {\sum }}\limits _{i\in \mathbb {Q}} c_it^i$
with
![]() $c_i\in K$
, subject to the following properties.
$c_i\in K$
, subject to the following properties.
-
• For any
 $c>0$
, the set
$c>0$
, the set
 $\{i\in \mathbb {Q}\mid |c_i|\geq c\}$
is well-ordered.
$\{i\in \mathbb {Q}\mid |c_i|\geq c\}$
is well-ordered. -
• For any
 $\rho \in [\alpha ,1)$
, we have
$\rho \in [\alpha ,1)$
, we have
 $\lim \limits _{i\to \pm \infty } |c_i|\rho ^i=0$
.
$\lim \limits _{i\to \pm \infty } |c_i|\rho ^i=0$
.
For any
![]() $\rho \in [\alpha ,1)$
, we define the
$\rho \in [\alpha ,1)$
, we define the
![]() $\rho $
-Gauss norm on
$\rho $
-Gauss norm on
![]() $\tilde {\mathcal {R}}_\alpha $
by setting
$\tilde {\mathcal {R}}_\alpha $
by setting
We define
![]() $\tilde {\mathcal {R}} := \tilde {\mathcal {R}}(K,t):= \bigcup \limits _{\alpha \in (0,1)} \tilde {\mathcal {R}}_\alpha $
, the extended Robba ring. The absolute Frobenius lift on
$\tilde {\mathcal {R}} := \tilde {\mathcal {R}}(K,t):= \bigcup \limits _{\alpha \in (0,1)} \tilde {\mathcal {R}}_\alpha $
, the extended Robba ring. The absolute Frobenius lift on
![]() $\tilde {\mathcal {R}}$
is the ring automorphism on
$\tilde {\mathcal {R}}$
is the ring automorphism on
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
given by
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
given by
![]() $\sum \limits _{i\in \mathbb {Q}} c_it^i \mapsto \sum \limits _{i\in \mathbb {Q}} \varphi (c_i)t^{iq}$
. We denote by
$\sum \limits _{i\in \mathbb {Q}} c_it^i \mapsto \sum \limits _{i\in \mathbb {Q}} \varphi (c_i)t^{iq}$
. We denote by
![]() $\operatorname {\mathrm {\tilde {\mathcal {E}}}}^{\dagger }$
the subring of
$\operatorname {\mathrm {\tilde {\mathcal {E}}}}^{\dagger }$
the subring of
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
consisting of bounded elements. By [Reference Kedlaya11, Proposition 2.2.6], we have a
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
consisting of bounded elements. By [Reference Kedlaya11, Proposition 2.2.6], we have a
![]() $\varphi $
-equivariant embedding
$\varphi $
-equivariant embedding
![]() $\psi :\mathcal {R}\to \tilde {\mathcal {R}}$
such that
$\psi :\mathcal {R}\to \tilde {\mathcal {R}}$
such that
![]() $|\psi (x)|_\rho =|x|_\rho $
for
$|\psi (x)|_\rho =|x|_\rho $
for
![]() $\rho $
sufficiently close to
$\rho $
sufficiently close to
![]() $1$
.
$1$
.
2.3 The slope filtration theorem
We recall Kedlaya’s theory of slopes. Let
![]() $R\in \{\mathcal {E}^{\dagger },\mathcal {R},\operatorname {\mathrm {\tilde {\mathcal {E}}}}^{\dagger },\operatorname {\mathrm {\tilde {\mathcal {R}}}}\}$
equipped with a Frobenius lift
$R\in \{\mathcal {E}^{\dagger },\mathcal {R},\operatorname {\mathrm {\tilde {\mathcal {E}}}}^{\dagger },\operatorname {\mathrm {\tilde {\mathcal {R}}}}\}$
equipped with a Frobenius lift
![]() $\varphi $
. For the notions of
$\varphi $
. For the notions of
![]() $\varphi $
-modules and
$\varphi $
-modules and
![]() $(\varphi ,\nabla )$
-modules over R, we refer to [Reference Kedlaya9, Section 2.5]. We denote by
$(\varphi ,\nabla )$
-modules over R, we refer to [Reference Kedlaya9, Section 2.5]. We denote by
![]() $\operatorname {\mathrm {\textbf {Mod}^{\varphi }_R}}$
(resp.
$\operatorname {\mathrm {\textbf {Mod}^{\varphi }_R}}$
(resp.
![]() $\operatorname {\mathrm {\textbf {Mod}^{\varphi ,\nabla }_R}}$
) the category of
$\operatorname {\mathrm {\textbf {Mod}^{\varphi ,\nabla }_R}}$
) the category of
![]() $\varphi $
-modules (resp.
$\varphi $
-modules (resp.
![]() $(\varphi ,\nabla )$
-modules) over R.
$(\varphi ,\nabla )$
-modules) over R.
Let
![]() $(M,\varphi )\in \operatorname {\mathrm {\textbf {Mod}^{\varphi }_R}}$
, and let n be a positive integer. Then,
$(M,\varphi )\in \operatorname {\mathrm {\textbf {Mod}^{\varphi }_R}}$
, and let n be a positive integer. Then,
![]() $(M,\varphi ^n)$
is a
$(M,\varphi ^n)$
is a
![]() $\varphi ^n$
-module over
$\varphi ^n$
-module over
![]() $(R,\varphi ^n)$
. The n-pushforward functor is given by
$(R,\varphi ^n)$
. The n-pushforward functor is given by
For any
![]() $s\in \mathbb {Z}$
, we define the twist
$s\in \mathbb {Z}$
, we define the twist
![]() $M(s)$
of
$M(s)$
of
![]() $(M,\varphi )$
by s to be the
$(M,\varphi )$
by s to be the
![]() $\varphi $
-module
$\varphi $
-module
![]() $(M,\varpi ^s\Phi )$
.
$(M,\varpi ^s\Phi )$
.
Now, let M be a
![]() $\varphi $
-module over R of rank d.
$\varphi $
-module over R of rank d.
-
(i) We say that M is a unit-root
 $\varphi $
-module if there exists a basis
$\varphi $
-module if there exists a basis
 $\textbf {v}_1,\ldots ,\textbf {v}_d$
of M over R in which
$\textbf {v}_1,\ldots ,\textbf {v}_d$
of M over R in which
 $\varphi $
acts via an invertible matrix in
$\varphi $
acts via an invertible matrix in
 $\operatorname {\mathrm {GL}}_d(\mathcal {O}_{\mathcal {E}^{\dagger }})$
if
$\operatorname {\mathrm {GL}}_d(\mathcal {O}_{\mathcal {E}^{\dagger }})$
if
 $R\in \{\mathcal {E}^{\dagger },\mathcal {R}\}$
, or
$R\in \{\mathcal {E}^{\dagger },\mathcal {R}\}$
, or
 $\operatorname {\mathrm {GL}}_d(\mathcal {O}_{\operatorname {\mathrm {\tilde {\mathcal {E}}}}^{\dagger }})$
if
$\operatorname {\mathrm {GL}}_d(\mathcal {O}_{\operatorname {\mathrm {\tilde {\mathcal {E}}}}^{\dagger }})$
if
 $R\in \{\operatorname {\mathrm {\tilde {\mathcal {E}}}}^{\dagger },\operatorname {\mathrm {\tilde {\mathcal {R}}}}\}$
.
$R\in \{\operatorname {\mathrm {\tilde {\mathcal {E}}}}^{\dagger },\operatorname {\mathrm {\tilde {\mathcal {R}}}}\}$
. -
(ii) Let
 $\mu =s/r \in \mathbb {Q}$
with
$\mu =s/r \in \mathbb {Q}$
with
 $r>0$
and
$r>0$
and
 $(s,r)=1$
. We say that M is pure of slope
$(s,r)=1$
. We say that M is pure of slope
 $\mu $
if
$\mu $
if
 $([r]_*M)(-s)$
is unit-root.
$([r]_*M)(-s)$
is unit-root.
Let
![]() $M\in \operatorname {\mathrm {\textbf {Mod}^{\varphi }_R}}$
. We have a canonical filtration
$M\in \operatorname {\mathrm {\textbf {Mod}^{\varphi }_R}}$
. We have a canonical filtration
![]() $0=M_0 \subseteq M_1 \subseteq \cdots \subseteq M_l=M$
of
$0=M_0 \subseteq M_1 \subseteq \cdots \subseteq M_l=M$
of
![]() $\varphi $
-submodules over R such that each quotient
$\varphi $
-submodules over R such that each quotient
![]() $M_i/M_{i-1}$
is pure of some slope
$M_i/M_{i-1}$
is pure of some slope
![]() $\mu _i$
with
$\mu _i$
with
![]() $\mu _1< \cdots <\mu _l$
, by [Reference Kedlaya11, Theorem 1.7.1] if
$\mu _1< \cdots <\mu _l$
, by [Reference Kedlaya11, Theorem 1.7.1] if
![]() $R=\mathcal {R}$
or [Reference Kedlaya11, Proposition 1.4.15 and Theorem 2.1.8]) if
$R=\mathcal {R}$
or [Reference Kedlaya11, Proposition 1.4.15 and Theorem 2.1.8]) if
![]() $R=\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
. This is called the slope filtration of M. We call
$R=\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
. This is called the slope filtration of M. We call
![]() $\mu _1,\ldots ,\mu _l$
the jumps of the slope filtration. The (uniquely determined, not necessarily strictly) increasing sequence
$\mu _1,\ldots ,\mu _l$
the jumps of the slope filtration. The (uniquely determined, not necessarily strictly) increasing sequence
![]() $(\mu _1,\ldots ,\mu _1,\ldots ,\mu _l,\ldots ,\mu _l)$
, with each
$(\mu _1,\ldots ,\mu _1,\ldots ,\mu _l,\ldots ,\mu _l)$
, with each
![]() $\mu _i$
appearing
$\mu _i$
appearing
![]() $\operatorname {\mathrm {rk}}_R(M_i/M_{i-1})$
times, is said to be the slope sequence for M. We call
$\operatorname {\mathrm {rk}}_R(M_i/M_{i-1})$
times, is said to be the slope sequence for M. We call
![]() $\operatorname {\mathrm {rk}}_R (M_i/M_{i-1})$
the multiplicity of
$\operatorname {\mathrm {rk}}_R (M_i/M_{i-1})$
the multiplicity of
![]() $\mu _i$
for all
$\mu _i$
for all
![]() $1\leq i\leq l$
.
$1\leq i\leq l$
.
Moreover, if M is a
![]() $(\varphi ,\nabla )$
-module over
$(\varphi ,\nabla )$
-module over
![]() $\mathcal {R}$
, then the slope filtration can be refined to a filtration of
$\mathcal {R}$
, then the slope filtration can be refined to a filtration of
![]() $(\varphi ,\nabla )$
-submodules. This is [Reference Kedlaya9, Theorem 6.12], and is referred to as the slope filtration theorem for
$(\varphi ,\nabla )$
-submodules. This is [Reference Kedlaya9, Theorem 6.12], and is referred to as the slope filtration theorem for
![]() $(\varphi ,\nabla )$
-modules over
$(\varphi ,\nabla )$
-modules over
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
To continue, we need to recall some notions introduced in [Reference Kedlaya12, Section 14]. A difference ring (resp. difference field) is a ring (resp. field) R equipped with an endomorphism
![]() $\phi $
. A difference module over R is an R-module M equipped with a
$\phi $
. A difference module over R is an R-module M equipped with a
![]() $\phi $
-linear endomorphism
$\phi $
-linear endomorphism
![]() $\Phi $
. A finite free difference module M over R is said to be dualizable (resp. trivial) if M admits a basis over R such that
$\Phi $
. A finite free difference module M over R is said to be dualizable (resp. trivial) if M admits a basis over R such that
![]() $\Phi $
acts via an invertible matrix (resp. the identity matrix). For example, a
$\Phi $
acts via an invertible matrix (resp. the identity matrix). For example, a
![]() $\varphi $
-module over R is a dualizable difference module over R where R is any of the rings constructed in Section 2.2. A dualizable difference module M over R is said to be standard if it admits a basis
$\varphi $
-module over R is a dualizable difference module over R where R is any of the rings constructed in Section 2.2. A dualizable difference module M over R is said to be standard if it admits a basis
![]() $e_1,\ldots ,e_d$
such that
$e_1,\ldots ,e_d$
such that
![]() $e_i=\Phi (e_{i-1})$
for
$e_i=\Phi (e_{i-1})$
for
![]() $2\leq i \leq d$
and
$2\leq i \leq d$
and
![]() $\Phi (e_d)=\lambda e_1$
for some
$\Phi (e_d)=\lambda e_1$
for some
![]() $\lambda \in R^{\times }$
. A difference field
$\lambda \in R^{\times }$
. A difference field
![]() $(k,\phi _k)$
is called strongly difference-closed if
$(k,\phi _k)$
is called strongly difference-closed if
![]() $\phi _k$
is an automorphism and any dualizable difference module over k is trivial.
$\phi _k$
is an automorphism and any dualizable difference module over k is trivial.
Let k be a complete nonarchimedean valued field and
![]() $(k,\phi _k)$
is a difference field in which
$(k,\phi _k)$
is a difference field in which
![]() $\phi _k$
is bijective. An admissible extension of
$\phi _k$
is bijective. An admissible extension of
![]() $(k,\phi _k)$
is a difference field
$(k,\phi _k)$
is a difference field
![]() $(\ell ,\phi _\ell )$
, where
$(\ell ,\phi _\ell )$
, where
![]() $\ell $
is a field extension of k complete for the valuation extending the one on k with the same value group, and
$\ell $
is a field extension of k complete for the valuation extending the one on k with the same value group, and
![]() $\phi _\ell $
is an automorphism of
$\phi _\ell $
is an automorphism of
![]() $\ell $
extending
$\ell $
extending
![]() $\phi _k$
. (See [Reference Kedlaya11, Definition 3.2.1].)
$\phi _k$
. (See [Reference Kedlaya11, Definition 3.2.1].)
Lemma 2.2 [Reference Liu15, Lemma 1.5.3] The field K admits an admissible extension E such that the residue field
![]() $\kappa _E$
of E is strongly difference-closed.
$\kappa _E$
of E is strongly difference-closed.
The following lemma is a recollection of some results which will be used in the sequel.
Lemma 2.3 Let E be an admissible extension of K such that
![]() $\kappa _E$
is strongly difference-closed.
$\kappa _E$
is strongly difference-closed.
-
(i) Let
 $M \in \operatorname {\mathrm {\textbf {Mod}^{\varphi }_{\mathcal {R}}}}$
. Then, tensoring the slope filtration of M with
$M \in \operatorname {\mathrm {\textbf {Mod}^{\varphi }_{\mathcal {R}}}}$
. Then, tensoring the slope filtration of M with
 $\tilde {\mathcal {R}}(E,t)$
gives the slope filtration of
$\tilde {\mathcal {R}}(E,t)$
gives the slope filtration of
 $M\bigotimes _{\mathcal {R}}\tilde {\mathcal {R}}(E,t)$
.
$M\bigotimes _{\mathcal {R}}\tilde {\mathcal {R}}(E,t)$
. -
(ii) Let
 $0 \operatorname {\mathrm {\longrightarrow }} M_1 \operatorname {\mathrm {\longrightarrow }} M \operatorname {\mathrm {\longrightarrow }} M_2 \operatorname {\mathrm {\longrightarrow }} 0$
be a short exact sequence of
$0 \operatorname {\mathrm {\longrightarrow }} M_1 \operatorname {\mathrm {\longrightarrow }} M \operatorname {\mathrm {\longrightarrow }} M_2 \operatorname {\mathrm {\longrightarrow }} 0$
be a short exact sequence of
 $\varphi $
-modules over
$\varphi $
-modules over
 $\tilde {\mathcal {R}}(E,t)$
such that the slopes of
$\tilde {\mathcal {R}}(E,t)$
such that the slopes of
 $M_1$
are all less than the smallest slope of
$M_1$
are all less than the smallest slope of
 $M_2$
. Then, the sequence splits.
$M_2$
. Then, the sequence splits. -
(iii) Every
 $\varphi $
-module over
$\varphi $
-module over
 $\tilde {\mathcal {R}}(E,t)$
admits a Dieudonné–Manin decomposition, i.e., it is a direct sum of standard
$\tilde {\mathcal {R}}(E,t)$
admits a Dieudonné–Manin decomposition, i.e., it is a direct sum of standard
 $\varphi $
-submodules.
$\varphi $
-submodules. -
(iv) Let M and N be
 $\varphi $
-modules over
$\varphi $
-modules over
 $\tilde {\mathcal {R}}(E,t)$
. If the slopes of M are all less than the smallest slope of N, then no nonzero morphism from M to N exists.
$\tilde {\mathcal {R}}(E,t)$
. If the slopes of M are all less than the smallest slope of N, then no nonzero morphism from M to N exists.
Assertion (i) is [Reference Liu15, Proposition 1.5.6]. Assertion (ii) is [Reference Liu15, Proposition 1.5.11], and assertion (iii) is Proposition 1.5.12 in loc. cit. Assertion (iv) is [Reference Kedlaya11, Proposition 1.4.18].
2.4 The Tannakian duality
In this subsection, k denotes a field unless otherwise specified. We follow the definitions and notations in [Reference Deligne and Milne7]. We denote by
![]() $\omega ^G$
the forgetful functor
$\omega ^G$
the forgetful functor
![]() $\operatorname {\mathrm {\textbf {Rep}}}_k(G)\to \operatorname {\mathrm {\textbf {Vec}}}_k$
, which is called the fiber functor.
$\operatorname {\mathrm {\textbf {Rep}}}_k(G)\to \operatorname {\mathrm {\textbf {Vec}}}_k$
, which is called the fiber functor.
The following Tannakian duality will be repeatedly used in this paper, whose proof can be found, e.g., in [Reference Milne18, Theorem 9.2].
Theorem 2.4 Let G be an affine algebraic k-group, and let
![]() $R\in \operatorname {\mathrm {\textbf {Alg}}}_k$
. Suppose that for any
$R\in \operatorname {\mathrm {\textbf {Alg}}}_k$
. Suppose that for any
![]() $(V,\rho _V) \in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
, we are given an R-linear map
$(V,\rho _V) \in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
, we are given an R-linear map
![]() $\lambda _V\colon V_R\to V_R$
. If the family
$\lambda _V\colon V_R\to V_R$
. If the family
![]() $\{\lambda _V\mid (V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)\}$
satisfies
$\{\lambda _V\mid (V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)\}$
satisfies
-
(i)
 $\lambda _{V\bigotimes W}=\lambda _V\otimes \lambda _W$
for all
$\lambda _{V\bigotimes W}=\lambda _V\otimes \lambda _W$
for all
 $V,W\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
;
$V,W\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
; -
(ii)
 is the identity map where
is the identity map where
 is the trivial representation on k;
is the trivial representation on k; -
(iii) for all G-equivariant maps
 $\alpha \colon V\to W$
, we have
$\alpha \colon V\to W$
, we have
 $\lambda _W\circ \alpha _R=\alpha _R\circ \lambda _V$
.
$\lambda _W\circ \alpha _R=\alpha _R\circ \lambda _V$
.
Then, there exists a unique
![]() $g\in G(R)$
such that
$g\in G(R)$
such that
![]() $\lambda _V=\rho _V(g)$
for all
$\lambda _V=\rho _V(g)$
for all
![]() $(V,\rho _V) \in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
.
$(V,\rho _V) \in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
.
Corollary 2.5 Let G be an affine algebraic k-group. We have an isomorphism
![]() $G \cong \operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega ^G)$
of affine algebraic k-groups.
$G \cong \operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega ^G)$
of affine algebraic k-groups.
Corollary 2.6 Let G be a smooth affine algebraic k-group. Let
![]() $\ell /k$
be a field extension, and let
$\ell /k$
be a field extension, and let
![]() $\eta \colon \operatorname {\mathrm {\textbf {Rep}}}_\ell (G)\to \operatorname {\mathrm {\textbf {Vec}}}_\ell $
be a fiber functor over
$\eta \colon \operatorname {\mathrm {\textbf {Rep}}}_\ell (G)\to \operatorname {\mathrm {\textbf {Vec}}}_\ell $
be a fiber functor over
![]() $\ell $
. Then,
$\ell $
. Then,
![]() $\operatorname {\mathrm {\underline {Hom}}}^{\otimes } (\omega ^G,\eta )$
is a G-torsor over
$\operatorname {\mathrm {\underline {Hom}}}^{\otimes } (\omega ^G,\eta )$
is a G-torsor over
![]() $\ell $
. In particular, if
$\ell $
. In particular, if
![]() $H^1(\ell ,G)=\{1\}$
and
$H^1(\ell ,G)=\{1\}$
and
![]() $G(\ell )\neq \emptyset $
, then
$G(\ell )\neq \emptyset $
, then
![]() $\omega ^G$
is isomorphic to
$\omega ^G$
is isomorphic to
![]() $\eta $
over
$\eta $
over
![]() $\ell $
.
$\ell $
.
Proof Notice that we have an action
by precomposition. By [Reference Deligne and Milne7, Theorem 3.2(i)],
![]() $\operatorname {\mathrm {\underline {Hom}}}^{\otimes } (\omega ^G,\eta )$
is an
$\operatorname {\mathrm {\underline {Hom}}}^{\otimes } (\omega ^G,\eta )$
is an
![]() $\operatorname {\mathrm {\underline {Aut}}}^{\otimes } (\omega ^G)$
-torsor. In particular, it is a G-torsor over
$\operatorname {\mathrm {\underline {Aut}}}^{\otimes } (\omega ^G)$
-torsor. In particular, it is a G-torsor over
![]() $\ell $
by Corollary 2.5.
$\ell $
by Corollary 2.5.
Because G is a
![]() $\ell $
-group variety, G-torsors over
$\ell $
-group variety, G-torsors over
![]() $\ell $
are
$\ell $
are
![]() $\ell $
-varieties by [Reference Milne18, Proposition 2.69], whose isomorphism classes are classified by
$\ell $
-varieties by [Reference Milne18, Proposition 2.69], whose isomorphism classes are classified by
![]() $H^1(\ell ,G)$
. It follows from the triviality of
$H^1(\ell ,G)$
. It follows from the triviality of
![]() $H^1(\ell ,G)$
that
$H^1(\ell ,G)$
that
![]() $\operatorname {\mathrm {\underline {Hom}}}^{\otimes } (\omega ^G,\eta )(\ell )\cong G(\ell )$
; hence,
$\operatorname {\mathrm {\underline {Hom}}}^{\otimes } (\omega ^G,\eta )(\ell )\cong G(\ell )$
; hence,
![]() $\operatorname {\mathrm {\underline {Hom}}}^{\otimes } (\omega ^G,\eta )(\ell )\neq \emptyset $
. [Reference Deligne and Milne7, Proposition 1.13] then implies the second assertion.▪
$\operatorname {\mathrm {\underline {Hom}}}^{\otimes } (\omega ^G,\eta )(\ell )\neq \emptyset $
. [Reference Deligne and Milne7, Proposition 1.13] then implies the second assertion.▪
To end this subsection, we give a Lie algebra version of Theorem 2.4. We start with recalling the notion of the Lie algebra of a k-group functor. (See [Reference Demazure and Gabriel8, Chapitre II, Section 4] for more details. Notice that k denotes a ring in loc. cit.)
For any
![]() $R\in \operatorname {\mathrm {\textbf {Alg}}}_k$
, we define the R-algebra of dual numbers
$R\in \operatorname {\mathrm {\textbf {Alg}}}_k$
, we define the R-algebra of dual numbers
![]() $R[\varepsilon ]:= R[X]/(X^2)$
. Put
$R[\varepsilon ]:= R[X]/(X^2)$
. Put
![]() $\varepsilon := X+(X^2)$
; we then have the canonical projection
$\varepsilon := X+(X^2)$
; we then have the canonical projection
![]() $\pi _R\colon R[\varepsilon ]\to R,~\varepsilon \mapsto 0$
. Let G be a k-group functor. We define
$\pi _R\colon R[\varepsilon ]\to R,~\varepsilon \mapsto 0$
. Let G be a k-group functor. We define
Let
![]() $f\colon G\to H$
be a morphism of k-group functors. The commutative diagram
$f\colon G\to H$
be a morphism of k-group functors. The commutative diagram

implies that
![]() $f(R[\epsilon ])\circ \iota _G(X)\in \operatorname {\mathrm {Lie}}(H)(R)$
for all
$f(R[\epsilon ])\circ \iota _G(X)\in \operatorname {\mathrm {Lie}}(H)(R)$
for all
![]() $X\in \operatorname {\mathrm {Lie}}(G)(R)$
. We define
$X\in \operatorname {\mathrm {Lie}}(G)(R)$
. We define
![]() $\operatorname {\mathrm {Lie}}(f):= f(R[\epsilon ])\circ \iota _G\colon \operatorname {\mathrm {Lie}}(G)(R) \to \operatorname {\mathrm {Lie}}(H)(R)$
. Hence,
$\operatorname {\mathrm {Lie}}(f):= f(R[\epsilon ])\circ \iota _G\colon \operatorname {\mathrm {Lie}}(G)(R) \to \operatorname {\mathrm {Lie}}(H)(R)$
. Hence,
![]() $\operatorname {\mathrm {Lie}}(\rule {2mm}{0.15mm})(R)$
is a functor from the category of k-group functors to that of abelian groups.
$\operatorname {\mathrm {Lie}}(\rule {2mm}{0.15mm})(R)$
is a functor from the category of k-group functors to that of abelian groups.
For an affine algebraic k-group G, we write I for the kernel of the counit
![]() $\epsilon _G\colon k[G]\to k$
. Because
$\epsilon _G\colon k[G]\to k$
. Because
![]() $k[G]$
is Noetherian,
$k[G]$
is Noetherian,
![]() $I/I^2$
is a finite-dimensional vector space over
$I/I^2$
is a finite-dimensional vector space over
![]() $k\cong k[G]/I$
. We then have
$k\cong k[G]/I$
. We then have
![]() $\operatorname {\mathrm {Hom}}_k(I/I^2,R) \cong \operatorname {\mathrm {Hom}}_k(I/I^2,k) \bigotimes _k R$
. By [Reference Demazure and Gabriel8, Corollaire II.3.3], we have canonical group isomorphisms
$\operatorname {\mathrm {Hom}}_k(I/I^2,R) \cong \operatorname {\mathrm {Hom}}_k(I/I^2,k) \bigotimes _k R$
. By [Reference Demazure and Gabriel8, Corollaire II.3.3], we have canonical group isomorphisms
![]() $\operatorname {\mathrm {Lie}}(G)(R)\cong \operatorname {\mathrm {Hom}}_k(I/I^2,R)$
and
$\operatorname {\mathrm {Lie}}(G)(R)\cong \operatorname {\mathrm {Hom}}_k(I/I^2,R)$
and
![]() $\mathfrak {g}=\operatorname {\mathrm {Lie}}(G)(k) \cong \operatorname {\mathrm {Hom}}_k(I/I^2,k)$
, whence
$\mathfrak {g}=\operatorname {\mathrm {Lie}}(G)(k) \cong \operatorname {\mathrm {Hom}}_k(I/I^2,k)$
, whence
![]() $\operatorname {\mathrm {Lie}}(G)(R) \cong \mathfrak {g}_R$
. The Lie structure on
$\operatorname {\mathrm {Lie}}(G)(R) \cong \mathfrak {g}_R$
. The Lie structure on
![]() $\mathfrak {g}$
then canonically gives a Lie structure on
$\mathfrak {g}$
then canonically gives a Lie structure on
![]() $\mathfrak {g}_R$
and hence on
$\mathfrak {g}_R$
and hence on
![]() $\operatorname {\mathrm {Lie}}(G)(R)$
. We call
$\operatorname {\mathrm {Lie}}(G)(R)$
. We call
![]() $\operatorname {\mathrm {Lie}}(G)(R)$
the Lie algebra of G over R, and will identify it with
$\operatorname {\mathrm {Lie}}(G)(R)$
the Lie algebra of G over R, and will identify it with
![]() $\mathfrak {g}_R$
. Moreover,
$\mathfrak {g}_R$
. Moreover,
![]() $\operatorname {\mathrm {Lie}}(\rule {2mm}{0.15mm})(R)$
is a functor from the category of affine algebraic k-groups to that of Lie algebras over R.
$\operatorname {\mathrm {Lie}}(\rule {2mm}{0.15mm})(R)$
is a functor from the category of affine algebraic k-groups to that of Lie algebras over R.
Remark 2.7 More generally, let k be a commutative ring with
![]() $1$
and let G be a smooth k-group scheme. For any k-algebra R, we can similarly define
$1$
and let G be a smooth k-group scheme. For any k-algebra R, we can similarly define
![]() $\operatorname {\mathrm {Lie}}(G)(R)$
as above. Because the
$\operatorname {\mathrm {Lie}}(G)(R)$
as above. Because the
![]() $\mathscr {O}_G$
-module
$\mathscr {O}_G$
-module
![]() $\Omega _{G/k}^1$
is finite locally free, we have
$\Omega _{G/k}^1$
is finite locally free, we have
![]() $\operatorname {\mathrm {Lie}}(G)(R)\cong \operatorname {\mathrm {Lie}}(G)(k)\bigotimes _k R$
by [Reference Demazure and Gabriel8, Proposition II.4.8].
$\operatorname {\mathrm {Lie}}(G)(R)\cong \operatorname {\mathrm {Lie}}(G)(k)\bigotimes _k R$
by [Reference Demazure and Gabriel8, Proposition II.4.8].
Remark 2.8 For any d-dimensional G-representation
![]() $(V,\rho _V)$
, we write
$(V,\rho _V)$
, we write
![]() $\operatorname {\mathrm {\mathfrak {gl}}}_V:= \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {GL}}_V)(k)$
. We then have
$\operatorname {\mathrm {\mathfrak {gl}}}_V:= \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {GL}}_V)(k)$
. We then have
![]() $\operatorname {\mathrm {\mathfrak {gl}}}_{V,R}=\{I_d+\varepsilon B \mid B\in \operatorname {\mathrm {Mat}}_{d,d}(R)\}$
, after choosing a k-basis for V. Then,
$\operatorname {\mathrm {\mathfrak {gl}}}_{V,R}=\{I_d+\varepsilon B \mid B\in \operatorname {\mathrm {Mat}}_{d,d}(R)\}$
, after choosing a k-basis for V. Then,
![]() $I_d+\varepsilon B \mapsto B$
gives a group isomorphism from
$I_d+\varepsilon B \mapsto B$
gives a group isomorphism from
![]() $\operatorname {\mathrm {\mathfrak {gl}}}_{V,R}$
to
$\operatorname {\mathrm {\mathfrak {gl}}}_{V,R}$
to
![]() $\operatorname {\mathrm {End}}_R(V_R)$
. Henceforth, we will identify
$\operatorname {\mathrm {End}}_R(V_R)$
. Henceforth, we will identify
![]() $\operatorname {\mathrm {Lie}}(\rho _V)(X)$
as an endomorphism of
$\operatorname {\mathrm {Lie}}(\rho _V)(X)$
as an endomorphism of
![]() $V_R$
, for all
$V_R$
, for all
![]() $X\in \mathfrak {g}_R$
.
$X\in \mathfrak {g}_R$
.
Replacing H with
![]() $\operatorname {\mathrm {GL}}_V$
and f with
$\operatorname {\mathrm {GL}}_V$
and f with
![]() $\rho _V$
in diagram (1), we obtain a morphism
$\rho _V$
in diagram (1), we obtain a morphism
![]() $\operatorname {\mathrm {Lie}}(\rho _V)=\rho _V(R[\epsilon ])\circ \iota _G \colon \mathfrak {g}_R \to \operatorname {\mathrm {\mathfrak {gl}}}_{V,R}$
of Lie algebras over R. Let
$\operatorname {\mathrm {Lie}}(\rho _V)=\rho _V(R[\epsilon ])\circ \iota _G \colon \mathfrak {g}_R \to \operatorname {\mathrm {\mathfrak {gl}}}_{V,R}$
of Lie algebras over R. Let
![]() $(W,\rho _W)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
, and let
$(W,\rho _W)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
, and let
![]() $\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
. We then have
$\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
. We then have
![]() $\alpha _R\circ \operatorname {\mathrm {Lie}}(\rho _V)(X)=\operatorname {\mathrm {Lie}}(\rho _W)(X)\circ \alpha _R$
for all
$\alpha _R\circ \operatorname {\mathrm {Lie}}(\rho _V)(X)=\operatorname {\mathrm {Lie}}(\rho _W)(X)\circ \alpha _R$
for all
![]() $X\in \mathfrak {g}_R$
.
$X\in \mathfrak {g}_R$
.
Applying the functor
![]() $\operatorname {\mathrm {Lie}}(\rule {2mm}{0.15mm})(R)$
on both sides of the isomorphism in Corollary 2.5 gives us an isomorphism
$\operatorname {\mathrm {Lie}}(\rule {2mm}{0.15mm})(R)$
on both sides of the isomorphism in Corollary 2.5 gives us an isomorphism
![]() $\mathfrak {g}_R\cong \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {\underline {Aut}}}^{\otimes } (\omega ^G))(R)$
of Lie algebras over R. The following corollary indicates that elements in
$\mathfrak {g}_R\cong \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {\underline {Aut}}}^{\otimes } (\omega ^G))(R)$
of Lie algebras over R. The following corollary indicates that elements in
![]() $\operatorname {\mathrm {Lie}}(\operatorname {\mathrm {\underline {Aut}}}^{\otimes } (\omega ^G))(R)$
are exactly the derivatives (in the sense of taking derivations of conditions (i–iii) in Theorem 2.4) of elements in
$\operatorname {\mathrm {Lie}}(\operatorname {\mathrm {\underline {Aut}}}^{\otimes } (\omega ^G))(R)$
are exactly the derivatives (in the sense of taking derivations of conditions (i–iii) in Theorem 2.4) of elements in
![]() $\operatorname {\mathrm {\underline {Aut}}}^{\otimes } (\omega ^G)(R)$
.
$\operatorname {\mathrm {\underline {Aut}}}^{\otimes } (\omega ^G)(R)$
.
Corollary 2.9 Let G be an affine algebraic k-group, and let R be a k-algebra. Suppose that for any
![]() $(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_k (G)$
, we are given an R-linear endomorphism
$(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_k (G)$
, we are given an R-linear endomorphism
![]() $\theta _V$
of
$\theta _V$
of
![]() $V_R$
subject to the conditions:
$V_R$
subject to the conditions:
-
(i)
 $\theta _{V\bigotimes W}=\theta _V\otimes \operatorname {\mathrm {Id}}_{W_R} +\operatorname {\mathrm {Id}}_{V_R}\otimes \theta _W$
for all
$\theta _{V\bigotimes W}=\theta _V\otimes \operatorname {\mathrm {Id}}_{W_R} +\operatorname {\mathrm {Id}}_{V_R}\otimes \theta _W$
for all
 $V,W\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
;
$V,W\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
; -
(ii)
 , where
, where
 is the trivial G-representation;
is the trivial G-representation; -
(iii)
 $\theta _W\circ \alpha _R=\alpha _R\circ \theta _V$
for all
$\theta _W\circ \alpha _R=\alpha _R\circ \theta _V$
for all
 $\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
.
$\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
.
Then, there exists a unique element
![]() $X\in \mathfrak {g}_R$
such that
$X\in \mathfrak {g}_R$
such that
![]() $\theta _V=\operatorname {\mathrm {Lie}}(\rho _V)(X)$
for all
$\theta _V=\operatorname {\mathrm {Lie}}(\rho _V)(X)$
for all
![]() $(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
.
$(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
.
Proof For any
![]() $(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
and
$(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
and
![]() $\theta _V\colon V_R\to V_R$
, we define an
$\theta _V\colon V_R\to V_R$
, we define an
![]() $R[\varepsilon ]$
-linear map
$R[\varepsilon ]$
-linear map
We define an
![]() $R[\varepsilon ]$
-linear endomorphism
$R[\varepsilon ]$
-linear endomorphism
Then,
![]() $\tilde \theta _V\in \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {GL}}_V)(R)\subseteq \operatorname {\mathrm {GL}}_V(R[\varepsilon ])$
, because
$\tilde \theta _V\in \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {GL}}_V)(R)\subseteq \operatorname {\mathrm {GL}}_V(R[\varepsilon ])$
, because
![]() $\pi _R(\tilde \theta _V)=\operatorname {\mathrm {Id}}_{V_R}$
.
$\pi _R(\tilde \theta _V)=\operatorname {\mathrm {Id}}_{V_R}$
.
We claim that the family
of
![]() $R[\varepsilon ]$
-linear endomorphisms satisfies conditions (i–iii) in Theorem 2.4. Granting this claim for a moment, we conclude that
$R[\varepsilon ]$
-linear endomorphisms satisfies conditions (i–iii) in Theorem 2.4. Granting this claim for a moment, we conclude that
![]() $\tilde \theta \in \operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega ^G)(R[\varepsilon ])$
. In particular, there exists a unique element
$\tilde \theta \in \operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega ^G)(R[\varepsilon ])$
. In particular, there exists a unique element
![]() $X\in G(R[\varepsilon ])$
such that
$X\in G(R[\varepsilon ])$
such that
![]() $\tilde \theta _V=\rho _V(X)$
for all
$\tilde \theta _V=\rho _V(X)$
for all
![]() $(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
. Because
$(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
. Because
![]() $\pi _R(\tilde \theta )=\operatorname {\mathrm {Id}}\in \operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega ^G)(R)$
, we have
$\pi _R(\tilde \theta )=\operatorname {\mathrm {Id}}\in \operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega ^G)(R)$
, we have
![]() $\tilde \theta \in \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega ^G))(R)$
. The isomorphism
$\tilde \theta \in \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega ^G))(R)$
. The isomorphism
![]() $\mathfrak {g}_R\cong \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {\underline {Aut}}}^{\otimes } (\omega ^G))(R)$
then implies that
$\mathfrak {g}_R\cong \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {\underline {Aut}}}^{\otimes } (\omega ^G))(R)$
then implies that
![]() $X\in \mathfrak {g}_R$
. Furthermore, it follows from the construction that
$X\in \mathfrak {g}_R$
. Furthermore, it follows from the construction that
![]() $\theta _V=\operatorname {\mathrm {Lie}}(\rho _V)(X)$
for all
$\theta _V=\operatorname {\mathrm {Lie}}(\rho _V)(X)$
for all
![]() $(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
, and the corollary follows.
$(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
, and the corollary follows.
It remains to prove the claim. Condition (ii) is clear from the construction. Given
![]() $(W,\rho _W)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
, we compute
$(W,\rho _W)\in \operatorname {\mathrm {\textbf {Rep}}}_k(G)$
, we compute
 $$ \begin{align*} \tilde \theta_{V\bigotimes W} &=\operatorname{\mathrm{Id}}_{(V\bigotimes W)_R}+\varepsilon \theta_{V\bigotimes W}\\ &=\operatorname{\mathrm{Id}}_{(V\otimes W)_R}+\varepsilon(\theta_V\otimes \operatorname{\mathrm{Id}}_{W_R} +\operatorname{\mathrm{Id}}_{V_R}\otimes \theta_W)\\ &=(\operatorname{\mathrm{Id}}_{V_R}+\varepsilon \theta_V)\otimes (\operatorname{\mathrm{Id}}_{W_R}+\varepsilon \theta_W)\\ &=\tilde \theta_V\otimes \tilde \theta_W. \end{align*} $$
$$ \begin{align*} \tilde \theta_{V\bigotimes W} &=\operatorname{\mathrm{Id}}_{(V\bigotimes W)_R}+\varepsilon \theta_{V\bigotimes W}\\ &=\operatorname{\mathrm{Id}}_{(V\otimes W)_R}+\varepsilon(\theta_V\otimes \operatorname{\mathrm{Id}}_{W_R} +\operatorname{\mathrm{Id}}_{V_R}\otimes \theta_W)\\ &=(\operatorname{\mathrm{Id}}_{V_R}+\varepsilon \theta_V)\otimes (\operatorname{\mathrm{Id}}_{W_R}+\varepsilon \theta_W)\\ &=\tilde \theta_V\otimes \tilde \theta_W. \end{align*} $$
Hence, (2) satisfies condition (i). It remains to show that Theorem 2.4 satisfies condition (iii). Let
![]() $\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
. For any
$\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
. For any
![]() $v\otimes (x+y\varepsilon )\in V_{R[\varepsilon ]}$
, we compute
$v\otimes (x+y\varepsilon )\in V_{R[\varepsilon ]}$
, we compute
 $$ \begin{align*} \alpha_{R[\varepsilon]}\circ \varepsilon \theta_V(v\otimes(x+y\varepsilon)) &=\alpha_{R[\varepsilon]} (\theta_V(v \otimes x)\otimes \varepsilon) =(\alpha_R\circ \theta_V)(v\otimes x )\otimes \varepsilon \\ &=(\theta_W\circ \alpha_R)(v\otimes x ) \otimes \varepsilon =\theta_W (\alpha(v)\otimes x)\otimes \varepsilon \\ &=\varepsilon\theta_W ( \alpha(v)\otimes (x+y\epsilon)) =\varepsilon\theta_W \circ \alpha_{R[\varepsilon]} (v\otimes (x+y\varepsilon)). \end{align*} $$
$$ \begin{align*} \alpha_{R[\varepsilon]}\circ \varepsilon \theta_V(v\otimes(x+y\varepsilon)) &=\alpha_{R[\varepsilon]} (\theta_V(v \otimes x)\otimes \varepsilon) =(\alpha_R\circ \theta_V)(v\otimes x )\otimes \varepsilon \\ &=(\theta_W\circ \alpha_R)(v\otimes x ) \otimes \varepsilon =\theta_W (\alpha(v)\otimes x)\otimes \varepsilon \\ &=\varepsilon\theta_W ( \alpha(v)\otimes (x+y\epsilon)) =\varepsilon\theta_W \circ \alpha_{R[\varepsilon]} (v\otimes (x+y\varepsilon)). \end{align*} $$
It follows that
 $$ \begin{align*} \alpha_{R[\varepsilon]}\circ \tilde \theta_V&=\alpha_{R[\varepsilon]}\circ (\operatorname{\mathrm{Id}}_{V_{R[\varepsilon]}}+\varepsilon \theta_V) =\alpha_{R[\varepsilon]}+\alpha_{R[\varepsilon]}\circ \varepsilon \theta_V\\ &=\alpha_{R[\varepsilon]}+\varepsilon\theta_W \circ \alpha_{R[\varepsilon]} =(\operatorname{\mathrm{Id}}_{W_{R[\varepsilon]}}+\varepsilon \theta_W)\circ \alpha_{R[\varepsilon]}\\ &=\tilde \theta_W \circ \alpha_{R[\varepsilon]}, \end{align*} $$
$$ \begin{align*} \alpha_{R[\varepsilon]}\circ \tilde \theta_V&=\alpha_{R[\varepsilon]}\circ (\operatorname{\mathrm{Id}}_{V_{R[\varepsilon]}}+\varepsilon \theta_V) =\alpha_{R[\varepsilon]}+\alpha_{R[\varepsilon]}\circ \varepsilon \theta_V\\ &=\alpha_{R[\varepsilon]}+\varepsilon\theta_W \circ \alpha_{R[\varepsilon]} =(\operatorname{\mathrm{Id}}_{W_{R[\varepsilon]}}+\varepsilon \theta_W)\circ \alpha_{R[\varepsilon]}\\ &=\tilde \theta_W \circ \alpha_{R[\varepsilon]}, \end{align*} $$
as desired.▪
2.5 Filtered and graded fiber functors
We recall the notions of filtered and graded fiber functors on Tannakian categories following [Reference Ziegler25]. Let
![]() $\Gamma $
be a totally ordered abelian group (written additively), and let
$\Gamma $
be a totally ordered abelian group (written additively), and let
![]() $R\in \operatorname {\mathrm {\textbf {Alg}}}_k$
. A
$R\in \operatorname {\mathrm {\textbf {Alg}}}_k$
. A
![]() $\Gamma $
-graded R-module is an R-module M together with a direct sum decomposition
$\Gamma $
-graded R-module is an R-module M together with a direct sum decomposition
![]() $M=\bigoplus \limits _{\gamma \in \Gamma } M_\gamma $
. A morphism between two
$M=\bigoplus \limits _{\gamma \in \Gamma } M_\gamma $
. A morphism between two
![]() $\Gamma $
-graded R modules M and N is an R-linear map
$\Gamma $
-graded R modules M and N is an R-linear map
![]() $f\colon M\to N$
such that
$f\colon M\to N$
such that
![]() $f(M_\gamma )\subseteq N_\gamma $
for all
$f(M_\gamma )\subseteq N_\gamma $
for all
![]() $\gamma \in \Gamma $
. We denote by
$\gamma \in \Gamma $
. We denote by
![]() $\Gamma $
-
$\Gamma $
-
![]() $\operatorname {\mathrm {\textbf {Grad}}}_R$
the category of
$\operatorname {\mathrm {\textbf {Grad}}}_R$
the category of
![]() $\Gamma $
-graded modules over R. For
$\Gamma $
-graded modules over R. For
![]() $M,N\in \Gamma $
-
$M,N\in \Gamma $
-
![]() $\operatorname {\mathrm {\textbf {Grad}}}_R$
, we define the tensor product
$\operatorname {\mathrm {\textbf {Grad}}}_R$
, we define the tensor product
![]() $(M\bigotimes _R N)_\gamma = \bigoplus \limits _{\gamma '+\gamma ''=\gamma } \big ( M_{\gamma '}\bigotimes _R N_{\gamma ''}\big )$
.
$(M\bigotimes _R N)_\gamma = \bigoplus \limits _{\gamma '+\gamma ''=\gamma } \big ( M_{\gamma '}\bigotimes _R N_{\gamma ''}\big )$
.
Let M be an R-module. A
![]() $\Gamma $
-filtration on M is an increasing map
$\Gamma $
-filtration on M is an increasing map
such that
![]() $\mathcal {F}^{\gamma } M=0$
for
$\mathcal {F}^{\gamma } M=0$
for
![]() $\gamma \ll 0$
and
$\gamma \ll 0$
and
![]() $\mathcal {F}^{\gamma } M=M$
for
$\mathcal {F}^{\gamma } M=M$
for
![]() $\gamma \gg 0$
, which is increasing in the sense that
$\gamma \gg 0$
, which is increasing in the sense that
![]() $\mathcal {F}^{\gamma } M \subseteq \mathcal {F}^{\gamma '} M$
whenever
$\mathcal {F}^{\gamma } M \subseteq \mathcal {F}^{\gamma '} M$
whenever
![]() $\gamma \leq \gamma '$
. A
$\gamma \leq \gamma '$
. A
![]() $\Gamma $
-filtered R-module is an R-module M with a
$\Gamma $
-filtered R-module is an R-module M with a
![]() $\Gamma $
-filtration. To abbreviate notations, we sometimes denote
$\Gamma $
-filtration. To abbreviate notations, we sometimes denote
![]() $\mathcal {F}^{\gamma } M$
by
$\mathcal {F}^{\gamma } M$
by
![]() $M^{\gamma }$
if no confusion shall arise. A morphism between two
$M^{\gamma }$
if no confusion shall arise. A morphism between two
![]() $\Gamma $
-filtered R-modules M and N is an R-linear map
$\Gamma $
-filtered R-modules M and N is an R-linear map
![]() $f\colon M\to N$
such that
$f\colon M\to N$
such that
![]() $f(M^{\gamma })\subseteq N^{\gamma }$
for all
$f(M^{\gamma })\subseteq N^{\gamma }$
for all
![]() $\gamma \in \Gamma $
. We denote by
$\gamma \in \Gamma $
. We denote by
![]() $\Gamma $
-
$\Gamma $
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_R$
the category of
$\operatorname {\mathrm {\textbf {Fil}}}_R$
the category of
![]() $\Gamma $
-filtered modules over R.
$\Gamma $
-filtered modules over R.
Let M be a
![]() $\Gamma $
-filtered module over R. For any
$\Gamma $
-filtered module over R. For any
![]() $\gamma \in \Gamma $
, we put
$\gamma \in \Gamma $
, we put
![]() $\mathcal {F}^{\gamma -} M:= \operatorname *{\mathrm {\sum }}\limits _{\gamma '<\gamma } \mathcal {F}^{\gamma '} M$
. We define
$\mathcal {F}^{\gamma -} M:= \operatorname *{\mathrm {\sum }}\limits _{\gamma '<\gamma } \mathcal {F}^{\gamma '} M$
. We define
Then,
![]() $\operatorname {\mathrm {gr}}_{\mathcal {F}} M:= \bigoplus \limits _{\gamma \in \Gamma } \operatorname {\mathrm {gr}}_{\mathcal {F}}^{\gamma } M$
is a
$\operatorname {\mathrm {gr}}_{\mathcal {F}} M:= \bigoplus \limits _{\gamma \in \Gamma } \operatorname {\mathrm {gr}}_{\mathcal {F}}^{\gamma } M$
is a
![]() $\Gamma $
-graded R module, and is called the
$\Gamma $
-graded R module, and is called the
![]() $\Gamma $
-graded R-module associated to
$\Gamma $
-graded R-module associated to
![]() $\mathcal {F}$
. We thus have a functor
$\mathcal {F}$
. We thus have a functor
Elements
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
![]() $\operatorname {\mathrm {gr}}_{\mathcal {F}}^{\gamma } M\neq 0$
are said to be the
$\operatorname {\mathrm {gr}}_{\mathcal {F}}^{\gamma } M\neq 0$
are said to be the
![]() $\Gamma $
-jumps (or simply jumps) of
$\Gamma $
-jumps (or simply jumps) of
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
The tensor product structure in
![]() $\Gamma $
-
$\Gamma $
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_R$
is defined by
$\operatorname {\mathrm {\textbf {Fil}}}_R$
is defined by
for all
![]() $\Gamma $
-filtered modules M and N over R.
$\Gamma $
-filtered modules M and N over R.
A morphism
![]() $f\colon M\to N$
in
$f\colon M\to N$
in
![]() $\Gamma $
-
$\Gamma $
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_R$
is said to be admissible (or strict) if
$\operatorname {\mathrm {\textbf {Fil}}}_R$
is said to be admissible (or strict) if
Following [Reference Ziegler25, Section 4.1], we say that a short sequence
![]()
![]() in
in
![]() $\Gamma $
-
$\Gamma $
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_R$
is exact if both of
$\operatorname {\mathrm {\textbf {Fil}}}_R$
is exact if both of
![]() $f'$
and
$f'$
and
![]() $f''$
are admissible, and the underlying short sequence in
$f''$
are admissible, and the underlying short sequence in
![]() $\operatorname {\mathrm {\textbf {Mod}}}_R$
is exact.
$\operatorname {\mathrm {\textbf {Mod}}}_R$
is exact.
Let
![]() $\mathcal T$
be a Tannakian category over k, and let R be a k-algebra.
$\mathcal T$
be a Tannakian category over k, and let R be a k-algebra.
-
(i) A
 $\Gamma $
-graded fiber functor on
$\Gamma $
-graded fiber functor on
 $\mathcal T$
over R is an exact faithful k-linear tensor functor
$\mathcal T$
over R is an exact faithful k-linear tensor functor
 $\tau \colon \mathcal T \to \Gamma $
-
$\tau \colon \mathcal T \to \Gamma $
-
 $\operatorname {\mathrm {\textbf {Grad}}}_R$
.
$\operatorname {\mathrm {\textbf {Grad}}}_R$
. -
(ii) A
 $\Gamma $
-filtered fiber functor on
$\Gamma $
-filtered fiber functor on
 $\mathcal T$
over R is an exact faithful k-linear tensor functor
$\mathcal T$
over R is an exact faithful k-linear tensor functor
 $\eta \colon \mathcal T \to \Gamma $
-
$\eta \colon \mathcal T \to \Gamma $
-
 $\operatorname {\mathrm {\textbf {Fil}}}_R$
.
$\operatorname {\mathrm {\textbf {Fil}}}_R$
. -
(iii) Given an object
 $M=\bigoplus \limits _{\gamma \in \Gamma } M_\gamma $
in
$M=\bigoplus \limits _{\gamma \in \Gamma } M_\gamma $
in
 $\Gamma $
-
$\Gamma $
-
 $\operatorname {\mathrm {\textbf {Grad}}}_R$
, we put
$\operatorname {\mathrm {\textbf {Grad}}}_R$
, we put
 $\mathcal {F}^{\gamma }(M):=\bigoplus \limits _{\gamma '\leq \gamma } M_{\gamma '}$
. This gives rise to a functor
$\mathcal {F}^{\gamma }(M):=\bigoplus \limits _{\gamma '\leq \gamma } M_{\gamma '}$
. This gives rise to a functor
 $\operatorname {\mathrm {fil}}\colon \Gamma $
-
$\operatorname {\mathrm {fil}}\colon \Gamma $
-
 $\operatorname {\mathrm {\textbf {Grad}}}_R \to \Gamma $
-
$\operatorname {\mathrm {\textbf {Grad}}}_R \to \Gamma $
-
 $\operatorname {\mathrm {\textbf {Fil}}}_R$
.
$\operatorname {\mathrm {\textbf {Fil}}}_R$
. -
(iv) A
 $\Gamma $
-filtered fiber functor
$\Gamma $
-filtered fiber functor
 $\eta $
is called splittable if there exists a
$\eta $
is called splittable if there exists a
 $\Gamma $
-graded fiber functor
$\Gamma $
-graded fiber functor
 $\tau $
such that
$\tau $
such that
 $\eta =\operatorname {\mathrm {fil}}\circ \tau $
, and
$\eta =\operatorname {\mathrm {fil}}\circ \tau $
, and
 $\tau $
is called a splitting of
$\tau $
is called a splitting of
 $\eta $
.
$\eta $
.
Remark 2.10 More concretely, a
![]() $\Gamma $
-filtered fiber functor is a k-linear functor
$\Gamma $
-filtered fiber functor is a k-linear functor
![]() $\eta \colon \mathcal T \to \Gamma $
-
$\eta \colon \mathcal T \to \Gamma $
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_R$
satisfying the following properties (cf. [Reference Dat, Orlik and Rapoport6, Definition 4.2.6 and Remark 4.2.7]).
$\operatorname {\mathrm {\textbf {Fil}}}_R$
satisfying the following properties (cf. [Reference Dat, Orlik and Rapoport6, Definition 4.2.6 and Remark 4.2.7]).
-
(i) It is admissibly (or strictly) functorial, i.e., for any morphism
 $\alpha \colon X\to Y$
in
$\alpha \colon X\to Y$
in
 $\mathcal T$
, we have
$\mathcal T$
, we have
 $\eta (\alpha )\big (\mathcal {F}^{\gamma } \eta (X)\big )=\eta (\alpha )(\eta (X))\cap \mathcal {F}^{\gamma } \eta (Y)$
for all
$\eta (\alpha )\big (\mathcal {F}^{\gamma } \eta (X)\big )=\eta (\alpha )(\eta (X))\cap \mathcal {F}^{\gamma } \eta (Y)$
for all
 $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
. -
(ii) It is compatible with tensor products, i.e., we have
for all $$ \begin{align*} \mathcal{F}^{\gamma} \big(\eta(X\bigotimes Y)\big)=\operatorname*{\mathrm{\sum}}\limits_{\gamma'+\gamma''=\gamma} \mathcal{F}^{\gamma'} \big(\eta(X)\big)\bigotimes \mathcal{F}^{\gamma''} \big(\eta(Y)\big),\end{align*} $$
$$ \begin{align*} \mathcal{F}^{\gamma} \big(\eta(X\bigotimes Y)\big)=\operatorname*{\mathrm{\sum}}\limits_{\gamma'+\gamma''=\gamma} \mathcal{F}^{\gamma'} \big(\eta(X)\big)\bigotimes \mathcal{F}^{\gamma''} \big(\eta(Y)\big),\end{align*} $$
 $X,Y\in \operatorname {\mathrm {Ob}}(\mathcal T)$
and
$X,Y\in \operatorname {\mathrm {Ob}}(\mathcal T)$
and
 $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
-
(iii)
where
 is the identity object in
is the identity object in
 $\mathcal T$
. Note that
$\mathcal T$
. Note that
 is the identity object in
is the identity object in
 $\Gamma $
-
$\Gamma $
-
 $\operatorname {\mathrm {\textbf {Fil}}}_R$
.
$\operatorname {\mathrm {\textbf {Fil}}}_R$
.
Construction 2.11 Let
![]() $(M,\mathcal {F})\in \mathbb {Z}$
-
$(M,\mathcal {F})\in \mathbb {Z}$
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_R$
be a
$\operatorname {\mathrm {\textbf {Fil}}}_R$
be a
![]() $\mathbb {Z}$
-filtered module with
$\mathbb {Z}$
-filtered module with
![]() $\mathbb {Z}$
-jumps
$\mathbb {Z}$
-jumps
![]() $\jmath _1< \cdots <\jmath _n$
. For any
$\jmath _1< \cdots <\jmath _n$
. For any
![]() $\gamma \in \mathbb {Q}_{>0}$
, we define a
$\gamma \in \mathbb {Q}_{>0}$
, we define a
![]() $\mathbb {Q}$
-filtered module
$\mathbb {Q}$
-filtered module
![]() $(M,[\gamma ]_*\mathcal {F})$
by
$(M,[\gamma ]_*\mathcal {F})$
by
 $$ \begin{align*}([\gamma]_*\mathcal{F})^{x} M:= \left\{ \begin{array}{ll} 0 &\text{for}~x< \jmath_1\gamma, \\ M^{\jmath_i} ~~~ &\text{for}~ \jmath_i\gamma \leq x <\jmath_{i+1}\gamma,~ 1\leq i\leq n-1,\\ M &\text{for}~x\geq \jmath_n\gamma. \end{array} \right.\end{align*} $$
$$ \begin{align*}([\gamma]_*\mathcal{F})^{x} M:= \left\{ \begin{array}{ll} 0 &\text{for}~x< \jmath_1\gamma, \\ M^{\jmath_i} ~~~ &\text{for}~ \jmath_i\gamma \leq x <\jmath_{i+1}\gamma,~ 1\leq i\leq n-1,\\ M &\text{for}~x\geq \jmath_n\gamma. \end{array} \right.\end{align*} $$
We then have a fully faithful embedding
![]() $[\gamma ]_*\colon \mathbb {Z}$
-
$[\gamma ]_*\colon \mathbb {Z}$
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_R \to \mathbb {Q}$
-
$\operatorname {\mathrm {\textbf {Fil}}}_R \to \mathbb {Q}$
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_R$
. Similarly, we have a fully faithful embedding
$\operatorname {\mathrm {\textbf {Fil}}}_R$
. Similarly, we have a fully faithful embedding
![]() $[\gamma ]_*\colon \mathbb {Z}$
-
$[\gamma ]_*\colon \mathbb {Z}$
-
![]() $\operatorname {\mathrm {\textbf {Grad}}}_R \to \mathbb {Q}$
-
$\operatorname {\mathrm {\textbf {Grad}}}_R \to \mathbb {Q}$
-
![]() $\operatorname {\mathrm {\textbf {Grad}}}_R$
by defining
$\operatorname {\mathrm {\textbf {Grad}}}_R$
by defining
![]() $[\gamma ]_* := \operatorname {\mathrm {gr}}\circ [\gamma ]_*\circ \operatorname {\mathrm {fil}}$
.
$[\gamma ]_* := \operatorname {\mathrm {gr}}\circ [\gamma ]_*\circ \operatorname {\mathrm {fil}}$
.
To end this subsection, we exhibit the following theorem for latter use. (Be aware that in [Reference Ziegler25], the author only considers
![]() $\Gamma $
-gradings and
$\Gamma $
-gradings and
![]() $\Gamma $
-filtrations for
$\Gamma $
-filtrations for
![]() $\Gamma = \mathbb{Z}$
.)
$\Gamma = \mathbb{Z}$
.)
Theorem 2.12 [Reference Ziegler25, Theorem 4.15] Let
![]() $\mathcal T$
be a Tannakian category over a field k, and let R be a k-algebra. Let
$\mathcal T$
be a Tannakian category over a field k, and let R be a k-algebra. Let
![]() $\eta \colon \mathcal T \to \mathbb {Z}$
-
$\eta \colon \mathcal T \to \mathbb {Z}$
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_R$
be a
$\operatorname {\mathrm {\textbf {Fil}}}_R$
be a
![]() $\mathbb {Z}$
-filtered fiber functor. If
$\mathbb {Z}$
-filtered fiber functor. If
![]() $\operatorname {\mathrm {\underline {Aut}}}^{\otimes }_R(\operatorname {\mathrm {forg}}\circ \eta )$
is prosmooth (i.e., a limit of smooth algebraic group schemes) over R, where
$\operatorname {\mathrm {\underline {Aut}}}^{\otimes }_R(\operatorname {\mathrm {forg}}\circ \eta )$
is prosmooth (i.e., a limit of smooth algebraic group schemes) over R, where
![]() $\operatorname {\mathrm {forg}}\colon \mathbb {Z}$
-
$\operatorname {\mathrm {forg}}\colon \mathbb {Z}$
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_R \to \operatorname {\mathrm {\textbf {Mod}}}_R$
is the forgetful functor, then
$\operatorname {\mathrm {\textbf {Fil}}}_R \to \operatorname {\mathrm {\textbf {Mod}}}_R$
is the forgetful functor, then
![]() $\eta $
is splittable.
$\eta $
is splittable.
3
G-
 $\varphi $
-modules over the Robba ring
$\varphi $
-modules over the Robba ring
We fix an affine algebraic F-group G in this section.
3.1 Definition
Let
![]() $R\in \{\mathcal {E}^{\dagger },\mathcal {R},\operatorname {\mathrm {\tilde {\mathcal {E}}}}^{\dagger },\operatorname {\mathrm {\tilde {\mathcal {R}}}}\}$
equipped with an absolute Frobenius lift
$R\in \{\mathcal {E}^{\dagger },\mathcal {R},\operatorname {\mathrm {\tilde {\mathcal {E}}}}^{\dagger },\operatorname {\mathrm {\tilde {\mathcal {R}}}}\}$
equipped with an absolute Frobenius lift
![]() $\varphi $
. The following definition is motivated by that of G-isocrystals introduced in [Reference Dat, Orlik and Rapoport6, Section IX.1].
$\varphi $
. The following definition is motivated by that of G-isocrystals introduced in [Reference Dat, Orlik and Rapoport6, Section IX.1].
Definition 3.1 A G-
![]() $\varphi $
-module over R is an exact faithful F-linear tensor functor
$\varphi $
-module over R is an exact faithful F-linear tensor functor
which satisfies
![]() $\operatorname {\mathrm {forg}} \circ \operatorname {\mathrm {I}} = \omega ^G \otimes R$
, where
$\operatorname {\mathrm {forg}} \circ \operatorname {\mathrm {I}} = \omega ^G \otimes R$
, where
![]() $\operatorname {\mathrm {forg}} \colon \operatorname {\mathrm {\textbf {Mod}^{\varphi }_R}} \to \operatorname {\mathrm {\textbf {Mod}}}_R$
is the forgetful functor. The category of G-
$\operatorname {\mathrm {forg}} \colon \operatorname {\mathrm {\textbf {Mod}^{\varphi }_R}} \to \operatorname {\mathrm {\textbf {Mod}}}_R$
is the forgetful functor. The category of G-
![]() $\varphi $
-modules over R is denoted by
$\varphi $
-modules over R is denoted by
![]() $\operatorname {\mathrm {G-\textbf {Mod}^{\varphi }_R}}$
, whose morphisms are morphisms of tensor functors.
$\operatorname {\mathrm {G-\textbf {Mod}^{\varphi }_R}}$
, whose morphisms are morphisms of tensor functors.
Let
![]() $(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, and let
$(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, and let
![]() $g\in G(R)$
. We define
$g\in G(R)$
. We define
![]() $\operatorname {\mathrm {I}}(g)(V):= (V_R,g\varphi )$
, where
$\operatorname {\mathrm {I}}(g)(V):= (V_R,g\varphi )$
, where
Let
![]() $V,W\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
. We have a canonical isomorphism
$V,W\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
. We have a canonical isomorphism
![]() $(V\otimes W)_{\mathcal {R}} \cong V_{\mathcal {R}} \otimes _{\mathcal {R}} W_{\mathcal {R}}$
, and we will henceforth identify them. Given any
$(V\otimes W)_{\mathcal {R}} \cong V_{\mathcal {R}} \otimes _{\mathcal {R}} W_{\mathcal {R}}$
, and we will henceforth identify them. Given any
![]() $\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
, we define
$\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
, we define
![]() $\operatorname {\mathrm {I}}(g)(\alpha ):= \alpha _R$
. We thus have the following G-
$\operatorname {\mathrm {I}}(g)(\alpha ):= \alpha _R$
. We thus have the following G-
![]() $\varphi $
-module over R (associated to g).
$\varphi $
-module over R (associated to g).
We call
![]() $\operatorname {\mathrm {I}}(g)(V)=(V_R,g\varphi )$
the G-
$\operatorname {\mathrm {I}}(g)(V)=(V_R,g\varphi )$
the G-
![]() $\varphi $
-module over R associated to g.
$\varphi $
-module over R associated to g.
For any
![]() $g\in G(R)$
, we sometimes write
$g\in G(R)$
, we sometimes write
![]() $\Phi _g= \Phi _{g,V}$
for the
$\Phi _g= \Phi _{g,V}$
for the
![]() $\varphi $
-linear action
$\varphi $
-linear action
![]() $g\varphi $
on
$g\varphi $
on
![]() $V_R$
. Both notations have their own advantages in practice.
$V_R$
. Both notations have their own advantages in practice.
Remark 3.2 For any
![]() $g\in G(R)$
, we define
$g\in G(R)$
, we define
![]() $\Phi (g):= G(\varphi )(g)$
. For any
$\Phi (g):= G(\varphi )(g)$
. For any
![]() $(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, we have a commutative diagram
$(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, we have a commutative diagram

Hence,
![]() $\rho (\varphi (g))=\varphi (\rho (g))$
. For any
$\rho (\varphi (g))=\varphi (\rho (g))$
. For any
![]() $h\in G(R)$
and
$h\in G(R)$
and
![]() $n,m\geq 0$
, we have the following formula in
$n,m\geq 0$
, we have the following formula in
![]() $G(R)\rtimes \operatorname {\mathrm {\langle }}\varphi \operatorname {\mathrm {\rangle }}$
:
$G(R)\rtimes \operatorname {\mathrm {\langle }}\varphi \operatorname {\mathrm {\rangle }}$
:
3.2 The
 $\mathbb {Q}$
-filtered fiber functor
$\mathbb {Q}$
-filtered fiber functor
 $\operatorname {\mathrm {{HN}}}_g$
$\operatorname {\mathrm {{HN}}}_g$
We fix an element
![]() $g\in G(\mathcal {R})$
.
$g\in G(\mathcal {R})$
.
Construction 3.3 For any
![]() $V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, we have a
$V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, we have a
![]() $\varphi $
-module
$\varphi $
-module
![]() $(V_{\mathcal {R}},g\varphi )$
over
$(V_{\mathcal {R}},g\varphi )$
over
![]() $\mathcal {R}$
. Kedlaya’s slope filtration theorem [Reference Kedlaya9, Theorem 6.10] then provides a filtration
$\mathcal {R}$
. Kedlaya’s slope filtration theorem [Reference Kedlaya9, Theorem 6.10] then provides a filtration
satisfying
-
•
 $V_{\mathcal {R}}^{\mu _1}$
is pure of some slope
$V_{\mathcal {R}}^{\mu _1}$
is pure of some slope
 $\mu _1\in \mathbb {Q}$
and each
$\mu _1\in \mathbb {Q}$
and each
 $V_{\mathcal {R}}^{\mu _i}/V_{\mathcal {R}}^{\mu _{i-1}}$
is pure of some slope
$V_{\mathcal {R}}^{\mu _i}/V_{\mathcal {R}}^{\mu _{i-1}}$
is pure of some slope
 $\mu _i\in \mathbb {Q}$
for
$\mu _i\in \mathbb {Q}$
for
 $2\leq i\leq l$
;
$2\leq i\leq l$
; -
•
 $\mu _1<\cdots <\mu _l$
.
$\mu _1<\cdots <\mu _l$
.
We thus have an increasing map
 $$ \begin{align*} \mathcal{HN}_g \colon \mathbb{Q} &\operatorname{\mathrm{\longrightarrow}} \{\mathcal{R}\text{-modules of}~V_{\mathcal{R}}\}\\ x &\longmapsto \mathcal{HN}_g^x(V_{\mathcal{R}}), \end{align*} $$
$$ \begin{align*} \mathcal{HN}_g \colon \mathbb{Q} &\operatorname{\mathrm{\longrightarrow}} \{\mathcal{R}\text{-modules of}~V_{\mathcal{R}}\}\\ x &\longmapsto \mathcal{HN}_g^x(V_{\mathcal{R}}), \end{align*} $$
where
 $$ \begin{align*}\mathcal{HN}_g^x(V_{\mathcal{R}})=\left\{ \begin{array}{ll} 0 &\text{for}~x<\mu_1,\\ V_{\mathcal{R}}^{\mu_i} ~~~ &\text{for}~ \mu_i\leq x <\mu_{i+1}, 1\leq i\leq l-1,\\ V_{\mathcal{R}} &\text{for}~x\geq \mu_l. \end{array} \right.\end{align*} $$
$$ \begin{align*}\mathcal{HN}_g^x(V_{\mathcal{R}})=\left\{ \begin{array}{ll} 0 &\text{for}~x<\mu_1,\\ V_{\mathcal{R}}^{\mu_i} ~~~ &\text{for}~ \mu_i\leq x <\mu_{i+1}, 1\leq i\leq l-1,\\ V_{\mathcal{R}} &\text{for}~x\geq \mu_l. \end{array} \right.\end{align*} $$
Then,
![]() $(V_{\mathcal {R}},\mathcal {HN}_g)$
is a
$(V_{\mathcal {R}},\mathcal {HN}_g)$
is a
![]() $\mathbb {Q}$
-filtered module over
$\mathbb {Q}$
-filtered module over
![]() $\mathcal {R}$
with
$\mathcal {R}$
with
![]() $\mathbb {Q}$
-jumps
$\mathbb {Q}$
-jumps
![]() $\mu _1<\cdots <\mu _l$
. We will denote
$\mu _1<\cdots <\mu _l$
. We will denote
![]() $\mathcal {HN}_g^x(V_{\mathcal {R}})$
by
$\mathcal {HN}_g^x(V_{\mathcal {R}})$
by
![]() $V_{\mathcal {R}}^x$
when
$V_{\mathcal {R}}^x$
when
![]() $\mathcal {HN}_g$
is clear in the context.
$\mathcal {HN}_g$
is clear in the context.
Theorem 3.4 The assignments
for all
![]() $\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
, define a
$\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
, define a
![]() $\mathbb {Q}$
-filtered fiber functor
$\mathbb {Q}$
-filtered fiber functor
For any admissible extension E of K, we first remark that the
![]() $\varphi $
-equivariant embedding
$\varphi $
-equivariant embedding
![]() $\psi \colon \mathcal {R}\to \operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)$
is faithfully flat (see [Reference Kedlaya11, Remark 3.5.3]). We also remark that, if
$\psi \colon \mathcal {R}\to \operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)$
is faithfully flat (see [Reference Kedlaya11, Remark 3.5.3]). We also remark that, if
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are pure
$M_2$
are pure
![]() $\varphi $
-modules over
$\varphi $
-modules over
![]() $\mathcal {R}$
of slopes
$\mathcal {R}$
of slopes
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
, respectively, then
$\mu _2$
, respectively, then
![]() $M_1 \bigotimes _{\mathcal {R}} M_2$
is pure of slope
$M_1 \bigotimes _{\mathcal {R}} M_2$
is pure of slope
![]() $\mu _1+\mu _2$
(cf. [Reference Kedlaya11, Corollary 1.6.4]). These facts will be repeatedly used in the sequel.
$\mu _1+\mu _2$
(cf. [Reference Kedlaya11, Corollary 1.6.4]). These facts will be repeatedly used in the sequel.
Proposition 3.5 The assignments in Theorem 3.4 yield a faithful F-linear tensor functor
![]() $\operatorname {\mathrm {{HN}}}_g \colon \operatorname {\mathrm {\textbf {Rep}}}_F(G) \to \mathbb {Q}$
-
$\operatorname {\mathrm {{HN}}}_g \colon \operatorname {\mathrm {\textbf {Rep}}}_F(G) \to \mathbb {Q}$
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_{\mathcal {R}}$
.
$\operatorname {\mathrm {\textbf {Fil}}}_{\mathcal {R}}$
.
Proof Let
![]() be the trivial G-representation. Then,
be the trivial G-representation. Then,
![]() is of rank
is of rank
![]() $1$
with slope
$1$
with slope
![]() $0$
, proving that
$0$
, proving that
![]() $\operatorname {\mathrm {{HN}}}_g$
preserves identity objects.
$\operatorname {\mathrm {{HN}}}_g$
preserves identity objects.
We claim that
![]() $\operatorname {\mathrm {{HN}}}_g$
is functorial. Let
$\operatorname {\mathrm {{HN}}}_g$
is functorial. Let
![]() $\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
be a morphism of finite-dimensional G-modules. We need to show that
$\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
be a morphism of finite-dimensional G-modules. We need to show that
![]() $\alpha _{\mathcal {R}}(V_{\mathcal {R}}^x)\subseteq W_{\mathcal {R}}^x$
for all
$\alpha _{\mathcal {R}}(V_{\mathcal {R}}^x)\subseteq W_{\mathcal {R}}^x$
for all
![]() ${x\in \mathbb {Q}}$
. Choose by Lemma 2.2 an admissible extension E of K such that
${x\in \mathbb {Q}}$
. Choose by Lemma 2.2 an admissible extension E of K such that
![]() $\kappa _E$
is strongly difference-closed. For any fixed
$\kappa _E$
is strongly difference-closed. For any fixed
![]() $x\in \mathbb {Q}$
, we set
$x\in \mathbb {Q}$
, we set
![]() $V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x := V_{\mathcal {R}}^x\bigotimes _{\mathcal {R}} {\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}$
, and
$V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x := V_{\mathcal {R}}^x\bigotimes _{\mathcal {R}} {\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}$
, and
![]() $W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x := W_{\mathcal {R}}^x\bigotimes _{\mathcal {R}} {\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}$
. By Lemma 2.3(iii), we have a decomposition
$W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x := W_{\mathcal {R}}^x\bigotimes _{\mathcal {R}} {\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}$
. By Lemma 2.3(iii), we have a decomposition
![]() $W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}=W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x \operatorname *{\mathrm {\bigoplus }} W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}'$
of
$W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}=W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x \operatorname *{\mathrm {\bigoplus }} W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}'$
of
![]() $\varphi $
-modules over
$\varphi $
-modules over
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)$
, where
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)$
, where
![]() $W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x$
(resp.
$W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x$
(resp.
![]() $W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}'$
) has slopes less or equal to x (resp. greater than x). By Lemma 2.3(iv), the induced morphism
$W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}'$
) has slopes less or equal to x (resp. greater than x). By Lemma 2.3(iv), the induced morphism
![]() $V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x \to W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}'$
of
$V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x \to W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}'$
of
![]() $\varphi $
-modules is zero. We thus have
$\varphi $
-modules is zero. We thus have
![]() $\alpha _{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)} \big (V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x \big )\subseteq W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x$
. Given any
$\alpha _{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)} \big (V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x \big )\subseteq W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x$
. Given any
![]() $\textbf {v}\in V_{\mathcal {R}}^x$
, we may write
$\textbf {v}\in V_{\mathcal {R}}^x$
, we may write
![]() $\alpha _{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}(\textbf {v}\otimes 1)=\alpha _{\mathcal {R}}(\textbf {v})\otimes 1=\operatorname *{\mathrm {\sum }}\limits _{i\in I} \textbf {w}_i\otimes s_i$
for some finite set I, with
$\alpha _{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}(\textbf {v}\otimes 1)=\alpha _{\mathcal {R}}(\textbf {v})\otimes 1=\operatorname *{\mathrm {\sum }}\limits _{i\in I} \textbf {w}_i\otimes s_i$
for some finite set I, with
![]() $\textbf {w}_i\in W_{\mathcal {R}}^x$
and
$\textbf {w}_i\in W_{\mathcal {R}}^x$
and
![]() $s_i\in {\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}$
for all
$s_i\in {\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}$
for all
![]() $i\in I$
. Let M be the
$i\in I$
. Let M be the
![]() $\mathcal {R}$
-submodule of
$\mathcal {R}$
-submodule of
![]() $W_{\mathcal {R}}$
generated by
$W_{\mathcal {R}}$
generated by
![]() $\alpha _{\mathcal {R}}(\textbf {v})$
and the
$\alpha _{\mathcal {R}}(\textbf {v})$
and the
![]() $\textbf {w}_i$
, and let N be the
$\textbf {w}_i$
, and let N be the
![]() $\mathcal {R}$
-submodule of
$\mathcal {R}$
-submodule of
![]() $W_{\mathcal {R}}^x$
generated by the
$W_{\mathcal {R}}^x$
generated by the
![]() $\textbf {w}_i$
. We then have
$\textbf {w}_i$
. We then have
![]() $(M/N)\bigotimes _{\mathcal {R}} \operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t) \cong (M\bigotimes _{\mathcal {R}} \operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t))/ (N\bigotimes _{\mathcal {R}} \operatorname {\mathrm {\tilde {\mathcal {R}}}}{(E,t))=0}$
. It follows that
$(M/N)\bigotimes _{\mathcal {R}} \operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t) \cong (M\bigotimes _{\mathcal {R}} \operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t))/ (N\bigotimes _{\mathcal {R}} \operatorname {\mathrm {\tilde {\mathcal {R}}}}{(E,t))=0}$
. It follows that
![]() $M/N=0$
as
$M/N=0$
as
![]() $\mathcal {R}\to \operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)$
is faithfully flat. We thus have
$\mathcal {R}\to \operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)$
is faithfully flat. We thus have
![]() $\alpha _{\mathcal {R}}(\textbf {v})\in N\subseteq W_{\mathcal {R}}^x$
, as desired.
$\alpha _{\mathcal {R}}(\textbf {v})\in N\subseteq W_{\mathcal {R}}^x$
, as desired.
It remains to show that
![]() $\operatorname {\mathrm {{HN}}}_g$
preserves tensor products (in the sense of Remark 2.10(ii)). Let V and W be two finite-dimensional G-modules, and suppose that the slope filtration of
$\operatorname {\mathrm {{HN}}}_g$
preserves tensor products (in the sense of Remark 2.10(ii)). Let V and W be two finite-dimensional G-modules, and suppose that the slope filtration of
![]() $(V_{\mathcal {R}},g\varphi )$
(resp.
$(V_{\mathcal {R}},g\varphi )$
(resp.
![]() $(W_{\mathcal {R}},g\varphi )$
) has jumps
$(W_{\mathcal {R}},g\varphi )$
) has jumps
![]() $\mu _1<\cdots <\mu _{l_V}$
(resp.
$\mu _1<\cdots <\mu _{l_V}$
(resp.
![]() ${\nu _1<\cdots <\nu _{l_W}}$
). By [Reference Kedlaya12, Lemma 16.4.3],
${\nu _1<\cdots <\nu _{l_W}}$
). By [Reference Kedlaya12, Lemma 16.4.3],
![]() $\big ((V\bigotimes _F W)_{\mathcal {R}},g\varphi \big )$
has jumps
$\big ((V\bigotimes _F W)_{\mathcal {R}},g\varphi \big )$
has jumps
![]() $\{\mu _i+\nu _j \mid 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\}$
. Fix any
$\{\mu _i+\nu _j \mid 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\}$
. Fix any
![]() $1\leq l\leq {l_V}$
and
$1\leq l\leq {l_V}$
and
![]() $1\leq s\leq {l_W}$
; we need to show
$1\leq s\leq {l_W}$
; we need to show
 $$ \begin{align} (V \bigotimes_F W)_{\mathcal{R}}^{\mu_{l}+\nu_{s}}= \operatorname*{\mathrm{\sum}}\limits_{\scriptstyle \begin{array}{c} x,y\in\mathbb{Q} \\ x+y=\mu_{l}+\nu_{s}\end{array}} V_{\mathcal{R}}^x \bigotimes_{\mathcal{R}} W_{\mathcal{R}}^y, \end{align} $$
$$ \begin{align} (V \bigotimes_F W)_{\mathcal{R}}^{\mu_{l}+\nu_{s}}= \operatorname*{\mathrm{\sum}}\limits_{\scriptstyle \begin{array}{c} x,y\in\mathbb{Q} \\ x+y=\mu_{l}+\nu_{s}\end{array}} V_{\mathcal{R}}^x \bigotimes_{\mathcal{R}} W_{\mathcal{R}}^y, \end{align} $$
and we will do so in the remainder of the proof.
We claim that
 $$ \begin{align*}\operatorname*{\mathrm{\sum}}\limits_{\scriptstyle \begin{array}{c} x,y\in\mathbb{Q} \\ x+y=\mu_{l}+\nu_{s}\end{array}} V_{\mathcal{R}}^x \bigotimes_{\mathcal{R}} W_{\mathcal{R}}^y= \operatorname*{\mathrm{\sum}}\limits_{\scriptstyle \begin{array}{c} \mu_i+\nu_j\leq \mu_l+\nu_s \\ 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\end{array}}V_{\mathcal{R}}^{\mu_i} \bigotimes_{\mathcal{R}} W_{\mathcal{R}}^{\nu_j}.\end{align*} $$
$$ \begin{align*}\operatorname*{\mathrm{\sum}}\limits_{\scriptstyle \begin{array}{c} x,y\in\mathbb{Q} \\ x+y=\mu_{l}+\nu_{s}\end{array}} V_{\mathcal{R}}^x \bigotimes_{\mathcal{R}} W_{\mathcal{R}}^y= \operatorname*{\mathrm{\sum}}\limits_{\scriptstyle \begin{array}{c} \mu_i+\nu_j\leq \mu_l+\nu_s \\ 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\end{array}}V_{\mathcal{R}}^{\mu_i} \bigotimes_{\mathcal{R}} W_{\mathcal{R}}^{\nu_j}.\end{align*} $$
It is clear that the RHS is contained in the LHS; we now show the reverse inclusion. Let
![]() $x,y\in \mathbb {Q}$
such that
$x,y\in \mathbb {Q}$
such that
![]() $x+y=\mu _{l}+\nu _{s}$
. If
$x+y=\mu _{l}+\nu _{s}$
. If
![]() $x<\mu _1$
or
$x<\mu _1$
or
![]() $y<\nu _1$
, then
$y<\nu _1$
, then
![]() $V_{\mathcal {R}}^x\bigotimes _{\mathcal {R}} W_{\mathcal {R}}^y=0$
which is contained in the RHS. Otherwise, there exists the largest integer
$V_{\mathcal {R}}^x\bigotimes _{\mathcal {R}} W_{\mathcal {R}}^y=0$
which is contained in the RHS. Otherwise, there exists the largest integer
![]() $1\leq i\leq {l_V}$
(resp.
$1\leq i\leq {l_V}$
(resp.
![]() $1\leq j\leq {l_W}$
) with the property that
$1\leq j\leq {l_W}$
) with the property that
![]() $\mu _i\leq x$
(resp.
$\mu _i\leq x$
(resp.
![]() $\nu _j\leq y$
). We then have
$\nu _j\leq y$
). We then have
![]() $V_{\mathcal {R}}^x\bigotimes _{\mathcal {R}} W_{\mathcal {R}}^y=V_{\mathcal {R}}^{\mu _i}\bigotimes _{\mathcal {R}} W_{\mathcal {R}}^{\nu _j}$
and
$V_{\mathcal {R}}^x\bigotimes _{\mathcal {R}} W_{\mathcal {R}}^y=V_{\mathcal {R}}^{\mu _i}\bigotimes _{\mathcal {R}} W_{\mathcal {R}}^{\nu _j}$
and
![]() $\mu _i+\nu _j\leq \mu _{l}+\nu _{s}$
. The claim is thus proved.
$\mu _i+\nu _j\leq \mu _{l}+\nu _{s}$
. The claim is thus proved.
From Lemma 2.3(iii), we see that
 $$ \begin{align*} \big(V \bigotimes_F W \big)_{\operatorname{\mathrm{\tilde{\mathcal{R}}}}(E,t)}^{\mu_{l}+\nu_{s}}= \Big( \operatorname*{\mathrm{\sum}}\limits_{\scriptstyle \begin{array}{c} \mu_i+\nu_j\leq \mu_{l}+\nu_{s} \\ 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\end{array}} V_{\mathcal{R}}^{\mu_i}\bigotimes_{\mathcal{R}} W_{\mathcal{R}}^{\nu_j} \Big)\bigotimes_{\mathcal{R}} {\operatorname{\mathrm{\tilde{\mathcal{R}}}}(E,t)}.\end{align*} $$
$$ \begin{align*} \big(V \bigotimes_F W \big)_{\operatorname{\mathrm{\tilde{\mathcal{R}}}}(E,t)}^{\mu_{l}+\nu_{s}}= \Big( \operatorname*{\mathrm{\sum}}\limits_{\scriptstyle \begin{array}{c} \mu_i+\nu_j\leq \mu_{l}+\nu_{s} \\ 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\end{array}} V_{\mathcal{R}}^{\mu_i}\bigotimes_{\mathcal{R}} W_{\mathcal{R}}^{\nu_j} \Big)\bigotimes_{\mathcal{R}} {\operatorname{\mathrm{\tilde{\mathcal{R}}}}(E,t)}.\end{align*} $$
Therefore, we have
 $$ \begin{align*} \big(V \bigotimes W \big)_{\mathcal{R}}^{\mu_{l}+\nu_{s}}=\operatorname*{\mathrm{\sum}}\limits_{\scriptstyle \begin{array}{c}\mu_i+\nu_j\leq \mu_{l}+\nu_{s} \\ 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\end{array}} V_{\mathcal{R}}^{\mu_i}\bigotimes_{\mathcal{R}} W_{\mathcal{R}}^{\nu_j}\end{align*} $$
$$ \begin{align*} \big(V \bigotimes W \big)_{\mathcal{R}}^{\mu_{l}+\nu_{s}}=\operatorname*{\mathrm{\sum}}\limits_{\scriptstyle \begin{array}{c}\mu_i+\nu_j\leq \mu_{l}+\nu_{s} \\ 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\end{array}} V_{\mathcal{R}}^{\mu_i}\bigotimes_{\mathcal{R}} W_{\mathcal{R}}^{\nu_j}\end{align*} $$
by Lemma 2.3(i) and the fact that
![]() $\mathcal {R} \to {\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}$
is faithfully flat. The desired equality (1) then follows from the preceding claim.▪
$\mathcal {R} \to {\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}$
is faithfully flat. The desired equality (1) then follows from the preceding claim.▪
Let
![]() $(M,\varphi )$
be a
$(M,\varphi )$
be a
![]() $\varphi $
-module over
$\varphi $
-module over
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
of rank d. Then,
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
of rank d. Then,
![]() $\Phi $
is invertible, because the Frobenius lift on
$\Phi $
is invertible, because the Frobenius lift on
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
is bijective, and
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
is bijective, and
![]() $(M,\varphi ^{-1})$
is a
$(M,\varphi ^{-1})$
is a
![]() $\varphi ^{-1}$
-module over
$\varphi ^{-1}$
-module over
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
. More explicitly, let
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
. More explicitly, let
![]() $A\in \operatorname {\mathrm {GL}}_d(\operatorname {\mathrm {\tilde {\mathcal {R}}}})$
be the matrix of action of
$A\in \operatorname {\mathrm {GL}}_d(\operatorname {\mathrm {\tilde {\mathcal {R}}}})$
be the matrix of action of
![]() $\varphi $
in some basis for M over
$\varphi $
in some basis for M over
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
. Then, in the same basis, the matrix of action of
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
. Then, in the same basis, the matrix of action of
![]() $\varphi ^{-1}$
is
$\varphi ^{-1}$
is
![]() $\varphi ^{-1}(A^{-1})$
. For example, if
$\varphi ^{-1}(A^{-1})$
. For example, if
![]() $M=V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}}$
for some
$M=V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}}$
for some
![]() $V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, and
$V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, and
![]() $\Phi =\psi (g)\varphi $
where
$\Phi =\psi (g)\varphi $
where
![]() $\psi $
denotes (by abuse of notation) the group morphism
$\psi $
denotes (by abuse of notation) the group morphism
![]() $G(\mathcal {R}) \to G(\operatorname {\mathrm {\tilde {\mathcal {R}}}})$
induced by the embedding
$G(\mathcal {R}) \to G(\operatorname {\mathrm {\tilde {\mathcal {R}}}})$
induced by the embedding
![]() $\psi \colon \mathcal {R} \to \operatorname {\mathrm {\tilde {\mathcal {R}}}}$
recalled above Proposition 3.5, then
$\psi \colon \mathcal {R} \to \operatorname {\mathrm {\tilde {\mathcal {R}}}}$
recalled above Proposition 3.5, then
in
![]() $G(\operatorname {\mathrm {\tilde {\mathcal {R}}}})\rtimes \operatorname {\mathrm {\langle }}\varphi \operatorname {\mathrm {\rangle }}$
(cf. Remark 3.2), which implies that
$G(\operatorname {\mathrm {\tilde {\mathcal {R}}}})\rtimes \operatorname {\mathrm {\langle }}\varphi \operatorname {\mathrm {\rangle }}$
(cf. Remark 3.2), which implies that
![]() $\varphi ^{-1}=\varphi ^{-1}(\psi (g^{-1}))\varphi ^{-1}$
.
$\varphi ^{-1}=\varphi ^{-1}(\psi (g^{-1}))\varphi ^{-1}$
.
Let M be a standard
![]() $\varphi $
-module over
$\varphi $
-module over
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
of slope
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
of slope
![]() $\mu =s/r$
with
$\mu =s/r$
with
![]() $r>0$
and
$r>0$
and
![]() $(s,r)=1$
. Namely, we have a standard basis
$(s,r)=1$
. Namely, we have a standard basis
![]() $e_1,\ldots ,e_r$
in which
$e_1,\ldots ,e_r$
in which
![]() $\varphi $
acts via
$\varphi $
acts via
 $$ \begin{align*}A= \left(\begin{smallmatrix} 0 & & &\varpi^s\\ 1 &\ddots & & \\ &\;\ddots &\;\;\ddots &\\ && 1 &0 \end{smallmatrix}\right). \end{align*} $$
$$ \begin{align*}A= \left(\begin{smallmatrix} 0 & & &\varpi^s\\ 1 &\ddots & & \\ &\;\ddots &\;\;\ddots &\\ && 1 &0 \end{smallmatrix}\right). \end{align*} $$
Then,
 $$ \begin{align*}\varphi^{-1}(A^{-1})= \left(\begin{smallmatrix} 0 &1 & &\\ &\ddots &\ddots & \\ & & \;\;\ddots & {{\scriptstyle 1}} \\ \varpi^{-s} & & &0 \end{smallmatrix}\right), \end{align*} $$
$$ \begin{align*}\varphi^{-1}(A^{-1})= \left(\begin{smallmatrix} 0 &1 & &\\ &\ddots &\ddots & \\ & & \;\;\ddots & {{\scriptstyle 1}} \\ \varpi^{-s} & & &0 \end{smallmatrix}\right), \end{align*} $$
which implies that
![]() $(M,\varphi ^{-1})$
is a standard
$(M,\varphi ^{-1})$
is a standard
![]() $\varphi ^{-1}$
-module pure of slope
$\varphi ^{-1}$
-module pure of slope
![]() $-\mu $
.
$-\mu $
.
Proposition 3.6 The functor
![]() $\operatorname {\mathrm {{HN}}}_g\colon \operatorname {\mathrm {\textbf {Rep}}}_F(G) \to \mathbb {Q}\text {-}\operatorname {\mathrm {\textbf {Fil}}}_{\mathcal {R}}$
is exact.
$\operatorname {\mathrm {{HN}}}_g\colon \operatorname {\mathrm {\textbf {Rep}}}_F(G) \to \mathbb {Q}\text {-}\operatorname {\mathrm {\textbf {Fil}}}_{\mathcal {R}}$
is exact.
Proof Let
![]() $\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
be a morphism of finite-dimensional G-modules. We need to show that
$\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
be a morphism of finite-dimensional G-modules. We need to show that
![]() $\alpha _{\mathcal {R}}(V_{\mathcal {R}}^x)=\alpha _{\mathcal {R}}(V_{\mathcal {R}})\cap W_{\mathcal {R}}^x$
for all
$\alpha _{\mathcal {R}}(V_{\mathcal {R}}^x)=\alpha _{\mathcal {R}}(V_{\mathcal {R}})\cap W_{\mathcal {R}}^x$
for all
![]() $x\in \mathbb {Q}$
. For any fixed
$x\in \mathbb {Q}$
. For any fixed
![]() $x\in \mathbb {Q}$
, the functoriality in Proposition 3.5 already implies that
$x\in \mathbb {Q}$
, the functoriality in Proposition 3.5 already implies that
![]() $\alpha _{\mathcal {R}}(V_{\mathcal {R}}^x)\subseteq \alpha _{\mathcal {R}}(V_{\mathcal {R}})\cap W_{\mathcal {R}}^x$
. Thus, it suffices to show that for any nonzero element
$\alpha _{\mathcal {R}}(V_{\mathcal {R}}^x)\subseteq \alpha _{\mathcal {R}}(V_{\mathcal {R}})\cap W_{\mathcal {R}}^x$
. Thus, it suffices to show that for any nonzero element
![]() $\textbf {v}\in V_{\mathcal {R}}$
such that
$\textbf {v}\in V_{\mathcal {R}}$
such that
![]() $\alpha _{\mathcal {R}}(\textbf {v})\in W_{\mathcal {R}}^x$
, there exists
$\alpha _{\mathcal {R}}(\textbf {v})\in W_{\mathcal {R}}^x$
, there exists
![]() $\textbf {v}'\in V_{\mathcal {R}}^x$
with
$\textbf {v}'\in V_{\mathcal {R}}^x$
with
![]() $\alpha _{\mathcal {R}}(\textbf {v})=\alpha _{\mathcal {R}}(\textbf {v}')$
.
$\alpha _{\mathcal {R}}(\textbf {v})=\alpha _{\mathcal {R}}(\textbf {v}')$
.
By Lemma 2.3(iii), we have decompositions
of
![]() $\varphi $
-modules over
$\varphi $
-modules over
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)$
, in which
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)$
, in which
![]() $V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x$
and
$V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x$
and
![]() $W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x$
have slopes less or equal to x, while
$W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x$
have slopes less or equal to x, while
![]() $V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}'$
and
$V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}'$
and
![]() $W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}'$
have slopes greater than x. Notice that the composition
$W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}'$
have slopes greater than x. Notice that the composition
is a morphism of
![]() $\varphi $
-modules. We claim that
$\varphi $
-modules. We claim that
![]() $\xi =0$
. We write
$\xi =0$
. We write
![]() $\varphi =\psi (g)\varphi $
, then
$\varphi =\psi (g)\varphi $
, then
![]() $\varphi ^{-1}=\varphi ^{-1}(\psi (g^{-1}))\varphi ^{-1}$
. Because
$\varphi ^{-1}=\varphi ^{-1}(\psi (g^{-1}))\varphi ^{-1}$
. Because
![]() $\alpha $
is G-equivariant and
$\alpha $
is G-equivariant and
![]() $\varphi ^{-1}(\psi (g^{-1}))\in G(\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t))$
, we have that
$\varphi ^{-1}(\psi (g^{-1}))\in G(\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t))$
, we have that
![]() $\alpha _{\operatorname {\mathrm {\tilde {\mathcal {R}}}}}\colon (V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)},\varphi ^{-1}) \to (W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)},\varphi ^{-1})$
is a morphism of
$\alpha _{\operatorname {\mathrm {\tilde {\mathcal {R}}}}}\colon (V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)},\varphi ^{-1}) \to (W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)},\varphi ^{-1})$
is a morphism of
![]() $\varphi ^{-1}$
-modules. On the other hand, we also have decompositions of
$\varphi ^{-1}$
-modules. On the other hand, we also have decompositions of
![]() $\varphi ^{-1}$
-modules as in (2), together with the induced morphism
$\varphi ^{-1}$
-modules as in (2), together with the induced morphism
![]() $\xi \colon V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}' \to W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x$
of
$\xi \colon V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}' \to W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x$
of
![]() $\varphi ^{-1}$
-modules. But in this case,
$\varphi ^{-1}$
-modules. But in this case,
![]() $V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}'$
has slopes less than x, while
$V_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}'$
has slopes less than x, while
![]() $W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x$
has slopes greater or equal to x. It then follows from Lemma 2.3(iv) that
$W_{\operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)}^x$
has slopes greater or equal to x. It then follows from Lemma 2.3(iv) that
![]() $\xi =0$
, as claimed.
$\xi =0$
, as claimed.
Therefore, we find
![]() $\textbf {v}_1,\ldots ,\textbf {v}_n \in V_{\mathcal {R}}^x$
and
$\textbf {v}_1,\ldots ,\textbf {v}_n \in V_{\mathcal {R}}^x$
and
![]() $s_1,\ldots ,s_n\in \operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)$
such that
$s_1,\ldots ,s_n\in \operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)$
such that
 $$ \begin{align*} \alpha_{\operatorname{\mathrm{\tilde{\mathcal{R}}}}(E,t)}(\textbf{v}\otimes 1)=\alpha_{\mathcal{R}}(\textbf{v})\otimes 1 =\operatorname*{\mathrm{\sum}}\limits_{i=1}^n \alpha_{\mathcal{R}}(\textbf{v}_i)\otimes s_i.\end{align*} $$
$$ \begin{align*} \alpha_{\operatorname{\mathrm{\tilde{\mathcal{R}}}}(E,t)}(\textbf{v}\otimes 1)=\alpha_{\mathcal{R}}(\textbf{v})\otimes 1 =\operatorname*{\mathrm{\sum}}\limits_{i=1}^n \alpha_{\mathcal{R}}(\textbf{v}_i)\otimes s_i.\end{align*} $$
Let M be the submodule of
![]() $W_{\mathcal {R}}$
generated by
$W_{\mathcal {R}}$
generated by
![]() $\alpha _{\mathcal {R}}(\textbf {v})$
and the
$\alpha _{\mathcal {R}}(\textbf {v})$
and the
![]() $\alpha _{\mathcal {R}}(\textbf {v}_i)$
, and let N be the submodule generated by the
$\alpha _{\mathcal {R}}(\textbf {v}_i)$
, and let N be the submodule generated by the
![]() $\alpha _{\mathcal {R}}(\textbf {v}_i)$
. We then have
$\alpha _{\mathcal {R}}(\textbf {v}_i)$
. We then have
It follows that
![]() $M/N=0$
as
$M/N=0$
as
![]() $\mathcal {R}\to \operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)$
is faithfully flat, and hence,
$\mathcal {R}\to \operatorname {\mathrm {\tilde {\mathcal {R}}}}(E,t)$
is faithfully flat, and hence,
![]() $\alpha _{\mathcal {R}}(\textbf {v})=\sum \limits _{i=1}^n r_i\alpha _{\mathcal {R}}(\textbf {v}_i)\in W_{\mathcal {R}}^x$
for some
$\alpha _{\mathcal {R}}(\textbf {v})=\sum \limits _{i=1}^n r_i\alpha _{\mathcal {R}}(\textbf {v}_i)\in W_{\mathcal {R}}^x$
for some
![]() $r_i\in \mathcal {R}$
. Put
$r_i\in \mathcal {R}$
. Put
![]() $\textbf {v}':= \sum \limits _{i=1}^n r_i\textbf {v}_i \in V_{\mathcal {R}}^x$
, we then have
$\textbf {v}':= \sum \limits _{i=1}^n r_i\textbf {v}_i \in V_{\mathcal {R}}^x$
, we then have
![]() $\alpha _{\mathcal {R}}(\textbf {v}')=\alpha _{\mathcal {R}}(\textbf {v})$
, as desired.▪
$\alpha _{\mathcal {R}}(\textbf {v}')=\alpha _{\mathcal {R}}(\textbf {v})$
, as desired.▪
3.3 Splittings of
 $\operatorname {\mathrm {{HN}}}_g$
$\operatorname {\mathrm {{HN}}}_g$
As before, we fix an element
![]() $g\in G(\mathcal {R})$
. In Section 3.2, we have constructed a
$g\in G(\mathcal {R})$
. In Section 3.2, we have constructed a
![]() $\mathbb {Q}$
-filtered fiber functor
$\mathbb {Q}$
-filtered fiber functor
![]() $\operatorname {\mathrm {{HN}}}_g\colon \operatorname {\mathrm {\textbf {Rep}}}_F(G) \to \mathbb {Q}$
-
$\operatorname {\mathrm {{HN}}}_g\colon \operatorname {\mathrm {\textbf {Rep}}}_F(G) \to \mathbb {Q}$
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_{\mathcal {R}}$
. In this subsection, we show that
$\operatorname {\mathrm {\textbf {Fil}}}_{\mathcal {R}}$
. In this subsection, we show that
![]() $\operatorname {\mathrm {{HN}}}_g$
is splittable whenever G is smooth. Our strategy goes as follows. We first use Lemma 3.10 reducing
$\operatorname {\mathrm {{HN}}}_g$
is splittable whenever G is smooth. Our strategy goes as follows. We first use Lemma 3.10 reducing
![]() $\operatorname {\mathrm {{HN}}}_g$
to a
$\operatorname {\mathrm {{HN}}}_g$
to a
![]() $\mathbb {Z}$
-filtered fiber functor
$\mathbb {Z}$
-filtered fiber functor
![]() $\operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
to which Theorem 2.12 is applicable. This
$\operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
to which Theorem 2.12 is applicable. This
![]() $\operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
then admits a
$\operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
then admits a
![]() $\mathbb {Z}$
-splitting. Finally, in Theorem 3.12, we lift such a
$\mathbb {Z}$
-splitting. Finally, in Theorem 3.12, we lift such a
![]() $\mathbb {Z}$
-splitting to a
$\mathbb {Z}$
-splitting to a
![]() $\mathbb {Q}$
-splitting of
$\mathbb {Q}$
-splitting of
![]() $\operatorname {\mathrm {{HN}}}_g$
.
$\operatorname {\mathrm {{HN}}}_g$
.
Definition 3.7 We define the support of
![]() $\operatorname {\mathrm {{HN}}}_g$
by
$\operatorname {\mathrm {{HN}}}_g$
by
Notice that
![]() $\operatorname {\mathrm {Supp}}(\operatorname {\mathrm {{HN}}}_g)$
is the set of jumps of the slope filtrations of
$\operatorname {\mathrm {Supp}}(\operatorname {\mathrm {{HN}}}_g)$
is the set of jumps of the slope filtrations of
![]() $(V_{\mathcal {R}},g\varphi )$
for all
$(V_{\mathcal {R}},g\varphi )$
for all
![]() $V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
.
$V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
.
The general idea of the following construction was addressed in [Reference Anschütz2], after Definition 2.5 in loc. cit.; we will make it more explicit in our case.
Construction 3.8 Let
![]() $W\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
be a faithful representation. Because G is algebraic, W is a tensor generator for
$W\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
be a faithful representation. Because G is algebraic, W is a tensor generator for
![]() $\operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, i.e., any representation V of G is a subquotient of a direct sum of representations
$\operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, i.e., any representation V of G is a subquotient of a direct sum of representations
![]() $\bigotimes ^m (W \bigoplus W^{\vee })$
for various
$\bigotimes ^m (W \bigoplus W^{\vee })$
for various
![]() $m\in \mathbb {N}$
. (See [Reference Milne18, Theorem 4.14].) Therefore,
$m\in \mathbb {N}$
. (See [Reference Milne18, Theorem 4.14].) Therefore,
![]() $\operatorname {\mathrm {Supp}}(\operatorname {\mathrm {{HN}}}_g)$
is the additive subgroup of
$\operatorname {\mathrm {Supp}}(\operatorname {\mathrm {{HN}}}_g)$
is the additive subgroup of
![]() $\mathbb {Q}$
finitely generated by the
$\mathbb {Q}$
finitely generated by the
![]() $\mathbb {Q}$
-jumps
$\mathbb {Q}$
-jumps
![]() $\nu _1,\ldots ,\nu _n$
of
$\nu _1,\ldots ,\nu _n$
of
![]() $(W_{\mathcal {R}},g\varphi )$
. We write
$(W_{\mathcal {R}},g\varphi )$
. We write
![]() $\nu _i=s_i/d_i$
with
$\nu _i=s_i/d_i$
with
![]() $d_i>0$
and
$d_i>0$
and
![]() $(s_i,d_i)=1$
for
$(s_i,d_i)=1$
for
![]() $1\leq i\leq n$
. Let
$1\leq i\leq n$
. Let
![]() $d_g\in \mathbb {N}$
be the least common multiple of the
$d_g\in \mathbb {N}$
be the least common multiple of the
![]() $d_i$
. We then have
$d_i$
. We then have
![]() $d_g\nu _i\in \mathbb {Z}$
for
$d_g\nu _i\in \mathbb {Z}$
for
![]() $1\leq i\leq n$
. In particular, we have
$1\leq i\leq n$
. In particular, we have
Therefore,
![]() $d_g$
is uniquely determined by g. We call
$d_g$
is uniquely determined by g. We call
![]() $d_g$
the least common denominator of g.
$d_g$
the least common denominator of g.
Remark 3.9 We conclude from Construction 3.8 that
![]() $\operatorname {\mathrm {Supp}}(\operatorname {\mathrm {{HN}}}_g)$
is isomorphic to
$\operatorname {\mathrm {Supp}}(\operatorname {\mathrm {{HN}}}_g)$
is isomorphic to
![]() $\mathbb {Z}$
or
$\mathbb {Z}$
or
![]() $0$
. In fact, if
$0$
. In fact, if
![]() $(W_{\mathcal {R}},g\varphi )$
has only one jump
$(W_{\mathcal {R}},g\varphi )$
has only one jump
![]() $0$
, then
$0$
, then
![]() $\operatorname {\mathrm {Supp}}(\operatorname {\mathrm {{HN}}}_g)=0$
. Otherwise, the choice of
$\operatorname {\mathrm {Supp}}(\operatorname {\mathrm {{HN}}}_g)=0$
. Otherwise, the choice of
![]() $d_g$
implies that
$d_g$
implies that
![]() $\gcd (d_g\nu _1,\ldots ,d_g\nu _n)=1$
. We then have
$\gcd (d_g\nu _1,\ldots ,d_g\nu _n)=1$
. We then have
![]() $d_g\operatorname {\mathrm {Supp}}(\operatorname {\mathrm {{HN}}}_g)=\mathbb {Z}$
, because the
$d_g\operatorname {\mathrm {Supp}}(\operatorname {\mathrm {{HN}}}_g)=\mathbb {Z}$
, because the
![]() $d_g\nu _i$
generate
$d_g\nu _i$
generate
![]() $\mathbb {Z}$
as a
$\mathbb {Z}$
as a
![]() $\mathbb {Z}$
-module. Therefore,
$\mathbb {Z}$
-module. Therefore,
![]() $x \mapsto d_gx$
gives an isomorphism
$x \mapsto d_gx$
gives an isomorphism
![]() $\operatorname {\mathrm {Supp}}(\operatorname {\mathrm {{HN}}}_g)\cong \mathbb {Z}$
.
$\operatorname {\mathrm {Supp}}(\operatorname {\mathrm {{HN}}}_g)\cong \mathbb {Z}$
.
Lemma 3.10
![]() $\operatorname {\mathrm {{HN}}}_g$
factors through a
$\operatorname {\mathrm {{HN}}}_g$
factors through a
![]() $\mathbb {Z}$
-filtered fiber functor
$\mathbb {Z}$
-filtered fiber functor
![]() $\operatorname {\mathrm {{HN}}}^{\mathbb {Z}}_g\colon \operatorname {\mathrm {\textbf {Rep}}}_F(G) \to \mathbb {Z}$
-
$\operatorname {\mathrm {{HN}}}^{\mathbb {Z}}_g\colon \operatorname {\mathrm {\textbf {Rep}}}_F(G) \to \mathbb {Z}$
-
![]() $\operatorname {\mathrm {\textbf {Fil}}}_{\mathcal {R}}$
which makes the diagram
$\operatorname {\mathrm {\textbf {Fil}}}_{\mathcal {R}}$
which makes the diagram

commute.
We remark that the functor
![]() ${[d_g^{-1}]}_*$
(see Construction 2.11) is nothing but relabeling the jumps by multiplying all jumps with
${[d_g^{-1}]}_*$
(see Construction 2.11) is nothing but relabeling the jumps by multiplying all jumps with
![]() $d_g^{-1}$
. In particular, this lemma implies that
$d_g^{-1}$
. In particular, this lemma implies that
![]() $\operatorname {\mathrm {gr}}^x_{\operatorname {\mathrm {{HN}}}_g}(V)=\operatorname {\mathrm {gr}}^{d_g^{-1}x}_{\operatorname {\mathrm {{HN}}}^{\mathbb {Z}}_g}(V)$
for all
$\operatorname {\mathrm {gr}}^x_{\operatorname {\mathrm {{HN}}}_g}(V)=\operatorname {\mathrm {gr}}^{d_g^{-1}x}_{\operatorname {\mathrm {{HN}}}^{\mathbb {Z}}_g}(V)$
for all
![]() $x\in \mathbb {Q}$
and
$x\in \mathbb {Q}$
and
![]() $V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
.
$V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
.
Proof of Lemma 3.10 Let
![]() $V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, and let
$V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, and let
![]() $\mu _1,\ldots ,\mu _l$
be the
$\mu _1,\ldots ,\mu _l$
be the
![]() $\mathbb {Q}$
-jumps of
$\mathbb {Q}$
-jumps of
![]() $(V_{\mathcal {R}},g\varphi )$
. We then have
$(V_{\mathcal {R}},g\varphi )$
. We then have
![]() $d_g\mu _i\in \mathbb {Z}$
for all i. We have an increasing map
$d_g\mu _i\in \mathbb {Z}$
for all i. We have an increasing map
 $$ \begin{align*} \mathcal{F}_g \colon \mathbb{Z} &\operatorname{\mathrm{\longrightarrow}} \{\mathcal{R}\text{-submodules of}~V_{\mathcal{R}}\},\\ x &\longmapsto \mathcal{F}_g^x(V_{\mathcal{R}}), \end{align*} $$
$$ \begin{align*} \mathcal{F}_g \colon \mathbb{Z} &\operatorname{\mathrm{\longrightarrow}} \{\mathcal{R}\text{-submodules of}~V_{\mathcal{R}}\},\\ x &\longmapsto \mathcal{F}_g^x(V_{\mathcal{R}}), \end{align*} $$
where
 $$ \begin{align*}\mathcal{F}_g^x(V_{\mathcal{R}}):= \left\{ \begin{array}{ll} 0 &\text{for}~x<d_g\mu_1,\\ \mathcal{HN}_g^{\mu_i}(V_{\mathcal{R}}) ~~~ &\text{for}~ d_g\mu_i\leq x <d_g\mu_{i+1}, 1\leq i\leq l-1,\\ V_{\mathcal{R}} &\text{for}~x\geq d_g\mu_l. \end{array} \right.\end{align*} $$
$$ \begin{align*}\mathcal{F}_g^x(V_{\mathcal{R}}):= \left\{ \begin{array}{ll} 0 &\text{for}~x<d_g\mu_1,\\ \mathcal{HN}_g^{\mu_i}(V_{\mathcal{R}}) ~~~ &\text{for}~ d_g\mu_i\leq x <d_g\mu_{i+1}, 1\leq i\leq l-1,\\ V_{\mathcal{R}} &\text{for}~x\geq d_g\mu_l. \end{array} \right.\end{align*} $$
Then,
![]() $(V_{\mathcal {R}},\mathcal {F}_g)$
is a
$(V_{\mathcal {R}},\mathcal {F}_g)$
is a
![]() $\mathbb {Z}$
-filtered module over
$\mathbb {Z}$
-filtered module over
![]() $\mathcal {R}$
with
$\mathcal {R}$
with
![]() $\mathbb {Z}$
-jumps
$\mathbb {Z}$
-jumps
![]() $d_g\mu _1<\cdots <d_g\mu _l$
. We thus have a
$d_g\mu _1<\cdots <d_g\mu _l$
. We thus have a
![]() $\mathbb {Z}$
-filtered fiber functor
$\mathbb {Z}$
-filtered fiber functor
 $$ \begin{align*} \operatorname{\mathrm{{HN}}}^{\mathbb{Z}}_g \colon \operatorname{\mathrm{\textbf{Rep}}}_F(G) &\operatorname{\mathrm{\longrightarrow}} \mathbb{Z}\text{-}\operatorname{\mathrm{\textbf{Fil}}}_{\mathcal{R}},\\ V &\longmapsto (V_{\mathcal{R}},\mathcal{F}_g), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{{HN}}}^{\mathbb{Z}}_g \colon \operatorname{\mathrm{\textbf{Rep}}}_F(G) &\operatorname{\mathrm{\longrightarrow}} \mathbb{Z}\text{-}\operatorname{\mathrm{\textbf{Fil}}}_{\mathcal{R}},\\ V &\longmapsto (V_{\mathcal{R}},\mathcal{F}_g), \end{align*} $$
satisfying
![]() $\operatorname {\mathrm {{HN}}}_g=[d_g^{-1}]_*\circ \operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
.▪
$\operatorname {\mathrm {{HN}}}_g=[d_g^{-1}]_*\circ \operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
.▪
By the definition of
![]() $\operatorname {\mathrm {\underline {Aut}}}^{\otimes }$
and Corollary 2.5, we have
$\operatorname {\mathrm {\underline {Aut}}}^{\otimes }$
and Corollary 2.5, we have
![]() $\operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega ^G)(R)=\operatorname {\mathrm {Aut}}^{\otimes } (\omega ^G_R)\cong G(R)$
for all
$\operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega ^G)(R)=\operatorname {\mathrm {Aut}}^{\otimes } (\omega ^G_R)\cong G(R)$
for all
![]() $R\in \operatorname {\mathrm {\textbf {Alg}}}_k$
. For any R-algebra S, we then have
$R\in \operatorname {\mathrm {\textbf {Alg}}}_k$
. For any R-algebra S, we then have
Proposition 3.11 Let G be a smooth F-group. Then,
![]() $\operatorname {\mathrm {{HN}}}^{\mathbb {Z}}_g$
is splittable.
$\operatorname {\mathrm {{HN}}}^{\mathbb {Z}}_g$
is splittable.
Proof Because
![]() $\operatorname {\mathrm {forg}}\circ \operatorname {\mathrm {{HN}}}^{\mathbb {Z}}_g=\omega ^G\otimes \mathcal {R}$
, we have
$\operatorname {\mathrm {forg}}\circ \operatorname {\mathrm {{HN}}}^{\mathbb {Z}}_g=\omega ^G\otimes \mathcal {R}$
, we have
Notice that
![]() $G_{\mathcal {R}}$
is smooth over
$G_{\mathcal {R}}$
is smooth over
![]() $\mathcal {R}$
; the proposition then follows from Theorem 2.12.▪
$\mathcal {R}$
; the proposition then follows from Theorem 2.12.▪
Theorem 3.12 Let G be a smooth F-group. Then, the
![]() $\mathbb {Q}$
-filtered fiber functor
$\mathbb {Q}$
-filtered fiber functor
![]() $\operatorname {\mathrm {{HN}}}_g$
is splittable.
$\operatorname {\mathrm {{HN}}}_g$
is splittable.
Proof Choose a splitting
![]() $\tau _g\colon \operatorname {\mathrm {\textbf {Rep}}}_F(G)\to \mathbb {Z}$
-
$\tau _g\colon \operatorname {\mathrm {\textbf {Rep}}}_F(G)\to \mathbb {Z}$
-
![]() $\operatorname {\mathrm {\textbf {Grad}}}_{\mathcal {R}}$
of
$\operatorname {\mathrm {\textbf {Grad}}}_{\mathcal {R}}$
of
![]() $\operatorname {\mathrm {{HN}}}^{\mathbb {Z}}_g$
by Proposition 3.11, we then have a
$\operatorname {\mathrm {{HN}}}^{\mathbb {Z}}_g$
by Proposition 3.11, we then have a
![]() $\mathbb {Q}$
-graded fiber functor
$\mathbb {Q}$
-graded fiber functor
![]() ${[d_g^{-1}]}_*\circ \tau _g\colon \operatorname {\mathrm {\textbf {Rep}}}_F(G)\to \mathbb {Q}$
-
${[d_g^{-1}]}_*\circ \tau _g\colon \operatorname {\mathrm {\textbf {Rep}}}_F(G)\to \mathbb {Q}$
-
![]() $\operatorname {\mathrm {\textbf {Grad}}}_{\mathcal {R}}$
. On the other hand, we have the diagram
$\operatorname {\mathrm {\textbf {Grad}}}_{\mathcal {R}}$
. On the other hand, we have the diagram

with the upper-left, the upper-right, and the bottom triangles commutative. Here, the commutativity of the upper-left (resp. the upper-right) triangle follows from Proposition 3.11 (resp. Lemma 3.10); for the bottom one, we note that
![]() ${[d_g^{-1}]}_*\circ \operatorname {\mathrm {fil}}=\operatorname {\mathrm {fil}}\circ {[d_g^{-1}]}_*$
. Hence, the outer diagram also commutes, which implies that
${[d_g^{-1}]}_*\circ \operatorname {\mathrm {fil}}=\operatorname {\mathrm {fil}}\circ {[d_g^{-1}]}_*$
. Hence, the outer diagram also commutes, which implies that
![]() $\operatorname {\mathrm {{HN}}}_g$
factors through the
$\operatorname {\mathrm {{HN}}}_g$
factors through the
![]() $\mathbb {Q}$
-graded fiber functor
$\mathbb {Q}$
-graded fiber functor
![]() ${[d_g^{-1}]}_*\circ \tau _g$
, as desired.▪
${[d_g^{-1}]}_*\circ \tau _g$
, as desired.▪
3.4 The slope morphism
Let R be a commutative ring with
![]() $1$
, and let
$1$
, and let
![]() $\Gamma $
be an abelian group (not necessarily finitely generated). We first continue the discussions in Section 2.5 to see how
$\Gamma $
be an abelian group (not necessarily finitely generated). We first continue the discussions in Section 2.5 to see how
![]() $\Gamma $
-gradings over R are related to
$\Gamma $
-gradings over R are related to
![]() $D_R(\Gamma )$
-modules, for some affine group scheme
$D_R(\Gamma )$
-modules, for some affine group scheme
![]() $D_R(\Gamma )$
which will be defined as follows.
$D_R(\Gamma )$
which will be defined as follows.
The group algebra
![]() $R[\Gamma ]:= \bigoplus \limits _{\gamma \in \Gamma } Re_\gamma $
carries a Hopf algebra structure, where the comultiplication is given by
$R[\Gamma ]:= \bigoplus \limits _{\gamma \in \Gamma } Re_\gamma $
carries a Hopf algebra structure, where the comultiplication is given by
![]() $\Delta (e_\gamma )=e_\gamma \otimes e_\gamma $
, the counit is given by
$\Delta (e_\gamma )=e_\gamma \otimes e_\gamma $
, the counit is given by
![]() $\epsilon (e_\gamma )=1$
, and the antipode is given by
$\epsilon (e_\gamma )=1$
, and the antipode is given by
![]() $S(e_\gamma )=e_{-\gamma }$
, for all
$S(e_\gamma )=e_{-\gamma }$
, for all
![]() $\gamma \in \Gamma $
. We denote by
$\gamma \in \Gamma $
. We denote by
![]() $D_R(\Gamma )$
the affine R-group scheme represented by
$D_R(\Gamma )$
the affine R-group scheme represented by
![]() $R[\Gamma ]$
. For any
$R[\Gamma ]$
. For any
![]() $\gamma \in \Gamma $
, the Hopf algebra morphism
$\gamma \in \Gamma $
, the Hopf algebra morphism
![]() $R[\mathbb {Z}] \to R[\Gamma ], e_1 \mapsto e_\gamma $
gives rise to a character
$R[\mathbb {Z}] \to R[\Gamma ], e_1 \mapsto e_\gamma $
gives rise to a character
![]() $\chi _\gamma \colon D_R(\Gamma ) \to \mathbb {G}_{m,R}$
of
$\chi _\gamma \colon D_R(\Gamma ) \to \mathbb {G}_{m,R}$
of
![]() $D_R(\Gamma )$
. For the remainder of this paper, we denote by
$D_R(\Gamma )$
. For the remainder of this paper, we denote by
![]() $\mathbb {D}_R$
the R-group scheme
$\mathbb {D}_R$
the R-group scheme
![]() $D_R(\mathbb {Q})$
.
$D_R(\mathbb {Q})$
.
Let
![]() $M=\bigoplus _{\gamma \in \Gamma } M_\gamma $
be a
$M=\bigoplus _{\gamma \in \Gamma } M_\gamma $
be a
![]() $\Gamma $
-graded module over R. Then, M becomes a
$\Gamma $
-graded module over R. Then, M becomes a
![]() $D_R(\Gamma )$
-module where
$D_R(\Gamma )$
-module where
![]() $D_R(\Gamma )$
acts on each
$D_R(\Gamma )$
acts on each
![]() $M_\gamma $
via
$M_\gamma $
via
![]() $\chi _\gamma $
. The following lemma shows that this assignment gives an equivalence of categories.
$\chi _\gamma $
. The following lemma shows that this assignment gives an equivalence of categories.
Lemma 3.13 [Reference Demazure and Gabriel8, Proposition II.2.5]
![]() $\Gamma $
-
$\Gamma $
-
![]() $\operatorname {\mathrm {\textbf {Grad}}}_R$
is equivalent to the category of
$\operatorname {\mathrm {\textbf {Grad}}}_R$
is equivalent to the category of
![]() $D_{R}(\Gamma )$
-modules.
$D_{R}(\Gamma )$
-modules.
Corollary 3.14 For any
![]() $\gamma \in \mathbb {Q}_{>0}$
, the functor
$\gamma \in \mathbb {Q}_{>0}$
, the functor
![]() $[\gamma ]_*\colon \mathbb {Z}\text {-}\operatorname {\mathrm {\textbf {Grad}}}_R \to \mathbb {Q}\text {-}\operatorname {\mathrm {\textbf {Grad}}}_R$
corresponds to the character
$[\gamma ]_*\colon \mathbb {Z}\text {-}\operatorname {\mathrm {\textbf {Grad}}}_R \to \mathbb {Q}\text {-}\operatorname {\mathrm {\textbf {Grad}}}_R$
corresponds to the character
![]() $\chi _\gamma \colon \mathbb {D}_R\to \mathbb {G}_{m,R}$
.
$\chi _\gamma \colon \mathbb {D}_R\to \mathbb {G}_{m,R}$
.
Proof Let
![]() $M\in \mathbb {Z}\text {-}\operatorname {\mathrm {\textbf {Grad}}}_R$
. By Lemma 3.13, we may write
$M\in \mathbb {Z}\text {-}\operatorname {\mathrm {\textbf {Grad}}}_R$
. By Lemma 3.13, we may write
![]() $M=\bigoplus \limits _{n\in \mathbb {Z}} M_n$
as a direct sum of eigenmodules. By construction, we have
$M=\bigoplus \limits _{n\in \mathbb {Z}} M_n$
as a direct sum of eigenmodules. By construction, we have
![]() $[\gamma ]_*(M)=\bigoplus \limits _{n\in \mathbb {Z}} ([\gamma ]_*(M))_{\gamma n}$
with
$[\gamma ]_*(M)=\bigoplus \limits _{n\in \mathbb {Z}} ([\gamma ]_*(M))_{\gamma n}$
with
![]() $([\gamma ]_*(M))_{\gamma n}=M_n$
for all n, which is also a decomposition into eigenmodules. Therefore, giving
$([\gamma ]_*(M))_{\gamma n}=M_n$
for all n, which is also a decomposition into eigenmodules. Therefore, giving
![]() $[\gamma ]_*$
is equivalent to giving the commutative diagram
$[\gamma ]_*$
is equivalent to giving the commutative diagram

of R-modules for all
![]() $n\in \mathbb {Z}$
such that
$n\in \mathbb {Z}$
such that
![]() $M_n\neq 0$
. Here, the left (resp. the right) vertical arrow is given by
$M_n\neq 0$
. Here, the left (resp. the right) vertical arrow is given by
![]() $m\mapsto m\otimes e_n$
(resp.
$m\mapsto m\otimes e_n$
(resp.
![]() $m\mapsto m\otimes e_{\gamma n}$
). The diagram then corresponds to
$m\mapsto m\otimes e_{\gamma n}$
). The diagram then corresponds to
![]() $R[\mathbb {Z}]\to R[\mathbb {Q}],~e_1\mapsto e_\gamma $
, as desired.▪
$R[\mathbb {Z}]\to R[\mathbb {Q}],~e_1\mapsto e_\gamma $
, as desired.▪
We now apply the preceding discussions to the functors constructed in Section 3.3, following [Reference Kottwitz14, Section 4].
Construction 3.15 Let
![]() $g\in G(\mathcal {R})$
; we fix a splitting
$g\in G(\mathcal {R})$
; we fix a splitting
![]() $\tau _g$
of
$\tau _g$
of
![]() $\operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
given by Proposition 3.11. For any
$\operatorname {\mathrm {{HN}}}_g^{\mathbb {Z}}$
given by Proposition 3.11. For any
![]() $(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
,
$(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
,
![]() $\tau _g$
gives a decomposition of
$\tau _g$
gives a decomposition of
![]() $V_{\mathcal {R}}$
, which induces a morphism
$V_{\mathcal {R}}$
, which induces a morphism
![]() $\lambda _{\rho ,g}\colon \mathbb {G}_{m,\mathcal {R}} \to \operatorname {\mathrm {GL}}_{V,\mathcal {R}}$
by Lemma 3.13. Let S be an
$\lambda _{\rho ,g}\colon \mathbb {G}_{m,\mathcal {R}} \to \operatorname {\mathrm {GL}}_{V,\mathcal {R}}$
by Lemma 3.13. Let S be an
![]() $\mathcal {R}$
-algebra, and let
$\mathcal {R}$
-algebra, and let
![]() $a\in \mathbb {G}_{m,\mathcal {R}}(S)$
. We then have a family
$a\in \mathbb {G}_{m,\mathcal {R}}(S)$
. We then have a family
of S-linear maps. Because
![]() $\tau _g$
is a tensor functor, this family satisfies conditions (i–iii) in Theorem 2.4. We thus find a unique element
$\tau _g$
is a tensor functor, this family satisfies conditions (i–iii) in Theorem 2.4. We thus find a unique element
![]() $b\in G_{\mathcal {R}}(S)$
such that
$b\in G_{\mathcal {R}}(S)$
such that
![]() $\lambda _{\rho ,g}(a)=\rho (b)$
for all
$\lambda _{\rho ,g}(a)=\rho (b)$
for all
![]() $(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
. The assignment
$(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
. The assignment
![]() $a\mapsto b$
is functorial in S, because both
$a\mapsto b$
is functorial in S, because both
![]() $\lambda _{\rho ,g}$
and
$\lambda _{\rho ,g}$
and
![]() $\rho $
are functorial. We then have a morphism of
$\rho $
are functorial. We then have a morphism of
![]() $\mathcal {R}$
-groups
$\mathcal {R}$
-groups
which is said to be the
![]() $\mathbb {Z}$
-slope morphism of g.
$\mathbb {Z}$
-slope morphism of g.
By Corollary 3.14,
![]() ${[d_g^{-1}]}_*$
gives a unique morphism
${[d_g^{-1}]}_*$
gives a unique morphism
![]() $\chi _{d_g^{-1}}\colon \mathbb {D}_{\mathcal {R}} \to \mathbb {G}_{m,\mathcal {R}}$
. We define
$\chi _{d_g^{-1}}\colon \mathbb {D}_{\mathcal {R}} \to \mathbb {G}_{m,\mathcal {R}}$
. We define
which is said to be the
![]() $\mathbb {Q}$
-slope morphism of g.
$\mathbb {Q}$
-slope morphism of g.
The following example demonstrates explicitly how
![]() $\lambda _g$
and
$\lambda _g$
and
![]() $\nu _g$
are related to the splittings constructed in Section 3.3 (see Diagram 3).
$\nu _g$
are related to the splittings constructed in Section 3.3 (see Diagram 3).
Example 3.16 Let
![]() $(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
and suppose that the slope filtration of
$(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
and suppose that the slope filtration of
![]() $(V_{\mathcal {R}},g\varphi )$
is
$(V_{\mathcal {R}},g\varphi )$
is
with jumps
![]() $\mu _1<\cdots <\mu _l$
. By Theorem 3.12, the functor
$\mu _1<\cdots <\mu _l$
. By Theorem 3.12, the functor
![]() $[d_g^{-1}]_* \circ \tau _g \colon \operatorname {\mathrm {\textbf {Rep}}}_F(G) \to \mathbb {Q}\text {-}\operatorname {\mathrm {\textbf {Grad}}}_{\mathcal {R}}$
gives a splitting
$[d_g^{-1}]_* \circ \tau _g \colon \operatorname {\mathrm {\textbf {Rep}}}_F(G) \to \mathbb {Q}\text {-}\operatorname {\mathrm {\textbf {Grad}}}_{\mathcal {R}}$
gives a splitting
of
![]() $\operatorname {\mathrm {{HN}}}_g(V)$
, i.e., we have
$\operatorname {\mathrm {{HN}}}_g(V)$
, i.e., we have
![]() $\bigoplus \limits _{i=1}^j V_{\mathcal {R},\mu _i}=V_{\mathcal {R}}^{\mu _j}$
for all
$\bigoplus \limits _{i=1}^j V_{\mathcal {R},\mu _i}=V_{\mathcal {R}}^{\mu _j}$
for all
![]() $1\leq j\leq l$
.
$1\leq j\leq l$
.
First, we fix
![]() $1\leq i\leq l$
. Let
$1\leq i\leq l$
. Let
![]() $S\in \operatorname {\mathrm {\textbf {Alg}}}_{\mathcal {R}}$
and
$S\in \operatorname {\mathrm {\textbf {Alg}}}_{\mathcal {R}}$
and
![]() $a\in \mathbb {D}_{\mathcal {R}}(S)$
, then
$a\in \mathbb {D}_{\mathcal {R}}(S)$
, then
![]() $\rho \circ \nu _g(a)$
acts on
$\rho \circ \nu _g(a)$
acts on
![]() $V_{\mathcal {R},\mu _i}\bigotimes _{\mathcal {R}} S$
via multiplication by
$V_{\mathcal {R},\mu _i}\bigotimes _{\mathcal {R}} S$
via multiplication by
![]() $\chi _{\mu _i}(a)$
. By Lemma 3.10,
$\chi _{\mu _i}(a)$
. By Lemma 3.10,
![]() $\rho \circ \lambda _g(b)$
acts on
$\rho \circ \lambda _g(b)$
acts on
![]() $V_{\mathcal {R},\mu _i}$
via multiplication by
$V_{\mathcal {R},\mu _i}$
via multiplication by
![]() $b^{d_g\mu _i}$
, for all
$b^{d_g\mu _i}$
, for all
![]() $b\in \mathbb {G}_{m,\mathcal {R}}(S)$
. Notice that for any
$b\in \mathbb {G}_{m,\mathcal {R}}(S)$
. Notice that for any
![]() $\frac {m}{n}\in \mathbb {Q}$
, we have
$\frac {m}{n}\in \mathbb {Q}$
, we have
![]() $e_{\frac {m}{n}}=(e_{\frac {1}{n}})^m \in \mathcal {R}[\mathbb {Q}]$
, and hence,
$e_{\frac {m}{n}}=(e_{\frac {1}{n}})^m \in \mathcal {R}[\mathbb {Q}]$
, and hence,
![]() $\chi _{\frac {m}{n}}=(\chi _{\frac {1}{n}})^m$
. In particular, we have
$\chi _{\frac {m}{n}}=(\chi _{\frac {1}{n}})^m$
. In particular, we have
![]() $\chi _{\mu _i}=\chi _{\frac {d_g\mu _i}{d_g}}=(\chi _{d_g^{-1}})^{d_g\mu _i}$
. Then, on
$\chi _{\mu _i}=\chi _{\frac {d_g\mu _i}{d_g}}=(\chi _{d_g^{-1}})^{d_g\mu _i}$
. Then, on
![]() $V_{\mathcal {R},\mu _i}\bigotimes _{\mathcal {R}} S$
, we have
$V_{\mathcal {R},\mu _i}\bigotimes _{\mathcal {R}} S$
, we have
We next apply this result to all
![]() $1\leq i\leq l$
. Because
$1\leq i\leq l$
. Because
![]() $V_{\mathcal {R}}=\bigoplus \limits _{i=1}^l V_{\mathcal {R},\mu _i}$
, we conclude that
$V_{\mathcal {R}}=\bigoplus \limits _{i=1}^l V_{\mathcal {R},\mu _i}$
, we conclude that
![]() $\rho \circ \nu _g=\rho \circ \lambda _g\circ \chi _{d_g^{-1}}$
. It follows that
$\rho \circ \nu _g=\rho \circ \lambda _g\circ \chi _{d_g^{-1}}$
. It follows that
![]() $\nu _g=\lambda _g\circ \chi _{d_g^{-1}}$
once we choose a faithful representation, as is expected from the definition of
$\nu _g=\lambda _g\circ \chi _{d_g^{-1}}$
once we choose a faithful representation, as is expected from the definition of
![]() $\nu _g$
.
$\nu _g$
.
If
![]() $G=\operatorname {\mathrm {GL}}_V$
for some
$G=\operatorname {\mathrm {GL}}_V$
for some
![]() $V\in \operatorname {\mathrm {\textbf {Vec}}}_F$
, we consider the standard representation
$V\in \operatorname {\mathrm {\textbf {Vec}}}_F$
, we consider the standard representation
![]() $(V,\rho )$
of G where
$(V,\rho )$
of G where
![]() $\rho $
is the identity. The discussion in the above example then indicates that the image of
$\rho $
is the identity. The discussion in the above example then indicates that the image of
![]() $\lambda _g$
is contained in a split maximal torus in
$\lambda _g$
is contained in a split maximal torus in
![]() $G_{\mathcal {R}}$
; we conjecture that this property holds true for an arbitrary split reductive F-group G, and we shall give one more evidence as follows.
$G_{\mathcal {R}}$
; we conjecture that this property holds true for an arbitrary split reductive F-group G, and we shall give one more evidence as follows.
Example 3.17 Fix a d-dimensional F-vector space V. For any
![]() $R\in \operatorname {\mathrm {\textbf {Alg}}}_F$
, we define
$R\in \operatorname {\mathrm {\textbf {Alg}}}_F$
, we define
The affine algebraic F-group
![]() $\operatorname {\mathrm {SL}}_V$
is called the special linear group (associated to V).
$\operatorname {\mathrm {SL}}_V$
is called the special linear group (associated to V).
Fix an arbitrary
![]() $g\in \operatorname {\mathrm {SL}}_V(\mathcal {R})$
. With the notation as in Construction 4.14, we suppose the jumps of the slope filtration of
$g\in \operatorname {\mathrm {SL}}_V(\mathcal {R})$
. With the notation as in Construction 4.14, we suppose the jumps of the slope filtration of
![]() $(V_{\mathcal {R}},\Phi _g)$
are
$(V_{\mathcal {R}},\Phi _g)$
are
![]() $\mu _1,\ldots ,\mu _l$
and
$\mu _1,\ldots ,\mu _l$
and
![]() $\xi _g(V)=\bigoplus \limits _{i=1}^l V_{\mathcal {R},\mu _i}$
. For each i, we write
$\xi _g(V)=\bigoplus \limits _{i=1}^l V_{\mathcal {R},\mu _i}$
. For each i, we write
![]() $r_i=\operatorname {\mathrm {rk}}_{\mathcal {R}} (V_{\mathcal {R},\mu _i})$
, then the
$r_i=\operatorname {\mathrm {rk}}_{\mathcal {R}} (V_{\mathcal {R},\mu _i})$
, then the
![]() $r_i$
-th exterior product
$r_i$
-th exterior product
![]() $\Lambda ^{r_i}(V_{\mathcal {R},\mu _i})$
is of rank
$\Lambda ^{r_i}(V_{\mathcal {R},\mu _i})$
is of rank
![]() $1$
. We choose a generator
$1$
. We choose a generator
![]() $m_i$
, then
$m_i$
, then
![]() $\Lambda ^{r_i}(\Phi _{g,\mu _i})(m_i)=f_i m_i$
for some
$\Lambda ^{r_i}(\Phi _{g,\mu _i})(m_i)=f_i m_i$
for some
![]() $f_i\in \mathcal {R}^{\times }=(\mathcal {E}^{\dagger })^{\times }$
. Let
$f_i\in \mathcal {R}^{\times }=(\mathcal {E}^{\dagger })^{\times }$
. Let
![]() $\nu $
be the valuation of the
$\nu $
be the valuation of the
![]() $1$
-Gauss norm on
$1$
-Gauss norm on
![]() $\mathcal {E}^{\dagger }$
. We then have
$\mathcal {E}^{\dagger }$
. We then have
![]() $\mu _i=\frac {\nu (f_i)}{r_i}$
by [Reference Kedlaya11, Definition 1.4.4].
$\mu _i=\frac {\nu (f_i)}{r_i}$
by [Reference Kedlaya11, Definition 1.4.4].
Let
![]() $e_1,\ldots ,e_d$
be a basis for V over F, and let
$e_1,\ldots ,e_d$
be a basis for V over F, and let
![]() $A\in \operatorname {\mathrm {SL}}_d(\mathcal {R})$
be the matrix of action of
$A\in \operatorname {\mathrm {SL}}_d(\mathcal {R})$
be the matrix of action of
![]() $\Phi _g$
in
$\Phi _g$
in
![]() $e_1\otimes 1,\ldots , e_d\otimes 1$
. Let
$e_1\otimes 1,\ldots , e_d\otimes 1$
. Let
![]() $B\in \operatorname {\mathrm {GL}}_d(\mathcal {R})$
represent a change-of-basis over
$B\in \operatorname {\mathrm {GL}}_d(\mathcal {R})$
represent a change-of-basis over
![]() $\mathcal {R}$
. Then, in the new basis, the matrix of action of
$\mathcal {R}$
. Then, in the new basis, the matrix of action of
![]() $\Phi _g$
is
$\Phi _g$
is
![]() $B^{-1}A \varphi (B)$
. Notice that
$B^{-1}A \varphi (B)$
. Notice that
![]() $\det (B)\in (\mathcal {E}^{\dagger })^{\times }$
and
$\det (B)\in (\mathcal {E}^{\dagger })^{\times }$
and
![]() $\varphi $
preserves
$\varphi $
preserves
![]() $\nu $
, we then have
$\nu $
, we then have
which implies that the valuation of the determinant of the matrix of action of
![]() $\Phi _g$
is invariant under change-of-basis. We denote by
$\Phi _g$
is invariant under change-of-basis. We denote by
![]() $\nu (\det (\Phi _g))$
this invariant. In particular, we have
$\nu (\det (\Phi _g))$
this invariant. In particular, we have
![]() $\nu (\det (\Phi _g))=0$
, because
$\nu (\det (\Phi _g))=0$
, because
![]() $\det (A)=1$
by assumption. Put
$\det (A)=1$
by assumption. Put
![]() $\Phi ^{\prime }_g := \bigoplus \limits _{i=1}^l \Phi _{g,\mu _i}$
, where each
$\Phi ^{\prime }_g := \bigoplus \limits _{i=1}^l \Phi _{g,\mu _i}$
, where each
![]() $\Phi _{g,\mu _i}$
is the projection of
$\Phi _{g,\mu _i}$
is the projection of
![]() $\Phi _g$
to the
$\Phi _g$
to the
![]() $\mu _i$
-th graded piece of
$\mu _i$
-th graded piece of
![]() $\xi _g(V)$
(cf. Construction 4.14 below). We thus have
$\xi _g(V)$
(cf. Construction 4.14 below). We thus have
Let
![]() $S\in \operatorname {\mathrm {\textbf {Alg}}}_{\mathcal {R}}$
and
$S\in \operatorname {\mathrm {\textbf {Alg}}}_{\mathcal {R}}$
and
![]() $t\in \mathbb {G}_{m,\mathcal {R}}(S)$
. Because
$t\in \mathbb {G}_{m,\mathcal {R}}(S)$
. Because
![]() $\lambda _g(t)$
acts on each
$\lambda _g(t)$
acts on each
![]() $V_{\mathcal {R},\mu _i}\bigotimes _{\mathcal {R}} S$
via multiplication by
$V_{\mathcal {R},\mu _i}\bigotimes _{\mathcal {R}} S$
via multiplication by
![]() $t^{d_g\mu _i}$
where
$t^{d_g\mu _i}$
where
![]() $d_g$
is the least common denominator of g, we then have
$d_g$
is the least common denominator of g, we then have
Therefore, the image of
![]() $\lambda _g$
is contained in a split maximal torus in
$\lambda _g$
is contained in a split maximal torus in
![]() $\operatorname {\mathrm {SL}}_{V,\mathcal {R}}$
.
$\operatorname {\mathrm {SL}}_{V,\mathcal {R}}$
.
4
G-
 $(\varphi ,\nabla )$
-modules over the Robba ring
$(\varphi ,\nabla )$
-modules over the Robba ring
In this section, we fix an affine algebraic group F-group G.
4.1 Definition and an identification
Let
![]() $R\in \{\mathcal {E}^{\dagger },\mathcal {R}\}$
equipped with an absolute Frobenius lift
$R\in \{\mathcal {E}^{\dagger },\mathcal {R}\}$
equipped with an absolute Frobenius lift
![]() $\varphi $
and the usual derivation
$\varphi $
and the usual derivation
![]() $\partial =\partial _t=d/dt$
on R.
$\partial =\partial _t=d/dt$
on R.
Definition 4.1 A G-
![]() $(\varphi ,\nabla )$
-module over R is an exact faithful F-linear tensor functor
$(\varphi ,\nabla )$
-module over R is an exact faithful F-linear tensor functor
which satisfies
![]() $\operatorname {\mathrm {forg}} \circ \operatorname {\mathrm {I}} = \omega ^G \otimes R$
, where
$\operatorname {\mathrm {forg}} \circ \operatorname {\mathrm {I}} = \omega ^G \otimes R$
, where
![]() $\operatorname {\mathrm {forg}} \colon \operatorname {\mathrm {\textbf {Mod}^{\varphi }_R}} \to \operatorname {\mathrm {\textbf {Mod}}}_R$
is the forgetful functor. The category of G-
$\operatorname {\mathrm {forg}} \colon \operatorname {\mathrm {\textbf {Mod}^{\varphi }_R}} \to \operatorname {\mathrm {\textbf {Mod}}}_R$
is the forgetful functor. The category of G-
![]() $(\varphi ,\nabla )$
-modules over R is denoted by
$(\varphi ,\nabla )$
-modules over R is denoted by
![]() $\operatorname {\mathrm {G-\textbf {Mod}^{\varphi ,\nabla }_R}}$
, whose morphisms are morphisms of tensor functors. A G-
$\operatorname {\mathrm {G-\textbf {Mod}^{\varphi ,\nabla }_R}}$
, whose morphisms are morphisms of tensor functors. A G-
![]() $(\varphi ,\nabla )$
-module
$(\varphi ,\nabla )$
-module
![]() $\operatorname {\mathrm {I}}$
over R is called unit-root if
$\operatorname {\mathrm {I}}$
over R is called unit-root if
![]() $\operatorname {\mathrm {I}}(V,\rho )$
is a unit-root
$\operatorname {\mathrm {I}}(V,\rho )$
is a unit-root
![]() $(\varphi ,\nabla )$
-module over R for all
$(\varphi ,\nabla )$
-module over R for all
![]() $(V,\rho ) \in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
.
$(V,\rho ) \in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
.
Remark 4.2 We remark that
![]() $\operatorname {\mathrm {G-\textbf {Mod}^{\varphi ,\nabla }_R}}$
is a groupoid, because both
$\operatorname {\mathrm {G-\textbf {Mod}^{\varphi ,\nabla }_R}}$
is a groupoid, because both
![]() $\operatorname {\mathrm {\textbf {Rep}}}_F(G)$
and
$\operatorname {\mathrm {\textbf {Rep}}}_F(G)$
and
![]() $\textbf {Mod}^{\varphi ,\nabla }_R$
are rigid tensor categories over F, and any morphism of tensor functors between rigid tensor categories is an isomorphism by [Reference Deligne and Milne7, Proposition 1.13]. Note that tensor products and duals in
$\textbf {Mod}^{\varphi ,\nabla }_R$
are rigid tensor categories over F, and any morphism of tensor functors between rigid tensor categories is an isomorphism by [Reference Deligne and Milne7, Proposition 1.13]. Note that tensor products and duals in
![]() $\textbf {Mod}^{\varphi ,\nabla }_R$
are defined as in [Reference Tsuzuki22, Section 3.1], and the identity object is
$\textbf {Mod}^{\varphi ,\nabla }_R$
are defined as in [Reference Tsuzuki22, Section 3.1], and the identity object is
![]() $(R,\varphi ,\partial )$
.
$(R,\varphi ,\partial )$
.
We put
Let
![]() $\Omega _R^1 := \Omega _{R/K}^1$
be the free R-module generated by the symbol
$\Omega _R^1 := \Omega _{R/K}^1$
be the free R-module generated by the symbol
![]() $dt$
, with the K-linear derivation
$dt$
, with the K-linear derivation
![]() $d\colon R \to \Omega ^1_R, f\mapsto \partial (f) dt$
. We also define a
$d\colon R \to \Omega ^1_R, f\mapsto \partial (f) dt$
. We also define a
![]() $\varphi $
-linear endomorphism
$\varphi $
-linear endomorphism
Given a finite-dimensional representation
![]() $\rho \colon G\to \operatorname {\mathrm {GL}}_V$
, we have a morphism
$\rho \colon G\to \operatorname {\mathrm {GL}}_V$
, we have a morphism
![]() $\operatorname {\mathrm {Lie}}(\rho ) \colon \mathfrak {g}\to \operatorname {\mathrm {\mathfrak {gl}}}_V$
of Lie algebras, and hence a morphism
$\operatorname {\mathrm {Lie}}(\rho ) \colon \mathfrak {g}\to \operatorname {\mathrm {\mathfrak {gl}}}_V$
of Lie algebras, and hence a morphism
![]() $ \mathfrak {g}_R \to \operatorname {\mathrm {\mathfrak {gl}}}_V\bigotimes R\cong \operatorname {\mathrm {End}}_R(V_R)$
of Lie algebras over R (which is injective if
$ \mathfrak {g}_R \to \operatorname {\mathrm {\mathfrak {gl}}}_V\bigotimes R\cong \operatorname {\mathrm {End}}_R(V_R)$
of Lie algebras over R (which is injective if
![]() $\rho $
is a closed embedding). For any
$\rho $
is a closed embedding). For any
![]() $X\in \mathfrak {g}_R$
, we denote by X the action of
$X\in \mathfrak {g}_R$
, we denote by X the action of
![]() $\operatorname {\mathrm {Lie}}(\rho )(X)$
on
$\operatorname {\mathrm {Lie}}(\rho )(X)$
on
![]() $V_R$
(see Remark 2.8). We define the connection
$V_R$
(see Remark 2.8). We define the connection
![]() $\nabla _X$
of
$\nabla _X$
of
![]() $V_R$
associated to X by
$V_R$
associated to X by
 $$ \begin{align*} \nabla_X := \nabla_{X,V} \colon V_R &\operatorname{\mathrm{\longrightarrow}} V_R \bigotimes_R \Omega_R^1,\\ v\otimes f &\longmapsto (v\otimes 1)\otimes d(f) + X(v\otimes f)\otimes dt. \end{align*} $$
$$ \begin{align*} \nabla_X := \nabla_{X,V} \colon V_R &\operatorname{\mathrm{\longrightarrow}} V_R \bigotimes_R \Omega_R^1,\\ v\otimes f &\longmapsto (v\otimes 1)\otimes d(f) + X(v\otimes f)\otimes dt. \end{align*} $$
Because
![]() $fdt\mapsto f$
gives an isomorphism
$fdt\mapsto f$
gives an isomorphism
![]() $\Omega _R^1 \cong R$
, we have an isomorphism
$\Omega _R^1 \cong R$
, we have an isomorphism
![]() $\iota \colon V_R\bigotimes _R \Omega ^1_R\to V_R$
. Let
$\iota \colon V_R\bigotimes _R \Omega ^1_R\to V_R$
. Let
![]() $\Theta _X := \Theta _{X,V}$
be the differential operator associated to
$\Theta _X := \Theta _{X,V}$
be the differential operator associated to
![]() $\nabla _X$
given by the following composition:
$\nabla _X$
given by the following composition:
We have that
![]() $\Theta _X(v\otimes f)=v\otimes \partial (f)+X(v\otimes f)$
for all
$\Theta _X(v\otimes f)=v\otimes \partial (f)+X(v\otimes f)$
for all
![]() $v\otimes f\in V_R$
.
$v\otimes f\in V_R$
.
When
![]() $G=\operatorname {\mathrm {GL}}_V$
for some
$G=\operatorname {\mathrm {GL}}_V$
for some
![]() $V\in \operatorname {\mathrm {\textbf {Vec}}}_F$
, we may canonically associate to any G-
$V\in \operatorname {\mathrm {\textbf {Vec}}}_F$
, we may canonically associate to any G-
![]() $(\varphi ,\nabla )$
-module
$(\varphi ,\nabla )$
-module
![]() $\operatorname {\mathrm {I}}$
over R a
$\operatorname {\mathrm {I}}$
over R a
![]() $(\varphi ,\nabla )$
-module
$(\varphi ,\nabla )$
-module
![]() $(V_R,\Phi ,\nabla )$
over R, where
$(V_R,\Phi ,\nabla )$
over R, where
![]() $(V_R,\Phi ,\nabla ) := \operatorname {\mathrm {I}}(V,\rho )$
and
$(V_R,\Phi ,\nabla ) := \operatorname {\mathrm {I}}(V,\rho )$
and
![]() $\rho \colon G\to G$
is the identity. Choose a basis
$\rho \colon G\to G$
is the identity. Choose a basis
![]() $e_1,\ldots ,e_d$
of V, we define elements
$e_1,\ldots ,e_d$
of V, we define elements
![]() $g\in G(R)$
and
$g\in G(R)$
and
![]() $X\in \mathfrak {g}_R$
by setting
$X\in \mathfrak {g}_R$
by setting
![]() $g(e_i\otimes 1) := \Phi (e_i\otimes 1)$
and
$g(e_i\otimes 1) := \Phi (e_i\otimes 1)$
and
![]() $X(e_i\otimes 1) := \iota \circ \nabla (e_i \otimes 1)$
, respectively. We then have
$X(e_i\otimes 1) := \iota \circ \nabla (e_i \otimes 1)$
, respectively. We then have
![]() $\Phi =g\varphi $
and
$\Phi =g\varphi $
and
![]() $\nabla =\nabla _X$
.
$\nabla =\nabla _X$
.
Lemma 4.3 Let
![]() $V,W \in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, and let
$V,W \in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, and let
![]() $\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
. We then have
$\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
. We then have
Proof The first equality holds, because
![]() $\alpha _R$
commutes with X (see Remark 2.8), and the second one follows from a direct computation.▪
$\alpha _R$
commutes with X (see Remark 2.8), and the second one follows from a direct computation.▪
Construction 4.4 We consider the R-algebra morphism
which induces a morphism
![]() $G(\hat \partial )\colon G(R)\to G(R[\varepsilon ])$
. Notice that
$G(\hat \partial )\colon G(R)\to G(R[\varepsilon ])$
. Notice that
![]() $\pi _R\circ \hat \partial =\operatorname {\mathrm {Id}}_R$
; we then have
$\pi _R\circ \hat \partial =\operatorname {\mathrm {Id}}_R$
; we then have
![]() $G(\pi _R)\circ G(\hat \partial )= \operatorname {\mathrm {Id}}_{G(R)}$
, in particular,
$G(\pi _R)\circ G(\hat \partial )= \operatorname {\mathrm {Id}}_{G(R)}$
, in particular,
![]() $G(\pi _R)\big (G(\hat \partial ) (g)\big )=g$
. Identifying g with its image in
$G(\pi _R)\big (G(\hat \partial ) (g)\big )=g$
. Identifying g with its image in
![]() $G(R[\varepsilon ])$
induced by the inclusion
$G(R[\varepsilon ])$
induced by the inclusion
![]() $R\to R[\varepsilon ],r\mapsto r$
, we then have
$R\to R[\varepsilon ],r\mapsto r$
, we then have
For
![]() $g\in G(R)$
, we define
$g\in G(R)$
, we define
![]() $\partial (g):= G(\hat \partial ) (g)\in G(R[\varepsilon ])$
, and put
$\partial (g):= G(\hat \partial ) (g)\in G(R[\varepsilon ])$
, and put
Example 4.5 Let
![]() $G=\operatorname {\mathrm {GL}}_d$
for some
$G=\operatorname {\mathrm {GL}}_d$
for some
![]() $d\in \mathbb {N}$
, and let
$d\in \mathbb {N}$
, and let
![]() $B\in G(R)$
. We have that
$B\in G(R)$
. We have that
![]() $\operatorname {\mathrm {dlog}}(B)=I_d+\varepsilon \partial (B)B^{-1}$
, where
$\operatorname {\mathrm {dlog}}(B)=I_d+\varepsilon \partial (B)B^{-1}$
, where
![]() $I_d$
is the
$I_d$
is the
![]() $d\times d$
identity matrix and
$d\times d$
identity matrix and
![]() $\partial $
acts on B entrywise. Using the isomorphism
$\partial $
acts on B entrywise. Using the isomorphism
![]() $\operatorname {\mathrm {Lie}}(G)(R)=\{I_d+ \varepsilon B \mid B\in \operatorname {\mathrm {Mat}}_{d,d}(R)\}\cong \{B\mid B\in \operatorname {\mathrm {Mat}}_{d,d}(R)\}$
, we may identify
$\operatorname {\mathrm {Lie}}(G)(R)=\{I_d+ \varepsilon B \mid B\in \operatorname {\mathrm {Mat}}_{d,d}(R)\}\cong \{B\mid B\in \operatorname {\mathrm {Mat}}_{d,d}(R)\}$
, we may identify
![]() $\operatorname {\mathrm {dlog}}(B)$
with
$\operatorname {\mathrm {dlog}}(B)$
with
![]() $\partial (B)B^{-1}$
.
$\partial (B)B^{-1}$
.
Definition 4.6
-
(i) We define the gauge transformation
where $$ \begin{align*}\Gamma_g\colon \mathfrak{g}_R \operatorname{\mathrm{\longrightarrow}} \mathfrak{g}_R,\;\;\;\;\; X \longmapsto \operatorname{\mathrm{Ad}}(g)(X)-\operatorname{\mathrm{dlog}}(g),\end{align*} $$
$$ \begin{align*}\Gamma_g\colon \mathfrak{g}_R \operatorname{\mathrm{\longrightarrow}} \mathfrak{g}_R,\;\;\;\;\; X \longmapsto \operatorname{\mathrm{Ad}}(g)(X)-\operatorname{\mathrm{dlog}}(g),\end{align*} $$
 $\operatorname {\mathrm {Ad}}\colon G\to \operatorname {\mathrm {GL}}_{\mathfrak {g}}$
is the adjoint representation.
$\operatorname {\mathrm {Ad}}\colon G\to \operatorname {\mathrm {GL}}_{\mathfrak {g}}$
is the adjoint representation.
-
(ii) We define
 $\textbf {B}^{\varphi ,\nabla }(G,R)$
to be the groupoid whose objects are
$\textbf {B}^{\varphi ,\nabla }(G,R)$
to be the groupoid whose objects are
 $(g,X)\in G(R)\times \mathfrak {g}_R$
satisfying
$(g,X)\in G(R)\times \mathfrak {g}_R$
satisfying
 $X=\Gamma _g(\operatorname {\mathrm {\boldsymbol \mu }}\varphi (X))$
, and whose morphisms
$X=\Gamma _g(\operatorname {\mathrm {\boldsymbol \mu }}\varphi (X))$
, and whose morphisms
 $(g,X) \to (g',X')$
are elements
$(g,X) \to (g',X')$
are elements
 $x\in G(R)$
such that
$x\in G(R)$
such that
 $g'=xg \varphi (x^{-1})$
and
$g'=xg \varphi (x^{-1})$
and
 $X'=\Gamma _x(X)$
.
$X'=\Gamma _x(X)$
.
Lemma 4.7 Let
![]() $(g,X)\in \textbf {B}^{\varphi ,\nabla }(G,R)$
. Then,
$(g,X)\in \textbf {B}^{\varphi ,\nabla }(G,R)$
. Then,
![]() $(V_R,g\varphi ,\nabla _X)$
is a
$(V_R,g\varphi ,\nabla _X)$
is a
![]() $(\varphi ,\nabla )$
-module over R for all
$(\varphi ,\nabla )$
-module over R for all
![]() $V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
.
$V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
.
Proof Choose a basis
![]() $e_1,\ldots ,e_d$
for V over F where
$e_1,\ldots ,e_d$
for V over F where
![]() $d=\dim _F V$
. Let
$d=\dim _F V$
. Let
![]() $A=(a_{ij})_{i,j} \in \operatorname {\mathrm {GL}}_d(R)$
(resp.
$A=(a_{ij})_{i,j} \in \operatorname {\mathrm {GL}}_d(R)$
(resp.
![]() $N=(n_{ij})_{i,j} \in \operatorname {\mathrm {Mat}}_{n,n}(R)$
) be the representing matrix of
$N=(n_{ij})_{i,j} \in \operatorname {\mathrm {Mat}}_{n,n}(R)$
) be the representing matrix of
![]() $\rho (g)$
(resp. X). For any
$\rho (g)$
(resp. X). For any
![]() $\textbf {v}=\sum \limits _{i=1}^d e_i\otimes f_i \in V_{\mathcal {R}}$
, we compute
$\textbf {v}=\sum \limits _{i=1}^d e_i\otimes f_i \in V_{\mathcal {R}}$
, we compute
 $$ \begin{align*} g\varphi(\Theta_X(\textbf{v})) &= g\varphi \Big(\operatorname*{\mathrm{\sum}}\limits_{i=1}^d e_i \otimes \partial(f_i) + \operatorname*{\mathrm{\sum}}\limits_{j=1}^d e_j \otimes \operatorname*{\mathrm{\sum}}\limits_{i=1}^d n_{ji}f_i \Big)\\ &=\operatorname*{\mathrm{\sum}} \limits_{j=1}^d e_j \otimes \operatorname*{\mathrm{\sum}} \limits_{i=1}^d a_{ji}\varphi(\partial(f_i)) + \operatorname*{\mathrm{\sum}}\limits_{k=1}^d e_k \otimes \operatorname*{\mathrm{\sum}} \limits_{i=1}^d \operatorname*{\mathrm{\sum}} \limits_{j=1}^d a_{kj}\varphi(n_{ji} f_i), \end{align*} $$
$$ \begin{align*} g\varphi(\Theta_X(\textbf{v})) &= g\varphi \Big(\operatorname*{\mathrm{\sum}}\limits_{i=1}^d e_i \otimes \partial(f_i) + \operatorname*{\mathrm{\sum}}\limits_{j=1}^d e_j \otimes \operatorname*{\mathrm{\sum}}\limits_{i=1}^d n_{ji}f_i \Big)\\ &=\operatorname*{\mathrm{\sum}} \limits_{j=1}^d e_j \otimes \operatorname*{\mathrm{\sum}} \limits_{i=1}^d a_{ji}\varphi(\partial(f_i)) + \operatorname*{\mathrm{\sum}}\limits_{k=1}^d e_k \otimes \operatorname*{\mathrm{\sum}} \limits_{i=1}^d \operatorname*{\mathrm{\sum}} \limits_{j=1}^d a_{kj}\varphi(n_{ji} f_i), \end{align*} $$
and
 $$ \begin{align*} \Theta_X (g\varphi(\textbf{v})) &=\Theta_X \Big( \operatorname*{\mathrm{\sum}}\limits_{j=1}^d e_j \otimes \operatorname*{\mathrm{\sum}}\limits_{i=1}^d a_{ji} \varphi(f_i) \Big) \\ &=\operatorname*{\mathrm{\sum}}\limits_{j=1}^d e_j \otimes \operatorname*{\mathrm{\sum}}\limits_{i=1}^d \partial(a_{ji}) \varphi(f_i) +\operatorname*{\mathrm{\sum}}\limits_{j=1}^d e_j \otimes \operatorname*{\mathrm{\sum}}\limits_{i=1}^d a_{ji}\partial( \varphi(f_i))\\ &\quad{}+ \operatorname*{\mathrm{\sum}}\limits_{k=1}^d e_k \otimes \operatorname*{\mathrm{\sum}} \limits_{i=1}^d \operatorname*{\mathrm{\sum}} \limits_{j=1}^d n_{kj} a_{ji} \varphi(f_i). \end{align*} $$
$$ \begin{align*} \Theta_X (g\varphi(\textbf{v})) &=\Theta_X \Big( \operatorname*{\mathrm{\sum}}\limits_{j=1}^d e_j \otimes \operatorname*{\mathrm{\sum}}\limits_{i=1}^d a_{ji} \varphi(f_i) \Big) \\ &=\operatorname*{\mathrm{\sum}}\limits_{j=1}^d e_j \otimes \operatorname*{\mathrm{\sum}}\limits_{i=1}^d \partial(a_{ji}) \varphi(f_i) +\operatorname*{\mathrm{\sum}}\limits_{j=1}^d e_j \otimes \operatorname*{\mathrm{\sum}}\limits_{i=1}^d a_{ji}\partial( \varphi(f_i))\\ &\quad{}+ \operatorname*{\mathrm{\sum}}\limits_{k=1}^d e_k \otimes \operatorname*{\mathrm{\sum}} \limits_{i=1}^d \operatorname*{\mathrm{\sum}} \limits_{j=1}^d n_{kj} a_{ji} \varphi(f_i). \end{align*} $$
Because
 $\operatorname {\mathrm {\boldsymbol \mu }}\cdot \sum \limits _{j=1}^d e_j \otimes \sum \limits _{i=1}^d a_{ji}\varphi (\partial (f_i))= \sum \limits _{j=1}^d e_j \otimes \sum \limits _{i=1}^d a_{ji}\partial ( \varphi (f_i))$
, we have that
$\operatorname {\mathrm {\boldsymbol \mu }}\cdot \sum \limits _{j=1}^d e_j \otimes \sum \limits _{i=1}^d a_{ji}\varphi (\partial (f_i))= \sum \limits _{j=1}^d e_j \otimes \sum \limits _{i=1}^d a_{ji}\partial ( \varphi (f_i))$
, we have that
![]() $\operatorname {\mathrm {\boldsymbol \mu }}\cdot g\varphi \circ \Theta _X= \Theta _X \circ g\varphi $
if and only if
$\operatorname {\mathrm {\boldsymbol \mu }}\cdot g\varphi \circ \Theta _X= \Theta _X \circ g\varphi $
if and only if
![]() $\mu A \varphi (N)=\partial (A)+NA$
, i.e.,
$\mu A \varphi (N)=\partial (A)+NA$
, i.e.,
![]() $N=\operatorname {\mathrm {\boldsymbol \mu }} A\varphi (N)A^{-1}-\partial (A)A^{-1}$
. The last equality holds because of the assumption
$N=\operatorname {\mathrm {\boldsymbol \mu }} A\varphi (N)A^{-1}-\partial (A)A^{-1}$
. The last equality holds because of the assumption
![]() $X=\Gamma _g\big (\operatorname {\mathrm {\boldsymbol \mu }}\varphi (X)\big )$
, which completes the proof.▪
$X=\Gamma _g\big (\operatorname {\mathrm {\boldsymbol \mu }}\varphi (X)\big )$
, which completes the proof.▪
As a consequence, we may define a functor
where
![]() $\operatorname {\mathrm {I}}(g,X)(V):= (V_R,g\varphi ,\nabla _X)$
. We next show that this functor is an isomorphism. To do this, we need the following elementary descent result.
$\operatorname {\mathrm {I}}(g,X)(V):= (V_R,g\varphi ,\nabla _X)$
. We next show that this functor is an isomorphism. To do this, we need the following elementary descent result.
Lemma 4.8 Fix a field k, and let A and B be finitely generated k-algebras. Let
![]() $\rho \colon X\to Y$
be a closed embedding of affine algebraic k-schemes for
$\rho \colon X\to Y$
be a closed embedding of affine algebraic k-schemes for
![]() $X=\operatorname {\mathrm {Spec}} A$
and
$X=\operatorname {\mathrm {Spec}} A$
and
![]() $Y=\operatorname {\mathrm {Spec}} B$
. Let
$Y=\operatorname {\mathrm {Spec}} B$
. Let
![]() $\iota \colon S\hookrightarrow \tilde S$
be an embedding in
$\iota \colon S\hookrightarrow \tilde S$
be an embedding in
![]() $\operatorname {\mathrm {\textbf {Alg}}}_k$
. Suppose that we are given an element
$\operatorname {\mathrm {\textbf {Alg}}}_k$
. Suppose that we are given an element
![]() $\tilde z\in X(\tilde S)$
such that
$\tilde z\in X(\tilde S)$
such that
![]() $\rho (\tilde z)\in Y(\iota (S))$
, then there exists a unique element
$\rho (\tilde z)\in Y(\iota (S))$
, then there exists a unique element
![]() $z\in X(S)$
such that
$z\in X(S)$
such that
![]() $\tilde z=X(\iota )(z)$
.
$\tilde z=X(\iota )(z)$
.
Proof We have a diagram

with the outer triangle commutative in which
![]() $\rho ^*$
is surjective. We prove the lemma by constructing a unique k-algebra morphism
$\rho ^*$
is surjective. We prove the lemma by constructing a unique k-algebra morphism
![]() $\alpha \colon A\to S$
such that
$\alpha \colon A\to S$
such that
![]() $\tilde z=\iota \circ \alpha $
, as follows. For any
$\tilde z=\iota \circ \alpha $
, as follows. For any
![]() $a\in A$
, the surjectivity of
$a\in A$
, the surjectivity of
![]() $\rho ^*$
gives us some
$\rho ^*$
gives us some
![]() $b\in B$
such that
$b\in B$
such that
![]() $\rho ^*(b)=a$
. We define
$\rho ^*(b)=a$
. We define
![]() $\alpha (a):= \beta (b)$
. Because
$\alpha (a):= \beta (b)$
. Because
![]() $\iota $
is injective, we have
$\iota $
is injective, we have
![]() $\operatorname {\mathrm {Ker}} \rho ^* \subseteq \operatorname {\mathrm {Ker}} \beta $
, which implies that
$\operatorname {\mathrm {Ker}} \rho ^* \subseteq \operatorname {\mathrm {Ker}} \beta $
, which implies that
![]() $\alpha $
is well-defined. We then have
$\alpha $
is well-defined. We then have
![]() $\tilde z\circ \rho ^*=\iota \circ \beta =\iota \circ \alpha \circ \rho ^*$
, which implies that
$\tilde z\circ \rho ^*=\iota \circ \beta =\iota \circ \alpha \circ \rho ^*$
, which implies that
![]() $\tilde z=\iota \circ \alpha $
, because
$\tilde z=\iota \circ \alpha $
, because
![]() $\rho ^*$
is surjective. Moreover,
$\rho ^*$
is surjective. Moreover,
![]() $\alpha $
is a k-algebra morphism, because
$\alpha $
is a k-algebra morphism, because
![]() $\iota $
is injective and both
$\iota $
is injective and both
![]() $\iota $
and
$\iota $
and
![]() $\tilde z=\iota \circ \alpha $
are k-algebra morphisms. Finally, we see that
$\tilde z=\iota \circ \alpha $
are k-algebra morphisms. Finally, we see that
![]() $\alpha $
is unique, again because
$\alpha $
is unique, again because
![]() $\iota $
is injective.▪
$\iota $
is injective.▪
Proposition 4.9 The functor
![]() $\textbf {B}^{\varphi ,\nabla }(G,R) \to \operatorname {\mathrm {G-\textbf {Mod}^{\varphi ,\nabla }_R}}$
defined in (7) is an isomorphism of categories.
$\textbf {B}^{\varphi ,\nabla }(G,R) \to \operatorname {\mathrm {G-\textbf {Mod}^{\varphi ,\nabla }_R}}$
defined in (7) is an isomorphism of categories.
Proof The proof is similar to that of [Reference Dat, Orlik and Rapoport6, Lemma 9.1.4]. We first show that the functor is fully faithful. Let
![]() $(g,X), (g',X')\in \textbf {B}^{\varphi ,\nabla }(G,R)$
. Then, any morphism
$(g,X), (g',X')\in \textbf {B}^{\varphi ,\nabla }(G,R)$
. Then, any morphism
![]() $\eta \colon \operatorname {\mathrm {I}}(g,x) \to \operatorname {\mathrm {I}}(g',X')$
is an isomorphism according to [Reference Deligne and Milne7, Proposition 1.13] (see also Remark 4.2). By composing
$\eta \colon \operatorname {\mathrm {I}}(g,x) \to \operatorname {\mathrm {I}}(g',X')$
is an isomorphism according to [Reference Deligne and Milne7, Proposition 1.13] (see also Remark 4.2). By composing
![]() $\eta $
with the forgetful functor, we then have an automorphism of the fiber functor
$\eta $
with the forgetful functor, we then have an automorphism of the fiber functor
![]() $\omega ^G\otimes R$
. By Corollary 2.5, this automorphism is given by a unique element
$\omega ^G\otimes R$
. By Corollary 2.5, this automorphism is given by a unique element
![]() $x\in G(R)$
, which then gives an isomorphism between
$x\in G(R)$
, which then gives an isomorphism between
![]() $(g,X)$
and
$(g,X)$
and
![]() $(g',X')$
, as desired.
$(g',X')$
, as desired.
It remains to show that, for any
![]() $\operatorname {\mathrm {I}}\in \operatorname {\mathrm {G-\textbf {Mod}^{\varphi ,\nabla }_R}}$
, there exists a unique
$\operatorname {\mathrm {I}}\in \operatorname {\mathrm {G-\textbf {Mod}^{\varphi ,\nabla }_R}}$
, there exists a unique
![]() $(g,X)\in \textbf {B}^{\varphi ,\nabla }(G,R)$
such that
$(g,X)\in \textbf {B}^{\varphi ,\nabla }(G,R)$
such that
![]() $\operatorname {\mathrm {I}}=\operatorname {\mathrm {I}}(g,X)$
. For any
$\operatorname {\mathrm {I}}=\operatorname {\mathrm {I}}(g,X)$
. For any
![]() $(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, we write
$(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, we write
![]() $\operatorname {\mathrm {I}}(V,\rho _V)=(V_R,\Phi _V,\nabla _V)$
for a
$\operatorname {\mathrm {I}}(V,\rho _V)=(V_R,\Phi _V,\nabla _V)$
for a
![]() $\varphi $
-linear map
$\varphi $
-linear map
![]() $\Phi _V$
and a connection
$\Phi _V$
and a connection
![]() $\nabla _V$
on
$\nabla _V$
on
![]() $V_R$
. The proof consists of two steps.
$V_R$
. The proof consists of two steps.
Step 1: There exists a unique
![]() $X\in \mathfrak {g}_R$
such that
$X\in \mathfrak {g}_R$
such that
![]() $\nabla _V=\nabla _X$
. We write
$\nabla _V=\nabla _X$
. We write
![]() $\Theta _V$
for the composition of
$\Theta _V$
for the composition of
where
![]() $\iota $
is induced by
$\iota $
is induced by
![]() $fdt\mapsto f$
, and put
$fdt\mapsto f$
, and put
![]() $\theta _V:= \Theta _V-\operatorname {\mathrm {Id}}_V\otimes \partial $
. It is clear that
$\theta _V:= \Theta _V-\operatorname {\mathrm {Id}}_V\otimes \partial $
. It is clear that
, where
denotes the trivial representation. Lemma 4.3 then implies that the family
of R-linear endomorphisms satisfies conditions (i–iii) in Corollary 2.9. We thus find a unique
![]() $X\in \mathfrak {g}_R$
such that
$X\in \mathfrak {g}_R$
such that
![]() $\theta _V=\operatorname {\mathrm {Lie}}(\rho _V)(X)$
for all
$\theta _V=\operatorname {\mathrm {Lie}}(\rho _V)(X)$
for all
![]() $(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, which implies that
$(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, which implies that
![]() $\nabla _V=\nabla _X$
.
$\nabla _V=\nabla _X$
.
Step 2: There exists a unique
![]() $g\in G(R)$
such that
$g\in G(R)$
such that
![]() $\Phi _V=g\varphi $
. We put
$\Phi _V=g\varphi $
. We put
![]() $\tilde \Phi _V := \Phi _V\otimes \varphi $
, where
$\tilde \Phi _V := \Phi _V\otimes \varphi $
, where
![]() $\varphi $
is the Frobenius lift on
$\varphi $
is the Frobenius lift on
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
(in particular,
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
(in particular,
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
is viewed as an
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
is viewed as an
![]() $\mathcal {R}$
-module via the
$\mathcal {R}$
-module via the
![]() $\varphi $
-equivariant embedding
$\varphi $
-equivariant embedding
![]() $\psi $
described in Section 2.3). The family
$\psi $
described in Section 2.3). The family
of
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
-linear endomorphisms satisfies conditions (i–) in Theorem 2.4, which provides a unique element
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
-linear endomorphisms satisfies conditions (i–) in Theorem 2.4, which provides a unique element
![]() $\tilde g\in G(\operatorname {\mathrm {\tilde {\mathcal {R}}}})$
such that
$\tilde g\in G(\operatorname {\mathrm {\tilde {\mathcal {R}}}})$
such that
![]() $\lambda _V=\rho _V(\tilde g)$
for all
$\lambda _V=\rho _V(\tilde g)$
for all
![]() $(V,\rho _V) \in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
. We next reduce
$(V,\rho _V) \in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
. We next reduce
![]() $\tilde g$
to an element in
$\tilde g$
to an element in
![]() $G(\mathcal {R})$
. We compute
$G(\mathcal {R})$
. We compute
which implies that
![]() $\tilde \Phi _V(v\otimes f)=\rho _V(\tilde g)(v\otimes \varphi (f))$
, and hence,
$\tilde \Phi _V(v\otimes f)=\rho _V(\tilde g)(v\otimes \varphi (f))$
, and hence,
![]() $\tilde \Phi _V=\tilde g \varphi $
. We now fix a d-dimensional faithful representation
$\tilde \Phi _V=\tilde g \varphi $
. We now fix a d-dimensional faithful representation
![]() $(V,\rho _V)$
, and an F-basis
$(V,\rho _V)$
, and an F-basis
![]() $e_1,\ldots ,e_d$
for V. Suppose that
$e_1,\ldots ,e_d$
for V. Suppose that
 $\Phi _V(e_i)=\sum \limits _{j=1}^d a_{ji}e_j$
, where
$\Phi _V(e_i)=\sum \limits _{j=1}^d a_{ji}e_j$
, where
![]() $a_{ij}\in R$
for all
$a_{ij}\in R$
for all
![]() $1\leq i,j \leq d$
. Put
$1\leq i,j \leq d$
. Put
![]() $A=(a_{ij})_{i,j} \in \operatorname {\mathrm {GL}}_d(R)$
. Then,
$A=(a_{ij})_{i,j} \in \operatorname {\mathrm {GL}}_d(R)$
. Then,
![]() $\psi (A)=(\psi (a_{ij}))_{i,j}\in \operatorname {\mathrm {GL}}_d(\operatorname {\mathrm {\tilde {\mathcal {R}}}})$
describes the
$\psi (A)=(\psi (a_{ij}))_{i,j}\in \operatorname {\mathrm {GL}}_d(\operatorname {\mathrm {\tilde {\mathcal {R}}}})$
describes the
![]() $\varphi $
-linear action of
$\varphi $
-linear action of
![]() $\tilde \Phi _V$
as well as the
$\tilde \Phi _V$
as well as the
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
-linear action
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
-linear action
![]() $\rho (\tilde g)$
in the basis
$\rho (\tilde g)$
in the basis
![]() $e_1\otimes 1,\ldots , e_d \otimes 1$
. By replacing X with G, Y with
$e_1\otimes 1,\ldots , e_d \otimes 1$
. By replacing X with G, Y with
![]() $\operatorname {\mathrm {GL}}_d$
, S with R,
$\operatorname {\mathrm {GL}}_d$
, S with R,
![]() $\tilde S$
with
$\tilde S$
with
![]() $\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
, and
$\operatorname {\mathrm {\tilde {\mathcal {R}}}}$
, and
![]() $\iota $
with
$\iota $
with
![]() $\psi $
in Lemma 4.8, we find a unique element
$\psi $
in Lemma 4.8, we find a unique element
![]() $g\in G(R)$
such that
$g\in G(R)$
such that
![]() $\psi (g)=\tilde g$
. It follows that
$\psi (g)=\tilde g$
. It follows that
![]() $\Phi _V=g\varphi $
, as desired.▪
$\Phi _V=g\varphi $
, as desired.▪
Example 4.10 Let
![]() $d\in \mathbb {N}$
. The affine algebraic F-group
$d\in \mathbb {N}$
. The affine algebraic F-group
![]() $\operatorname {\mathrm {SL}}_d$
is defined by
$\operatorname {\mathrm {SL}}_d$
is defined by
for all
![]() $S\in \operatorname {\mathrm {\textbf {Alg}}}_F$
, whose Lie algebra
$S\in \operatorname {\mathrm {\textbf {Alg}}}_F$
, whose Lie algebra
![]() $\operatorname {\mathrm {\mathfrak {sl}}}_d$
consists of
$\operatorname {\mathrm {\mathfrak {sl}}}_d$
consists of
![]() $d\times d$
matrices with entries in F and with trace zero.
$d\times d$
matrices with entries in F and with trace zero.
-
(i) We claim that any pair
 $(A,N) \in \operatorname {\mathrm {SL}}_d(\mathcal {R}) \times \operatorname {\mathrm {Mat}}_{d,d}(\mathcal {E}^{\dagger })$
satisfying
$(A,N) \in \operatorname {\mathrm {SL}}_d(\mathcal {R}) \times \operatorname {\mathrm {Mat}}_{d,d}(\mathcal {E}^{\dagger })$
satisfying
 $N=\operatorname {\mathrm {\boldsymbol \mu }} A \varphi (N) A^{-1}-\partial (A)A^{-1}$
is already an object in
$N=\operatorname {\mathrm {\boldsymbol \mu }} A \varphi (N) A^{-1}-\partial (A)A^{-1}$
is already an object in
 $\textbf {B}^{\varphi ,\nabla }(\operatorname {\mathrm {SL}}_d,\mathcal {R})$
. It is equivalent to showing that the trace
$\textbf {B}^{\varphi ,\nabla }(\operatorname {\mathrm {SL}}_d,\mathcal {R})$
. It is equivalent to showing that the trace
 $\operatorname {\mathrm {Tr}}(N)$
of N is zero. Recall that the Frobenius lift
$\operatorname {\mathrm {Tr}}(N)$
of N is zero. Recall that the Frobenius lift
 $\varphi $
on
$\varphi $
on
 $\mathcal {E}^{\dagger }$
is given by
$\mathcal {E}^{\dagger }$
is given by
 $\varphi \big (\sum \limits _{i\in \mathbb {Z}} c_it^i \big )=\sum \limits _{i\in \mathbb {Z}} \varphi (c_i) u^i$
, where
$\varphi \big (\sum \limits _{i\in \mathbb {Z}} c_it^i \big )=\sum \limits _{i\in \mathbb {Z}} \varphi (c_i) u^i$
, where
 $u=\varphi (t)$
satisfies
$u=\varphi (t)$
satisfies
 $|u-t^q|_1<1$
. If we write
$|u-t^q|_1<1$
. If we write
 $u=\sum \limits _{i\in \mathbb {Z}} u_it^i, u_i\in K$
, we then have
$u=\sum \limits _{i\in \mathbb {Z}} u_it^i, u_i\in K$
, we then have
 $|u_j|<1$
for all
$|u_j|<1$
for all
 $j \neq q$
and
$j \neq q$
and
 $|u_q|=1$
. It follows that
$|u_q|=1$
. It follows that
 $|\operatorname {\mathrm {\boldsymbol \mu }}|_1=|\partial (u)|_1=|\sum \limits _{i\in \mathbb {Z}} i u_i t^{i-1}|_1 <1$
. On the other hand, we have
$|\operatorname {\mathrm {\boldsymbol \mu }}|_1=|\partial (u)|_1=|\sum \limits _{i\in \mathbb {Z}} i u_i t^{i-1}|_1 <1$
. On the other hand, we have
 $\operatorname {\mathrm {Tr}}\big (\partial (A)A^{-1} \big )=0$
, because
$\operatorname {\mathrm {Tr}}\big (\partial (A)A^{-1} \big )=0$
, because
 $\partial (A)A^{-1} \in \operatorname {\mathrm {\mathfrak {sl}}}_{d,\mathcal {R}}$
(see Construction 4.4). Assume, to the contrary, that
$\partial (A)A^{-1} \in \operatorname {\mathrm {\mathfrak {sl}}}_{d,\mathcal {R}}$
(see Construction 4.4). Assume, to the contrary, that
 $\operatorname {\mathrm {Tr}}(N)\neq 0$
, we have a contradiction (we have the last equality, because
$\operatorname {\mathrm {Tr}}(N)\neq 0$
, we have a contradiction (we have the last equality, because $$ \begin{align*} |\operatorname{\mathrm{Tr}}(N)|_1= |\operatorname{\mathrm{\boldsymbol\mu}} \operatorname{\mathrm{Tr}}(\varphi(N))|_1 = |\operatorname{\mathrm{\boldsymbol\mu}} \varphi(\operatorname{\mathrm{Tr}}(N))|_1 < |\varphi(\operatorname{\mathrm{Tr}}(N))|_1= |\operatorname{\mathrm{Tr}}(N)|_1, \end{align*} $$
$$ \begin{align*} |\operatorname{\mathrm{Tr}}(N)|_1= |\operatorname{\mathrm{\boldsymbol\mu}} \operatorname{\mathrm{Tr}}(\varphi(N))|_1 = |\operatorname{\mathrm{\boldsymbol\mu}} \varphi(\operatorname{\mathrm{Tr}}(N))|_1 < |\varphi(\operatorname{\mathrm{Tr}}(N))|_1= |\operatorname{\mathrm{Tr}}(N)|_1, \end{align*} $$
 $\varphi $
preserves the
$\varphi $
preserves the
 $1$
-Gauss norm on
$1$
-Gauss norm on
 $\mathcal {E}^{\dagger }$
).
$\mathcal {E}^{\dagger }$
).
-
(ii) We use the Bessel isocrystal as described in [Reference Kedlaya12, Example 20.2.1] (see also [Reference Kedlaya9, Section 1.5] and [Reference Tsuzuki24, Example 6.2.6]) to construct an object in
 $\textbf {B}^{\varphi ,\nabla }(\operatorname {\mathrm {SL}}_2,\mathcal {R})$
. We first briefly recall the Bessel isocrystal. In Hypothesis 2.1, we let
$\textbf {B}^{\varphi ,\nabla }(\operatorname {\mathrm {SL}}_2,\mathcal {R})$
. We first briefly recall the Bessel isocrystal. In Hypothesis 2.1, we let
 $q=p$
be an odd prime,
$q=p$
be an odd prime,
 $\kappa =\mathbb {F}_p$
, and
$\kappa =\mathbb {F}_p$
, and
 $F=\mathbb {Q}_p(\pi )$
, where
$F=\mathbb {Q}_p(\pi )$
, where
 $\pi $
is a
$\pi $
is a
 $(p-1)$
st root of
$(p-1)$
st root of
 $-p$
in
$-p$
in
 $\bar {\mathbb {Q}}_p$
. Then, the (p-power) Frobenius on
$\bar {\mathbb {Q}}_p$
. Then, the (p-power) Frobenius on
 $K=F$
is the identity. Let
$K=F$
is the identity. Let
 $\varphi $
be the Frobenius lift on
$\varphi $
be the Frobenius lift on
 $\mathcal {R}$
given by
$\mathcal {R}$
given by
 $\varphi (t)=t^p$
. Then, [Reference Kedlaya12, Example 20.2.1] gives rise to a pair
$\varphi (t)=t^p$
. Then, [Reference Kedlaya12, Example 20.2.1] gives rise to a pair
 $(A_0,N_0)\in \operatorname {\mathrm {GL}}_2(\mathcal {R}) \times \operatorname {\mathrm {Mat}}_{2,2}(\mathcal {E}^{\dagger })$
with
$(A_0,N_0)\in \operatorname {\mathrm {GL}}_2(\mathcal {R}) \times \operatorname {\mathrm {Mat}}_{2,2}(\mathcal {E}^{\dagger })$
with
 $\det (A_0)=p$
satisfying the gauge compatibility condition, in which
$\det (A_0)=p$
satisfying the gauge compatibility condition, in which
 $N_0= \left ( \begin {smallmatrix} 0 & t^{-1}\\ \pi ^2 t^{-2} & 0 \end {smallmatrix}\right ) \in \operatorname {\mathrm {\mathfrak {sl}}}_{2,\mathcal {E}^{\dagger }}.$
We now assume that
$N_0= \left ( \begin {smallmatrix} 0 & t^{-1}\\ \pi ^2 t^{-2} & 0 \end {smallmatrix}\right ) \in \operatorname {\mathrm {\mathfrak {sl}}}_{2,\mathcal {E}^{\dagger }}.$
We now assume that
 $p \equiv 1 (\operatorname {\mathrm {mod}} 4)$
, and
$p \equiv 1 (\operatorname {\mathrm {mod}} 4)$
, and
 $\textbf {i}$
is a square root of
$\textbf {i}$
is a square root of
 $-1$
in
$-1$
in
 $\mathbb {Q}_p$
. Because
$\mathbb {Q}_p$
. Because
 $p-1$
is even, we may set
$p-1$
is even, we may set
 $\alpha := \frac {\textbf {i}}{\pi ^{(p-1)/2}}\in F^{\times }$
. We then have
$\alpha := \frac {\textbf {i}}{\pi ^{(p-1)/2}}\in F^{\times }$
. We then have
 $\alpha ^2=p^{-1}=\det (A_0)^{-1}$
. Put
$\alpha ^2=p^{-1}=\det (A_0)^{-1}$
. Put
 $D_0 = \left ( \begin {smallmatrix} 0 & 1\\ \alpha & 0 \end {smallmatrix}\right ) \in \operatorname {\mathrm {GL}}_2(F).$
Then,
$D_0 = \left ( \begin {smallmatrix} 0 & 1\\ \alpha & 0 \end {smallmatrix}\right ) \in \operatorname {\mathrm {GL}}_2(F).$
Then,
 $D_0A_0D_0\in \operatorname {\mathrm {SL}}_2(\mathcal {R})$
. Moreover, we see that
$D_0A_0D_0\in \operatorname {\mathrm {SL}}_2(\mathcal {R})$
. Moreover, we see that
 $D_0N_0D_0^{-1}=D_0^{-1}N_0 D_0 \in \operatorname {\mathrm {\mathfrak {sl}}}_{2,\mathcal {E}^{\dagger }}$
. Put
$D_0N_0D_0^{-1}=D_0^{-1}N_0 D_0 \in \operatorname {\mathrm {\mathfrak {sl}}}_{2,\mathcal {E}^{\dagger }}$
. Put
 $A := D_0A_0 D_0$
and
$A := D_0A_0 D_0$
and
 $N := D_0 N_0 D_0^{-1}$
. Then, a straightforward verification shows
$N := D_0 N_0 D_0^{-1}$
. Then, a straightforward verification shows
 $N=\operatorname {\mathrm {\boldsymbol \mu }} A \varphi (N)A^{-1}-\partial (A)A^{-1}$
(noting that
$N=\operatorname {\mathrm {\boldsymbol \mu }} A \varphi (N)A^{-1}-\partial (A)A^{-1}$
(noting that
 $\varphi (D_0)=D_0$
and
$\varphi (D_0)=D_0$
and
 $\partial (D_0)=0$
). We thus have
$\partial (D_0)=0$
). We thus have
 $(A,N)\in \textbf {B}^{\varphi ,\nabla }(\operatorname {\mathrm {SL}}_2,\mathcal {R})$
, as desired.
$(A,N)\in \textbf {B}^{\varphi ,\nabla }(\operatorname {\mathrm {SL}}_2,\mathcal {R})$
, as desired. -
(iii) Let
 $(A,N) \in \textbf {B}^{\varphi ,\nabla }(\operatorname {\mathrm {SL}}_d,\mathcal {R})$
. We show that
$(A,N) \in \textbf {B}^{\varphi ,\nabla }(\operatorname {\mathrm {SL}}_d,\mathcal {R})$
. We show that
 $(A,N)$
is“
$(A,N)$
is“
 $\operatorname {\mathrm {SL}}_d$
-quasi-unipotent” (as described in the introduction) by modifying the classical monodromy as follows. By the classical pLMT, we find a finite separable extension L of
$\operatorname {\mathrm {SL}}_d$
-quasi-unipotent” (as described in the introduction) by modifying the classical monodromy as follows. By the classical pLMT, we find a finite separable extension L of
 $\kappa (\!( t )\!)$
and
$\kappa (\!( t )\!)$
and
 $B\in \operatorname {\mathrm {GL}}_d(\mathcal {R}_L)$
such that
$B\in \operatorname {\mathrm {GL}}_d(\mathcal {R}_L)$
such that
 $BNB^{-1}-\partial (B)B^{-1}$
has trace zero being an upper-triangular block matrix with zero blocks in the diagonal. We wish to replace B with an element in
$BNB^{-1}-\partial (B)B^{-1}$
has trace zero being an upper-triangular block matrix with zero blocks in the diagonal. We wish to replace B with an element in
 $\operatorname {\mathrm {SL}}_d(\mathcal {R}_L)$
. To this end, we deduce first that
$\operatorname {\mathrm {SL}}_d(\mathcal {R}_L)$
. To this end, we deduce first that
 $\operatorname {\mathrm {Tr}}(\partial (B)B^{-1})= \operatorname {\mathrm {Tr}}(BNB^{-1})=\operatorname {\mathrm {Tr}}(N)=0$
. It then follows from Jacobi’s formula that
$\operatorname {\mathrm {Tr}}(\partial (B)B^{-1})= \operatorname {\mathrm {Tr}}(BNB^{-1})=\operatorname {\mathrm {Tr}}(N)=0$
. It then follows from Jacobi’s formula that
 $\partial (\det (B))= \det (B) \cdot \operatorname {\mathrm {Tr}}(B^{-1} \partial (B))=0$
. Put
$\partial (\det (B))= \det (B) \cdot \operatorname {\mathrm {Tr}}(B^{-1} \partial (B))=0$
. Put
 $D := \operatorname {\mathrm {Diag}}( \det (B)^{-1},1,\ldots ,1)$
. Then,
$D := \operatorname {\mathrm {Diag}}( \det (B)^{-1},1,\ldots ,1)$
. Then,
 $DB\in \operatorname {\mathrm {SL}}_d(\mathcal {R}_L)$
and
$DB\in \operatorname {\mathrm {SL}}_d(\mathcal {R}_L)$
and
 $\partial (D)=0$
. We then have which is an upper-triangular block matrix with zero blocks, and the sizes of the blocks are the same as those in
$\partial (D)=0$
. We then have which is an upper-triangular block matrix with zero blocks, and the sizes of the blocks are the same as those in $$ \begin{align*} (DB) N (DB)^{-1}- \partial(DB)(DB)^{-1} = D \big( B N B^{-1} -\partial(B)B^{-1} \big) D^{-1}, \end{align*} $$
$$ \begin{align*} (DB) N (DB)^{-1}- \partial(DB)(DB)^{-1} = D \big( B N B^{-1} -\partial(B)B^{-1} \big) D^{-1}, \end{align*} $$
 $B N B^{-1} -\partial (B)B^{-1}$
(the said properties are preserved under conjugation by a diagonal matrix). Hence,
$B N B^{-1} -\partial (B)B^{-1}$
(the said properties are preserved under conjugation by a diagonal matrix). Hence,
 $DB$
is a desired replacement of B and we are done.
$DB$
is a desired replacement of B and we are done.
Example 4.11 For any matrix X, we denote by
![]() $X^{\operatorname {\mathrm {T}}}$
its transpose, and by
$X^{\operatorname {\mathrm {T}}}$
its transpose, and by
![]() $X^{-\operatorname {\mathrm {T}}}$
the inverse of transpose if X is invertible.
$X^{-\operatorname {\mathrm {T}}}$
the inverse of transpose if X is invertible.
We fix the skew-symmetric matrix
![]() $J=\left (\begin {smallmatrix} & & & 1 \\ & & -1 & \\ & 1 & &\\ -1 & & & \end {smallmatrix}\right )$
. The affine algebraic F-group
$J=\left (\begin {smallmatrix} & & & 1 \\ & & -1 & \\ & 1 & &\\ -1 & & & \end {smallmatrix}\right )$
. The affine algebraic F-group
![]() $\operatorname {\mathrm {Sp}}_4$
is defined by
$\operatorname {\mathrm {Sp}}_4$
is defined by
for all
![]() $S\in \operatorname {\mathrm {\textbf {Alg}}}_F$
. We denote by
$S\in \operatorname {\mathrm {\textbf {Alg}}}_F$
. We denote by
![]() $\operatorname {\mathrm {\mathfrak {sp}}}_4$
the Lie algebra of
$\operatorname {\mathrm {\mathfrak {sp}}}_4$
the Lie algebra of
![]() $\operatorname {\mathrm {Sp}}_4$
. For any
$\operatorname {\mathrm {Sp}}_4$
. For any
![]() $S\in \operatorname {\mathrm {\textbf {Alg}}}_F$
, we then have
$S\in \operatorname {\mathrm {\textbf {Alg}}}_F$
, we then have
![]() $\operatorname {\mathrm {\mathfrak {sp}}}_{4,S}=\{X\in \operatorname {\mathrm {Mat}}_{4,4}(S) \mid X=J X^{\operatorname {\mathrm {T}}} J\}$
. We remark that the specific choice of J preserves Borel subgroups under conjugation, which will be useful in the monodromy considered below.
$\operatorname {\mathrm {\mathfrak {sp}}}_{4,S}=\{X\in \operatorname {\mathrm {Mat}}_{4,4}(S) \mid X=J X^{\operatorname {\mathrm {T}}} J\}$
. We remark that the specific choice of J preserves Borel subgroups under conjugation, which will be useful in the monodromy considered below.
Given any
![]() $(\varphi ,\nabla )$
-module over
$(\varphi ,\nabla )$
-module over
![]() $\mathcal {R}$
of rank
$\mathcal {R}$
of rank
![]() $2$
, e.g., the Bessel isocrystal described above, we obtain a pair
$2$
, e.g., the Bessel isocrystal described above, we obtain a pair
![]() $(A_0,N_0)\in \operatorname {\mathrm {GL}}_2(\mathcal {R}) \times \operatorname {\mathrm {Mat}}_{2,2}(\mathcal {R})$
satisfying
$(A_0,N_0)\in \operatorname {\mathrm {GL}}_2(\mathcal {R}) \times \operatorname {\mathrm {Mat}}_{2,2}(\mathcal {R})$
satisfying
![]() $N_0=\operatorname {\mathrm {\boldsymbol \mu }} A_0\varphi (N_0)A_0^{-1}-\partial (A_0)A_0^{-1}$
. Put
$N_0=\operatorname {\mathrm {\boldsymbol \mu }} A_0\varphi (N_0)A_0^{-1}-\partial (A_0)A_0^{-1}$
. Put
 $$ \begin{align*} A := \begin{pmatrix} A_0 & 0 \\ 0 & \left(\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\right)^{-1} A_0^{-\operatorname{\mathrm{T}}} \left(\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\right) \end{pmatrix} ~~~\text{and}~~~ N := \begin{pmatrix} N_0 &0 \\ 0 & \left(\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\right) N_0^{\operatorname{\mathrm{T}}} \left(\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\right) \end{pmatrix}. \end{align*} $$
$$ \begin{align*} A := \begin{pmatrix} A_0 & 0 \\ 0 & \left(\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\right)^{-1} A_0^{-\operatorname{\mathrm{T}}} \left(\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\right) \end{pmatrix} ~~~\text{and}~~~ N := \begin{pmatrix} N_0 &0 \\ 0 & \left(\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\right) N_0^{\operatorname{\mathrm{T}}} \left(\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\right) \end{pmatrix}. \end{align*} $$
A straightforward verification shows that
![]() $A\in \operatorname {\mathrm {Sp}}_4(\mathcal {R}),N\in \operatorname {\mathrm {\mathfrak {sp}}}_{4,\mathcal {R}}$
, and, moreover,
$A\in \operatorname {\mathrm {Sp}}_4(\mathcal {R}),N\in \operatorname {\mathrm {\mathfrak {sp}}}_{4,\mathcal {R}}$
, and, moreover,
![]() $N=\operatorname {\mathrm {\boldsymbol \mu }} A \varphi (N)A^{-1}-\partial (A)A^{-1}$
(noting that
$N=\operatorname {\mathrm {\boldsymbol \mu }} A \varphi (N)A^{-1}-\partial (A)A^{-1}$
(noting that
![]() $\left (\begin {smallmatrix} 0 & 1\\ -1 & 0 \end {smallmatrix}\right )^{-1} =-\left (\begin {smallmatrix} 0 & 1\\ -1 & 0\end {smallmatrix} \right )$
), which implies that
$\left (\begin {smallmatrix} 0 & 1\\ -1 & 0 \end {smallmatrix}\right )^{-1} =-\left (\begin {smallmatrix} 0 & 1\\ -1 & 0\end {smallmatrix} \right )$
), which implies that
![]() $(A,N) \in \textbf {B}^{\varphi ,\nabla }(\operatorname {\mathrm {Sp}}_4,\mathcal {R})$
.
$(A,N) \in \textbf {B}^{\varphi ,\nabla }(\operatorname {\mathrm {Sp}}_4,\mathcal {R})$
.
We next show that
![]() $(A,N)$
is “
$(A,N)$
is “
![]() $\operatorname {\mathrm {Sp}}_4$
-quasi-unipotent.” By the classical pLMT, we find a finite separable extension L of
$\operatorname {\mathrm {Sp}}_4$
-quasi-unipotent.” By the classical pLMT, we find a finite separable extension L of
![]() $\kappa (\!( t )\!)$
and
$\kappa (\!( t )\!)$
and
![]() $B_0 \in \operatorname {\mathrm {GL}}_2(\mathcal {R}_L)$
such that
$B_0 \in \operatorname {\mathrm {GL}}_2(\mathcal {R}_L)$
such that
for some
![]() $n\in \mathcal {R}_L$
(n could be
$n\in \mathcal {R}_L$
(n could be
![]() $0$
). Put
$0$
). Put
 $$ \begin{align*} B := \begin{pmatrix} B_0 & 0 \\ 0 & \left(\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\right)^{-1} B_0^{-\operatorname{\mathrm{T}}} \left(\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\right) \end{pmatrix}. \end{align*} $$
$$ \begin{align*} B := \begin{pmatrix} B_0 & 0 \\ 0 & \left(\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\right)^{-1} B_0^{-\operatorname{\mathrm{T}}} \left(\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\right) \end{pmatrix}. \end{align*} $$
We then have
![]() $B\in \operatorname {\mathrm {Sp}}_4(\mathcal {R}_L)$
, and
$B\in \operatorname {\mathrm {Sp}}_4(\mathcal {R}_L)$
, and
again by straightforward computations.
4.2 The pushforward functor
Let
![]() $R\in \{\mathcal {E}^{\dagger },\mathcal {R}\}$
. For any
$R\in \{\mathcal {E}^{\dagger },\mathcal {R}\}$
. For any
![]() $g\in G(R)$
and
$g\in G(R)$
and
![]() $n\in \mathbb {N}$
, we define
$n\in \mathbb {N}$
, we define
the n-pushforward of g. Notice that
![]() $[n]_*(g)\varphi ^n=(g\varphi )^n\in G(R)\rtimes \operatorname {\mathrm {\langle }}\varphi \operatorname {\mathrm {\rangle }}$
for all
$[n]_*(g)\varphi ^n=(g\varphi )^n\in G(R)\rtimes \operatorname {\mathrm {\langle }}\varphi \operatorname {\mathrm {\rangle }}$
for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
We define the n-pushforward functor by
and
![]() $[n]_*(x)=x$
for all morphisms
$[n]_*(x)=x$
for all morphisms
![]() $x\in \textbf {B}^{\varphi ,\nabla }(G,R)$
. The following lemma shows that this functor is well-defined (in particular, faithful).
$x\in \textbf {B}^{\varphi ,\nabla }(G,R)$
. The following lemma shows that this functor is well-defined (in particular, faithful).
Lemma 4.12 Let
![]() $(g,X)\in \textbf {B}^{\varphi ,\nabla }(G,R)$
. We then have
$(g,X)\in \textbf {B}^{\varphi ,\nabla }(G,R)$
. We then have
![]() $\big ([n]_*(g), X \big )\in \textbf {B}^{\varphi ^n,\nabla }(G,R)$
for all
$\big ([n]_*(g), X \big )\in \textbf {B}^{\varphi ^n,\nabla }(G,R)$
for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Proof We show by induction on n that
There is nothing to show when
![]() $n=1$
. We now assume by the induction hypothesis that
$n=1$
. We now assume by the induction hypothesis that
We notice that
![]() $\operatorname {\mathrm {\boldsymbol \mu }}(\varphi ^{n-1},t)=\operatorname {\mathrm {\boldsymbol \mu }}\varphi (\operatorname {\mathrm {\boldsymbol \mu }})\cdots \varphi ^{n-2}(\operatorname {\mathrm {\boldsymbol \mu }})$
, and hence,
$\operatorname {\mathrm {\boldsymbol \mu }}(\varphi ^{n-1},t)=\operatorname {\mathrm {\boldsymbol \mu }}\varphi (\operatorname {\mathrm {\boldsymbol \mu }})\cdots \varphi ^{n-2}(\operatorname {\mathrm {\boldsymbol \mu }})$
, and hence,
which implies that
On the other hand, because
![]() $X+\operatorname {\mathrm {dlog}}(g)=\operatorname {\mathrm {\boldsymbol \mu }} \operatorname {\mathrm {Ad}}(g)(\varphi (X))$
, we have
$X+\operatorname {\mathrm {dlog}}(g)=\operatorname {\mathrm {\boldsymbol \mu }} \operatorname {\mathrm {Ad}}(g)(\varphi (X))$
, we have
We now compute
 $$ \begin{align*} X+\operatorname{\mathrm{dlog}}\big([n]_*(g)\big) &=X+\operatorname{\mathrm{dlog}}\big([n-1]_*(g)\big)+\operatorname{\mathrm{Ad}}\big([n-1]_*(g)\big)\big(\operatorname{\mathrm{dlog}}(\varphi^{n-1}(g))\big)\\ &=\operatorname{\mathrm{\boldsymbol\mu}}(\varphi^{n-1},t)\operatorname{\mathrm{Ad}}\big([n-1]_*(g)\big) \big(\varphi^{n-1}(X)\big)\\ &\;\;\;\; +\operatorname{\mathrm{\boldsymbol\mu}}(\varphi^{n-1},t)\operatorname{\mathrm{Ad}}\big([n-1]_*(g)\big) \big(\varphi^{n-1}(\operatorname{\mathrm{dlog}}(g)) \big)\\ &=\operatorname{\mathrm{\boldsymbol\mu}}(\varphi^{n-1},t) \operatorname{\mathrm{Ad}}\big([n-1]_*(g)\big) \big(\varphi^{n-1}(X)+\varphi^{n-1}(\operatorname{\mathrm{dlog}}(g)) \big)\\ &= \operatorname{\mathrm{\boldsymbol\mu}}(\varphi^{n-1},t)\operatorname{\mathrm{Ad}}\big([n-1]_*(g)\big) \big(\varphi^{n-1}(\operatorname{\mathrm{\boldsymbol\mu}})\operatorname{\mathrm{Ad}}\big(\varphi^{n-1}(g)\big)\big(\varphi^n(X)\big)\big)\\ &=\operatorname{\mathrm{\boldsymbol\mu}}(\varphi^n,t) \operatorname{\mathrm{Ad}}\big([n]_*(g)\big)\big(\varphi^{n}(X)\big), \end{align*} $$
$$ \begin{align*} X+\operatorname{\mathrm{dlog}}\big([n]_*(g)\big) &=X+\operatorname{\mathrm{dlog}}\big([n-1]_*(g)\big)+\operatorname{\mathrm{Ad}}\big([n-1]_*(g)\big)\big(\operatorname{\mathrm{dlog}}(\varphi^{n-1}(g))\big)\\ &=\operatorname{\mathrm{\boldsymbol\mu}}(\varphi^{n-1},t)\operatorname{\mathrm{Ad}}\big([n-1]_*(g)\big) \big(\varphi^{n-1}(X)\big)\\ &\;\;\;\; +\operatorname{\mathrm{\boldsymbol\mu}}(\varphi^{n-1},t)\operatorname{\mathrm{Ad}}\big([n-1]_*(g)\big) \big(\varphi^{n-1}(\operatorname{\mathrm{dlog}}(g)) \big)\\ &=\operatorname{\mathrm{\boldsymbol\mu}}(\varphi^{n-1},t) \operatorname{\mathrm{Ad}}\big([n-1]_*(g)\big) \big(\varphi^{n-1}(X)+\varphi^{n-1}(\operatorname{\mathrm{dlog}}(g)) \big)\\ &= \operatorname{\mathrm{\boldsymbol\mu}}(\varphi^{n-1},t)\operatorname{\mathrm{Ad}}\big([n-1]_*(g)\big) \big(\varphi^{n-1}(\operatorname{\mathrm{\boldsymbol\mu}})\operatorname{\mathrm{Ad}}\big(\varphi^{n-1}(g)\big)\big(\varphi^n(X)\big)\big)\\ &=\operatorname{\mathrm{\boldsymbol\mu}}(\varphi^n,t) \operatorname{\mathrm{Ad}}\big([n]_*(g)\big)\big(\varphi^{n}(X)\big), \end{align*} $$
which proves the lemma.▪
In connection with the pushforward functor on
![]() $\varphi $
-modules as recalled in Section 2.3, we state the following lemma resulting from [Reference Kedlaya11, Lemma 1.6.3 and Remark 1.7.2], which will not be explicitly used in the sequel.
$\varphi $
-modules as recalled in Section 2.3, we state the following lemma resulting from [Reference Kedlaya11, Lemma 1.6.3 and Remark 1.7.2], which will not be explicitly used in the sequel.
Lemma 4.13 Let
![]() $g\in G(R)$
. Then,
$g\in G(R)$
. Then,
![]() $(V_R,g\varphi )$
is pure of slope
$(V_R,g\varphi )$
is pure of slope
![]() $\mu $
if and only if
$\mu $
if and only if
![]() $(V_R,[n]_*(g)\varphi ^n)$
is pure of slope
$(V_R,[n]_*(g)\varphi ^n)$
is pure of slope
![]() $n\mu $
for all
$n\mu $
for all
![]() $n\in \mathbb {N}$
. Moreover, if
$n\in \mathbb {N}$
. Moreover, if
![]() $(V_R,g\varphi )$
has jumps
$(V_R,g\varphi )$
has jumps
![]() $\mu _1,\ldots ,\mu _l$
, then
$\mu _1,\ldots ,\mu _l$
, then
![]() $(V_R,[n]_*(g)\varphi ^n)$
has jumps
$(V_R,[n]_*(g)\varphi ^n)$
has jumps
![]() $n\mu _1,\ldots ,n\mu _l$
.
$n\mu _1,\ldots ,n\mu _l$
.
4.3
G-
 $\varphi $
-modules attached to splittings
$\varphi $
-modules attached to splittings
Let
![]() $g\in G(\mathcal {R})$
. We fix a splitting
$g\in G(\mathcal {R})$
. We fix a splitting
![]() $\xi _g$
of
$\xi _g$
of
![]() $\operatorname {\mathrm {{HN}}}_g$
by Theorem 3.12.
$\operatorname {\mathrm {{HN}}}_g$
by Theorem 3.12.
Construction 4.14 Let
![]() $(V_{\mathcal {R}},g\varphi ,\nabla _X)$
be a
$(V_{\mathcal {R}},g\varphi ,\nabla _X)$
be a
![]() $(\varphi ,\nabla )$
-module over
$(\varphi ,\nabla )$
-module over
![]() $\mathcal {R}$
with the slope filtration
$\mathcal {R}$
with the slope filtration
with jumps
![]() $\mu _1<\cdots <\mu _l$
. Then,
$\mu _1<\cdots <\mu _l$
. Then,
![]() $\xi _g(V)$
is the decomposition
$\xi _g(V)$
is the decomposition
 $$ \begin{align*} V_{\mathcal{R}}=\operatorname*{\mathrm{\bigoplus}}\limits_{i=1}^l V_{\mathcal{R},\mu_i}\end{align*} $$
$$ \begin{align*} V_{\mathcal{R}}=\operatorname*{\mathrm{\bigoplus}}\limits_{i=1}^l V_{\mathcal{R},\mu_i}\end{align*} $$
of
![]() $\mathcal {R}$
-modules such that
$\mathcal {R}$
-modules such that
![]() $\bigoplus \limits _{i=1}^j V_{\mathcal {R},\mu _i} =V_{\mathcal {R}}^{\mu _j}$
for
$\bigoplus \limits _{i=1}^j V_{\mathcal {R},\mu _i} =V_{\mathcal {R}}^{\mu _j}$
for
![]() $j=1,\ldots ,l$
.
$j=1,\ldots ,l$
.
-
(i) For any
 $1\leq j\leq l$
and
$1\leq j\leq l$
and
 $\textbf {v}\in V_{\mathcal {R},\mu _j}$
, we have
$\textbf {v}\in V_{\mathcal {R},\mu _j}$
, we have
 $\Phi _g(\textbf {v})\in V_{\mathcal {R}}^{\mu _j}$
, whence a unique expression
$\Phi _g(\textbf {v})\in V_{\mathcal {R}}^{\mu _j}$
, whence a unique expression
 $\Phi _g(\textbf {v})=\operatorname *{\mathrm {\sum }}\limits _{i=1}^j \textbf {v}_i$
with
$\Phi _g(\textbf {v})=\operatorname *{\mathrm {\sum }}\limits _{i=1}^j \textbf {v}_i$
with
 $\textbf {v}_i\in V_{\mathcal {R},\mu _i}$
. We thus have a
$\textbf {v}_i\in V_{\mathcal {R},\mu _i}$
. We thus have a
 $\varphi $
-linear map We then define
$\varphi $
-linear map We then define $$ \begin{align*}\Phi_{g,\mu_j} \colon V_{\mathcal{R},\mu_j} \operatorname{\mathrm{\longrightarrow}} V_{\mathcal{R},\mu_j},~~~~ \textbf{v} \longmapsto \textbf{v}_j.\end{align*} $$
$$ \begin{align*}\Phi_{g,\mu_j} \colon V_{\mathcal{R},\mu_j} \operatorname{\mathrm{\longrightarrow}} V_{\mathcal{R},\mu_j},~~~~ \textbf{v} \longmapsto \textbf{v}_j.\end{align*} $$
 $\Phi _g':= \bigoplus \limits _{i=1}^l \Phi _{g,{\mu _i}}$
. We define For a morphism
$\Phi _g':= \bigoplus \limits _{i=1}^l \Phi _{g,{\mu _i}}$
. We define For a morphism $$ \begin{align*}\operatorname{\mathrm{I}}'(g)(V):= (V_{\mathcal{R}},\Phi_g').\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{I}}'(g)(V):= (V_{\mathcal{R}},\Phi_g').\end{align*} $$
 $\alpha \colon V\to W$
of finite-dimensional G-modules, we define
$\alpha \colon V\to W$
of finite-dimensional G-modules, we define
 $\operatorname {\mathrm {I}}'(g)(\alpha ):= \alpha _{\mathcal {R}}$
.
$\operatorname {\mathrm {I}}'(g)(\alpha ):= \alpha _{\mathcal {R}}$
.
-
(ii) Similarly, for any
 $1\leq j\leq l$
and
$1\leq j\leq l$
and
 $\textbf {v}\in V_{\mathcal {R},\mu _j}$
, we have
$\textbf {v}\in V_{\mathcal {R},\mu _j}$
, we have
 $\Theta _X(\textbf {v})\in V_{\mathcal {R}}^{\mu _j}$
, whence a unique expression
$\Theta _X(\textbf {v})\in V_{\mathcal {R}}^{\mu _j}$
, whence a unique expression
 $\Theta _X(\textbf {v})=\sum _{i=1}^j \textbf {v}_i$
with
$\Theta _X(\textbf {v})=\sum _{i=1}^j \textbf {v}_i$
with
 $\textbf {v}_i\in V_{\mathcal {R},\mu _i}$
. We thus have a K-linear differential operator We then define
$\textbf {v}_i\in V_{\mathcal {R},\mu _i}$
. We thus have a K-linear differential operator We then define $$ \begin{align*}\Theta_{X,\mu_j} \colon V_{\mathcal{R},\mu_j} \operatorname{\mathrm{\longrightarrow}} V_{\mathcal{R},\mu_j},~~~~ \textbf{v} \longmapsto \textbf{v}_j.\end{align*} $$
$$ \begin{align*}\Theta_{X,\mu_j} \colon V_{\mathcal{R},\mu_j} \operatorname{\mathrm{\longrightarrow}} V_{\mathcal{R},\mu_j},~~~~ \textbf{v} \longmapsto \textbf{v}_j.\end{align*} $$
 $\Theta _X':= \bigoplus \limits _{i=1}^l \Theta _{X,{\mu _i}}$
.
$\Theta _X':= \bigoplus \limits _{i=1}^l \Theta _{X,{\mu _i}}$
.
Notice that
![]() $\big ( V_{\mathcal {R},\mu _1},\Phi _{g,{\mu _1}}\big )=\big ( V_{\mathcal {R}}^{\mu _1},\Phi _g|_{V_{\mathcal {R}}^{\mu _1}} \big )$
, and
$\big ( V_{\mathcal {R},\mu _1},\Phi _{g,{\mu _1}}\big )=\big ( V_{\mathcal {R}}^{\mu _1},\Phi _g|_{V_{\mathcal {R}}^{\mu _1}} \big )$
, and
![]() $\big ( V_{\mathcal {R},\mu _i},\Phi _{g,{\mu _i}}\big )$
is isomorphic to
$\big ( V_{\mathcal {R},\mu _i},\Phi _{g,{\mu _i}}\big )$
is isomorphic to
![]() $V_{\mathcal {R}}^{\mu _i}/V_{\mathcal {R}}^{\mu _{i-1}}$
as
$V_{\mathcal {R}}^{\mu _i}/V_{\mathcal {R}}^{\mu _{i-1}}$
as
![]() $\varphi $
-modules for
$\varphi $
-modules for
![]() $2\leq i\leq l$
. Similarly, we have
$2\leq i\leq l$
. Similarly, we have
![]() $\big ( V_{\mathcal {R},\mu _1},\Theta _{X,{\mu _1}} \big )=\big ( V_{\mathcal {R}}^{\mu _1},\Theta _X|_{V_{\mathcal {R}}^{\mu _1}} \big )$
, and
$\big ( V_{\mathcal {R},\mu _1},\Theta _{X,{\mu _1}} \big )=\big ( V_{\mathcal {R}}^{\mu _1},\Theta _X|_{V_{\mathcal {R}}^{\mu _1}} \big )$
, and
![]() $\big ( V_{\mathcal {R},\mu _i},\Theta _{X,\mu _i}\big )$
is isomorphic to
$\big ( V_{\mathcal {R},\mu _i},\Theta _{X,\mu _i}\big )$
is isomorphic to
![]() $V_{\mathcal {R}}^{\mu _i}/V_{\mathcal {R}}^{\mu _{i-1}}$
as a differential module for
$V_{\mathcal {R}}^{\mu _i}/V_{\mathcal {R}}^{\mu _{i-1}}$
as a differential module for
![]() $2\leq i\leq l$
.
$2\leq i\leq l$
.
The remainder of this subsection is devoted to the consequences of Construction 4.14 (i). We will continue to discuss (ii) in Section 4.4; we will show, in particular, that both constructions assemble to give a G-
![]() $(\varphi ,\nabla )$
-module over
$(\varphi ,\nabla )$
-module over
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
Lemma 4.15
![]() $\operatorname {\mathrm {I}}'(g) \colon \operatorname {\mathrm {\textbf {Rep}}}_F(G) \to \varphi \text {-}\operatorname {\mathrm {\textbf {Mod}}}_{\mathcal {R}}$
is a G-
$\operatorname {\mathrm {I}}'(g) \colon \operatorname {\mathrm {\textbf {Rep}}}_F(G) \to \varphi \text {-}\operatorname {\mathrm {\textbf {Mod}}}_{\mathcal {R}}$
is a G-
![]() $\varphi $
-module over
$\varphi $
-module over
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
Proof By Definition 3.1, it amounts to show that
![]() $\operatorname {\mathrm {I}}'(g)$
is an exact faithful F-linear tensor functor. In this proof, we fix
$\operatorname {\mathrm {I}}'(g)$
is an exact faithful F-linear tensor functor. In this proof, we fix
![]() $V,W\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, and suppose the slope filtration of
$V,W\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, and suppose the slope filtration of
![]() $(V_{\mathcal {R}},g\varphi )$
(resp. of
$(V_{\mathcal {R}},g\varphi )$
(resp. of
![]() $(W_{\mathcal {R}},g\varphi )$
) has jumps
$(W_{\mathcal {R}},g\varphi )$
) has jumps
![]() $\mu _1<\cdots <\mu _{l_V}$
(resp.
$\mu _1<\cdots <\mu _{l_V}$
(resp.
![]() $\nu _1<\cdots <\nu _{l_W}$
).
$\nu _1<\cdots <\nu _{l_W}$
).
We first check the functoriality of
![]() $\operatorname {\mathrm {I}}'(g)$
(the exactness, faithfulness, and F-linearity will follow immediately). Given
$\operatorname {\mathrm {I}}'(g)$
(the exactness, faithfulness, and F-linearity will follow immediately). Given
![]() $\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
, we need to show that
$\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
, we need to show that
For any fixed
![]() $1\leq l \leq {l_V}$
, we have that
$1\leq l \leq {l_V}$
, we have that
![]() $\alpha _{\mathcal {R}}(V_{\mathcal {R},\mu _l})\subseteq W_{\mathcal {R},\mu _l}$
by Theorem 3.12. Notice that
$\alpha _{\mathcal {R}}(V_{\mathcal {R},\mu _l})\subseteq W_{\mathcal {R},\mu _l}$
by Theorem 3.12. Notice that
![]() $W_{\mathcal {R},\mu _l}=W_{\mathcal {R},\nu _s}$
if
$W_{\mathcal {R},\mu _l}=W_{\mathcal {R},\nu _s}$
if
![]() $\mu _l=\nu _s$
for some
$\mu _l=\nu _s$
for some
![]() $1\leq s\leq {l_W}$
, and
$1\leq s\leq {l_W}$
, and
![]() $W_{\mathcal {R},\mu _l}=0$
otherwise. In the latter case, it is clear that
$W_{\mathcal {R},\mu _l}=0$
otherwise. In the latter case, it is clear that
![]() $\alpha _{\mathcal {R}}\circ \Phi _g'=\Phi _g'\circ \alpha _{\mathcal {R}}=0$
on
$\alpha _{\mathcal {R}}\circ \Phi _g'=\Phi _g'\circ \alpha _{\mathcal {R}}=0$
on
![]() $V_{\mathcal {R},\mu _l}$
, and we are done. Suppose now we are in the former case. Let
$V_{\mathcal {R},\mu _l}$
, and we are done. Suppose now we are in the former case. Let
![]() $\textbf {v}$
be a nonzero element in
$\textbf {v}$
be a nonzero element in
![]() $V_{\mathcal {R},\mu _l}$
. We then have
$V_{\mathcal {R},\mu _l}$
. We then have
![]() $\Phi _g(\textbf {v})\in V_{\mathcal {R}}^{\mu _l}$
and
$\Phi _g(\textbf {v})\in V_{\mathcal {R}}^{\mu _l}$
and
![]() $\alpha _{\mathcal {R}}(\textbf {v})\in W_{\mathcal {R},\nu _s}$
. We have unique expressions
$\alpha _{\mathcal {R}}(\textbf {v})\in W_{\mathcal {R},\nu _s}$
. We have unique expressions
 $$ \begin{align*} \Phi_g(\textbf{v})= \operatorname*{\mathrm{\sum}}\limits_{i=1}^l \textbf{v}_i,~~~~~\textbf{v}_i\in V_{\mathcal{R},\mu_i},\end{align*} $$
$$ \begin{align*} \Phi_g(\textbf{v})= \operatorname*{\mathrm{\sum}}\limits_{i=1}^l \textbf{v}_i,~~~~~\textbf{v}_i\in V_{\mathcal{R},\mu_i},\end{align*} $$
and
 $$ \begin{align*} \alpha_{\mathcal{R}}\circ\Phi_g(\textbf{v})=\operatorname*{\mathrm{\sum}}\limits_{i=1}^s \textbf{w}_i,~~~~~\textbf{w}_i\in W_{\mathcal{R},\nu_i};\end{align*} $$
$$ \begin{align*} \alpha_{\mathcal{R}}\circ\Phi_g(\textbf{v})=\operatorname*{\mathrm{\sum}}\limits_{i=1}^s \textbf{w}_i,~~~~~\textbf{w}_i\in W_{\mathcal{R},\nu_i};\end{align*} $$
therefore
![]() $\alpha _{\mathcal {R}}(\textbf {v}_l)=\textbf {w}_s$
. We also write
$\alpha _{\mathcal {R}}(\textbf {v}_l)=\textbf {w}_s$
. We also write
 $$ \begin{align*} \Phi_g\circ \alpha_{\mathcal{R}}(\textbf{v})=\operatorname*{\mathrm{\sum}}\limits_{i=1}^s \textbf{w}_i', \;\;\;\textbf{w}_i'\in W_{\mathcal{R},\nu_i};\end{align*} $$
$$ \begin{align*} \Phi_g\circ \alpha_{\mathcal{R}}(\textbf{v})=\operatorname*{\mathrm{\sum}}\limits_{i=1}^s \textbf{w}_i', \;\;\;\textbf{w}_i'\in W_{\mathcal{R},\nu_i};\end{align*} $$
we then have
![]() $\textbf {w}_i=\textbf {w}_i'$
for
$\textbf {w}_i=\textbf {w}_i'$
for
![]() $i=1,\ldots ,s$
, as
$i=1,\ldots ,s$
, as
![]() $\alpha _{\mathcal {R}}\circ \Phi _g=\Phi _g\circ \alpha _{\mathcal {R}}$
. We thus have
$\alpha _{\mathcal {R}}\circ \Phi _g=\Phi _g\circ \alpha _{\mathcal {R}}$
. We thus have
![]() $\alpha _{\mathcal {R}}\circ \Phi _{g,{\mu _l}}(\textbf {v})=\alpha _{\mathcal {R}}(\textbf {v}_l)=\textbf {w}_s$
and
$\alpha _{\mathcal {R}}\circ \Phi _{g,{\mu _l}}(\textbf {v})=\alpha _{\mathcal {R}}(\textbf {v}_l)=\textbf {w}_s$
and
![]() $\Phi _{g,{\nu _s}}\circ \alpha _{\mathcal {R}}(\textbf {v})= \textbf {w}_s'=\textbf {w}_s$
, which implies that
$\Phi _{g,{\nu _s}}\circ \alpha _{\mathcal {R}}(\textbf {v})= \textbf {w}_s'=\textbf {w}_s$
, which implies that
![]() $\alpha _{\mathcal {R}}\circ \Phi _{g,{\mu _l}}=\Phi _{g,{\nu _s}}\circ \alpha _{\mathcal {R}}$
, as desired.
$\alpha _{\mathcal {R}}\circ \Phi _{g,{\mu _l}}=\Phi _{g,{\nu _s}}\circ \alpha _{\mathcal {R}}$
, as desired.
It remains to show that
![]() $\operatorname {\mathrm {I}}'(g)$
preserves tensor products. Because
$\operatorname {\mathrm {I}}'(g)$
preserves tensor products. Because
![]() $\tau _g$
is a tensor functor, the
$\tau _g$
is a tensor functor, the
![]() $(\mu _l+\nu _s)$
th graded piece of
$(\mu _l+\nu _s)$
th graded piece of
![]() $\tau _g(V\otimes W)$
is then
$\tau _g(V\otimes W)$
is then
 $$ \begin{align*} \big(V\bigotimes\limits_F W \big)_{\mathcal{R},\mu_l+\nu_s}= \operatorname*{\mathrm{\bigoplus}}\limits_{\scriptstyle \begin{array}{c}\mu_i+\nu_j=\mu_l+\nu_s \\ 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\end{array}} \big( V_{\mathcal{R},\mu_i}\bigotimes\limits_{\mathcal{R}} W_{\mathcal{R},\nu_j } \big),\end{align*} $$
$$ \begin{align*} \big(V\bigotimes\limits_F W \big)_{\mathcal{R},\mu_l+\nu_s}= \operatorname*{\mathrm{\bigoplus}}\limits_{\scriptstyle \begin{array}{c}\mu_i+\nu_j=\mu_l+\nu_s \\ 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\end{array}} \big( V_{\mathcal{R},\mu_i}\bigotimes\limits_{\mathcal{R}} W_{\mathcal{R},\nu_j } \big),\end{align*} $$
for all
![]() $1\leq l\leq l_V$
and
$1\leq l\leq l_V$
and
![]() $1\leq s \leq l_W$
. It then follows from Construction 4.14(i) that
$1\leq s \leq l_W$
. It then follows from Construction 4.14(i) that
 $$ \begin{align*} \Phi^{\prime}_{g,\mu_l+\nu_s}=\operatorname*{\mathrm{\bigoplus}}\limits_{\scriptstyle \begin{array}{c} \mu_i+\nu_j=\mu_l+\nu_s \\ 1\leq i\leq {l_V},1\leq j\leq {l_W}\end{array}} \big(\Phi^{\prime}_{g,\mu_i} \otimes \Phi^{\prime}_{g,\nu_j}\big),\end{align*} $$
$$ \begin{align*} \Phi^{\prime}_{g,\mu_l+\nu_s}=\operatorname*{\mathrm{\bigoplus}}\limits_{\scriptstyle \begin{array}{c} \mu_i+\nu_j=\mu_l+\nu_s \\ 1\leq i\leq {l_V},1\leq j\leq {l_W}\end{array}} \big(\Phi^{\prime}_{g,\mu_i} \otimes \Phi^{\prime}_{g,\nu_j}\big),\end{align*} $$
which implies that
![]() $\operatorname {\mathrm {I}}'(g)(V\bigotimes W)$
coincides with
$\operatorname {\mathrm {I}}'(g)(V\bigotimes W)$
coincides with
![]() $\operatorname {\mathrm {I}}'(g)(V)\bigotimes \operatorname {\mathrm {I}}'(g)(W)$
on all
$\operatorname {\mathrm {I}}'(g)(V)\bigotimes \operatorname {\mathrm {I}}'(g)(W)$
on all
![]() $(V\bigotimes W)_{\mathcal {R},\mu _l+\nu _s}$
, whence on
$(V\bigotimes W)_{\mathcal {R},\mu _l+\nu _s}$
, whence on
![]() $(V\bigotimes W)_{\mathcal {R}}$
. This completes the proof.▪
$(V\bigotimes W)_{\mathcal {R}}$
. This completes the proof.▪
With Lemma 4.15, we imitate Step 2 in the proof of Proposition 4.9 and have the following proposition.
Proposition 4.16 There exists a unique element
![]() $z\in G(\mathcal {R})$
such that
$z\in G(\mathcal {R})$
such that
![]() $\operatorname {\mathrm {I}}'(g)=\operatorname {\mathrm {I}}(z)$
.
$\operatorname {\mathrm {I}}'(g)=\operatorname {\mathrm {I}}(z)$
.
4.4
G-
 $(\varphi ,\nabla )$
-modules attached to splittings
$(\varphi ,\nabla )$
-modules attached to splittings
We fix
![]() $(g,X)\in \textbf {B}^{\varphi ,\nabla }(G,\mathcal {R})$
. We also fix a splitting
$(g,X)\in \textbf {B}^{\varphi ,\nabla }(G,\mathcal {R})$
. We also fix a splitting
![]() $\xi _g$
of
$\xi _g$
of
![]() $\operatorname {\mathrm {{HN}}}_g$
given by Theorem 3.12.
$\operatorname {\mathrm {{HN}}}_g$
given by Theorem 3.12.
We now look back at Construction 4.14(ii). We claim that
![]() $\Theta _X'-\operatorname {\mathrm {Id}}_V\otimes \partial \colon V_R \to V_R$
is R-linear for all
$\Theta _X'-\operatorname {\mathrm {Id}}_V\otimes \partial \colon V_R \to V_R$
is R-linear for all
![]() $(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
. Let
$(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
. Let
![]() $1\leq j\leq l$
and let
$1\leq j\leq l$
and let
![]() $v\otimes f\in V_{\mathcal {R},\mu _j}$
. Suppose that
$v\otimes f\in V_{\mathcal {R},\mu _j}$
. Suppose that
![]() $\Theta _X(v\otimes f)=\operatorname *{\mathrm {\sum }}_{i=1}^j \textbf {v}_i$
with
$\Theta _X(v\otimes f)=\operatorname *{\mathrm {\sum }}_{i=1}^j \textbf {v}_i$
with
![]() $\textbf {v}_i\in V_{\mathcal {R},\mu _i}$
. Then,
$\textbf {v}_i\in V_{\mathcal {R},\mu _i}$
. Then,
![]() $\Theta _X'(v\otimes f)=\textbf {v}_j$
by construction. Let
$\Theta _X'(v\otimes f)=\textbf {v}_j$
by construction. Let
![]() $f'\in R$
. We compute
$f'\in R$
. We compute
 $$ \begin{align*} \Theta^{\prime}_X(v\otimes ff') &=v\otimes \partial(f)f'+v\otimes f\partial(f')+X (v\otimes ff')\\ &= \big( v\otimes \partial(f)+ X(v\otimes f) \big)f'+v\otimes f\partial(f')\\ &= \Theta^{\prime}_X(v\otimes f)f' +v\otimes f\partial(f')\\ &=f' \operatorname*{\mathrm{\sum}}_{i=1}^j \textbf{v}_i+v\otimes f\partial(f'), \end{align*} $$
$$ \begin{align*} \Theta^{\prime}_X(v\otimes ff') &=v\otimes \partial(f)f'+v\otimes f\partial(f')+X (v\otimes ff')\\ &= \big( v\otimes \partial(f)+ X(v\otimes f) \big)f'+v\otimes f\partial(f')\\ &= \Theta^{\prime}_X(v\otimes f)f' +v\otimes f\partial(f')\\ &=f' \operatorname*{\mathrm{\sum}}_{i=1}^j \textbf{v}_i+v\otimes f\partial(f'), \end{align*} $$
which implies that
![]() $\Theta ^{\prime }_X(v\otimes ff')=f'\textbf {v}_j+v\otimes f\partial (f')$
. We thus have
$\Theta ^{\prime }_X(v\otimes ff')=f'\textbf {v}_j+v\otimes f\partial (f')$
. We thus have
 $$ \begin{align*} (\Theta_X'-\operatorname{\mathrm{Id}}_V\otimes \partial)(v\otimes ff') &=f'\textbf{v}_j+v\otimes f\partial(f')- v\otimes \partial(ff')\\ &= f'\textbf{v}_j+v\otimes f\partial(f')-v\otimes \partial(f)f'-v\otimes f\partial(f')\\ &=f' (\textbf{v}_j-v\otimes \partial(f))\\ &= f' (\Theta_X'-\operatorname{\mathrm{Id}}_V\otimes \partial)(v\otimes f), \end{align*} $$
$$ \begin{align*} (\Theta_X'-\operatorname{\mathrm{Id}}_V\otimes \partial)(v\otimes ff') &=f'\textbf{v}_j+v\otimes f\partial(f')- v\otimes \partial(ff')\\ &= f'\textbf{v}_j+v\otimes f\partial(f')-v\otimes \partial(f)f'-v\otimes f\partial(f')\\ &=f' (\textbf{v}_j-v\otimes \partial(f))\\ &= f' (\Theta_X'-\operatorname{\mathrm{Id}}_V\otimes \partial)(v\otimes f), \end{align*} $$
as desired.
The following proposition (and its proof) is analogous to Lemma 4.15.
Proposition 4.17 There exists a unique element
![]() $X_0\in \mathfrak {g}_{\mathcal {R}}$
such that
$X_0\in \mathfrak {g}_{\mathcal {R}}$
such that
![]() $\Theta _X'=\Theta _{X_0}$
.
$\Theta _X'=\Theta _{X_0}$
.
Proof For any
![]() $(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, we define
$(V,\rho _V)\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, we define
![]() $\theta _V:= \Theta _X'-\operatorname {\mathrm {Id}}_V\otimes \partial $
. We claim that the family
$\theta _V:= \Theta _X'-\operatorname {\mathrm {Id}}_V\otimes \partial $
. We claim that the family
of R-linear endomorphisms satisfies conditions (i–iii) in Corollary 2.9. The lemma will follow immediately.
It is clear that
![]() $\theta _V=0$
if
$\theta _V=0$
if
![]() $V=F$
is the trivial G-representation. For the remainder of the proof, we fix
$V=F$
is the trivial G-representation. For the remainder of the proof, we fix
![]() $(V,\rho _V),(W,\rho _W)\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, and suppose the slope filtration of
$(V,\rho _V),(W,\rho _W)\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, and suppose the slope filtration of
![]() $(V_{\mathcal {R}},g\varphi )$
(resp. of
$(V_{\mathcal {R}},g\varphi )$
(resp. of
![]() $(W_{\mathcal {R}},g\varphi )$
) has jumps
$(W_{\mathcal {R}},g\varphi )$
) has jumps
![]() $\mu _1<\cdots <\mu _{l_V}$
(resp.
$\mu _1<\cdots <\mu _{l_V}$
(resp.
![]() $\nu _1<\cdots <\nu _{l_W}$
). Let
$\nu _1<\cdots <\nu _{l_W}$
). Let
![]() $\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
. To show that
$\alpha \in \operatorname {\mathrm {Hom}}_G(V,W)$
. To show that
![]() $\theta _V\circ \alpha _{\mathcal {R}} =\alpha _{\mathcal {R}}\circ \theta _W$
, it suffices to show that
$\theta _V\circ \alpha _{\mathcal {R}} =\alpha _{\mathcal {R}}\circ \theta _W$
, it suffices to show that
![]() $\Theta _X'\circ \alpha _{\mathcal {R}} =\alpha _{\mathcal {R}} \circ \Theta _X'$
. Notice that
$\Theta _X'\circ \alpha _{\mathcal {R}} =\alpha _{\mathcal {R}} \circ \Theta _X'$
. Notice that
![]() $\alpha _{\mathcal {R}}$
respects gradings. Replacing
$\alpha _{\mathcal {R}}$
respects gradings. Replacing
![]() $\Phi _g$
with
$\Phi _g$
with
![]() $\Theta _X$
(possibly with proper decorations) in the second paragraph of the proof of Lemma 4.15, we have the desired result.
$\Theta _X$
(possibly with proper decorations) in the second paragraph of the proof of Lemma 4.15, we have the desired result.
It remains to show that
Because
![]() $\tau _g$
is a tensor functor, the
$\tau _g$
is a tensor functor, the
![]() $(\mu _l+\nu _s)$
th graded piece of
$(\mu _l+\nu _s)$
th graded piece of
![]() $\tau _g(V\bigotimes W)$
is then
$\tau _g(V\bigotimes W)$
is then
 $$ \begin{align*} \big(V \bigotimes W \big)_{\mathcal{R},\mu_l+\nu_s}= \operatorname*{\mathrm{\bigoplus}}\limits_{\scriptstyle \begin{array}{c}\mu_i+\nu_j=\mu_l+\nu_s \\ 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\end{array}} \big( V_{\mathcal{R},\mu_i}\bigotimes_{\mathcal{R}} W_{\mathcal{R},\nu_j } \big),\end{align*} $$
$$ \begin{align*} \big(V \bigotimes W \big)_{\mathcal{R},\mu_l+\nu_s}= \operatorname*{\mathrm{\bigoplus}}\limits_{\scriptstyle \begin{array}{c}\mu_i+\nu_j=\mu_l+\nu_s \\ 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\end{array}} \big( V_{\mathcal{R},\mu_i}\bigotimes_{\mathcal{R}} W_{\mathcal{R},\nu_j } \big),\end{align*} $$
for all
![]() $1\leq l\leq l_V$
and
$1\leq l\leq l_V$
and
![]() $1\leq s \leq l_W$
. It follows from Lemma 4.3 and Construction 4.14 that
$1\leq s \leq l_W$
. It follows from Lemma 4.3 and Construction 4.14 that
 $$ \begin{align*} \Theta^{\prime}_{X,\mu_l+\nu_s}=\operatorname*{\mathrm{\bigoplus}}\limits_{\scriptstyle \begin{array}{c}\mu_i+\nu_j=\mu_l+\nu_s \\ 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\end{array}} \big(\Theta^{\prime}_{X,\mu_i}\otimes \operatorname{\mathrm{Id}}_{W_{\mathcal{R},\nu_j }}+ \operatorname{\mathrm{Id}}_{V_{\mathcal{R},\mu_i }} \otimes \Theta^{\prime}_{X,\nu_j} \big).\end{align*} $$
$$ \begin{align*} \Theta^{\prime}_{X,\mu_l+\nu_s}=\operatorname*{\mathrm{\bigoplus}}\limits_{\scriptstyle \begin{array}{c}\mu_i+\nu_j=\mu_l+\nu_s \\ 1\leq i\leq {l_V}, 1\leq j\leq {l_W}\end{array}} \big(\Theta^{\prime}_{X,\mu_i}\otimes \operatorname{\mathrm{Id}}_{W_{\mathcal{R},\nu_j }}+ \operatorname{\mathrm{Id}}_{V_{\mathcal{R},\mu_i }} \otimes \Theta^{\prime}_{X,\nu_j} \big).\end{align*} $$
Let
![]() $v\otimes f\otimes w\otimes f'\in V_{\mathcal {R},\mu _i}\bigotimes _{\mathcal {R}} W_{\mathcal {R},\nu _j }$
. We compute
$v\otimes f\otimes w\otimes f'\in V_{\mathcal {R},\mu _i}\bigotimes _{\mathcal {R}} W_{\mathcal {R},\nu _j }$
. We compute
 $$ \begin{align*} & \big( \theta_V\otimes \operatorname{\mathrm{Id}}_{W_{\mathcal{R}}} +\operatorname{\mathrm{Id}}_{V_{\mathcal{R}}} \otimes \theta_W \big)(v\otimes f\otimes w\otimes f')\\ =& \big(\Theta^{\prime}_{X,\mu_i}(v\otimes f)-v\otimes \partial(f)\big) \otimes w\otimes f'+ v\otimes f \otimes \big( \Theta^{\prime}_{X,\nu_j}(w\otimes f')-w\otimes\partial(f') \big)\\ =& \big( \Theta^{\prime}_{X,\mu_i}\otimes \operatorname{\mathrm{Id}}_{W_{\mathcal{R},\nu_j }}+ \operatorname{\mathrm{Id}}_{V_{\mathcal{R},\mu_i }} \otimes \Theta^{\prime}_{X,\nu_j}\big)(v\otimes f\otimes w\otimes f')- v\otimes 1\otimes w\otimes \partial(ff') \\ =& \big(\Theta^{\prime}_{X,\mu_l+\nu_s}-\operatorname{\mathrm{Id}}_{V\otimes W}\otimes \partial \big)(v\otimes w\otimes ff')\\ =& \theta_{V\otimes W} (v\otimes w\otimes ff'), \end{align*} $$
$$ \begin{align*} & \big( \theta_V\otimes \operatorname{\mathrm{Id}}_{W_{\mathcal{R}}} +\operatorname{\mathrm{Id}}_{V_{\mathcal{R}}} \otimes \theta_W \big)(v\otimes f\otimes w\otimes f')\\ =& \big(\Theta^{\prime}_{X,\mu_i}(v\otimes f)-v\otimes \partial(f)\big) \otimes w\otimes f'+ v\otimes f \otimes \big( \Theta^{\prime}_{X,\nu_j}(w\otimes f')-w\otimes\partial(f') \big)\\ =& \big( \Theta^{\prime}_{X,\mu_i}\otimes \operatorname{\mathrm{Id}}_{W_{\mathcal{R},\nu_j }}+ \operatorname{\mathrm{Id}}_{V_{\mathcal{R},\mu_i }} \otimes \Theta^{\prime}_{X,\nu_j}\big)(v\otimes f\otimes w\otimes f')- v\otimes 1\otimes w\otimes \partial(ff') \\ =& \big(\Theta^{\prime}_{X,\mu_l+\nu_s}-\operatorname{\mathrm{Id}}_{V\otimes W}\otimes \partial \big)(v\otimes w\otimes ff')\\ =& \theta_{V\otimes W} (v\otimes w\otimes ff'), \end{align*} $$
which completes the proof.▪
We now summarize what we have shown thus far. The splitting
![]() $\xi _g$
of
$\xi _g$
of
![]() $\operatorname {\mathrm {{HN}}}_g$
gives a unique element
$\operatorname {\mathrm {{HN}}}_g$
gives a unique element
![]() $z\in G(\mathcal {R})$
such that
$z\in G(\mathcal {R})$
such that
![]() $\operatorname {\mathrm {I}}'(g)=\operatorname {\mathrm {I}}(z)$
by Proposition 4.16, and a unique element
$\operatorname {\mathrm {I}}'(g)=\operatorname {\mathrm {I}}(z)$
by Proposition 4.16, and a unique element
![]() $X_0\in \mathfrak {g}_{\mathcal {R}}$
such that
$X_0\in \mathfrak {g}_{\mathcal {R}}$
such that
![]() $\Theta ^{\prime }_X=\Theta _{X_0}$
by Proposition 4.17. These two elements are related as in Proposition 4.19 below.
$\Theta ^{\prime }_X=\Theta _{X_0}$
by Proposition 4.17. These two elements are related as in Proposition 4.19 below.
We next recall some notions from [Reference Conrad, Gabber and Prasad4, Section 2.1]. Let k be a commutative ring with
![]() $1$
, and let
$1$
, and let
![]() $\mathfrak {G}$
be a reductive k-group. Hereupon, we denote by
$\mathfrak {G}$
be a reductive k-group. Hereupon, we denote by
![]() $\kappa (s)$
the residue field of s and
$\kappa (s)$
the residue field of s and
![]() $\bar {\kappa }(s)$
an algebraic closure of
$\bar {\kappa }(s)$
an algebraic closure of
![]() $\kappa (s)$
, for all
$\kappa (s)$
, for all
![]() $s\in \operatorname {\mathrm {Spec}} k$
. A subgroup
$s\in \operatorname {\mathrm {Spec}} k$
. A subgroup
![]() $\mathfrak {P}$
of
$\mathfrak {P}$
of
![]() $\mathfrak {G}$
is a parabolic (resp. Borel) subgroup if
$\mathfrak {G}$
is a parabolic (resp. Borel) subgroup if
![]() $\mathfrak {P}$
is smooth and
$\mathfrak {P}$
is smooth and
![]() $\mathfrak {P}_{\bar {\kappa }(s)}$
is a parabolic (resp. Borel) subgroup of
$\mathfrak {P}_{\bar {\kappa }(s)}$
is a parabolic (resp. Borel) subgroup of
![]() $\mathfrak {G}_{\bar {\kappa }(s)}$
, for all
$\mathfrak {G}_{\bar {\kappa }(s)}$
, for all
![]() $s\in \operatorname {\mathrm {Spec}} k$
.
$s\in \operatorname {\mathrm {Spec}} k$
.
Suppose we have a cocharacter
![]() $\lambda \colon \mathbb {G}_m\to \mathfrak {G}$
over k. For any k-algebra R, we let
$\lambda \colon \mathbb {G}_m\to \mathfrak {G}$
over k. For any k-algebra R, we let
![]() $\mathbb {G}_{m,R}$
act on
$\mathbb {G}_{m,R}$
act on
![]() $\mathfrak {G}_R$
via the conjugation
$\mathfrak {G}_R$
via the conjugation
for all R-algebra S. For any
![]() $x\in \mathfrak {G}(R)$
, we have an orbit map
$x\in \mathfrak {G}(R)$
, we have an orbit map
![]() $\alpha _x\colon \mathbb {G}_{m,R} \to \mathfrak {G}_R$
given by
$\alpha _x\colon \mathbb {G}_{m,R} \to \mathfrak {G}_R$
given by
for all R-algebras S. Let
![]() $\mathbb {A}^1$
be the affine k-line. We say that the limit
$\mathbb {A}^1$
be the affine k-line. We say that the limit
![]() $\lim \limits _{t \to 0} t.x$
exists if
$\lim \limits _{t \to 0} t.x$
exists if
![]() $\alpha _x$
extends (necessarily uniquely) to a morphism
$\alpha _x$
extends (necessarily uniquely) to a morphism
![]() $\tilde \alpha _x\colon \mathbb {A}^1_R \to \mathfrak {G}_R$
of affine R-schemes, and put
$\tilde \alpha _x\colon \mathbb {A}^1_R \to \mathfrak {G}_R$
of affine R-schemes, and put
![]() $\lim \limits _{t \to 0} t.x := \tilde \alpha _x(0)\in \mathfrak {G}_R(R)$
. We define
$\lim \limits _{t \to 0} t.x := \tilde \alpha _x(0)\in \mathfrak {G}_R(R)$
. We define
and
where
![]() $-\lambda $
is the reciprocal of
$-\lambda $
is the reciprocal of
![]() $\lambda $
. Then,
$\lambda $
. Then,
![]() $P_{\mathfrak {G}}(\lambda )$
is a closed k-subgroup of
$P_{\mathfrak {G}}(\lambda )$
is a closed k-subgroup of
![]() $\mathfrak {G}$
[Reference Conrad, Gabber and Prasad4, Lemma 2.1.4],
$\mathfrak {G}$
[Reference Conrad, Gabber and Prasad4, Lemma 2.1.4],
![]() $U_{\mathfrak {G}}(\lambda )$
is an affine algebraic k-normal subgroup of
$U_{\mathfrak {G}}(\lambda )$
is an affine algebraic k-normal subgroup of
![]() $P_{\mathfrak {G}}(\lambda )$
, and
$P_{\mathfrak {G}}(\lambda )$
, and
![]() $Z_{\mathfrak {G}}(\lambda )$
is the centralizer of the
$Z_{\mathfrak {G}}(\lambda )$
is the centralizer of the
![]() $\mathbb {G}_m$
-action in
$\mathbb {G}_m$
-action in
![]() $\mathfrak {G}$
[Reference Conrad, Gabber and Prasad4, Lemma 2.1.5]. By [Reference Conrad, Gabber and Prasad4, Proposition 2.1.8(3)], these subgroups are smooth, because
$\mathfrak {G}$
[Reference Conrad, Gabber and Prasad4, Lemma 2.1.5]. By [Reference Conrad, Gabber and Prasad4, Proposition 2.1.8(3)], these subgroups are smooth, because
![]() $\mathfrak {G}$
is smooth.
$\mathfrak {G}$
is smooth.
It follows from the definitions that the formations of
![]() $P_{\mathfrak {G}}(\lambda ),U_{\mathfrak {G}}(\lambda )$
, and
$P_{\mathfrak {G}}(\lambda ),U_{\mathfrak {G}}(\lambda )$
, and
![]() $Z_{\mathfrak {G}}(\lambda )$
commute with any base extension on k. In particular, for every
$Z_{\mathfrak {G}}(\lambda )$
commute with any base extension on k. In particular, for every
![]() $s\in \operatorname {\mathrm {Spec}} k$
, we have
$s\in \operatorname {\mathrm {Spec}} k$
, we have
![]() $P_{\mathfrak {G}}(\lambda )_{\bar {\kappa }(s)} =P_{\mathfrak {G}_{\bar {\kappa }(s)}}(\lambda _{\bar {\kappa }(s)})$
, which is a parabolic subgroup of
$P_{\mathfrak {G}}(\lambda )_{\bar {\kappa }(s)} =P_{\mathfrak {G}_{\bar {\kappa }(s)}}(\lambda _{\bar {\kappa }(s)})$
, which is a parabolic subgroup of
![]() $\mathfrak {G}_{\bar {\kappa }(s)}$
by [Reference Springer20, Proposition 8.4.5]. Hence,
$\mathfrak {G}_{\bar {\kappa }(s)}$
by [Reference Springer20, Proposition 8.4.5]. Hence,
![]() $P_{\mathfrak {G}}(\lambda )$
is a parabolic k-group.
$P_{\mathfrak {G}}(\lambda )$
is a parabolic k-group.
By [Reference Conrad, Gabber and Prasad4, Proposition 2.1.8(2)], the multiplication map gives an isomorphism
of affine algebraic k-groups.
Now, let
![]() $\mathbb {G}_m$
act on
$\mathbb {G}_m$
act on
![]() $\mathfrak {g}=\operatorname {\mathrm {Lie}}(\mathfrak {G})(k)$
through the adjoint representation. We then have
$\mathfrak {g}=\operatorname {\mathrm {Lie}}(\mathfrak {G})(k)$
through the adjoint representation. We then have
![]() $\mathfrak {g}=\operatorname *{\mathrm {\bigoplus }}\limits _{n\in \mathbb {Z}} \mathfrak {g}_n$
, where
$\mathfrak {g}=\operatorname *{\mathrm {\bigoplus }}\limits _{n\in \mathbb {Z}} \mathfrak {g}_n$
, where
![]() $\mathfrak {g}_n=\{X\in \mathfrak {g} \mid t.X=t^nX,\forall t\in \mathbb {G}_m\}$
for all
$\mathfrak {g}_n=\{X\in \mathfrak {g} \mid t.X=t^nX,\forall t\in \mathbb {G}_m\}$
for all
![]() $n\in \mathbb {Z}$
. We have
$n\in \mathbb {Z}$
. We have
![]() $\operatorname {\mathrm {Lie}}\big (Z_{\mathfrak {G}}(\lambda ) \big ) =\mathfrak {g}_0$
(which is the centralizer of the
$\operatorname {\mathrm {Lie}}\big (Z_{\mathfrak {G}}(\lambda ) \big ) =\mathfrak {g}_0$
(which is the centralizer of the
![]() $\mathbb {G}_m$
-action on
$\mathbb {G}_m$
-action on
![]() $\mathfrak {g}$
),
$\mathfrak {g}$
),
![]() $\operatorname {\mathrm {Lie}}\big (U_{\mathfrak {G}}(\lambda ) \big ) =\operatorname *{\mathrm {\bigoplus }}\limits _{n>0} \mathfrak {g}_n$
, and
$\operatorname {\mathrm {Lie}}\big (U_{\mathfrak {G}}(\lambda ) \big ) =\operatorname *{\mathrm {\bigoplus }}\limits _{n>0} \mathfrak {g}_n$
, and
![]() $\operatorname {\mathrm {Lie}}\big (P_{\mathfrak {G}}(\lambda ) \big ) =\operatorname *{\mathrm {\bigoplus }}\limits _{n\geq 0} \mathfrak {g}_n$
. In particular, we have the following decomposition:
$\operatorname {\mathrm {Lie}}\big (P_{\mathfrak {G}}(\lambda ) \big ) =\operatorname *{\mathrm {\bigoplus }}\limits _{n\geq 0} \mathfrak {g}_n$
. In particular, we have the following decomposition:
Lemma 4.18 With the notion above, we have
for all
![]() $u\in U_{\mathfrak {G}}(\lambda )(k)$
and
$u\in U_{\mathfrak {G}}(\lambda )(k)$
and
![]() $Z\in \operatorname {\mathrm {Lie}}\big ( Z_{\mathfrak {G}}(\lambda )\big )$
.
$Z\in \operatorname {\mathrm {Lie}}\big ( Z_{\mathfrak {G}}(\lambda )\big )$
.
Proof Recall that
![]() $Z\in Z_{\mathfrak {G}}(\lambda )(k[\varepsilon ])$
by definition; we may also view u as an element in
$Z\in Z_{\mathfrak {G}}(\lambda )(k[\varepsilon ])$
by definition; we may also view u as an element in
![]() $U_{\mathfrak {G}}(\lambda )(k[\varepsilon ])$
via the inclusion
$U_{\mathfrak {G}}(\lambda )(k[\varepsilon ])$
via the inclusion
![]() $\iota \colon k\hookrightarrow k[\varepsilon ]$
. By the definition of the adjoint representation, we have
$\iota \colon k\hookrightarrow k[\varepsilon ]$
. By the definition of the adjoint representation, we have
Because
![]() $U_{\mathfrak {G}}(\lambda )$
is normal in
$U_{\mathfrak {G}}(\lambda )$
is normal in
![]() $P_{\mathfrak {G}}(\lambda )$
, we have that
$P_{\mathfrak {G}}(\lambda )$
, we have that
![]() $ZuZ^{-1}\in U_{\mathfrak {G}}(\lambda )(k[\varepsilon ])$
, and so is
$ZuZ^{-1}\in U_{\mathfrak {G}}(\lambda )(k[\varepsilon ])$
, and so is
![]() $ZuZ^{-1}u^{-1}$
. Consider the following commutative diagram:
$ZuZ^{-1}u^{-1}$
. Consider the following commutative diagram:

Because both Z and
![]() $uZ^{-1}u^{-1}$
lie in the kernel of the right vertical map, so does their product
$uZ^{-1}u^{-1}$
lie in the kernel of the right vertical map, so does their product
![]() $ZuZ^{-1}u^{-1}$
. Hence,
$ZuZ^{-1}u^{-1}$
. Hence,
![]() $ZuZ^{-1}u^{-1}\in U_{\mathfrak {G}}(\lambda )(k[\varepsilon ])$
lies in the kernel of the left vertical map. The lemma then follows.▪
$ZuZ^{-1}u^{-1}\in U_{\mathfrak {G}}(\lambda )(k[\varepsilon ])$
lies in the kernel of the left vertical map. The lemma then follows.▪
Proposition 4.19 Let
![]() $z\in G(\mathcal {R})$
and
$z\in G(\mathcal {R})$
and
![]() $X_0\in \mathfrak {g}_{\mathcal {R}}$
be the unique elements given by Propositions 4.16 and 4.17, respectively. We have
$X_0\in \mathfrak {g}_{\mathcal {R}}$
be the unique elements given by Propositions 4.16 and 4.17, respectively. We have
![]() $X_0=\Gamma _z \big (\operatorname {\mathrm {\boldsymbol \mu }}\varphi (X_0)\big )$
. In particular,
$X_0=\Gamma _z \big (\operatorname {\mathrm {\boldsymbol \mu }}\varphi (X_0)\big )$
. In particular,
![]() $\operatorname {\mathrm {I}}(z,X_0)$
is a G-
$\operatorname {\mathrm {I}}(z,X_0)$
is a G-
![]() $(\varphi ,\nabla )$
-module over
$(\varphi ,\nabla )$
-module over
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
Proof The second assertion follows from the first assertion and Lemma 4.7. For the first assertion, we need to show
It suffices to show (3) with both sides understood as elements in
![]() $\operatorname {\mathrm {End}}_{\mathcal {R}}(V_{\mathcal {R}})$
for some faithful representation
$\operatorname {\mathrm {End}}_{\mathcal {R}}(V_{\mathcal {R}})$
for some faithful representation
![]() $(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
. Suppose that
$(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
. Suppose that
![]() $\dim _F V=d$
, and suppose that
$\dim _F V=d$
, and suppose that
![]() $\nu _g(V)$
is the decomposition
$\nu _g(V)$
is the decomposition
![]() $V_{\mathcal {R}}=\bigoplus \limits _{i=1}^l V_{\mathcal {R},\mu _i}$
. We choose for each graded-piece
$V_{\mathcal {R}}=\bigoplus \limits _{i=1}^l V_{\mathcal {R},\mu _i}$
. We choose for each graded-piece
![]() $V_{\mathcal {R},\mu _i}$
a basis. They altogether give a basis
$V_{\mathcal {R},\mu _i}$
a basis. They altogether give a basis
![]() $\textbf {v}_1,\ldots ,\textbf {v}_d$
of
$\textbf {v}_1,\ldots ,\textbf {v}_d$
of
![]() $V_{\mathcal {R}}$
, in which
$V_{\mathcal {R}}$
, in which
![]() $\Phi _g$
acts via a block-upper-triangular matrix
$\Phi _g$
acts via a block-upper-triangular matrix
 $$ \begin{align*} A= \left(\begin{smallmatrix} A_1 & &\\ & A_2 &~~~~{\ast}\\ && \ddots \\ && &A_l \end{smallmatrix}\right) \in\operatorname{\mathrm{GL}}_d(\mathcal{R}), \end{align*} $$
$$ \begin{align*} A= \left(\begin{smallmatrix} A_1 & &\\ & A_2 &~~~~{\ast}\\ && \ddots \\ && &A_l \end{smallmatrix}\right) \in\operatorname{\mathrm{GL}}_d(\mathcal{R}), \end{align*} $$
where each
![]() $A_i$
is an
$A_i$
is an
![]() $m_i$
by
$m_i$
by
![]() $m_i$
invertible matrix with
$m_i$
invertible matrix with
![]() $m_i$
the multiplicity of
$m_i$
the multiplicity of
![]() $\mu _i$
. Then,
$\mu _i$
. Then,
![]() $\Phi _z$
acts in this basis via
$\Phi _z$
acts in this basis via
![]() $Z:= \operatorname {\mathrm {Diag}}(A_1,\ldots ,A_l)$
. Likewise,
$Z:= \operatorname {\mathrm {Diag}}(A_1,\ldots ,A_l)$
. Likewise,
![]() $\Theta _X$
acts in the basis
$\Theta _X$
acts in the basis
![]() $\textbf {v}_1,\ldots ,\textbf {v}_d$
via a block-upper-triangular matrix
$\textbf {v}_1,\ldots ,\textbf {v}_d$
via a block-upper-triangular matrix
 $$ \begin{align*} N= \left(\begin{smallmatrix} N_1 & &\\ & N_2 &~~~~{{\ast}} \\ && \ddots \\ && &N_l \end{smallmatrix}\right) \in\operatorname{\mathrm{Mat}}_{d,d}(\mathcal{R}), \end{align*} $$
$$ \begin{align*} N= \left(\begin{smallmatrix} N_1 & &\\ & N_2 &~~~~{{\ast}} \\ && \ddots \\ && &N_l \end{smallmatrix}\right) \in\operatorname{\mathrm{Mat}}_{d,d}(\mathcal{R}), \end{align*} $$
where each
![]() $N_i$
is an
$N_i$
is an
![]() $m_i$
by
$m_i$
by
![]() $m_i$
matrix, and
$m_i$
matrix, and
![]() $\Theta _{X_0}$
acts via
$\Theta _{X_0}$
acts via
![]() $\overline N:= \operatorname {\mathrm {Diag}}(N_1,\ldots ,N_l)$
. Write
$\overline N:= \operatorname {\mathrm {Diag}}(N_1,\ldots ,N_l)$
. Write
![]() $A=ZU$
for
$A=ZU$
for
![]() $U\in \operatorname {\mathrm {GL}}_d(\mathcal {R})$
, and
$U\in \operatorname {\mathrm {GL}}_d(\mathcal {R})$
, and
![]() $N=\overline N+N_+$
for
$N=\overline N+N_+$
for
![]() $N_+\in \operatorname {\mathrm {Mat}}_{d,d}(\mathcal {R})$
. Because
$N_+\in \operatorname {\mathrm {Mat}}_{d,d}(\mathcal {R})$
. Because
![]() $X=\Gamma _g\big (\operatorname {\mathrm {\boldsymbol \mu }}\varphi (X)\big )$
, we have
$X=\Gamma _g\big (\operatorname {\mathrm {\boldsymbol \mu }}\varphi (X)\big )$
, we have
![]() $N=\operatorname {\mathrm {\boldsymbol \mu }}\cdot A \varphi (N) A^{-1}-\partial (A)A^{-1}$
, and then
$N=\operatorname {\mathrm {\boldsymbol \mu }}\cdot A \varphi (N) A^{-1}-\partial (A)A^{-1}$
, and then
 $$ \begin{align*} \overline N+N_+ =& \operatorname{\mathrm{\boldsymbol\mu}}\cdot (UZ)(\varphi(\overline N+N_+))(UZ)^{-1}-\partial(UZ)(UZ)^{-1}\\ =& \operatorname{\mathrm{\boldsymbol\mu}}\cdot(\!UZ)\varphi(\overline N)Z^{-1}U^{-1}\!+\operatorname{\mathrm{\boldsymbol\mu}}\cdot(\!UZ)\varphi(N_+)Z^{-1}U^{-1}\!-\partial(\!U)U^{-1}\!-U\partial(Z)Z^{-1}U^{-1}. \end{align*} $$
$$ \begin{align*} \overline N+N_+ =& \operatorname{\mathrm{\boldsymbol\mu}}\cdot (UZ)(\varphi(\overline N+N_+))(UZ)^{-1}-\partial(UZ)(UZ)^{-1}\\ =& \operatorname{\mathrm{\boldsymbol\mu}}\cdot(\!UZ)\varphi(\overline N)Z^{-1}U^{-1}\!+\operatorname{\mathrm{\boldsymbol\mu}}\cdot(\!UZ)\varphi(N_+)Z^{-1}U^{-1}\!-\partial(\!U)U^{-1}\!-U\partial(Z)Z^{-1}U^{-1}. \end{align*} $$
Applying
![]() $\operatorname {\mathrm {Ad}}(U^{-1})$
on both sides, we then have
$\operatorname {\mathrm {Ad}}(U^{-1})$
on both sides, we then have
 $$ \begin{align*} &\operatorname{\mathrm{\boldsymbol\mu}}\cdot Z\varphi(\overline N)Z^{-1}-\partial(Z)Z^{-1}+\operatorname{\mathrm{\boldsymbol\mu}}\cdot Z\varphi(N_+)Z^{-1}-U^{-1}\partial(U)\\ =& U^{-1}\overline NU+U^{-1}N_+U = \overline N -(\overline N-U^{-1}\overline NU-U^{-1}N_+U). \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{\boldsymbol\mu}}\cdot Z\varphi(\overline N)Z^{-1}-\partial(Z)Z^{-1}+\operatorname{\mathrm{\boldsymbol\mu}}\cdot Z\varphi(N_+)Z^{-1}-U^{-1}\partial(U)\\ =& U^{-1}\overline NU+U^{-1}N_+U = \overline N -(\overline N-U^{-1}\overline NU-U^{-1}N_+U). \end{align*} $$
We claim that
![]() $\operatorname {\mathrm {\boldsymbol \mu }}\cdot Z\varphi (\overline N)Z^{-1}-\partial (Z)Z^{-1}=\overline N$
. Put
$\operatorname {\mathrm {\boldsymbol \mu }}\cdot Z\varphi (\overline N)Z^{-1}-\partial (Z)Z^{-1}=\overline N$
. Put
![]() $\lambda _{\rho ,g}:= \rho \circ \lambda _g \colon \mathbb {G}_{m,\mathcal {R}} \to \operatorname {\mathrm {GL}}_{V,\mathcal {R}}$
, where
$\lambda _{\rho ,g}:= \rho \circ \lambda _g \colon \mathbb {G}_{m,\mathcal {R}} \to \operatorname {\mathrm {GL}}_{V,\mathcal {R}}$
, where
![]() $\lambda _g\colon \mathbb {G}_{m,\mathcal {R}} \to G_{\mathcal {R}}$
is the slope morphism defined in Construction 3.15. Identifying
$\lambda _g\colon \mathbb {G}_{m,\mathcal {R}} \to G_{\mathcal {R}}$
is the slope morphism defined in Construction 3.15. Identifying
![]() $\operatorname {\mathrm {GL}}_{V,\mathcal {R}}$
with
$\operatorname {\mathrm {GL}}_{V,\mathcal {R}}$
with
![]() $\operatorname {\mathrm {GL}}_{d,\mathcal {R}}$
via the basis
$\operatorname {\mathrm {GL}}_{d,\mathcal {R}}$
via the basis
![]() $\textbf {v}_1,\ldots ,\textbf {v}_d$
given in the preceding paragraph, and letting
$\textbf {v}_1,\ldots ,\textbf {v}_d$
given in the preceding paragraph, and letting
![]() $\mathfrak {G}=\operatorname {\mathrm {GL}}_{d,\mathcal {R}}$
, we then have an isomorphism
$\mathfrak {G}=\operatorname {\mathrm {GL}}_{d,\mathcal {R}}$
, we then have an isomorphism
of affine algebraic
![]() $\mathcal {R}$
-groups. Because
$\mathcal {R}$
-groups. Because
![]() $\mu _1< \cdots < \mu _l$
, we have
$\mu _1< \cdots < \mu _l$
, we have
It follows from Lemma 4.18 that
![]() $\overline N-U^{-1}\overline NU \in \operatorname {\mathrm {Lie}} \big ( U_{\mathfrak {G}}(-\lambda _{\rho ,g})\big )$
. In particular, we have
$\overline N-U^{-1}\overline NU \in \operatorname {\mathrm {Lie}} \big ( U_{\mathfrak {G}}(-\lambda _{\rho ,g})\big )$
. In particular, we have
![]() $\overline N-U^{-1}\overline NU-U^{-1}N_+U \in \operatorname {\mathrm {Lie}} \big ( U_{\mathfrak {G}}(-\lambda _{\rho ,g})\big )$
. On the other hand, it is clear that
$\overline N-U^{-1}\overline NU-U^{-1}N_+U \in \operatorname {\mathrm {Lie}} \big ( U_{\mathfrak {G}}(-\lambda _{\rho ,g})\big )$
. On the other hand, it is clear that
![]() $\operatorname {\mathrm {\boldsymbol \mu }}\cdot Z\varphi (\overline N)Z^{-1}-\partial (Z)Z^{-1}\in \operatorname {\mathrm {Lie}}\big ( Z_{\mathfrak {G}}(-\lambda _{\rho ,g})\big )$
and
$\operatorname {\mathrm {\boldsymbol \mu }}\cdot Z\varphi (\overline N)Z^{-1}-\partial (Z)Z^{-1}\in \operatorname {\mathrm {Lie}}\big ( Z_{\mathfrak {G}}(-\lambda _{\rho ,g})\big )$
and
![]() $\operatorname {\mathrm {\boldsymbol \mu }}\cdot Z\varphi (N_+)Z^{-1}-U^{-1}\partial (U)\in \operatorname {\mathrm {Lie}} \big ( U_{\mathfrak {G}}(-\lambda _{\rho ,g})\big )$
. By decomposition (2), we have
$\operatorname {\mathrm {\boldsymbol \mu }}\cdot Z\varphi (N_+)Z^{-1}-U^{-1}\partial (U)\in \operatorname {\mathrm {Lie}} \big ( U_{\mathfrak {G}}(-\lambda _{\rho ,g})\big )$
. By decomposition (2), we have
![]() $\operatorname {\mathrm {\boldsymbol \mu }}\cdot Z\varphi (\overline N)Z^{-1}-\partial (Z)Z^{-1}=\overline N$
, and the desired equality (3) follows.▪
$\operatorname {\mathrm {\boldsymbol \mu }}\cdot Z\varphi (\overline N)Z^{-1}-\partial (Z)Z^{-1}=\overline N$
, and the desired equality (3) follows.▪
Recall that the least common denominator
![]() $d_g$
of g is constructed in Construction 3.8, and
$d_g$
of g is constructed in Construction 3.8, and
![]() $\lambda _g \colon \mathbb {G}_{m,\mathcal {R}} \to G_{\mathcal {R}}$
is the slope morphism (see Construction 3.15). We next reduce the G-
$\lambda _g \colon \mathbb {G}_{m,\mathcal {R}} \to G_{\mathcal {R}}$
is the slope morphism (see Construction 3.15). We next reduce the G-
![]() $(\varphi ,\nabla )$
-module
$(\varphi ,\nabla )$
-module
![]() $(z,X_0)$
over
$(z,X_0)$
over
![]() $\mathcal {R}$
to a unit-root one by applying the pushforward functor
$\mathcal {R}$
to a unit-root one by applying the pushforward functor
![]() $[d_g]_*$
and twisting by
$[d_g]_*$
and twisting by
![]() $\lambda _g(\varpi ^{-1})$
.
$\lambda _g(\varpi ^{-1})$
.
Corollary 4.20
![]() $\operatorname {\mathrm {I}} \big (\lambda _g(\varpi ^{-1})[d_g]_*(z),X_0 \big )$
is a unit-root G-
$\operatorname {\mathrm {I}} \big (\lambda _g(\varpi ^{-1})[d_g]_*(z),X_0 \big )$
is a unit-root G-
![]() $(\varphi ^{d_g},\nabla )$
-module over
$(\varphi ^{d_g},\nabla )$
-module over
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
Proof For any
![]() $V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, it suffices to show that
$V\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, it suffices to show that
![]() $(V_{\mathcal {R}},[d_g]_*(z)\varphi ^{d_g},\nabla _{X_0})$
is unit-root. By Proposition 4.19 and Lemma 4.12,
$(V_{\mathcal {R}},[d_g]_*(z)\varphi ^{d_g},\nabla _{X_0})$
is unit-root. By Proposition 4.19 and Lemma 4.12,
![]() $(V_{\mathcal {R}},[d_g]_*(z)\varphi ^{d_g},\nabla _{X_0})$
is a
$(V_{\mathcal {R}},[d_g]_*(z)\varphi ^{d_g},\nabla _{X_0})$
is a
![]() $(\varphi ^{d_g},\nabla )$
-module over
$(\varphi ^{d_g},\nabla )$
-module over
![]() $\mathcal {R}$
. Equivalently, we have
$\mathcal {R}$
. Equivalently, we have
![]() $\Theta _{X_0}\circ \Phi _z^{d_g}= \operatorname {\mathrm {\boldsymbol \mu }}\cdot \Phi _z^{d_g}\circ \Theta _{X_0}$
. Suppose that
$\Theta _{X_0}\circ \Phi _z^{d_g}= \operatorname {\mathrm {\boldsymbol \mu }}\cdot \Phi _z^{d_g}\circ \Theta _{X_0}$
. Suppose that
![]() $(V_{\mathcal {R}},g\varphi )$
has jumps
$(V_{\mathcal {R}},g\varphi )$
has jumps
![]() $\mu _1,\ldots ,\mu _l$
, then
$\mu _1,\ldots ,\mu _l$
, then
![]() $\big ( V_{\mathcal {R}},[d_g]_*(z)\varphi ^{d_g} \big )$
has jumps
$\big ( V_{\mathcal {R}},[d_g]_*(z)\varphi ^{d_g} \big )$
has jumps
![]() $d_g\mu _1,\ldots ,d_g\mu _l$
by Lemma 4.13. For any
$d_g\mu _1,\ldots ,d_g\mu _l$
by Lemma 4.13. For any
![]() $1\leq i \leq l$
,
$1\leq i \leq l$
,
![]() $\rho (\lambda _g(\varpi ^{-1}))$
acts via multiplication by
$\rho (\lambda _g(\varpi ^{-1}))$
acts via multiplication by
![]() $\varpi ^{-d_g\mu _i}\in K$
on the graded-piece
$\varpi ^{-d_g\mu _i}\in K$
on the graded-piece
![]() $V_{\mathcal {R},\mu _i}$
, which implies that
$V_{\mathcal {R},\mu _i}$
, which implies that
![]() $\big ( V_{\mathcal {R},\mu _i},\lambda _g(\varpi ^{-1})[d_g]_*(z)\varphi ^{d_g} \big )$
is unit-root. It follows from [Reference Kedlaya10, Proposition 4.6.3(a)] that
$\big ( V_{\mathcal {R},\mu _i},\lambda _g(\varpi ^{-1})[d_g]_*(z)\varphi ^{d_g} \big )$
is unit-root. It follows from [Reference Kedlaya10, Proposition 4.6.3(a)] that
![]() $\big ( V_{\mathcal {R}},\lambda _g(\varpi ^{-1})[d_g]_*(z)\varphi ^{d_g} \big )$
is unit-root. Moreover, because
$\big ( V_{\mathcal {R}},\lambda _g(\varpi ^{-1})[d_g]_*(z)\varphi ^{d_g} \big )$
is unit-root. Moreover, because
![]() $\Theta _{X_0}$
is K-linear, we have
$\Theta _{X_0}$
is K-linear, we have
which completes the proof.▪
4.5 A G-version of the p-adic local monodromy theorem
Let L be a finite separable extension of
![]() $\kappa (\!( t )\!)$
, and let
$\kappa (\!( t )\!)$
, and let
![]() $\mathcal {E}^{\dagger }_L$
be the unique unramified extension of
$\mathcal {E}^{\dagger }_L$
be the unique unramified extension of
![]() $\mathcal {E}^{\dagger }$
with residue field L. We put
$\mathcal {E}^{\dagger }$
with residue field L. We put
![]() $\mathcal {R}_L := \mathcal {R}\bigotimes _{\mathcal {E}^{\dagger }} \mathcal {E}^{\dagger }_L$
.
$\mathcal {R}_L := \mathcal {R}\bigotimes _{\mathcal {E}^{\dagger }} \mathcal {E}^{\dagger }_L$
.
We put
where L runs through all finite separable extensions of
![]() $\kappa (\!( t )\!)$
. In fact,
$\kappa (\!( t )\!)$
. In fact,
![]() $\mathcal {E}^{\dagger ,\operatorname {\mathrm {nr}}}$
is the maximal unramified extension of
$\mathcal {E}^{\dagger ,\operatorname {\mathrm {nr}}}$
is the maximal unramified extension of
![]() $\mathcal {E}^{\dagger }$
with residue field
$\mathcal {E}^{\dagger }$
with residue field
![]() $\kappa (\!( t )\!)^{\operatorname {\mathrm {sep}}}$
, the separable closure of
$\kappa (\!( t )\!)^{\operatorname {\mathrm {sep}}}$
, the separable closure of
![]() $\kappa (\!( t )\!)$
.
$\kappa (\!( t )\!)$
.
The main result of this paper is the following theorem.
Theorem 4.21 Let G be a connected reductive F-group, and let
![]() $(g,X)\in \textbf {B}^{\varphi ,\nabla }(G,\mathcal {R})$
. Then, there exist a finite separable extension L of
$(g,X)\in \textbf {B}^{\varphi ,\nabla }(G,\mathcal {R})$
. Then, there exist a finite separable extension L of
![]() $\kappa (\!( t )\!)$
and an element
$\kappa (\!( t )\!)$
and an element
![]() $b\in G(\mathcal {R}_L)$
such that
$b\in G(\mathcal {R}_L)$
such that
![]() $\Gamma _b(X)\in \operatorname {\mathrm {Lie}} \big (U_{G_{\mathcal {R}}}(-\lambda _g)\big )_{\mathcal {R}_L}$
.
$\Gamma _b(X)\in \operatorname {\mathrm {Lie}} \big (U_{G_{\mathcal {R}}}(-\lambda _g)\big )_{\mathcal {R}_L}$
.
We will make use of the following lemma, which is often mentioned as Steinberg’s theorem. The theory of fields of cohomological dimension
![]() $\leq 1$
can be found in, e.g., [Reference Serre19, Chapter II, Section 3]; for us, the most important example will be a Henselian discretely valued field of characteristic
$\leq 1$
can be found in, e.g., [Reference Serre19, Chapter II, Section 3]; for us, the most important example will be a Henselian discretely valued field of characteristic
![]() $0$
with algebraically closed residue field (see [Reference Serre19, Chapter II, Section 3.3]).
$0$
with algebraically closed residue field (see [Reference Serre19, Chapter II, Section 3.3]).
Lemma 4.22 ([Reference Steinberg21, Theorem 1.9])
Suppose that k is a field of cohomological dimension
![]() $\leq 1$
and
$\leq 1$
and
![]() $\mathfrak {G}$
is a connected reductive k-group, then
$\mathfrak {G}$
is a connected reductive k-group, then
![]() $H^1(k,\mathfrak {G})=1$
.
$H^1(k,\mathfrak {G})=1$
.
Proof of Theorem 4.21 Let
![]() $z\in G(\mathcal {R})$
and
$z\in G(\mathcal {R})$
and
![]() $X_0\in \mathfrak {g}_{\mathcal {R}}$
be the unique elements given by Propositions 4.16 and 4.17, respectively.
$X_0\in \mathfrak {g}_{\mathcal {R}}$
be the unique elements given by Propositions 4.16 and 4.17, respectively.
Let
![]() $(V,\rho )$
be a d-dimensional G-representation (not necessarily faithful). Suppose the slope filtration of
$(V,\rho )$
be a d-dimensional G-representation (not necessarily faithful). Suppose the slope filtration of
![]() $(V_{\mathcal {R}},g\varphi )$
has jumps
$(V_{\mathcal {R}},g\varphi )$
has jumps
![]() $\mu _1,\ldots ,\mu _l$
. Suppose that
$\mu _1,\ldots ,\mu _l$
. Suppose that
![]() $\xi _g(V)=\bigoplus \limits _{i=1}^l V_{\mathcal {R},\mu _i}$
, we put
$\xi _g(V)=\bigoplus \limits _{i=1}^l V_{\mathcal {R},\mu _i}$
, we put
![]() $d_i:= \operatorname {\mathrm {rk}}_{\mathcal {R}} (V_{\mathcal {R},\mu _i})$
for all i. In the proof of Corollary 4.20, we see that
$d_i:= \operatorname {\mathrm {rk}}_{\mathcal {R}} (V_{\mathcal {R},\mu _i})$
for all i. In the proof of Corollary 4.20, we see that
![]() $\big (V_{\mathcal {R},\mu _i},\lambda _g(\varpi ^{-1})[d_g]_*(z)\varphi ^{d_g},\nabla _{X_0} \big )$
is a unit-root
$\big (V_{\mathcal {R},\mu _i},\lambda _g(\varpi ^{-1})[d_g]_*(z)\varphi ^{d_g},\nabla _{X_0} \big )$
is a unit-root
![]() $(\varphi ,\nabla )$
-module over
$(\varphi ,\nabla )$
-module over
![]() $\mathcal {R}$
for all
$\mathcal {R}$
for all
![]() $1\leq i\leq l$
. Let
$1\leq i\leq l$
. Let
![]() $\Phi _z=z\varphi $
, and let
$\Phi _z=z\varphi $
, and let
![]() $\Theta _{X_0}\colon V_{\mathcal {R}}\to V_{\mathcal {R}}$
be the differential operator associated to
$\Theta _{X_0}\colon V_{\mathcal {R}}\to V_{\mathcal {R}}$
be the differential operator associated to
![]() $\nabla _{X_0}$
. Then,
$\nabla _{X_0}$
. Then,
![]() $\Phi _z$
(resp.
$\Phi _z$
(resp.
![]() $\Theta _{X_0}$
) may be extended to
$\Theta _{X_0}$
) may be extended to
![]() $V\bigotimes _F \mathcal {B}_0$
, which is still denoted by
$V\bigotimes _F \mathcal {B}_0$
, which is still denoted by
![]() $\Phi _z$
(resp.
$\Phi _z$
(resp.
![]() $\Theta _{X_0}$
). By the unit-root pLMT [Reference Kedlaya9, Theorem 6.11], we find:
$\Theta _{X_0}$
). By the unit-root pLMT [Reference Kedlaya9, Theorem 6.11], we find:
-
(i) a finite separable extension
 $L(V)$
of
$L(V)$
of
 $\kappa (\!( t )\!)$
;
$\kappa (\!( t )\!)$
; -
(ii) for each
 $1\leq i\leq l$
, a basis
$1\leq i\leq l$
, a basis
 $\textbf {w}_1^{(i)},\ldots ,\textbf {w}_{d_i}^{(i)}$
for
$\textbf {w}_1^{(i)},\ldots ,\textbf {w}_{d_i}^{(i)}$
for
 $V_{\mathcal {R},\mu _i}\bigotimes _{\mathcal {R}} \mathcal {R}_{L(V)}$
over
$V_{\mathcal {R},\mu _i}\bigotimes _{\mathcal {R}} \mathcal {R}_{L(V)}$
over
 $\mathcal {R}_{L(V)}$
such that
$\mathcal {R}_{L(V)}$
such that
 $\Theta _{X_0}(\textbf {w}_j^{(i)})=0$
, for all
$\Theta _{X_0}(\textbf {w}_j^{(i)})=0$
, for all
 $1\leq j\leq d_i$
.
$1\leq j\leq d_i$
.
Then, for each
![]() $1\leq i\leq l$
, we have that
$1\leq i\leq l$
, we have that
is a
![]() $d_i$
-dimensional
$d_i$
-dimensional
![]() $K^{\operatorname {\mathrm {nr}}}$
-vector space spanned by
$K^{\operatorname {\mathrm {nr}}}$
-vector space spanned by
![]() $\textbf {w}_1^{(i)},\ldots ,\textbf {w}_{d_i}^{(i)}$
. In particular, we have
$\textbf {w}_1^{(i)},\ldots ,\textbf {w}_{d_i}^{(i)}$
. In particular, we have
 $$ \begin{align*} (V_{\mathcal{B}_0} )^{\Theta_{X_0}=0}= \big\{ x\in V_{\mathcal{B}_0} \mid \Theta_{X_0}(x)=0 \big\}=\operatorname*{\mathrm{\bigoplus}}\limits_{i=1}^l W_i,\end{align*} $$
$$ \begin{align*} (V_{\mathcal{B}_0} )^{\Theta_{X_0}=0}= \big\{ x\in V_{\mathcal{B}_0} \mid \Theta_{X_0}(x)=0 \big\}=\operatorname*{\mathrm{\bigoplus}}\limits_{i=1}^l W_i,\end{align*} $$
which is a
![]() $d_i$
-dimensional
$d_i$
-dimensional
![]() $K^{\operatorname {\mathrm {nr}}}$
-vector space.
$K^{\operatorname {\mathrm {nr}}}$
-vector space.
We now have two
![]() $K^{\operatorname {\mathrm {nr}}}$
-valued fiber functors
$K^{\operatorname {\mathrm {nr}}}$
-valued fiber functors
and
Moreover, we have an action
of
![]() $\operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega _1)$
on
$\operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega _1)$
on
![]() $\operatorname {\mathrm {\underline {Isom}}}^{\otimes }(\omega _1,\omega _2)$
, given by precomposition. We note that
$\operatorname {\mathrm {\underline {Isom}}}^{\otimes }(\omega _1,\omega _2)$
, given by precomposition. We note that
![]() $\operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega _1)=\operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega ^G\otimes K^{\operatorname {\mathrm {nr}}})\cong G_{K^{\operatorname {\mathrm {nr}}}}$
,Footnote
2
so
$\operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega _1)=\operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega ^G\otimes K^{\operatorname {\mathrm {nr}}})\cong G_{K^{\operatorname {\mathrm {nr}}}}$
,Footnote
2
so
![]() $\operatorname {\mathrm {\underline {Isom}}}^{\otimes }(\omega _1,\omega _2)$
may be viewed as a
$\operatorname {\mathrm {\underline {Isom}}}^{\otimes }(\omega _1,\omega _2)$
may be viewed as a
![]() $G_{K^{\operatorname {\mathrm {nr}}}}$
-torsor over
$G_{K^{\operatorname {\mathrm {nr}}}}$
-torsor over
![]() $K^{\operatorname {\mathrm {nr}}}$
. By Lemma 4.22, we have
$K^{\operatorname {\mathrm {nr}}}$
. By Lemma 4.22, we have
![]() $H^1(K^{\operatorname {\mathrm {nr}}},G_{K^{\operatorname {\mathrm {nr}}}})=1$
. Thus,
$H^1(K^{\operatorname {\mathrm {nr}}},G_{K^{\operatorname {\mathrm {nr}}}})=1$
. Thus,
![]() $\operatorname {\mathrm {\underline {Isom}}}^{\otimes }(\omega _1,\omega _2)$
is isomorphic to the trivial
$\operatorname {\mathrm {\underline {Isom}}}^{\otimes }(\omega _1,\omega _2)$
is isomorphic to the trivial
![]() $G_{K^{\operatorname {\mathrm {nr}}}}$
-torsor over
$G_{K^{\operatorname {\mathrm {nr}}}}$
-torsor over
![]() $K^{\operatorname {\mathrm {nr}}}$
, i.e., we have
$K^{\operatorname {\mathrm {nr}}}$
, i.e., we have
![]() $\operatorname {\mathrm {\underline {Isom}}}^{\otimes }(\omega _1,\omega _2)_{K^{\operatorname {\mathrm {nr}}}} \cong G_{K^{\operatorname {\mathrm {nr}}}}$
.
$\operatorname {\mathrm {\underline {Isom}}}^{\otimes }(\omega _1,\omega _2)_{K^{\operatorname {\mathrm {nr}}}} \cong G_{K^{\operatorname {\mathrm {nr}}}}$
.
On the other hand, we have an isomorphism
![]() $\gamma \colon \omega _2\otimes \mathcal {B}_0 \to \omega _1 \otimes \mathcal {B}_0$
of tensor functors, induced by the
$\gamma \colon \omega _2\otimes \mathcal {B}_0 \to \omega _1 \otimes \mathcal {B}_0$
of tensor functors, induced by the
![]() $\mathcal {B}_0$
-linear extension of the inclusion
$\mathcal {B}_0$
-linear extension of the inclusion
for all
![]() $(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
. We now fix
$(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
. We now fix
![]() $\beta \in \operatorname {\mathrm {\underline {Isom}}}^{\otimes }(\omega _1,\omega _2)(K^{\operatorname {\mathrm {nr}}})$
; we then have an element
$\beta \in \operatorname {\mathrm {\underline {Isom}}}^{\otimes }(\omega _1,\omega _2)(K^{\operatorname {\mathrm {nr}}})$
; we then have an element
![]() $\tilde \beta := \gamma \circ \beta _{\mathcal {B}_0} \in \operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega _1\otimes \mathcal {B}_0)(\mathcal {B}_0)=G(\mathcal {B}_0)$
. Let
$\tilde \beta := \gamma \circ \beta _{\mathcal {B}_0} \in \operatorname {\mathrm {\underline {Aut}}}^{\otimes }(\omega _1\otimes \mathcal {B}_0)(\mathcal {B}_0)=G(\mathcal {B}_0)$
. Let
![]() $b\in G(\mathcal {B}_0)$
be the inverse of the image of
$b\in G(\mathcal {B}_0)$
be the inverse of the image of
![]() $\tilde \beta $
under the following isomorphism:
$\tilde \beta $
under the following isomorphism:
Because
![]() $F[G]$
is finitely presented over F, the functor
$F[G]$
is finitely presented over F, the functor
![]() $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {\textbf {Alg}}}_F}(F[G],\rule {2mm}{0.15mm})$
commutes with colimits. We have
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {\textbf {Alg}}}_F}(F[G],\rule {2mm}{0.15mm})$
commutes with colimits. We have
where L runs over all finite separable extensions of
![]() $\kappa (\!( t )\!)$
; we thus find a finite separable extension L of
$\kappa (\!( t )\!)$
; we thus find a finite separable extension L of
![]() $\kappa (\!( t )\!)$
such that
$\kappa (\!( t )\!)$
such that
![]() $b\in G(\mathcal {R}_L)$
.
$b\in G(\mathcal {R}_L)$
.
For any
![]() $(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, it follows from the construction of b that the automorphism
$(V,\rho )\in \operatorname {\mathrm {\textbf {Rep}}}_F(G)$
, it follows from the construction of b that the automorphism
![]() $\rho (b^{-1})\colon V_{\mathcal {B}_0} \to V_{\mathcal {B}_0}$
factors through
$\rho (b^{-1})\colon V_{\mathcal {B}_0} \to V_{\mathcal {B}_0}$
factors through
![]() $(V_{\mathcal {B}_0})^{\Theta _{X_0}=0} \otimes \mathcal {B}_0$
. Notice that
$(V_{\mathcal {B}_0})^{\Theta _{X_0}=0} \otimes \mathcal {B}_0$
. Notice that
![]() $\Theta _{X_0}$
and
$\Theta _{X_0}$
and
![]() $X_0$
agree on
$X_0$
agree on
![]() $\omega _1(V)=V_{K^{\operatorname {\mathrm {nr}}}}$
. Therefore, we have
$\omega _1(V)=V_{K^{\operatorname {\mathrm {nr}}}}$
. Therefore, we have
We now fix a faithful representation
![]() $(V,\rho )$
. The equality (4) then implies
$(V,\rho )$
. The equality (4) then implies
Put
![]() $X_1:= X-X_0\in \mathfrak {g}_{\mathcal {R}}$
; we then have
$X_1:= X-X_0\in \mathfrak {g}_{\mathcal {R}}$
; we then have
 $$ \begin{align*} \Gamma_{b}(X) &=\operatorname{\mathrm{Ad}}(b)(X_0+X_1)-\operatorname{\mathrm{dlog}}(b)\\ &= \operatorname{\mathrm{Ad}}(b)(X_0)-\operatorname{\mathrm{dlog}}(b)+\operatorname{\mathrm{Ad}}(b)(X_1)\\ &=\Gamma_{b}(X_0)+\operatorname{\mathrm{Ad}}(b)(X_1)\\ &=\operatorname{\mathrm{Ad}}(b)(X_1). \end{align*} $$
$$ \begin{align*} \Gamma_{b}(X) &=\operatorname{\mathrm{Ad}}(b)(X_0+X_1)-\operatorname{\mathrm{dlog}}(b)\\ &= \operatorname{\mathrm{Ad}}(b)(X_0)-\operatorname{\mathrm{dlog}}(b)+\operatorname{\mathrm{Ad}}(b)(X_1)\\ &=\Gamma_{b}(X_0)+\operatorname{\mathrm{Ad}}(b)(X_1)\\ &=\operatorname{\mathrm{Ad}}(b)(X_1). \end{align*} $$
Conserving the notation as in the second paragraph,
![]() $\Theta _X=\rho (b) X_1 \rho (b^{-1})$
acts in the basis
$\Theta _X=\rho (b) X_1 \rho (b^{-1})$
acts in the basis
![]() $\textbf {w}_1^{(1)},\ldots ,\textbf {w}_{d_1}^{(1)},\ldots ,\textbf {w}_1^{(l)},\ldots ,\textbf {w}_{d_l}^{(l)}$
via a matrix of the form
$\textbf {w}_1^{(1)},\ldots ,\textbf {w}_{d_1}^{(1)},\ldots ,\textbf {w}_1^{(l)},\ldots ,\textbf {w}_{d_l}^{(l)}$
via a matrix of the form
Here, the ith
![]() $0$
in the diagonal denotes the zero matrix of size
$0$
in the diagonal denotes the zero matrix of size
![]() $d_i\times d_i$
. Hence,
$d_i\times d_i$
. Hence,
![]() $\Gamma _{b}(X)\in \operatorname {\mathrm {Lie}} \big (U_{G_{\mathcal {R}_L}}(-\lambda _{g,\mathcal {R}_L})\big )=\operatorname {\mathrm {Lie}}\big ( U_{G_{\mathcal {R}}}(-\lambda _g)_{\mathcal {R}_L} \big )=\operatorname {\mathrm {Lie}} \big (U_{G_{\mathcal {R}}}(-\lambda _g)\big )_{\mathcal {R}_L}$
, as desired.▪
$\Gamma _{b}(X)\in \operatorname {\mathrm {Lie}} \big (U_{G_{\mathcal {R}_L}}(-\lambda _{g,\mathcal {R}_L})\big )=\operatorname {\mathrm {Lie}}\big ( U_{G_{\mathcal {R}}}(-\lambda _g)_{\mathcal {R}_L} \big )=\operatorname {\mathrm {Lie}} \big (U_{G_{\mathcal {R}}}(-\lambda _g)\big )_{\mathcal {R}_L}$
, as desired.▪
Acknowledgment
The content of this paper is part of the author’s Ph.D. thesis carried out at Humboldt-Universität zu Berlin. He owes a deep gratitude to his supervisor Elmar Grosse-Klönne for providing him this problem, and for all the helpful discussions. He would like to thank the external examiners of the thesis for their valuable feedback. He is also indebted to Claudius Heyer for many constructive suggestions. Finally, he would like to thank the anonymous referees for very helpful comments and suggestions which have greatly improved the presentation of this paper.