Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-11T07:15:55.934Z Has data issue: false hasContentIssue false
  • English
  • Français

Further inequalities and properties of p-inner parallel bodies

Part of: General convexity

Published online by Cambridge University Press:  09 November 2020

Yingying Lou ,
Dongmeng Xi  and
Zhenbing Zeng
Yingying Lou*
Affiliation:
Department of Mathematics, Shanghai University, Shanghai200444, China e-mail: dongmeng.xi@live.comzbzeng@shu.edu.cn
Dongmeng Xi
Affiliation:
Department of Mathematics, Shanghai University, Shanghai200444, China e-mail: dongmeng.xi@live.comzbzeng@shu.edu.cn
Zhenbing Zeng
Affiliation:
Department of Mathematics, Shanghai University, Shanghai200444, China e-mail: dongmeng.xi@live.comzbzeng@shu.edu.cn
*
e-mail: louyingying@i.shu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A. R. Martínez Fernández obtained upper bounds for quermassintegrals of the p-inner parallel bodies: an extension of the classical inner parallel body to the 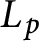$L_p$ -Brunn-Minkowski theory. In this paper, we establish (sharp) upper and lower bounds for quermassintegrals of p-inner parallel bodies. Moreover, the sufficient and necessary conditions of the equality case for the main inequality are obtained, which characterize the so-called tangential bodies.

Keywords

p-Inner parallel body0-extreme normal vectortangential body

MSC classification

Primary: 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces)
Secondary: 52A39: Mixed volumes and related topics 52A40: Inequalities and extremum problems
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 2 , April 2022 , pp. 368 - 380
Check for updates
Copyright
© Canadian Mathematical Society 2020

Footnotes

D. X. was supported by the NSFC 11601310. Z. Z. was supported by the NSFC 11471209.

References

Firey, W. J., $p$ -Means of convex bodies . Math. Scand. 10(1962), 17–24. https://doi.org/10.7146/math.scand.a-10510 CrossRefGoogle Scholar
Gardner, R. J., Geometric tomography . 2nd ed., Encyclopedia of Mathematics and its Applications, 58, Cambridge University Press, Cambridge, MA, 2006. http://doi.org/10.1017/CBO9781107341029 CrossRefGoogle Scholar
Hardy, G. H., Littlewood, J. E., and Pólya, G., Inequalities . 2nd ed., Cambridge University Press, Cambridge, MA, 1952.Google Scholar
Cifre, M. A. Hernández, Fernández, A. R. Martínez, and Gómez, E. Saorín, Differentiability properties of the family of $p$ -parallel bodies . Appl. Anal. Discrete Math. 10(2016), no. 1, 186–207. https://doi.org/10.2298/aadm160325005c CrossRefGoogle Scholar
Cifre, M. A. Hernández and Saorín, E., On inner parallel bodies and quermassintegrals . Israel J. Math. 177(2010), 29–47. https://doi.org/10.1007/s11856-010-0037-6 CrossRefGoogle Scholar
Lutwak, E., The Brunn–Minkowski–Firey theory. I. Mixed volumes and the Minkowski problem . J. Differ. Geom. 38(1993), no. 1, 131–150. https://doi.org/10.4310/jdg/1214454097 Google Scholar
Lutwak, E., The Brunn–Minkowski–Firey theory II: Affine and geominimal surface areas . Adv. Math. 118(1996), no. 2, 244–294. https://doi.org/10.1006/aima.1996.0022 CrossRefGoogle Scholar
Fernández, A. R. Martínez, Going further in the ${L}_p$ -Brunn–Minkowski theory: a $p$ -difference of convex bodies. Ph. D. thesis, University of Murcia, 2016. https://doi.org/10.13140/RG.2.2.22938.44482 CrossRefGoogle Scholar
Fernández, A. R. Martínez, Gómez, E. Saorín, and Nicolás, J. Yepes, $p$ -difference: a counterpart of Minkowski difference in the framework of the ${L}_p$ -Brunn–Minkowski theory . Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 110(2016), no. 2, 613–631. https://doi.org/10.1007/s13398-015-0253-3 Google Scholar
Schneider, R., On the Aleksandrov–Fenchel inequality . Ann. N. Y. Acad. Sci. 440(1985), no. 1, 132–141. https://doi.org/10.1111/j.1749-6632.1985.tb14547.x CrossRefGoogle Scholar
Schneider, R., Convex bodies: The Brunn–Minkowski theory . 2nd ed., Encyclopedia of Mathematics and its Applications, 151, Cambridge University Press, Cambridge, MA, 2014.Google Scholar