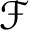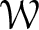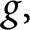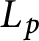1 Introduction
In [Reference Lei, Loeffler and ZerbesLLZ14] (and more generally [Reference Kings, Loeffler and ZerbesKLZ15]) Kings, Lei, Loeffler, and Zerbes constructed an Euler system for the Galois representation attached to the convolution of two modular forms. This Euler system is constructed from Beilinson–Flach classes, which are norm-compatible classes in the (absolute) étale cohomology of the fibre product of two modular curves. It turns out that these Euler system classes exist in families in the sense that there exist classes
 $$\begin{align*}{{}_{c}\mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]}} \in \operatorname{H}^1\left( \mathbb{Q}(\mu_m), D^{\mathrm{la}}(\Gamma, M(\mathcal{F})^* \hat{\otimes} M(\mathcal{G})^* ) \right) \end{align*}$$
$$\begin{align*}{{}_{c}\mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]}} \in \operatorname{H}^1\left( \mathbb{Q}(\mu_m), D^{\mathrm{la}}(\Gamma, M(\mathcal{F})^* \hat{\otimes} M(\mathcal{G})^* ) \right) \end{align*}$$
that specialise to the Beilinson–Flach Euler system at classical points. Here,
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
are Coleman families with associated Galois representations
$\mathcal {G}$
are Coleman families with associated Galois representations
![]() $M(\mathcal {F})$
and
$M(\mathcal {F})$
and
![]() $M(\mathcal {G}),$
respectively, and
$M(\mathcal {G}),$
respectively, and
![]() $D^{\mathrm {la}}(\Gamma , -)$
denotes the space of locally analytic distributions on
$D^{\mathrm {la}}(\Gamma , -)$
denotes the space of locally analytic distributions on
![]() $\Gamma \cong \mathbb {Z}_p^{\times }$
.
$\Gamma \cong \mathbb {Z}_p^{\times }$
.
The above classes are constructed in [Reference Loeffler and ZerbesLZ16] and shown to satisfy an “explicit reciprocity law” relating the bottom class
![]() $(m=1$
) to the three variable p-adic L-function constructed by Urban [Reference UrbanUrb14]. This relation can then be used to prove instances of the Bloch–Kato conjecture for the Galois representation attached to the convolution of two modular forms (including the case of an elliptic curve twisted by an Artin representation).
$(m=1$
) to the three variable p-adic L-function constructed by Urban [Reference UrbanUrb14]. This relation can then be used to prove instances of the Bloch–Kato conjecture for the Galois representation attached to the convolution of two modular forms (including the case of an elliptic curve twisted by an Artin representation).
Building on the work of Nekovář, Pottharst [Reference PottharstPot13] describes how one can put the Bloch–Kato Selmer group of a Galois representation into a family. More precisely, given a family of
![]() $G_{\mathbb {Q}}$
-representations over a rigid analytic space X, he constructs a coherent sheaf
$G_{\mathbb {Q}}$
-representations over a rigid analytic space X, he constructs a coherent sheaf
![]() $\mathcal {S}$
on X which specialises to the Bloch–Kato Selmer group at certain “crystalline” points of X, i.e., points where the Galois representation is crystalline at p. This gives rise to the natural question:
$\mathcal {S}$
on X which specialises to the Bloch–Kato Selmer group at certain “crystalline” points of X, i.e., points where the Galois representation is crystalline at p. This gives rise to the natural question:
-
• Do the Beilinson–Flach classes
 ${{}_{c}\mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}}$
(and hence the three-variable p-adic L-function) control the behaviour of
${{}_{c}\mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}}$
(and hence the three-variable p-adic L-function) control the behaviour of
 $\mathcal {S}$
?
$\mathcal {S}$
?
In this paper, we provide a partial answer to this question.
1.1 Summary of Results
Fix an odd prime
![]() $p \geq 5$
. To explain the results, we introduce the following notation. Let
$p \geq 5$
. To explain the results, we introduce the following notation. Let
![]() $N \geq 1$
be an integer prime to p and let f and g be two normalised cuspidal newforms of levels
$N \geq 1$
be an integer prime to p and let f and g be two normalised cuspidal newforms of levels
![]() $\Gamma _1(N_1)$
and
$\Gamma _1(N_1)$
and
![]() $\Gamma _1(N_2)$
and weights
$\Gamma _1(N_2)$
and weights
![]() $k+2$
and
$k+2$
and
![]() $k^{\prime }+2$
respectively, such that
$k^{\prime }+2$
respectively, such that
![]() $N_1, N_2$
both divide N and
$N_1, N_2$
both divide N and
![]() $k^{\prime }, k \geq 0$
.
$k^{\prime }, k \geq 0$
.
We assume that
![]() $k \neq k^{\prime }$
, and that one of the p-stabilisations of f and both of the p-stabilisations of g are noble (Definition 3.2.2). This implies that all three of these modular forms can be put into Coleman families. We denote the weight space parameterising all continuous characters
$k \neq k^{\prime }$
, and that one of the p-stabilisations of f and both of the p-stabilisations of g are noble (Definition 3.2.2). This implies that all three of these modular forms can be put into Coleman families. We denote the weight space parameterising all continuous characters
![]() $\mathbb {Z}_p^{\times } \to \mathbb {C}_p^{\times }$
by
$\mathbb {Z}_p^{\times } \to \mathbb {C}_p^{\times }$
by
![]() $\mathcal {W,}$
and for an integer i, we denote the character
$\mathcal {W,}$
and for an integer i, we denote the character
![]() $x \mapsto x^i$
simply by i.
$x \mapsto x^i$
simply by i.
Let E be a p-adic field and
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
two Coleman families over affinoid domains
$\mathcal {G}$
two Coleman families over affinoid domains
![]() $V_1 \subset \mathcal {W}_E$
and
$V_1 \subset \mathcal {W}_E$
and
![]() $V_2 \subset \mathcal {W}_E$
passing through p-stabilisations of f and
$V_2 \subset \mathcal {W}_E$
passing through p-stabilisations of f and
![]() $g,$
respectively (see Definition 3.1.2 for the definition of
$g,$
respectively (see Definition 3.1.2 for the definition of
![]() $\mathcal {W}_E$
). We impose the following hypotheses on f and g:
$\mathcal {W}_E$
). We impose the following hypotheses on f and g:
-
(a) The image of the Galois representation attached to the convolution of f and g is big (see (BI) in Section 7.3).
-
(b) The inertia invariants at ramified primes of the Galois representation attached to the convolution of f and g is free (flatness of inertia, see §8.1).
-
(c) f and g are not congruent modulo p to forms of a lower level (minimally ramified, see §8.1).
-
(d) The p-adic L-function attached to the convolution of f and g does not have a trivial zero, which is a condition on the Fourier coefficients of f and g (condition (NLZ) for the point
 $\mathbf {x}$
corresponding to f and g in §7.3).
$\mathbf {x}$
corresponding to f and g in §7.3).
Under these hypotheses, there exists a coherent analytic sheaf
![]() $\mathcal {S}$
on
$\mathcal {S}$
on
![]() $X:= V_1 \times V_2 \times \mathcal {W}$
, such that for all
$X:= V_1 \times V_2 \times \mathcal {W}$
, such that for all
![]() $\mathbf {x} = (k_1,\, k_2,\, j) \in X$
with
$\mathbf {x} = (k_1,\, k_2,\, j) \in X$
with
![]() $k_1,\, k_2,\, j$
integers and
$k_1,\, k_2,\, j$
integers and
![]() $1 \leq k_2+1 \leq j \leq k_1$
, the specialisation of
$1 \leq k_2+1 \leq j \leq k_1$
, the specialisation of
![]() $\mathcal {S}$
satisfies
$\mathcal {S}$
satisfies
 $$\begin{align*}\mathcal{S}_{\mathbf{x}} \cong \operatorname{H}^1_f\big(\mathbb{Q}, [M(\mathcal{F}_{k_1}) \otimes M(\mathcal{G}_{k_2})](1+j)\big)^*,\end{align*}$$
$$\begin{align*}\mathcal{S}_{\mathbf{x}} \cong \operatorname{H}^1_f\big(\mathbb{Q}, [M(\mathcal{F}_{k_1}) \otimes M(\mathcal{G}_{k_2})](1+j)\big)^*,\end{align*}$$
where
![]() $M(-)$
denotes the Galois representation attached to a modular form (in the sense of Deligne) and the right-hand side is the (dual of the) Bloch–Kato Selmer group. We recall the construction of this sheaf in Section 8 following [Reference PottharstPot13, §3.4]; the construction relies on the machinery of Selmer complexes developed by Nekovář [Reference NekovářNek06] and Pottharst [Reference PottharstPot13].
$M(-)$
denotes the Galois representation attached to a modular form (in the sense of Deligne) and the right-hand side is the (dual of the) Bloch–Kato Selmer group. We recall the construction of this sheaf in Section 8 following [Reference PottharstPot13, §3.4]; the construction relies on the machinery of Selmer complexes developed by Nekovář [Reference NekovářNek06] and Pottharst [Reference PottharstPot13].
To be more precise, one can construct a family
![]() $\overline {D}$
of overconvergent
$\overline {D}$
of overconvergent
![]() $(\varphi , \Gamma )$
-modules corresponding to the representation
$(\varphi , \Gamma )$
-modules corresponding to the representation
![]() $\overline {M} := [M(\mathcal {F})^* \hat {\otimes } M(\mathcal {G})^*](-\mathbf {j})$
, where
$\overline {M} := [M(\mathcal {F})^* \hat {\otimes } M(\mathcal {G})^*](-\mathbf {j})$
, where
![]() $-\mathbf {j}$
denotes the twist by the inverse of the universal character of
$-\mathbf {j}$
denotes the twist by the inverse of the universal character of
![]() $\mathcal {W}$
, and it is shown in [Reference LiuLiu15] that this family has a canonical triangulation (provided that
$\mathcal {W}$
, and it is shown in [Reference LiuLiu15] that this family has a canonical triangulation (provided that
![]() $V_1$
and
$V_1$
and
![]() $V_2$
are small enough). In Section 8, we define a Selmer complex with unramified local conditions away from p, and at p we choose local conditions defined by the cohomology of a family
$V_2$
are small enough). In Section 8, we define a Selmer complex with unramified local conditions away from p, and at p we choose local conditions defined by the cohomology of a family
![]() $\overline {D}^+$
of two-dimensional sub
$\overline {D}^+$
of two-dimensional sub
![]() $(\varphi , \Gamma )$
-modules appearing in the triangulation of
$(\varphi , \Gamma )$
-modules appearing in the triangulation of
![]() $\overline {D}$
; at classical weights, the local condition at p specialises to a so-called Panchishkin submodule, i.e., the Hodge–Tate weights for
$\overline {D}$
; at classical weights, the local condition at p specialises to a so-called Panchishkin submodule, i.e., the Hodge–Tate weights for
 $\overline {D}_{\mathbf {x}}^+$
(resp.
$\overline {D}_{\mathbf {x}}^+$
(resp.
 $\overline {D}_{\mathbf {x}}/\overline {D}_{\mathbf {x}}^+$
) are positive (resp. non-positive). Then, under some very mild conditions, this local condition corresponds to the Bloch–Kato local condition for the specialisation of the representation
$\overline {D}_{\mathbf {x}}/\overline {D}_{\mathbf {x}}^+$
) are positive (resp. non-positive). Then, under some very mild conditions, this local condition corresponds to the Bloch–Kato local condition for the specialisation of the representation
![]() $\overline {M}$
. We define
$\overline {M}$
. We define
![]() $\mathcal {S}$
to be
$\mathcal {S}$
to be
![]() $\operatorname {H}^2$
of this Selmer complex.
$\operatorname {H}^2$
of this Selmer complex.
In [Reference UrbanUrb14] (and [Reference Andreatta and IovitaAI17, Appendix II]) Urban constructs a three variable p-adic L-function, denoted
![]() $L_p$
, associated to
$L_p$
, associated to
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
over
$\mathcal {G}$
over
![]() $X:= V_1 \times V_2 \times \mathcal {W}$
. This p-adic L-function is constructed via the theory of families of nearly overconvergent modular forms and interpolates the critical values of the Rankin–Selberg L-function at classical specialisations. We recall the interpolation property of
$X:= V_1 \times V_2 \times \mathcal {W}$
. This p-adic L-function is constructed via the theory of families of nearly overconvergent modular forms and interpolates the critical values of the Rankin–Selberg L-function at classical specialisations. We recall the interpolation property of
![]() $L_p$
in Section 3.6. In analogy with the Bloch–Kato conjecture—which predicts that the Bloch–Kato Selmer group is controlled by the L-function for the corresponding representation—we expect that the sheaf
$L_p$
in Section 3.6. In analogy with the Bloch–Kato conjecture—which predicts that the Bloch–Kato Selmer group is controlled by the L-function for the corresponding representation—we expect that the sheaf
![]() $\mathcal {S}$
is controlled by the three variable p-adic L-function.
$\mathcal {S}$
is controlled by the three variable p-adic L-function.
More precisely, the ring
![]() $\mathcal {O}(X)$
is a disjoint union of
$\mathcal {O}(X)$
is a disjoint union of
![]() $p-1$
integral domains indexed by characters
$p-1$
integral domains indexed by characters
![]() $\eta $
of the group
$\eta $
of the group
![]() $(\mathbb {Z}/p\mathbb {Z} )^{\times }$
(each of which correspond to an irreducible component of
$(\mathbb {Z}/p\mathbb {Z} )^{\times }$
(each of which correspond to an irreducible component of
![]() $\mathcal {W}$
). For each character
$\mathcal {W}$
). For each character
![]() $\eta $
, let
$\eta $
, let
![]() $e_{\eta }$
denote the corresponding idempotent of
$e_{\eta }$
denote the corresponding idempotent of
![]() $\mathcal {O}(X)$
projecting to the domain indexed by
$\mathcal {O}(X)$
projecting to the domain indexed by
![]() $\eta $
. Since X is quasi-Stein, a coherent sheaf on X is determined by its global sections, so we will pass between these two perspectives freely. We expect the analogue of [Reference Kings, Loeffler and ZerbesKLZ17, Theorem 11.6.4] to hold in our situation, namely
$\eta $
. Since X is quasi-Stein, a coherent sheaf on X is determined by its global sections, so we will pass between these two perspectives freely. We expect the analogue of [Reference Kings, Loeffler and ZerbesKLZ17, Theorem 11.6.4] to hold in our situation, namely
Conjecture Suppose that
![]() $e_{\eta } \cdot L_p \neq 0$
. Under the hypotheses on f and g above, we expect that:
$e_{\eta } \cdot L_p \neq 0$
. Under the hypotheses on f and g above, we expect that:
-
•
 $e_{\eta } \cdot \mathcal {S}$
is a torsion
$e_{\eta } \cdot \mathcal {S}$
is a torsion
 $e_{\eta } \cdot \mathcal {O}(X)$
-module;
$e_{\eta } \cdot \mathcal {O}(X)$
-module; -
• the
 $0$
-th Fitting ideal
$0$
-th Fitting ideal
 $ \operatorname {Fitt}_0(e_{\eta } \cdot \mathcal {S}) $
divides the ideal sheaf generated by the p-adic L-function
$ \operatorname {Fitt}_0(e_{\eta } \cdot \mathcal {S}) $
divides the ideal sheaf generated by the p-adic L-function
 $e_{\eta } \cdot L_p$
.
$e_{\eta } \cdot L_p$
.
Note that the factor
![]() $\Omega $
appearing in loc. cit. is unnecessary for our formulation, since it is invertible in
$\Omega $
appearing in loc. cit. is unnecessary for our formulation, since it is invertible in
![]() $\mathcal {O}(X)$
. A particular case of this conjecture is that the support of the sheaf is contained in the vanishing locus of the p-adic L-function. We prove a partial result in this direction.
$\mathcal {O}(X)$
. A particular case of this conjecture is that the support of the sheaf is contained in the vanishing locus of the p-adic L-function. We prove a partial result in this direction.
Theorem A Let
![]() $\mathcal {S}_{k^{\prime }}$
denote the specialisation of the above sheaf at
$\mathcal {S}_{k^{\prime }}$
denote the specialisation of the above sheaf at
![]() $k^{\prime }$
in the second variable. If
$k^{\prime }$
in the second variable. If
![]() $V_1$
is small enough and the above hypotheses hold for f and g, then
$V_1$
is small enough and the above hypotheses hold for f and g, then
where “
![]() $\, \operatorname {supp}$
” denotes the support of a sheaf.
$\, \operatorname {supp}$
” denotes the support of a sheaf.
Remark 1.1.1 By Krull’s principal ideal theorem, the vanishing locus of the three-variable p-adic L-function has codimension
![]() $\leq 1$
in X. Furthermore, since
$\leq 1$
in X. Furthermore, since
![]() $L_p \neq 0$
, there exists a character
$L_p \neq 0$
, there exists a character
![]() $\eta $
such that
$\eta $
such that
![]() $e_{\eta } \cdot L_p \neq 0$
. In this case, the vanishing locus of
$e_{\eta } \cdot L_p \neq 0$
. In this case, the vanishing locus of
![]() $e_{\eta } \cdot L_p$
has codimension one in
$e_{\eta } \cdot L_p$
has codimension one in
![]() $V_1 \times V_2 \times \mathcal {W}_{\eta }$
, where
$V_1 \times V_2 \times \mathcal {W}_{\eta }$
, where
![]() $\mathcal {W}_{\eta }$
denotes the component of weight space indexed by
$\mathcal {W}_{\eta }$
denotes the component of weight space indexed by
![]() $\eta $
.
$\eta $
.
To prove Theorem A, we actually show that if
![]() $\mathbf {x}$
is a point in
$\mathbf {x}$
is a point in
![]() $V_1 \times \{k^{\prime }\} \times \mathcal {W}$
and
$V_1 \times \{k^{\prime }\} \times \mathcal {W}$
and
![]() $L_p(\mathbf {x}) \neq 0,$
then the group
$L_p(\mathbf {x}) \neq 0,$
then the group
 $\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
vanishes. Here,
$\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
vanishes. Here,
 $\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
is the cohomology in degree
$\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
is the cohomology in degree
![]() $2$
of a certain Selmer complex attached to the representation
$2$
of a certain Selmer complex attached to the representation
![]() $\overline {M}_{\mathbf {x}}$
(see §7.2), which will be shown to coincide with the specialisation of
$\overline {M}_{\mathbf {x}}$
(see §7.2), which will be shown to coincide with the specialisation of
![]() $\mathcal {S}$
at
$\mathcal {S}$
at
![]() $\mathbf {x}$
. To show that this group vanishes, we generalise the proof of [Reference Loeffler and ZerbesLZ16, Theorem 8.2.1] to non-classical specialisations; this relies heavily on the theory of
$\mathbf {x}$
. To show that this group vanishes, we generalise the proof of [Reference Loeffler and ZerbesLZ16, Theorem 8.2.1] to non-classical specialisations; this relies heavily on the theory of
![]() $(\varphi , \Gamma )$
-modules and involves a careful analysis of the Perrin–Riou logarithm (see Section 6).
$(\varphi , \Gamma )$
-modules and involves a careful analysis of the Perrin–Riou logarithm (see Section 6).
Unfortunately, with the current methods, we were unable to prove a three-variable version of this result. Indeed, a crucial step in the proof relies on the fact that
![]() $\mathcal {G}_{k^{\prime }}$
is the p-stabilisation of a classical modular form of level
$\mathcal {G}_{k^{\prime }}$
is the p-stabilisation of a classical modular form of level
![]() $N_2$
, whose other p-stabilisation is noble. By putting the other p-stabilisation into a Coleman family, we obtain two linearly independent Euler systems that can be used to bound the Bloch–Kato Selmer group, rather than just the strict Selmer group (this is also the technique used in the proof of [Reference Loeffler and ZerbesLZ16, Theorem 8.2.1]). For a general (non-classical) weight
$N_2$
, whose other p-stabilisation is noble. By putting the other p-stabilisation into a Coleman family, we obtain two linearly independent Euler systems that can be used to bound the Bloch–Kato Selmer group, rather than just the strict Selmer group (this is also the technique used in the proof of [Reference Loeffler and ZerbesLZ16, Theorem 8.2.1]). For a general (non-classical) weight
![]() $k_2$
, the specialisation
$k_2$
, the specialisation
![]() $\mathcal {G}_{k_2}$
will be the unique point on the eigencurve with associated Galois representation
$\mathcal {G}_{k_2}$
will be the unique point on the eigencurve with associated Galois representation
![]() $M(\mathcal {G}_{k_2})$
, so the above strategy will not work.
$M(\mathcal {G}_{k_2})$
, so the above strategy will not work.
1.2 Notation
Throughout the paper fix a prime
![]() $p \geq 5$
. If K is a field, then we often denote its absolute Galois group by
$p \geq 5$
. If K is a field, then we often denote its absolute Galois group by
![]() $G_K = \operatorname {\mathrm {Gal}}(K^{\mathrm {sep}}/K)$
, where
$G_K = \operatorname {\mathrm {Gal}}(K^{\mathrm {sep}}/K)$
, where
![]() $K^{\mathrm {sep}}$
denotes a fixed maximal separable closure of K.
$K^{\mathrm {sep}}$
denotes a fixed maximal separable closure of K.
Let R be a topological ring and G a topological group. We say M is a G-module over R (or an
![]() $R[G]$
-module) if M is a continuous R-module equipped with a continuous homomorphism
$R[G]$
-module) if M is a continuous R-module equipped with a continuous homomorphism
![]() $\rho : G \to \operatorname {Aut}_RM$
. We will often work within the category of
$\rho : G \to \operatorname {Aut}_RM$
. We will often work within the category of
![]() $R[G]$
-modules. This is not an abelian category in general, but it is additive and has kernels and cokernels, so we can still talk about its derived category. If M is an
$R[G]$
-modules. This is not an abelian category in general, but it is additive and has kernels and cokernels, so we can still talk about its derived category. If M is an
![]() $R[G]$
-module and the action is commutative (i.e., the map
$R[G]$
-module and the action is commutative (i.e., the map
![]() $\rho $
factors through
$\rho $
factors through
![]() $G^{\operatorname {ab}}$
), then we write
$G^{\operatorname {ab}}$
), then we write
![]() $M^{\iota }$
to mean the module M with the action given by
$M^{\iota }$
to mean the module M with the action given by
![]() $g \cdot m = \rho (g^{-1})m$
for all
$g \cdot m = \rho (g^{-1})m$
for all
![]() $g \in G$
and
$g \in G$
and
![]() $m \in M$
.
$m \in M$
.
We will often take R to be a
![]() $\mathbb {Q}_p$
-Banach algebra (or more generally, the global sections of a rigid analytic space). In this case, we write
$\mathbb {Q}_p$
-Banach algebra (or more generally, the global sections of a rigid analytic space). In this case, we write
![]() $R^\circ $
for the subring of power-bounded elements. When R is a reduced affinoid algebra, this coincides with the unit ball with respect to the supremum norm.
$R^\circ $
for the subring of power-bounded elements. When R is a reduced affinoid algebra, this coincides with the unit ball with respect to the supremum norm.
For an
![]() $R[G]$
-module M, let
$R[G]$
-module M, let
![]() $M^* := \operatorname {Hom}_{\text {cont}}(M, R)$
denote the dual representation of M and, where appropriate, we write
$M^* := \operatorname {Hom}_{\text {cont}}(M, R)$
denote the dual representation of M and, where appropriate, we write
![]() $M(n)$
to mean the representation M tensored with the n-th Tate twist. We fix a compatible system of p-th power roots of unity in
$M(n)$
to mean the representation M tensored with the n-th Tate twist. We fix a compatible system of p-th power roots of unity in
![]() $\bar {\mathbb {Q}}_p$
, so in the case where M is a Galois representation,
$\bar {\mathbb {Q}}_p$
, so in the case where M is a Galois representation,
![]() $M(1)$
is just M twisted by the cyclotomic character
$M(1)$
is just M twisted by the cyclotomic character
![]() $\chi _{\text {cycl}}$
. In this paper, the cyclotomic character will always have Hodge–Tate weight
$\chi _{\text {cycl}}$
. In this paper, the cyclotomic character will always have Hodge–Tate weight
![]() $1$
.
$1$
.
If M is an
![]() $R[G]$
-module, then we denote its i-th group cohomology by
$R[G]$
-module, then we denote its i-th group cohomology by
![]() $\operatorname {H}^i(G, M)$
. If
$\operatorname {H}^i(G, M)$
. If
![]() $G_K$
is the absolute Galois group of a field
$G_K$
is the absolute Galois group of a field
![]() $K,$
then we will also sometimes write
$K,$
then we will also sometimes write
![]() $\mathrm {H}^{i}(K, M)$
for
$\mathrm {H}^{i}(K, M)$
for
![]() $\operatorname {H}^i(G_K, M)$
.
$\operatorname {H}^i(G_K, M)$
.
When talking about left (resp. right) exact functors F, we write
![]() $\mathbf {R}F$
(resp.
$\mathbf {R}F$
(resp.
![]() $\mathbf {L}F$
) for the right (resp. left) derived functors of F. In particular, if M is a
$\mathbf {L}F$
) for the right (resp. left) derived functors of F. In particular, if M is a
![]() $R[G]$
-module, then we write
$R[G]$
-module, then we write
![]() $\mathbf {R}\Gamma _{\mathrm {cont}}(G, M)$
for the image of the complex of continuous cochains of M in the derived category of R-modules.
$\mathbf {R}\Gamma _{\mathrm {cont}}(G, M)$
for the image of the complex of continuous cochains of M in the derived category of R-modules.
If X is an object defined over a ring R and we have a homomorphism
![]() $R \to R'$
, then we denote the base change of X to
$R \to R'$
, then we denote the base change of X to
![]() $R'$
by
$R'$
by
![]() $X_{R^{\prime }}$
.
$X_{R^{\prime }}$
.
For a positive integer m, we let
![]() $\mu _m^\circ $
denote the group scheme (over
$\mu _m^\circ $
denote the group scheme (over
![]() $\mathbb {Q}$
) of m-th roots of unity.
$\mathbb {Q}$
) of m-th roots of unity.
Finally, we note that throughout the paper, any étale cohomology group refers to continuous étale cohomology in the sense of Jannsen [Reference JannsenJan88].
2 Modular Curves
In this section we will define the modular curves that will be used throughout the paper. Let
![]() $\mathcal {H}^{\pm } := \mathbb {C} - \mathbb {R}$
denote the upper and lower complex half-space and denote the finite adeles of
$\mathcal {H}^{\pm } := \mathbb {C} - \mathbb {R}$
denote the upper and lower complex half-space and denote the finite adeles of
![]() $\mathbb {Q}$
by
$\mathbb {Q}$
by
![]() $\mathbb {A}_f$
. For a compact open subgroup
$\mathbb {A}_f$
. For a compact open subgroup
![]() $K \subset \operatorname {GL}_2(\mathbb {A}_f)$
, we let
$K \subset \operatorname {GL}_2(\mathbb {A}_f)$
, we let
 $$ \begin{align} Y_K := \operatorname{GL}_2(\mathbb{Q}) \backslash \left[ \mathcal{H}^{\pm} \times \operatorname{GL}_2(\mathbb{A}_f)/K \right] \,. \end{align} $$
$$ \begin{align} Y_K := \operatorname{GL}_2(\mathbb{Q}) \backslash \left[ \mathcal{H}^{\pm} \times \operatorname{GL}_2(\mathbb{A}_f)/K \right] \,. \end{align} $$
We assume that K is sufficiently small so that
![]() $Y_K$
has the structure of a Shimura variety. This Shimura variety has a canonical model over
$Y_K$
has the structure of a Shimura variety. This Shimura variety has a canonical model over
![]() $\mathbb {Q}$
(which we will also denote by
$\mathbb {Q}$
(which we will also denote by
![]() $Y_K$
), and we will refer to this as the modular curve of level K. In this paper, we are interested in the following choices of K.
$Y_K$
), and we will refer to this as the modular curve of level K. In this paper, we are interested in the following choices of K.
Let
![]() $m, N$
be two positive integers such that
$m, N$
be two positive integers such that
![]() $m(N+1) \geq 5$
. Then the subgroup
$m(N+1) \geq 5$
. Then the subgroup
 $$\begin{align*}K_{m, N} := \bigg\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{GL}_2(\widehat{\mathbb{Z}}) \Bigm| \begin{array}{ccc} a \equiv 1, & b \equiv 0 & \mod{m\widehat{\mathbb{Z}}} \\ c \equiv 0, & d \equiv 1 & \mod{mN\widehat{\mathbb{Z}}} \end{array} \bigg\} \end{align*}$$
$$\begin{align*}K_{m, N} := \bigg\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{GL}_2(\widehat{\mathbb{Z}}) \Bigm| \begin{array}{ccc} a \equiv 1, & b \equiv 0 & \mod{m\widehat{\mathbb{Z}}} \\ c \equiv 0, & d \equiv 1 & \mod{mN\widehat{\mathbb{Z}}} \end{array} \bigg\} \end{align*}$$
is sufficiently small, and we denote the corresponding modular curve by
![]() $Y(m, mN) := Y_{K_{m, N}}$
. If
$Y(m, mN) := Y_{K_{m, N}}$
. If
![]() $m=1$
we simply denote this curve by
$m=1$
we simply denote this curve by
![]() $Y_1(N)$
. The modular curve
$Y_1(N)$
. The modular curve
![]() $Y(m, mN)$
represents the contravariant functor taking a
$Y(m, mN)$
represents the contravariant functor taking a
![]() $\mathbb {Q}$
-scheme S to the set of isomorphism classes of triples
$\mathbb {Q}$
-scheme S to the set of isomorphism classes of triples
![]() $(E, P, Q)$
, where
$(E, P, Q)$
, where
![]() $E/S$
is an elliptic scheme, P is a torsion section of order
$E/S$
is an elliptic scheme, P is a torsion section of order
![]() $m,$
and Q is a torsion section of order
$m,$
and Q is a torsion section of order
![]() $mN$
, such that P and Q are linearly independent, in the sense that the map
$mN$
, such that P and Q are linearly independent, in the sense that the map
![]() $\mathbb {Z}/m\mathbb {Z} \times \mathbb {Z}/mN\mathbb {Z} \to E(S)$
given by
$\mathbb {Z}/m\mathbb {Z} \times \mathbb {Z}/mN\mathbb {Z} \to E(S)$
given by
![]() $(a, b) \mapsto aP +bQ$
is injective. There is a natural morphism
$(a, b) \mapsto aP +bQ$
is injective. There is a natural morphism
![]() $Y(m, mN) \to \mu _m^\circ $
given by the Weil pairing on the points
$Y(m, mN) \to \mu _m^\circ $
given by the Weil pairing on the points
![]() $P, NQ$
, and the fibres of this map are smooth, geometrically connected curves.
$P, NQ$
, and the fibres of this map are smooth, geometrically connected curves.
For an integer
![]() $N \geq 1$
not divisible by p, we also set
$N \geq 1$
not divisible by p, we also set
 $$\begin{align*}K_1(N(p)) := \bigg\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{GL}_2(\widehat{\mathbb{Z}}) \Bigm| c \equiv 0 \mod{pN \widehat{\mathbb{Z}}}, \quad d \equiv 1 \mod{N \widehat{\mathbb{Z}}} \bigg\}. \end{align*}$$
$$\begin{align*}K_1(N(p)) := \bigg\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{GL}_2(\widehat{\mathbb{Z}}) \Bigm| c \equiv 0 \mod{pN \widehat{\mathbb{Z}}}, \quad d \equiv 1 \mod{N \widehat{\mathbb{Z}}} \bigg\}. \end{align*}$$
This is a sufficiently small subgroup, and we denote the corresponding modular curve by
![]() $Y_1(N(p))$
. This has a moduli interpretation as the contravariant functor taking a
$Y_1(N(p))$
. This has a moduli interpretation as the contravariant functor taking a
![]() $\mathbb {Q}$
-scheme S to the set of isomorphism classes of triples
$\mathbb {Q}$
-scheme S to the set of isomorphism classes of triples
![]() $(E, P, C)$
, where
$(E, P, C)$
, where
![]() $E/S$
is an elliptic scheme, P is a torsion section of order
$E/S$
is an elliptic scheme, P is a torsion section of order
![]() $N,$
and C is a finite flat subgroup scheme of
$N,$
and C is a finite flat subgroup scheme of
![]() $E[p]$
(the p-torsion of E) of order p.
$E[p]$
(the p-torsion of E) of order p.
It will also be useful to introduce several maps between these modular curves.
-
• For a positive integer d, we define the following map:
(2.0.2)as the morphism that sends a triple $$ \begin{align} \Xi_d \colon Y(dm, dmN) \longrightarrow Y(m, m N) \end{align} $$
$$ \begin{align} \Xi_d \colon Y(dm, dmN) \longrightarrow Y(m, m N) \end{align} $$
 $(E, P, Q)$
to the triple
$(E, P, Q)$
to the triple
 $(E/\langle mP \rangle , P \! \! \mod {mP}, dQ \! \! \mod {mP})$
, where
$(E/\langle mP \rangle , P \! \! \mod {mP}, dQ \! \! \mod {mP})$
, where
 $\langle mP \rangle $
denotes the cyclic subgroup generated by
$\langle mP \rangle $
denotes the cyclic subgroup generated by
 $mP$
.
$mP$
.
-
• Recall that
 $\mu _m^\circ $
denotes the group scheme (over
$\mu _m^\circ $
denotes the group scheme (over
 $\mathbb {Q}$
) of
$\mathbb {Q}$
) of
 $m^{\prime }$
-th roots of unity. We define the following map (2.0.3)as the morphism given by
$m^{\prime }$
-th roots of unity. We define the following map (2.0.3)as the morphism given by $$ \begin{align} t_m \colon Y(m, mN) \longrightarrow Y_1(N) \times_{\mathbb{Q}} \mu_m^\circ \end{align} $$
$$ \begin{align} t_m \colon Y(m, mN) \longrightarrow Y_1(N) \times_{\mathbb{Q}} \mu_m^\circ \end{align} $$
 $(E, P, Q) \mapsto ((E/\langle P \rangle , mQ \! \! \mod {P}), \langle P, NQ \rangle )$
, where
$(E, P, Q) \mapsto ((E/\langle P \rangle , mQ \! \! \mod {P}), \langle P, NQ \rangle )$
, where
 $\langle -, - \rangle $
denotes the Weil pairing on
$\langle -, - \rangle $
denotes the Weil pairing on
 $E[m]$
and
$E[m]$
and
 $\langle P \rangle $
is the subgroup generated by P.
$\langle P \rangle $
is the subgroup generated by P.
-
• Let
 $N^{\prime }$
be a positive integer dividing N. We define the following map: (2.0.4)to be the morphism sending
$N^{\prime }$
be a positive integer dividing N. We define the following map: (2.0.4)to be the morphism sending $$ \begin{align} s_{N^{\prime}} \colon Y_1(Np) \longrightarrow Y_1(N^{\prime}(p)) \end{align} $$
$$ \begin{align} s_{N^{\prime}} \colon Y_1(Np) \longrightarrow Y_1(N^{\prime}(p)) \end{align} $$
 $(E, Q)$
to
$(E, Q)$
to
 $\big (E, \frac {Np}{N^{\prime }} \cdot Q, \langle N \cdot Q \rangle \big )$
, where
$\big (E, \frac {Np}{N^{\prime }} \cdot Q, \langle N \cdot Q \rangle \big )$
, where
 $\langle N \cdot Q \rangle $
denotes the cyclic group scheme generated by the p-torsion section
$\langle N \cdot Q \rangle $
denotes the cyclic group scheme generated by the p-torsion section
 $N \cdot Q$
.
$N \cdot Q$
.
The first two maps are compatible in the following sense.
Lemma 2.0.5 Let
![]() $m, N$
be two positive integers with
$m, N$
be two positive integers with
![]() $m(N+1) \geq 5$
and let d be a positive integer. Then we have the following commutative diagram:
$m(N+1) \geq 5$
and let d be a positive integer. Then we have the following commutative diagram:

where the bottom map is induced from the d-th power map
![]() $\mu _{dm}^\circ \to \mu _{m}^\circ $
.
$\mu _{dm}^\circ \to \mu _{m}^\circ $
.
Proof This is immediate from the definitions. ▪
3 Families of Modular Forms and Galois Representations
3.1 Weight Space
Definition 3.1.1 Let
 $\Lambda := \mathbb {Z}_p \left [\!\!\left [ \mathbb {Z}_p^{\times } \right ]\!\!\right ]$
. The weight space
$\Lambda := \mathbb {Z}_p \left [\!\!\left [ \mathbb {Z}_p^{\times } \right ]\!\!\right ]$
. The weight space
![]() $\mathcal {W}$
is defined to be the rigid generic fibre of the formal spectrum
$\mathcal {W}$
is defined to be the rigid generic fibre of the formal spectrum
![]() $\operatorname {Spf}\Lambda $
. It represents the functor taking a rigid analytic space X over
$\operatorname {Spf}\Lambda $
. It represents the functor taking a rigid analytic space X over
![]() $\operatorname {Sp}\mathbb {Q}_p$
to the set
$\operatorname {Sp}\mathbb {Q}_p$
to the set
 $\operatorname {Hom}_{\text {cont}}(\mathbb {Z}_p^{\times }, \mathcal {O}_X(X)^{\times })$
. Let
$\operatorname {Hom}_{\text {cont}}(\mathbb {Z}_p^{\times }, \mathcal {O}_X(X)^{\times })$
. Let
 $$\begin{align*}\kappa \colon \mathbb{Z}_p^{\times} \longrightarrow \Lambda^{\times} \subset \mathcal{O}_{\mathcal{W}}(\mathcal{W})^{\times} \end{align*}$$
$$\begin{align*}\kappa \colon \mathbb{Z}_p^{\times} \longrightarrow \Lambda^{\times} \subset \mathcal{O}_{\mathcal{W}}(\mathcal{W})^{\times} \end{align*}$$
denote the tautological character.
The space
![]() $\mathcal {W}$
is isomorphic to a union of
$\mathcal {W}$
is isomorphic to a union of
![]() $p-1$
wide open discs (recall that we have assumed
$p-1$
wide open discs (recall that we have assumed
![]() $p>2$
).
$p>2$
).
Definition 3.1.2 Let E be a finite extension of
![]() $\mathbb {Q}_p$
with ring of integers
$\mathbb {Q}_p$
with ring of integers
![]() $\mathcal {O}_E$
, and let
$\mathcal {O}_E$
, and let
![]() $\mathcal {U}$
be a wide open disc in
$\mathcal {U}$
be a wide open disc in
![]() $\mathcal {W}_E := \mathcal {W} \times _{\operatorname {Sp}(\mathbb {Q}_p)} \operatorname {Sp}(E)$
. Define
$\mathcal {W}_E := \mathcal {W} \times _{\operatorname {Sp}(\mathbb {Q}_p)} \operatorname {Sp}(E)$
. Define
![]() $\Lambda _{\mathcal {U}} := \mathcal {O}_{\mathcal {W}}(\mathcal {U})^{\circ }$
, the subring of power-bounded elements of
$\Lambda _{\mathcal {U}} := \mathcal {O}_{\mathcal {W}}(\mathcal {U})^{\circ }$
, the subring of power-bounded elements of
![]() $\mathcal {O}_{\mathcal {W}}(\mathcal {U})$
(so
$\mathcal {O}_{\mathcal {W}}(\mathcal {U})$
(so
![]() $\Lambda $
is non-canonically isomorphic to
$\Lambda $
is non-canonically isomorphic to
![]() $\mathcal {O}_E \left [\!\!\left [ t \right ]\!\!\right ]$
), and write
$\mathcal {O}_E \left [\!\!\left [ t \right ]\!\!\right ]$
), and write
 $$\begin{align*}\kappa_{\mathcal{U}} \colon \mathbb{Z}_p^{\times} \to \Lambda_{\mathcal{U}}^{\times} \end{align*}$$
$$\begin{align*}\kappa_{\mathcal{U}} \colon \mathbb{Z}_p^{\times} \to \Lambda_{\mathcal{U}}^{\times} \end{align*}$$
for the map induced by
![]() $\kappa $
.
$\kappa $
.
Definition 3.1.3 The m-accessible part of the weight space, denoted
![]() $\mathcal {W}_m$
, is the union of wide open discs defined by the inequality
$\mathcal {W}_m$
, is the union of wide open discs defined by the inequality
 $$\begin{align*}\big| \kappa(1+p^{m+1}) - 1 \big|^{p-1} < |p|. \end{align*}$$
$$\begin{align*}\big| \kappa(1+p^{m+1}) - 1 \big|^{p-1} < |p|. \end{align*}$$
We will eventually restrict our attention to
![]() $\mathcal {W}_0$
.
$\mathcal {W}_0$
.
Definition 3.1.4 A classical point of
![]() $\mathcal {W}$
is a point corresponding to the character
$\mathcal {W}$
is a point corresponding to the character
![]() $z \mapsto z^k$
for some nonnegative integer k.
$z \mapsto z^k$
for some nonnegative integer k.
Remark 3.1.5 The previous definition is an abuse of notation, since the weight
![]() $z \mapsto \chi (z) z^k$
, for
$z \mapsto \chi (z) z^k$
, for
![]() $\chi $
a finite order character, can be the weight of a point on the eigencurve corresponding to a classical modular form. But we will not need to consider this more general class of weights.
$\chi $
a finite order character, can be the weight of a point on the eigencurve corresponding to a classical modular form. But we will not need to consider this more general class of weights.
3.2 Families of Overconvergent Modular Forms
Definition 3.2.1 Let E be a finite extension of
![]() $\mathbb {Q}_p$
with ring of integers
$\mathbb {Q}_p$
with ring of integers
![]() $\mathcal {O}_E$
, and let
$\mathcal {O}_E$
, and let
![]() $\mathcal {U} \subseteq (\mathcal {W}_0)_E$
be a wide open disc containing a classical point. A Coleman family
$\mathcal {U} \subseteq (\mathcal {W}_0)_E$
be a wide open disc containing a classical point. A Coleman family
![]() ${\mathcal {F}}$
over
${\mathcal {F}}$
over
![]() $\mathcal {U}$
(of tame level N) is formal power series
$\mathcal {U}$
(of tame level N) is formal power series
![]() $\sum _{n=1}^{\infty } a_n({\mathcal {F}}) q^n \in q \Lambda _{\mathcal {U}} \left [\!\!\left [ q \right ]\!\!\right ]$
satisfying the following properties:
$\sum _{n=1}^{\infty } a_n({\mathcal {F}}) q^n \in q \Lambda _{\mathcal {U}} \left [\!\!\left [ q \right ]\!\!\right ]$
satisfying the following properties:
-
(i)
 $a_1({\mathcal {F}}) = 1$
and
$a_1({\mathcal {F}}) = 1$
and
 $a_p({\mathcal {F}}) \in \Lambda _{\mathcal {U}}[\frac {1}{p}]^{\times }$
.
$a_p({\mathcal {F}}) \in \Lambda _{\mathcal {U}}[\frac {1}{p}]^{\times }$
. -
(ii) For all but finitely many classical weights k contained in
 $\mathcal {U}$
, the restriction of
$\mathcal {U}$
, the restriction of
 ${\mathcal {F}}$
to k is the q-expansion of a classical modular form of weight
${\mathcal {F}}$
to k is the q-expansion of a classical modular form of weight
 $k+2$
and level
$k+2$
and level
 $\Gamma _1(N) \cap \Gamma _0(p)$
that is a normalized eigenform for the Hecke operators (away from
$\Gamma _1(N) \cap \Gamma _0(p)$
that is a normalized eigenform for the Hecke operators (away from
 $Np$
).
$Np$
).
We denote the character associated with
![]() $\mathcal {F}$
by
$\mathcal {F}$
by
![]() $\varepsilon _{\mathcal {F}}$
, so that for all but finitely many classical weights k in
$\varepsilon _{\mathcal {F}}$
, so that for all but finitely many classical weights k in
![]() $\mathcal {U,}$
the specialisation of
$\mathcal {U,}$
the specialisation of
![]() $\varepsilon _{\mathcal {F}}$
at k coincides with the nebentypus of
$\varepsilon _{\mathcal {F}}$
at k coincides with the nebentypus of
![]() $\mathcal {F}_k$
.
$\mathcal {F}_k$
.
The following definition gives a criterion for when a modular form lies in a Coleman family.
Definition 3.2.2 We say that a cuspidal eigenform f of level
![]() $\Gamma _1(N) \cap \Gamma _0(p)$
and weight
$\Gamma _1(N) \cap \Gamma _0(p)$
and weight
![]() $k+2$
is noble if the following two conditions are satisfied.
$k+2$
is noble if the following two conditions are satisfied.
-
• f is the p-stabilisation of normalised cuspidal newform
 $f^{\prime }$
of level
$f^{\prime }$
of level
 $\Gamma _1(N)$
such that the roots
$\Gamma _1(N)$
such that the roots
 $\{\alpha _{f^{\prime }}, \beta _{f^{\prime }}\}$
of the Hecke polynomial
$\{\alpha _{f^{\prime }}, \beta _{f^{\prime }}\}$
of the Hecke polynomial  $$\begin{align*}X^2 - a_p(f^{\prime})X + p^{k+1}\varepsilon_{f^{\prime}}(p) \end{align*}$$
$$\begin{align*}X^2 - a_p(f^{\prime})X + p^{k+1}\varepsilon_{f^{\prime}}(p) \end{align*}$$
are distinct. Here,
 $a_p(f^{\prime })$
is the p-th Fourier coefficient of
$a_p(f^{\prime })$
is the p-th Fourier coefficient of
 $f^{\prime }$
and
$f^{\prime }$
and
 $\varepsilon _{f^{\prime }}$
is the nebentypus.
$\varepsilon _{f^{\prime }}$
is the nebentypus. -
• If the
 $U_p$
-eigenvalue of f has p-adic valuation
$U_p$
-eigenvalue of f has p-adic valuation
 $k+1,$
then the local Galois representation attached to
$k+1,$
then the local Galois representation attached to
 $f^{\prime }$
at p is not the direct sum of two characters.
$f^{\prime }$
at p is not the direct sum of two characters.
Lemma 3.2.3 Let f be a noble eigenform of weight
![]() $k+2$
. Then for any sufficiently small
$k+2$
. Then for any sufficiently small
![]() $\mathcal {U} \owns k$
in
$\mathcal {U} \owns k$
in
![]() $\mathcal {W}$
, there is a unique Coleman family
$\mathcal {W}$
, there is a unique Coleman family
![]() ${\mathcal {F}}$
over
${\mathcal {F}}$
over
![]() $\mathcal {U}$
such that
$\mathcal {U}$
such that
![]() ${\mathcal {F}}_k = f$
.
${\mathcal {F}}_k = f$
.
Proof This is essentially proved in [Reference BellaïcheBel12, Lemma 2.8]. In particular, the lemma shows that if x is an E-point on the eigencurve of weight
![]() $k+2$
, then there is a neighborhood
$k+2$
, then there is a neighborhood
![]() $\mathcal {V} \owns x$
and an open disc
$\mathcal {V} \owns x$
and an open disc
![]() $\mathcal {U} \subseteq \mathcal {W}$
such that
$\mathcal {U} \subseteq \mathcal {W}$
such that
![]() $\mathcal {V} \to \mathcal {U}$
is finite flat of degree
$\mathcal {V} \to \mathcal {U}$
is finite flat of degree
 $\dim M^{\dagger }_{k+2,(x)}$
, where
$\dim M^{\dagger }_{k+2,(x)}$
, where
 $M^{\dagger }_{k+2,(x)}$
is the space of overconvergent modular forms of weight
$M^{\dagger }_{k+2,(x)}$
is the space of overconvergent modular forms of weight
![]() $k+2$
that are Hecke eigenforms with eigenvalues given by x. Suppose x is noble; then it has slope less than
$k+2$
that are Hecke eigenforms with eigenvalues given by x. Suppose x is noble; then it has slope less than
![]() $k+1$
, so Coleman’s control theorem [Reference ColemanCol96, Thm. 6.1] implies that
$k+1$
, so Coleman’s control theorem [Reference ColemanCol96, Thm. 6.1] implies that
 $M^{\dagger }_{k+2,(x)}$
consists of classical modular forms. Moreover, x corresponds to a newform, so the subspace of classical modular forms is one-dimensional (see, for example, [Reference LangLan95, Thm. VIII.3.3]). ▪
$M^{\dagger }_{k+2,(x)}$
consists of classical modular forms. Moreover, x corresponds to a newform, so the subspace of classical modular forms is one-dimensional (see, for example, [Reference LangLan95, Thm. VIII.3.3]). ▪
3.3 Locally Analytic Distribution Modules
Now we begin defining a family of Galois representations on
![]() $\mathcal {W}$
as in [Reference Loeffler and ZerbesLZ16, §4].
$\mathcal {W}$
as in [Reference Loeffler and ZerbesLZ16, §4].
Let
![]() $Y = Y_1(N(p))$
be the modular curve at level
$Y = Y_1(N(p))$
be the modular curve at level
![]() $\Gamma _1(N) \cap \Gamma _0(p)$
, and let
$\Gamma _1(N) \cap \Gamma _0(p)$
, and let
![]() $\pi \colon \mathcal {E} \to Y$
be the universal elliptic curve over Y. Let
$\pi \colon \mathcal {E} \to Y$
be the universal elliptic curve over Y. Let
 $$\begin{align*}\mathscr{H} := \mathbf{R}^1 \pi_* \mathbb{Z}_p(1) \end{align*}$$
$$\begin{align*}\mathscr{H} := \mathbf{R}^1 \pi_* \mathbb{Z}_p(1) \end{align*}$$
be the relative Tate module of
![]() $\mathcal {E}$
. We will define several pro-sheaves of “functions and distributions on
$\mathcal {E}$
. We will define several pro-sheaves of “functions and distributions on
![]() $\mathscr {H}$
.” By this, we mean the following. Let
$\mathscr {H}$
.” By this, we mean the following. Let
![]() $Y(p^{\infty }, p^{\infty }N)$
denote the pro-scheme
$Y(p^{\infty }, p^{\infty }N)$
denote the pro-scheme
 $\varprojlim _n Y(p^n, p^nN)$
and
$\varprojlim _n Y(p^n, p^nN)$
and
![]() $t \colon Y(p^{\infty }, p^{\infty }N) \to Y$
the natural projection; it is a Galois covering, and its Galois group can be identified with the Iwahori subgroup
$t \colon Y(p^{\infty }, p^{\infty }N) \to Y$
the natural projection; it is a Galois covering, and its Galois group can be identified with the Iwahori subgroup
![]() $U_0(p) \subset \mathrm {GL}_2(\mathbb {Z}_p)$
(with respect to the standard Borel).
$U_0(p) \subset \mathrm {GL}_2(\mathbb {Z}_p)$
(with respect to the standard Borel).
The pro-sheaf
![]() $t^* \mathscr {H}$
is canonically isomorphic to the constant pro-sheaf
$t^* \mathscr {H}$
is canonically isomorphic to the constant pro-sheaf
![]() $\underline {H}$
, where
$\underline {H}$
, where
 $H=\mathbb {Z}_p^2$
. We will define several spaces of functions and distributions on subsets of H that are equipped with actions of
$H=\mathbb {Z}_p^2$
. We will define several spaces of functions and distributions on subsets of H that are equipped with actions of
![]() $U_0(p)$
. Since a
$U_0(p)$
. Since a
![]() $U_0(p)$
-module determines a
$U_0(p)$
-module determines a
![]() $U_0(p)$
-equivariant pro-sheaf on
$U_0(p)$
-equivariant pro-sheaf on
![]() $Y(p^{\infty },p^{\infty }N)$
, these spaces will descend to pro-sheaves on Y.
$Y(p^{\infty },p^{\infty }N)$
, these spaces will descend to pro-sheaves on Y.
First, we recall the definition of two locally analytic distribution modules following [Reference Loeffler and ZerbesLZ16, §4.2].
Definition 3.3.1 Let
![]() $T_0$
,
$T_0$
,
![]() $T_0^{\prime }$
be the subsets of H defined by
$T_0^{\prime }$
be the subsets of H defined by
 $$\begin{align*}T_0 := \mathbb{Z}_p^{\times} \times \mathbb{Z}_p \quad \text{and}\quad T_0^{\prime} := p\mathbb{Z}_p \times \mathbb{Z}_p^{\times}, \end{align*}$$
$$\begin{align*}T_0 := \mathbb{Z}_p^{\times} \times \mathbb{Z}_p \quad \text{and}\quad T_0^{\prime} := p\mathbb{Z}_p \times \mathbb{Z}_p^{\times}, \end{align*}$$
and let
![]() $\Sigma _0(p)$
,
$\Sigma _0(p)$
,
![]() $\Sigma _0^{\prime }(p)$
be the submonoids of
$\Sigma _0^{\prime }(p)$
be the submonoids of
![]() $M_2(\mathbb {Z}_p)$
defined by
$M_2(\mathbb {Z}_p)$
defined by
 $$\begin{align*}\Sigma_0(p) := \begin{pmatrix} \mathbb{Z}_p^{\times} & \mathbb{Z}_p \\ p\mathbb{Z}_p & \mathbb{Z}_p \end{pmatrix} \quad\text{and}\quad \Sigma_0^{\prime}(p) := \begin{pmatrix} \mathbb{Z}_p & \mathbb{Z}_p \\ p\mathbb{Z}_p & \mathbb{Z}_p^{\times} \end{pmatrix}. \end{align*}$$
$$\begin{align*}\Sigma_0(p) := \begin{pmatrix} \mathbb{Z}_p^{\times} & \mathbb{Z}_p \\ p\mathbb{Z}_p & \mathbb{Z}_p \end{pmatrix} \quad\text{and}\quad \Sigma_0^{\prime}(p) := \begin{pmatrix} \mathbb{Z}_p & \mathbb{Z}_p \\ p\mathbb{Z}_p & \mathbb{Z}_p^{\times} \end{pmatrix}. \end{align*}$$
The monoids
![]() $\Sigma _0(p)$
and
$\Sigma _0(p)$
and
![]() $\Sigma _0^{\prime }(p)$
act on the right on
$\Sigma _0^{\prime }(p)$
act on the right on
![]() $T_0$
and
$T_0$
and
![]() $T_0^{\prime }$
, respectively.
$T_0^{\prime }$
, respectively.
Let R be a complete topological
![]() $\mathbb {Z}_p$
-algebra, and let
$\mathbb {Z}_p$
-algebra, and let
![]() $w \colon \mathbb {Z}_p^{\times } \to R^{\times }$
be a continuous homomorphism. Suppose there exists an integer
$w \colon \mathbb {Z}_p^{\times } \to R^{\times }$
be a continuous homomorphism. Suppose there exists an integer
![]() $m \geq 0$
such that the restriction of w to
$m \geq 0$
such that the restriction of w to
![]() $1+p^{m+1} \mathbb {Z}_p$
is analytic. We are primarily interested in the following cases:
$1+p^{m+1} \mathbb {Z}_p$
is analytic. We are primarily interested in the following cases:
-
(a)
 $R = \Lambda _{\mathcal {U}}$
,
$R = \Lambda _{\mathcal {U}}$
,
 $w=\kappa _{\mathcal {U}}$
for some finite extension
$w=\kappa _{\mathcal {U}}$
for some finite extension
 $E/\mathbb {Q}_p$
and some
$E/\mathbb {Q}_p$
and some
 $\mathcal {U} \subset (\mathcal {W}_m)_E$
.
$\mathcal {U} \subset (\mathcal {W}_m)_E$
. -
(b)
 $R = \mathcal {O}_E$
,
$R = \mathcal {O}_E$
,
 $w(z) = z^k$
for some finite extension
$w(z) = z^k$
for some finite extension
 $E/\mathbb {Q}_p$
and some nonnegative integer k.
$E/\mathbb {Q}_p$
and some nonnegative integer k.
Definition 3.3.2 Let T be either
![]() $T_0$
or
$T_0$
or
![]() $T_0^{\prime }$
. Let
$T_0^{\prime }$
. Let
![]() $A^{\circ }_{w,m}(T)$
denote the space of functions
$A^{\circ }_{w,m}(T)$
denote the space of functions
![]() $f \colon T \to R$
satisfying the following properties:
$f \colon T \to R$
satisfying the following properties:
-
(i) The function f is homogeneous of weight w, i.e.
 $f(\lambda v) = w(\lambda ) f(v)$
for any
$f(\lambda v) = w(\lambda ) f(v)$
for any
 $v \in T$
,
$v \in T$
,
 $\lambda \in \mathbb {Z}_p^{\times }$
.
$\lambda \in \mathbb {Z}_p^{\times }$
. -
(ii) The function f is analytic on discs of radius
 $p^{-m}$
, i.e. for any
$p^{-m}$
, i.e. for any
 $v \in T$
, the restriction of f to
$v \in T$
, the restriction of f to
 $v+p^m T$
is given by a power series with coefficients in R.
$v+p^m T$
is given by a power series with coefficients in R.
Let
 $$ \begin{align*} D^{\circ}_{w,m}(T)&:= \operatorname{\mathrm{Hom}}_{R, \mathrm{cont}}(A^{\circ}_{w,m}(T), R), \\ D_{w,m}(T)& := D^{\circ}_{w,m}(T)[ 1/p ]. \end{align*} $$
$$ \begin{align*} D^{\circ}_{w,m}(T)&:= \operatorname{\mathrm{Hom}}_{R, \mathrm{cont}}(A^{\circ}_{w,m}(T), R), \\ D_{w,m}(T)& := D^{\circ}_{w,m}(T)[ 1/p ]. \end{align*} $$
When
![]() $R=\Lambda _{\mathcal {U}}$
,
$R=\Lambda _{\mathcal {U}}$
,
![]() $w=\kappa _{\mathcal {U}}$
, we will denote the modules by
$w=\kappa _{\mathcal {U}}$
, we will denote the modules by
![]() $A^{\circ }_{\mathcal {U},m}$
,
$A^{\circ }_{\mathcal {U},m}$
,
![]() $D^{\circ }_{\mathcal {U},m}$
,
$D^{\circ }_{\mathcal {U},m}$
,
![]() $D_{\mathcal {U},m}$
. When
$D_{\mathcal {U},m}$
. When
![]() $R = \mathcal {O}_E$
,
$R = \mathcal {O}_E$
,
![]() $w(z)=z^k$
, we will denote the modules by
$w(z)=z^k$
, we will denote the modules by
![]() $A^{\circ }_{k,m}$
,
$A^{\circ }_{k,m}$
,
![]() $D^{\circ }_{k,m}$
,
$D^{\circ }_{k,m}$
,
![]() $D_{k,m}$
.
$D_{k,m}$
.
The modules
![]() $A^{\circ }_{w,m}(T)$
,
$A^{\circ }_{w,m}(T)$
,
![]() $D^{\circ }_{w,m}(T)$
,
$D^{\circ }_{w,m}(T)$
,
![]() $D_{w,m}(T)$
inherit an action of
$D_{w,m}(T)$
inherit an action of
![]() $\Sigma _0(p)$
or
$\Sigma _0(p)$
or
![]() $\Sigma _0^{\prime }(p)$
from the action on T. If the disc
$\Sigma _0^{\prime }(p)$
from the action on T. If the disc
![]() $\mathcal {U}$
contains the point corresponding to the homomorphism
$\mathcal {U}$
contains the point corresponding to the homomorphism
![]() $z \mapsto z^k$
, then the specialization map
$z \mapsto z^k$
, then the specialization map
![]() $\Lambda _{\mathcal {U}} \to \mathbb {Z}_p$
induces a homomorphism
$\Lambda _{\mathcal {U}} \to \mathbb {Z}_p$
induces a homomorphism
and similarly there are specialization maps with
![]() $D^{\circ }$
replaced by
$D^{\circ }$
replaced by
![]() $A^{\circ }$
or D.
$A^{\circ }$
or D.
As mentioned at the beginning of this subsection, each of the modules defined above determines a pro-sheaf on Y. We let
![]() $\mathcal {D}^{\circ }_{w,m}(\mathscr {H}_0)$
,
$\mathcal {D}^{\circ }_{w,m}(\mathscr {H}_0)$
,
![]() $\mathcal {D}^{\circ }_{w,m}(\mathscr {H}_0^{\prime })$
, be the pro-sheaves corresponding to
$\mathcal {D}^{\circ }_{w,m}(\mathscr {H}_0^{\prime })$
, be the pro-sheaves corresponding to
![]() $D^{\circ }_{w,m}(T_0)$
,
$D^{\circ }_{w,m}(T_0)$
,
![]() $D^{\circ }_{w,m}(T_0^{\prime })$
, respectively.
$D^{\circ }_{w,m}(T_0^{\prime })$
, respectively.
3.4 Galois Representations
Now we define families of Galois representations coming from the cohomology of the sheaves defined above. For a wide open disc
![]() $\mathcal {U} \subset (\mathcal {W}_0)_E$
we set
$\mathcal {U} \subset (\mathcal {W}_0)_E$
we set
 $B_{\mathcal {U}} := \Lambda _{\mathcal {U}}[\frac {1}{p}]$
.
$B_{\mathcal {U}} := \Lambda _{\mathcal {U}}[\frac {1}{p}]$
.
Definition 3.4.1 As before, let
![]() $Y = Y_1(N(p))$
denote the modular curve of level
$Y = Y_1(N(p))$
denote the modular curve of level
![]() $\Gamma _1(N) \cap \Gamma _0(p)$
. Set
$\Gamma _1(N) \cap \Gamma _0(p)$
. Set
 $$ \begin{align*} M^{\circ}_{w,m}(\mathscr{H}_0) & := \operatorname{H}^1_{\acute{\mathrm{e}}\mathrm{t}}(Y_{\overline{\mathbb{Q}}}, \mathcal{D}^{\circ}_{w,m}(\mathscr{H}_0))(-\kappa_{\mathcal{U}}) \\ M^{\circ}_{w,m}(\mathscr{H}_0^{\prime}) & := \operatorname{H}^1_{\acute{\mathrm{e}}\mathrm{t}}(Y_{\overline{\mathbb{Q}}}, \mathcal{D}^{\circ}_{w,m}(\mathscr{H}_0^{\prime}))(1). \end{align*} $$
$$ \begin{align*} M^{\circ}_{w,m}(\mathscr{H}_0) & := \operatorname{H}^1_{\acute{\mathrm{e}}\mathrm{t}}(Y_{\overline{\mathbb{Q}}}, \mathcal{D}^{\circ}_{w,m}(\mathscr{H}_0))(-\kappa_{\mathcal{U}}) \\ M^{\circ}_{w,m}(\mathscr{H}_0^{\prime}) & := \operatorname{H}^1_{\acute{\mathrm{e}}\mathrm{t}}(Y_{\overline{\mathbb{Q}}}, \mathcal{D}^{\circ}_{w,m}(\mathscr{H}_0^{\prime}))(1). \end{align*} $$
Proposition 3.4.2 [Reference Loeffler and ZerbesLZ16, Thm. 4.6.6]
Let
![]() $f_0$
be a noble eigenform of weight
$f_0$
be a noble eigenform of weight
![]() $k_0 + 2$
, and let
$k_0 + 2$
, and let
![]() ${\mathcal {F}}$
be the Coleman family passing through
${\mathcal {F}}$
be the Coleman family passing through
![]() $f_0$
. If the disc
$f_0$
. If the disc
![]() $\mathcal {U} \owns k_0$
is sufficiently small, then the following hold.
$\mathcal {U} \owns k_0$
is sufficiently small, then the following hold.
-
(i) The modules
are direct summands (as $$ \begin{align*} M_{\mathcal{U}}({\mathcal{F}}) &:= M_{\mathcal{U},0}(\mathscr{H}_0) \big[ T_n = a_n({\mathcal{F}}) \quad \forall n \ge 1 \big] \\ M_{\mathcal{U}}({\mathcal{F}})^* &:= M_{\mathcal{U},0}(\mathscr{H}_0^{\prime}) \big[ T_n^{\prime} = a_n({\mathcal{F}}) \quad \forall n \ge 1 \big] \end{align*} $$
$$ \begin{align*} M_{\mathcal{U}}({\mathcal{F}}) &:= M_{\mathcal{U},0}(\mathscr{H}_0) \big[ T_n = a_n({\mathcal{F}}) \quad \forall n \ge 1 \big] \\ M_{\mathcal{U}}({\mathcal{F}})^* &:= M_{\mathcal{U},0}(\mathscr{H}_0^{\prime}) \big[ T_n^{\prime} = a_n({\mathcal{F}}) \quad \forall n \ge 1 \big] \end{align*} $$
 $B_{\mathcal {U}}$
-modules) of
$B_{\mathcal {U}}$
-modules) of
 $M_{\mathcal {U},0}(\mathscr {H}_0)$
and
$M_{\mathcal {U},0}(\mathscr {H}_0)$
and
 $M_{\mathcal {U},0}(\mathscr {H}_0^{\prime })$
respectively, where
$M_{\mathcal {U},0}(\mathscr {H}_0^{\prime })$
respectively, where
 $[-]$
stands for isotypic component and
$[-]$
stands for isotypic component and
 $T_n'$
is the transpose of the usual Hecke operator. Each is free of rank
$T_n'$
is the transpose of the usual Hecke operator. Each is free of rank
 $2$
over
$2$
over
 $B_{\mathcal {U}}$
.
$B_{\mathcal {U}}$
.
-
(ii) The Ohta pairing (see [Reference Loeffler and ZerbesLZ16, §4.3]) induces an isomorphism of
 $B_{\mathcal {U}}[G_{\mathbb {Q}}]$
-modules
$B_{\mathcal {U}}[G_{\mathbb {Q}}]$
-modules  $$\begin{align*}M_{\mathcal{U}}({\mathcal{F}})^* \cong \operatorname{\mathrm{Hom}}_{B_{\mathcal{U}}}(M_{\mathcal{U}}({\mathcal{F}}),B_{\mathcal{U}}) . \end{align*}$$
$$\begin{align*}M_{\mathcal{U}}({\mathcal{F}})^* \cong \operatorname{\mathrm{Hom}}_{B_{\mathcal{U}}}(M_{\mathcal{U}}({\mathcal{F}}),B_{\mathcal{U}}) . \end{align*}$$
Given two Coleman families
![]() ${\mathcal {F}}$
and
${\mathcal {F}}$
and
![]() $\mathcal {G}$
defined over
$\mathcal {G}$
defined over
![]() $\mathcal {U}_1, \mathcal {U}_2 \subset \mathcal {W}_E$
, respectively, we will write
$\mathcal {U}_1, \mathcal {U}_2 \subset \mathcal {W}_E$
, respectively, we will write
![]() $M := M_{\mathcal {U}_1}({\mathcal {F}})^* \hat {\otimes } M_{\mathcal {U}_2}(\mathcal {G})^*$
for the family of Galois representations on
$M := M_{\mathcal {U}_1}({\mathcal {F}})^* \hat {\otimes } M_{\mathcal {U}_2}(\mathcal {G})^*$
for the family of Galois representations on
![]() $\mathcal {U}_1 \times \mathcal {U}_2$
given by the
$\mathcal {U}_1 \times \mathcal {U}_2$
given by the
![]() $B_{\mathcal {U}_1} \hat {\otimes } B_{\mathcal {U}_2}$
-module
$B_{\mathcal {U}_1} \hat {\otimes } B_{\mathcal {U}_2}$
-module
and to ease notation, we will often omit the subscripts when the spaces
![]() $\mathcal {U}_1$
and
$\mathcal {U}_1$
and
![]() $\mathcal {U}_2$
are clear. Furthermore, we will often restrict this representation to open affinoids
$\mathcal {U}_2$
are clear. Furthermore, we will often restrict this representation to open affinoids
![]() $V_1 \subset \mathcal {U}_1$
and
$V_1 \subset \mathcal {U}_1$
and
![]() $V_2 \subset \mathcal {U}_2$
; in this case, M is a Banach module over the affinoid algebra
$V_2 \subset \mathcal {U}_2$
; in this case, M is a Banach module over the affinoid algebra
![]() $\mathcal {O}_{\mathcal {W}}(V_1 \times V_2)$
that is free of rank four.
$\mathcal {O}_{\mathcal {W}}(V_1 \times V_2)$
that is free of rank four.
Definition 3.4.3 Let A be a
![]() $\mathbb {Q}_p$
-affinoid algebra and let M be an A-valued (continuous) representation of
$\mathbb {Q}_p$
-affinoid algebra and let M be an A-valued (continuous) representation of
![]() $G_{\mathbb {Q}}$
. Let
$G_{\mathbb {Q}}$
. Let
![]() $D^{\mathrm {la}}(\Gamma , A)$
denote the space of locally analytic distributions with values in A; this comes equipped with an action of
$D^{\mathrm {la}}(\Gamma , A)$
denote the space of locally analytic distributions with values in A; this comes equipped with an action of
![]() $G_{\mathbb {Q}}$
given by
$G_{\mathbb {Q}}$
given by
 $$ \begin{align} \int_{\Gamma} f \; d(g \cdot \mu) := \int_{\Gamma} f([g]^{-1}x) \; d\mu(x), \end{align} $$
$$ \begin{align} \int_{\Gamma} f \; d(g \cdot \mu) := \int_{\Gamma} f([g]^{-1}x) \; d\mu(x), \end{align} $$
where
![]() $[g]$
denotes the image of
$[g]$
denotes the image of
![]() $g \in G_{\mathbb {Q}}$
in
$g \in G_{\mathbb {Q}}$
in
![]() $\Gamma = \operatorname {\mathrm {Gal}}(\mathbb {Q}(\mu _{p^{\infty }})/\mathbb {Q})$
, and is isomorphic (as
$\Gamma = \operatorname {\mathrm {Gal}}(\mathbb {Q}(\mu _{p^{\infty }})/\mathbb {Q})$
, and is isomorphic (as
![]() $A[G_{\mathbb {Q}}]$
-modules) to
$A[G_{\mathbb {Q}}]$
-modules) to
![]() $\mathcal {O}_{\mathcal {W}}(\mathcal {W})^{\iota } \hat {\otimes } A$
. The cyclotomic deformation of M is defined to be
$\mathcal {O}_{\mathcal {W}}(\mathcal {W})^{\iota } \hat {\otimes } A$
. The cyclotomic deformation of M is defined to be
 $$\begin{align*}M(-\kappa) := D^{\mathrm{la}}(\Gamma, M) := M \widehat{\otimes}_{\mathbb{Q}_p} D^{\mathrm{la}}(\Gamma, A). \end{align*}$$
$$\begin{align*}M(-\kappa) := D^{\mathrm{la}}(\Gamma, M) := M \widehat{\otimes}_{\mathbb{Q}_p} D^{\mathrm{la}}(\Gamma, A). \end{align*}$$
with the diagonal Galois action.
Similarly, for any
![]() $\lambda \in \mathbb {R}_{\ge 0}$
, let
$\lambda \in \mathbb {R}_{\ge 0}$
, let
![]() $D_{\lambda }(\Gamma ,\mathbb {Q}_p)$
be the space of
$D_{\lambda }(\Gamma ,\mathbb {Q}_p)$
be the space of
![]() $\mathbb {Q}_p$
-valued distributions on
$\mathbb {Q}_p$
-valued distributions on
![]() $\Gamma $
of order
$\Gamma $
of order
![]() $\lambda $
as in [Reference ColmezCol10, §II.3], with Galois action given by the same formula in (3.4.4). Define
$\lambda $
as in [Reference ColmezCol10, §II.3], with Galois action given by the same formula in (3.4.4). Define
![]() $D_{\lambda }(\Gamma ,M) := D_{\lambda }(\Gamma ,\mathbb {Q}_p) \widehat {\otimes }_{\mathbb {Q}_p} M$
.
$D_{\lambda }(\Gamma ,M) := D_{\lambda }(\Gamma ,\mathbb {Q}_p) \widehat {\otimes }_{\mathbb {Q}_p} M$
.
3.5 Some Properties of Locally Analytic Distribution Modules
We mention some properties of the modules defined above that will be useful in Section 4.
Definition 3.5.1 Define
![]() $\Lambda (H)$
to be the space of continuous
$\Lambda (H)$
to be the space of continuous
![]() $\mathbb {Z}_p$
-valued distributions on H, and let
$\mathbb {Z}_p$
-valued distributions on H, and let
![]() $\Lambda (\mathscr {H})$
be the corresponding pro-sheaf on Y. This coincides with the sheaf of Iwasawa modules for
$\Lambda (\mathscr {H})$
be the corresponding pro-sheaf on Y. This coincides with the sheaf of Iwasawa modules for
![]() $\mathscr {H}$
, i.e.,
$\mathscr {H}$
, i.e.,
![]() $\Lambda (\mathscr {H})$
is the pro-system of étale sheaves corresonding to the inverse system
$\Lambda (\mathscr {H})$
is the pro-system of étale sheaves corresonding to the inverse system
![]() $\left ( \mathbb {Z}/p^n \mathbb {Z} [\mathscr {H} /p^n \mathscr {H} ] \right )_{n \geq 1}$
with the natural transition maps.
$\left ( \mathbb {Z}/p^n \mathbb {Z} [\mathscr {H} /p^n \mathscr {H} ] \right )_{n \geq 1}$
with the natural transition maps.
For any nonnegative integer k, let
 $ \operatorname {\mathrm {TSym}}^k H$
be the space of degree k symmetric tensors over H, i.e., it is the subgroup of
$ \operatorname {\mathrm {TSym}}^k H$
be the space of degree k symmetric tensors over H, i.e., it is the subgroup of
![]() $H^{\otimes k}$
that is invariant under the action of the symmetric group
$H^{\otimes k}$
that is invariant under the action of the symmetric group
![]() $S_k$
. Let
$S_k$
. Let
 $ \operatorname {\mathrm {TSym}}^k \mathscr {H}$
be the corresponding pro-sheaf on Y.
$ \operatorname {\mathrm {TSym}}^k \mathscr {H}$
be the corresponding pro-sheaf on Y.
For
![]() $j \geq 0$
, set
$j \geq 0$
, set
![]() $\Lambda ^{[j]}(\mathscr {H}) := \Lambda (\mathscr {H}) \otimes \operatorname {TSym}^j\mathscr {H}$
and
$\Lambda ^{[j]}(\mathscr {H}) := \Lambda (\mathscr {H}) \otimes \operatorname {TSym}^j\mathscr {H}$
and
![]() $\Lambda ^{[j, j]} = \Lambda ^{[j]}(\mathscr {H}) \boxtimes \Lambda ^{[j]}(\mathscr {H})$
. Then there is a Clebsch–Gordon map (see [Reference Loeffler and ZerbesLZ16, §3.2])
$\Lambda ^{[j, j]} = \Lambda ^{[j]}(\mathscr {H}) \boxtimes \Lambda ^{[j]}(\mathscr {H})$
. Then there is a Clebsch–Gordon map (see [Reference Loeffler and ZerbesLZ16, §3.2])
 $$\begin{align*}\operatorname{CG}^{[j]} \colon \Lambda(\mathscr{H}) \longrightarrow \big( \Lambda^{[j]}(\mathscr{H}) \hat{\otimes} \Lambda^{[j]}(\mathscr{H}) \big) (-j). \end{align*}$$
$$\begin{align*}\operatorname{CG}^{[j]} \colon \Lambda(\mathscr{H}) \longrightarrow \big( \Lambda^{[j]}(\mathscr{H}) \hat{\otimes} \Lambda^{[j]}(\mathscr{H}) \big) (-j). \end{align*}$$
For any
![]() $\mathcal {U}$
, m, there is a natural restriction map
$\mathcal {U}$
, m, there is a natural restriction map
and for any nonnegative integer k,
 $ \operatorname {\mathrm {TSym}}^k H$
can be identified with the space of distributions on homogeneous degree k polynomial functions on H. Hence, there is a natural surjection
$ \operatorname {\mathrm {TSym}}^k H$
can be identified with the space of distributions on homogeneous degree k polynomial functions on H. Hence, there is a natural surjection
 $$\begin{align*}\mathcal{D}^{\circ}_{k,m}(T) \longrightarrow \operatorname{\mathrm{TSym}}^k \mathscr{H}. \end{align*}$$
$$\begin{align*}\mathcal{D}^{\circ}_{k,m}(T) \longrightarrow \operatorname{\mathrm{TSym}}^k \mathscr{H}. \end{align*}$$
3.6 The Three-variable p-adic L-function
Let f and g be two normalised cuspidal eigenforms of weights
![]() $k +2, k^{\prime }+2$
and levels
$k +2, k^{\prime }+2$
and levels
![]() $\Gamma _1(N_1)$
and
$\Gamma _1(N_1)$
and
![]() $\Gamma _1(N_2),$
respectively, where
$\Gamma _1(N_2),$
respectively, where
![]() $k> k' \geq 0$
. Let
$k> k' \geq 0$
. Let
![]() $\chi $
be a Dirichlet character of conductor
$\chi $
be a Dirichlet character of conductor
![]() $N_{\chi }$
and suppose that p does not divide
$N_{\chi }$
and suppose that p does not divide
![]() $N_1 \cdot N_2$
. With this data, one has the associated (imprimitive) Rankin–Selberg L-function, defined as
$N_1 \cdot N_2$
. With this data, one has the associated (imprimitive) Rankin–Selberg L-function, defined as
 $$\begin{align*}L(f, g, \chi, s) = L_{(N_1 N_2 N_{\chi})}(\varepsilon_f \varepsilon_g \chi^2, 2s - 2 - k - k^{\prime}) \cdot \sum_{\substack{n \geq 1 \\ (n, N_{\chi}) = 1}} a_n(f) a_n(g) \chi(n) n^{-s} \end{align*}$$
$$\begin{align*}L(f, g, \chi, s) = L_{(N_1 N_2 N_{\chi})}(\varepsilon_f \varepsilon_g \chi^2, 2s - 2 - k - k^{\prime}) \cdot \sum_{\substack{n \geq 1 \\ (n, N_{\chi}) = 1}} a_n(f) a_n(g) \chi(n) n^{-s} \end{align*}$$
for
![]() $\operatorname {Re}(s)$
sufficiently large. Here the subscript
$\operatorname {Re}(s)$
sufficiently large. Here the subscript
![]() $(N_1 N_2 N_{\chi })$
denotes the omission of the Euler factors at primes dividing
$(N_1 N_2 N_{\chi })$
denotes the omission of the Euler factors at primes dividing
![]() $N_1 N_2 N_{\chi }$
. This L-function differs from the automorphic L-function attached to the representation
$N_1 N_2 N_{\chi }$
. This L-function differs from the automorphic L-function attached to the representation
![]() $\pi _f \otimes \pi _g \otimes \chi $
by only finitely many Euler factors. Since we have assumed
$\pi _f \otimes \pi _g \otimes \chi $
by only finitely many Euler factors. Since we have assumed
![]() $k \neq k^{\prime }$
, the function
$k \neq k^{\prime }$
, the function
![]() $L(f, g, \chi , -)$
has analytic continuation to all of
$L(f, g, \chi , -)$
has analytic continuation to all of
![]() $\mathbb {C}$
(see [Reference LoefflerLoe18, §2.1]).
$\mathbb {C}$
(see [Reference LoefflerLoe18, §2.1]).
Using the theory of nearly overconvergent families of modular forms as described in [Reference Andreatta and IovitaAI17], Urban has constructed a three-variable p-adic L-function that interpolates critical values of the above Rankin–Selberg L-function. More precisely, suppose that there exist noble p-stabilisations of f and g (as in Definition 3.2.2) and let
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
be Coleman families over affinoid domains
$\mathcal {G}$
be Coleman families over affinoid domains
![]() $V_1$
and
$V_1$
and
![]() $V_2$
, passing through these p-stabilisations. We can shrink
$V_2$
, passing through these p-stabilisations. We can shrink
![]() $V_1$
and
$V_1$
and
![]() $V_2$
to ensure that all classical specialisations of
$V_2$
to ensure that all classical specialisations of
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
are noble (see Remark 8.2.5)—if
$\mathcal {G}$
are noble (see Remark 8.2.5)—if
![]() $\mathcal {F}_{k_1}$
denotes such a specialisation, then we let
$\mathcal {F}_{k_1}$
denotes such a specialisation, then we let
![]() $\mathcal {F}^\circ _{k_1}$
denote the associated newform, and similarly for
$\mathcal {F}^\circ _{k_1}$
denote the associated newform, and similarly for
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Theorem 3.6.1 (Urban)
There exists an element
![]() $L_p(\mathcal {F}, \mathcal {G}, 1 + \mathbf {j}) \in \mathcal {O}(V_1 \times V_2 \times \mathcal {W})$
satisfying the following interpolation property:
$L_p(\mathcal {F}, \mathcal {G}, 1 + \mathbf {j}) \in \mathcal {O}(V_1 \times V_2 \times \mathcal {W})$
satisfying the following interpolation property:
-
• For all integers
 $k_1,\, k_2,\, j$
satisfying
$k_1,\, k_2,\, j$
satisfying
 $k_i \in V_i$
and
$k_i \in V_i$
and
 $0 \leq k_2 + 1 \leq j \leq k_1$
, and all Dirichlet characters
$0 \leq k_2 + 1 \leq j \leq k_1$
, and all Dirichlet characters
 $\chi $
of p-power conductor, we have where
$\chi $
of p-power conductor, we have where $$ \begin{align*} &L_p(\mathcal{F}_{k_1}, \mathcal{G}_{k_2}, 1 + j + \chi) = C(\mathcal{F}_{k_1}, \mathcal{G}_{k_2}, 1 + j + \chi )\\[-3pt] &\quad\quad\quad\quad\quad\cdot \frac{j! (j-k_2 - 1)! i^{k_1 - k_2}}{\pi^{2j + 1 - k_2}2^{2j + 2 + k_1 - k_2} \langle \mathcal{F}_{k_1}^{\circ}, \mathcal{F}_{k_1}^{\circ} \rangle_{N_1}} L(\mathcal{F}_{k_1}^{\circ}, \mathcal{G}_{k_2}^{\circ}, \chi^{-1}, 1+j), \end{align*} $$
$$ \begin{align*} &L_p(\mathcal{F}_{k_1}, \mathcal{G}_{k_2}, 1 + j + \chi) = C(\mathcal{F}_{k_1}, \mathcal{G}_{k_2}, 1 + j + \chi )\\[-3pt] &\quad\quad\quad\quad\quad\cdot \frac{j! (j-k_2 - 1)! i^{k_1 - k_2}}{\pi^{2j + 1 - k_2}2^{2j + 2 + k_1 - k_2} \langle \mathcal{F}_{k_1}^{\circ}, \mathcal{F}_{k_1}^{\circ} \rangle_{N_1}} L(\mathcal{F}_{k_1}^{\circ}, \mathcal{G}_{k_2}^{\circ}, \chi^{-1}, 1+j), \end{align*} $$
 $C(\mathcal {F}_{k_1}, \mathcal {G}_{k_2}, 1 + j + \chi )$
is an explicit product of Euler factors and Gauss sums.
$C(\mathcal {F}_{k_1}, \mathcal {G}_{k_2}, 1 + j + \chi )$
is an explicit product of Euler factors and Gauss sums.
Proof This follows from the interpolation property in [Reference UrbanUrb14, Theorem 4.4.7] (which is valid by the results of [Reference Andreatta and IovitaAI17, Appendix II]). The calculation is only for
![]() $N=1,$
but its generalisation is immediate. See also the computation of the Rankin–Selberg period in [Reference LoefflerLoe18, Prop 2.10]. ▪
$N=1,$
but its generalisation is immediate. See also the computation of the Rankin–Selberg period in [Reference LoefflerLoe18, Prop 2.10]. ▪
In the following section, we will recall the construction of the Beilinson–Flach classes in families. It turns out that this p-adic L-function
![]() $L_p$
is closely related to the images of these Beilinson–Flach classes under Perrin–Riou’s “big logarithm”. This will be important in Proposition 6.2.2 later on.
$L_p$
is closely related to the images of these Beilinson–Flach classes under Perrin–Riou’s “big logarithm”. This will be important in Proposition 6.2.2 later on.
4 Beilinson–Flach Classes
In this section, we recall the construction of classes
 $$\begin{align*}{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]} \in \operatorname{H}^1 \big(\mathbb{Q}(\mu_m), D^{\mathrm{la}}(\Gamma, M) \big), \end{align*}$$
$$\begin{align*}{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]} \in \operatorname{H}^1 \big(\mathbb{Q}(\mu_m), D^{\mathrm{la}}(\Gamma, M) \big), \end{align*}$$
where
![]() $M = M_{V_1}(\mathcal {F})^* \hat {\otimes } M_{V_2}(\mathcal {G})^*$
following [Reference Loeffler and ZerbesLZ16]. These classes are obtained from so-called Rankin–Iwasawa classes under the pushforward of a certain sequence of morphisms. In particular we show that these classes satisfy certain norm relations that interpolate the (tame) Euler system relations at classical weights.
$M = M_{V_1}(\mathcal {F})^* \hat {\otimes } M_{V_2}(\mathcal {G})^*$
following [Reference Loeffler and ZerbesLZ16]. These classes are obtained from so-called Rankin–Iwasawa classes under the pushforward of a certain sequence of morphisms. In particular we show that these classes satisfy certain norm relations that interpolate the (tame) Euler system relations at classical weights.
None of the results in this section are new, apart from perhaps Proposition 4.3.1 and §4.4, although we suspect this is already known to the experts.
4.1 Rankin–Iwasawa Classes
Let
![]() $(\mathcal {E}, P, Q)$
denote the universal triple over the curve
$(\mathcal {E}, P, Q)$
denote the universal triple over the curve
![]() $Y:= Y(m, mN)$
as defined in Section 2, and recall that
$Y:= Y(m, mN)$
as defined in Section 2, and recall that
 $$\begin{align*}\mathscr{H} = \mathscr{H}_{\mathbb{Z}_p} := \mathbf{R}^1\pi_* \mathbb{Z}_p(1) \end{align*}$$
$$\begin{align*}\mathscr{H} = \mathscr{H}_{\mathbb{Z}_p} := \mathbf{R}^1\pi_* \mathbb{Z}_p(1) \end{align*}$$
denotes the relative p-adic Tate module of
![]() $\mathcal {E}/Y$
. Here,
$\mathcal {E}/Y$
. Here,
![]() $\pi \colon \mathcal {E} \to Y$
denotes the structure map, and
$\pi \colon \mathcal {E} \to Y$
denotes the structure map, and
![]() $\mathbb {Z}_p(1)$
is the Tate twist by the cyclotomic character. This is a locally free étale pro-sheaf on Y of rank
$\mathbb {Z}_p(1)$
is the Tate twist by the cyclotomic character. This is a locally free étale pro-sheaf on Y of rank
![]() $2$
.
$2$
.
Let
![]() $c \geq 1$
be an integer prime to
$c \geq 1$
be an integer prime to
![]() $6mN$
. In [Reference KingsKin16], Kings constructs Eisenstein classes
$6mN$
. In [Reference KingsKin16], Kings constructs Eisenstein classes
 ${{}_{c}\operatorname {Eis}^k_{\mathbb {Q}_p}}$
arising from motivic classes whose de Rham realisations recover the usual Eisenstein series of weight
${{}_{c}\operatorname {Eis}^k_{\mathbb {Q}_p}}$
arising from motivic classes whose de Rham realisations recover the usual Eisenstein series of weight
![]() $k+2$
(see also [Reference Kings, Loeffler and ZerbesKLZ15, §4]). In addition to this, he constructs so-called Eisenstein–Iwasawa classes
$k+2$
(see also [Reference Kings, Loeffler and ZerbesKLZ15, §4]). In addition to this, he constructs so-called Eisenstein–Iwasawa classes
 $$\begin{align*}{{}_{c} \mathcal{EI}_{m, mN}} \in \operatorname{H}^1_{\acute{\mathrm{e}}\mathrm{t}}\big(Y(m, mN), \Lambda(\mathscr{H})(1) \big), \end{align*}$$
$$\begin{align*}{{}_{c} \mathcal{EI}_{m, mN}} \in \operatorname{H}^1_{\acute{\mathrm{e}}\mathrm{t}}\big(Y(m, mN), \Lambda(\mathscr{H})(1) \big), \end{align*}$$
which interpolate
 ${ {}_{c}\operatorname {Eis}^k_{\mathbb {Q}_p}}$
via the “moment maps”
${ {}_{c}\operatorname {Eis}^k_{\mathbb {Q}_p}}$
via the “moment maps”
 $$\begin{align*}\operatorname{mom}^k \colon \Lambda(\mathscr{H}) \longrightarrow \operatorname{TSym}^k \mathscr{H}. \end{align*}$$
$$\begin{align*}\operatorname{mom}^k \colon \Lambda(\mathscr{H}) \longrightarrow \operatorname{TSym}^k \mathscr{H}. \end{align*}$$
From these classes, one obtains Rankin–Iwasawa classes in the following way.
Definition 4.1.1 Let
![]() $c \geq 1$
be an integer that is coprime to
$c \geq 1$
be an integer that is coprime to
![]() $6mN$
. We define the Rankin–Iwasawa class to be
$6mN$
. We define the Rankin–Iwasawa class to be
 $$\begin{align*}{}_{c} \mathcal{RI}_{m, mN, 1}^{[j]} := \big[ (u_1)_* \circ \Delta_* \circ \operatorname{CG}^{[j]} \big]({}_{c}\mathcal{EI}_{m, mN}), \end{align*}$$
$$\begin{align*}{}_{c} \mathcal{RI}_{m, mN, 1}^{[j]} := \big[ (u_1)_* \circ \Delta_* \circ \operatorname{CG}^{[j]} \big]({}_{c}\mathcal{EI}_{m, mN}), \end{align*}$$
which lies in the cohomology group
 $\operatorname {H}^3_{\acute {\mathrm {e}}\mathrm {t}}(Y(m, mN)^2, \Lambda ^{[j, j]}(2-j) )$
. Here
$\operatorname {H}^3_{\acute {\mathrm {e}}\mathrm {t}}(Y(m, mN)^2, \Lambda ^{[j, j]}(2-j) )$
. Here
-
•
 $\operatorname {CG}^{[j]}$
is the Clebsch–Gordon map described in Definition 3.5.1.
$\operatorname {CG}^{[j]}$
is the Clebsch–Gordon map described in Definition 3.5.1. -
•
 $\Delta \colon Y(m, mN) \rightarrow Y(m, mN)^2$
denotes the diagonal embedding where, by abuse of notation, we write
$\Delta \colon Y(m, mN) \rightarrow Y(m, mN)^2$
denotes the diagonal embedding where, by abuse of notation, we write
 $Y(m, mN)^2$
for the fibre product
$Y(m, mN)^2$
for the fibre product  $$\begin{align*}Y(m, mN) \times_{\mu_m^{\circ}} Y(m, mN). \end{align*}$$
$$\begin{align*}Y(m, mN) \times_{\mu_m^{\circ}} Y(m, mN). \end{align*}$$
-
•
 $u_1 \colon Y(m, mN)^2 \to Y(m, mN)^2$
denotes the automorphism that is the identity on the first factor and acts on the moduli interpretation as on the second factor.
$u_1 \colon Y(m, mN)^2 \to Y(m, mN)^2$
denotes the automorphism that is the identity on the first factor and acts on the moduli interpretation as on the second factor. $$\begin{align*}(E, P, Q) \longmapsto (E, P + NQ, Q) \end{align*}$$
$$\begin{align*}(E, P, Q) \longmapsto (E, P + NQ, Q) \end{align*}$$
The Rankin–Iwasawa classes satisfy the following norm compatibility relations.
Proposition 4.1.2 Let
![]() $c \geq 1$
be an integer prime to
$c \geq 1$
be an integer prime to
![]() $6Np$
and let m be an integer prime to
$6Np$
and let m be an integer prime to
![]() $6cN$
. Let l be a prime not dividing
$6cN$
. Let l be a prime not dividing
![]() $6cNp$
and recall that we have defined the following morphism
$6cNp$
and recall that we have defined the following morphism
![]() $\Xi _l\colon Y(lm, lmN) \to Y(m, mN)$
in (2.0.2).
$\Xi _l\colon Y(lm, lmN) \to Y(m, mN)$
in (2.0.2).
-
(i) If l divides
 $m,$
then the Rankin–Iwasawa classes satisfy the following norm compatibility relation
$m,$
then the Rankin–Iwasawa classes satisfy the following norm compatibility relation  $$\begin{align*}(\Xi_l \times \Xi_l)_*({}_{c} \mathcal{RI}_{lm, lmN, 1}^{[j]}) = (U_l^{\prime}, U_l^{\prime}) \cdot {{}_{c} \mathcal{RI}_{m, mN, 1}^{[j]}}. \end{align*}$$
$$\begin{align*}(\Xi_l \times \Xi_l)_*({}_{c} \mathcal{RI}_{lm, lmN, 1}^{[j]}) = (U_l^{\prime}, U_l^{\prime}) \cdot {{}_{c} \mathcal{RI}_{m, mN, 1}^{[j]}}. \end{align*}$$
-
(ii) If l does not divide
 $m,$
then the Rankin–Iwasawa classes satisfy the following norm compatibility relation where
$m,$
then the Rankin–Iwasawa classes satisfy the following norm compatibility relation where $$\begin{align*}(\Xi_l \times \Xi_l)_*({}_{c} \mathcal{RI}_{lm, lmN, 1}^{[j]}) = \widetilde{Q}_l \cdot {{}_{c} \mathcal{RI}_{m, mN, 1}^{[j]}}, \end{align*}$$
$$\begin{align*}(\Xi_l \times \Xi_l)_*({}_{c} \mathcal{RI}_{lm, lmN, 1}^{[j]}) = \widetilde{Q}_l \cdot {{}_{c} \mathcal{RI}_{m, mN, 1}^{[j]}}, \end{align*}$$
 $\widetilde {Q}_l$
is the operator and
$\widetilde {Q}_l$
is the operator and $$ \begin{align*} -l^j \sigma_l + (T_l^{\prime}, T_l^{\prime}) &+ \big((l+1)l^j(\langle l \rangle^{-1} [l]_*, \langle l \rangle^{-1} [l]_*) - (\langle l \rangle^{-1} [l]_*, T_l^{{\prime}2}) - [l]_*, T_l^{{\prime}2})\\ & - (T_l^{{\prime}2}, \langle l \rangle^{-1} [l]_*) \big)\sigma_l^{-1} + \big(\langle l^{-1} \rangle [l]_* T_l^{\prime}, \langle l^{-1} \rangle [l]_* T_l^{\prime}) \sigma_l^{-2}\\ & - l^{1+j}([l^2]_* \langle l^{-2} \rangle, [l^2]_* \langle l^{-2} \rangle\big)\sigma_l^{-3} \end{align*} $$
$$ \begin{align*} -l^j \sigma_l + (T_l^{\prime}, T_l^{\prime}) &+ \big((l+1)l^j(\langle l \rangle^{-1} [l]_*, \langle l \rangle^{-1} [l]_*) - (\langle l \rangle^{-1} [l]_*, T_l^{{\prime}2}) - [l]_*, T_l^{{\prime}2})\\ & - (T_l^{{\prime}2}, \langle l \rangle^{-1} [l]_*) \big)\sigma_l^{-1} + \big(\langle l^{-1} \rangle [l]_* T_l^{\prime}, \langle l^{-1} \rangle [l]_* T_l^{\prime}) \sigma_l^{-2}\\ & - l^{1+j}([l^2]_* \langle l^{-2} \rangle, [l^2]_* \langle l^{-2} \rangle\big)\sigma_l^{-3} \end{align*} $$
-
•
 $T_l^{\prime }$
(resp.
$T_l^{\prime }$
(resp.
 $U_l'$
) is the transpose of the usual Hecke operator
$U_l'$
) is the transpose of the usual Hecke operator
 $T_l$
(resp.
$T_l$
(resp.
 $U_l$
) on
$U_l$
) on
 $Y(m, mN);$
$Y(m, mN);$
-
•
 $[a]_* \colon \Lambda ^{[j]}(\mathscr {H}) \to \Lambda ^{[j]}(\mathscr {H})$
is the map induced from multiplication by a on the first factor and the identity on the second;
$[a]_* \colon \Lambda ^{[j]}(\mathscr {H}) \to \Lambda ^{[j]}(\mathscr {H})$
is the map induced from multiplication by a on the first factor and the identity on the second; -
•
 $\langle b \rangle $
is the diamond operator on
$\langle b \rangle $
is the diamond operator on
 $Y(m, mN)$
that acts on the moduli interpretation as
$Y(m, mN)$
that acts on the moduli interpretation as
 $(E, P, Q) \mapsto (E, b^{-1}P, bQ)$
;
$(E, P, Q) \mapsto (E, b^{-1}P, bQ)$
; -
•
 $\sigma _l$
is the automorphism of
$\sigma _l$
is the automorphism of
 $Y(m ,mN)$
that acts on the moduli interpretation as
$Y(m ,mN)$
that acts on the moduli interpretation as
 $(E, P, Q) \mapsto (E, lP, Q)$
.
$(E, P, Q) \mapsto (E, lP, Q)$
.
Proof In the notation of [Reference Kings, Loeffler and ZerbesKLZ17, §5], the map
![]() $(\Xi _l \times \Xi _l)_*$
is the composition
$(\Xi _l \times \Xi _l)_*$
is the composition
![]() $(\operatorname {pr}_1 \times \operatorname {pr}_1)_* (\hat {\operatorname {pr}}_2 \times \hat {\operatorname {pr}}_2)_*$
, and if
$(\operatorname {pr}_1 \times \operatorname {pr}_1)_* (\hat {\operatorname {pr}}_2 \times \hat {\operatorname {pr}}_2)_*$
, and if
![]() $l | m,$
one can check that
$l | m,$
one can check that
![]() $(\operatorname {pr}_1 \times \operatorname {pr}_1)_*$
commutes with
$(\operatorname {pr}_1 \times \operatorname {pr}_1)_*$
commutes with
![]() $(U_l^{\prime }, U_l')$
. The first part then follows by combining the norm relations in Theorem 5.3.1 and Theorem 5.4.1 in op. cit. For the second part, this is just Proposition 5.6.1 in op. cit. ▪
$(U_l^{\prime }, U_l')$
. The first part then follows by combining the norm relations in Theorem 5.3.1 and Theorem 5.4.1 in op. cit. For the second part, this is just Proposition 5.6.1 in op. cit. ▪
4.2 Beilinson–Flach Classes in Families
Let E be a finite extension of
![]() $\mathbb {Q}_p$
with ring of integers
$\mathbb {Q}_p$
with ring of integers
![]() $\mathcal {O}_E$
, and
$\mathcal {O}_E$
, and
![]() $\mathcal {U}_1, \mathcal {U}_2 \subset (\mathcal {W}_0)_E$
two wide open discs, where
$\mathcal {U}_1, \mathcal {U}_2 \subset (\mathcal {W}_0)_E$
two wide open discs, where
![]() $\mathcal {W}_0 \subset \mathcal {W}$
is the wide open subspace of
$\mathcal {W}_0 \subset \mathcal {W}$
is the wide open subspace of
![]() $0$
-accessible weights (see Definition 3.1.3). Recall that
$0$
-accessible weights (see Definition 3.1.3). Recall that
![]() $\Lambda (\mathscr {H}^{\prime }_0)$
and
$\Lambda (\mathscr {H}^{\prime }_0)$
and
![]() $\mathcal {D}_{\mathcal {U}_i}^{\circ }(\mathscr {H}^{\prime }_0) := \mathcal {D}_{\mathcal {U}_i, 0}^{\circ }(\mathscr {H}^{\prime }_0)$
are the sheaves of continuous (resp. locally analytic)
$\mathcal {D}_{\mathcal {U}_i}^{\circ }(\mathscr {H}^{\prime }_0) := \mathcal {D}_{\mathcal {U}_i, 0}^{\circ }(\mathscr {H}^{\prime }_0)$
are the sheaves of continuous (resp. locally analytic)
![]() $\mathbb {Z}_p$
-valued (resp.
$\mathbb {Z}_p$
-valued (resp.
![]() $\Lambda _{\mathcal {U}_i}$
-valued) distributions on
$\Lambda _{\mathcal {U}_i}$
-valued) distributions on
![]() $\mathscr {H}^{\prime }_0$
, the subsheaf of
$\mathscr {H}^{\prime }_0$
, the subsheaf of
![]() $\mathscr {H}$
which is locally isomorphic to
$\mathscr {H}$
which is locally isomorphic to
![]() $T^{\prime }_0$
.
$T^{\prime }_0$
.
Consider the map of sheaves
 $$ \begin{align} \Lambda^{[j, j]}(\mathscr{H}_0^{\prime}) \longrightarrow \mathcal{D}_{[\mathcal{U}_1, \mathcal{U}_2]}(\mathscr{H}_0^{\prime}) := \big( \mathcal{D}^{\circ}_{\mathcal{U}_i}(\mathscr{H}_0^{\prime}) \boxtimes \mathcal{D}^{\circ}_{\mathcal{U}_2}(\mathscr{H}_0') \big) \Big[ \frac{1}{p} \Big] \end{align} $$
$$ \begin{align} \Lambda^{[j, j]}(\mathscr{H}_0^{\prime}) \longrightarrow \mathcal{D}_{[\mathcal{U}_1, \mathcal{U}_2]}(\mathscr{H}_0^{\prime}) := \big( \mathcal{D}^{\circ}_{\mathcal{U}_i}(\mathscr{H}_0^{\prime}) \boxtimes \mathcal{D}^{\circ}_{\mathcal{U}_2}(\mathscr{H}_0') \big) \Big[ \frac{1}{p} \Big] \end{align} $$
induced from the composition
 $$ \begin{align} \Lambda(\mathscr{H}_0^{\prime}) \otimes \operatorname{TSym}^j\mathscr{H} \longrightarrow \mathcal{D}^{\circ}_{\mathcal{U}_i - j}(\mathscr{H}_0^{\prime}) \otimes \operatorname{TSym}^j\mathscr{H} \xrightarrow{\delta^*_j} \mathcal{D}_{\mathcal{U}_i}(\mathscr{H}_0^{\prime}) \end{align} $$
$$ \begin{align} \Lambda(\mathscr{H}_0^{\prime}) \otimes \operatorname{TSym}^j\mathscr{H} \longrightarrow \mathcal{D}^{\circ}_{\mathcal{U}_i - j}(\mathscr{H}_0^{\prime}) \otimes \operatorname{TSym}^j\mathscr{H} \xrightarrow{\delta^*_j} \mathcal{D}_{\mathcal{U}_i}(\mathscr{H}_0^{\prime}) \end{align} $$
described in [Reference Loeffler and ZerbesLZ16, Definition 5.3.1]. We will not need an explicit description of these maps, but we do note that we have the following commutative diagram.
Lemma 4.2.3 We have the following commutative diagram of sheaves

where the horizontal arrows are the composition in (4.2.2) and, as usual, l is a prime not dividing
![]() $Np$
and
$Np$
and
![]() $\kappa _i$
is the universal character of
$\kappa _i$
is the universal character of
![]() $\mathcal {U}_i$
.
$\mathcal {U}_i$
.
Proof One can check this étale locally and this follows from the homogeneity condition in the definition of
![]() $D^{\circ }_{\mathcal {U}_i}$
and the fact that
$D^{\circ }_{\mathcal {U}_i}$
and the fact that
 $\delta _j^* \circ ([l]_* \otimes \operatorname {id}) = l^{-j}([l]_* \otimes \operatorname {id}) \circ \delta _j^*$
. ▪
$\delta _j^* \circ ([l]_* \otimes \operatorname {id}) = l^{-j}([l]_* \otimes \operatorname {id}) \circ \delta _j^*$
. ▪
We are now in a position to define the Beilinson–Flach classes. Consider the following composition, which we will denote by
![]() $\tau _m$
$\tau _m$
 $$\begin{align*}\tau_m\colon Y(m, mNp)^2 \xrightarrow{t_m \times t_m} Y_1(Np)^2 \times \mu_m^{\circ} \rightarrow Y_1(N_1(p)) \times Y_1(N_2(p)) \times \mu_m^{\circ} \end{align*}$$
$$\begin{align*}\tau_m\colon Y(m, mNp)^2 \xrightarrow{t_m \times t_m} Y_1(Np)^2 \times \mu_m^{\circ} \rightarrow Y_1(N_1(p)) \times Y_1(N_2(p)) \times \mu_m^{\circ} \end{align*}$$
where
![]() $t_m \colon Y(m, mNp) \to Y_1(Np) \times \mu _m^{\circ }$
is the map defined in (2.0.3), and the second map is induced from the maps
$t_m \colon Y(m, mNp) \to Y_1(Np) \times \mu _m^{\circ }$
is the map defined in (2.0.3), and the second map is induced from the maps
![]() $s_{N_i}\colon Y_1(Np) \to Y_1(N_i(p))$
as defined in (2.0.4).
$s_{N_i}\colon Y_1(Np) \to Y_1(N_i(p))$
as defined in (2.0.4).
Definition 4.2.4 We define the Beilinson–Flach class
 $$\begin{align*}{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{U}_1, \mathcal{U}_2, j]} \in \operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}\big(Y_1(N_1(p)) \times Y_1(N_2(p)) \times \mu_m^{\circ}, \mathcal{D}_{[\mathcal{U}_1, \mathcal{U}_2]}(\mathscr{H}_0^{\prime})(2-j) \big) \end{align*}$$
$$\begin{align*}{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{U}_1, \mathcal{U}_2, j]} \in \operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}\big(Y_1(N_1(p)) \times Y_1(N_2(p)) \times \mu_m^{\circ}, \mathcal{D}_{[\mathcal{U}_1, \mathcal{U}_2]}(\mathscr{H}_0^{\prime})(2-j) \big) \end{align*}$$
to be the pushforward of
 ${}_{c} \mathcal {RI}_{m, mNp, 1}^{[j]}$
under
${}_{c} \mathcal {RI}_{m, mNp, 1}^{[j]}$
under
![]() $\tau _m$
composed with the map in (4.2.1).
$\tau _m$
composed with the map in (4.2.1).
Let
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
be Coleman families over
$\mathcal {G}$
be Coleman families over
![]() $\mathcal {U}_1$
and
$\mathcal {U}_1$
and
![]() $\mathcal {U}_2$
respectively. To specialise the Beilinson–Flach classes at
$\mathcal {U}_2$
respectively. To specialise the Beilinson–Flach classes at
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
one introduces the following differential operators
$\mathcal {G}$
one introduces the following differential operators
 ${\nabla _i \choose j}$
on
${\nabla _i \choose j}$
on
![]() $\Lambda _{\mathcal {U}_i}[1/p]$
given by the formula
$\Lambda _{\mathcal {U}_i}[1/p]$
given by the formula
 $$\begin{align*}\binom{\nabla_i}{j} := \frac{1}{j!}\prod_{k = 0}^{j-1}{(\nabla_i - k)}, \end{align*}$$
$$\begin{align*}\binom{\nabla_i}{j} := \frac{1}{j!}\prod_{k = 0}^{j-1}{(\nabla_i - k)}, \end{align*}$$
where
![]() $\nabla _i$
is given by
$\nabla _i$
is given by
 $(\nabla _if)(x) = \frac {d}{dt}f(tx) \mid _{t=1}$
(see [Reference Loeffler and ZerbesLZ16, Proposition 5.1.2] for more details). Let
$(\nabla _if)(x) = \frac {d}{dt}f(tx) \mid _{t=1}$
(see [Reference Loeffler and ZerbesLZ16, Proposition 5.1.2] for more details). Let
![]() $V_1$
and
$V_1$
and
![]() $V_2$
be open affinoid subdomains in
$V_2$
be open affinoid subdomains in
![]() $\mathcal {U}_1$
and
$\mathcal {U}_1$
and
![]() $\mathcal {U}_2$
respectively and
$\mathcal {U}_2$
respectively and
![]() $j \geq 0$
an integer not contained in either
$j \geq 0$
an integer not contained in either
![]() $V_1$
or
$V_1$
or
![]() $V_2$
. Then the operators
$V_2$
. Then the operators
 ${\nabla _1 \choose j}$
and
${\nabla _1 \choose j}$
and
 $\binom {\nabla _2}{ j}$
are injective and there exist unique classes
$\binom {\nabla _2}{ j}$
are injective and there exist unique classes
 $$\begin{align*}{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}, j]} \in \operatorname{H}^1\left(\mathbb{Q}(\mu_m), [M_{V_1}(\mathcal{F})^* \hat{\otimes} M_{V_2}(\mathcal{G})^*](-j) \right) \end{align*}$$
$$\begin{align*}{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}, j]} \in \operatorname{H}^1\left(\mathbb{Q}(\mu_m), [M_{V_1}(\mathcal{F})^* \hat{\otimes} M_{V_2}(\mathcal{G})^*](-j) \right) \end{align*}$$
such that
 ${\nabla _1 \choose j}{\nabla _2 \choose j} {{}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}, j]}}$
equals the image of
${\nabla _1 \choose j}{\nabla _2 \choose j} {{}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}, j]}}$
equals the image of
 ${}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {U}_1, \mathcal {U}_2, j]}$
under the Abel–Jacobi map
${}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {U}_1, \mathcal {U}_2, j]}$
under the Abel–Jacobi map
![]() $\operatorname {AJ}_{\mathcal {F}, \mathcal {G}}$
defined below.
$\operatorname {AJ}_{\mathcal {F}, \mathcal {G}}$
defined below.
Definition 4.2.5 The Abel–Jacobi map
![]() $\operatorname {AJ}_{\mathcal {F}, \mathcal {G}}$
is defined to be the composition
$\operatorname {AJ}_{\mathcal {F}, \mathcal {G}}$
is defined to be the composition
 $$\begin{align*} & \operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}\big(Y_1(N_1(p)) \times Y_1(N_2(p) ) \times \mu_m^{\circ}, \mathcal{D}_{[\mathcal{U}_1, \mathcal{U}_2]}(\mathscr{H}_0^{\prime})(2-j)\big) \\ & \quad \longrightarrow \operatorname{H}^1\big(\mathbb{Q}(\mu_m), \operatorname{H}^2_{\acute{\mathrm{e}}\mathrm{t}}(Y_1(N_1(p))_{\bar{\mathbb{Q}}} \times Y_1(N_2(p))_{\bar{\mathbb{Q}}}, \mathcal{D}_{[\mathcal{U}_1, \mathcal{U}_2]}(\mathscr{H}_0^{\prime})(2-j) \big) \\ & \quad \xrightarrow{\sim} \operatorname{H}^1(\mathbb{Q}(\mu_m), \operatorname{H}^1_{\acute{\mathrm{e}}\mathrm{t}}(Y_1(N_1(p))_{\bar{\mathbb{Q}}}, \mathcal{D}_{\mathcal{U}_1}(\mathscr{H}_0^{\prime})(1)) \\ & \qquad \hat{\otimes} \operatorname{H}^1_{\acute{\mathrm{e}}\mathrm{t}}(Y_1(N_2(p))_{\bar{\mathbb{Q}}}, \mathcal{D}_{\mathcal{U}_2}(\mathscr{H}_0^{\prime})(1))(-j)) \\ & \quad \longrightarrow \operatorname{H}^1\big(\mathbb{Q}(\mu_m), \big[ M_{V_1}(\mathcal{F})^* \hat{\otimes} M_{V_2}(\mathcal{G})^* \big] (-j) \big), \end{align*}$$
$$\begin{align*} & \operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}\big(Y_1(N_1(p)) \times Y_1(N_2(p) ) \times \mu_m^{\circ}, \mathcal{D}_{[\mathcal{U}_1, \mathcal{U}_2]}(\mathscr{H}_0^{\prime})(2-j)\big) \\ & \quad \longrightarrow \operatorname{H}^1\big(\mathbb{Q}(\mu_m), \operatorname{H}^2_{\acute{\mathrm{e}}\mathrm{t}}(Y_1(N_1(p))_{\bar{\mathbb{Q}}} \times Y_1(N_2(p))_{\bar{\mathbb{Q}}}, \mathcal{D}_{[\mathcal{U}_1, \mathcal{U}_2]}(\mathscr{H}_0^{\prime})(2-j) \big) \\ & \quad \xrightarrow{\sim} \operatorname{H}^1(\mathbb{Q}(\mu_m), \operatorname{H}^1_{\acute{\mathrm{e}}\mathrm{t}}(Y_1(N_1(p))_{\bar{\mathbb{Q}}}, \mathcal{D}_{\mathcal{U}_1}(\mathscr{H}_0^{\prime})(1)) \\ & \qquad \hat{\otimes} \operatorname{H}^1_{\acute{\mathrm{e}}\mathrm{t}}(Y_1(N_2(p))_{\bar{\mathbb{Q}}}, \mathcal{D}_{\mathcal{U}_2}(\mathscr{H}_0^{\prime})(1))(-j)) \\ & \quad \longrightarrow \operatorname{H}^1\big(\mathbb{Q}(\mu_m), \big[ M_{V_1}(\mathcal{F})^* \hat{\otimes} M_{V_2}(\mathcal{G})^* \big] (-j) \big), \end{align*}$$
where the first map arises from the Leray spectral sequence (using the fact that
![]() $Y_1(N_1(p))_{\bar {\mathbb {Q}}} \times Y_1(N_2(p))_{\bar {\mathbb {Q}}}$
is an affine scheme, so its étale cohomology vanishes in degree
$Y_1(N_1(p))_{\bar {\mathbb {Q}}} \times Y_1(N_2(p))_{\bar {\mathbb {Q}}}$
is an affine scheme, so its étale cohomology vanishes in degree
![]() $3$
and above); the second isomorphism is the Künneth formula (again using the fact that
$3$
and above); the second isomorphism is the Künneth formula (again using the fact that
![]() $Y_1(N_i(p))_{\bar {\mathbb {Q}}}$
is affine), and the third map is the projection down to the Galois representations associated with
$Y_1(N_i(p))_{\bar {\mathbb {Q}}}$
is affine), and the third map is the projection down to the Galois representations associated with
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
The Beilinson–Flach classes associated with
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
satisfy norm compatibility relations similar to those for the Rankin–Iwasawa classes.
$\mathcal {G}$
satisfy norm compatibility relations similar to those for the Rankin–Iwasawa classes.
Proposition 4.2.6 Let
![]() $c \geq 1$
be an integer prime to
$c \geq 1$
be an integer prime to
![]() $6Np$
and let m be an integer prime to
$6Np$
and let m be an integer prime to
![]() $6cN$
. Let l be a prime not dividing
$6cN$
. Let l be a prime not dividing
![]() $6cNp$
and let
$6cNp$
and let
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
be two Coleman families over the affinoid subdomains
$\mathcal {G}$
be two Coleman families over the affinoid subdomains
![]() $V_1$
and
$V_1$
and
![]() $V_2,$
respectively. Suppose that
$V_2,$
respectively. Suppose that
![]() $j \geq 0$
is an integer not contained in
$j \geq 0$
is an integer not contained in
![]() $V_1$
or
$V_1$
or
![]() $V_2$
.
$V_2$
.
-
(i) If l divides
 $m,$
then the Beilinson–Flach classes satisfy the following norm-compatibility relation
$m,$
then the Beilinson–Flach classes satisfy the following norm-compatibility relation  $$\begin{align*}\operatorname{cores}^{\mathbb{Q}(\mu_{ml})}_{\mathbb{Q}(\mu_m)} \big( {}_{c} \mathcal{BF}_{ml, 1}^{[\mathcal{F}, \mathcal{G}, j]} \big) = \big(a_l(\mathcal{F})a_l(\mathcal{G})\big){{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}, j]}}. \end{align*}$$
$$\begin{align*}\operatorname{cores}^{\mathbb{Q}(\mu_{ml})}_{\mathbb{Q}(\mu_m)} \big( {}_{c} \mathcal{BF}_{ml, 1}^{[\mathcal{F}, \mathcal{G}, j]} \big) = \big(a_l(\mathcal{F})a_l(\mathcal{G})\big){{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}, j]}}. \end{align*}$$
-
(ii) If l does not divide
 $m,$
then the Beilinson–Flach classes satisfy the following norm-compatibility relation where
$m,$
then the Beilinson–Flach classes satisfy the following norm-compatibility relation where $$\begin{align*}\operatorname{cores}^{\mathbb{Q}(\mu_{ml})}_{\mathbb{Q}(\mu_m)} \left( {}_{c} \mathcal{BF}_{ml, 1}^{[\mathcal{F}, \mathcal{G}, j]} \right) = \mathcal{Q}_l(l^{-j}\sigma_l^{-1}) \cdot {{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}, j]}}, \end{align*}$$
$$\begin{align*}\operatorname{cores}^{\mathbb{Q}(\mu_{ml})}_{\mathbb{Q}(\mu_m)} \left( {}_{c} \mathcal{BF}_{ml, 1}^{[\mathcal{F}, \mathcal{G}, j]} \right) = \mathcal{Q}_l(l^{-j}\sigma_l^{-1}) \cdot {{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}, j]}}, \end{align*}$$
 $\mathcal {Q}_l(X) \in \mathcal {O}(V_1 \times V_2)[X, X^{-1}]$
is the polynomial where, as before,
$\mathcal {Q}_l(X) \in \mathcal {O}(V_1 \times V_2)[X, X^{-1}]$
is the polynomial where, as before, $$\begin{align*}\begin{aligned} \mathcal{Q}_l(X) = & -X^{-1} + a_l(\mathcal{F})a_l(\mathcal{G}) \\ & + \big((l+1)l^{\kappa_1 + \kappa_2}\varepsilon_{\mathcal{F}}(l)\varepsilon_{\mathcal{G}}(l) - l^{\kappa_1}\varepsilon_{\mathcal{F}}(l)a_l(\mathcal{G})^2 - l^{\kappa_2}\varepsilon_{\mathcal{G}}(l)a_l(\mathcal{F})^2\big)X \\ & + l^{\kappa_1 + \kappa_2}\varepsilon_{\mathcal{F}}(l)\varepsilon_{\mathcal{G}}(l)a_l(\mathcal{F})a_l(\mathcal{G}) X^2 - l^{1+2\kappa_1 + 2\kappa_2}\varepsilon_{\mathcal{F}}(l^{2})\varepsilon_{\mathcal{G}}(l^{2})X^3, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \mathcal{Q}_l(X) = & -X^{-1} + a_l(\mathcal{F})a_l(\mathcal{G}) \\ & + \big((l+1)l^{\kappa_1 + \kappa_2}\varepsilon_{\mathcal{F}}(l)\varepsilon_{\mathcal{G}}(l) - l^{\kappa_1}\varepsilon_{\mathcal{F}}(l)a_l(\mathcal{G})^2 - l^{\kappa_2}\varepsilon_{\mathcal{G}}(l)a_l(\mathcal{F})^2\big)X \\ & + l^{\kappa_1 + \kappa_2}\varepsilon_{\mathcal{F}}(l)\varepsilon_{\mathcal{G}}(l)a_l(\mathcal{F})a_l(\mathcal{G}) X^2 - l^{1+2\kappa_1 + 2\kappa_2}\varepsilon_{\mathcal{F}}(l^{2})\varepsilon_{\mathcal{G}}(l^{2})X^3, \end{aligned} \end{align*}$$
 $\sigma _l$
is the image of the arithmetic Frobenius at l in
$\sigma _l$
is the image of the arithmetic Frobenius at l in
 $ \operatorname {\mathrm {Gal}}(\mathbb {Q}(\mu _m)/\mathbb {Q})$
.
$ \operatorname {\mathrm {Gal}}(\mathbb {Q}(\mu _m)/\mathbb {Q})$
.
Proof Consider the composition
 $$ \begin{align*} &\operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}\big(Y(m, mNp)^2, \Lambda^{[j, j]}(2-j) \big) \\ &\qquad \xrightarrow{\tau_{m, *}} \operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}(Y_1(N_1(p)) \times Y_1(N_2(p)) \times \mu_m^{\circ}, \Lambda^{[j, j]}(\mathscr{H}_0^{\prime}) ) \\ &\qquad \longrightarrow \operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}\big(Y_1(N_1(p)) \times Y_1(N_2(p)) \times \mu_m^{\circ}, \mathcal{D}_{[\mathcal{U}_1, \mathcal{U}_2]}(\mathscr{H}_0^{\prime})\big). \end{align*} $$
$$ \begin{align*} &\operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}\big(Y(m, mNp)^2, \Lambda^{[j, j]}(2-j) \big) \\ &\qquad \xrightarrow{\tau_{m, *}} \operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}(Y_1(N_1(p)) \times Y_1(N_2(p)) \times \mu_m^{\circ}, \Lambda^{[j, j]}(\mathscr{H}_0^{\prime}) ) \\ &\qquad \longrightarrow \operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}\big(Y_1(N_1(p)) \times Y_1(N_2(p)) \times \mu_m^{\circ}, \mathcal{D}_{[\mathcal{U}_1, \mathcal{U}_2]}(\mathscr{H}_0^{\prime})\big). \end{align*} $$
By applying Lemma 2.0.5, the morphisms
![]() $(\Xi _l)_*$
and
$(\Xi _l)_*$
and
 $\operatorname {cores}^{\mathbb {Q}(\mu _{lm})}_{\mathbb {Q}(\mu _m)}$
are compatible under the map
$\operatorname {cores}^{\mathbb {Q}(\mu _{lm})}_{\mathbb {Q}(\mu _m)}$
are compatible under the map
 $$ \begin{align} {\operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}(Y(m, mN)^2, \Lambda^{[j, j]}(2-j))} \longrightarrow {\operatorname{H}^1(\mathbb{Q}(\mu_m), [M(\mathcal{F})^* \hat{\otimes} M(\mathcal{G})^*](-j))} \end{align} $$
$$ \begin{align} {\operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}(Y(m, mN)^2, \Lambda^{[j, j]}(2-j))} \longrightarrow {\operatorname{H}^1(\mathbb{Q}(\mu_m), [M(\mathcal{F})^* \hat{\otimes} M(\mathcal{G})^*](-j))} \end{align} $$
obtained by composing the above map with
![]() $\operatorname {AJ}_{\mathcal {F}, \mathcal {G}}$
.
$\operatorname {AJ}_{\mathcal {F}, \mathcal {G}}$
.
Immediately we see that if l divides m, then
 $$ \begin{align*} &\binom{\nabla_1}{ j} \binom{\nabla_2}{ j} \operatorname{cores}^{\mathbb{Q}(\mu_{ml})}_{\mathbb{Q}(\mu_m)} {{}_{c} \mathcal{BF}_{lm, 1}^{[\mathcal{F}, \mathcal{G}, j]}}\\ &\qquad = \operatorname{cores}^{\mathbb{Q}(\mu_{ml})}_{\mathbb{Q}(\mu_m)} \binom{\nabla_1}{ j} \binom{\nabla_2}{ j} {{}_{c} \mathcal{BF}_{lm, 1}^{[\mathcal{F}, \mathcal{G}, j]}} \\ &\qquad = (a_l(\mathcal{F})a_l(\mathcal{G}))\binom{\nabla_1}{ j} \binom{\nabla_2}{ j} {{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}, j]}}, \end{align*} $$
$$ \begin{align*} &\binom{\nabla_1}{ j} \binom{\nabla_2}{ j} \operatorname{cores}^{\mathbb{Q}(\mu_{ml})}_{\mathbb{Q}(\mu_m)} {{}_{c} \mathcal{BF}_{lm, 1}^{[\mathcal{F}, \mathcal{G}, j]}}\\ &\qquad = \operatorname{cores}^{\mathbb{Q}(\mu_{ml})}_{\mathbb{Q}(\mu_m)} \binom{\nabla_1}{ j} \binom{\nabla_2}{ j} {{}_{c} \mathcal{BF}_{lm, 1}^{[\mathcal{F}, \mathcal{G}, j]}} \\ &\qquad = (a_l(\mathcal{F})a_l(\mathcal{G}))\binom{\nabla_1}{ j} \binom{\nabla_2}{ j} {{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}, j]}}, \end{align*} $$
where the second equality follows from Proposition 4.1.2(i) and the fact that
![]() $T_l^{\prime }$
acts as multiplication by
$T_l^{\prime }$
acts as multiplication by
![]() $a_l(\mathcal {F})$
(resp.
$a_l(\mathcal {F})$
(resp.
![]() $a_l(\mathcal {G})$
) on
$a_l(\mathcal {G})$
) on
![]() $M(\mathcal {F})^*$
(resp.
$M(\mathcal {F})^*$
(resp.
![]() $M(\mathcal {G})^*$
). Note that under the morphism
$M(\mathcal {G})^*$
). Note that under the morphism
![]() $t_m$
the operators
$t_m$
the operators
![]() $U_l'$
and
$U_l'$
and
![]() $T_l'$
are compatible. Since j is not contained in
$T_l'$
are compatible. Since j is not contained in
![]() $V_1$
or
$V_1$
or
![]() $V_2$
, the operator
$V_2$
, the operator
 $\binom {\nabla _1 }{ j} \binom {\nabla _2}{ j}$
is invertible, and we have the required relation.
$\binom {\nabla _1 }{ j} \binom {\nabla _2}{ j}$
is invertible, and we have the required relation.
For the second part, recall that by Proposition 4.1.2(ii), the Rankin–Iwasawa classes satisfy
 $(\Xi _l \times \Xi _l)_*({}_{c} \mathcal {RI}_{lm, lmN, 1}^{[j]}) = \widetilde {Q}_l \cdot {{}_{c} \mathcal {RI}_{m, mN, 1}^{[j]}}$
. We have the following commutative diagram:
$(\Xi _l \times \Xi _l)_*({}_{c} \mathcal {RI}_{lm, lmN, 1}^{[j]}) = \widetilde {Q}_l \cdot {{}_{c} \mathcal {RI}_{m, mN, 1}^{[j]}}$
. We have the following commutative diagram:

where the horizontal arrows are the maps in (4.2.7). Indeed,
![]() $M(\mathcal {F})^*$
can be described as the quotient of
$M(\mathcal {F})^*$
can be described as the quotient of
 $$\begin{align*}\operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}\big(Y_1(N_1(p))_{\bar{\mathbb{Q}}}, \mathcal{D}_{V_1}(1)\big) \end{align*}$$
$$\begin{align*}\operatorname{H}^3_{\acute{\mathrm{e}}\mathrm{t}}\big(Y_1(N_1(p))_{\bar{\mathbb{Q}}}, \mathcal{D}_{V_1}(1)\big) \end{align*}$$
such that
![]() $T^{\prime }_l$
acts as multiplication by
$T^{\prime }_l$
acts as multiplication by
![]() $a_l(\mathcal {F})$
and
$a_l(\mathcal {F})$
and
![]() $\langle l \rangle $
acts as multiplication by
$\langle l \rangle $
acts as multiplication by
![]() $\varepsilon _{\mathcal {F}}(l)^{-1}$
. We have a similar description for
$\varepsilon _{\mathcal {F}}(l)^{-1}$
. We have a similar description for
![]() $M(\mathcal {G})^*$
. Furthermore, the action of
$M(\mathcal {G})^*$
. Furthermore, the action of
![]() $\sigma _l$
becomes the natural action of
$\sigma _l$
becomes the natural action of
![]() $\sigma _l$
under the horizontal map in the above diagram (this is an application of the push-pull lemma for étale cohomology). Finally, by Lemma 4.2.3,
$\sigma _l$
under the horizontal map in the above diagram (this is an application of the push-pull lemma for étale cohomology). Finally, by Lemma 4.2.3,
![]() $[l]_*$
becomes multiplication by
$[l]_*$
becomes multiplication by
![]() $l^{\kappa _i - j}$
. This shows that the above diagram is commutative and completes the proof of the proposition. ▪
$l^{\kappa _i - j}$
. This shows that the above diagram is commutative and completes the proof of the proposition. ▪
4.3 Interpolation in the Cyclotomic Variable
In this section, we recall how to interpolate the Beilinson–Flach classes
 ${}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}, j]}$
in the cyclotomic variable j. As a consequence, we show that the three-variable Beilinson–Flach classes satisfy a norm-compatibility relation closely related to the Euler system relations.
${}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}, j]}$
in the cyclotomic variable j. As a consequence, we show that the three-variable Beilinson–Flach classes satisfy a norm-compatibility relation closely related to the Euler system relations.
Let
 $p^{-\lambda _1} = \|a_p(\mathcal {F})\|$
(resp.
$p^{-\lambda _1} = \|a_p(\mathcal {F})\|$
(resp.
 $p^{-\lambda _2} = \|a_p(\mathcal {G})\|$
) where
$p^{-\lambda _2} = \|a_p(\mathcal {G})\|$
) where
![]() $\|\cdot \|$
denotes the canonical supremum norm on
$\|\cdot \|$
denotes the canonical supremum norm on
![]() $\mathcal {O}(V_i)$
(which exists because we have restricted our Coleman families to reduced affinoid subdomains). Let
$\mathcal {O}(V_i)$
(which exists because we have restricted our Coleman families to reduced affinoid subdomains). Let
![]() $\lambda = \lambda _1 + \lambda _2$
and
$\lambda = \lambda _1 + \lambda _2$
and
![]() $h \geq \lambda $
a positive integer. Define the following elements
$h \geq \lambda $
a positive integer. Define the following elements
 $$\begin{align*}x_{n, j} := \big(a_p(\mathcal{F})a_p(\mathcal{G})\big)^{-n} \frac{{}_{c} \mathcal{BF}_{mp^n, 1}^{[\mathcal{F}, \mathcal{G}, j]}}{(-1)^jj!} \end{align*}$$
$$\begin{align*}x_{n, j} := \big(a_p(\mathcal{F})a_p(\mathcal{G})\big)^{-n} \frac{{}_{c} \mathcal{BF}_{mp^n, 1}^{[\mathcal{F}, \mathcal{G}, j]}}{(-1)^jj!} \end{align*}$$
for
![]() $0 \leq j \leq h$
,
$0 \leq j \leq h$
,
![]() $n \geq 1$
, and set
$n \geq 1$
, and set
 $$\begin{align*}x_{0, j} := \Big(1 - \frac{p^j}{a_p(\mathcal{F})a_p(\mathcal{G})} \Big) \frac{{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}, j]}}{(-1)^jj!} \end{align*}$$
$$\begin{align*}x_{0, j} := \Big(1 - \frac{p^j}{a_p(\mathcal{F})a_p(\mathcal{G})} \Big) \frac{{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}, j]}}{(-1)^jj!} \end{align*}$$
for
![]() $0 \leq j \leq h$
. These elements are compatible under corestriction and satisfy a certain growth bound (see [Reference Loeffler and ZerbesLZ16, Proposition 5.4.1]), so by Proposition 2.3.3 in op. cit. there exists a unique element
$0 \leq j \leq h$
. These elements are compatible under corestriction and satisfy a certain growth bound (see [Reference Loeffler and ZerbesLZ16, Proposition 5.4.1]), so by Proposition 2.3.3 in op. cit. there exists a unique element
 $$\begin{align*}{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]} \in \operatorname{H}^1 \big(\mathbb{Q}(\mu_{mp^{\infty}}), D_{\lambda}(\Gamma, M)\big)^{\Gamma} \cong \operatorname{H}^1\big(\mathbb{Q}(\mu_m), D_{\lambda}(\Gamma, M)\big) \end{align*}$$
$$\begin{align*}{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]} \in \operatorname{H}^1 \big(\mathbb{Q}(\mu_{mp^{\infty}}), D_{\lambda}(\Gamma, M)\big)^{\Gamma} \cong \operatorname{H}^1\big(\mathbb{Q}(\mu_m), D_{\lambda}(\Gamma, M)\big) \end{align*}$$
satisfying
 $$\begin{align*}\int_{\Gamma_n} \chi_{\mathrm{cycl}}^j \; {{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]}} = x_{n, j} \end{align*}$$
$$\begin{align*}\int_{\Gamma_n} \chi_{\mathrm{cycl}}^j \; {{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]}} = x_{n, j} \end{align*}$$
for all
![]() $n, j$
. Here,
$n, j$
. Here,
![]() $M = M_{V_1}(\mathcal {F})^* \hat {\otimes } M_{V_2}(\mathcal {G})^*$
and
$M = M_{V_1}(\mathcal {F})^* \hat {\otimes } M_{V_2}(\mathcal {G})^*$
and
![]() $\Gamma _n \subset \Gamma $
is the unique subgroup of index
$\Gamma _n \subset \Gamma $
is the unique subgroup of index
![]() $p^{n-1}(p-1)$
(we set
$p^{n-1}(p-1)$
(we set
![]() $\Gamma _0 = \Gamma $
). The class
$\Gamma _0 = \Gamma $
). The class
 ${}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}$
is independent of the choice of h.
${}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}$
is independent of the choice of h.
Proposition 4.3.1 The Beilinson–Flach classes
 ${}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}$
satisfy the following norm compatibility relations:
${}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}$
satisfy the following norm compatibility relations:
-
• If l divides
 $m,$
then
$m,$
then  $$\begin{align*}\operatorname{cores}^{\mathbb{Q}(\mu_{lm})}_{\mathbb{Q}(\mu_m)} \big( {}_{c} \mathcal{BF}_{lm, 1}^{[\mathcal{F}, \mathcal{G}]} \big) = \big(a_l(\mathcal{F})a_l(\mathcal{G})\big) \cdot {{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]}}. \end{align*}$$
$$\begin{align*}\operatorname{cores}^{\mathbb{Q}(\mu_{lm})}_{\mathbb{Q}(\mu_m)} \big( {}_{c} \mathcal{BF}_{lm, 1}^{[\mathcal{F}, \mathcal{G}]} \big) = \big(a_l(\mathcal{F})a_l(\mathcal{G})\big) \cdot {{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]}}. \end{align*}$$
-
• If l does not divide
 $m,$
then where
$m,$
then where $$\begin{align*}\operatorname{cores}^{\mathbb{Q}(\mu_{lm})}_{\mathbb{Q}(\mu_m)} \left( {}_{c} \mathcal{BF}_{lm, 1}^{[\mathcal{F}, \mathcal{G}]} \right) = \mathcal{Q}_l(l^{-\mathbf{j}}\sigma_l^{-1}) \cdot {{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]}} \end{align*}$$
$$\begin{align*}\operatorname{cores}^{\mathbb{Q}(\mu_{lm})}_{\mathbb{Q}(\mu_m)} \left( {}_{c} \mathcal{BF}_{lm, 1}^{[\mathcal{F}, \mathcal{G}]} \right) = \mathcal{Q}_l(l^{-\mathbf{j}}\sigma_l^{-1}) \cdot {{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]}} \end{align*}$$
 $\mathcal {Q}_l(X)$
is the polynomial defined in Proposition 4.2.6 and
$\mathcal {Q}_l(X)$
is the polynomial defined in Proposition 4.2.6 and
 $\mathbf {j}$
is the universal character
$\mathbf {j}$
is the universal character
 $\Gamma \to D_{\lambda }(\Gamma , E)$
( i.e., the homomorphism taking
$\Gamma \to D_{\lambda }(\Gamma , E)$
( i.e., the homomorphism taking
 $x \mapsto \operatorname {ev}_x$
where
$x \mapsto \operatorname {ev}_x$
where
 $\operatorname {ev}_x$
is the evaluation-at-x map).
$\operatorname {ev}_x$
is the evaluation-at-x map).
Proof Let
![]() $\mathcal {Q}_l(X)$
denote the polynomial appearing in Proposition 4.2.6 and let l be a prime not dividing
$\mathcal {Q}_l(X)$
denote the polynomial appearing in Proposition 4.2.6 and let l be a prime not dividing
![]() $6mpNc$
. Set
$6mpNc$
. Set
 $$\begin{align*}\nu_m = \mathcal{Q}_l(l^{-\mathbf{j}}\sigma_l^{-1}) \cdot {{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]}} - \operatorname{cores}^{\mathbb{Q}(\mu_{lm})}_{\mathbb{Q}(\mu_m)} \left( {}_{c} \mathcal{BF}_{lm, 1}^{[\mathcal{F}, \mathcal{G}]} \right). \end{align*}$$
$$\begin{align*}\nu_m = \mathcal{Q}_l(l^{-\mathbf{j}}\sigma_l^{-1}) \cdot {{}_{c} \mathcal{BF}_{m, 1}^{[\mathcal{F}, \mathcal{G}]}} - \operatorname{cores}^{\mathbb{Q}(\mu_{lm})}_{\mathbb{Q}(\mu_m)} \left( {}_{c} \mathcal{BF}_{lm, 1}^{[\mathcal{F}, \mathcal{G}]} \right). \end{align*}$$
Then for all
![]() $n,j \geq 0$
the specialisation
$n,j \geq 0$
the specialisation
 $\int _{\Gamma _n}{\chi ^j \nu _m}$
is zero; so
$\int _{\Gamma _n}{\chi ^j \nu _m}$
is zero; so
![]() $\nu _m$
interpolates only zero classes. By uniqueness, this implies that
$\nu _m$
interpolates only zero classes. By uniqueness, this implies that
![]() $\nu _m = 0$
. A similar argument works for
$\nu _m = 0$
. A similar argument works for
![]() $l | m$
.▪
$l | m$
.▪
4.4 Euler System Relations in Families
In Proposition 4.3.1, we showed that the Beilinson–Flach classes satisfy norm compatible relations. It turns out that we can adjust these classes so that we obtain cohomology classes satisfying the Euler system relations.
As before, let
![]() $M = M_{V_1}(\mathcal {F})^* \hat {\otimes } M_{V_2}(\mathcal {G})^*$
and let
$M = M_{V_1}(\mathcal {F})^* \hat {\otimes } M_{V_2}(\mathcal {G})^*$
and let
![]() $\mathcal {P}_l(X)$
denote the polynomial
$\mathcal {P}_l(X)$
denote the polynomial
 $\operatorname {det}\left (1 - \operatorname {Frob}_l^{-1} X | M^*(1) \right )$
, where
$\operatorname {det}\left (1 - \operatorname {Frob}_l^{-1} X | M^*(1) \right )$
, where
![]() $\operatorname {Frob}_l$
denotes any lift of the arithmetic Frobenius at l. Then one can observe that
$\operatorname {Frob}_l$
denotes any lift of the arithmetic Frobenius at l. Then one can observe that
 $$\begin{align*}\mathcal{Q}_l(X) = X^{-1}\big( (l-1)(1-l^{\kappa_1 + \kappa_2 + 2}\varepsilon_{\mathcal{F}}(l)\varepsilon_{\mathcal{G}}(l) X^2 ) - l \mathcal{P}_l(X) \big), \end{align*}$$
$$\begin{align*}\mathcal{Q}_l(X) = X^{-1}\big( (l-1)(1-l^{\kappa_1 + \kappa_2 + 2}\varepsilon_{\mathcal{F}}(l)\varepsilon_{\mathcal{G}}(l) X^2 ) - l \mathcal{P}_l(X) \big), \end{align*}$$
so in particular,
![]() $\mathcal {Q}_l(X) \equiv -X^{-1}\mathcal {P}_l(X)$
modulo
$\mathcal {Q}_l(X) \equiv -X^{-1}\mathcal {P}_l(X)$
modulo
![]() $l-1$
. Such a congruence allows us to adjust the classes
$l-1$
. Such a congruence allows us to adjust the classes
 ${}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}$
so that we obtain Euler system relations.
${}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}$
so that we obtain Euler system relations.
Proposition 4.4.1 Let
![]() $c \geq 1$
be an integer prime to
$c \geq 1$
be an integer prime to
![]() $6pN$
and let A denote the set of all square-free positive integers that are coprime to
$6pN$
and let A denote the set of all square-free positive integers that are coprime to
![]() $6pNc$
. Then for all
$6pNc$
. Then for all
![]() $m \in A$
, there exist cohomology classes
$m \in A$
, there exist cohomology classes
 ${{}_{c}\mathcal {Z}_m^{[\mathcal {F}, \mathcal {G}]}} \in \operatorname {H}^1(\mathbb {Q}(\mu _m), D^{\mathrm {la}}(\Gamma , M) )$
such that
${{}_{c}\mathcal {Z}_m^{[\mathcal {F}, \mathcal {G}]}} \in \operatorname {H}^1(\mathbb {Q}(\mu _m), D^{\mathrm {la}}(\Gamma , M) )$
such that
-
(i) The bottom class satisfies
 ${}_{c}\mathcal {Z}_1^{[\mathcal {F}, \mathcal {G}]} = {{}_{c} \mathcal {BF}_{1, 1}^{[\mathcal {F}, \mathcal {G}]}}$
.
${}_{c}\mathcal {Z}_1^{[\mathcal {F}, \mathcal {G}]} = {{}_{c} \mathcal {BF}_{1, 1}^{[\mathcal {F}, \mathcal {G}]}}$
. -
(ii) If l is a prime such that
 $lm \in A$
(so in particular
$lm \in A$
(so in particular
 $l \nmid m$
), we have the following Euler system relation: Note that
$l \nmid m$
), we have the following Euler system relation: Note that $$\begin{align*}\operatorname{cores}^{\mathbb{Q}(\mu_{lm})}_{\mathbb{Q}(\mu_m)}{{}_{c}\mathcal{Z}_{lm}^{[\mathcal{F}, \mathcal{G}]}} = \mathcal{P}_l(l^{-\mathbf{j}} \sigma_l^{-1} ) \cdot {{}_{c}\mathcal{Z}_{m}^{[\mathcal{F}, \mathcal{G}]}}. \end{align*}$$
$$\begin{align*}\operatorname{cores}^{\mathbb{Q}(\mu_{lm})}_{\mathbb{Q}(\mu_m)}{{}_{c}\mathcal{Z}_{lm}^{[\mathcal{F}, \mathcal{G}]}} = \mathcal{P}_l(l^{-\mathbf{j}} \sigma_l^{-1} ) \cdot {{}_{c}\mathcal{Z}_{m}^{[\mathcal{F}, \mathcal{G}]}}. \end{align*}$$
 $\mathcal {P}_l(l^{-\mathbf {j}}X) = \operatorname {det}( 1 - \operatorname {Frob}_l^{-1} X | M^*(1 + \mathbf {j}))$
.
$\mathcal {P}_l(l^{-\mathbf {j}}X) = \operatorname {det}( 1 - \operatorname {Frob}_l^{-1} X | M^*(1 + \mathbf {j}))$
.
Moreover,
 ${{}_{c}\mathcal {Z}_m^{[\mathcal {F}, \mathcal {G}]}}$
differs from
${{}_{c}\mathcal {Z}_m^{[\mathcal {F}, \mathcal {G}]}}$
differs from
 ${{}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}}$
by an element of
${{}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}}$
by an element of
![]() $\mathcal {O}(V_1 \times V_2 \times \mathcal {W})^{\circ }[(\mathbb {Z}/m\mathbb {Z})^{\times }]$
.
$\mathcal {O}(V_1 \times V_2 \times \mathcal {W})^{\circ }[(\mathbb {Z}/m\mathbb {Z})^{\times }]$
.
Proof This follows from the same argument in [Reference Lei, Loeffler and ZerbesLLZ14, §7.3]. ▪
Unfortunately, in general, there is no way to force these classes to lie in a Galois stable lattice inside
![]() $D^{\mathrm {la}}(\Gamma , M)$
, so we do not get an Euler system for this representation. However, this is possible after specialisation so long as we use a weaker notion of an Euler system.
$D^{\mathrm {la}}(\Gamma , M)$
, so we do not get an Euler system for this representation. However, this is possible after specialisation so long as we use a weaker notion of an Euler system.
Corollary 4.4.2 Let
![]() $\mathbf {x} = (k_1,\, k_2, \eta ) \in V_1 \times V_2 \times \mathcal {W}$
defined over a finite extension
$\mathbf {x} = (k_1,\, k_2, \eta ) \in V_1 \times V_2 \times \mathcal {W}$
defined over a finite extension
![]() $E/\mathbb {Q}_p$
, and let
$E/\mathbb {Q}_p$
, and let
![]() $T(\eta ^{-1})$
be a Galois stable lattice inside
$T(\eta ^{-1})$
be a Galois stable lattice inside
![]() $M_E(\mathcal {F}_{k_1})^* \otimes M_E(\mathcal {G}_{k_2})^* (\eta ^{-1})$
. Assume that
$M_E(\mathcal {F}_{k_1})^* \otimes M_E(\mathcal {G}_{k_2})^* (\eta ^{-1})$
. Assume that
![]() $k_1 \neq k_2$
. Let
$k_1 \neq k_2$
. Let
![]() $c \geq 1$
be an integer prime to
$c \geq 1$
be an integer prime to
![]() $6Np$
and let
$6Np$
and let
![]() $\mathcal {N}$
be a finite product of primes containing all primes dividing
$\mathcal {N}$
be a finite product of primes containing all primes dividing
![]() $6cNp$
. Let S denote the set of positive integers divisible only by primes not dividing
$6cNp$
. Let S denote the set of positive integers divisible only by primes not dividing
![]() $\mathcal {N}$
. Then for
$\mathcal {N}$
. Then for
![]() $m \in S$
and
$m \in S$
and
![]() $V_1$
and
$V_1$
and
![]() $V_2$
small enough, there exist cohomology classes
$V_2$
small enough, there exist cohomology classes
 $$\begin{align*}c_m \in \operatorname{H}^1\big(\mathbb{Q}(\mu_m), T(\eta^{-1}) \big) \end{align*}$$
$$\begin{align*}c_m \in \operatorname{H}^1\big(\mathbb{Q}(\mu_m), T(\eta^{-1}) \big) \end{align*}$$
that satisfy
 $$\begin{align*}\operatorname{cores}^{\mathbb{Q}(\mu_{lm})}_{\mathbb{Q}(\mu_m)} {c_{lm}} = \begin{cases} c_m & \text{if } l | m, \\ P_l(\eta^{-1}(l)\sigma_l^{-1}) \cdot c_m & \text{if } l \nmid m, \end{cases} \end{align*}$$
$$\begin{align*}\operatorname{cores}^{\mathbb{Q}(\mu_{lm})}_{\mathbb{Q}(\mu_m)} {c_{lm}} = \begin{cases} c_m & \text{if } l | m, \\ P_l(\eta^{-1}(l)\sigma_l^{-1}) \cdot c_m & \text{if } l \nmid m, \end{cases} \end{align*}$$
where l is a prime not dividing
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $P_l(\eta ^{-1}(l)X)$
is the specialisation of
$P_l(\eta ^{-1}(l)X)$
is the specialisation of
![]() $\mathcal {P}_l(l^{-\mathbf {j}}X)$
at
$\mathcal {P}_l(l^{-\mathbf {j}}X)$
at
![]() $(k_1,\, k_2, \eta )$
. Furthermore, the bottom class
$(k_1,\, k_2, \eta )$
. Furthermore, the bottom class
![]() $c_1$
is a non-zero multiple of
$c_1$
is a non-zero multiple of
 ${{}_{c} \mathcal {BF}_{1, 1}^{[\mathcal {F}, \mathcal {G}]}}$
.
${{}_{c} \mathcal {BF}_{1, 1}^{[\mathcal {F}, \mathcal {G}]}}$
.
Proof First, note that
 $\operatorname {H}^0(\mathbb {Q}(\mu _{mp^{\infty }}), M_{\mathbf {x}}) = 0$
for all
$\operatorname {H}^0(\mathbb {Q}(\mu _{mp^{\infty }}), M_{\mathbf {x}}) = 0$
for all
![]() $m \in S$
, where
$m \in S$
, where
Indeed this is true, because we have assumed
![]() $k_1 \neq k_2$
, for the following reason. Shrinking
$k_1 \neq k_2$
, for the following reason. Shrinking
![]() $V_1$
and
$V_1$
and
![]() $V_2$
if necessary, we can assume that
$V_2$
if necessary, we can assume that
![]() $M_{\mathbf {x}}$
is (absolutely) irreducible. Hence, any twist of
$M_{\mathbf {x}}$
is (absolutely) irreducible. Hence, any twist of
![]() $M_{\mathbf {x}}$
by a character is also irreducible. But if
$M_{\mathbf {x}}$
by a character is also irreducible. But if
![]() $M_{\mathbf {x}}$
has any non-trivial invariants under the group
$M_{\mathbf {x}}$
has any non-trivial invariants under the group
![]() $G_{\mathbb {Q}^{ab}}$
then there is a one-dimensional submodule of
$G_{\mathbb {Q}^{ab}}$
then there is a one-dimensional submodule of
![]() $M_{\mathbf {x}}$
on which
$M_{\mathbf {x}}$
on which
![]() $G_{\mathbb {Q}}$
acts via a character. This is a contradiction to irreducibility.
$G_{\mathbb {Q}}$
acts via a character. This is a contradiction to irreducibility.
Therefore, by applying [Reference Loeffler and ZerbesLZ16, Proposition 2.4.7], there exists a constant
![]() $R> 0$
independent of m such that
$R> 0$
independent of m such that
 $R \cdot {{}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}}$
specialised at
$R \cdot {{}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}}$
specialised at
![]() $\mathbf {x}$
lands in the cohomology of the Galois stable lattice
$\mathbf {x}$
lands in the cohomology of the Galois stable lattice
![]() $T(\eta ^{-1})$
.
$T(\eta ^{-1})$
.
But since
 ${{}_{c}\mathcal {Z}_m^{[\mathcal {F}, \mathcal {G}]}}$
differs from
${{}_{c}\mathcal {Z}_m^{[\mathcal {F}, \mathcal {G}]}}$
differs from
 ${{}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}}$
by an element of
${{}_{c} \mathcal {BF}_{m, 1}^{[\mathcal {F}, \mathcal {G}]}}$
by an element of
![]() $\mathcal {O}(V_1 \times V_2 \times \mathcal {W})^{\circ }[(\mathbb {Z}/m\mathbb {Z})^{\times }]$
, this implies that the specialisation of
$\mathcal {O}(V_1 \times V_2 \times \mathcal {W})^{\circ }[(\mathbb {Z}/m\mathbb {Z})^{\times }]$
, this implies that the specialisation of
 $R \cdot {{}_{c}\mathcal {Z}_m^{[\mathcal {F}, \mathcal {G}]}}$
lands in the cohomology of the Galois stable lattice
$R \cdot {{}_{c}\mathcal {Z}_m^{[\mathcal {F}, \mathcal {G}]}}$
lands in the cohomology of the Galois stable lattice
![]() $T(\eta ^{-1})$
. We set
$T(\eta ^{-1})$
. We set
![]() $c_m$
to be the specialisation of
$c_m$
to be the specialisation of
 $R \cdot {{}_{c}\mathcal {Z}_m^{[\mathcal {F}, \mathcal {G}]}}$
at
$R \cdot {{}_{c}\mathcal {Z}_m^{[\mathcal {F}, \mathcal {G}]}}$
at
![]() $\mathbf {x}$
.
$\mathbf {x}$
.
By Proposition 4.4.1, we obtain the Euler system relations for the classes
![]() $c_m$
, and this proves the corollary for all
$c_m$
, and this proves the corollary for all
![]() $m \in A$
, where A is the subset of S consisting of all square-free integers.
$m \in A$
, where A is the subset of S consisting of all square-free integers.
But we can extend the classes
![]() $\{c_m : m \in A\}$
to a collection of classes indexed over the set S by defining
$\{c_m : m \in A\}$
to a collection of classes indexed over the set S by defining
![]() $c_m$
to be
$c_m$
to be
 $$\begin{align*}c_m := \prod_{l | m}\frac{1}{l^{v_l(m) - 1}} \operatorname{res}^{\mathbb{Q}(\mu_m)}_{\mathbb{Q}(\mu_{m^{\prime}})} c_{m^{\prime},} \end{align*}$$
$$\begin{align*}c_m := \prod_{l | m}\frac{1}{l^{v_l(m) - 1}} \operatorname{res}^{\mathbb{Q}(\mu_m)}_{\mathbb{Q}(\mu_{m^{\prime}})} c_{m^{\prime},} \end{align*}$$
where
![]() $m^{\prime }$
is the radical of m (i.e., the product of all prime factors that divide m) and
$m^{\prime }$
is the radical of m (i.e., the product of all prime factors that divide m) and
![]() $v_l(m)$
is the l-adic valuation of m. We do not lose integrality of the classes because all integers in S are coprime to p.▪
$v_l(m)$
is the l-adic valuation of m. We do not lose integrality of the classes because all integers in S are coprime to p.▪
5 Preliminaries on
 $(\varphi , \Gamma )$
-modules
$(\varphi , \Gamma )$
-modules
5.1 Period Rings
In this section, we (briefly) recall the period rings that will be used throughout the paper. Since we only work with representations of
![]() $G_{\mathbb {Q}_p}$
, we specialise immediately to this case and refer the reader to [Reference BergerBer03] for the definitions over more general p-adic fields; proofs and their corresponding references for all of the assertions in this section can also be found in op. cit..
$G_{\mathbb {Q}_p}$
, we specialise immediately to this case and refer the reader to [Reference BergerBer03] for the definitions over more general p-adic fields; proofs and their corresponding references for all of the assertions in this section can also be found in op. cit..
Let
![]() $\mathbb {C}_p$
denote a fixed completed algebraic closure of
$\mathbb {C}_p$
denote a fixed completed algebraic closure of
![]() $\mathbb {Q}_p$
and let
$\mathbb {Q}_p$
and let
![]() $v_p$
denote the unique valuation on
$v_p$
denote the unique valuation on
![]() $\mathbb {C}_p$
such that
$\mathbb {C}_p$
such that
![]() $v_p(p) = 1$
. Set
$v_p(p) = 1$
. Set
 $\mathcal {O}_{\mathbb {C}_p}^{\flat } := \varprojlim \mathcal {O}_{\mathbb {C}_p}/p$
, where the inverse limit is over the p-th power map, and fix
$\mathcal {O}_{\mathbb {C}_p}^{\flat } := \varprojlim \mathcal {O}_{\mathbb {C}_p}/p$
, where the inverse limit is over the p-th power map, and fix
 $\varepsilon := (\varepsilon _n) \in \mathcal {O}_{\mathbb {C}_p}^{\flat }$
a compatible system of p-th roots of unity, i.e.,
$\varepsilon := (\varepsilon _n) \in \mathcal {O}_{\mathbb {C}_p}^{\flat }$
a compatible system of p-th roots of unity, i.e.,
![]() $\varepsilon _n$
is a
$\varepsilon _n$
is a
![]() $p^n$
-th root of unity such that
$p^n$
-th root of unity such that
 $\varepsilon _{n+1}^p = \varepsilon _n$
.
$\varepsilon _{n+1}^p = \varepsilon _n$
.
Let
![]() $\widetilde {\mathbf {A}}^+$
denote the (p-typical) Witt vectors of
$\widetilde {\mathbf {A}}^+$
denote the (p-typical) Witt vectors of
 $\mathcal {O}_{\mathbb {C}_p}^{\flat }$
and let
$\mathcal {O}_{\mathbb {C}_p}^{\flat }$
and let
 $\widetilde {\mathbf {B}}^+ = \widetilde {\mathbf {A}}^+[\frac {1}{p}]$
. One has a canonical homomorphism
$\widetilde {\mathbf {B}}^+ = \widetilde {\mathbf {A}}^+[\frac {1}{p}]$
. One has a canonical homomorphism
 $ \theta \colon \widetilde {\mathbf {B}}^+ \rightarrow \mathbb {C}_p $
whose kernel is a principal ideal of
$ \theta \colon \widetilde {\mathbf {B}}^+ \rightarrow \mathbb {C}_p $
whose kernel is a principal ideal of
![]() $\widetilde {\mathbf {B}}^+$
generated by
$\widetilde {\mathbf {B}}^+$
generated by
![]() $\omega := ([\varepsilon ] - 1)/([\varepsilon ^{\prime }] - 1)$
where
$\omega := ([\varepsilon ] - 1)/([\varepsilon ^{\prime }] - 1)$
where
![]() $\varepsilon ^{\prime } = (\varepsilon _{n+1})_{n \geq 0}$
and
$\varepsilon ^{\prime } = (\varepsilon _{n+1})_{n \geq 0}$
and
![]() $[\cdot ]$
denotes the Teichmüller lift. We set
$[\cdot ]$
denotes the Teichmüller lift. We set
![]() $t := \operatorname {log}([\varepsilon ])$
to be the period of Fontaine.
$t := \operatorname {log}([\varepsilon ])$
to be the period of Fontaine.
We define the de Rham period rings
![]() $\mathbf {B}_{\mathrm {dR}}^+$
and
$\mathbf {B}_{\mathrm {dR}}^+$
and
![]() $\mathbf {B}_{\mathrm {dR}}$
to be the
$\mathbf {B}_{\mathrm {dR}}$
to be the
![]() $(\operatorname {ker}\theta )$
-adic completion of
$(\operatorname {ker}\theta )$
-adic completion of
![]() $\widetilde {\mathbf {B}}^+$
and the fraction field of
$\widetilde {\mathbf {B}}^+$
and the fraction field of
![]() $\mathbf {B}_{\mathrm {dR}}^+$
, respectively. Similarly, we define the crystalline period rings
$\mathbf {B}_{\mathrm {dR}}^+$
, respectively. Similarly, we define the crystalline period rings
![]() $\mathbf {B}_{\mathrm {cris}}^+$
and
$\mathbf {B}_{\mathrm {cris}}^+$
and
![]() $\mathbf {B}_{\mathrm {cris}}$
to be the divided-power envelope of
$\mathbf {B}_{\mathrm {cris}}$
to be the divided-power envelope of
![]() $\widetilde {\mathbf {B}}^+$
(with respect to
$\widetilde {\mathbf {B}}^+$
(with respect to
![]() $\omega $
) and
$\omega $
) and
![]() $\mathbf {B}_{\mathrm {cris}} = \mathbf {B}_{\mathrm {cris}}^+[t^{-1}],$
respectively. The field
$\mathbf {B}_{\mathrm {cris}} = \mathbf {B}_{\mathrm {cris}}^+[t^{-1}],$
respectively. The field
![]() $\mathbf {B}_{\mathrm {dR}}$
comes equipped with a decreasing filtration given by
$\mathbf {B}_{\mathrm {dR}}$
comes equipped with a decreasing filtration given by
 $\operatorname {Fil}^i\mathbf {B}_{\mathrm {dR}} = t^i\mathbf {B}_{\mathrm {dR}}^+$
, and since
$\operatorname {Fil}^i\mathbf {B}_{\mathrm {dR}} = t^i\mathbf {B}_{\mathrm {dR}}^+$
, and since
![]() $\mathbf {B}_{\mathrm {cris}} \subset \mathbf {B}_{\mathrm {dR}}$
, the ring
$\mathbf {B}_{\mathrm {cris}} \subset \mathbf {B}_{\mathrm {dR}}$
, the ring
![]() $\mathbf {B}_{\mathrm {cris}}$
also inherits a filtration from
$\mathbf {B}_{\mathrm {cris}}$
also inherits a filtration from
![]() $\mathbf {B}_{\mathrm {dR}}$
. Furthermore,
$\mathbf {B}_{\mathrm {dR}}$
. Furthermore,
![]() $\mathbf {B}_{\mathrm {cris}}$
comes equipped with a Frobenius endomorphism
$\mathbf {B}_{\mathrm {cris}}$
comes equipped with a Frobenius endomorphism
![]() $\varphi $
extending the natural Frobenius on
$\varphi $
extending the natural Frobenius on
![]() $\widetilde {\mathbf {B}}^+$
.
$\widetilde {\mathbf {B}}^+$
.
In addition to these constructions, we define overconvergent period rings as follows. For
![]() $r, s$
two positive rational numbers, let
$r, s$
two positive rational numbers, let
 $\widetilde {\mathbf {A}}^{[r, s]}$
denote the p-adic completion of
$\widetilde {\mathbf {A}}^{[r, s]}$
denote the p-adic completion of
 $\widetilde {\mathbf {A}}^+\big [\frac {p}{[\varepsilon - 1]^r}, \frac {[\varepsilon - 1]^s}{p}\big ]$
and set
$\widetilde {\mathbf {A}}^+\big [\frac {p}{[\varepsilon - 1]^r}, \frac {[\varepsilon - 1]^s}{p}\big ]$
and set
 $\widetilde {\mathbf {B}}^{[r, s]} = \widetilde {\mathbf {A}}^{[r, s]}[1/p]$
. We define
$\widetilde {\mathbf {B}}^{[r, s]} = \widetilde {\mathbf {A}}^{[r, s]}[1/p]$
. We define
 $\widetilde {\mathbf {B}}^{\dagger , r}_{\text {rig}}$
to be the intersection
$\widetilde {\mathbf {B}}^{\dagger , r}_{\text {rig}}$
to be the intersection
 $\widetilde {\mathbf {B}}^{\dagger , r}_{\text {rig}} := \cap _{r \leq s < +\infty }\widetilde {\mathbf {B}}^{[r, s]}$
, and if we set
$\widetilde {\mathbf {B}}^{\dagger , r}_{\text {rig}} := \cap _{r \leq s < +\infty }\widetilde {\mathbf {B}}^{[r, s]}$
, and if we set
![]() $\pi = [\varepsilon ] -1$
, then this ring contains the following subring:
$\pi = [\varepsilon ] -1$
, then this ring contains the following subring:
 $$\begin{align*}\mathbf{B}^{\dagger, r}_{\text{rig}, \mathbb{Q}_p} := \bigg\{ f(\pi) = \sum_{k = -\infty}^{\infty}{a_k \pi^k} : \begin{array}{c} a_k \in \mathbb{Q}_p \\ f(x) \text{ converges for } 0 < v_p(x) \leq \frac{1}{r} \end{array} \!\!\!\bigg\}. \end{align*}$$
$$\begin{align*}\mathbf{B}^{\dagger, r}_{\text{rig}, \mathbb{Q}_p} := \bigg\{ f(\pi) = \sum_{k = -\infty}^{\infty}{a_k \pi^k} : \begin{array}{c} a_k \in \mathbb{Q}_p \\ f(x) \text{ converges for } 0 < v_p(x) \leq \frac{1}{r} \end{array} \!\!\!\bigg\}. \end{align*}$$
Note that the period t defined previously is equal to
![]() $\operatorname {log}(1+\pi )$
.
$\operatorname {log}(1+\pi )$
.
The union of these rings, namely
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} := \varinjlim {\mathbf {B}^{\dagger , r}_{\mathrm {rig}, \mathbb {Q}_p}}$
, is the Robba ring associated to the p-adic field
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} := \varinjlim {\mathbf {B}^{\dagger , r}_{\mathrm {rig}, \mathbb {Q}_p}}$
, is the Robba ring associated to the p-adic field
![]() $\mathbb {Q}_p$
and can be identified with all power series in
$\mathbb {Q}_p$
and can be identified with all power series in
 $\mathbb {Q}_p\left [\!\!\left [ \pi , \pi ^{-1} \right ]\!\!\right ]$
that converge on an annulus of the form
$\mathbb {Q}_p\left [\!\!\left [ \pi , \pi ^{-1} \right ]\!\!\right ]$
that converge on an annulus of the form
![]() $\{x \in \mathbb {C}_p : 0 < v_p(x) \leq 1/r \}$
for some positive rational number r. We let
$\{x \in \mathbb {C}_p : 0 < v_p(x) \leq 1/r \}$
for some positive rational number r. We let
 $\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \subset \mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p}$
denote the subring of power series which converge on the whole open unit disc, i.e.,
$\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \subset \mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p}$
denote the subring of power series which converge on the whole open unit disc, i.e.,
![]() $f(x)$
converges for all
$f(x)$
converges for all
![]() $v_p(x)> 0$
. Both of these rings come equipped with an action of Frobenius given by the formula
$v_p(x)> 0$
. Both of these rings come equipped with an action of Frobenius given by the formula
 $$\begin{align*}(\varphi \cdot f) (\pi) = f\big((1+\pi)^p - 1\big) \end{align*}$$
$$\begin{align*}(\varphi \cdot f) (\pi) = f\big((1+\pi)^p - 1\big) \end{align*}$$
and
![]() $\Gamma := \operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^{\infty }})/\mathbb {Q}_p)$
given by the formula
$\Gamma := \operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^{\infty }})/\mathbb {Q}_p)$
given by the formula
 $$\begin{align*}(\gamma \cdot f) (\pi) = f\big((1+\pi)^{\chi_{\mathrm{cycl}}(\gamma)} - 1\big), \end{align*}$$
$$\begin{align*}(\gamma \cdot f) (\pi) = f\big((1+\pi)^{\chi_{\mathrm{cycl}}(\gamma)} - 1\big), \end{align*}$$
where
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $\chi _{\mathrm {cycl}}\colon \Gamma \to \mathbb {Z}_p^{\times }$
is the cyclotomic character. The morphism
$\chi _{\mathrm {cycl}}\colon \Gamma \to \mathbb {Z}_p^{\times }$
is the cyclotomic character. The morphism
![]() $\varphi $
has a left inverse, denoted by
$\varphi $
has a left inverse, denoted by
![]() $\psi $
, which satisfies the following relation:
$\psi $
, which satisfies the following relation:
 $$\begin{align*}(\varphi \psi \cdot f)(\pi) = \frac{1}{p} \sum_{\xi^p = 1}{f\big((1+\pi)\xi - 1\big)}, \end{align*}$$
$$\begin{align*}(\varphi \psi \cdot f)(\pi) = \frac{1}{p} \sum_{\xi^p = 1}{f\big((1+\pi)\xi - 1\big)}, \end{align*}$$
where the sum is over all p-th roots of unity.
If A is an affinoid
![]() $\mathbb {Q}_p$
-algebra, we define the Robba ring over A to be the completed tensor product
$\mathbb {Q}_p$
-algebra, we define the Robba ring over A to be the completed tensor product
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A$
, and similarly, we denote the subring of bounded power series by
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A$
, and similarly, we denote the subring of bounded power series by
 $\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A$
. As above, both of these rings come equipped with an action of
$\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A$
. As above, both of these rings come equipped with an action of
![]() $\varphi $
,
$\varphi $
,
![]() $\psi ,$
and
$\psi ,$
and
![]() $\Gamma $
by the exact same formulae.
$\Gamma $
by the exact same formulae.
5.2 Overconvergent
 $(\varphi , \Gamma )$
-modules Over Affinoid Algebras
$(\varphi , \Gamma )$
-modules Over Affinoid Algebras
Definition 5.2.1 Let A be an affinoid algebra over
![]() $\mathbb {Q}_p$
. We say that D is a
$\mathbb {Q}_p$
. We say that D is a
![]() $(\varphi , \Gamma )$
-module over
$(\varphi , \Gamma )$
-module over
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A$
if D is a finite projective
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A$
if D is a finite projective
 $(\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A)$
-module with commuting semilinear actions of
$(\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A)$
-module with commuting semilinear actions of
![]() $\varphi $
and
$\varphi $
and
![]() $\Gamma $
, such that
$\Gamma $
, such that
![]() $\varphi (D)$
generates D as a
$\varphi (D)$
generates D as a
 $(\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A)$
-module.
$(\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A)$
-module.
If M is a Galois representation over an affinoid algebra A (i.e., a finite projective A-module with a continuous A-linear action of
![]() $G_{\mathbb {Q}}$
), then Berger and Colmez [Reference Berger and ColmezBC08] (and more generally Kedlaya and Liu [Reference Kedlaya and LiuKL10]) have constructed a functor
$G_{\mathbb {Q}}$
), then Berger and Colmez [Reference Berger and ColmezBC08] (and more generally Kedlaya and Liu [Reference Kedlaya and LiuKL10]) have constructed a functor
 $$\begin{align*}M \mapsto \mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \end{align*}$$
$$\begin{align*}M \mapsto \mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \end{align*}$$
that associates with a Galois representation a
![]() $(\varphi , \Gamma )$
-module over the Robba ring
$(\varphi , \Gamma )$
-module over the Robba ring
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A$
. This agrees with the usual functor as constructed by Berger [Reference BergerBer02] when A is a finite field extension of
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A$
. This agrees with the usual functor as constructed by Berger [Reference BergerBer02] when A is a finite field extension of
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
For the rest of this section let
![]() $A=E$
be a finite field extension of
$A=E$
be a finite field extension of
![]() $\mathbb {Q}_p$
and let D be a
$\mathbb {Q}_p$
and let D be a
![]() $(\varphi , \Gamma )$
-module over
$(\varphi , \Gamma )$
-module over
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } E$
. By taking the “stalk at
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } E$
. By taking the “stalk at
![]() $\zeta _{p^n} - 1$
”, one can define a
$\zeta _{p^n} - 1$
”, one can define a
![]() $\mathbb {Q}_p(\mu _{p^{\infty }})(\!(t)\!)$
-module
$\mathbb {Q}_p(\mu _{p^{\infty }})(\!(t)\!)$
-module
![]() $D_{\mathrm {dif}}$
with a semilinear action of
$D_{\mathrm {dif}}$
with a semilinear action of
![]() $\Gamma $
(see [Reference NakamuraNak14]). We set
$\Gamma $
(see [Reference NakamuraNak14]). We set
and note that both
![]() $D_{\mathrm {dR}}$
and
$D_{\mathrm {dR}}$
and
![]() $D_{\mathrm {cris}}$
are finite-dimensional vector spaces over E.
$D_{\mathrm {cris}}$
are finite-dimensional vector spaces over E.
Definition 5.2.2 Let
![]() $E/\mathbb {Q}_p$
be a finite extension and D a
$E/\mathbb {Q}_p$
be a finite extension and D a
![]() $(\varphi , \Gamma )$
-module over
$(\varphi , \Gamma )$
-module over
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E$
.
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E$
.
-
(i) We say that D is de Rham (resp. crystalline) if the E-dimension of
 $D_{\mathrm {dR}}$
(resp.
$D_{\mathrm {dR}}$
(resp.
 $D_{\mathrm {cris}}$
) is equal to the rank of D as a
$D_{\mathrm {cris}}$
) is equal to the rank of D as a
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } E$
-module.
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } E$
-module. -
(ii) If D is de Rham then
 $D_{\mathrm {dR}}$
comes equipped with a decreasing filtration induced from the t-adic filtration on
$D_{\mathrm {dR}}$
comes equipped with a decreasing filtration induced from the t-adic filtration on
 $\mathbb {Q}_p(\mu _{p^{\infty }})\left [\!\!\left [ t \right ]\!\!\right ]$
. The Hodge–Tate weights of D are defined to be the negatives of the jumps in the filtration on
$\mathbb {Q}_p(\mu _{p^{\infty }})\left [\!\!\left [ t \right ]\!\!\right ]$
. The Hodge–Tate weights of D are defined to be the negatives of the jumps in the filtration on
 $D_{\mathrm {dR}}$
(so in particular the cyclotomic character has Hodge–Tate weight
$D_{\mathrm {dR}}$
(so in particular the cyclotomic character has Hodge–Tate weight
 $1$
).
$1$
).
If D is a crystalline
![]() $(\varphi , \Gamma )$
-module, then one can associate a sub-
$(\varphi , \Gamma )$
-module, then one can associate a sub-
 $(\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E)$
-module of D, denoted
$(\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E)$
-module of D, denoted
![]() $\mathbf {N}_{\mathrm {rig}}(D)$
, that is free of rank equal to the rank of D and is stable under
$\mathbf {N}_{\mathrm {rig}}(D)$
, that is free of rank equal to the rank of D and is stable under
![]() $\Gamma $
. Furthermore,
$\Gamma $
. Furthermore,
![]() $\varphi $
restricts to a morphism
$\varphi $
restricts to a morphism
 $$\begin{align*}\varphi \colon \mathbf{N}_{\mathrm{rig}}(D) \longrightarrow \mathbf{N}_{\mathrm{rig}}(D)[q^{-1}], \end{align*}$$
$$\begin{align*}\varphi \colon \mathbf{N}_{\mathrm{rig}}(D) \longrightarrow \mathbf{N}_{\mathrm{rig}}(D)[q^{-1}], \end{align*}$$
where
![]() $q = \varphi (\pi )/\pi $
; and if D has non-negative Hodge–Tate weights, then
$q = \varphi (\pi )/\pi $
; and if D has non-negative Hodge–Tate weights, then
![]() $\mathbf {N}_{\mathrm {rig}}(D)$
is in fact stable under
$\mathbf {N}_{\mathrm {rig}}(D)$
is in fact stable under
![]() $\varphi $
. This submodule is called the Wach module associated with D and will be important in Section 6 when we recall the construction of the Perrin–Riou logarithm. For more details on the construction and properties of this module, see [Reference PottharstPot12, §3]. Note that if D comes from a crystalline p-adic representation V and
$\varphi $
. This submodule is called the Wach module associated with D and will be important in Section 6 when we recall the construction of the Perrin–Riou logarithm. For more details on the construction and properties of this module, see [Reference PottharstPot12, §3]. Note that if D comes from a crystalline p-adic representation V and
![]() $\mathbf {N}(V)$
denotes the usual Wach module (over
$\mathbf {N}(V)$
denotes the usual Wach module (over
 $\mathbf {B}_{\mathbb {Q}_p}^+$
) associated with V, then
$\mathbf {B}_{\mathbb {Q}_p}^+$
) associated with V, then
![]() $\mathbf {N}_{\mathrm {rig}}(D)$
satisfies the relation
$\mathbf {N}_{\mathrm {rig}}(D)$
satisfies the relation
 $$\begin{align*}\mathbf{N}_{\mathrm{rig}}(D) = \mathbf{N}(V) \otimes_{\mathbf{B}^+_{\mathbb{Q}_p}} \mathbf{B}^{+}_{\mathrm{rig}, \mathbb{Q}_p} . \end{align*}$$
$$\begin{align*}\mathbf{N}_{\mathrm{rig}}(D) = \mathbf{N}(V) \otimes_{\mathbf{B}^+_{\mathbb{Q}_p}} \mathbf{B}^{+}_{\mathrm{rig}, \mathbb{Q}_p} . \end{align*}$$
Here,
 $\mathbf {B}^+_{\mathbb {Q}_p}$
is a period ring that can be identified with the subring
$\mathbf {B}^+_{\mathbb {Q}_p}$
is a period ring that can be identified with the subring
 $\mathbb {Z}_p \left [\!\!\left [ \pi \right ]\!\!\right ][1/p] \subset \mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p}$
.
$\mathbb {Z}_p \left [\!\!\left [ \pi \right ]\!\!\right ][1/p] \subset \mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p}$
.
5.3 Cohomology of
 $(\varphi , \Gamma )$
-modules
$(\varphi , \Gamma )$
-modules
If D is a
![]() $(\varphi ,\Gamma )$
-module over
$(\varphi ,\Gamma )$
-module over
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } A$
, then we define the Herr complex
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } A$
, then we define the Herr complex
 $$\begin{align*}C^{\bullet}_{\varphi, \gamma}(D) := D \xrightarrow{\varphi-1,\gamma-1} D \oplus D \xrightarrow{1-\gamma,\varphi-1} D \, \end{align*}$$
$$\begin{align*}C^{\bullet}_{\varphi, \gamma}(D) := D \xrightarrow{\varphi-1,\gamma-1} D \oplus D \xrightarrow{1-\gamma,\varphi-1} D \, \end{align*}$$
concentrated in degrees
![]() $0, 1, 2$
, where
$0, 1, 2$
, where
![]() $\gamma $
is a choice of topological generator for
$\gamma $
is a choice of topological generator for
![]() $\Gamma $
(such an element exists because we have assumed
$\Gamma $
(such an element exists because we have assumed
![]() $p> 2$
). We define
$p> 2$
). We define
![]() $\mathbf {R}\Gamma _{\mathrm {cont}}(\mathbb {Q}_p, D)$
to be the corresponding object in the derived category of bounded complexes of (continuous) A-modules, and we denote the cohomology of this complex by
$\mathbf {R}\Gamma _{\mathrm {cont}}(\mathbb {Q}_p, D)$
to be the corresponding object in the derived category of bounded complexes of (continuous) A-modules, and we denote the cohomology of this complex by
 $\operatorname {H}^i(\mathbb {Q}_p, D) := \operatorname {H}^i(C^{\bullet }_{\varphi , \gamma }(D))$
.
$\operatorname {H}^i(\mathbb {Q}_p, D) := \operatorname {H}^i(C^{\bullet }_{\varphi , \gamma }(D))$
.
By [Reference PottharstPot13, Thm. 2.8], for any A-representation M of
![]() $G_{\mathbb {Q}_p}$
there is a canonical quasi-isomorphism
$G_{\mathbb {Q}_p}$
there is a canonical quasi-isomorphism
 $$\begin{align*}\mathbf{R}\Gamma_{\mathrm{cont}}(\mathbb{Q}_p, M) \cong \mathbf{R}\Gamma_{\mathrm{cont}}(\mathbb{Q}_p, \mathbf{D}^{\dagger}_{\mathrm{rig}}(M)) \,. \end{align*}$$
$$\begin{align*}\mathbf{R}\Gamma_{\mathrm{cont}}(\mathbb{Q}_p, M) \cong \mathbf{R}\Gamma_{\mathrm{cont}}(\mathbb{Q}_p, \mathbf{D}^{\dagger}_{\mathrm{rig}}(M)) \,. \end{align*}$$
Since
![]() $\varphi (D)$
generates D as an
$\varphi (D)$
generates D as an
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A$
-module, the map
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A$
-module, the map
![]() $\varphi \colon D \to D$
has a unique semilinear left inverse
$\varphi \colon D \to D$
has a unique semilinear left inverse
![]() $\psi $
. As the following lemma shows, the cohomology of D can be computed with
$\psi $
. As the following lemma shows, the cohomology of D can be computed with
![]() $\psi $
in place of
$\psi $
in place of
![]() $\varphi $
.
$\varphi $
.
Lemma 5.3.1 [Reference Kedlaya, Pottharst and XiaoKPX14, Proposition 2.3.6]
Let
 $C^{\bullet }_{\psi ,\gamma }(D)$
be the bottom row of the commutative diagram
$C^{\bullet }_{\psi ,\gamma }(D)$
be the bottom row of the commutative diagram

(here the top row is
 $C^{\bullet }_{\varphi , \gamma }(D)$
). Then the map
$C^{\bullet }_{\varphi , \gamma }(D)$
). Then the map
 $C^{\bullet }_{\varphi , \gamma }(D) \to C^{\bullet }_{\psi ,\gamma }(D)$
defined above is a quasi-isomorphism.
$C^{\bullet }_{\varphi , \gamma }(D) \to C^{\bullet }_{\psi ,\gamma }(D)$
defined above is a quasi-isomorphism.
We finish this section by stating an Euler–Poincaré characteristic formula for
![]() $(\varphi , \Gamma )$
-modules, which will be used in the proof of Theorem 7.3.3.
$(\varphi , \Gamma )$
-modules, which will be used in the proof of Theorem 7.3.3.
Proposition 5.3.2 [Reference LiuLiu08, Theorem 5.3]
Let
![]() $A=E$
be a finite field extension of
$A=E$
be a finite field extension of
![]() $\mathbb {Q}_p$
and let D be a
$\mathbb {Q}_p$
and let D be a
![]() $(\varphi , \Gamma )$
-module over
$(\varphi , \Gamma )$
-module over
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } E$
. Then, for
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } E$
. Then, for
![]() $i=0, 1, 2$
,
$i=0, 1, 2$
,
 $\operatorname {H}^i(\mathbb {Q}_p, D)$
are finite-dimensional vector spaces over E and
$\operatorname {H}^i(\mathbb {Q}_p, D)$
are finite-dimensional vector spaces over E and
 $$\begin{align*}\chi(D) := \sum_{i=0}^{2}(-1)^i\operatorname{dim}_E\operatorname{H}^i(\mathbb{Q}_p, D) = -\operatorname{rank}D, \end{align*}$$
$$\begin{align*}\chi(D) := \sum_{i=0}^{2}(-1)^i\operatorname{dim}_E\operatorname{H}^i(\mathbb{Q}_p, D) = -\operatorname{rank}D, \end{align*}$$
where
![]() $\operatorname {rank}D$
is the rank of D as a
$\operatorname {rank}D$
is the rank of D as a
 $(\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } E)$
-module.
$(\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } E)$
-module.
5.4 Iwasawa Cohomology
Recall that for an affinoid algebra A, we denote its unit ball by
![]() $A^\circ $
. Let M be a Galois representation over A and let T be a Galois stable lattice inside M (i.e., a sub-
$A^\circ $
. Let M be a Galois representation over A and let T be a Galois stable lattice inside M (i.e., a sub-
![]() $A^\circ $
-module that is stable under the action of
$A^\circ $
-module that is stable under the action of
![]() $G_{\mathbb {Q}}$
and satisfies
$G_{\mathbb {Q}}$
and satisfies
![]() $T[1/p] = M$
). The classical Iwasawa cohomology of M is defined to be
$T[1/p] = M$
). The classical Iwasawa cohomology of M is defined to be
 $$\begin{align*}\operatorname{H}^i_{\mathrm{cl.Iw}}(\mathbb{Q}_{\infty}, M) := \big( \varprojlim_n \operatorname{H}^i(\mathbb{Q}(\mu_{p^n}), T)\big) \Big[\frac{1}{p}\Big], \end{align*}$$
$$\begin{align*}\operatorname{H}^i_{\mathrm{cl.Iw}}(\mathbb{Q}_{\infty}, M) := \big( \varprojlim_n \operatorname{H}^i(\mathbb{Q}(\mu_{p^n}), T)\big) \Big[\frac{1}{p}\Big], \end{align*}$$
where the inverse limit is over the corestriction maps, and the (analytic) Iwasawa cohomology of M is
 $$\begin{align*}\operatorname{H}^i_{\mathrm{Iw}}(\mathbb{Q}_{\infty}, M) := \operatorname{H}^i(\mathbb{Q}, D^{\mathrm{la}}(\Gamma, M) ), \end{align*}$$
$$\begin{align*}\operatorname{H}^i_{\mathrm{Iw}}(\mathbb{Q}_{\infty}, M) := \operatorname{H}^i(\mathbb{Q}, D^{\mathrm{la}}(\Gamma, M) ), \end{align*}$$
where
![]() $D^{\mathrm {la}}(\Gamma , M)$
denotes the space of locally analytic distributions on
$D^{\mathrm {la}}(\Gamma , M)$
denotes the space of locally analytic distributions on
![]() $\Gamma $
, valued in M. For a finite place v of
$\Gamma $
, valued in M. For a finite place v of
![]() $\mathbb {Q}$
, the Iwasawa cohomology groups
$\mathbb {Q}$
, the Iwasawa cohomology groups
![]() $\operatorname {H}^i_{\mathrm {cl.Iw}}(\mathbb {Q}_{v, \infty }, M)$
and
$\operatorname {H}^i_{\mathrm {cl.Iw}}(\mathbb {Q}_{v, \infty }, M)$
and
![]() $\operatorname {H}^i_{\mathrm {Iw}}(\mathbb {Q}_{v, \infty }, M)$
are defined analogously. These two constructions satisfy the relation
$\operatorname {H}^i_{\mathrm {Iw}}(\mathbb {Q}_{v, \infty }, M)$
are defined analogously. These two constructions satisfy the relation
 $$\begin{align*}\operatorname{H}^i_{\mathrm{Iw}}(\mathbb{Q}_{\infty}, M) = \operatorname{H}^i_{\mathrm{cl.Iw}}(\mathbb{Q}_{\infty}, M) \hat{\otimes}_{\mathbb{Z}_p\left[\!\!\left[ \Gamma \right]\!\!\right]} D^{\mathrm{la}}(\Gamma, A). \end{align*}$$
$$\begin{align*}\operatorname{H}^i_{\mathrm{Iw}}(\mathbb{Q}_{\infty}, M) = \operatorname{H}^i_{\mathrm{cl.Iw}}(\mathbb{Q}_{\infty}, M) \hat{\otimes}_{\mathbb{Z}_p\left[\!\!\left[ \Gamma \right]\!\!\right]} D^{\mathrm{la}}(\Gamma, A). \end{align*}$$
Remark 5.4.1 Our notation for Iwasawa cohomology differs from that in [Reference Loeffler and ZerbesLZ16]; in op. cit.,
![]() $\operatorname {H}_{\mathrm {Iw}}$
denotes classical Iwasawa cohomology, whereas in this paper it refers to analytic Iwasawa cohomology.
$\operatorname {H}_{\mathrm {Iw}}$
denotes classical Iwasawa cohomology, whereas in this paper it refers to analytic Iwasawa cohomology.
Definition 5.4.2 Let D be a
![]() $(\varphi , \Gamma )$
-module over
$(\varphi , \Gamma )$
-module over
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A$
. The Iwasawa Herr complex is defined to be
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } A$
. The Iwasawa Herr complex is defined to be
 $$\begin{align*}C_{\mathrm{Iw}}^{\bullet}(D)\colon D \xrightarrow{\psi - 1} D \end{align*}$$
$$\begin{align*}C_{\mathrm{Iw}}^{\bullet}(D)\colon D \xrightarrow{\psi - 1} D \end{align*}$$
concentrated in degrees
![]() $1$
and
$1$
and
![]() $2$
, where
$2$
, where
![]() $\psi $
is the left inverse to
$\psi $
is the left inverse to
![]() $\varphi $
as discussed in the previous section. We denote the cohomology of this complex by
$\varphi $
as discussed in the previous section. We denote the cohomology of this complex by
 $\operatorname {H}^i_{\mathrm {Iw}}(\mathbb {Q}_p, D)$
.
$\operatorname {H}^i_{\mathrm {Iw}}(\mathbb {Q}_p, D)$
.
We have the following relation between Iwasawa cohomology for M and Iwasawa cohomology for
 $\mathbf {D}^{\dagger }_{\mathrm {rig}}(M)$
.
$\mathbf {D}^{\dagger }_{\mathrm {rig}}(M)$
.
Proposition 5.4.3 Let M be a Galois representation over an affinoid algebra A. Then one has the following isomorphism
 $$\begin{align*}\operatorname{H}^i_{\mathrm{Iw}}(\mathbb{Q}_{p, \infty}, M) \cong \operatorname{H}^i_{\mathrm{Iw}}\big(\mathbb{Q}_p, \mathbf{D}^{\dagger}_{\mathrm{rig}}(M)\big). \end{align*}$$
$$\begin{align*}\operatorname{H}^i_{\mathrm{Iw}}(\mathbb{Q}_{p, \infty}, M) \cong \operatorname{H}^i_{\mathrm{Iw}}\big(\mathbb{Q}_p, \mathbf{D}^{\dagger}_{\mathrm{rig}}(M)\big). \end{align*}$$
In particular ,
 $\operatorname {H}^i_{\mathrm {Iw}}(\mathbb {Q}_{p, \infty }, M)$
vanishes for
$\operatorname {H}^i_{\mathrm {Iw}}(\mathbb {Q}_{p, \infty }, M)$
vanishes for
![]() $i \neq 1, 2$
.
$i \neq 1, 2$
.
Proof See [Reference Kedlaya, Pottharst and XiaoKPX14, Corollary 4.4.11]. ▪
6 Some p-adic Hodge Theory
In this section, we recall the construction of the Perrin–Riou logarithm following [Reference PottharstPot12, §3] and use this map to show that if the p-adic L-function does not vanish, then we obtain two linearly independent classes in
 $\operatorname {H}^1(\mathbb {Q}_p, D^-(\eta ^{-1}))$
, where
$\operatorname {H}^1(\mathbb {Q}_p, D^-(\eta ^{-1}))$
, where
![]() $D^-(\eta ^{-1})$
is a certain
$D^-(\eta ^{-1})$
is a certain
![]() $2$
-dimensional
$2$
-dimensional
![]() $(\varphi , \Gamma )$
-module defined in (6.2.1). Throughout this section, E is a finite extension of
$(\varphi , \Gamma )$
-module defined in (6.2.1). Throughout this section, E is a finite extension of
![]() $\mathbb {Q}_p$
and D will denote a
$\mathbb {Q}_p$
and D will denote a
![]() $(\varphi , \Gamma )$
-module over the Robba ring
$(\varphi , \Gamma )$
-module over the Robba ring
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E$
.
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E$
.
Recall from Section 5.2 that if D is a crystalline
![]() $(\varphi , \Gamma )$
-module, then one can associate to D the Wach module
$(\varphi , \Gamma )$
-module, then one can associate to D the Wach module
![]() $\mathbf {N}_{\mathrm {rig}}(D)$
. This is a sub
$\mathbf {N}_{\mathrm {rig}}(D)$
. This is a sub
 $(\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } E)$
-module of D that is free of rank equal to the rank of D and is stable under
$(\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } E)$
-module of D that is free of rank equal to the rank of D and is stable under
![]() $\Gamma $
. It will be useful to impose the following hypothesis on D:
$\Gamma $
. It will be useful to impose the following hypothesis on D:
-
(H) The Hodge–Tate weights of D are non-negative and
 $p^n$
is not an eigenvalue of
$p^n$
is not an eigenvalue of
 $\varphi $
on
$\varphi $
on
 $D_{\mathrm {cris}}$
for all integers
$D_{\mathrm {cris}}$
for all integers
 $n \geq 0$
.
$n \geq 0$
.
The reason for imposing this hypothesis is to ensure that the “big logarithm” as constructed in [Reference PottharstPot12, §3] lands in the lattice
![]() $D_{\mathrm {cris}} \otimes \Lambda _{\infty }$
.
$D_{\mathrm {cris}} \otimes \Lambda _{\infty }$
.
Lemma 6.0.4 Let D be a crystalline
![]() $(\varphi , \Gamma )$
-module satisfying hypothesis (H).
$(\varphi , \Gamma )$
-module satisfying hypothesis (H).
-
(i) The inclusion
 $\mathbf {N}_{\mathrm {rig}}(D) \rightarrow D$
induces an isomorphism
$\mathbf {N}_{\mathrm {rig}}(D) \rightarrow D$
induces an isomorphism
 $\mathbf {N}_{\mathrm {rig}}(D)^{\psi = 1} \cong D^{\psi = 1}$
, where
$\mathbf {N}_{\mathrm {rig}}(D)^{\psi = 1} \cong D^{\psi = 1}$
, where
 $\psi $
is the left inverse to
$\psi $
is the left inverse to
 $\varphi $
coming from the trace map (see §5.2).
$\varphi $
coming from the trace map (see §5.2). -
(ii) Let
 $\varphi ^*\mathbf {N}_{\mathrm {rig}}(D)$
denote the sub
$\varphi ^*\mathbf {N}_{\mathrm {rig}}(D)$
denote the sub
 $(\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } E)$
-module of D generated by
$(\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \hat {\otimes } E)$
-module of D generated by
 $\varphi (\mathbf {N}_{\mathrm {rig}}(D))$
. Then there is an inclusion
$\varphi (\mathbf {N}_{\mathrm {rig}}(D))$
. Then there is an inclusion  $$\begin{align*}(\varphi^*\mathbf{N}_{\mathrm{rig}}(D))^{\psi = 0} \subset D_{\mathrm{cris}} \otimes_{E} (\mathbf{B}^{+}_{\mathrm{rig}, \mathbb{Q}_p} \hat{\otimes} E)^{\psi = 0}. \end{align*}$$
$$\begin{align*}(\varphi^*\mathbf{N}_{\mathrm{rig}}(D))^{\psi = 0} \subset D_{\mathrm{cris}} \otimes_{E} (\mathbf{B}^{+}_{\mathrm{rig}, \mathbb{Q}_p} \hat{\otimes} E)^{\psi = 0}. \end{align*}$$
-
(iii) We have an inclusion
where $$\begin{align*}\mathbf{N}_{\mathrm{rig}}(D) \subset q^{h_1} \varphi^*\mathbf{N}_{\mathrm{rig}}(D) \subset \varphi^*\mathbf{N}_{\mathrm{rig}}(D), \end{align*}$$
$$\begin{align*}\mathbf{N}_{\mathrm{rig}}(D) \subset q^{h_1} \varphi^*\mathbf{N}_{\mathrm{rig}}(D) \subset \varphi^*\mathbf{N}_{\mathrm{rig}}(D), \end{align*}$$
 $h_1$
is the smallest Hodge–Tate weight of D and
$h_1$
is the smallest Hodge–Tate weight of D and
 $q = \varphi (\pi )/\pi $
.
$q = \varphi (\pi )/\pi $
.
Proof Let
![]() $h_1 \leq h_2 \leq \cdots \leq h_d$
be the Hodge–Tate weights of D. Since D has non-negative Hodge–Tate weights and
$h_1 \leq h_2 \leq \cdots \leq h_d$
be the Hodge–Tate weights of D. Since D has non-negative Hodge–Tate weights and
![]() $p^n$
is not an eigenvalue for
$p^n$
is not an eigenvalue for
![]() $\varphi $
for all
$\varphi $
for all
![]() $n \geq 0$
, the quantity
$n \geq 0$
, the quantity
![]() $a(D) := \operatorname {max}\{-h_1, \lambda (D) +1 \}$
is non-positive, where
$a(D) := \operatorname {max}\{-h_1, \lambda (D) +1 \}$
is non-positive, where
![]() $\lambda (D)$
is the largest integer (or
$\lambda (D)$
is the largest integer (or
![]() $-\infty $
if there is no such one) such that
$-\infty $
if there is no such one) such that
![]() $\varphi - p^{\lambda (D)}$
is not bijective on
$\varphi - p^{\lambda (D)}$
is not bijective on
![]() $D_{\mathrm {cris}}$
. The first part then follows from [Reference PottharstPot12, Theorem 3.3].
$D_{\mathrm {cris}}$
. The first part then follows from [Reference PottharstPot12, Theorem 3.3].
For the second part, we note that from the second bullet point in Theorem 3.1 in op. cit.
 $$\begin{align*}\mathbf{N}_{\mathrm{rig}}(D) \subset \Big(\frac{t}{\pi}\Big)^{h_1} (D_{\mathrm{cris}} \otimes (\mathbf{B}^{+}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E) ) \subset (D_{\mathrm{cris}} \otimes (\mathbf{B}^{+}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E)), \end{align*}$$
$$\begin{align*}\mathbf{N}_{\mathrm{rig}}(D) \subset \Big(\frac{t}{\pi}\Big)^{h_1} (D_{\mathrm{cris}} \otimes (\mathbf{B}^{+}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E) ) \subset (D_{\mathrm{cris}} \otimes (\mathbf{B}^{+}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E)), \end{align*}$$
where the last inclusion follows, because the Hodge–Tate weights are non-negative. Since
![]() $\varphi $
is an isomorphism on
$\varphi $
is an isomorphism on
![]() $D_{\mathrm {cris}}$
,
$D_{\mathrm {cris}}$
,
![]() $\psi $
is also an isomorphism, and we have
$\psi $
is also an isomorphism, and we have
 $\varphi ^*(D_{\mathrm {cris}} \otimes (\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E)) = (D_{\mathrm {cris}} \otimes (\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E))$
. Combining these facts we obtain the inclusion in (ii).
$\varphi ^*(D_{\mathrm {cris}} \otimes (\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E)) = (D_{\mathrm {cris}} \otimes (\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E))$
. Combining these facts we obtain the inclusion in (ii).
Similarly, the third part follows from the third bullet point in Theorem 3.1 in loc. cit., using the fact that
![]() $h_1 \geq 0$
and that
$h_1 \geq 0$
and that
 $q \in \mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p}$
.▪
$q \in \mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p}$
.▪
6.1 Perrin-Riou’s Big Logarithm
Let
![]() $\Lambda _{\infty }$
denote the global sections of
$\Lambda _{\infty }$
denote the global sections of
![]() $\mathcal {W}_E$
; this can be identified with a subring of the ring of power series
$\mathcal {W}_E$
; this can be identified with a subring of the ring of power series
![]() $E[\Delta ]\left [\!\!\left [ \gamma - 1 \right ]\!\!\right ]$
, where
$E[\Delta ]\left [\!\!\left [ \gamma - 1 \right ]\!\!\right ]$
, where
![]() $\Delta $
is the torsion subgroup of
$\Delta $
is the torsion subgroup of
![]() $\Gamma $
and
$\Gamma $
and
![]() $\gamma $
is a topological generator of
$\gamma $
is a topological generator of
![]() $\Gamma /\Delta $
. The ring
$\Gamma /\Delta $
. The ring
 $(\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E)^{\psi = 0}$
has an action of
$(\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E)^{\psi = 0}$
has an action of
![]() $\Gamma $
that extends to an action of
$\Gamma $
that extends to an action of
![]() $\Lambda _{\infty }$
via the Mellin transform:
$\Lambda _{\infty }$
via the Mellin transform:
 $$ \begin{align*} \mathfrak{M}\colon \Lambda_{\infty} & \xrightarrow{\sim} (\mathbf{B}^{+}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E)^{\psi = 0} \nonumber \\ f(\gamma - 1) & \mapsto f(\gamma - 1) \cdot (1 + \pi). \nonumber \end{align*} $$
$$ \begin{align*} \mathfrak{M}\colon \Lambda_{\infty} & \xrightarrow{\sim} (\mathbf{B}^{+}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E)^{\psi = 0} \nonumber \\ f(\gamma - 1) & \mapsto f(\gamma - 1) \cdot (1 + \pi). \nonumber \end{align*} $$
Therefore,
 $(\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E)^{\psi = 0}$
can be viewed as a free
$(\mathbf {B}^{+}_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E)^{\psi = 0}$
can be viewed as a free
![]() $\Lambda _{\infty }$
-module of rank one.
$\Lambda _{\infty }$
-module of rank one.
Definition 6.1.1 Suppose that D is a crystalline
![]() $(\varphi , \Gamma )$
-module satisfying hypothesis (H). The Perrin-Riou logarithm
$(\varphi , \Gamma )$
-module satisfying hypothesis (H). The Perrin-Riou logarithm
 $\mathcal {L} = \mathcal {L}_D : \operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_{p}, D) \to D_{\mathrm {cris}} \widehat {\otimes } \Lambda _{\infty }$
is defined as the composition of the following maps:
$\mathcal {L} = \mathcal {L}_D : \operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_{p}, D) \to D_{\mathrm {cris}} \widehat {\otimes } \Lambda _{\infty }$
is defined as the composition of the following maps:
 $$ \begin{align*} \operatorname{H}^1_{\mathrm{Iw}}(\mathbb{Q}_{p}, D) \cong D^{\psi = 1} & = \mathbf{N}_{\mathrm{rig}}(D)^{\psi = 1} \nonumber \\ & \xrightarrow{1 - \varphi} (\varphi^*\mathbf{N}_{\mathrm{rig}}(D))^{\psi = 0} \nonumber \\ & \longrightarrow D_{\mathrm{cris}} \widehat{\otimes}_{E} (\mathbf{B}^{+}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E)^{\psi = 0} \xrightarrow{\sim} D_{\mathrm{cris}} \widehat{\otimes}_{E} \Lambda_{\infty}, \nonumber \end{align*} $$
$$ \begin{align*} \operatorname{H}^1_{\mathrm{Iw}}(\mathbb{Q}_{p}, D) \cong D^{\psi = 1} & = \mathbf{N}_{\mathrm{rig}}(D)^{\psi = 1} \nonumber \\ & \xrightarrow{1 - \varphi} (\varphi^*\mathbf{N}_{\mathrm{rig}}(D))^{\psi = 0} \nonumber \\ & \longrightarrow D_{\mathrm{cris}} \widehat{\otimes}_{E} (\mathbf{B}^{+}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E)^{\psi = 0} \xrightarrow{\sim} D_{\mathrm{cris}} \widehat{\otimes}_{E} \Lambda_{\infty}, \nonumber \end{align*} $$
where the second, third, and fourth maps exist by Lemma 6.0.4. Here the last map is given by the inverse of the Mellin transform described above. Since all of the maps above are functorial in D, we see that
![]() $\mathcal {L}$
is a map of
$\mathcal {L}$
is a map of
![]() $\Lambda _{\infty }$
-modules that is also functorial in D.
$\Lambda _{\infty }$
-modules that is also functorial in D.
In the case where D comes from a crystalline p-adic representation, the map
![]() $\mathcal {L}$
is a special case of a more general construction by Perrin-Riou ([Reference Perrin-RiouPR00]), which was later interpreted using
$\mathcal {L}$
is a special case of a more general construction by Perrin-Riou ([Reference Perrin-RiouPR00]), which was later interpreted using
![]() $(\varphi , \Gamma )$
-modules by Lei, Loeffler, and Zerbes ([Reference Lei, Loeffler and ZerbesLLZ11]). This was generalised to potentially crystalline
$(\varphi , \Gamma )$
-modules by Lei, Loeffler, and Zerbes ([Reference Lei, Loeffler and ZerbesLLZ11]). This was generalised to potentially crystalline
![]() $(\varphi , \Gamma )$
-modules by Pottharst ([Reference PottharstPot12]) and to de Rham
$(\varphi , \Gamma )$
-modules by Pottharst ([Reference PottharstPot12]) and to de Rham
![]() $(\varphi , \Gamma )$
-modules by Nakamura ([Reference NakamuraNak14]). The key property of this map is that it interpolates the Bloch–Kato logarithm and dual exponential maps at certain classical specialisations. More precisely, let
$(\varphi , \Gamma )$
-modules by Nakamura ([Reference NakamuraNak14]). The key property of this map is that it interpolates the Bloch–Kato logarithm and dual exponential maps at certain classical specialisations. More precisely, let
![]() $\eta \colon \Gamma \to (E^{\prime })^{\times }$
be a continuous character, where
$\eta \colon \Gamma \to (E^{\prime })^{\times }$
be a continuous character, where
![]() $\Gamma = \operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^{\infty }})/\mathbb {Q}_p)$
, and consider the induced map
$\Gamma = \operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^{\infty }})/\mathbb {Q}_p)$
, and consider the induced map
![]() $\Lambda _{\infty } \to E^{\prime },$
which we will also denote by
$\Lambda _{\infty } \to E^{\prime },$
which we will also denote by
![]() $\eta $
. Then we have two specialisation maps: the first on Iwasawa cohomology
$\eta $
. Then we have two specialisation maps: the first on Iwasawa cohomology
 $$\begin{align*}\operatorname{H}^1_{\mathrm{Iw}}(\mathbb{Q}_{p}, D) \xrightarrow{\mathrm{pr}_{\eta}} \operatorname{H}^1\big(\mathbb{Q}_p, D_{E^{\prime}}(\eta^{-1}) \big) \end{align*}$$
$$\begin{align*}\operatorname{H}^1_{\mathrm{Iw}}(\mathbb{Q}_{p}, D) \xrightarrow{\mathrm{pr}_{\eta}} \operatorname{H}^1\big(\mathbb{Q}_p, D_{E^{\prime}}(\eta^{-1}) \big) \end{align*}$$
induced from the map on the Herr complexes
 $C^{\bullet }_{Iw}(D) \to C^{\bullet }_{\psi , \gamma }(D(\eta ^{-1}))$
which in degree one is given by
$C^{\bullet }_{Iw}(D) \to C^{\bullet }_{\psi , \gamma }(D(\eta ^{-1}))$
which in degree one is given by
![]() $x \mapsto (0, x)$
(recall that by Lemma 5.3.1 the cohomology of a
$x \mapsto (0, x)$
(recall that by Lemma 5.3.1 the cohomology of a
![]() $(\varphi , \Gamma )$
-module can be calculated with
$(\varphi , \Gamma )$
-module can be calculated with
![]() $\psi $
in place of
$\psi $
in place of
![]() $\varphi $
). The second specialisation map is
$\varphi $
). The second specialisation map is
 $$\begin{align*}D_{\mathrm{cris}} \widehat{\otimes} \Lambda_{\infty} \xrightarrow{\mathrm{ev}_{\eta}} D_{\mathrm{cris}} \otimes_{\mathbb{Q}_p} E^{\prime} \end{align*}$$
$$\begin{align*}D_{\mathrm{cris}} \widehat{\otimes} \Lambda_{\infty} \xrightarrow{\mathrm{ev}_{\eta}} D_{\mathrm{cris}} \otimes_{\mathbb{Q}_p} E^{\prime} \end{align*}$$
induced from
![]() $\eta \colon \Lambda _{\infty } \to E^{\prime }$
. Then for classical
$\eta \colon \Lambda _{\infty } \to E^{\prime }$
. Then for classical
![]() $\eta $
(i.e.,
$\eta $
(i.e.,
 $\eta = \chi _{\mathrm {cycl}}^j$
for some integer j) there is a commutative diagram
$\eta = \chi _{\mathrm {cycl}}^j$
for some integer j) there is a commutative diagram

where the dotted arrow is (up to some Euler factors) the Bloch–Kato logarithm in the range
![]() $j < h_1$
, and the dual exponential map in the range
$j < h_1$
, and the dual exponential map in the range
![]() $j \geq h_1$
, where
$j \geq h_1$
, where
![]() $h_1$
is the smallest Hodge–Tate weight of D (see [Reference NakamuraNak14]). We will study this map at non-classical specialisations.
$h_1$
is the smallest Hodge–Tate weight of D (see [Reference NakamuraNak14]). We will study this map at non-classical specialisations.
Proposition 6.1.2 Let D be a crystalline
![]() $(\varphi , \Gamma )$
-module that satisfies hypothesis (H). The map
$(\varphi , \Gamma )$
-module that satisfies hypothesis (H). The map
![]() $\mathcal {L} = \mathcal {L}_D$
satisfies the following properties:
$\mathcal {L} = \mathcal {L}_D$
satisfies the following properties:
-
(i) Let
 $k \geq 0$
be an integer and let
$k \geq 0$
be an integer and let
 $\omega _{-k}$
denote the automorphism of
$\omega _{-k}$
denote the automorphism of
 $\Lambda _{\infty }$
which sends
$\Lambda _{\infty }$
which sends
 $\gamma \in \Gamma $
to the element
$\gamma \in \Gamma $
to the element
 $\chi _{\mathrm {cycl}}(\gamma )^{-k}\gamma $
. Then we have a commutative diagram
$\chi _{\mathrm {cycl}}(\gamma )^{-k}\gamma $
. Then we have a commutative diagram

where for a
 $\Lambda _{\infty }$
-module M,
$\Lambda _{\infty }$
-module M,
 $\omega _{-k}^*M$
denotes the pull-back
$\omega _{-k}^*M$
denotes the pull-back
 $M \otimes _{\Lambda _{\infty }, \omega _{-k}} \Lambda _{\infty }$
.
$M \otimes _{\Lambda _{\infty }, \omega _{-k}} \Lambda _{\infty }$
. -
(ii) For any character
 $\eta \colon \Gamma \to (E^{\prime })^{\times }$
, there exists a
$\eta \colon \Gamma \to (E^{\prime })^{\times }$
, there exists a
 $\Lambda _{\infty }$
-linear morphism making the following diagram commute:
$\Lambda _{\infty }$
-linear morphism making the following diagram commute:

where
 $E^{\prime }$
is a finite extension of E.
$E^{\prime }$
is a finite extension of E.
Proof The first part follows from carefully tracing through the definitions.
For the second part, it is enough to show that if
 $\mathrm {pr}_{\eta }(x) = 0,$
then
$\mathrm {pr}_{\eta }(x) = 0,$
then
![]() $\mathrm {ev}_{\eta }(\mathcal {L}(x)) = 0$
, because then we can just define the map by taking a lift to
$\mathrm {ev}_{\eta }(\mathcal {L}(x)) = 0$
, because then we can just define the map by taking a lift to
 $\operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_{p}, D)$
. If
$\operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_{p}, D)$
. If
 $\mathrm {pr}_{\eta }(x) = 0,$
then there exists
$\mathrm {pr}_{\eta }(x) = 0,$
then there exists
![]() $y \in D^{\psi = 1}$
such that
$y \in D^{\psi = 1}$
such that
But
![]() $\mathcal {L}$
is
$\mathcal {L}$
is
![]() $\Lambda _{\infty }$
-linear so (after base-changing D and
$\Lambda _{\infty }$
-linear so (after base-changing D and
![]() $\Lambda _{\infty }$
to
$\Lambda _{\infty }$
to
![]() $D_{E^{\prime }}$
and
$D_{E^{\prime }}$
and
![]() $(\Lambda _{\infty })_{E^{\prime }},$
respectively)
$(\Lambda _{\infty })_{E^{\prime }},$
respectively)
But this is precisely mapped to zero under
![]() $\mathrm {ev}_{\eta }$
.▪
$\mathrm {ev}_{\eta }$
.▪
From the above proposition, we obtain the following corollary, which will be useful in later sections.
Corollary 6.1.3 Let D be a
![]() $(\varphi , \Gamma )$
-module satisfying hypothesis (H) and
$(\varphi , \Gamma )$
-module satisfying hypothesis (H) and
![]() $D_1, D_2 \subset D$
two sub-
$D_1, D_2 \subset D$
two sub-
![]() $(\varphi , \Gamma )$
-modules satisfying
$(\varphi , \Gamma )$
-modules satisfying
![]() $D_{\mathrm {cris}} = (D_1)_{\mathrm {cris}} \oplus (D_2)_{\mathrm {cris}}$
. Let
$D_{\mathrm {cris}} = (D_1)_{\mathrm {cris}} \oplus (D_2)_{\mathrm {cris}}$
. Let
![]() $x_1$
and
$x_1$
and
![]() $x_2$
be two elements of
$x_2$
be two elements of
 $\operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_p, D)$
that lie in the images of the maps
$\operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_p, D)$
that lie in the images of the maps
 $\operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_p, D_1) \to \operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_p, D)$
and
$\operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_p, D_1) \to \operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_p, D)$
and
 $\operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_p, D_2) \to \operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_p, D),$
respectively. Then for any character
$\operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_p, D_2) \to \operatorname {H}^1_{\mathrm {Iw}}(\mathbb {Q}_p, D),$
respectively. Then for any character
![]() $\eta \colon G \to E^{\times }$
the elements
$\eta \colon G \to E^{\times }$
the elements
 $\mathrm {pr}_{\eta }(x_1)$
and
$\mathrm {pr}_{\eta }(x_1)$
and
 $\mathrm {pr}_{\eta }(x_2)$
are linearly independent if both
$\mathrm {pr}_{\eta }(x_2)$
are linearly independent if both
![]() $\mathrm {ev}_{\eta }\mathcal {L}(x_1)$
and
$\mathrm {ev}_{\eta }\mathcal {L}(x_1)$
and
![]() $\mathrm {ev}_{\eta }\mathcal {L}(x_2)$
are non-zero.
$\mathrm {ev}_{\eta }\mathcal {L}(x_2)$
are non-zero.
Proof This follows from functoriality of
![]() $\mathcal {L}$
and the existence of the bottom map in Proposition 6.1.2(ii). Indeed, if both
$\mathcal {L}$
and the existence of the bottom map in Proposition 6.1.2(ii). Indeed, if both
![]() $\mathrm {ev}_{\eta }\mathcal {L}(x_1)$
and
$\mathrm {ev}_{\eta }\mathcal {L}(x_1)$
and
![]() $\mathrm {ev}_{\eta }\mathcal {L}(x_2)$
are non-zero, then because they lie in different direct summands of
$\mathrm {ev}_{\eta }\mathcal {L}(x_2)$
are non-zero, then because they lie in different direct summands of
![]() $D_{\mathrm {cris}},$
they must be linearly independent in
$D_{\mathrm {cris}},$
they must be linearly independent in
![]() $D_{\mathrm {cris}} \widehat {\otimes } \Lambda _{\infty }$
. ▪
$D_{\mathrm {cris}} \widehat {\otimes } \Lambda _{\infty }$
. ▪
6.2 Application to Beilinson–Flach Classes
Returning to the situation in the paper, let f and g denote eigenforms satisfying the assumptions in Section 1.1, so we have Coleman families
![]() $\mathcal {F}, \mathcal {G}_{\alpha }, \mathcal {G}_{\beta }$
over
$\mathcal {F}, \mathcal {G}_{\alpha }, \mathcal {G}_{\beta }$
over
 $V_1, V_2^{\alpha }, V_2^{\beta }$
passing through the p-stabilisations
$V_1, V_2^{\alpha }, V_2^{\beta }$
passing through the p-stabilisations
![]() $f_{\alpha }, g_{\alpha }, g_{\beta }$
respectively. Here
$f_{\alpha }, g_{\alpha }, g_{\beta }$
respectively. Here
![]() $f_{\alpha }$
denotes the p-stabilisation of f that satisfies
$f_{\alpha }$
denotes the p-stabilisation of f that satisfies
![]() $U_p f = \alpha f$
; and similarly for
$U_p f = \alpha f$
; and similarly for
![]() $g_{\alpha }$
and
$g_{\alpha }$
and
![]() $g_{\beta }$
. Since we have assumed that the weights of f and g are not equal, we can choose
$g_{\beta }$
. Since we have assumed that the weights of f and g are not equal, we can choose
![]() $V_1$
such that it does not contain the character
$V_1$
such that it does not contain the character
![]() $k^{\prime }$
. In this subsection,
$k^{\prime }$
. In this subsection,
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $V_2$
will denote either
$V_2$
will denote either
![]() $\mathcal {G}_{\alpha }$
and
$\mathcal {G}_{\alpha }$
and
![]() $V_2^{\alpha }$
or
$V_2^{\alpha }$
or
![]() $\mathcal {G}_{\beta }$
and
$\mathcal {G}_{\beta }$
and
![]() $V_2^{\beta }$
, respectively.
$V_2^{\beta }$
, respectively.
Let
![]() $M_{V_1}(\mathcal {F})$
and
$M_{V_1}(\mathcal {F})$
and
![]() $M_{V_2}(\mathcal {G})$
denote the Galois representations associated with
$M_{V_2}(\mathcal {G})$
denote the Galois representations associated with
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
and let
$\mathcal {G}$
and let
 $\mathbf {D}^{\dagger }_{\mathrm {rig}}(\mathcal {F})^*$
and
$\mathbf {D}^{\dagger }_{\mathrm {rig}}(\mathcal {F})^*$
and
 $\mathbf {D}^{\dagger }_{\mathrm {rig}}(\mathcal {G})^*$
denote the
$\mathbf {D}^{\dagger }_{\mathrm {rig}}(\mathcal {G})^*$
denote the
![]() $(\varphi , \Gamma )$
-modules of
$(\varphi , \Gamma )$
-modules of
![]() $M_{V_1}(\mathcal {F})^*$
and
$M_{V_1}(\mathcal {F})^*$
and
![]() $M_{V_2}(\mathcal {G})^*,$
respectively. If
$M_{V_2}(\mathcal {G})^*,$
respectively. If
![]() $V_1$
and
$V_1$
and
![]() $V_2$
are small enough, both of these modules come with a canonical triangulation, which we will denote as
$V_2$
are small enough, both of these modules come with a canonical triangulation, which we will denote as
 $$\begin{align*}0 \longrightarrow \mathscr{F}^{+}\mathbf{D}^{\dagger}_{\mathrm{rig}}(?)^* \longrightarrow \mathbf{D}^{\dagger}_{\mathrm{rig}}(?)^* = \mathscr{F}^{o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(?)^* \longrightarrow \mathscr{F}^{-}\mathbf{D}^{\dagger}_{\mathrm{rig}}(?)^* \longrightarrow 0 \end{align*}$$
$$\begin{align*}0 \longrightarrow \mathscr{F}^{+}\mathbf{D}^{\dagger}_{\mathrm{rig}}(?)^* \longrightarrow \mathbf{D}^{\dagger}_{\mathrm{rig}}(?)^* = \mathscr{F}^{o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(?)^* \longrightarrow \mathscr{F}^{-}\mathbf{D}^{\dagger}_{\mathrm{rig}}(?)^* \longrightarrow 0 \end{align*}$$
for
![]() $? = \mathcal {F}$
or
$? = \mathcal {F}$
or
![]() $?=\mathcal {G}$
. In fact, there is an explicit description for both the kernel and the cokernel (see [Reference Loeffler and ZerbesLZ16, Theorem 6.3.2]).
$?=\mathcal {G}$
. In fact, there is an explicit description for both the kernel and the cokernel (see [Reference Loeffler and ZerbesLZ16, Theorem 6.3.2]).
Let
![]() $k_1$
be a (not necessarily classical) weight in
$k_1$
be a (not necessarily classical) weight in
![]() $V_1$
and let
$V_1$
and let
![]() $\eta $
be a character of
$\eta $
be a character of
![]() $\Gamma = \operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^{\infty }})/\mathbb {Q}_p)$
, and let E be a finite extension of
$\Gamma = \operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^{\infty }})/\mathbb {Q}_p)$
, and let E be a finite extension of
![]() $\mathbb {Q}_p$
that contains the fields of definition of
$\mathbb {Q}_p$
that contains the fields of definition of
![]() $k_1$
and
$k_1$
and
![]() $\eta $
. Recall that
$\eta $
. Recall that
![]() $k^{\prime }+2$
denotes the weight of g. Let
$k^{\prime }+2$
denotes the weight of g. Let
![]() $M(\mathcal {F}_{k_1})$
and
$M(\mathcal {F}_{k_1})$
and
![]() $M(\mathcal {G}_{k^{\prime }})$
denote the specialisations of
$M(\mathcal {G}_{k^{\prime }})$
denote the specialisations of
![]() $M_{V_1}(\mathcal {F})$
and
$M_{V_1}(\mathcal {F})$
and
![]() $M_{V_2}(\mathcal {G})$
at
$M_{V_2}(\mathcal {G})$
at
![]() $k_1$
and
$k_1$
and
![]() $k^{\prime }$
respectively, and note that we have isomorphisms
$k^{\prime }$
respectively, and note that we have isomorphisms
 $$ \begin{align*} M((\mathcal{G}_{\alpha})_{k^{\prime}}) & \xrightarrow{\mathrm{pr}^{\alpha}} M_E(g), \nonumber \\ M((\mathcal{G}_{\beta})_{k^{\prime}}) & \xrightarrow{\mathrm{pr}^{\beta}} M_E(g) \nonumber \end{align*} $$
$$ \begin{align*} M((\mathcal{G}_{\alpha})_{k^{\prime}}) & \xrightarrow{\mathrm{pr}^{\alpha}} M_E(g), \nonumber \\ M((\mathcal{G}_{\beta})_{k^{\prime}}) & \xrightarrow{\mathrm{pr}^{\beta}} M_E(g) \nonumber \end{align*} $$
both of which follow from the fact that g is classical and the Galois representation does not change after p-stabilisation. We let
 $\mathbf {D}^{\dagger }_{\mathrm {rig}}(\mathcal {F}_{k_1})^*$
,
$\mathbf {D}^{\dagger }_{\mathrm {rig}}(\mathcal {F}_{k_1})^*$
,
 $\mathbf {D}^{\dagger }_{\mathrm {rig}}(\mathcal {G}_{k^{\prime }})^*$
, and
$\mathbf {D}^{\dagger }_{\mathrm {rig}}(\mathcal {G}_{k^{\prime }})^*$
, and
 $\mathbf {D}^{\dagger }_{\mathrm {rig}}(g)^*$
denote the
$\mathbf {D}^{\dagger }_{\mathrm {rig}}(g)^*$
denote the
![]() $(\varphi , \Gamma )$
-modules associated with
$(\varphi , \Gamma )$
-modules associated with
![]() $M(\mathcal {F}_{k_1})^*$
,
$M(\mathcal {F}_{k_1})^*$
,
![]() $M(\mathcal {G}_{k^{\prime }})^*$
and
$M(\mathcal {G}_{k^{\prime }})^*$
and
![]() $M_E(g)^*$
, respectively. By specialising the triangulation above and applying
$M_E(g)^*$
, respectively. By specialising the triangulation above and applying
![]() $\mathrm {pr}^{\alpha }$
or
$\mathrm {pr}^{\alpha }$
or
![]() $\mathrm {pr}^{\beta }$
if necessary, we obtain triangulations for these three
$\mathrm {pr}^{\beta }$
if necessary, we obtain triangulations for these three
![]() $(\varphi , \Gamma )$
-modules.
$(\varphi , \Gamma )$
-modules.
Let
![]() $D^-$
be the
$D^-$
be the
![]() $(\varphi , \Gamma )$
-module
$(\varphi , \Gamma )$
-module
 $$ \begin{align} D^- = \mathscr{F}^{-}\mathbf{D}^{\dagger}_{\mathrm{rig}}(\mathcal{F}_{k_1})^* \otimes \mathscr{F}^{o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(g)^*. \end{align} $$
$$ \begin{align} D^- = \mathscr{F}^{-}\mathbf{D}^{\dagger}_{\mathrm{rig}}(\mathcal{F}_{k_1})^* \otimes \mathscr{F}^{o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(g)^*. \end{align} $$
Since g is classical,
![]() $D^-$
is crystalline with Hodge–Tate weights
$D^-$
is crystalline with Hodge–Tate weights
![]() ${0, 1+k^{\prime }}$
and by the explicit description in [Reference Loeffler and ZerbesLZ16, Theorem 6.3.2],
${0, 1+k^{\prime }}$
and by the explicit description in [Reference Loeffler and ZerbesLZ16, Theorem 6.3.2],
![]() $p^n$
is not an eigenvalue for
$p^n$
is not an eigenvalue for
![]() $\varphi $
on
$\varphi $
on
![]() $D^-_{\mathrm {cris}}$
for any integer
$D^-_{\mathrm {cris}}$
for any integer
![]() $n \geq 0$
(so
$n \geq 0$
(so
![]() $D^-$
satisfies hypothesis (H)). Consider the following submodules
$D^-$
satisfies hypothesis (H)). Consider the following submodules
 $$ \begin{align*} D_1 = D^{\alpha} & = \mathrm{pr}^{\alpha} \big( \mathscr{F}^{-}\mathbf{D}^{\dagger}_{\mathrm{rig}}(\mathcal{F}_{k_1})^* \otimes \mathscr{F}^{+}\mathbf{D}^{\dagger}_{\mathrm{rig}}((\mathcal{G}_{\alpha})_{k^{\prime}})^* \big), \nonumber \\ D_2 = D^{\beta} & = \mathrm{pr}^{\beta} \big( \mathscr{F}^{-}\mathbf{D}^{\dagger}_{\mathrm{rig}}(\mathcal{F}_{k_1})^* \otimes \mathscr{F}^{+}\mathbf{D}^{\dagger}_{\mathrm{rig}}((\mathcal{G}_{\beta})_{k^{\prime}})^* \big), \nonumber \end{align*} $$
$$ \begin{align*} D_1 = D^{\alpha} & = \mathrm{pr}^{\alpha} \big( \mathscr{F}^{-}\mathbf{D}^{\dagger}_{\mathrm{rig}}(\mathcal{F}_{k_1})^* \otimes \mathscr{F}^{+}\mathbf{D}^{\dagger}_{\mathrm{rig}}((\mathcal{G}_{\alpha})_{k^{\prime}})^* \big), \nonumber \\ D_2 = D^{\beta} & = \mathrm{pr}^{\beta} \big( \mathscr{F}^{-}\mathbf{D}^{\dagger}_{\mathrm{rig}}(\mathcal{F}_{k_1})^* \otimes \mathscr{F}^{+}\mathbf{D}^{\dagger}_{\mathrm{rig}}((\mathcal{G}_{\beta})_{k^{\prime}})^* \big), \nonumber \end{align*} $$
where
![]() $\mathrm {pr}^{\alpha }$
and
$\mathrm {pr}^{\alpha }$
and
![]() $\mathrm {pr}^{\beta }$
are the isomorphisms described above. Again, by the explicit description in loc. cit.,
$\mathrm {pr}^{\beta }$
are the isomorphisms described above. Again, by the explicit description in loc. cit.,
![]() $(D_1)_{\mathrm {cris}}$
and
$(D_1)_{\mathrm {cris}}$
and
![]() $(D_2)_{\mathrm {cris}}$
are both rank one sub
$(D_2)_{\mathrm {cris}}$
are both rank one sub
![]() $\varphi $
-modules of
$\varphi $
-modules of
![]() $D_{\mathrm {cris}}^-$
on which
$D_{\mathrm {cris}}^-$
on which
![]() $\varphi $
acts by multiplication by
$\varphi $
acts by multiplication by
 $\alpha _{\mathcal {F}_{k_1}}^{-1}\beta _g^{-1}$
and
$\alpha _{\mathcal {F}_{k_1}}^{-1}\beta _g^{-1}$
and
 $\alpha _{\mathcal {F}_{k_1}}^{-1}\alpha _g^{-1}$
respectively. Since we have assumed that g is p-regular (i.e.,
$\alpha _{\mathcal {F}_{k_1}}^{-1}\alpha _g^{-1}$
respectively. Since we have assumed that g is p-regular (i.e.,
![]() $\alpha _g \neq \beta _g$
), we must have
$\alpha _g \neq \beta _g$
), we must have
![]() $D_{\mathrm {cris}}^- = (D_1)_{\mathrm {cris}} \oplus (D_2)_{\mathrm {cris}}$
.
$D_{\mathrm {cris}}^- = (D_1)_{\mathrm {cris}} \oplus (D_2)_{\mathrm {cris}}$
.
Let
![]() $c> 6$
be an integer that is coprime to
$c> 6$
be an integer that is coprime to
![]() $6Np$
and let
$6Np$
and let
![]() $z_1^{\alpha }$
be the image of the Beilinson–Flach class
$z_1^{\alpha }$
be the image of the Beilinson–Flach class
 ${}_{c} \mathcal {BF}^{[\mathcal {F}, \mathcal {G}_{\alpha }]}_{1, 1}$
(see §4.3) under the composition
${}_{c} \mathcal {BF}^{[\mathcal {F}, \mathcal {G}_{\alpha }]}_{1, 1}$
(see §4.3) under the composition
 $$ \begin{align*} \operatorname{H}^1\big(\mathbb{Q}, D^{\mathrm{la}}(\Gamma, M(\mathcal{F}_{k_1})^* &\otimes M((\mathcal{G}_{\alpha})_{k^{\prime}})^*)\big)\\ &\longrightarrow \operatorname{H}^1_{\mathrm{Iw}}\big(\mathbb{Q}_{p, \infty}, M(\mathcal{F}_{k_1})^* \otimes M(g)^*\big) \longrightarrow \operatorname{H}^1_{\mathrm{Iw}}(\mathbb{Q}_p, D^-) \end{align*} $$
$$ \begin{align*} \operatorname{H}^1\big(\mathbb{Q}, D^{\mathrm{la}}(\Gamma, M(\mathcal{F}_{k_1})^* &\otimes M((\mathcal{G}_{\alpha})_{k^{\prime}})^*)\big)\\ &\longrightarrow \operatorname{H}^1_{\mathrm{Iw}}\big(\mathbb{Q}_{p, \infty}, M(\mathcal{F}_{k_1})^* \otimes M(g)^*\big) \longrightarrow \operatorname{H}^1_{\mathrm{Iw}}(\mathbb{Q}_p, D^-) \end{align*} $$
and similarly for
![]() $z_1^{\beta }$
, where the first map is restriction to the decomposition group at p composed with the isomorphism
$z_1^{\beta }$
, where the first map is restriction to the decomposition group at p composed with the isomorphism
![]() $\mathrm {pr}^{\alpha }$
. Recall that
$\mathrm {pr}^{\alpha }$
. Recall that
![]() $L_p(\mathcal {F}, g, 1 +\mathbf {j})$
is the two-variable p-adic L-function associated with the Coleman family
$L_p(\mathcal {F}, g, 1 +\mathbf {j})$
is the two-variable p-adic L-function associated with the Coleman family
![]() $\mathcal {F}$
and the universal twist
$\mathcal {F}$
and the universal twist
![]() $\mathbf {j}$
(see [Reference UrbanUrb14] or [Reference Loeffler and ZerbesLZ16, §9]).
$\mathbf {j}$
(see [Reference UrbanUrb14] or [Reference Loeffler and ZerbesLZ16, §9]).
Proposition 6.2.2 We can choose the auxiliary integer c such that, if
![]() $L_p(\mathcal {F}_{k_1}, g, 1 + \eta ) \neq 0,$
then
$L_p(\mathcal {F}_{k_1}, g, 1 + \eta ) \neq 0,$
then
 $\mathrm {pr}_{\eta }(z_1^{\alpha })$
and
$\mathrm {pr}_{\eta }(z_1^{\alpha })$
and
 $\mathrm {pr}_{\eta }(z_1^{\beta })$
are linearly independent in
$\mathrm {pr}_{\eta }(z_1^{\beta })$
are linearly independent in
 $\operatorname {H}^1(\mathbb {Q}_p, D^-(\eta ^{-1}))$
.
$\operatorname {H}^1(\mathbb {Q}_p, D^-(\eta ^{-1}))$
.
Proof Recall that
![]() $D^-$
is a crystalline
$D^-$
is a crystalline
![]() $(\varphi , \Gamma )$
-module satisfying hypothesis (H). Therefore, we have the Perrin–Riou logarithm
$(\varphi , \Gamma )$
-module satisfying hypothesis (H). Therefore, we have the Perrin–Riou logarithm
 $$\begin{align*}\mathcal{L}\colon \operatorname{H}^1_{\mathrm{Iw}}(\mathbb{Q}_{p}, D^-) \longrightarrow D^-_{\mathrm{cris}} \widehat{\otimes} \Lambda_{\infty}. \end{align*}$$
$$\begin{align*}\mathcal{L}\colon \operatorname{H}^1_{\mathrm{Iw}}(\mathbb{Q}_{p}, D^-) \longrightarrow D^-_{\mathrm{cris}} \widehat{\otimes} \Lambda_{\infty}. \end{align*}$$
By Proposition 6.1.2(i), this map agrees with the map (also denoted by
![]() $\mathcal {L}$
) constructed in [Reference Loeffler and ZerbesLZ16, Theorem 7.1.4] after specialising at
$\mathcal {L}$
) constructed in [Reference Loeffler and ZerbesLZ16, Theorem 7.1.4] after specialising at
![]() $(k_1, k^{\prime })$
. Indeed, the map in loc. cit. is defined as the pull back of
$(k_1, k^{\prime })$
. Indeed, the map in loc. cit. is defined as the pull back of
![]() $\mathcal {L}_{D^-(-1-k^{\prime })}$
under the automorphism
$\mathcal {L}_{D^-(-1-k^{\prime })}$
under the automorphism
![]() $\omega _{-1-k^{\prime }}$
.
$\omega _{-1-k^{\prime }}$
.
By the “explicit reciprocity law” of Theorem 7.1.5 in op. cit., we see that
![]() $\mathrm {ev}_{\eta }(\mathcal {L}(z_1^{\alpha }))$
and
$\mathrm {ev}_{\eta }(\mathcal {L}(z_1^{\alpha }))$
and
 $\mathrm {ev}_{\eta }(\mathcal {L}(z_1^{\beta }))$
are both non-zero if the quantity
$\mathrm {ev}_{\eta }(\mathcal {L}(z_1^{\beta }))$
are both non-zero if the quantity
 $$ \begin{align} \big( c^2 - c^{-(k_1 + k^{\prime} - 2\eta)} \varepsilon_{\mathcal{F}_{k_1}}(c)^{-1}\varepsilon_g(c)^{-1} \big) (-1)^{1+ \eta} \lambda_N(\mathcal{F}_{k_1} )^{-1} L_p(\mathcal{F}_{k_1}, g, 1+ \eta ) \end{align} $$
$$ \begin{align} \big( c^2 - c^{-(k_1 + k^{\prime} - 2\eta)} \varepsilon_{\mathcal{F}_{k_1}}(c)^{-1}\varepsilon_g(c)^{-1} \big) (-1)^{1+ \eta} \lambda_N(\mathcal{F}_{k_1} )^{-1} L_p(\mathcal{F}_{k_1}, g, 1+ \eta ) \end{align} $$
is non-zero, where
![]() $\lambda _N(\mathcal {F}_{k_1} )$
denotes the specialisation of the Atkin–Lehner pseudo-eigenvalue of
$\lambda _N(\mathcal {F}_{k_1} )$
denotes the specialisation of the Atkin–Lehner pseudo-eigenvalue of
![]() $\mathcal {F}$
(see [Reference Kings, Loeffler and ZerbesKLZ17, §2.5] for the definition of the Atkin–Lehner operators). Since our assumption at the start of §6.2 implies that
$\mathcal {F}$
(see [Reference Kings, Loeffler and ZerbesKLZ17, §2.5] for the definition of the Atkin–Lehner operators). Since our assumption at the start of §6.2 implies that
![]() $k_1 \neq k^{\prime }$
, we can choose the integer c such that the first factor in (6.2.3) is non-zero. The result then follows by applying Corollary 6.1.3. ▪
$k_1 \neq k^{\prime }$
, we can choose the integer c such that the first factor in (6.2.3) is non-zero. The result then follows by applying Corollary 6.1.3. ▪
7 Bounding the Selmer Group
Let f and g be two cuspidal new eigenforms satisfying the assumptions in section 1.1, and let
![]() $\mathcal {F}$
be a Coleman family over
$\mathcal {F}$
be a Coleman family over
![]() $V_1 \subset \mathcal {W}_E$
passing through a p-stabilisation of f. In this section, we show that, if
$V_1 \subset \mathcal {W}_E$
passing through a p-stabilisation of f. In this section, we show that, if
![]() $V_1$
is taken to be small enough and certain hypotheses are satisfied, then the cohomology group
$V_1$
is taken to be small enough and certain hypotheses are satisfied, then the cohomology group
 $\widetilde {\operatorname {H}}^2_f(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
vanishes if
$\widetilde {\operatorname {H}}^2_f(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
vanishes if
![]() $L_p(\mathbf {x}) = 0$
. Here,
$L_p(\mathbf {x}) = 0$
. Here,
![]() $\mathbf {x} = (k_1, k^{\prime }, \eta ) \in V_1 \times \{k^{\prime }\} \times \mathcal {W}$
is a tuple of weights,
$\mathbf {x} = (k_1, k^{\prime }, \eta ) \in V_1 \times \{k^{\prime }\} \times \mathcal {W}$
is a tuple of weights,
![]() $\overline {M}_{\mathbf {x}}$
denotes the representation
$\overline {M}_{\mathbf {x}}$
denotes the representation
![]() $[M(\mathcal {F}_{k_1})^* \otimes M(g)^*](\eta ^{-1})$
and
$[M(\mathcal {F}_{k_1})^* \otimes M(g)^*](\eta ^{-1})$
and
 $\widetilde {\operatorname {H}}^2_f(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
is the second cohomology group of the Selmer complex defined in Section 7.2.
$\widetilde {\operatorname {H}}^2_f(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
is the second cohomology group of the Selmer complex defined in Section 7.2.
7.1 Cohomological Preliminaries
In [Reference NekovářNek06], Nekovář defined the concept of a Selmer complex: an object in a certain derived category whose cohomology is closely related to the usual definition of Selmer groups. This construction is useful because the resulting complex has nice base-change and duality properties; attributes that one does not necessarily have for the classical Selmer groups. In [Reference PottharstPot13], Pottharst extends this construction to families of Galois representations over well-behaved rigid analytic spaces. This is the tool we will use to construct a sheaf interpolating the Bloch–Kato Selmer groups. We now summarise this construction.
Let A be an affinoid algebra over
![]() $\mathbb {Q}_p$
and let M be an A-valued representation of
$\mathbb {Q}_p$
and let M be an A-valued representation of
![]() $G_{\mathbb {Q}} = \operatorname {\mathrm {Gal}}(\bar {\mathbb {Q}}/\mathbb {Q})$
(i.e., a finitely generated, projective A-module with a continuous action of
$G_{\mathbb {Q}} = \operatorname {\mathrm {Gal}}(\bar {\mathbb {Q}}/\mathbb {Q})$
(i.e., a finitely generated, projective A-module with a continuous action of
![]() $G_{\mathbb {Q}}$
). Let
$G_{\mathbb {Q}}$
). Let
![]() $\Sigma $
be a set of places of
$\Sigma $
be a set of places of
![]() $\mathbb {Q}$
containing
$\mathbb {Q}$
containing
![]() $p, \infty $
and all primes where M is ramified, and assume that
$p, \infty $
and all primes where M is ramified, and assume that
![]() $\Sigma $
is finite. Let
$\Sigma $
is finite. Let
![]() $G_{\Sigma }$
denote the Galois group of the maximal algebraic unramified-outside-
$G_{\Sigma }$
denote the Galois group of the maximal algebraic unramified-outside-
![]() $\Sigma $
extension of
$\Sigma $
extension of
![]() $\mathbb {Q}$
and, for a place
$\mathbb {Q}$
and, for a place
![]() $v \in \Sigma $
, let
$v \in \Sigma $
, let
![]() $G_v$
denote a fixed decomposition group in
$G_v$
denote a fixed decomposition group in
![]() $G_{\Sigma }$
associated with the place v.
$G_{\Sigma }$
associated with the place v.
Definition 7.1.1 A collection of local conditions
![]() $\Delta $
for M is a set of pairs
$\Delta $
for M is a set of pairs
![]() $\{ (\Delta _v, \iota _v): v \in \Sigma \}$
where
$\{ (\Delta _v, \iota _v): v \in \Sigma \}$
where
![]() $\Delta _v$
is an object in the derived category of bounded complexes of (continuous) A-modules, and
$\Delta _v$
is an object in the derived category of bounded complexes of (continuous) A-modules, and
![]() $\iota _v$
is a morphism
$\iota _v$
is a morphism
 $$\begin{align*}\Delta_v \xrightarrow{\iota_v} \mathbf{R}\Gamma_{\mathrm{cont}}(G_v, M). \end{align*}$$
$$\begin{align*}\Delta_v \xrightarrow{\iota_v} \mathbf{R}\Gamma_{\mathrm{cont}}(G_v, M). \end{align*}$$
One defines the Selmer complex
![]() ${\mathbf {R}\widetilde {\Gamma }({G_{\Sigma }}, {M}; {\Delta })}$
in the following way.
${\mathbf {R}\widetilde {\Gamma }({G_{\Sigma }}, {M}; {\Delta })}$
in the following way.
Definition 7.1.2 Let
![]() $\Delta $
be a set of local conditions for M. Then the Selmer complex
$\Delta $
be a set of local conditions for M. Then the Selmer complex
![]() ${\mathbf {R}\widetilde {\Gamma }({G_{\Sigma }}, {M}; {\Delta })}$
is the mapping fibre
${\mathbf {R}\widetilde {\Gamma }({G_{\Sigma }}, {M}; {\Delta })}$
is the mapping fibre
 $$\begin{align*}{\mathbf{R}\widetilde{\Gamma}({G_{\Sigma}}, {M}; {\Delta})} := \operatorname{Cone}\Big( \mathbf{R}\Gamma_{\mathrm{cont}}(G_{\Sigma}, M) \oplus \bigoplus_{v \in \Sigma}{\Delta_v} \xrightarrow{\operatorname{res}_v - \iota_v} \bigoplus_{v \in \Sigma} \mathbf{R}\Gamma_{\mathrm{cont}}(G_v, M) \Big)[-1]. \end{align*}$$
$$\begin{align*}{\mathbf{R}\widetilde{\Gamma}({G_{\Sigma}}, {M}; {\Delta})} := \operatorname{Cone}\Big( \mathbf{R}\Gamma_{\mathrm{cont}}(G_{\Sigma}, M) \oplus \bigoplus_{v \in \Sigma}{\Delta_v} \xrightarrow{\operatorname{res}_v - \iota_v} \bigoplus_{v \in \Sigma} \mathbf{R}\Gamma_{\mathrm{cont}}(G_v, M) \Big)[-1]. \end{align*}$$
We denote the i-th cohomology of this complex by
![]() $\widetilde {H}^{i}(G_{\Sigma }, M; \Delta )$
.
$\widetilde {H}^{i}(G_{\Sigma }, M; \Delta )$
.
If
![]() $\Delta _v$
is quasi-isomorphic to a complex of finitely generated A-modules concentrates in degrees
$\Delta _v$
is quasi-isomorphic to a complex of finitely generated A-modules concentrates in degrees
![]() $[0, 2]$
(all our local conditions in this paper will satisfy this), then
$[0, 2]$
(all our local conditions in this paper will satisfy this), then
![]() ${\mathbf {R}\widetilde {\Gamma }({G_{\Sigma }}, {M}; {\Delta })}$
is quasi-isomorphic to a complex of finitely generated A-modules, concentrated in degrees
${\mathbf {R}\widetilde {\Gamma }({G_{\Sigma }}, {M}; {\Delta })}$
is quasi-isomorphic to a complex of finitely generated A-modules, concentrated in degrees
![]() $[0, 3]$
(see [Reference PottharstPot13, §1.5]).
$[0, 3]$
(see [Reference PottharstPot13, §1.5]).
This construction also works in more general situations. For example, if X is a quasi-Stein rigid analytic space, then
![]() ${\mathbf {R}\widetilde {\Gamma }({G_{\Sigma }}, {M}; {\Delta })}$
is quasi-isomorphic to a complex of coherent
${\mathbf {R}\widetilde {\Gamma }({G_{\Sigma }}, {M}; {\Delta })}$
is quasi-isomorphic to a complex of coherent
![]() $\mathcal {O}_X$
-modules, concentrated in degrees
$\mathcal {O}_X$
-modules, concentrated in degrees
![]() $[0, 3]$
(this is situation (4) described in [Reference PottharstPot13, §1.5]).
$[0, 3]$
(this is situation (4) described in [Reference PottharstPot13, §1.5]).
Proposition 7.1.3 Selmer complexes satisfy the following properties:
-
(i) (Duality, [Reference PottharstPot13, Theorem 1.16]) Suppose that the local condition
 $\Delta _v$
is quasi-isomorphic to a perfect complex of A-modules concentrated in degrees
$\Delta _v$
is quasi-isomorphic to a perfect complex of A-modules concentrated in degrees
 $[0, 2]$
, for all
$[0, 2]$
, for all
 $v \in \Sigma $
. We define the dual local conditions
$v \in \Sigma $
. We define the dual local conditions
 $\Delta ^*(1)$
to be
$\Delta ^*(1)$
to be
 $\{(\Delta _v^*(1), j_v^*[-2]) \}$
, where
$\{(\Delta _v^*(1), j_v^*[-2]) \}$
, where  $$\begin{align*}\Delta_v^*(1) := Q_v^*[-2] \xrightarrow{j_v^*[-2]} \mathbf{R}\Gamma_{\mathrm{cont}}(G_v, M)^*[-2] \cong \mathbf{R}\Gamma_{\mathrm{cont}}(G_v, M^*(1)) \end{align*}$$
$$\begin{align*}\Delta_v^*(1) := Q_v^*[-2] \xrightarrow{j_v^*[-2]} \mathbf{R}\Gamma_{\mathrm{cont}}(G_v, M)^*[-2] \cong \mathbf{R}\Gamma_{\mathrm{cont}}(G_v, M^*(1)) \end{align*}$$
and
 $Q_v$
is the mapping cone of
$Q_v$
is the mapping cone of
 $\iota _v$
, we write
$\iota _v$
, we write
 $j_v: \mathbf {R}\Gamma _{\mathrm {cont}}(G_v, M) \to Q_v$
for the natural map and
$j_v: \mathbf {R}\Gamma _{\mathrm {cont}}(G_v, M) \to Q_v$
for the natural map and
 $(-)^*$
denotes the dual (in the underived sense).One has an isomorphism
$(-)^*$
denotes the dual (in the underived sense).One has an isomorphism  $$\begin{align*}\mathbf{R}\widetilde{\Gamma}(G_{\Sigma}, M^*(1); \Delta^*(1)) \cong {\mathbf{R}\widetilde{\Gamma}({G_{\Sigma}}, {M}; {\Delta})}^*[-3]. \end{align*}$$
$$\begin{align*}\mathbf{R}\widetilde{\Gamma}(G_{\Sigma}, M^*(1); \Delta^*(1)) \cong {\mathbf{R}\widetilde{\Gamma}({G_{\Sigma}}, {M}; {\Delta})}^*[-3]. \end{align*}$$
-
(ii) (Comparison of local conditions) If
 $\Delta ^{\prime } = \{(\Delta ^{\prime }_v, \iota ^{\prime }_v): v \in \Sigma \}$
is another set of local conditions and
$\Delta ^{\prime } = \{(\Delta ^{\prime }_v, \iota ^{\prime }_v): v \in \Sigma \}$
is another set of local conditions and
 $\{\tau _v\}$
are morphisms such that
$\{\tau _v\}$
are morphisms such that
 $\iota ^{\prime }_v$
is equal to the composition then we obtain a Poitou–Tate style long exact sequence
$\iota ^{\prime }_v$
is equal to the composition then we obtain a Poitou–Tate style long exact sequence $$\begin{align*}\Delta^{\prime}_v \xrightarrow{\tau_v} \Delta_v \xrightarrow{\iota_v} \mathbf{R}\Gamma_{\mathrm{cont}}(G_v, M), \end{align*}$$
where
$$\begin{align*}\Delta^{\prime}_v \xrightarrow{\tau_v} \Delta_v \xrightarrow{\iota_v} \mathbf{R}\Gamma_{\mathrm{cont}}(G_v, M), \end{align*}$$
where $$\begin{align*}\begin{aligned} \bigoplus_{v \in \Sigma}\operatorname{H}^0(Q_v) \longrightarrow \widetilde{H}^{1}(G_{\Sigma}, M; \Delta^{\prime}) \longrightarrow \widetilde{H}^{1}(G_{\Sigma}, M; \Delta) \xrightarrow{\xi} \bigoplus_{v \in \Sigma}\operatorname{H}^1(Q_v) \longrightarrow \\ \longrightarrow \widetilde{H}^{2}(G_{\Sigma}, M; \Delta^{\prime}) \longrightarrow \widetilde{H}^{2}(G_{\Sigma}, M; \Delta) \longrightarrow \bigoplus_{v \in \Sigma}\operatorname{H}^2(Q_v), \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \bigoplus_{v \in \Sigma}\operatorname{H}^0(Q_v) \longrightarrow \widetilde{H}^{1}(G_{\Sigma}, M; \Delta^{\prime}) \longrightarrow \widetilde{H}^{1}(G_{\Sigma}, M; \Delta) \xrightarrow{\xi} \bigoplus_{v \in \Sigma}\operatorname{H}^1(Q_v) \longrightarrow \\ \longrightarrow \widetilde{H}^{2}(G_{\Sigma}, M; \Delta^{\prime}) \longrightarrow \widetilde{H}^{2}(G_{\Sigma}, M; \Delta) \longrightarrow \bigoplus_{v \in \Sigma}\operatorname{H}^2(Q_v), \end{aligned} \end{align*}$$
 $Q_v$
is the mapping cone of
$Q_v$
is the mapping cone of
 $\tau _v$
.
$\tau _v$
.
Proof For the second part, this is immediate from the definition of the Selmer complexes associated with the local conditions
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta ^{\prime }$
. ▪
$\Delta ^{\prime }$
. ▪
In §7.3 we will use the Poitou–Tate long exact sequence described above to show that the cohomology of the Selmer complex vanishes in degree two if the corresponding value of the p-adic L-function is non-zero. In particular we will use the following result:
Proposition 7.1.4 If the map
![]() $\xi $
in Proposition 7.1.3 (ii) is surjective, then we have an injective map
$\xi $
in Proposition 7.1.3 (ii) is surjective, then we have an injective map
In particular, if
![]() $\widetilde {H}^{2}(G_{\Sigma }, M; \Delta )$
vanishes, then so does
$\widetilde {H}^{2}(G_{\Sigma }, M; \Delta )$
vanishes, then so does
![]() $\widetilde {H}^{2}(G_{\Sigma }, M; \Delta ^{\prime })$
.
$\widetilde {H}^{2}(G_{\Sigma }, M; \Delta ^{\prime })$
.
7.2 Convolution of Two Coleman Families
Let
![]() $\mathbf {x} = (k_1, k^{\prime }, \eta ) \in V_1 \times \{k^{\prime }\} \times \mathcal {W}$
be a tuple of weights defined over a finite extension
$\mathbf {x} = (k_1, k^{\prime }, \eta ) \in V_1 \times \{k^{\prime }\} \times \mathcal {W}$
be a tuple of weights defined over a finite extension
![]() $E / \mathbb {Q}_p$
.
$E / \mathbb {Q}_p$
.
Let
![]() $\overline {M}_{\mathbf {x}}$
denote the representation
$\overline {M}_{\mathbf {x}}$
denote the representation
![]() $[M(\mathcal {F}_{k_1})^* \otimes M(g)^*](\eta ^{-1})$
and let
$[M(\mathcal {F}_{k_1})^* \otimes M(g)^*](\eta ^{-1})$
and let
![]() $\Sigma $
be a finite set of places of
$\Sigma $
be a finite set of places of
![]() $\mathbb {Q}$
that contains
$\mathbb {Q}$
that contains
![]() $p, \infty $
and all the primes where
$p, \infty $
and all the primes where
![]() $\overline {M}_{\mathbf {x}}$
ramifies. Let
$\overline {M}_{\mathbf {x}}$
ramifies. Let
 $D_{\mathbf {x}} := \mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}_{\mathbf {x}})$
denote the
$D_{\mathbf {x}} := \mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}_{\mathbf {x}})$
denote the
![]() $(\varphi , \Gamma )$
-module associated with
$(\varphi , \Gamma )$
-module associated with
![]() $\overline {M}_{\mathbf {x}}$
and recall that we have a two dimensional quotient
$\overline {M}_{\mathbf {x}}$
and recall that we have a two dimensional quotient
 $\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}_{\mathbf {x}}) \rightarrow D^-(\eta ^{-1}) =: D^-_{\mathbf {x}}$
, where
$\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}_{\mathbf {x}}) \rightarrow D^-(\eta ^{-1}) =: D^-_{\mathbf {x}}$
, where
![]() $D^-$
is defined as in (6.2.1). We denote the kernel of this quotient by
$D^-$
is defined as in (6.2.1). We denote the kernel of this quotient by
![]() $D^+_{\mathbf {x}}$
. For
$D^+_{\mathbf {x}}$
. For
![]() $v \in \Sigma \backslash \{p\},$
we call
$v \in \Sigma \backslash \{p\},$
we call
 $(\mathbf {R}\Gamma _{\mathrm {cont}}(G_v/I_v, {\overline {M}_{\mathbf {x}}}^{I_v}), \iota _v)$
the unramified local condition at v, where
$(\mathbf {R}\Gamma _{\mathrm {cont}}(G_v/I_v, {\overline {M}_{\mathbf {x}}}^{I_v}), \iota _v)$
the unramified local condition at v, where
![]() $\iota _v$
is the natural map induced by inflation. We are interested in the following examples of local conditions:
$\iota _v$
is the natural map induced by inflation. We are interested in the following examples of local conditions:
-
• (Relaxed) For
 $v \in \Sigma ,$
take
$v \in \Sigma ,$
take
 $\Delta _{\mathrm {rel}}$
to be the set of unramified local conditions for
$\Delta _{\mathrm {rel}}$
to be the set of unramified local conditions for
 $v \neq p$
and We denote the cohomology of the associated Selmer complex by
$v \neq p$
and We denote the cohomology of the associated Selmer complex by $$\begin{align*}\Delta_{\mathrm{rel}, p} := \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \overline{M}_{\mathbf{x}}) \xrightarrow{\sim} \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \overline{M}_{\mathbf{x}}). \end{align*}$$
$$\begin{align*}\Delta_{\mathrm{rel}, p} := \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \overline{M}_{\mathbf{x}}) \xrightarrow{\sim} \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \overline{M}_{\mathbf{x}}). \end{align*}$$
 $\widetilde {\operatorname {H}}_{\mathrm {rel}}^{i}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
.
$\widetilde {\operatorname {H}}_{\mathrm {rel}}^{i}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
.
-
• (Strict) For
 $v \in \Sigma ,$
take
$v \in \Sigma ,$
take
 $\Delta _{\mathrm {str}}$
to be the set of unramified local conditions for
$\Delta _{\mathrm {str}}$
to be the set of unramified local conditions for
 $v \neq p$
and We denote the cohomology of the associated Selmer complex by
$v \neq p$
and We denote the cohomology of the associated Selmer complex by $$\begin{align*}\Delta_{\mathrm{str}, p} := 0 \longrightarrow \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \overline{M}_{\mathbf{x}}). \end{align*}$$
$$\begin{align*}\Delta_{\mathrm{str}, p} := 0 \longrightarrow \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \overline{M}_{\mathbf{x}}). \end{align*}$$
 $\widetilde {\operatorname {H}}_{\mathrm {str}}^{i}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
.
$\widetilde {\operatorname {H}}_{\mathrm {str}}^{i}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
.
-
• (Panchishkin) For
 $v \in \Sigma $
take
$v \in \Sigma $
take
 $\Delta _{f}$
to be the set of unramified local conditions for
$\Delta _{f}$
to be the set of unramified local conditions for
 $v \neq p$
and We denote the cohomology of the associated Selmer complex by
$v \neq p$
and We denote the cohomology of the associated Selmer complex by $$\begin{align*}\Delta_{f, p} := \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, D^+_{\mathbf{x}}) \longrightarrow \mathbf{R}\Gamma_{\mathrm{cont}}(\mathbb{Q}_p, \mathbf{D}^{\dagger}_{\mathrm{rig}}(\overline{M}_{\mathbf{x}})) \cong \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \overline{M}_{\mathbf{x}}). \end{align*}$$
$$\begin{align*}\Delta_{f, p} := \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, D^+_{\mathbf{x}}) \longrightarrow \mathbf{R}\Gamma_{\mathrm{cont}}(\mathbb{Q}_p, \mathbf{D}^{\dagger}_{\mathrm{rig}}(\overline{M}_{\mathbf{x}})) \cong \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \overline{M}_{\mathbf{x}}). \end{align*}$$
 $\widetilde {\operatorname {H}}_f^{i}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
. The reason for choosing this local condition is because it is closely related to the Bloch–Kato local condition when
$\widetilde {\operatorname {H}}_f^{i}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
. The reason for choosing this local condition is because it is closely related to the Bloch–Kato local condition when
 $\mathbf {x}$
lies in the critical range (the range where the p-adic L-function interpolates critical values of the global L-function). We will discuss this relation in §7.4.
$\mathbf {x}$
lies in the critical range (the range where the p-adic L-function interpolates critical values of the global L-function). We will discuss this relation in §7.4.
Remark 7.2.1
-
(i) All three of the above Selmer complexes do not change if we enlarge the set
 $\Sigma $
, so we suppress this auxiliary set from the notation.
$\Sigma $
, so we suppress this auxiliary set from the notation. -
(ii) The relaxed and strict conditions are dual to each other. The dual of the Panchishkin local condition is a Panchishkin local condition for
 $\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}_{\mathbf {x}})^*(1) = \mathbf {D}^{\dagger }_{\mathrm {rig}}({\overline {M}_{\mathbf {x}}}^*(1))$
.
$\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}_{\mathbf {x}})^*(1) = \mathbf {D}^{\dagger }_{\mathrm {rig}}({\overline {M}_{\mathbf {x}}}^*(1))$
.
Let
![]() $c> 6$
be an integer prime to
$c> 6$
be an integer prime to
![]() $6Np$
and recall from §4.3 that, for an integer m coprime to
$6Np$
and recall from §4.3 that, for an integer m coprime to
![]() $6Ncp$
, there is a Beilinson–Flach class
$6Ncp$
, there is a Beilinson–Flach class
 $$\begin{align*}{}_{c}\mathcal{BF}^{[\mathcal{F}, \mathcal{G}]}_{m, 1} \in \operatorname{H}^1 \big(\mathbb{Q}(\mu_m), D^{\mathrm{la}}(\Gamma, M) \big), \end{align*}$$
$$\begin{align*}{}_{c}\mathcal{BF}^{[\mathcal{F}, \mathcal{G}]}_{m, 1} \in \operatorname{H}^1 \big(\mathbb{Q}(\mu_m), D^{\mathrm{la}}(\Gamma, M) \big), \end{align*}$$
where
![]() $M = M_{V_1}(\mathcal {F})^* \widehat {\otimes } M_{V_2}(\mathcal {G})^*$
. By specialising these Beilinson–Flach classes at
$M = M_{V_1}(\mathcal {F})^* \widehat {\otimes } M_{V_2}(\mathcal {G})^*$
. By specialising these Beilinson–Flach classes at
![]() $\mathbf {x}$
and identifying
$\mathbf {x}$
and identifying
![]() $M((\mathcal {G}_{\alpha })_{k^{\prime }})$
and
$M((\mathcal {G}_{\alpha })_{k^{\prime }})$
and
![]() $M((\mathcal {G}_{\beta })_{k^{\prime }})$
with
$M((\mathcal {G}_{\beta })_{k^{\prime }})$
with
![]() $M_E(g)$
as before, we obtain classes in
$M_E(g)$
as before, we obtain classes in
![]() $\operatorname {H}^1(\mathbb {Q}(\mu _m), \overline {M}_{\mathbf {x}} )$
.
$\operatorname {H}^1(\mathbb {Q}(\mu _m), \overline {M}_{\mathbf {x}} )$
.
In Section 4.4, we showed that these classes satisfy certain norm relations and that we could produce an Euler system from these classes. More precisely, let
![]() $\overline {T}_{\mathbf {x}}$
be a Galois stable lattice inside
$\overline {T}_{\mathbf {x}}$
be a Galois stable lattice inside
![]() $\overline {M}_{\mathbf {x}}$
. Then there exist collections
$\overline {M}_{\mathbf {x}}$
. Then there exist collections
![]() $\{c^{\alpha }_m \in \operatorname {H}^1(\mathbb {Q}(\mu _m), \overline {T}_{\mathbf {x}}) : m \in S \}$
and
$\{c^{\alpha }_m \in \operatorname {H}^1(\mathbb {Q}(\mu _m), \overline {T}_{\mathbf {x}}) : m \in S \}$
and
 $\{c^{\beta }_m \in \operatorname {H}^1(\mathbb {Q}(\mu _m), \overline {T}_{\mathbf {x}}) : m \in S \}$
satisfying the Euler system relations, and
$\{c^{\beta }_m \in \operatorname {H}^1(\mathbb {Q}(\mu _m), \overline {T}_{\mathbf {x}}) : m \in S \}$
satisfying the Euler system relations, and
![]() $c_1^{\alpha }$
and
$c_1^{\alpha }$
and
![]() $c_1^{\beta }$
are equal to non-zero multiples of the specialisations of
$c_1^{\beta }$
are equal to non-zero multiples of the specialisations of
 ${{}_{c} \mathcal {BF}_{1, 1}^{[\mathcal {F}, \mathcal {G}_{\alpha }]}}$
and
${{}_{c} \mathcal {BF}_{1, 1}^{[\mathcal {F}, \mathcal {G}_{\alpha }]}}$
and
 ${{}_{c} \mathcal {BF}_{1, 1}^{[\mathcal {F}, \mathcal {G}_{\beta }]}}$
at
${{}_{c} \mathcal {BF}_{1, 1}^{[\mathcal {F}, \mathcal {G}_{\beta }]}}$
at
![]() $\mathbf {x}$
respectively.
$\mathbf {x}$
respectively.
We choose the integer c in such a way that the conclusion of Proposition 6.2.2 holds at the point
![]() $\mathbf {x}$
(this choice may depend on
$\mathbf {x}$
(this choice may depend on
![]() $\mathbf {x}$
). After making this choice, the classes
$\mathbf {x}$
). After making this choice, the classes
 $c_{m}^{\alpha }, c_{m}^{\beta }$
satisfy the following local conditions.
$c_{m}^{\alpha }, c_{m}^{\beta }$
satisfy the following local conditions.
Proposition 7.2.2 Keeping the same notation as above, the classes
 $c_{m}^{\alpha }, c_{m}^{\beta }$
satisfy the following properties:
$c_{m}^{\alpha }, c_{m}^{\beta }$
satisfy the following properties:
-
(i) Both
 $c_{m}^{\alpha }$
and
$c_{m}^{\alpha }$
and
 $c_{m}^{\beta }$
are unramified outside p. In particular, both
$c_{m}^{\beta }$
are unramified outside p. In particular, both
 $c_1^{\alpha }$
and
$c_1^{\alpha }$
and
 $c_1^{\beta }$
lie in
$c_1^{\beta }$
lie in
 $\widetilde {\operatorname {H}}_{\mathrm {rel}}^{1}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
. This implies that the collection
$\widetilde {\operatorname {H}}_{\mathrm {rel}}^{1}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
. This implies that the collection
 $\{c_m : m \in S \}$
forms an Euler system in the sense of [Reference RubinRub00, Definition 2.1.1], with condition (ii) replaced by (ii)’(b) (see §9.1 in op. cit. ).
$\{c_m : m \in S \}$
forms an Euler system in the sense of [Reference RubinRub00, Definition 2.1.1], with condition (ii) replaced by (ii)’(b) (see §9.1 in op. cit. ). -
(ii) Let
 $\bar {c}_{1}^{\alpha }, \bar {c}_{1}^{\beta }$
denote the images of
$\bar {c}_{1}^{\alpha }, \bar {c}_{1}^{\beta }$
denote the images of
 $c_{1}^{\alpha }, c_{1}^{\beta }$
under the map where
$c_{1}^{\alpha }, c_{1}^{\beta }$
under the map where $$\begin{align*}\widetilde{\operatorname{H}}_{\mathrm{rel}}^{1}(\mathbb{Q}, \overline{M}_{\mathbf{x}}) \xrightarrow{\xi} \operatorname{H}^1(\mathbb{Q}_p, D^-_{\mathbf{x}}), \end{align*}$$
$$\begin{align*}\widetilde{\operatorname{H}}_{\mathrm{rel}}^{1}(\mathbb{Q}, \overline{M}_{\mathbf{x}}) \xrightarrow{\xi} \operatorname{H}^1(\mathbb{Q}_p, D^-_{\mathbf{x}}), \end{align*}$$
 $\xi $
is given by first restricting to p and then mapping to the quotient (this map is the same map as in Proposition 7.1.4 if we compare the relaxed and Panchishkin local conditions defined above). Then, if
$\xi $
is given by first restricting to p and then mapping to the quotient (this map is the same map as in Proposition 7.1.4 if we compare the relaxed and Panchishkin local conditions defined above). Then, if
 $\bar {c}_{1}^{\alpha }$
and
$\bar {c}_{1}^{\alpha }$
and
 $\bar {c}_{1}^{\beta }$
are both non-zero, they are linearly independent. In particular, this happens when
$\bar {c}_{1}^{\beta }$
are both non-zero, they are linearly independent. In particular, this happens when
 $L_p(\mathcal {F}_{k_1}, g, 1 +\eta ) \neq 0$
.
$L_p(\mathcal {F}_{k_1}, g, 1 +\eta ) \neq 0$
.
Proof The first part is the same proof as in [Reference Loeffler and ZerbesLZ16, Theorem 8.1.4]. For the second part, note that
![]() $\bar {c}_{1}^{\alpha }$
and
$\bar {c}_{1}^{\alpha }$
and
![]() $\bar {c}_{1}^{\beta }$
are two elements satisfying the conditions of Corollary 6.1.3. The result then follows from Proposition 6.2.2. ▪
$\bar {c}_{1}^{\beta }$
are two elements satisfying the conditions of Corollary 6.1.3. The result then follows from Proposition 6.2.2. ▪
7.3 A Vanishing Result
Let
![]() $\mathcal {F}$
be a Coleman family over an affinoid domain V. For ease of notation we set
$\mathcal {F}$
be a Coleman family over an affinoid domain V. For ease of notation we set
![]() $\alpha _{\mathcal {F}} := a_p(\mathcal {F})$
and similarly for specialisations of
$\alpha _{\mathcal {F}} := a_p(\mathcal {F})$
and similarly for specialisations of
![]() $\mathcal {F}$
. Moreover, recall that if the specialisation of
$\mathcal {F}$
. Moreover, recall that if the specialisation of
![]() $\mathcal {F}$
at
$\mathcal {F}$
at
![]() $k_1$
is a noble eigenform (so it is the p-stabilisation of an eigenform h), then
$k_1$
is a noble eigenform (so it is the p-stabilisation of an eigenform h), then
![]() $\alpha _{\mathcal {F}_{k_1}} = \alpha _h$
and
$\alpha _{\mathcal {F}_{k_1}} = \alpha _h$
and
![]() $\beta _h$
denote the roots of the Hecke polynomial at p associated with h, and satisfy
$\beta _h$
denote the roots of the Hecke polynomial at p associated with h, and satisfy
![]() $\alpha _h \beta _h = p^{k_1 + 1}\varepsilon _h(p)$
. In this case, we will also write
$\alpha _h \beta _h = p^{k_1 + 1}\varepsilon _h(p)$
. In this case, we will also write
![]() $\beta _{\mathcal {F}_{k_1}} := \beta _h$
(although the notation
$\beta _{\mathcal {F}_{k_1}} := \beta _h$
(although the notation
![]() $\beta _{\mathcal {F}}$
is, of course, meaningless).
$\beta _{\mathcal {F}}$
is, of course, meaningless).
The goal of this section is to show that if the p-adic L-function does not vanish at
![]() $\mathbf {x}$
then the Selmer group
$\mathbf {x}$
then the Selmer group
 $\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
is trivial. The strategy is to combine Propositions 7.1.4 and 7.2.2 by comparing the Panchishkin and relaxed local conditions. In particular, we must show that the hypothesis in Proposition 7.1.4 is satisfied. Unfortunately this is not true in general and fails when
$\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
is trivial. The strategy is to combine Propositions 7.1.4 and 7.2.2 by comparing the Panchishkin and relaxed local conditions. In particular, we must show that the hypothesis in Proposition 7.1.4 is satisfied. Unfortunately this is not true in general and fails when
![]() $\overline {M}_{\mathbf {x}}$
has a “local zero”, i.e., the local Euler factor of
$\overline {M}_{\mathbf {x}}$
has a “local zero”, i.e., the local Euler factor of
![]() $\overline {M}_{\mathbf {x}}$
at p vanishes at
$\overline {M}_{\mathbf {x}}$
at p vanishes at
![]() $s = 1$
. Therefore, we impose the following hypothesis on
$s = 1$
. Therefore, we impose the following hypothesis on
![]() $\overline {M}_{\mathbf {x}}$
:
$\overline {M}_{\mathbf {x}}$
:
-
(NLZ) None of the products
are equal to $$\begin{align*}\{ \alpha_{\mathcal{F}_{k_1}} \alpha_{g}, \quad \alpha_{\mathcal{F}_{k_1}} \beta_{g}, \quad \alpha_{\mathcal{F}_{k_1}}^{-1} \varepsilon_{\mathcal{F}_{k_1}}(p) \alpha_{g}, \quad \alpha_{\mathcal{F}_{k_1}}^{-1} \varepsilon_{\mathcal{F}_{k_1}}(p) \beta_{g} \} \end{align*}$$
$$\begin{align*}\{ \alpha_{\mathcal{F}_{k_1}} \alpha_{g}, \quad \alpha_{\mathcal{F}_{k_1}} \beta_{g}, \quad \alpha_{\mathcal{F}_{k_1}}^{-1} \varepsilon_{\mathcal{F}_{k_1}}(p) \alpha_{g}, \quad \alpha_{\mathcal{F}_{k_1}}^{-1} \varepsilon_{\mathcal{F}_{k_1}}(p) \beta_{g} \} \end{align*}$$
 $p^j$
for some integer j (recall that
$p^j$
for some integer j (recall that
 $\mathbf {x} = (k_1, k^{\prime }, \eta )$
).
$\mathbf {x} = (k_1, k^{\prime }, \eta )$
).
Remark 7.3.1 The (NLZ) hypothesis is an open condition, i.e., if it holds at the point
![]() $\mathbf {x,}$
then it also holds for all specialisations in an open neighbourhood of
$\mathbf {x,}$
then it also holds for all specialisations in an open neighbourhood of
![]() $\mathbf {x}$
. In particular, if
$\mathbf {x}$
. In particular, if
![]() $\mathcal {F}$
is a Coleman family passing through a p-stabilisation of f defined over an affinoid subdomain
$\mathcal {F}$
is a Coleman family passing through a p-stabilisation of f defined over an affinoid subdomain
![]() $V_1 \subset \mathcal {W}_E$
, and if the (NLZ) hypothesis holds for f and g, i.e., none of the products
$V_1 \subset \mathcal {W}_E$
, and if the (NLZ) hypothesis holds for f and g, i.e., none of the products
are equal to a power of p, then we can shrink
![]() $V_1$
so that the (NLZ) hypothesis holds for all specialisations of
$V_1$
so that the (NLZ) hypothesis holds for all specialisations of
![]() $\overline {M}$
at
$\overline {M}$
at
![]() $\mathbf {x} = (k_1, k^{\prime }, \eta ) \in V_1 \times \{k^{\prime }\} \times \mathcal {W}$
.
$\mathbf {x} = (k_1, k^{\prime }, \eta ) \in V_1 \times \{k^{\prime }\} \times \mathcal {W}$
.
The second ingredient to proving the vanishing result is to apply the “Euler system machine” to the representation
![]() $\overline {M}_{\mathbf {x}}$
. To be able to apply this we need to assume the following “Big Image” hypothesis.
$\overline {M}_{\mathbf {x}}$
. To be able to apply this we need to assume the following “Big Image” hypothesis.
-
(BI) There exists an element
 $\sigma \in \operatorname {\mathrm {Gal}}(\bar {\mathbb {Q}}/\mathbb {Q}(\mu _{p^{\infty }}))$
such that
$\sigma \in \operatorname {\mathrm {Gal}}(\bar {\mathbb {Q}}/\mathbb {Q}(\mu _{p^{\infty }}))$
such that
 $\overline {M}_{\mathbf {x}}/(\sigma - 1)\overline {M}_{\mathbf {x}}$
is one-dimensional (over E).
$\overline {M}_{\mathbf {x}}/(\sigma - 1)\overline {M}_{\mathbf {x}}$
is one-dimensional (over E).
Remark 7.3.2 It turns out that for the “Big Image” hypothesis to hold, we only need to assume that the image of the mod p representation of
![]() $\overline {M}_{\mathbf {x}}$
is sufficiently large, and this is almost always the case provided that
$\overline {M}_{\mathbf {x}}$
is sufficiently large, and this is almost always the case provided that
![]() ${\mathcal {F}}_{k_1}$
and g are not of CM type and
${\mathcal {F}}_{k_1}$
and g are not of CM type and
![]() ${\mathcal {F}}_{k_1}$
is not Galois conjugate to a twist of g. In particular, since the mod p representation of a Coleman family is locally constant, this implies that the “Big Image” hypothesis will hold in an open neighbourhood of the point
${\mathcal {F}}_{k_1}$
is not Galois conjugate to a twist of g. In particular, since the mod p representation of a Coleman family is locally constant, this implies that the “Big Image” hypothesis will hold in an open neighbourhood of the point
![]() $\mathbf {x}$
. We provide justifications for this in the appendix (§A).
$\mathbf {x}$
. We provide justifications for this in the appendix (§A).
Under these two assumptions, we have the following vanishing result.
Theorem 7.3.3 Keeping the same notation at the start of Section 7.2, assume that the (NLZ) and (BI) hypotheses hold. If
![]() $L_p(\mathcal {F}_{k_1}, g, 1+\eta ) \neq 0,$
then
$L_p(\mathcal {F}_{k_1}, g, 1+\eta ) \neq 0,$
then
 $\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}}) = 0$
.
$\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}}) = 0$
.
Proof Consider the local conditions
![]() $\Delta = \Delta _{\mathrm {rel}}$
and
$\Delta = \Delta _{\mathrm {rel}}$
and
![]() $\Delta ^{\prime } = \Delta _f$
and suppose for the moment that, as in the statement of Proposition 7.1.4, the map
$\Delta ^{\prime } = \Delta _f$
and suppose for the moment that, as in the statement of Proposition 7.1.4, the map
![]() $\xi $
is surjective. Then there is an injective map
$\xi $
is surjective. Then there is an injective map
 $$\begin{align*}\widetilde{\operatorname{H}}_f^{2}(\mathbb{Q}, \overline{M}_{\mathbf{x}}) \hookrightarrow \widetilde{\operatorname{H}}_{\mathrm{rel}}^{2}(\mathbb{Q}, \overline{M}_{\mathbf{x}}), \end{align*}$$
$$\begin{align*}\widetilde{\operatorname{H}}_f^{2}(\mathbb{Q}, \overline{M}_{\mathbf{x}}) \hookrightarrow \widetilde{\operatorname{H}}_{\mathrm{rel}}^{2}(\mathbb{Q}, \overline{M}_{\mathbf{x}}), \end{align*}$$
so it is enough to show that
 $\widetilde {\operatorname {H}}_{\mathrm {rel}}^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}}) = 0$
.
$\widetilde {\operatorname {H}}_{\mathrm {rel}}^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}}) = 0$
.
Let
![]() $\overline {T}_{\mathbf {x}}$
be a Galois stable lattice inside
$\overline {T}_{\mathbf {x}}$
be a Galois stable lattice inside
![]() $\overline {M}_{\mathbf {x}}$
and set
$\overline {M}_{\mathbf {x}}$
and set
 $A = \overline {M}_{\mathbf {x}}^*(1)/\overline {T}_{\mathbf {x}}^*(1)$
. Then by the duality of the relaxed and strict local conditions, we see that
$A = \overline {M}_{\mathbf {x}}^*(1)/\overline {T}_{\mathbf {x}}^*(1)$
. Then by the duality of the relaxed and strict local conditions, we see that
 $\widetilde {\operatorname {H}}_{\mathrm {rel}}^{2}(\mathbb {Q}, \overline {T}_{\mathbf {x}})^{\vee } := \operatorname {Hom}_{\mathcal {O}_E}(\widetilde {\operatorname {H}}_{\mathrm {rel}}^{2}(\mathbb {Q}, \overline {T}_{\mathbf {x}}), E/\mathcal {O}_E)$
is equal to
$\widetilde {\operatorname {H}}_{\mathrm {rel}}^{2}(\mathbb {Q}, \overline {T}_{\mathbf {x}})^{\vee } := \operatorname {Hom}_{\mathcal {O}_E}(\widetilde {\operatorname {H}}_{\mathrm {rel}}^{2}(\mathbb {Q}, \overline {T}_{\mathbf {x}}), E/\mathcal {O}_E)$
is equal to
 $\widetilde {\operatorname {H}}^1_{\mathrm {str}}(\mathbb {Q}, A)$
(see [Reference NekovářNek06] for more details). Furthermore, since
$\widetilde {\operatorname {H}}^1_{\mathrm {str}}(\mathbb {Q}, A)$
(see [Reference NekovářNek06] for more details). Furthermore, since
 $\widetilde {\operatorname {H}}_{\mathrm {rel}}^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}}) = \widetilde {\operatorname {H}}_{\mathrm {rel}}^{2}(\mathbb {Q}, \overline {T}_{\mathbf {x}})[1/\varpi ]$
, where
$\widetilde {\operatorname {H}}_{\mathrm {rel}}^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}}) = \widetilde {\operatorname {H}}_{\mathrm {rel}}^{2}(\mathbb {Q}, \overline {T}_{\mathbf {x}})[1/\varpi ]$
, where
![]() $\varpi $
is a uniformiser for
$\varpi $
is a uniformiser for
![]() $\mathcal {O}_E$
, it is enough to show
$\mathcal {O}_E$
, it is enough to show
 $\widetilde {\operatorname {H}}^1_{\mathrm {str}}(\mathbb {Q}, A)$
is finite.
$\widetilde {\operatorname {H}}^1_{\mathrm {str}}(\mathbb {Q}, A)$
is finite.
Recall that
![]() $\{c^{\alpha }_m\}$
forms an Euler system for
$\{c^{\alpha }_m\}$
forms an Euler system for
![]() $\overline {T}_{\mathbf {x}}$
and the bottom class
$\overline {T}_{\mathbf {x}}$
and the bottom class
![]() $c^{\alpha }_1$
is non-zero because
$c^{\alpha }_1$
is non-zero because
![]() $L_p(\mathcal {F}_{k_1}, g, 1+\eta )$
is non-zero. Coupling this with the (BI) assumption, we can apply [Reference RubinRub00, Theorem 2.2.3] and conclude that
$L_p(\mathcal {F}_{k_1}, g, 1+\eta )$
is non-zero. Coupling this with the (BI) assumption, we can apply [Reference RubinRub00, Theorem 2.2.3] and conclude that
 $\widetilde {\operatorname {H}}^1_{\mathrm {str}}(\mathbb {Q}, A)$
is finite. Indeed, by comparing the strict and relaxed local conditions, the group
$\widetilde {\operatorname {H}}^1_{\mathrm {str}}(\mathbb {Q}, A)$
is finite. Indeed, by comparing the strict and relaxed local conditions, the group
 $\widetilde {\operatorname {H}}^1_{\mathrm {str}}(\mathbb {Q}, A)$
differs from the strict Selmer group in op.cit. by the group
$\widetilde {\operatorname {H}}^1_{\mathrm {str}}(\mathbb {Q}, A)$
differs from the strict Selmer group in op.cit. by the group
 $\operatorname {H}^0(\mathbb {Q}_p, A)$
, which is finite because
$\operatorname {H}^0(\mathbb {Q}_p, A)$
, which is finite because
 $\operatorname {H}^0(\mathbb {Q}_p, \overline {M}_{\mathbf {x}}^*(1)) = 0$
. So we are left to show the map
$\operatorname {H}^0(\mathbb {Q}_p, \overline {M}_{\mathbf {x}}^*(1)) = 0$
. So we are left to show the map
![]() $\xi $
is surjective.
$\xi $
is surjective.
The mapping cone
![]() $Q_p$
is precisely the same thing as the image of the Herr complex
$Q_p$
is precisely the same thing as the image of the Herr complex
 $C_{\varphi , \gamma }^{\bullet }(D^-_{\mathbf {x}})$
and by the local Euler characteristic formula (Proposition 5.3.2) for
$C_{\varphi , \gamma }^{\bullet }(D^-_{\mathbf {x}})$
and by the local Euler characteristic formula (Proposition 5.3.2) for
![]() $(\varphi , \Gamma )$
-modules, we have
$(\varphi , \Gamma )$
-modules, we have
![]() $\chi (D^-_{\mathbf {x}}) = -2$
. Therefore, if we show that
$\chi (D^-_{\mathbf {x}}) = -2$
. Therefore, if we show that
 $\operatorname {H}^0(\mathbb {Q}_p, D^-_{\mathbf {x}})$
and
$\operatorname {H}^0(\mathbb {Q}_p, D^-_{\mathbf {x}})$
and
 $\operatorname {H}^2(\mathbb {Q}_p, D^-_{\mathbf {x}})$
both vanish, then this would imply that
$\operatorname {H}^2(\mathbb {Q}_p, D^-_{\mathbf {x}})$
both vanish, then this would imply that
 $\operatorname {H}^1(\mathbb {Q}_p, D^-_{\mathbf {x}})$
is two-dimensional. Combining this with Proposition 7.2.2(ii), this would imply that the map
$\operatorname {H}^1(\mathbb {Q}_p, D^-_{\mathbf {x}})$
is two-dimensional. Combining this with Proposition 7.2.2(ii), this would imply that the map
![]() $\xi $
is surjective.
$\xi $
is surjective.
By duality, we have
 $\operatorname {H}^2(\mathbb {Q}_p, D^-_{\mathbf {x}}) \cong \operatorname {H}^0(\mathbb {Q}_p, (D^-_{\mathbf {x}})^*(1))^*$
and from the explicit description of the triangulation ([Reference Loeffler and ZerbesLZ16, Theorem 6.3.2]), we have the following short exact sequences:
$\operatorname {H}^2(\mathbb {Q}_p, D^-_{\mathbf {x}}) \cong \operatorname {H}^0(\mathbb {Q}_p, (D^-_{\mathbf {x}})^*(1))^*$
and from the explicit description of the triangulation ([Reference Loeffler and ZerbesLZ16, Theorem 6.3.2]), we have the following short exact sequences:
 $$ \begin{align*} 0 &\longrightarrow [\mathbf{B}^{\dagger}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E](\alpha_{\mathcal{F}_{k_1}}^{-1}\alpha_g \varepsilon_g(p)^{-1})(\chi_{\mathrm{cycl}}^{1+k^{\prime}}\cdot\eta^{-1}) \longrightarrow D^-_{\mathbf{x}}\\[-3pt]& \longrightarrow [\mathbf{B}^{\dagger}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E](\alpha_{\mathcal{F}_{k_1}}^{-1}\alpha_g^{-1})(\eta^{-1}) \longrightarrow 0, \\[-3pt] 0 &\longrightarrow [\mathbf{B}^{\dagger}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E](\alpha_{\mathcal{F}_{k_1}}\alpha_g)(\chi_{\mathrm{cycl}} \cdot \eta) \longrightarrow (D^-_{\mathbf{x}})^*(1) \\[-3pt]&\longrightarrow [\mathbf{B}^{\dagger}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E](\alpha_{\mathcal{F}_{k_1}}\alpha_g^{-1} \varepsilon_g(p))(\chi_{\mathrm{cycl}}^{-k^{\prime}} \cdot \eta) \longrightarrow 0, \nonumber \end{align*} $$
$$ \begin{align*} 0 &\longrightarrow [\mathbf{B}^{\dagger}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E](\alpha_{\mathcal{F}_{k_1}}^{-1}\alpha_g \varepsilon_g(p)^{-1})(\chi_{\mathrm{cycl}}^{1+k^{\prime}}\cdot\eta^{-1}) \longrightarrow D^-_{\mathbf{x}}\\[-3pt]& \longrightarrow [\mathbf{B}^{\dagger}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E](\alpha_{\mathcal{F}_{k_1}}^{-1}\alpha_g^{-1})(\eta^{-1}) \longrightarrow 0, \\[-3pt] 0 &\longrightarrow [\mathbf{B}^{\dagger}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E](\alpha_{\mathcal{F}_{k_1}}\alpha_g)(\chi_{\mathrm{cycl}} \cdot \eta) \longrightarrow (D^-_{\mathbf{x}})^*(1) \\[-3pt]&\longrightarrow [\mathbf{B}^{\dagger}_{\mathrm{rig}, \mathbb{Q}_p} \widehat{\otimes} E](\alpha_{\mathcal{F}_{k_1}}\alpha_g^{-1} \varepsilon_g(p))(\chi_{\mathrm{cycl}}^{-k^{\prime}} \cdot \eta) \longrightarrow 0, \nonumber \end{align*} $$
where we denote by
 $[\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E](\lambda )(\omega )$
the one-dimensional
$[\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E](\lambda )(\omega )$
the one-dimensional
![]() $(\varphi , \Gamma )$
-module over
$(\varphi , \Gamma )$
-module over
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E$
with a basis e such that
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E$
with a basis e such that
![]() $\varphi (e) = \lambda e$
and
$\varphi (e) = \lambda e$
and
![]() $\gamma \cdot e = \omega (\gamma )e$
for all
$\gamma \cdot e = \omega (\gamma )e$
for all
![]() $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
From the above sequences, one sees that if either
 $\operatorname {H}^0(\mathbb {Q}_p, D^-_{\mathbf {x}})$
or
$\operatorname {H}^0(\mathbb {Q}_p, D^-_{\mathbf {x}})$
or
 $\operatorname {H}^2(\mathbb {Q}_p, D^-_{\mathbf {x}})$
did not vanish then this would contradict the (NLZ) hypothesis. ▪
$\operatorname {H}^2(\mathbb {Q}_p, D^-_{\mathbf {x}})$
did not vanish then this would contradict the (NLZ) hypothesis. ▪
Remark 7.3.4 To prove the above theorem, we only needed to assume that the two products
![]() $\alpha _{{\mathcal {F}}_{k_1}} \alpha _g$
and
$\alpha _{{\mathcal {F}}_{k_1}} \alpha _g$
and
![]() $\alpha _{{\mathcal {F}}_{k_1}} \beta _g$
are not equal to a power of p. However, in the following section, we will relate
$\alpha _{{\mathcal {F}}_{k_1}} \beta _g$
are not equal to a power of p. However, in the following section, we will relate
 $\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
to the usual Bloch–Kato Selmer group at classical specialisations, and for this, we will need to assume that all four products in the statement of (NLZ) are not equal to a power of p.
$\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}})$
to the usual Bloch–Kato Selmer group at classical specialisations, and for this, we will need to assume that all four products in the statement of (NLZ) are not equal to a power of p.
Furthermore, for most non-classical specialisations, we do not have to impose a (NLZ) condition. Indeed by [Reference ColmezCol08, Proposition 2.1 and Théorème 2.9], it is often the case that
![]() $\operatorname {H}^1(D^-_{\mathbf {x}})$
is automatically two-dimensional unless the weights in
$\operatorname {H}^1(D^-_{\mathbf {x}})$
is automatically two-dimensional unless the weights in
![]() $\mathbf {x}$
are classical.
$\mathbf {x}$
are classical.
7.4 Relation to the Bloch–Kato Selmer Group
Theorem 7.3.3 is a generalisation of [Reference Loeffler and ZerbesLZ16, Theorem 8.2.1] to non-classical specialisations. Indeed, suppose that
![]() $k_1$
and
$k_1$
and
 $\eta = \chi _{\mathrm {cycl}}^j$
are classical, and we have
$\eta = \chi _{\mathrm {cycl}}^j$
are classical, and we have
![]() $k^{\prime } +1 \leq j \leq k_1$
. Then by the duality property of Selmer complexes and the fact that the Panchishkin condition is self-dual, we have
$k^{\prime } +1 \leq j \leq k_1$
. Then by the duality property of Selmer complexes and the fact that the Panchishkin condition is self-dual, we have
 $\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}})^* \cong \widetilde {\operatorname {H}}_f^{1}(\mathbb {Q}, \overline {M}_{\mathbf {x}}^*(1))$
. But by the (NLZ) hypothesis, we have the following equalities:
$\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}})^* \cong \widetilde {\operatorname {H}}_f^{1}(\mathbb {Q}, \overline {M}_{\mathbf {x}}^*(1))$
. But by the (NLZ) hypothesis, we have the following equalities:
-
•
 $\operatorname {H}^0(\mathbb {Q}_p, (D^+_{\mathbf {x}})^*(1)) = 0$
,
$\operatorname {H}^0(\mathbb {Q}_p, (D^+_{\mathbf {x}})^*(1)) = 0$
, -
•
 $\operatorname {H}^0(\mathbb {Q}_p, D_{\mathbf {x}}/D^+_{\mathbf {x}}) = \operatorname {H}^0(\mathbb {Q}_p, D^-_{\mathbf {x}}) = 0$
.
$\operatorname {H}^0(\mathbb {Q}_p, D_{\mathbf {x}}/D^+_{\mathbf {x}}) = \operatorname {H}^0(\mathbb {Q}_p, D^-_{\mathbf {x}}) = 0$
.
Indeed, by the conditions on the Hodge–Tate weights, we have
-
•
 $\operatorname {H}^0(\mathbb {Q}_p, (D^+_{\mathbf {x}})^*(1)) = (D^+_{\mathbf {x}})^*(1)_{\mathrm {cris}}^{\varphi = 1}$
,
$\operatorname {H}^0(\mathbb {Q}_p, (D^+_{\mathbf {x}})^*(1)) = (D^+_{\mathbf {x}})^*(1)_{\mathrm {cris}}^{\varphi = 1}$
, -
•
 $\operatorname {H}^0(\mathbb {Q}_p, D_{\mathbf {x}}/D^+_{\mathbf {x}}) = (D_{\mathbf {x}}/D^+_{\mathbf {x}})_{\mathrm {cris}}^{\varphi = 1}$
.
$\operatorname {H}^0(\mathbb {Q}_p, D_{\mathbf {x}}/D^+_{\mathbf {x}}) = (D_{\mathbf {x}}/D^+_{\mathbf {x}})_{\mathrm {cris}}^{\varphi = 1}$
.
But
![]() $\varphi $
has eigenvalues
$\varphi $
has eigenvalues
 $\{p^{-1-j}\beta _{\mathcal {F}_{k_1}}\alpha _g, p^{-1-j}\beta _{\mathcal {F}_{k_1}} \beta _g \}$
and
$\{p^{-1-j}\beta _{\mathcal {F}_{k_1}}\alpha _g, p^{-1-j}\beta _{\mathcal {F}_{k_1}} \beta _g \}$
and
 $\{p^j \alpha _{\mathcal {F}_{k_1}}^{-1}\alpha _g^{-1}, p^j \alpha _{\mathcal {F}_{k_1}}^{-1}\beta _g^{-1} \}$
on
$\{p^j \alpha _{\mathcal {F}_{k_1}}^{-1}\alpha _g^{-1}, p^j \alpha _{\mathcal {F}_{k_1}}^{-1}\beta _g^{-1} \}$
on
![]() $(D^+_{\mathbf {x}})^*(1)_{\mathrm {cris}}$
and
$(D^+_{\mathbf {x}})^*(1)_{\mathrm {cris}}$
and
![]() $(D_{\mathbf {x}}/D^+_{\mathbf {x}})_{\mathrm {cris}},$
respectively, and these products can never be equal to
$(D_{\mathbf {x}}/D^+_{\mathbf {x}})_{\mathrm {cris}},$
respectively, and these products can never be equal to
![]() $1$
by the (NLZ) hypothesis. Therefore, by [Reference PottharstPot13, Proposition 3.7], we see that
$1$
by the (NLZ) hypothesis. Therefore, by [Reference PottharstPot13, Proposition 3.7], we see that
 $$\begin{align*}\widetilde{\operatorname{H}}_f^{1}(\mathbb{Q}, \overline{M}_{\mathbf{x}}^*(1)) = \operatorname{H}^1_f(\mathbb{Q}, \overline{M}_{\mathbf{x}}^*(1)), \end{align*}$$
$$\begin{align*}\widetilde{\operatorname{H}}_f^{1}(\mathbb{Q}, \overline{M}_{\mathbf{x}}^*(1)) = \operatorname{H}^1_f(\mathbb{Q}, \overline{M}_{\mathbf{x}}^*(1)), \end{align*}$$
where the latter is the Bloch–Kato Selmer group. This recovers Theorem 8.3.1 in [Reference Loeffler and ZerbesLZ16]. In fact the proof of Theorem 7.3.3 is modelled on the proof in loc. cit..
8 The Selmer sheaf
In the previous section, we showed that (under certain hypotheses) if the specialisation of
![]() $L_p$
is non-zero, then
$L_p$
is non-zero, then
 $\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}}) = 0$
. It turns out that we can package together all of these cohomology groups into a coherent sheaf over
$\widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M}_{\mathbf {x}}) = 0$
. It turns out that we can package together all of these cohomology groups into a coherent sheaf over
![]() $V_1 \times V_2 \times \mathcal {W}$
using the machinery of Selmer complexes. We follow closely the construction in [Reference PottharstPot13].
$V_1 \times V_2 \times \mathcal {W}$
using the machinery of Selmer complexes. We follow closely the construction in [Reference PottharstPot13].
8.1 Assumptions
Recall that
![]() $\mathcal {W}/\mathbb {Q}_p$
denotes the rigid analytic space parameterising continuous characters
$\mathcal {W}/\mathbb {Q}_p$
denotes the rigid analytic space parameterising continuous characters
 $\Gamma = \operatorname {\mathrm {Gal}}(\mathbb {Q}(\mu _{p^{\infty }})/\mathbb {Q}) \to \mathbb {C}_p^{\times }$
. Let
$\Gamma = \operatorname {\mathrm {Gal}}(\mathbb {Q}(\mu _{p^{\infty }})/\mathbb {Q}) \to \mathbb {C}_p^{\times }$
. Let
![]() $V_1$
and
$V_1$
and
![]() $V_2$
be two affinoid subdomains of
$V_2$
be two affinoid subdomains of
![]() $(\mathcal {W})_E$
and set
$(\mathcal {W})_E$
and set
![]() $X = V_1 \times V_2 \times \mathcal {W}$
. Then X has admissible cover
$X = V_1 \times V_2 \times \mathcal {W}$
. Then X has admissible cover
![]() $\mathcal {U} = (Y_n)_{n \geq 1}$
given by
$\mathcal {U} = (Y_n)_{n \geq 1}$
given by
where
![]() $\mathcal {W}_n$
is the open affinoid subdomain of
$\mathcal {W}_n$
is the open affinoid subdomain of
![]() $\mathcal {W}$
parameterising all characters
$\mathcal {W}$
parameterising all characters
![]() $\eta $
that satisfy
$\eta $
that satisfy
 $|\eta (\gamma )^{p^{n-1}} - 1|_p \leq p^{-1}$
, where
$|\eta (\gamma )^{p^{n-1}} - 1|_p \leq p^{-1}$
, where
![]() $\gamma $
is a topological generator of
$\gamma $
is a topological generator of
![]() $\Gamma /\Gamma _{\mathrm {tors}}$
. The restriction maps
$\Gamma /\Gamma _{\mathrm {tors}}$
. The restriction maps
![]() $\mathcal {O}(Y_{n+1}) \to \mathcal {O}(Y_n)$
have dense image. Hence, X is a quasi-Stein space.
$\mathcal {O}(Y_{n+1}) \to \mathcal {O}(Y_n)$
have dense image. Hence, X is a quasi-Stein space.
Let
![]() $A_{\infty } := \mathcal {O}(X)$
,
$A_{\infty } := \mathcal {O}(X)$
,
![]() $A_n := \mathcal {O}(Y_n)$
. Note that for all
$A_n := \mathcal {O}(Y_n)$
. Note that for all
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $A_n$
is flat over
$A_n$
is flat over
![]() $A_{\infty }$
.
$A_{\infty }$
.
Let
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
be two Coleman families over
$\mathcal {G}$
be two Coleman families over
![]() $V_1$
and
$V_1$
and
![]() $V_2$
passing through p-stabilisations of f and
$V_2$
passing through p-stabilisations of f and
![]() $g,$
respectively, and let M denote the representation
$g,$
respectively, and let M denote the representation
![]() $M(\mathcal {F})^* \widehat {\otimes } M(\mathcal {G})^*$
. Fix a Galois stable lattice T inside M, i.e., a free rank four
$M(\mathcal {F})^* \widehat {\otimes } M(\mathcal {G})^*$
. Fix a Galois stable lattice T inside M, i.e., a free rank four
![]() $\mathcal {O}(V_1 \times V_2)^\circ $
-submodule that is stable under the action of
$\mathcal {O}(V_1 \times V_2)^\circ $
-submodule that is stable under the action of
![]() $G_{\mathbb {Q}}$
.
$G_{\mathbb {Q}}$
.
Let
![]() $\overline {M} = D^{\mathrm {la}}(\Gamma , M)$
denote the cyclotomic deformation of M, and for any
$\overline {M} = D^{\mathrm {la}}(\Gamma , M)$
denote the cyclotomic deformation of M, and for any
![]() $n \geq 1$
we set
$n \geq 1$
we set
![]() $M_n = M(-\kappa _n)$
, where
$M_n = M(-\kappa _n)$
, where
![]() $(-\kappa _n)$
denotes the twist by the inverse of the universal character of
$(-\kappa _n)$
denotes the twist by the inverse of the universal character of
![]() $\mathcal {W}_n$
. Then we also obtain a Galois stable lattice
$\mathcal {W}_n$
. Then we also obtain a Galois stable lattice
![]() $T_n := T(-\kappa _n)$
inside
$T_n := T(-\kappa _n)$
inside
![]() $M_n$
.
$M_n$
.
Let
![]() $\Sigma $
be a finite set of places containing
$\Sigma $
be a finite set of places containing
![]() $p, \infty $
and all primes where M ramifies. Then
$p, \infty $
and all primes where M ramifies. Then
![]() $\overline {M}$
is a family of
$\overline {M}$
is a family of
![]() $G_{\Sigma }$
-representations over the space X and we place ourselves in situation (4) in [Reference PottharstPot13, §1.5].
$G_{\Sigma }$
-representations over the space X and we place ourselves in situation (4) in [Reference PottharstPot13, §1.5].
By an
![]() $\mathcal {O}_{\mathcal {U}}$
-module we mean a compatible system of
$\mathcal {O}_{\mathcal {U}}$
-module we mean a compatible system of
![]() $A_n$
-modules. Let
$A_n$
-modules. Let
![]() $\mathbf {R}\Gamma _{\mathrm {cont}}(G_{\Sigma }, \overline {M})$
denote the image of the complex of continuous cochains
$\mathbf {R}\Gamma _{\mathrm {cont}}(G_{\Sigma }, \overline {M})$
denote the image of the complex of continuous cochains
![]() $C^{\bullet }_{\mathrm {cont}}(G_{\Sigma }, \overline {M})$
in the derived category of
$C^{\bullet }_{\mathrm {cont}}(G_{\Sigma }, \overline {M})$
in the derived category of
![]() $\mathcal {O}_{\mathcal {U}}$
-modules. Explicitly,
$\mathcal {O}_{\mathcal {U}}$
-modules. Explicitly,
![]() $C^{\bullet }_{\mathrm {cont}}(G_{\Sigma }, \overline {M})$
is defined by the rule
$C^{\bullet }_{\mathrm {cont}}(G_{\Sigma }, \overline {M})$
is defined by the rule
where we note that
![]() $M_n = \Gamma (Y_n, \overline {M})$
.
$M_n = \Gamma (Y_n, \overline {M})$
.
Lemma 8.1.1
-
(i)
 $\mathbf {R}\Gamma _{\mathrm {cont}}(G_{\Sigma }, \overline {M})$
is a perfect complex, in the sense that it is quasi-isomorphic to a complex
$\mathbf {R}\Gamma _{\mathrm {cont}}(G_{\Sigma }, \overline {M})$
is a perfect complex, in the sense that it is quasi-isomorphic to a complex
 $D^{\bullet }$
, concentrated in finitely many degrees, such that
$D^{\bullet }$
, concentrated in finitely many degrees, such that
 $\Gamma (Y_n, D^{\bullet })$
is a finite projective
$\Gamma (Y_n, D^{\bullet })$
is a finite projective
 $A_n$
-module.
$A_n$
-module. -
(ii) Let
 $\iota _n: Y_n \hookrightarrow X$
denote the inclusion. Then
$\iota _n: Y_n \hookrightarrow X$
denote the inclusion. Then  $$\begin{align*}\mathbf{L}\iota_n^* \mathbf{R}\Gamma_{\mathrm{cont}}(G_{\Sigma}, \overline{M}) \cong \mathbf{R}\Gamma_{\mathrm{cont}}(G_{\Sigma}, M_n). \end{align*}$$
$$\begin{align*}\mathbf{L}\iota_n^* \mathbf{R}\Gamma_{\mathrm{cont}}(G_{\Sigma}, \overline{M}) \cong \mathbf{R}\Gamma_{\mathrm{cont}}(G_{\Sigma}, M_n). \end{align*}$$
Proof For the first part, this follows from the discussion in [Reference PottharstPot13, §1.2], and the second part is just Theorem 1.6 in op.cit. ▪
Since X is a quasi-Stein space, we also have an alternative description of
![]() $\mathbf {R}\Gamma _{\mathrm {cont}}(G_{\Sigma }, \overline {M})$
, namely as the image of the complex
$\mathbf {R}\Gamma _{\mathrm {cont}}(G_{\Sigma }, \overline {M})$
, namely as the image of the complex
 $\varprojlim _n C^{\bullet }_{\mathrm {cont}}(G_{\Sigma }, M_n)$
in the derived category of
$\varprojlim _n C^{\bullet }_{\mathrm {cont}}(G_{\Sigma }, M_n)$
in the derived category of
![]() $A_{\infty }$
-modules. By the above lemma and Kiehl’s theorem,
$A_{\infty }$
-modules. By the above lemma and Kiehl’s theorem,
![]() $\mathbf {R}\Gamma _{\mathrm {cont}}(G_{\Sigma }, \overline {M})$
is quasi-isomorphic to a complex of locally free (of finite rank)
$\mathbf {R}\Gamma _{\mathrm {cont}}(G_{\Sigma }, \overline {M})$
is quasi-isomorphic to a complex of locally free (of finite rank)
![]() $\mathcal {O}_X$
-modules, so in particular, its cohomology groups are coherent sheaves on X. Furthermore, since X is quasi-Stein, a coherent sheaf on X is determined by its global sections, so we will often use these two descriptions interchangeably. We say an
$\mathcal {O}_X$
-modules, so in particular, its cohomology groups are coherent sheaves on X. Furthermore, since X is quasi-Stein, a coherent sheaf on X is determined by its global sections, so we will often use these two descriptions interchangeably. We say an
![]() $A_{\infty }$
-module is coadmissible if it arises as the global sections of a coherent sheaf on X.
$A_{\infty }$
-module is coadmissible if it arises as the global sections of a coherent sheaf on X.
As in §7.1, for a collection
![]() $\Delta = \{\Delta _v\}_{v \in \Sigma }$
of local conditions
$\Delta = \{\Delta _v\}_{v \in \Sigma }$
of local conditions
 $$\begin{align*}\begin{aligned} \Delta_v \xrightarrow{\iota_v} \mathbf{R}\Gamma_{\mathrm{cont}}({G_v}, {\overline{M}}) & \; \; \; \; & \Delta_v \in \mathbf{D}_{\mathrm{ft}}^{[0, 2]}(A_{\infty}\text{-Mod}), \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \Delta_v \xrightarrow{\iota_v} \mathbf{R}\Gamma_{\mathrm{cont}}({G_v}, {\overline{M}}) & \; \; \; \; & \Delta_v \in \mathbf{D}_{\mathrm{ft}}^{[0, 2]}(A_{\infty}\text{-Mod}), \end{aligned} \end{align*}$$
where
 $\mathbf {D}_{\mathrm {ft}}^{[0, 2]}(A_{\infty }\text {-Mod})$
is the derived category of complexes of
$\mathbf {D}_{\mathrm {ft}}^{[0, 2]}(A_{\infty }\text {-Mod})$
is the derived category of complexes of
![]() $A_{\infty }$
-modules concentrated in degrees
$A_{\infty }$
-modules concentrated in degrees
![]() $[0, 2]$
whose cohomology groups are coadmissible, we can construct the Selmer complex
$[0, 2]$
whose cohomology groups are coadmissible, we can construct the Selmer complex
![]() ${\mathbf {R}\widetilde {\Gamma }({G_{\Sigma }}, \overline {M}; {\Delta })}$
which is an object in the derived category of
${\mathbf {R}\widetilde {\Gamma }({G_{\Sigma }}, \overline {M}; {\Delta })}$
which is an object in the derived category of
![]() $A_{\infty }$
-modules, concentrated in degrees
$A_{\infty }$
-modules, concentrated in degrees
![]() $[0, 3]$
, whose cohomology groups are coadmissible (see [Reference PottharstPot13, §1.5]).
$[0, 3]$
, whose cohomology groups are coadmissible (see [Reference PottharstPot13, §1.5]).
We impose the following assumptions on f and g. Let
![]() $x_0 = (k, k^{\prime }, 0) \in X$
, where
$x_0 = (k, k^{\prime }, 0) \in X$
, where
![]() $k+2$
and
$k+2$
and
![]() $k^{\prime }+2$
are the weights of f and
$k^{\prime }+2$
are the weights of f and
![]() $g,$
respectively, and choose n such that
$g,$
respectively, and choose n such that
![]() $x_0 \in Y_n$
.
$x_0 \in Y_n$
.
-
(a) (Flatness of inertia) If
 $\mathfrak {p}_0$
denotes the prime ideal of
$\mathfrak {p}_0$
denotes the prime ideal of
 $A_n^\circ $
corresponding to the point
$A_n^\circ $
corresponding to the point
 $x_0$
, then we let
$x_0$
, then we let
 $A_{n, \mathfrak {p}_0}^\circ $
and
$A_{n, \mathfrak {p}_0}^\circ $
and
 $T_{n, \mathfrak {p}_0}$
denote the localisations of
$T_{n, \mathfrak {p}_0}$
denote the localisations of
 $A_n^\circ $
and
$A_n^\circ $
and
 $T_n$
at
$T_n$
at
 $\mathfrak {p}_0$
. For every place
$\mathfrak {p}_0$
. For every place
 $v \in \Sigma $
not equal to p, we let
$v \in \Sigma $
not equal to p, we let
 $I_v$
denote the inertia subgroup of the fixed decomposition group at v. Then we assume that
$I_v$
denote the inertia subgroup of the fixed decomposition group at v. Then we assume that
 $T_{n, \mathfrak {p}_0}^{I_v}$
is a flat
$T_{n, \mathfrak {p}_0}^{I_v}$
is a flat
 $A_n^\circ $
-module, for all
$A_n^\circ $
-module, for all
 $v \in \Sigma \backslash \{p\}$
. Since
$v \in \Sigma \backslash \{p\}$
. Since
 $A_n^\circ $
is a commutative Noetherian local ring, this is equivalent to
$A_n^\circ $
is a commutative Noetherian local ring, this is equivalent to
 $T_{n, \mathfrak {p}_0}^{I_v}$
being free.In particular, by generic flatness this implies that there exists a Zariski open subset U of
$T_{n, \mathfrak {p}_0}^{I_v}$
being free.In particular, by generic flatness this implies that there exists a Zariski open subset U of
 $Y_n$
containing
$Y_n$
containing
 $x_0$
such that
$x_0$
such that
 $(T_n)_U^{I_v}$
is a flat
$(T_n)_U^{I_v}$
is a flat
 $\mathcal {O}(U)^\circ $
-module.
$\mathcal {O}(U)^\circ $
-module. -
(b) (Minimally ramified) Let
 $\mathfrak {m}_0$
denote the maximal ideal in
$\mathfrak {m}_0$
denote the maximal ideal in
 $A_n^{\circ }$
containing a uniformiser
$A_n^{\circ }$
containing a uniformiser
 $\varpi $
of E and the prime ideal
$\varpi $
of E and the prime ideal
 $\mathfrak {p}_0$
corresponding to
$\mathfrak {p}_0$
corresponding to
 $x_0$
. Then
$x_0$
. Then
 $A_n^{\circ }/\mathfrak {m}_0 = k$
, where k is the residue field of
$A_n^{\circ }/\mathfrak {m}_0 = k$
, where k is the residue field of
 $\mathcal {O}_E$
, and the “mod p representation” of
$\mathcal {O}_E$
, and the “mod p representation” of
 $T_n$
at the point
$T_n$
at the point
 $x_0$
is defined to be where ss stands for semi-simplification and the tensor product is via the map
$x_0$
is defined to be where ss stands for semi-simplification and the tensor product is via the map $$\begin{align*}T_{\bar{\mathbb{F}}_p} := (T_n \otimes_{A_n^{\circ}} \bar{\mathbb{F}}_p)^{\mathrm{ss}}, \end{align*}$$
$$\begin{align*}T_{\bar{\mathbb{F}}_p} := (T_n \otimes_{A_n^{\circ}} \bar{\mathbb{F}}_p)^{\mathrm{ss}}, \end{align*}$$
 $A_n^{\circ } \to A_n^{\circ }/\mathfrak {m}_0 \hookrightarrow \bar {\mathbb {F}}_p$
.
$A_n^{\circ } \to A_n^{\circ }/\mathfrak {m}_0 \hookrightarrow \bar {\mathbb {F}}_p$
.
We assume that we have the following equality
for all $$\begin{align*}\operatorname{dim}_k T_n^{I_v}/\mathfrak{m}_0 = \operatorname{dim}_{\bar{\mathbb{F}}_p} (T_{\bar{\mathbb{F}}_p})^{I_v}, \end{align*}$$
$$\begin{align*}\operatorname{dim}_k T_n^{I_v}/\mathfrak{m}_0 = \operatorname{dim}_{\bar{\mathbb{F}}_p} (T_{\bar{\mathbb{F}}_p})^{I_v}, \end{align*}$$
 $v \in \Sigma \backslash \{p\}$
. In other words, f and g are not congruent to forms of a lower level.
$v \in \Sigma \backslash \{p\}$
. In other words, f and g are not congruent to forms of a lower level.
Remark 8.1.2 We give examples of pairs of modular forms satisfying the above assumptions in the appendix (§1.2).
Lemma 8.1.3 Assume that conditions (a) and (b) above hold. Then, after possibly shrinking
![]() $V_1$
and
$V_1$
and
![]() $V_2$
, we have
$V_2$
, we have
-
• for all
 $n \geq 1$
and
$n \geq 1$
and
 $v \in \Sigma \backslash \{p\}$
,
$v \in \Sigma \backslash \{p\}$
,
 $T_n^{I_v}$
is a flat
$T_n^{I_v}$
is a flat
 $A_n^\circ $
-module;
$A_n^\circ $
-module; -
• let
 $\eta \in \mathcal {W}_n$
be a closed point and let
$\eta \in \mathcal {W}_n$
be a closed point and let
 $\mathbf {x} = (k, k^{\prime }, \eta )$
(so
$\mathbf {x} = (k, k^{\prime }, \eta )$
(so
 $\mathbf {x} \in Y_n$
). If
$\mathbf {x} \in Y_n$
). If
 $\mathfrak {m}$
denotes the maximal ideal of
$\mathfrak {m}$
denotes the maximal ideal of
 $A_n^\circ $
containing
$A_n^\circ $
containing
 $\varpi $
and the prime ideal associated with
$\varpi $
and the prime ideal associated with
 $\mathbf {x}$
, then for all
$\mathbf {x}$
, then for all
 $v \in \Sigma \backslash \{p\},$
where
$v \in \Sigma \backslash \{p\},$
where $$\begin{align*}\operatorname{dim}_k T_n^{I_v}/\mathfrak{m} = \operatorname{dim}_{\bar{\mathbb{F}}_p} \left( (T_n \otimes_{A_n^\circ} \bar{\mathbb{F}}_p )^{\mathrm{ss}} \right)^{I_v}, \end{align*}$$
$$\begin{align*}\operatorname{dim}_k T_n^{I_v}/\mathfrak{m} = \operatorname{dim}_{\bar{\mathbb{F}}_p} \left( (T_n \otimes_{A_n^\circ} \bar{\mathbb{F}}_p )^{\mathrm{ss}} \right)^{I_v}, \end{align*}$$
 $k = A_n^\circ /\mathfrak {m}$
and the tensor product in the right-hand side is via the map
$k = A_n^\circ /\mathfrak {m}$
and the tensor product in the right-hand side is via the map
 $A_n^\circ \to k \hookrightarrow \bar {\mathbb {F}}_p$
.
$A_n^\circ \to k \hookrightarrow \bar {\mathbb {F}}_p$
.
Proof By shrinking
![]() $V_1$
and
$V_1$
and
![]() $V_2$
if necessary, we can assume that the set U in (a) above contains
$V_2$
if necessary, we can assume that the set U in (a) above contains
![]() $V_1 \times V_2 \times U^{\prime }$
for some open affinoid
$V_1 \times V_2 \times U^{\prime }$
for some open affinoid
![]() $U^{\prime } \subset \mathcal {W}_n$
. The lemma then follows from the fact that any character of
$U^{\prime } \subset \mathcal {W}_n$
. The lemma then follows from the fact that any character of
![]() $\Gamma $
restricted to
$\Gamma $
restricted to
![]() $I_v$
is trivial, for
$I_v$
is trivial, for
![]() $v \neq p$
. ▪
$v \neq p$
. ▪
8.2 The Selmer Sheaf
We first fix some notation. If
![]() $D_1$
and
$D_1$
and
![]() $D_2$
are rank two
$D_2$
are rank two
![]() $(\varphi , \Gamma )$
-modules over
$(\varphi , \Gamma )$
-modules over
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E$
equipped with a triangulation
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } E$
equipped with a triangulation
where
![]() $\mathscr {F}^{\pm }D_i$
are rank one
$\mathscr {F}^{\pm }D_i$
are rank one
![]() $(\varphi , \Gamma )$
-modules, then we set
$(\varphi , \Gamma )$
-modules, then we set
for
![]() $\diamondsuit , \clubsuit \in \{+, -, o \}$
, where
$\diamondsuit , \clubsuit \in \{+, -, o \}$
, where
![]() $D = D_1 \widehat {\otimes } D_2$
.
$D = D_1 \widehat {\otimes } D_2$
.
Let
 $\mathbf {D}^{\dagger }_{\mathrm {rig}}(M)$
denote the
$\mathbf {D}^{\dagger }_{\mathrm {rig}}(M)$
denote the
![]() $(\varphi , \Gamma )$
-module over
$(\varphi , \Gamma )$
-module over
 $\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } A$
associated with the representation M, where
$\mathbf {B}^{\dagger }_{\mathrm {rig}, \mathbb {Q}_p} \widehat {\otimes } A$
associated with the representation M, where
![]() $A = \mathcal {O}(V_1) \widehat {\otimes } \mathcal {O}(V_2)$
. As in Section 6.2, assuming
$A = \mathcal {O}(V_1) \widehat {\otimes } \mathcal {O}(V_2)$
. As in Section 6.2, assuming
![]() $V_1$
and
$V_1$
and
![]() $V_2$
are small enough, we have two possible triangulations for
$V_2$
are small enough, we have two possible triangulations for
 $\mathbf {D}^{\dagger }_{\mathrm {rig}}(M)$
, namely,
$\mathbf {D}^{\dagger }_{\mathrm {rig}}(M)$
, namely,
 $$\begin{align*}\{0\} \subset \mathscr{F}^{+ +}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \subset \mathscr{F}^{+ o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \subset \mathscr{F}^{+ o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) + \mathscr{F}^{o +}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \subset \mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \end{align*}$$
$$\begin{align*}\{0\} \subset \mathscr{F}^{+ +}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \subset \mathscr{F}^{+ o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \subset \mathscr{F}^{+ o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) + \mathscr{F}^{o +}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \subset \mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \end{align*}$$
and
 $$\begin{align*}\{0\} \subset \mathscr{F}^{+ +}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \subset \mathscr{F}^{o +}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \subset \mathscr{F}^{+ o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) + \mathscr{F}^{o +}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \subset \mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \end{align*}$$
$$\begin{align*}\{0\} \subset \mathscr{F}^{+ +}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \subset \mathscr{F}^{o +}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \subset \mathscr{F}^{+ o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) + \mathscr{F}^{o +}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \subset \mathbf{D}^{\dagger}_{\mathrm{rig}}(M) \end{align*}$$
differing only by the middle term in the filtration.
Let
![]() $\mathbf {x} = (k_1,\, k_2,\, j)$
be a classical point in X satisfying
$\mathbf {x} = (k_1,\, k_2,\, j)$
be a classical point in X satisfying
![]() $0 \leq k_2 < k_1$
and denote the specialisation of
$0 \leq k_2 < k_1$
and denote the specialisation of
![]() $\overline {M}$
at
$\overline {M}$
at
![]() $\mathbf {x}$
by
$\mathbf {x}$
by
![]() $\overline {M}_{\mathbf {x}}$
. The Hodge–Tate weights of
$\overline {M}_{\mathbf {x}}$
. The Hodge–Tate weights of
![]() $\overline {M}_{\mathbf {x}}$
are
$\overline {M}_{\mathbf {x}}$
are
We want to define a sheaf that interpolates the classical Bloch–Kato Selmer group; the correct local condition that we will need to take will therefore depend on the range we want to interpolate over. For example:
-
• Suppose that
 $\mathbf {x}$
lies in the geometric range, i.e., one has
$\mathbf {x}$
lies in the geometric range, i.e., one has
 $0 \leq j \leq \operatorname {min}\{k_1, k_2\}$
. Then one can take the local condition at p to be the cohomology of
$0 \leq j \leq \operatorname {min}\{k_1, k_2\}$
. Then one can take the local condition at p to be the cohomology of
 $\mathscr {F}^{+o} + \mathscr {F}^{o+}$
. Indeed, this specialises to a Panchishkin submodule at
$\mathscr {F}^{+o} + \mathscr {F}^{o+}$
. Indeed, this specialises to a Panchishkin submodule at
 $\mathbf {x}$
(recall that a Panchishkin submodule of a de Rham
$\mathbf {x}$
(recall that a Panchishkin submodule of a de Rham
 $(\varphi , \Gamma )$
-module D is a submodule
$(\varphi , \Gamma )$
-module D is a submodule
 $D^+$
such that
$D^+$
such that
 $D^+$
(resp.
$D^+$
(resp.
 $D/D^+$
) has positive (resp. non-negative) Hodge–Tate weights).
$D/D^+$
) has positive (resp. non-negative) Hodge–Tate weights). -
• Suppose that
 $\mathbf {x}$
lies in the critical range, i.e., one has
$\mathbf {x}$
lies in the critical range, i.e., one has
 $k_2+1 \leq j \leq k_1$
. Then one can take the local condition at p to be the cohomology of
$k_2+1 \leq j \leq k_1$
. Then one can take the local condition at p to be the cohomology of
 $\mathscr {F}^{+o}$
.
$\mathscr {F}^{+o}$
.
In this paper, we are interested in interpolating in the critical range, since it is precisely the range where the p-adic L-function interpolates (critical) values of the global L-function.
We denote by
 $\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M})$
the family of
$\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M})$
the family of
![]() $(\varphi , \Gamma )$
-modules over X satisfying
$(\varphi , \Gamma )$
-modules over X satisfying
 $\Gamma (Y_n, \mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M})) = \mathbf {D}^{\dagger }_{\mathrm {rig}}(M_n)$
. This comes equipped with the triangulations
$\Gamma (Y_n, \mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M})) = \mathbf {D}^{\dagger }_{\mathrm {rig}}(M_n)$
. This comes equipped with the triangulations
 $\mathscr {F}^{\diamondsuit \clubsuit }\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M})$
defined previously, i.e.,
$\mathscr {F}^{\diamondsuit \clubsuit }\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M})$
defined previously, i.e.,
 $\mathscr {F}^{\diamondsuit \clubsuit }\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M})$
is the family of
$\mathscr {F}^{\diamondsuit \clubsuit }\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M})$
is the family of
![]() $(\varphi , \Gamma )$
-modules satisfying
$(\varphi , \Gamma )$
-modules satisfying
 $$\begin{align*}\Gamma(Y_n, \mathscr{F}^{\diamondsuit \clubsuit}\mathbf{D}^{\dagger}_{\mathrm{rig}}(\overline{M})) = \mathscr{F}^{\diamondsuit \clubsuit}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M)(-\kappa_n), \end{align*}$$
$$\begin{align*}\Gamma(Y_n, \mathscr{F}^{\diamondsuit \clubsuit}\mathbf{D}^{\dagger}_{\mathrm{rig}}(\overline{M})) = \mathscr{F}^{\diamondsuit \clubsuit}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M)(-\kappa_n), \end{align*}$$
where
![]() $(-\kappa _n)$
denotes the twist by the inverse of the universal character of
$(-\kappa _n)$
denotes the twist by the inverse of the universal character of
![]() $\mathcal {W}_n$
.
$\mathcal {W}_n$
.
We consider the following set of local conditions
![]() $\Delta = \{\Delta _v\}_{v \in \Sigma }$
where
$\Delta = \{\Delta _v\}_{v \in \Sigma }$
where
-
• for
 $v \neq p$
,
$v \neq p$
,
 $\Delta _v$
is the unramified condition, i.e.
$\Delta _v$
is the unramified condition, i.e.
 $\Delta _v$
is the complex
$\Delta _v$
is the complex  $$\begin{align*}\Delta_v := \mathbf{R}\Gamma_{\mathrm{cont}}(G_v/I_v, \overline{M}^{I_v}) \rightarrow \mathbf{R}\Gamma_{\mathrm{cont}}({G_v}, {\overline{M}}); \end{align*}$$
$$\begin{align*}\Delta_v := \mathbf{R}\Gamma_{\mathrm{cont}}(G_v/I_v, \overline{M}^{I_v}) \rightarrow \mathbf{R}\Gamma_{\mathrm{cont}}({G_v}, {\overline{M}}); \end{align*}$$
-
• for
 $v = p$
we take
$v = p$
we take
 $\Delta _p$
to be the Panchishkin local condition given by where
$\Delta _p$
to be the Panchishkin local condition given by where $$\begin{align*}\Delta_p := \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \mathscr{F}^{+ o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(\overline{M})) \rightarrow \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \mathbf{D}^{\dagger}_{\mathrm{rig}}(\overline{M})) \cong \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \overline{M}), \end{align*}$$
$$\begin{align*}\Delta_p := \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \mathscr{F}^{+ o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(\overline{M})) \rightarrow \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \mathbf{D}^{\dagger}_{\mathrm{rig}}(\overline{M})) \cong \mathbf{R}\Gamma_{\mathrm{cont}}(G_p, \overline{M}), \end{align*}$$
 $\mathbf {R}\Gamma _{\mathrm {cont}}(G_p, \mathscr {F}^{+ o}\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}))$
denotes the image of the family of Herr complexes
$\mathbf {R}\Gamma _{\mathrm {cont}}(G_p, \mathscr {F}^{+ o}\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}))$
denotes the image of the family of Herr complexes
 $\mathcal {C}_{\varphi , \gamma }^{\bullet }(\mathscr {F}^{+ o}\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}))$
in the derived category of
$\mathcal {C}_{\varphi , \gamma }^{\bullet }(\mathscr {F}^{+ o}\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}))$
in the derived category of
 $\mathcal {O}_{\mathcal {U}}$
-modules, as defined in §5.3.
$\mathcal {O}_{\mathcal {U}}$
-modules, as defined in §5.3.
By Lemma 8.1.3, if
![]() $V_1$
and
$V_1$
and
![]() $V_2$
are small enough (which we will assume from now on), then the above local conditions lie in
$V_2$
are small enough (which we will assume from now on), then the above local conditions lie in
 $\mathbf {D}_{\mathrm {ft}}^{[0, 2]}(A_{\infty }\mathrm {-Mod})$
so we can talk about the corresponding Selmer complex.
$\mathbf {D}_{\mathrm {ft}}^{[0, 2]}(A_{\infty }\mathrm {-Mod})$
so we can talk about the corresponding Selmer complex.
Remark 8.2.1 We have defined the local conditions in terms of
![]() $\mathcal {O}_{\mathcal {U}}$
-modules, but this is equivalent to specifying local conditions in terms of coadmissible modules by [Reference PottharstPot13, Theorem 1.13] and the discussion preceding it.
$\mathcal {O}_{\mathcal {U}}$
-modules, but this is equivalent to specifying local conditions in terms of coadmissible modules by [Reference PottharstPot13, Theorem 1.13] and the discussion preceding it.
Definition 8.2.2 Let
 $\mathbf {R}\widetilde {\Gamma }_f(G_{\Sigma }, \overline {M})$
denote the Selmer complex associated to
$\mathbf {R}\widetilde {\Gamma }_f(G_{\Sigma }, \overline {M})$
denote the Selmer complex associated to
![]() $\overline {M}$
and the local conditions
$\overline {M}$
and the local conditions
![]() $\Delta $
, with cohomology groups denoted by
$\Delta $
, with cohomology groups denoted by
 $\widetilde {H}_f^i(\mathbb {Q}, \overline {M})$
.
$\widetilde {H}_f^i(\mathbb {Q}, \overline {M})$
.
As explained in the paragraph preceding Proposition 7.1.3, the groups
 $\widetilde {H}_f^i(\mathbb {Q}, \overline {M})$
are coherent sheaves on X and satisfy
$\widetilde {H}_f^i(\mathbb {Q}, \overline {M})$
are coherent sheaves on X and satisfy
 $\widetilde {H}_f^i(\mathbb {Q}, \overline {M}) = 0$
for
$\widetilde {H}_f^i(\mathbb {Q}, \overline {M}) = 0$
for
![]() $i \neq 0, 1, 2, 3$
.
$i \neq 0, 1, 2, 3$
.
Theorem 8.2.3 We can take
![]() $V_1$
and
$V_1$
and
![]() $V_2$
small enough such that the following hold:
$V_2$
small enough such that the following hold:
-
(i) For each
 $n \geq 0$
,
$n \geq 0$
,
 $A_n$
is a flat
$A_n$
is a flat
 $A_{\infty }$
-module and the natural map is an isomorphism, where
$A_{\infty }$
-module and the natural map is an isomorphism, where $$\begin{align*}\mathbf{R}\widetilde{\Gamma}_f(G_{\Sigma}, \overline{M}) \otimes_{A_{\infty}} A_n \rightarrow \mathbf{R}\widetilde{\Gamma}_f(G_{\Sigma}, M_n) \end{align*}$$
$$\begin{align*}\mathbf{R}\widetilde{\Gamma}_f(G_{\Sigma}, \overline{M}) \otimes_{A_{\infty}} A_n \rightarrow \mathbf{R}\widetilde{\Gamma}_f(G_{\Sigma}, M_n) \end{align*}$$
 $\mathbf {R}\widetilde {\Gamma }_f(G_{\Sigma }, M_n)$
denotes the Selmer complex associated to
$\mathbf {R}\widetilde {\Gamma }_f(G_{\Sigma }, M_n)$
denotes the Selmer complex associated to
 $M_n = \Gamma (Y_n, \overline {M})$
with unramified local conditions at
$M_n = \Gamma (Y_n, \overline {M})$
with unramified local conditions at
 $v \neq p$
and the Panchishkin condition
$v \neq p$
and the Panchishkin condition
 $\mathcal {C}_{\varphi , \gamma }^{\bullet }(\mathscr {F}^{+ o}\mathbf {D}^{\dagger }_{\mathrm {rig}}(M_n))$
at p.
$\mathcal {C}_{\varphi , \gamma }^{\bullet }(\mathscr {F}^{+ o}\mathbf {D}^{\dagger }_{\mathrm {rig}}(M_n))$
at p.
-
(ii) Let
 $\mathbf {x}$
be an
$\mathbf {x}$
be an
 $E^{\prime }$
-valued point in
$E^{\prime }$
-valued point in
 $Y_n$
and v a prime in
$Y_n$
and v a prime in
 $\Sigma $
not equal to p. Then the natural map is an isomorphism and hence we have an isomorphism
$\Sigma $
not equal to p. Then the natural map is an isomorphism and hence we have an isomorphism $$\begin{align*}(M_n^{I_v})_{\mathbf{x}} \rightarrow (\overline{M}_{\mathbf{x}})^{I_v} \end{align*}$$
where
$$\begin{align*}(M_n^{I_v})_{\mathbf{x}} \rightarrow (\overline{M}_{\mathbf{x}})^{I_v} \end{align*}$$
where $$\begin{align*}\mathbf{R}\widetilde{\Gamma}_f(G_{\Sigma}, M_n) \otimes^{\mathbf{L}}_{A_n, \mathbf{x}} E^{\prime} \cong \mathbf{R}\widetilde{\Gamma}_f(G_{\Sigma}, \overline{M}_{\mathbf{x}}) \end{align*}$$
$$\begin{align*}\mathbf{R}\widetilde{\Gamma}_f(G_{\Sigma}, M_n) \otimes^{\mathbf{L}}_{A_n, \mathbf{x}} E^{\prime} \cong \mathbf{R}\widetilde{\Gamma}_f(G_{\Sigma}, \overline{M}_{\mathbf{x}}) \end{align*}$$
 $\mathbf {R}\widetilde {\Gamma }_f(G_{\Sigma }, \overline {M}_{\mathbf {x}})$
is the Selmer complex associated to
$\mathbf {R}\widetilde {\Gamma }_f(G_{\Sigma }, \overline {M}_{\mathbf {x}})$
is the Selmer complex associated to
 $\overline {M}_{\mathbf {x}}$
with unramified local conditions away from p and the Panchishkin condition
$\overline {M}_{\mathbf {x}}$
with unramified local conditions away from p and the Panchishkin condition
 $\mathcal {C}_{\varphi , \gamma }^{\bullet }(\mathscr {F}^{+ o}\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}_{\mathbf {x}}))$
at p (compare with the definition in Section 7.2).
$\mathcal {C}_{\varphi , \gamma }^{\bullet }(\mathscr {F}^{+ o}\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}_{\mathbf {x}}))$
at p (compare with the definition in Section 7.2).
We will prove this theorem in the next section. Combining this with Theorem 7.3.3, we obtain the following corollary.
Corollary 8.2.4 Let f and g be two modular forms as in Section 1.1 and let
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
be Coleman families over
$\mathcal {G}$
be Coleman families over
![]() $V_1$
and
$V_1$
and
![]() $V_2$
passing through p-stabilisations of f and g respectively. Let
$V_2$
passing through p-stabilisations of f and g respectively. Let
![]() $\overline {M}$
denote the cyclotomic deformation of
$\overline {M}$
denote the cyclotomic deformation of
![]() $M(\mathcal {F})^* \widehat {\otimes } M(\mathcal {G})^*$
as above, and let
$M(\mathcal {F})^* \widehat {\otimes } M(\mathcal {G})^*$
as above, and let
 $\mathcal {S} = \widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M})$
denote the coherent sheaf obtained as the second cohomology group of the Selmer complex attached to
$\mathcal {S} = \widetilde {\operatorname {H}}_f^{2}(\mathbb {Q}, \overline {M})$
denote the coherent sheaf obtained as the second cohomology group of the Selmer complex attached to
![]() $\overline {M}$
.
$\overline {M}$
.
-
(i) Suppose that the (NLZ) hypothesis holds for f and g and that the “flatness of inertia” and “minimally ramified” hypotheses hold for
 $\overline {M}$
and
$\overline {M}$
and
 $x_0 = (k, k^{\prime }, 0)$
. Then, shrinking
$x_0 = (k, k^{\prime }, 0)$
. Then, shrinking
 $V_1$
and
$V_1$
and
 $V_2$
if necessary, for all
$V_2$
if necessary, for all
 $\mathbf {x} = (k_1,\, k_2,\, j) \in X$
with
$\mathbf {x} = (k_1,\, k_2,\, j) \in X$
with
 $k_1,\, k_2,\, j$
integers satisfying
$k_1,\, k_2,\, j$
integers satisfying
 $1 \leq k_2 + 1 \leq j \leq k_1$
, the specialisation of
$1 \leq k_2 + 1 \leq j \leq k_1$
, the specialisation of
 $\mathcal {S}$
satisfies where the right-hand side is the (dual of the) Bloch–Kato Selmer group.
$\mathcal {S}$
satisfies where the right-hand side is the (dual of the) Bloch–Kato Selmer group. $$\begin{align*}\mathcal{S}_{\mathbf{x}} \cong \operatorname{H}^1_f(\mathbb{Q}, [M(\mathcal{F}_{k_1}) \otimes M(\mathcal{G}_{k_2})](1+j) )^* \end{align*}$$
$$\begin{align*}\mathcal{S}_{\mathbf{x}} \cong \operatorname{H}^1_f(\mathbb{Q}, [M(\mathcal{F}_{k_1}) \otimes M(\mathcal{G}_{k_2})](1+j) )^* \end{align*}$$
-
(ii) (Theorem A) Suppose that the (NLZ) hypothesis holds for f and g, and that the (BI), “flatness of inertia” and “minimally ramified” hypotheses hold for
 $\overline {M}$
and
$\overline {M}$
and
 $x_0 = (k , k^{\prime }, 0)$
. Then, shrinking
$x_0 = (k , k^{\prime }, 0)$
. Then, shrinking
 $V_1$
if necessary, we have the following inclusion where “
$V_1$
if necessary, we have the following inclusion where “ $$\begin{align*}\operatorname{supp}\mathcal{S}_{k^{\prime}} \subset \{L_p = 0\}, \end{align*}$$
$$\begin{align*}\operatorname{supp}\mathcal{S}_{k^{\prime}} \subset \{L_p = 0\}, \end{align*}$$
 $\,\operatorname {supp}$
” denotes the support of a sheaf,
$\,\operatorname {supp}$
” denotes the support of a sheaf,
 $L_p$
is the three-variable p-adic L-function, and
$L_p$
is the three-variable p-adic L-function, and
 $\mathcal {S}_{k^{\prime }}$
denotes the specialisation of
$\mathcal {S}_{k^{\prime }}$
denotes the specialisation of
 $\mathcal {S}$
at
$\mathcal {S}$
at
 $k^{\prime }$
in the second variable.
$k^{\prime }$
in the second variable.
Remark 8.2.5 If we take
![]() $V_2$
to be small enough, then the conclusion of Corollary 8.2.4(ii) holds for all classical specialisations in
$V_2$
to be small enough, then the conclusion of Corollary 8.2.4(ii) holds for all classical specialisations in
![]() $V_2$
(provided that the same hypotheses also hold). More precisely, if
$V_2$
(provided that the same hypotheses also hold). More precisely, if
![]() $k_2$
is a classical weight in
$k_2$
is a classical weight in
![]() $V_2$
, then
$V_2$
, then
or to put it another way, the “slices” of
![]() $\mathcal {S}$
in the second variable are controlled by the p-adic L-function
$\mathcal {S}$
in the second variable are controlled by the p-adic L-function
![]() $L_p$
provided that the weight in the second variable is classical.
$L_p$
provided that the weight in the second variable is classical.
The reason for this is as follows. By [Reference BellaïcheBel12, Lemma 2.7], if
![]() $V_2$
is small enough, then any classical specialisation of
$V_2$
is small enough, then any classical specialisation of
![]() $\mathcal {G}$
is the p-stabilisation of a new eigenform h of level
$\mathcal {G}$
is the p-stabilisation of a new eigenform h of level
![]() $\Gamma _1(N_2)$
, and both p-stabilisations of h are noble. This allows us to prove the analogue of Theorem 7.3.3 for the pair
$\Gamma _1(N_2)$
, and both p-stabilisations of h are noble. This allows us to prove the analogue of Theorem 7.3.3 for the pair
![]() $f, h$
of modular forms (instead of f and g). Here we are crucially using the fact that
$f, h$
of modular forms (instead of f and g). Here we are crucially using the fact that
![]() $k \neq k^{\prime }$
.
$k \neq k^{\prime }$
.
Proof Let
![]() $\mathbf {x} \in X$
be an
$\mathbf {x} \in X$
be an
![]() $E^{\prime }$
-valued point. By Theorem 8.2.3, we have the following isomorphism
$E^{\prime }$
-valued point. By Theorem 8.2.3, we have the following isomorphism
 $$\begin{align*}\mathbf{R}\widetilde{\Gamma}_f(G_{\Sigma}, \overline{M}) \otimes_{A_{\infty}, x}^{\mathbf{L}} E^{\prime} \xrightarrow{\sim} \mathbf{R}\widetilde{\Gamma}_f(G_{\Sigma}, \overline{M}_{\mathbf{x}}), \end{align*}$$
$$\begin{align*}\mathbf{R}\widetilde{\Gamma}_f(G_{\Sigma}, \overline{M}) \otimes_{A_{\infty}, x}^{\mathbf{L}} E^{\prime} \xrightarrow{\sim} \mathbf{R}\widetilde{\Gamma}_f(G_{\Sigma}, \overline{M}_{\mathbf{x}}), \end{align*}$$
which gives the following Tor-spectral sequence
 $$\begin{align*}E^{i, j}_2 \colon \operatorname{Tor}_{-i}^{A_{\infty}}\big(\widetilde{H}_f^j(\mathbb{Q}, \overline{M}), E^{\prime} \big) \Longrightarrow \widetilde{H}_f^{i+j}(\mathbb{Q}, \overline{M}_{\mathbf{x}}). \end{align*}$$
$$\begin{align*}E^{i, j}_2 \colon \operatorname{Tor}_{-i}^{A_{\infty}}\big(\widetilde{H}_f^j(\mathbb{Q}, \overline{M}), E^{\prime} \big) \Longrightarrow \widetilde{H}_f^{i+j}(\mathbb{Q}, \overline{M}_{\mathbf{x}}). \end{align*}$$
If
![]() $\mathbf {x}$
does not lie in the support of
$\mathbf {x}$
does not lie in the support of
 $\widetilde {H}_f^3(\mathbb {Q}, \overline {M})$
, then, since
$\widetilde {H}_f^3(\mathbb {Q}, \overline {M})$
, then, since
 $\widetilde {H}_f^i(\mathbb {Q}, \overline {M}) = 0$
for
$\widetilde {H}_f^i(\mathbb {Q}, \overline {M}) = 0$
for
![]() $i \geq 4$
, we see that
$i \geq 4$
, we see that
 $$\begin{align*}\widetilde{H}_f^2(\mathbb{Q}, \overline{M}) \otimes_{A_{\infty}, x} E^{\prime} \cong \widetilde{H}_f^2(\mathbb{Q}, \overline{M}_{\mathbf{x}}). \end{align*}$$
$$\begin{align*}\widetilde{H}_f^2(\mathbb{Q}, \overline{M}) \otimes_{A_{\infty}, x} E^{\prime} \cong \widetilde{H}_f^2(\mathbb{Q}, \overline{M}_{\mathbf{x}}). \end{align*}$$
If
![]() $\mathbf {x} = (k_1,\, k_2,\, j)$
where
$\mathbf {x} = (k_1,\, k_2,\, j)$
where
![]() $k_1,\, k_2,\, j$
are integers satisfying
$k_1,\, k_2,\, j$
are integers satisfying
![]() $1 \leq k_2 + 1 \leq j \leq k_1$
, then by the discussion in Section 7.4, we see that the right-hand side of the above isomorphism is isomorphic to the dual of the Bloch–Kato Selmer group for the representation
$1 \leq k_2 + 1 \leq j \leq k_1$
, then by the discussion in Section 7.4, we see that the right-hand side of the above isomorphism is isomorphic to the dual of the Bloch–Kato Selmer group for the representation
 $\overline {M}_{\mathbf {x}}^*(1)$
. This proves part (i) assuming that
$\overline {M}_{\mathbf {x}}^*(1)$
. This proves part (i) assuming that
![]() $\mathbf {x}$
does not lie in the support of
$\mathbf {x}$
does not lie in the support of
 $\widetilde {H}_f^3(\mathbb {Q}, \overline {M})$
.
$\widetilde {H}_f^3(\mathbb {Q}, \overline {M})$
.
Now let
![]() $\mathbf {x} = (k_1, k^{\prime }, \eta ) \in X$
with
$\mathbf {x} = (k_1, k^{\prime }, \eta ) \in X$
with
![]() $k_1$
and
$k_1$
and
![]() $\eta $
not necessarily classical. Assume that
$\eta $
not necessarily classical. Assume that
![]() $L_p(\mathbf {x}) \neq 0$
. Then we can apply Theorem 7.3.3, which says that
$L_p(\mathbf {x}) \neq 0$
. Then we can apply Theorem 7.3.3, which says that
 $\widetilde {H}_f^2(\mathbb {Q}, \overline {M}_{\mathbf {x}}) = 0$
.
$\widetilde {H}_f^2(\mathbb {Q}, \overline {M}_{\mathbf {x}}) = 0$
.
Let
![]() $\mathfrak {m}$
denote the kernel of the map
$\mathfrak {m}$
denote the kernel of the map
![]() $A_{\infty } \to E^{\prime }$
and let
$A_{\infty } \to E^{\prime }$
and let
![]() $A_{\infty , \mathfrak {m}}$
denote the localisation of
$A_{\infty , \mathfrak {m}}$
denote the localisation of
![]() $A_{\infty }$
at
$A_{\infty }$
at
![]() $\mathfrak {m}$
. Since
$\mathfrak {m}$
. Since
 $\mathcal {S} = \widetilde {H}_f^2(\mathbb {Q}, \overline {M})$
is a coadmissible module,
$\mathcal {S} = \widetilde {H}_f^2(\mathbb {Q}, \overline {M})$
is a coadmissible module,
is a finitely generated
![]() $A_{\infty , \mathfrak {m}}$
-module; so by Nakayama’s lemma we must have
$A_{\infty , \mathfrak {m}}$
-module; so by Nakayama’s lemma we must have
![]() $\mathcal {S} \otimes _{A_{\infty }} A_{\infty , \mathfrak {m}} = 0$
. But this precisely means that
$\mathcal {S} \otimes _{A_{\infty }} A_{\infty , \mathfrak {m}} = 0$
. But this precisely means that
![]() $\mathbf {x}$
is not in the support of
$\mathbf {x}$
is not in the support of
![]() $\mathcal {S}$
(because the set of points where the stalk of a coherent sheaf is non-zero is automatically closed). This proves part (ii) for the points that don’t lie in the support of
$\mathcal {S}$
(because the set of points where the stalk of a coherent sheaf is non-zero is automatically closed). This proves part (ii) for the points that don’t lie in the support of
 $\widetilde {\operatorname {H}}_f^{3}(\mathbb {Q}, \overline {M})$
.
$\widetilde {\operatorname {H}}_f^{3}(\mathbb {Q}, \overline {M})$
.
But since
![]() $M(\mathcal {F})$
and
$M(\mathcal {F})$
and
![]() $M(\mathcal {G})$
are irreducible, we have
$M(\mathcal {G})$
are irreducible, we have
 $\widetilde {H}_f^3(\mathbb {Q}, \overline {M}) = 0$
. Indeed by duality
$\widetilde {H}_f^3(\mathbb {Q}, \overline {M}) = 0$
. Indeed by duality
 $$\begin{align*}\widetilde{H}_f^3(\mathbb{Q}, M_n)^* \cong \widetilde{H}_f^0(\mathbb{Q}, M_n^*(1)) \subset \operatorname{H}^0(\mathbb{Q}, M_n^*(1)) \end{align*}$$
$$\begin{align*}\widetilde{H}_f^3(\mathbb{Q}, M_n)^* \cong \widetilde{H}_f^0(\mathbb{Q}, M_n^*(1)) \subset \operatorname{H}^0(\mathbb{Q}, M_n^*(1)) \end{align*}$$
and
 $\operatorname {H}^0(\mathbb {Q}, M_n^*(1)) = \operatorname {Hom}_{G_{\mathbb {Q}}}(M(\mathcal {F})^*, M(\mathcal {G})(\kappa _n + 1))$
. If this group is non-zero, then because
$\operatorname {H}^0(\mathbb {Q}, M_n^*(1)) = \operatorname {Hom}_{G_{\mathbb {Q}}}(M(\mathcal {F})^*, M(\mathcal {G})(\kappa _n + 1))$
. If this group is non-zero, then because
![]() $M(\mathcal {F})^*$
and
$M(\mathcal {F})^*$
and
![]() $M(\mathcal {G})(\kappa _n +1)$
are irreducible, they must be isomorphic as representations. But (taking
$M(\mathcal {G})(\kappa _n +1)$
are irreducible, they must be isomorphic as representations. But (taking
![]() $V_1$
and
$V_1$
and
![]() $V_2$
to be small enough) the generalised Hodge–Tate weights of these representations can never be the same (because
$V_2$
to be small enough) the generalised Hodge–Tate weights of these representations can never be the same (because
![]() $k \neq k^{\prime }$
).▪
$k \neq k^{\prime }$
).▪
8.3 Proof of Theorem 8.2.3
We start by proving the following lemma.
Lemma 8.3.1 Suppose that
![]() $V_1$
and
$V_1$
and
![]() $V_2$
are small enough so that
$V_2$
are small enough so that
![]() $T_n^{I_v}$
is a flat
$T_n^{I_v}$
is a flat
![]() $A^{\circ }_n$
-module, and suppose that the “minimally ramified” hypothesis is satisfied. Then for any maximal ideal
$A^{\circ }_n$
-module, and suppose that the “minimally ramified” hypothesis is satisfied. Then for any maximal ideal
![]() $\mathfrak {m}$
in
$\mathfrak {m}$
in
![]() $A_n$
, the natural map
$A_n$
, the natural map
is an isomorphism.
Proof As explained previously (see Lemma 8.1.3 following the “minimally ramified” assumption), the result is invariant under twisting in the third variable, so we may assume that we are working over the space
Shrinking
![]() $V_1$
and
$V_1$
and
![]() $V_2$
if necessary, we can assume that V is an irreducible affinoid space over E. Let R denote its global sections; this is an integral domain. Let
$V_2$
if necessary, we can assume that V is an irreducible affinoid space over E. Let R denote its global sections; this is an integral domain. Let
![]() $I = I_v$
be an inertia group and set
$I = I_v$
be an inertia group and set
![]() $M = M(\mathcal {F})^* \widehat {\otimes } M(\mathcal {G})^*$
, thought of as a representation over R. It is enough to prove that the natural map
$M = M(\mathcal {F})^* \widehat {\otimes } M(\mathcal {G})^*$
, thought of as a representation over R. It is enough to prove that the natural map
is an isomorphism, for all maximal ideals
![]() $\mathfrak {m}$
of R.
$\mathfrak {m}$
of R.
Let
![]() $|\cdot |_E$
denote the norm on E (normalised so that
$|\cdot |_E$
denote the norm on E (normalised so that
![]() $|p|_E = 1/p$
) and for any finite field extension
$|p|_E = 1/p$
) and for any finite field extension
![]() $E^{\prime }$
of E, let
$E^{\prime }$
of E, let
![]() $|\cdot |_{E^{\prime }}$
denote the unique norm on
$|\cdot |_{E^{\prime }}$
denote the unique norm on
![]() $E^{\prime }$
extending
$E^{\prime }$
extending
![]() $|\cdot |_E$
. Since R is a reduced affinoid algebra it comes with a Banach norm given by
$|\cdot |_E$
. Since R is a reduced affinoid algebra it comes with a Banach norm given by
where
![]() $k(\mathfrak {m})$
denotes the residue field of
$k(\mathfrak {m})$
denotes the residue field of
![]() $\mathfrak {m}$
.
$\mathfrak {m}$
.
Let
![]() $R^{\circ }$
denote the unit ball inside R and from now on
$R^{\circ }$
denote the unit ball inside R and from now on
![]() $E^{\prime }$
will denote the residue field of a maximal ideal
$E^{\prime }$
will denote the residue field of a maximal ideal
![]() $\mathfrak {m}$
inside R. If
$\mathfrak {m}$
inside R. If
![]() $R \to E^{\prime }$
is the continuous surjective homomorphism corresponding to
$R \to E^{\prime }$
is the continuous surjective homomorphism corresponding to
![]() $\mathfrak {m}$
then, by the description of
$\mathfrak {m}$
then, by the description of
![]() $\|\cdot \|$
above, we see that
$\|\cdot \|$
above, we see that
![]() $R^{\circ }$
is mapped into the unit ball
$R^{\circ }$
is mapped into the unit ball
![]() $\mathcal {O}_{E^{\prime }}$
inside
$\mathcal {O}_{E^{\prime }}$
inside
![]() $E^{\prime }$
. Let
$E^{\prime }$
. Let
![]() $\mathfrak {p} = \mathfrak {m} \cap R^{\circ }$
. We also let
$\mathfrak {p} = \mathfrak {m} \cap R^{\circ }$
. We also let
![]() $\mathfrak {m}_0$
denote the maximal ideal corresponding to the point
$\mathfrak {m}_0$
denote the maximal ideal corresponding to the point
![]() $(k, k^{\prime }, 0)$
, and let
$(k, k^{\prime }, 0)$
, and let
![]() $\mathfrak {p}_0 = \mathfrak {m}_0 \cap R^{\circ }$
.
$\mathfrak {p}_0 = \mathfrak {m}_0 \cap R^{\circ }$
.
Since
![]() $\mathcal {O}_E$
embeds isometrically into
$\mathcal {O}_E$
embeds isometrically into
![]() $R^{\circ }$
, we have
$R^{\circ }$
, we have
Now
![]() $R^{\circ }/\mathfrak {p}$
is an integral domain with fraction field
$R^{\circ }/\mathfrak {p}$
is an integral domain with fraction field
![]() $E^{\prime }$
, so
$E^{\prime }$
, so
![]() $R^{\circ }/\mathfrak {p}$
is an
$R^{\circ }/\mathfrak {p}$
is an
![]() $\mathcal {O}_E$
-algebra that is finite free of rank
$\mathcal {O}_E$
-algebra that is finite free of rank
![]() $[E^{\prime }:E]$
as an
$[E^{\prime }:E]$
as an
![]() $\mathcal {O}_E$
-module (
$\mathcal {O}_E$
-module (
![]() $R^{\circ }/\mathfrak {p}$
is torsion-free and
$R^{\circ }/\mathfrak {p}$
is torsion-free and
![]() $\mathcal {O}_E$
is a principal ideal domain). Let
$\mathcal {O}_E$
is a principal ideal domain). Let
![]() $\varpi ^{\prime }$
be a uniformiser of
$\varpi ^{\prime }$
be a uniformiser of
![]() $E^{\prime }$
and set
$E^{\prime }$
and set
![]() $J = (\varpi ^{\prime }) \cap R^{\circ }/\mathfrak {p}$
. This corresponds to a maximal ideal of
$J = (\varpi ^{\prime }) \cap R^{\circ }/\mathfrak {p}$
. This corresponds to a maximal ideal of
![]() $R^{\circ },$
which we will denote by
$R^{\circ },$
which we will denote by
![]() $\mathfrak {n}$
.
$\mathfrak {n}$
.
Let k and
![]() $k^{\prime }$
denote the residue fields of
$k^{\prime }$
denote the residue fields of
![]() $\mathcal {O}_E$
and
$\mathcal {O}_E$
and
![]() $\mathcal {O}_{E^{\prime }}$
respectively. Then we have
$\mathcal {O}_{E^{\prime }}$
respectively. Then we have
Take
![]() $T \subset M$
to be a Galois stable
$T \subset M$
to be a Galois stable
![]() $R^{\circ }$
-lattice (which exists by compactness). The representation
$R^{\circ }$
-lattice (which exists by compactness). The representation
![]() $T/\mathfrak {p}T \otimes \mathcal {O}_{E^{\prime }}$
is a Galois stable lattice inside
$T/\mathfrak {p}T \otimes \mathcal {O}_{E^{\prime }}$
is a Galois stable lattice inside
![]() $M/\mathfrak {m}M$
and the “mod p representation” attached to
$M/\mathfrak {m}M$
and the “mod p representation” attached to
![]() $M/\mathfrak {m}M$
is
$M/\mathfrak {m}M$
is
 $$\begin{align*}\left( \left( (T/\mathfrak{p}T \otimes \mathcal{O}_{E^{\prime}}) \otimes \mathcal{O}_{E^{\prime}}/\varpi^{\prime} \right) \otimes \bar{\mathbb{F}}_p \right)^{\mathrm{ss}} = \left( T/\mathfrak{n}T \otimes_{R^{\circ}/\mathfrak{n}} \bar{\mathbb{F}}_p \right)^{\mathrm{ss}}, \end{align*}$$
$$\begin{align*}\left( \left( (T/\mathfrak{p}T \otimes \mathcal{O}_{E^{\prime}}) \otimes \mathcal{O}_{E^{\prime}}/\varpi^{\prime} \right) \otimes \bar{\mathbb{F}}_p \right)^{\mathrm{ss}} = \left( T/\mathfrak{n}T \otimes_{R^{\circ}/\mathfrak{n}} \bar{\mathbb{F}}_p \right)^{\mathrm{ss}}, \end{align*}$$
where ss stands for semi-simplification. Since the “mod p representation” for a Coleman family is constant, we have
 $$\begin{align*}\left( T/\mathfrak{n}T \otimes_{R^{\circ}/\mathfrak{n}} \bar{\mathbb{F}}_p \right)^{\operatorname{ss}} \cong \left( T/\mathfrak{n}_0T \otimes_{R^{\circ}/\mathfrak{n}_0} \bar{\mathbb{F}}_p \right)^{\operatorname{ss}}. \end{align*}$$
$$\begin{align*}\left( T/\mathfrak{n}T \otimes_{R^{\circ}/\mathfrak{n}} \bar{\mathbb{F}}_p \right)^{\operatorname{ss}} \cong \left( T/\mathfrak{n}_0T \otimes_{R^{\circ}/\mathfrak{n}_0} \bar{\mathbb{F}}_p \right)^{\operatorname{ss}}. \end{align*}$$
Here, we are using the property that if
![]() $\nu $
and
$\nu $
and
![]() $\nu ^{\prime }$
are two representations, then
$\nu ^{\prime }$
are two representations, then
![]() $(\nu \otimes \nu ^{\prime })^{\mathrm {ss}} = (\nu ^{\mathrm {ss}} \otimes (\nu ^{\prime })^{\mathrm {ss}})^{\operatorname {ss}}$
. Now consider the short exact sequence
$(\nu \otimes \nu ^{\prime })^{\mathrm {ss}} = (\nu ^{\mathrm {ss}} \otimes (\nu ^{\prime })^{\mathrm {ss}})^{\operatorname {ss}}$
. Now consider the short exact sequence
Taking inertia invariants and using the fact that
![]() $(\mathfrak {n}T)^I = \mathfrak {n}T^I$
, we see that
$(\mathfrak {n}T)^I = \mathfrak {n}T^I$
, we see that
 $$ \begin{align} T^I/\mathfrak{n}T^I \hookrightarrow \left(T/\mathfrak{n}T\right)^I. \end{align} $$
$$ \begin{align} T^I/\mathfrak{n}T^I \hookrightarrow \left(T/\mathfrak{n}T\right)^I. \end{align} $$
Similarly we have two more injective maps
The map in (8.3.2) factors as (8.3.3) modulo J followed by (8.3.4); i.e., it factors as
 $$\begin{align*}T^I/\mathfrak{n}T^I \rightarrow \left(T/\mathfrak{p}T\right)^I/J \hookrightarrow \left(T/\mathfrak{n}T\right)^I, \end{align*}$$
$$\begin{align*}T^I/\mathfrak{n}T^I \rightarrow \left(T/\mathfrak{p}T\right)^I/J \hookrightarrow \left(T/\mathfrak{n}T\right)^I, \end{align*}$$
and the first map is injective. We then have
 $$\begin{align*}T^I/\mathfrak{n}T^I \otimes_{R^{\circ}/\mathfrak{n}} \bar{\mathbb{F}}_p \hookrightarrow (T/\mathfrak{n}T)^I \otimes \bar{\mathbb{F}}_p \hookrightarrow (T/\mathfrak{n}T \otimes \bar{\mathbb{F}}_p)^I, \end{align*}$$
$$\begin{align*}T^I/\mathfrak{n}T^I \otimes_{R^{\circ}/\mathfrak{n}} \bar{\mathbb{F}}_p \hookrightarrow (T/\mathfrak{n}T)^I \otimes \bar{\mathbb{F}}_p \hookrightarrow (T/\mathfrak{n}T \otimes \bar{\mathbb{F}}_p)^I, \end{align*}$$
and we obtain the following sequence of inequalities:
 $$ \begin{align} \operatorname{dim}_{R^{\circ}/\mathfrak{n}}T^I/\mathfrak{n}T^I & \leq \operatorname{dim}_{R^{\circ}/\mathfrak{n}}(T/\mathfrak{n}T)^I \nonumber \\ & \leq \operatorname{dim}_{\bar{\mathbb{F}}_p}\left(T/\mathfrak{n}T \otimes \bar{\mathbb{F}}_p \right)^I \nonumber \\ & \leq \operatorname{dim}_{\bar{\mathbb{F}}_p}\left((T/\mathfrak{n}T \otimes \bar{\mathbb{F}}_p)^{\operatorname{ss}} \right)^I \nonumber \\ & = \operatorname{dim}_{\bar{\mathbb{F}}_p}\big((T/\mathfrak{n}_0T \otimes \bar{\mathbb{F}}_p)^{\operatorname{ss}} \big)^I. \end{align} $$
$$ \begin{align} \operatorname{dim}_{R^{\circ}/\mathfrak{n}}T^I/\mathfrak{n}T^I & \leq \operatorname{dim}_{R^{\circ}/\mathfrak{n}}(T/\mathfrak{n}T)^I \nonumber \\ & \leq \operatorname{dim}_{\bar{\mathbb{F}}_p}\left(T/\mathfrak{n}T \otimes \bar{\mathbb{F}}_p \right)^I \nonumber \\ & \leq \operatorname{dim}_{\bar{\mathbb{F}}_p}\left((T/\mathfrak{n}T \otimes \bar{\mathbb{F}}_p)^{\operatorname{ss}} \right)^I \nonumber \\ & = \operatorname{dim}_{\bar{\mathbb{F}}_p}\big((T/\mathfrak{n}_0T \otimes \bar{\mathbb{F}}_p)^{\operatorname{ss}} \big)^I. \end{align} $$
All of these inequalities become equalities when
![]() $\mathfrak {n} = \mathfrak {n}_0$
by the “minimially ramified” assumption.
$\mathfrak {n} = \mathfrak {n}_0$
by the “minimially ramified” assumption.
Now we use the fact that
![]() $T^I$
is a flat
$T^I$
is a flat
![]() $R^{\circ }$
-module. In particular, the localisation
$R^{\circ }$
-module. In particular, the localisation
![]() $(T^I)_{\mathfrak {n}}$
is free, and so
$(T^I)_{\mathfrak {n}}$
is free, and so
 $$\begin{align*}\operatorname{dim}_{R^{\circ}/\mathfrak{n}}T^I/\mathfrak{n} = \operatorname{dim}_{R^{\circ}/\mathfrak{n}}(T^I)_{\mathfrak{n}}/\mathfrak{n} = \operatorname{dim}_{\mathcal{K}}T^I \otimes_{R^{\circ}} \mathcal{K},\end{align*}$$
$$\begin{align*}\operatorname{dim}_{R^{\circ}/\mathfrak{n}}T^I/\mathfrak{n} = \operatorname{dim}_{R^{\circ}/\mathfrak{n}}(T^I)_{\mathfrak{n}}/\mathfrak{n} = \operatorname{dim}_{\mathcal{K}}T^I \otimes_{R^{\circ}} \mathcal{K},\end{align*}$$
where
![]() $\mathcal {K}$
denotes the fraction field of
$\mathcal {K}$
denotes the fraction field of
![]() $R^{\circ }$
(recall that
$R^{\circ }$
(recall that
![]() $R^{\circ }$
is an integral domain). Hence, the quantity
$R^{\circ }$
is an integral domain). Hence, the quantity
 $\operatorname {dim}_{R^{\circ }/\mathfrak {n}}T^I/\mathfrak {n}$
is constant and so all inequalities in (8.3.5) become equalities, for general
$\operatorname {dim}_{R^{\circ }/\mathfrak {n}}T^I/\mathfrak {n}$
is constant and so all inequalities in (8.3.5) become equalities, for general
![]() $\mathfrak {n}$
. This implies that the map
$\mathfrak {n}$
. This implies that the map
 $$\begin{align*}T^I/\mathfrak{n}T^I \hookrightarrow \left(T/\mathfrak{p}T\right)^I/J \end{align*}$$
$$\begin{align*}T^I/\mathfrak{n}T^I \hookrightarrow \left(T/\mathfrak{p}T\right)^I/J \end{align*}$$
is an isomorphism.
Consider the exact sequence
where W is a finitely generated
![]() $R^{\circ }/\mathfrak {p}$
-module. Then we have
$R^{\circ }/\mathfrak {p}$
-module. Then we have
![]() $W/JW = 0$
, which implies that
$W/JW = 0$
, which implies that
 $W[\frac {1}{\varpi }] = 0$
. Indeed, W is a finitely generated
$W[\frac {1}{\varpi }] = 0$
. Indeed, W is a finitely generated
![]() $\mathcal {O}_E$
-module and
$\mathcal {O}_E$
-module and
![]() $\varpi \in J$
. Since inverting
$\varpi \in J$
. Since inverting
![]() $\varpi $
commutes with taking inertia invariants, we localise the above sequence, and we see that the natural map
$\varpi $
commutes with taking inertia invariants, we localise the above sequence, and we see that the natural map
 $$\begin{align*}M^I/\mathfrak{m}M^I \longrightarrow \left(M/\mathfrak{m}M\right)^I \end{align*}$$
$$\begin{align*}M^I/\mathfrak{m}M^I \longrightarrow \left(M/\mathfrak{m}M\right)^I \end{align*}$$
is an isomorphism, as required. ▪
We are now in a position to prove Theorem 8.2.3.
Proof It is clear from the definition of
![]() $A_n$
as the global sections of
$A_n$
as the global sections of
![]() $Y_n$
that
$Y_n$
that
![]() $A_n$
is a flat
$A_n$
is a flat
![]() $A_{\infty }$
-module. So for the first part we need to check that taking cohomology and constructing the local conditions both commute with
$A_{\infty }$
-module. So for the first part we need to check that taking cohomology and constructing the local conditions both commute with
![]() $- \otimes _{A_{\infty }} A_n$
.
$- \otimes _{A_{\infty }} A_n$
.
By Lemma 8.1.1(ii) and finiteness, we have
for
![]() $G = G_{\Sigma }$
or
$G = G_{\Sigma }$
or
![]() $G = G_v$
. Similarly
$G = G_v$
. Similarly
![]() $\overline {M}^{I_v}$
is a family of representations over X of the group
$\overline {M}^{I_v}$
is a family of representations over X of the group
![]() $G_v/I_v$
and, after shrinking
$G_v/I_v$
and, after shrinking
![]() $V_1$
and
$V_1$
and
![]() $V_2$
, we can assume that
$V_2$
, we can assume that
![]() $\overline {M}^{I_v}$
is a flat family, in the sense that
$\overline {M}^{I_v}$
is a flat family, in the sense that
 $$\begin{align*}\Gamma(Y_n, \overline{M}^{I_v}) = M_n^{I_v} \end{align*}$$
$$\begin{align*}\Gamma(Y_n, \overline{M}^{I_v}) = M_n^{I_v} \end{align*}$$
is a flat
![]() $A_n$
-module, for all n. The pair
$A_n$
-module, for all n. The pair
![]() $(G_v/I_v, M_n^{I_v})$
satisfies “hypothesis A” in [Reference PottharstPot13], so in fact (by the same proof) the conclusion in Lemma 8.1.1(ii) holds for
$(G_v/I_v, M_n^{I_v})$
satisfies “hypothesis A” in [Reference PottharstPot13], so in fact (by the same proof) the conclusion in Lemma 8.1.1(ii) holds for
![]() $G_v/I_v$
and
$G_v/I_v$
and
![]() $\overline {M}^{I_v}$
in place of
$\overline {M}^{I_v}$
in place of
![]() $G_v$
and
$G_v$
and
![]() $\overline {M}$
, i.e.,
$\overline {M}$
, i.e.,
 $$\begin{align*}\mathbf{L}\iota_n^* \mathbf{R}\Gamma_{\mathrm{cont}}(G_v/I_v, \overline{M}^{I_v}) \cong \mathbf{R}\Gamma_{\mathrm{cont}}(G_v/I_v, M_n^{I_v}). \end{align*}$$
$$\begin{align*}\mathbf{L}\iota_n^* \mathbf{R}\Gamma_{\mathrm{cont}}(G_v/I_v, \overline{M}^{I_v}) \cong \mathbf{R}\Gamma_{\mathrm{cont}}(G_v/I_v, M_n^{I_v}). \end{align*}$$
Again by finiteness, this implies that
 $$\begin{align*}\mathbf{R}\Gamma_{\mathrm{cont}}(G_v/I_v, \overline{M}^{I_v}) \otimes_{A_{\infty}} A_n \cong \mathbf{R}\Gamma_{\mathrm{cont}}(G_v/I_v, M_n^{I_v}). \end{align*}$$
$$\begin{align*}\mathbf{R}\Gamma_{\mathrm{cont}}(G_v/I_v, \overline{M}^{I_v}) \otimes_{A_{\infty}} A_n \cong \mathbf{R}\Gamma_{\mathrm{cont}}(G_v/I_v, M_n^{I_v}). \end{align*}$$
To complete the proof of part (i), we just need to check that the local condition at p commutes with base change to
![]() $A_n$
. By [Reference PottharstPot13, Theorem 2.5], the Herr complex
$A_n$
. By [Reference PottharstPot13, Theorem 2.5], the Herr complex
 $\mathcal {C}^{\bullet }_{\varphi , \gamma }(\mathscr {F}^{{+}{o}}\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}))$
is quasi-isomorphic to a complex
$\mathcal {C}^{\bullet }_{\varphi , \gamma }(\mathscr {F}^{{+}{o}}\mathbf {D}^{\dagger }_{\mathrm {rig}}(\overline {M}))$
is quasi-isomorphic to a complex
![]() $C^{\bullet }$
of coadmissible
$C^{\bullet }$
of coadmissible
![]() $A_{\infty }$
-modules. Since
$A_{\infty }$
-modules. Since
![]() $A_n$
is a flat
$A_n$
is a flat
![]() $A_{\infty }$
-module, we have
$A_{\infty }$
-module, we have
 $$\begin{align*}C^{\bullet} \widehat{\otimes}_{A_{\infty}} A_n \cong C^{\bullet} \widehat{\otimes}^{\mathbf{L}}_{A_{\infty}} A_n \cong \mathcal{C}^{\bullet}_{\varphi, \gamma}(\mathscr{F}^{{+}{o}}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M_n)). \end{align*}$$
$$\begin{align*}C^{\bullet} \widehat{\otimes}_{A_{\infty}} A_n \cong C^{\bullet} \widehat{\otimes}^{\mathbf{L}}_{A_{\infty}} A_n \cong \mathcal{C}^{\bullet}_{\varphi, \gamma}(\mathscr{F}^{{+}{o}}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M_n)). \end{align*}$$
By finiteness of cohomology, this implies that the natural map
 $$\begin{align*}\mathbf{R}\Gamma_{\mathrm{cont}}(\mathbb{Q}_p, \mathscr{F}^{+ o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(\overline{M})) \otimes_{A_{\infty}} A_n \rightarrow \mathbf{R}\Gamma_{\mathrm{cont}}(\mathbb{Q}_p, \mathscr{F}^{+ o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M_n)) \end{align*}$$
$$\begin{align*}\mathbf{R}\Gamma_{\mathrm{cont}}(\mathbb{Q}_p, \mathscr{F}^{+ o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(\overline{M})) \otimes_{A_{\infty}} A_n \rightarrow \mathbf{R}\Gamma_{\mathrm{cont}}(\mathbb{Q}_p, \mathscr{F}^{+ o}\mathbf{D}^{\dagger}_{\mathrm{rig}}(M_n)) \end{align*}$$
is an isomorphism.
Let
![]() $\mathbf {x}$
be an
$\mathbf {x}$
be an
![]() $E^{\prime }$
-valued point in
$E^{\prime }$
-valued point in
![]() $Y_n$
. We now restrict ourselves to the setting where we have a representation
$Y_n$
. We now restrict ourselves to the setting where we have a representation
![]() $M_n$
over
$M_n$
over
![]() $A_n$
that comes from a
$A_n$
that comes from a
![]() $A_n^{\circ }$
-lattice
$A_n^{\circ }$
-lattice
![]() $T_n \subset M_n$
. Shrinking
$T_n \subset M_n$
. Shrinking
![]() $V_1$
and
$V_1$
and
![]() $V_2$
if necessary, we can assume that
$V_2$
if necessary, we can assume that
![]() $T_n^{I_v}$
is a flat
$T_n^{I_v}$
is a flat
![]() $A_n^{\circ }$
-module for all
$A_n^{\circ }$
-module for all
![]() $v \in \Sigma $
not equal to p. Furthermore, by Lemma 8.3.1, specialisation at
$v \in \Sigma $
not equal to p. Furthermore, by Lemma 8.3.1, specialisation at
![]() $\mathbf {x}$
commutes with taking inertia invariants. The result then follows from [Reference PottharstPot13, §3.4] (see, in particular, equation (3.3)). ▪
$\mathbf {x}$
commutes with taking inertia invariants. The result then follows from [Reference PottharstPot13, §3.4] (see, in particular, equation (3.3)). ▪
A Justification of hypotheses
In this appendix, we give justifications for the hypotheses made throughout the paper.
A.1 The “Big Image” Hypothesis
Let f and g be normalised new cuspidal eigenforms of levels
![]() $\Gamma _1(N_1)$
and
$\Gamma _1(N_1)$
and
![]() $\Gamma _1(N_2)$
, weights
$\Gamma _1(N_2)$
, weights
![]() $k+2, k^{\prime }+2$
and characters
$k+2, k^{\prime }+2$
and characters
![]() $\varepsilon _f$
and
$\varepsilon _f$
and
![]() $\varepsilon _g$
respectively. Let
$\varepsilon _g$
respectively. Let
![]() $L_f$
and
$L_f$
and
![]() $L_g$
be the coefficient fields of f and g. Assume that f and g are not of CM type and that f is not a Galois twist of g, i.e., there does not exist an embedding
$L_g$
be the coefficient fields of f and g. Assume that f and g are not of CM type and that f is not a Galois twist of g, i.e., there does not exist an embedding
![]() $\gamma : L_f \to \mathbb {C}$
and a Dirichlet character
$\gamma : L_f \to \mathbb {C}$
and a Dirichlet character
![]() $\chi $
such that
$\chi $
such that
![]() $f^{\gamma } = g \otimes \chi $
.
$f^{\gamma } = g \otimes \chi $
.
Let V be a p-adic representation of
![]() $G_{\mathbb {Q}}$
with coefficients in a finite extension E of
$G_{\mathbb {Q}}$
with coefficients in a finite extension E of
![]() $\mathbb {Q}_p$
. Recall the “Big Image” hypothesis from Section 7.3:
$\mathbb {Q}_p$
. Recall the “Big Image” hypothesis from Section 7.3:
-
(BI) There exists an element
 $\sigma \in \operatorname {\mathrm {Gal}}(\bar {\mathbb {Q}}/\mathbb {Q}(\mu _{p^{\infty }}))$
such that
$\sigma \in \operatorname {\mathrm {Gal}}(\bar {\mathbb {Q}}/\mathbb {Q}(\mu _{p^{\infty }}))$
such that
 $V/(\sigma - 1)V$
is one-dimensional (over E).
$V/(\sigma - 1)V$
is one-dimensional (over E).
Let
![]() $\mathfrak {p}$
be a prime in the compositum
$\mathfrak {p}$
be a prime in the compositum
![]() $L = L_f L_g$
and consider the representation
$L = L_f L_g$
and consider the representation
![]() $V = M_{L_{\mathfrak {p}}}(f)^* \otimes M_{L_{\mathfrak {p}}}(g)^*$
. Then it is shown in [Reference LoefflerLoe17] that for all but finitely many primes
$V = M_{L_{\mathfrak {p}}}(f)^* \otimes M_{L_{\mathfrak {p}}}(g)^*$
. Then it is shown in [Reference LoefflerLoe17] that for all but finitely many primes
![]() $\mathfrak {p}$
, the “Big Image” hypothesis holds for the representation V. Let
$\mathfrak {p}$
, the “Big Image” hypothesis holds for the representation V. Let
![]() $\mathfrak {p}$
be such a prime (lying above a prime
$\mathfrak {p}$
be such a prime (lying above a prime
![]() $p \geq 7$
say) and suppose that we have a Coleman family
$p \geq 7$
say) and suppose that we have a Coleman family
![]() $\mathcal {F}$
defined over
$\mathcal {F}$
defined over
![]() $V_1$
passing through a p-stabilisation of f. Then it is not immediately obvious whether we can shrink
$V_1$
passing through a p-stabilisation of f. Then it is not immediately obvious whether we can shrink
![]() $V_1$
such that the “Big Image” hypothesis holds for the representation
$V_1$
such that the “Big Image” hypothesis holds for the representation
for all specialisations
![]() $k_1 \in V_1$
, even if we were to restrict
$k_1 \in V_1$
, even if we were to restrict
![]() $k_1$
to just classical weights. In this section we show that this is indeed possible by using the fact that the mod p reduction of the above representation is constant, for
$k_1$
to just classical weights. In this section we show that this is indeed possible by using the fact that the mod p reduction of the above representation is constant, for
![]() $V_1$
small enough.
$V_1$
small enough.
Lemma A.1.1 Let G be a profinite group, let
![]() $\rho \colon G \to \mathrm {GL}_n(\mathcal {O}_E)$
be a continuous representation, and let
$\rho \colon G \to \mathrm {GL}_n(\mathcal {O}_E)$
be a continuous representation, and let
![]() $\bar {\rho } \colon G \to \mathrm {GL}_n(k_E)$
be the corresponding residual representation. Suppose there exists
$\bar {\rho } \colon G \to \mathrm {GL}_n(k_E)$
be the corresponding residual representation. Suppose there exists
![]() $g_0 \in G$
so that
$g_0 \in G$
so that
![]() $\bar {\rho }(g_0)$
has eigenvalue
$\bar {\rho }(g_0)$
has eigenvalue
![]() $1$
with multiplicity one. Then there exists
$1$
with multiplicity one. Then there exists
![]() $g \in G$
such that
$g \in G$
such that
![]() $\rho (g)$
has eigenvalue
$\rho (g)$
has eigenvalue
![]() $1$
with multiplicity one.
$1$
with multiplicity one.
Proof Take
 $g=\lim _{n \to \infty } (g_0)^{p^{n!}}$
. Indeed, to show this sequence converges in
$g=\lim _{n \to \infty } (g_0)^{p^{n!}}$
. Indeed, to show this sequence converges in
![]() $G,$
it is enough to show that its image in any finite quotient of G is eventually constant, and this is a routine check. Furthermore, the eigenvalues of
$G,$
it is enough to show that its image in any finite quotient of G is eventually constant, and this is a routine check. Furthermore, the eigenvalues of
![]() $\rho (g)$
are the Teichmüller lifts of the eigenvalues of
$\rho (g)$
are the Teichmüller lifts of the eigenvalues of
![]() $\bar {\rho }(g_0)$
, so
$\bar {\rho }(g_0)$
, so
![]() $1$
is an eigenvalue for
$1$
is an eigenvalue for
![]() $\rho (g)$
with multiplicity one. ▪
$\rho (g)$
with multiplicity one. ▪
In particular, the above lemma can be applied to the tensor product of a pair of Galois representations whose residual representations are “good” in the following sense.
Definition A.1.2 For
![]() $i=1, 2$
let
$i=1, 2$
let
 $\sigma _i: G_{\mathbb {Q}} \to \operatorname {GL}_2(\bar {\mathbb {F}}_p)$
be (continuous) Galois representations. We say the pair
$\sigma _i: G_{\mathbb {Q}} \to \operatorname {GL}_2(\bar {\mathbb {F}}_p)$
be (continuous) Galois representations. We say the pair
![]() $(\sigma _1, \sigma _2)$
is good if
$(\sigma _1, \sigma _2)$
is good if
-
•
 $\chi _i := \operatorname {det} \circ \sigma _i : G_{\mathbb {Q}(\mu _{p^{\infty }})} \to \bar {\mathbb {F}}_p^{\times }$
is a Dirichlet character of conductor
$\chi _i := \operatorname {det} \circ \sigma _i : G_{\mathbb {Q}(\mu _{p^{\infty }})} \to \bar {\mathbb {F}}_p^{\times }$
is a Dirichlet character of conductor
 $N_i$
, and p does not divide the order of the group
$N_i$
, and p does not divide the order of the group
 $(\mathbb {Z}/N\mathbb {Z})^{\times }$
, where N is the lowest common multiple of
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
, where N is the lowest common multiple of
 $N_1$
and
$N_1$
and
 $N_2$
.
$N_2$
. -
• There exists an element
 $u \in (\mathbb {Z}/N\mathbb {Z})^{\times }$
such that the group contains the subgroup generated by
$u \in (\mathbb {Z}/N\mathbb {Z})^{\times }$
such that the group contains the subgroup generated by $$\begin{align*}\big\{(\sigma_1(g), \sigma_2(g)) \in \operatorname{GL}_2(\bar{\mathbb{F}}_p) \times \operatorname{GL}_2(\bar{\mathbb{F}}_p) : g \in G_{\mathbb{Q}(\mu_{p^{\infty}})} \big\} \end{align*}$$
$$\begin{align*}\big\{(\sigma_1(g), \sigma_2(g)) \in \operatorname{GL}_2(\bar{\mathbb{F}}_p) \times \operatorname{GL}_2(\bar{\mathbb{F}}_p) : g \in G_{\mathbb{Q}(\mu_{p^{\infty}})} \big\} \end{align*}$$
 $\operatorname {SL}_2(\mathbb {F}_p) \times \operatorname {SL}_2(\mathbb {F}_p)$
and the element
$\operatorname {SL}_2(\mathbb {F}_p) \times \operatorname {SL}_2(\mathbb {F}_p)$
and the element  $$\begin{align*}\bigg( \begin{pmatrix} 1 & 0 \\ 0 & \chi_1(u) \end{pmatrix} , \begin{pmatrix} 1 & 0 \\ 0 & \chi_2(u) \end{pmatrix} \bigg). \end{align*}$$
$$\begin{align*}\bigg( \begin{pmatrix} 1 & 0 \\ 0 & \chi_1(u) \end{pmatrix} , \begin{pmatrix} 1 & 0 \\ 0 & \chi_2(u) \end{pmatrix} \bigg). \end{align*}$$
If we want to specify the element
![]() $u,$
we also call
$u,$
we also call
![]() $(\sigma _1, \sigma _2, u)$
good.
$(\sigma _1, \sigma _2, u)$
good.
Lemma A.1.3 Assume
![]() $p \ge 7$
and let E be a finite extension of
$p \ge 7$
and let E be a finite extension of
![]() $\mathbb {Q}_p$
. Let
$\mathbb {Q}_p$
. Let
![]() $\rho _1, \rho _2 \colon G_{\mathbb {Q}} \to \mathrm {GL}_2(\mathcal {O}_E)$
be two p-adic representations, and let
$\rho _1, \rho _2 \colon G_{\mathbb {Q}} \to \mathrm {GL}_2(\mathcal {O}_E)$
be two p-adic representations, and let
![]() $\bar {\rho }_1$
,
$\bar {\rho }_1$
,
![]() $\bar {\rho }_2$
denote the corresponding residual representations. If there exists an element
$\bar {\rho }_2$
denote the corresponding residual representations. If there exists an element
![]() $u \in (\mathbb {Z}/N\mathbb {Z})^{\times }$
such that
$u \in (\mathbb {Z}/N\mathbb {Z})^{\times }$
such that
![]() $(\bar {\rho }_1, \bar {\rho }_2, u)$
is good and
$(\bar {\rho }_1, \bar {\rho }_2, u)$
is good and
![]() $\chi _1(u) \chi _2(u) \neq 1$
, then
$\chi _1(u) \chi _2(u) \neq 1$
, then
![]() $\rho _1 \otimes _E \rho _2$
satisfies condition (BI).
$\rho _1 \otimes _E \rho _2$
satisfies condition (BI).
Proof Since
![]() $p \ge 7$
, there exists
$p \ge 7$
, there exists
![]() $x \in \mathbb {F}_p^{\times }$
such that
$x \in \mathbb {F}_p^{\times }$
such that
![]() $x^{-2} \chi _1(u)$
and
$x^{-2} \chi _1(u)$
and
![]() $x^2 \chi _2(u)$
are different from
$x^2 \chi _2(u)$
are different from
![]() $1$
. Since
$1$
. Since
![]() $(\bar {\rho }_1, \bar {\rho }_2, u)$
is a good triple, there exists an element
$(\bar {\rho }_1, \bar {\rho }_2, u)$
is a good triple, there exists an element
![]() $g_0 \in G_{\mathbb {Q}(\mu _{p^\infty })}$
such that
$g_0 \in G_{\mathbb {Q}(\mu _{p^\infty })}$
such that
 $$\begin{align*}\bar{\rho}_1(g_0) = \begin{pmatrix} x & 0 \\ 0 & x^{-1} \chi_1(u) \end{pmatrix} \, \quad \bar{\rho}_2(g_0) = \begin{pmatrix} x^{-1} & 0 \\ 0 & x \chi_2(u) \end{pmatrix} \,. \end{align*}$$
$$\begin{align*}\bar{\rho}_1(g_0) = \begin{pmatrix} x & 0 \\ 0 & x^{-1} \chi_1(u) \end{pmatrix} \, \quad \bar{\rho}_2(g_0) = \begin{pmatrix} x^{-1} & 0 \\ 0 & x \chi_2(u) \end{pmatrix} \,. \end{align*}$$
The eigenvalues of
![]() $\bar {\rho }_1(g_0) \otimes \bar {\rho }_2(g_0)$
are
$\bar {\rho }_1(g_0) \otimes \bar {\rho }_2(g_0)$
are
![]() $\{1,x^{-2} \chi _1(u),x^2 \chi _2(u),\chi _1(u)\chi _2(u)\}$
, so the eigenvalue
$\{1,x^{-2} \chi _1(u),x^2 \chi _2(u),\chi _1(u)\chi _2(u)\}$
, so the eigenvalue
![]() $1$
has multiplicity one and we may apply Lemma A.1.1. ▪
$1$
has multiplicity one and we may apply Lemma A.1.1. ▪
A.1.1 A.1.1 Examples of Good Triples
 $(\sigma _1, \sigma _2, u)$
$(\sigma _1, \sigma _2, u)$
Returning to the situation at the start of Section 1.1, let
![]() $\mathfrak {p}$
be a prime of the compositum
$\mathfrak {p}$
be a prime of the compositum
![]() $L = L_fL_g$
lying above a prime
$L = L_fL_g$
lying above a prime
![]() $p \geq 7$
. We have Galois representations
$p \geq 7$
. We have Galois representations
 $$ \begin{align*} \rho_{f, \mathfrak{p}}^* \colon G_{\mathbb{Q}} \longrightarrow \operatorname{GL}(M_{L_{\mathfrak{p}}}(f)^*) \nonumber \\ \rho_{g, \mathfrak{p}}^* \colon G_{\mathbb{Q}} \longrightarrow \operatorname{GL}(M_{L_{\mathfrak{p}}}(g)^*) \nonumber \end{align*} $$
$$ \begin{align*} \rho_{f, \mathfrak{p}}^* \colon G_{\mathbb{Q}} \longrightarrow \operatorname{GL}(M_{L_{\mathfrak{p}}}(f)^*) \nonumber \\ \rho_{g, \mathfrak{p}}^* \colon G_{\mathbb{Q}} \longrightarrow \operatorname{GL}(M_{L_{\mathfrak{p}}}(g)^*) \nonumber \end{align*} $$
which satisfy
 $\operatorname {det} \circ \rho _{f, \mathfrak {p}}^* = \varepsilon _f^{-1} \chi _{\mathrm {cycl}}^{1+k}$
and
$\operatorname {det} \circ \rho _{f, \mathfrak {p}}^* = \varepsilon _f^{-1} \chi _{\mathrm {cycl}}^{1+k}$
and
 $\operatorname {det} \circ \rho _{g, \mathfrak {p}}^* = \varepsilon _g^{-1} \chi _{\mathrm {cycl}}^{1+k^{\prime }}$
. Let
$\operatorname {det} \circ \rho _{g, \mathfrak {p}}^* = \varepsilon _g^{-1} \chi _{\mathrm {cycl}}^{1+k^{\prime }}$
. Let
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
denote the reductions modulo
$\sigma _2$
denote the reductions modulo
![]() $\mathfrak {p}$
of
$\mathfrak {p}$
of
 $\rho _{f, \mathfrak {p}}^*$
and
$\rho _{f, \mathfrak {p}}^*$
and
![]() $\rho _{g, \mathfrak {p}}^*$
, respectively.
$\rho _{g, \mathfrak {p}}^*$
, respectively.
Then it is shown in [Reference LoefflerLoe17] that, for a very large amount of primes
![]() $\mathfrak {p}$
,
$\mathfrak {p}$
,
![]() $(\sigma _1, \sigma _2)$
is a good pair.Footnote
1
In particular, for all but finitely many
$(\sigma _1, \sigma _2)$
is a good pair.Footnote
1
In particular, for all but finitely many
![]() $\mathfrak {p}$
that split completely in
$\mathfrak {p}$
that split completely in
![]() $L/\mathbb {Q}$
the triple
$L/\mathbb {Q}$
the triple
![]() $(\sigma _1, \sigma _2, u)$
is a good triple for any
$(\sigma _1, \sigma _2, u)$
is a good triple for any
![]() $u \in (\mathbb {Z}/N\mathbb {Z})^{\times }$
, where
$u \in (\mathbb {Z}/N\mathbb {Z})^{\times }$
, where
![]() $N = 4 \operatorname {lcm}(N_1, N_2)$
.
$N = 4 \operatorname {lcm}(N_1, N_2)$
.
Now suppose that
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
are two Coleman families over open affinoids
$\mathcal {G}$
are two Coleman families over open affinoids
![]() $V_1, V_2$
passing through p-stabilisations of f and g respectively. Let
$V_1, V_2$
passing through p-stabilisations of f and g respectively. Let
be the tensor product of the Galois representations attached to
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
and take
$\mathcal {G}$
and take
![]() $V_1$
and
$V_1$
and
![]() $V_2$
to be small enough such that M is constant modulo p. Note that the representations
$V_2$
to be small enough such that M is constant modulo p. Note that the representations
 $$ \begin{align*} \rho_{\mathcal{F}}^* \colon G_{\mathbb{Q}}& \longrightarrow \operatorname{GL}(M_{V_1}(\mathcal{F})^*), \nonumber \\ \rho_{\mathcal{G}}^* \colon G_{\mathbb{Q}} &\longrightarrow \operatorname{GL}(M_{V_2}(\mathcal{G})^*) \nonumber \end{align*} $$
$$ \begin{align*} \rho_{\mathcal{F}}^* \colon G_{\mathbb{Q}}& \longrightarrow \operatorname{GL}(M_{V_1}(\mathcal{F})^*), \nonumber \\ \rho_{\mathcal{G}}^* \colon G_{\mathbb{Q}} &\longrightarrow \operatorname{GL}(M_{V_2}(\mathcal{G})^*) \nonumber \end{align*} $$
satisfy
![]() $\operatorname {det} \circ \rho _{\mathcal {F}}^*(g) = \varepsilon _{\mathcal {F}}^{-1}(g)$
and
$\operatorname {det} \circ \rho _{\mathcal {F}}^*(g) = \varepsilon _{\mathcal {F}}^{-1}(g)$
and
 $\operatorname {det} \circ \rho _{\mathcal {G}}^*(g) = \varepsilon _{\mathcal {G}}^{-1}(g)$
, for all
$\operatorname {det} \circ \rho _{\mathcal {G}}^*(g) = \varepsilon _{\mathcal {G}}^{-1}(g)$
, for all
![]() $g \in G_{\mathbb {Q}(\mu _{p^{\infty }})}$
. In particular, we can shrink
$g \in G_{\mathbb {Q}(\mu _{p^{\infty }})}$
. In particular, we can shrink
![]() $V_1$
and
$V_1$
and
![]() $V_2$
so that
$V_2$
so that
![]() $\varepsilon _{\mathcal {F}_{k_1}} = \varepsilon _f$
and
$\varepsilon _{\mathcal {F}_{k_1}} = \varepsilon _f$
and
![]() $\varepsilon _{\mathcal {G}_{k_2}} = \varepsilon _g$
for all specialisations
$\varepsilon _{\mathcal {G}_{k_2}} = \varepsilon _g$
for all specialisations
![]() $\mathbf {x} = (k_1, k_2) \in V_1 \times V_2$
.
$\mathbf {x} = (k_1, k_2) \in V_1 \times V_2$
.
Then, assuming
![]() $\varepsilon _f(u)\varepsilon _g(u) \not \equiv 1$
modulo p, by Lemma A.1.3 we have that the (BI) condition holds for the representation
$\varepsilon _f(u)\varepsilon _g(u) \not \equiv 1$
modulo p, by Lemma A.1.3 we have that the (BI) condition holds for the representation
![]() $M_{\mathbf {x}}$
for any specialisation at
$M_{\mathbf {x}}$
for any specialisation at
![]() $\mathbf {x} \in V_1 \times V_2$
.
$\mathbf {x} \in V_1 \times V_2$
.
A.2 The “Flatness of Inertia” and “Minimally Ramified” Hypotheses
An example of a pair of modular forms f and g that satisfy the “flatness of inertia” and “minimally ramified” hypotheses are as follows. Let
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
be two distinct primes
$\ell _2$
be two distinct primes
![]() $\geq 7$
both different from p, and let f and g be two normalised cuspidal new eigenforms of levels
$\geq 7$
both different from p, and let f and g be two normalised cuspidal new eigenforms of levels
![]() $\Gamma _1(\ell _1)$
and
$\Gamma _1(\ell _1)$
and
![]() $\Gamma _1(\ell _2)$
, weights
$\Gamma _1(\ell _2)$
, weights
![]() $k+2$
and
$k+2$
and
![]() $k^{\prime }+2$
, and characters
$k^{\prime }+2$
, and characters
![]() $\varepsilon _f = \varepsilon _1$
and
$\varepsilon _f = \varepsilon _1$
and
![]() $\varepsilon _g = \varepsilon _2$
respectively. Suppose that
$\varepsilon _g = \varepsilon _2$
respectively. Suppose that
![]() $\varepsilon _1$
and
$\varepsilon _1$
and
![]() $\varepsilon _2$
are both non-trivial modulo p. Let E be a p-adic field containing
$\varepsilon _2$
are both non-trivial modulo p. Let E be a p-adic field containing
![]() $a_n(f)$
,
$a_n(f)$
,
![]() $a_n(g)$
and the images of
$a_n(g)$
and the images of
![]() $\varepsilon _1$
and
$\varepsilon _1$
and
![]() $\varepsilon _2$
, and suppose that
$\varepsilon _2$
, and suppose that
![]() $a_{\ell _1}(f)$
and
$a_{\ell _1}(f)$
and
![]() $a_{\ell _2}(g)$
are both non-zero.
$a_{\ell _2}(g)$
are both non-zero.
Let
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
denote the restriction of
$\rho _2$
denote the restriction of
![]() $M_E(f)$
and
$M_E(f)$
and
![]() $M_E(g)$
to the inertia group at
$M_E(g)$
to the inertia group at
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
respectively. By [Reference Loeffler and WeinsteinLW12, §5], the local components at
$\ell _2$
respectively. By [Reference Loeffler and WeinsteinLW12, §5], the local components at
![]() $\ell _i$
of the automorphic representations associated to f and g are prinicipal series representations; therefore by the local Langlands correspondence (and local-global compatibility) we have
$\ell _i$
of the automorphic representations associated to f and g are prinicipal series representations; therefore by the local Langlands correspondence (and local-global compatibility) we have
where
![]() $\mathbf {1}$
is the trivial character.
$\mathbf {1}$
is the trivial character.
Let
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
be Coleman families over
$\mathcal {G}$
be Coleman families over
![]() $V_1$
and
$V_1$
and
![]() $V_2$
passing through p-stabilisations of f and
$V_2$
passing through p-stabilisations of f and
![]() $g,$
respectively. Let M denote the representation
$g,$
respectively. Let M denote the representation
![]() $M_{V_1}(\mathcal {F})^* \widehat {\otimes } M_{V_2}(\mathcal {G})^*$
and let
$M_{V_1}(\mathcal {F})^* \widehat {\otimes } M_{V_2}(\mathcal {G})^*$
and let
![]() $M_i$
denote the restriction of M to the inertia group
$M_i$
denote the restriction of M to the inertia group
![]() $I_{\ell _i}$
.
$I_{\ell _i}$
.
Since inertial types are locally constant, we can shrink
![]() $V_1$
and
$V_1$
and
![]() $V_2$
so that for every classical weight
$V_2$
so that for every classical weight
![]() $\mathbf {k} = (k_1, k_2) \in V_1 \times V_2$
the specialisation of M satisfies
$\mathbf {k} = (k_1, k_2) \in V_1 \times V_2$
the specialisation of M satisfies
for
![]() $i=1, 2$
. It is not hard to see that the action of
$i=1, 2$
. It is not hard to see that the action of
![]() $I_{\ell _i}$
on M factors through a finite quotient isomorphic to
$I_{\ell _i}$
on M factors through a finite quotient isomorphic to
![]() $\left (\mathbb {Z}/\ell _i \mathbb {Z}\right )^{\times }$
(it is true on a Zariski dense subset) and that
$\left (\mathbb {Z}/\ell _i \mathbb {Z}\right )^{\times }$
(it is true on a Zariski dense subset) and that
![]() $M_i$
must decompose as
$M_i$
must decompose as
Indeed the action factors though a finite group and we can define idempotents corresponding to each direct summand. Taking
![]() $\Sigma = \{\ell _1, \ell _2, p, \infty \},$
we see that the “flatness of inertia” and “minimally ramified” hypotheses hold for f and g (provided that
$\Sigma = \{\ell _1, \ell _2, p, \infty \},$
we see that the “flatness of inertia” and “minimally ramified” hypotheses hold for f and g (provided that
![]() $V_1$
and
$V_1$
and
![]() $V_2$
are small enough).
$V_2$
are small enough).
A similar argument can be applied if either (or both) of
![]() $\varepsilon _i$
are trivial, except now the local component can be an unramified twist of the Steinberg representation and the action of inertia factors through a (not necessarily finite) abelian quotient. However we are primarily interested in the case
$\varepsilon _i$
are trivial, except now the local component can be an unramified twist of the Steinberg representation and the action of inertia factors through a (not necessarily finite) abelian quotient. However we are primarily interested in the case
![]() $\varepsilon _1 \cdot \varepsilon _2 \neq 1$
anyway, otherwise the “Big Image” hypothesis would not hold for the representation
$\varepsilon _1 \cdot \varepsilon _2 \neq 1$
anyway, otherwise the “Big Image” hypothesis would not hold for the representation
![]() $M_E(f)^* \otimes M_E(g)^*$
.
$M_E(f)^* \otimes M_E(g)^*$
.
Acknowledgment
This paper grew out of our group project at the 2018 Arizona Winter School. We would like to thank David Loeffler and Sarah Zerbes for suggesting the project that led to this article and for offering us their invaluable advice and guidance. We are grateful for their continued encouragements during the preparation of this paper. We also thank Rodolfo Venerucci for many helpful conversations and suggestions. Special thanks are also due to the organizers of the Arizona Winter School for making the winter school an enjoyable and fruitful experience. AG would like to thank Ashwin Iyengar and Pol van Hoften for their helpful comments and suggestions. The authors would like to thank the anonymous referees for their helpful suggestions.