Published online by Cambridge University Press: 20 November 2018
For 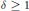 $\delta \ge 1$ and
$\delta \ge 1$ and  $n\ge 1$, consider the simplicial complex of graphs on
$n\ge 1$, consider the simplicial complex of graphs on  $n$ vertices in which each vertex has degree at most
$n$ vertices in which each vertex has degree at most  $\delta$; we identify a given graph with its edge set and admit one loop at each vertex. This complex is of some importance in the theory of semigroup algebras. When
$\delta$; we identify a given graph with its edge set and admit one loop at each vertex. This complex is of some importance in the theory of semigroup algebras. When 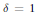 $\delta =1$, we obtain the matching complex, for which it is known that there is 3-torsion in degree
$\delta =1$, we obtain the matching complex, for which it is known that there is 3-torsion in degree  $d$ of the homology whenever
$d$ of the homology whenever 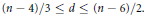 $\left( n-4 \right)/3\le d\le \left( n-6 \right)/2$. This paper establishes similar bounds for
$\left( n-4 \right)/3\le d\le \left( n-6 \right)/2$. This paper establishes similar bounds for 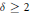 $\delta \ge 2$. Specifically, there is 3-torsion in degree
$\delta \ge 2$. Specifically, there is 3-torsion in degree  $d$ whenever
$d$ whenever
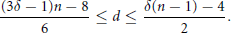 $$\frac{\left( 3\delta -1 \right)n-8}{6}\le d\le \frac{\delta \left( n-1 \right)-4}{2}.$$
$$\frac{\left( 3\delta -1 \right)n-8}{6}\le d\le \frac{\delta \left( n-1 \right)-4}{2}.$$
The procedure for detecting torsion is to construct an explicit cycle  $z$ that is easily seen to have the property that
$z$ that is easily seen to have the property that 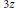 $3z$ is a boundary. Defining a homomorphism that sends
$3z$ is a boundary. Defining a homomorphism that sends  $z$ to a non-boundary element in the chain complex of a certain matching complex, we obtain that
$z$ to a non-boundary element in the chain complex of a certain matching complex, we obtain that  $z$ itself is a non-boundary. In particular, the homology class of
$z$ itself is a non-boundary. In particular, the homology class of  $z$ has order 3.
$z$ has order 3.