Let X be a real Banach space with a uniformly convex dual, X*, and let C be a nonempty closed convex and bounded subset of X. Let T: C → C be a strongly accretive and a continuous mapping. For any f ∈ C, let S: C → C be defined by Sx = f + x – Tx for each x ∈ C. Then, the iteration process xo ∈ C,
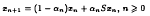
under suitable conditions on the real sequence  converges strongly to a solution of the equation Tx = f in C. Furthermore, if T is strongly accretive and Lipschitz with Lipschitz constant L ≥ 1 then the iteration process x0 ∈ C,
converges strongly to a solution of the equation Tx = f in C. Furthermore, if T is strongly accretive and Lipschitz with Lipschitz constant L ≥ 1 then the iteration process x0 ∈ C,

under suitable conditions on the real sequences  and
and  converges strongly to a solution of the equation Tx = f in C. Explicit error estimates are obtained.
converges strongly to a solution of the equation Tx = f in C. Explicit error estimates are obtained.