The total irregularity of a simple undirected graph $G$ is defined as $\text{irr}_{t}(G)=\frac{1}{2}\sum _{u,v\in V(G)}|d_{G}(u)-d_{G}(v)|$, where $d_{G}(u)$ denotes the degree of a vertex $u\in V(G)$. Obviously, $\text{irr}_{t}(G)=0$ if and only if $G$ is regular. Here, we characterise the nonregular graphs with minimal total irregularity and thereby resolve the recent conjecture by Zhu et al. [‘The minimal total irregularity of graphs’, Preprint, 2014, arXiv:1404.0931v1 ] about the lower bound on the minimal total irregularity of nonregular connected graphs. We show that the conjectured lower bound of $2n-4$ is attained only if nonregular connected graphs of even order are considered, while the sharp lower bound of $n-1$ is attained by graphs of odd order. We also characterise the nonregular graphs with the second and the third smallest total irregularity.

Lladó and Moragas [‘Cycle-magic graphs’, Discrete Math.307 (2007), 2925–2933] showed the cyclic-magic and cyclic-supermagic behaviour of several classes of connected graphs. They discussed cycle-magic labellings of subdivided wheels and friendship graphs, but there are no further results on cycle-magic labellings of other families of subdivided graphs. In this paper, we find cycle-magic labellings for subdivided graphs. We show that if a graph has a cycle-(super)magic labelling, then its uniform subdivided graph also has a cycle-(super)magic labelling. We also discuss some cycle-supermagic labellings for nonuniform subdivided fans and triangular ladders.

For two given graphs $G_{1}$ and $G_{2}$, the Ramsey number $R(G_{1},G_{2})$ is the smallest integer $N$ such that, for any graph $G$ of order $N$, either $G$ contains $G_{1}$ as a subgraph or the complement of $G$ contains $G_{2}$ as a subgraph. A fan $F_{l}$ is $l$ triangles sharing exactly one vertex. In this note, it is shown that $R(F_{n},F_{m})=4n+1$ for $n\geq \max \{m^{2}-m/2,11m/2-4\}$.

Let $G$ be a finite abelian group and $A\subseteq G$. For $n\in G$, denote by $r_{A}(n)$ the number of ordered pairs $(a_{1},a_{2})\in A^{2}$ such that $a_{1}+a_{2}=n$. Among other things, we prove that for any odd number $t\geq 3$, it is not possible to partition $G$ into $t$ disjoint sets $A_{1},A_{2},\dots ,A_{t}$ with $r_{A_{1}}=r_{A_{2}}=\cdots =r_{A_{t}}$.

In this paper, we present a decomposition of the elements of a finite field and illustrate the efficiency of this decomposition in evaluating some specific exponential sums over finite fields. The results can be employed in determining the Walsh spectrum of some Boolean functions.

In this paper, we find a power series expansion of the invariant differential ${\it\omega}_{E}$ of an elliptic curve $E$ defined over $\mathbb{Q}$, where $E$ is described by certain families of Weierstrass equations. In addition, we derive several congruence relations satisfied by the trace of the Frobenius endomorphism of $E$.

Podoski and Szegedy [‘On finite groups whose derived subgroup has bounded rank’, Israel J. Math.178 (2010), 51–60] proved that for a finite group $G$ with rank $r$, the inequality $[G:Z_{2}(G)]\leq |G^{\prime }|^{2r}$ holds. In this paper we omit the finiteness condition on $G$ and show that groups with finite derived subgroup satisfy the same inequality. We also construct an $n$-capable group which is not $(n+1)$-capable for every $n\in \mathbf{N}$.

In the present paper, a coupled algorithm refining recursively the Hermite–Hadamard inequality on a simplex is investigated. Our approach allows us to express the integral mean value $M_{f}$ of a convex function $f$ on a simplex as both the limit of sequences and sum of series involving iterative lower and upper bounds of $M_{f}$. Two examples of interest are discussed.

Let $f$ be a transcendental meromorphic function with at least one direct tract. In this note, we investigate the structure of the escaping set which is in the same direct tract. We also give a theorem about the slow escaping set.

Let $G$ be a commutative group and 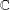$\mathbb{C}$ the field of complex numbers, $\mathbb{R}^{+}$ the set of positive real numbers and $f,g,h,k:G\times \mathbb{R}^{+}\rightarrow \mathbb{C}$. In this paper, we first consider the Levi-Civitá functional inequality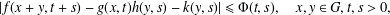

$$\begin{eqnarray}\displaystyle |f(x+y,t+s)-g(x,t)h(y,s)-k(y,s)|\leq {\rm\Phi}(t,s),\quad x,y\in G,t,s>0, & & \displaystyle \nonumber\end{eqnarray}$$

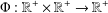${\rm\Phi}:\mathbb{R}^{+}\times \mathbb{R}^{+}\rightarrow \mathbb{R}^{+}$

${\rm\Phi}(t_{2},s_{2})\leq {\rm\Phi}(t_{1},s_{1})$

$0<t_{1}\leq t_{2}$

$0<s_{1}\leq s_{2}$

$$\begin{eqnarray}\displaystyle u\circ S-v\otimes w-k\circ {\rm\Pi}\in {\mathcal{D}}_{L^{\infty }}^{\prime }(\mathbb{R}^{2n})\quad [\text{respectively}\;{\mathcal{A}}_{L^{\infty }}^{\prime }(\mathbb{R}^{2n})] & & \displaystyle \nonumber\end{eqnarray}$$

$u,v,w,k$

$S(x,y)=x+y,{\rm\Pi}(x,y)=y,x,y\in \mathbb{R}^{n}$

$\circ$

$\otimes$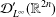

${\mathcal{D}}_{L^{\infty }}^{\prime }(\mathbb{R}^{2n})$

${\mathcal{A}}_{L^{\infty }}^{\prime }(\mathbb{R}^{2n})$

In this paper we improve the inequalities obtained by Chen in 2009 for the Euler–Mascheroni constant.

The Dunkl transform ${\mathcal{F}}_{k}$ is a generalisation of the usual Fourier transform to an integral transform invariant under a finite reflection group. The goal of this paper is to prove a strong uncertainty principle for orthonormal bases in the Dunkl setting which states that the product of generalised dispersions cannot be bounded for an orthonormal basis. Moreover, we obtain a quantitative version of Shapiro’s uncertainty principle on the time–frequency concentration of orthonormal sequences and show, in particular, that if the elements of an orthonormal sequence and their Dunkl transforms have uniformly bounded dispersions then the sequence is finite.

We give a positive answer to the question of Bouras [‘Almost Dunford–Pettis sets in Banach lattices’, Rend. Circ. Mat. Palermo (2) 62 (2013), 227–236] concerning weak compactness of almost Dunford–Pettis sets in Banach lattices. That is, every almost Dunford–Pettis set in a Banach lattice $E$ is relatively weakly compact if and only if $E$ is a $\mathit{KB}$-space.

In this paper, for an arbitrary $\ell ^{1}$-Munn algebra $\mathfrak{A}$ over a Banach algebra $A$ with a sandwich matrix $P$, we characterise all homomorphisms from $\mathfrak{A}$ to a commutative Banach algebra $B$. Especially, we study the character space of this algebra. Then, as an application, its character amenability is investigated. Finally, we apply these results to certain semigroups, which are called Rees matrix semigroups.

We define the quotient and complete NUOS-quotient map (NUOS stands for nonunital operator system) in the category of nonunital operator systems. We prove that the greatest reduced tensor product max0 is projective in some sense. Moreover, we define a pseudo unit in a nonunital operator system and give some necessary and sufficient conditions under which a nonunital operator system has an operator system structure.

We prove ${\it\epsilon}$-closeness of hypersurfaces to a sphere in Euclidean space under the assumption that the traceless second fundamental form is ${\it\delta}$-small compared to the mean curvature. We give the explicit dependence of ${\it\delta}$ on ${\it\epsilon}$ within the class of uniformly convex hypersurfaces with bounded volume.

For every countable group $G$ we construct a compact path connected subspace $K$ of $\mathbb{R}^{4}$ such that ${\it\pi}_{1}(K)\cong G$. Our construction is much simpler than the one found recently by Virk.

Exact upper and lower bounds on the difference between the arithmetic and geometric means are obtained. The inequalities providing these bounds may be viewed, respectively, as a reverse Jensen inequality and an improvement of the direct Jensen inequality, in the case when the convex function is the exponential.

For triangular arrays $\{X_{n,k}:1\leqslant k\leqslant n,n\geqslant 1\}$ of upper extended negatively dependent random variables weakly mean dominated by a random variable $X$ and sequences $\{b_{n}\}$ of positive constants, conditions are given to guarantee an almost sure finite upper bound to $\sum _{k=1}^{n}(X_{n,k}-\mathbb{E}X_{n,k})/\!\sqrt{b_{n}\,\text{Log}\,n}$, where $\text{Log}\,n:=\max \{1,\log n\}$, thus getting control over the limiting rate in terms of the prescribed sequence $\{b_{n}\}$ and permitting us to weaken or strengthen the assumptions on the random variables.