Let (T, T, μ) be a σ-finite measure space and X a Suslin space. Let A be a class of normal integrands on T × X. We discuss the existence of an essential supremum of A, namely, a normal integrand l with
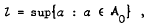
where A0 is a countable subclass of A, and, for each α ∈ A,

In this way we obtain an extension of the classical essential supremum concept. The applications include a result on measurable selectors of nonmeasurable multifunctions.