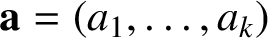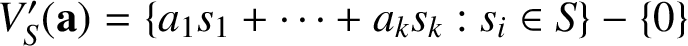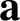1 Introduction
For a positive integer m greater than or equal to 3, the polynomial
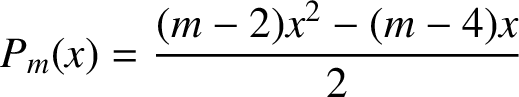$$ \begin{align*}P_m(x)=\frac{(m-2)x^2-(m-4)x}{2} \end{align*} $$
is an integer-valued quadratic polynomial and
$P_m(s)$
is the sth m-gonal number for a nonnegative integer s. For a vector
$\mathbf {a}=(a_1,a_2,\ldots ,a_k)$
of positive integers, a polynomial of the form
$$ \begin{align*}p_m(\mathbf{a})=p_m(\mathbf{a})(x_1,\ldots,x_k)=a_1P_m(x_1)+\cdots+a_kP_m(x_k) \end{align*} $$
in variables
$x_1,x_2,\ldots ,x_k$
is called a k-ary m-gonal form (or a k-ary sum of generalised m-gonal numbers). We say that an integer N is represented by an m-gonal form
$p_m(\mathbf {a})$
if the equation
$$ \begin{align*}p_m(\mathbf{a})(x_1,\ldots,x_k)=N \end{align*} $$
has an integer solution. The minimum of
$p_m(\mathbf {a})$
, denoted by
$\min (p_m(\mathbf {a}))$
, is the smallest positive integer represented by
$p_m(\mathbf {a})$
. We call an m-gonal form tight universal if it represents every positive integer greater than its minimum. A tight universal m-gonal form having minimum 1 is simply called universal. There are several results on the classification of universal m-gonal forms (see, for example, [Reference Bosma and Kane2, Reference Ju6, Reference Ju and Oh7, Reference Kim8]). Note that
$P_4(x)=x^2$
and the classification of universal diagonal quadratic forms can be easily done by using the Conway–Schneeberger 15 theorem (see [Reference Bhargava1, Reference Conway3]).
Recently, the author and Oh [Reference Kim and Oh10] studied (positive definite integral) quadratic forms which represent every positive integer greater than the minimum of the form. We called such a quadratic form f tight
$\mathcal T(n)$
-universal, where n is the minimum of the quadratic form f. We classified ‘diagonal’ tight universal quadratic forms, which gives the classification of tight universal m-gonal forms in the case of
$m=4$
.
We follow the notation and terminologies used in [Reference Kim and Oh10]. For
$n=1,2,3,\ldots ,$
we denote by
$\mathcal T(n)$
the set of integers greater than or equal to n. We say that an m-gonal form is tight
$\mathcal T(n)$
-universal if it is tight universal with minimum n. In Section 3, we resolve the classification problem of tight
$\mathcal T(n)$
-universal m-gonal forms in the following cases:
$$ \begin{align*}\mathrm{(i)} \ m=5, \ n\ge 7; \quad \mathrm{(ii)} \ m=7, \ n\ge 11; \quad \mathrm{(iii)} \ m\ge 8, \ n\ge 2m-5.\end{align*} $$
In fact, it will be proved that there are ‘essentially’ two tight
$\mathcal T(n)$
-universal m-gonal forms in the cases (ii) and (iii). It will also be shown that there is a unique tight
$\mathcal T(n)$
-universal pentagonal form for any
$n\ge 7$
. In addition, we classify tight
$\mathcal T(n)$
-universal sums of m-gonal numbers (for the definition, see Section 3). In Section 4, we classify tight universal triangular forms by finding all tight
$\mathcal T(n)$
-universal triangular forms for every integer
$n\ge 3$
. Universal triangular forms were classified in [Reference Bosma and Kane2] and tight
$\mathcal T(2)$
-universal triangular forms were found by Ju [‘Almost universal sums of triangular numbers with one exception’, submitted for publication]. To classify tight universal triangular forms, we use the theory of quadratic forms and adapt the geometric language of quadratic spaces and lattices, generally following [Reference Kitaoka11, Reference O’Meara12]. Some basic notation and terminologies will be given in Section 2.
2 Preliminaries
Let R be the ring of rational integers
${\mathbb Z}$
or the ring of p-adic integers
${\mathbb Z}_p$
for a prime p and let F be the field of fractions of R. An R-lattice is a finitely generated R-submodule of a quadratic space
$(W,Q)$
over F. We let
$B:W\times W\to F$
be the symmetric bilinear form associated to the quadratic map Q so that
$B(x,x)=Q(x)$
for every
$x\in W$
. For an element a in R and an R-lattice L, we say that a is represented by L over R and write
$a{\ \longrightarrow \ } L$
over R if
$Q(\mathbf {x})=a$
for some vector
$\mathbf {x}\in L$
.
Let L be a
${\mathbb Z}$
-lattice on a quadratic space W over
${\mathbb Q}$
. The genus of L, denoted
$\text {gen}(L)$
, is the set of all
${\mathbb Z}$
-lattices on W which are locally isometric to L. The number of isometry classes in
$\text {gen}(L)$
is called the class number of L and denoted by
$h(L)$
. If an integer a is represented by L over
${\mathbb Z}_p$
for all primes p (including
$\infty $
), then there is a
${\mathbb Z}$
-lattice K in
$\text {gen}(L)$
such that
$a{\ \longrightarrow \ } K$
(see [Reference O’Meara12, 102:5 Example]). In this case, we say that a is represented by the genus of L and write
$a{\ \longrightarrow \ } \text {gen}(L)$
. For a
${\mathbb Z}$
-basis
$\{ \mathbf {v}_1,\mathbf {v}_2,\ldots ,\mathbf {v}_k\}$
of L, the corresponding quadratic form
$f_L$
is defined by
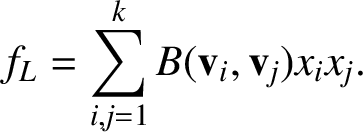$$ \begin{align*}f_L=\sum_{i,j=1}^k B(\mathbf{v}_i,\mathbf{v}_j)x_ix_j. \end{align*} $$
If L admits an orthogonal basis
$\{\mathbf {w}_1,\mathbf {w}_2,\ldots ,\mathbf {w}_k\}$
, then we simply write
$$ \begin{align*}L\simeq \langle Q(\mathbf{w}_1),Q(\mathbf{w}_2),\ldots,Q(\mathbf{w}_k)\rangle. \end{align*} $$
We abuse the notation and the diagonal quadratic form
$a_1x_1^2+a_2x_2^2+\cdots +a_kx_k^2$
will also be denoted by
$\langle a_1,a_2,\ldots ,a_k\rangle $
. The scale of L is denoted by
$\mathfrak {s}(L)$
. Throughout, we always assume that every
${\mathbb Z}$
-lattice is positive definite and primitive in the sense that
$\mathfrak {s}(L)={\mathbb Z}$
. Any unexplained notation and terminologies on the representation of quadratic forms can be found in [Reference Kitaoka11] or [Reference O’Meara12].
Throughout this section, S always denotes a set of nonnegative integers containing
$0$
and
$1$
, unless otherwise stated. For a vector
$\mathbf {a}=(a_1,a_2,\ldots ,a_k)\in {\mathbb N}^k$
, we define
$$ \begin{align*}V_S(\mathbf{a})=\{ a_1s_1+a_2s_2+\cdots+a_ks_k : s_i\in S\} \end{align*} $$
and define
$V^{\prime }_S(\mathbf {a})=V_S(\mathbf {a})-\{0\}$
. For example, if S is the set of squares of integers, then
$$ \begin{align*}V^{\prime}_S(1,1,1,1)={\mathbb N},\quad V^{\prime}_S(1,1,1)={\mathbb N}-\{4^a(8b+7) : a,b\in {\mathbb N}_0\} \end{align*} $$
by Lagrange’s four-square theorem and Legendre’s three-square theorem, respectively. We denote the set of nonnegative integers by
${\mathbb N}_0$
for simplicity. For two vectors
$\mathbf {u}=(u_1,u_2,\ldots ,u_r)\in {\mathbb N}^r$
and
$\mathbf {v}=(v_1,v_2,\ldots ,v_s)\in {\mathbb N}^s$
, we write
$$ \begin{align*}\mathbf{u}\preceq \mathbf{v}\quad (\mathbf{u}\prec \mathbf{v}) \end{align*} $$
if
$\{u_i\}_{1\le i\le r}$
is a subsequence (proper subsequence, respectively) of
$\{v_j\}_{1\le j\le s}$
. Let n be a positive integer and let
$\mathbf {a}$
be a vector of positive integers. We say that
$\mathbf {a}$
is tight
$\mathcal T(n)$
-universal with respect to S if
$V^{\prime }_S(\mathbf {a})=\mathcal T(n)$
. When
$n=1$
, we simply say that
$\mathbf {a}$
is universal with respect to S. We say that
$\mathbf {a}$
is new tight
$\mathcal T(n)$
-universal with respect to S if
$V^{\prime }_S(\mathbf {a})=\mathcal T(n)$
and
$V^{\prime }_S(\mathbf {b})\subsetneq \mathcal T(n)$
whenever
$\mathbf {b}\prec \mathbf {a}$
. For
$n_1,n_2,\ldots ,n_r\in {\mathbb N}$
and
$e_1,e_2,\ldots ,e_r\in {\mathbb N}_0$
, we denote by
$ \mathbf {n_1}^{e_1}\mathbf {n_2}^{e_2}\cdots \mathbf {n_r}^{e_r} $
the vector
$$ \begin{align*}(n_1,\ldots,n_1,n_2,\ldots,n_2,\ldots,n_r,\ldots,n_r)\in {\mathbb Z}^{e_1+e_2+\cdots+e_r}, \end{align*} $$
where each
$n_i$
is repeated
$e_i$
times for
$i=1,2,\ldots ,r$
. The first lemma is straightforward.
Lemma 2.1. Let
$\mathbf {a},\mathbf {b}$
be vectors of positive integers such that
$\mathbf {a}\preceq \mathbf {b}$
and let
$S, S^{\prime }$
be sets of nonnegative integers containing
$0$
and
$1$
such that
$S\subseteq S^{\prime }$
. Then:
-
(i)
$V_S(\mathbf {a})\subseteq V_S(\mathbf {b})$
; -
(ii)
$V_S(\mathbf {a})\subseteq V_{S^{\prime }}(\mathbf {a})$
; -
(iii)
$V_S(u+v)\subset V_S(u,v)$
for any
$u,v\in {\mathbb N}$
; -
(iv)
$\min (V^{\prime }_S(\mathbf {a}))=\min \{a_i : 1\le i\le k\}$
, where
$\mathbf {a}=(a_1,a_2,\ldots ,a_k)$
.
Lemma 2.2. Let
$\mathbf {a}=\mathbf {1}^{e_1}\mathbf {2}^{e_2}\mathbf {3}^{e_3}$
be a vector with a positive integer
$e_1$
and nonnegative integers
$e_2$
and
$e_3$
. Assume that
$V_S(\mathbf {a})={\mathbb N}_0$
. Then, for any integer
$n\ge 2e_3+3$
, the vector
$$ \begin{align*}\mathbf{b}=\mathbf{n}^{e_1}\mathbf{n+1}^1\mathbf{n+2}^1\cdots \mathbf{2n-1}^1\mathbf{2n}^{e_2} \end{align*} $$
is tight
$\mathcal T(n)$
-universal with respect to S.
Proof. Let n be an integer with
$n\ge 2e_3+3$
and let m be an integer greater than or equal to n. Then m can be written in the form
$un+v$
for a nonnegative integer u and an integer v with
$n\le v\le 2n-1$
. To prove the lemma, it suffices to show that
$un+v\in V_S(\mathbf {b})$
. Since
$$ \begin{align*}u\in {\mathbb N}_0 =V_S(\mathbf{a})=V_S(\mathbf{1}^{e_1}\mathbf{2}^{e_2}\mathbf{3}^{e_3}), \end{align*} $$
we have
$$ \begin{align*}un\in V_S(\mathbf{n}^{e_1}\mathbf{2n}^{e_2}\mathbf{3n}^{e_3}). \end{align*} $$
Since the other cases can be dealt with in a similar manner, we only provide the proof when
$$ \begin{align*}n+1\le v\le e_3+1\quad \text{or}\quad 2n-e_3-1\le v\le 2n-1. \end{align*} $$
By applying Lemma 2.1(iii)
$e_3$
times,
$$ \begin{align*}V_S(\mathbf{3n}^{e_3})\subseteq V_S(n+1,2n-1,n+2,2n-2,\ldots,\widehat{v},\widehat{3n-v},\ldots,n+e_3+1,2n-e_3-1), \end{align*} $$
where the hat symbol
$\,\hat {}\,$
indicates that the component is omitted. It follows that
$$ \begin{align*} un&\in V_S(\mathbf{n}^{e_1}\mathbf{2n}^{e_2}\mathbf{3n}^{e_3})\\ &\subseteq V_S(\mathbf{n}^{e_1}\mathbf{2n}^{e_2}\mathbf{n+1}^1\mathbf{2n-1}^1\cdots \widehat{\mathbf{v}^1}\widehat{\mathbf{3n-v}^1}\cdots \mathbf{n+e_3+1}^1\mathbf{2n-e_3-1}^1). \end{align*} $$
Therefore,
$$ \begin{align*} un+v&\in V_S(\mathbf{n}^{e_1}\mathbf{2n}^{e_2}\mathbf{n+1}^1\mathbf{2n-1}^1\cdots \mathbf{v}^1\mathbf{3n-v}^1\cdots \mathbf{n+e_3+1}^1\mathbf{2n-e_3-1}^1)\\ &\subseteq V_S(\mathbf{n}^{e_1}\mathbf{n+1}^1\mathbf{n+2}^1\cdots \mathbf{2n-1}^1\mathbf{2n}^{e_2}). \end{align*} $$
This completes the proof.
For
$n=1,2,3,\ldots $
, we define vectors
$\mathbf {x}_n, \mathbf {y}_n\in {\mathbb Z}^{n+1}$
by
$$ \begin{align*}\mathbf{x}_n=(n,n,n+1,n+2,\ldots,2n-1),\quad \mathbf{y}_n=(n,n+1,n+2,\ldots,2n). \end{align*} $$
Lemma 2.3. Let n be a positive integer and let
$\mathbf {a}=(a_1,a_2,\ldots ,a_k)\in {\mathbb N}^k$
with
$a_1\le a_2\le \cdots \le a_k$
such that
$V^{\prime }_S(\mathbf {a})=\mathcal T(n)$
. Then
$(n,n+1,n+2,\ldots ,2n-1)\preceq \mathbf {a}$
. Furthermore, if
$2\not \in S$
, then
$\mathbf {x}_n\preceq \mathbf {a}$
or
$\mathbf {y}_n\preceq \mathbf {a}$
.
Proof. Since
$V^{\prime }_S(\mathbf {a})=\mathcal T(n)$
,
$$ \begin{align} n=a_1\le a_2\le \cdots \le a_k. \end{align} $$
To prove the first assertion, it suffices to show that for any integer v with
$n+1\le v\le 2n-1$
, there is an integer
$j_v$
with
$1\le j_v\le k$
such that
$a_{j_v}=v$
. Let v be an integer such that
$n+1\le v\le 2n-1$
. Since
$v\in V^{\prime }_S(\mathbf {a})$
, we have
$ v=a_1s_1+a_2s_2+\cdots +a_ks_k $
for some
$s_1,s_2,\ldots ,s_k\in S$
. Since
$v>0$
, there is an integer
$j_v$
with
$1\le j_v\le k$
such that
$s_{j_v}>0$
. If
$s_l>0$
for some l different from
$j_v$
, then
$$ \begin{align*}v=a_1s_1+a_2s_2+\cdots+a_ks_k\ge a_{j_v}s_{j_v}+a_ls_l\ge a_{j_v}+a_l\ge 2n \end{align*} $$
by (2.1) and this is absurd since
$v\le 2n-1$
. It follows that
$s_{j_v}=1$
and
$s_l=0$
for any
$l\neq j_v$
. Thus,
$v=a_{j_v}$
and the first assertion follows.
Now we assume further that
$2\not \in S$
. Then clearly
$$ \begin{align*}2n\in V_S(\mathbf{a})-V_S(n,n+1,n+2,\ldots,2n-1). \end{align*} $$
From this, one may easily deduce that
$$ \begin{align*}(n,n,n+1,n+2,\ldots,2n-1)\preceq \mathbf{a}\quad\text{or}\quad(n,n+1,n+2,\ldots,2n-1,2n)\preceq \mathbf{a}. \end{align*} $$
This completes the proof.
3 Tight
$\mathcal T(n)$
-universal sums of (generalised) m-gonal numbers
Let m be an integer greater than or equal to 3. We denote the set of (generalised) m-gonal numbers by
$\mathcal {P}_m$
(respectively,
$\mathcal {GP}_m$
), that is,
$$ \begin{align*}\mathcal{P}_m=\bigg\{ \frac{(m-2)x^2-(m-4)x}2 : x\in {\mathbb N}_0 \bigg\}, \quad \mathcal{GP}_m=\bigg\{ \frac{(m-2)x^2-(m-4)x}2 : x\in {\mathbb Z} \bigg\}. \end{align*} $$
One may easily check that:
-
(i)
$\{0,1\} \subset \mathcal {P}_m\subseteq \mathcal {GP}_m$
for any
$m\ge 3$
; -
(ii)
$2\not \in \mathcal {P}_m$
for any
$m\ge 3$
; -
(iii)
$2\in \mathcal {GP}_m$
only if
$m=5$
; -
(iv)
$\mathcal {P}_3=\mathcal {GP}_3=\mathcal {GP}_6$
; -
(v)
$\mathcal {P}_4=\mathcal {GP}_4$
.
Proposition 3.1. Let m be an integer greater than or equal to
$8$
. If
$n\ge 2m-5$
, then both
$\mathbf {x}_n$
and
$\mathbf {y}_n$
are tight
$\mathcal T(n)$
-universal with respect to
$\mathcal {GP}_m$
.
Proof. By [Reference Sun13, Theorem 1.1] and [Reference Kim8, Theorem 3.2],
$ V_{\mathcal {GP}_m}(\mathbf {1}^{m-4})={\mathbb N}_0. $
From this, one may easily deduce that
$ V_{\mathcal {GP}_m}(\mathbf {1}^{e_1}\mathbf {2}^{e_2}\mathbf {3}^{m-4})={\mathbb N}_0 $
for
$(e_1,e_2)\in \{(2,0),(1,1)\}$
. Now the proposition follows immediately from Lemma 2.2.
Theorem 3.2. Let m be an integer greater than or equal to
$8$
. If
$n\ge 2m-5$
, then there are exactly two new tight
$\mathcal T(n)$
-universal m-gonal forms.
Proof. Note that
$2\not \in \mathcal {GP}_m$
since
$m\neq 5$
. The theorem follows immediately from the second assertion of Lemma 2.3 and Proposition 3.1.
Proposition 3.3. There is only one new tight
$\mathcal T(n)$
-universal pentagonal form for any
$n\ge 7$
.
Proof. Note that the vector
$(1,3,3)$
is universal with respect to
$\mathcal {GP}_5$
(see [Reference Ge and Sun4]). By Lemma 2.2, the vector
$ (n,n+1,n+2,\ldots ,2n-1) $
is tight
$\mathcal T(n)$
-universal with respect to
$\mathcal {GP}_5$
for any
$n\ge 7$
. Now the proposition follows immediately from the first assertion of Lemma 2.3.
Proposition 3.4. There are exactly two new tight
$\mathcal T(n)$
-universal heptagonal forms for any
$n\ge 11$
.
Proof. Note that
$V_{\mathcal {GP}_7}(1,1,1,1)={\mathbb N}_0$
(see [Reference Sun13] or [Reference Kim8, Theorem 1.2]). It follows that
$ V_{\mathcal {GP}_7}(\mathbf {1}^{e_1}\mathbf {2}^{e_2}\mathbf {3}^4)={\mathbb N}_0 $
for
$(e_1,e_2)\in \{(2,0),(1,1)\}$
. The proposition follows immediately from Lemma 2.2 and the second assertion of Lemma 2.3.
Let n be a positive integer. Now we define (new) tight
$\mathcal T(n)$
-universal sums of m-gonal numbers. For an integer
$m\ge 3$
and a vector
$\mathbf {a}$
of positive integers, we call the pair
$(\mathcal P_m,\mathbf {a})$
a sum of m-gonal numbers. We say that
$(\mathcal P_m,\mathbf {a})$
is tight
$\mathcal T(n)$
-universal if
$V^{\prime }_{\mathcal P_m}(\mathbf {a})=\mathcal T(n)$
. A tight
$\mathcal T(n)$
-universal sum of m-gonal numbers
$(\mathcal P_m,\mathbf {a})$
is called new if
$(\mathcal P_m,\mathbf {b})$
is not
$\mathcal T(n)$
-universal whenever
$\mathbf {b}\prec \mathbf {a}$
or, equivalently,
$V^{\prime }_{\mathcal P_m}(\mathbf {b})\subsetneq \mathcal T(n)$
whenever
$\mathbf {b}\prec \mathbf {a}$
.
Proposition 3.5. Let m be an integer greater than or equal to
$3$
. If
$n\ge 2m+3$
, then both
$(\mathcal P_m,\mathbf {x}_n)$
and
$(\mathcal P_m,\mathbf {y}_n)$
are tight
$\mathcal T(n)$
-universal.
Proof. Fermat’s polygonal number theorem says that
$ V_{\mathcal {P}_m}(\mathbf {1}^m)={\mathbb N}_0. $
From this, one may easily deduce that
$ V_{\mathcal {P}_m}(\mathbf {1}^{e_1}\mathbf {2}^{e_2}\mathbf {3}^m)={\mathbb N}_0 $
for
$(e_1,e_2)\in \{(2,0),(1,1)\}$
. Now the tight
$\mathcal T(n)$
-universalities (with respect to
$\mathcal {P}_m$
) of
$\mathbf {x}_n$
and
$\mathbf {y}_n$
follow immediately from Lemma 2.2.
Theorem 3.6. Let m be an integer greater than or equal to
$3$
. If
$n\ge 2m+3$
, then there are exactly two new tight
$\mathcal T(n)$
-universal sums of m-gonal numbers.
4 Tight universal triangular forms
In this section, we classify tight universal triangular forms. As noted in the introduction, for
$n=1,2$
, tight
$\mathcal T(n)$
-universal triangular forms were already classified. We first prove that there are exactly 12 new tight
$\mathcal T(3)$
-universal triangular forms as listed in Table 1. We also prove that there are exactly two new tight
$\mathcal T(n)$
-universal triangular forms
$$ \begin{align*}X_n=p_3(n,n,n+1,n+2,\ldots,2n-1)\quad \text{and}\quad Y_n=p_3(n,n+1,n+2,\ldots,2n-1,2n) \end{align*} $$
for any
$n\ge 4$
. We introduce some notation which will be used throughout this section. Recall that a triangular form is a polynomial of the form
$$ \begin{align*}p_3(a_1,a_2,\ldots,a_k)=a_1\frac{x_1(x_1+1)}{2}+\cdots+a_k\frac{x_k(x_k+1)}{2}, \end{align*} $$
where
$(a_1,a_2,\ldots ,a_k)$
is a vector of positive integers. For a nonnegative integer g and a triangular form
$p_3(a_1,a_2,\ldots ,a_k)$
, we write
$$ \begin{align*}g{\ \longrightarrow \ } p_3(a_1,a_2,\ldots,a_k) \end{align*} $$
if g is represented by
$p_3(a_1,a_2,\ldots ,a_k)$
. For a positive integer u and a diagonal quadratic form
$\langle a_1,a_2,\ldots ,a_k\rangle $
, we write
$$ \begin{align*}u{\ \overset{2}{\longrightarrow} \ } \langle a_1,a_2,\ldots,a_k\rangle \end{align*} $$
if there is a vector
$(x_1,x_2,\ldots ,x_k)\in {\mathbb Z}^k$
with
$(2,x_1x_2\cdots x_k)=1$
such that
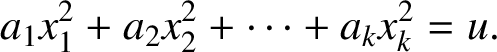$$ \begin{align*}a_1x_1^2+a_2x_2^2+\cdots+a_kx_k^2=u. \end{align*} $$
One may easily see the following observation, which will be used to show the tight universality of triangular forms: a nonnegative integer g is represented by a triangular form
$p_3(a_1,a_2,\ldots ,a_k)$
if and only if
$$ \begin{align*}8g+a_1+a_2+\cdots+a_k{\ \overset{2}{\longrightarrow} \ } \langle a_1,a_2,\ldots,a_k\rangle. \end{align*} $$
A ternary triangular form
$p_3(a,b,c)$
is called regular if, for every nonnegative integer g, the following holds: if
$8g+a+b+c{\ \longrightarrow \ } \langle a,b,c\rangle $
over
${\mathbb Z}_p$
for every odd prime p, then
$8g+a+b+c{\ \overset {2}{\longrightarrow } \ } \langle a,b,c\rangle $
. For more information about regular ternary triangular forms, we refer the reader to [Reference Kim and Oh9].
Table 1 New tight
$\mathcal T(3)$
-universal triangular forms
$p_3(a_1,a_2,\ldots ,a_k)$
.
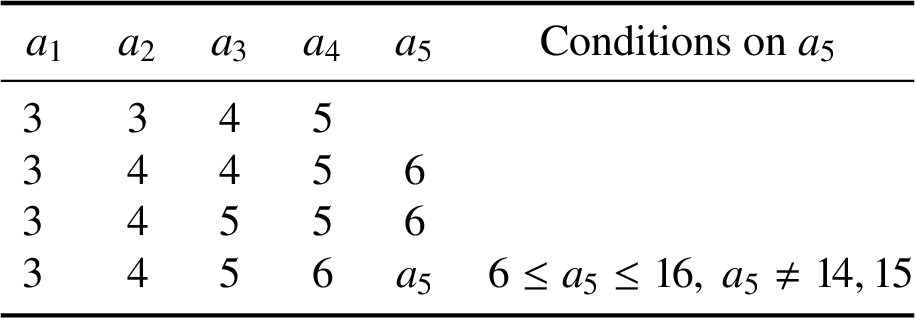
Proposition 4.1. The quaternary triangular form
$X_3=p_3(3,3,4,5)$
is tight
$\mathcal T(3)$
-universal.
Proof. One may directly check that
$X_3$
represents all integers from 3 to 14. Let g be a positive integer greater than 14 and put
$g^{\prime }=8g+15$
. To show that g is represented by
$X_3$
, it suffices to show that
$ g^{\prime }{\ \overset {2}{\longrightarrow } \ } \langle 3,3,4,5\rangle. $
Define sets A and B by
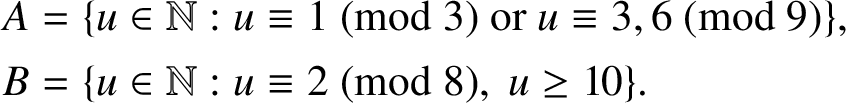$$ \begin{align*} A&=\{ u\in {\mathbb N} : u\equiv 1\ (\mathrm{mod}\ 3 ) \ \text{or}\ u\equiv 3,6\ (\mathrm{mod}\ 9 ) \}, \\ B&=\{ u\in {\mathbb N} : u\equiv 2\ (\mathrm{mod}\ 8 ),\ u\ge 10\}. \end{align*} $$
We assert that
$ v{\ \overset {2}{\longrightarrow } \ } \langle 3,3,4\rangle $
for any
$v\in A\cap B$
. To show the assertion, let
$v\in A\cap B$
. One may easily check that every positive integer in A is represented by the diagonal quadratic form
$\langle 3,3,4\rangle $
over
${\mathbb Z}_3$
. Note that
$\langle 3,3,4\rangle $
represents all elements in
${\mathbb Z}_p$
over
${\mathbb Z}_p$
for any prime
$p\ge 5$
. Thus,
$ v{\ \longrightarrow \ } \langle 3,3,4\rangle $
over
${\mathbb Z}_p$
for all odd primes p. Furthermore,
$v=8v^{\prime }+10$
for some nonnegative integer
$v^{\prime }$
since
$v\in B$
. From these statements and the fact that the ternary triangular form
$p_3(3,3,4)$
is regular (see [Reference Kim and Oh9]), it follows that
$ v{\ \overset {2}{\longrightarrow } \ } \langle 3,3,4\rangle. $
So, we have the assertion.
If we define an odd positive integer d by
$$ \begin{align*}d=\begin{cases} 1\quad &\text{if } g^{\prime}\equiv 0\ (\mathrm{mod}\ 3 ) \ \ \text{or}\ \ g^{\prime}\equiv 2,8\ (\mathrm{mod}\ 9 ) ,\\ 3\quad&\text{if } g^{\prime}\equiv 1\ (\mathrm{mod}\ 3 ) ,\\ 5\quad&\text{if } g^{\prime}\equiv 5\ (\mathrm{mod}\ 9 ) ,\end{cases} \end{align*} $$
then one may easily check that
$g^{\prime }-5d^2\in A\cap B$
. Thus,
$ g^{\prime }-5d^2{\ \overset {2}{\longrightarrow } \ } \langle 3,3,4\rangle. $
Since d is odd, it follows that
$ g^{\prime }{\ \overset {2}{\longrightarrow } \ } \langle 3,3,4,5\rangle. $
This completes the proof.
We use the following lemma proved by B. W. Jones in his unpublished thesis [Reference Jones5].
Lemma 4.2 (Jones).
Let p be an odd prime and k be a positive integer not divisible by p such that the Diophantine equation
$x^2+ky^2=p$
has an integer solution. If the Diophantine equation
$$ \begin{align*}x^2+ky^2=N\quad (N>0) \end{align*} $$
has an integer solution, then it also has an integer solution
$(x_0,y_0)$
satisfying
$$ \begin{align*}\gcd(x_0,y_0,p)=1. \end{align*} $$
Proposition 4.3. Let g be a positive integer congruent to
$5$
modulo
$8$
. Assume that g is congruent to
$1$
modulo
$3$
or is a multiple of
$9$
. Then g is represented by the diagonal ternary quadratic form
$3x^2+4y^2+6z^2$
.
Proof. Let
$L=\langle 3,4,6\rangle $
. The class number
$h(L)$
of L is 2 and the genus mate is
$\langle 1,6,12\rangle $
. From the assumptions, one may easily check that
$ g{\ \longrightarrow \ } \text {gen}(\langle 3,4,6\rangle ). $
We may assume that
$g{\ \longrightarrow \ } \langle 1,6,12\rangle $
since otherwise we are done. Thus, there is a vector
$(x_1,y_1,z_1)\in {\mathbb Z}^3$
such that
$$ \begin{align*}g=x_1^2+6y_1^2+12z_1^2. \end{align*} $$
First, assume that
$g\equiv 0\ (\mathrm {mod}\ 9 )$
. One may easily check that
$x_1\equiv 0\ (\mathrm {mod}\ 3 )$
and that
$y_1\equiv 0\ (\mathrm {mod}\ 3 )$
if and only if
$z_1\equiv 0\ (\mathrm {mod}\ 3 )$
. By changing the sign of
$z_1$
if necessary, we may further assume that
$y_1\equiv z_1\ (\mathrm {mod}\ 3 )$
. Thus,
$x_1=3x_2$
and
$y_1=z_1-3y_2$
with integers
$x_2$
and
$y_2$
. Now
$$ \begin{align*} g&=x_1^2+6y_1^2+12z_1^2\\ &=(3x_2)^2+6(z_1-3y_2)^2+12z_1^2\\ &=3(x_2+2y_2-2z_1)^2+4(3y_2)^2+6(x_2-y_2+z_1)^2. \end{align*} $$
Second, assume that
$g\equiv 1\ (\mathrm {mod}\ 3 )$
. If
$y_1^2+2z_1^2=0$
, then
$g=x_1^2$
and this is absurd since
$g\equiv 5\ (\mathrm {mod}\ 8 )$
. Hence,
$y_1^2+2z_1^2\neq 0$
and thus, by Lemma 4.2, there are integers
$y_3$
and
$z_3$
with
$\gcd (y_3,z_3,3)=1$
such that
$$ \begin{align*}y_1^2+2z_1^2=y_3^2+2z_3^2. \end{align*} $$
Note that
$x_1\not \equiv 0\ (\mathrm {mod}\ 3 )$
since
$g\equiv 1\ (\mathrm {mod}\ 3 )$
. After changing the signs of
$y_3$
and
$z_3$
if necessary, we may assume that
$x_1+y_3+2z_3\equiv 0\ (\mathrm {mod}\ 3 )$
. Then
$$ \begin{align*} g&=x_1^2+6y_3^2+12z_3^2\\ &=3\bigg( \frac{x_1-2y_3-4z_3}{3}\bigg)^2+4( y_3-z_3)^2+6\bigg( \frac{x_1+y_3+2z_3}{3}\bigg)^2. \end{align*} $$
Since
$x_1-2y_3-4z_3\equiv x_1+y_3+2z_3\equiv 0\ (\mathrm {mod}\ 3 )$
, we have
$g{\ \longrightarrow \ } L$
. This completes the proof.
Proposition 4.4. The quaternary triangular form
$Y_3=p_3(3,4,5,6)$
represents all positive integers except
$1$
,
$2$
and
$16$
.
Proof. One may directly check that
$Y_3$
represents all integers from 3 to 29 except 16. Let g be an integer greater than 29 and put
$g^{\prime }=8g+18$
. If we define an odd positive integer d by
$$ \begin{align*}d=\begin{cases} 1\quad&\text{if } g^{\prime}\equiv 0\ (\mathrm{mod}\ 3 ) \ \ \text{or}\ \ g^{\prime}\equiv 5\ (\mathrm{mod}\ 9 ) ,\\ 3\quad&\text{if } g^{\prime}\equiv 1\ (\mathrm{mod}\ 3 ) ,\\ 5\quad&\text{if } g^{\prime}\equiv 8\ (\mathrm{mod}\ 9 ) ,\\ 7\quad&\text{if } g^{\prime}\equiv 2\ (\mathrm{mod}\ 9 ) ,\end{cases} \end{align*} $$
then one may easily check that
$g^{\prime }-5d^2\equiv 1\ (\mathrm {mod}\ 3 )$
or
$g^{\prime }-5d^2\equiv 0\ (\mathrm {mod}\ 9 )$
. Furthermore,
$g^{\prime }-5d^2\equiv 5\ (\mathrm {mod}\ 8 )$
since d is odd. Hence,
$g^{\prime }-5d^2{\ \longrightarrow \ } \langle 3,4,6\rangle $
by Proposition 4.3. Thus, there is a vector
$(x,y,z)\in {\mathbb Z}^3$
such that
$ g^{\prime }\kern-3pt -5d^2{\kern2pt=\kern2pt}3x^2{\kern1.5pt+\kern2pt}4y^2{\kern1.5pt+\kern2pt}6z^2. $
One may easily deduce from
$g^{\prime }-5d^2\equiv 5\ (\mathrm {mod}\ 8 )$
that
$xyz\equiv 1\ (\mathrm {mod}\ 2 )$
. Thus,
$g^{\prime }{\ \overset {2}{\longrightarrow } \ } \langle 3,4,5,6\rangle $
. This completes the proof.
Corollary 4.5. All of the quinary triangular forms in Table 1 are tight
$\mathcal T(3)$
-universal.
Proof. Let
$Z=p_3(a_1,a_2,a_3,a_4,a_5)$
be any quinary triangular form in Table 1. One may see that
$$ \begin{align*}(3,4,5,6)\prec (a_1,a_2,a_3,a_4,a_5). \end{align*} $$
From this and Proposition 4.4, it follows that Z represents every integer greater than or equal to 3 except 16. One may directly check that Z also represents 16. This completes the proof.
Proposition 4.6. Every new tight
$\mathcal T(3)$
-universal triangular form appears in Table 1.
Proof. Let
$p_3=p_3(a_1,a_2,\ldots ,a_k)$
be a new tight
$\mathcal T(3)$
-universal triangular form. By Lemma 2.3, we have
$X_3\preceq p_3$
or
$Y_3\preceq p_3$
.
First, assume that
$X_3\preceq p_3$
. From the fact that
$X_3$
is tight
$\mathcal T(3)$
-universal and the assumption that
$p_3$
is new tight
$\mathcal T(3)$
-universal, it follows that
$p_3=X_3$
.
Second, assume that
$Y_3\preceq p_3$
. Since
$Y_3$
is not
$\mathcal T(3)$
-universal, it follows that
$k>4$
and there is a vector
$(\kern2pt j_1,j_2,j_3,j_4)\in {\mathbb Z}^4$
with
$ (\kern2pt j_1,j_2,j_3,j_4)\prec (1,2,\ldots ,k) $
such that
$(a_{j_1},a_{j_2},a_{j_3},a_{j_4})=(3,4,5,6)$
. We put
$ A=\{u\in {\mathbb N} : 3\le u\le 16, u\neq 14,15\}. $
If
$a_j\not \in A$
for every
$j\in \{1,2,\ldots ,k\} \setminus \{\kern2pt j_1,j_2,j_3,j_4\}$
, then one may easily show that
$p_3$
cannot represent 16, which is absurd. Thus, there is an integer j with
$$ \begin{align*}j\in \{1,2,\ldots,k\} \setminus \{\kern2pt j_1,j_2,j_3,j_4\} \end{align*} $$
such that
$a_j\in A$
. One may check that
$p_3(a_{j_1},a_{j_2},a_{j_3},a_{j_4},a_j)$
is in Table 1 and thus it is tight
$\mathcal T(3)$
-universal. It follows that
$k=5$
and
$p_3=p_3(a_{j_1},a_{j_2},a_{j_3},a_{j_4},a_j)$
since otherwise
$p_3$
is not new. This completes the proof.
Theorem 4.7. For any integer n greater than or equal to
$3$
, the triangular form
$X_n=p_3(n,n,n+1,n+2,\ldots ,2n-1)$
is tight
$\mathcal T(n)$
-universal.
Proof. First, assume that
$n\ge 6$
. Let g be an integer greater than or equal to n. Then g can be written in the form
$g=un+v$
for some nonnegative integer u and an integer v with
$n\le v\le 2n-1$
. Note that the ternary triangular form
$p_3(1,1,4)$
is universal and thus it represents u. Thus,
$un$
is represented by
$p_3(n,n,4n)$
. It follows that
$un$
is represented by
$p_3(n,n,n+1,n+2,2n-3)$
. Thus, if
$v\not \in \{n+1,n+2,2n-3\}$
, then
$un+v$
is represented by
$p_3(n,n,n+1,n+2,2n-3,v)$
and thus by
$X_n$
. On the other hand, the ternary triangular form
$p_3(1,1,5)$
is also universal. Hence,
$un$
is represented by
$p_3(n,n,5n)$
and thus also represented by
$p_3(n,n,n+3,2n-2,2n-1)$
. From this we deduce that if
$v \not\in \{n+3,2n-2,2n-1\}$
, then
$un+v$
is represented by
$p_3(n,n,n+3,2n-2,2n-1,v)$
and thus by
$X_n$
.
Second, assume that
$n=5$
. Let g be an integer greater than or equal to 236. We write
$g=15u+v$
, where u is a positive integer and v is an integer such that
$0\le v\le 14$
. Note that the ternary triangular form
$p_3(1,1,3)$
is regular. For any nonnegative integer w, both
$8\cdot 3w+5$
and
$8(3w+1)+5$
are represented by
$\langle 1,1,3\rangle $
over
${\mathbb Z}_3$
. Thus,
$p_3(1,1,3)$
represents every nonnegative integer not equivalent to 2 modulo 3. It follows that
$p_3(5,5,6+9)$
represents every nonnegative integer congruent to 0 or 5 modulo 15. Hence, if
$v\in \{0,5\}$
, then
$ g=15u+v{\ \longrightarrow \ } p_3(5,5,6+9) $
and so
$ g{\ \longrightarrow \ } p_3(5,5,6,9). $
One may directly check that the binary triangular form
$p_3(7,8)$
represents all integers in the set
$$ \begin{align*}\{31,122,48,94,80,231,7,8,24\}. \end{align*} $$
If
$v\not \in \{0,5\}$
, then one may easily see that there is a positive integer a in the above set such that
$g-a$
is a nonnegative integer congruent to 0 or 5 modulo 15. Thus, we have
$g-a{\ \longrightarrow \ } p_3(5,5,6+9,7,8)$
. One may directly check that
$p_3(5,5,6,7,8,9)$
represents all integers from 5 to 235.
Third, assume that
$n=4$
. Note that the ternary triangular form
$p_3(2,2,3)$
is regular. From this, one may easily show that it represents every nonnegative integer not congruent to 1 modulo 3. Thus,
$p_3(4,4,6)$
represents every nonnegative integer of the form
$6u$
and
$6u+4$
, where
$u\in {\mathbb Z}_{\ge 0}$
. Note that
$p_3(5,7)$
represents 5, 7, 15 and 26 as
$$ \begin{align*}5=5\cdot 1+7\cdot 0,\ 7=5\cdot 0+7\cdot 1,\ 15=5\cdot 3+7\cdot 0,\ 26=5\cdot 1+7\cdot 3. \end{align*} $$
From this and the fact that
$p_3(4,4,6)$
represents every nonnegative integer of the form
$6u$
, it follows that
$p_3(4,4,5,6,7)$
represents every nonnegative integer of the form
$$ \begin{align*}6u+7,\quad 6u+26,\quad 6u+15\quad \text{and}\quad 6u+5. \end{align*} $$
One may directly check that
$p_3(4,4,5,6,7)$
represents all integers from 4 to 25.
The case of
$n=3$
was already proved in Proposition 4.1. This completes the proof.
Theorem 4.8. For any integer n greater than or equal to
$4$
, the triangular form
$Y_n=p_3(n,n+1,n+2,\ldots ,2n)$
is tight
$\mathcal T(n)$
-universal.
Proof. First, assume that the integer n is greater than 4. Let g be an integer greater than or equal to n. We write
$g=un+v$
for some nonnegative integer u and an integer v with
$n\le v\le 2n-1$
. Since
$n\ge 5$
, there is an integer
$n_1$
with
$1\le n_1\le [ n/2 ]$
such that the three integers
$n+n_1$
,
$2n-n_1$
and v are all distinct. Since the ternary triangular form
$p_3(1,2,3)$
is universal, every nonnegative integer which is a multiple of n is represented by
$p_3(n,2n,3n)$
and thus also by
$p_3(n,2n,n+n_1,2n-n_1)$
. It follows that
$g=un+v$
is represented by
$p_3(n,2n,n+n_1,2n-n_1,v)$
. From this and the choice of v, it follows that g is represented by
$Y_n$
.
Now we assume that
$n=4$
. Let
$g_1$
be an integer greater than or equal to 830. If we define two odd positive integers
$\alpha $
and
$\beta $
as
$$ \begin{align*}(\alpha,\beta)=\begin{cases} (1,1)\quad&\text{if } g_1\equiv 0\ (\mathrm{mod}\ 6 ),\\ (1,17)\quad&\text{if } g_1\equiv 1\ (\mathrm{mod}\ 6 ),\\ (3,43)\quad&\text{if } g_1\equiv 2\ (\mathrm{mod}\ 6 ),\\ (3,27)\quad&\text{if } g_1\equiv 3\ (\mathrm{mod}\ 6 ),\\ (1,33)\quad&\text{if } g_1\equiv 4\ (\mathrm{mod}\ 6 ),\\ (5,37)\quad&\text{if } g_1\equiv 5\ (\mathrm{mod}\ 6 ),\end{cases} \end{align*} $$
then one may easily check that
$8g_1+30-5\alpha ^2-7\beta ^2$
is a nonnegative integer congruent to 18 modulo 48. Put
$$ \begin{align*}s=8g_1+30-5\alpha^2-7\beta^2 \end{align*} $$
and let
$L=\langle 4,6,8\rangle $
. We assert that
$s{\ \overset {2}{\longrightarrow } \ } L$
. One may easily check that s is locally represented by L. Note that the class number of L is 2 and the genus mate is
$M=\langle 2,4,24\rangle $
. If
$s{\ \longrightarrow \ } L$
, then we have
$s{\ \overset {2}{\longrightarrow } \ } L$
since
$s\equiv 2\ (\mathrm {mod}\ 16 )$
. Hence, we may assume that
$s{\ \longrightarrow \ } M$
. Thus, there is a vector
$(x,y,z)\in {\mathbb Z}^3$
such that
$$ \begin{align*}s=2x^2+4y^2+24z^2. \end{align*} $$
Since
$s\equiv 0\ (\mathrm {mod}\ 3 )$
, either
$xy\not \equiv 0\ (\mathrm {mod}\ 3 )$
or
$x\equiv y\equiv 0\ (\mathrm {mod}\ 3 )$
holds. After changing the sign of y if necessary, we may assume that
$x\equiv y\ (\mathrm {mod}\ 3 )$
. If we put
$x=y-3x_1$
, then
$$ \begin{align*} s&=2x^2+4y^2+24z^2\\ &=2(y-3x_1)^2+4y^2+24z^2\\ &=4(x_1+2z)^2+6(x_1-y)^2+8(x_1-z)^2. \end{align*} $$
In the above equation, one may easily deduce that
$$ \begin{align*}x_1+2z\equiv x_1-y\equiv x_1-z\equiv 1\ (\mathrm{mod}\ 2 ) \end{align*} $$
from the fact that
$s\equiv 2\ (\mathrm {mod}\ 16 )$
. Thus, we have
$s{\ \overset {2}{\longrightarrow } \ } L$
. It follows immediately from this that
$$ \begin{align*}8g_1+30{\ \overset{2}{\longrightarrow} \ } \langle 4,5,6,7,8\rangle, \end{align*} $$
which is equivalent to
$g_1{\ \longrightarrow \ } Y_4$
. On the other hand, one may directly check that
$Y_4$
represents all integers from 4 to 829. This completes the proof.
Theorem 4.9. For any integer n exceeding
$3$
, there are exactly two new tight
$\mathcal T(n)$
-universal triangular forms
$X_n$
and
$Y_n$
.
