Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-06T18:43:44.393Z Has data issue: false hasContentIssue false
  • English
  • Français

STABLE SOLUTIONS TO THE STATIC CHOQUARD EQUATION

Part of: Partial differential equations Equations of mathematical physics and other areas of application Elliptic equations and systems

Published online by Cambridge University Press:  10 June 2020

PHUONG LE
PHUONG LE*
Affiliation:
Division of Computational Mathematics and Engineering, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam email lephuong@tdtu.edu.vn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is concerned with the static Choquard equation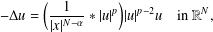

$$\begin{eqnarray}-\unicode[STIX]{x1D6E5}u=\bigg(\frac{1}{|x|^{N-\unicode[STIX]{x1D6FC}}}\ast |u|^{p}\bigg)|u|^{p-2}u\quad \text{in }\mathbb{R}^{N},\end{eqnarray}$$
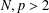where $N,p>2$ and 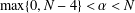$\max \{0,N-4\}<\unicode[STIX]{x1D6FC}<N$. We prove that if 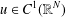$u\in C^{1}(\mathbb{R}^{N})$ is a stable weak solution of the equation, then 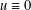$u\equiv 0$. This phenomenon is quite different from that of the local Lane–Emden equation, where such a result only holds for low exponents in high dimensions. Our result is the first Liouville theorem for Choquard-type equations with supercritical exponents and 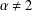$\unicode[STIX]{x1D6FC}\neq 2$.

Keywords

Choquard equationstable solutionLiouville theoremsupercritical exponent

MSC classification

Primary: 35J61: Semilinear elliptic equations
Secondary: 35B35: Stability 35B53: Liouville theorems, Phragmén-Lindelöf theorems 35Q40: PDEs in connection with quantum mechanics
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 3 , December 2020 , pp. 471 - 478
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

References

Chen, C., Song, H. and Yang, H., ‘Liouville type theorems for stable solutions of p-Laplace equation in ℝN’, Nonlinear Anal. 160 (2017), 44–52.10.1016/j.na.2017.05.004CrossRefGoogle Scholar
Dai, W., Huang, J., Qin, Y., Wang, B. and Fang, Y., ‘Regularity and classification of solutions to static Hartree equations involving fractional Laplacians’, Discrete Contin. Dyn. Syst. 39(3) (2019), 1389–1403.10.3934/dcds.2018117CrossRefGoogle Scholar
Damascelli, L., Farina, A., Sciunzi, B. and Valdinoci, E., ‘Liouville results for m-Laplace equations of Lane–Emden–Fowler type’, Ann. Inst. H. Poincaré Anal. Non Linéaire 26(4) (2009), 1099–1119.10.1016/j.anihpc.2008.06.001CrossRefGoogle Scholar
Dávila, J., Dupaigne, L., Wang, K. and Wei, J., ‘A monotonicity formula and a Liouville-type theorem for a fourth order supercritical problem’, Adv. Math. 258 (2014), 240–285.10.1016/j.aim.2014.02.034CrossRefGoogle Scholar
Dupaigne, L., Stable Solutions of Elliptic Partial Differential Equations, Chapman and Hall/CRC Monographs and Surveys in Pure and Applied Mathematics, 143 (Chapman and Hall/CRC, Boca Raton, FL, 2011).10.1201/b10802CrossRefGoogle Scholar
Farina, A., ‘On the classification of solutions of the Lane–Emden equation on unbounded domains of ℝN’, J. Math. Pures Appl. (9) 87(5) (2007), 537–561.10.1016/j.matpur.2007.03.001CrossRefGoogle Scholar
Gidas, B. and Spruck, J., ‘Global and local behavior of positive solutions of nonlinear elliptic equations’, Comm. Pure Appl. Math. 34(4) (1981), 525–598.10.1002/cpa.3160340406CrossRefGoogle Scholar
Guo, L., T., Hu, S., Peng and Shuai, W., ‘Existence and uniqueness of solutions for Choquard equation involving Hardy–Littlewood–Sobolev critical exponent’, Calc. Var. Partial Differential Equations 58(4) (2019), 58–128.10.1007/s00526-019-1585-1CrossRefGoogle Scholar
Huynh, N. V. and Le, P., ‘Instability of solutions to Kirchhoff type problems in low dimension’, Ann. Polon. Math. 124(1) (2020), 75–91.10.4064/ap181120-3-5CrossRefGoogle Scholar
Joseph, D. D. and Lundgren, T. S., ‘Quasilinear Dirichlet problems driven by positive sources’, Arch. Ration. Mech. Anal. 49 (1972–1973), 241–269.10.1007/BF00250508CrossRefGoogle Scholar
Le, P., ‘Liouville theorem for stable weak solutions of elliptic equations involving Grushin operator’, Commun. Pure Appl. Anal. 19 (2020), 511–525.10.3934/cpaa.2020025CrossRefGoogle Scholar
Le, P., ‘On classical solutions to the Hartree equation’, J. Math. Anal. Appl. 485(2) (2020), 123859.10.1016/j.jmaa.2020.123859CrossRefGoogle Scholar
Le, P. and Ho, V., ‘Liouville results for stable solutions of quasilinear equations with weights’, Acta Math. Sci. Ser. B (Engl. Ed.) 39(2) (2019), 357–368.Google Scholar
Lei, Y., ‘Liouville theorems and classification results for a nonlocal Schrödinger equation’, Discrete Contin. Dyn. Syst. 38(11) (2018), 5351–5377.10.3934/dcds.2018236CrossRefGoogle Scholar
Lieb, E. H., ‘Existence and uniqueness of the minimizing solution of Choquard’s nonlinear equation’, Stud. Appl. Math. 57(2) (1976–1977), 93–105.10.1002/sapm197757293CrossRefGoogle Scholar
Lieb, E. H. and Simon, B., ‘The Hartree–Fock theory for Coulomb systems’, Comm. Math. Phys. 53(3) (1977), 185–194.10.1007/BF01609845CrossRefGoogle Scholar
Lions, P.-L., ‘The Choquard equation and related questions’, Nonlinear Anal. 4(6) (1980), 1063–1072.10.1016/0362-546X(80)90016-4CrossRefGoogle Scholar
Ma, L. and Zhao, L., ‘Classification of positive solitary solutions of the nonlinear Choquard equation’, Arch. Ration. Mech. Anal. 195(2) (2010), 455–467.10.1007/s00205-008-0208-3CrossRefGoogle Scholar
Moroz, I. M., Penrose, R. and Tod, P., ‘Spherically-symmetric solutions of the Schrödinger–Newton equations’, Classical Quantum Gravity 15(9) (1998), 2733–2742; Topology of the Universe Conf., Cleveland, OH, 1997.10.1088/0264-9381/15/9/019CrossRefGoogle Scholar
Moroz, V. and Van Schaftingen, J., ‘Groundstates of nonlinear Choquard equations: existence, qualitative properties and decay asymptotics’, J. Funct. Anal. 265(2) (2013), 153–184.10.1016/j.jfa.2013.04.007CrossRefGoogle Scholar
Moroz, V. and Van Schaftingen, J., ‘A guide to the Choquard equation’, J. Fixed Point Theory Appl. 19(1) (2017), 773–813.10.1007/s11784-016-0373-1CrossRefGoogle Scholar
Nazin, G. I., ‘Limit distribution functions of systems with many-particle interactions in classical statistical physics’, Teoret. Mat. Fiz. 25(1) (1975), 132–140.Google Scholar
Wang, C. and Ye, D., ‘Some Liouville theorems for Hénon type elliptic equations’, J. Funct. Anal. 262(4) (2012), 1705–1727.10.1016/j.jfa.2011.11.017CrossRefGoogle Scholar
Yang, J. and Yu, X., ‘Liouville type theorems for Hartree and Hartree–Fock equations’, Nonlinear Anal. 183 (2019), 191–213.10.1016/j.na.2019.01.012CrossRefGoogle Scholar
Zhao, X., ‘Liouville theorem for Choquard equation with finite Morse indices’, Acta Math. Sci. Ser. B (Engl. Ed.) 38(2) (2018), 673–680.Google Scholar