Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-14T09:15:41.848Z Has data issue: false hasContentIssue false
  • English
  • Français

STABILITY OF AN EXPONENTIAL-MONOMIAL FUNCTIONAL EQUATION

Published online by Cambridge University Press:  28 March 2018

CHANG-KWON CHOI Open the ORCID record for CHANG-KWON CHOI [Opens in a new window]
CHANG-KWON CHOI*
Affiliation:
Department of Mathematics and Liberal Education Institute, Kunsan National University, Gunsan 54150, Republic of Korea email ck38@kunsan.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $N$ be a fixed positive integer and 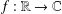$f:\mathbb{R}\rightarrow \mathbb{C}$. As a generalisation of the superstability of the exponential functional equation we consider the functional inequalities

$$\begin{eqnarray}\displaystyle & \displaystyle \big|f\big(\!\sqrt[N]{x^{N}+y^{N}}\big)-f(x)f(y)\big|\leq \unicode[STIX]{x1D719}(x), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \big|f\big(\!\sqrt[N]{x^{N}+y^{N}}\big)-f(x)f(y)\big|\leq \unicode[STIX]{x1D713}(x,y) & \displaystyle \nonumber\end{eqnarray}$$
for all $x,y\in \mathbb{R}$, where 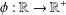$\unicode[STIX]{x1D719}:\mathbb{R}\rightarrow \mathbb{R}^{+}$ is an arbitrary function and 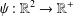$\unicode[STIX]{x1D713}:\mathbb{R}^{2}\rightarrow \mathbb{R}^{+}$ satisfies a certain condition.

Keywords

exponential functional equationexponential-monomial functional equationstability

MSC classification

Primary: 39B82: Stability, separation, extension, and related topics
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 3 , June 2018 , pp. 471 - 479
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Baker, J. A., ‘The stability of the cosine functional equation’, Proc. Amer. Math. Soc. 80 (1980), 411–416.CrossRefGoogle Scholar
Baker, J. A., Lawrence, J. and Zorzitto, F., ‘The stability of the equation f (x + y) = f (x)f (y)’, Proc. Amer. Math. Soc. 74 (1979), 242–246.Google Scholar
Brzdȩk, J., ‘Remarks on solutions to the functional equations of the radical type’, Adv. Theor. Nonlinear Anal. Appl. 1(2) (2017), 125–135.Google Scholar
Brzdȩk, J., Najdecki, A. and Xu, B., ‘Two general theorems on superstability of functional equations’, Aequationes Math. 89 (2015), 771–783.Google Scholar
Chung, J., ‘General stability of the exponential and Lobačevskiǐ functional equations’, Bull. Aust. Math. Soc. 94(2) (2016), 278–285.Google Scholar
Gǎvruţǎ, P., ‘An answer to a question of Th. M. Rassias and J. Tabor on mixed stability of mappings’, Bul. St. Univ. ‘Politehnica’ Timisoara Ser. Mat. Fiz. 42(56) (1997), 1–6.Google Scholar
Hyers, D. H., ‘On the stability of the linear functional equation’, Proc. Natl. Acad. Sci. USA 27 (1941), 222–224.Google Scholar
Hyers, D. H., Isac, G. and Rassias, Th. M., Stability of Functional Equations in Several Variables (Birkhauser, Basel, 1998).Google Scholar
Jung, S.-M., Hyers–Ulam–Rassias Stability of Functional Equations in Nonlinear Analysis (Springer, New York, 2011).Google Scholar
Székelyhidi, L., ‘On a theorem of Baker, Lawrence and Zorzitto’, Proc. Amer. Math. Soc. 84 (1982), 95–96.Google Scholar
Ulam, S. M., Problems in Modern Mathematics (Wiley, New York, 1940), Ch. 6.Google Scholar