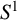1 Introduction
In [Reference Spielberg14], Spielberg showed that every Kirchberg (that is, simple, nuclear, purely infinite and separable) algebra which satisfies the universal coefficient theorem (UCT) admits a Hausdorff groupoid model and hence admits a Cartan subalgebra. Conversely, it was shown by Barlak and Li in [Reference Barlak and Li2] that any separable and nuclear
$C^*$
-algebra which has a Cartan subalgebra satisfies the UCT.
Given an étale non-Hausdorff groupoid G, there are dynamical criteria which ensure that the essential
$C^*$
-algebra of G is a Kirchberg algebra. Since, in general,
$C^*_{\mathrm {ess}}(G)$
does not admit any obvious Cartan subalgebra, it seems natural to look at such groupoids as potential sources of counterexamples to the UCT problem (which asks whether every separable nuclear
$C^*$
-algebra satisfies the UCT).
Let
$G(T,S^1)$
be the groupoid of germs of the action of Thompson’s group T on
$S^1$
. In [Reference Kalantar and Scarparo7], Kalantar and the author showed that the reduced
$C^*$
-algebra of
$G(T,S^1)$
is not simple, even though
$G(T,S^1)$
is minimal and effective. Moreover, as observed in [Reference Kalantar and Scarparo7], it follows from results of Kwaśniewski and Meyer [Reference Kwaśniewski and Meyer8] that
$C^*_{\mathrm {ess}}(G(T,S^1))$
is purely infinite and simple. In this paper, we show that
$G(T,S^1)$
is Borel amenable. Since, as observed by Renault in [Reference Renault13], the results on nuclearity of groupoid
$C^*$
-algebras from the work of Anantharaman-Delaroche and Renault [Reference Anantharaman-Delaroche and Renault1] use only Borel amenability and hold in the non-Hausdorff setting as well, we conclude that
$C^*_{\mathrm {ess}}(G(T,S^1))$
is a Kirchberg algebra. We leave open the question of whether
$C^*_{\mathrm {ess}}(G(T,S^1))$
admits a Cartan subalgebra (equivalently, whether it satisfies the UCT).
Let
$\Gamma $
be a group acting on a locally compact Hausdorff space X and on a set K. In [Reference Ozawa11], Ozawa studied the existence of nets of continuous approximately equivariant maps
$\mu _i\colon X\to \operatorname {Prob}(K)$
. Clearly, the existence of such maps generalises both topological amenability (in the case
$K=\Gamma )$
and set-theoretical amenability (in the case that X consists of a single point). If such a property holds in the case that K is a set of left cosets
$\Gamma /\Lambda $
, we say that X is
$(\Gamma ,\Lambda)$
-amenable. We show that this property generalises the notion of relative co-amenability introduced by Caprace and Monod in [Reference Caprace and Monod6] (in the more general setting of locally compact groups).
Consider Thompson’s groups
$F\leq T$
. We show that
$S^1$
is
$(T,F)$
-amenable and use this fact to conclude that F is exact if and only if T is exact.
2 Relatively amenable actions
Given a set Y, we consider
$\operatorname {Prob}(Y):=\{\mu \in \ell ^1(Y):\mu \geq 0, \|\mu \|_1=1\}$
equipped with the pointwise convergence topology.
Given a group
$\Gamma $
acting by homeomorphisms on a locally compact Hausdorff space X, we say that X is a locally compact
$\Gamma $
-space. Given
$\Lambda \leq \Gamma $
, we say that X is
$(\Gamma ,\Lambda )$
-amenable if there exists a net of continuous functions
$\mu _i\colon X\to \operatorname {Prob}(\Gamma /\Lambda )$
which is approximately invariant in the sense that
$$ \begin{align*} \lim_i\sup_{x\in K}\|s\mu_i(x)-\mu_i(sx)\|_1= 0 \end{align*} $$
for all
$s\in \Gamma $
and
$K\subset X$
compact. If
$\Lambda =\{e\}$
, this is the usual notion of (topologically) amenable action on a space X [Reference Anantharaman-Delaroche and Renault1, Example 2.2.14(2)]. If
$\Lambda $
is co-amenable in
$\Gamma $
, then any
$\Gamma $
-space is
$(\Gamma ,\Lambda )$
-amenable.
We will need the following result.
Proposition 2.1 [Reference Brown and Ozawa4, Proposition 5.2.1]
Let X be a compact
$\Gamma $
-space which is
$(\Gamma ,\Lambda )$
-amenable for some
$\Lambda \leq \Gamma $
. If
$\Lambda $
is exact, then
$\Gamma $
is exact.
Let us now characterise
$(\Gamma ,\Lambda )$
-amenability in the case of a discrete
$\Gamma $
-space.
Proposition 2.2. Let S be a discrete
$\Gamma $
-space and
$\Lambda \leq \Gamma $
. The space S is
$(\Gamma ,\Lambda )$
-amenable if and only if there exists a unital positive
$\Gamma $
-equivariant linear map
$\varphi \colon \ell ^\infty (\Gamma /\Lambda )\to \ell ^\infty (S)$
.
Proof. We identify the space of bounded linear maps
$\mathcal {L}(\ell ^\infty (\Gamma /\Lambda ),\ell ^\infty (S))$
with
$\ell ^\infty (S,\ell ^\infty (\Gamma /\Lambda )^*)$
. Under this identification, a unital positive
$\Gamma $
-equivariant map
$\varphi \in \mathcal {L}(\ell ^\infty (\Gamma /\Lambda ),\ell ^\infty (S))$
corresponds to a map
$\psi \colon S\to \ell ^\infty (\Gamma /\Lambda )^*$
such that
$\psi (s)$
is a state and
$\psi (gs)=g(\psi (s))$
for every
$s\in S$
and
$g\in \Gamma $
.
Suppose that S is
$(\Gamma ,\Lambda )$
-amenable and let
$\mu _i\colon S\to \operatorname {Prob}(\Gamma /\Lambda )\subset \ell ^\infty (\Gamma /\Lambda )^*$
be a net of approximately invariant functions. By taking a subnet, we may assume that, for each
$s\in S$
,
$\mu _i(s)$
converges in the weak-
$*$
topology to a state
$\psi (s)\in \ell ^\infty (\Gamma /\Lambda )^*$
. Clearly,
$\psi \colon S\to \ell ^\infty (\Gamma /\Lambda )^*$
has the desired properties.
Conversely, suppose that there exists a map
$\psi \in \ell ^\infty (S,\ell ^\infty (\Gamma /\Lambda )^*)$
which is unital, positive and
$\Gamma $
-equivariant. Since
$\ell ^1(\Gamma )$
is weak-
$*$
dense in
$\ell ^\infty (\Gamma )^*$
, we can find a net
$\mu _i\colon S\to \operatorname {Prob}(\Gamma /\Lambda )\subset \ell ^\infty (\Gamma /\Lambda )^*$
such that, for each
$s\in S$
,
$\mu _i(s)\to \psi (s)$
in the weak-
$*$
topology. By
$\Gamma $
-equivariance of
$\psi $
, the net
$g\mu _i(s)-\mu _i(gs)$
converges to zero weakly in
$\ell ^1(\Gamma /\Lambda )$
for each
$g\in \Gamma $
and
$s\in S$
.
Given
$\epsilon>0$
and finite subsets
$E\subset \Gamma $
and
$F\subset S$
, we claim that there is a function
$\mu \colon S\to \operatorname {Prob}(\Gamma /\Lambda )$
such that
$\|g\mu (x)-\mu (gx)\|_1<\epsilon $
for each
$x\in F$
and
$g\in E$
. From the previous paragraph, it follows that
$0$
is in the weak closure of the convex set
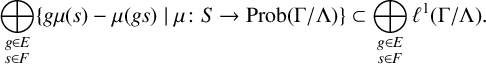$$ \begin{align*}\bigoplus_{\substack{g\in E\\s\in F}}\{g\mu(s)-\mu(gs)\mid\mu\colon S\to\operatorname{Prob}(\Gamma/\Lambda)\}\subset\bigoplus_{\substack{g\in E\\s\in F}}\ell^1(\Gamma/\Lambda).\end{align*} $$
By the Hahn–Banach separation theorem, the claim follows. Thus, S is
$(\Gamma ,\Lambda )$
- amenable.
Remark 2.3. Given a group
$\Gamma $
and subgroups
$\Lambda _1,\Lambda _2\leq \Gamma $
, Proposition 2.2 implies that
$\Gamma /\Lambda _2$
is
$(\Gamma ,\Lambda _1)$
-amenable if and only if
$\Lambda _1$
is co-amenable to
$\Lambda _2$
relative to
$\Gamma $
in the sense of [Reference Caprace and Monod6, Section 7.C].
For completeness, we record the following permanence property. The proof follows the argument in [Reference Brown and Ozawa4, Proposition 5.2.1].
Proposition 2.4. Let X be a locally compact
$\Gamma $
-space and
$\Lambda _1\leq \Lambda _2\leq \Gamma $
be such that X is
$(\Gamma ,\Lambda _2)$
-amenable and
$(\Lambda _2,\Lambda _1)$
-amenable. Then X is
$(\Gamma ,\Lambda _1)$
-amenable.
Proof. Fix
$E\subset \Gamma $
finite,
$\epsilon>0$
and
$K\subset X$
compact. Take
$\eta \colon X\to \operatorname {Prob}(\Gamma /\Lambda _2)$
continuous such that
$\sup _{x\in K}\|s\eta ^x-\eta ^{sx}\|<\epsilon /2$
for all
$s\in E$
. By arguing as in [Reference Brown and Ozawa4, Lemma 4.3.8], we may assume that there is
$F\subset \Gamma /\Lambda _2$
finite such that
$\operatorname {supp}\eta ^x\subset F$
for all
$x\in X$
.
Fix a cross-section
$\sigma \colon \Gamma /\Lambda _2\to \Gamma $
. Let
$$ \begin{align*}E^*:=\{\sigma(sa)^{-1}s\sigma(a ):a\in F, s\in E\}\subset\Lambda_2\end{align*} $$
and
$$ \begin{align*}L:=\bigcup_{a\in F}\sigma(a)^{-1}K.\end{align*} $$
Take
$\nu \colon X\to \operatorname {Prob}(\Lambda _2/\Lambda _1)\subset \operatorname {Prob}(\Gamma /\Lambda _1)$
continuous such that
$$ \begin{align*}\max_{s\in E^*}\sup_{y\in L}\|s\nu(y)-\nu(sy)\|_1<\epsilon/2.\end{align*} $$
Let
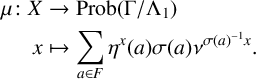$$ \begin{align*} \mu\colon X&\to \operatorname{Prob}(\Gamma/\Lambda_1)\\ x&\mapsto \sum_{a\in F}\eta^x(a)\sigma(a)\nu^{\sigma(a)^{-1}x}. \end{align*} $$
Given
$s\in E$
and
$x\in K$
,
$$ \begin{align*} s\mu(x)&=\sum_{a\in F}\eta^x(a)s\sigma(a)\nu^{\sigma(a)^{-1}x}\\ &=\sum_{a\in \Gamma/\Lambda_2}\eta^x(a)\sigma(sa)\sigma(sa)^{-1}s\sigma(a)\nu^{\sigma(a)^{-1}x}\\ &\approx_{\epsilon/2} \sum_{a\in \Gamma/\Lambda_2}\eta^x(a)\sigma(sa)\nu^{\sigma(sa)^{-1}sx}\\ &\approx_{\epsilon/2} \sum_{a\in \Gamma/\Lambda_2}\eta^{sx}(sa)\sigma(sa)\nu^{\sigma(sa)^{-1}sx}\\ &=\sum_{b\in \Gamma/\Lambda_2}\eta^{sx}(b)\sigma(b)\nu^{\sigma(b)^{-1}sx}=\mu(sx).\\[-46pt] \end{align*} $$
Thompson’s groups. Thompson’s group V consists of piecewise linear, right continuous bijections on
$[0,1)$
which have finitely many points of nondifferentiability, all being dyadic rationals, and have a derivative which is an integer power of two at each point of differentiability.
Let
$\mathcal {W}$
be the set of finite words in the alphabet
$\{0,1\}$
. Given
$w\in \mathcal {W}$
with length
$|w|$
, let
$\mathcal {C}(w):=\{(x_n)\in \{0,1\}^{\mathbb {N}}:x_{[1,|w|]}=w\}$
. Also let
$\psi \colon \mathcal {W}\to [0,1]$
be the map given by
$\psi (w):=\sum _{n=1}^{|w|} x_n2^{-n}$
for
$w\in \mathcal {W}$
. By identifying a set of the form
$\mathcal {C}(w)$
with the half-open interval
$[\psi (w),\psi (w)+2^{-|w|})$
, we can view V as the group of homeomorphisms of
$\{0,1\}^{\mathbb {N}}$
consisting of elements g for which there exist two partitions
$\{\mathcal {C}(w_1),\dots ,\mathcal {C}(w_n)\}$
and
$\{\mathcal {C}_{z_1},\dots ,\mathcal {C}_{z_n}\}$
of
$\{0,1\}^{\mathbb {N}}$
such that
$g(w_ix)=z_ix$
for every i and infinite binary sequence x.
Let
$D:=\{(x_n)\in \{0,1\}^{\mathbb {N}}:\text {there exists}\ k\in {\mathbb {N}}\ \text {such that}\ x_l=0 \ \text {for all}\ l\geq k\}$
. Notice that D is V-invariant. Given
$w\in \mathcal {W}$
, let
$w0^\infty $
be the element of D obtained by extending w with infinitely many
$0$
’s.
Theorem 2.5. There is a sequence of continuous maps
$\mu _N\colon \{0,1\}^{\mathbb {N}}\to \operatorname {Prob}(D)$
such that
$$ \begin{align} \lim_N\sup_{x\in \{0,1\}^{\mathbb{N}}}\|s\mu_N(x)-\mu_N(sx)\|_1=0 \end{align} $$
for every
$s\in V$
.
Proof. Given
$N\in \mathbb {N}$
, let
$\mu _N\colon \{0,1\}^{\mathbb {N}}\to \operatorname {Prob}(D)$
be defined by
$$ \begin{align*}\mu_N(x):=\frac{1}{N}\sum_{j=1}^N\delta_{x_{[1,j]}0^\infty}.\end{align*} $$
Clearly, for each
$d\in D$
and
$N\in \mathbb {N}$
, the map
$x\mapsto \mu _N(x)(d)$
is continuous. We claim that
$(\mu _N)$
satisfies (2.1).
Fix
$s\in V$
. There exist two partitions
$\{\mathcal {C}(w_1),\dots ,\mathcal {C}(w_n)\}$
and
$\{\mathcal {C}_{z_1},\dots ,\mathcal {C}_{z_n}\}$
of
$\{0,1\}^{\mathbb {N}}$
such that
$s(w_ix)=z_ix$
for every i and infinite binary sequence x.
Let
$k(s):=\max _i\{|w_i|,|z_i|-|w_i|\}$
. Fix
$1\leq i \leq n$
and
$x\in \mathcal {C}(w_i)$
. Let
$\alpha _i:=|z_i|-|w_i|$
. Given
$k> k(s)$
,
$$ \begin{align*}s(x_{[1,k]}0^\infty) =z_ix_{[|w_i|+1,k]}0^\infty =s(x)_{[1,|z_i|]}s(x)_{[|z_i|+1,k+|z_i|-|w_i|]}0^\infty =s(x)_{[1,k+\alpha_i]}0^\infty.\end{align*} $$
For
$N>2k(s)$
,
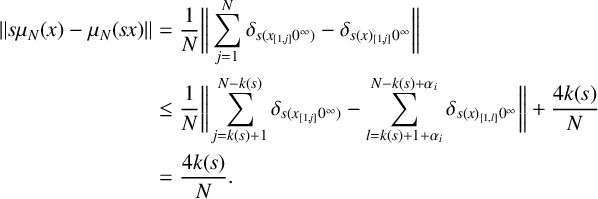$$ \begin{align*} \|s\mu_N(x)-\mu_N(sx)\|&=\frac{1}{N}\bigg\|\sum_{j=1}^N\delta_{s(x_{[1,j]}0^\infty)}-\delta_{s(x)_{[1,j]}0^\infty}\bigg\|\\ &\leq \frac{1}{N}\bigg\|\sum_{j=k(s)+1}^{N-k(s)}\delta_{s(x_{[1,j]}0^\infty)}-\sum_{l=k(s)+1+\alpha_i}^{N-k(s)+\alpha_i}\delta_{s(x)_{[1,l]}0^\infty}\bigg\| + \frac{4k(s)}{N} \\ &=\frac{4k(s)}{N}.\\[-44pt] \end{align*} $$
Thompson’s group T is the subgroup of V consisting of elements which have at most one point of discontinuity. By identifying
$[0,1)$
with
$S^1$
, the elements of T can be seen as homeomorphisms on
$S^1$
. Thompson’s group F is the subgroup of T which stabilises
$1\in S^1$
.
Corollary 2.6. The spaces
$\{0,1\}^{\mathbb {N}}$
and
$S^1$
are
$(T,F)$
-amenable.
Proof. Notice that T acts transitively on
$D\subset \{0,1\}^{\mathbb {N}}$
. Since F is the stabiliser of
$0^\infty \in D$
, it follows immediately from Theorem 2.5 that
$\{0,1\}^{\mathbb {N}}$
is
$(T,F)$
-amenable.
Let
$\varphi \colon S^1\to \{0,1\}^{\mathbb {N}}$
be the map which, given
$\theta \in [0,1)$
, sends
$e^{2\pi i \theta }$
to the binary expansion of
$\theta $
. Clearly,
$\varphi $
is T-equivariant and Borel measurable. Since
$\{0,1\}^{\mathbb {N}}$
is
$(T,F)$
-amenable, composition with
$\varphi $
gives rise to a sequence
$u_n\colon S^1\to \operatorname {Prob}(T/F)$
of approximately T-equivariant pointwise Borel maps (in the sense that for each
$d\in T/F$
, the map
$x\mapsto u_n(x)(d)$
is Borel). It follows from [Reference Brown and Ozawa4, Proposition 5.2.1] (or [Reference Ozawa11, Proposition 11]) that
$S^1$
is
$(T,F)$
-amenable.
The next result follows immediately from Proposition 2.1 and Corollary 2.6.
Corollary 2.7. Thompson’s group F is exact if and only if Thompson’s group T is exact.
The next result has been recorded in [Reference Monod9, Section 3.2] as a consequence of hyperfiniteness of the equivalence relation of T on
$S^1$
. It also follows from the fact that stabilisers of amenable actions are amenable, Proposition 2.4 and Corollary 2.6.
Corollary 2.8 [Reference Monod9]
The following conditions are equivalent:
-
(i) F is amenable;
-
(ii)
$T\!\curvearrowright \! \{0,1\}^{\mathbb {N}}$
is amenable; -
(iii)
$T\!\curvearrowright \! S^1$
is amenable.
3 Groupoids of germs
We say that a topological groupoid G is étale if its unit space
$G^{(0)}$
is Hausdorff and the range and source maps
$r,s\colon G\to G^{(0)}$
are local homeomorphisms. If G is also second countable, then G is said to be Borel amenable [Reference Renault13, Definition 2.1] if there exists a sequence
$(m_n)_{n\in \mathbb {N}}$
, where each
$m_n$
is a family
$(m_n^x)_{x\in G^{(0)}}$
of probability measures on
$r^{-1}(x)$
such that:
-
(i) for all
$n\in \mathbb {N}$
,
$m_n$
is Borel in the sense that for all bounded Borel functions f on G,
$x\mapsto \sum _{g\in r^{-1}(x)}f(g)m_n^x(g)$
is Borel; -
(ii) for all
$g\in G$
, we have
$\sum _{h\in r^{-1}(r(g))}|m_n^{s(g)}(g^{-1}h)-m_n^{r(g)}(h)|\to 0$
.
Remark 3.1. Let G be a second countable étale groupoid and
$A\subset G^{(0)}$
a measurable subset which is invariant in the sense that
$r^{-1}(A)=s^{-1}(A)$
. In this case,
$G_A:=s^{-1}(A)$
is a subgroupoid of G. If G is Borel amenable, then clearly
$G_A$
is also Borel amenable. Conversely, if
$G_A$
and
$G_{G^{(0)}\setminus A}$
are Borel amenable, then, since
$G=G_A\sqcup G_{G^{(0)}\setminus A}$
, also G is Borel amenable.
Let
$\Gamma $
be a group acting on a compact Hausdorff space X. Given
$x\in X$
, let
$\Gamma _x^{0}:=\{g\in \Gamma :g\ \text {fixes pointwise a neighbourhood of}\ x\}$
be the open stabiliser at x. Consider the following equivalence relation on
$\Gamma \times X$
:
$(g,x)\sim (h,y)$
if and only if
$x=y$
and
$g\Gamma _x^{(0)}=h\Gamma _x^{(0)}$
. As a set, the groupoid of germs of
$\Gamma \!\curvearrowright \! X$
is
$G(\Gamma ,X):={(\Gamma \times X)}/{\sim }$
. The topology on
$G(\Gamma ,X)$
is the one generated by sets of the form
$[g,U]:=\{[g,x]:x\in U\}$
for
$U\subset X$
open and
$g\in \Gamma $
. Inversion in
$G(\Gamma ,X)$
is given by
$[g,x]^{-1}=[g^{-1},gx]$
. Two elements
$[h,y],[g,x]\in G(\Gamma ,X)$
are multipliable if and only if
$y=gx$
, in which case
$[h,y][g,x]:=[hg,x]$
. With this structure,
$G(\Gamma ,X)$
is an étale groupoid.
Example 3.2. Let
$G_{[2]}$
be the Cuntz groupoid introduced in [Reference Renault12, Definition III.2.1]. Since Thompson’s group T can be seen as a covering subgroup of the topological full group of
$G_{[2]}$
[Reference Brix and Scarparo3, Example 3.3], it follows from [Reference Nyland and Ortega10, Proposition 4.10] that
$G(T,\{0,1\}^{\mathbb {N}})\simeq G_{[2]}$
. Hence,
$G(T,\{0,1\}^{\mathbb {N}})$
is Borel amenable by [Reference Renault12, Proposition III.2.5].
Theorem 3.3. The groupoid of germs of
$T\!\curvearrowright \! S^1$
is Borel amenable.
Proof. Let
$X:=\{e^{2\pi i\theta }:\theta \in \mathbb {Z}[1/2]\}$
and
$Y:=S^1\setminus X$
. Notice that X is T-invariant. We will show that
$G(T,S^1)_X$
and
$G(T,S^1)_Y$
are Borel amenable. From Remark 3.1, it will follow that
$G(T,S^1)$
is Borel amenable.
Let
$\varphi \colon S^1\to \{0,1\}^{\mathbb {N}}$
be the T-equivariant map, which, given
$\theta \in [0,1)$
, sends
$e^{2\pi i \theta }$
to the binary expansion of
$\theta $
. Notice that
$\varphi |_Y\colon Y\to \varphi (Y)$
is a homeomorphism. Furthermore, the map
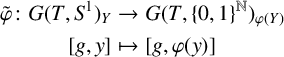$$ \begin{align*}\tilde{\varphi}\colon G(T,S^1)_Y&\to G(T,\{0,1\}^{\mathbb{N}})_{\varphi(Y)}\\[1pt][g,y]&\mapsto[g,\varphi(y)] \end{align*} $$
is an isomorphism of topological groupoids. Therefore,
$G(T,S^1)_Y$
is Borel amenable by Remark 3.1 and Example 3.2.
Notice that
$G(T,S^1)_X$
is a countable set. It follows from [Reference Cannon, Floyd and Parry5, Theorem 4.1] that the open stabiliser
$T_1^0$
is equal to the commutator subgroup
$[F,F]$
and
$F/{[F,F]}\simeq \mathbb {Z}^2$
. Therefore,
$\kern-1ptG(T,S^1\kern-1pt)_X$
is Borel isomorphic to the transitive discrete groupoid
$X\kern-1pt\times X\kern-1pt\times \mathbb {Z}^2$
, which, due to the amenability of the isotropy group, is Borel amenable.
Acknowledgement
I am grateful to Nicolas Monod for comments on a preliminary version.
