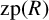1 Introduction
Group theoretical problems related to discrete probabilities have been extensively studied (see, for example, [Reference Barry, MacHale and Ni She2, Reference Guralnick and Robinson8, Reference Gustafson9, Reference Lescot12, Reference Rusin16]). Recently, there has been interest in using a similar approach with rings, mainly concerning the commuting probability (also called the commutativity degree) [Reference Buckley and MacHale3–Reference Dutta, Basnet and Nath5, Reference MacHale13] and the probability of zero multiplication (also called the nullity degree) [Reference Esmkhani and Jafarian Amiri6, Reference Esmkhani and Jafarian Amiri7] of finite rings. However, all recent results regarding the nullity degree have been obtained in the setting of finite commutative rings.
We investigate the nullity degree of an arbitrary finite ring with identity. The nullity degree of R is
![]() ${\mathrm {zp}}(R) = {|\{(x, y) \in R \times R: xy = 0\}|}/{|R|^2}$
, that is, the probability that the multiplication of two randomly chosen elements of R is zero. In Section 2, we find the nullity degree of an arbitrary semisimple ring. In Section 3, we generalise the notion of a nullity degree to ideals and consider the relations between the nullity degree of the ring and the nullity degree of an ideal, with an emphasis on the Jacobson radical. In the final section, we find upper and lower bounds for the nullity degree, whereby we also generalise and improve some of the results from [Reference Esmkhani and Jafarian Amiri6].
${\mathrm {zp}}(R) = {|\{(x, y) \in R \times R: xy = 0\}|}/{|R|^2}$
, that is, the probability that the multiplication of two randomly chosen elements of R is zero. In Section 2, we find the nullity degree of an arbitrary semisimple ring. In Section 3, we generalise the notion of a nullity degree to ideals and consider the relations between the nullity degree of the ring and the nullity degree of an ideal, with an emphasis on the Jacobson radical. In the final section, we find upper and lower bounds for the nullity degree, whereby we also generalise and improve some of the results from [Reference Esmkhani and Jafarian Amiri6].
We recall some basic definitions that are needed in this paper. Let
![]() $Z(R)$
be the set of zero divisors of the finite ring R. Note that by [Reference Kobayashi and Koh10, Proposition 1.3], every left zero divisor is also a right zero divisor and vice versa, so we do not need to make a distinction between left and right zero divisors. We denote by
$Z(R)$
be the set of zero divisors of the finite ring R. Note that by [Reference Kobayashi and Koh10, Proposition 1.3], every left zero divisor is also a right zero divisor and vice versa, so we do not need to make a distinction between left and right zero divisors. We denote by
![]() $R^*$
the group of invertible elements of R, while for an element
$R^*$
the group of invertible elements of R, while for an element
![]() $x \in R$
, we denote the right annihilator of x in R by
$x \in R$
, we denote the right annihilator of x in R by
![]() ${\mathrm {Ann}}(x)=\{y \in R: xy=0\}$
. We say that
${\mathrm {Ann}}(x)=\{y \in R: xy=0\}$
. We say that
![]() $e \in R$
is an idempotent if
$e \in R$
is an idempotent if
![]() $e^2=e$
, and e is a nontrivial idempotent if
$e^2=e$
, and e is a nontrivial idempotent if
![]() $e \neq 0,1$
. Idempotents e and f are orthogonal if
$e \neq 0,1$
. Idempotents e and f are orthogonal if
![]() $ef=fe=0$
. We introduce a binary relation on the set of idempotents with
$ef=fe=0$
. We introduce a binary relation on the set of idempotents with
![]() $e \geq f$
if
$e \geq f$
if
![]() $ef=fe=e$
. The set of all idempotents is partially ordered with this relation, and we call any smallest nonzero idempotent under this relation a minimal idempotent. For a set X, let
$ef=fe=e$
. The set of all idempotents is partially ordered with this relation, and we call any smallest nonzero idempotent under this relation a minimal idempotent. For a set X, let
![]() $|X|$
denote its cardinality. If p is a prime, we say that R is a p-ring if
$|X|$
denote its cardinality. If p is a prime, we say that R is a p-ring if
![]() $|R|=p^k$
for some integer k. We denote the Jacobson radical of R by
$|R|=p^k$
for some integer k. We denote the Jacobson radical of R by
![]() $J(R)$
and say that R is a basic ring if
$J(R)$
and say that R is a basic ring if
![]() $R/J(R)$
is a direct product of finite fields. Also, we denote by
$R/J(R)$
is a direct product of finite fields. Also, we denote by
![]() $\overline {x} \in R/J(R)$
the image of
$\overline {x} \in R/J(R)$
the image of
![]() $x \in R$
under the canonical homomorphism. For a field F, let
$x \in R$
under the canonical homomorphism. For a field F, let
![]() $M_n(F)$
denote the full matrix ring of n-by-n matrices over F, while the ring of integers modulo n will be denoted by
$M_n(F)$
denote the full matrix ring of n-by-n matrices over F, while the ring of integers modulo n will be denoted by
![]() ${\mathbb {Z}}_n$
. We denote the disjoint union of two sets A and B by
${\mathbb {Z}}_n$
. We denote the disjoint union of two sets A and B by
![]() $A \sqcup B$
.
$A \sqcup B$
.
2 Semisimple rings
In this section, we investigate the nullity degree of a semisimple ring. The following lemma is obvious.
Lemma 2.1. For any finite ring R, we have
![]() ${\mathrm {zp}}(R) = {\sum _{x \in R}{|{\mathrm {Ann}}(x)|}}/{|R|^2}$
.
${\mathrm {zp}}(R) = {\sum _{x \in R}{|{\mathrm {Ann}}(x)|}}/{|R|^2}$
.
The following lemma will be useful.
Lemma 2.2. For any finite rings
![]() $R_1, R_2, \ldots , R_n$
, we have
$R_1, R_2, \ldots , R_n$
, we have
![]() ${\mathrm {zp}}(R_1 \times R_2 \times \cdots \times R_n) = {\mathrm {zp}}(R_1) {\mathrm {zp}}(R_2) \cdots {\mathrm {zp}} (R_n)$
.
${\mathrm {zp}}(R_1 \times R_2 \times \cdots \times R_n) = {\mathrm {zp}}(R_1) {\mathrm {zp}}(R_2) \cdots {\mathrm {zp}} (R_n)$
.
Proof. Observe that
![]() ${\mathrm {Ann}}(x_1, x_2, \ldots , x_n) = {\mathrm {Ann}} (x_1) \times {\mathrm {Ann}} (x_2) \times \cdots \times {\mathrm {Ann}}(x_n)$
and use Lemma 2.1.
${\mathrm {Ann}}(x_1, x_2, \ldots , x_n) = {\mathrm {Ann}} (x_1) \times {\mathrm {Ann}} (x_2) \times \cdots \times {\mathrm {Ann}}(x_n)$
and use Lemma 2.1.
Any finite semisimple ring is a direct product of fields and full matrix rings over fields. Thus, to find the nullity degree of an arbitrary finite semisimple ring, we have to investigate the nullity degrees of finite fields and matrix rings over finite fields.
Proposition 2.3. Let F be a finite field and n an integer. Then, the following equations hold:
-
(1)
 ${\mathrm {zp}}(F)={(2 |F| - 1)}/{|F|^2}$
;
${\mathrm {zp}}(F)={(2 |F| - 1)}/{|F|^2}$
; -
(2)
 ${\mathrm {zp}}(M_n(F))={(1+\sum _{r=1}^n{(\prod _{j=0}^{r-1}{{(|F|^n-|F|^j)^2}/{|F|^n(|F|^r-|F|^j)}})})}/{|F|^{n^2}}$
.
${\mathrm {zp}}(M_n(F))={(1+\sum _{r=1}^n{(\prod _{j=0}^{r-1}{{(|F|^n-|F|^j)^2}/{|F|^n(|F|^r-|F|^j)}})})}/{|F|^{n^2}}$
.
Proof. (1) follows from [Reference Esmkhani and Jafarian Amiri6, Lemma 3.1]. To see (2), observe first that
![]() ${\mathrm {zp}}(M_n(F))={\sum _{r=0}^{n}\sum _{{\mathrm {rank}}(A)=r}{{\mathrm {Ann}}(A)}}/{|F|^{2n^2}}$
. Now,
${\mathrm {zp}}(M_n(F))={\sum _{r=0}^{n}\sum _{{\mathrm {rank}}(A)=r}{{\mathrm {Ann}}(A)}}/{|F|^{2n^2}}$
. Now,
![]() $\dim _F(\ker (A))=n-r$
for any matrix A of rank r. Thus, every column of a matrix
$\dim _F(\ker (A))=n-r$
for any matrix A of rank r. Thus, every column of a matrix
![]() $B \in {\mathrm {Ann}}(A)$
is a linear combination of
$B \in {\mathrm {Ann}}(A)$
is a linear combination of
![]() $n-r$
vectors from
$n-r$
vectors from
![]() $\ker (A)$
and thus
$\ker (A)$
and thus
![]() $|{\mathrm {Ann}}(A)|=|F|^{n(n-r)}$
. By [Reference Morrison15], the number of matrices of rank r in
$|{\mathrm {Ann}}(A)|=|F|^{n(n-r)}$
. By [Reference Morrison15], the number of matrices of rank r in
![]() $M_n(F)$
is exactly
$M_n(F)$
is exactly
![]() $\prod _{j=0}^{r-1}{(|F|^n-|F|^j)^2}/{(|F|^r-|F|^j)}$
. Therefore,
$\prod _{j=0}^{r-1}{(|F|^n-|F|^j)^2}/{(|F|^r-|F|^j)}$
. Therefore,
 $$ \begin{align*}{\mathrm{zp}}(M_n(F))=\frac{|F|^{n^2}+\sum_{r=1}^n{|F|^{n(n-r)}(\prod_{j=0}^{r-1}{{(|F|^n-|F|^j)^2}/{(|F|^r-|F|^j)}})}}{|F|^{2n^2}}\end{align*} $$
$$ \begin{align*}{\mathrm{zp}}(M_n(F))=\frac{|F|^{n^2}+\sum_{r=1}^n{|F|^{n(n-r)}(\prod_{j=0}^{r-1}{{(|F|^n-|F|^j)^2}/{(|F|^r-|F|^j)}})}}{|F|^{2n^2}}\end{align*} $$
and thus the desired equality follows.
Since for any ring R, the factor ring
![]() $R/J(R)$
is a semisimple ring, we can now calculate its nullity degree. We thus have the following upper bound for
$R/J(R)$
is a semisimple ring, we can now calculate its nullity degree. We thus have the following upper bound for
![]() ${\mathrm {zp}}(R)$
.
${\mathrm {zp}}(R)$
.
Proposition 2.4. For any finite ring R, we have
![]() ${\mathrm {zp}}(R) \leq {\mathrm {zp}}(R/J(R))$
.
${\mathrm {zp}}(R) \leq {\mathrm {zp}}(R/J(R))$
.
Proof. Denote
![]() $J=J(R)$
. By Lemma 2.1,
$J=J(R)$
. By Lemma 2.1,
 $$ \begin{align*} {\mathrm{zp}}(R/J) = \frac{\sum_{x+J \in R/J}{|{\mathrm{Ann}}(x+J)|}}{|R/J|^2} &\geq \frac{\sum_{x+J \in R/J}{{|{\mathrm{Ann}}(x)|}/{|J|}}}{|R/J|^2} \\ &=\frac{\sum_{x \in R}{{|{\mathrm{Ann}}(x)|}/{|J|^2}}}{|R/J|^2}=\frac{\sum_{x \in R}{|{\mathrm{Ann}}(x)|}}{|R|^2}={\mathrm{zp}}(R).\\[-41pt] \end{align*} $$
$$ \begin{align*} {\mathrm{zp}}(R/J) = \frac{\sum_{x+J \in R/J}{|{\mathrm{Ann}}(x+J)|}}{|R/J|^2} &\geq \frac{\sum_{x+J \in R/J}{{|{\mathrm{Ann}}(x)|}/{|J|}}}{|R/J|^2} \\ &=\frac{\sum_{x \in R}{{|{\mathrm{Ann}}(x)|}/{|J|^2}}}{|R/J|^2}=\frac{\sum_{x \in R}{|{\mathrm{Ann}}(x)|}}{|R|^2}={\mathrm{zp}}(R).\\[-41pt] \end{align*} $$
3 Generalised nullity degree
In this section, we generalise the nullity degree of the ring to the ideals. Let I be an ideal of R.
Definition 3.1. The generalised nullity degree of a finite ring R corresponding to an ideal I is equal to
Obviously,
![]() ${\mathrm {zp}}_{(0)}(R)={\mathrm {zp}}(R)$
. In the general case, we have the following lemma.
${\mathrm {zp}}_{(0)}(R)={\mathrm {zp}}(R)$
. In the general case, we have the following lemma.
Lemma 3.2. For any finite ring R and an ideal I of R, we have
![]() ${\mathrm {zp}}_I(R)={\mathrm {zp}}(R/I)$
.
${\mathrm {zp}}_I(R)={\mathrm {zp}}(R/I)$
.
Proof. Observe that for every
![]() $x, y \in R$
,
$x, y \in R$
,
![]() $xy \in I$
if and only if
$xy \in I$
if and only if
![]() $(x+I)(y+I)=I$
, so for every
$(x+I)(y+I)=I$
, so for every
![]() $x \in R$
we have
$x \in R$
we have
![]() $|\{y \in R; xy \in I \}|{{\kern-1pt}={\kern-1pt}}|{\mathrm {Ann}}(x+I)| |I|$
. Therefore,
$|\{y \in R; xy \in I \}|{{\kern-1pt}={\kern-1pt}}|{\mathrm {Ann}}(x+I)| |I|$
. Therefore,
![]() $\sum _{x \in R}{|\{y \in R; xy \in I \}|}{{\kern-1pt}=} \sum _{x \in R}{|{\mathrm {Ann}}(x+I)||I|}=\sum _{x+I \in R/I}{|{\mathrm {Ann}}(x+I)||I|^2}$
, which is equal to
$\sum _{x \in R}{|\{y \in R; xy \in I \}|}{{\kern-1pt}=} \sum _{x \in R}{|{\mathrm {Ann}}(x+I)||I|}=\sum _{x+I \in R/I}{|{\mathrm {Ann}}(x+I)||I|^2}$
, which is equal to
![]() ${{\mathrm {zp}}(R/I)}/{|R|^2}$
by Lemma 2.1.
${{\mathrm {zp}}(R/I)}/{|R|^2}$
by Lemma 2.1.
We can now prove the following theorem.
Theorem 3.3. For any finite ring R and an ideal I of R, we have
![]() ${\mathrm {zp}}_I(R) \geq |I| {(2|R|-|I|)}/{|R|^2}$
, and the equality holds if and only if the factor ring
${\mathrm {zp}}_I(R) \geq |I| {(2|R|-|I|)}/{|R|^2}$
, and the equality holds if and only if the factor ring
![]() $R/I$
is a field.
$R/I$
is a field.
Proof. Choose
![]() $x \in R$
. If
$x \in R$
. If
![]() $x \in I$
then
$x \in I$
then
![]() $xy \in I$
for all
$xy \in I$
for all
![]() $y \in R$
, and if
$y \in R$
, and if
![]() $x \notin I$
then
$x \notin I$
then
![]() $xy \in I$
for all
$xy \in I$
for all
![]() $y \in I$
. Thus,
$y \in I$
. Thus,
![]() $\sum _{x \in R}{|\{y \in R; xy \in I \}|} \geq |I| |R| + |R \setminus I| |I| = |I| (2|R|-|I|)$
and
$\sum _{x \in R}{|\{y \in R; xy \in I \}|} \geq |I| |R| + |R \setminus I| |I| = |I| (2|R|-|I|)$
and
![]() ${\mathrm {zp}}_I(R) \geq |I| {(2|R|-|I|)}/{|R|^2}$
. Suppose now that
${\mathrm {zp}}_I(R) \geq |I| {(2|R|-|I|)}/{|R|^2}$
. Suppose now that
![]() $R/I$
is a field. Choose
$R/I$
is a field. Choose
![]() $x \in R \setminus I$
. Since
$x \in R \setminus I$
. Since
![]() $\overline {x} \in R/I$
is invertible, the fact that
$\overline {x} \in R/I$
is invertible, the fact that
![]() $xy \in I$
implies
$xy \in I$
implies
![]() $\overline {y}=\overline {0}$
and thus
$\overline {y}=\overline {0}$
and thus
![]() $y \in I$
. So,
$y \in I$
. So,
![]() $xy \in I$
if and only if
$xy \in I$
if and only if
![]() $y \in I$
. We have proved that
$y \in I$
. We have proved that
![]() ${\mathrm {zp}}_I(R) = |I| {(2|R|-|I|)}/{|R|^2}$
. On the other hand, if
${\mathrm {zp}}_I(R) = |I| {(2|R|-|I|)}/{|R|^2}$
. On the other hand, if
![]() ${\mathrm {zp}}_I(R) = |I|{(2|R|-|I|)}/{|R|^2}$
, then for every
${\mathrm {zp}}_I(R) = |I|{(2|R|-|I|)}/{|R|^2}$
, then for every
![]() $x \in R \setminus I$
, the fact that
$x \in R \setminus I$
, the fact that
![]() $xy \in I$
has to imply that
$xy \in I$
has to imply that
![]() $y \in I$
. So, for every nonzero
$y \in I$
. So, for every nonzero
![]() $\overline {x} \in R/I$
, the fact that
$\overline {x} \in R/I$
, the fact that
![]() $\overline {x}\overline {y}=\overline {0}$
implies that
$\overline {x}\overline {y}=\overline {0}$
implies that
![]() $\overline {y}=\overline {0}$
. We have proved that
$\overline {y}=\overline {0}$
. We have proved that
![]() $R/I$
is a ring without nontrivial zero divisors and hence a field.
$R/I$
is a ring without nontrivial zero divisors and hence a field.
This immediately yields the following corollary.
Corollary 3.4. For any finite ring R, we have
![]() ${\mathrm {zp}}(R/J(R)) \geq |J(R)| {(2|R|-|J(R)|)}/{|R|^2}$
, and the equality holds if and only if R is a local ring.
${\mathrm {zp}}(R/J(R)) \geq |J(R)| {(2|R|-|J(R)|)}/{|R|^2}$
, and the equality holds if and only if R is a local ring.
4 Bounds for the nullity degree
In this section, we find some further upper and lower bounds for the nullity degree of finite rings. First, we investigate the upper bounds for
![]() ${\mathrm {zp}}(R)$
.
${\mathrm {zp}}(R)$
.
Theorem 4.1. For a finite ring R, we have
![]() ${\mathrm {zp}}(R) \leq {(|Z(R)|^2+2|R \setminus Z(R)|)}/{|R|^2}$
, and the equality holds if and only if R is a local ring with
${\mathrm {zp}}(R) \leq {(|Z(R)|^2+2|R \setminus Z(R)|)}/{|R|^2}$
, and the equality holds if and only if R is a local ring with
![]() $J(R)^2=0$
.
$J(R)^2=0$
.
Proof. By Lemma 2.1, we have
![]() ${\mathrm {zp}}(R) = {\sum _{x \in R}{|{\mathrm {Ann}}(x)|}}/{|R|^2}$
. Obviously,
${\mathrm {zp}}(R) = {\sum _{x \in R}{|{\mathrm {Ann}}(x)|}}/{|R|^2}$
. Obviously,
![]() $|{\mathrm {Ann}}(x)|=1$
for every x that is not a zero divisor, and
$|{\mathrm {Ann}}(x)|=1$
for every x that is not a zero divisor, and
![]() $|{\mathrm {Ann}}(x)| \leq |Z(R)|$
for any nonzero zero divisor x, and thus
$|{\mathrm {Ann}}(x)| \leq |Z(R)|$
for any nonzero zero divisor x, and thus
![]() ${\mathrm {zp}}(R) \leq {(|R \setminus Z(R)| + |R| + (|Z(R)|-1)|Z(R)|)}/{|R|^2}$
, so we have proved the desired inequality. If R is local with
${\mathrm {zp}}(R) \leq {(|R \setminus Z(R)| + |R| + (|Z(R)|-1)|Z(R)|)}/{|R|^2}$
, so we have proved the desired inequality. If R is local with
![]() $J(R)^2=0$
, then
$J(R)^2=0$
, then
![]() $|{\mathrm {Ann}}(x)| = |Z(R)|$
for every nonzero zero divisor x, so the equality does indeed hold. Conversely, if R is not a local ring, then by [Reference McDonald14, Theorem VII.7] there exists a nontrivial idempotent
$|{\mathrm {Ann}}(x)| = |Z(R)|$
for every nonzero zero divisor x, so the equality does indeed hold. Conversely, if R is not a local ring, then by [Reference McDonald14, Theorem VII.7] there exists a nontrivial idempotent
![]() $e \in Z(R)$
. However, if the equality holds, then
$e \in Z(R)$
. However, if the equality holds, then
![]() $|{\mathrm {Ann}}(x)| = |Z(R)|$
for every nonzero zero divisor x, which implies that
$|{\mathrm {Ann}}(x)| = |Z(R)|$
for every nonzero zero divisor x, which implies that
![]() $e^2=0$
, a contradiction. So, R is local and thus
$e^2=0$
, a contradiction. So, R is local and thus
![]() $J(R)=Z(R)$
, so
$J(R)=Z(R)$
, so
![]() $J(R)^2=0$
.
$J(R)^2=0$
.
We can actually find an even better bound if we have some knowledge of the structure of the orthogonal minimal idempotents in R and the corresponding Peirce decomposition of R. Recall at this point that R is called a basic ring if the factor ring
![]() $R/J(R)$
is a direct product of fields.
$R/J(R)$
is a direct product of fields.
Theorem 4.2. Let R be a finite ring, and let
![]() $e_1,e_2, \ldots , e_n$
be mutually orthogonal minimal idempotents in R such that
$e_1,e_2, \ldots , e_n$
be mutually orthogonal minimal idempotents in R such that
![]() $\sum _{i=1}^n{e_i=1}$
. Denote
$\sum _{i=1}^n{e_i=1}$
. Denote
![]() $N=\{1,2,\ldots ,n\}$
. Then,
$N=\{1,2,\ldots ,n\}$
. Then,
 $$ \begin{align} \mathrm{zp}(R) \leq \sum\limits_{I_1 \sqcup I_2 \subseteq N}{\prod\limits_{i \in I_1}{\frac{|(e_iRe_i)^*|}{|e_iR||e_iRe_i|}}\prod\limits_{j \in I_2}{\frac{|J(e_iRe_i)|-1}{|(e_jRe_j)^*||e_jRe_j|}}}, \end{align} $$
$$ \begin{align} \mathrm{zp}(R) \leq \sum\limits_{I_1 \sqcup I_2 \subseteq N}{\prod\limits_{i \in I_1}{\frac{|(e_iRe_i)^*|}{|e_iR||e_iRe_i|}}\prod\limits_{j \in I_2}{\frac{|J(e_iRe_i)|-1}{|(e_jRe_j)^*||e_jRe_j|}}}, \end{align} $$
and the equality holds if and only if R is a basic ring with
![]() $J(R)^2=0$
.
$J(R)^2=0$
.
Proof. By Lemma 2.1, we have
![]() ${\mathrm {zp}}(R) = {\sum _{x \in R}{|{\mathrm {Ann}}(x)|}}/{|R|^2}$
. Choose
${\mathrm {zp}}(R) = {\sum _{x \in R}{|{\mathrm {Ann}}(x)|}}/{|R|^2}$
. Choose
![]() $x \in R$
. Let
$x \in R$
. Let
![]() $I_1(x)=\{i: e_ixe_i \in (e_iRe_i)^*\} \subseteq N$
and
$I_1(x)=\{i: e_ixe_i \in (e_iRe_i)^*\} \subseteq N$
and
![]() $I_2(x)=\{i: 0 \neq e_ixe_i \in J(e_iRe_i)\} \subseteq N$
. Observe that
$I_2(x)=\{i: 0 \neq e_ixe_i \in J(e_iRe_i)\} \subseteq N$
. Observe that
![]() $I_1(x)$
and
$I_1(x)$
and
![]() $I_2(x)$
are disjoint sets. Note also that every x can be written as
$I_2(x)$
are disjoint sets. Note also that every x can be written as
![]() $x=\sum _{i,j=1}^n{e_ixe_j}$
. Thus, for any disjoint sets
$x=\sum _{i,j=1}^n{e_ixe_j}$
. Thus, for any disjoint sets
![]() $I_1, I_2 \subseteq N$
, there exist exactly
$I_1, I_2 \subseteq N$
, there exist exactly
 $$ \begin{align*}\prod_{i \in I_1}{|(e_iRe_i)^*|} \prod_{j \in I_2}{(|J(e_iRe_i)|-1)} \frac{|R|}{\prod\limits_{i \in I_1 \cup I_2}{|e_iRe_i|}}\end{align*} $$
$$ \begin{align*}\prod_{i \in I_1}{|(e_iRe_i)^*|} \prod_{j \in I_2}{(|J(e_iRe_i)|-1)} \frac{|R|}{\prod\limits_{i \in I_1 \cup I_2}{|e_iRe_i|}}\end{align*} $$
elements in R such that
![]() $I_1(x)=I_1$
and
$I_1(x)=I_1$
and
![]() $I_2(x)=I_2$
. Choose
$I_2(x)=I_2$
. Choose
![]() $y \in {\mathrm {Ann}}(x)$
. For any
$y \in {\mathrm {Ann}}(x)$
. For any
![]() $i \in I_1(x)$
, we have
$i \in I_1(x)$
, we have
![]() $e_ixe_iy=0$
and therefore
$e_ixe_iy=0$
and therefore
![]() $e_iy=0$
. Also, if
$e_iy=0$
. Also, if
![]() $j \in I_2(x)$
then
$j \in I_2(x)$
then
![]() $j \notin I_1(y)$
. Thus,
$j \notin I_1(y)$
. Thus,
![]() $y \in \sum _{k \notin I_1 \cup I_2}{e_kR} + \sum _{k \in I_2, l \neq k}{e_kRe_l} + \sum _{k \in I_2}{J(e_kRe_k)}$
. Therefore,
$y \in \sum _{k \notin I_1 \cup I_2}{e_kR} + \sum _{k \in I_2, l \neq k}{e_kRe_l} + \sum _{k \in I_2}{J(e_kRe_k)}$
. Therefore,
![]() $|{\mathrm {Ann}}(x)|$
is bounded by
$|{\mathrm {Ann}}(x)|$
is bounded by
 $$ \begin{align*}\prod\limits_{i \notin I_1 \cup I_2}{|e_iR|} \prod\limits_{j \in I_2}\frac{|e_jR|}{|(e_jRe_j)^*|}=\frac{|R|}{\prod\limits_{i \in I_1 \cup I_2}{|e_iR|}} \prod\limits_{j \in I_2}\frac{|e_jR|}{|(e_jRe_j)^*|}=\frac{|R|}{\prod\limits_{i \in I_1}{|e_iR|}} \prod\limits_{j \in I_2}\frac{1}{|(e_jRe_j)^*|},\end{align*} $$
$$ \begin{align*}\prod\limits_{i \notin I_1 \cup I_2}{|e_iR|} \prod\limits_{j \in I_2}\frac{|e_jR|}{|(e_jRe_j)^*|}=\frac{|R|}{\prod\limits_{i \in I_1 \cup I_2}{|e_iR|}} \prod\limits_{j \in I_2}\frac{|e_jR|}{|(e_jRe_j)^*|}=\frac{|R|}{\prod\limits_{i \in I_1}{|e_iR|}} \prod\limits_{j \in I_2}\frac{1}{|(e_jRe_j)^*|},\end{align*} $$
and (4.1) holds.
Now, if R is a basic ring with
![]() $J(R)^2=0$
then
$J(R)^2=0$
then
![]() $e_kRe_l \in J(R)$
for all
$e_kRe_l \in J(R)$
for all
![]() $k \neq l$
, so the equality holds in (4.1). Conversely, assume that the equality holds in (4.1). If R is not a basic ring, then by the Wedderburn–Artin theorem there exists a full matrix ring
$k \neq l$
, so the equality holds in (4.1). Conversely, assume that the equality holds in (4.1). If R is not a basic ring, then by the Wedderburn–Artin theorem there exists a full matrix ring
![]() $M_r(F)$
as a subring of
$M_r(F)$
as a subring of
![]() $R/J(R)$
for a field F and an integer r. Thus, there exist two orthogonal minimal idempotents
$R/J(R)$
for a field F and an integer r. Thus, there exist two orthogonal minimal idempotents
![]() $\overline {e}, \overline {f} \in M_r(F) \subseteq R/J(R)$
such that
$\overline {e}, \overline {f} \in M_r(F) \subseteq R/J(R)$
such that
![]() $\overline {e}=P\overline {f}P^{-1}$
for some invertible (permutation) matrix
$\overline {e}=P\overline {f}P^{-1}$
for some invertible (permutation) matrix
![]() $P \in M_r(F)$
. Therefore,
$P \in M_r(F)$
. Therefore,
![]() $\overline {e}P\overline {f}P^{-1}\overline {e}=\overline {e}$
. By [Reference McDonald14, Theorem VII.12], there exist orthogonal idempotents
$\overline {e}P\overline {f}P^{-1}\overline {e}=\overline {e}$
. By [Reference McDonald14, Theorem VII.12], there exist orthogonal idempotents
![]() $e, f \in R$
such that
$e, f \in R$
such that
![]() $e+J(R)=\overline {e}$
and
$e+J(R)=\overline {e}$
and
![]() $f+J(R)=\overline {f}$
. Also, by [Reference McDonald14, Theorem VII.13], there exist
$f+J(R)=\overline {f}$
. Also, by [Reference McDonald14, Theorem VII.13], there exist
![]() $a \in R^*$
and
$a \in R^*$
and
![]() $i, j \in N$
such that
$i, j \in N$
such that
![]() $e=ae_ia^{-1}$
and
$e=ae_ia^{-1}$
and
![]() $f=ae_ja^{-1}$
. Choose an invertible
$f=ae_ja^{-1}$
. Choose an invertible
![]() $p \in R$
such that
$p \in R$
such that
![]() $p+J(R)=P$
. The equality in (4.1) now implies that
$p+J(R)=P$
. The equality in (4.1) now implies that
![]() $(e_ia^{-1}pae_j)(e_ja^{-1}p^{-1}ae_i)=0$
; thus,
$(e_ia^{-1}pae_j)(e_ja^{-1}p^{-1}ae_i)=0$
; thus,
![]() $(epf)(fp^{-1}e)=0$
and consequently
$(epf)(fp^{-1}e)=0$
and consequently
![]() $\overline {e}P\overline {f}P^{-1}\overline {e}=\overline {0}$
, a contradiction. We have proved that
$\overline {e}P\overline {f}P^{-1}\overline {e}=\overline {0}$
, a contradiction. We have proved that
![]() $R/J$
is indeed a basic ring. Now,
$R/J$
is indeed a basic ring. Now,
![]() $J(R) = \sum _{i \in N}{J(e_iRe_i)} + \sum _{i \neq j \in N}{e_iRe_j}$
, so the fact that
$J(R) = \sum _{i \in N}{J(e_iRe_i)} + \sum _{i \neq j \in N}{e_iRe_j}$
, so the fact that
![]() $J(R)^2=0$
follows immediately from the equality in (4.1).
$J(R)^2=0$
follows immediately from the equality in (4.1).
Next, we investigate lower bounds for
![]() ${\mathrm {zp}}(R)$
. Obviously, by Lemma 2.2, there is no nonzero constant that can be a lower bound for the nullity degree of an arbitrary ring. However, since every finite ring is uniquely expressible as a direct product of rings of prime power order (see, for example, [Reference McDonald14, Theorem I.1]), we can limit ourselves (again by Lemma 2.2) to studying the bounds for the nullity degrees of rings of prime power orders.
${\mathrm {zp}}(R)$
. Obviously, by Lemma 2.2, there is no nonzero constant that can be a lower bound for the nullity degree of an arbitrary ring. However, since every finite ring is uniquely expressible as a direct product of rings of prime power order (see, for example, [Reference McDonald14, Theorem I.1]), we can limit ourselves (again by Lemma 2.2) to studying the bounds for the nullity degrees of rings of prime power orders.
We can prove the following lemma, thereby improving upon the lower bound of [Reference Esmkhani and Jafarian Amiri6, Lemma 2.5] and generalising it to noncommutative and nonlocal rings.
Lemma 4.3. Let R be a p-ring that is not a field. Then,
where the equality holds if and only if
![]() $R={\mathbb {Z}}_{p^2}$
or
$R={\mathbb {Z}}_{p^2}$
or
![]() $R={\mathbb {Z}}_p[x]/(x^2)$
.
$R={\mathbb {Z}}_p[x]/(x^2)$
.
Proof. By Lemma 2.1, we have
![]() ${\mathrm {zp}}(R) = {\sum _{x \in R}{|{\mathrm {Ann}}(x)|}}/{|R|^2}$
. Since any element in R that is not a zero divisor is invertible and
${\mathrm {zp}}(R) = {\sum _{x \in R}{|{\mathrm {Ann}}(x)|}}/{|R|^2}$
. Since any element in R that is not a zero divisor is invertible and
![]() ${\mathrm {Ann}}(x)$
is a nontrivial subgroup of the group
${\mathrm {Ann}}(x)$
is a nontrivial subgroup of the group
![]() $(R,+)$
,
$(R,+)$
,
 $$ \begin{align*} {\mathrm{zp}}(R) = \frac{|R \setminus Z(R)| + \sum_{x \in Z(R)}{|{\mathrm{Ann}}(x)|}}{|R|^2} & = \frac{2|R| - |Z(R)| + \sum_{0 \neq x \in Z(R)}{|{\mathrm{Ann}}(x)|}}{|R|^2} \\ &\geq \frac{2|R| - |Z(R)| + p(|Z(R)|-1)}{|R|^2}. \end{align*} $$
$$ \begin{align*} {\mathrm{zp}}(R) = \frac{|R \setminus Z(R)| + \sum_{x \in Z(R)}{|{\mathrm{Ann}}(x)|}}{|R|^2} & = \frac{2|R| - |Z(R)| + \sum_{0 \neq x \in Z(R)}{|{\mathrm{Ann}}(x)|}}{|R|^2} \\ &\geq \frac{2|R| - |Z(R)| + p(|Z(R)|-1)}{|R|^2}. \end{align*} $$
Since
![]() $|Z(R)| \geq \sqrt {|R|}$
by [Reference Koh11], this implies that
$|Z(R)| \geq \sqrt {|R|}$
by [Reference Koh11], this implies that
![]() ${\mathrm {zp}}(R) \geq {(2|R| + (p-1)\sqrt {|R|}-p)}/{|R|^2}$
. Obviously, if
${\mathrm {zp}}(R) \geq {(2|R| + (p-1)\sqrt {|R|}-p)}/{|R|^2}$
. Obviously, if
![]() $R={\mathbb {Z}}_{p^2}$
or
$R={\mathbb {Z}}_{p^2}$
or
![]() $R={\mathbb {Z}}_p[x]/(x^2)$
, we have
$R={\mathbb {Z}}_p[x]/(x^2)$
, we have
![]() ${\mathrm {zp}}(R)={(2p^2+(p-1)p-p)}/{p^2}$
, so the equality holds. On the other hand, if
${\mathrm {zp}}(R)={(2p^2+(p-1)p-p)}/{p^2}$
, so the equality holds. On the other hand, if
![]() ${\mathrm {zp}}(R) = {(2|R|+(p-1)\sqrt {|R|}-p)}/{|R|^2}$
then
${\mathrm {zp}}(R) = {(2|R|+(p-1)\sqrt {|R|}-p)}/{|R|^2}$
then
![]() $|Z(R)| = \sqrt {|R|}$
and
$|Z(R)| = \sqrt {|R|}$
and
![]() $|{\mathrm {Ann}}(x)|=p$
for any nonzero
$|{\mathrm {Ann}}(x)|=p$
for any nonzero
![]() $x \in Z(R)$
. Now,
$x \in Z(R)$
. Now,
![]() $|Z(R)| = \sqrt {|R|}$
together with [Reference Kobayashi and Koh10, Corollary 2.6] implies that R is a local ring with
$|Z(R)| = \sqrt {|R|}$
together with [Reference Kobayashi and Koh10, Corollary 2.6] implies that R is a local ring with
![]() $J(R)^2=0$
. Since
$J(R)^2=0$
. Since
![]() $|{\mathrm {Ann}}(x)|=p$
, we conclude that
$|{\mathrm {Ann}}(x)|=p$
, we conclude that
![]() $|J(R)| = p$
. Finally, we use [Reference Akbari and Mohammadian1, Theorem 3] to see that
$|J(R)| = p$
. Finally, we use [Reference Akbari and Mohammadian1, Theorem 3] to see that
![]() $R={\mathbb {Z}}_{p^2}$
or
$R={\mathbb {Z}}_{p^2}$
or
![]() $R={\mathbb {Z}}_p[x]/(x^2)$
.
$R={\mathbb {Z}}_p[x]/(x^2)$
.
This immediately yields the following theorem, which is an improvement on [Reference Esmkhani and Jafarian Amiri6, Theorem 3.2] and a generalisation of it to noncommutative rings.
Theorem 4.4. Let R be a finite ring such that no direct factor of R is a field. Suppose that
![]() $|R|=p_1^{\alpha _1}p_2^{\alpha _2}\ldots p_k^{\alpha _k}$
for distinct primes
$|R|=p_1^{\alpha _1}p_2^{\alpha _2}\ldots p_k^{\alpha _k}$
for distinct primes
![]() $p_1,p_2,\ldots ,p_k$
and integers
$p_1,p_2,\ldots ,p_k$
and integers
![]() $\alpha _1, \alpha _2, \ldots , \alpha _k$
. Then,
$\alpha _1, \alpha _2, \ldots , \alpha _k$
. Then,
![]() ${\mathrm {zp}}(R) \geq {\prod _{i=1}^{k}{(2p_i^{\alpha _i}+(p_i-1)p_i^{\alpha _i/2}-p_i)}}/{|R|^2}$
, where the equality holds if and only if R is a direct product of rings isomorphic to
${\mathrm {zp}}(R) \geq {\prod _{i=1}^{k}{(2p_i^{\alpha _i}+(p_i-1)p_i^{\alpha _i/2}-p_i)}}/{|R|^2}$
, where the equality holds if and only if R is a direct product of rings isomorphic to
![]() ${\mathbb {Z}}_{p^2}$
or
${\mathbb {Z}}_{p^2}$
or
![]() $R={\mathbb {Z}}_p[x]/(x^2)$
.
$R={\mathbb {Z}}_p[x]/(x^2)$
.
Proof. This follows directly from Lemmas 2.2 and 4.3 and [Reference McDonald14, Theorem I.1].