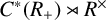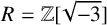1 Introduction
Motivated by the pioneering paper of Bost and Connes [Reference Bost and Connes2], Cuntz in [Reference Cuntz, Cortiñas, Cuntz, Karoubi, Nest and Weibel8] constructed the first ring
$C^*$
-algebra. Cuntz and Li [Reference Cuntz, Li, Blanchard, Ellwood, Khalkhali, Marcolli, Moscovici and Popa11] generalised the work of [Reference Cuntz, Cortiñas, Cuntz, Karoubi, Nest and Weibel8] to an integral domain with finite quotients. Eventually, Li [Reference Li18] generalised the work of [Reference Cuntz, Cortiñas, Cuntz, Karoubi, Nest and Weibel8] to arbitrary rings. There is more than one way of studying
$C^*$
-algebras associated to rings. Hirshberg [Reference Hirshberg12], Larsen and Li [Reference Larsen and Li17], and Kaliszewski et al. [Reference Kaliszewski, Omland and Quigg13] independently investigated
$C^*$
-algebras from p-adic rings. Li [Reference Li19] defined the notion of semigroup
$C^*$
-algebras and proved that the
$ax+b$
-semigroup
$C^*$
-algebra of a ring is an extension of the ring
$C^*$
-algebra. When the ring is the ring of integers of a field, Li [Reference Li19] proved that the
$ax+b$
-semigroup
$C^*$
-algebra is isomorphic to another construction due to Cuntz et al. [Reference Cuntz, Deninger and Laca9]. Very recent work due to Bruce and Li [Reference Bruce and Li5, Reference Bruce and Li6] and Bruce et al. [Reference Bruce, Kubota and Takeishi4] on algebraic dynamical systems and their associated
$C^*$
-algebras solves quite a few open problems.
For an integral domain R, denote by
$R_+$
the additive group
$(R,+)$
and by
$R^\times $
the multiplicative semigroup
$(R\setminus \{0\},\cdot )$
. There is a natural unital and injective action of
$R^\times $
on
$C^*(R_+)$
by multiplication. Thus, we obtain a semigroup crossed product
$C^*(R_+) \rtimes R^\times $
. We characterise the primitive ideal space and its Jacobson topology for the semigroup crossed product
$C^*(R_+) \rtimes R^\times $
under certain conditions. Our main example is
$R=\mathbb {Z}[\sqrt {-3}]$
. The semigroup crossed product
$C^*(R_+) \rtimes R^\times $
is closely related to other constructions. In the Appendix, we show that
$C^*(R_+) \rtimes R^\times $
is an extension of the boundary quotient of the opposite semigroup of the
$ax+b$
-semigroup of the ring and that when the ring is a greatest common divisor (GCD) domain,
$C^*(R_+) \rtimes R^\times $
is isomorphic to the boundary quotient of the opposite semigroup of the
$ax+b$
-semigroup of the ring. There are only a few investigations of the opposite semigroup
$C^*$
-algebra of the
$ax+b$
-semigroup of a ring (see for example [Reference Cuntz, Echterhoff and Li10, Reference Li20, Reference Li and Norling21]).
Standing assumptions
Throughout the paper, any semigroup is assumed to be discrete, countable, unital and left cancellative; any group is assumed to be discrete and countable; any subsemigroup of a semigroup is assumed to inherit the unit of the semigroup; any ring is assumed to be countable and unital with
$0 \neq 1$
; and any topological space is assumed to be second countable.
2 Laca’s dilation theorem revisited
Laca [Reference Laca14] proved an important theorem which dilates a semigroup dynamical system
$(A,P,\alpha )$
to a
$C^*$
-dynamical system
$(B,G,\beta )$
so that the semigroup crossed product
$A \rtimes _{\alpha }^{e} P$
is Morita equivalent to the crossed product
$B \rtimes _{\beta } G$
. In this section, we revisit Laca’s theorem when A is a unital commutative
$C^*$
-algebra.
Notation 2.1. Let P be a subsemigroup of a group G satisfying
$G=P^{-1}P$
. For
${p,q \in P}$
, define
$p \leq q$
if
$qp^{-1} \in P$
. Then,
$\leq $
is a reflexive, transitive and directed relation on P.
Theorem 2.2 (See [Reference Laca14, Theorem 2.1])
Let P be a subsemigroup of a group G satisfying
$G=P^{-1}P$
, let
$A=C(X)$
, where X is a compact Hausdorff space, and let
$\alpha :P \to \mathrm {End}(A)$
be a semigroup homomorphism such that
$\alpha _p$
is unital and injective for all
$p \in P$
. Then, there exists a dynamical system
$(X_\infty ,G,\gamma )$
(where
$X_\infty $
is compact Hausdorff) such that
$A \rtimes _{\alpha }^{e} P$
is Morita equivalent to
$C(X_\infty ) \rtimes _\gamma G$
.
Proof. By [Reference Laca14, Theorem 2.1], there exists a
$C^*$
-dynamical system
$(A_\infty ,G,\beta )$
such that
$A \rtimes _{\alpha }^{e} P$
is Morita equivalent to
$A_\infty \rtimes _\beta G$
. We cite the proof of [Reference Laca14, Theorem 2.1] to sketch the construction of
$A_\infty $
and the definition of
$\beta $
.
For
$p \in P$
, define
$A_p:=A$
. For
$p,q \in P$
with
$p \leq q$
, define
$\alpha _{p,q}:A_p \to A_q$
to be
$\alpha _{qp^{-1}}$
. Then,
$\{(A_p,\alpha _{p,q}):p,q \in P,p \leq q\}$
is an inductive system. Let
${A_\infty :=\lim _{p}(A_p,\alpha _{p,q})}$
, let
$\alpha ^{p}:A_p \to A_\infty $
be the natural unital embedding for all
$p \in P$
and let
$\beta :G \to \mathrm {Aut}(A_\infty )$
be the homomorphism satisfying
$\beta _{p_0}\circ \alpha ^{pp_0}=\alpha ^p$
for all
$p_0,p\in P$
.
For
$p \in P$
, denote by
$f_p:X \to X$
the unique surjective continuous map induced from
$\alpha _p$
and set
$X_p:=X$
. For
$p,q \in P$
with
$p \leq q$
, denote by
$f_{q,p}:X_q \to X_p$
the unique surjective continuous map induced from
$\alpha _{p,q}$
. Since
$\alpha _{p,q}=\alpha _{qp^{-1}}$
, we have
${f_{q,p}=f_{qp^{-1}}}$
. Then,
$\{(X_p,f_{q,p}):p,q \in P,p \leq q\}$
is an inverse system. Set
$$ \begin{align} X_\infty :=\bigg\{(x_p)_{p \in P} \in \prod _{p \in P}X_p:f_{q,p}(x_q)=x_p\mbox { for all } p \leq q\bigg\}, \end{align} $$
which is the inverse limit of the inverse system. By [Reference Blackadar1, Example II.8.2.2(i)],
${A_\infty \cong C(X_\infty )}$
. For
$p \in P$
, denote by
$f^p:X_\infty \to X_p$
the unique projection induced from
$\alpha ^p$
. Then,
$f_{q,p}\circ f^q=f^p$
for all
$p,q \in P,p \leq q$
. For
$p,p_0 \in P,f \in C(X_\infty )$
, denote by
$\gamma _{p_0}:X_\infty \to X_\infty $
the unique homeomorphism such that
$\beta _{p_0}(f)=f\circ \gamma _{p_0}^{-1}$
.
From this construction,
$(X_\infty ,G,\gamma )$
is a dynamical system with
$C(X_\infty ) \rtimes _\gamma G \cong A_\infty \rtimes _\beta G$
. Hence,
$A \rtimes _{\alpha }^{e} P$
is Morita equivalent to
$C(X_\infty ) \rtimes _\gamma G$
.
Notation 2.3. We give an explicit description of
$X_\infty $
and the action of G on
$X_\infty $
given in Theorem 2.2. We start with the definition of
$X_\infty$
in (2.1). Then, for
$p_0,p,q \in P$
with
$q \geq p_0,p$
, and for
$(x_p)_{p \in P} \in X_\infty $
, we have
$$ \begin{align*}(p_0\cdot (x_p))(p)=x_{pp_0},\quad (p_0^{-1}\cdot (x_p))(p)=f_{q,p}(x_{qp_0^{-1}}).\end{align*} $$
In particular, when G is abelian, we have a simpler form of the group action given by
$$ \begin{align*}\frac{p_0}{q_0} \cdot (x_p)=(f_{q_0}(x_{pp_0})).\end{align*} $$
Our goal is to apply Theorem 2.2 to characterise the primitive ideal space of the semigroup crossed product
$C^{*}(R_+)\rtimes R^{\times }$
of an integral domain. Since
$R^{\times }$
is abelian, we will need the following version of Williams’ theorem.
Definition 2.4. Let G be an abelian group, let X be a locally compact Hausdorff space and let
$\alpha :G \to \mathrm {Homeo}(X)$
be a homomorphism. For
$x,y\in X$
, define
$x \sim y$
if
$\overline {G\cdot x} =\overline {G \cdot y}$
. Then,
$\sim $
is an equivalence relation on X. For
$x \in X$
, define
$[x] := \overline {G\cdot x}$
, called the quasi-orbit of x. The quotient space
$Q(X /G)$
by the relation
$\sim $
is called the quasi-orbit space. For
$x \in X$
, define
$G_{x}:=\{ g \in G : g \cdot x = x\}$
, called the isotropy group (or stability group) at x. For
$([x],\phi ), ([y],\psi ) \in Q(X/ G)\times \widehat {G}$
, define
$([x],\phi )\approx ([y],\psi )$
if
$[x] = [y]$
and
$\phi \vert _{G_{x}}= \psi \vert _{G_{x}}$
. Then,
$\approx $
is an equivalence relation on
$Q(X /G) \times \widehat {G}$
.
Theorem 2.5 [Reference Laca and Raeburn16, Theorem 1.1]
Let G be an abelian group, let X be a locally compact Hausdorff space and let
$\alpha : G \to \mathrm {Homeo}(X)$
be a homomorphism. Then,
${\mathrm {Prim}(C_{0}(X)\rtimes _\alpha G)\cong (Q(X /G)\times \widehat {G})/\approx} $
.
3 Primitive ideal structure of
$C^*(R_+)\rtimes R^\times $
In this section, we characterise the primitive ideal space and its Jacobson topology for the semigroup crossed product
$C^*(R_+) \rtimes R^\times $
under certain conditions.
Notation 3.1. Let R be an integral domain. Denote by Q the field of fractions of R, by
$R_+$
the additive group
$(R,+)$
, by
$\widehat {R_+}$
the dual group of
$R_+$
, by
$R^\times $
the multiplicative semigroup
$(R\setminus \{0\},\cdot )$
, by
$Q^\times $
the enveloping group
$(Q\setminus \{0\},\cdot )$
of
$R^\times $
, by
$\{u_r\}_{r \in R_+}$
the family of unitaries generating
$C^*(R_+)$
and by
$\alpha :R^\times \to \mathrm {End}(C^*(R_+))$
the homomorphism such that
$\alpha _{p}(u_r)=u_{pr}$
for all
$p \in R^\times ,r \in R_+$
. Observe that for any
$p \in R^\times , \alpha _p$
is unital and injective, and the map
$f_p:\widehat {R_+} \to \widehat {R_+},\phi \mapsto \phi (p \cdot )$
is the unique surjective continuous map induced from
$\alpha _p$
. Denote by
$$ \begin{align*}X_\infty(R):=\bigg\{\phi=(\phi_p)_{p\in R^\times}\in\prod_{p\in R^\times}\widehat{R_+}:\phi_q\bigg(\frac{q}{p}\cdot \bigg)=\phi_p,\text{ whenever } p \mid q\bigg\}.\end{align*} $$
Then,
$({p_0}/{q_0})\cdot (\phi _p)=(\phi _{pp_0}(q_0\cdot ))$
.
Lemma 3.2. Let R be an integral domain. Fix
$(\phi _p)_{p\in R^\times } \in X_\infty (R)$
. If
$(\phi _p)_{p\in R^\times }\neq (1)_{p \in R^\times }$
, then
$Q^{\times }_{\phi }=\{1_R\}$
. If
$(\phi _p)_{p\in R^\times }= (1)_{p\in R^\times }$
, then
$Q^{\times }_{\phi }=Q^{\times }$
.
Proof. To prove the first statement, suppose for a contradiction that there exists
$p_0/q_0 \in Q^\times$
with
$p_0/q_0 \ne 1$
and such that
$({p_0}/{q_0}) \cdot \phi =\phi $
. Since
$(\phi _p)_{p\in R^\times }\neq (1)_{p \in R^\times }$
, there exists
${p_1 \in R^\times }$
such that
$\phi _{p_1} \neq 1$
. Then,
$\phi _p=\phi _{pp_0}(q_0 \cdot )$
for any
$p \in R^{\times }$
. Since
$\phi _{pp_0}(p_0\cdot )=\phi _p$
for any
$p \in R^\times $
, we deduce that
$\phi _{pp_0}(p_0\cdot )=\phi _{pp_0}(q_0 \cdot )$
for all
$p \in R^\times $
. So
${\phi _{pp_0}((p_0-q_0)\cdot )= 1}$
for any
$p \in R^\times $
. Hence,
$\phi _{pp_0}((p_0-q_0)p_0\cdot )= 1$
for any
${p \in R^\times }$
. When
$p=p_1(p_0-q_0)$
, we get
$\phi _{p_1}=\phi _{p_1(p_0-q_0)p_0}(((p_0-q_0)p_0\cdot )= 1$
, which is a contradiction. Therefore,
${Q^{\times }_{\phi }=\{1_R\}}$
.
To prove the second statement, suppose that
$(\phi _p)_{p\in R^\times }= (1)_{p\in R^\times }$
. For
${{p_0}/{q_0} \in Q^{\times }}$
, we have
$({p_0}/{q_0})\cdot (1)_{p\in R^\times }\kern1.3pt{=}\kern1.3pt({p_0}/{q_0})\cdot (\phi _p)_{p\in R^\times }\kern1.3pt{=}\kern1.3pt(\phi _{pp_0}(q_0\cdot ))_{p\in R^\times }\kern1.3pt{=}\kern1.3pt(1)_{p\in R^\times }$
. So
$Q^{\times }_{\phi }=Q^{\times }$
.
Lemma 3.3. Let R be an integral domain. Suppose that for
$\epsilon>0$
,
$(1)_{p \in R^\times }\neq (\phi _p)_{p\in R^\times } \in X_\infty (R)$
,
$\pi \in \widehat {R_+}$
,
$P \in R^\times $
and
$r_1,r_2,\ldots , r_n \in R_+$
, there exist
$p,q \in R^\times $
with
$P \mid p$
such that
$\vert \phi _{p}(qr_i)-\pi (r_i)\vert <\epsilon ,i=1,2,\ldots ,n$
. Then,
$Q(X_\infty (R)/Q^\times )$
consists of only two points with the only nontrivial closed subset
$\{[(1)_{p \in R^\times }]\}$
.
Proof. Since
$\overline {Q^{\times } \cdot (1)_{p \in R^\times }}=\overline {(1)_{p \in R^\times }}=(1)_{p \in R^\times }$
, we have
$[(\phi _p)_{p\in R^\times }] \neq [(1)_{p \in R^\times }]$
whenever
$(1)_{p \in R^\times }\neq (\phi _p)_{p\in R^\times } \in X_\infty (R)$
.
Fix
$(\phi _p)_{p\in R^\times }, (\psi _p)_{p\in R^\times } \in X_\infty (R)$
such that
$(\phi _p)_{p\in R^\times }, (\psi _p)_{p\in R^\times } \neq (1)_{p \in R^\times }$
. We aim to show that
$[(\phi _p)_{p\in R^\times }]=[(\psi _p)_{p\in R^\times }]$
. It suffices to show that
$(\psi _p)_{p\in R^\times } \in \overline {Q^{\times } \cdot (\phi _p)_{p\in R^\times }}$
since
$(\phi _p)_{p\in R^\times } \in \overline {Q^{\times } \cdot (\psi _p)_{p\in R^\times }}$
follows from the same argument. Fix
$\epsilon>0$
,
$p_1,p_2,\ldots ,p_n \in R^\times $
and
$r_1,r_2,\ldots ,r_n \in R$
. By the condition imposed in the lemma, there exist
$p_0,q_0 \in R^{\times }$
such that
$$ \begin{align*}\vert \phi_{p_1p_2\cdots p_np_0}(q_0p_1\cdots p_{i-1}p_{i+1}\cdots p_nr_j)-\psi_{p_1p_2\cdots p_n}(p_1\cdots p_{i-1}p_{i+1}\cdots p_nr_j)\vert<\epsilon\end{align*} $$
for
$1\leq i,j\leq n$
. So
$\vert \phi _{p_ip_0}(q_0r_j)-\psi _{p_i}(r_j)\vert <\epsilon $
for
$1\leq i,j\leq n$
. Hence,
$(\psi _p)_{p\in R^\times } \in \overline {Q^{\times } \cdot (\phi _p)_{p\in R^\times }}$
. Therefore,
$[(\phi _p)_{p\in R^\times }]=[(\psi _p)_{p\in R^\times }]$
.
We conclude that
$Q(X_\infty (R)/Q^\times )$
consists of only two points. For any
$(1)_{p \in R^\times }\neq (\phi _p)_{p\in R^\times } \in X_\infty (R)$
,
$\overline {Q^{\times } \cdot (\phi _p)_{p\in R^\times }}=X_\infty (R) \setminus \{(1)_{p \in R^\times }\}$
is open but not closed. Finally, we deduce that
$\{[(1)_{p \in R^\times }]\}$
is the only nontrivial closed subset of
$Q(X_\infty (R)/Q^\times )$
.
Theorem 3.4. Let R be an integral domain satisfying the condition of Lemma 3.3. Take an arbitrary element
$(\phi _p)_{p\in R^\times } \in X_\infty (R)$
with
$(1)_{p \in R^\times } \neq (\phi _p)_{p\in R^\times }$
. Then, we have
$\mathrm {Prim}(C^*(R_+) \rtimes R^\times ) \cong \{[(\phi _p)_{p\in R^\times }]\} \amalg \{[(1)_{p \in R^\times }]\} \times \widehat {Q^\times }$
, and the open sets of
${\mathrm {Prim}(C^*(R_+) \rtimes R^\times )}$
comprise
$\{[(\phi _p)_{p\in R^\times }]\} \amalg \{[(1)_{p \in R^\times }]\} \times N$
, where N is an open subset of
$\widehat {Q^\times }$
.
Proof. By Theorem 2.2,
$(C^*(R_+) \rtimes R^\times )$
is Morita equivalent to
$C(X_\infty (R)) \rtimes Q^\times $
. So
$\mathrm {Prim}(C^*(R_+) \rtimes R^\times ) \cong \mathrm {Prim}(C(X_\infty (R)) \rtimes Q^\times )$
. By Theorem 2.5 and Lemma 3.3,
$\mathrm {Prim}(C(X_\infty (R)) \rtimes Q^\times ) \cong \{[(\phi _p)_{p\in R^\times }],[(1)_{p \in R^\times }]\} \times \widehat {Q^\times } /\approx $
. By Lemma 3.2,
$Q^{\times }_{(\phi _p)_{p\in R^\times }}=\{1_R\}$
and
$Q^{\times }_{(1)_{p \in R^\times }}=Q^{\times }$
. So,
$\mathrm {Prim}(C(X_\infty (R)) \rtimes Q^\times ) \cong \{[(\phi _p)_{p\in R^\times }]\} \amalg \{[(1)_{p \in R^\times }]\} \times \widehat {Q^\times }$
. Hence,
$\mathrm {Prim}(C^*(R_+) \rtimes R^\times ) \cong \{[(\phi _p)_{p\in R^\times }]\} \amalg \{[(1)_{p \in R^\times }]\} \times \widehat {Q^\times }$
, and the open sets of
$\mathrm {Prim}(C^*(R_+) \rtimes R^\times )$
are
$\{[(\phi _p)_{p\in R^\times }]\} \amalg \{[(1)_{p \in R^\times }]\} \times N$
, where N is an open subset of
$\widehat {Q^\times }$
.
Example 3.5. Let
$R=\mathbb {Z}$
. Then,
$\widehat {R_+}=\mathbb {T}$
. Fix
$\epsilon>0$
,
$(1)_{p \in \mathbb {Z}^\times }\neq (\phi _p)_{p\in \mathbb {Z}^\times } \in X_\infty (\mathbb {Z})$
,
$\pi \in \mathbb {T}$
,
$P \in \mathbb {Z}^\times $
and
$r_1,r_2,\ldots , r_n \in \mathbb {Z}_+$
. Take an arbitrary
$p_0 \in \mathbb {Z}^\times $
such that
$P\mid p_0$
and let
$\phi _{p_0}=e^{2\pi i \theta }$
for some
$\theta \in (0,1)$
.
Case 1:
$\theta $
is rational. Then,
$\phi _{p_0}^{\mathbb {Z}}=\{e^{{2\pi i k}/{n}}\}_{k=0}^{n-1}$
for some
$n \geq 1$
. Since
$\phi _{pp_0}^p=\phi _{p_0}$
for any
$p \geq 1$
, we get
$\phi _{pp_0}^{\mathbb {Z}}=\{e^{{2\pi i k}/{pn}} \}_{k=0}^{pn-1}$
. Choose
$p_1 \geq 1$
such that
$\vert e^{{2\pi i}/{p_1n}}-1 \vert <\epsilon /\sum _{i=1}^{n}\vert r_i \vert $
. Then, there exists
$q_0 \in \mathbb {Z}^\times $
such that
$\vert \phi _{p_1p_0}^{q_0}-\pi \vert <\epsilon /\sum _{i=1}^{n}\vert r_i \vert $
.
Case 2:
$\theta $
is irrational. Then, by the properties of an irrational rotation,
$\{\phi _{p_0}^z\}_{z \in \mathbb {Z}}$
is a dense subset of
$\mathbb {T}$
. So, there exists
$q_0 \in \mathbb {Z}^\times $
such that
$\vert \phi _{p_0}^{q_0}-\pi \vert <\epsilon /\sum _{i=1}^{n}\vert r_i \vert $
.
In both cases, there exist
$p,q \in \mathbb {Z}^\times $
with
$P \mid p$
such that
$\vert \phi _{p}^{q}-\pi \vert <\epsilon /\sum _{i=1}^{n}\vert r_i \vert $
. For
$1\leq i\leq n$
, we may assume that
$r_i \geq 0$
and we calculate that
$$ \begin{align*} \vert\phi_{p}(qr_i)-\pi(r_i)\vert=\vert\phi_{p}^{qr_i}-\pi^{r_i}\vert =\vert \phi_{p}^{q}-\pi\vert\,\bigg\vert\sum_{j=0}^{r_i-1}\phi_{p}^{q(r_i-1-j)}\pi^{j}\bigg\vert &\leq\vert \phi_{p}^{q}-\pi\vert\sum_{j=0}^{r_i-1}\vert\phi_{p}^{q(r_i-1-j)}\pi^{j}\vert \\&<\epsilon r_i\Big/\sum_{i=1}^{n}\vert r_i \vert <\epsilon. \end{align*} $$
So,
$\mathbb {Z}$
satisfies the condition of Lemma 3.3.
Example 3.6. Let
$R=\mathbb {Z}[\sqrt {-3}]$
. Then,
$\mathbb {Z}[\sqrt {-3}]_+\cong \mathbb {Z}^2$
and
$\widehat {\mathbb {Z}[\sqrt {-3}]_+}\cong \mathbb {T}^2$
. Fix
$\epsilon>0$
,
$((1,1))_{p \in R^\times }\kern1.3pt{\neq}\kern1.3pt ((a_p,b_p))_{p\in R^\times } \kern1.3pt{\in}\kern1.3pt X_\infty (\mathbb {Z}[\sqrt {-3}])$
,
$(\pi ,\rho ) \kern1.3pt{\in}\kern1.3pt \mathbb {T}^2$
,
$P \kern1.4pt{\in}\kern1.4pt R^\times $
and
$r_i\kern1.4pt{+}\kern1.4pt s_i\sqrt{-3} \kern1.4pt{\in}\kern1.4pt \mathbb{Z}[\sqrt{-3}]_+ \mathrm{for}\ i=1,2\ldots,n$
. Take an arbitrary
$P \mid p_0 \in R^\times $
such that
$(a_{p_0},b_{p_0}) \neq (1,1)$
. There exist
$p,q=q_1+q_2\sqrt {-3} \in R^\times $
with
$P \mid p$
such that
$\vert a_{p}^{q_1}b_p^{q_2}-\pi \vert ,\vert a_p^{-3q_2}b_p^{q_1}-\rho \vert <{\epsilon }/{\sum _{i=1}^{n}(\vert r_i \vert +\vert s_i \vert )}$
. For
$1\leq i\leq n$
, we may assume that
$r_i \geq 0$
and we estimate
$$ \begin{align*} &\vert(a_p,b_p)(q(r_i+s_i\sqrt{-3}))-(\pi,\rho)(r_i+s_i\sqrt{-3})\vert \\&\quad=\vert (a_{p}^{q_1}b_p^{q_2})^{r_i}(a_p^{-3q_2}b_p^{q_1})^{s_i}-\pi^{r_i}\rho^{s_i}\vert \\&\quad=\vert ((a_{p}^{q_1}b_p^{q_2})^{r_i}-\pi^{r_i})(a_p^{-3q_2}b_p^{q_1})^{s_i}+\pi^{r_i}((a_p^{-3q_2}b_p^{q_1})^{s_i}-\rho^{s_i})\vert \\&\quad\leq\vert (a_{p}^{q_1}b_p^{q_2})^{r_i}-\pi^{r_i}\vert+\vert(a_p^{-3q_2}b_p^{q_1})^{s_i}-\rho^{s_i}\vert \\&\quad< \frac{\epsilon\vert r_i\vert}{\sum_{i=1}^{n}\vert r_i \vert+\vert s_i \vert}+\frac{\epsilon \vert s_i \vert}{\sum_{i=1}^{n}\vert r_i \vert+\vert s_i \vert} \leq\epsilon. \end{align*} $$
So,
$\mathbb {Z}[\sqrt {-3}]$
satisfies the condition of Lemma 3.3.
By a similar argument to this example, we conclude that any (concrete) order of a number field satisfies the condition of Lemma 3.3. (For the background about number fields, one may refer to [Reference Neukirch22].)
Appendix The relationship between
$C^*(R_+) \rtimes R^\times $
and semigroup
$C^*$
-algebras
In this appendix, we show that
$C^*(R_+) \rtimes R^\times $
is an extension of the boundary quotient of the opposite semigroup of the
$ax+b$
-semigroup of the ring and that when the ring is a GCD domain,
$C^*(R_+) \rtimes R^\times $
is isomorphic to the boundary quotient of the opposite semigroup of the
$ax+b$
-semigroup of the ring.
Definition A.1 ([Reference Laca and Raeburn15, Section 2], [Reference Li19, Definition 2.13])
Let P be a semigroup, A be a unital
$C^*$
-algebra and
$\alpha :P \to \mathrm {End}(A)$
be a semigroup homomorphism such that
$\alpha _p$
is injective for all
$p \in P$
. Define the semigroup crossed product
$A \rtimes _{\alpha } P$
to be the universal unital
$C^*$
-algebra generated by the image of a unital homomorphism
${i_A:A \to A \rtimes _{\alpha } P}$
and a semigroup homomorphism
$i_P:P \to \mathrm {Isom}(A \rtimes _{\alpha } P)$
satisfying the following conditions:
-
(1)
$i_P(p)i_A(a)i_P(p)^*=i_A(\alpha _p(a))$
for all
$p \in P,a \in A$
; -
(2) for any unital
$C^*$
-algebra B, unital homomorphism
$j_A:A \to B$
and semigroup homomorphism
$j_P:P \to \mathrm {Isom}(B)$
satisfying
$j_P(p)j_A(a)j_P(p)^*=j_A(\alpha _p(a))$
, there exists a unique unital homomorphism
$\Phi :A \rtimes _{\alpha } P \to B$
such that
$\Phi \circ i_A=j_A$
and
$\Phi \circ i_P=j_P$
.
Remark A.2. We have
$i_A(1_A)=i_P(1_P) = \mbox { the unit of } A \rtimes _{\alpha } P$
.
If
$\alpha _p$
is unital for all
$p \in P$
, then
$i_P(p)$
is a unitary for any
$p \in P$
. To see this, we calculate that
$i_P(p)i_P(p)^*=i_P(p)i_A(1_A)i_P(p)^*=i_A(\alpha _p(1_A))=i_A(1_A)$
.
Notation A.3 [Reference Brownlowe, Ramagge, Robertson and Whittaker3, Reference Li19]
Let P be a semigroup. For
$p \in P$
, we also denote by p the left multiplication map
$q \mapsto pq$
. The set of constructible right ideals is defined to be
$$ \begin{align*} \mathcal{J}(P):=\{p_1^{-1}q_1\cdots p_n^{-1}q_nP:n \geq 1, p_1,q_1,\ldots, p_n,q_n \in P\} \cup \{\emptyset\}. \end{align*} $$
A finite subset
$F \subset \mathcal {J}(P)$
is called a foundation set if for any nonempty
$X \in \mathcal {J}(P)$
, there exists
$Y \in F$
such that
$X \cap Y \neq \emptyset $
.
Definition A.4 ([Reference Brownlowe, Ramagge, Robertson and Whittaker3, Remark 5.5], [Reference Li19, Definition 2.2])
Let P be a semigroup. Define the full semigroup
$C^*$
-algebra
$C^*(P)$
of P to be the universal unital
$C^*$
-algebra generated by a family of isometries
$\{v_p\}_{p \in P}$
and a family of projections
$\{e_X\}_{X \in \mathcal {J}(P)}$
satisfying the following relations:
-
(1)
$v_p v_q=v_{pq}$
for all
$p,q \in P$
; -
(2)
$v_p e_X v_p^*=e_{pX}$
for all
$p \in P,X \in \mathcal {J}(P)$
; -
(3)
$e_\emptyset =0$
and
$e_P=1$
; -
(4)
$e_X e_Y=e_{X \cap Y}$
for all
$X,Y \in \mathcal {J}(P)$
.
Define the boundary quotient
$\mathcal {Q}(P)$
of
$C^*(P)$
to be the universal unital
$C^*$
-algebra generated by a family of isometries
$\{v_p\}_{p \in P}$
and a family of projections
$\{e_X\}_{X \in \mathcal {J}(P)}$
satisfying conditions (1)–(4) and
$\prod _{X \in F}(1-e_X)=0$
for any foundation set
$F \subset \mathcal {J}(P)$
.
Definition A.5 ([Reference Brownlowe, Ramagge, Robertson and Whittaker3, Definition 2.1], [Reference Norling23, Definition 2.17])
Let P be a semigroup. Then, P is said to be right LCM (or to satisfy the Clifford condition) if the intersection of two principal right ideals is either empty or a principal right ideal.
Notation A.6. Let P be a semigroup. Denote by
$P^{\mathrm {op}}$
the opposite semigroup of P. Let R be an integral domain. Denote by
$R_+ \rtimes R^\times $
the
$ax+b$
-semigroup of R. Denote by
$\times $
the multiplication of
$(R_+ \rtimes R^\times )^{\mathrm {op}}$
, that is,
$(r_1,p_1)\times (r_2,p_2)=(r_2,p_2)(r_1,p_1)=(r_2+p_2r_1,p_1p_2)$
.
Remark A.7. Let R be an integral domain. We claim that any nonempty element of
$\mathcal {J}((R_+ \rtimes R^\times )^{\mathrm {op}})$
is a foundation set of
$(R_+ \rtimes R^\times )^{\mathrm {op}}$
. To see this, for any
$(r_1,p_1),(r_2,p_2) \in (R_+ \rtimes R^\times )^{\mathrm {op}}$
, we compute
$$ \begin{align*} (r_1,p_1) \times (p_1r_2,p_2)=(p_1r_2,p_2)(r_1,p_1) &=(p_1r_2+p_2r_1,p_1p_2) \\ &=(p_2r_1,p_1)(r_2,p_2) =(r_2,p_2)\times (p_2r_1,p_1). \end{align*} $$
Theorem A.8. Let R be an integral domain. Then, the crossed product
$C^*(R_+) \rtimes R^\times $
is an extension of
$\mathcal {Q}((R_+ \rtimes R^\times )^{\mathrm {op}})$
. Moreover, if R is a GCD domain (see [Reference Chapman and Glaz7]), then we have
$C^*(R_+) \rtimes R^\times \cong \mathcal {Q}((R_+ \rtimes R^\times )^{\mathrm {op}})$
.
Proof. Denote by
$i_A:C^*(R_+) \to C^*(R_+) \rtimes R^\times $
and
$i_P:R^{\times } \to \mathrm {Isom}(C^*(R_+) \rtimes R^\times )$
the canonical homomorphisms generating
$C^*(R_+) \rtimes R^\times $
. Let
$\{v_{(r,p)}:(r,p) \in (R_+ \rtimes R^\times )^{\mathrm {op}}\}$
be the family of isometries and
$\{e_X:X \in \mathcal {J}((R_+ \rtimes R^\times )^{\mathrm {op}})\}$
be the family of projections generating
$\mathcal {Q}((R_+ \rtimes R^\times )^{\mathrm {op}})$
.
For any
$(r,p)\in (R_+ \rtimes R^\times )^{\mathrm {op}}$
, note that
$1-v_{(r,p)}v_{(r,p)}^*=1-e_{(r,p) \times (R_+ \rtimes R^\times )^{\mathrm {op}}}=0$
because
$\{(r,p)\times (R_+ \rtimes R^\times )^{\mathrm {op}} \}$
is a foundation set. So each
$v_{(r,p)}$
is a unitary.
For
$r \in R_+$
, define
$U_r:=v_{(r,1)}$
. For any
$r,s \in R_+$
,
$$ \begin{align*} U_r U_s=v_{(r,1)}v_{(s,1)}=v_{(s,1)(r,1)}=v_{(r+s,1)}=v_{(r,1)(s,1)}=v_{(s,1)}v_{(r,1)}=U_sU_r, \end{align*} $$
so
$j_A:C^*(R_+) \to \mathcal {Q}((R_+ \rtimes R^\times )^{\mathrm {op}}),u_r \mapsto v_{(r,1)}$
is a homomorphism by the universal property of
$C^*(R_+)$
. For
$p \in R^\times $
, define
$j_P(p):=v_{(0,p)}^*$
. For any
$p,q \in R^\times $
,
$$ \begin{align*} j_P(p)j_P(q)=v_{(0,p)}^*v_{(0,q)}^*=(v_{(0,q)}v_{(0,p)})^*=(v_{(0,p)(0,q)})^*=v_{(0,pq)}^*=j_P(pq), \end{align*} $$
so
$j_P:R^{\times } \to \mathrm {Isom}(\mathcal {Q}((R_+ \rtimes R^\times )^{\mathrm {op}}))$
is a semigroup homomorphism. For any
$p \in R^\times $
,
$r \in R_+$
, we compute
$$ \begin{align*} j_P(p)j_A(u_r)j_P(p)^*=v_{(0,p)}^*v_{(r,1)}v_{(0,p)}=v_{(0,p)}^*v_{(pr,p)}=v_{(pr,1)}=j_A(u_{pr})=j_A(\alpha_p(u_r)). \end{align*} $$
By the universal property of
$C^*(R_+) \rtimes R^\times $
, there exists a unique homomorphism
$\Phi :C^*(R_+) \rtimes R^\times \to \mathcal {Q}((R_+ \rtimes R^\times )^{\mathrm {op}})$
such that
$\Phi \circ i_A=j_A$
and
$\Phi \circ i_P=j_P$
. Since
$v_{(r,p)}=v_{(0,p)}v_{(r,1)}$
for any
$(r,p) \in (R_+ \rtimes R^\times )^{\mathrm {op}}$
, we see that
$\Phi $
is surjective. So,
$C^*(R_+) \rtimes R^\times $
is an extension of
$\mathcal {Q}((R_+ \rtimes R^\times )^{\mathrm {op}})$
.
Now, we assume that R is a GCD domain. By [Reference Norling23, Proposition 2.23],
$R^\times $
is right LCM. For
$(r_1,p_1),(r_2,p_2) \in (R_+ \rtimes R^\times )^{\mathrm {op}}$
, suppose that
$p_1R^\times \cap p_2R^\times =pR^\times $
for some
$p \in R^\times $
. We claim that
$$ \begin{align*}(r_1,p_1)\times (R_+ \rtimes R^\times)^{\mathrm{op}}\cap(r_2,p_2) \times (R_+ \rtimes R^\times)^{\mathrm{op}}=(0,p) \times (R_+ \rtimes R^\times)^{\mathrm{op}}.\end{align*} $$
Indeed, for any
$(s_1,q_1),(s_2,q_2) \in (R_+ \rtimes R^\times )^{\mathrm {op}}$
, if
$(r_1,p_1)\times (s_1,q_1)=(r_2,p_2) \times (s_2,q_2)$
, then
$(r_1,p_1)\times (s_1,q_1)=(r_2,p_2) \times (s_2,q_2)=(0,p) \times (s_1+q_1r_1,{q_1p_1}/{p})$
. Conversely, for any
$(s,q) \in (R_+ \rtimes R^\times )^{\mathrm {op}}$
,
$$ \begin{align*}(0,p) \times (s,q)=(r_1,p_1)\times \bigg(s-\frac{pqr_1}{p_1},\frac{pq}{p_1}\bigg)=(r_2,p_2) \times \bigg(s-\frac{pqr_2}{p_2},\frac{pq}{p_2}\bigg).\end{align*} $$
This proves the claim. Hence,
$(R_+ \rtimes R^\times )^{\mathrm {op}}$
is right LCM as well.
Since
$(R_+ \rtimes R^\times )^{\mathrm {op}}$
is right LCM, it follows from [Reference Starling24, Lemma 3.4] that
${\mathcal {Q}((R_+ \rtimes R^\times )^{\mathrm {op}})}$
is the universal unital
$C^*$
-algebra generated by a family of unitaries
$\{v_{(r,p)}:(r,p) \in (R_+ \rtimes R^\times )^{\mathrm {op}}\}$
satisfying the conditions:
-
(1)
$v_{(r_1,p_1)}v_{(r_2,p_2)}=v_{(r_1,p_1) \times (r_2,p_2)}$
; -
(2)
$v_{(r_1,p_1)}^*v_{(r_2,p_2)}=v_{(s_1,q_1)}v_{(s_2,q_2)}^*$
, whenever
$(r_1,p_1)\times (s_1,q_1)=(r_2,p_2) \times (s_2,q_2)$
and
$(r_1,p_1)\times (R_+ \rtimes R^\times )^{\mathrm {op}}\cap (r_2,p_2)\times (R_+ \rtimes R^\times )^{\mathrm {op}}=(r_1,p_1)\times (s_1,q_1)\times (R_+ \rtimes R^\times )^{\mathrm {op}}$
.
For
$(r,p) \in (R_+ \rtimes R^\times )^{\mathrm {op}}$
, define
$V_{(r,p)}:=i_P(p)^*i_A(u_r)$
. Finally, we check that
$\{V_{(r,p)}\}$
satisfies the above two conditions. For any
$(r_1,p_1) ,(r_2,p_2) \in (R_+ \rtimes R^\times )^{\mathrm {op}}$
,
$$ \begin{align*} V_{(r_1,p_1)}V_{(r_2,p_2)}&=i_P(p_1)^*i_A(u_{r_1})i_P(p_2)^*i_A(u_{r_2}) =i_P(p_1)^*i_P(p_2)^*i_A(\alpha_{p_2}(u_{r_1}))i_A(u_{r_2}) \\ &=(i_P(p_2)i_P(p_1))^*i_A(u_{p_2r_1})i_A(u_{r_2}) =i_P(p_1p_2)^*i_A(u_{r_2+p_2r_1}) \\ &=V_{(r_2+p_2r_1,p_1p_2)} =V_{(r_1,p_1) \times (r_2,p_2)}. \end{align*} $$
For
$(r_1,p_1),(r_2,p_2) \in (R_+ \rtimes R^\times )^{\mathrm {op}}$
, suppose that
$p_1R^\times \cap p_2R^\times =pR^\times $
for some
$p \in R^\times $
. By the above claim,
$(r_1,p_1)\times (R_+ \rtimes R^\times )^{\mathrm {op}}\cap (r_2,p_2)\times (R_+ \rtimes R^\times )^{\mathrm {op}}=(0,p)\times (R_+ \rtimes R^\times )^{\mathrm {op}}$
. It is not hard to see that
$(r_1,p_1) \times (-{pr_1}/{p_1},{p}/{p_1})=(r_2,p_2) \times (-{pr_2}/{p_2},{p}/{p_2})=(0,p)$
. So,
$$ \begin{align*} V_{(r_1,p_1)}^*V_{(r_2,p_2)}&=i_A(u_{-r_1})i_P(p_1)i_P(p_2)^*i_A(u_{r_2}) =i_A(u_{-r_1})i_P\bigg(\frac{p}{p_1}\bigg)^*i_P\bigg(\frac{p}{p_2})i_A(u_{r_2}\bigg) \\ &=i_P\bigg(\frac{p}{p_1}\bigg)^*i_A(u_{-{pr_1}/{p_1}})i_A(u_{{pr_2}/{p_2}})i_P\bigg(\frac{p}{p_2}\bigg) \\&=V_{(-{pr_1}/{p_1},{p}/{p_1})}V_{(-{pr_2}/{p_2},{p}/{p_2})}^*. \end{align*} $$
By the universal property of
$\mathcal {Q}((R_+ \rtimes R^\times )^{\mathrm {op}})$
, there exists a homomorphism
${\Psi :\mathcal {Q}((R_+ \rtimes R^\times )^{\mathrm {op}}) \to C^*(R_+) \rtimes R^\times }$
such that
$\Psi (v_{(r,p)})=i_P(p)^*i_A(u_r)$
. Since
$$ \begin{align*} \Phi \circ \Psi(v_{(r,p)})=\Phi(i_P(p)^*i_A(u_r))=j_P(p)^*j_A(u_r)=v_{(0,p)}v_{(r,1)}=v_{(r,p)}, \end{align*} $$
$$ \begin{align*} \Psi\circ \Phi(i_A(u_r))=\Psi(j_A(u_r))=\Psi(v_{(r,1)})=i_A(u_r), \end{align*} $$
$$ \begin{align*} \Psi\circ \Phi(i_P(p))=\Psi(j_P(p))=\Psi(v_{(0,p)})^*=i_P(p), \end{align*} $$
we conclude that
$C^*(R_+) \rtimes R^\times \cong \mathcal {Q}((R_+ \rtimes R^\times )^{\mathrm {op}})$
.
Acknowledgement
The first author thanks the second author for his encouragement and patient supervision.
