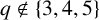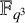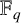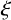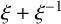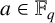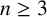1 Introduction
Let q be a prime power and n an integer at least
$3$
, and let
$\mathbb {F}_{q^{n}}$
denote a degree-n extension of the finite field
$\mathbb {F}_{q}$
. We say that
$(q,n)\in \mathfrak {P}$
if, for any
$a\in \mathbb {F}_{q}$
, we can find a primitive element
$\xi \in \mathbb {F}_{q^{n}}$
such that
$\xi +\xi ^{-1}$
is also primitive and
$\operatorname {\mathrm {Tr}}(\xi )=a$
. This problem was considered by Gupta et al., who proved a complete result for
$n\ge 5$
[Reference Gupta, Sharma and Cohen4]. We refer the reader to [Reference Gupta, Sharma and Cohen4] for an introduction to similar problems. Cohen and Gupta [Reference Cohen and Gupta2] extended the work of [Reference Gupta, Sharma and Cohen4], providing a complete result for
$n=4$
and some preliminary results for
$n=3$
. We improved the latter results in [Reference Booker, Cohen, Leong and Trudgian1, Section 7], showing in particular that
$(q,3)\in \mathfrak {P}$
for all
$q\ge 8\times 10^{12}$
. It is a formidable task to try to prove the result for the remaining values of q and, indeed, the computation involved in [Reference Cohen and Gupta2] is extensive.
In this paper, we combine theory and novel computation to resolve the remaining cases with
$n=3$
, proving the following theorem and affirming [Reference Gupta, Sharma and Cohen4, Conjecture 1].
Theorem 1.1. We have
$(q,n)\in \mathfrak {P}$
for all q and all
$n\ge 3$
, with the exception of the pairs
$(3,3)$
,
$(4,3)$
and
$(5,3)$
.
The main theoretical input that we need is the following result, which Cohen and Gupta term the ‘modified prime sieve criterion’ (MPSC).
Theorem 1.2 [Reference Cohen and Gupta2, Theorem 4.1].
Let q be a prime power, and write
$\operatorname {\mathrm {rad}}(q^{3}-1)=kPL$
, where
$k,P,L$
are positive integers. Define
$$ \begin{align*} \delta=1-2\sum_{p\mid P}\frac1p, \quad\varepsilon=\sum_{p\mid L}\frac1p, \quad\theta=\frac{\varphi(k)}{k} \quad\text{and}\quad C_{q}=\begin{cases} 2&\text{if } \, 2\mid q,\\ 3&\text{if } \, 2\nmid q. \end{cases} \end{align*} $$
Then
$(q,3)\in \mathfrak {P}$
provided that
$$ \begin{align} \theta^{2}\delta>2\varepsilon \quad\text{and}\quad q^{1/2}> \frac{C_{q}\big(\theta^{2}4^{\omega(k)}(2\omega(P)-1+2\delta)+\omega(L)-\varepsilon\big)} {\theta^{2}\delta-2\varepsilon}. \end{align} $$
In practice, we take k to be the product of the first few prime factors of
$q^{3}-1$
and L the product of the last few. In particular, taking
$L=1$
, we recover the simpler ‘prime sieve criterion’ (PSC) [Reference Cohen and Gupta2, Theorem 3.2], in which the hypothesis (1.1) reduces to
$$ \begin{align*} \delta>0 \quad\text{and}\quad q^{1/2}>C_{q}4^{\omega(k)}\bigg(\frac{2\omega(P)-1}{\delta}+2\bigg). \end{align*} $$
We will use this simpler criterion in most of what follows.
2 Proof of Theorem 1.1
2.1 Applying the modified prime sieve
Thanks to [Reference Booker, Cohen, Leong and Trudgian1, Theorem 7.2], to complete the proof of Theorem 1.1 for
$n=3$
, it suffices to check all
$q<8\times 10^{12}$
. To reduce this to a manageable list of candidates, we seek to apply the MPSC. For prime
$q<10^{10}$
and composite
$q<8\times 10^{12}$
, we do this directly with a straightforward implementation in PARI/GP [6], first trying the PSC and then the general MPSC when necessary.
For larger primes q, the direct approach becomes too time-consuming, mostly because of the time taken to factor
$q^{3}-1$
. To remedy this, we developed and coded in C the following novel strategy that makes use of a partial factorisation. Using sliding window sieves, we find the complete factorisation of
$q-1$
, as well as all prime factors of
$q^{2}+q+1$
below
$X=2^{20}$
. Let
$u=(q^{2}+q+1)\prod _{p<X}p^{-\operatorname {\mathrm {ord}}_{p}(q^{2}+q+1)}$
denote the remaining unfactored part. If
$u<X^{2}$
, then u must be 1 or a prime number, so we have enough information to compute the full prime factorisation of
$q^{3}-1$
and can apply the PSC directly.
Otherwise, let
$\{p_{1},\ldots ,p_{s}\}$
be the set of prime factors of u. Although the
$p_{i}$
are unknown to us, we can bound their contribution to the PSC via
$$ \begin{align*} s\le\lfloor\log_{X}{u}\rfloor \quad\text{and}\quad \sum_{i=1}^{s}\frac1{p_{i}}\le\frac{\lfloor\log_{X}{u}\rfloor}{X}. \end{align*} $$
We then check the PSC with all possibilities for P divisible by
$p_{1}\cdots p_{s}$
. This sufficed to rule out all primes
$q\in [10^{10},8\times 10^{12}]$
in less than a day using one 16-core machine.
The end result is a list of
$46896$
values of q that are not ruled out by the MPSC, the largest of which is
$4708304701$
. Of these,
$483$
are composite, the largest being
$37951^{2}=1440278401$
. We remark that with only the PSC, there would be
$87157$
exceptions, so using the MPSC reduces the number of candidates by 46% and reduces the time taken to test the candidates (see Section 2.2) by an estimated 61%. This represents an instance when the MPSC makes a substantial and not merely an incidental contribution to a computation.
2.2 Testing the possible exceptions
Next we aim to test each putative exception directly, by exhibiting, for each
$a\in \mathbb {F}_{q}$
, a primitive pair
$(\xi ,\xi +\xi ^{-1})$
satisfying
$\operatorname {\mathrm {Tr}}(\xi )=a$
. Although greatly reduced from the initial set of all
$q<8\times 10^{12}$
from [Reference Booker, Cohen, Leong and Trudgian1, Theorem 7.2], the candidate list is still rather large, so we employed an optimised search strategy based on the following lemma.
Lemma 2.1. Let
$g\in \mathbb {F}_{q}^{\times }$
be a primitive root, let
$d\in \mathbb {Z}$
and define the polynomial
${P=x^{3}-x^{2}+g^{d-1}x-g^{d}\in \mathbb {F}_{q}[x]}$
. Suppose P is irreducible. Let
$\xi _{0}=x+(P)$
be a root of P in
$\mathbb {F}_{q}[x]/(P)\cong \mathbb {F}_{q^{3}}$
and assume that
$\xi _{0}$
is not a pth power in
$\mathbb {F}_{q^{3}}$
for any
$p\mid q^{2}+q+1$
. Then for any
$k\in \mathbb {Z}$
such that
$\gcd (3k+d,q-1)=1$
,
$\xi _{k}:=g^{k}\xi _{0}$
is a primitive root of
$\mathbb {F}_{q^{3}}^{\times }$
satisfying
$\operatorname {\mathrm {Tr}}(\xi _{k})=g^{k}$
and
$\operatorname {\mathrm {Tr}}(\xi _{k}^{-1})=g^{-k-1}$
.
Proof. Note that
$\xi _{0}$
has trace
$1$
and norm
$g^{d}$
, so
$\xi _{k}$
has trace
$g^{k}$
and norm
$\xi _{k}^{q^{2}+q+1}=g^{3k+d}$
. Furthermore,
$$ \begin{align*} \xi_{0}^{3}-\xi_{0}^{2}+g^{d-1}\xi_{0}-g^{d}=0{\implies} \xi_{0}^{-3}-g^{-1}\xi_{0}^{-2}+g^{-d}\xi_{0}^{-1}-g^{-d}=0, \end{align*} $$
so
$\operatorname {\mathrm {Tr}}(\xi _{k}^{-1})=g^{-k}\operatorname {\mathrm {Tr}}(\xi _{0}^{-1})=g^{-k-1}$
.
Let p be a prime dividing
$q^{3}-1$
. If
$p\mid q^{2}+q+1$
, then
$$ \begin{align*} \xi_{k}^{{(q^{3}-1)}/{p}}=(g^{k}\xi_{0})^{{(q^{3}-1)}/{p}} =g^{k{(q^{2}+q+1)}(q-1)/{p}}\xi_{0}^{{(q^{3}-1)}/{p}} =\xi_{0}^{{(q^{3}-1)}/{p}}\ne1, \end{align*} $$
since
$\xi _{0}$
is not a pth power. However, if
$p\mid q-1$
, then
$$ \begin{align*} \xi_{k}^{{(q^{3}-1)}/{p}}=\xi_{k}^{(q^{2}+q+1){(q-1)}/{p}} =g^{(3k+d){(q-1)}/{p}}\ne1, \end{align*} $$
since
$\gcd (3k+d,q-1)=1$
. Hence
$\xi _{k}$
is a primitive root.
Remark 2.2. If
$q\equiv 1\pmod 3$
, then the hypotheses of Lemma 2.1 imply that
${3\nmid d}$
. Hence there always exists k such that
$\gcd (3k+d,q-1)=1$
, and this condition is equivalent to
$\gcd (k+\bar {d},r)=1$
, where
$r=\prod _{{p\mid q-1,\, p\ne 3}}p$
and
$3\bar {d}\equiv d\pmod {r}$
.
Thanks to the symmetry between
$\xi $
and
$\xi ^{-1}$
, if we find a
$\xi $
that works for a given
$g^{k}$
via Lemma 2.1, we also obtain a solution for
$g^{-k-1}$
. Furthermore, when
$q\equiv 1\pmod 4$
,
$\alpha \in \mathbb {F}_{q^{3}}^{\times }$
is primitive if and only if
$-\alpha $
is primitive, and thus a solution for
$g^{k}$
yields one for
$-g^{k}$
by replacing
$\xi $
with
$-\xi $
. Therefore, to find a solution for every
$a\in \mathbb {F}_{q}^{\times }$
, it suffices to check
$k\in \{0,\ldots ,K-1\}$
, where
$$ \begin{align*} K=\begin{cases} \lfloor{q/4}\rfloor&\text{if } q\equiv1\pmod4,\\ \lfloor{q/2}\rfloor&\text{otherwise}. \end{cases} \end{align*} $$
Note that this does not handle
$a=0$
, for which we conduct a separate search over randomly chosen
$\xi \in \mathbb {F}_{q^{3}}$
of trace
$0$
.
Our strategy for applying Lemma 2.1 is as follows. First we choose random values of
$d\pmod {q-1}$
until we find sufficiently many (
$2^{10}$
in our implementation) satisfying the hypotheses. (We allow repetition among the d values, but for some small q there are no suitable d, in which case we fall back on a brute-force search strategy.) For each d, we precompute and store
$\bar {d}=d/3\ \mod {r}$
and
$g^{-d}$
, so we can quickly compute
$\xi _{k}+\xi _{k}^{-1}=a^{-1}g^{-d}(\xi _{0}^{2}-\xi _{0})+a\xi _{0}+a^{-1}g^{-1}$
given the pair
$(a,a^{-1})=(g^{k},g^{-k})$
. Then for each k, we run through the precomputed values of d satisfying
$\gcd (k+\bar {d},r)=1$
, and check whether
$(\xi _{k}+\xi _{k}^{-1})^{(q^{3}-1)/p}\ne 1$]
for every prime
$p\mid q^{3}-1$
.
Thanks to Lemma 2.1, our test for whether
$\xi _{k}$
itself is a primitive root, which is just a coprimality check, is very fast. In fact, since we run through values of k in linear order, we could avoid computing the gcd by keeping track of
$k\ \mod {p}$
and
$-\bar {d}\ \mod {p}$
for each prime
$p\mid r$
, and looking for collisions between them. However, in our numerical tests, this gave only a small reduction in the overall running time.
We are therefore able to save a factor of roughly
$(q^{3}-1)/\varphi (q^{3}-1)$
over a more naive approach that tests both
$\xi $
and
$\xi +\xi ^{-1}$
. Combined with the savings from symmetries noted above, we estimate that the total running time of our algorithm over the candidate set is approximately
$1/15$
th of what it would be with a direct approach testing random
$\xi \in \mathbb {F}_{q^{3}}$
of trace a for every
$a\in \mathbb {F}_{q}$
.
We are not aware of any reason why this strategy should fail systematically, though we observed that for some fields of small characteristic (the largest q we encountered is
$3^{12}=531441$
),
$\xi _{k}+\xi _{k}^{-1}$
is always a square for a particular k. Whenever this occurred, we fell back on a more straightforward randomised search for
$\xi $
of trace
$g^{k}$
and
$g^{-k-1}$
.
We used PARI/GP [6] to handle the brute-force search for
$q\le 211$
, as well as the remaining composite q with a basic implementation of the above strategy. For prime
$q>211$
, we used Andrew Sutherland’s fast C library ff_poly [Reference Sutherland5] for arithmetic in
$\mathbb {F}_{q}[x]/(P)$
, together with an implementation of the Bos–Coster algorithm for vector addition chains described in [Reference de Rooij3, Section 4]. The total running time for all parts was approximately 13 days on a computer with 64 cores (AMD Opteron processors running at 2.5 GHz). The same system handles the largest value
$q=4708304701$
in approximately one hour. Our code is available upon request.
