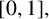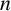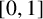1 Introduction
When the line joining
$0$
to
$1$
(or a rectangular piece of paper with
$ [0,1] $
at its edge) is folded in half, right over left, the point
$1/2$
is at the fold. When the line is then folded in half again, right over left, the points
$1/4$
and
$3/4$
are at this second fold, in that order, as indicated by the horizontal arrow, from the outside of the fold to its interior in Figure 1. We have ignored the fact that, strictly speaking, a line with no thickness, when halved and completely folded back upon itself, would have all points superimposed, not juxtaposed at the fold.
Figure 1 Points in a fold after two folds.
Proceeding in this way, the sequence of points from the outside of the third fold to the inside becomes
$\langle 1/8,7/8,5/8,3/8\rangle $
. Their placing, prior to the third fold, is indicated by the vertical arrow in Figure 1.
Definition 1.1 (nth fold sequence)
After we have folded the line n times, the sequence of points from the outside of the nth fold to the inside is designated as the nth fold sequence,
$S_{n}$
, and the
$ j $
th term in
$S_{n}$
is designated as
$S_{n,j}.$
Example 1.2. The sequences after 2, 3 and 4 folds are:
$$ \begin{align*} S_{2} =\langle S_{2,1},S_{2,2}\rangle &=\Big\langle \tfrac{1}{4}, \tfrac{3}{4}\Big\rangle , \\ S_{3} =\langle S_{3,1},S_{3,2},S_{3,3},S_{3,4}\rangle &=\Big\langle \tfrac{1}{8},\tfrac{7}{8},\tfrac{5}{8},\tfrac{3}{8}\Big\rangle, \\ S_{4} =\langle S_{4,1},S_{4,2},S_{4,3},S_{4,4},S_{4,5},S_{4,6},S_{4,7},S_{4,8}\rangle &=\Big\langle \tfrac{1}{16},\tfrac{15}{16},\tfrac{9}{16},\tfrac{7}{16},\tfrac{5}{ 16},\tfrac{11}{16},\tfrac{13}{16},\tfrac{3}{16}\Big\rangle. \end{align*} $$
The line after n folds has the following properties:
-
• the nth fold,
$S_{n},$
is on the right; -
• the ends of the line appear at the bottom on the left;
-
• the first fold,
$S_{1},$
then the second fold,
$S_{2},$
all the way through to the
$(n-1)$
th fold,
$S_{n-1},$
appear immediately above the ends of the line, in ascending order.
For points found in the folds in
$[0,1]$
, we will determine:
-
• the jth term,
$S_{n,j}$
, in
$S_{n}$
in terms of n and j (Theorems 3.2 and 3.4); -
• the relationship between points in the same fold (Theorems 3.5 and 3.6);
-
• the exact position in the folded structure of any point of
$[0,1]$
(Theorems 3.7 and 3.9); -
• given a point on the bottom line of the structure, which point lies at any level above it (Theorem 3.1).
The line when unfolded shows a sequence of
$\vee $
and
$\wedge $
creases, which form the paperfolding sequence which has been studied in [Reference Bates, Bunder and Tognetti1, Reference Dekking, Mendès France and van der Poorten2–Reference Mendès France and van der Poorten4, Reference van der Poorten and Shallit7].
2 Folds and prefolds
We now show one of the properties of
$S_{n}$
.
Theorem 2.1 (Points of
$S_{n}$
)
The set of points in
$S_{n}$
is
$$ \begin{align*} \bigg\{ \frac{2k+1}{2^{n}}\,\Big|\, 0\leq k<2^{n-1}\bigg\}. \end{align*} $$
Proof. Each new fold places a crease midway between creases from earlier folds as well as a new crease midway between 0 and the first crease and another crease midway between 1 and the last crease. Thus the nth fold places a new crease at
$1/2^{n}$
and further new creases thereafter at intervals of
$ 1/2^{n-1}$
units. Thus for
$k=0,1,2,\ldots ,2^{n-1}-1,$
points in the nth fold occur at the locations
$$ \begin{align*} \frac{1}{2^{n}}+\frac{k}{2^{n-1}}=\frac{2k+1}{2^{n}}.\\[-41pt] \end{align*} $$
We note that
$S_{n}$
is the sequence of middle points of the set of overlaid intervals, each of length
$1/2^{n-1}$
, formed after
$n-1$
folds and listed from bottom to top. To help determine this order we introduce the concept of prefolds. We begin with the definition of an nth prefold sequence.
Definition 2.2 (nth prefold)
Fold the line from
$0$
to
$1$
n times, where
$n\geq 0$
. Let j be an integer such that
$ 0<j\leq 2^{n}$
and a be a real number such that
$0<a<1/2^{n}$
. Then we have the following properties.
-
(1)
$F_{n}(a,j)$
is the jth term from the bottom, lying at, or directly above a; we call
$F_{n}(a,j)$
the jth term of the nth prefold sequence at a. -
(2)
$F_{n}(a)$
is the sequence of all terms in the nth prefold sequence at a, that is,
$$ \begin{align*} F_{n}(a)=\langle F_{n}(a,1),F_{n}(a,2),F_{n}(a,3),\ldots ,F_{n}(a,2^{n})\rangle. \end{align*} $$
-
(3)
$\widetilde {F_{n}}(a)$
is the reverse nth prefold sequence at a, that is,
$$ \begin{align*} \widetilde{F_{n}}(a)=\langle F_{n}(a,2^{n}),\ldots ,F_{n}(a,3),F_{n}(a,2),F_{n}(a,1)\rangle. \end{align*} $$
By Definition 2.2,
$F_{n}(a,1)=a$
and we can express
$S_n$
in terms of
$F_{n-1}$
.
Theorem 2.3. For
$n>0,$
$$ \begin{align*} S_{n} =F_{n-1}\bigg(\frac{1}{2^n}\bigg) =\bigg\langle F_{n-1}\bigg(\frac{1}{2^n},1\bigg),F_{n-1}\bigg(\frac{1}{2^n} ,2\bigg),F_{n-1}\bigg(\frac{1}{2^n},3\bigg),\ldots ,F_{n-1}\bigg(\frac{1}{2^n} ,2^{n-1}\bigg)\bigg\rangle. \end{align*} $$
Example 2.4. For
$n=3$
,
$$ \begin{align*} S_{3} =\Big\langle F_{2}\Big(\tfrac{1}{8},1\Big),F_{2}\Big(\tfrac{1}{8},2\Big),F_{2}\Big(\tfrac{1 }{8},3\Big),F_{2}\Big(\tfrac{1}{8},4\Big)\Big\rangle =\Big\langle \tfrac{1}{8},\tfrac{7}{8},\tfrac{5}{8},\tfrac{3}{8}\Big\rangle. \end{align*} $$
We now derive connections between prefolds.
Lemma 2.5 (Form of
$F_{n}(a)$
)
For
$0<a<1/2^{n},$
$$ \begin{align*} F_{n}(a)=\bigg\langle F_{n-1}(a),\widetilde{F_{n-1}}\bigg(\frac{1}{2^{n-1}} -a\bigg)\bigg\rangle. \end{align*} $$
Proof. The nth fold occurs at
$1/2^{n}.$
It involves
$F_{n-1}(({1}/{2^{n-1})} -a) $
for
$0<a<1/2^{n}$
being rotated anticlockwise around
$1/2^{n}$
and then placed atop
$F_{n-1}(a)$
to form
$F_{n}(a),$
giving the result
$.$
Lemma 2.5 gives a recursion for
$F_n$
.
Theorem 2.6 (Recursive expression of prefolds)
$$ \begin{align*} F_{n}(a,j)= \begin{cases} F_{n-1}(a,j),& \quad \text{if }1\leq j\leq 2^{n-1}, \\ F_{n-1}(({1}/{2^{n-1})}-a,2^{n}-j+1), & \quad \text{if }2^{n-1}<j\leq 2^{n}. \end{cases} \end{align*} $$
Theorem 2.7 (Prefold expression of folds)
$$ \begin{align*} S_{n} &=\bigg\langle F_{n-2}\bigg(\frac{1}{2^{n}}\bigg),\widetilde{F_{n-2}}\bigg(\frac{3}{ 2^{n}}\bigg)\bigg\rangle \\ &=\bigg\langle F_{n-2}\bigg(\frac{1}{2^{n}},1\bigg),F_{n-2}\bigg(\frac{1}{2^{n}},2\bigg),\ldots ,F_{n-2}\bigg(\frac{1}{2^{n}},2^{n-2}\bigg), \\ &\quad\ \ F_{n-2}\bigg(\frac{3}{2^{n}},2^{n-2}\bigg),F_{n-2}\bigg(\frac{3}{2^{n}} ,2^{n-2}-1\bigg),\ldots ,F_{n-2}\bigg(\frac{3}{2^{n}},1\bigg)\bigg\rangle. \end{align*} $$
3 The main result
Theorem 3.1. Let
$s\leq 2^{n}$
.
-
(i) If
$s=j+1$
where
$j=\sum _{p=1}^{r}2^{t_{p}}\leq 2^{n}$
with
$r\geq 0 $
and
$t_{1}>t_{2}>\cdots >t_{r}>0$
if
$r>0,$
then
$$ \begin{align*} F_{n}(a,s)=\sum_{p=1}^{r}\frac{1}{2^{t_{p}}}+a. \end{align*} $$
-
(ii) If
$s=j$
with j as in (i), then
$$ \begin{align*} F_{n}(a,s)=\frac{1}{2^{t_{r}-1}}-\sum_{p=1}^{r-1}\frac{1}{2^{t_{p}}}-a. \end{align*} $$
Proof. The proof is by induction on
$n.$
If
$n=1$
and
$j=0$
then
$r=0$
and
$F_{n}(a,j+1)=a$
, so we have (i). If
$n=1$
and
$j=2$
then
$r=t_{r}=1$
and
$F_{n}(a,j)=1-a$
, so we have (ii).
Assume the result for
$n.$
If
$1\leq s\leq 2^{n},$
by Theorem 2.6(i),
$F_{n+1}(a,s)=F_{n}(a,s)$
. The induction hypothesis for
$s=j$
gives (ii) with
$n+1$
for n and, for
$s=j+1\leq 2^{n}$
, it gives (i) with
$n+1$
for n.
If
$2^{n}<s\leq 2^{n+1},$
we have
$t_{1}=n$
and by Theorem 2.6(ii),
$$ \begin{align*} F_{n+1}(a,s)=F_{n}\bigg(\frac{1}{2^{n}}-a,2^{n+1}-s+1\bigg). \end{align*} $$
If
$s=j+1$
, we can write
$$ \begin{align*} 2^{n+1}-( j+1) +1=\sum_{i=1}^{r-1}\bigg( \sum_{p=t_{i}-1}^{t_{i+1}+1}2^{p}\bigg) +2^{t_{r}} \end{align*} $$
because the double sum is the sum of the powers of
$2$
from
$2^{t_{1}-1}$
to
$ 2^{t_{r}+1}$
omitting
$2^{t_{2}},2^{t_{3}},\ldots ,2^{t_{r-1}}.$
By the induction hypothesis,
$$ \begin{align*} F_{n+1}(a,j+1)=\frac{1}{2^{t_{r}-1}}-\sum_{i=1}^{r-1}\bigg( \sum_{p=t_{i}-1}^{t_{i+1}+1}\frac{1}{2^{p}}\bigg) +a-\frac{1}{2^{n}}, \end{align*} $$
where the double sum is the sum of the powers of
$\tfrac 12$
from
${1 }/{2^{t_{1}-1}}$
to
${1}/{2^{t_{r}+1}},$
omitting
${1}/{2^{t_{2}}}, {1}/{2^{t_{3}}},\ldots ,{1}/{2^{t_{r-1}}}.$
This shows
$F_{n+1}(a,s)$
is as in (i) because
$$ \begin{align*} \frac{1}{2^{t_{r}-1}}-\frac{1}{2^{n}}=\frac{1}{2^{t_{r}}}+\frac{1}{ 2^{t_{r}+1}}+\cdots +\frac{1}{2^{t_{1}-1}}+\frac{1}{2^{t_{1}}}. \end{align*} $$
If
$s=j$
, we can write
$$ \begin{align*} 2^{n+1}-j+1=\sum_{i=1}^{r-1}\bigg( \sum_{p=t_{i}-1}^{t_{i+1}+1}2^{p}\bigg) +2^{t_{r}}+1. \end{align*} $$
By the induction hypothesis,
$$ \begin{align*} F_{n+1}(a,j)=\sum_{i=1}^{r-1}\bigg( \sum_{p=t_{i}-1}^{t_{i+1}+1}\frac{1}{ 2^{p}}\bigg) +\frac{1}{2^{t_{r}}}+\frac{1}{2^{n}}-a, \end{align*} $$
where the double sums are as in the
$s=j+1$
case. Since
$$ \begin{align*} \frac{1}{2^{t_{r}}}+\frac{1}{2^{n}}=\frac{1}{2^{t_{r}-1}}-\bigg( \frac{1}{ 2^{t_{r}+1}}+\cdots +\frac{1}{2^{t_{1}-1}}+\frac{1}{2^{t_{1}}}\bigg) , \end{align*} $$
$F_{n+1}(a,s)$
is as in (ii).
Theorem 3.2. Let
$s\leq 2^{n}$
.
-
(i) If
$s=j+1$
where
$j=\sum _{p=1}^{r}2^{t_{p}}\leq 2^{n}$
with
$r\geq 0 $
and
$t_{1}>t_{2}>\cdots >t_{r}>0$
if
$r>0,$
then
$$ \begin{align*} S_{n,s}=\sum_{p=1}^{r}\frac{1}{2^{t_{p}}}+\frac{1}{2^{n}}. \end{align*} $$
-
(ii) If
$s=j$
with j as in (i), then
$$ \begin{align*} S_{n,s}=\frac{1}{2^{t_{r}-1}}-\sum_{p=1}^{r-1}\frac{1}{2^{t_{p}}}-\frac{1}{ 2^{n}}. \end{align*} $$
Proof. The result follows from Theorem 3.1 with
$a={1}/{2^{n}}.$
Example 3.3. Since
$11=2^{3}+2+1$
, we can take
$r=2,t_{1}=3$
and
$t_{2}=1$
in Theorem 3.2(i) to give
$$ \begin{align*} S_{6,11} =\frac{1}{2^{3}}+\frac{1}{2}+\frac{1}{2^{6}} =\frac{41}{64}. \end{align*} $$
Similarly, since
$26=2^{4}+2^{3}+2$
, we can take
$r=3,t_{1}=4$
and
$t_{2}=3$
in Theorem 3.2(ii) to give
$$ \begin{align*} S_{6,26} =\frac{3}{2}-\bigg( \frac{1}{2^{4}}+\frac{1}{2^{3}}+\frac{1}{2}+ \frac{1}{2^{6}}\bigg) =\frac{51}{64}. \end{align*} $$
The next result gives some special cases of Theorem 3.2.
Theorem 3.4. Let
$p\in \mathbb {N}$
.
-
(i)
$S_{n,2^{p}-1}=1-({1}/{2^{p-1}})+({1}/{2^{n}})$
if
$n\geq 1, 0<p\leq n$
. -
(ii)
$S_{n,2^{p}}=({1}/{2^{p-1}})-({1}/{2^{n}})$
if
$n>1,0<p<n$
. -
(iii)
$S_{n,2^{p}+1}=({1}/{2^{p}})+({1}/{2^{n}})$
if
$n>2,0<p<n$
. -
(iv)
$S_{n,2^{p}+2}=1-({1}/{2^{p}})-({1}/{2^{n}})$
if
$n>2,0<p<n$
.
We can relate consecutive elements of
$S_{n}.$
Theorem 3.5. If
$j=\sum _{p=1}^{r}2^{t_{p}}\leq 2^{n-1},r>0$
and
$t_{1}>t_{2}>\cdots >t_{r}>0,$
then
-
(i)
$S_{n,j+1}+S_{n,j}={3}/{2^{t_{r}}}$
, -
(ii)
$S_{n,j-1}+S_{n,j}=1$
.
Proof. (i) This follows from Theorem 3.2.
(ii) As
$j-1= \sum _{p=1}^{r-1}2^{t_{p}}+2^{t_{r}-1}+2^{t_{r}-2}+\cdots +2+1,$
by Theorem 3.2(i),
$$ \begin{align*} S_{n,j-1} =\sum_{p=1}^{r-1}\frac{1}{2^{t_{p}}}+\sum_{i=1}^{t_{r}-1}\frac{1 }{2^{i}}+\frac{1}{2^{n}} =\sum_{p=1}^{r-1}\frac{1}{2^{t_{p}}}+1-\frac{1}{2^{t_{r}}}+\frac{1}{2^{n}}. \end{align*} $$
The result follows because
$$ \begin{align*} S_{n,j}=\frac{1}{2^{t_{r}}}-\sum_{p=1}^{r-1}\frac{1}{2^{t_{p}}}-\frac{1}{ 2^{n}}.\\[-48pt] \end{align*} $$
Theorem 3.6. For
$n\geq 2,$
$$ \begin{align*} S_{n,j}=S_{n,2^{n-1}-j+1}+\frac{( -1) ^{j}}{2^{n-1}}. \end{align*} $$
Proof. For j even, if
$j=\sum _{p=1}^{r}2^{t_{p}}\leq 2^{n-1}$
where
$r>0$
and
$ t_{1}>t_{2}>\cdots >t_{r}>0,$
then
$$ \begin{align*} 2^{n-1}-j+1=\sum_{i=t_{1}+1}^{n-2}2^{i}+\sum_{i=1}^{r-1}\bigg( \sum_{p=t_{i+1}+1}^{t_{i}-1}2^{p}\bigg) +2^{t_{r}}+1. \end{align*} $$
By Theorem 3.2,
$$ \begin{align*} S_{n,2^{n-1}-j+1}=\sum_{i=t_{1}+1}^{n-2}\frac{1}{2^{i}}+\sum_{i=1}^{r-1} \bigg( \sum_{p=t_{i+1}+1}^{t_{i}-1}\frac{1}{2^{p}}\bigg) +\frac{1}{2^{t_{r}} }+\frac{1}{2^{n}} \end{align*} $$
and
$$ \begin{align*} S_{n,j}=\frac{1}{2^{t_{r}-1}}-\sum_{p=1}^{r-1}\frac{1}{2^{t_{p}}}-\frac{1}{ 2^{n}}. \end{align*} $$
So
$$ \begin{align*} S_{n,2^{n-1}-j+1}-S_{n,j} =\sum_{i=t_{1}+1}^{n-2}\frac{1}{2^{i}} +\sum_{i=t_{1}}^{t_{r}+1}\frac{1}{2^{i}}-\frac{1}{2^{t_{r}}}+\frac{1}{2^{n-1} } =-\frac{1}{2^{n-1}}. \end{align*} $$
For j odd, let
$j=\sum _{p=1}^{r}2^{t_{p}}+1$
with
$r>0$
and
$ t_{1}>t_{2}>\cdots >t_{r}>0.$
Then
$$ \begin{align*} 2^{n-1}-j+1=\sum_{i=t_{1}+1}^{n-2}2^{i}+\sum_{i=1}^{r-1}\bigg( \sum_{p=t_{i+1}+1}^{t_{i}-1}2^{p}\bigg) +2^{t_{r}}. \end{align*} $$
So, by Theorem 3.2,
$$ \begin{align*} S_{n,2^{n-1}-j+1}=\frac{1}{2^{t_{r}-1}}-\sum_{i=t_{1}+1}^{n-2}\frac{1}{2^{i}} +\sum_{i=1}^{r-1}\bigg( \sum_{p=t_{i+1}+1}^{t_{i}-1}\frac{1}{2^{p}}\bigg) - \frac{1}{2^{n}} \end{align*} $$
and
$$ \begin{align*} S_{n,j}=\sum_{p=1}^{r}\frac{1}{2^{t_{p}}}+\frac{1}{2^{n}}. \end{align*} $$
Thus
$$ \begin{align*} S_{n,2^{n-1}-j+1}-S_{n,j} =\frac{1}{2^{t_{r}-1}}-\sum_{i=t_{1}+1}^{n-2} \frac{1}{2^{i}}-\sum_{i=t_{1}}^{t_{r}+1}\frac{1}{2^{i}}-\frac{1}{2^{n-1}} =\frac{1}{2^{n-1}}.\\[-46pt] \end{align*} $$
The next two theorems allow us to determine exactly where in the n times folded structure any point b of
$[0,1]$
appears.
Theorem 3.7. If
$0\leq b\leq 1$
,
$b\neq {(2k+1)}/{2^{n+1}}$
, then b lies on level j of the n times folded structure at, or directly above,
$a,$
where
$0\leq a< {1}/{2^{n}}$
.
-
(i) If
$\lfloor 2^{n}b\rfloor $
is even, that is,
$ \lfloor 2^{n}b\rfloor =\sum _{p=1}^{s}2^{u_{p}}$
where
$s=0,$
or
$ s=1$
and
$u_{1}=n,$
or
$n>u_{1}>u_{2}>\cdots >u_{s}>0,$
then
$$ \begin{align*} a =b-\frac{\lfloor 2^{n}b\rfloor }{2^{n}} \quad\text{and}\quad j =1+\sum_{p=1}^{s}2^{n-u_{s}-p+1}. \end{align*} $$
-
(ii) If
$\lfloor 2^{n}b\rfloor $
is odd, that is, for some
$m,0\leq m<n,\lfloor 2^{n}b\rfloor =2^{n-m}-1-\sum _{p=1}^{v}2^{w_{p}}$
where
$v=0$
or
$v>0$
and
$ n-m-1>w_{1}>w_{2}>\cdots >w_{s}>0,$
then
$$ \begin{align*} a =\frac{\lfloor 2^{n}b\rfloor }{2^{n}}+\frac{1}{2^{n}}-b \quad\text{and}\quad j =\sum_{p=1}^{v}2^{n-w_{v}-p+1}+2^{m+1}. \end{align*} $$
Proof. Note that a and j are such that
$0\leq a<{1}/{2^{n}}$
,
$1\leq j\leq 2^{n}$
and
$b=F_{n}(a,j).$
(i) Let
$j=\sum _{p=1}^{r}2^{t_{p}}+1,$
where
$n>t_{1}>t_{2}> \cdots >t_{r}>0$
if
$r>0$
. By Theorem 3.1(i),
$$ \begin{align*} b=\sum_{p=1}^{r}\frac{1}{2^{t_{p}}}+a. \end{align*} $$
Consequently
$\lfloor 2^{n}b\rfloor =\sum _{p=1}^{r}2^{n-t_{p}}$
. If
$ \lfloor 2^{n}b\rfloor =\sum _{p=1}^{s}2^{u_{p}},$
then
$r=s$
and
$t_{p}=n-u_{s-p+1}$
for
$1\leq p\leq s$
. So
$$ \begin{align*} j=1+\sum_{p=1}^{s}2^{n-u_{s-p+1}}. \end{align*} $$
As
$t_{1}<n$
, j can only be odd if
$u_{s}>0,$
that is,
$\lfloor 2^{n}b\rfloor $
is even.
(ii) Let
$j=\sum _{p=1}^{r}2^{t_{p}},$
where
$r>0$
and
$ t_{1}>t_{2}>\cdots >t_{r}>0$
. By Theorem 3.1(ii),
$$ \begin{align*} b=\frac{1}{2^{t_{r}-1}}-\sum_{p=1}^{r-1}\frac{1}{2^{t_{p}}}-a. \end{align*} $$
Consequently
$\lfloor 2^{n}b\rfloor =2^{n-t_{r}+1}-1-\sum _{p=1}^{r-1}2^{n-t_{p}}$
. If j is even then
$\lfloor 2^{n}b\rfloor $
must be odd. If, for some m with
$0\leq m<n,$
we have
$\lfloor 2^{n}b\rfloor =2^{n-m}-1-\sum _{p=1}^{v}2^{w_{p}}$
with
$v=0$
or
$v>0$
and
$n-m-1>w_{1}>w_{2}>\cdots >w_{p}>0,$
then
$$ \begin{align*} 2^{n-m}-\sum_{p=1}^{v}2^{w_{p}}=2^{n-t_{r}+1}-\sum_{p=1}^{r-1}2^{n-t_{p}}. \end{align*} $$
As
$n-m>w_{1}+1$
and
$n-t_{r}+1>n-t_{r-1}+1,$
we must have
$t_{r}=m+1,r=v+1$
and
$t_{p}=n-w_{v-p+1}$
for
$0\leq p\leq r-1$
. So
$$ \begin{align*} j=\sum_{p=1}^{v}2^{n-w_{v-p+1}}+2^{m+1}.\\[-48pt] \end{align*} $$
Example 3.8. If
$n=5$
and
$$ \begin{align*} b =\frac{9}{32}+\frac{\pi }{180} =\frac{2^{5}-2^{4}-2^{2}-2-1}{2^{5}}+\frac{\pi }{180}. \end{align*} $$
then
$\lfloor 2^{5}b\rfloor =2^{5}-2^{4}-2^{2}-2-1=9.$
So by Theorem 3.7(ii) with
$n=5,m=0$
,
$v=3, w_{1}=4,w_{2}=2$
and
$w_{3}=1,$
$$ \begin{align*} a =\frac{5}{16}-\frac{9}{32}-\frac{\pi }{180}\text{ } =\frac{1}{32}-\frac{\pi }{180} \quad\text{and}\quad j =2^{4}+2^{3}+2 =26. \end{align*} $$
If
$n=5$
and
$$ \begin{align*}b=\frac{5}{16}+\frac{\pi }{180},\end{align*} $$
then
$\lfloor 2^{5}b\rfloor =2^{3}+2=10.$
So by Theorem 3.7(i) with
$ s=2,u_{1}=3$
and
$u_{2}=1,$
$$ \begin{align*} a =\frac{5}{16}+\frac{\pi }{180}-\frac{5}{16} =\frac{\pi }{180} \quad\text{and}\quad j =1+2^{2}+2^{4} =21. \end{align*} $$
Theorem 3.9. Let
$S_{n,j}={(2k+1)}/{2^{n}}$
.
-
(i) If
$k=\sum _{p=1}^{s}2^{u_{p}}$
where
$n-1>u_{1}>u_{2}>\cdots >u_{s}>0 $
or
$s=1$
and
$u_{1}=n-1,$
then
$$ \begin{align*} j=1+\sum_{p=1}^{s}2^{n-1-u_{s-p+1}}. \end{align*} $$
-
(ii) If
$k=2^{n-1-m}-1-\sum _{p=1}^{v}2^{w_{p}}$
where
$v=0$
or
$v>0$
and
$n-m-2>w_{1}>w_{2}>\cdots >w_{v}>0,$
then
$$ \begin{align*} j=2^{m+1}+\sum_{p=1}^{v}2^{n-1-w_{v-p+1}}. \end{align*} $$
Proof. If
$S_{n,j}={(2k+1)}/{2^{n}},$
then
$F_{n-1}({1}/{2^{n}},j)={(2k+1) }/{2^{n}}$
and
$\lfloor 2^{n-1}{(2k+1)/}{2^{n}}\rfloor =k,$
so we use Theorem 3.7 with
${(2k+1)}/{2^{n}}$
for b and
$n-1$
for
$n.$
-
(i) If
$k=\sum _{p=1}^{s}2^{u_{p}}$
where
$s=1$
and
$u_{1}=n-1$
or
$ n-1>u_{1}>u_{2}>\cdots >u_{s}>0,$
then
$$ \begin{align*} j=1+\sum_{p=1}^{s}2^{n-1-u_{s-p+1}}. \end{align*} $$
-
(ii) If
$k=2^{n-1-m}-1-\sum _{p=1}^{v}2^{w_{p}}$
where
$v=0$
or
$v>0$
and
$n-m-2>w_{1}>w_{2}>\cdots >w_{v}>0,$
then
$$ \begin{align*} j=2^{m+1}+\sum_{p=1}^{v}2^{n-1-w_{v-p+1}}.\\[-46pt] \end{align*} $$
Example 3.10. For
$n=5,k=9,m=0,v=2,w_{1}=2$
and
$w_{2}=1,$
we have
$S_{5,14}={19}/{32}.$
For
$n=5,k=14,u_{1}=3,u_{2}=2,u_{3}=1$
and
$s=3$
, we have
$S_{5,15}={29}/{32}.$
4 Folds and the triangular array
$T(n,k)$
We thank the referee for drawing our attention to Sigrist’s triangular array
$T(n,i)$
[Reference Sigrist6] which also arises from paperfolding. Our sequences
$S_{n,i}$
are related to
$T(n,i)$
by
$$ \begin{align*} T(n,i) =2^{n-1}S_{n,i}+\tfrac{1}{2}. \end{align*} $$
As a result, our Theorem 3.2 gives the following result for
$T(n,i)$
.
Theorem 4.1. Let
$s\leq 2^{n}$
.
-
(i) If
$s=j+1$
where
$j=\sum _{p=1}^{r}2^{t_{p}}\leq 2^{n}, r\geq 0$
and
$t_{1}>t_{2}>\cdots >t_{r}>0$
if
$r>0$
, then
$$ \begin{align*} T(n,s) =\sum_{p=1}^{r}2^{n-t_{p}-1}+1. \end{align*} $$
-
(ii) If
$s=j,$
with j as in (i), then
$$ \begin{align*} T( n,s) =2^{n-t_{r}}-\sum_{p=1}^{r-1}2^{n-t_{p}-1}. \end{align*} $$
Proof. The statements follow from Theorem 3.2. If s is as in (i), then
$$ \begin{align*} T( n,s) =2^{n-1}\bigg( \sum_{p=1}^{r}\frac{1}{2^{t_{p}}}+\frac{1 }{2^{n}}\bigg) +\frac{1}{2} =\sum_{p=1}^{r}2^{n-t_{p}-1}+1. \end{align*} $$
If s is as in (ii), then
$$ \begin{align*} T( n,s) =2^{n-1}\bigg( \frac{1}{2^{t_{r}-1}}-\sum_{p=1}^{r-1} \frac{1}{2^{t_{p}}}-\frac{1}{2^{n}}\bigg) +\frac{1}{2} =2^{n-t_{r}}-\sum_{p=1}^{r-1}2^{n-t_{p}-1}.\\[-46pt] \end{align*} $$
Similarly, Theorems 3.4 and 3.5 give the following results.
Theorem 4.2. We have:
-
(i)
$T( n,2^{p}-1) =2^{n-1}-2^{n-p}+1$
if
$n\geq 1$
,
$0<p\leq n$
; -
(ii)
$T( n,2^{p}) =2^{n-p}$
if
$n>1$
,
$0<p<n$
; -
(iii)
$T( n,2^{p}+1) =2^{n-p-1}+1$
if
$n>2$
,
$0<p<n$
; -
(iv)
$T( n,2^{p}+2) =2^{n-1}-2^{n-p-1}$
if
$n>2$
,
$0<p<n$
.
Theorem 4.3. If
$j=\sum _{p=1}^{r}2^{t_{p}}\leq 2^{n-1}$
,
$r>0$
and
$t_{1}>t_{2}>\cdots >t_{r}>0,$
then:
-
(i)
$T( n,j+1) +T( n,j) =3.2^{n+t_{r}-1}+1$
; -
(ii)
$T( n,j-1) +T( n,j) =2^{n-1}+1$
.
Write out the elements of
$T(n,i)$
as
$$ \begin{align*}\begin{array}{c} T( 1,1) =a( 1) , \\[3pt] T( 2,1) =a( 2),T( 2,2) =a(3) , \\[3pt] T( 3,1) =a( 4) ,T( 3,2) =a(5) ,T( 3,3) =a( 6), \\[3pt]\vdots \end{array}\end{align*} $$
Shallit [Reference Shallit5] observed that
$a( n) $
is a 2-regular sequence defined by the recursion
$$ \begin{align*} a( 4n) &=a( 2n), \\ a( 4n+2) &=a( 2n) -a( 2n+1) +a(4n+1), \\ a( 4n+3) &=a( 2n+1), \\ a( 8n+1) &=-2a( 2n+1) +3a( 4n+1), \\ a( 8n+5) &=-a( 2n+1) +2a( 4n+1). \end{align*} $$
As, clearly,
$T( n,i) =a( 2^{n-1}+i-1) ,$
we have
$a( 2^{n-1}+i-1) =2^{n-1}S_{n,i}+{1}/{2}$
. This leads to the following result.
Theorem 4.4. We have:
-
(i)
$2S_{n,4j+1}=S_{n-1,2j+1}$
if
$n>2$
; -
(ii)
$2S_{n,4j+3}=S_{n-1,2j+1}-S_{n-1,2j+2}+2S_{n,4j+2}$
if
$n>2$
; -
(iii)
$2S_{n,4j+4}=S_{n-1,2j+2}$
if
$n>2$
; -
(iv)
$2S_{n,8j+2}=3S_{n-1,4j+2}-S_{n-2,2j+2}$
if
$n>3$
; -
(v)
$4S_{n,8j+6}=4S_{n-1,4j+2}-S_{n-2,2j+2}$
if
$n>3$
.
Proof. If
$n>2$
, then
$a( 2^{n-1}+4j) =a( 2^{n-2}+2j)$
, so
$2^{n-1}S_{n,4j+1}=2^{n-2}S_{n-1,2j+1}$
, giving (i). A similar approach gives the remaining results.
