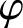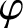1. Introduction
In his memoir, Johnson [Reference Johnson3] introduced the cohomological notion of an amenable Banach algebra. The concept of
$\varphi $
-amenability, which is a modification of Johnson’s amenability, was introduced by Kaniuth et al. [Reference Kaniuth, Lau and Pym4] and independently by Monfared [Reference Monfared8]. By way of background,
$\varphi $
-amenability is a generalisation of the notion of (left) amenability for Lau algebras (or F-algebras); these are Banach algebras that are preduals of a von Neumann algebra where the identity element of the von Neumann algebra is a character [Reference Lau5]. The notion of injectivity for dual Banach algebras was introduced by Daws [Reference Daws1]. We recall the definitions in Definitions 2.1 and 2.4 below.
Motivated by these concepts, we define and study
$\varphi $
-injective dual Banach algebras. In Section 2, we recall some background definitions and notation. In Section 3, we introduce and investigate
$\varphi $
-injectivity of a dual Banach algebra
$\mathfrak {A}$
. Among other things, we prove that
$\varphi $
-injectivity is equivalent to
$\varphi $
-amenability whenever
$\varphi : \mathfrak {A} \longrightarrow \mathbb {C}$
is a
$w^*$
-continuous homomorphism. In Section 4, using the idea of
$\varphi $
-injectivity, we discuss
$\varphi $
-amenability of the enveloping dual Banach algebra
${\textrm {WAP}}(\mathfrak {A}^*)^*$
of a Banach algebra
$\mathfrak {A}$
. Besides examples, we will characterise
$\varphi $
-amenability of
${\textrm {WAP}}(\mathfrak {A}^*)^*$
in terms of continuous representations from
$\mathfrak {A}$
on reflexive Banach spaces. Section 5 is devoted to non-
$\tilde {\varphi }$
-amenability of the algebra
$ {\textrm {WAP}}(\ell ^1(\mathbb {N}_\wedge )^*)^*$
where
$\varphi $
is the augmentation character on
$\ell ^1(\mathbb {N}_\wedge )$
. Finally, in Appendix A, we shall see that every nonzero homomorphism
$\varphi : \mathfrak {A} \longrightarrow \mathbb {C}$
becomes automatically a
$w^*$
-continuous homomorphism
$\varphi : {\textrm {WAP}}(\mathfrak {A}^*)^* \longrightarrow \mathbb {C}$
.
2. Preliminaries
For a Banach algebra
$\mathfrak {A}$
, the projective tensor product
$ \mathfrak {A} \widehat {\otimes } \mathfrak {A}$
is a Banach
$\mathfrak {A}$
-bimodule in a canonical way. The diagonal operator
$ \pi : \mathfrak {A} \widehat {\otimes } \mathfrak {A} \longrightarrow \mathfrak {A}$
defined by
$\pi (a \otimes b) = ab$
is an
$\mathfrak {A}$
-bimodule homomorphism. Let E be a Banach
$\mathfrak {A}$
-bimodule. A continuous linear operator
$D: \mathfrak {A} \longrightarrow E$
is called a derivation if it satisfies
$ D(ab) = D(a) \cdot b + a \cdot D(b) $
for all
$a,b \in \mathfrak {A}$
. Given
$x \in E$
, the inner derivation
$ad_x : \mathfrak {A} \longrightarrow E$
is defined by
$ad_x(a) = a \cdot x - x \cdot a$
. We write
$\Delta (\mathfrak {A})$
for the set of all homomorphisms from
$\mathfrak {A}$
onto
$ \mathbb {C}$
.
Definition 2.1 [Reference Kaniuth, Lau and Pym4].
Let
$\mathfrak {A}$
be a Banach algebra and let
$\varphi \in \Delta (\mathfrak {A})$
. The algebra
$\mathfrak {A}$
is
$\varphi $
-amenable if there exists a bounded linear functional m on
$\mathfrak {A}^*$
satisfying
$m(\varphi ) = 1$
and
$ m(f \cdot a) = \varphi (a) m(f)$
for all
$a \in \mathfrak {A}$
and
$f \in \mathfrak {A}^*$
.
Proposition 2.2 [Reference Kaniuth, Lau and Pym4, Theorem 1.1].
Let
$\mathfrak {A}$
be a Banach algebra and let
$\varphi \in \Delta (\mathfrak {A})$
. Then
$\mathfrak {A}$
is
$\varphi $
-amenable if and only if every derivation
$D: \mathfrak {A} \longrightarrow E^*$
is inner, where E is a Banach
$\mathcal A$
-bimodule such that
$ a \cdot x = \varphi (a) x $
for all
$a \in \mathfrak {A}$
and
$x \in E$
.
Let
$\mathfrak {A}$
be a Banach algebra. A Banach
$\mathfrak {A}$
-bimodule E is dual if there is a closed submodule
$E_*$
of
$E^*$
such that
$E = (E_*)^*$
. We call
$E_*$
the predual of E. A Banach algebra
$\mathfrak {A}$
is dual if it is dual as a Banach
$\mathfrak {A}$
-bimodule. We write
$\mathfrak {A} = (\mathfrak {A}_*)^*$
if we wish to stress that
$\mathfrak {A}$
is a dual Banach algebra with predual
$\mathfrak {A}_*$
.
Let
$\mathfrak {A} $
be a dual Banach algebra and let E be a Banach
$\mathfrak {A}$
-bimodule. Then
$\sigma wc(E)$
stands for the set of all elements
$ x \in E$
such that the maps
$$ \begin{align} \mathfrak{A} \longrightarrow E, \quad a \longmapsto \left \{ \begin{array}{@{}ll} a\cdot x \\ x \cdot a \end{array} \right. \end{align} $$
are
$w^*$
-
$wk$
-continuous. It is well known that
$\sigma wc(E)$
is a closed submodule of E.
Suppose that
$\mathfrak {A}$
is a Banach algebra and that E is a Banach
$\mathfrak {A}$
-bimodule. An element
$x \in E$
is weakly almost periodic if the maps in
$(*)$
are weakly compact. The set of all weakly almost periodic elements in E is denoted by
$ {\textrm {WAP}}(E)$
.
Let
$\mathfrak {A}$
be a Banach algebra. For
$ \varphi \in {\textrm {WAP}}(\mathfrak {A}^*)$
and
$\Psi \in {\textrm {WAP}}(\mathfrak {A}^*)^*,$
define
$ \Psi \cdot \varphi \in {\textrm {WAP}}(\mathfrak {A}^*)$
by
$ \langle a , \Psi \cdot \varphi \rangle = \langle \varphi \cdot a , \Psi \rangle $
for all
$a \in \mathfrak {A}$
. This turns
${\textrm {WAP}}(\mathfrak {A}^*)^*$
into a Banach algebra by letting
$$\begin{align*}\langle \varphi , \Phi \Psi \rangle = \langle \Psi \cdot \varphi , \Phi \rangle \quad ( \Phi , \Psi \in {\textrm{WAP}}(\mathfrak{A}^*)^* ,\ \varphi \in {\textrm{WAP}}(\mathfrak{A}^*) ).\end{align*}$$
More precisely,
${\textrm {WAP}}(\mathfrak {A}^*)^*$
is a dual Banach algebra and there is a (continuous) homomorphism
$ \imath : \mathfrak {A} \longrightarrow {\textrm {WAP}} (\mathfrak {A}^*)^*$
whose range is
$w^*$
-dense. Indeed, the map
$ \imath $
is obtained by composing the canonical inclusion
$ \mathfrak {A} \longrightarrow \mathfrak {A}^{**}$
with the adjoint of the inclusion map
$ {\textrm {WAP}} (\mathfrak {A}^*) \hookrightarrow \mathfrak {A} ^*$
[Reference Runde10].
Proposition 2.3 [Reference Runde10, Theorem 4.10].
Let
$\mathfrak {A}$
be a Banach algebra, let
$\mathfrak {B}$
be a dual Banach algebra and let
$ \theta : \mathfrak {A} \longrightarrow \mathfrak {B}$
be a (continuous) homomorphism. Then there exists a unique
$w^*$
-continuous homomorphism
$ \tilde {\theta } : {\textrm {WAP}}(\mathfrak {A}^*)^* \longrightarrow \mathfrak {B}$
such that
$ \theta = \tilde {\theta } \circ \imath $
. In particular, every
$w^*$
-continuous homomorphism from
${\textrm {WAP}}(\mathfrak {A}^*)^*$
into
$\mathfrak {B}$
is uniquely determined by its restriction to
$\mathfrak {A}$
.
Let
$ \mathcal {S}$
be a subset of an algebra
$ \mathcal {H}$
. We use
$ \mathcal {S}^c$
to denote the commutant of
$ \mathcal {S}$
in
$ \mathcal {H}$
, that is,
$ \mathcal {S}^c = \{ h \in \mathcal {H} \ : \ hs = sh , \ s \in \mathcal {S} \} $
. It is obvious that
$\mathcal {S}^c$
is a closed subalgebra of
$ \mathcal {H}$
. For Banach spaces E and F, we write
$ \mathcal {L}(E,F)$
for the set of all bounded linear maps from E into F and
$ \mathcal {L}(E)$
for
$ \mathcal {L}(E,E)$
. We also write
$I_{E}$
for the identity map on E.
Let E be a Banach space and let
$ \mathcal {S} \subseteq \mathcal {L}(E)$
be a subalgebra. A quasi expectation for
$ \mathcal {S}$
is a projection
$ Q : \mathcal {L}(E) \longrightarrow \mathcal {S}^c $
such that
$ Q( c T d) = c Q(T) d$
for
$ c,d \in \mathcal {S}^c$
and
$T \in \mathcal {L}(E)$
.
Definition 2.4 [Reference Daws1, Definition 6.12].
A dual Banach algebra
$\mathfrak {A}$
is injective if, whenever
$ \varrho : \mathfrak {A} \longrightarrow \mathcal {L}(E)$
is a
$w^*$
-continuous unital representation, then there is a quasi expectation
$ Q : \mathcal {L}(E) \longrightarrow \varrho (\mathfrak {A})^c$
.
Connes amenable dual Banach algebras were systematically introduced by Runde in [Reference Runde9]. The remarkable point is that injectivity and Connes amenability are the same notions [Reference Daws1, Theorem 6.13].
3. On
$\varphi $
-injectivity of dual Banach algebras
Let
$\mathfrak {A}$
and
$\mathfrak {B}$
be Banach algebras and let
$ \theta : \mathfrak {A} \longrightarrow \mathfrak {B}$
be a homomorphism. For
$\varphi \in \Delta (\mathfrak {A})$
, we define
$$\begin{align*}\theta(\mathfrak{A})^\varphi = \{ b \in \mathfrak{B}: \theta(a) b = \varphi(a) b \ \ (a \in \mathfrak{A}) \}.\end{align*}$$
Obviously,
$\theta (\mathfrak {A})^\varphi $
is a (closed) right ideal of
$\mathfrak {B}$
. One may see Lemma 5.1 below as a concrete example of such a set.
Definition 3.1. Let
$\mathfrak {A}$
and
$\mathfrak {B}$
be Banach algebras, let
$ \theta : \mathfrak {A} \longrightarrow \mathfrak {B}$
be a homomorphism and let
$\varphi \in \Delta (\mathfrak {A})$
. A
$ \varphi $
-quasi expectation
$ Q : \mathfrak {B} \longrightarrow \theta (\mathfrak {A})^\varphi $
is a projection from
$ \mathfrak {B}$
onto
$ \theta (\mathfrak {A})^\varphi $
satisfying
$ Q ( cbd) = c Q(b) d$
for
$ c,d \in \theta (\mathfrak {A})^c$
and
$b \in \mathfrak {B}$
.
It is standard that
$\mathcal {L}(E) = (E^* \hat {\otimes } E)^* $
is a dual Banach algebra whenever E is a reflexive Banach space [Reference Runde9]. For a dual Banach algebra
$\mathfrak {A}$
, we denote by
$\Delta _{w^*}(\mathfrak {A})$
the set of all
$w^*$
-continuous homomorphisms from
$\mathfrak {A}$
onto
$\mathbb {C}$
.
Definition 3.2. Let
$\mathfrak {A}$
be a dual Banach algebra and let
$\varphi \in \Delta _{w^*}(\mathfrak {A})$
. We say that
$\mathfrak {A}$
is
$ \varphi $
-injective if, whenever
$ \varrho : \mathfrak {A} \longrightarrow \mathcal {L}(E)$
is a
$w^*$
-continuous representation on a reflexive Banach space E, then there is a
$ \varphi $
-quasi expectation
$ Q : \mathcal {L}(E) \longrightarrow \varrho (\mathfrak {A})^\varphi $
.
It should be stressed that Definition 3.2 is in fact a generalisation of the classical definition of injectivity (see Corollary 3.7 below).
Let
$\mathfrak {A}$
be a dual Banach algebra. It is known that its unitisation
$\mathfrak {A}^\sharp = \mathfrak {A} \oplus \mathbb {C} $
is a dual Banach algebra as well. Let
$\varphi \in \Delta _{w^*}(\mathfrak {A})$
and let
$\varphi ^\sharp $
be its unique extension to
$\mathfrak {A}^\sharp $
. It is obvious that
$\varphi ^\sharp \in \Delta _{w^*}(\mathfrak {A}^\sharp ) $
.
Theorem 3.3. Suppose that
$\mathfrak {A}$
is a dual Banach algebra and that
$\varphi \in \Delta _{w^*}(\mathfrak {A})$
. Then
$\mathfrak {A}$
is
$ \varphi $
-injective if and only if
$\mathfrak {A}^\sharp $
is
$ \varphi ^\sharp $
-injective.
Proof. Let
$\mathfrak {A}$
be
$ \varphi $
-injective and let
$ \varrho : \mathfrak {A}^\sharp \longrightarrow \mathcal {L}(E)$
be a
$w^*$
-continuous representation where E is a reflexive Banach space. Clearly,
$\hat {\varrho } = \varrho |_{\mathfrak {A}}$
is a
$w^*$
-continuous representation for
$\mathfrak {A}$
. Hence, there is a
$ \varphi $
-quasi expectation
$ Q : \mathcal {L}(E) \longrightarrow \hat {\varrho }(\mathfrak {A})^\varphi $
. Since
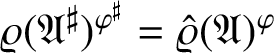$ \varrho (\mathfrak {A}^\sharp )^{\varphi ^\sharp } = \hat {\varrho }(\mathfrak {A})^\varphi $
and
$ \varrho (\mathfrak {A}^\sharp )^c = \hat {\varrho }(\mathfrak {A})^c$
, we are done.
Conversely, suppose that
$ \mathfrak {A}^\sharp $
is
$ \varphi ^\sharp $
-injective and that
$ \varrho : \mathfrak {A} \longrightarrow \mathcal {L}(E)$
is a
$w^*$
-continuous representation on a reflexive Banach space E. We extend
$\varrho $
to
$\hat {\varrho }$
from
$\mathfrak {A}$
into
$\mathfrak {A}^\sharp $
by setting
$\hat {\varrho }(a, \lambda ) = \varrho (a) + \lambda I_E$
for
$a \in \mathfrak {A}$
and
$ \lambda \in \mathbb {C}$
. It is readily seen that
$\hat {\varrho }$
is a
$w^*$
-continuous representation. By the assumption, there is a
$ \varphi ^\sharp $
-quasi expectation
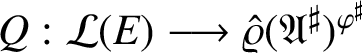$ Q : \mathcal {L}(E) \longrightarrow \hat {\varrho }(\mathfrak {A}^\sharp )^{\varphi ^\sharp }$
. Because
$\hat {\varrho } (\mathfrak {A}^\sharp )^c = \varrho (\mathfrak {A})^c$
and
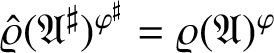$\hat {\varrho } (\mathfrak {A}^\sharp )^{\varphi ^\sharp } = \varrho (\mathfrak {A})^\varphi $
, we conclude that
$\mathfrak {A}$
is
$ \varphi $
-injective.
Theorem 3.4. Suppose that
$\mathfrak {A} = (\mathfrak {A}_*)^* $
and
$\mathfrak {B} = (\mathfrak {B}_*)^*$
are dual Banach algebras,
$\varphi \in \Delta _{w^*}(\mathfrak {A})$
and that
$\theta : \mathfrak {A} \longrightarrow \mathfrak {B} $
is a
$w^*$
-continuous homomorphism. If
$\mathfrak {A}$
is
$\varphi $
-amenable, then there exists a
$ \varphi $
-quasi expectation
$ Q :\mathfrak {B} \longrightarrow \theta (\mathfrak {A})^\varphi $
.
Proof. Here we follow the standard argument in [Reference Runde11, Theorem 5.1.24]. Let
$ E= \mathfrak {B} \hat {\otimes } \mathfrak {B}_*$
be equipped with the
$\mathfrak {A}$
-bimodule operation given through
$$\begin{align*}a \cdot (b \otimes f) = \varphi(a) (b \otimes f) \quad \text{and} \quad \ (b \otimes f) \cdot a = b \otimes f \cdot \theta(a)\end{align*}$$
for
$a \in \mathfrak {A}$
,
$f \in \mathfrak {B}_*$
and
$b \in \mathfrak {B}$
. Identifying
$E^*$
with
$\mathcal {L}(\mathfrak {B})$
as
$$\begin{align*}T (b \otimes f) = \langle f , T(b) \rangle \quad(T \in \mathcal{L}(\mathfrak{B}), \ f \in \mathfrak{B}_*, \ b \in \mathfrak{B}),\end{align*}$$
we obtain as the corresponding dual
$\mathfrak {A}$
-bimodule operation on
$\mathcal {L}(\mathfrak {B})$
$$\begin{align*}(a \cdot T)(b) = \theta(a) T(b) \quad \text{and} \quad (T \cdot a)(b) = \varphi(a) T(b) \quad (a \in \mathfrak{A}, \ b \in \mathfrak{B}, \ T \in \mathcal{L}(\mathfrak{B})). \end{align*}$$
Let F be the subspace of
$E^*$
consisting of those
$T \in E^*$
such that
$$\begin{align*}\langle zb \otimes f - b \otimes f \cdot z , T \rangle =0, \quad \langle bz\otimes f - b \otimes z \cdot f , T \rangle =0 \quad\mbox{and}\quad \langle {z}^\prime \otimes f , T \rangle =0 \end{align*}$$
for all
$ b \in \mathfrak {B}$
,
$f \in \mathfrak {B}_*$
,
$ z \in \theta (\mathfrak {A})^c$
and
${z}^\prime \in \theta (\mathfrak {A})^\varphi $
. It is routine to verify that F is a
$w^*$
-closed
$\mathfrak {A}$
-submodule of
$E^*$
and thus a dual Banach
$\mathfrak {A}$
-bimodule in its own right. Considering the derivation
$ D = ad_{I_{\mathfrak {B}}} : \mathfrak {A} \longrightarrow \mathcal {L}(\mathfrak {B})$
, we claim that D attains its values in F. To see this, let
$ b \in \mathfrak {B}$
,
$f \in \mathfrak {B}_*$
,
$z \in \theta (\mathfrak {A})^c$
,
$ {z}^\prime \in \theta (\mathfrak {A})^\varphi $
and
$a \in \mathfrak {A}$
. Then
$$ \begin{align*} \langle {z}^\prime \otimes f, Da \rangle = \langle {z}^\prime \otimes f \cdot \theta(a) , I_{\mathfrak{B}} \rangle - \varphi(a) \langle {z}^\prime \otimes f , I_{\mathfrak{B}} \rangle = \langle f , \theta(a) {z}^\prime \rangle - \langle f , \varphi(a) {z}^\prime \rangle = 0 \end{align*} $$
and
$$ \begin{align*} \langle zb \otimes f &- b \otimes f \cdot z , Da \rangle = \langle zb \otimes f - b \otimes f \cdot z , a \cdot I_{\mathfrak{B}} - I_{\mathfrak{B}} \cdot a \rangle \\&= \langle (zb \otimes f ) \cdot a - (b \otimes f \cdot z ) \ \cdot \ a - a \cdot ( zb \otimes f ) + a \cdot (b \otimes f \cdot z) , I_{\mathfrak{B}} \rangle \\& =\langle zb \otimes f \cdot \theta(a) - b \otimes f \cdot z \theta(a) - \varphi(a) z b \otimes f + \varphi(a) b \otimes f \cdot z , I_{\mathfrak{B}} \rangle \\&= \langle zb , f \cdot \theta(a) \rangle - \langle b , f \cdot z \theta(a) \rangle - \varphi(a) \langle z b , f \rangle + \varphi(a) \langle b , f \cdot z \rangle \\&= \langle \theta(a) zb , f \rangle - \langle z \theta(a) b , f \rangle - \varphi(a) \langle z b , f \rangle + \varphi(a) \langle z b , f \rangle = 0, \end{align*} $$
because
$ z \in \theta (\mathfrak {A})^c$
. Also,
$$ \begin{align*} \langle bz\otimes f &- b \otimes z \cdot f , Da \rangle = \langle b z \otimes f - b \otimes z \cdot f , a \cdot I_{\mathfrak{B}} - I_{\mathfrak{B}} \cdot a \rangle \\&= \langle (b z \otimes f ) \cdot a - (b \otimes z \cdot f ) \cdot a - a \cdot ( bz \otimes f ) + a \cdot (b \otimes z \cdot f ) , I_{\mathfrak{B}} \rangle \\& =\langle b z \otimes f \cdot \theta(a) - b \otimes z \cdot f \cdot \theta(a) - \varphi(a) b z \otimes f + \varphi(a) b \otimes z \cdot f , I_{\mathfrak{B}} \rangle \\ &= \langle b z , f \cdot \theta(a) \rangle - \langle b , z \cdot f \cdot \theta(a) \rangle - \varphi(a) \langle b z , f \rangle + \varphi(a) \langle b , z \cdot f \rangle \\ &= \langle \theta(a) b z , f \rangle - \langle \theta(a) b z , f \rangle - \varphi(a) \langle b z , f \rangle + \varphi(a) \langle b z , f \rangle = 0. \end{align*} $$
Then, by Proposition 2.2, there exists
$\rho \in F$
such that
$ D= ad_\rho $
. Setting
$Q =I_{\mathfrak {B}} - \rho $
, we see that
$ a \cdot Q = Q \cdot a$
for all
$a \in \mathfrak {A}$
. Hence,
$ \theta (a) Q(b) = \varphi (a) Q(b)$
for
$b \in \mathfrak {B}$
and so Q takes values in
$\theta (\mathfrak {A})^\varphi $
.
Because
$\rho \in F $
, we have
$ 0 = \langle {z}^\prime \otimes f , \rho \rangle = \langle \rho ({z}^\prime ) , f \rangle $
for
$ f \in \mathfrak {B}_*$
,
$ {z}^\prime \in \theta (\mathfrak {A})^\varphi $
. That is,
$\rho ({z}^\prime ) = 0 $
and thus
$ Q ({z}^\prime ) = {z}^\prime $
for each
$ {z}^\prime \in \theta (\mathfrak {A})^\varphi $
. Therefore, Q is the identity on
$\theta (\mathfrak {A})^\varphi $
and thus a projection onto
$\theta (\mathfrak {A})^\varphi $
.
Next, for each
$b \in \mathfrak {B}$
,
$f \in \mathfrak {B}_*$
and
$ z \in \theta (\mathfrak {A})^c$
,
$$\begin{align*}0 = \langle z b \otimes f - b \otimes f \cdot z , \rho \rangle = \langle \rho( z b) , f \rangle - \langle \rho( b) , f \cdot z \rangle = \langle \rho( z b) - z \rho( b) , f \rangle\end{align*}$$
and so
$\rho ( z b) = z \rho ( b) $
. Similarly,
$$\begin{align*}0 = \langle b z \otimes f - b \otimes z \cdot f , \rho \rangle = \langle \rho(b z) , f \rangle - \langle \rho( b) , z \cdot f \rangle = \langle \rho(b z) - \rho( b) z , f \rangle,\end{align*}$$
so that
$\rho ( b z) = \rho ( b) z $
. Thus,
$$\begin{align*}Q(z b )= z b - \rho (z b ) = z b - z \rho ( b ) = z Q(b), \quad Q(b z )= b z - \rho (b z ) = b z - \rho ( b ) z = Q(b) z .\end{align*}$$
We then have
$Q( z_1 b z_2) = z_1 Q( b z_2) = z_1 Q( b ) z_2$
for
$z_1 , z_2 \in \theta (\mathfrak {A})^c , b \in \mathfrak {B}$
. Therefore, Q is a
$\varphi $
-quasi expectation.
To establish Theorem 3.6 below, we need some preliminaries from [Reference Daws1, pages 253–255]. Let
$ \mathfrak {A} $
be a Banach algebra. First, recall that
$ ( \mathfrak {A} \widehat {\otimes } \mathfrak {A} )^* = \mathcal {L}(\mathfrak {A}, \mathfrak {A}^*)$
, where we choose the convention that
$ \langle a \otimes b , T \rangle = \langle a , T(b) \rangle $
for
$a, b \in \mathfrak {A}$
,
$T \in \mathcal {L}(\mathfrak {A}, \mathfrak {A}^*)$
. Next, let
$\varrho : \mathfrak {A} \longrightarrow \mathcal {L}(E)$
be a (continuous) representation on a reflexive Banach space E. Then
$\mathcal {L}(E)$
becomes a Banach
$ \mathfrak {A}$
-bimodule with actions
$ a \cdot T =\varrho (a) T $
and
$ T \cdot a = T \varrho (a) $
for
$a \in \mathfrak {A} $
,
$T \in \mathcal {L}(E)$
. Also,
$\mathcal {L}(E)$
is a Banach
$\varrho (\mathfrak {A})^c$
-bimodule in the obvious way. We write
$\mathcal {L}_{\mathfrak {A}}(\mathcal {L}(E))$
for the collection of all
$\varrho (\mathfrak {A})^c$
-bimodule homomorphisms, that is, maps
$Q \in \mathcal {L}(\mathcal {L}(E)) $
such that
$ Q( S T) = S Q(T)$
and
$Q(T S) = Q(T) S $
for all
$S \in \varrho (\mathfrak {A})^c$
and
$ T \in \mathcal {L}(E)$
. We turn
$ \mathcal {L}_{\mathfrak {A}}(\mathcal {L}(E))$
into a Banach
$\mathfrak {A}$
-bimodule by setting
$$\begin{align*}(a \,. \,Q) (T) = \varrho(a) Q(T) \quad \text{and} \quad (Q \,. \,a)T = Q(T) \varrho(a) \end{align*}$$
for
$ a \in \mathfrak {A}$
,
$ T \in \mathcal {L}(E)$
and
$ Q \in \mathcal {L}_{\mathfrak {A}}(\mathcal {L}(E))$
. We notice that
$ \mathcal {L}(\mathcal {L}(E)) $
is a dual Banach algebra with predual
$ \mathcal {L}(E) \widehat {\otimes } ( E \widehat {\otimes } E^*)$
. Let
$X \subseteq \mathcal {L}(E) \widehat {\otimes } ( E \widehat {\otimes } E^*)$
be the closure of the linear span of the set consisting of all elements of the form
$ ST \otimes x \otimes \mu - T \otimes x \otimes S^*(\mu )$
and
$ T S \otimes x \otimes \mu - T \otimes S(x) \otimes \mu $
for all
$ S \in \varrho (\mathfrak {A})^c$
,
$T \in \mathcal {L}(E)$
,
$x \in E$
,
$\mu \in E^*$
. Because
$ X ^\perp = \mathcal {L}_{\mathfrak {A}}(\mathcal {L}(E))$
, we see that
$\mathcal {L}_{\mathfrak {A}}(\mathcal {L}(E))$
is a dual Banach algebra with the predual
$ Y= { \mathcal {L}(E) \widehat {\otimes } E \widehat {\otimes } E^*}/{X}$
. Now define
$ \psi : Y \longrightarrow \mathcal {L}(\mathfrak {A}, \mathfrak {A}^*)$
via
$$ \begin{align*} & \langle a \otimes b , \psi(T \otimes x \otimes \mu + X) \rangle = \langle \varrho (a) T \varrho (b) (x) , \mu \rangle \quad (a,b \in \mathfrak{A},\ x \in E,\ \mu \in E^*,\ T \in \mathcal{L}(E) ). \end{align*} $$
We turn
$ \mathcal {L}(E) \widehat {\otimes } E \widehat {\otimes } E^*$
into a Banach
$\mathfrak {A}$
-bimodule through
$$\begin{align*}a \cdot (T \otimes x \otimes \mu ) = T \otimes \varrho (a) (x) \otimes \mu \quad \text{and} \quad (T \otimes x \otimes \mu ) \cdot a =T \otimes x \otimes \varrho (a)^* (\mu) \end{align*}$$
for
$ a \in \mathfrak {A}, x \in E, \mu \in E^*, T \in \mathcal {L}(E)$
. Observe that
$\psi $
is an
$\mathfrak {A}$
-bimodule homomorphism.
The next proposition shows that it is possible to choose E to make
$\psi $
a bijection onto
$ \sigma wc ( \mathcal {L}(\mathfrak {A}, \mathfrak {A}^*))$
.
Proposition 3.5 [Reference Daws1, Theorem 6.11].
Let
$ \mathfrak {A} = ( \mathfrak {A}_*)^*$
be a unital dual Banach algebra. There exist a reflexive normal Banach left
$\mathfrak {A}$
-module E and an isometric
$w^*$
-continuous representation
$ \varrho : \mathfrak {A} \longrightarrow \mathcal {L}(E)$
such that
$\psi $
(associated with
$\varrho $
as above) maps into
$ \sigma wc ( \mathcal {L}(\mathfrak {A}, \mathfrak {A}^*))$
and is a bijection. In particular,
$\psi ^* : \sigma wc ( \mathcal {L}(\mathfrak {A}, \mathfrak {A}^*))^* \longrightarrow \mathcal {L}_{\mathfrak {A}}(\mathcal {L}(E)) $
is an isomorphism.
Let
$\mathfrak {A}$
be a dual Banach algebra and let
$\varphi \in \Delta _{w^*}(\mathfrak {A})$
. From [Reference Mahmoodi6],
$\mathfrak {A}$
is
$\varphi $
-Connes amenable if there exists a bounded linear functional m on
$ \sigma wc (\mathfrak {A}^*)$
satisfying
$ m(\varphi ) = 1$
and
$ m ( f \,. \,a) = \varphi (a) m(f)$
for all
$a \in \mathfrak {A}$
and
$ f \in \sigma wc (\mathfrak {A}^*)$
.
The following result could be compared with [Reference Daws1, Theorem 6.13].
Theorem 3.6. Suppose that
$\mathfrak {A}$
is a dual Banach algebra and
$\varphi \in \Delta _{w^*}(\mathfrak {A})$
. Then the following are equivalent:
-
(i)
$\mathfrak {A}$
is
$\varphi $
-amenable; -
(ii)
$\mathfrak {A}$
is
$\varphi $
-contractible (in the sense of [Reference Hu, Monfared and Traynor2]); -
(iii)
$\mathfrak {A}$
is
$\varphi $
-Connes amenable; -
(iv)
$\mathfrak {A}$
is
$\varphi $
-injective.
Proof. The equivalence (i)
$\Longleftrightarrow $
(ii)
$\Longleftrightarrow $
(iii) is [Reference Mahmoodi7, Theorem 2.4].
(i)
$\Longrightarrow $
(iv) Suppose that
$\mathfrak {A}$
is
$\varphi $
-amenable and
$ \varrho : \mathfrak {A} \longrightarrow \mathcal {L}(E)$
is a
$w^*$
-continuous representation on some reflexive Banach space E. By Theorem 3.4, there is a
$\varphi $
-quasi expectation
$ Q : \mathcal {L}(E) \longrightarrow \varrho (\mathfrak {A})^\varphi $
, that is,
$\mathfrak {A}$
is
$ \varphi $
-injective.
(iv)
$\Longrightarrow $
(iii) Suppose that
$\mathfrak {A}$
is
$\varphi $
-injective. By Theorem 3.3 and [Reference Kaniuth, Lau and Pym4, Lemma 3.2], without loss of generality, we may suppose that
$\mathfrak {A}$
is unital. Take the
$w^*$
-continuous representation
$ \varrho : \mathfrak {A} \longrightarrow \mathcal {L}(E)$
and the map
$ \psi $
as in Proposition 3.5. By the assumption, there exists a
$\varphi $
-quasi expectation
$ Q : \mathcal {L}(E) \longrightarrow \varrho (\mathfrak {A})^\varphi $
. Notice that
$ Q \in \mathcal {L}_{\mathfrak {A}}(\mathcal {L}(E))$
. Define
$ M:= (\psi ^*)^{-1}(Q) \in \sigma wc ((\mathfrak {A} \hat {\otimes } \mathfrak {A})^*)^*$
. As Q maps into
$\varrho (\mathfrak {A})^\varphi $
, it follows that
$ a \,. \,Q = \varphi (a) Q$
for
$a \in \mathfrak {A}$
, so that
$ a \,. \,M = \varphi (a) M$
. Next, for some
$\alpha \in \mathbb {C}$
, we have
$ \langle \varphi \otimes \varphi , M \rangle = \alpha $
. Hence, putting
$ N= ({1}/{\alpha }) M$
, it is readily seen that
$ \langle \varphi \otimes \varphi , N \rangle = 1 $
and
$ a \,. \,N = \varphi (a) N$
for
$ a \in \mathfrak {A}$
. On the other hand, from [Reference Runde10],
$ \pi ^*(\sigma wc (\mathfrak {A}^*)) \subseteq \sigma wc (( \mathfrak {A} \hat {\otimes } \mathfrak {A})^*).$
We then set
$ m:=(\pi ^*|_{\sigma wc (\mathfrak {A}^*)})^*(N) \in \sigma wc (\mathfrak {A}^*)^*$
. One may check that
$ m(\varphi ) = 1$
and
$ m ( f \,. \,a) = \varphi (a) m(f)$
for all
$a \in \mathfrak {A}$
and
$ f \in \sigma wc (\mathfrak {A}^*)$
. Thus,
$\mathfrak {A}$
is
$\varphi $
-Connes amenable.
Corollary 3.7. An injective dual Banach algebra
$\mathfrak {A}$
is
$\varphi $
-injective for all
$\varphi \in \Delta _{w^*}(\mathfrak {A})$
.
Proof. Since
$\mathfrak {A}$
is injective, it is Connes amenable [Reference Daws1, Theorem 6.13]. It then follows from [Reference Mahmoodi6, Theorem 2.2] that
$\mathfrak {A}$
is
$\varphi $
-Connes amenable for each
$\varphi \in \Delta _{w^*}(\mathfrak {A})$
. The result is now immediate by Theorem 3.6.
4. Application to
${\textrm {WAP}}(\mathfrak {A}^*)^*$
and examples
The following result is analogous to [Reference Kaniuth, Lau and Pym4, Proposition 3.5].
Theorem 4.1. Suppose that
$\mathfrak {A}$
is a Banach algebra,
$\mathfrak {B} = (\mathfrak {B}_* )^*$
is a dual Banach algebra,
$\theta : \mathfrak {A} \longrightarrow \mathfrak {B} $
is a continuous homomorphism with
$w^*$
-dense range and
$\varphi \in \Delta _{w^*}(\mathfrak {B})$
. If
$\mathfrak {A}$
is
$\varphi \circ \theta $
-amenable, then
$\mathfrak {B}$
is
$\varphi $
-amenable.
Proof. Take
$ m \in \mathfrak {A}^{**}$
with
$ m(\varphi \circ \theta ) = 1$
and
$ m ( f \cdot a) = (\varphi \circ \theta )(a) m(f)$
for all
$a \in \mathfrak {A}$
and
$ f \in \mathfrak {A}^*$
. Define
$ n \in \sigma wc ( \mathfrak {B}^*)^*$
by
$ n(g) = m(g \circ \theta )$
for
$ g \in \sigma wc ( \mathfrak {B}^*)$
. Note that
$ \varphi \in \sigma wc ( \mathfrak {B}^*)$
as
$ \varphi \in \mathfrak {B}_*$
(see also [Reference Mahmoodi7, Lemma 2.3]). Then
$n(\varphi ) = m(\varphi \circ \theta ) = 1 $
. For
$a , {a}^\prime \in \mathfrak {A}$
and
$ g \in \sigma wc ( \mathfrak {B}^*)$
,
$$\begin{align*}n( g \cdot \theta(a) ) = m ( ( g \cdot \theta(a)) \circ \theta ) = m( ( g \circ \theta) \cdot a) = ( \varphi \circ \theta ) (a) m(g \circ \theta )= (\varphi \circ \theta) (a) n(g) , \end{align*}$$
because
$$\begin{align*}\langle ( g \cdot \theta(a) ) \circ \theta , {a}^\prime \rangle = \langle g , \theta(a) \theta({a}^\prime) \rangle = \langle ( g \circ \theta) \cdot a , {a}^\prime \rangle .\end{align*}$$
Next, for an arbitrary element
$b \in \mathfrak {B} $
, there is a net
$(a_i)_i \subseteq \mathfrak {A}$
such that
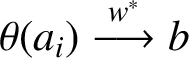$ \theta (a_i) \stackrel {w^*} \longrightarrow b$
. For each
$ g \in \sigma wc ( \mathfrak {B}^*)$
, we then have
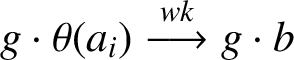$g \cdot \theta (a_i) \stackrel {wk} \longrightarrow g \cdot b$
. Hence,
$$\begin{align*}n ( g \cdot b )= \lim_i n(g \cdot \theta(a_i) ) = \lim_i \varphi ( \theta(a_i)) n(g) = \varphi(b) n(g).\end{align*}$$
Thus,
$\mathfrak {B}$
is
$\varphi $
-amenable, by Theorem 3.6(iii).
Remark 4.2. Let
$\mathfrak {A}$
be a Banach algebra and let
$\varphi \in \Delta (\mathfrak {A})$
. By Proposition 2.3, there exists a unique element
$\tilde {\varphi } \in \Delta _{w^*}({\textrm {WAP}}(\mathfrak {A}^*)^* )$
extending
$\varphi $
. We shall henceforth keep the notation
$\tilde {\varphi }$
.
Corollary 4.3. Let
$\mathfrak {A}$
be a Banach algebra and let
$ \varphi \in \Delta (\mathfrak {A})$
. If
$\mathfrak {A}$
is
$\varphi $
-amenable, then
${\textrm {WAP}}(\mathfrak {A}^*)^*$
is
$\tilde {\varphi }$
-amenable.
Proof. As
$\varphi =\tilde {\varphi } \circ \imath $
, this is a consequence of Remark 4.2 and Theorem 4.1.
Example 4.4. Let G be a locally compact group and let
$A(G)$
and
$VN(G)=A(G)^*$
be the Fourier algebra and the von Neumann algebra of G, respectively. From [Reference Kaniuth, Lau and Pym4, Example 2.6],
$A(G)$
is
$\varphi _t$
-amenable for every
$t \in G$
, where
$\varphi _t$
is the point evaluation at
$t \in G$
, that is,
$\varphi _t(f) = f(t) $
,
$f \in A(G)$
. So, by Corollary 4.3,
${\textrm {WAP}}(VN(G))^*$
is
$\tilde {\varphi }_t$
-amenable for every
$t \in G$
.
The converse of Corollary 4.3 holds for dual Banach algebras as follows.
Theorem 4.5. Let
$\mathfrak {A} = (\mathfrak {A}_*)^*$
be a dual Banach algebra and let
$ \varphi \in \Delta _{w^*}(\mathfrak {A})$
. Then
$\mathfrak {A}$
is
$\varphi $
-amenable if and only if
${\textrm {WAP}}(\mathfrak {A}^*)^*$
is
$\tilde {\varphi }$
-amenable.
Proof. Since
$ \mathfrak {A}_* \subseteq \sigma wc(\mathfrak {A}^*) \subseteq {\textrm {WAP}}(\mathfrak {A}^*)$
from [Reference Runde10], there exists an inclusion map
$ \varepsilon : \mathfrak {A}_* \longrightarrow {\textrm {WAP}}(\mathfrak {A}^*)$
. Then
$\varepsilon ^*$
is an
$ \mathfrak {A}$
-bimodule homomorphism from
${\textrm {WAP}}(\mathfrak {A}^*)^*$
onto
$ \mathfrak {A}$
.
Suppose that
${\textrm {WAP}}(\mathfrak {A}^*)^*$
is
$\tilde {\varphi }$
-amenable. Let E be a Banach
$ \mathfrak {A}$
-bimodule for which
$ a \,. \,x = \varphi (a) x$
for all
$a \in \mathfrak {A}$
and
$x \in E$
and let
$D : \mathfrak {A} \longrightarrow E^*$
be a derivation. We turn E into a Banach
${\textrm {WAP}}(\mathfrak {A}^*)^*$
-bimodule through
$$\begin{align*}\Lambda \,. \, x := \tilde{\varphi}(\Lambda) x \quad \text{and} \quad x \,. \, \Lambda :=\varepsilon^* (\Lambda) \,. \,x \quad ( x \in E,\ \Lambda \in {\textrm{WAP}}(\mathfrak{A}^*)^*) \ .\end{align*}$$
Now, by Proposition 2.2, the derivation
$ D \varepsilon ^* : {\textrm {WAP}}(\mathfrak {A}^*)^* \longrightarrow E^*$
is inner. Thus, there exists
$x \in E$
such that
$ (D \varepsilon ^*) (\Lambda ) = \Lambda \, .\, x - x \,. \, \Lambda $
for all
$\Lambda \in {\textrm {WAP}}(\mathfrak {A}^*)^* $
. Consequently,
$D a = a \,. \, x - x \,. \, a$
,
$a \in \mathfrak {A}$
. Again by Proposition 2.2,
$\mathfrak {A}$
is
$\varphi $
-amenable.
We write
$\mathbb {D}$
for the open unit disk. For the discrete convolution algebra
$\ell ^1(\mathbb {Z}^+)$
, it is known that
$ \Delta (\ell ^1(\mathbb {Z}^+)) \equiv \bar {\mathbb {D}}$
under the bijective map
$ z \longmapsto \varphi _z$
, where
$\varphi _z$
is the point evaluation at z, that is,
$ \varphi _z ( \sum _{n=0}^\infty c_n \delta _n)= \sum _{n=0}^\infty c_n z^n$
. It is not hard to see that
$ \Delta _{w^*}(\ell ^1(\mathbb {Z}^+)) = \mathbb {D}$
. It was shown in [Reference Kaniuth, Lau and Pym4, Example 2.5] that
$\ell ^1(\mathbb {Z}^+)$
is
$\varphi _z$
-amenable when
$|z| = 1$
and it is not
$\varphi _z$
-amenable if
$ z \in \mathbb {D}$
. Hence, by Corollary 4.3,
${\textrm {WAP}}(\ell ^\infty (\mathbb {Z}^+))^*$
is
$\tilde {\varphi }_z$
-amenable when
$|z| = 1$
. As
$\ell ^1(\mathbb {Z}^+)$
is a dual Banach algebra, we conclude from Theorem 4.5 that
${\textrm {WAP}}(\ell ^\infty (\mathbb {Z}^+))^*$
is not
$\tilde {\varphi }_z$
-amenable for each
$ z \in \mathbb {D}$
. Notice that
${\textrm {WAP}}(\ell ^\infty (\mathbb {Z}^+))^*$
is not amenable. To see this, we first observe that there exists a continuous homomorphism from
${\textrm {WAP}}(\ell ^\infty (\mathbb {Z}^+))^*$
onto
$\ell ^1(\mathbb {Z}^+)$
by the universal property (with
$\ell ^1(\mathbb {Z}^+)$
and the identity map in place of
$\mathfrak {B}$
and
$\theta $
, respectively). Therefore, amenability of
${\textrm {WAP}}(\ell ^\infty (\mathbb {Z}^+))^*$
forces
$\ell ^1(\mathbb {Z}^+)$
to be amenable, which is not the case.
Putting all these results together gives the following example.
Example 4.6.
-
(i)
${\textrm {WAP}}(\ell ^\infty (\mathbb {Z}^+))^*$
is not amenable; -
(ii)
${\textrm {WAP}}(\ell ^\infty (\mathbb {Z}^+))^*$
is not
$\tilde {\varphi }_z$
-amenable for each
$ z \in \mathbb {D}$
; -
(iii)
${\textrm {WAP}}(\ell ^\infty (\mathbb {Z}^+))^*$
is
$\tilde {\varphi }_z$
-amenable when
$|z| = 1$
.
Let
$\mathfrak {A}$
be a Banach algebra and let
$ \varrho : \mathfrak {A} \longrightarrow \mathcal {L}(E)$
be a continuous representation on a Banach space E. We use
$ \tilde {\varrho } : {\textrm {WAP}}(\mathfrak {A}^*)^* \longrightarrow \mathcal {L}(E) $
for the unique
$w^*$
-continuous representation obtained by Proposition 2.3.
Lemma 4.7. Let
$\mathfrak {A}$
be a Banach algebra, let
$ \varrho : \mathfrak {A} \longrightarrow \mathcal {L}(E)$
be a continuous representation and
$ \varphi \in \Delta (\mathfrak {A})$
. Then every
$\varphi $
-quasi expectation
$ Q : \mathcal {L}(E) \longrightarrow \varrho (\mathfrak {A})^\varphi $
is exactly a
$\tilde {\varphi } $
-quasi expectation
$ Q : \mathcal {L}(E) \longrightarrow \tilde {\varrho } ( {\textrm {WAP}}(\mathfrak {A}^*)^*)^{\tilde {\varphi }}$
and vice versa.
Proof. The same argument as that in the proof of [Reference Daws1, Proposition 6.15] shows that
$\varrho (\mathfrak {A})^c = \tilde {\varrho } ( {\textrm {WAP}}(\mathfrak {A}^*)^*)^c$
. To complete the proof, we show that
$ \tilde {\varrho } ( {\textrm {WAP}}(\mathfrak {A}^*)^*)^{\tilde {\varphi }} = \varrho (\mathfrak {A})^\varphi $
. It is obvious that
$ \tilde {\varrho } ( {\textrm {WAP}}(\mathfrak {A}^*)^*)^{\tilde {\varphi }} \subseteq \varrho (\mathfrak {A})^\varphi $
. For the converse, suppose that
$T \in \varrho (\mathfrak {A})^\varphi $
. Thus,
$ \langle \varrho (a) T , \eta \rangle =\varphi (a) \langle T , \eta \rangle $
for each
$a \in \mathfrak {A}$
and
$ \eta \in E^*\hat {\otimes } E$
. Take
$ \Psi \in {\textrm {WAP}}(\mathfrak {A}^*)^*$
and take a bounded net
$ (a_i) \subseteq \mathfrak {A}$
which converges to
$\Psi $
in the
$w^*$
-topology on
${\textrm {WAP}}(\mathfrak {A}^*)^*$
. Then, for
$x \in E$
,
$\mu \in E^*$
and
$ T \in \varrho (\mathfrak {A})^\varphi $
,
$$ \begin{align*} \langle \mu, \tilde{\varrho}(\Psi) T(x) \rangle &= \langle \mu \otimes T(x) , \tilde{\varrho}(\Psi) \rangle = \langle \Psi , \varrho_* (\mu \otimes T(x)) \rangle = \lim_i \langle \varrho_* (\mu \otimes T(x)) , a_i \rangle \\&= \lim_i \langle \mu , \varrho(a_i) T(x) \rangle = \lim_i \varphi(a_i) \langle \mu , T(x) \rangle = \langle \mu , \tilde{\varphi}(\Psi) T(x) \rangle, \end{align*} $$
so that
$ T \in \tilde {\varrho } ( {\textrm {WAP}}(\mathfrak {A}^*)^*)^{\tilde {\varphi }}$
, as required.
The next step is a useful characterisation.
Theorem 4.8. Let
$\mathfrak {A}$
be a Banach algebra and let
$ \varphi \in \Delta (\mathfrak {A})$
. Then the following are equivalent:
-
(i)
${\textrm {WAP}}(\mathfrak {A}^*)^*$
is
$\tilde {\varphi }$
-amenable; -
(ii) whenever
$ \varrho : \mathfrak {A}\longrightarrow \mathcal {L}(E)$
is a continuous representation on a reflexive Banach space E, there exists a
$\varphi $
-quasi expectation
$ Q : \mathcal {L}(E) \longrightarrow \varrho (\mathfrak {A})^\varphi $
.
Proof. (i)
$\Longrightarrow $
(ii) Let
$ \varrho : \mathfrak {A}\longrightarrow \mathcal {L}(E)$
be a continuous representation on a reflexive Banach space E and let
$ \tilde {\varrho } : {\textrm {WAP}}(\mathfrak {A}^*)^* \longrightarrow \mathcal {L}(E) $
be its unique extension to a
$w^*$
-continuous representation. By Theorem 3.6,
${\textrm {WAP}}(\mathfrak {A}^*)^*$
is
$\tilde {\varphi }$
-injective and there exists a
$\tilde {\varphi } $
-quasi expectation
$ Q : \mathcal {L}(E) \longrightarrow \tilde {\varrho } ( {\textrm {WAP}}(\mathfrak {A}^*)^*)^{\tilde {\varphi }}$
by Definition 3.2. Now, by Lemma 4.7,
$ Q : \mathcal {L}(E) \longrightarrow \varrho (\mathfrak {A})^\varphi $
is indeed a
$\varphi $
-quasi expectation.
(ii)
$\Longrightarrow $
(i) Suppose that
$ \varrho : {\textrm {WAP}}(\mathfrak {A}^*)^*\longrightarrow \mathcal {L}(E)$
is a
$w^*$
-continuous representation on a reflexive Banach space E. Thus,
$ \varrho |_{\mathfrak {A}} : \mathfrak {A}\longrightarrow \mathcal {L}(E)$
is a continuous representation. By the assumption, there exists a
$\varphi $
-quasi expectation
$ Q : \mathcal {L}(E) \longrightarrow \varrho (\mathfrak {A})^\varphi $
. Again by Lemma 4.7,
$ Q : \mathcal {L}(E) \longrightarrow \tilde {\varrho } ( {\textrm {WAP}}(\mathfrak {A}^*)^*)^{\tilde {\varphi }}$
is a
$\tilde {\varphi } $
-quasi expectation, as required.
5. For
$ {\textrm {WAP}}(\ell ^1(\mathbb {N}_\wedge )^*)^*$
Let
$\mathbb {N}_\wedge $
be the semigroup
$\mathbb {N}$
with the product
$ m \wedge n = \min \{ m , n \}$
for
$ m , n \in \mathbb {N}$
. In this section, we write
$\varphi $
for the augmentation character on
$\ell ^1(\mathbb {N}_\wedge )$
, which is given by
$ \varphi ( \sum _{n=1}^\infty \alpha _i \delta _i)= \sum _{n=1}^\infty \alpha _i$
. In the light of Theorem 4.8, we will show that
$ {\textrm {WAP}}(\ell ^1(\mathbb {N}_\wedge )^*)^*$
is not
$\tilde {\varphi }$
-amenable. To this end, some preliminaries are needed.
Let E be a Banach space with a normalised basis
$(e_n)_n$
. For each
$n \in \mathbb {N}$
, we consider the linear functional
$f_n \in E^*$
,
$n \in \mathbb {N}$
, given by
$ \langle f_n , \sum \alpha _i e_i \rangle = \alpha _n $
. Throughout the section, we use the notation
$\varrho $
for the representation
$\varrho : \ell ^1(\mathbb {N}_\wedge ) \longrightarrow \mathcal {L}(E)$
given by
$$\begin{align*}\varrho(\delta_n)(e_m) = \left \{ \begin{array}{@{}lc} e_m & \mbox{for } m \leq n \\ 0 & \mbox{for }m> n \end{array} \right. \quad(m ,n \in \mathbb{N})\end{align*}$$
and linearity. In fact,
$ \varrho (\delta _n)$
is the projection onto the linear span of
$ \{ e_1, \ldots , e_n \}$
. It is standard that each element of
$\mathcal {L}(E)$
can be considered as a matrix with respect to the basis
$(e_n)_n$
. We denote by
$ \mathcal {E}_{i,j}$
the matrix with
$1$
in the
$(i,j)$
th place and
$0$
elsewhere.
The next result shows that the set
$\varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi $
consists of all matrices in
$\mathcal {L}(E)$
with zero entries from the second row on.
Lemma 5.1.
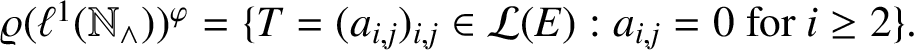$\varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi = \{ T= (a_{i,j})_{i,j} \in \mathcal {L}(E) : a_{i,j} = 0 \ \text {for} \ i \geq 2 \} .$
Proof. Set
$ \mathcal {R}= \{ T= (a_{i,j})_{i,j} \in \mathcal {L}(E) : a_{i,j} = 0 \ \text {for} \ i \geq 2 \} $
and notice that
$\varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi = \{ T \in \mathcal {L}(E) : \varrho (\delta _n) T = \varphi (\delta _n) T = T \} .$
It is easily checked that
$\mathcal {R} \subseteq \varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi $
.
Conversely, for
$ T \in \varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi $
,
$$\begin{align*}\mathcal{E}_{n,n} T = (\varrho(\delta_n) - \varrho(\delta_{n-1}) ) T = \varrho(\delta_n) T - \varrho(\delta_{n-1}) T = T - T = 0 \quad ( n \geq 2) .\end{align*}$$
A simple verification then shows that
$$\begin{align*}0 = \mathcal{E}_{n,n} T (e_m) = \langle f_n , T(e_m) \rangle e_n \quad (m \geq 1,\ n \geq 2) \end{align*}$$
and therefore
$ \langle f_n , T(e_m) \rangle = 0$
for
$m \geq 1,n \geq 2 $
. So,
$ T(e_m) \in \mathbb {C}e_1$
for each
$m \geq 1$
, which proves that
$ T \in \mathcal {R}$
.
Remark 5.2. Compared to Lemma 5.1,
$\varrho (\ell ^1(\mathbb {N}_\wedge ))^c$
is exactly the set of all diagonal matrices in
$\mathcal {L}(E)$
[Reference Daws1].
We write
$ P_{\varphi } : \mathcal {L}(E) \longrightarrow \varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi $
for the canonical projection onto
$\varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi $
defined by
$ T= (a_{i,j})_{i,j} \longmapsto P_{\varphi }(T)= (b_{i,j})_{i,j}$
, where
$ b_{1,j} = a_{1,j}$
and
$ b_{i,j} = 0$
for
$i \geq 2$
and all j. Next, we show that every
$\varphi $
-quasi expectation
$ Q : \mathcal {L}(E) \longrightarrow \varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi $
must be the canonical projection onto
$\varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi $
.
Lemma 5.3. Let
$ Q : \mathcal {L}(E) \longrightarrow \varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi $
be a
$\varphi $
-quasi expectation. Then
$Q = P_{\varphi }$
.
Proof. Let
$m ,n \in \mathbb {N}$
and
$T \in \mathcal {L}(E)$
. From Remark 5.2,
$\mathcal {E}_{n,n} , \mathcal {E}_{m,m} \in \varrho (\ell ^1(\mathbb {N}_\wedge ))^c$
. Then
$$\begin{align*}\langle f_m , T(e_n) \rangle Q(\mathcal{E}_{m,n}) = Q(\mathcal{E}_{m,m} T \mathcal{E}_{n,n}) =\mathcal{E}_{m,m} Q(T) \mathcal{E}_{n,n} = \langle f_m , Q(T)(e_n) \rangle \mathcal{E}_{m,n}.\end{align*}$$
As
$ \mathcal {E}_{m,n}$
is not in
$\varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi $
for
$ m> 1$
by Lemma 5.1, it follows that
$ \langle f_m , Q(T)(e_n) \rangle = 0$
for
$ m> 1$
. Thus,
$Q(T)(e_n) \in \mathbb {C}e_1 $
for each n. Next, since
$\mathcal {E}_{1,n} \in \varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi $
,
$$ \begin{align*} \langle f_1 , T(e_n) \rangle \mathcal{E}_{1,n} = \langle f_1 , T(e_n) \rangle Q(\mathcal{E}_{1,n}) & = Q(\mathcal{E}_{1,1} T \mathcal{E}_{n,n}) \\ & = \mathcal{E}_{1,1} Q(T) \mathcal{E}_{n,n} = \langle f_1 , Q(T)(e_n) \rangle \mathcal{E}_{1,n} \end{align*} $$
and hence
$Q(T)(e_n) = \langle f_1 , T(e_n) \rangle e_1$
for each
$n \in \mathbb {N}$
, as required.
Theorem 5.4. The algebra
$ {\textrm {WAP}}(\ell ^1(\mathbb {N}_\wedge )^*)^*$
is not
$\tilde {\varphi }$
-amenable.
Proof. By Theorem 4.8 and Lemma 5.3, it suffices to find a reflexive Banach space E such that
$P_{\varphi }$
is not bounded. It is clear that there is an isometric isomorphism
$\Theta $
from
$\varrho (\ell ^1(\mathbb {N}_\wedge ))^c$
onto
$\varrho (\ell ^1(\mathbb {N}_\wedge ))^\varphi $
. From [Reference Daws1, Theorem 7.6], there is a reflexive Banach space E for which the canonical projection
$P_c : \mathcal {L}(E) \longrightarrow \varrho (\ell ^1(\mathbb {N}_\wedge ))^c$
is not bounded. Thus,
$P_{\varphi } = \Theta \circ P_c$
is not bounded, as required.
A combination of Corollary 4.3 and Theorem 5.4 yields the following result.
Corollary 5.5. The algebra
$\ell ^1(\mathbb {N}_\wedge )$
is not
$\varphi $
-amenable.
Appendix A
In this section, we show that
$\Delta _{w^*}({\textrm {WAP}}(\mathfrak {A}^*)^* )$
contains
$ \Delta (\mathfrak {A})$
as a subset, as pointed out by an anonymous referee in response to a previous version of this work.
Proposition A.1. Let
$\mathfrak {A}$
be a Banach algebra. Then
$ \Delta (\mathfrak {A}) \subseteq \Delta _{w^*}({\textrm {WAP}}(\mathfrak {A}^*)^* )$
.
Proof. Take
$\varphi \in \Delta (\mathfrak {A})$
, so that
$\varphi \in \mathfrak {A}^*$
. Then
$ \langle b , a \cdot \varphi \rangle = \varphi (a ) \varphi (b)$
for every
$a , b \in \mathfrak {A}$
, so that
$a \cdot \varphi =\varphi (a ) \varphi $
. Similarly,
$\varphi \cdot a = \varphi (a ) \varphi $
. So, obviously,
$ \varphi \in {\textrm {WAP}}(\mathfrak {A}^*)$
. Hence, we may treat
$\varphi $
as a bounded linear map on
${\textrm {WAP}}(\mathfrak {A}^*)^* $
. As a consequence,
$\varphi $
is
$w^*$
-continuous. Next, for
$ \Psi \in {\textrm {WAP}}(\mathfrak {A}^*)^* $
and
$ a \in \mathfrak {A}$
, it follows that
$ \langle a , \Psi \cdot \varphi \rangle = \langle \varphi \cdot a , \Psi \rangle = \varphi (a) \langle \varphi , \Psi \rangle $
, so that
$ \Psi \cdot \varphi = \langle \varphi , \Psi \rangle \varphi $
. Then, for each
$ \Phi , \Psi \in {\textrm {WAP}}(\mathfrak {A}^*)^* $
,
$$\begin{align*}\langle \varphi , \Phi \Psi \rangle = \langle \Psi \cdot \varphi , \Phi \rangle = \langle \langle \varphi , \Psi \rangle \varphi , \Phi \rangle = \langle \varphi , \Psi \rangle \langle \varphi , \Phi \rangle .\end{align*}$$
Thus,
$ \varphi \in \Delta _{w^*}({\textrm {WAP}}(\mathfrak {A}^*)^* )$
.
The following consequence should be compared with Corollary 4.3.
Corollary A.2. Let
$\mathfrak {A}$
be a Banach algebra and let
$ \varphi \in \Delta (\mathfrak {A})$
. If
$\mathfrak {A}$
is
$\varphi \circ \imath $
-amenable, then
${\textrm {WAP}}(\mathfrak {A}^*)^*$
is
$\varphi $
-amenable.
