Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-21T19:59:14.407Z Has data issue: false hasContentIssue false
  • English
  • Français

ON 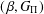$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-UNFAVOURABLE SPACES

Part of: Spaces with richer structures Fairly general properties Topological and differentiable algebraic systems

Published online by Cambridge University Press:  16 March 2020

HANFENG WANG Open the ORCID record for HANFENG WANG [Opens in a new window] ,
WEI HE Open the ORCID record for WEI HE [Opens in a new window]  and
JING ZHANG Open the ORCID record for JING ZHANG [Opens in a new window]
HANFENG WANG*
Affiliation:
Department of Mathematics, Shandong Agricultural University, Taian 271018, China email whfeng@sdau.edu.cn
WEI HE
Affiliation:
Institute of Mathematics, Nanjing Normal University, Nanjing 210046, China email weihe@njnu.edu.cn
JING ZHANG
Affiliation:
School of Mathematics and Statistics, Minnan Normal University, Zhangzhou 363000, China email zhangjing86@126.com
*
✉whfeng@sdau.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

To study when a paratopological group becomes a topological group, Arhangel’skii et al. [‘Topological games and topologies on groups’, Math. Maced. 8 (2010), 1–19] introduced the class of 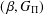$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourable spaces. We show that every 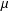$\unicode[STIX]{x1D707}$-complete (or normal) 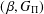$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourable semitopological group is a topological group. We prove that the product of a 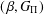$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourable space and a strongly Fréchet 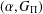$(\unicode[STIX]{x1D6FC},G_{\unicode[STIX]{x1D6F1}})$-favourable space is 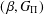$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourable. We also show that continuous closed irreducible mappings preserve the 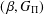$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-unfavourableness in both directions.

Keywords

G𝛱 game( 𝛽, G𝛱)-unfavourablestrategytopological group

MSC classification

Primary: 22A05: Structure of general topological groups
Secondary: 54D40: Remainders 54E35: Metric spaces, metrizability
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 3 , December 2020 , pp. 439 - 450
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Footnotes

Project supported by SDNSF (No. ZR2018MA013) and NSFC (Nos. 11571175, 11801254).

References

Arhangelskii, A. V., ‘Two types of remainders of topological groups’, Comment. Math. Univ. Carolin. 49(4) (2008), 119–126.Google Scholar
Arhangel’skii, A. V., Choban, M. M. and Kenderov, P. S., ‘Topological games and topologies on groups’, Math. Maced. 8 (2010), 1–19.Google Scholar
Arhangel’skii, A. V., Choban, M. M. and Kenderov, P. S., ‘Topological games and continuity of group operations’, Topology Appl. 157 (2010), 2542–2552.10.1016/j.topol.2010.08.001CrossRefGoogle Scholar
Arhangel’skii, A. V. and Reznichenko, E. A., ‘Paratopological and semitopological groups versus topological groups’, Topology Appl. 151 (2005), 107–119.CrossRefGoogle Scholar
Arhangelskii, A. V. and Tkachenko, M. G., Topological Groups and Related Structures (Atlantis Press, Amsterdam, 2008).CrossRefGoogle Scholar
Bouziad, A., ‘Every C̆ech-analytic Baire semitopological group is a topological group’, Proc. Amer. Math. Soc. 124(3) (1996), 953–959.10.1090/S0002-9939-96-03384-9CrossRefGoogle Scholar
Ellis, R., ‘A note on the continuity of the inverse’, Proc. Amer. Math. Soc. 8 (1957), 119–125.10.1090/S0002-9939-1957-0083681-9CrossRefGoogle Scholar
Engelking, R., General Topology, revised and completed edition (Heldermann, Berlin, 1989).Google Scholar
Kenderov, P., Kortezov, I. S. and Moors, W. B., ‘Topological games and topological groups’, Topology Appl. 109 (2001), 157–165.CrossRefGoogle Scholar