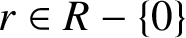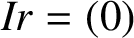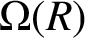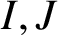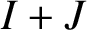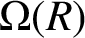1 Introduction
The metric dimension of a graph was introduced by Harary and Melter [Reference Harary and Melter6] and it has been studied for a wide variety of graphs, for example trees and unicyclic graphs [Reference Chartrand, Eroh, Johnson and Oellermann3], wheel graphs [Reference Shanmukha, Sooryanarayana and Harinath14] and cartesian product graphs [Reference Khuller, Raghavachari and Rosenfeld7]. A number of results have been presented on the strong metric dimension of cartesian product graphs and Cayley graphs [Reference Oellermann and Peters-Fransen10] and distance-hereditary graphs [Reference May and Oellermann9]. Later, the metric dimension and strong metric dimension were applied to graphs associated to commutative rings (see, for example, [Reference Dolžan4, Reference Dolžan5, Reference Pirzada and Aijaz11–Reference Pirzada and Raja13]). In [Reference Abachi and Sahebi1], the authors studied the metric dimension of the total graph of nonzero annihilating ideals. In this paper, we study the strong metric dimension for such graphs.
Throughout, all rings are assumed to be commutative with identity. The sets of all maximal ideals and the Jacobson radical of R are denoted by
$\mathrm {Max}(R)$
and
$J(R)$
, respectively. An ideal I of a ring R is called an annihilating ideal if there exists
$r\in R- \{0\}$
such that
$Ir=(0)$
. The set of annihilating ideals of R is denoted by
$\mathbb {A}(R)$
. For every ideal I of R, we denote the
$\textit {annihilator}$
of I by
$\mathrm{ann}(I)$
. Further definitions relating to commutative rings can be found in [Reference Atiyah and Macdonald2].
We use the standard terminology of graphs following [Reference West16]. By
$G=(V,E)$
, we mean a graph where V and E are the sets of vertices and edges, respectively. If we can find at least one path between any two vertices of G, then G is called
$\textit {connected}$
. The length of the shortest path between two distinct vertices x and y is denoted by
$d(x,y)$
and
$\mathrm{diam}(G)=\max \{d(x,y) \mid x,y\in V\}$
is called the
$\textit {diameter}$
of G. (Note that
$d(x,y)=\infty $
, if there is no path between x and y.)
The graph
$H=(V_0,E_0)$
is a subgraph of G if
$V_0\subseteq V$
and
$E_0 \subseteq E$
. Moreover, H is called an
$\textit {induced}$
subgraph by
$V_0$
, denoted by
$G[V_0]$
, if
$V_0\subseteq V$
and the edge set is
$E_0=\{\{u,v\}\in E \mid u,v\in V_0\}$
. For
$x\in V$
, let
$N(x)=\{y\in V \mid \{x,y\}\in E\}$
. Then
$N[x]=N(x)\cup \{x\}$
. A
$\textit {complete}$
graph is a graph such that there exists an edge between each pair of vertices; the complete graph on n vertices is denoted by
$K_n$
. For a graph G,
$S\subseteq V(G)$
is called a
$\textit {clique}$
if the subgraph induced on S is complete. The number of vertices in the largest clique of a graph G is called the
$\textit {clique number}$
of G and is often denoted by
$\omega (G)$
.
Let
$G=(V,E)$
be a connected graph,
$S=\{v_1,v_2,\ldots ,v_k\}$
an ordered subset of V and
$v\in V(G)\setminus S$
. The metric representation of v with respect to S is the k-vector
$D(v|S)=(d(v,v_1),d(v,v_2),\ldots , d(v,v_k))$
. For
$S\subseteq V$
, if for every
$v,u\in V(G)\setminus S$
,
$D(u|S)=D(v|S)$
implies that
$u=v$
, then S is called a resolving set for G. A metric basis for G is a resolving set S of minimum cardinality and the number of elements in S is called the metric dimension of G, denoted by
$\dim _M(G)$
.
In a connected graph G, for two distinct vertices u and v, the interval
$I[u,v]$
is the collection of all vertices that belong to some shortest
$u-v$
path. A vertex
$w\in V(G)$
strongly resolves two vertices u and v if
$v\in I[u,w]$
or
$u\in I[v,w]$
. In other words, two vertices u and v are strongly resolved by w if
$d(w,u)=d(w,v)+d(v,u)$
or
$d(w,v)=d(w,u)+d(v,u)$
. A set W of vertices is a strong resolving set of G if every two distinct vertices of G are strongly resolved by some vertex of W. A minimal strong resolving set is called a strong metric basis and its cardinality is the strong metric dimension of G, denoted by
$\mathrm{sdim}_M(G)$
. One can immediately see that a strong resolving set is also a resolving set, so that
$\dim _M(G)\leq \mathrm{sdim}_M(G)$
.
Let R be a commutative ring with identity which is not an integral domain. Visweswaran and Patel [Reference Visweswaran and Patel15] associated a graph
$\Omega (R)$
with the set of all nonzero annihilating ideals of R. It is the graph with vertex set
$A(R)^*$
, the set of all nonzero annihilating ideals of R, and two distinct vertices
$I,J$
are joined if and only if
$I+J$
is also an annihilating ideal of R. In [Reference Abachi and Sahebi1], the authors studied the metric dimension of this total graph of nonzero annihilating ideals. In this paper, we study the strong metric dimension of the total graph of nonzero annihilating ideals. We completely characterise the rings whose metric dimension and strong metric dimension are equal.
2 Strong metric dimension of a total graph of a reduced ring
In this section, we derive a formula for the strong metric dimension of the total graph of nonzero annihilating ideals when R is reduced. Also, we characterise the rings R such that
$\dim _M({\Omega }(R))=\mathrm{sdim}_M({\Omega }(R))$
. We begin with the necessary background definitions and results. The first lemma is a simple consequence of the definitions.
Lemma 2.1. Let G be a connected graph. Then the following statements hold.
-
(1) If
$W\subset V(G)$
is a strong resolving set of G and
$u,v\in V(G)$
are such that
$N(u)=N(v)$
or
$N[u]=N[v]$
, then
$u\in W$
or
$v\in W$
. -
(2) If
$W\subset V(G)$
is a strong resolving set of G and
$u,v\in V(G)$
are such that
$d(u,v)=\mathrm{diam}(G)$
, then
$u\in W$
or
$v\in W$
.
Let G be a graph. A set S of vertices of G is a vertex cover of G if every edge of G is incident with at least one vertex of S. The vertex cover number of G, denoted by
$\alpha (G)$
, is the smallest cardinality of a vertex cover of G.
The largest cardinality of a set of vertices of G, no two of which are adjacent, is called the independence number of G and is denoted by
$\beta (G)$
. The following well-known result, due to Gallai, states the relationship between the independence number and the vertex cover number of a graph G.
Theorem 2.2 (Gallai’s theorem).
For any graph G of order n,
$\alpha (G)+\beta (G)=n$
.
A vertex u of G is maximally distant from v if
$d(v,w)\leq d(u,v)$
for every
$w\in N(u)$
. If u is maximally distant from v and v is maximally distant from u, then we say that u and v are mutually maximally distant. The boundary of G is
$$ \begin{align*} \partial(G)=\{u\in V(G) \mid \text{there is } v\in V(G) \text{ such that } u,v \text{ are mutually maximally distant} \}.\end{align*} $$
We use the notion of strong resolving graph introduced by Oellermann and Peters-Fransen in [Reference Oellermann and Peters-Fransen10]. The strong resolving graph of G is a graph
$G_{\textit {SR}}$
with vertex set
$V(G_{\textit {SR}})=\partial (G)$
where two vertices
$u,v$
are adjacent in
$G_{\textit {SR}}$
if and only u and v are mutually maximally distant.
It was shown in [Reference Oellermann and Peters-Fransen10] that the problem of finding the strong metric dimension of a graph G can be transformed into the problem of computing the vertex cover number of
$G_{\textit {SR}}$
.
Theorem 2.3 [Reference Oellermann and Peters-Fransen10].
For any connected graph G,
$\mathrm{sdim}_M(G)=\alpha (G_{\textit {SR}})$
.
Example 2.4.
$(1)$
Since
$(K_n)_{\textit {SR}}=K_n$
,
$\mathrm{sdim}_M(K_n)=n-1$
.
$(2)$
Suppose that G is the graph in Figure 1. Set
$X=\{V_2,V_3,V_4\}$
and
$Y=\{V_1, V_5, V_6\}$
. We can easily see that for any
$u\in X$
, there is no
$u\in V(G)$
such that u and v are mutually maximally distant, whereas the vertices of Y are mutually maximally distant from each other. It follows that
$\partial (G)=\{V_1, V_5, V_6\}$
and
$G_{\textit {SR}}=K_3$
. Since
$\alpha (G_{\textit {SR}})=2$
, by Theorem 2.3,
$\mathrm{sdim}_M(G)=2$
. On the other hand,
$W=\{V_1, V_6 \}$
is a minimum strong resolving set, so we see again that
$\mathrm{sdim}_M(G)=2$
.
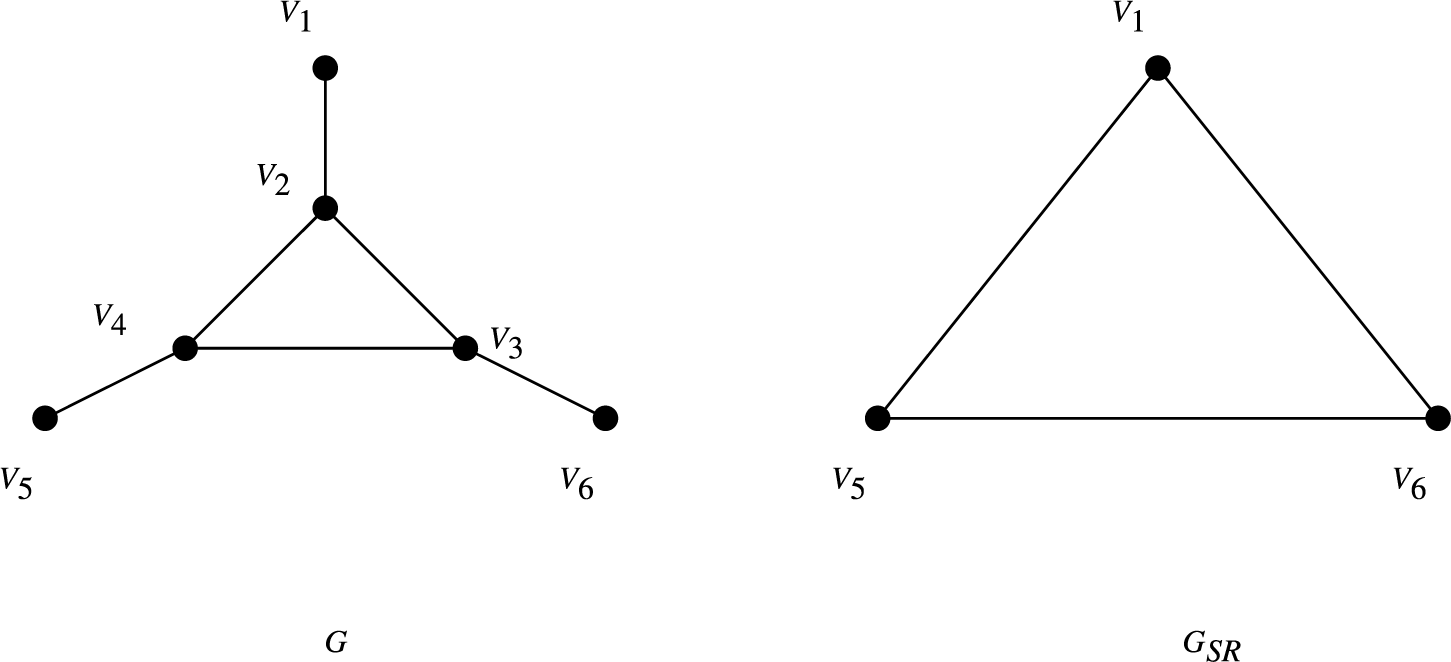
Figure 1 The graphs G and
$G_{\textit {SR}}$
.
Example 2.5. Let
$R=F_1\times F_2\times F_3$
. From Figure 2, we can easily see that
$$ \begin{align*} W=\{(0)\times F_2\times F_3,F_1\times (0)\times F_3, F_1\times F_2\times (0) \} \end{align*} $$
is the only minimum strong resolving set and hence
$\mathrm{sdim}_M({\Omega }(R) )=3$
. On the other hand, we have
$\partial ({\Omega }(R))=V({\Omega }(R))$
and
$\alpha ({\Omega }(R)_{SR})=6-\beta ({\Omega }(R)_{SR})=6-3=3$
, which also give
$\mathrm{sdim}_M({\Omega }(R) )=3$
.
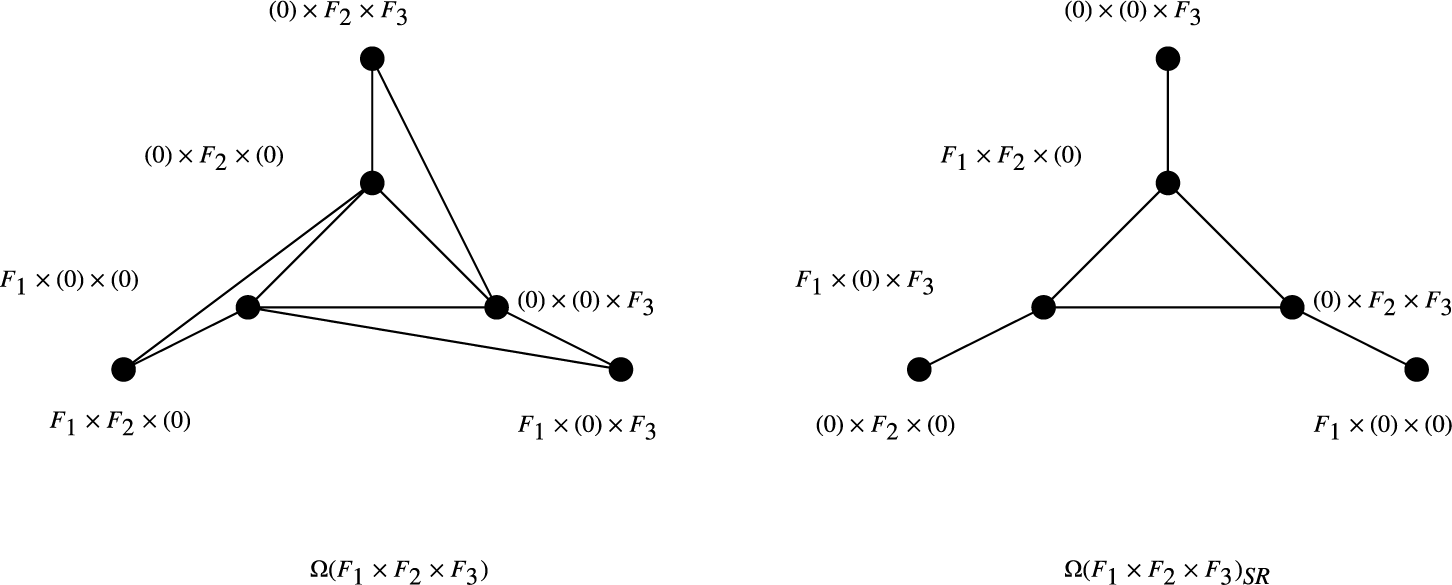
Figure 2 The graphs
${\Omega }(R) $
and
${\Omega }(R)_{\textit {SR}} $
.
Theorem 2.6. Suppose that
$R\cong F_1\times \cdots \times F_n$
, where
$F_i$
is a field for
$1\leq i\leq n$
. Then:
-
(1)
$\partial ({\Omega }(R))=V({\Omega }(R))$
; -
(2)
${\Omega }(R)_{\textit {SR}}$
is connected,
$\mathrm{diam}({\Omega }(R)_{\textit {SR}})\leq 3$
and
$\beta ({\Omega }(R)_{\textit {SR}})=2^{n-1}-1$
if
$n\geq 3$
.
Proof.
$(1)$
Assume that
$I\in V({\Omega }(R))$
. Since
$I+J=R$
for some
$J\in V({\Omega }(R))$
, it follows that
$I+J$
is not an annihilating ideal of R and so
$d(I,J)_{{\Omega }(R)}=2=\mathrm{diam}({\Omega }(R))$
. (Note that
$\mathrm{diam}({\Omega }(R))\leq 2$
.) This implies that
$I,J$
are mutually maximally distant and hence
$I\in \partial ({\Omega }(R))$
.
$(2)$
Assume that
$I,J\in V({\Omega }(R)_{\textit {SR}})$
. If
$I,J\in \mathrm {Max}(R)$
, then
$I+J=R$
. So,
$d(I,J)_{{\Omega }(R)}=2=\mathrm{diam}({\Omega }(R))$
. This implies that
$I,J$
are mutually maximally distant and hence I is adjacent to J in
${\Omega }(R)_{\textit {SR}}$
. Therefore, the induced subgraph on
$\mathrm {Max}(R)$
is a clique in
${\Omega }(R)_{\textit {SR}}$
. Now, we show that if
$I\not \in \mathrm {Max}(R)$
, then I is adjacent to some of the maximal ideals in
${\Omega }(R)_{\textit {SR}}$
. Since
$I\not \in \mathrm {Max}(R)$
and
$J(R)=(0)$
, there exists a maximal ideal J such that
$I\nsubseteq J$
. It follows that
$I+J=R$
. This implies that
$I,J$
are mutually maximally distant and hence I is adjacent to J in
${\Omega }(R)_{\textit {SR}}$
. Since the induced subgraph on
$\mathrm {Max}(R)$
is a clique in
${\Omega }(R)_{\textit {SR}}$
, this implies that
${\Omega }(R)_{SR}$
is connected and
$\mathrm{diam}({\Omega }(R)_{\textit {SR}})\leq 3$
.
Next, we show that
$\beta ({\Omega }(R)_{\textit {SR}})=2^{n-1}-1$
. For this, put
$$ \begin{align*} V_{1} & =\{(0,I_2,\ldots, I_n) \mid I_i\in \{0,F_i\} \text{ for } 2\leq i\leq n\}, \\ V_{2} &=\{(F_1,0,I_3,\ldots, I_n) \mid I_i\in \{0,F_i\} \text{ for } 3\leq i\leq n\}, \\ &\ \ \vdots \\ V_{n} & =\{(F_1,F_2,\ldots, F_{n-1}, 0)\}. \end{align*} $$
It is easy to see that
$$ \begin{align*} 1=|V_n|< |V_2|<\cdots <|V_1|=2^{n-1}-1 = \tfrac{1}{2} V({\Omega}(R)_{\textit{SR}}). \end{align*} $$
Since every vertex of
$V({\Omega }(R)_{SR})\setminus V_1$
is adjacent to some of the vertices of
$V_1$
, it follows that
$|V_1|$
is the largest cardinality of a set of vertices of
${\Omega }(R)_{\textit {SR}}$
, where no two of them are adjacent. Therefore,
$\beta ({\Omega }(R)_{\textit {SR}})=2^{n-1}-1$
.
If R is a reduced ring with finitely many ideals, then R is an artinian ring and so, by [Reference Atiyah and Macdonald2, Theorem 8.7], R is a direct product of finitely many fields. This remark gives the following result.
Theorem 2.7. Suppose that R is a reduced ring. If
$\dim _M({\Omega }(R))$
is finite and we set
$n=|\mathrm {Max}(R)|$
, then
$\mathrm{sdim}_M({\Omega }(R))=2^n-2^{n-1}-1$
.
Proof. Since
$\dim _M({\Omega }(R))$
is finite, R has finitely many ideals by [Reference Abachi and Sahebi1, Lemma 2.1] and so
$R\cong F_1\times \cdots \times F_n$
, where
$F_i$
is a field for
$1\leq i\leq n$
. By Theorem 2.3,
$$ \begin{align*}\text{sdim}_M({\Omega}(R))=\alpha({\Omega}(R)_{\textit{SR}})=V({\Omega}(R)_{\textit{SR}})-\beta({\Omega}(R)_{\textit{SR}}).\end{align*} $$
On the other hand,
$\partial ({\Omega }(R))=V({\Omega }(R))=2^{n}-2$
and
$\beta ({\Omega }(R)_{SR})=2^{n-1}-1$
, by Theorem 2.6. Therefore,
$\mathrm{sdim}_M({\Omega }(R))=2^{n}-2-(2^{n-1}-1)=2^n-2^{n-1}-1$
.
The next result is an immediate consequence of Theorem 2.7 and [Reference Abachi and Sahebi1, Theorem 2.1].
Corollary 2.8. Suppose that R is a reduced ring with
$|\mathrm {Max}(R)|\geq 3$
. If
$\dim _M({\Omega }(R))$
is finite, then
$\mathrm{sdim}_M({\Omega }(R))\neq \dim _M({\Omega }(R))$
.
3 Strong metric dimension of a total graph of a nonreduced ring
In this section, we study the strong metric dimension of
$\Omega (R)$
when R is nonreduced. We begin with the following useful lemma.
Lemma 3.1 [Reference Abachi and Sahebi1].
Let
$R\cong R_1\times \cdots \times R_n$
, where
$R_i$
is an artinian local ring for
$1\leq i\leq n$
, and let
$I= (I_1,\ldots , I_n)$
,
$J= (J_1,\ldots ,J_n)$
.
-
(1)
$I-J$
is an edge of
$\Omega (R)$
if and only if
$I_i,J_i\subseteq \mathrm{Nil}(R_i)$
for some
$1\leq i\leq n$
. -
(2) If
$0\neq I\subseteq J(R)$
, then I is adjacent to all other vertices in
$\Omega (R)$
.
Theorem 3.2. Suppose that
$R\cong R_1\times \cdots \times R_n$
, where
$R_i$
is an artinian local ring such that
$|A(R_i)^*|\geq 1$
for
$1\leq i\leq n$
. Then
$\mathrm{sdim}_M(\Omega (R))=|A(R)^*|-2^{n-1}$
.
Proof. Let
$X=\{I\in A(R) \mid 0\neq I\subseteq J(R)\}$
. Since every element of X is adjacent to all other vertices in
$\Omega (R)$
by Lemma 3.1, all elements except one of X must belong to a strong resolving set W of
$\Omega (R)$
. We can assume that
$X\setminus \{J(R)\}\subseteq W$
. Now, suppose that
$I= (I_1,\ldots , I_n)$
and
$J= (J_1,\ldots ,J_n)$
are vertices of
$\Omega (R)\setminus X$
. Define the relation
$\thicksim $
on
$\Omega (R)\setminus X$
by
$I\thicksim J$
whenever
$I_i\subseteq \mathrm{Nil}(R_i)$
if and only if
$J_i\subseteq \mathrm{Nil}(R_i)$
for
$1\leq i\leq n$
,
Clearly,
$\thicksim $
is an equivalence relation on
$\Omega (R)\setminus X$
. The equivalence class of I is denoted by
$[I]$
. Suppose that X and Y are two elements of the equivalence class of I. Since
$X\thicksim Y$
, by Lemma 3.1(1),
$N[X]=N[Y]$
. So, by Lemma 2.1(1),
$[I]\setminus \{I\}\subseteq W$
. If
$A=\{(I_1,\ldots ,I_n)\in V(\Omega (R)) \mid I_i\in \{0,R_1,\ldots ,R_n\} \mathrm{ for } 1\leq i\leq n\}$
, then
$|A\cap [I]|=1$
for every equivalence class
$[I]$
. Therefore, we can assume that
$A(R)^*\setminus A\cup \{J(R)\} \subseteq W$
. To complete the proof, we investigate the elements of A. For this, let
$I,J\in A$
and
$I\neq J$
be such that I is not adjacent to J. Then
$d(I,J)=\mathrm{diam}(\Omega (R))=2$
and, by Lemma 2.1(1),
$I\in W$
or
$J\in W$
. This clearly shows that
$\mathrm{sdim}_M(\Omega (R))\geq |A(R)^*|-\omega (\Omega (R)[A])-1$
.
To calculate
$\omega (\Omega (R)[A])$
, we put
$$ \begin{align*} V_{1} & =\{(0,I_2,\ldots, I_n)\,|\, I_i\in \{0,F_i\} \text{ for } 2\leq i\leq n\}, \\ V_{2} & =\{(F_1,0,I_3,\ldots, I_n)\,|\, I_i\in \{0,F_i\} \text{ for } 3\leq i\leq n\}, \\ &\ \ \vdots \\ V_{n} & =\{(F_1,F_2,\ldots, F_{n-1}, 0)\}. \end{align*} $$
It is easy to see that
$$ \begin{align*} 1=|V_n|<|V_2|<\cdots |V_1|=2^{n-1}-1 = \tfrac{1}{2}|A|. \end{align*} $$
Since every vertex of
$V(\Omega (R)[A])\setminus V_1$
is not adjacent to some vertex of
$V_1$
, this implies that
$V_1$
is a largest clique of vertices of
${\Omega }(R)[A]$
. Therefore,
$$ \begin{align*} \text{sdim}_M(\Omega(R))\geq |A(R)^*|-\omega(\Omega(R)[A])-1=|A(R)^*|-2^{n-1}+1-1=|A(R)^*|-2^{n-1}. \end{align*} $$
Next, we show that
$\mathrm{sdim}_M(\Omega (R))\leq |A(R)^*|-2^{n-1}$
. For this, let
$W=A(R)^*\setminus B$
, where
$B=V_1\cup \{J(R)\}$
. We prove that W is a strong resolving set of
$\Omega (R)$
. Let
$I,J\in V_1$
with
$I= (0,I_2,\ldots , I_n)$
and
$J= (0,J_2,\ldots ,J_n)$
. Since
$I\neq J$
, without loss of generality, we can assume that
$I_2=F_2$
and
$J_2=0$
. Set
$K=(F_1, J(R_2),F_3,\ldots ,F_n)$
. Then
$d(I,K)=2$
and
$d(J,K)=1$
. This means that I and J are strongly resolved by
$K\in W$
(note that I is adjacent to J). Similarly, if
$I=J(R)$
and
$J\in V_1$
, then I and J are strongly resolved by some vertex of W. Therefore, W is a strong resolving set for
$\Omega (R)$
and hence
$\mathrm{sdim}_M(\Omega (R))\leq |A(R)^*|- |B|=|A(R)^*|-2^{n-1}$
.
Example 3.3. Let
$R=\mathbb {Z}_4\times \mathbb {Z}_4\times \mathbb {Z}_8$
. We have
$$ \begin{align*} X = J(R) & = \{((2),(2),(2)),((2),(2),(4)), ((0),(2),(2)),((0),(2),(4)),((2),(0),(2)), \\ &\quad \ ((2),(0),(4)),((2),(2),(0)), ((0),(0),(2)),((0),(0),(4)),((2),(0),(0)), \\ & \quad \ ((0),(2),(0))\}, \\ [(\mathbb{Z}_4,\mathbb{Z}_4,(0))] & =\{(\mathbb{Z}_4,\mathbb{Z}_4,(0)), (\mathbb{Z}_4,\mathbb{Z}_4,(2)),(\mathbb{Z}_4,\mathbb{Z}_4,(4))\}, \\ [(\mathbb{Z}_4,(0),\mathbb{Z}_8)] & =\{(\mathbb{Z}_4,(0),\mathbb{Z}_8),(\mathbb{Z}_4,(2),\mathbb{Z}_8)\}, \\ [((0),\mathbb{Z}_4,\mathbb{Z}_8)] & =\{((0),\mathbb{Z}_4,\mathbb{Z}_8),((2),\mathbb{Z}_4,\mathbb{Z}_8)\}, \\ [((0),(0),\mathbb{Z}_8)] & =\{((0),(0),\mathbb{Z}_8),((2),(0),\mathbb{Z}_8), ((0),(2),\mathbb{Z}_8),((2),(2),\mathbb{Z}_8)\}, \\ [(\mathbb{Z}_4,(0),(0))] & =\{(\mathbb{Z}_4,(0),(0)),(\mathbb{Z}_4,(0),(2)),(\mathbb{Z}_4,(0),(4)),(\mathbb{Z}_4,(2),(0)), (\mathbb{Z}_4,(2),(2)), \\ & \quad \ (\mathbb{Z}_{4}, (2), (4)) \}, \\ [((0),\mathbb{Z}_4,(0))] & =\{((0),\mathbb{Z}_4,(0)),((0),\mathbb{Z}_4,(2)),((0),\mathbb{Z}_4,(4)),((2),\mathbb{Z}_4,(0)), ((2),\mathbb{Z}_4,(2)), \\ & \quad \ ((2),{\mathbb{Z}}_{4},(4)) \} \end{align*} $$
and
$$ \begin{align*} A = \{(\mathbb{Z}_4,\mathbb{Z}_4,(0)), (\mathbb{Z}_4,(0),\mathbb{Z}_8), ((0),\mathbb{Z}_4,\mathbb{Z}_8), ((0),(0),\mathbb{Z}_8),(\mathbb{Z}_4,(0),(0)),((0),\mathbb{Z}_4,(0))\}. \end{align*} $$
By the proof of Theorem 3.2,
$A(R)^*\setminus A \subseteq W$
, where W is a strong resolving set of
$\Omega (R)$
. Now, we investigate the elements of A. Put
$$ \begin{align*} V_{1} & =\{((0),\mathbb{Z}_4,(0)),((0),\mathbb{Z}_4,\mathbb{Z}_8),((0),(0),\mathbb{Z}_8)\}, \\ V_{2} & =\{(\mathbb{Z}_4,(0),\mathbb{Z}_8), (\mathbb{Z}_4,(0), (0))\}, \\ V_{3} & =\{(\mathbb{Z}_4,\mathbb{Z}_4,(0))\}. \end{align*} $$
For every
$I\in \{V_2\cup V_3\}$
, there exists
$J\in V_1$
such that I and J are not adjacent. So, we can assume that
$A(R)^*\setminus (V_1\cup J(R)) \subseteq W$
and hence
$|W|\geq |A(R)^*\setminus (V_1\cup J(R))|= 34-4=30$
. On the other hand, for every
$v\in V_1$
, there exists
$u\in A(R)^*\setminus (V_1\cup J(R))$
with
$v+u=R$
. Since
$J(R)$
is adjacent to all the other vertices in
$\Omega (R)$
, this implies that
$J(R)$
and every vertex of
$V_1$
are strongly resolved by some of the vertices of
${A(R)^*\setminus (V_1\cup J(R))}$
. Similarly, the vertices
$((0),\mathbb {Z}_4,(0))$
and
$((0),\mathbb {Z}_4,\mathbb {Z}_8)$
are strongly resolved by the vertex
$(\mathbb {Z}_4,(2),(0))$
, the vertices
$((0),\mathbb {Z}_4,(0))$
and
$((0),(0),\mathbb {Z}_8)$
are strongly resolved by the vertex
$(\mathbb {Z}_4,\mathbb {Z},(2))$
and the vertices
$((0),\mathbb {Z}_4,\mathbb {Z}_8)$
and
$((0),(0),\mathbb {Z}_8)$
are strongly resolved by the vertex
$(\mathbb {Z}_4,(2),(2))$
. Thus
$|W|\leq |A(R)^*\setminus (V_1\cup J(R))|=30$
. Therefore,
$\mathrm{sdim}_M(\Omega (R))=|W|=30$
.
In view of Theorem 3.2, we have the following results.
Corollary 3.4. Suppose that
$R\cong R_1\times \cdots \times R_n$
, where
$R_i$
is an artinian local ring such that
$|A(R_i)^*|= 1$
for
$1\leq i\leq n$
. Then
$\mathrm{sdim}_M(\Omega (R))=3^n-2^{n-1}-2$
.
Corollary 3.5. Suppose that
$R\cong R_1\times \cdots \times R_n$
, where
$R_i$
is an artinian local ring such that
$|A(R_i)^*|\geq 1$
for
$1\leq i\leq n$
. If
$\dim _M({\Omega }(R))$
is finite, then
$\mathrm{sdim}_M({\Omega }(R))=\dim _M({\Omega }(R))$
if and only if
$n=1$
.
Proof. The assertions follow from Theorem 3.4 and [Reference Abachi and Sahebi1, Theorem 3.1].
Theorem 3.6. Let
$R\cong R_1\times \cdots \times R_n\times F_1\times \cdots \times F_m$
be a ring,
$n\geq 1$
and
$m\geq 1$
, where each
$(R_i,\mathfrak {m}_i)$
is an artinian local ring with
$\mathfrak {m}_i\neq (0)$
and each
$F_i$
is a field. Then
$\mathrm{sdim}_M(\Omega (R))=|A(R)^*|-2^{n+m-1}$
.
Proof. The argument is a refinement of the proof of Theorem 3.2. Arguing as in the proof of Theorem 3.2,
$\mathrm{sdim}_M(\Omega (R))=|A(R)^*|-\omega (\Omega (R)[A])-1$
, where
$$ \begin{align*} A=\{(I_1,\ldots,I_{n+m})\in V(\Omega(R))\,\,|\,\, I_i\in \{0,R_1,\ldots,R_n,F_1,\ldots,F_m\}\}. \end{align*} $$
Since
$\omega (\Omega (R)[A])=2^{n+m-1}-1$
, it follows that
$\mathrm{sdim}_M(\Omega (R))=|A(R)^*|-2^{n+m-1}$
.
Corollary 3.7. Let
$R\cong R_1\times \cdots \times R_n\times F_1\times \cdots \times F_m$
be a ring,
$n\geq 1$
and
$m\geq 1$
, where each
$(R_i,\mathfrak {m}_i)$
is an artinian local ring with
$\mathfrak {m}_i\neq (0)$
and each
$F_i$
is a field. If
$\dim _M({\Omega }(R))$
is finite, then
$\mathrm{sdim}_M({\Omega }(R))=\dim _M({\Omega }(R))$
if and only if
$n=m=1$
.
Proof. The assertion follows from Theorem 3.4 and [Reference Abachi and Sahebi1, Theorem 3.1].
We close this section with two examples which are related to Theorem 3.6 and Corollary 3.7.
Example 3.8. (1) Let
$R=\mathbb {Z}_4\times \mathbb {Z}_2$
. By Theorem 3.6 and Corollary 3.7,
$\mathrm{sdim}_M ({\Omega }(R))=\dim _M({\Omega }(R))=2$
. This is confirmed by Figure 3.
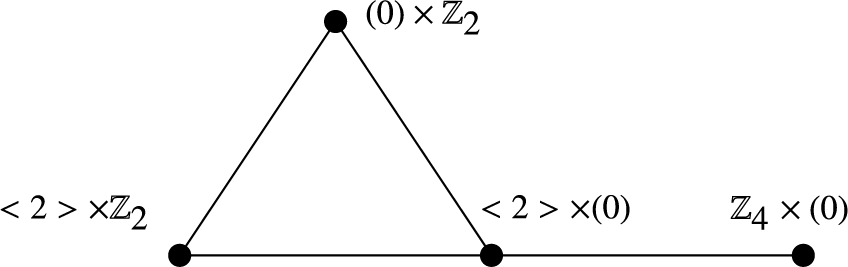
Figure 3
$ \Omega (\mathbb {Z}_4\times \mathbb {Z}_2) $
.
(2) Let
$R=\mathbb {Z}_4\times \mathbb {Z}_4\times \mathbb {Z}_2\times \mathbb {Z}_2$
. From the proof of Theorem 3.6,
$\mathrm{sdim}_M(\Omega (R))=|A(R)^*|-\omega (\Omega (R)[A])-1$
, where
$$ \begin{align*} A & =\{((0),\mathbb{Z}_4,\mathbb{Z}_2, \mathbb{Z}_2), (\mathbb{Z}_4,(0),\mathbb{Z}_2, \mathbb{Z}_2),(\mathbb{Z}_4,\mathbb{Z}_4,(0), \mathbb{Z}_2),(\mathbb{Z}_4,\mathbb{Z}_4, \mathbb{Z}_2,(0)), \\ & \quad\ ((0),(0),\mathbb{Z}_2,\mathbb{Z}_2), ((0),\mathbb{Z}_4, (0),\mathbb{Z}_2),((0),\mathbb{Z}_4, \mathbb{Z}_2,(0)),(\mathbb{Z}_4,(0), \mathbb{Z}_2,(0)), \\ & \quad\ (\mathbb{Z}_4,(0),(0),\mathbb{Z}_2), (\mathbb{Z}_4,\mathbb{Z}_4,(0),(0)), (\mathbb{Z}_4,(0),(0),(0)), ((0),\mathbb{Z}_4,(0),(0)), \\ & \quad\ ((0),(0), \mathbb{Z}_2,(0)),((0),(0), (0),\mathbb{Z}_2)\}. \end{align*} $$
Now, let
$$ \begin{align*} V_1 & =\{((0),\mathbb{Z}_4,\mathbb{Z}_2, \mathbb{Z}_2),((0),(0),\mathbb{Z}_2,\mathbb{Z}_2),((0),\mathbb{Z}_4,(0), \mathbb{Z}_2), ((0),\mathbb{Z}_4,\mathbb{Z}_2,(0)), \\ & \quad\ ((0),(0),(0), \mathbb{Z}_2),((0),\mathbb{Z}_4,(0), (0)), ((0),(0),\mathbb{Z}_2, (0))\}, \\ V_2 & =A\setminus V_1. \end{align*} $$
For every element
$I\in V_2$
, there exists
$J\in V_1$
such that
$I+J=R$
. So, for every element of
$ V_2$
, there exist elements of
$ V_1$
which are not adjacent to it. Since
$\Omega (R)[V_1]$
is a clique, this implies that
$\omega (\Omega (R)[A])=|V_1|=7$
. Therefore,
$$ \begin{align*}\text{sdim}_M(\Omega(R))=|A(R)^*|-\omega(\Omega(R)[A])-1=34-7-1=26.\end{align*} $$
Again, Theorem 3.6 confirms that
$\mathrm{sdim}_M(\Omega (R))=|A(R)^*|-2^{n+m-1}=34-2^3=26$
.
Acknowledgement
The authors thank the referee for careful reading and excellent suggestions.
